Continuous-wave parallel interferometric near-infrared spectroscopy (CW πNIRS) with a fast two-dimensional camera

Abstract

Interferometric near-infrared spectroscopy (iNIRS) is an optical method that noninvasively measures the optical and dynamic properties of the human brain in vivo. However, the original iNIRS technique uses single-mode fibers for light collection, which reduces the detected light throughput. The reduced light throughput is compensated by the relatively long measurement or integration times (∼1 sec), which preclude monitoring of rapid blood flow changes that could be linked to neural activation. Here, we propose parallel interferometric near-infrared spectroscopy (πNIRS) to overcome this limitation. In πNIRS we use multi-mode fibers for light collection and a high-speed, two-dimensional camera for light detection. Each camera pixel acts effectively as a single iNIRS channel. So, the processed signals from each pixel are spatially averaged to reduce the overall integration time. Moreover, interferometric detection provides us with the unique capability of accessing complex information (amplitude and phase) about the light remitted from the sample, which with more than 8000 parallel channels, enabled us to sense the cerebral blood flow with only a 10 msec integration time (∼100x faster than conventional iNIRS). In this report, we have described the theoretical foundations and possible ways to implement πNIRS. Then, we developed a prototype continuous wave (CW) πNIRS system and validated it in liquid phantoms. We used our CW πNIRS to monitor the pulsatile blood flow in a human forearm in vivo. Finally, we demonstrated that CW πNIRS could monitor activation of the prefrontal cortex by recording the change in blood flow in the forehead of the subject while he was reading an unknown text.

1. Introduction

Diffuse optics offers a noninvasive portable approach for examining biological tissues, including the human brain in vivo [1]. Near-infrared spectroscopy (NIRS) [2] and diffuse correlation spectroscopy (DCS) [3,4] are the primary diffuse optical modalities. In both approaches, the light illuminates the tissue, and diffusively scattered photons are collected at a distance $(\rho )$ from the emitter (typically 2-3 cm). NIRS uses the detected signal to estimate optical properties (absorption and scattering), while DCS quantifies the blood flow from temporal changes of the remitted light intensity. Although these methods have been applied to monitor brain oxygenation and blood flow, their most widely adopted versions rely on continuous wavelength (CW) lasers, precluding absolute measures of the optical and dynamical tissue properties [5].

Time-domain NIRS (TD-NIRS) enables quantification of the optical properties through the photon time-of-flight distribution (DTOF) within the sample [6–9]. The measured DTOF is analyzed using statistical moments [10,11], fitted to the theoretical model [12], analyzed with the finite element method (FEM) [13,14], or Monte-Carlo simulated DTOF [15,16] to extract optical properties. The time-of-flight (TOF) resolution can also be combined with correlation spectroscopy to achieve TOF- (or photon path-length-) resolved blood flow information [17]. With TOF, we could better distinguish photons traversing superficial layers (short TOFs) from photons traveling deep into the brain (long TOFs). Also, given the TOF distribution, we could estimate the optical properties to achieve the blood flow index (BFI), effectively combining the capabilities of TD-NIRS with DCS into a single modality.

Recently, there was significant progress in this research area. Sutin et al. introduced time-domain DCS and applied it to examine the cerebral blood flow in rodents [18]. Shortly after, TD-DCS was used for blood flow monitoring in the human forearm in vivo [19]. Tamborini et al. developed a portable TD-DCS system [20]. Colombo and others demonstrated TD-DCS with a custom-made pulsed laser operating at a wavelength of 1000 nm [21]. A narrow-linewidth pulsed laser with the novel processing methods [22] unlocked the full potential of TD-DCS to sense the depth-dependent blood flow index in human tissues in vivo. Recently, Ozana et al. improved TD-DCS by employing a pulsed 1064-nm laser with superconducting nanowire single-photon detectors (SNSPDs) to improve the SNR [23]. This wavelength increases maximum permissible exposure, enabling illumination powers up to 100 mW, while SNSPDs provide fast single photon counting.

Though TD-DCS is a powerful technique that was even applied in clinics [24], it relies only on light intensity. Therefore, TD-DCS does not enable detection of the optical phase, which carries a significant amount of information about scatterers moving inside the sample [25]. The optical phase is accessible in interferometric near-infrared spectroscopy (iNIRS) [26]. iNIRS employs Fourier-domain light interferometry to rapidly measure the two-dimensional autocorrelation function, from which optical and dynamical properties of liquid phantoms [26], mouse brain [27], and human brain [28] in vivo have been extracted. However, the original iNIRS (as TD-DCS) uses single-mode fibers for light collection, requiring integration times on the order of 0.5-1 second. This time frame is too long, obviating the ability to detect rapid blood flow changes in the human brain that could be linked to neural signals [29]. Also, the low fiber throughput limits the extent of the source-collector separation $(\rho ).$ Conventionally, the longer the source-collector separation, the better the depth sensitivity [4,30,31].

Zhou et al. developed interferometric diffusing wave spectroscopy (iDWS) to overcome those limitations and applied it to monitor pulsatile blood flow in the human brain in vivo [31,32]. iDWS uses a similar setup as iNIRS but employs a single- or a few-mode fiber for illumination, and multi-mode fiber for light collection. The resulting interference pattern is detected using a high-speed line scan (one-dimensional) camera. The field autocorrelation functions are estimated independently, using appropriately binned pixels. Subsequently, autocorrelations are spatially averaged to reduce the overall integration time to 100 msec. This approach enabled recordings at long (up to ∼5 cm) source-collector separations $(\rho )$ .

A similar approach of spatial autocorrelation averaging was also presented for diffuse correlation spectroscopy. Dietsche et al. employed a fiber bundle and an avalanche photodiode (APD) array to concurrently measure intensity autocorrelations from different speckles. By averaging these autocorrelations, they reduced the integration time to 6.5-29 msec at a source-collector separation up to 2.9 cm [33]. Several groups have developed parallel or multi-speckle DCS to examine the dynamical properties of phantoms [34], volar forearm [35], and the human forehead in vivo [36]. The parallel DCS detects intensity light fluctuations using single-photon avalanche diode (SPAD) arrays. The intensity autocorrelations are estimated using the photon count fluctuations at N individual SPAD detectors and then spatially averaged. This strategy improves the signal-to-noise ratio (SNR) proportionally to $\sqrt{N},$ enabling integration times of about 30-100 msec. However, the parallel DCS was only demonstrated at short source-collector separations (0.5-1.5 cm), limiting the sensitivity to deep tissue layers [30].

Here, we introduce parallel interferometric near-infrared spectroscopy (πNIRS). πNIRS extends iNIRS by parallel detection. To achieve this, we use multi-mode fibers for light delivery and collection. The detected light is recorded using an ultra-high speed two-dimensional camera operating at frame rates up to 1.1 MHz with the number N of active pixels between 2048-8096. Each pixel in the recorded image sequence represents an individual iNIRS detection channel. By processing signals from each channel and then averaging them spatially, we achieve similar information as in iNIRS, but $\sqrt{N}$ times faster. With the unique capability of accessing complex information (amplitude and phase) about the sample with more than 8000 parallel detection channels, we can sense the dynamic properties, including deep tissue blood flow at long source-collector separations (2-3 cm) with only 2-10 msec integration times. This time interval is up to 50-100-times faster than single-channel iNIRS and TD-DCS based on a single SPAD. Contrary to SPAD arrays, which have low active areas, our 2D camera has a higher active area, enabling such short integration times.

In this paper, we describe the theoretical foundations for πNIRS and discuss its possible applications. Accordingly, we constructed the optical system with a continuous wave (CW) laser, and a fast two-dimensional camera to monitor the sample dynamics. We applied CW πNIRS to analyze the dynamics of tissue-mimicking liquid phantoms and to monitor deep blood flow in the human forearm and forehead in vivo.

Though the camera offers frame rates up to 1 Mfps it is still too slow to achieve fast renderings of the TOF-resolved autocorrelations by employing the tunable laser. Here, we decided to sacrifice TOF-resolution to favor ultra-short integration times, making our CW πNIRS system a promising approach for monitoring the dynamics of biological tissues with diffuse light at long source-collector separations.

2. Theory

Interferometric near-infrared spectroscopy measures the spectral interference pattern S over time $t_d$ as a function of optical frequency, $\nu =c/\lambda$ [25]:

$$S(\nu ,t_d)=S_{DC}(\nu ,t_d)+2\text{Re}[W_{rs}(\nu ,t_d)],$$ (1)

where the first term $S_{DC}(\nu ,t_d)$ denotes the so-called DC offset (the sum of light intensities in the sample and reference arms), and the second term $2\text{Re}[W_{rs}(\nu ,t_d)]$ is the real part of the cross-spectral density function $W_{rs}(\nu ,t_d)$ between the optical fields associated with the light propagating in the reference ( $r$ ) and sample ( $s$ ) interferometer arm.

We then subtract $S_{DC}(\nu ,t_d)$ from Eq. (1), and inverse Fourier-transform the resulting function $2\text{Re}[W_{rs}(\nu ,t_d)]$ to achieve the mutual coherence function:

$${\mathrm{\Gamma }}_{rs}^{\left(\text{iNIRS}\right)}\left({\tau }_s,t_d\right)={⟨U_r^{\text{*}}\left(t_s,t_d\right)U_s\left(t_s+{\tau }_s,t_d\right)⟩}_{t_s},$$ (2)

where ${\tau }_s$ is the time-of-flight (a conjugate variable to $\nu$ [26]), while $U_r$ and $U_s$ denote the optical fields propagating in the reference and sample arms of the interferometer.

Given ${\mathrm{\Gamma }}_{rs}^{(\text{iNIRS})}({\tau }_s,t_d),$ we estimate the two-dimensional TOF-resolved field autocorrelation:

$$G_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)={⟨{\mathrm{\Gamma }}_{rs}^{\ast \left(\text{iNIRS}\right)}\left({\tau }_s,t_d\right){\mathrm{\Gamma }}_{rs}^{\left(\text{iNIRS}\right)}\left({\tau }_s,t_d+{\tau }_d\right)⟩}_{t_d}.$$ (3)

Here, ${\tau }_d$ is the autocorrelation lag time, whose sampling depends on the laser tuning rate and is typically on the order of a few to tens of microseconds. The measured $G_1^{(\text{iNIRS})}({\tau }_s,{\tau }_d)$ is related to the true TOF-resolved field autocorrelation, $G_1^{}\left({\tau }_s,{\tau }_d\right)={⟨U_{\text{s}}^{\ast }\left({\tau }_s,t_d\right)U_s\left({\tau }_s,t_d+{\tau }_d\right)⟩}_{t_d}$ through convolution with the instrument response function (IRF):

$$G_1^{(\text{iNIRS})}({\tau }_s,{\tau }_d)=G_1({\tau }_s,t_d)\ast \mathrm{I}\mathrm{R}\mathrm{F}({\tau }_s).$$ (4)

For ${\tau }_d=0$ we obtain the temporal point spread function (TPSF):

$$I_s^{(\text{iNIRS})}({\tau }_s)=G_1^{(\text{iNIRS})}({\tau }_s,0),$$ (5)

which is related to the true time-of-flight distribution (DTOF) by the convolution with the IRF [Eq. (4)].

In iNIRS, the IRF is governed by the laser tuning bandwidth $\mathrm{\Delta }\lambda$ [37]. The wider the $\mathrm{\Delta }\lambda$ , the narrower the IRF. For the Gaussian spectrum, the theoretical full width at half maximum (FWHM) TOF resolution is:

$$\delta {\tau }_s=\frac{2\sqrt{2}\text{ln}(2)}{\pi }\frac{{\lambda }_c^2}{c\mathrm{\Delta }\lambda }\approx 0.62\frac{{\lambda }_c^2}{c\mathrm{\Delta }\lambda },$$ (6)

where ${\lambda }_c$ is the center wavelength. Also, the tuning bandwidth determines the maximum TOF value (or the sensing range) [38]:

$${\tau }_{s,max}=\frac{f_s}{f_l}\frac{{\lambda }_c^2}{c\mathrm{\Delta }\lambda },$$ (7)

where $f_s$ is the sampling rate, and $f_l$ denotes the laser tuning rate.

In practice, the IRF is measured similarly to TD-NIRS [26,27,37], by incorporating the free space transmission measurement with an optional diffuser. When estimating the optical properties, the measured IRF is convolved with the theoretical model [27].

We now see that the iNIRS performance strongly depends on the spectral and tuning parameters of the tunable laser. By increasing $\mathrm{\Delta }\lambda$ , we achieve finer TOF resolution $(\delta {\tau }_s)$ but decrease the TOF range. On the other hand, increasing the autocorrelation sampling rate,

$$\delta t_d=\frac{1}{f_l},$$ (8)

requires us to tune the laser faster; this would also degrade the TOF range unless the sampling rate is increased. Consequently, the iNIRS operating parameters cannot be freely chosen and are adjusted to either achieve fine TOF resolution (required for estimating optical properties) or high autocorrelation sampling rate (for estimating dynamical properties) [37].

In $\pi$ NIRS, the spectral fringe pattern and thus the mutual coherence function are now spatially resolved by the transverse modes propagating in the multi-mode fiber and detected by the two-dimensional camera (Fig. 1). So, ${\mathrm{\Gamma }}_{rs}^{(\text{iNIRS})}({\tau }_s,t_d)$ becomes a function of spatial dimensions ( $x,y$ ):

$${\mathrm{\Gamma }}_{rs}^{\left(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S}\right)}\left(x,y,{\tau }_s,t_d\right)={⟨U_{\text{r}}^{\text{*}}\left(x,y,{\text{t}}_s+{\tau }_s,t_d\right)U_s\left(x,y,{\tau }_s,t_d\right)⟩}_{t_s}.$$ (9)

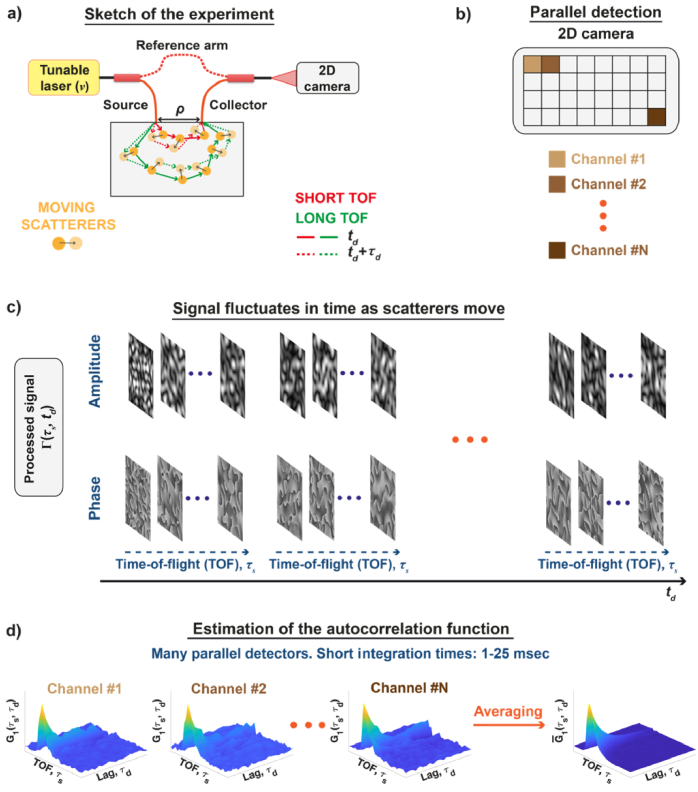
Fig. 1.

Parallel interferometric near infrared spectroscopy ( $\pi$ NIRS) can rapidly measure the two-dimensional, time-of-flight-resolved autocorrelation, $G_1({\tau }_s,{\tau }_d)$ by parallel detection of the light remitted from the sample. (a) To this end, the spectral interference of the reference and the light scattered from the moving particles is recorded using the Mach-Zehnder interferometer with the tunable laser. The output of the interferometer is projected on the two-dimensional camera, whose pixels act as the individual detection channels (b). The complex signal on each pixel fluctuates in time as the scatterers move (c). The latter is used to estimate the autocorrelation for each channel independently (d). However, each autocorrelation is noisy, so averaging $G_1({\tau }_s,{\tau }_d)$ over many detection channels improves the SNR, enabling faster estimation of autocorrelation.

This leads to the spatially- and TOF-resolved autocorrelation function:

$$G_1^{\left(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S}\right)}\left(x,y,{\tau }_s,{\tau }_d\right)={⟨{\mathrm{\Gamma }}_{rs}^{\ast \left(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S}\right)}\left(x,y,{\tau }_s,t_d\right){\mathrm{\Gamma }}_{rs}^{\left(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S}\right)}\left(x,y,{\tau }_s,t_d+{\tau }_d\right)⟩}_{t_d}.$$ (10)

Then, we spatially average $G_1^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}(x,y,{\tau }_s,{\tau }_d)$ to improve our estimate:

$${\overline{G}}_1^{\left(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S}\right)}\left({\tau }_s,{\tau }_d\right)={⟨G_1^{\left(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S}\right)}\left(x,y,{\tau }_s,{\tau }_d\right)⟩}_{x,y}.$$ (11)

Ideally, each detection channel should measure a statistically independent mutual coherence function ${\mathrm{\Gamma }}_{rs}^{}$ , acting effectively as a separate iNIRS channel. In such a case, each camera pixel senses the temporal evolution of the independent speckle. Hence, after spatial averaging in Eq. (11), the SNR will increase as $\sqrt{N}$ , where N is the number of detection channels [39]. To achieve this ideal condition, we must match the camera pixel size to the speckle size, as explained in section 4.6.

An increased SNR makes it possible to shorten the overall integration time needed to estimate the two-dimensional autocorrelation function. Specifically, for $N=1000,$ the integration time can be reduced from 0.5 sec (iNIRS) to 15 msec ( $\pi$ NIRS). A further increase of the channel number $N=10,000$ , reduces the integration time to 5 msec.

Similarly, as in iNIRS, we can estimate the TPSF by setting ${\tau }_d=0$ in Eq. (10):

$$I_s^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}({\tau }_s)={\overline{G}}_1^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}({\tau }_s,0).$$ (12)

On the other hand, after integrating $G_1^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}(x,y,{\tau }_s,{\tau }_d)$ over time-of-flights, we get the one-dimensional field autocorrelation function:

$${\overline{G}}_1^{\left(\pi \mathrm{D}\mathrm{C}\mathrm{S}\right)}\left({\tau }_d\right)={⟨{\int }_0^{\mathrm{\infty }}d{\tau }_s{G}_1^{\left(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S}\right)}\left(x,y,{\tau }_s,{\tau }_d\right)⟩}_{x,y}.$$ (13)

The latter represents the signal that would be obtained when the laser tuning is disabled or a fixed wavelength instead of a tunable laser is used. Since we still use interferometric detection, we call this approach parallel interferometric diffuse correlation spectroscopy, abbreviated as piDCS or $\pi$ DCS.

After setting ${\tau }_d=0$ in Eq. (13) we get the TOF-integrated intensity,

$$I_s^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}={\overline{G}}_1^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}({\tau }_d=0)={\int }_0^{\mathrm{\infty }}d{\tau }_s{I}_s^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}({\tau }_s).$$ (14)

The above quantity can be used to monitor absorption changes since $I_s^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}$ is reduced when absorption increases according to the modified Beer-Lambert law [40,41].

Finally, by following the standard DCS approach, we normalize the autocorrelation functions with respect to their values at ${\tau }_d=0$ ,

$$g_1^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}({\tau }_s,{\tau }_d)=\frac{{\overline{G}}_1^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}({\tau }_s,{\tau }_d)}{{\overline{G}}_1^{(\pi \mathrm{N}\mathrm{I}\mathrm{R}\mathrm{S})}({\tau }_s,0)},$$ (15)

$$g_1^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}({\tau }_d)=\frac{{\overline{G}}_1^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}({\tau }_d)}{{\overline{G}}_1^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}(0)}.$$ (16)

3. System design considerations

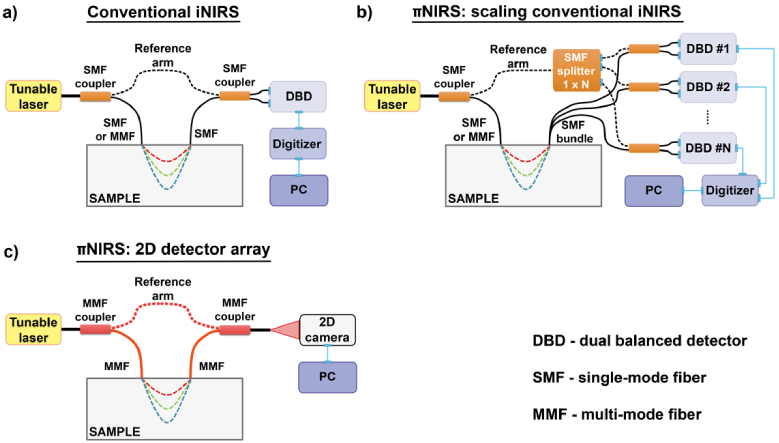
Before assembling the experimental setup, we considered possible optical setups for $\pi$ NIRS, and compared them to the conventional single channel iNIRS (Fig. 2). In all systems, the light from the tunable laser is split into the reference and sample arms. In the conventional iNIRS, we split the light using the single-mode fiber (SMF) coupler [Fig. 2(a)]. The “sample” output of the coupler can be optionally connected to the multi-mode fiber patch cord to improve light delivery to the sample. The diffusively reemitted light is collected by the single-mode fiber and recombined with the reference light through another SMF coupler. The resulting interference pattern is detected by the dual balanced detector (DBD), digitized, stored, and then processed in the PC. Optionally, the interferometer can be equipped with an additional k-clock, which provides a signal, enabling uniform sampling of the nonlinearly swept laser in the k-domain required for Fourier transformation; when converting $W_{rs}(\nu ,t_d)$ to ${\mathrm{\Gamma }}_{rs}^{}({\tau }_s,t_d)$ [42].

Fig. 2.

A schematic diagram of conventional interferometric near-infrared spectroscopy (iNIRS, a) is compared to two possible implementations of parallel iNIRS (πNIRS, b, c).

Figure 2(b) demonstrates the first approach to increasing the number of detection channels in iNIRS. A light from the tunable laser is also split into the sample and reference arms using an SMF coupler, and the light delivery system is the same as in conventional iNIRS. However, now we use N single-mode fibers (or the fiber bundle) to collect the remitted light. Also, we split the reference light into multiple channels using a $1\times N$ fiber splitter. Each output of the splitter is connected to one of N separate DBDs and re-combined with the collected light using SMF couplers. Again, the DBD signal is digitized, stored, and processed in the PC. Consequently, we need N digitization channels.

In the second approach, “2D detector array,” we split the light from the laser using the multi-mode fiber (MMF) coupler [Fig. 2(c)]. The light is delivered and collected using the MMF. The collected light is recombined with the reference light using the MMF coupler. The resulting fringe pattern is detected with the two-dimensional detector having N active pixels. The recorded camera images are then transferred to the PC for processing. In this approach, we cannot use the single detector, as the speckles would average out, decreasing the ability to resolve the autocorrelation function [32].

The significant advantages and disadvantages of both approaches are summarized in Table 1. Scaling conventional iNIRS has two essential benefits. Thanks to DBDs, the DC level ( $S_{DC}$ ) can be diminished. The DBD has two photodiodes, which are shifted in phase. The output of the photodiodes is subtracted to retrieve only the oscillatory part of the spectral fringes ( $Re[W_{rs}]$ ), so that the dynamic range of the detected signal increases. Moreover, current digitizers offer high sampling rates ( $f_s$ can be as large as 50 Gs/sec), which enables us to keep a long TOF range at rapid laser tuning rates, as demonstrated for swept-source optical coherence tomography [43].

Table 1. Comparison of the possible $\mathit{\pi }$ NIRS implementations.

	Scaling conventional iNIRS	2D detector array
Advantages	Balanced detection diminishes DC level and enhances the dynamic range	No need for fiber splitting
	Digitizers offer fast sampling rates	Enables a very large number of parallel channels (1000 and beyond)
Disadvantages	Achieving a large number of channels (100-1000) can be challenging and requires more digitizers.	Balanced detection is challenging
	High-power lasers are needed due to fiber splitting	Sampling rates are currently limited to ∼1Ms/sec
Cost factors	DBDs (∼2,000 USD each) Digitizers (>10,000 USD each)	High-speed camera (∼50,000 USD)

However, scaling the iNIRS in this way is challenging for many channels. Specifically, for $N=100$ channels, we would need to split the reference arm into 100 paths. This would require a much more powerful laser than conventionally used in iNIRS. Moreover, we would need 100 DBDs. A commercial, off-the-shelf DBD typically costs ∼2,000 USD, which leads to about 200,000 USD for the detector cost. Moreover, digitizers can accommodate up to several input channels. Hence, for 100 iNIRS channels, we would need several digitizers and, most likely several PCs. This problem can be partially balanced by multiplexing several iNIRS signals into a single DBD [38] to reduce the total number of required detectors. Nevertheless, such multiplexing would limit the practical application of the iNIRS scaling unless custom ADCs are used, similarly as in optical communication [44]. Finally, averaging signals from different channels requires additional calibration steps, as the signals can be shifted with each other due to different propagation times in each channel and differences in DBDs responsivity. This makes the averaging procedure challenging, especially at low signal levels, which we face at long source-collector separations.

By using a 2D detector array, we end up with a straightforward optical setup. We do not need fiber splitting, can use the same laser as in iNIRS, and we achieve a vast number of parallel channels (typically, $N=1000-10000$ ). The latter is limited only by the number of camera pixels.

However, this approach comes at the cost of a lack of balanced detection, so that the DC level can saturate the camera pixels, decreasing the dynamic range. Second, though ultra-high-speed cameras are commercially available, the frame rate, equivalent to the fringe sampling rate, is about 1 Ms/sec (1 Mfps), limiting the TOF sensing range. Finally, the cost is mainly governed by the camera (∼50,000 USD). So, it is beneficial to use the 2D detector array when many parallel channels are needed. This is especially important for sensing rapid dynamic changes at long source-collector separations, which can be achieved in the $\pi$ DCS mode. For all those reasons, here we use the 2D detector array approach.

Our main goal here is to achieve the fastest possible approach for sensing the dynamic properties of the biological tissues. For such samples, the decorrelation time, defined as the lag time when the autocorrelation drops to 1/e of its initial value, is on the order of tens to hundreds of microseconds, depending on the source-collector separation.

As previously explained [Eqs. (6)-(8)], concurrently achieving high TOF-resolution at such decorrelation times would require fast tuning rates and large sampling rates. Even though the frame rate of the 2D detector can reach 1 Mfps, it is still not enough to sample the two-dimensional autocorrelation function to recover rapidly decorrelating signals in the biological tissue at long source-collector separations. For this reason, we decided to sacrifice the TOF resolution to favor the maximum autocorrelation sampling $(\delta {\tau }_d).$ So, we disabled the laser tuning and operate at a fixed wavelength. Thus, we effectively measure ${\overline{G}}_1^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}({\tau }_d)$ . This approach is also motivated by the fact that the dynamic signal can achieve better brain sensitivity than optical property changes [31].

4. Methods

4.1. Two-dimensional, ultra-high-speed camera

Here, we use the Photron FASTCAM NOVA S16 camera as the two-dimensional detector. Intrinsically, the camera uses the CMOS image sensor (pixel size of 20 $\times$ 20 $\mu$ m) with a resolution of up to 1024 $\times$ 1024 px. At this maximum resolution, the camera frame rate is 16,000 fps. The frame rate can be increased up to 1,100,000 fps by reducing the image resolution down to 128 $\times$ 16 px. We typically operate at a resolution of 128 $\times$ 32 px or 128 $\times$ 64 px and 600,000 fps, which provides 1.67 $\mu$ s autocorrelation sampling in the $\pi$ DCS mode.

We use the camera frame rate to define the measurement window or integration time, $T_{int}=\frac{M}{cameraframerate}$ , where M is the number of camera frames used to estimate the autocorrelation function. In practice, we record the data for up to several seconds and then select continuous range of frames for analysis.

The relative spectral response of the camera achieves maximum for 660-680 nm wavelengths. For the 785 nm wavelength used in this study, the relative spectral response of the camera is 80%.

The camera was connected to the PC using a 10-Gigabit Ethernet interface. The 16-bit images were first saved to the camera internal memory (128 GB), and then transferred to a dedicated FASTDrive SSD (4 TB). Finally, the images were downloaded to the PC for processing. During the download, the camera recording was stopped. Hence, the duration of the acquisition is currently limited by the size of the camera internal memory.

4.2. Optical setup

The optical setup was assembled using the schematic diagram shown in Fig. 2(c), but with the CW laser (CrystaLaser, DL785-120-SO) replacing the tunable laser. The free space output of the laser was coupled to the first fiber coupler (Thorlabs TH200R5F1B, 1 × 2, splitting ratio 50:50, 0.5 NA, 200 $\mu$ m core diameter) using a semi-apochromat objective (OLYMPUS UPLFLN 4x NA 0.13) and a two-axis fiber launch system (Thorlabs KT120). The optical power injected into the sample was $P_s=50$ mW for the phantom and in vivo experiments. The reference arm was equipped with a custom-made variable optical attenuator (VOA) to control the reference arm power. The VOA comprises two collimators (Thorlabs F240FC-850) and a continuously variable ND filter (Thorlabs NDC-50C-2M-B). The light remitted from the sample was collected using one input of another fiber coupler (Thorlabs TH200R5F1B, 1 × 2, splitting ratio 50:50 or 90:10, 0.5 NA, 200 $\mu$ m core diameter), and then recombined with the reference light injected through the second output of the fiber coupler. The fiber tip at the output of the interferometer was placed on the manual translation stage to control the distance between the tip and the camera sensor. By controlling this distance, we can vary the speckle size to optimize the detection channel count.

4.3. Liquid phantoms

We carried out measurements on homogeneous liquid phantoms, mimicking the reduced scattering coefficient of biological tissues. We made the phantoms by mixing homogenized milk (3.2% fat) with distilled water to achieve three different levels of reduced scattering, ${\mu }_s^{\mathrm{\prime }}=7.5-12.5\text{c}{\text{m}}^{-1}$ in steps of $2.5\text{c}{\text{m}}^{-1},$ and fixed absorption, ${\mu }_a=0.03\text{c}{\text{m}}^{-1}$ . The optical properties were estimated using a separate TD-NIRS instrument and moment approach, as described in detail in one of our previous works [22]. For the measurements we used a custom-made cubic compartment to simulate the semi-infinite geometry and satisfy the light diffusion approximation. The source and collection fiber tips were placed on a 3D-printed fiber holder. We used 5 different separations, $\rho =1-3$ cm in steps of $0.5$ cm.

4.4. Human in vivo measurements

We performed human in vivo measurements on the forearm and forehead of a healthy 39-year-old volunteer, using a source-collector separation of 3 cm. To calculate the blood flow indices we estimated the subject’s optical properties using a multi-wavelength time-domain NIRS system at $\rho =3$ cm [45], and moments approach. The resulting optical properties are summarized in Table 2.

Table 2. Optical properties of the healthy volunteer.

Location	${\mathit{\mu }}_{\mathit{a}}$ [cm-1]	${\mathit{\mu }}_{\mathit{s}}\mathbf{\prime }$ [cm-1]
Center forearm	0.14	7.16
Right forearm	0.15	7.14
Forehead	0.14	11.85

All experimental procedures and protocols were reviewed and approved by the Commission of Bioethics at the Military Institute of Medicine, Poland (permission no. 90/WIM/2018). The experiments were conducted following the tenets of the Declaration of Helsinki. Written informed consent was obtained from all subjects before measurements, and all possible risks related to the examination were explained.

4.5. Signal processing

In $\pi$ DCS mode, the laser tuning is disabled. So, we record, the fixed-wavelength or TOF-integrated, signal

$$S(x,y,t_d)=S_{DC}(x,y,t_d)+2Re[W(x,y,t_d)],$$ (17)

from which we suppress the DC level by subtracting the rolling average over time $t_d$ with the window length of 100-1000 msec. The resulting function,

$$S\mathrm{\prime }(x,y,t_d)=S(x,y,t_d)-S_{DC}(x,y,t_d)$$ (18)

represents the real part of $W(x,y,t_d)$ [Eq. (1)]: $S\mathrm{\prime }(x,y,t_d)=2\text{Re}[W(x,y,t_d)].$

We use measured $S\mathrm{\prime }(x,y,t_d)$ to estimate the TOF-integrated autocorrelation ${\hat{G}}_1\left(x,y,{\tau }_d\right)={⟨S^{\text{'*}}\left(x,y,t_d\right)S\left(x,y,t_d+{\tau }_d\right)⟩}_{t_d}$ (the Fourier transformation is omitted since we do not tune the laser and do not have the frequency-resolved measurement). The autocorrelation estimate is then corrected for white noise, ${\hat{G}}_{1,corr}(x,y,{\tau }_d)={\hat{G}}_1(x,y,{\tau }_d)-{\hat{G}}_{1,bg}(x,y)\delta ({\tau }_d=0),$ and spatially averaged:

$${\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d)=\frac{1}{W\times H}\sum _{x=1}^W\sum _{y=1}^H{\hat{G}}_{1,corr}(x,y,{\tau }_d),$$ (19)

where W, and H denote the width and height of the active camera region.

By setting ${\tau }_d=0$ in Eq. (19) we get the intensity estimate [Eq. (14)]: ${\hat{I}}_s^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}={\overline{\hat{G}}}_1^{(\pi \text{DCS})}(0)$ . We use the latter to monitor absorption changes since ${\hat{I}}_s^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}$ is reduced when absorption increases, according to the modified Beer-Lambert law [40,41].

To get the blood flow, we normalize the ${\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d)$ estimate using zero lag:

$${\overline{\hat{g}}}_1^{(\pi \text{DCS})}({\tau }_d)={\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d)/{\overline{\hat{G}}}_1^{(\pi \text{DCS})}(0).$$ (20)

As with diffuse correlation spectroscopy, the decay of the above function encodes the blood flow [3]. The steeper the decay, the faster the blood flow. To decode the blood flow, we fit our experimental estimates of ${\overline{\hat{g}}}_1^{(\pi \text{DCS})}({\tau }_d)$ to the correlation diffusion equation, as explained under section 4.7.

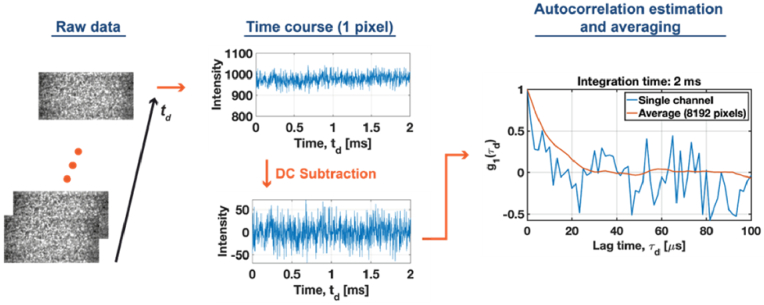
An example of the processing pipeline for ${\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d)$ is illustrated in Fig. 3. The raw data were collected from the non-absorbing tissue-mimicking phantom with ${\mu }_s^{\mathrm{\prime }}=10\text{c}{\text{m}}^{-1}$ at a source-collector of 1.5 cm.

Fig. 3.

A demonstration of the $\pi$ DCS processing pipeline shows a clear SNR improvement by spatial autocorrelation averaging.

4.6. System optimization

We control the reference arm power ( $P_r$ ) through a variable optical attenuator (VOA), while the speckle size at the camera is adjusted by varying the distance z between the interferometer output’s fiber tip and the camera sensor. As discussed earlier, the speckle size should be matched to the camera pixel size, so that each camera pixel represents an independent detection channel. To determine the distance $z,$ we use the following relationship [34]:

$$z=\frac{d_s\times d_c}{\lambda },$$ (21)

where $d_s$ and $d_c$ are the average speckle and fiber core diameters, respectively. In our case, $\lambda =785nm$ , $d_c=200\mu m$ , and $d_s=20\mu m$ (the side length of the camera pixel). So, $z=5.1$ mm.

To confirm that this distance provides the optimum number of detection channels, which should be equal to the total number of camera pixels ( $N_T)$ we rely on the speckle contrast:

$$SC(x,y)=\frac{{\sigma }_{S(x,y,t_d)}}{S{(x,y,t_d)}_{t_d}},$$ (22)

where ${⟨S\left(x,y,t_d\right)⟩}_{t_d}$ is the average pixel intensity, and ${\sigma }_{S(x,y,t_d)}$ is the standard deviation of $S(x,y,t_d).$ According to the theory of statistical optics, averaging intensities over N independent speckles, the speckle contrast should decrease as $1/\sqrt{N}$ . Hence, we estimate the number $N_d$ of detection channels as:

$$N_d={\left(\frac{SC(x_m,y_m)}{SC{(x,y)}_{x,y}}\right)}^2,$$ (23)

where $x_m$ and $y_m$ are the coordinates of the image for which the single speckle contrast achieves the maximum value, while ${⟨SC\left(x,y\right)⟩}_{x,y}$ is the speckle contrast of the spatially averaged intensity ( $S{(x,y,t_d)}_{x,y}$ ), and $\cdots$ denotes the floor function.

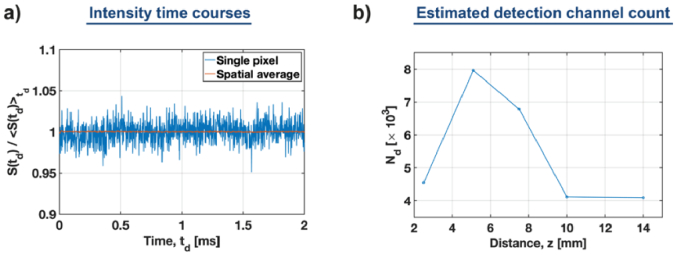
We calculated the speckle contrast using the 2-msec time courses of the data acquired for the non-absorbing tissue-mimicking phantom ( ${\mu }_s^{\mathrm{\prime }}=10\text{c}{\text{m}}^{-1}$ ) at a source-detector distance of 1.5 cm. The representative intensity time course of the center pixel $[S(x_c,y_c,t_d)$ ] is compared to the spatially averaged intensity [ ${⟨S\left(x,y,t_d\right)⟩}_{x,y}$ ] in Fig. 4(a). From this, we estimate $N_d=7963$ , which is very close to the total number of camera pixels, $N_T=8192$ . The difference can be attributed to the practical difficulties in precisely setting the distance between the fiber tip and the camera sensor. This adjustment, however, can be improved in the future by adopting a closed-feedback control system, which will precisely and automatically adjust the distance z.

Fig. 4.

Estimation of the detection channel count using speckle contrast analysis. (a) Representative time courses of the single pixel and spatially averaged intensities. (b) The estimated detection channel count, $N_d$ for the variable distance ( $z)$ between the fiber tip and the camera sensor, achieves an optimum at $z=5.1$ mm.

Subsequently, we repeated the measurements and speckle calculations for variable z and the fixed reference arm power, $P_r=0.15\mathrm{\%}$ of the sample arm power ( $P_s$ ) to confirm that $z=5.1\text{mm}$ leads to the optimum number of detection channels [Fig. 4(b)].

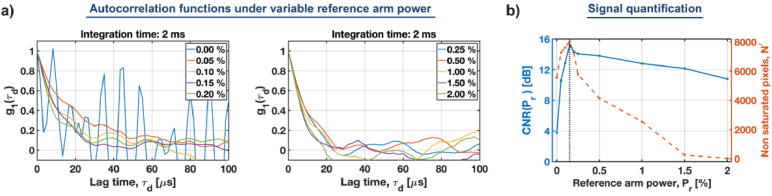
Concurrently, the reference arm power $(P_r)$ enables us to gain the amplitude of the cross-spectral density function $W(x,y,t_d)$ . However, $P_r$ must be balanced against the camera dynamic range. If the reference arm power is too high, it will increase the DC level, leading to saturation of the camera sensor [Eq. (15)]. To determine the optimum value of $P_r$ , we performed a series of measurements on the same liquid phantom as used above by varying $P_r$ from $0.0\mathrm{\%}$ to $2\mathrm{\%}$ of $P_s$ [ Fig. 5(a)].

Fig. 5.

Determining the optimum reference arm power by quantifying autocorrelation functions. (a) Autocorrelation functions for the variable reference arm power $(P_r).$ (b) Contrast to noise ratio (CNR) and the number of non-saturated camera pixels as a function of $P_r.$ The vertical dotted line indicates the optimum $P_r$ of 0.15%.

For $P_r=0.0\mathrm{\%}$ , the system works as a multi-speckle DCS. In this case, the estimated autocorrelation is very noisy. By increasing the reference arm power to only 0.0 $5\mathrm{\%}$ , we clearly improve the autocorrelation function. To quantify this improvement, we used the contrast to noise ratio ( $CNR$ ) of ${\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d)$ , defined as:

$$CNR=10{\log }_{10}\left[\frac{{\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d=0)}{{\sigma }_{{\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d\to \mathrm{\infty })}}\right],$$ (24)

where ${\sigma }_{{\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d\to \mathrm{\infty })}$ denotes the standard deviation of ${\overline{\hat{G}}}_1^{(\pi \text{DCS})}$ at large lag times. In practice, to calculate ${\sigma }_{{\overline{\hat{G}}}_1^{(\pi \text{DCS})}({\tau }_d\to \mathrm{\infty })}$ we select the region of ${\overline{\hat{G}}}_1^{(\pi \text{DCS})}$ where it drops to 0. For example, in Fig. 2(c) that would be the range of 65-100 $\mu \text{s}$ . The reason for using CNR is that it provides a single, lag time-independent indicator of the ${\overline{\hat{G}}}_1^{(\pi \text{DCS})}$ quality.

The resulting CNRs are plotted as a function of $P_r$ in Fig. 5(b). Initially, the CNR rapidly increases with $P_r$ , and after reaching the maximum at $P_r=0.15\mathrm{\%}$ (indicated by the dotted line), the CNR starts to gradually decrease. Additionally, for large $P_r$ we observe faster decorrelation, because the increased reference arm power starts to saturate the camera. To evaluate this effect, we analyzed the number of non-saturated pixels, $N^{\mathrm{\prime }}$ [red curve in Fig. 5(b)]. As shown there, $N^{\mathrm{\prime }}$ starts to rapidly decrease for $P_r>0.15\mathrm{\%}$ . This analysis enabled us to find the optimum reference arm power of 0.1 $5\mathrm{\%}$ (black dotted line).

4.7. Autocorrelation fitting

To estimate the sample dynamics, we use the solution of the correlation diffusion equation (CDE) for the semi-infinite model with the Brownian motion model for the mean square scatterer displacement [40,46]:

$$G_1^{(CDE)}({\tau }_d)=\frac{3{\mu }_s\mathrm{\prime }}{4\pi }\left[\frac{\text{exp}[K({\tau }_d)r_1]}{r_1}-\frac{\text{exp}[K({\tau }_d)r_2]}{r_2}\right],$$ (25)

where

$$K({\tau }_d)=\sqrt{3{\mu }_s\mathrm{\prime }[{\mu }_a+2{\mu }_s^{\mathrm{\prime }}{k}^2\alpha D_B{\tau }_d]},$$ (26)

$$r_1=\sqrt{{\rho }^2+z_0^2},$$ (27)

$$r_2=\sqrt{{\rho }^2+{(z_0+2z_b^2)}^2},$$ (28)

and $z_0=\frac{1}{{{\mu }_s}^{\mathrm{\prime }}},$ $z_b=\frac{2}{3{{\mu }_s}^{\mathrm{\prime }}}\frac{1+R_{\mathit{eff}}}{1-R_{\mathit{eff}}},$ $\rho$ is the source-collector separation, whereas

$$R_{\mathit{eff}}=-1.4399n^{-2}+0.7099n^{-1}+0.6681+0.0636n.$$ (29)

We fit the normalized CDE equation:

$$g_1^{(CDE)}({\tau }_d)=G_1^{(CDE)}({\tau }_d)/G_1^{(CDE)}(0)$$ (30)

to our experimental estimates using the non-linear least square method. We assume optical properties ( ${\mu }_a,{{\mu }_s}^{\mathrm{\prime }}$ ) and keep $\alpha D_B$ as the fit parameter. We interpret the resulting values of $\alpha D_B$ as the blood flow index (BFI) for in vivo experiments.

5. Results

5.1. Tissue-mimicking phantoms

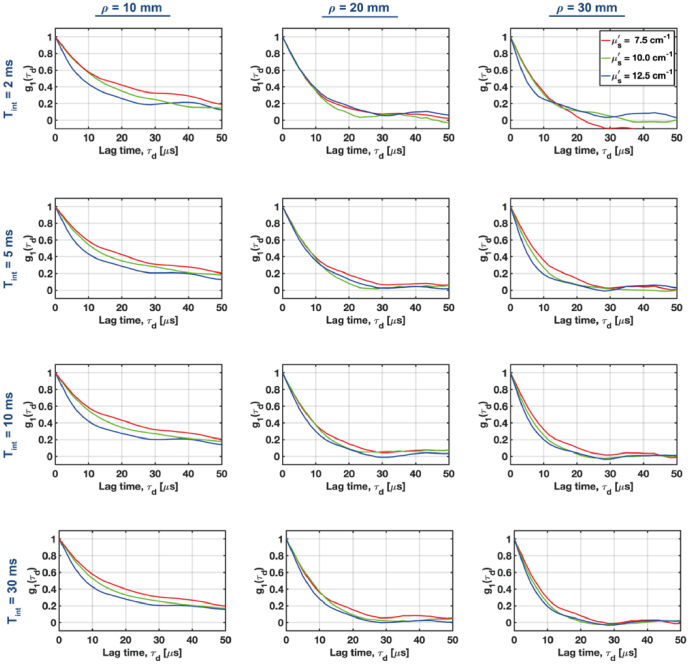
According to Eqs. (25)-(28), the autocorrelation function (ACF) decay varies with the product of $\alpha D_B$ and the reduced scattering coefficients ( ${{\mu }_s}^{\mathrm{\prime }}$ ), and the source-collector separations ( $\rho$ ). So, tuning the value of ${{\mu }_s}^{\mathrm{\prime }}$ has the similar effect on the ACF decay as varying $\alpha D_B$ . Hence, we first analyzed if we could resolve changes in ACF for the tissue-mimicking phantoms under various source-collector separations ( $\rho$ ) at three different levels of ${\mu }_s^{\mathrm{\prime }}$ (7.5, 10, 12.5 cm^-1) (Fig. 6).

Fig. 6.

Normalized autocorrelation functions for the tissue-mimicking non-absorbing phantoms with a variable reduced scattering coefficient ( ${{\mu }_s}^{\mathrm{\prime }}$ ) at increasing source-collector separations (columns) were estimated using variable integration times (rows). Autocorrelations for the variable ${{\mu }_s}^{\mathrm{\prime }}$ can be distinguished at long separations, provided the integration time is 5-10 msec.

The expected differences in $g_1({\tau }_d$ ) for variable scattering can be rapidly (integration time, $T_{\text{int}}=2$ msec) resolved for a short $\rho =10$ mm. However, to resolve changes in the $g_1({\tau }_d)$ decay for longer source-collector separations we need to increase the integration time to 5-10 msec.

The results from Fig. 6 also enable us to qualitatively assess at which lag times the ACF provides the largest contrast, $\mathrm{\Delta }{g}_1({\tau }_d)$ (which is defined as the absolute difference between two ACFs estimated for the different optical properties and/or source-collector separations).

We see that for $\rho =10\text{mm}$ , we get the largest $\mathrm{\Delta }{g}_1({\tau }_d)$ for ${\tau }_d\le 20\mu s$ , while for $\rho =30\text{mm}$ , the best contrast appears for ${\tau }_d\le 15\mu s$ . This analysis enables us to calibrate the autocorrelation fitting window, and reject the lag times for which ACF drops below 20-30% of its initial value.

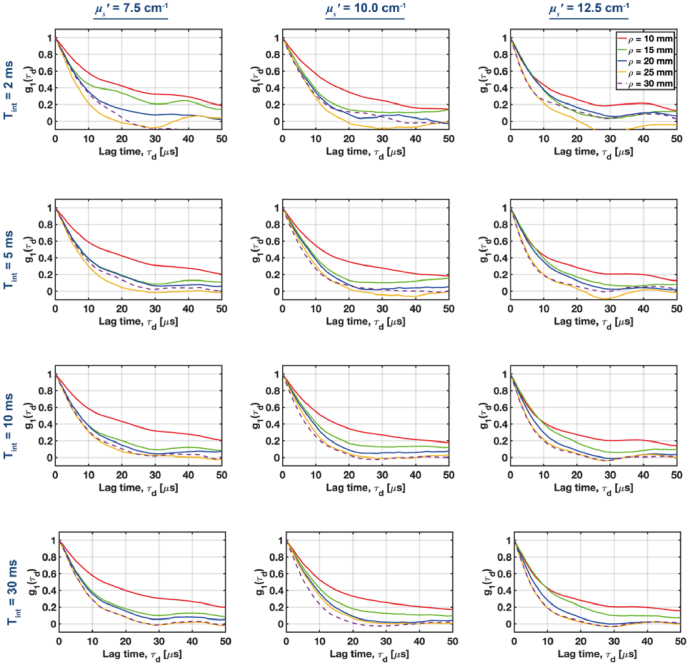
Then, we performed a similar analysis for the variable source-collector separations (Fig. 7). For the lowest reduced scattering ( ${\mu }_s^{\mathrm{\prime }}=7.5\text{c}{\text{m}}^{-1}$ ), we can resolve changes in the ACF decay when $\rho \le 20\text{mm}$ (first row in Fig. 7). To reliably resolve various ACF decays for higher values of ${\mu }_s^{\mathrm{\prime }}$ ,we need to increase the integration time to 5-10 msec. In such cases, the ACF decays can be resolved for all analyzed combinations of the reduced scattering and source-collector separations. By further increasing the integration time to 30 msec, we do not observe significant improvements in the ACF contrast. Hence, we decided to fix the integration time at 10 msec.

Fig. 7.

A comparison of the normalized autocorrelation functions (ACFs) for increasing source-collector separations $(\rho )$ at three different levels of the reduced scattering coefficient $({\mu }_s^{\mathrm{\prime }},\text{columns})$ . ACFs were estimated for the variable integration times $(T_{\text{int},}$ rows).

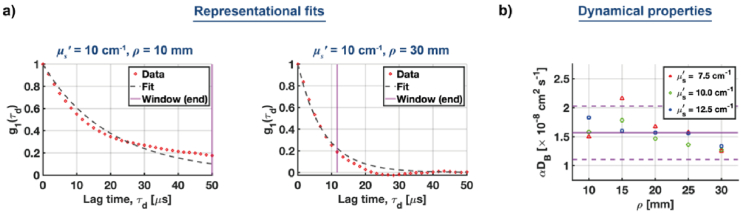
After fixing the integration time, we fitted the experimentally estimated autocorrelations to the normalized correlation diffusion equation [CDE, Eq. (28)] to estimate values of $\alpha D_B.$ Fig. 8 depicts representative fits, and the resulting values of $\alpha D_B.$

Fig. 8.

An estimation of dynamic properties by fitting experimental autocorrelations to the correlation diffusion equation (CDE). (a) Representative fits of the experimental data to CDE for short (left) and long (right) source-collector separations $(\rho )$ . The vertical purple line denotes the end of the fitting window (which is the last lag time used for fitting). (b) The values of $\alpha D_B$ are plotted for various values of $\rho$ and ${{\mu }_s}^{\mathrm{\prime }}$ . The horizontal purple line denotes the mean value, $⟨\alpha D_B⟩$ , while the dashed purple lines denote the region $⟨\alpha D_B⟩\pm 1.96{\sigma }_{\alpha D_B}$ , where ${\sigma }_{\alpha D_B}$ is the standard deviation of $\alpha D_B$ .

At short source-collector separations, we observe a mismatch between the experimental and theoretical ACFs, which is due to invalidated CDE assumptions at short values of $\rho$ . However, the extracted values of $\alpha D_B$ are consistent for almost all measurements with the mean value of $\alpha D_B=(1.57\pm 0.24)\times {10}^{-8}\frac{\text{c}{\text{m}}^2}{\text{s}}$ [Fig. 8(b)].

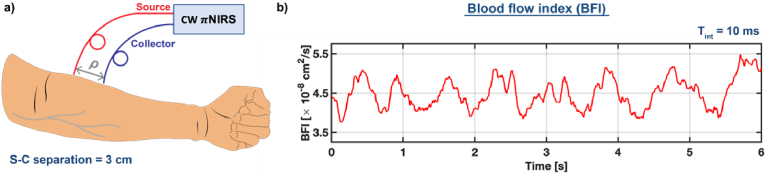
5.2. Human forearm in vivo

We evaluated the possibility of sensing deep blood flow with πNIRS in the human forearm in vivo. The source and collector fibers were separated by 3 cm and fixed in a black 3D-printed fiber holder. We attached the probe to the forearm with an elastic bandage. The recorded data were processed to estimate the averaged autocorrelations. The autocorrelations were estimated using 10 msec data chunks with 9 msec overlap. The resulting autocorrelations were fit to the correlation diffusion equation [CDE, Eq. (28)] to estimate the blood flow index, using the optical properties from Table 1.

Our results, shown in Fig. 9, demonstrate the feasibility of this approach in detecting the pulsatile blood flow in human tissue in vivo. Notably, the integration time necessary to estimate the ACF was only 10 msec, approximately 100 times shorter than conventional iNIRS. However, the pulse waveforms do not reveal all features due to limited sensitivity at long source-collector separation. We can improve the sensitivity by further optimizing the system as described in section 6.

Fig. 9.

$\pi$ NIRS enables measuring the pulsatile blood flow in the human forearm in vivo at long source-collector separation and a short integration time of only 10 msec. (a) A diagram of the experiment. (b) The estimated blood flow index renders the pulsatility.

The measurement lasted for several seconds due to the limited internal memory of our camera. These initial proof-of-concept experiments demonstrate that we can monitor the deep pulsatile blood flow.

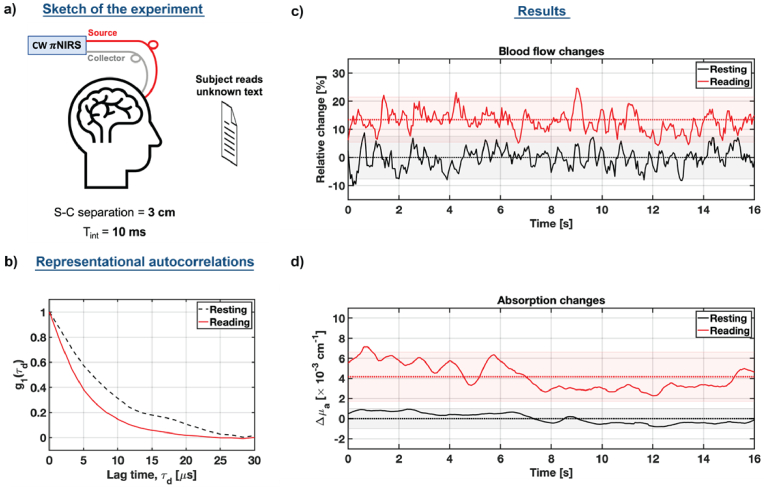
5.3. Human forehead in vivo

Finally, we employed our system to monitor activation of the subject’s prefrontal cortex when he read an unfamiliar text [ Fig. 10(a)]. A healthy 39-year-old volunteer sat on the rotating chair and put his head on the chinrest to eliminate the motion artifacts. We then attached the probe, consisting of the 3D-printed fiber holder mounted on the elastic band. The source-collector separation was set to 3 cm to reduce the effects of superficial layers. We reduced the image resolution to 128 × 32 pixels to increase the recording length to 16 seconds. This, however, reduced the effective number of channels by half.

Fig. 10.

$\pi$ NIRS monitors prefrontal cortex activation. (a) Schematic diagram of the experiment. (b) Representative autocorrelations (10 msec integration time) for the resting (baseline) and reading stage (activation). (c) Relative blood flow index and (d) relative absorption changes during the reading stage are compared to the resting stage, demonstrating the increase in blood flow and absorption during the prefrontal activation.

First, we recorded the baseline when the subject was resting. Then, the subject was asked to read an unfamiliar text, and we repeated the measurement. Due to the limited internal memory of our camera, we recorded the baseline and the activation stage separately.

The recorded data were processed to estimate autocorrelations [Fig. 10(b)], from which we extracted the relative changes of the blood flow index, $\mathrm{\Delta }$ rBFi:

$$\mathrm{\Delta }\mathrm{r}\mathrm{B}\mathrm{F}\mathrm{I}=100\mathrm{\%}\times \frac{\text{BF}{\text{I}}_{\text{reading}}-\text{BF}{\text{I}}_{\text{baseline}}}{\text{BF}{\text{I}}_{\text{baselie}}},$$ (31)

where to estimate the rBFI baseline, we averaged the BFI time courses during the resting stage. The resulting relative rBFI changes during the resting (baseline) and reading stage (brain activation) are plotted in Fig. 10(c). We noticed an approximately 14% rBFI increase during the reading stage. This rBFI change is consistent with previous reports, which used parallel SPAD-based DCS [36], and single-channel iNIRS at null source-collector separation [28]. However, at the source collector separation of 3 cm, we did not achieve clear pulsatility traces, most likely due to the reduced number of channels. Importantly, our integration time is 10 times shorter than in other approaches.

We also estimated the complementary absorption changes. To do so, we first estimated the intensity using Eq. (14). Then, we calculated the differential absorption changes $\mathrm{\Delta }{\mu }_a$ , using the modified Beer-Lambert law:

$$\mathrm{\Delta }{\mu }_a=\frac{1}{⟨l⟩}\ln \left[\frac{I_{s,\text{baseline}}^{\left(\pi \mathrm{D}\mathrm{C}\mathrm{S}\right)}}{I_s^{\left(\pi \mathrm{D}\mathrm{C}\mathrm{S}\right)}}\right]=\frac{1}{⟨l⟩}\ln \left[\frac{{\overline{G}}_{1,\text{baseline}}^{\left(\pi \mathrm{D}\mathrm{C}\mathrm{S}\right)}\left({\tau }_d=0\right)}{{\overline{G}}_1^{\left(\pi \mathrm{D}\mathrm{C}\mathrm{S}\right)}\left({\tau }_d=0\right)}\right],$$ (32)

where $⟨l⟩$ is the average photon path length. To determine $⟨l⟩$ we used the centroid of the photon time-of-flight distribution achieved using TD-NIRS and obtained $⟨l⟩=18.95$ cm. To estimate the baseline intensity, we averaged $I_{s,\text{baseline}}^{(\pi \mathrm{D}\mathrm{C}\mathrm{S})}$ acquired during the resting stage. Then, assuming that $⟨l⟩$ did not change during the activation, we plotted the resulting absorption changes in Fig. 10(d). The absorption, consistent with the blood flow, increased during the reading stage. These results demonstrate the ability of our approach to monitor prefrontal cortex activation due to reading of unfamiliar text.

The system could be further enhanced by an additional channel with the source-collector separation to further regress superficial signal components [47]. We can use the single 2D camera and project the output of the short source-collector separation onto a different active area than the long S-C channel.

6. Discussion

In this report, we introduced the basis for interferometric near-infrared spectroscopy with parallel Fourier-domain detection and implemented its continuous wave version. The main goal was to achieve fast renderings of the autocorrelations of the light remitted from a turbid sample at long source-collector separations (up to 3 cm). Achieving this goal with time-of-flight resolution would require at least two-order-of-magnitude faster cameras than currently available. Hence, our initial experimental setup is based on a fixed wavelength instead of a tunable laser. So, our approach enables us to estimate absorption changes (like in continuous wave NIRS) and relative blood flow index (like in diffuse correlation spectroscopy), effectively combining CW NIRS and DCS into a single modality.

We demonstrated ways to optimize the optical setup using tissue-mimicking phantoms and then applied the system to monitor human pulsatile blood flow in vivo. One of the significant advantages of our approach is the relatively small size of the system. Usually, multi-channel diffuse optical systems, like TD-NIRS or DCS, are enclosed in medical carts. After further optimizations, our system could be deployed to clinics in a more compact form. The main components include the multi-mode fiber couplers, compact laser, and the compact 2D camera, which already has a carrying handle.

The major challenge of our approach is related to data size. Two-dimensional image acquisition at very high frame rates generates extensive data. A typical recording of 128 × 64 px images produces about 9 GB per second. These data must then be downloaded to the PC for processing. The camera for this study uses an Ethernet interface, which is currently the major bottleneck for practical applications. Therefore, one of our future goals is to optimize the recording and downloading strategy to achieve nearly real-time renderings of autocorrelations. This will enable continuous and long measurements to unlock the full potential of our approach.

We also noticed an overestimation of the diffusion coefficient ( $\alpha D_B$ ) in phantoms compared to TD-DCS [22]. The different fitting models most likely caused this discrepancy. Specifically, TD-DCS extracts the diffusion coefficient using diffusing wave spectroscopy theory, in which the normalized field autocorrelation does not depend on the absorption coefficient. On the contrary, the diffuse correlation equation used here depends on ${\mu }_a$ . Since the latter was estimated using a separate measurement, it can lead to inaccuracies in $\alpha D_B$ .

Our approach is compared to the state-of-the-art in Table 3. For this comparison, we used three parameters: the resolution of the autocorrelation function (ACF resolution), integration time, and source-collector separation. Interferometric diffusing wave spectroscopy (iDWS) provides a ACF resolution of 3 $\mu$ s and requires integration times of 100 msec, and enables renderings of the ACF at very long source-collector separations, reaching 5 cm. SPAD array-based multi-speckle DCS provides the same ACF resolution as iDWS and can shorten the integration time to 30 msec. Still, it operates at short source-collector separations (up to 1.5 cm). Multi-speckle DCS based on the fiber bundle and APD array provides the finest ACF resolution, and very short integration times (6.5–29 msec) and operates at long source-collector separations. The approach presented here provides ACF resolution of up to 0.9 $\mu$ s, with integration times of 2-10 msec, and can operate at source-collector separations up to 3 cm. These values are comparable to parallel DCS based on the fiber bundle and APD array.

Table 3. A comparison of CW πNIRS to the state-of-the-art.

Approach	References	ACF resolution [ $\mathit{\mu }$ s]	Integration time [msec]	Source-collector separation [cm]
iDWS	[31,32]	3	100	1–5
SPAD array	[34,36]	3	30–100	1–1.5
Fiber bundle and APD array	[33]	0.2–3.2	6.5–29	1.4–2.9
CW $\pi$ NIRS	herein	0.9–1.6	2–10	1–3

Here, we also mention alternative approaches to detect the dynamics of biological tissues using low-frame rate two-dimensional cameras. These include interferometric speckle visibility spectroscopy (ISVS) [48] and Fourier-domain DCS [49]. Both methods were demonstrated to significantly improve the SNR, even an order of magnitude better than multi-speckle DCS. However, ISVS and Fourier-domain DCS were demonstrated only at short source-collector separations (0.75–1.5 cm).

Our system can be further optimized to improve the sensitivity. This refinement would include optimization of the illumination and collection paths. Specifically, the illumination fiber could have a lower numerical aperture or use a collimated light beam to improve light delivery to the tissue, as in interferometric diffuse wave spectroscopy (iDWS) [31]. On the other hand, we could also increase the diameter of the collection fiber to improve light collection efficiency. This could possibly improve the SNR in two ways. First, the larger core diameter would increase the number of modes $N_m$ , which with more camera pixels would further boost the SNR. To estimate the number of modes, we use the relation [50]: $N_m\approx \frac{2{\pi }^2{a}^{2}N{A}^2}{{\lambda }^2},$ where a is the fiber core radius, and $NA$ is numerical aperture. In our current setup $a=100\mu m,NA=0.5$ , and $\lambda =785nm$ , which leads to $N_m\approx 80000$ . We also see that number of modes scales with the square of a or $NA$ . So, doubling the core radius, and keeping NA constant, can increase the number of modes up to 320 000. This estimation further confirms the potential of multi-speckle detection systems. Second, an increased diameter of the collection fiber would increase the number of collected photons since the reflected light is integrated over a larger area [12]. Finally, we could optimize the fiber coupler splitting ratios to increase the number of collected sample photons.

One of the interesting future avenues for this project would be to use a longer wavelength; e.g., 1064 nm, as already demonstrated for other techniques, including DCS [51] and TD-DCS [21,23]. The longer wavelength would be beneficial for two reasons. First, the power incident on the tissue could be increased roughly 3-4 times, which would linearly improve the signal-to-noise ratio. Secondly, the decorrelation time would be slower, which would enable using slower camera frame rates. This change would enable using slower InGaAs 2D cameras, sensitive to a 1064-nm wavelength.

Signal processing can account for absorption changes and eventual distortions from the subject’s motion. We can also correct the signal for a non-uniform distribution of the intensity at the detector (due to beam expansion after the fiber tip [Fig. 2(c)]) [52]. Ultimately, renderings of true TOF-resolved autocorrelations would be made possible by employing a tunable laser. This modification, however, as explained above, would require us to reduce the autocorrelation sampling rate. Alternative approaches to this problem are currently being investigated in our lab.

7. Summary

We introduced the theoretical foundations for parallel interferometric (π) NIRS and demonstrated its possible hardware implementations. Then, we constructed continuous wavelength (CW) πNIRS and validated it in tissue-mimicking phantoms. Then, by utilizing more than 8000 parallel channels, we monitored the pulsatile blood flow in a human forearm in vivo. Finally, we applied CW πNIRS to monitor activation of the prefrontal cortex in vivo.

The major limitation of our technique is the relatively high cost of the CMOS camera. However, we expect that applications of the CMOS technology in LiDAR [53] and ultra-fast volumetric eye imaging [50,54] will lead to reduction of the camera cost soon. Thus, CW πNIRS could be extended to monitor the cerebral blood flow and absorption changes from more than a single spatial location. Also, utilizing the tunable laser should enable us to employ time gating to shorten the source-collector separation to $\rho <1$ cm. Such a short source-collector separation would improve the light detection efficiency further. This modification would allow us to use sub-millisecond integration times.

Funding

Fundacja na rzecz Nauki Polskiej10.13039/501100001870 (MAB/2019/12); Narodowe Centrum Nauki10.13039/501100004281 (2016/22/A/ST2/00313, 2020/38/L/ST2/00556).

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.