Abstract
In this paper, we propose an accurate and rapid non-rigid registration method between blood vessels in temporal 3D cardiac computed tomography angiography images of the same patient. This method provides auxiliary information that can be utilized in the diagnosis and treatment of coronary artery diseases. The proposed method consists of the following four steps. First, global registration is conducted through rigid registration between the 3D vessel centerlines obtained from temporal 3D cardiac CT angiography images. Second, point matching between the 3D vessel centerlines in the rigid registration results is performed, and the corresponding points are defined. Third, the outliers in the matched corresponding points are removed by using various information such as thickness and gradient of the vessels. Finally, non-rigid registration is conducted for hierarchical local transformation using an energy function. The experiment results show that the average registration error of the proposed method is 0.987 mm, and the average execution time is 2.137 s, indicating that the registration is accurate and rapid. The proposed method that enables rapid and accurate registration by using the information on blood vessel characteristics in temporal CTA images of the same patient.
Keywords: Medical imaging, Rigid registration, Non-rigid registration, Cardiac CT angiography
Introduction
Coronary artery disease (CAD) is one of the leading causes of death worldwide [1]. It is a disease caused by insufficient blood supply to the cardiac muscle, resulting from the narrowing or clogging of the blood vessels due to stricture, calcification, and lipid deposits in the coronary arteries. Cardiac CT angiography (CTA), known for its non-invasive nature and high accuracy, is utilized for an accurate diagnosis of CAD [2]. CTA can take 3D images of blood vessels using radiopaque contrast media for various tasks. For example, these tasks can be comparing the effects of surgery, searching for coronary artery movements according to the heart cycle, and checking the progress based on the images taken during the initial and follow-up visits. However, the coronary arteries in the CTA images taken from the same patient may entail differences in disease status, imaging equipment, patient posture, protocol, and heart movement. These differences can prolong comparative observations and analysis of multiple CTA images. Active research is conducted on auxiliary technologies that allow direct comparative observations and monitoring of coronary arteries through automatic registration methods of the vessels to compensate for these shortcomings.
Related work
Studies on registration related to medical imaging have been conducted in various modalities such as US/US, CT/CT, CT/MR, and MR/MR.
Studies on MR/MR registration are as follows [3, 4]. Zhang et al. [3] performed an hippocampus segmentation through pre-prepared brain cross-section atlas model registration and then performed sophisticated segmentation using the broad learning model. This method has a potential problem of causing misalignment if the predefined atlas model is different from the brain cross-section of the segmented target. Fontana et al. [4] performed thresholding-based muscle segmentation for skeletal muscle registration in MRI images, performed initial registration through rigid body registration, and then performed non-rigid registration using a B-spline-based free-form transform (FFD). However, as this method matches the divided muscle by a simple thresholding method, it implies a disadvantage because a large matching error may occur depending on the degree of division.
Studies on CT/MR registration include as follows [5–7]. For knee joint registration, Kuniper et al. [5] performed initial registration using the Iterative Closest Point (ICP) method between the point cloud data obtained in the area where water/fat/muscle is divided, and then performed B-spline non-rigid registration based on intensity information. As the matching performance in this method is affected by the brightness similarity of the images, registration becomes difficult if changes occur in the protocol of the imaging equipment or in the patient’s body. Xu et al. [6] segmented the liver area using a U-Net++-based deep learning model applied with the 3D MR images taken before the procedure and the 3D CT images taken during the procedure, and after global alignment via rigid body registration, performed non-rigid registration using the B-spine-based FFD. This method may cause inaccurate segmentation because it does not consider the inter-images of adjacent upper/lower frames in liver segmentation, which could affect the registration performance. Tang et al. [7] divided the liver area through the active contour using the seed points specified by the user and performed non-rigid body registration between the divided liver areas using the B-spline-based FFD. This method has a disadvantage in that a user has to define several seed points through intervention manually.
Studies on US/US registration include as follows [8–11]. Ou et al. [8] conducted supervised-learning based on the texture information extracted from US images using the Gabor filter in order to select meaningful features. Based on this, they performed registration using an FFD technique. For the purpose of registration of brain images for brain shift compensation, Luo et al. [9] performed registration through the Gaussian process between the feature points acquired using Scale-invariant feature transform (SIFT) in the 2D US images, and further improved the registration accuracy by using preoperative US-MRI image information. Machado et al. [10] performed the SIFT-based affine and thin-plate spline registration for 3D US Volume registration. Zhou et al. [11] performed registration through intensity similarity comparison using NCC, for US volume matching. However, registration between US/US images presents difficulties due to the characteristics of ultrasound images such as low contrast detectability and poor quality [12].
Studies of CT/CT registration include as follows [13–18]. Park et al. [13] performed liver segmentation on 3D CT images using a level-set method, initial registration using the boundary regions, then precise registration through the non-rigid registration technique and local affine transformation using the B-spline deformation model. This method has a disadvantage in that the matching technique using the local affine transformation model takes a long time due to the complexity of the calculation. Zhang et al. [14] registered blood vessels divided into each cardiac phase through registration using the B-spline method and the template matching technique based on the blood vessel at the end-diastole point in the 4D CTA image. This method takes a long time to conduct owing to vessel division and registration for each cardiac phase. In addition, it entails a disadvantage of onerous registration because of the rapid heart movement causing blurring and ghost effect phenomena in the image. Hadjiiski et al. [15] proposed a method for performing inter-phase registration between adjacent phases with little changes in the blood vessels by using affine transformation and cubic B-spline transformation methods in the multi-phase CTA images. However, this method makes it challenging to divide blood vessels in the phase image excluding end-diastole and end-systole because of the image noise caused by the rapid transformation of blood vessels due to heartbeats. Furthermore, it can cause registration errors owing to incorrect input of blood vessel information. Luo et al. [16] proposed a registration method using a hidden Markov model (HMM) based on the intensity of the CTA image and the geometry of the 3D vessel centerline. However, registration becomes difficult if the protocol of the imaging equipment changes or internal changes occur in the patient body because such techniques are influenced by the brightness similarity of the images. Zeng et al. [17] matched branching points between two blood vessels using a feature engineering technique by means of SIFT. Next, the authors conducted registration based on thin plate spline on all blood vessels using the matched branching points. Subsequently, the registration correction on blood vessel segments was performed using the Levelset and B-spline transform technique in order to register between 3D vessel centerlines. This method takes a long time to perform, as the operation is performed on the entire blood vessel and some segments. Cao et al. [18] performed rigid registration using coherent point drift to register between 3D vessel centerlines. However, this method can cause registration errors by converging to a local minimum if the transformation between the vessel centerlines is substantial.
In this paper, we propose a non-rigid registration method based on the characteristics of the temporal CTA image of the same patient to overcome the aforementioned shortcomings. Translation, rotation, and rigid transformations between two blood vessels are sequentially optimized to conduct global registration. Next, point matching is performed based on the gradient to consider the corresponding points between the two blood vessels. In this step, outliers are removed to consider CAD and errors in the feature extraction process. Non-rigid registration involves conducting hierarchical local transformation so that transformations occur accurately and naturally. In addition, a more natural transformation is enabled by using an energy function that utilizes blood vessel characteristics, as the phase of the two blood vessels is maintained. In this study, rapid and accurate registration is enabled through outlier removal using blood vessel characteristics and hierarchical local transformations.
The structure of this paper is as follows. Chapter 2 introduces the proposed method, and Chap. 3 details the experimental environment and the results. Finally, Chap. 4 presents the conclusions of this study.
Methodology
In this study, a rapid and robust 3D-3D non-rigid registration process is proposed using a flow chart (Fig. 1) to register blood vessels between 3D CTA images of the same patient photographed with a time difference.
Fig. 1.
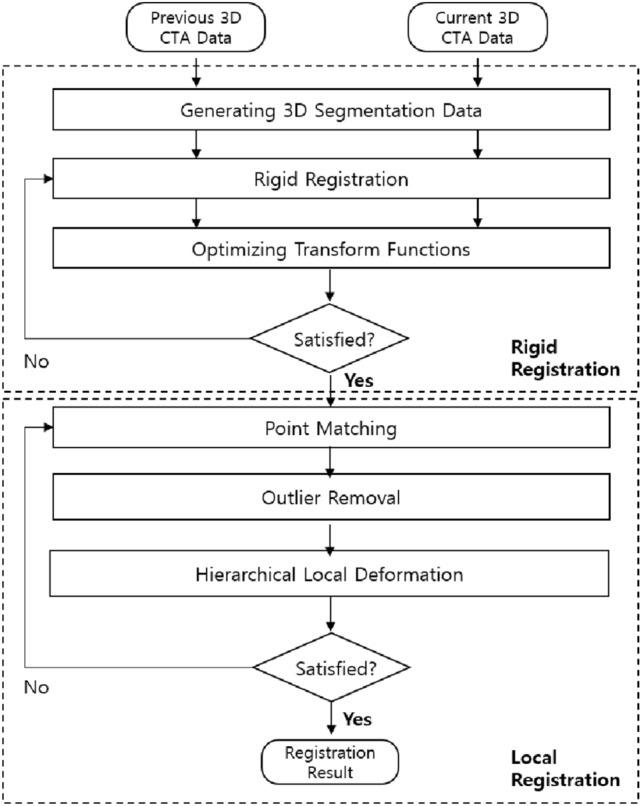
3D-3D non-rigid registration process
3D CTA images of the same patient photographed with a time difference are defined as fixed and moving images. Feature-based registration methods [19] allow faster registration compared to light intensity-based registration methods [20], which have relatively high computational complexity. A 3D vessel centerline is extracted [21] from the 3D CTA image to acquire information on blood vessel characteristics for rapid registration. Here, registration is performed based on the assumption that the shapes are similar because the blood vessels of the fixed and moving images are photographed from the same patient.
Rigid Registration
The location or shape of the blood vessel may differ even for the same patient owing to CAD, imaging equipment, patient posture, and protocols [22]. A global registration is performed through rigid registration [23] proposed by Park et al. [23] to minimize these errors before conducting non-rigid registration. First, Eq. (1) is used to optimize the conversion function regarding the two 3D centerlines of the fixed and moving images [24].
| 1 |
Here, , , and refer to the motion vector of the , , and axes, respectively, and , , and refer to the center size vectors. Further, represents translation transformation, represents translation and rotation transformations, and refers to rigid transformations. Finally, and refer to and , respectively. Equation (2) is used to evaluate the conversion function [25].
| 2 |
Here, refers to the i-th point on the moving 3D centerline, and shows the 3D distance map of the fixed 3D centerline [25].
Point matching based on the gradient
In this study, non-rigid registration for the local deformation of each blood vessel was conducted, following global registration through rigid registration. Consequently, all the points, , were matched to the 3D centerline acquired from the fixed image based on the 3D centerline obtained from the moving image [24]. The global registration of the two blood vessels occurred through the rigid registration in the previous process, so a gradient-based searching technique was used to search for points instead of a distance-based technique. In the gradient-based searching method, partial derivatives (, , ) were calculated for all the points and were matched as shown in Fig. 2 [24].
Fig. 2.
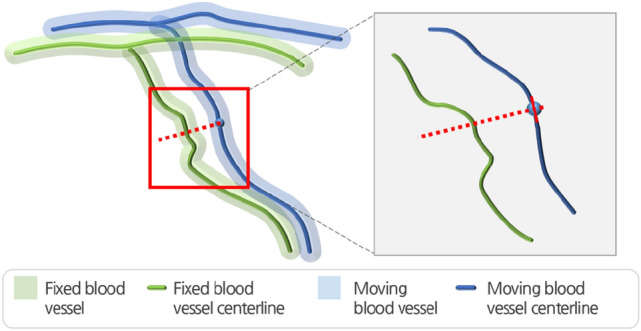
Point matching between points on the 3D-3D centerlines
Outlier removal
Errors can occur in the gradient-based point matching process because of errors that can occur in the extraction process of CAD or the centerline even if the data of the same patient are used in registration. The registration efficiency through the removal of outliers between the matched points was enhanced as follows. First, we assumed the difference in the shape of the two blood vessels to not be significantly different in the CTA images taken from the same patient. Second, was defined assuming the error in the blood vessels was not too substantial, as the global registration of the two blood vessels occurred through rigid registration. The uses the distance (, gradient (), and thickness .
| 3 |
is used as the outlier if no matched points exist or the distance between the matched points is greater than .
| 4 |
.
Here, refers to the adjacent gradient, and the surrounding adjacent points are used to consider the presence of a disease, errors that occur in the division process, and errors that occur during the point matching process.
| 5 |
Similar to the gradient, adjacent points are also used for the information regarding the vessel thickness.
Hierarchical local transformation
The non-rigid registration process involves repeated local transformations from the upper level, which includes the root node of the vessel tree, to the lower level to achieve more accurate and natural vessel transformations (Fig. 3).
Fig. 3.
Upper and lower local transformations
Thus, the phase information of the actual blood vessels is first maintained through sampling point matching and transformations, and local errors are reduced. The transformation involves repeated rotations using the angle between matched sampling points (Fig. 4).
Fig. 4.

a LCA registration result. b RCA registration result
After repeated local transformations, the energy minimization method proposed by Park et al. [17] is extended and applied.
| 6 |
Here, α, β, and γ refer to the weight of each function; represents the i-th point on the 3D centerline; and N represents the number of points constituting the 3D centerline. The energy function controls the continuity of the points constituting the 3D centerline and maintains equal spacing between adjacent points. The refers to the average distance between neighboring points. The energy function controls the slowness of the 3D centerline and induces a gentle, natural shape to prevent sudden curvature changes and vibrations. The energy function controls the location and shape transformations according to the reference 3D centerline. The is the corresponding point of .
Statistical analysis
The matching performance was compared by verifying the statistical significance between the rigid and non-rigid registration methods of the 3D vessel centerlines. A t-test was conducted to examine the significance of the accuracy, in which the statistical significance was confirmed when the P-value was less than 0.05. Statistical analysis was performed using Medcalc version 20.116 (Frank Schoonjans, Mariakerke, Belgium).
Experiments and results
This experiment was conducted on a system with an Intel Core i7-7800 CPU(3.2 GHz) RAM 32GB. Seven sets of left coronary artery (LCA) CTA images and four sets of right coronary artery (RCA) images photographed with a time difference on 11 patients were used as the experimental data.
Qualitative evaluation
Figure 5 shows the results of registering the blood vessels between 3D CTA images with the method proposed in this study. Figure 5a and b show the LCA and RCA registration results, respectively. The registration results visually confirm that the two 3D vessel centerlines extracted from the CTA images photographed with a time difference are well registered.
Fig. 5.

a LCA registration result. b RCA registration result
Quantitative evaluation
This study uses a distance-based error measurement method to measure the registration accuracy between registered 3D vessel centerlines. Distance-based error measurements are taken by calculating the Euclidean distance-based average of distance difference (ADD) using Eq. (7) between the registered results and the ground truth centerline manually divided in fixed images by an expert [23, 26].
| 7 |
.
Here, refers to the number of points constituting the input 3D vessel centerline, and are the matched points in the two 3D vessel centerlines extracted from the fixed and moving images, and represents the Euclidean distance between these two points.
Figure 6 shows the error in average distance between the two 3D vessel centerlines after applying the rigid and non-rigid registration methods proposed in this study to each patient data. Compared to the case where only the rigid registration method was applied, the non-rigid registration method decreased the error in the left and right coronary arteries of the 11 patients by an average of 0.479 mm and 0.442 mm, respectively. These results indicate that the proposed method successfully enhanced the registration accuracy.
Fig. 6.
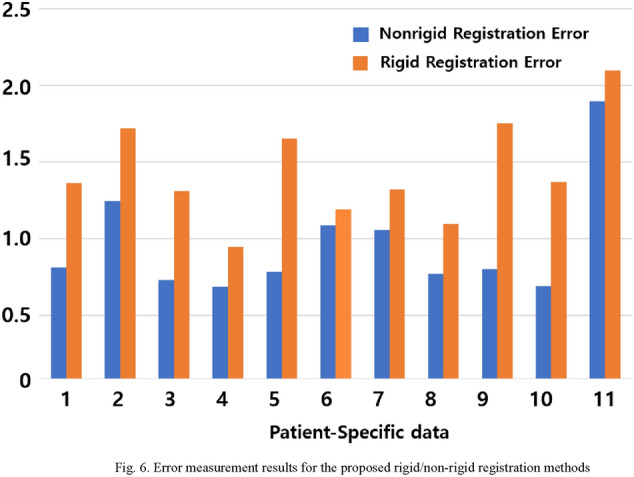
Error measurement results for the proposed rigid/non-rigid registration methods
Table 1 shows the registration performance results of the proposed method in this study and previous studies. The average registration error of the proposed method for the data of the 11 patients is 0.987 mm, and the standard deviation of the registration error is 0.397 mm. The average registration error in the left coronary artery is 0.913 mm, and the standard deviation is 0.213 mm. The average registration error in the right coronary artery is 1.061 mm, and the standard deviation is 0.582 mm.
Table 1.
Comparing the proposed method with previous studies
| Author | Modality | No. of test subjects | Accuracy |
|---|---|---|---|
| Kaila et al. [27] | Biplane XA / CTA | 7 |
1.41 mm (RMSE1) |
| Hadjiiski et al. [15] | CTA / CTA | 22 |
LCA − 1.49 pixels RCA − 1.43 pixels |
| Luo et al. [16] | CTA / CTA | 5 |
1.6 mm (ADD1) |
| Park et al. [13] | CTA / CTA | 10 | 1.7964 mm |
| Proposed method | CTA / CTA | 11 |
LCA − 0.913 mm RCA − 1.061 mm (ADD1) |
aRMSE: Root mean square error
bADD: Average of distance difference
In the result of the comparison between the accuracy of the non-rigid registration method of the 3D vessel centerlines (proposed in this paper) and that of the rigid registration method, the p-value was 0.0129, confirming the statistical significance of the method proposed in this paper.
The imaging modality, accuracy measurement method, and additional data used for registration differ between the studies. However, we acquired superior performance compared to that of the method proposed in the most recent paper. Furthermore, the average time to conduct the proposed method in this study is 2.137 s.
Conclusion
In this study, we propose a non-rigid registration method that enables rapid and accurate registration by using the information on blood vessel characteristics in temporal CTA images of the same patient. First, global registration is conducted through rigid registration between the 3D vessel centerlines. This procedure minimizes the error in the blood vessel location that occurs owing to the patient posture during imaging and imaging protocols and reduces the time required for non-rigid registration. After global registration, the corresponding points between the two 3D vessel centerlines are defined by point matching using a gradient-based searching method. At this point, the point matching error caused by errors in the feature extraction process is reduced using an outlier removal method, which considers the thickness and gradient of the blood vessels to enhance the registration efficacy. Non-rigid registration maintains the topology through hierarchical local transformations and improves the registration accuracy by reducing the error caused by local deformation of the blood vessels according to breathing and CAD. Here, an energy function defined based on vessel characteristics is used to induce a natural blood vessel transformation.
The non-rigid registration method proposed in this paper was able to provide accurate blood vessel information compared to the rigid registration method, by correcting the location and shape of blood vessels that are deformed due to heartbeat and respiration through hierarchical local transformation.
The experimental results show that the average registration error is 0.987 mm, and the standard deviation is 0.397 mm. The average registration error is improved by 0.479 mm compared to that before non-rigid registration. The average conduction time is 2.137 s, indicating that the proposed method enables rapid and accurate registration of the two 3D vessel centerlines.
As a limitation of this study, since blood vessel feature information of the 3D CTA image is extracted using the Han et al. [2] method, the feature information that can be used for registration is limited. In the future, we will collect more data and study a blood vessel feature extraction method using the deep learning, which is being actively studied recently, and link it with registration method. It can be expected to improve the accuracy and processing time by utilizing additional blood vessel features and removing unnecessary computation.
Acknowledgements
This study was a basic research project (No. 2020R1A2C1102727) supported by the National Research Foundation of Korea and financed by the Government (Ministry of Science and ICT) in 2020. In addition, this study was a basic research project (No. 2020R1A6A3A01099507) supported by the National Research Foundation of Korea and financed by the Government (Ministry of Education) in 2020.
Declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Heeryeol Jeong, Email: heeya8876@naver.com.
Taeyong Park, Email: taeyong@mach.hallym.or.kr.
Seungwoo Khang, Email: swkhang@naver.com.
Kyoyeong Koo, Email: koomaro@naver.com.
Juneseuk Shin, Email: jsshin@skku.edu.
Kyung Won Kim, Email: medimash@gmail.com.
Jeongjin Lee, Email: leejeongjin@ssu.ac.kr.
References
- 1.Murray CJ, Lopez AD. Alternative projections of mortality and disability by cause 1990–2020: global burden of disease study. Lancet. 1997;349(9064):1498–504. doi: 10.1016/S0140-6736(96)07492-2. [DOI] [PubMed] [Google Scholar]
- 2.Min JK, Shaw LJ, Berman DS. The present state of coronary computed tomography angiography: a process in evolution. J Am Coll Cardiol. 2010;55(10):957–65. doi: 10.1016/j.jacc.2009.08.087. [DOI] [PubMed] [Google Scholar]
- 3.Zhang W, Yuqian Z. Hierarchical registration of brain images based on B-splines and laplacian commutators. Optik. 2021;241:167022. doi: 10.1016/j.ijleo.2021.167022. [DOI] [Google Scholar]
- 4.Fontana L, Mastropietro A, Scalco E, Peruzzo D, Beretta E, Strazzer S, Arrigoni F, Rizzo G. Multi-steps registration protocol for multimodal MR images of hip skeletal muscles in a longitudinal study. Appl Sci. 2020;10(21):7823. doi: 10.3390/app10217823. [DOI] [Google Scholar]
- 5.Kuiper RJ, van Stralen M, Sakkers RJ, Bergmans RH, Zijlstra F, Viergever MA, Weinans H, Seevinck PR. CT to MR registration of complex deformations in the knee joint through dual quaternion interpolation of rigid transforms. Phys Med Biol. 2021;66(17):175024. doi: 10.1088/1361-6560/ac1769. [DOI] [PubMed] [Google Scholar]
- 6.Xu P, Chen C, Wang X, Li W, Sun J. ROI-based intraoperative MR-CT registration for image-guided multimode tumor ablation therapy in hepatic malignant tumors. IEEE Access. 2020;8:13613–9. doi: 10.1109/ACCESS.2020.2966518. [DOI] [Google Scholar]
- 7.Tang S, Wang Y. MR-guided liver cancer surgery by nonrigid registration. In: Proceedings of the international conference on medical image analysis and clinical application 2010 2010, pp. 113–7.
- 8.Ou Y, Sotiras A, Paragios N. Deformable registration via attribute matching and mutual-saliency weighting. Med Image Anal. 2011;15(4):622–39. doi: 10.1016/j.media.2010.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Luo J, Toews M, Machado I, Frisken S, Zhang M, Preiswerk F, Sedghi A, Ding H, Pieper S, Golland P, Sugiyama M, Golby A, Wells WM. A feature-driven active framework for ultrasound-based brain shift compensation. In: Proceedings of the international conference on medical image computing and computer-assisted intervention 2018, pp. 30–8.
- 10.Machado I, Toews M, Luo J, Unadkat P, Essayed W, George E, Wells WM. Non-rigid registration of 3D ultrasound for neurosurgery using automatic feature detection and matching. Int J Comput Assist Radiol Surg. 2018;13(10):1525–38. doi: 10.1007/s11548-018-1786-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhou H, Rivaz H. Registration of pre-and postresection ultrasound volumes with noncorresponding regions in neurosurgery. IEEE J Biomed Health Inform. 2016;20(5):1240–9. doi: 10.1109/JBHI.2016.2554122. [DOI] [PubMed] [Google Scholar]
- 12.Gerard IJ, Kersten-Oertel M, Petrecca K, Sirhan D, Hall JA, Collins DL. 2017 brain shift in neuronavigation of brain tumors: a review. Med Image Anal. 2017;35:403–20. doi: 10.1016/j.media.2016.08.007. [DOI] [PubMed] [Google Scholar]
- 13.Park TY, Lee J, Shin J, Kim KW, Kang HC. Non-rigid liver registration in liver computed tomography images using elastic method with global and local deformation. J Med Imaging Health Inform. 2021;11(3):810–6. doi: 10.1166/jmihi.2021.3355. [DOI] [Google Scholar]
- 14.Zhang DP, Risser L, Friman O, Metz C, Neefjes L, Mollet N, Niessen W, Rueckert D. Nonrigid registration and template matching for coronary motion modeling from 4D CTA. Lecture notes in computer science. 2010, vol 6204, pp. 210–21.
- 15.Hadjiiski L, Zhou C, Chan HP, Chughtai A, Agarwal P, Kuriakose J, Patel S, Wei J, Kazerooni E. Automated registration of coronary arterial trees from multiple phases in coronary CT angiography (cCTA). In: Proceedings of the SPIE medical imaging 2013, p. 8670:86703 M. [DOI] [PMC free article] [PubMed]
- 16.Luo Y, Feng J, Xu M, Zhou J, Min JK, Xiong G. Registration of coronary arteries in computed tomography angiography images using hidden markov model. In: Proceedings of the annual international conference of the ieee engineering in medicine and biology society. 2015, pp. 1993–6. [DOI] [PMC free article] [PubMed]
- 17.Zeng S, Feng J, An Y, Lu B, Lu J, Zhou J. Towards Accurate and Complete Registration of Coronary Arteries in CTA Images. In: Proceedings of the medical image computing and computer-assisted intervention 2018, pp. 419–27.
- 18.Cao Q, Broersen A, Kitslaar PH, Yuan M, Lelieveldt BP, Dijkstra J. Automatic coronary artery plaque thickness comparison between baseline and follow-up CCTA images. Med Phys. 2020;47(3):1083–93. doi: 10.1002/mp.13993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lim S, Park TY, Jeong H, Lee J. Accurate vascular structure extraction method in 2D X-ray angiogram. J King Comput. 2017;13(1):82–90. [Google Scholar]
- 20.Song Y, Lee J, Shin Y. B-spline based accurate nonrigid registration of ROI: application to chest CT. J King Comput. 2016;12(2):87–96. [Google Scholar]
- 21.Han D, Shim H, Jeon B, Jang Y, Hong Y, Jung S, Ha S, Chang HJ. Automatic coronary artery segmentation using active search for branches and seemingly disconnected vessel segments from coronary CT angiography. PLoS ONE. 2016;11(8):e0156837. doi: 10.1371/journal.pone.0156837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lee W. Technical aspect of coronary CT angiography: imaging tips and safety issues. J Korean Med Assoc. 2007;50(2):104–8. doi: 10.5124/jkma.2007.50.2.104. [DOI] [Google Scholar]
- 23.Park TY, Kang S, Koo G, Lee J. Fast and accurate rigid Registration Method of Cardiac vessels in 3D follow-up cardiac CTA images. J King Comput. 2017;13(4):59–67. [Google Scholar]
- 24.Rivest-Henault D, Sundar H, Cheriet M. Nonrigid 2D/3D registration of coronary artery models with live fluoroscopy for guidance of cardiac interventions. IEEE Trans Med Imaging. 2012;31(8):1557–72. doi: 10.1109/TMI.2012.2195009. [DOI] [PubMed] [Google Scholar]
- 25.Hong H, Lee J, Yim Y. Automatic lung nodule matching on sequential CT images. Comput Biol Med. 2008;38(5):623–34. doi: 10.1016/j.compbiomed.2008.02.010. [DOI] [PubMed] [Google Scholar]
- 26.Park TY. Convolutional neural network-based segmentation and non-rigid registration in multi-modality images for image-guided intervention. Ph. D. Thesis, Soong-Sil University, 2019.
- 27.Kaila G, Kitslaar P, Tu S, Penicka M, Dijkstra J, Lelieveldt B. Fusion of CTA and XA data using 3D centerline registration for plaque visualization during coronary intervention. In: Proceedings of the medical imaging 2016: image-guided procedures, robotic interventions, and modeling. 2016;9786, p. 978606.



