The IoT-enabled sustainable reverse supply chain for COVID-19 Pandemic Wastes (CPW)

Abstract

Supply chains have been impacted by the COVID-19 pandemic, which is the most recent worldwide disaster. After the world health organization recognized the latest phenomena as a pandemic, nations became incapacitated to provide the required medical supplies. In the current situation, the world seeks an essential solution for COVID-19 Pandemic Wastes (CPWs) by pushing the pandemic to a stable condition. In this study, the development of a supply chain network is contrived for CPWs utilizing optimization modeling tools. Also, an IoT platform is devised to enable the proposed model to retrieve real-time data from IoT devices and set them as the model’s inputs. Moreover, sustainability aspects are appended to the proposed IoT-enabled model considering its triplet pillars as objective functions. A real case of Puebla city and 15 experiments are used to validate the model. Furthermore, a combination of metaheuristic algorithms utilized to solve the model and also seven evaluation indicators endorse the selection of efficient solution approaches. The evaluation indicators are appointed as the inputs of statistical and multicriteria decision-making hybridization to prioritize the algorithms. The result of the Entropy Weights method and Combined Compromise Solution approach confirms that MOGWO has better performance for the medium-sizes, case study and an overall view. Also, NSHHO outclasses the small-size and large-size experiments.

1. Introduction

Global concerns regarding environmental issues have increased in recent decades, and organizations have sought to supplement environmental and greening ideas with Supply Chain (SC) practices (Cheraghalipour et al., 2017). However, organizations must detect the negative impacts of current SCs, and reshape their processes in which handling environmental aspects, economic progress, and social upliftment are considered, and it also helps to adjust the efficiency of the businesses (Hashemi-Amiri et al., 2022). Generally, SC can be grouped differently based on the flow of products throughout the system; however, the main categories are identified as forward, reverse, and closed-loop SCs (Hajiaghaei-Keshteli et al., 2011, Golmohamadi et al., 2017). Compared to forward SC, in which the products move from supplier or producers to end customers, reverse supply chain (RSC) encompasses reassigning used goods from consumers to separation centers, treatment centers, recyclers, and remanufacturers (Matsui, 2022).

Generally, the collection process in the RSC includes receiving used products and goods from different customers, examining these items for residual benefit, and shipping gathered products to the recycling unit. Goods with a terminated shelf life that are not economically repairable for consumers are the fitted raw material for RSC that is valuable to be recycled and reused. After COVID-19 pneumonia spread, the world encountered enormous pressure to obtain medical, personal protective equipment (PPE), and sanitizing equipment (Mosallanezhad et al., 2021a). According to Fig. 1, it is estimated that discarded masks worldwide might be more than three billion pieces. Predictably, this drastic change is a consequence of the COVID-19 outbreak, which needs significant consideration for this item’s reverse network.

Fig. 1.

The estimated daily amount of discarded masks (Benson et al., 2021).

Policies and guidelines made communities protect themselves by using PPEs, which has left an extreme load of waste (de Sousa, 2020). COVID-19 pandemic wastes (CPWs) refer to the wastes produced during a novel pandemic and are generated during a novel outbreak. As Fig. 2 shows, CPWs have nine main categories: syringes, surgical aprons, masks, shoe covers, blades and scalpels, medical/surgical gowns, latex gloves, sanitizer containers, and shields (Al-Omran et al., 2021).

Fig. 2.

COVID-19 Pandemic wastes.

Most CPWs are solid waste associated with medical activities such as examination, vaccination, and medication of individuals and even animals (Nzediegwu and Chang, 2020). Health professionals (nurses and physicians), patients, and healthy persons who touch infected patients are required to wear standard PPE. Currently, all people in most nations worldwide need to use facial protection like a mask or shield during all outside activities. Thus, inevitably disposable PPEs occupy the environment and bring about a tremendous amount of infectious CPW as an inevitable threat to our health and environment (Al-Omran et al., 2021, Hantoko et al., 2021).

Moreover, due to the unique, versatile characteristics of COVID-19, the healthcare system has recently been involved with a complicated situation caused by new variants such as Alpha, Beta, etc. Concerning the infectiousness of new variants and their effects on human beings’ well-being, generated CPWs by societies require more observation and consideration to be treated prior to the treatment process (Purnomo et al., 2021). Fig. 3 displays the discarded infectious wastes in the environment, which will become a massive disaster for our world.

Fig. 3.

Infectious wastes and environment.

The nations that make excessive CPW must assess their waste management policies and systems to suitably deal with these wastes during the pandemic. In particular, waste management has different processes like collection, separation, pre-treatment, delivery, transportation, disposal, and recycling (Valizadeh et al., 2021). These phases may provide another avenue to spread the coronavirus, predominantly by contact with infected areas and objects. Thereby, to hinder the domination of the contaminated virus and its new variants, provisions and protections should be provided by authorities, and safety guidelines, both for human beings and the environment, must be considered (Sangkham, 2020).

One of the most critical problems in organizations is a structure that enables them to achieve real-time SCs information. Also, this structure ensures organizations that the transmission of information throughout the SC systems is safe and secure (Kordi et al., 2022, Kargar et al., 2020a). Information technology (IT) excels in this situation and plays an outstanding role because it generates, stores, processes, and distributes information (Garrido-Hidalgo et al., 2020). IT has risen to the forefront of the SC and RSC field in recent decades, providing more substantial and adaptable decision-making processes with economic expenditures, as is empowered with the appearance of the Internet of Things (IoT). Connected devices are the main constituents of IoT platforms that transfer and receive information, leading to corresponding decisions based on perceived data (Wang and Wang, 2022). Undoubtedly, the amplification of quality and integration of Supply Chain Management depends on the ingenious use of IoT in SCs and RSCs (Garrido-Hidalgo et al., 2020).

In fact, due to RSC’s high-risk characteristics for CPWs, IoT guarantees prodigious development in the context of RSC, where convectional waste management policies are incompetent for collecting, separating, treatment, and recycling (Valizadeh et al., 2021). The adoption of IoT facilitates the exploitation of information to make processes of RSC for CPWs a more sustainable and quicker style, which results in the exclusion of unnecessary expenses in the network, controlling sustainable aspects in the network, and finally, managing the hazards caused by a novel coronavirus and its recent variants.

In this paper, we propose an RSC for CPWs empowered by IoT as a tool to collaborate with RSC design to control and overcome the potential harms of coronavirus spread and its effect on all parties within the network. Hence, this study expects to deal with several primary goals, including (I) improvement of RSC processes to the highest safety level in a way that minimizes the risk of collection, transportation, treatment, and recycling of CPWs, (II) managing the cost of RSC according to the authorities’ regulations and necessities, (III) taking into account the sustainability aspects for the network. Considering these three goals and healthcare challenges and guidelines enforced by WHO for the governments result in presenting a multi-objective IoT-enabled RSC network for CPWs. The merit of this study is that the proposed network embraces all centers exposed to generate CPWs and implements appropriate waste management using the information provided by IoT devices to centers and the calculation of the right amount of waste generated over the network. It is noteworthy that the waste amount of each center is estimated using customized formulation so that IoT devices ascertain the required information for healthcare centers by befittingly calibrating the proposed model. Moreover, a metaheuristic framework is proposed to enable the network as well as the IoT devices to pursue the computational complexity of the problem and quickly obtain the solutions. Last but not least, Puebla City, Mexico, is chosen as a real-life example alongside a set of instances for the validation of the model.

2. Literature review

There is substantial progress and development in the studies and research in RSC. This part of the study tries to recapitulate the contemporary and RSC-related studies during the pandemic to identify the research gap in recent literature.

2.1. Reverse supply chain

One of the research fields that has drawn much attention in the past years is RSC. Many studies have focused on RSC with a wide range of variety in assumption and problem formulation. Furthermore, numerous studies specifically focus on the RSC and its different aspects, such as Hrouga et al. (2022), and Doan et al. (2019).

Several research perspectives and methodologies have been conducted in the field of RSC. Hosseini-Motlagh et al. (2022) investigated a novel saving-cost sharing contract for a sustainable pharmaceutical RSC network that fortifies the supply chain in profitmaking under competition conditions. Shetty et al. (2022) modeled an RSC network to collect plastic wastes from end-consumers and reinject the recycled products into the network for future applications. The proposed network manages profitability, emission reduction, and new product usage. Integrating technological and economic policies such as hard and soft path technologies as well as subsidizing considerations, Xu et al. (2022) conducted a study on the RSC network for municipal solid wastes. They followed three goals controlling costs, emissions, and employment. An optimized timing model was proposed by Matsui (2022) for dual-channel RSC. A supply chain was selected as the real case to corroborate the practicability of the model.

Furthermore, Rau et al. (2021) invoked a multi-echelon RSC network under demand uncertainty in which they assumed the network is multi-period and multi-products. So, to cope with this problem, they conducted postponement strategies. Moreover, Yılmaz et al. (2021), to investigate the ripple effect in an RSC, carried out stochastic mathematical modeling. Also, an $\alpha$-reliability approach and multiple scenarios were arranged to reinforce the model. A forward SC and RSC are conducted by Alizadeh et al. (2020) to examine the biological risk within the medical supply chain network and modify it by the Bounded De Novo programming method. In this model, the authors tried to find the optimal location for the warehouses, sterilization centers, and collection centers while dealing with the biological risks in clinics and sterilization centers.

One of the critical issues in the globe’s current situation is to keep the lead–acid battery RSC under control. For this purpose, Tosarkani and Amin (2019) designed a fuzzy and stochastic RSC to optimize the profit and environmental compliance in the network for all parties. This multi-objective model, which considered the environmental aspects, was implemented in Canada. Analogously, Jin et al. (2019) developed an RSC network to optimize the model’s profit and environmental benefits. This study tried to monitor the locations and trade-offs of services and transportation at all points in the network. They formed a methodological procedure using the exact technique to cope with a case in California, the United States. A two-layer RSC was designed by Guo et al. (2018), which adopted a differential game model concerning publicity activities. Also, the model considered collection strategies to find optimal recycling channels. Finally, a stochastic optimization problem was discussed by Heydari et al. (2018) to obtain the optimal paid reward under two specific cases: decentralized and centralized.

2.2. Reverse supply chain for pandemics

As a step toward controlling COVID-19 phenomena, scholars and practitioners started to conduct studies in different fields, especially SCM (Hosseini et al., 2021, Alizadeh et al., 2022). After the rapid proliferation of CPWs, RSC as one of SCM arms and an important and necessary problem during the pandemic attracted much attention.

A metaheuristic-oriented solution approach was implemented by Tirkolaee et al. (2022) to solve the mask face supply chain problem taking into account sustainable aspects as well as RSC activities, specifically recycling and reusing. They attempted to monitor the economic, social, and environmental aspects of a sustainable network by approaching the lowest amount of cost, pollution, and risk. Shadkam (2022) carried out a reverse logistics (RL) model to optimize the network’s related costs and increase customer satisfaction. The developed MILP concentrated on vaccination waste management more than other medical wastes. Luo and Liao (2022) conceptualized RSC for the COVID-19 outbreak by designing a multi-component routing-location optimization model. Also, they firstly armed the distribution processes by mobile processing centers to improve the network’s agility.

An RSC network formulated by Balci et al. (2022) for medical waste during the pandemic in the metropolitan region of Istanbul, Turkey. In addition to finding the optimum level of cost for the network, the model helps the government with human resource and financial decision-making. In order to outline a setting with the optimal level of profit, environment impact, and social risk, Cao et al. (2022) implemented mathematical modeling for medical waste management, taking into account the diversity of wastes on multiple time windows under the pandemic situation. Santos et al. (2022) designed an RSC network for hazardous materials during COVID-19 to financially minimize the network’s processes. In order to fortify the traceability, security, and transparency of the supply chain network for the medical waste management processes through the pandemic, Ahmad et al. (2021) structured a decentralized blockchain-oriented framework.

Additionally, Govindan et al. (2021) evoked a MILP model for COVID-19 medical waste. This bi-objective model intends to optimize infected individuals’ total costs and risks. Moreover, they tried to identify the optimal solution for the proposed uncertain fuzzified model using the goal programming technique. Lotfi et al. (2021) recommended a two-echelon mathematical model for medical waste, which considered resiliency and sustainability. This model was presented in a robust stochastic setting. An optimization model was elicited by Mei et al. (2021) to optimize total cost, safety risk, and disposal time throughout the RSC network related to healthcare waste. A case was elaborated to investigate the applicability of the proposed nonlinear model. Since secure and safe transportation of COVID-19 medical waste performs a vital task in stopping the increase of infected persons, Eren and Rıfat Tuzkaya (2021) conducted a study to design an RSC for the COVID-19 pandemic’s medical waste. The model attempts to render the optimal vehicle routing considering safety and distance.

A fuzzy chance-constrained RSC model based on medical waste management was suggested by Tirkolaee et al. (2021), according to the feature of COVID-19. They contrived a model with sustainability constraints for their subject of interest and then solved the model using the goal programming technique. The revised multi-choice goal programming (RMCGP) is an approach to cope with the optimization models. In addition to all the preceding, Kargar et al. (2020b) presented a linear context to design an RSC for medical waste of COVID-19-involved locations. They used a case in Iran to justify the network and solved it using RMCG. In developed structures, sustainability factors also are regarded in picking treatment methods (see Table 1).

Table 1.

A review of state-of-the-art studies in the reverse supply chain.

Row	Author	Model configuration											Solution approach				Objective function(s)	IoT-based design	Waste type
		S	M	SC	MC	LP/ILP	MILP	NP	MINLP	SIO	BIO	MUO	EX	MT	HU	SM
1	Parker et al. (2010)	✔		✔					✔	✔			✔				C		AW
2	Faccio et al. (2011)	✔		✔					✔			✔	✔				C/T/D	✔	MW
3	Hiete et al. (2011)		✔		✔		✔			✔			✔				C		SW
4	Ghiani et al. (2012)	✔		✔			✔			✔			✔				NF		SW
5	Samanlioglu (2013)	✔			✔				✔			✔	✔				C/TR/R		HW
6	Zhang et al. (2014)		✔	✔			✔			✔			✔				C		SW
7	Bing et al. (2015)	✔			✔		✔				✔		✔				C/CE		SW
8	Zhao et al. (2016)	✔			✔				✔		✔		✔				C/R		HW
9	Xu et al. (2017)	✔			✔		✔				✔		✔				C/CE		SW
10	Shah et al. (2018)	✔		✔			✔				✔		✔				C/RV	✔	MW
11	Heydari et al. (2018)	✔			✔	✔				✔			✔				P		SW
12	Guo et al. (2018)		✔		✔			✔		✔			✔				P		EW
13	Jin et al. (2019)		✔	✔					✔		✔		✔				C/EI		CW
14	Tosarkani and Amin (2019)		✔	✔			✔			✔			✔				P		CW
15	Alizadeh et al. (2020)	✔			✔		✔				✔		✔				P/R		MW
16	Kargar et al. (2020b)		✔		✔		✔				✔		✔				C/TR		CPW
17	Mishra and Kumar Ray (2020)	✔		✔			✔			✔					✔		C	✔	SW
18	Yılmaz et al. (2021)	✔			✔		✔			✔			✔				C		SW
19	Rau et al. (2021)		✔		✔				✔	✔			✔				P		SW
20	Matsui (2022)	✔			✔	✔				✔			✔				P		EW
21	Akbarpour et al. (2021)	✔		✔			✔			✔				✔			D	✔	SMW
22	Tirkolaee et al. (2021)		✔	✔			✔					✔		✔			T/DL/R		CPW
23	Eren and Rıfat Tuzkaya (2021)	✔			✔		✔				✔		✔				D/SF		CPW
24	Mei et al. (2021)		✔		✔				✔			✔	✔				C/R/T		CPW
25	Lotfi et al. (2021)		✔	✔			✔			✔			✔				C		CPW
26	Govindan et al. (2021)		✔		✔		✔				✔		✔				C/R		CPW
27	Roy et al. (2022)	✔		✔			✔			✔				✔			C	✔	SW
28	Salehi-Amiri et al. (2022)	✔		✔			✔					✔		✔			C/P/EI	✔	MW
29	Xu et al. (2022)		✔		✔		✔					✔	✔				C/E/JO		MSW
30	Shetty et al. (2022)		✔		✔				✔	✔			✔				RW		SW
31	Hosseini-Motlagh et al. (2022)	✔			✔	✔				✔			✔				C		PhW
32	Tirkolaee et al. (2022)		✔		✔		✔					✔		✔			C/CE/R		CPW
33	Shadkam (2022)	✔		✔			✔			✔				✔			C		CPW
34	Luo and Liao (2022)		✔	✔			✔				✔		✔				C/R		CPW
35	Balci et al. (2022)	✔		✔			✔					✔	✔				C/E/P		CPW
36	Cao et al. (2022)	✔			✔				✔			✔	✔				P/E/R		CPW
37	Santos et al. (2022)	✔			✔		✔			✔			✔				C		CPW
38	This study		✔		✔		✔					✔		✔			C/TR/EI/CE/JO	✔	CPW

Model Configuration: Single-Period (S); Multi-Period (M); Single-Commodity (SC); Multi-Commodity (MC); Linear Programming (LP); Integer Linear Programming (ILP); Mixed Integer Linear Programming (MILP); Non-linear Programming (NP); Mixed Integer Non-Linear Programming (MINLP); Single Objective (SIO); Bi-Objective (BIO); MUO (Multi-Objective). Solution Approach: Exact (EX); Metaheuristic (MT); Heuristic (HU); Simulation (SM). Objective Function(s): Total Cost (C), Profit (P); Time (T); Distance (D); Transportation Risk (TR); Risk (R); Environmental Impacts (EI); CO₂ Emission (CE); Job Opportunities (JO), Recycled Waste (RW); Number of Facilities (NF); Recovery Value (RV); Safety (SF); Time Violation and Delay (DL). Waste Type: COVID-19 Pandemic Wastes (CPW); Medical Wastes (MW); Pharmaceutical Waste (PhW); Municipal Waste (MW); Solid Municipal Waste (SMW); Agricultural Waste (AW); Hazardous Wastes (HW); Electronic/Electrical Waste (EW); Chemical Waste (CW).

2.3. Application of IoT in reverse supply chain

Different studies, frameworks, schemes, and configurations have been carried out to reinforce the RSC networks and waste management processes. The IoT-based RSC networks and models strongly overlap with waste management studies. For this section, research and works on both fields, RSC and waste management, are reviewed. Also, some literature reviews have been presented on this research area: Akram et al. (2021), Anagnostopoulos et al. (2017), and de Souza Melaré et al. (2017).

Roy et al. (2022) carried out an IoT-based routing optimization problem for solid waste collection procedures based on financial objectives, including allocation, routing, and human resources costs. Waste bins are equipped with IoT devices responsible for detecting bins’ filling levels. Salehi-Amiri et al. (2022) sought out a smart city skeleton by embedding IoT kits throughout the waste collection system and tried to optimize the system using a mathematical modeling problem, both financially and environmentally. Akbarpour et al. (2021) presented a model for MSW of smart cities to obtain the lowest possible total cost for the model by setting up IoT devices. The main model of the study is divided into two sub-models, including the vehicle routing problem (VRP) and the allocation problem.

Alqahtani et al. (2020) combined IoT concepts and recurrent neural network structure to scrutinize the information regarding collection processes in cities so that they can easily analyze waste type and source as well as vehicle capacity. Mishra and Kumar Ray (2020) tailored a new routing modeling to financially control the waste collection framework equipped with IoT cloud-based devices. Moreover, the retrieved data from IoT devices were exploited to propose a novel cost function.

An IoT-empowered architecture designed by Shah et al. (2018) for a routing problem in a waste collection system. The proposed routing problem attempts to handle the network at the lowest transportation cost and highest recovery value. Anagnostopoulos et al. (2015) devised an IoT structure by embedding a sensor in bins all over the RSC network. This structure recalls data from sensors for a dynamic routing system and prioritizes the collection of bins. Among the early studies, Faccio et al. (2011) configured a framework including several IoT devices such as Global Positioning Systems (GPSs) and Radio Frequency Identifications (RFIDs) to find the best locations and routes in the waste collection system.

2.4. Research gap

Reviewing the recent works in previous sections endorses a dearth of comprehensive and inclusive RSC designs for CPWs. Most communities are entangled by the novel outbreak, and demand for PPEs, in addition to medical equipment, is escalated. As a result, the mentioned situation leads to an increase in CPWs, so the authorities in the healthcare system should thwart this pandemonium. Although many studies might be listed in RSC and waste management, limited works discuss CPWs’ supply chain design. Above and beyond all other considerations, the literature review revealed that the number of studies that developed a mathematical model for CPWs is a few with many shortcomings.

A multi-objective RSC network is presented in the current work, which simultaneously optimizes the network’s total cost, transportation risk, environmental impact, CO₂ emission, and job opportunity. Also, the IoT platform empowers the model to obtain the required information as the model’s inputs and is constrained by the sustainability aspects to provide a nature-friendly RSC network. The pivotal merits and contributions of current work are digested as follows:

• •A comprehensive network is devised to contain all CPW producers, including hospitals, temporary hospitals, clinics, laboratories, residential locations, vaccination centers, and environmental zones.
• •A well-formed IoT platform is considered for the network to use real-time information as parameters of a mathematical program.
• •The IoT platform is empowered by an all-embracing setting to help IoT-platform estimate the roughly accurate amount of CPWs generated by each producer.
• •The optimization model attempts to optimally track the total cost, transportation risk, environmental impact, CO₂ emission, and job opportunity at the same time.
• •The model facilitates moving toward sustainable settings.

3. Problem definition

The overall structure of this section takes the form of three parts. The proposed RSC for CPWs is established in the first part. Afterward, the configuration of IoT features for the proposed RSC is provided. Lastly, the mathematical modeling of RSC for CPWs is developed.

3.1. Reverse supply chain for COVID-19 pandemic wastes

The proposed RSC structure for CPWs has been presented in Fig. 4. There are several main constituents in this network. As the first layer of the network, CPW producers generate waste based on their activities. In order to keep the waste, they follow the regulations and guidelines established by the WHO. CPW producers are hospitals, temporary hospitals, clinics, laboratories, residential locations, and vaccination centers. These points involve infected patients, or they might produce waste because of health and safety procedures. On the other side, during the outbreak, our environment was filled with CPWs, thoughtlessly discarded. So, one of the primary responsibilities of governments and nature friends non-governmental organizations (NF-NGOs) is to protect the mother of nature from these destructive wastes. Therefore, as social responsibility in the RSC, we consider that naturally discarded wastes are moved to collection centers.

Fig. 4.

Schema of RSC for CPWs.

It is worth noting that the next level also needs to be informed about the type of waste, the risk of waste, the possibility of infection, and the policies that must be considered. The IoT devices communicate this information throughout the network. As previously declared, IoT supports the network in the highest health and safety situation.

Then, after collecting waste from the environment and CPW producers, the separation center is the next destination of CPWs. CPWs are grouped into two categories in this sector: recyclable and non-recyclable. Through IoT devices, all information related to CPWs is transmitted to the next level. They are moved to treatment centers to protect society and the environment from non-recyclable CPWs such as testing kits, facemasks, and gloves. In the centers, non-recyclable CPWs are disinfected and decontaminated using a medium-temperature microwave, high-temperature pyrolysis technique, and chemical disinfection (Ilyas et al., 2020). Thereafter, unrecyclable items are transported to determined locations for disposal or burial.

Recyclable pieces such as sanitizer containers, vaccine vials, or broken plastic/glass shields become the raw material for recycling centers. Like other segments of the RSC network, Recycling centers get informed by IoT devices. However, in comparison to separation or treatment centers and even transportation sections, recycling centers just need details on the types, infection risk, and amount of waste. Subsequently, information sharing using IoT is explained comprehensively.

3.2. IoT-enabled RSC

Here, we explain how IoT assists the RSC in monitoring and transferring essential information to each party within the network. In this regard, the IoT structure is first presented, and the data analysis method by IoT devices is presented.

3.2.1. IoT platform

The platform of IoT for CPWs-RSC is displayed in Fig. 5. The conceptualized platform has been inspired by Liu et al. (2021) and Rezaei et al. (2017), which entails four layers: the configuration, process, application, and users. The configuration layer is responsible for coordinating IoT devices’ sensing ability in RSC. Put differently, IoT devices in this platform are handheld devices such as smartphones or temperature data loggers, monitors, sensors, and closed-circuit television cameras (CCTVs). These devices are implemented in different locations, such as CPW producers’ locations, vehicles, collection centers, separation centers, and treatment centers, and connected via Wi-Fi, Bluetooth, and the internet. In this layer, data are gathered by IoT devices and sent to the process layer.

Fig. 5.

IoT platform for CPWs-RSC.

The process layer undertakes the data processing and converting data to required information by each sector. Obtaining information in this layer includes four main tasks: data clustering, data classification, data analysis, and data validation. After completing these steps, information is sent to the sector for their situation and needs. This information helps RSC control special conditions caused by the pandemic, thwart the proliferation of coronavirus infection, mitigate the accompanying effects of the virus in waste management activities, and monitor policies and regulations.

The application layer encompasses six services: CPWs analysis, waste management, pandemic management, risk analysis, infection prevention and control, and tracking and tracing of WHO’s policies. This layer has multiple application programming interfaces (APIs). They support and interact with users to make decisions according to the different conditions of the RSC network. For instance, CPWs analysis means that the waste producers should provide data in an API related to the kind of waste, coronavirus/its variants, and amount of waste. According to data provided by the waste producer, waste management and pandemic management devise their process according to data. For example, waste producers assert a load of CPW containing 100 kg PPEs of infected patients by delta variant. Thereby, the transportation workforce and other sectors know the guidelines to transport, separate, treat, recycle, and bury this waste. The users layer indicates the user groups: CPW producers, separation centers, collection centers, treatment centers, recycling centers, and transportation units. The users are responsible for providing exact data for each waste load and using processed data and information for further procedures. The detailed IoT architecture for the reverse supply chain network and processes within the network are available in Fig. 6.

Fig. 6.

The detailed IoT architecture for the reverse supply chain network and processes within the network.

3.2.2. IoT data analytics structure

As we previously stated, IoT devices collect data and convert them to helpful information in the network. Among all the information, two cases play critical roles in authorities’ decision-making and each segment of the RSC network: estimating the quantity of daily PPE and measuring the amount of medical waste respective to each CPW producer. In this regard, we explain how IoT devices compute this information.

Nzediegwu and Chang (2020) adapted Eq. (1). to approximate the amount of face masks in a day.

$$\tau =\rho \times Pop\times \alpha \times \mu$$ (1)

where:

$$\tau =\text{ used mask pieces on a daily basis}$$

$$\mathrm{Pop}=\text{Population}$$

$$\rho =\text{Percentage of population in urban}$$

$$\alpha =\text{Perfection rate of the mask}$$

$$\mu =\frac{\text{Average consumption of face masks per capita}}{10,000}\text{(per day)}$$

To customize Eq. (1) for the proposed model, we consider that $\tau$ is the used PPE pieces per ton, $\alpha$ is the acceptance rate of PPE, $\mu$ denotes the average used PPEs per capita in a day divided by 10,000, and $\omega$ is the weight of each piece of PPE. Consequently, we extend the previous equation to Eq. (2) as follows:

$$\tau =\rho \times Pop\times \alpha \times \mu \times \frac{\omega }{10,000}$$ (2)

To estimate the quantity of waste generated at each CPWs producer location, IoT devices use the proposed equation by Sangkham (2020) as Eq. (3):

$$\phi =\frac{\pi \times \beta }{1000}$$ (3)

where:

$\phi$$=$  CPW produced by patients (tons/day)

$\pi$ = Total number of infected persons by COVID-19 cases

$\beta$$=$  generation rate of CPWs.

It is worth noting that $\beta$ for hospitals and clinics is 3.95 kg/bed/day (Sangkham, 2020). However, the daily PPE weight per worker per each center is proposed by Al-Omran et al. (2021) calculated as Eq. (4):

$$e=\frac{l\times k}{1000}$$ (4)

where:

$\mathrm{e}$$=$  CPW produced by medical staff (tons/day)

$\mathrm{l}$ = Average PPE weight per medical staff (kg/day)

$\mathrm{k}$$=$  Total number of medical staff.

Also, Al-Omran et al. (2021) proposed an estimation method for waste weight in vaccination centers and laboratories. These equations are as follows:

$$o=\frac{w\times t}{1000}$$ (5)

where:

$\mathrm{o}$$=$  CPW produced in laboratories (tons/day)

$\mathrm{w}$$=$ Weight of COVID-19 test kit (kg)

$\mathrm{t}$$=$  Total number of performed COVID-19 tests per day in laboratories.

$$j=\frac{r\times f}{1000}$$ (6)

where:

$j$$=$  CPW produced in vaccination centers (tons/day)

$r$ = weight of syringe and vial (kg)

$f$$=$  Total number of vaccinated people per day in vaccination centers.

3.3. RSC problem formulation

The formulation for the RSC problem for CPWs is maintained in this section. In this model, five objective functions are formulated to optimize the model’s sustainability perspective (see Table 2).

Table 2.

Notation for the proposed RSC model.

Indices
$i\in I$	PPE waste producer
$j\in J$	Selected location in the environment
$k\in K$	Collection center
$l\in L$	Separation center
$m\in M$	Treatment center
$n\in N$	Recycling center
$o\in O$	Burial center
$q\in Q$	Market
$p\in P$	Waste type
$t\in T$	Period
Parameters
- Transportation Cost (TC)
$TC{I}_{il}$	TC between waste producer (i) and separation center (l)
$TC{J}_{jk}$	TC between location (j) and collection center (k)
$TC{K}_{kl}$	TC between collection center (k) and separation center (l)
$TC{L}_{lm}$	TC between PPE separation center (l) and treatment center (m)
$TC{T}_{ln}$	TC between PPE separation center (l) and recycling center (n)
$TC{M}_{mo}$	TC between PPE treatment center (m) and burial center (o)
$TC{N}_{nq}$	TC between PPE recycling center (n) and market (q)
- Operation Cost (OC)
$OC{K}_k$	Collection cost for collection center (k) if opens
$OC{L}_l$	Separation cost for treatment center (l) if opens
$OC{M}_m$	Treatment cost for treatment center (m) if opens
$OC{N}_n$	Recycle cost for recycling center (n) if opens
$OC{O}_o$	Burial cost for burial center (o) if opens
- Fixed Cost (FC)
$FC{K}_k$	FC for collection center (k) if opens
$FC{L}_l$	FC for separation center (l) if opens
$FC{M}_m$	FC for treatment center (m) if opens
$FC{N}_n$	FC for recycling center (n) if opens
$FC{O}_o$	FC for burial center (o) if opens
- Transportation Risk Possibility (RP) for waste type (p)
$RP{I}_{ilp}$	RP between waste producer (i) and separation center (l)
$RP{J}_{jkp}$	RP between location (j) and collection center (k)
$RP{K}_{klp}$	RP between collection center (k) and separation center (l)
$RP{L}_{lmp}$	RP between separation center (l) and treatment center (m)
$RP{T}_{lnp}$	RP between separation center (l) and recycling center (n)
$RP{M}_{mop}$	RP between treatment center (m) and burial center (o)
$RP{N}_{nqp}$	RP between recycling center (n) and market (q)
- The number of created Job Opportunities (JO) in period (t)
$JO{C}_{kt}$	By collection center (k)
$JO{S}_{lt}$	By separation center (l)
$JO{T}_{mt}$	By treatment center (m)
$JO{R}_{nt}$	By recycling center (n)
$JO{B}_{ot}$	By burial center (o)
- Environmental Impact per unit (EI) for waste type (p) in period (t)
$EI{I}_{ilpt}$	Transportation between waste producer (i) and separation center (l)
$EI{J}_{jkpt}$	Transportation between location (j) and collection center (k)
$EI{K}_{klpt}$	Transportation between collection center (k) and separation center (l)
$EI{L}_{lmpt}$	Transportation between separation center (l) and treatment center (m)
$EI{G}_{lnpt}$	Transportation between separation center (l) and recycling center (n)
$EI{M}_{mopt}$	Transportation between treatment center (m) and burial center (o)
$EI{N}_{nqpt}$	Transportation between recycling center (n) and market (q) per unit
$EI{C}_{kt}$	Establishment of collection center (k)
$EI{S}_{lt}$	Establishment of separation center (l)
$EI{T}_{mt}$	Establishment of treatment center (m)
$EI{R}_{nt}$	Establishment of recycling center (n)
$EI{B}_{ot}$	Establishment of burial center (o)
- CO2Emission per unit (CE) in period (t) for waste type (p)
$CE{I}_{ilpt}$	Transportation between waste producer (i) and separation center (l)
$CE{J}_{jkpt}$	Transportation between location (j) and collection center (k)
$CE{K}_{klpt}$	Transportation between collection center (k) and separation center (l)
$CE{L}_{lmpt}$	Transportation between separation center (l) and treatment center (m)
$CE{T}_{lnpt}$	Transportation between separation center (l) and recycling center (n)
$CE{M}_{mopt}$	Transportation between treatment center (m) and burial center (o)
$CE{N}_{nqpt}$	Transportation between recycling center (n) and market (q)
- Rate (R)
${\alpha }^{cc}$	The processing rate of collection centers
${\alpha }^{sp}$	The processing rate of separation centers
${\alpha }^{tr}$	The processing rate of treatment centers
${\alpha }^{rc}$	The processing rate of recycling centers
${\alpha }_t$	Recyclable amount of waste in period (t)
$1-{\alpha }_t$	Non-recyclable amount of waste in period (t)
Variables
- Transported Amount (TA) in period (t) for waste type (p)
$TA{I}_{ilpt}$	TA between waste producer (i) and separation center (l)
$TA{J}_{jkpt}$	TA between environment (j) and collection center (k)
$TA{K}_{klpt}$	TA between collection center (k) and separation center (l)
$TA{L}_{lmpt}$	TA between separation center (l) and treatment center (m)
$TA{T}_{lnpt}$	TA between separation center (l) and recycling center (n)
$TA{M}_{mopt}$	TA between treatment center (m) and burial center (o)
$TA{N}_{nqpt}$	TA between recycling center (n) and market (q)
- Processed Amount (PA) in period (t)
$PA{C}_{kt}$	The collected amount by collection center (k)
$PA{S}_{lt}$	The separated amount by separation center (l)
$PA{T}_{mt}$	The treated amount by treatment center (m)
$PA{R}_{nt}$	The recycled amount by recycling center (n)
- Implementation (IP) in period (t)
$IP{C}_{kt}$	If collection center (k) is implemented equals 1; otherwise, 0.
$IP{S}_{lt}$	If separation center (l) is implemented equals 1; otherwise, 0.
$IP{T}_{mt}$	If treatment center (m) is implemented equals 1; otherwise, 0.
$IP{R}_{nt}$	If recycling center (n) is implemented equals 1; otherwise, 0.
$IP{B}_{ot}$	If burial center (o) is implemented equals 1; otherwise, 0.

Governments, policy-makers, businesses, and industries are incredibly enthusiastic to process their supply chain at the lowest cost (Gupta et al., 2022, Tarei et al., 2022). Thereby, the leading objective function aims to optimize the entire RSC network economically. As Eq. (7) shows, its constituents are the transportation cost (Eq. (8)), operation cost (Eq. (9)), and fixed cost (Eq. (10)).

$$\mathit{Objective}\mathit{Function}1=\mathit{Transportation}Cost+\mathit{Operation}Cost$$$$+\mathit{Fixed}Cost$$ (7)

$$\begin{array}{c}\mathit{Transportation}Cost=\sum _i\sum _l\sum _p\sum _{t}TA{I}_{ilpt}\times TC{I}_{ilp}\hfill \\ +\sum _j\sum _k\sum _p\sum _{t}TA{J}_{jkpt}\times TC{J}_{jkp}+\hfill \\ \sum _k\sum _l\sum _p\sum _{t}TA{K}_{klpt}\times TC{K}_{klp}+\sum _l\sum _m\sum _p\sum _{t}TA{L}_{lmpt}\times TC{L}_{lmp}\hfill \\ +\sum _l\sum _n\sum _p\sum _{t}TA{T}_{lnpt}\times TC{T}_{lnp}+\hfill \\ \sum _m\sum _o\sum _p\sum _{t}TA{M}_{mopt}\times TC{M}_{mop}+\sum _n\sum _q\sum _p\sum _{t}TA{N}_{nqpt}\times TC{N}_{nqp}\hfill \end{array}$$ (8)

$$\begin{array}{c}\mathit{Operation}Cost=\sum _k\sum _{t}PA{C}_{kt}\times OC{K}_k+\sum _l\sum _{t}PA{S}_{lt}\times OC{L}_l\hfill \\ +\sum _m\sum _{t}PA{T}_{mt}\times OC{M}_m+\hfill \\ \sum _n\sum _{t}PA{R}_{nt}\times OC{N}_n\hfill \end{array}$$ (9)

$$\begin{array}{c}\mathit{Fixed}Cost=\sum _k\sum _{t}IP{C}_{kt}\times FC{K}_k+\sum _l\sum _{t}IP{S}_{lt}\times FC{L}_l\hfill \\ +\sum _m\sum _{t}IP{T}_{mt}\times FC{M}_m+\hfill \\ \sum _n\sum _{t}IP{R}_{nt}\times FC{N}_n+\sum _o\sum _{t}IP{B}_{ot}\times FC{O}_o\hfill \end{array}$$ (10)

Transportation of hazardous material (Hazmat) typically is accompanied by high-risk physical, social, and financial consequences for businesses (Ziaei and Jabbarzadeh, 2021). Undoubtedly, CPWs are highly potential to be labeled as Hazmats, and the transportation risk of CPWs certainly needs to be controlled within the network. Therefore, transportation risk in the proposed model stems from contagious CPWs, which minimizes using the second objective function. This objective function uses risk possibility parameters, which IoT devices evaluate. The risk possibility of each location is multiplied by the amount of CPWs transported from that location to obtain the risk of CPWs’ transportation.

Objective Function 2 $=$ Risk of Transportation

$$\begin{array}{c}Riskof\mathit{Transportation}=\sum _i\sum _l\sum _p\sum _{t}TA{I}_{ilpt}\times RP{I}_{ilp}\hfill \\ +\sum _j\sum _k\sum _p\sum _{t}TA{J}_{jkpt}\times RP{J}_{jkp}+\hfill \\ \sum _k\sum _l\sum _p\sum _{t}TA{K}_{klpt}\times RP{K}_{klp}+\sum _l\sum _m\sum _p\sum _{t}TA{L}_{lmpt}\times RP{L}_{lmp}\hfill \\ +\sum _l\sum _n\sum _p\sum _{t}TA{T}_{lnpt}\times RP{T}_{lnp}+\hfill \\ \sum _m\sum _o\sum _p\sum _{t}TA{M}_{mopt}\times RP{M}_{mop}+\sum _n\sum _q\sum _p\sum _{t}TA{N}_{nqpt}\times RP{N}_{nqp}\hfill \end{array}$$ (11)

The environmental impacts of Hazmats, such as CPWs and CO₂ emissions related to supply chain processes and logistic activities within the network, are nonnegligible (Mohammadi et al., 2017, Klemeš et al., 2021). Recently, a paucity of studies has highlighted the significance of awareness and severe action against ever-increasing environmental impacts and CO₂ emissions (Teimoury et al., 2017, Van Fan et al., 2021). Consequently, minimization of environmental impacts and CO₂ emissions is inevitable, even though the priorities are altered toward decreasing the casualties of the pandemic and enhancing the health security of societies.

The third objective function is to minimize the environmental impacts caused by transportation activities and each location’s implementation.

Objective Function 3 $=$ Transportation EI $+$ Implementation EI

$$\begin{array}{c}\mathit{Transportation}\mathit{EI}=\sum _{\mathit{i}}\sum _{\mathit{l}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAI}}_{\mathit{ilpt}}\times {\mathit{EII}}_{\mathit{ilpt}}\hfill \\ +\sum _{\mathit{j}}\sum _{\mathit{k}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAJ}}_{\mathit{jkpt}}\times {\mathit{EIJ}}_{\mathit{jkpt}}+\hfill \\ \sum _{\mathit{k}}\sum _{\mathit{l}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAK}}_{\mathit{klpt}}\times {\mathit{EIK}}_{\mathit{klpt}}+\sum _{\mathit{l}}\sum _{\mathit{m}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAL}}_{\mathit{lmpt}}\times {\mathit{EIL}}_{\mathit{lmpt}}\hfill \\ +\sum _{\mathit{l}}\sum _{\mathit{n}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAT}}_{\mathit{lnpt}}\times {\mathit{EIG}}_{\mathit{lnpt}}\hfill \\ +\sum _{\mathit{m}}\sum _{\mathit{o}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAM}}_{\mathit{mopt}}\times {\mathit{EIM}}_{\mathit{mopt}}+\sum _{\mathit{n}}\sum _{\mathit{q}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAN}}_{\mathit{nqpt}}\hfill \\ \times {\mathit{EIN}}_{\mathit{nqpt}}\hfill \end{array}$$ (12)

$$\begin{array}{c}\mathit{Implementation}\mathit{EI}=\sum _{\mathit{k}}\sum _{\mathit{t}}{\mathit{IPC}}_{\mathit{kt}}\times {\mathit{EIC}}_{\mathit{kt}}+\sum _{\mathit{l}}\sum _{\mathit{t}}{\mathit{IPS}}_{\mathit{lt}}\times {\mathit{EIS}}_{\mathit{lt}}\hfill \\ +\sum _{\mathit{m}}\sum _{\mathit{t}}{\mathit{IPT}}_{\mathit{mt}}\times {\mathit{EIT}}_{\mathit{mt}}+\hfill \\ \sum _{\mathit{n}}\sum _{\mathit{t}}{\mathit{IPR}}_{\mathit{nt}}\times {\mathit{EIR}}_{\mathit{nt}}+\sum _{\mathit{o}}\sum _{\mathit{t}}{\mathit{IPB}}_{\mathit{ot}}\times {\mathit{EIB}}_{\mathit{ot}}\hfill \end{array}$$ (13)

The following objective function is responsible for optimizing the CO${}_2$ emission caused by both transportation activities.

Objective Function 4 $=$ CO ₂ Emission

$$\begin{array}{c}{\mathbf{CO}}_{\mathbf{2}}\mathit{Emission}=\sum _{\mathit{i}}\sum _{\mathit{l}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAI}}_{\mathit{ilpt}}\times {\mathit{CEI}}_{\mathit{ilpt}}\hfill \\ +\sum _{\mathit{j}}\sum _{\mathit{k}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAJ}}_{\mathit{jkpt}}\times {\mathit{CEJ}}_{\mathit{jkpt}}+\hfill \\ \sum _{\mathit{k}}\sum _{\mathit{l}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAK}}_{\mathit{klpt}}\times {\mathit{CEK}}_{\mathit{klpt}}+\sum _{\mathit{l}}\sum _{\mathit{m}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAL}}_{\mathit{lmpt}}\times {\mathit{CEL}}_{\mathit{lmpt}}\hfill \\ +\sum _{\mathit{l}}\sum _{\mathit{n}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAT}}_{\mathit{lnpt}}\times {\mathit{CET}}_{\mathit{lnpt}}\hfill \\ +\sum _{\mathit{m}}\sum _{\mathit{o}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAM}}_{\mathit{mopt}}\times {\mathit{CEM}}_{\mathit{mopt}}+\sum _{\mathit{n}}\sum _{\mathit{q}}\sum _{\mathit{p}}\sum _{\mathit{t}}{\mathit{TAN}}_{\mathit{nqpt}}\hfill \\ \times {\mathit{CEN}}_{\mathit{nqpt}}\hfill \end{array}$$ (14)

Equitable distribution of job opportunities for the local population is counted as one of the principal corporation social responsibilities (CSRs) challenging every movement and business. Moreover, many individuals lost their jobs or are susceptible to being laid off during the pandemic. Therefore, it could be advantageous for stakeholders to concentrate on social aspects of their network by adjusting job employment (Vali-Siar and Roghanian, 2022, Pahlevan et al., 2021). Finally, the fifth objective function optimizes the job opportunities created by implementing each center throughout the network.

Objective Function 5$=$Job Opportunities

$$\begin{array}{c}\mathit{Job}\mathit{Opportunities}=\sum _{\mathit{k}}\sum _{\mathit{t}}{\mathit{IPC}}_{\mathit{kt}}\times {\mathit{JOC}}_{\mathit{kt}}+\sum _{\mathit{l}}\sum _{\mathit{t}}{\mathit{IPS}}_{\mathit{lt}}\times {\mathit{JOS}}_{\mathit{lt}}\hfill \\ +\sum _{\mathit{m}}\sum _{\mathit{t}}{\mathit{IPT}}_{\mathit{mt}}\times {\mathit{JOT}}_{\mathit{mt}}\hfill \\ +\sum _{\mathit{n}}\sum _{\mathit{t}}{\mathit{IPR}}_{\mathit{nt}}\times {\mathit{JOR}}_{\mathit{nt}}+\sum _{\mathit{o}}\sum _{\mathit{t}}{\mathit{IPB}}_{\mathit{ot}}\times {\mathit{JOB}}_{\mathit{ot}}\hfill \end{array}$$ (15)

Constraints:

$$\sum _l\sum _{p}TA{I}_{ilpt}=\sum _{p}W{A}_{ipt}\forall i,t$$ (16)

Previous studies are inadequate considering CPW producers; hence, current work covers all possible producers. Eq. (16) implies that the amount of waste shipped from the CPW producer to the separation center matches the estimated waste produced by the CPW producer (${\mathrm{WA}}_{\mathrm{ipt}}$), which is periodically estimated by IoT devices and used by the model.

$$\sum _k\sum _{p}TA{J}_{jkpt}=\sum _{p}W{V}_{jpt}\forall j,t$$ (17)

What is not yet considered in previous publications is CPWs discarded in the environment. Therefore, Eq. (17) asserts that the amount of waste shipped from the selected location in the environment to a collection center equals the estimated waste in that location.

$$\sum _{\mathrm{j}}\sum _{\mathrm{p}}{\mathrm{TAJ}}_{\text{jkpt}}\le {\text{CAPK}}_{\mathrm{k}}\times {\mathrm{IPC}}_{\mathrm{kt}}\forall \mathrm{k},\mathrm{t}$$ (18)

Eq. (18) declares that the amount of waste transported between the environment and the collection center should match the capacity of the implemented collection center.

$$\sum _{\mathrm{k}}{\mathrm{IPC}}_{\mathrm{kt}}\ge 1\forall \mathrm{t}$$ (19)

Eq. (19) ensures that at least one collection center must be implemented. Eq. (20) considers the processing amount of CPWs at the collection center.

$$\sum _{\mathrm{j}}\sum _{\mathrm{p}}{\mathrm{TAJ}}_{\text{jkpt}}\times {\alpha }^{cc}\le {\mathrm{PAC}}_{\mathrm{kt}}\forall \mathrm{k},\mathrm{t}$$ (20)

$$\sum _{\mathrm{l}}\sum _{\mathrm{p}}{\mathrm{TAK}}_{\text{klpt}}={\mathrm{PAC}}_{\mathrm{kt}}\forall \mathrm{k},\mathrm{t}$$ (21)

Eq. (21) implies that the amount of collected waste type moved between the collection and separation center should be equal to the amount of processed waste in the collection center.

$$\sum _{\mathrm{i}}\sum _{\mathrm{p}}{\mathrm{TAI}}_{\text{ilpt}}+\sum _{\mathrm{k}}\sum _{\mathrm{p}}{\mathrm{TAK}}_{\text{klpt}}\le {\text{CAPL}}_{\mathrm{l}}\times {\mathrm{IPS}}_{\mathrm{lt}}\forall \mathrm{l},\mathrm{t}$$ (22)

Eq. (22) specifies that the amount of waste shipped from the CPW producer to the separation center and the collected waste shipped between the collection and separation centers should be fitted to the capacity of implemented separation center.

$$\sum _{\mathrm{l}}{\mathrm{IPS}}_{\mathrm{lt}}\ge 1\forall \mathrm{t}$$ (23)

Eq. (23) ensures that at least one separation center must be implemented. Eq. (24) considers the processing amount of CPWs at separation centers.

$$(\sum _{\mathrm{i}}\sum _{\mathrm{p}}{\mathrm{TAI}}_{\text{ilpt}}+\sum _{\mathrm{k}}\sum _{\mathrm{p}}{\mathrm{TAK}}_{\text{klpt}})\times {\alpha }^{sp}\le {\mathrm{PAS}}_{\mathrm{lt}}\forall \mathrm{l},\mathrm{t}$$ (24)

$$\sum _{\mathrm{p}}\sum _{\mathrm{m}}{\mathrm{TAL}}_{\text{lmpt}}+\sum _{\mathrm{p}}\sum _{\mathrm{n}}{\mathrm{TAT}}_{\text{lnpt}}={\mathrm{PAS}}_{\mathrm{lt}}\forall \mathrm{l},\mathrm{t}$$ (25)

Eq. (25) implies that the waste moved between separation and treatment centers and recycling centers should be equal to the amount of processed waste in the separation center.

$$\sum _{\mathrm{p}}\sum _{\mathrm{m}}{\mathrm{TAL}}_{\text{lmpt}}={\alpha }_{\mathrm{t}}\times {\mathrm{PAS}}_{\mathrm{lt}}\forall \mathrm{l},\mathrm{t}$$ (26)

$$\sum _{\mathrm{p}}\sum _{\mathrm{n}}{\mathrm{TAT}}_{\text{lnpt}}=\left(1-{\alpha }_{\mathrm{t}}\right)\times {\mathrm{PAS}}_{\mathrm{lt}}\forall \mathrm{l},\mathrm{t}$$ (27)

Eqs. (26), (27) express the amount of waste moved between separation, treatment, and recycling centers.

$$\sum _{\mathrm{l}}\sum _{\mathrm{p}}{\mathrm{TAL}}_{\text{lmpt}}\le {\text{CAPM}}_{\mathrm{m}}\times {\mathrm{IPT}}_{\mathrm{mt}}\forall \mathrm{m},\mathrm{t}$$ (28)

Eq. (28) points out the amount of waste transported between separation and treatment centers and satisfies the capacity of the implemented treatment center.

$$\sum _{\mathrm{m}}{\mathrm{IPT}}_{\mathrm{mt}}\ge 1\forall \mathrm{t}$$ (29)

Eq. (29) ensures that at least one treatment center must be implemented in each period.

$$\sum _{\mathrm{l}}\sum _{\mathrm{p}}{\mathrm{TAT}}_{\text{lnpt}}\le {\text{CAPN}}_{\mathrm{n}}\times {\mathrm{IPR}}_{\mathrm{nt}}\forall \mathrm{n},\mathrm{t}$$ (30)

Eq. (30) points out the amount of waste moved between the separation and recycling center and meets the capacity of the implemented recycling center.

$$\sum _{\mathrm{n}}{\mathrm{IPR}}_{\mathrm{nt}}\ge 1\forall \mathrm{t}$$ (31)

Eq. (31) ensures that at least one recycling center must be implemented in each period. Eq. (32) considers the processing amount of CPWs at the collection center.

$$\sum _{\mathrm{p}}\sum _{\mathrm{m}}{\mathrm{TAL}}_{\text{lmpt}}\times {\alpha }^{tr}\le {\mathrm{PAT}}_{\mathrm{mt}}\forall \mathrm{m},\mathrm{t}$$ (32)

$$\sum _{\mathrm{o}}\sum _{\mathrm{p}}{\mathrm{TAM}}_{\text{mopt}}={\mathrm{PAT}}_{\mathrm{mt}}\forall \mathrm{m},\mathrm{t}$$ (33)

Eq. (33) organizes that the amount of waste type shipped from the treatment center to the burial location should be equal to the amount of processed waste in the treatment center. Eq. (34) considers the processing amount of CPWs at the collection center.

$$\sum _{\mathrm{p}}\sum _{\mathrm{n}}{\mathrm{TAT}}_{\text{lnpt}}\times {\alpha }^{rc}\le {\mathrm{PAR}}_{\mathrm{nt}}\forall \mathrm{n},\mathrm{t}$$ (34)

$$\sum _{\mathrm{q}}\sum _{\mathrm{p}}{\mathrm{TAN}}_{\text{nqpt}}={\mathrm{PAR}}_{\mathrm{nt}}\forall \mathrm{n},\mathrm{t}$$ (35)

Eq. (35) confirms that the amount of waste shipped from the recycling center to the market should be equal to the amount of processed waste in the recycling center.

$$\sum _{\mathrm{m}}\sum _{\mathrm{p}}{\mathrm{TAM}}_{\text{mopt}}\le {\text{CAPO}}_{\mathrm{o}}\times {\mathrm{IPB}}_{\mathrm{ot}}\forall \mathrm{o},\mathrm{t}$$ (36)

Eq. (36) points out the amount of waste shipped from the treatment center to the burial location and is equal to or less than the capacity of implemented burial location.

$$\sum _{\mathrm{n}}{\mathrm{IPB}}_{\mathrm{ot}}\ge 1\forall \mathrm{t}$$ (37)

Eq. (37) ensures that at least one burial location must be considered in each period.

$$\sum _{\mathrm{n}}\sum _{\mathrm{p}}{\mathrm{TAN}}_{\text{nqpt}}={\mathrm{DM}}_{\mathrm{qt}}\forall \mathrm{q},\mathrm{t}$$ (38)

Eq. (38) points out that recycled waste is transported between the recycling center and the market and is equal to the demand of the market. Eq. (39) specifies the transportation amount of CPWs and the processed amount of CPWs in the network. Also, binary variables for the assignment of facilities are established by Eq. (40)

$$\begin{array}{c}TA{I}_{ilpt},TA{J}_{jkpt},TA{K}_{klpt},TA{L}_{lmpt},TA{T}_{lnpt},\hfill \\ TA{M}_{mopt},TA{N}_{nqpt},\hfill \\ PA{C}_{kt},PA{S}_{lt},PA{T}_{mt},PA{R}_{nt}\ge 0\hfill \end{array}\forall \mathrm{i},\mathrm{j},\mathrm{k},\mathrm{l},\mathrm{m},\mathrm{n},\mathrm{o},\mathrm{q},\mathrm{p},\mathrm{t}$$ (39)

$$IP{C}_{kt},IP{S}_{lt},IP{T}_{mt},IP{R}_{nt},IP{B}_{ot}\in \{0,1\}\forall \mathrm{k},\mathrm{l},\mathrm{m},\mathrm{n},\mathrm{o},\mathrm{q},\mathrm{t}$$ (40)

4. Solution approach

This section discusses solution approaches for the proposed model, which is classified into two parts. The first part introduces the encoding and decoding strategies to form feasible chromosomes. In the second part, metaheuristic algorithms are presented. These four well-known optimizers are classic, modern, and hybrid algorithms.

4.1. Encoding and decoding

Various methods can be found in the literature for encoding and decoding purposes, among which random key (RK), as the most competent method, is selected for this study. The RK suggests that the chromosome should be made in a matrix with values specified by uniform random distribution between 0 and 1. Then, the matrix values are sorted in descending order so that the largest value possesses the highest prioritization. This matrix is recognized as the priority-based matrix. To make it clear, an example is provided (Bahadori-Chinibelagh et al., 2022, Liao et al., 2020).

Suppose an RSC network for CPWs with 2, 1, 2, 3, 2, 2, 1, and 2 waste producers, selected location in the environment, collection center, separation center, treatment center, recycling center, burial center, and market, respectively. Fig. 7 displays the RK method’s mentioned procedures and priority-based chromosome matrix for the proposed RSC model. Each column of chromosomes in Fig. 7 has a value between 0 and 1 and represents a facility within the network. These values are arranged in descending order to support the flow of material between the different segments of the model. It is worthwhile to add that flows in the RSC network are forward.

Fig. 7.

The proposed chromosome for the RSC model.

4.2. Metaheuristics

In optimization problems, different features significantly influence the problem’s computational complexity. The RSC problems are grouped as NP-hard optimization problems (Khezerlou et al., 2021, Boonmee et al., 2018, Farrokhi-Asl et al., 2017, Ghezavati and Beigi, 2016). In other words, the exact method is incompetent to solve the NP-hard models in logical execution time, and it encounters high computational complexity and exponential time consumption, particularly in large-size problems. This condition is entitled to NP-hardness in optimization terms. Therefore, scholars engage metaheuristic algorithms in the solution approach to overcome the NP-harness of the problems. Consequently, six multi-objective metaheuristic algorithms are the proposed tools for the RSC model. Here, the metaheuristic algorithms are expounded in a brief manner.

4.2.1. Multi-objective Keshtel Algorithm

Keshtel Algorithm (KA) is attributed as one of the modern, efficient metaheuristics founded on the population base structure. It was firstly proposed by Hajiaghaei-Keshteli and Aminnayeri (2014) and applied in many fields (Chouhan et al., 2021). The concept of MOKA is almost similar to conventional KA (Mosallanezhad et al., 2021a). In the first step of MOKA, an initial population, namely Keshtels, is selected. Based on on-dominating sorting and crowding distance, the primary Keshtels are sorted. Then, they are grouped into three subpopulations: (I) ${\mathit{N}}_{\mathit{1}}$: the lucky Keshtels; (II) ${\mathit{N}}_{\mathit{2}}$: the Keshtels that are exposed to movement operator; and (III) ${\mathit{N}}_{\mathit{3}}$: the worst Keshtels that are replaced by new Keshtels. Due to the fact that this algorithm has both intensification and diversification phases, two operators named swirling and movement are responsible for each of those phases in the algorithm. This algorithm has both intensification, and diversification phases, so two operators named swirling and movement are responsible for each of those phases. Chouhan et al. (2022) is a proper reference for more information and pseudo-code.

4.2.2. Multi-objective social engineering optimizer

The SEO was primarily developed by Fathollahi-Fard et al. (2018) and applied in numerous studies involving supply chain network design. It is a point-based optimizer with considerable processing time and incredible potential to find the feasible global point. The SEO gets the two initial solutions as capabilities of human beings and labels them attacker and defender. Therefore, the attacker evaluates the defender’s capabilities to discriminate against the dominant capability. To study more about the MOSEO, refer to (Mousavi et al., 2021).

4.2.3. Non-dominated sorting genetic algorithm II

The first development of the genetic algorithm (GA) was proposed by Holland (1975), and it was employed in many problems in different fields. Due to the nature of the real case problem, researchers sought a multi-objective alternative for GA. Meanwhile, numerous versions of multi-objective GA were developed, among which the most recognized algorithm happened to be NSGA-II. It is famous due to its non-dominating sorting and crowding distance estimation procedure. The non-dominating sorting technique enables the algorithms to classify the feasible solution into multiple Pareto frontiers. Then, nominated feasible solutions for the next generation are obtained using crowding distance. Also, the NSGA-II preserved the natural operators of traditional GA, i.e., crossover and mutation. To obtain more information, refer to Mousavi et al. (2021).

4.2.4. Multi-Objective Grey Wolf Optimizer (MOGWO)

This recently-devised metaheuristic algorithm possesses a population-based structure and imitates the hierarchical hunting of grey wolves. The algorithm considers an initial pack of grey wolves, selects the top three wolves, and nominates them as the pack’s leaders. The conventional GWO algorithm was primarily propounded by Mirjalili et al. (2014), and lately, the multi-objective GWO was established by Mirjalili et al. (2016). Interested readers may check the mentioned studies to follow the details of the algorithm.

4.2.5. Non-Dominated Harris Hawks Optimizer (NSHHO)

The hunting fashion of Harris hawk birds became an inspiration for Heidari et al. (2019) to implement Harris Hawks Optimization (HHO). In the global search phase, the birds seeking for prey at various places, and in each iteration, the birds’ positions are updated. On the other hand, the birds perform attacks in the exploitation phase in order to embezzle and slow down the prey. Recently, Jangir et al. (2021) developed the non-sorted multi-objective HHO (NSHHO), which inclines toward the elitism and non-dominated sorting process.

4.2.6. Hybrid multi-objective Keshtel algorithm and social engineering optimizer

The proposed MOKASEO, a hybrid form of MOKA and MOSEO, is proposed in this study. As previously mentioned, the MOKA is a population-based algorithm with three subpopulations, including $N_1,N_2$ and, $N_3$. It also possesses both diversification and intensification phases. The former phase is performed to help the algorithm in the local optimization process while a point-based metaheuristic can reinforce it. Here, we propose the SEO optimization approach to help MOKA in the diversification phase. The pseudo-code for the MOKASEO is available in Fig. 8.

Fig. 8.

The Pseudo-code of the MOKASEO.

5. Evaluation outline

We provide an evaluation outline to enlighten the practicability of the proposed model and solution methodology in real-world and experimental situations by presenting a case of Puebla city, Mexico, and 15 practical experiments. In the following subsections, the details of the evaluation outline are explained.

5.1. Case study and practical experiments

During the ongoing pandemic era, Mexico is recognized as one of the nations struggling with an enormous number of infected populations, casualties, and fatalities (Piña-García and Espinoza, 2022). The Mexican government could control the shocking situation of the current pandemic through numerous strategies, such as hygiene and healthcare regulations or extensive vaccination coverage in all states (Peci et al., 2022). Undoubtedly, controlling CPWs by federal and local governments is listed as one of the high-priority actions in the current position. Puebla city is positioned in the southern part of Mexico and belongs to Puebla State (Fig. 9). We consider Puebla city as the real case for the study to examine our network in reality.

Fig. 9.

Map of Puebla state.

From the beginning moments, the Secretary of Health of the State of Puebla1 endeavored to handle the situation. It appointed hospitals, medical centers, and outpatient departments to admit infected individuals and hospitalize emergency cases. Furthermore, they repetitively advertised a weekly scheduling scheme for vaccination against COVID-19 in predefined zones throughout the Puebla state. Also, certified laboratories by the Secretary of Health of the State of Puebla were responsible for COVID diagnosis tests. Therefore, these healthcare and medical centers are recognized as the main CPW producers, as well as a number of nominated residential locations. The required data of CPW producers are obtained from the official portal of the Secretary of Health of the State of Puebla.2 Also, selected residential locations are determined based on municipality classification and the existing accessibility of waste collection in related areas. Fig. 10 reveals the location of CPWs and potential points for the centers within the proposed RSC network. It is worthwhile to mention that the planning duration for the case study is six months, and 18 types of CPW are considered, among which discarded or used masks, gloves, sanitizer containers, and shields are the most significant.

Fig. 10.

Position of CPW producers in Puebla city.

In addition to a real case in Puebla city, 15 practical experiments are designed to comprehensively evaluate the performance of algorithms. The practical experiments are partitioned into three groups: small, medium, and large. These experiments aim to explore the computational performance and solution quality of metaheuristic algorithms under different sizes of problems. The details of practical experiments are stated in Table 3. Moreover, Table 4 contains the range of parameters for the RSC network.

Table 3.

Problem dimensions for the case study and practical experiments.

Problem	Small					Medium					Large					Puebla City
	${\mathrm{S}}_1$	${\mathrm{S}}_2$	${\mathrm{S}}_3$	${\mathrm{S}}_4$	${\mathrm{S}}_5$	${\mathrm{M}}_1$	${\mathrm{M}}_2$	${\mathrm{M}}_3$	${\mathrm{M}}_4$	${\mathrm{M}}_5$	${\mathrm{L}}_1$	${\mathrm{L}}_2$	${\mathrm{L}}_3$	${\mathrm{L}}_4$	${\mathrm{L}}_5$
i	10	15	20	25	30	40	45	55	60	70	90	100	110	120	150	44
j	2	3	3	3	3	15	20	25	35	40	50	55	60	70	80	5
k	2	3	5	5	5	8	8	9	9	10	20	25	30	35	40	2
l	3	4	4	5	5	6	7	8	9	10	20	25	30	35	40	3
m	4	5	5	5	6	6	7	8	9	10	20	25	30	35	40	2
n	2	4	5	5	6	6	7	8	9	10	20	25	30	35	40	2
o	4	5	6	6	7	8	10	10	15	20	30	35	40	45	50	5
q	4	5	5	5	6	6	7	8	9	10	20	25	30	35	40	2
p	6	6	6	9	9	9	12	12	12	12	15	15	18	18	18	18
t	3	3	3	4	4	4	6	6	6	6	12	12	12	12	12	6

Table 4.

Values for the parameters of the network.

Parameter	Distribution	Range		Parameter	Distribution	Range
		Lower bound	Upper bound			Lower bound	Upper bound
$TC{I}_{il}$	Uniform	100	200	$FC{L}_l$	Uniform	10	20
$TC{J}_{jk}$	Uniform	20	50	$FC{M}_m$	Uniform	8	15
$TC{K}_{kl}$	Uniform	20	30	$FC{N}_n$	Uniform	8	20
$TC{L}_{lm}$	Uniform	75	105	$FC{O}_o$	Uniform	10	14
$TC{T}_{ln}$	Uniform	30	70	$D{M}_{qt}$	Uniform	10	15
$TC{M}_{mo}$	Uniform	5	15	${\alpha }_t$	Uniform	0.3	0.5
$TC{N}_{nq}$	Uniform	50	75	${\alpha }^{cc}$	Uniform	0.90	0.95
$FC{K}_k$	Uniform	10	20	${\alpha }^{sp}$	Uniform	0.90	0.95
$OC{K}_k$	Uniform	100	800	${\alpha }^{tr}$	Uniform	0.90	0.95
$OC{L}_l$	Uniform	500	2500	${\alpha }^{rc}$	Uniform	0.90	0.95
$OC{M}_m$	Uniform	650	1150	$CAP{M}_m$	Uniform	500	600
$OC{N}_n$	Uniform	1100	1200	$CAP{K}_k$	Uniform	20	30
$OC{O}_o$	Uniform	400	850	$CAP{L}_l$	Uniform	200	360
$W{A}_{ipt}$	Uniform	0.1	2	$CAP{N}_n$	Uniform	200	300
$W{V}_{jpt}$	Uniform	0.1	0.2	$CAP{O}_o$	Uniform	100	250
RP	Uniform	0.05	0.4	$JO{C}_{kt}$	–	{5, 6, …, 10}
EIT	Uniform	0.2	10	$JO{S}_{lt}$	–	{7, 8, …, 15}
EIIM	Uniform	0.1	2	$JO{T}_{mt}$	–	{3, 4, …, 10}
CE	–	{1,2, … , 10}		$JO{R}_{nt}$	–	{10, 11, …, 20}
				$JO{B}_{ot}$	–	{1, 2, …, 10}

RP (All parameters related to transportation risk possibility); EIT (All parameters related to the environmental impact of transportation); EIIM (All parameters related to the establishment of facilities); CE (All parameters related to CO₂ emission).

5.1.1. Evaluation indicators

The results of multi-objective metaheuristic algorithms are Pareto solutions which can be analyzed in two ways to demonstrate the performance of algorithms and their solutions qualities: quantifying them as single values using different techniques such as weighted sum values or evaluating by well-known indicators. Here, we pursue the latter to examine the Pareto solutions and the performance of algorithms. Although numerous studies have recommended evaluation indicators for multi-objective metaheuristic algorithms, the most applicable indicators for supply chain network design and RSC problems are deployed for this study. The indicators are as follows (Gholian-Jouybari et al., 2023, Yacoubi et al., 2022):

• 1.
  Spread of non-dominated solutions (SNS): It is calculated using Eq. (41), which is a tool to quantify the spread of the solution. SNS is a profit-type indicator, so the higher value is merely the superior optimizer.

  $$\mathrm{SNS}=\sqrt{\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left(\overline{\gamma }-{\gamma }_{\mathrm{i}}\right)}^2}{\mathrm{n}-1}}$$ (41)

  where ${\gamma }_{\mathrm{i}}=\Vert {\mathrm{f}}_{\mathrm{i}}-{\mathrm{f}}_{\mathrm{\ast }}\Vert$, $\overline{\gamma }=\frac{{\mathrm{f}}_{\mathrm{i}}}{\mathrm{n}}$, ${\mathrm{f}}_{\mathrm{\ast }}=\{min\left({\mathrm{f}}_1\right),\dots ,min\left({\mathrm{f}}_{\mathrm{k}}\right)\}$.
• 2.
  Mean ideal distance (MID): It concentrates on the distance of solutions from the ideal reference point. Thus, MID is marked as a cost metric in which the lower value is preferable. Considering m and n represent the number of objective functions and optimal solutions, the formulation of MID is as follows:

  $$\mathrm{MID}=\sum _{\mathrm{i}=1}^{\mathrm{n}}\sqrt{\sum _{\mathrm{j}=1}^{\mathrm{m}}{\left(\raisebox{1ex}{${\mathrm{f}}_{\mathrm{ji}}-{\mathrm{f}}_{\mathrm{j}}^{\mathrm{\ast }}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{f}}_{\mathrm{j}}^{\text{max*}}-{\mathrm{f}}_{\mathrm{j}}^{\text{min*}}$}\right.\right)}^2}/\mathrm{n}$$ (42)

  where $f_j^{\ast }$, $f_j^{max\ast }$ and $f_j^{min\ast }$ stand for the best, the maximum, and the minimum case for each algorithm.
• 3.
  Maximum Spread (MS): It aims to measure the dispersion of Pareto optimal solutions, and is a profit-type indicator. Suppose m is the number of objective functions, and $f_j^{max\ast }$ and $f_j^{min\ast }$ denote the maximum and the minimum case for each algorithm. MS is computed as follows:

  $$MS=\sqrt{\sum _{j=1}^m{\left(f_j^{max\ast }-f_j^{min\ast }\right)}^2}$$ (43)
• 4.
  Hyper-Volume (HV): This profit-type indicator aims to scalarize the portion of objective space occupied by the Pareto front solutions. Given RF is a set of reference solutions, PF is the set of Pareto frontier, and ${\mathcal{L}}_m$ then HV is computed in the following manner:

  $$HV={\mathcal{L}}_m\left(\bigcup _{\gamma \in PF}\left[\gamma ,RF\right]\right)$$ (44)

  The m-dimensional Lebesgue measure is denoted by ${\mathcal{L}}_m$.
• 5.
  Generational Distance (GD): The distance between each solution of the Pareto frontier and nominated reference solutions is obtained by GD, a cost-type indicator. The reference solutions can be either the true Pareto front or non-dominated solutions that are superior compared to other non-dominated solutions of the algorithm. This indicator is calculated as follows:

  $$GD=\frac{1}{n}\left(\sum _{i=1}^n\sqrt{\sum _{j=1}^m{\left(f_{i,j}^{PF}-f_j^{RF}\right)}^2}\right)$$ (45)

  which $f_{i,j}^{PF}$ is the $j$th objective function value of $i$th solution in the Pareto front (PF) and $f_j^{RF}$ is the $j$th objective function value in the reference solution (RF). Also, m and n denote the number of objective functions and solutions in the Pareto front, respectively.
• 6.Inverted Generational Distance (IGD): This cost-type indicator is an extended formulation of GD in which the difference between IGD and GD is the reference solution. To be more specific, $f_j^{RF}$ is considered the nearest solution to $f_{i,j}^{PF}$ in IGD calculations.
• 7.CPU Time (CT): The computational time of an algorithm is distinguished as CT, and a lower value of CT is satisfactory.

5.1.2. Parameters tuning

Typically, each metaheuristic algorithm contains multiple parameters that directly influence the quality of the solution. Each algorithm renders better solutions for an optimization problem under a specific level of parameters (Mosallanezhad et al., 2021b). So, tuning parameters defines as finding the optimal level for an algorithm’s parameters so that it shows sound performance compared to other levels (Sadeghi-Moghaddam et al., 2019). Parameter tuning prevents time-taking execution of algorithms and improves the reliability of obtained solutions (Babaveisi et al., 2018). Among existing design of experiment (DOE) techniques, Taguchi has recorded a solid background in tuning parameters of metaheuristic algorithms, and it has extensive application in this field of research (Arjomandi et al., 2022, Colombaroni et al., 2020). The response value (Y) for the Taguchi technique is defined as Eq. (46) to preserve the convergence and diversity of Pareto solutions:

$$MCOV=\frac{MID}{MS}$$ (46)

Then, the ${\mathit{L}}_{\mathit{9}}$ orthogonal array is formed for MOGWO, and the rest of the algorithm is adjusted by ${\mathit{L}}_{\mathit{27}}$ orthogonal arrays. S/N ratio as Eq. (47) is used for experiment ${\mathit{M}}_{\mathit{3}}$ to find the optimal level for the parameters (Gholian Jouybari et al., 2016):

$$\frac{S}{N}=-10\times log\left(\sum \frac{Y^2}{n}\right)$$ (47)

The results of the Taguchi technique and parameter tuning process are available in Table 5.

Table 5.

The optimal level of algorithms.

Algorithm	Parameter
NSGA-II	Maximum Iterations (200a, 300, 400); Population Number (100, 200a, 300); Crossover Population (0.75, 0.80a, 0.85); Mutation Population (0.10, 0.15a, 0.20)
MOSEO	Maximum Iterations (200, 300a, 400); Number of Connection (100, 150a, 200); a (0.30, 0.40a, 0.50); b (0.20, 0.35a, 0.50)
MOKA	Maximum Iterations (200, 300a, 400); Number of Keshtels (100, 200a, 300); Maximum Swirling (10, 15, 20); ${\mathit{N}}_1$ Percentage (0.05, 0.1a, 0.15); ${\mathit{N}}_2$ Percentage (0.2a, 0.25, 0.30);
MOKASEO	Maximum Iterations (200, 300a, 400); Number of Keshtels (100, 200, 300a); Maximum Swirling (10, 15, 20); ${\mathit{N}}_1$ Percentage (0.05, 0.1, 0.15); ${\mathit{N}}_2$ Percentage (0.2, 0.25, 0.30a); Number of Connection (100a, 150, 200); a (0.30a, 0.40, 0.50); b (0.20, 0.35a, 0.50);
MOGWO	Maximum Iterations (200a, 300, 400); Population Number (100, 200a, 300); Propensity to attackb ($p_a^0=0.5$; $p_a^T=2$); Propensity to cruiseb ($p_c^0=1$; $p_c^T=0.5$)
NSHHO	Maximum Iterations (200a, 300, 400); Population Number (100a, 200, 300); Mutation Probability (0.6, 0.7a, 0.8); Scaling Factor (0.5, 0.7, 0.8a); Recovery Number (10, 12, 15a)

^aThe optimal level.

^bThe selected parameters have the default value based on the conventional form.

6. Computational outputs

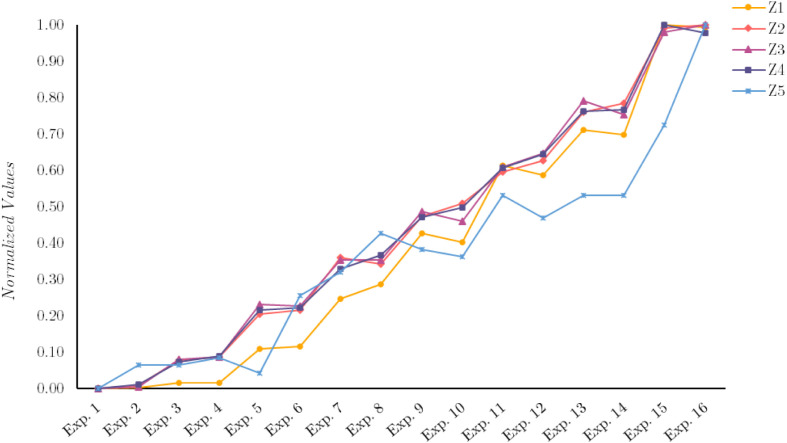
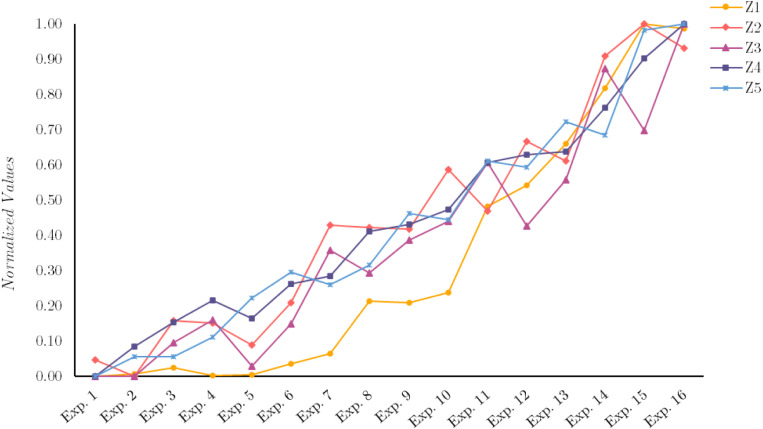
In this part, the outputs of metaheuristic algorithms for the proposed problem are reviewed and compared using both statistical and decision-making approaches. The metaheuristic algorithms were coded in MATLAB 2022a software to solve the designed networks using a laptop with the following features: Intel® Core i5-3320M CPU @ 2.60 GHz, 8 GB RAM, and Interl® 4 GB graphic card. To begin with, the distribution of the Pareto solution for problem ${\mathit{S}}_{\mathit{3}}$ is shown in Fig. 11 to visually provide the behavior of algorithms. Then, the evaluation indicators’ results are obtained and separately reported in Table 6. The results of statistical tests and decision-making approaches are thoroughly explained in the next two subsections. Since the RSC problem is a multi-objective problem, analyzing the algorithm’s convergence based on a single objective function is impossible. Then, we need a substitution to demonstrate the convergence of the proposed algorithms. To this end, we employ IGD and HV, two of the well-known indicators for multi-objective optimizers, instead of single objective function value and plot the convergence plots as in Fig. 12. Here, the maximum iteration of all optimizers is set on the 200 iterations to perform the convergence analysis justifiably. Then, three problems, namely ${\mathit{S}}_{\mathit{3}}$, ${\mathit{M}}_{\mathit{3}}$, and ${\mathit{L}}_{\mathit{3}}$, out of 16 designed problems, are nominated for the convergence analysis. The IGD plots for ${\mathit{S}}_{\mathit{3}}$, ${\mathit{M}}_{\mathit{3}}$, and ${\mathit{L}}_{\mathit{3}}$ demonstrate that although algorithms are unstable in initial iterations, they reach the convergence status in the middle.

Fig. 11.

Pareto solutions for experiment ${\mathit{S}}_{\mathit{3}}$.

Table 6.

Evaluation Indicators of Algorithms.

	SNS						MID						MS						CT
	NSGA-II	MOSEO	MOKA	MOKASEO	MOGWO	NSHHO	NSGA-II	MOSEO	MOKA	MOKASEO	MOGWO	NSHHO	NSGA-II	MOSEO	MOKA	MOKASEO	MOGWO	NSHHO	NSGA-II	MOSEO	MOKA	MOKASEO	MOGWO	NSHHO
${\mathit{S}}_1$	2.6969E＋05	3.4973E＋05	2.4597E＋05	3.1029E＋05	3.0889E＋05	3.3985E＋05	1.7170	1.6419	1.6833	1.9251	1.5350	1.5291	1.6477E＋06	2.1014E＋06	2.1446E＋06	2.3529E＋06	2.1313E＋06	2.4711E＋06	81	144	145	269	87	83
${\mathit{S}}_2$	7.3679E＋05	6.6907E＋05	7.1612E＋05	7.3025E＋05	7.4561E＋05	8.1775E＋05	1.3140	1.4512	1.3239	1.0573	1.0294	1.0752	6.8308E＋06	7.1208E＋06	8.1554E＋06	8.7054E＋06	7.8566E＋06	8.6359E＋06	146	233	514	520	163	143
${\mathit{S}}_3$	1.0624E＋06	9.1421E＋05	9.9589E＋05	1.0691E＋06	1.0166E＋06	1.0777E＋06	1.0318	1.8511	1.8123	1.6580	1.7129	1.5728	6.9132E＋06	6.7267E＋06	6.6897E＋06	8.5205E＋06	9.0613E＋06	9.9392E＋06	246	318	426	705	231	237
${\mathit{S}}_4$	1.6507E＋06	1.2453E＋06	1.5486E＋06	1.6178E＋06	1.6987E＋06	1.5728E＋06	1.7729	1.5147	1.1959	1.3541	1.1430	1.0589	1.1452E＋07	1.2094E＋07	1.2177E＋07	1.4593E＋07	1.4691E＋07	1.3143E＋07	589	976	1429	1782	599	564
${\mathit{S}}_5$	2.1039E＋06	2.1084E＋06	2.1962E＋06	2.0378E＋06	2.1842E＋06	1.9282E＋06	1.2439	1.1213	1.6858	1.9952	1.2548	1.0835	2.4665E＋07	2.4706E＋07	2.4713E＋07	2.6141E＋07	2.3752E＋07	2.7096E＋07	1996	3122	3248	4015	1883	1898
${\mathit{M}}_1$	2.7055E＋06	2.5817E＋06	2.6766E＋06	2.6079E＋06	2.3976E＋06	2.3726E＋06	1.4618	1.0870	1.7418	1.9411	1.1900	1.0666	2.3504E＋07	2.3425E＋07	2.6502E＋07	2.9424E＋07	3.1356E＋07	2.7616E＋07	1451	1542	1743	3132	1450	1304
${\mathit{M}}_2$	2.9359E＋06	3.1957E＋06	3.1123E＋06	3.1815E＋06	2.9978E＋06	3.5835E＋06	1.1700	1.0947	1.4254	1.3945	1.0140	1.0952	4.7953E＋07	6.1157E＋07	7.3536E＋07	6.5282E＋07	8.0775E＋07	8.0653E＋07	3822	4740	5473	6339	3408	3412
${\mathit{M}}_3$	3.8323E＋06	3.6492E＋06	3.5215E＋06	3.6224E＋06	3.6969E＋06	3.8157E＋06	1.2479	1.5985	1.5534	1.4465	1.5464	1.5835	3.5644E＋07	4.1871E＋07	5.0141E＋07	8.6921E＋07	7.8962E＋07	8.1366E＋07	2570	2748	3400	4334	2884	2412
${\mathit{M}}_4$	5.6336E＋06	5.6763E＋06	4.9401E＋06	4.9816E＋06	6.3452E＋06	5.6807E＋06	1.1434	1.7932	1.5971	1.9380	1.5468	1.3941	6.1055E＋07	7.0446E＋07	7.1974E＋07	7.3504E＋07	6.7106E＋07	8.1431E＋07	2669	4966	9185	9483	2773	2568
${\mathit{M}}_5$	5.8271E＋06	5.5189E＋06	5.9371E＋06	6.0554E＋06	5.8725E＋06	5.3213E＋06	1.6872	1.9713	1.2689	1.9370	1.2699	1.1494	5.2789E＋07	6.5766E＋07	7.0473E＋07	8.5672E＋07	7.5753E＋07	7.5988E＋07	12 533	14 117	16 078	22 858	13 250	11 815
${\mathit{L}}_1$	6.1509E＋06	6.1263E＋06	6.0351E＋06	6.1748E＋06	5.9639E＋06	6.8815E＋06	1.1657	1.7215	1.9880	1.7991	1.6935	1.8327	3.1849E＋08	3.4594E＋08	1.0133E＋09	1.0151E＋09	9.6172E＋08	1.0448E＋09	14 834	18 204	24 959	26 551	16 000	15 095
${\mathit{L}}_2$	6.0881E＋06	6.2981E＋06	6.3425E＋06	5.9525E＋06	7.0011E＋06	6.1197E＋06	1.0468	1.1441	1.4433	1.6832	1.0972	1.1780	3.9234E＋08	4.8026E＋08	1.3751E＋08	7.7991E＋08	7.4326E＋08	7.4702E＋08	18 627	25 555	32 205	37 423	20 755	19 780
${\mathit{L}}_3$	6.9775E＋06	6.3392E＋06	7.0118E＋06	6.4905E＋06	6.6092E＋06	6.8911E＋06	1.2126	1.5143	1.5391	1.9726	1.5740	1.3980	2.7606E＋08	3.9634E＋08	4.1966E＋08	1.2325E＋09	1.2845E＋09	1.3908E＋09	27 379	28 198	37 331	37 368	28 928	24 391
${\mathit{L}}_4$	7.3635E＋06	7.0202E＋06	6.9056E＋06	7.1657E＋06	7.5588E＋06	7.4162E＋06	1.0861	1.2135	1.1536	1.7183	1.1791	1.1450	1.8357E＋08	4.6347E＋08	8.7116E＋08	9.6806E＋08	1.0832E＋09	1.0384E＋09	24 097	34 878	49 053	55 857	29 259	24 171
${\mathit{L}}_5$	7.8728E＋06	7.7302E＋06	7.6602E＋06	7.5814E＋06	8.0486E＋06	8.8305E＋06	1.8568	1.5611	1.3912	1.6778	1.3544	1.3289	4.3563E＋08	8.6714E＋08	9.8257E＋08	1.1758E＋09	1.2112E＋09	1.1315E＋09	24 364	28 078	36 852	46 255	24 899	25 516
Puebla	2.9931E＋06	2.8764E＋06	2.9768E＋06	3.1723E＋06	2.7983E＋06	2.7375E＋06	1.6693	1.0628	1.1811	1.8284	1.0583	1.0732	5.0377E＋07	6.2913E＋07	7.5195E＋07	6.6759E＋07	7.4163E＋07	8.2822E＋07	28 173	35 435	56 900	60 216	30 027	31 011

	HV						GD						IGD
	NSGA-II	MOSEO	MOKA	MOKASEO	MOGWO	NSHHO	NSGA-II	MOSEO	MOKA	MOKASEO	MOGWO	NSHHO	NSGA-II	MOSEO	MOKA	MOKASEO	MOGWO	NSHHO
${\mathit{S}}_1$	0.5858	0.8156	0.5194	0.7442	0.8680	0.7222	0.0678	0.0824	0.0474	0.0654	0.0463	0.0430	0.2709	0.2240	0.2874	0.1533	0.1652	0.1410
${\mathit{S}}_2$	0.5240	0.4515	0.5758	0.6187	0.5870	0.6172	0.0630	0.0777	0.0476	0.0590	0.0527	0.0521	0.2093	0.2416	0.3112	0.1984	0.2140	0.1901
${\mathit{S}}_3$	0.5265	0.5168	0.8139	0.7611	0.9061	0.7932	0.0564	0.0764	0.0524	0.0496	0.0537	0.0463	0.2849	0.2724	0.3041	0.2174	0.2305	0.2411
${\mathit{S}}_4$	0.4037	0.3311	0.6460	0.7642	0.6432	0.5875	0.0733	0.0646	0.0460	0.0627	0.0486	0.0441	0.2217	0.2159	0.3484	0.1664	0.1749	0.1542
${\mathit{S}}_5$	0.4726	0.7281	0.3327	0.8141	0.8061	0.6741	0.0651	0.0616	0.0554	0.0554	0.0609	0.0522	0.4230	0.2586	0.3761	0.1550	0.1697	0.1427
${\mathit{M}}_1$	0.3481	0.7261	0.4320	0.7640	0.7582	0.7283	0.0719	0.0391	0.0471	0.0365	0.0417	0.0343	0.3930	0.2873	0.3542	0.2274	0.2194	0.2487
${\mathit{M}}_2$	0.4866	0.6521	0.3616	0.8412	0.7193	0.6514	0.0524	0.0115	0.0473	0.0102	0.0126	0.0121	0.2649	0.2474	0.3242	0.1513	0.1634	0.1364
${\mathit{M}}_3$	0.4675	0.6151	0.2687	0.8790	0.6798	0.5585	0.0284	0.0537	0.0578	0.0258	0.0311	0.0250	0.2924	0.2398	0.3450	0.1338	0.1386	0.1198
${\mathit{M}}_4$	0.4372	0.8554	0.4334	0.8168	0.9361	0.8773	0.0213	0.0597	0.0585	0.0206	0.0223	0.0231	0.4465	0.2239	0.3292	0.1616	0.1750	0.1647
${\mathit{M}}_5$	0.7789	0.3146	0.3724	0.7312	0.8555	0.7118	0.0095	0.0640	0.0483	0.0087	0.0095	0.0093	0.4385	0.2351	0.3985	0.2102	0.2248	0.1986
${\mathit{L}}_1$	0.8241	0.3234	0.3534	0.7912	0.8782	0.7816	0.0209	0.0270	0.0514	0.0179	0.0211	0.0211	0.5525	0.2523	0.3714	0.0748	0.0664	0.0839
${\mathit{L}}_2$	0.6754	0.2712	0.4665	0.7431	0.7199	0.6296	0.0118	0.0381	0.0478	0.0113	0.0128	0.0107	0.4339	0.2284	0.3076	0.2344	0.2541	0.2104
${\mathit{L}}_3$	0.7356	0.2777	0.2876	0.9128	0.7895	0.6761	0.0103	0.0377	0.0575	0.0093	0.0106	0.0097	0.5646	0.2983	0.4305	0.0507	0.0548	0.0502
${\mathit{L}}_4$	0.2067	0.7174	0.3918	0.8144	0.6698	0.6997	0.0280	0.0409	0.0606	0.0252	0.0264	0.0246	0.3850	0.3046	0.3499	0.2053	0.1851	0.2166
${\mathit{L}}_5$	0.2624	0.7125	0.4955	0.7732	0.7157	0.6925	0.0109	0.0218	0.0458	0.0104	0.0122	0.0113	0.3216	0.2567	0.3636	0.1158	0.1173	0.1249
Puebla	0.1793	0.7689	0.5836	0.7843	0.6811	0.7860	0.0121	0.0083	0.0514	0.0079	0.0084	0.0079	0.4522	0.3559	0.3689	0.2688	0.2897	0.2544

Fig. 12.

Convergency analysis: (a) IGD of ${\mathit{S}}_{\mathit{3}}$, (b) IGD of ${\mathit{M}}_{\mathit{3}}$, (c) IGD of ${\mathit{L}}_{\mathit{3}}$, (e) HV of ${\mathit{S}}_{\mathit{3}}$, (f) HV of ${\mathit{M}}_{\mathit{3}}$, (e) HV of ${\mathit{L}}_{\mathit{3}}$.

Moreover, these plots assert that MGWO and NSHHO converge in a shorter time. HV plots confirm the capability and effectiveness of the algorithms in solving the problems while convergent to the highest value of HV. It is however possible to differentiate between the convergence behavior of optimizers in terms of HV for different problem sizes.

6.1. Statistical comparison

It was previously mentioned that 15 test problems and a case study are designed to investigate the performance of the proposed network under various dimensions. As a result, the indicators values for each defined problem are completely distinguishable. So, we transform these values into [0, 1] intervals using the Relative Deviation Index (RDI) to facilitate the next steps of the study (Abdi et al., 2020):

$$RDI=\frac{|E{I}_{Alg}-E{I}_{best}|}{E{I}_{max}-E{I}_{min}}$$ (48)

where the best, maximum, and minimum value of the indicator in each experiment are $E{I}_{best}$, $E{I}_{max}$, and $E{I}_{min}$ while $E{I}_{Alg}$ the obtained value of the indicator by a specific algorithm in each experiment. Now, interval plots with a 5% acceptance threshold or 95% confidence distance are plotted as shown in Fig. 13, Fig. 14, Fig. 15, Fig. 16, Fig. 17, Fig. 18, Fig. 19 and categorized into four groups. The mean of interval plots at the lowest RDI confidence distances appoints the superior algorithms. The results declare that the performance of all optimizers is considerable and close in terms of various metrics.

Fig. 13.

Interval plots of SNS for four cases.

Fig. 14.

Interval plots of MID for four cases.

Fig. 15.

Interval plots of MS for four cases.

Fig. 16.

Interval plots of CT for four cases.

Fig. 17.

Interval plots of HV for four cases.

Fig. 18.

Interval plots of GD for four cases.

Fig. 19.

Interval plots of IGD for four cases.

The interval plots affirm that NSGA-II, MOGWO, and NSHHO conquer other metaheuristics in terms of SNS for all four categories. With respect to the MID indicator, it is discernible that MOGWO and NSHHO have tight competition in small and medium size experiments. Nonetheless, NSHHO outperforms the first two categories, and for large-size experiments, NSGA-II is the superior algorithm. In an overall view, NSHHO overcomes other metaheuristic algorithms. In terms of MS, MOKASEO, MOGWO, and NSHHO outpace every other algorithm in all sizes. Still, NSHHO surpasses other algorithms’ performance for small-size, medium-size, large-size, and overall views in terms of MS.

NSGA-II, MOGWO, and NSHHO are unrivaled in terms of computational time for all problem sizes and overall views. Additionally, the computational duration of all four algorithms is available in Fig. 20, in which the details of execution times for all algorithms and problems are represented. With respect to HV, GD and IGD three algorithms have close performance: MOKASEO, MOGWO, and NSHHO. The interval plots of HV contend that MOKASEO is superior for medium-size problems and in general perspective, but NSHHO has better performance for small-size and large-size problems. From the GD standpoint, NSHHO is the top optimizer for all problem sizes. Finally, MOGWO outpaces large-size problems in terms of IGD. Nonetheless, NSHHO is specified as the superior optimizer with respect to IGD.

Fig. 20.

CT plot of metaheuristics for experiments.

6.2. Algorithm comparison using entropy weights method and CoCoSo

Generally, MCDM tools are recognized and prevalent for prioritization or ranking purposes (Arjomandi and Mosallanezhad, 2022, Cheraghalipour et al., 2017). A hybrid MCDM structure is proposed in this section to prioritize the algorithm based on the result of evaluation indicators in a general manner. Typically, the hybrid MCDM architecture constitutes two or more techniques to first find the significance weights of decision-making criteria and then prioritize the alternatives (Arjomandi et al., 2021). The hybrid structure encompasses two MCDM methods: Entropy Weights Method (EWM), a popular MCDM tool to determine the weights of criteria or indicators in our case, as well as Combined Compromise Solution (CoCoSo) to rank the alternatives or metaheuristic algorithms in this study. The inputs of the proposed hybrid MCDM are the means RDI value of each indicator for different problem sizes. It is suggested to refer to Chodha et al. (2021) and Yazdani et al. (2019) for details on the EWM and CoCoSo. Here are the steps of hybrid​ MCDM:

Step 1: Construct the decision matrix ($X$): Here, there are four indicators and algorithms in this study. So, the decision matrix is a 6 × 7 matrix, including the mean RDI value of indicators. For instance, $x_{11}$ is the RDI of the first indicator (SNS) for the first algorithm (NSGA-II). Thus, for this problem, the number of rows and columns is denoted by n, and m equals 6 and 7, respectively.

$$\mathrm{X}=\left[\begin{array}{ccc}\hfill {\mathrm{x}}_{11}\hfill & \hfill \cdots \hfill & \hfill {\mathrm{x}}_{1\mathrm{m}}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathrm{x}}_{\mathrm{n}1}\hfill & \hfill \cdots \hfill & \hfill {\mathrm{x}}_{\mathrm{nm}}\hfill \end{array}\right]$$

Step 2: Normalize the decision matrix ($\tilde{X}$): Using Eq. (49) matrix X is normalized.

$${\rho }_{\mathrm{ij}}=\frac{{\mathrm{x}}_{\mathrm{ij}}}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{ij}}}\mathrm{j}=\left[1,\dots ,\mathrm{m}\right]$$ (49)

Step 3: Obtain entropy value (e): The entropy value is calculated by Eq. (50) which quantifies the amount of decision information in $\tilde{X}$.

$${\mathrm{e}}_{\mathrm{j}}=-\frac{1}{\text{logn}}\sum _{\mathrm{i}=1}^{\mathrm{n}}{\rho }_{\mathrm{ij}}log\left({\rho }_{\mathrm{ij}}\right)\mathrm{j}\in \left[1,\dots ,\mathrm{m}\right]$$ (50)

Step 4: Compute diversification degree (d): This value is attained by Eq. (51)

$${\mathrm{d}}_{\mathrm{j}}=1-{\mathrm{e}}_{\mathrm{j}}\mathrm{j}\in \left[1,\dots ,\mathrm{m}\right]$$ (51)

Step 5: Assess the weight (w): Using Eq. (52) the weights of all indicators are calculated.

$${\mathrm{w}}_{\mathrm{j}}=\frac{{\mathrm{d}}_{\mathrm{ij}}}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{ij}}}\mathrm{j}\in \left[1,\dots ,\mathrm{m}\right]$$ (52)

Step 6: Calculate the${\delta }_{ij}$: Normal matrix ($\tilde{X}$) related to the CoCoSo technique is formed.

$${\delta }_{\mathrm{ij}}=\frac{\underset{i}{max}{\rho }_{\mathrm{ij}}-{\rho }_{\mathrm{ij}}}{\underset{i}{min}{\rho }_{\mathrm{ij}}-\underset{i}{max}{\rho }_{\mathrm{ij}}}\mathrm{j}\in \left[1,\dots ,\mathrm{m}\right]$$ (53)

Step 7: Determine ($S_i$) and ($P_i$): The weighted comparability sequence (${\mathrm{S}}_{\mathrm{i}}$) and power weight of comparability sequences (${\mathrm{P}}_{\mathrm{i}})$ are computed using Eqs. (54), (55).

$${\mathrm{S}}_{\mathrm{i}}=\sum _{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{w}}_{\mathrm{j}}{\delta }_{\mathrm{ij}}\mathrm{i}\in \left[1,\dots ,\mathrm{n}\right]$$ (54)

$${\mathrm{P}}_{\mathrm{i}}=\sum _{\mathrm{j}=1}^{\mathrm{m}}{\left({\delta }_{\mathrm{ij}}\right)}^{{\mathrm{w}}_{\mathrm{j}}}\mathrm{i}\in \left[1,\dots ,\mathrm{n}\right]$$ (55)

Step 8: Calculate relative weights ($k_{ia}$), ($k_{ib}$) and ($k_{ic}$): Using three guidelines as Eqs. (56), (57), and (58), $k_{ia}$ (relative weights embracing arithmetic mean of $S_i$ and $P_i$), $k_{ib}$ (the sum of relative scores of $S_i$ and $P_i$), and $k_{ic}$ (the balanced compromise of ${\mathrm{S}}_{\mathrm{i}}$ and ${\mathrm{P}}_{\mathrm{i}}$) are calculated. In Eq. (58), $\lambda$ is considered 0.5.

$${\mathrm{k}}_{\mathrm{ia}}=\frac{{\mathrm{S}}_{\mathrm{i}}+{\mathrm{P}}_{\mathrm{i}}}{\sum _{\mathrm{j}=1}^{\mathrm{m}}({\mathrm{S}}_{\mathrm{i}}+{\mathrm{P}}_{\mathrm{i}})}\mathrm{i}\in \left[1,\dots ,\mathrm{n}\right]$$ (56)

$${\mathrm{k}}_{\mathrm{ib}}=\frac{{\mathrm{S}}_{\mathrm{i}}}{\underset{i}{min}{\mathrm{S}}_{\mathrm{i}}}+\frac{{\mathrm{P}}_{\mathrm{i}}}{\underset{i}{min}{\mathrm{P}}_{\mathrm{i}}}\mathrm{i}\in \left[1,\dots ,\mathrm{n}\right]$$ (57)

$${\mathrm{k}}_{\mathrm{ic}}=\frac{\lambda \left({\mathrm{S}}_{\mathrm{i}}\right)+(1-\lambda )\left({\mathrm{P}}_{\mathrm{i}}\right)}{(\lambda \left(\underset{i}{max}{\mathrm{S}}_{\mathrm{i}}\right)+(1-\lambda )\left(\underset{i}{max}{\mathrm{P}}_{\mathrm{i}}\right))}\mathrm{i}\in \left[1,\dots ,\mathrm{n}\right],0\le \lambda \le 1$$ (58)

Step 9: Prioritize the algorithms: The final prioritization is established using Eq. (59)

$${\mathrm{k}}_{\mathrm{i}}={\left({\mathrm{k}}_{\mathrm{ia}}{\mathrm{k}}_{\mathrm{ib}}{\mathrm{k}}_{\mathrm{ic}}\right)}^{\frac{1}{3}}+\frac{1}{3}({\mathrm{k}}_{\mathrm{ia}}+{\mathrm{k}}_{\mathrm{ib}}+{\mathrm{k}}_{\mathrm{ic}})\mathrm{i}\in \left[1,\dots ,\mathrm{n}\right]$$ (59)

This hybrid MCDM structure helps us sort algorithms according to evaluation indicators for four scales small, medium, large, and all problems together. Table 7, Table 8, Table 9, Table 10 includes implementation steps related to the entropy weights method. Using these steps, weights of evaluation indicators are obtained. Then, Table 11, Table 12, Table 13, Table 14 shows the steps of the CoCoSo technique. The result of hybrid entropy-CoCoSo certifies that for small and large sizes, NSHHO has more superiority than other algorithms. For the Medium size experiments, MOGWO overcomes other metaheuristics. In the entire perspective, the hybrid suggests that MOGWO is better with regard to all evaluation indicators.

Table 7.

Initial decision matrix for all problem sizes.

	All experiments								Small size								Medium size and case study								Large size
	SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD
NSGA-II	0.281	0.328	0.953	0.045	0.685	0.372	0.841		0.229	0.302	0.932	0.023	0.779	0.695	0.634		0.268	0.253	0.998	0.064	0.758	0.372	0.908		0.305	0.320	0.200	0.046	0.684	0.056	0.944
MOSEO	0.222	0.336	0.718	0.292	0.545	0.615	0.429		0.401	0.344	0.760	0.335	0.666	0.886	0.472		0.100	0.432	0.706	0.257	0.351	0.507	0.400		0.081	0.157	0.373	0.292	0.461	0.343	0.560
MOKA	0.324	0.283	0.521	0.670	0.722	0.658	0.827		0.271	0.230	0.636	0.617	0.553	0.125	0.967		0.338	0.295	0.452	0.616	0.838	0.817	0.796		0.307	0.285	0.455	0.788	0.629	1.000	0.801
MOKASEO	0.285	0.210	0.178	1.000	0.085	0.129	0.050		0.194	0.327	0.179	1.000	0.146	0.388	0.052		0.329	0.114	0.267	1.000	0.078	0.014	0.051		0.136	0.137	0.886	1.000	0.001	0.004	0.058
MOGWO	0.298	0.250	0.239	0.088	0.115	0.132	0.093		0.190	0.240	0.427	0.023	0.097	0.266	0.143		0.334	0.270	0.238	0.090	0.128	0.085	0.094		0.356	0.224	0.278	0.150	0.153	0.035	0.062
NSHHO	0.376	0.232	0.100	0.016	0.246	0.025	0.043		0.291	0.203	0.103	0.006	0.283	0.030	0.055		0.412	0.259	0.146	0.015	0.232	0.020	0.030		0.237	0.216	0.271	0.028	0.192	0.008	0.065

Table 8.

Normalized decision matrix for all problem sizes.

	All experiments								Small size								Medium size and case study								Large size
	SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD
NSGA-II	0.157	0.200	0.352	0.022	0.286	0.193	0.368		0.145	0.183	0.307	0.011	0.309	0.291	0.273		0.150	0.156	0.356	0.031	0.318	0.205	0.399		0.215	0.239	0.081	0.020	0.323	0.039	0.379
MOSEO	0.124	0.205	0.265	0.138	0.227	0.319	0.188		0.255	0.209	0.250	0.167	0.264	0.371	0.203		0.056	0.266	0.251	0.126	0.147	0.279	0.175		0.057	0.117	0.152	0.127	0.218	0.237	0.225
MOKA	0.182	0.172	0.192	0.317	0.301	0.341	0.362		0.172	0.140	0.209	0.308	0.219	0.052	0.416		0.190	0.182	0.161	0.302	0.351	0.450	0.349		0.216	0.213	0.185	0.342	0.296	0.691	0.322
MOKASEO	0.160	0.128	0.066	0.473	0.035	0.067	0.022		0.123	0.199	0.059	0.499	0.058	0.162	0.022		0.185	0.070	0.095	0.490	0.033	0.008	0.023		0.096	0.102	0.360	0.434	0.000	0.003	0.023
MOGWO	0.167	0.152	0.088	0.042	0.048	0.068	0.041		0.120	0.146	0.141	0.011	0.038	0.111	0.062		0.188	0.166	0.085	0.044	0.054	0.047	0.041		0.250	0.168	0.113	0.065	0.072	0.024	0.025
NSHHO	0.211	0.142	0.037	0.008	0.103	0.013	0.019		0.185	0.123	0.034	0.003	0.112	0.013	0.024		0.231	0.159	0.052	0.007	0.097	0.011	0.013		0.167	0.161	0.110	0.012	0.091	0.006	0.026

Table 9.

Entropy value and diversification degree for all problem sizes.

	All experiments								Small size								Medium size and case study								Large size
	SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD
$e_j$	0.993	0.992	0.866	0.694	0.867	0.820	0.747		0.980	0.990	0.890	0.629	0.883	0.824	0.775		0.964	0.965	0.891	0.700	0.842	0.709	0.733		0.945	0.976	0.926	0.726	0.819	0.480	0.749
$d_j$	0.007	0.008	0.134	0.306	0.133	0.180	0.253		0.020	0.010	0.110	0.371	0.117	0.176	0.225		0.036	0.035	0.109	0.300	0.158	0.291	0.267		0.055	0.024	0.074	0.274	0.181	0.520	0.251

Table 10.

Weights of evaluation indicators all problem sizes.

	All experiments								Small size								Medium size and case study								Large size
	SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD		SNS	MID	MS	CPU	HV	GD	IGD
$w_j$	0.007	0.008	0.131	0.299	0.130	0.177	0.248		0.044	0.023	0.242	0.815	0.257	0.388	0.495		0.080	0.076	0.241	0.659	0.346	0.640	0.587		0.120	0.052	0.163	0.603	0.398	1.143	0.552

Table 11.

CoCoSo’s normalized matrix.

	All experiments							Small size							Medium size and case study							Large size
	SNS	MID	MS	CPU	HV	GD	IGD	SNS	MID	MS	CPU	HV	GD	IGD	SNS	MID	MS	CPU	HV	GD	IGD	SNS	MID	MS	CPU	HV	GD
NSGA-II	0.615	0.060	0.000	0.970	0.058	0.451	0.000	0.815	0.299	0.000	0.983	0.000	0.223	0.363	0.463	0.562	0.000	0.950	0.105	0.554	0.000	0.184	0.000	1.000	0.981	0.000	0.947
MOSEO	1.000	0.000	0.276	0.719	0.278	0.068	0.516	0.000	0.000	0.207	0.669	0.165	0.000	0.541	1.000	0.000	0.343	0.754	0.641	0.386	0.579	1.000	0.888	0.747	0.728	0.326	0.659
MOKA	0.336	0.423	0.507	0.335	0.000	0.000	0.017	0.616	0.804	0.357	0.385	0.331	0.888	0.000	0.237	0.432	0.641	0.389	0.000	0.000	0.128	0.179	0.192	0.628	0.218	0.082	0.000
MOKASEO	0.589	1.000	0.908	0.000	1.000	0.836	0.991	0.979	0.118	0.908	0.000	0.929	0.581	1.000	0.267	1.000	0.859	0.000	1.000	1.000	0.976	0.797	1.000	0.000	0.000	1.000	1.000
MOGWO	0.504	0.684	0.837	0.927	0.952	0.830	0.937	1.000	0.733	0.609	0.983	1.000	0.725	0.900	0.251	0.509	0.893	0.923	0.935	0.912	0.927	0.000	0.522	0.886	0.874	0.777	0.969
NSHHO	0.000	0.822	1.000	1.000	0.746	1.000	1.000	0.519	1.000	1.000	1.000	0.727	1.000	0.997	0.000	0.545	1.000	1.000	0.798	0.992	1.000	0.431	0.566	0.897	1.000	0.720	0.996

Table 12.

The $S_i$ and $P_i$ values.

	All experiments		Small size		Medium size and case study		Large size
	Si	Pi	Si	Pi	Si	Pi	Si	Pi
NSGA-II	0.382	4.524	1.110	4.115	1.097	4.008	1.860	3.745
MOSEO	0.434	5.067	0.905	2.771	1.469	4.730	1.851	5.665
MOKA	0.177	3.986	0.875	4.920	0.538	3.564	0.387	3.790
MOKASEO	0.655	5.951	1.225	5.720	1.863	5.850	2.241	4.973
MOGWO	0.899	6.892	1.992	6.698	2.334	6.644	2.666	5.736
NSHHO	0.959	5.961	2.170	6.891	2.440	5.875	2.804	6.725

Table 13.

Relative weights value for all problem sizes.

	All experiments			Small size			Medium size and case study			Large size
	kia	kib	kic	kia	kib	kic	kia	kib	kic	kia	kib	kic
NSGA-II	0.137	3.298	0.625	0.133	2.754	0.577	0.126	3.164	0.562	0.132	5.811	0.588
MOSEO	0.153	3.728	0.701	0.093	2.035	0.406	0.153	4.057	0.682	0.177	6.298	0.789
MOKA	0.116	2.000	0.530	0.147	2.776	0.640	0.102	2.000	0.452	0.098	2.012	0.438
MOKASEO	0.184	5.198	0.841	0.176	3.464	0.766	0.191	5.105	0.849	0.170	7.123	0.757
MOGWO	0.217	6.815	0.992	0.221	4.695	0.959	0.222	6.202	0.988	0.198	8.426	0.882
NSHHO	0.193	6.920	0.881	0.230	4.968	1.000	0.206	6.184	0.915	0.225	9.046	1.000

Table 14.

Final ranking of each algorithm.

	All experiments		Small size		Medium size and case study		Large size
	ki	Rank	ki	Rank	ki	Rank	ki	Rank
NSGA-II	2.009	5	1.749	5	1.892	5	2.944	5
MOSEO	2.264	4	1.270	6	2.383	4	3.380	4
MOKA	1.379	6	1.827	4	1.302	6	1.292	6
MOKASEO	3.005	3	2.245	3	2.987	3	3.655	3
MOGWO	3.811	1	2.956	2	3.579	1	4.306	2
NSHHO	3.720	2	3.111	1	3.487	2	4.690	1

6.3. Sensitivity analysis

Sensitivity analysis considerably supports a meticulous view of the proposed model’s behavior in every study by changing the model’s main parameters (Gholian-Jouybari et al., 2018, Hajiaghaei-Keshteli and Sajadifar, 2010). Here, we consider problem S₃ to perform the sensitivity analysis. On the other hand, the hybrid MCDM approach selected the NSHHO as the most well-performed algorithm for small-size problems; therefore, we utilize the NSHHO optimizer alongside the ${\mathrm{S}}_3$ model for sensitivity analysis. The goal parameters for this process are partitioned into three categories: (I) processing rates (${\alpha }^{cc}$, ${\alpha }^{sp}$, ${\alpha }^{tr}$, ${\alpha }^{rc}$), (II) CPW production amount (${\mathrm{WA}}_{\mathrm{ipt}}$ and ${\mathrm{WV}}_{\mathrm{jpt}}$) and (III) facilities capacities (${\text{CAPK}}_{\mathrm{k}}$, ${\text{CAPL}}_{\mathrm{l}}$, ${\text{CAPM}}_{\mathrm{m}}$ and ${\text{CAPN}}_{\mathrm{n}}$). 16 experiments with multiple values of parameters are designed and solved in each category.

The first sets of experiments are designed based on the smallest and largest processing rates (0.7 and 0.95). Other parameters are kept fixed. The outputs for the first group of experiments rates are captured in Table A.1, and the normalized values are displayed in Fig. A.1. It is concluded that the Z1, Z2, and Z3 are very sensitive to an increase in processing rates, especially ${\alpha }^{sp}$, ${\alpha }^{tr}$ and ${\alpha }^{rc}$. Also, it can be revealed that separation, recycling, and treatment centers are the most effective facilities in the RSC network.

Fig. A.1.

The behavior of the RSC model under processing rates analysis.

The second set of experiments concentrates on the production of CPWs in different medical centers. These experiments are formed based on the maximum and minimum amount CPW production rate. The experiments are sorted in ascending order of $W{A}_{ipt}$. The results are exhibited in Table A.2, and the normalized values of the results are outlined in Fig. A.2. It is concluded that the behavior of objective function tightly follows the change of CPWs amounts. Notice Exp. 16, which has performed at the maximum level of both CPWs’ production rates. It proves that more optimal objective function values stem from the higher CPWs production.

Fig. A.2.

The behavior of the RSC model under CPW amount analysis.

Finally, the last set of experiments is created based on a 10% increase in the lowest value of the main facilities’ capacities. Also, to avoid the potential resistance of the model to objective function changes, the other capacity parameters are increased in parallel. The results of these experiments are provided in Table A.3 and Fig. A.3. The results prove that the objective functions trail the increase of the model’s main facilities. Therefore, the more capacity of the facilities would bring about a higher value of objective functions.

Fig. A.3.

The behavior of the RSC model under facilities’ capacity analysis.

7. Conclusion

In today’s world, SC is one of the focal components of the global economy and stability. The occurrence of any kind of disruptions in SCs, even natural or even-made disasters, may raise global concerns. In the last widespread disruption in global SCs, namely the COVID-19 pandemic, many nations, and governments encountered severe difficulties in supplying medical supplies and materials, particularly PPEs. In the current situation, after finding a vaccination for the novel coronavirus, the main trouble for global societies is finding a way to confront hazardous pandemic waste or CPWs steadily.

Reviewing the recent studies and related literature revealed that although there are a few numbers of research on controlling the CPWs, there is an unfilled spot for a comprehensive RSC model to cope with CPWs’ problems. Furthermore, technologies can also be involved in the RSC model to highly empower the RSC. This study developed an IoT-enabled RSC structure for CPWs to underpin the global healthcare systems and nations. The proposed model aims to consider all potential CPW producers in the structure. At the same time, it forms a well-structured IoT platform to feed RSC models with real-time data. In addition to current issues, global agencies and institutions have proceeded with extreme cautions concerning sustainability matters. Thus, the current study designed the RSC model according to sustainability guidelines so that total cost, transportation risk, environmental impact, CO₂ emission, and job opportunity guarantee three aspects of a sustainable model, i.e., economic, environmental, and social.

To examine the practicability of the RSC network, in reality, a real instance in Puebla city, Mexico, and 15 experiments are created. Then, a mixture of modern, classic, and hybrid metaheuristic algorithms are utilized to solve experiments. Moreover, four evaluation indicators become in charge of finding the efficient solution approach. To this aim, statistical as well as MCDM approaches analyze the evaluation indicators. For the statistical procedure, interval plots and LSD are conducted. A hybrid entropy weight method and CoCoSo construct a potent decision-making tool. The results show that metaheuristic algorithms behave differently in the case of various sizes of problems. Nevertheless, the MCDM corroborates that for small-size and large-size RSC problems, NSHHO is preferable. The performance of MOGWO for solving medium-size problems is better than other algorithms. But, in the overall view, conducting a hybrid MCDM technique chooses MOGWO as the leading algorithm.

The barriers and limitations are entangled with research processes, and scholars likely encounter both expected and unforeseen boundaries that affect the research. Owing to privacy issues in regulations of healthcare and medical organization and confidentiality of information during the pandemic, finding required data for parameters of mathematical modeling was the most substantial restriction of this study and beyond the authors’ control. The next formidable obstacle of the current research was the lack of information on the processing capacity of collection, treatment, recycling, and burial centers which prevented accurate implementation of the model and correspondingly lack deviation from reality. Last but not least, the validation and comparison of the current study and previous works remain out of reach due to the fact that there is no scientific research with similar scope or framework to our study.

From an applicability point of view, this study not only provides an excellent opportunity for bewildered policymakers and governments to survive the overloaded burden of CPWs in their territory but also takes sustainability standards into account to establish a reliable solution for the future of human beings. Nonetheless, numerous suggestions can be made for potential prospective research. To begin with, machine learning techniques are powerful toolkits for IoT platforms. For instance, a multilayer perceptron (MLP) network can help IoT devices to predict RSC model parameters. This framework engenders a different method for authorities to arrange required resources within the RSC network in advance.

The RSC problems for a pandemic similar to COVID-19 can face uncertainty due to chaotic situations during disasters, such as constantly changing infected populations, limitations in the capacity of healthcare centers, etc. Hence, key parameters of the model, like demand for medical supplies, PPE, test kits, and vaccines or capacity of main components of the network, are unpredictable. Correspondingly, this situation extremely affects the relations and processes within the proposed RSC. Thereby, uncertain capacities and demands can be joined into the RSC model to provide a realistic view of the pandemic atmosphere. Previously, we mentioned that supply chains are susceptible to disruption by any disaster. For future studies, the proposed RSC network can be framed under scenario-based considerations such that relevant responses and preparation will exist based occurrence of each scenario. On the other hand, the processing rate in each center depends on various elements like full attendance of human capital or lack of restrictions for businesses. These factors could be considered during the formulation of RSC to approach reality.

CRediT authorship contribution statement

Behzad Mosallanezhad: Designed the project, The principal conceptual ideas, The proof outline, Technical details, Mathematical formulation, Implemented the optimization, Discussed the results, Contributed to the final manuscript, Investigataion, Methodology, and Software. Fatemeh Gholian-Jouybari: Designed the project, The principal conceptual ideas, The proof outline, Technical details, Mathematical formulation, Implemented the optimization, Discussed the results, Contributed to the final manuscript, Investigataion, Methodology, and Writing-original draft. Leopoldo Eduardo Cárdenas-Barrón: Supervised the design of the methodology, technical details, and mathematical formulation, Validation, Writing – review & editing, Editing, Reviewing of the paper, Discussed the results, Contributed to the final manuscript. Mostafa Hajiaghaei-Keshteli: Supervised the design of the methodology, technical details, and mathematical formulation, Validation, Methodology, Supervision, Writing – review & editing, Editing, Reviewing of the paper, Discussed the results, Contributed to the final manuscript.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

See Fig. A.1, Fig. A.2, Fig. A.3 and Table A.1, Table A.2, Table A.3.

Table A.1.

Sensitivity analysis on processing rates.

Experiments	Parameters				Objective functions
	${\alpha }^{cc}$	${\alpha }^{sp}$	${\alpha }^{tr}$	${\alpha }^{rc}$	${\mathit{Z}}_1$	${\mathit{Z}}_2$	${\mathit{Z}}_3$	${\mathit{Z}}_4$	${\mathit{Z}}_5$
Exp. 1	0.70	0.70	0.70	0.70	631,650.14	55.5	527.3	958.006	616
Exp. 2	0.70	0.70	0.70	0.95	637,200.94	55.1	532.8	1027.72	631
Exp. 3	0.70	0.70	0.95	0.70	613,436.76	57.9	556.1	1014.40	599
Exp. 4	0.70	0.70	0.95	0.95	623,722.49	56.3	554	1001.10	608
Exp. 5	0.70	0.95	0.70	0.70	594,576.26	54.3	529.8	1034.80	583
Exp. 6	0.70	0.95	0.70	0.95	627,611.86	57.6	551.9	973.258	607
Exp. 7	0.70	0.95	0.95	0.70	627,234.37	55.9	542.9	1044.96	612
Exp. 8	0.70	0.95	0.95	0.95	633,225.79	55.9	546.3	1047.28	625
Exp. 9	0.95	0.70	0.70	0.70	595,729.07	55.2	533.8	1029.27	588
Exp. 10	0.95	0.70	0.70	0.95	595,412.69	55.8	544.1	971.872	577
Exp. 11	0.95	0.70	0.95	0.70	607,644.36	60.5	543.4	1053.57	599
Exp. 12	0.95	0.70	0.95	0.95	604,711.57	60.6	581.2	1005.12	584
Exp. 13	0.95	0.95	0.70	0.70	625,421.31	57.4	531.3	1001.80	605
Exp. 14	0.95	0.95	0.70	0.95	632,355.24	53.6	556.8	996.331	611
Exp. 15	0.95	0.95	0.95	0.70	634,397.77	58.8	578.4	996.70	632
Exp. 16	0.95	0.95	0.95	0.95	643,771.83	57.5	551.1	1075.33	633

Table A.2.

Sensitivity analysis on CPW amounts.

Experiments	Parameters		Objective functions
	$W{A}_{ipt}$	$W{V}_{jpt}$	${\mathit{Z}}_1$	${\mathit{Z}}_2$	${\mathit{Z}}_3$	${\mathit{Z}}_4$	${\mathit{Z}}_5$
Exp. 1	0.1	0.1	198,190.88	6.28	102.5	110.426	576
Exp. 2	0.1	0.18	200,150.55	7.25	106.5	129.302	579
Exp. 3	0.25	0.1	211,964.11	13.9	172	242.216	579
Exp. 4	0.25	0.18	212,901.19	14.7	177.3	270.532	580
Exp. 5	0.5	0.1	295,960.47	26.2	302.3	492.773	578
Exp. 6	0.5	0.18	302,366.20	27.4	299.6	508.398	588
Exp. 7	0.75	0.1	420,617.67	41.5	408.1	696.52	591
Exp. 8	0.75	0.18	456,142.44	39.8	407.8	764.244	596
Exp. 9	1	0.15	582,944.15	52.5	523.5	949.469	594
Exp. 10	1	0.2	561,255.23	56	500.8	998.42	593
Exp. 11	1.25	0.15	750,369.93	64.5	629.4	1190.95	601
Exp. 12	1.25	0.2	726,561.10	67.6	661.9	1257.21	598
Exp. 13	1.5	0.15	839,623.53	80.5	787.3	1469.67	601
Exp. 14	1.5	0.2	828,212.70	82.9	754	1475.48	601
Exp. 15	2	0.15	1,100,416.03	103	951.1	1892.55	610
Exp. 16	2	0.2	1,094,207.40	104	968.9	1851.42	623

Table A.3.

Sensitivity analysis on facilities’ capacity.

Experiments	Parameters				Objective functions
	$CAP{K}_k$	$CAP{L}_l$	$CAP{M}_m$	$CAP{N}_n$	${\mathit{Z}}_1$	${\mathit{Z}}_2$	${\mathit{Z}}_3$	${\mathit{Z}}_4$	${\mathit{Z}}_5$
Exp. 1	20	200	500	200	1,552,624.65	60.8	526.8	957.047	574
Exp. 2	22	220	550	220	1,569,428.76	59.5	526.9	1005.87	577
Exp. 3	24	242	605	242	1,609,751.79	63.8	549.4	1045.77	577
Exp. 4	27	266	666	266	1,557,695.43	63.6	564.7	1082.13	580
Exp. 5	29	293	732	293	1,561,906.32	61.9	533.8	1052.73	586
Exp. 6	32	322	805	322	1,631,961.69	65.2	561.6	1109.11	590
Exp. 7	35	354	886	354	1,697,337.79	71.2	610.8	1121.86	588
Exp. 8	39	390	974	390	2,031,893.58	71	595.6	1194.15	591
Exp. 9	43	429	1072	429	2,021,971.35	70.9	617.5	1205.62	599
Exp. 10	47	472	1179	472	2,087,346.41	75.5	630.5	1230.02	598
Exp. 11	52	519	1297	519	2,631,363.95	72.3	669.6	1307.59	607
Exp. 12	57	571	1427	571	2,768,844.14	77.7	627	1319.90	606
Exp. 13	63	628	1569	628	3,033,875.89	76.2	657.9	1325.33	613
Exp. 14	69	690	1726	690	3,388,091.16	84.3	732.2	1397.49	611
Exp. 15	76	759	1899	759	3,795,222.73	86.8	690.8	1478.46	627
Exp. 16	84	835	2089	835	3,765,090.37	84.9	762	1534.88	628

Data availability

No data was used for the research described in the article.