Skip to main content
NCBI home page
JACS Au logoLink to JACS Au
. 2022 Dec 30;3(1):86–92. doi: 10.1021/jacsau.2c00627

A General Framework of Scanning Tunneling Microscopy Based on Bardeen’s Approximation for Isolated Molecules

Sai Duan †, Guangjun Tian , Xin Xu †,‡,*
PMCID: PMC9875243  PMID: 36711086

Abstract

graphic file with name au2c00627_0005.jpg

Scanning tunneling microscopy (STM) is one of the most popular techniques for precise characterization. Yet, its current theoretical implementation is often based on the periodic boundary condition with the Tersoff–Hamann approximation, which is inefficient to explore the tip states other than the s-wave and to treat properly the charged molecules that are ubiquitous in chemistry. In this work, we establish a general theoretical framework for STM image simulations, which is based on the Bardeen’s approximation and utilizes the boundary condition of the cluster model. We develop an analytic algorithm for the precise evaluation of the transfer Hamiltonian matrix, addressing correctly the asymptotic behaviors of the tip states. Numerical results demonstrate that the molecular images under different STM tip states and mapping modes can be quantitatively simulated in the present framework, which paves the avenue for the conclusive investigation of the ground state electronic structures for either neutral or charged molecules.

Keywords: scanning tunneling microscope, general theoretical framework, charged molecules, Bardeen’s approximation, analytic algorithm

Utilizing quantum tunneling currents between tips and substrates under a certain bias voltage, the invention of the scanning tunneling microscope (STM)1 in 1982 opened a door for direct visualizations of the investigated samples at the atomic scale and thus has been extensively applied in physics,2 chemistry,3 material science,4 and biology.5 It is well-known that high-resolution STM images can be associated with the local density of states of the adsorbates, which provides a unique tool for the exploration of the electronic characteristic of the samples.6 Although direct adsorption of the sample molecules on prerequisite metallic substrates would inevitably lead to undesired strong perturbations, for instance, energy broadening, charge transfer, and geometrical distortion, on molecular electronic structures, these difficulties have been largely circumvented, and pristine molecular electronic structures can be obtained by using an epitaxial growing of insulating spacers, such as metal oxides,7,8 alkali halogenides,9−11 two-dimensional materials,12 and organic layers,13,14 on metallic substrates to suppress the undesired dissipation effects (Figure 1a). Therefore, besides the frontier molecular orbitals that can be visualized by STM images,15 other molecular orbitals at arbitrary energy can also be obtained by the scanning tunneling spectroscopy (STS),16,17 i.e., the derivative of tunneling current with respect to the applied bias voltages, providing a powerful technique to precisely understand electronic structures in chemistry.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic of the experimental STM setup for investigating electronic structures of a single molecule that is decoupled from the metallic substrate by a thin insulating spacer. The gray-filled circle represents the adatom as in the spherical tip, i.e., a metal atom or an oxygen atom for metallic and CO-decorated tips, respectively. The left panel represents the truncated tip potential in the region of the red-dotted rectangle, where the blue-dotted line indicates the separation plane between the tip and sample regions. (b) The analytical (left) and Gaussian mimicked (right) wave functions of a typical STM tip at the ground state (top) and their derivatives with respect to the z-direction (bottom) on the plane 2.5 Å under the tip.

Accompanying the experimental efforts, developments of theoretical modeling for STM are also indispensable to unambiguously identify the molecular structures from the measurements. The theory of STM can be traced back to Bardeen’s seminal work of perturbative treatment for tunneling currents between two separated metal layers.18 The symmetric current density operator, i.e., the so-called transfer Hamiltonian matrix, was defined.18 Although theoretical levels beyond perturbation have to be applied in large current regions,19 Bardeen’s approximation is always valid in STM/STS simulations, as the strong perturbations have to be deliberately suppressed so as to explore the electronic characteristic of the samples.20 In other words, with the rational control of experimental setups, the tunneling channel that allows the adsorbates to stay in their ground states rather than excited or charging states21,22 during STM processes is dominant and thus is the focus of the present work. Assuming a locally spherical potential well, Tersoff and Hamann derived a simple version for the ground state wave function of the tip in the asymptotic region.23 Substituting this analytic tip’s wave function into Bardeen’s approximation, the well-known conclusion as mentioned above, i.e., STM/STS images reflect the local density of states of samples,6 can be obtained. Later, Chen highlighted that the whole system could be divided into tip and sample regions by a separation plane and modified the tip’s potential by truncating it in the sample region (Figure 1a), deriving a general formalism of the tip’s wave function.6,24,25 Specifically, the radial and angular parts of the tip’s wave function in the sample region are spherical modified Bessel functions and spherical harmonics, respectively (Section S1), which was supported by recent numerical simulations at the first-principles level.26 In this context, the Tersoff–Hamann approximation corresponds only to an s-wave tip. Chen’s results revealed that for the same electronic structure, p-wave tips could produce different STM images from s-wave, which has been experimentally confirmed by the STM images of pentacene on a bilayer NaCl above Cu(111) with and without CO decorated tip,27 highlighting the symbiotic relationship between experimental measurements and theoretical simulations.28,29

It is straightforward to simulate STM images with the Tersoff–Hamann approximation once the wave functions of samples were obtained.28−30 However, the Tersoff–Hamann approximation is only reliable for images with feature sizes well above 1 or 2 Å.20 Besides, extra efforts should be made for the non-s-wave tips that can not only increase the image resolution but also gain new information with important implication for molecular orbital engineering.27 The intrinsic limitations restrict applications of the Tersoff–Hamann approximation in precise determinations of electronic structures, resulting in a demand for the original Bardeen’s approximation. In contrast to the Tersoff–Hamann approximation, few implementations of Bardeen’s approximation are available even up to date.26,31−34 All these realizations are in the framework with periodic boundary conditions (PBCs). This is understandable because there is a naturally defined energy level in PBCs. However, the asymptotic behavior of the tip’s wave function that can extend the validation of Bardeen’s approximation6 was not considered in these implementations.31−34 More importantly, in PBCs, only neutral systems can be effectively treated because extremely large supercells that bring unnecessarily heavy computational costs have to be adopted to suppress the effects of the inevitable neutralization background charges owing to the long-range characteristic of the electrostatic interaction in charged samples. With suitable spacers, STM/STS experiments have the ability to visualize the electronic structures of charged systems.8,11,17 Recent experiments further revealed that the charged states could facilitate the rational on-surface synthesis under STM tips.35 Thus, accurate simulations of the (charged) isolated molecular systems are starting to play an increasingly important role in chemistry.

In the present work, we proposed a general theoretical framework for STM simulations with Bardeen’s approximation for isolated molecules whose wave functions are expanded by Gaussian functions (Section S2), where the asymptotic behavior of the tip’s wave function could be taken into account. Specifically, the transfer Hamiltonian matrix element18,23

graphic file with name au2c00627_m001.jpg 1

can be analytically evaluated (Section S3). Here Ψt and Ψs are quasi-particle wave functions of the tip and sample, respectively, Σ is the separation surface between the tip and sample regions, and s is the vector surface element on Σ.

As noted above, after truncation of the potential, the radial part of analytical Ψt is spherical modified Bessel functions (Table S1).6,24,25 For example, the wave function of an s-wave tip is proportional to e–κr/r, where κ is the decay rate and r is the distance from the tip. Owing to the appearance of the Coulomb operator (1/r) in Ψt, Mts cannot be factorized,36 which prevents its analytical evaluation.

On the other hand, Gill and Adamson found that the Coulomb operator could be accurately expanded by37

graphic file with name au2c00627_m002.jpg 2

where erfc is the complementary error function, ω is the short-range constant, and the coefficients cj and exponents αj are dimensionless constants. In the asymptotic region of ωr ≫ 1, the erfc part can be naturally dropped. In this context, further expanding the Slater function by Gaussian functions and taking the advantage of the Gaussian product theorem, the spherical modified Bessel functions on Σ can be mimicked solely by Gaussian functions.

As shown in Figure 1b, using only one Gaussian function can well reproduce the analytical s-wave as well as its derivative on Σ except for a slight contraction. More Gaussian functions and allowing different exponents in different directions are expected to further improve the reproduction of the analytical results, which is a direction worth trying in the future. The freely adjustable exponents in Gaussian functions significantly relieve the too-rapid decay feature into the vacuum. Furthermore, incorporating molecular wave functions that are expanded by Gaussian basis sets in the state-of-the-art quantum chemistry codes, the utilization of Gaussian functions allows the factorization of the integral in Mst, which thus leads to an analytic and fast recursive evaluation of the desired transfer Hamiltonian matrix for isolated systems. It should be stressed that in the present work, the asymptotic decay of the tip’s wave function is implicitly taken into account, which agrees well with the numerical simulations based on the modified potentials.26 We should also emphasize that the current algorithm could be readily extended for accurate simulations of the complex intermedia sates, especially many-body excitations of different charging states,12,21,22 in STM processes owing to the capacity of the cluster model. In practical calculations, the exponent in the tip’s wave function was set to be the same as that in Figure 1b.

To validate the current theoretical framework, we first simulated the STM images of pentacene, which is a widely used benchmark system in experiments.15,27,38 The theoretical results of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of an isolated pentacene are depicted in Figure 2a. The measured STM images at negative ion resonance (NIR) at −2.4 V and positive ion resonance (PIR) at 1.7 V in previous experiments (Figure 2b, top panel)15 nicely resemble the features of native HOMO and LUMO, respectively. As shown in Figure 2b (bottom panel), the calculated STM images with an s-wave tip in the present work are in agreement with their experimental counterparts. The resemblances highlight the ability of the exploration of molecular structures by STM images with s-wave tips, which is the key conclusion in the Tersoff–Hamann approximation.6,23 We should note that although the calculated HOMO–LUMO gap, which is 2.3 eV, is only around half of the experimental results, the insulating spacer helps by suppressing the substrate perturbations on the adsorbates to allow for an accurate assignment as shown in the present work.

Figure 2.

Figure 2

Open in a new tab

(a) Calculated HOMO (left) and LUMO (right) of isolated pentacene molecule with isovalue of ±2.0 × 10–3 au. (b) Top, experimentally measured constant current STM images of a decoupled single pentacene with a pentacene tip at the positive (PIR, left) and negative (NIR, right) ion resonance. Bottom, theoretically simulated constant current STM images for HOMO (left) and LUMO (right) of an isolated pentacene with an s-wave tip. (c) Top, experimentally measured constant current STM images of a decoupled single pentacene with a CO-decorated tip at PIR (left) and NIR (right). Bottom, theoretically simulated constant current STM images for HOMO (left) and LUMO (right) of an isolated pentacene with an sp-mix tip state. Experimental results in (b) and (c) were reproduced from ref (15) and ref (27) (copyright 2005 and 2011 by the American Physical Society), respectively.

For the same molecular electronic structure, different tip’s wave functions could lead to different STM images as shown in eq 1. Using a CO-functionalized tip, Gross et al. reported27 that the PIR and NIR STM images (Figure 2c, top panel) have dramatically changed as compared to their counterparts from s-wave tip states, emphasizing the significant contribution of p-wave tip states. Our constant current simulations reveal that the p-wave state can reproduce the experimentally measured outer lobes very well, while including some s-wave contribution improves the overall agreement with the experimental observations, especially the corner patterns in the PIR image (Figure S1). Our simulations confirm the previous proposal of using the sp-mix tip state for the CO-decorated tip,27 while, at the same time, show the importance of using a suitable mapping mode to discriminate constant height images and constant current images (Figure S2). This conclusion is further validated by comparing the constant height and constant current simulations using the sp-mix tip state for the PIR and NIR STM images of naphthalocyanine (Figure S3). The good agreement with the corresponding experimental results has manifested the accuracy of the proposed framework for STM simulations that goes beyond the commonly used Tersoff–Hamann approximation.

We then move on to investigate charged systems that distinguish the new STM framework in the present work from all other implementations currently available. Because the insulating spacer can alter the work function of the substrate, the charge states of adsorbates can be rationally controlled.39 For example, by dragging a ladder phenylene oligomer with nine benzene rings and steric methyl substitution groups (LP9) from Au(111) to NaCl(2 monolayer)/Au(111) via STM tip manipulation, an electron transfer from LP9 to the substrate automatically occurs, resulting in a positively charged LP9 (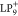Inline graphic).17 It should be noted that this charged state is not the intermedia state during the tunneling processes. Utilizing constant height STS mapping, not only the frontier molecular orbitals, i.e., the singly occupied molecular orbital (SOMO) and singly unoccupied molecular orbital (SUMO), but also the SOMO-1 and SUMO+1 of Inline graphic have been recently visualized in experiments.17

According to the experimentally used tungsten tip with gold coating,17 an s-wave tip was used in the practical calculations. The simulated constant height STS images are in excellent agreement with the corresponding experimental measurements (Figure 3). For SUMO+1, both experimental and theoretical STS images display six observable patterns along the long axis with an obscure central band, which should be attributed to the contributions from the cyclobutadiene rings in Inline graphic. Although the cyclobutadiene and fused benzene ring both contribute to SOMO-1, the destructive interferences between them result in an obscure central pattern and two bright patterns located around the outermost benzene groups. Theoretical results reveal that the methyl groups that were deliberately introduced for increasing the selectivity of on-surface synthesis17 can contribute to the SOMO-1 image despite their effects being underestimated in simulations. Specifically, the fuzzy patterns adjoining the molecular center moiety should be attributed to the methyl groups therein. In addition, the methyl groups in the outermost benzene can also contribute to the STS image, resulting in two crescent patterns around the molecular ends. It is interesting to note that the calculated images with PBC can also reproduce the SUMO+1 and SOMO-1 measurements of 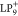Inline graphic, indicating that images of some orbitals would suffer less from the artificial extra neutralization background charges.

Figure 3.

Figure 3

Open in a new tab

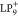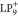Top, calculated SOMO-1, SOMO, SUMO, and SUMO+1 (from left to right) of an isolated Inline graphic molecule with an isovalue of ±2.0 × 10–3 au. Middle, experimentally measured constant height STS images of a decoupled single Inline graphic molecule with a metal tip at bias voltages of −0.85, –0.65, +0.5, and +1.05 V (from left to right). Bottom, theoretically simulated constant height STS images for SOMO-1, SOMO, SUMO, and SUMO+1 (from left to right) of an isolated Inline graphic with an s-wave tip. All experimental results were reproduced from ref (17). Copyright 2021 American Chemical Society.

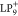It was anticipated that STS images of SOMO and SUMO in Inline graphic would have the same shapes because they are split from the HOMO of neutral LP9 by removing an electron.17 Indeed, the calculated results with PBC gave nearly identical STS images of SOMO and SUMO in Inline graphic (Figure S4).17 Nevertheless, the actual experimental measurements showed that the most bright pattern in the SUMO image is located at the molecular center, while in the SOMO image, the terminal patterns become brighter. Besides this remarkable difference, the connection regions between the central and terminal patterns also have noticeable differences, where more diffuse patterns with higher contrast exist in the measured SUMO image. Our calculated constant height STS images for SOMO and SUMO of Inline graphic faithfully reflect all the measured differences. As shown in Figure 3, the contributions from the second and third outermost methyl groups in SOMO are suppressed after the relaxation of the electronic structure when removing an electron from LP9 (Figure S5), which should be responsible for the compact and low contrast patterns in the connection regions. On the other hand, the brighter central pattern in SUMO should be attributed to the subtle coefficient changes of pz-orbitals of the conjugated carbon atoms in the positively charged state. It should be stressed that the above electronic relaxations were not observed in the calculations with PBC,17 which could originate from the indispensable neutralization background charges or plane wave basis sets. It is also noted that in this isolated system, we can correctly assign the high-resolution STS images once the order of energy level maintains (Table S2).

The last examples in the present work are anionic water clusters that are analogies of hydrated electrons.40 There are two kinds of localization for the excess electron in anionic water clusters, namely interior and surface.40 The visualization of the excess electron by STM would shed light on the precise nature of different local solvation environments as well as the dynamics between them. 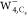Although there are no experimental STM measurements for these species, we simulate here the STM images of anionic water tetramers (Inline graphic, Figure 4a) to demonstrate the predictive power of the proposed framework. 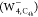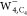The structures with the C4 (Inline graphic) and Cs (Inline graphic) symmetry point groups represent the surface localization. 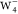Meanwhile, the structure with the C4h point group Inline graphic was considered for the interior localization. 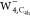It should be noted that the prepared precursor observed on NaCl layers41 would facilitate the formation of Inline graphic, although it has a very weak binding energy of the excess electron.42 The “free” water moiety with the double proton acceptor in the neutral precursor43 would be helpful for the formation of Inline graphic since it is the most stable Inline graphic.44 Besides, we also expect that the tetrahedral conformer45 would be flattened owing to the substrates, resulting in Kevan structure-like Inline graphic.46

Figure 4.

Figure 4

Open in a new tab

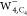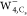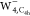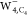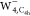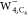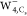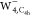(a) Calculated spin density in anionic water tetramers Inline graphic, Inline graphic, and Inline graphic (from left to right). The isovalue for Inline graphic is set to 5.0 × 10–5 au, while for Inline graphic and Inline graphic to 5.0 × 10–4 au. Calculated constant current (top) and constant height (bottom) STM images for SOMO of Inline graphic, Inline graphic, and Inline graphic (from left to right) with an s-wave tip (b) and a p-wave tip (c). The red solid and dotted lines in (b) and (c) represent the skeleton of the water molecules and the hydrogen bonds between them, respectively.

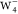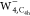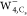All calculated STM images with the s-wave tip for the excess electron in Inline graphic were depicted in Figure 4b. All constant current STM images (Figure 4b, top panel) exhibit a quite diffuse pattern, which faithfully reflects the dispersion nature of the extra electron far away from the water molecules either in the surface or in interior structures. 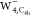The constant height STM images of Inline graphic and Inline graphic as shown in the bottom panel in Figure 4b present a more focused pattern, indicating the contraction of the extra electron in the vicinity of the molecular kernel. 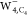Thus, the electron distributions should be a solid structure in Inline graphic and Inline graphic. On the other hand, the four bright patterns associated with the free O–H bonds and the dim central pattern reveal a hollow structure of the excess electron in Inline graphic.

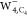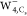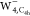The calculated constant current STM image of Inline graphic with the p-wave tip as shown in the top panel in Figure 4c exhibits an obscure central pattern with four fused protrusions along the free O–H bonds, well capturing the hollow feature of the excess electron. Meanwhile, the constant current STM images of Inline graphic and Inline graphic with the p-wave tip are similar to their counterparts with the s-wave tip except for a slight translation in the Inline graphic image and some minor deformations around the outer region in the Inline graphic image. 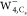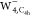The single pattern should be attributed to the large curvature of the electron distributions in the central region in Inline graphic and Inline graphic.

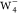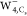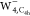With the p-wave tip, all constant height STM images of Inline graphic are distinguishable (Figure 4c, bottom panel). Specifically, the Inline graphic image displays two ring shape patterns, where the outer ring is brighter. The constructive and destructive interferences inside and between the ring patterns are clearly exhibited in the image. For the Inline graphic image, a bright crescent pattern located at the right side of the “free” water moiety and an obscure ring pattern around it are observed. Furthermore, a ring shape with four bright crescent patterns emerges in the Inline graphic image. All these results should be attributed to the fact that no matter the surface and interior localizations, the extra electron in anionic water clusters is accommodated by the diffuse atomic orbitals of the hydrogen atoms in the “free” O–H bonds, which can be well characterized via the p-wave’s quantum interaction.

Therefore, we make a theoretical proposal here. Owing to the extreme diffusion nature of the excess electron in Inline graphic, the s-wave contributions have to be suppressed as much as possible to observe the above p-wave characteristic. Our test calculations indicate that the maximum s-wave contribution to distinguish different kinds of 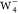Inline graphic is ∼20% (Figure S6). According to the formation of the dπ band when CO adsorbed on metal surfaces,47 strong interactions between CO’s 1π/2π* orbitals and metal’s d orbitals would facilitate the promotion of the p-wave contributions.

In summary, we propose a general theoretical framework of STM simulations for isolated molecular systems with different charge states. The effects of different states in functionalized tips can also be accurately considered in the framework. The quantitative agreement between the simulated and experimentally observed STM images for HOMO and LUMO in neutral pentacene under different tip states and mapping modes manifests the accuracy of the proposed framework. 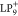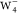Furthermore, the excellent reproduction of the experimentally measured STS images of Inline graphic, especially the subtle relaxations in the frontier molecular orbitals after ionization, highlights the advantages of the current framework in the exploration of the electronic structures in charged molecules. Taking Inline graphic clusters as an example, our results demonstrate that with the CO-decorated tip, the detailed local solvation environments of different kinds of hydrated electron can be well characterized by STM images. Thus, with the cooperation of high-resolution STM measurements, the present framework provides a unique means for understanding molecular electronic structures and thus would have extensive applications in physics, chemistry, material science, and biology.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (22233002, 22073017, 21973015, and 91427301), the Science Challenge Project (TZ2018004), and Innovation Program for Quantum Science and Technology (2021ZD0303305).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.2c00627.

  • Summary of tip’s asymptotic behavior, theoretical methodology, computational details, and additional calculated results (PDF)

Author Contributions

CRediT: Sai Duan conceptualization, investigation, methodology, software, writing-original draft, writing-review & editing; Guangjun Tian investigation, writing-original draft; Xin Xu supervision, writing-review & editing.

The authors declare no competing financial interest.

Supplementary Material

au2c00627_si_001.pdf (2MB, pdf)

References

  1. Binnig G.; Rohrer H.; Gerber Ch.; Weibel E. Tunneling Through a Controllable Vacuum Gap. Appl. Phys. Lett. 1982, 40, 178–180. 10.1063/1.92999. [DOI] [Google Scholar]
  2. Yin J.-X. Y.; Pan S. H.; Hasan M. Z. Probing Topological Quantum Matter with Scanning Tunnelling Microscopy. Nat. Rev. Phys. 2021, 3, 249–263. 10.1038/s42254-021-00293-7. [DOI] [Google Scholar]
  3. Wang X.; Wang Y.-Q.; Feng Y.-C.; Wang D.; Wan L.-J. Insights Into Electrocatalysis By Scanning Tunnelling Microscopy. Chem. Soc. Rev. 2021, 50, 5832–5849. 10.1039/D0CS01078B. [DOI] [PubMed] [Google Scholar]
  4. Salmeron M.; Eren B. High-Pressure Scanning Tunneling Microscopy. Chem. Rev. 2021, 121, 962–1006. 10.1021/acs.chemrev.0c00429. [DOI] [PubMed] [Google Scholar]
  5. Hansma P. K.; Elings V. B.; Marti O.; Bracker C. E. Scanning Tunneling Microscopy and Atomic Force Microscopy: Application to Biology and Technology. Science 1988, 242, 209–216. 10.1126/science.3051380. [DOI] [PubMed] [Google Scholar]
  6. Chen C. J.Introduction to Scanning Tunneling Microscopy; Oxford University Press, Inc.: New York, 1993. [Google Scholar]
  7. Brown N. M. D.; You H.-X. The Observation of The Structure of The Natural Oxide Layer on a Cr(110) Surface By Scanning Tunnelling Microscopy. Surf. Sci. 1990, 233, 317–322. 10.1016/0039-6028(90)90644-N. [DOI] [Google Scholar]
  8. Qiu X. H.; Nazin G. V.; Ho W. Vibrationally Resolved Fluorescence Excited with Submolecular Precision. Science 2003, 299, 542–546. 10.1126/science.1078675. [DOI] [PubMed] [Google Scholar]
  9. Glöckler K.; Sokolowski M.; Soukopp A.; Umbach E. Initial Growth of Insulating Overlayers of NaCl on Ge(100) Observed By Scanning Tunneling Microscopy with Atomic Resolution. Phys. Rev. B 1996, 54, 7705–7708. 10.1103/PhysRevB.54.7705. [DOI] [PubMed] [Google Scholar]
  10. Bennewitz R.; Barwich V.; Bammerlin M.; Loppacher C.; Guggisberg M.; Baratoff A.; Meyer E.; Güntherodt H.-J. Ultrathin Films of NaCl on Cu(111): A LEED and Dynamic Force Microscopy Study. Surf. Sci. 1999, 438, 289–296. 10.1016/S0039-6028(99)00586-5. [DOI] [Google Scholar]
  11. Repp J.; Meyer G.; Olsson F. E.; Persson M. Controlling The Charge State of Individual Gold Adatoms. Science 2004, 305, 493–495. 10.1126/science.1099557. [DOI] [PubMed] [Google Scholar]
  12. Schulz F.; Ijäs M.; Drost R.; Hämäläinen S. K.; Harju A.; Seitsonen A. P.; Liljeroth P. Many-Body Transitions in a Single Molecule Visualized by Scanning Tunnelling Microscopy. Nat. Phys. 2015, 11, 229–234. 10.1038/nphys3212. [DOI] [Google Scholar]
  13. Schunack M.; Petersen L.; Kühnle A.; Lægsgaard E.; Stensgaard I.; Johannsen I.; Besenbacher F. Anchoring of Organic Molecules to a Metal Surface: HtBDC on Cu(110). Phys. Rev. Lett. 2001, 86, 456–459. 10.1103/PhysRevLett.86.456. [DOI] [PubMed] [Google Scholar]
  14. Moresco F.; Gourdon A. Scanning Tunneling Microscopy Experiments on Single Molecular Landers. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 8809–8814. 10.1073/pnas.0500915102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Repp J.; Meyer G.; Stojković S. M.; Gourdon A.; Joachim C. Molecules on Insulating Films: Scanning-Tunneling Microscopy Imaging of Individual Molecular Orbitals. Phys. Rev. Lett. 2005, 94, 026803. 10.1103/PhysRevLett.94.026803. [DOI] [PubMed] [Google Scholar]
  16. Liljeroth P.; Repp J.; Meyer G. Current-Induced Hydrogen Tautomerization and Conductance Switching of Naphthalocyanine Molecules. Science 2007, 317, 1203–1206. 10.1126/science.1144366. [DOI] [PubMed] [Google Scholar]
  17. Li D.-Y.; Qiu X.; Li S.-W.; Ren Y.-T.; Zhu Y.-C.; Shu C.-H.; Hou X.-Y.; Liu M.; Shi X.-Q.; Qiu X.; Liu P.-N. Ladder Phenylenes Synthesized on Au(111) Surface via Selective [2 + 2] Cycloaddition. J. Am. Chem. Soc. 2021, 143, 12955–12960. 10.1021/jacs.1c05586. [DOI] [PubMed] [Google Scholar]
  18. Bardeen J. Tunnelling From a Many-Particle Point of View. Phys. Rev. Lett. 1961, 6, 57–59. 10.1103/PhysRevLett.6.57. [DOI] [Google Scholar]
  19. Sautet P.; Joachim C. Calculation of The Benzene on Rhodium STM Images. Chem. Phys. Lett. 1991, 185, 23–30. 10.1016/0009-2614(91)80133-I. [DOI] [Google Scholar]
  20. Hofer W. A.; Foster A. S.; Shluger A. L. Theories of Scanning Probe Microscopes At The Atomic Scale. Rev. Mod. Phys. 2003, 75, 1287–1331. 10.1103/RevModPhys.75.1287. [DOI] [Google Scholar]
  21. Baratz A.; Galperin M.; Baer R. Gate-Induced Intramolecular Charge Transfer in a Tunnel Junction: A Nonequilibrium Analysis. J. Phys. Chem. C 2013, 117, 10257–10263. 10.1021/jp312776c. [DOI] [Google Scholar]
  22. Miwa K.; Imada H.; Imai-Imada M.; Kimura K.; Galperin M.; Kim Y. Many-Body State Description of Single-Molecule Electroluminescence Driven by a Scanning Tunneling Microscope. Nano Lett. 2019, 19, 2803–2811. 10.1021/acs.nanolett.8b04484. [DOI] [PubMed] [Google Scholar]
  23. Tersoff J.; Hamann D. R. Theory of The Scanning Tunneling Microscope. Phys. Rev. B 1985, 31, 805–813. 10.1103/PhysRevB.31.805. [DOI] [PubMed] [Google Scholar]
  24. Chen C. J. Theory of Scanning Tunneling Spectroscopy. J. Vac. Sci. Technol. A 1988, 6, 319–322. 10.1116/1.575444. [DOI] [Google Scholar]
  25. Chen C. J. Tunneling Matrix Elements in Three-Dimensional Space: The Derivative Rule and The Sum Rule. Phys. Rev. B 1990, 42, 8841–8857. 10.1103/PhysRevB.42.8841. [DOI] [PubMed] [Google Scholar]
  26. Gustafsson A.; Paulsson M. Scanning Tunneling Microscopy Current From Localized Basis Orbital Density Functional Theory. Phys. Rev. B 2016, 93, 115434. 10.1103/PhysRevB.93.115434. [DOI] [Google Scholar]
  27. Gross L.; Moll N.; Mohn F.; Curioni A.; Meyer G.; Hanke F.; Persson M. High-Resolution Molecular Orbital Imaging Using a p-Wave STM Tip. Phys. Rev. Lett. 2011, 107, 086101. 10.1103/PhysRevLett.107.086101. [DOI] [PubMed] [Google Scholar]
  28. Carrasco J.; Hodgson A.; Michaelides A. A Molecular Perspective of Water at Metal Interfaces. Nat. Mater. 2012, 11, 667–674. 10.1038/nmat3354. [DOI] [PubMed] [Google Scholar]
  29. Duan S.; Zhang I. Y.; Xie Z.; Xu X. Identification of Water Hexamer on Cu(111) Surfaces. J. Am. Chem. Soc. 2020, 142, 6902–6906. 10.1021/jacs.0c01549. [DOI] [PubMed] [Google Scholar]
  30. Duan S.; Tian G.; Ji Y.; Shao J.; Dong Z.; Luo Y. Theoretical Modeling of Plasmon-Enhanced Raman Images of a Single Molecule with Subnanometer Resolution. J. Am. Chem. Soc. 2015, 137, 9515–9518. 10.1021/jacs.5b03741. [DOI] [PubMed] [Google Scholar]
  31. Tsukada M.; Shima N. Theory of Electronic Processes of Scanning Tunneling Microscopy. J. Phys. Soc. Jpn. 1987, 56, 2875–2885. 10.1143/JPSJ.56.2875. [DOI] [Google Scholar]
  32. Hofer W. A.; Redinger J. Scanning Tunneling Microscopy of Binary Alloys: First Principles Calculation of The Current for PtX(100) Surfaces. Surf. Sci. 2000, 447, 51–61. 10.1016/S0039-6028(99)01053-5. [DOI] [Google Scholar]
  33. Paz Ó.; Soler J. M. Efficient and Reliable Method for The Simulation of Scanning Tunneling Images and Spectra with Local Basis Sets. Phys. Stat. Sol. B 2006, 243, 1080–1094. 10.1002/pssb.200541453. [DOI] [Google Scholar]
  34. Zhang R.; Hu Z.; Li B.; Yang J. Efficient Method for Fast Simulation of Scanning Tunneling Microscopy with a Tip Effect. J. Phys. Chem. A 2014, 118, 8953–8959. 10.1021/jp5018218. [DOI] [PubMed] [Google Scholar]
  35. Albrecht F.; Fatayer S.; Pozo I.; Tavernelli I.; Repp J.; Peña D.; Gross L. Selectivity in Single-Molecule Reactions by Tip-Induced Redox Chemistry. Science 2022, 377, 298–301. 10.1126/science.abo6471. [DOI] [PubMed] [Google Scholar]
  36. Dupuis M.; Rys J.; King H. F. Evaluation of Molecular Integrals Over Gaussian Basis Functions. J. Chem. Phys. 1976, 65, 111–116. 10.1063/1.432807. [DOI] [Google Scholar]
  37. Gill P. M. W.; Adamson R. D. A Family of Attenuated Coulomb Operators. Chem. Phys. Lett. 1996, 261, 105–110. 10.1016/0009-2614(96)00931-1. [DOI] [Google Scholar]
  38. Xu J.; Zhu X.; Tan S.; Zhang Y.; Li B.; Tian Y.; Shan H.; Cui X.; Zhao A.; Dong Z.; Yang J.; Luo Y.; Wang B.; Hou J. G. Determining Structural and Chemical Heterogeneities of Surface Species At The Single-Bond Limit. Science 2021, 371, 818–822. 10.1126/science.abd1827. [DOI] [PubMed] [Google Scholar]
  39. Bennewitz R.; Bammerlin M.; Guggisberg M.; Loppacher C.; Baratoff A.; Meyer E.; Güntherodt H.-J. Aspects of Dynamic Force Microscopy on NaCl/Cu(111): Resolution, Tip–Sample Interactions and Cantilever Oscillation Characteristics. Surf. Interface Anal. 1999, 27, 462–466. . [DOI] [Google Scholar]
  40. Herbert J. M.; Coons M. P. The Hydrated Electron. Annu. Rev. Phys. Chem. 2017, 68, 447–472. 10.1146/annurev-physchem-052516-050816. [DOI] [PubMed] [Google Scholar]
  41. Guo J.; Meng X.; Chen J.; Peng J.; Sheng J.; Li X.-Z.; Xu L.; Shi J.-R.; Wang E.; Jiang Y. Real-Space Imaging of Interfacial Water with Submolecular Resolution. Nat. Mater. 2014, 13, 184–189. 10.1038/nmat3848. [DOI] [PubMed] [Google Scholar]
  42. Shin J.-W.; Hammer N. I.; Headrick J. M.; Johnson M. A. Preparation and Photoelectron Spectrum of The ‘Missing’ (H2O)4– Cluster. Chem. Phys. Lett. 2004, 399, 349–353. 10.1016/j.cplett.2004.10.015. [DOI] [Google Scholar]
  43. Dong A.; Yan L.; Sun L.; Yan S.; Shan X.; Guo Y.; Meng S.; Lu X. Identifying Few-Molecule Water Clusters with High Precision on Au(111) Surface. ACS Nano 2018, 12, 6452–6457. 10.1021/acsnano.8b02264. [DOI] [PubMed] [Google Scholar]
  44. Hammer N. I.; Shin J.-W.; Headrick J. M.; Diken E. G.; Roscioli J. R.; Weddle G. H.; Johnson M. A. How Do Small Water Clusters Bind an Excess Electron?. Science 2004, 306, 675–679. 10.1126/science.1102792. [DOI] [PubMed] [Google Scholar]
  45. Kumar A.; Walker J. A.; Bartels D. M.; Sevilla M. D. A Simple ab Initio Model for the Hydrated Electron That Matches Experiment. J. Phys. Chem. A 2015, 119, 9148–9159. 10.1021/acs.jpca.5b04721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Kevan L. Solvated Electron Structure in Glassy Matrixes. Acc. Chem. Res. 1981, 14, 138–145. 10.1021/ar00065a002. [DOI] [Google Scholar]
  47. Föhlisch A.; Nyberg M.; Hasselström J.; Karis O.; Pettersson L. G. M.; Nilsson A. How Carbon Monoxide Adsorbs in Different Sites. Phys. Rev. Lett. 2000, 85, 3309–3312. 10.1103/PhysRevLett.85.3309. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au2c00627_si_001.pdf (2MB, pdf)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES