Optimal control by deep learning techniques and its applications on epidemic models

Abstract

We represent the optimal control functions by neural networks and solve optimal control problems by deep learning techniques. Adjoint sensitivity analysis is applied to train the neural networks embedded in differential equations. This method can not only be applied in classic epidemic control problems, but also in epidemic forecasting, discovering unknown mechanisms, and the ideas behind can give new insights to traditional mathematical epidemiological problems.

Introduction

Optimal control is a branch of optimization theory that deals with finding a control for a dynamical system over a period of time, which shares tremendous popularity and plays a critical role in numerous applications in science, engineering and operations research (Betts 2010; Lenhart and Workman 2007). Optimal control is also believed to be foundation of many ecology and epidemiology problems, such as cost-effectiveness analysis, optimal vaccine distributions (Lenhart and Workman 2007), and many epidemiology problems such as epidemic forecasting, model discovery can be regarded as optimal control problems. However, efficiently and accurately solving optimal control problems is a challenging work. Most of real world optimal control problems have no explicit solutions and strongly rely on numerical methods like direct method, indirect method or dynamic programming (Betts 2010). Direct methods transform an optimal control problem to a nonlinear programming problem (NLP), so that some well-developed and mature NLP optimizers can be seamlessly applied at a low cost. But direct methods do not include adjoint information such as Pontryagin’s maximum principle (Pontryagin 1962) or Hamilton–Jacobi–Bellman equation (Bellman 1966), which makes direct methods less accurate. By using Pontryagin’s maximum principle (Pontryagin 1962), indirect methods transform an optimal control problem to a two points boundary value problem (TPBVP). But solving TPBVP depends on a good initial guess. Dynamic programming methods deal with an optimal control problem by solving a Hamilton–Jacobi–Bellman equation (Bellman 1966), but faces well-known Bellman curse of dimensionality (Bellman 1966). Hence, it still repays much more studies to develop new approaches to tackle optimal control problems efficiently and accurately.

In recent years, deep neural network (LeCun et al. 2015; Goodfellow et al. 2016), as a universal approximator for unknown functions or operators (Hornik et al. 1990; Lu et al. 2021), shows an unreasonable effectiveness (Sejnowski 2020) in solving traditional difficult problems, such as pattern recognition, learning unknown mechanisms, image recognition (He et al. 2016), and natural language processing (Devlin et al. 2018). Deep neural networks can even be used to aid mathematicians in discovering new conjectures and theorems (Davies et al. 2021), and physicians in finding new physical laws (Cranmer et al. 2020). To better understand the essence and improve the performance of deep learning methods on scientific problems such as physics, chemistry, ecology and epidemiology, more and more works pay attention to coupling or embedding differential equations and deep neural networks. Such attempts can be traced back at least to 1990s, which solves partial differential equations by neural networks (Dissanayake and Phan-Thien 1994; Lagaris et al. 1998). One important idea is regarding deep neural network (DNN) as numerical discretization schemes of ordinary or partial differential equation, which inspires researchers to redesign traditional neural architectures based on discretization methods (Niu et al. 2019; Chen 2019; Lu et al. 2018; Ruthotto and Haber 2020) or to replace DNN by a continuous differential equation (Chen et al. 2018; De Brouwer et al. 2019; Rubanova et al. 2019). Another revolutionary idea is training DNN from the perspective of optimal control theory. This extends the idea of backpropogation (Goodfellow et al. 2016) for functions to include adjoint sensitivity analysis (Cao et al. 2003) for dynamic systems, which opens the mind in differential programming (Baydin et al. 2018) and inspires a lot of architectures coupling neural network and differential equation, such as neural differential equation (Chen et al. 2018) and universal differential equations which embed neural networks into the differential equations (Rackauckas et al. 2020).

Despite the remarkable progress in coupling the differential equation and deep neural networks, deep learning methods like universal differential equations (Rackauckas et al. 2020) haven’t attracted enough attention (Song and Xiao 2022) and widely used in epidemiology problems such as epidemic control, epidemic forecasting and epidemic model discovery. This may be because coupling of transmission models and deep learning requires the researchers to have a strong background of mathematical epidemiology and deep learning as well as a basic understanding of differential programming and scientific computation, which might not always be expected in aforementioned fields. To fill this gap, we introduce universal differential equations, and apply universal differential equations to solve optimal epidemic control problems, which will also give new insights to traditional mathematical epidemiological problems.

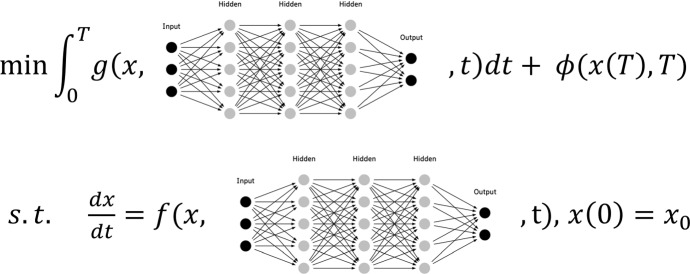
In this paper, we will consider the following optimal control problem in Bolza form (Betts 2010; Lenhart and Workman 2007):

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \underset{u(·),x(·)}{min}J={\int }_0^{T}g(x,u,t)dt+\varphi (x(T),T)\hfill \\ \hfill & s.t.\frac{\text{d}x}{\text{dt}}=f(x,u,t),x(0)=x_0,t\in [0,T],\hfill \\ \hfill & u_i(t)\in [a_i,b_i],1\le i\le m,t\in [0,T],\hfill \end{array}\right)\end{array}$$ 1

where the functions $u:\mathbb{R}\to {\mathbb{R}}^m$, $f:{\mathbb{R}}^n\times {\mathbb{R}}^m\times \mathbb{R}\to {\mathbb{R}}^n$, $g:{\mathbb{R}}^n\times {\mathbb{R}}^m\times \mathbb{R}\to \mathbb{R}$ and $\varphi :{\mathbb{R}}^n\times \mathbb{R}\to \mathbb{R}$ are assumed to be continuously differentiable. By representing the optimal control function u(t) as a neural network

$$\begin{array}{c}\hfill u(t)={\text{NeuralNetwork}}_{\theta }(t,x)\end{array}$$ 2

receiving t and x as inputs (see Fig. 1), the optimal control problem (1) becomes a parameter optimization problem as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \underset{\theta }{min}J={\int }_0^{T}g(x,{\text{NeuralNetwork}}_{\theta }(t,x),t)dt+\varphi (x(T),T)\hfill \\ \hfill & s.t.\frac{\text{d}x}{\text{dt}}=f(x,{\text{NeuralNetwork}}_{\theta }(t,x),t),x(0)=x_0,t\in [0,T],\hfill \\ \hfill \end{array}\right)\end{array}$$ 3

which can be learned by modern differential programming methods such as auto differentiation (Baydin et al. 2018; Ma et al. 2021) and adjoint sensitivity analysis method (Cao et al. 2003), and mature first order optimizers like Adam (Kingma and Ba 2014, Kochenderfer and Wheeler 2019, Chapter 5) or other second order optimizers like L-BFGS (Jorge and Stephen 2006, Kochenderfer and Wheeler 2019, Chapter 6). The last layer of the neural network is defined as

$$\begin{array}{c}\hfill \text{Lastlayer}(u):=\left(\begin{array}{cc}& a_1+(b_1-a_1)\sigma (u_1)\hfill \\ \hfill & a_2+(b_2-a_2)\sigma (u_2)\hfill \\ \hfill & \cdots \hfill \\ \hfill & a_m+(b_m-a_m)\sigma (u_m)\hfill \\ \hfill \end{array}\right),\end{array}$$ 4

where $\sigma (x):=1/(1+exp(-x))$ is sigmoid function. The last layer can be regarded as a hard constraint to satisfy $u_i(t)\in [a_i,b_i],1\le i\le m$ in optimal control problem (1).

Fig. 1.

Scheme of deep learning method to solve optimal control problem (1)

To better introduce deep learning techniques, we focus on optimal control problems without path constraints. However, general optimal control problems with additional continuously differentiable path constraints condition $h:{\mathbb{R}}^n\times {\mathbb{R}}^m\to {\mathbb{R}}^k$,

$$\begin{array}{c}\hfill h(x(t),u(t))\le 0,t\in [0,T],\end{array}$$ 5

can be transformed into optimal control problem (1) by augmented lagrangian method (Ito and Kunisch 1990), penalty method (Jorge and Stephen 2006, Chapter 17), barrier or relaxed barrier method (Auslender 1999; Feller and Ebenbauer 2016).

Optimal control is a broad concept, and it is core or engine of many real world problems, even the essence of training deep learning models is to solve optimal control problems (Benning et al. 2019). Many data driven epidemic problems can be regarded as or transformed to optimal control problems. By fixing control function u(t) as constant vector, epidemic models calibration is a special case of optimal control problems (1). Moreover, epidemic forecasting and epidemic model discovery can also be treated as optimal control problem. Let u(t) be some unknown epidemic mechanisms which needs to be learned by some kind of loss function

$$\begin{array}{c}\hfill \text{Loss}=\sum _{i=1}^N\Vert \tilde{g}(x(t_i))-y_i\Vert ,\end{array}$$

where $y\in {\mathbb{R}}^N$ is observation data, then the objective function in (1) can be represented by Dirac function

$$\begin{array}{c}\hfill L={\int }_0^{T}g(x,u,t)dt={\int }_0^T\sum _{i=1}^N\Vert \tilde{g}(x(t))-y_i\Vert \delta (t-t_i)dt.\end{array}$$

The rest of the paper is organized as follows. In Sect. 2, we will introduce deep learning techniques (universal differential equation method) and algorithm to train the neural networks embedded in differential equations. In Sect. 3, we will briefly review traditional methods to solve optimal control problems including direct, indirect and dynamic programming methods, compare deep learning method with these methods, and see how traditional methods can be combined with deep learning method. We will give several examples in Sect. 4 including classic optimal control, epidemic forecasting and model discovery problems. Conclusion and discussion will be in Sect. 5.

Universal differential equation method

Universal differential equation (UDE) (Rackauckas et al. 2020) is a special kind of differential equation with universal approximators embedded. “Universal” here means universal approximators and can be neural networks, Gaussian process, decision trees, Chebyshev polynomials, Fourier series and other parametric or nonparametric approximator kernels. Throughout this paper, we use neural networks as universal approximator. UDE couples differential equation and deep learning architectures for scientific machine learning, and can be accurately and efficiently extrapolate beyond the original partially observation data, obtain differentiable and fully observed fitting data, all in a time and data-efficient manner. In this section, we will introduce deep neural network and universal differential equation, and show how to train the parameter optimization problem (3) with neural network embedded.

Deep neural network

Deep neural network (DNN), as a universal approximator or feature extractor, is a special kind of compositional function which applies linear and nonlinear transformations to the inputs recursively (see the diagram of a deep neural network in Fig. 1). In recent years, a lot of different deep neural networks architectures are proposed (Goodfellow et al. 2016), such as feed-forward neural network (FNN, also called multi-layer perceptron (MLP)), convolution neural network (CNN), recurrent neural network (RNN), long short-term memory (LSTM), gate recurrent unit (GRU). Throughout this paper, we only use the simplest feed-forward neural network architectures, which is sufficient for approximating the optimal control functions. However, the core ideas and training techniques can also be extended to other complicated neural network architecture. For example, CNN can be applied in spatial epidemic models with human or host diffusion.

Let ${\mathcal{L}}^L(x):{\mathbb{R}}^{d_{\mathit{input}}}\to {\mathbb{R}}^{d_{\mathit{output}}}$ be an L-layer feed-forward neural network, also called as $(L-1)$-hidden layer neural network. $N_k,k=0,1,2,\dots ,L$ denotes the number of neurons in the kth layer with $N_0=d_{\mathit{input}}$ and $N_L=d_{\mathit{output}}$. Denote the weight matrix and bias vector in the kth layer by $W^k\in {\mathbb{R}}^{N_k\times N_{k-1}}$ and $b^k\in {\mathbb{R}}^{N_k}$, respectively. Then the FNN can be recursively defined as follows:

• input layer: ${\mathcal{L}}^0(\mathbf{U})=\mathbf{U}\in {\mathbb{R}}^{d_{\text{input}}}$.

• hidden layers: ${\mathcal{L}}^k(\mathbf{U})=\sigma \left(W^k,{\mathcal{L}}^{k-1},(\mathbf{U}),+,b^k\right)\in {\mathbb{R}}^{N_k}$ for $1\le k\le L-1$.

• output layer: ${\mathcal{L}}^L(\mathbf{U})=W^L{\mathcal{L}}^{L-1}(\mathbf{U})+b^L\in {\mathbb{R}}^{d_{\mathit{output}}}$,

where $W^k$ is a matrix or tensor, and $\sigma$ is a nonlinear activation function, and can be logistic sigmoid, the hyperbolic tangent (tanh), the rectified linear unit (ReLU, $max\{x,0\}$) and swish function ($x\ast \text{sigmoid}(x)$) or other activation functions (see Dubey et al. 2022 for review). Here, activation functions in different layers can be different.

The most fundamental and important property of DNN is that a single layer neural network can simultaneously and uniformly approximate a function and its partial derivatives, which is often called as universal approximation theorem. Let ${\mathbb{Z}}^{d+}$ be d-dimensional nonnegative integers set. For $m=(m_1,\cdots ,m_d)\in {\mathbb{Z}}^{d+}$, set $|m|:=m_1+\cdots +m_d$, and

$$\begin{array}{c}\hfill D^{\mathbf{m}}:=\frac{{\partial }^{|\mathbf{m}|}}{\partial x_1^{m_1}\dots \partial x_d^{m_d}}.\end{array}$$

We say $f\in C^m({\mathbb{R}}^d)$ if $D^{k}f\in C({\mathbb{R}}^d)$ for all $k\le m,k\in {\mathbb{Z}}^{d+}$, where $C({\mathbb{R}}^d)=\{f:{\mathbb{R}}^d\to \mathbb{R}|fiscontinuous\}$ is the space of continuous functions. Then we have the following universal approximate theorem of derivatives using single hidden layer neural networks (Pinkus 1999).

Theorem 1

(Pinkus 1999) Let $m_i\in {\mathbb{Z}}^{d+},i=1,\dots ,s$, and set $m={min}_{i=1,\dots ,s}|m_i|$. Assume $\sigma \in C({\mathbb{R}}^d)$ and that $\sigma$ is not a polynomial. Then a single hidden layer neural network:

$$\begin{array}{c}\hfill \mathcal{M}(\sigma ):=\mathbf{span}\left\{\sigma ,(\mathbf{w}·\mathbf{U}+b),:,\mathbf{w},\in ,{\mathbb{R}}^d,,,b,\in ,\mathbb{R}\right\}\end{array}$$

is dense in

$$\begin{array}{c}\hfill C^{{\mathbf{m}}^1,\dots ,{\mathbf{m}}^s}\left({\mathbb{R}}^d\right):={\cap }_{i=1}^s{C}^{{\mathbf{m}}^t}\left({\mathbb{R}}^d\right).\end{array}$$

Universal approximation theorem theoretically ensures that deep neural networks can approximate unknown mappings or operators by directly learning the entire set of nonlinear interactions from data. Deep neural networks method is shown practically to easily find good surrogate to fit the data or do model calibration. More importantly, good surrogate doesn’t need to be unique, which implies a belief in practice that for large neural networks, a local minima is enough and global minima often leads to over-fitting, which is still under theoretical investigating.

Universal differential equation

Before UDE, we first introduce neural differential equations (Chen et al. 2018), which inspired the ideas in UDE and can be regarded as a special case of UDE. Neural differential equations are initial value problems with the following form:

$$\begin{array}{c}\hfill u^{\prime }={\text{NeuralNetwork}}_{\theta }(u,t),\end{array}$$ 6

where ${\text{NeuralNetwork}}_{\theta }$ is a deep neural network receiving [u, t] as input and $\theta$ is weight parameter vector. From the perspective of deep learning, neural differential equations are redesigned sequential neural networks based on numerical schemes of differential equation, and they can be regarded as continuous-depth or “infinitely deep” ResNet-like deep learning models. Since the embedded neural network in Neural ODE is a universal approximator, it follows that neural differential equations can learn to approximate any differential equation with sufficient regularity.

However, neural differential equations haven’t broken away from the category of deep learning and are still data driven methods without including knowledge or known mechanisms. UDE extends the previous data-driven neural ODE approaches to directly utilize mechanistic modeling simultaneously with universal approximators. UDE are initial value problems as follows:

$$\begin{array}{c}\hfill u^{\prime }=f_{{\theta }_2}(u,t,{\text{NeuralNetwork}}_{{\theta }_1}(u,t)),\end{array}$$ 7

where f is a knowledge based or known mechanistic model and $\text{NeuralNetwork}$ denotes the missing or unknown terms, ${\theta }_1$ and ${\theta }_2$ are parameters of known mechanisms and neural networks, respectively, which can be estimated simultaneously. UDE is data-driven, knowledge based method, which has stronger explainability than black box deep neural networks or neural differential equations, since they keep known mechanisms in physics, chemistry, ecology or epidemiology. UDE is proved to be a method with good generalization and can be trained with less sample data (Rackauckas et al. 2020).

Adjoint sensitivity analysis and training techniques

Now it remains to solve the differential equation constrained parameter optimization problem (3). Let ${\Phi }_{\theta }(t):{\mathbb{R}}^n\to {\mathbb{R}}^n$ be solution map of the ODE

$$\begin{array}{c}\hfill \frac{\text{d}x}{\text{dt}}=f(x,{\text{NeuralNetwork}}_{\theta }(t,x),t),x(0)=x_0,t\in [0,T].\end{array}$$

Then $x(t)={\Phi }_{\theta }(t)x_0$, which transform optimization problem (3) to an unconstrained optimization problem

$$\begin{array}{cc}\hfill \underset{\theta }{min}J=F(\theta )=& {\int }_0^{T}g({\Phi }_{\theta }(t)x_0,\hfill \\ \hfill & {\text{NeuralNetwork}}_{\theta }(t,{\Phi }_{\theta }(t)x_0),t)dt+\varphi ({\Phi }_{\theta }(T)x_0,T).\hfill \end{array}$$ 8

Except for the solution map ${\Phi }_{\theta }$, problem (8) is no mystery and only concerned with parameter $\theta$. However, first order optimizers like Adam (Kingma and Ba 2014, Kochenderfer and Wheeler 2019, Chapter 5) or second order optimizers like L-BFGS (Jorge and Stephen 2006, Kochenderfer and Wheeler 2019, Chapter 6) can not directly be applied on unconstrained optimization problem (8), for large neural networks. The reason is that “backpropagation” (Goodfellow et al. 2016) does not work anymore. To apply modern differential programming techniques, we need to evaluate

$$\begin{array}{cc}\hfill \frac{\text{d}F(\theta )}{\text{d}\theta }=& {\int }_0^T\left[g_x,\frac{\text{d}{\Phi }_{\theta }(t)x_0}{\text{d}\theta },+,g_u,\left(\frac{\text{d}{\text{NeuralNetwork}}_{\theta }}{\text{d}\theta }\right)\right)\hfill \\ \hfill & \left(\left(+,{({\text{NeuralNetwork}}_{\theta })}_x,\frac{\text{d}{\Phi }_{\theta }(t)x_0}{\text{d}\theta }\right)\right]dt.\hfill \end{array}$$ 9

This is not a trivial task, at least for calculation $\frac{\text{d}{\Phi }_{\theta }(t)x_0}{\mathrm{d}\theta }.$ Assume that $\theta$ is $N_{\theta }$-dimensional, to calculate $\frac{\text{d}{\Phi }_{\theta }(t)x_0}{\mathrm{d}\theta }$, we need to solve the following $n+N_{\theta }$ dimensional ODE:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \frac{\text{d}x}{\text{dt}}=f(x,{\text{NeuralNetwork}}_{\theta }(t,x),t),\hfill \\ \hfill & \frac{\text{d}\left(\frac{\text{d}{\Phi }_{\theta }(t)x_0}{\text{d}\theta }\right)}{\text{dt}}=f_x\frac{\text{d}{\Phi }_{\theta }(t)x_0}{\text{d}\theta }\hfill \\ \hfill & +f_u\left(\frac{\text{d}{\text{NeuralNetwork}}_{\theta }}{\text{d}\theta },+,{({\text{NeuralNetwork}}_{\theta })}_x,\frac{\text{d}{\Phi }_{\theta }(t)x_0}{\text{d}\theta }\right),\hfill \end{array}\right)\end{array}$$ 10

where $f_u,f_x$ are dense jacobians also needing a lot of computation resources. In large neural networks ($N_{\theta }$ is large), for every step in the loop of optimization, we will need to solve $n+n\ast N_{\theta }$ dimensional ODE, which spends huge computational resources.

Therefore, the key issue of solving parameter optimization problem (3) is how to implement “backpropagation” (Goodfellow et al. 2016) for differential equations. Fortunately, it is not new story in optimal control theory. “Backpropagation” for differential equations can date back to 1960s when Pontryagin’s maximium principle (Pontryagin 1962) was developed. From the perspective of optimal control, the training of neural differential equations can be regarded as optimal control problems, which extend the idea of backpropagation (Goodfellow et al. 2016) in differential programming to include adjoint sensitivity analysis (Cao et al. 2003).

In what follows, we will introduce adjoint sensitivity analysis in detail. With adjoint sensitivity analysis results, first order optimizers like Adam (Kingma and Ba 2014) can be directly applied with no mystery even for large neural networks. For simplicity, we consider the following reformulated differential equation constrained parameter optimization problem:

$$\begin{array}{c}\hfill \underset{\theta }{min}J(\theta )={\int }_0^{T}e(y,t)dt,s.t.y^{\prime }=m(y,\theta ,t),y(0)=y_0.\end{array}$$ 11

Here y can be regarded as neural networks (neural differential equations) or dynamics including neural networks (universal differential equations). Note that optimal control problem (3) can be rewritten to (11) by Dirac function

$$\begin{array}{c}\hfill \varphi (x(T),T)={\int }_0^T\delta (t-T)\varphi (x(t),t).\end{array}$$

Moreover, if the optimal control problem is data-driven and the loss function is discrete, i.e.,

$$\begin{array}{c}\hfill \sum _{i=1}^{N}l(y(t_i)),\end{array}$$

we can rewrite discrete loss function by Dirac function

$$\begin{array}{c}\hfill \sum _{i=1}^{N}l(y(t_i))={\int }_0^T\sum _{i=1}^{N}l(y(t))\delta (t-t_i)dt.\end{array}$$

Our purpose here is to derive the “backpropagation” of derivatives of $J(\theta )={\int }_0^{T}e(y)dt$ to $\theta$. By introducing adjoint variable $\lambda (t)$, we obtain

$$\begin{array}{c}\hfill J(\theta )={\int }_0^{T}e(y,t)dt={\int }_0^{T}e(y,t)dt+{\int }_0^T\lambda (t)\left(m,(y,\theta ,t),-,y^{\prime },(t)\right)dt.\end{array}$$

Then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\text{d}J}{\text{d}\theta }& ={\int }_0^T{e}_y{y}_{\theta }dt+\lambda (T)y_{\theta }{|}_{t=T}+{\int }_0^T{\lambda }^{\prime }(t)y_{\theta }dt\hfill \\ \hfill & +{\int }_0^T\lambda (t)\left(m_y,y_{\theta },+,m_{\theta }\right)dt\hfill \\ \hfill & ={\int }_0^T\left[{\lambda }^{\prime },(t),+,e_y,+,m_y,\lambda ,(t)\right]y_{\theta }dt+{\int }_0^T\lambda (t)m_{\theta }dt+\lambda (T)y_{\theta }{|}_{t=T}.\hfill \end{array}\end{array}$$

Let

$$\begin{array}{c}\hfill {\lambda }^{\prime }(t)=-e_y-m_y\lambda (t),\lambda (T)=0.\end{array}$$ 12

We obtain

$$\begin{array}{c}\hfill \frac{\text{d}J}{\text{d}\theta }={\int }_0^T\lambda (t)m_{\theta }dt.\end{array}$$ 13

If the loss function is discrete, i.e.,

$$\begin{array}{c}\hfill e(u,t)=\sum _{i=1}^{N}l(y(t))\delta (t-t_i),\end{array}$$

then system (12) becomes an impulsive system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\lambda }^{\prime }(t)=-m_y\lambda (t),\hfill \\ \hfill & \lambda (t_i^{+})=\lambda (t_i^{-})+l_y(y(t_i)),i=1,2,\cdots ,N.\hfill \end{array}\right)\end{array}$$ 14

We have the following adjoint sensitivity result:

Theorem 2

Let

$$\begin{array}{c}\hfill J(\theta )={\int }_0^{T}e(y,t)dt,y^{\prime }=m(y,\theta ,t),y(0)=y_0,\end{array}$$

where $\theta \in {\mathbb{R}}^k$ and the functions $m:{\mathbb{R}}^n\times {\mathbb{R}}^k\times \mathbb{R}\to {\mathbb{R}}^n$, $e:{\mathbb{R}}^n\times {\mathbb{R}}^m\times \mathbb{R}\to \mathbb{R}$ are continuously differentiable. Then we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \frac{\text{d}J}{\text{d}\theta }={\int }_0^T\lambda (t)m_{\theta }dt,\hfill \\ \hfill & {\lambda }^{\prime }(t)=-e_y-m_y\lambda (t),\lambda (T)=0,\hfill \\ \hfill & y^{\prime }=m(y,\theta ,t),y(0)=y_0.\hfill \end{array}\right)\end{array}$$ 15

From Theorem 2, to calculate $\frac{\text{d}J}{\mathrm{d}\theta }$, we only need to solve 2n dimensional ODE. The dimensional is not dependent on the dimension of parameter $\theta$, which makes the couple of large scale neural networks and differential equations possible. Two approaches are possible to numerically solve $\frac{\text{d}J}{\mathrm{d}\theta }$ in (15). One is continuous adjoint method, also called the differentiate-then-discretize approach, which applies a numerical discretization to solve the adjoint ODE ($\lambda (t)$) in (15). Another is discrete adjoint sensitivity, also called as discretize-then- differentiate method, which first numerically approximates the forward system (y(t)) and then obtain the adjoint of the discrete system of (y(t)). The detailed comparison of these two methods to evaluate adjoint sensitivities is not our focus and can be seen in Zhang and Sandu 2014; Ma et al. 2021. The algorithm to train the universal differential equation is shown in Algorithm 1.

Comparison and combination with traditional optimal control methods

We will briefly review traditional methods to solve optimal control problems including direct, indirect and dynamic programming methods, compare deep learning methods with these traditional methods, and see how traditional methods can be combined with deep learning method to improve the training efficiency and reduce the training time. This part can also be regarded as additional materials for Optimal Control Applied to Biological Models (2007)Lenhart and Workman (2007). All methods mentioned are shown in Fig. 2.

Fig. 2.

Optimal control methods including direct, indirect, dynamic programming and deep learning

Direct method

The core of a direct method is to transform the original optimal control problem (1) to a nonlinear programming problem (NLP) without including adjoint information, and then some well-developed and mature NLP optimizers can be seamlessly applied at a low cost. These NLP optimizers include Ipopt (open source, Wächter and Biegler (2006)), SNOPT (limited academic license, Gill et al. (2005)), Knitro (commercial with limited academic license, Byrd et al. (2006)) and so on (see review Kronqvist et al. (2019) for more details). Compared with indirect and dynamic programming methods, direct methods do not need adjoint information such as Pontryagin’s maximum principle (Pontryagin 1962) or Hamilton–Jacobi–Bellman equation (Bellman 1966). This makes direct methods less accurate but possible to be easily posted and widely used to solve highly complicated nonlinear optimal control problems in real-life application.

Direct methods are quite broad and encompasses many techniques (Betts 2010), different from the way control and states to be discretized, how to handle differential equations. These transcription methods can be divided into two main classes: shooting methods and collection methods. Shooting methods includes direct single shooting (Hicks and Ray 1971) and multiple shooting (Bock and Plitt 1984). Direct single shooting method is the simplest method for transcribing an optimal control problem to NLP. It first parameterizes the control function u(t) by using surrogates like polynomials, piecewise polynomials, or simply piecewise constants, and then use embedded numerical ODE solvers to eliminate the differential equations, and apply adjoint sensitivity analysis (Cao et al. 2003) to compute the jacobians of the continuity and boundary conditions with respect to the parameters. Choose a fixed time grid

$$\begin{array}{c}\hfill 0=t_0<t_1<\cdots <t_N=T\end{array}$$

and set the control function

$$\begin{array}{c}\hfill u(t,c)=c_i,1\le i\le N,t\in [t_i,t_{i+1}],\end{array}$$

where the parameter $c=[c_0,c_1,\cdots ,c_{N-1}]$ is mN dimensional vector. By using robust ODE solvers, we can obtain x(t, c), which transcribe the optimal control problem to the following NLP:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \underset{c\in {\mathbb{R}}^{\mathit{mN}}}{min}J={\int }_0^{T}g(x(t,c),u(t,c),t)dt+\varphi (x(T,c),T)\hfill \\ \hfill & c_{\mathit{ij}}\in [a_j,b_j],0\le i\le N-1,1\le j\le m.\hfill \end{array}\right)\end{array}$$ 16

Multiple shooting (Bock and Plitt 1984) breaks up the time grid into some number of segments, and using single shooting method to solve for each segment. The idea behind the direct multiple shooting method stems from the observation that long integration of dynamics can be counterproductive for transcribing continuous optimal control problems into NLP, and this problem can be tackled by limiting the integration over arbitrarily short time intervals. In contrast to single shooting methods, multiple shooting solves the ODE separately on each interval $[t_i,t_{i+1}]$,

$$\begin{array}{c}\hfill \frac{\text{d}{x}_i(t,c_i,s_i)}{\text{dt}}=f(x_i(t,c_i,s_i),c_i,t),x_i(t_i,c_i,s_i)=s_i,t\in [t_i,t_{i+1}],\end{array}$$

which transcribe the optimal control problem to the following NLP:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \underset{c\in {\mathbb{R}}^{\mathit{mN}},s\in {\mathbb{R}}^{N+1}}{min}J=\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}g(x_i(t,c_i,s_i),c_i,t)dt+\varphi (s_N)\hfill \\ \hfill & c_{\mathit{ij}}\in [a_j,b_j],0\le i\le N-1,1\le j\le m,\hfill \\ \hfill & x_i(t_{i+1},c_i,s_i)=s_{i+1},0\le i\le N-1,\hfill \\ \hfill & x_0=s_0.\hfill \end{array}\right)\end{array}$$ 17

For direct collection method, both state and control functions are parameterized by surrogates like high order polynomial functions, which avoid the adjoint sensitivity analysis of direct shooting methods at the cost of a larger NLP. The collocation points (knots) for these methods are located at the roots of an orthogonal polynomial, for example, using Chebyshev or Legendre basis (Darby et al. 2011). In contrast to direct shooting method, the state function is approximated by a combination of polynomial basis. For time interval $[t_i,t_{i+1}]$, choose collocation points

$$\begin{array}{c}\hfill t_i=t_{i,0}<t_{i,1}<\cdots <t_{i,d}=t_{i+1}\end{array}$$

and set

$$\begin{array}{c}\hfill x(t)=p_i\left(t,,,v_i\right)=\sum _{k=0}^d{v}_{i,k}{\ell }_{i,k}(t)\end{array}$$

and the Lagrange basis for example,

$$\begin{array}{c}\hfill {\ell }_{i,k}(t)=\prod _{j=0,j\ne k}^d\frac{t-t_{i,k}}{t_{i,k}-t_{i,j}}\in \mathbb{R}.\end{array}$$

Then optimal control problem can be transposed to the following sparse NLP problem:

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{v\in {\mathbb{R}}^{\mathit{dN}},q\in \mathbb{R}\mathit{mN}}{min}\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}g(p_i\left(t,,,v_i\right),c_i,t)dt+\varphi (v_{N,0})\hfill \\ \hfill & \text{s.t.}{\dot{p}}_i\left(t_{i,k},,,v_i\right)-f\left(v_{i,k},,,q_i\right)=0,i=0,\cdots ,N-1,k=1,\cdots ,d,\hfill \\ \hfill & p_i\left(t_{i+1},,,v_i\right)-v_{i+1,0}=0,i=0,\cdots ,N-1,\hfill \\ \hfill & v_{0,0}-x_0=0,\hfill \end{array}\end{array}$$ 18

where the derivatives are concerned with polynomials and the integration can be handled by methods like Gaussian quadrature. To increase the accuracy of direct collection method, either the number of trajectory segments (h-method) or the order of the polynomial in each segment (p-method). One important reason to use high-order orthogonal polynomials in direct collection method is that they provide accurate approximations that converge exponentially for problems whose solutions are smooth (Rao 2009).

Indirect method

The essence of indirect methods is to change the optimal control problem (1) to a fixed point problem by Pontryagin’s maximium principle (Pontryagin 1962). Indirect methods use the Hamiltonian function

$$\begin{array}{c}\hfill H(x,u,\lambda )=g(x,u,t)+\lambda {(t)}^{T}f(x,u,t)\end{array}$$ 19

to derive the necessary conditions for optimality which is a two-point boundary value problem (TPBVP),

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{\text{d}x}{\text{dt}}={\mathrm{\nabla }}_{\lambda }{H}^{\ast }(x(t),\lambda (t)),t\in [0,T],\hfill \\ \hfill & x(0)=x_0,\hfill \\ \hfill & \frac{\text{d}\lambda }{\text{dt}}=-{\mathrm{\nabla }}_x{H}^{\ast }(x(t),\lambda (t)),t\in [0,T],\hfill \\ \hfill & \lambda (T)=\mathrm{\nabla }\varphi (x(T)),\hfill \\ \hfill \end{array}\end{array}$$ 20

where $H^{\ast }(x(t),\lambda (t))=H(x,u^{\ast }(t),\lambda (t))$ and

$$\begin{array}{c}\hfill u^{\ast }(x,\lambda )=\underset{u\in \mathcal{U}}{argmin}H(x,u,\lambda ),\mathcal{U}=[a_1,b_1]\times [a_2,b_2]\times \cdots \times [a_m,b_m]\subset {\mathbb{R}}^m.\end{array}$$ 21

Note here that for state function x(t), the boundary condition is at $t=0$, while for adjoint function $\lambda (t)$, the boundary condition is at $t=T$. Thus TPBVP (20) can not be solved by numerical ODE solver (Rackauckas and Nie 2017). Similar to direct methods, shooting methods or collection (pseudo-spectral) methods are ofen applied to solve TPBVP (Betts 2010). The ideas behind indirect shooting method and indirect collection method are similar to direct methods, so we omit the details here. Moreover, the derivation of TPBVP can be equivalently obtained by Pontryagin’s maximum principle (Pontryagin 1962), calculus of variational or dynamic programming. We didn’t give much detail here since it is not our focus, one can see (Li and Yong 1995, Chapter 4) for more details.

Compared with direct methods, indirect methods include adjoint information of optimal control problem (1). Thus indirect methods are more accurate. However, derivation of TPBVP by Pontryagin’s maximum principle (Pontryagin 1962) or Hamilton–Jacobi–Bellman equation (Bellman 1966) makes optimal control problem (1) hard to be posted, thus it is not easy to solve highly complicated nonlinear optimal control problems in real-life application. Moreover, solving TPBVP greatly depends on a good initial guess, which can not be easily obtained for large optimal control problem.

Dynamic programming method

Dynamic programming (DP) method was developed in the fifties and sixties of the 19th century, most prominently by Bellman (1966), and now it attracts much attention due to the popularity of Reinforcement Learning (Sutton and Barto 2018). Thanks to Bellman principle, optimal control problem (1) can be transformed to the following Hamilton–Jacobi–Bellman (HJB) equation

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{\partial }{\partial t}V(x,t)+\underset{u\in \mathcal{U}}{min}H\left(x,,,u,,,{\mathrm{\nabla }}_x,V,(x,t),,,t\right)=\mathbf{0},t\in (0,T),\hfill \\ \hfill & V(x,T)=\varphi (x),x\in {\mathbb{R}}^n,\hfill \end{array}\end{array}$$ 22

where H is Hamiltonian defined as (19), V(x, t) is the value function

$$\begin{array}{c}\hfill V(x,t)=\underset{u(·)}{min}J={\int }_t^{T}g(x,u,s)ds+\varphi (x(T),T).\end{array}$$

After solving the HJB equation (22), the optimal control function can be obtained from

$$\begin{array}{c}\hfill u^{\ast }(t)=\underset{u\in \mathcal{U}}{min}H\left(x,,,u,,,{\mathrm{\nabla }}_x,V,(x,t),,,t\right),\end{array}$$

and the state function is the solution of the following ODE

$$\begin{array}{c}\hfill \frac{\text{d}x}{\text{dt}}=f(x,u^{\ast },t),x(0)=x_0,t\in [0,T].\end{array}$$

However, solving HJB equation (22) is not an easy task and faces well-known Bellman curse of dimensionalty. The easiest way to solve HJB equation (22) is using DP to directly discrete state space, control space and time space. Assume that each state dimension has $N_x$ alternative values, each control dimension has $N_u$ alternative values and time [0, T] is divided to N segments, then the computation complexity will be $\mathcal{O}(N\ast N_x^n\ast N_u^m)$. Due to curse of dimensionality, simple DP can only be used in low-dimensional optimal control problem. To reduce the computation complexity, methods like Differential Dynamic Programming (Jacobson and Mayne 1970) or iterative LQR (Li and Todorov 2004) were proposed to break the problem into cascaded of subproblems. Approximate dynamic programming methods like DDP are fast and have a low memory, making them amenable to embedded implementation. However, DDP or iLQR methods are less numerically robust and less well-suited to handling nonlinearity in state and constraints.

Finally, we listed several frequently used open source packages to solve optimal control problem, especially on Julia Language (Bezanson et al. 2017) in Table 1.

Table 1.

Open source packages to solve optimal control problem

Packages	Methods	Languages
Casadi (Andersson et al. 2019)	Direct, Indirect	Python, C++, Julia
PSOPT (Becerra 2010)	Direct	Python, C++
InfiniteOpt.jl (Pulsipher et al. 2022)	Direct	Julia
DifferentialEquations.jl (Rackauckas and Nie 2017)	Indirect	Julia
TrajectoryOptimization.jl (Howell et al. 2019)	DP	Julia

Comparison and combination between different methods

Without relying on adjoint information such as Pontryagin’s maximum principle (Pontryagin 1962) or Hamilton–Jacobi–Bellman equation (Bellman 1966), direct methods are less accurate but more flexible to solve highly complicated nonlinear optimal control problems in real-life application. Compared with direct methods, indirect methods include adjoint information of optimal control problem. Indirect methods are more accurate but hard to be posted since derivation of TPBVP by Pontryagin’s maximum principle (Pontryagin 1962) needs much manually work, especially for pure state constraints. Moreover, solving TPBVP greatly depends on a good initial guess, making indirect methods not easy to solve highly complicated nonlinear optimal control problems in real-life application. Dynamic programming is easy to be posted and accurate, but solving HJB equation (22) is not an easy task and faces well-known Bellman curse of dimensionalty. Compared with traditional methods such as direct , indirect and dynamic programming, deep learning methods can integrate modern differential programming tools and neural networks are believed to some extent share bless of dimensionality. The comparison details are shown in Table 2.

Table 2.

Comparisons of different methods to solve optimal control. (DtO: discretize-then-optimize)

Methods	Direct method	Indirect method	HJB method	Deep learning
Transcriptions	Nonlinear programming problem (NLP)	Two point boundary value problem (TPBVP)	Dynamic programming	Parameter optimization
Trajectory or Parameter Optimization	Trajectory	Trajectory	Trajectory	Parameter
u(x, t) or x(u, t)	–	x(u, t)	u(x, t)	x(u, t)
OtD or DtO	DtO	OtD	DtO	DtO and OtD
Advantages	Mature Optimizers, easy to post, easy to solve	Accurate	Accurate	Accurate, bless of dimensionality, extendable
Disadvantages	Less accurate	Hard to post, hard to solve, initial guess	Curse of dimensionality	Theoretically under exploring, slow

Although deep learning method (UDE) is different from other methods, they can be combined. For long range time horizon optimal control problem or oscillation data driven problems, multiple shooting can be used to train the neural networks which helps to escape “flattened out” fitting for oscillation data (Turan and Jäschke 2022). Moreover, multiple shooting can also be combined with neural differential equation and become differential multiple shooting layer (Massaroli et al. 2021).

For data driven problems, training universal differential equations is computation consuming, especially for solving differential equations and adjoint sensitivity analysis. Collection methods can be combined to reduce the computation time. By using collection methods, we directly obtain $\frac{\text{d}x}{\text{dt}}$ from observation data points, which escapes from solving differential equations at a cost of low accuracy. Thus, collection method can be combined to pretrain the neural networks and help to obtain good initial value of parameters, and then Algorithm 1 can be applied to finish the training procedures.

Numerical simulations

In this section, we will use universal differential equation method to solve classic optimal control, epidemic forecasting and epidemic model discovery problems. For traditional methods to solve classic optimal control problems, only direct method is implemented since it is mostly used. Deep learning methods and direct collection methods are implemented in open source Julia language 1.8.2 (Bezanson et al. 2017), Laptop Y7000P with i5-9300HF CPU, 16G RAM. All algorithms and codes in this section are available in https://github.com/Song921012/OptEpiDeepL.

Optimal control problem with analytic solution

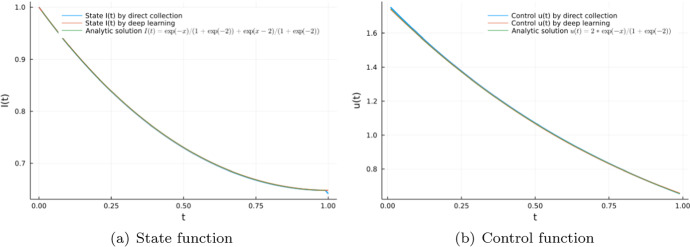
To start with, we solve Example 3.2 in Optimal Control Applied to Biological Models Lenhart and Workman (2007) with little modification

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{u}{min}{\int }_0^{1}u{(t)}^{2}dt+I{(1)}^2\hfill \\ \hfill & s.t.\frac{\text{d}I}{\text{dt}}=I(t)-u(t),I(0)=1,\hfill \end{array}\end{array}$$ 23

where I(t) can be regarded as infected population and u(t) are concerned with control measures. Optimal control problem (23) admits analytic solution

$$\begin{array}{c}\hfill I(t)=exp(-t)/(1+exp(-2))+exp(t-2)/(1+exp(-2))\end{array}$$

and

$$\begin{array}{c}\hfill u(t)=2exp(-t)/(1+exp(-2)).\end{array}$$

By representing u(t) as a $1\times 64\times 1$ full connected neural networks with $tanh$ activation function, optimal control problem (23) becomes a parameter optimization problem, which can be trained by Algorithm 1. From Fig. 3, both direct collection method and deep learning method fit the analytic solution well.

Fig. 3.

a State function for optimal control problem (22) by direct collection and deep learning method; b control function for optimal control problem (22) by direct collection and deep learning method optimal

SEIR model based epidemic control

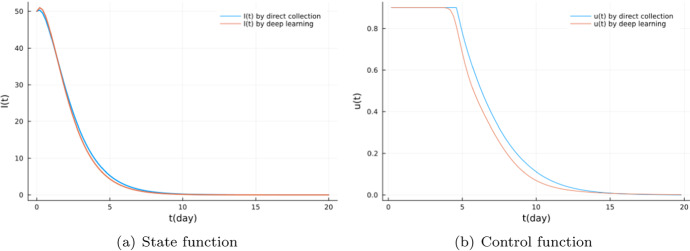
In this example, we will use universal differential equation method to solve the following epidemic control problem

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{u(t)}{min}{\int }_0^T\beta S(t)I(t)+Au{(t)}^{2}dt\hfill \\ \hfill & s.t.S^{\prime }=\Lambda -\beta SI-dS-u(t)S,\hfill \\ \hfill & E^{\prime }=\beta SI-(d+\sigma )E,\hfill \\ \hfill & I^{\prime }=\sigma E-(d+\gamma )I,\hfill \\ \hfill & S(0)=S_0,E(0)=E_0,I(0)=I_0,\hfill \\ \hfill & u(t)\in [a,b],\hfill \end{array}\end{array}$$ 24

where S(t), E(t), I(t) denote the expected number of suspected, exposed and infected individuals, respectively, and u(t) are concerned with permanently removal rate of S, for example, vaccination rate. The objective of the epidemic control is less control strategies, less health resources and less total infections. A is the weight between the trade-off pair. A two hidden layer $1\times 32\times 32\times 1$ neural network is used to represent control function u(t),

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{\theta }{min}{\int }_0^T\beta S(t)I(t)+A{\text{NeuralNetwork}}_{\theta }{(t)}^{2}dt\hfill \\ \hfill & s.t.S^{\prime }=\Lambda -\beta SI-dS-{\text{NeuralNetwork}}_{\theta }(t)S,\hfill \\ \hfill & E^{\prime }=\beta SI-(d+\sigma )E,\hfill \\ \hfill & I^{\prime }=\sigma E-(d+\gamma )I,\hfill \\ \hfill & S(0)=S_0,E(0)=E_0,I(0)=I_0,\hfill \\ \hfill & u(t)\in [a,b],\hfill \end{array}\end{array}$$ 25

and the training procedures are similar to optimal control problem (23). Figure 4 shows that deep learning techniques obtains more accurate optimal control solution with similar training time.

Fig. 4.

a State function for optimal epidemic control problem (24) by direct collection and deep learning method; b control function for optimal epidemic control problem (24) by direct collection and deep learning method

Epidemic forecasting

In this example, we will transform epidemic forecasting problem to an optimal control problem. Particularly, we will apply UDE method on the first wave Covid-19 cases in Ontario, Canada, i.e., using UDE model (3) to fit the case data and training the neural networks embedded in differential equations, and doing epidemic forecasting. Traditional architectures like LSTM, RNN, GRU (Goodfellow et al. 2016), or neural ordinary differential equations $x^{\prime }=\text{NeuralNetworks}(x,t)$ are often undifferentiatedly applied to handle time series data without including knowledge or mechanisms. However, all of them omit the epidemiology. Here, we use the following universal differential equation model with part of epidemiology:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \frac{\text{d}S}{\text{dt}}=-{\text{NeuralNetwork}}_{\theta }(I)S,\hfill \\ \hfill & \frac{\text{d}I}{\text{dt}}={\text{NeuralNetwork}}_{\theta }(I)S-\gamma I,\hfill \\ \hfill & \frac{\text{d}H}{\text{dt}}={\text{NeuralNetwork}}_{\theta }(I)S,\hfill \end{array}\right)\end{array}$$ 26

where S(t), I(t) and H(t) denote the number of suspected individuals, infected individuals and accumulated confirmed cases at time t, $1/\gamma$ is infection period of infectious disease, and ${\text{NeuralNetwork}}_{\theta }(I)$ denotes force of infection. To fit the observation data, we need to solve the following ordinary differential equation constrained optimization problem:

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{\theta }{min}J=\sum _{i=1}^N{(H(t_i)-o_i)}^2\hfill \\ \hfill & s.t.\frac{\text{d}S}{\text{dt}}=-{\text{NeuralNetwork}}_{\theta }(I)S,\hfill \\ \hfill & \frac{\text{d}I}{\text{dt}}={\text{NeuralNetwork}}_{\theta }(I)S-\gamma I,\hfill \\ \hfill & \frac{\text{d}H}{\text{dt}}={\text{NeuralNetwork}}_{\theta }(I)S,\hfill \\ \hfill & S(0)=S_0,I(0)=I_0,H_0=I_0.\hfill \end{array}\end{array}$$ 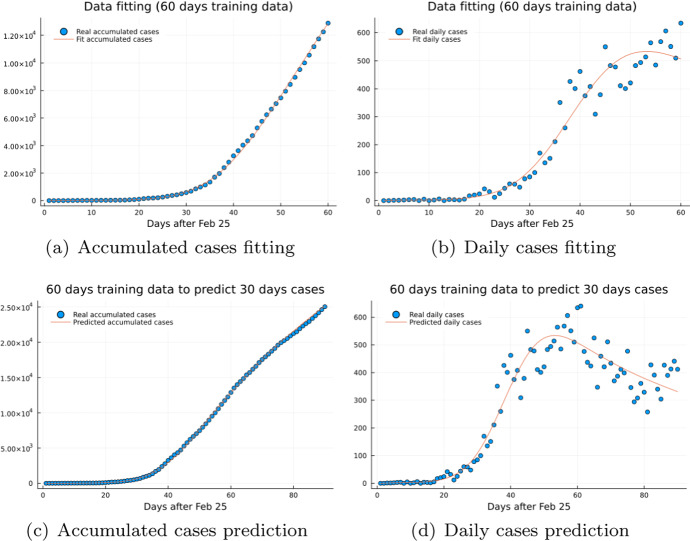27

Ontario’s first wave data began on Feb 25, 2020 and continued for about 150 days. In Fig. 5, 60 days Ontario’s first wave accumulated case data was used to train the neural network in (27), and the trained model is applied to forecast the epidemic in further 30 days. Figure 5a, b show that the trained model (26) fits the 60 days observation data very well, and generalize very well and is able to predict further 30 days cases (Fig. 5c, d).

Fig. 5.

60 days Ontario’s first wave case data to train neural networks in (27) and predict further 30 days case data. a, b Accumulated and daily cases data fitting. c Real accumulated cases and predicted accumulated cases. d Real daily cases and predicted daily cases

Epidemic model discovery

In this example, we generate data from the following SIR epidemic model with behavior change mechanism (Funk 2010; Verelst et al. 2016)

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \frac{\text{d}S}{\text{dt}}=-\beta Sexp(-\alpha I)I,\hfill \\ \hfill & \frac{\text{d}I}{\text{dt}}=\beta Sexp(-\alpha I)I-\gamma I.\hfill \end{array}\right)\end{array}$$ 28

Here, $\beta exp(-\alpha I)I$ is force of infection with media impact (Song and Xiao 2018). Our task here is to learn the force of infection function $exp(-\alpha I)I$ from the generated data, which can be done by three steps:

• Step one: setting up the optimal control problem,

  $$\begin{array}{c}\hfill \begin{array}{cc}& \underset{u(·),S(·),I(·)}{min}J=\sum _{i=1}^N[{(S(t_i)-o_{S,i})}^2+{(I(t_i)-o_{I,i})}^2]\hfill \\ \hfill & s.t.\frac{\text{d}S}{\text{dt}}=-u(t)S,\hfill \\ \hfill & \frac{\text{d}I}{\text{dt}}=u(t)S-\gamma I,\hfill \\ \hfill & S(0)=S_0,I(0)=I_0.\hfill \end{array}\end{array}$$ 29
• Step two: representing force of infection function by neural networks and training the resulting universal differential equation:

  $$\begin{array}{cc}& \underset{\theta }{min}J=\sum _{i=1}^N[{(S(t_i)-o_{S,i})}^2+{(I(t_i)-o_{I,i})}^2]\hfill \\ \hfill & s.t.\frac{\text{d}S}{\text{dt}}=-{\text{NeuralNetwork}}_{\theta }(I)S,\hfill \\ \hfill & \frac{\text{d}I}{\text{dt}}={\text{NeuralNetwork}}_{\theta }(I)S-\gamma I,\hfill \\ \hfill & S(0)=S_0,I(0)=I_0.\hfill \end{array}$$ 30

• Step three: recovering the simplest equation from neural networks by symbolic regression Schmidt and Lipson (2009).

From Fig. 6a, we can see that the training data in time span [0, 1] is enough to train universal differential equation (30), and it generalize well in time span [1, 4]. Moreover, Fig. 6b shows that neural networks fits the force of infection function $exp(-\alpha I)I$ well.

Fig. 6.

Universal differential equation (4) to learn the force of infection in transmission model (28). a Data fitting and prediction. b Real force of infection and learned force of infection

However, black box neural network is not what epidemiologist really need. In epidemiology, researchers care about both learning ability and interpreticity. We want to efficiently learn the missing mechanisms in transmission models and wish the missing mechanisms represented as simplest equation rather than black-box neural network, which is difficult to interpret in epidemiology. Symbolic Regression (SR) is a type of regression analysis that searches the space of mathematical expressions to find the model that best fits a given dataset, both in terms of accuracy and simplicity (Schmidt and Lipson 2009). After learning the parameters of neural networks, we generate data from neural networks and use the generated data to search the simplest equation:

$$\begin{array}{c}\hfill {\text{NeuralNetwork}}_{\theta }(I)\approx exp(-\alpha I)\ast I.\end{array}$$

Since this paper doesn’t focus on equation finding methods, we omit the details of symbolic regression here, one can see Schmidt and Lipson (2009), Song et al. (2022) for more details.

Conclusion and discussion

Deep neural network (LeCun et al. 2015; Goodfellow et al. 2016) is shown to be a universal approximator for unknown mappings with bless of dimensionality (Hornik et al. 1990; Han et al. 2018), which shows an unreasonable effectiveness (Sejnowski 2020) in pattern recognition, learning unknown mechanisms and solving traditional difficult problems such as image recognition (He et al. 2016), natural language processing (Devlin et al. 2018). In this paper, we use neural network to represent control functions and solve optimal control problems by deep learning techniques. The applications are not restricted in classical epidemic control problems, many data driven epidemiological problems like epidemic forecasting, unraveling missing transmission mechanisms, can be regarded as optimal control problems and solved by deep learning techniques. Compared with traditional methods such as direct, indirect and dynamic programming methods, deep learning methods can integrate modern differential programming tools and solve large scale optimal control problems.

We show how to extend the idea of backpropagation (Goodfellow et al. 2016) in differential programming to include adjoint sensitivity analysis (Pontryagin 1962; Cao et al. 2003). Thanks to adjoint sensitivity analysis, deep neural networks and dynamic systems can be coupled seamlessly. In this paper, only control function is represented by neural networks. Actually, high dimensional state function, for example, human mobility epidemic models with many patches, can also be approximated by neural networks,

$$\begin{array}{c}\hfill x(t)={\text{NeuralNetwork}}_{\tau }(t)\end{array}$$

and optimal control problem (1) can be transformed into

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{\theta }{min}J& ={\int }_0^{T}g({\text{NeuralNetwork}}_{{\tau }^{\ast }(\theta )}(t),{\text{NeuralNetwork}}_{\theta }(t),t)dt\hfill \\ \hfill & +\varphi ({\text{NeuralNetwork}}_{{\tau }^{\ast }(\theta )}(T),T),\hfill \end{array}\end{array}$$ 31

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tau }^{\ast }(\theta )& =arg\underset{\tau }{min}{\int }_0^T\left|\frac{\text{d}{\text{NeuralNetwork}}_{\tau }(t)}{\text{dt}}\right)\hfill \\ \hfill & -\left(f,(,{\text{NeuralNetwork}}_{\tau },(t),,,{\text{NeuralNetwork}}_{\theta },(t),,,t,)\right|dt\hfill \\ \hfill & +w|{\text{NeuralNetwork}}_{\tau }(0)-x_0|.\hfill \end{array}\end{array}$$ 32

The way in (32) to solve ODE by neural networks is often called physical informed neural networks (PINNs) (Raissi et al. 2019; Karniadakis et al. 2021). Moreover, neural networks (NNs) are not only universal approximators of continuous functions but also universal approximators of nonlinear continuous operator in infinite dimensional space, which implies that optimal control problem (1) can also be solved by neural operator (Lu et al. 2021).

This study also has some limitations. First, we didn’t add many details on solving general optimal control problems with path constraints. The tricks on how to transform general optimal control into problem (1) by augmented lagrangian method (Ito and Kunisch 1990), penalty method (Jorge and Stephen 2006, Chapter 17), barrier or relaxed barrier method (Auslender 1999; Feller and Ebenbauer 2016), are not included in our study. Second, we didn’t give much theoretical proof and complexity analysis which theoretically shows that deep learning methods can solve optimal control problems with bless of dimensionality. These problems will be our future work.