A pandemic business interruption insurance

Abstract

We analyze how pandemic business interruption coverage can be put in place by building on capitalization mechanisms and a portfolio management strategy. As evidenced with COVID-19, pandemics affect economic sectors in differentiated ways: some are very severely affected because their activity is heavily impacted by travel bans and constraints on work organization, while others are more resistant. This opens the door to risk-coverage mechanisms based on a portfolio of financial securities, including long-short positions and options in stock markets. We show that such a strategy allows insurers to offer business interruption coverage in pandemic states, while simultaneously hedging the risks associated with alternating bullish and bearish non-pandemic states. These conclusions contrast sharply with the idea of governments being the only solution to the pandemic insurability problem. They are derived from a theoretical model of corporate risk management, and their practical relevance is illustrated by numerical simulations, using data from the French stock exchange.

Introduction

In many countries, COVID-19 has been at the origin of dramatic losses due to business interruption. Because of the pandemic, workers, customers, and entrepreneurs were unable to pursue their activities normally, and therefore, firms were prevented from conducting business as usual. In this context, many firms turned to their insurance policies, in the hope that business interruption claims could be filed to recover losses resulting from the health crisis. Business interruption coverage is typically included as part of a company’s commercial property insurance policy, and is most commonly triggered when there is direct damage to insured property, particularly in the event of fire or natural disasters, such as floods, hurricanes, and earthquakes. Contingent business interruption coverage can also apply when a government limits access to a specific geographic area, thereby hindering admission to the policyholder’s premises. However, for COVID-19-related claims, policy wording appears to be crucial, and many insurers have denied coverage, contending that claims do not meet the “direct physical loss” requirement contained within standard business interruption policies.

Before COVID-19, business interruption was merely viewed as an indirect loss induced by property damage, with specific loss evaluation principles, which should be covered through similar mutualization mechanisms. In the recent period, the emergence of cyber risk has been a reason for considering that the mutualization of business interruption risk could be undermined by common factors affecting the whole economy. COVID-19 is another step in this direction, but with a much greater magnitude.1

Put in simple terms, a worldwide pandemic is an insurance risk that cannot be covered by standard mutualization mechanisms, because it is characterized by a high correlation between policyholders’ losses, and it is sometimes argued that only government intervention may make pandemic insurance feasible.2 This view is supported by Hartwig et al. (2020) in the following terms: “Business continuity losses arising from pandemics ... have the potential to impact virtually all policyholders, irrespective of location and nearly simultaneously, with losses continuing over the span of months or even years. The resulting accumulation of losses of the many (rather than the few) prevents the pooling and redistribution of those losses, as essentially all policyholders are impacted, requiring the insurer to hold prohibitively large amounts of capital. Pandemic risk therefore cannot be readily spread, shared or diversified across policyholders.” This capital requirement leads the authors to conclude that “government involvement is needed to solve the private insurance market failure, due to government’s unique ability to tax, borrow and pool risk across time.”

It is usually considered that mutualization and capitalization3 are relevant in areas that are clearly separate from one another: P&C lines and health insurance are based on mutualization, while the accumulation phase of life insurance works through capitalization. Issues are more complex in the case of corporate pandemic insurance, since the coverage of business interruption is a key line of business of P&C insurers, yet cannot be mutualized in the event of a pandemics. We will explore this avenue, by analyzing how capitalization mechanisms may yield business interruption coverage in the event of a pandemic, without government intervention.

At first glance, going through the capitalization channel conflicts with the systemic nature of the pandemic risk. The perspective of suffering from a major macroeconomic downturn in the event of a pandemic makes it harder to create risk-sharing mechanisms for the benefit of firms affected by business interruption. However, this concomitance between a well-defined event (mainly, the movement restrictions and ability to operate normal business activity) causing severe corporate losses, and a macroeconomic crisis is too narrow a view that overlooks the uneven impacts of the pandemic throughout the economy. Pandemics affect sectors of the economy to a greater or lesser extent, according to the effect of travel and work restrictions on their activities, while some may even take advantage of the situation. Tourism and restaurants, transport and distribution, manufacturing and crafts, the entertainment, retail and luxury industries, and all industries reliant on an international supply chain have been penalized the most severely by COVID-19, while pharmaceutical and biotech industries, online BtoB and BtoC platforms, and high-tech industries have benefited either from the increase in demand for health care, or from changes in consumption patterns, or from the propensity of firms to digitize their activity. These uneven effects of the COVID-19 pandemic across sectors were reflected in stock market performance, with contrasting movements of stock prices resulting from interactions between sector-specific economic disruptions and asset management strategies triggered by the financial crisis.4

The remainder of this paper exploits this heterogeneity in stock price movements in building a corporate insurance scheme against pandemic risks. It is organized as follows: Section 2 develops a conceptual framework that shows how corporate pandemic insurance can be based on a self-funded mechanism, by exploiting the heterogeneity of sectoral reactions to a pandemic event. We start with a one-period model of an economy, where two stocks are traded, differing according to how their returns react to the occurrence of a pandemic. Type 1 stocks perform relatively well, and may even benefit from the pandemic event. By contrast, type 2 stocks are struck with full force, with a strong decline in their returns, in the event of a pandemic. A small or medium-sized risk-averse firm seeks protection from the consequences of a pandemic on its cash flows by contributing to an insurance fund. The optimal financial investment strategy consists in going long on stock 1 and short on stock 2, so as to obtain benefits from their opposite reaction to pandemic events, while hedging the bearish and bullish non-pandemic episodes affecting the stock market. Equivalently, the risk-averse firm may be protected by a portfolio of call options on stock 1 and put options on stock 2. This results in total or partial coverage of the pandemic and non-pandemic risks, according to whether or not stock returns include a risk premium.

Section 3 extends this analysis to the case where the future pandemic’s characteristics are imperfectly known, in which case several forms of market incompleteness may arise. When the pandemic creates uncertain losses for the insured firm, prudent firms use the long–short strategy to obtain a higher level of coverage than in the absence of uncertainty on the consequence of the pandemic. In this respect, we draw a parallel with the precautionary motive for insurance highlighted by Schlesinger (2013). The case where the effects of a pandemic on future stock prices are imperfectly known and markets are incomplete is also discussed. It is shown that the firm may need to choose a portfolio that delivers higher expected cash flows in the pandemic state than in the non-pandemic states.

In a nutshell, we will show how a small or medium-sized risk-averse firm may cover its exposure to pandemic risk through portfolio choices. It should not come as a surprise that optimal risk coverage is complete or partial, according to whether security pricing reflects the preferences of risk-neutral or risk-averse investors. This reflects a well-known property of Pareto-optimal risk sharing in a economy where risk-averse individuals may coexist with risk-neutral economic agents or only with risk-averse individuals. Keeping that in mind, our contribution is threefold. Firstly, we show how this optimal risk-sharing property is extended to idiosyncratic risks that are correlated with macroeconomic shocks reflected in asset prices. Secondly, we characterize the optimal portfolio choices that sustain this optimal risk sharing. And thirdly, we extend these results to the case where various types of pandemic may occur and financial markets are incomplete.

From a more general standpoint, our analysis leads to take a view on the insurability of the pandemic risk that differs from Hartwig et al. (2020) : in our perspective, the correlation of risks invites insurers to substitute capitalization and portfolio management to mutualization, rather than being per se a motive for government intervention.

While this conclusion is of a theoretical nature, it remains to appraise whether such a strategy is plausible in practice. Is this market-centered approach without government involvement a realistic one? Does it correspond to a quantitatively important risk-coverage mechanism that would significantly reduce the need for government intervention? Section 4 addresses these questions through numerical simulations that give an idea of the strength of the mechanism we described, and that highlight its practical relevance. Our approach will consist in simulating the coverage at the outbreak of a future pandemic, when the insured firm invests in two option-based funds, with underlyings similar to stocks 1 and 2 of our theoretical model. Fund 1 is composed of call options whose underlyings are stocks that are expected to resist well to a pandemic shock, while Fund 2 includes put options on stocks that are expected to underperform the overall market in the pandemic state. We use data from the French market, and we simulate future stock price trajectories starting in 2020, with a new pandemic outbreak in 2031. Using reserving with riskless assets as a benchmark highlights the strength and relevance of the option-based strategy.

Section 5 concludes and the Appendix includes an extension of the model to a multi-period setting and proofs.

The model

Basis framework

We analyze the financial choices of a firm facing a pandemic risk, in a one-period model, starting at time $t=0$ and ending at $t=1$. The firm owns initial assets, including productive assets and financial reserves, with total value A. The firm is a small or medium-sized undertaking, entirely held by an entrepreneur with no outside equity. Hence, A corresponds to the initial wealth of the entrepreneur, and it is exogenously given. Because of transaction costs related to the firm’s size—including imperfect information and agency costs—the firm cannot directly trade with outside investors, and security prices depend on the attitude toward risk of the latter. Implicitly, the economy includes a large number of firms facing the pandemic risk, and each one has its own specific characteristics. We postulate that outside investors cannot run these firms, because of a lack of capacity regarding firm-specific information, management and control. A part I of this initial capital available at $t=0$ is kept as financial assets from $t=0$ to $t=1$, and the remainder is invested as additional productive assets. Hence, the firm has productive assets $K=A-I$ during the current period. In the absence of a pandemic, these productive assets provide cash flows f(K), with $f^{\prime }>0,f^{″}\le 0$, available at $t=1$. The firm chooses K and I under constraint $K+I=A$.

The firm’s environment is characterized by two types of uncertainty. Firstly, a pandemic occurs with probability $\pi \in (0,1)$. Secondly, in the absence of pandemic, stock markets are either bullish or bearish, with probability ${\alpha }_u$ and ${\alpha }_d$, respectively, with ${\alpha }_u+{\alpha }_d=1$. Thus, there are three states $s\in \{u,d,p\}$, where u (up) and d (down) are the two non-pandemic states (with a bullish and bearish market, respectively) and p is the pandemic state, with probability ${\alpha }_u(1-\pi ),{\alpha }_d(1-\pi )$ and $\pi$, respectively.

Three securities, indexed by $i\in \{0,1,2\}$, are traded on the financial market, and may be held as reserves by the firm: security $i=0$ is a risk-free asset, with interest rate $r_f$, and $i=1$ and 2 are two types of stocks. Both stocks are similarly affected by the vicissitudes of the business cycle in the non-pandemic states. In the absence of pandemic, the expected return on stock i is denoted $R_i$, with returns $R_i+h$ and $R_i-h^{\prime }$ in states u and d, respectively, with ${\alpha }_{u}h={\alpha }_d{h}^{\prime }$. Stocks $i=1$ and $i=2$ differ in their reaction to the occurrence of a pandemic: stock 1 is a defensive asset, while stock 2 is severely affected should a pandemic occur: their returns in state p are $R_1+H$ and $R_2-H^{\prime }$, respectively. We assume $H^{\prime }>h^{\prime }$ and $H+H^{\prime }>0$. Condition $H^{\prime }>h^{\prime }$ reflects the fact that stock 2 is severely affected by the pandemic. As regards stock 1, H may be positive or negative: the assumption $H+H^{\prime }>0$ simply means that stock 1 reacts better than stock 2 to the occurrence of a pandemic.5 We have $R_2>R_1$ because the higher expected return on stock 2 in the non-pandemic states compensates its stronger downward reaction in the event of a pandemic. Overall, the returns on the three assets are summarized in Table 1.

Table 1.

Return on securities

$s\backslash i$	0	1	2
u	$r_f$	$R_1+h$	$R_2+h$
d	$r_f$	$R_1-h^{\prime }$	$R_2-h^{\prime }$
p	$r_f$	$R_1+H$	$R_2-H^{\prime }$

The matrix of security returns is of rank 3, and the financial market is thus complete. In particular, for each state s, an Arrow–Debreu security (i.e., a security that pays one unit of numeraire in state s, and zero otherwise) can be obtained through a portfolio of available assets.

Covering pandemic losses

We view the firm as a small or medium-sized enterprise, whose business is not significantly correlated with the ups and downs of the stock market, except when a pandemic is at the origin of a business interruption, causing losses in an amount equal to L. Thus, the final cash flow derived from productive assets is f(K) in states u and d, and $f(K)-L$ in state p. The firm is assumed to be risk-averse with respect to its final net cash flow including the payoff of its financial holdings (in short, its cash flow), either due to the investment crowding-out mechanism analyzed by Froot et al. (1993), or because its owner has non-diversified wealth, or because a decrease in cash flow exacerbates the risk of bankruptcy in the future. All firms are simultaneously affected by a loss in the pandemic state (i.e., their losses are perfectly correlated), thereby making it impossible to cover this risk by standard insurance mechanisms.

The firm makes its financial choices so as to maximize the expected utility of its cash flows

$$\begin{array}{c}\hfill \sum _{s\in \{u,d,p\}}{\pi }_{s}u(w_s),\end{array}$$

where $w_s$ is the firm’s cash flow in state s (more precisely defined below), ${\pi }_s$ is the probability of state s (i.e., ${\pi }_u={\alpha }_u(1-\pi ),{\pi }_d={\alpha }_d(1-\pi )$ and ${\pi }_p=\pi$), and u(.) is a von Neumann-Morgenstern utility function that represents the firm’s risk aversion, with $u^{\prime }>0$ and $u^{″}<0$.

The firm allocates a part $x_i$ of its financial reserves to security i with

$$\begin{array}{c}\hfill \sum _{i\in \{0,1,2\}}{x}_i=I.\end{array}$$

The firm’s cash flow is the sum of the cash flow $f(K)=f(A-I)$ derived from its productive assets, reduced by the loss L in the event of a pandemic, and of the payoff of its financial holdings, which gives

$$\begin{array}{cc}\hfill w_s=& f\left(A,-,\sum _{i\in \{0,1,2\}},x_i\right)+\sum _{i\in \{0,1,2\}}(1+r_{\mathit{si}})x_i\text{if}s\in \{u,d\},\hfill \end{array}$$ 1

$$\begin{array}{cc}\hfill w_p=& f\left(A,-,\sum _{i\in \{0,1,2\}},x_i\right)+\sum _{i\in \{0,1,2\}}(1+r_{\mathit{pi}})x_i-L,\hfill \end{array}$$ 2

where $r_{\mathit{si}}$ is the return on security i in state s, as described in Table 1. The firm’s optimal financial policy is obtained by maximizing the expected utility of cash flows with respect to $x_{0,}{x}_1$ and $x_2$. Furthermore, and more realistically, the financial positions of the firm may be assumed by a financial institution, such as an insurance company, offering self-funded hedging mechanisms.

Since financial markets are complete, the price of Arrow–Debreu securities (or state prices) $q_u,q_d$ and $q_p$ can be recovered from the matrix of asset returns. When there are risk-neutral investors in the financial markets, the expected return on stocks is equal to the risk-free interest rate, i.e.,

$$\begin{array}{c}\hfill r_f=R_1+\pi H=R_2-\pi H^{\prime },\end{array}$$ 3

and in that case, the vector of state prices is proportional to the state probability vector. More realistically, we may assume that the stock returns include a risk premium because of investors’ risk aversion, a case in which we have

$$\begin{array}{c}\hfill r_f<R_1+\pi H\text{and}{r}_f<R_2-\pi H^{\prime }.\end{array}$$ 4

States u, d, and p correspond to various degrees of macroeconomic prosperity, with state p corresponding to a most severe economic downturn. Lemma 1 provides a sufficient condition on the security returns for this to be reflected in a simple hierarchy of probability-weighted state prices.

Lemma 1

When (3) holds, i.e., there are risk-neutral investors, the Arrow–Debreu security prices are such that

$$\begin{array}{c}\hfill \frac{1}{1+r_f}=\frac{q_u}{{\alpha }_u(1-\pi )}=\frac{q_d}{{\alpha }_d(1-\pi )}=\frac{q_p}{\pi }.\end{array}$$ 5

When (4) holds, i.e., all investors are risk-averse, then we have

$$\begin{array}{c}\hfill \frac{q_u}{{\alpha }_u(1-\pi )}<\frac{1}{1+r_f}<\frac{q_d}{{\alpha }_d(1-\pi )}.\end{array}$$ 6

If in addition we have

$$\begin{array}{c}\hfill \frac{R_2-\pi H^{\prime }-r_f}{R_1+\pi H-r_f}>\frac{h+\pi H^{\prime }}{h-\pi H},\end{array}$$ 7

then

$$\begin{array}{c}\hfill \frac{q_d}{{\alpha }_d(1-\pi )}<\frac{q_p}{\pi }.\end{array}$$ 8

Condition (7) means that the risk premium is substantially larger for stock 2 than for stock 1. This reflects the catastrophic nature of state p in which stock 2 has a very low return $R_2-H^{\prime }$ by comparison with its non-pandemic expected return $R_2$, while the relative performance is better for stock 1. In what follows, we refer to (5), and (6–8) as the investors’ risk neutrality and risk aversion cases, respectively, in relationship to the attitude toward risk of a representative investor who may require risk premiums to hold the securities in its portfolio. As assumed, the firm under consideration is risk-averse.

The firm chooses its portfolio $(x_0,x_1,x_2)$ of assets 0, 1, and 2 (or, equivalently, it chooses a portfolio of Arrow–Debreu Securities) in order to maximize its expected utility. Let $y_s$ denote the quantity of type s Arrow–Debreu security purchased by the firm, with $s\in \{u,d,p\}$, with

$$\begin{array}{cc}\hfill w_s=& f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_s\text{if}s\in \{u,d\},\hfill \end{array}$$ 9

$$\begin{array}{cc}\hfill w_p=& f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_p-L\text{.}\hfill \end{array}$$ 10

The firm chooses $y_u,y_d$ and $y_p$ in order to maximize its expected utility ${\sum }_{s\in \{u,d,p\}}{\pi }_{s}u(w_s)$, and its portfolio $(x_0,x_1,x_2)$ can then be deduced from the data on asset returns.

Proposition 1

If investors are risk-neutral, then

$$\begin{array}{c}\hfill w_u=w_d=w_p,\end{array}$$ 11

and the firm’s portfolio is such that

$$\begin{array}{cc}\hfill x_0=& A-K,\hfill \end{array}$$ 12

$$\begin{array}{cc}\hfill x_1=& -x_2=\frac{L}{H+H^{\prime }},\hfill \end{array}$$ 13

If investors are risk-averse, then

$$\begin{array}{c}\hfill w_u>w_d>w_p,\end{array}$$ 14

and the firm’s portfolio is such that

$$\begin{array}{cc}\hfill & x_0<A-K,\hfill \end{array}$$ 15

$$\begin{array}{cc}\hfill & x_1+x_2=\frac{w_u-w_d}{h+h^{\prime }}>0,\hfill \end{array}$$ 16

$$\begin{array}{cc}\hfill & -x_2<\frac{L}{H+H^{\prime }}.\hfill \end{array}$$ 17

In both cases, we have $K=K^{\ast }$ given by

$$\begin{array}{c}\hfill f^{\prime }(K^{\ast })=1+r_f.\end{array}$$ 18

Hence, when investors are risk-neutral, an optimal financial strategy for the firm consists of going long on stock 1 and short on stock 2, for exactly the same amount, i.e., $x_1+x_2=0$. In more concrete terms, at $t=0$ the firm sells stock 2 after borrowing it on the spot market and uses the proceeds of this sale to purchase stock 1. Hence, no net disbursement is required for these stock market operations. At $t=1$, the firm purchases stock 2 and cancels its short position, Because of the zero aggregate net position of the firm’s stock portfolio from $t=0$ to $t=1$, in state u, the high return from the long position on stock 1 exactly compensates the low return from the short position on stock 2, and vice versa in state d. Hence, these opposite positions enable the firm to perfectly hedge its market exposure in the non-pandemic states u and d, with an aggregate return equal to the riskless interest rate $r_f$. The size of these long and short positions is chosen in order to perfectly cover the firm’s loss $L$ in the event of a pandemic, which will be the case when (13) holds. The firm holds reserves or borrows money at the riskless interest rate $r_f$, according to whether A is higher or lower than its optimal productive capital $K^{\ast }$, respectively. When there are risk-neutral investors, the firm therefore uses stock market operations to cover the losses caused by a pandemic fully, while perfectly hedging its exposures to non-pandemic market fluctuations, and ultimately its cash flows are independent of the state that may occur.

When investors are risk-averse, the return on stocks includes risk premiums, and the higher these returns, the higher the probability-weighted state prices. More explicitly, from (6) and (8), transferring wealth from state u to state d can be done at rate $q_d/q_u$ which is larger than the odds ratio ${\alpha }_d/{\alpha }_u$, and similarly $q_p/q_d$ is larger than $\pi /{\alpha }_d(1-\pi )$. These distortions between state-price ratios and odds ratios make the hedging of pandemic and non-pandemic risks more costly, hence the partial coverage of cash flows reflected in inequalities (14): the firm is better off in state u than in state d, the pandemic state p being the worst. In the case of risk-neutral investors, it was optimal to hedge the non-pandemic risk by going long on stock 1 and short on stock 2, with equal positions in absolute value. When the aggregate firm’s position in the stock market is long, i.e., when $x_1+x_2>0$, the firm’s financial performance is higher in state u than in state d, which corresponds to the partial hedging of non-pandemic financial risk. As expressed by (16), the aggregate position $x_1+x_2$ is proportional to $w_u-w_d$, which depends on the firm’s degree of risk aversion. Conditions (13) and (17) show that partial coverage of the pandemic risk goes through a short position on stock 2, which is smaller than in the risk-neutral case.

Finally, in both cases, for an optimal level of productive capital $K^{\ast }$, the discounted marginal productivity of capital $f^{\prime }(K^{\ast })/(1+r_f)$ should equal 1, which corresponds to a standard corporate value maximization rule.6

Remarks

1. Obviously, there is a relationship between Proposition 1 and conclusions of the basic model of insurance demand, whose origin goes back to Mossin (1968) and Smith (1968). In both cases, the policyholder’s idiosyncratic risks are fully covered when the relationship between insurer and insured is actuarially fair, while partial insurance is optimal when there are transaction costs in one form or another. More specifically, Proposition 1 shows how the optimal insurance coverage can be implemented in a setting where the law of large numbers does not apply (and thus its mutualization by standard insurance mechanisms is not possible), and where the operating event behind the loss is at the origin of a financial shock reflected by stock returns. The vector of optimal state-contingent cash flows $(w_u,w_d,w_p)$ maximizes the firm’s expected utility and it depends on the vector of Arrow–Debreu security prices $(q_u,q_d,q_p)$. Proposition 1 characterizes the portfolio composed of stocks and risk-free asset that implements this vector of contingent cash flows, and how the optimal portfolio depends on security characteristics, particularly the effect of pandemic and non-pandemic shocks on their return. We will show below how the optimal coverage can also be reached through options on stocks.

2. From an organizational standpoint, we have assumed so far that financial assets are held by the firm itself. It is more realistic, particularly for a small or medium-sized firm, to restrict its financial operations to the holding of a remunerated bank account if $x_0>0$ and to the issuance of debt if $x_0<0$, the riskless interest rate $r_f$ applying in both cases, and to relate the return from stocks to contractual links to a financial institution. In this interpretation, the return on stocks 1 and 2 corresponds to the payout of a self-funded pandemic insurance scheme managed by an insurance company or a bank.

3. Another approach, worthy of further study, would consist in considering the case of an insurer that offers standard indemnity insurance against the pandemic risk to risk-averse firms and that holds costly risk capital to prevent insolvency. The portfolio strategy described in Proposition 1 would reduce the capital cost of such an insurer, by comparison with the case where only a risk-free asset is available. The capital cost problem highlighted by Hartwig et al. (2020) would be smaller, thereby allowing the insurer to offer pandemic insurance more easily, and thus reducing here also the need for government intervention.7 The advantage of this approach would be to allow insurers to offer indemnity cover reflecting firms’actual losses. Note however that the cost of the risk capital held by the insurer (possibly motivated by asymmetric information, agency problems or taxes) would reduce the efficiency of such a strategy, by comparison with the self-funded insurance mechanism that we have described.

Using options to cover the pandemic risk

One may easily show that a portfolio of call and put options purchased at $t=0$ with maturity date $t=1$ allows the firm to hedge its risks, in the same way as if it were going long and short on the stocks themselves. Consider call options on stock 1 and put options on stock 2, with strike price $1+R_1$ and $1+R_2$, respectively, the value of each stock being equal to 1 at $t=0$. Hence, for each option, the strike price is equal to the expected payoff of the stock in the non-pandemic states. We consider the case where $H>0$ so that the call option on stock 1 is in the money in states u and p (with payoffs h and H, respectively), while the put option on stock 2 is in the money in states d and p (with payoffs $h^{\prime }$ and $H^{\prime }$, respectively). Let $q_{c1}$ and $q_{p2}$ be the price of the call and put options, on stocks 1 and 2, respectively. For simplicity, consider the case where investors are risk-neutral, and thus the price of securities is equal to the discounted value of their expected payoff, which gives

$$\begin{array}{cc}\hfill q_{c1}=& \frac{{\alpha }_{u}h(1-\pi )+\pi H}{1+r_f},\hfill \end{array}$$ 19

$$\begin{array}{cc}\hfill q_{p2}=& \frac{{\alpha }_d{h}^{\prime }(1-\pi )+\pi H^{\prime }}{1+r_f}.\hfill \end{array}$$ 20

Let $n_{c1}$ and $n_{p2}$ be the number of calls and puts (on stocks 1 and 2, respectively) purchased at $t=0$.8 When investors are risk-neutral, the optimal insurance scheme provides perfect hedging of non-pandemic risks and full coverage of the loss in the event of a pandemic, which gives

$$\begin{array}{c}\hfill y=y_u=y_d=y_p-L.\end{array}$$ 21

These state-dependent financial cash flows are associated with a portfolio $(x_0,n_{c1},n_{c2})$ if the following conditions are satisfied:

$$\begin{array}{cc}\hfill & x_0(1+r_f)+n_{c1}h=y,\hfill \end{array}$$ 22

$$\begin{array}{cc}\hfill & x_0(1+r_f)+n_{p2}{h}^{\prime }=y,\hfill \end{array}$$ 23

$$\begin{array}{cc}\hfill & x_0(1+r_f)+n_{c1}H+n_{p2}{H}^{\prime }=y+L.\hfill \end{array}$$ 24

Solving (22–24) for $x_0,n_{c1}$ and $n_{p2}$ yields

$$\begin{array}{cc}\hfill & x_0=\frac{1}{1+r_f}[y-\frac{h{h}^{\prime }L}{H{h}^{\prime }+h(H^{\prime }-h^{\prime })}],\hfill \\ \hfill & n_{c1}=\frac{h^{\prime }L}{H{h}^{\prime }+h(H^{\prime }-h^{\prime })}>0,\hfill \\ \hfill & n_{p2}=\frac{\mathit{hL}}{H{h}^{\prime }+h(H^{\prime }-h^{\prime })}>0.\hfill \end{array}$$

Hence, following a long–short portfolio management strategy and holding a portfolio of call and put options are two ways to reach the same goal, i.e., covering simultaneously the non-pandemic market risks and the loss that may result from a pandemic.

Various types of pandemic

So far we have restricted ourselves to a unique type of pandemic, with well-defined effects on the firm’s cash flows and on stock returns. We may, however, extend our analysis to a more general setting, where pandemics take several forms. As we will see, this may lead to two forms of market incompleteness.

Uncertain losses for the insured firm

Let us first consider the case where pandemics are at the origin of random losses $\tilde{L}$ for the firm, with expected value $\overline{L}=\mathbb{E}\tilde{L}$.9 The matrix of security returns is unchanged and still defined by Table 1. Hence, we here consider the case where a pandemic may entail more or less severe consequences for the firm, while there is only one type of stocks 1 and 2. If each type of pandemic that may occur (in terms of loss incurred by the firm) is viewed as a state of nature, there are more states of nature than available securities, which corresponds to a first form of incomplete financial markets. In this setting, the firm’s cash flow in the pandemic state is random and written as

$$\begin{array}{c}\hfill {\tilde{w}}_p=f\left(A,-,\sum _{i\in \{0,1,2\}},x_i\right)+\sum _{i\in \{0,1,2\}}(1+r_{\mathit{pi}})x_i-\tilde{L},\end{array}$$ 25

and we denote ${\overline{w}}_p=\mathbb{E}{\tilde{w}}_p$. The firm chooses $x_0,x_1$ and $x_2$ in order to maximize its expected utility

$$\begin{array}{c}\hfill {\pi }_{u}u(w_u)+{\pi }_{d}u(w_d)+{\pi }_p\mathbb{E}u({\tilde{w}}_p),\end{array}$$ 26

where $\mathbb{E}u({\tilde{w}}_p)$ is the expected utility, conditional on the occurrence of a pandemic event. Proposition 2 characterizes the firm’s portfolio choices in this setting.

Proposition 2

Assume that the firm is prudent (i.e., $u^{″\prime }>0$). When facing a risk of random loss $\tilde{L}$, the firm’s optimal portfolio choices are the same as in the case of a deterministic loss L larger than expected loss $\overline{L}$. More particularly, when investors are risk-neutral, we have $x_1=-x_2>\overline{L}/(H+H^{\prime })$ and $w_u=w_d<{\overline{w}}_p$.

Hence, when pandemics create losses of uncertain amounts, the prudent firm behaves as though its losses in case of pandemic were known in advance, but larger than their expected value. In other words, the uncertainty regarding losses incentivizes the firm to overinsure its exposure to the pandemic risk, by comparison with the case where losses would be certain and equal to their expected value. In the particular case where investors are risk-neutral, the return on the firm’s portfolio should provide resources that exceed expected losses $\overline{L}$.

It is easy to see where this conclusion comes from. Writing $\tilde{L}=\overline{L}+\epsilon$, with $\mathbb{E}\epsilon =0$, shows that assuming uncertain pandemic losses is equivalent to adding a zero-mean background risk $\epsilon$ to a deterministic pandemic loss $L=\overline{L}$, which makes insurance even more attractive to prudent policyholders. In fact, Proposition 3 is similar to the precautionary motive of the prudent agent highlighted by Schlesinger (2013), whose intuition can be found in Eeckhoudt and Schlesinger (2006), and which states that uncertainty about losses stimulates insurance demand. We can conclude that the uncertainty about the pandemic cost is likely to incentivize firms to extend their insurance coverage beyond the level that they would choose if pandemics affect their cash flows in a perfectly predictable way.

Uncertain stock returns in the pandemic state

Let us now turn to the case where stock returns react differently, according to the type of pandemic that may occur. Our analysis would be qualitatively unchanged if financial markets were complete, with a large number of stocks reacting differently according to the type of pandemic. More explicitly, if the set of state-contingent stock returns span the full space of state-contingent claims (each type of pandemic corresponding to a specific state), then asset portfolios would allow us to replicate Arrow–Debreu securities for all pandemic and non-pandemic states. If there are risk-neutral investors, Arrow–Debreu security prices are proportional to state probabilities, and it is optimal for the risk-averse firm to fully cover all its pandemic and non-pandemic risks, through a portfolio of long–short positions, or call and put options. If investors are risk-averse, then partial coverage is optimal. In other words, in this complete market setting, the diversity of pandemic types would not affect our conclusions.

This is not the case when there are various types of pandemics, but the set of available stocks is not large enough to allow investors to reach a target payoff whatever the pandemic. To get an idea of how this second form of market incompleteness affects the firm’s risk management strategy, let us extend our base model to a case where the returns on stocks 1 and 2 in the pandemic state $s=p$ are affected by independently distributed random variables ${\epsilon }_1$ and ${\epsilon }_2$, respectively, with $\mathbb{E}{\epsilon }_1=\mathbb{E}{\epsilon }_2=0$. The diversity of possible pandemics in incomplete market is reflected in the distribution of ${\epsilon }_1$ and ${\epsilon }_2$, while only two stocks are traded. Table 2 describes the state-contingent asset returns.

Table 2.

Return on securities under multiple pandemic states

$s\backslash i$	0	1	2
u	$r_f$	$R_1+h$	$R_2+h$
d	$r_f$	$R_1-h^{\prime }$	$R_2-h^{\prime }$
p	$r_f$	$R_1+H+{\epsilon }_1$	$R_2-H^{\prime }+{\epsilon }_2$

Let $r_{\mathit{si}}$ be the expected state-contingent return on asset i as defined in Table 2. The firm’s cash flow $w_s$ in state s is still defined by (1) for $s=u$ and p, while the state-p random payoff ${\tilde{w}}_p$ with deterministic loss L is written as

$$\begin{array}{c}\hfill {\tilde{w}}_p=f\left(A,-,\sum _{i\in \{0,1,2\}},x_i\right)+\sum _{i\in \{0,1,2\}}(1+r_{\mathit{pi}})x_i+{\epsilon }_1{x}_1+{\epsilon }_2{x}_2-L,\end{array}$$ 27

and we denote ${\overline{w}}_p=\mathbb{E}{\tilde{w}}_p$. Comparing (27) and (25) shows that portfolio choices now affect the probability distribution of the firm’s cash flow in the pandemic state, and not only its expected value. Thus, the analysis of portfolio choices under multiple pandemic types can no longer be reduced to simply adding a background risk to a deterministic loss level. Proposition 3 characterizes the optimal solution to this problem when investors are risk-neutral, under technical assumptions that simplify our analysis.

Proposition 3

Assume $h^{\prime }=h,{\alpha }_u={\alpha }_d=1/2,H=0$. If investors are risk-neutral and the support of ${\epsilon }_1$ and ${\epsilon }_2$ is not too large, then the firm’s optimal portfolio choices are such that $w_u<w_d$, and $x_1+x_2<0$. Furthermore, if $\pi H^{\prime }<h$ and u(.) is quadratic, then we have ${\overline{w}}_p>w_u$.

We know from Proposition 1 that under complete financial markets and risk-neutral security pricing, it is optimal for the firm to perfectly hedge its non-pandemic risks and also to fully cover the loss that may result from a pandemic event. Proposition 3 shows that this is no longer the case in incomplete markets. When $h^{\prime }=h$ and ${\alpha }_u={\alpha }_d=1/2$, the bullish and bearish non-pandemic states are treated symmetrically, which makes the analysis more straightforward. Assumption $H=0$ is a sufficient condition, but not a necessary one, to obtain the first part of the Proposition. It means that stock 1 plays a neutral role in the event of a pandemic (its return being equal to its expected value $R_1$), while the effect of the pandemic shock is fully concentrated on stock 2, with a downward effect $-H^{\prime }$.10

In our setting, non-pandemic risks can be perfectly hedged by long–short positions that balance each other out, with $x_1+x_2=0$. Should a pandemic occur, then a long position on stock 1 (when H is positive) and a short position on stock 2 provide expected financial resources to the firm that compensate its loss L. However, perturbations ${\epsilon }_1$ and ${\epsilon }_2$ make this compensation random, which is detrimental to the risk-averse firm. When $H=0$, the balance of these effects tips more in favor of obtaining compensation through the short position on stock 2, than through the long position on stock 1, which gives $-x_2>x_1$, i.e., $x_1+x_2<0$.11 Consequently, we have $w_u<w_d$, the firm being better off when the stock market is bearish than when it is bullish. Since the short position on stock 2 is larger than the long position on stock 1, we may even have the paradoxical result ${\overline{w}}_p>w_u$, meaning that the expected cash flow is larger in the pandemic state than when the market is bullish in the absence of a pandemic. As stated in the second part of Proposition 3, this is the case when $\pi H^{\prime }<h$ and u(.) is quadratic.12

These results are obtained under the assumption of investors’ risk neutrality. As shown in the second part of Proposition 1, the investors’ risk aversion pulls in the opposite direction, the long position on stock 1 being larger than the short position on stock 2 when there is only one type of pandemic. In practice, the optimal structure of the firm’s portfolio results from the complex interaction between these two effects: the pricing of securities under investors’ risk aversion incentivizes the firm to have more long positions on stock 1 than short positions on stock 2, while the uncertainty of stock returns in the pandemic state may have the opposite effect.13

Numerical simulations

Simulations are performed with data from the French stock exchange. The investment strategy of the insured firm is characterized as follows. Every year, €20,000 is invested in two funds. Fund 1 is composed of call options, whose underlyings are twelve stocks that overperformed the CAC 40 index during the initial phase of COVID-19 and are expected to resist well to a future pandemic shock. Fund 2 is composed of put options on the stocks that are expected to underperform the CAC 40 in the pandemic state.14 Once a year, the firm rebalances its portfolio with an equal allocation to each fund. The symmetry between the funds aims to neutralize the effect of a potential trend in stock prices, since a general price increase benefits the calls and harms the puts, while a general price drop benefits the puts at the expense of the calls. The yields of the two funds are computed by calculating the value of options with the following characteristics: options purchased at the beginning of each year have a maturity of two years and are sold at the end of the year, with a remaining maturity of one year. The strike price is equal to the simulated current price of the underlying asset at the moment of purchase. Option prices are calculated using the Black–Scholes formula, on the basis of underlying prices and option characteristics. At the beginning of each year, the additional €20,000 contribution is added to the total fund value, which is split into two equal parts to finance the purchase of new put and call options and helps to increase the overall fund value.

We simulate a large number of future stock price trajectories by using the log-normal assumption on stock prices, on which the Black–Scholes model is built. The means and variances of the return processes are calibrated to their historical values, measured before the 2020 pandemics, between January 1, 2007 and February 1, 2020. The outcome of the financial investments made by the firm at the beginning of each year is evaluated on each simulated price path. This allows us to construct a histogram of potential payoffs to the insured firm, should another pandemic occur in the future.

The data set is composed of daily price fluctuations of the twenty-four stocks listed in Tables 3 and 4 between January 1, 2007 and April 1, 2020. In our baseline scenario, the firm starts contributing to the funds on April 1, 2020. The firm makes twelve yearly payments of €20,000 and a pandemic crisis occurs in 2031. We assume that this new pandemic affects expected stock returns in the same proportions as the 2020 crisis. More specifically, we postulate that the expected value of each daily stock return during the 2031 pandemic is equal to the average return observed during the 2020 pandemic.15 We consider the case of a pandemic crisis starting on August 1, 2031, the funds being liquidated on October 1, 2031. Hence, for each underlying stock, the daily expected return from August 1st to October 1, 2031 is equal to the average return from February 1, to April 1st 2020. However, each return is affected by its own volatility, and thus returns during the future pandemic differ from what was observed during the 2020 pandemic crisis, which leads to a distribution of the two-fund portfolio liquidation value.

Table 3.

Over performing stocks with their activity sectors, their yields measured between January 1 and April 1, 2020 and their associated call yields measured over the same time period

Stock	Sub-industry	YTD	CALL YTD
HERMES	Clothing	2.0%	10.40%
SANOFI	Pharmaceutical	− 0.1%	44.90%
STMICRO	Semi-conductors	− 2.5%	2.80%
L’OREAL	Cosmetics	− 4.0%	− 28%
DASSAULT SYSTEMES	Software	− 4.2%	37.90%
AIR LIQUIDE	Chemicals	− 5.0%	− 7.50%
ATOS	Computer services	− 11.0%	44.20%
CARREFOUR	Food retailer	− 11.1%	− 41.90%
SCHNEIDER ELECTRIC	Electrical components	− 12.1%	0.30%
DANONE	Food products	− 13.3%	− 46.40%
PERNOD RICARD	Distiller and vintner	− 14.2%	− 27.50%
LVMH	Clothing	− 15.0%	− 14.00%

The call yields reported are averages of all warrant calls traded during the first quarter of 2020

Table 4.

Underperforming stocks with their activity sectors, their yields measured between January 1 and April 1 2020 and their associated put yields measured over the same time period

Stock	Sub-industry	YTD	PUT YTD
UNIB-RODAM-WES	Real estate	− 64.1%	807.92%
RENAULT	Automobiles	− 58.4%	252.25%
SOCIETE GENERALE	Bank	− 57.2%	152.61%
AIRBUS	Aerospace	− 57.0%	164.47%
BNP PARIBAS	Bank	− 45.5%	116.70%
ACCOR	Hotels	− 45.0%	220.33%
CREDIT AGRICOLE	Bank	− 43.8%	118.29%
SAFRAN	Aerospace	− 41.1%	170.40%
SODEXO	Restaurants	− 38.0%	538.70%
PEUGEOT	Automobiles	− 37.0%	122.60%
AXA	Insurance	− 35.4%	157.20%
PUBLICIS GROUPE	Media agency	− 35.0%	192.40%

The put yields reported are averages of all warrant puts traded during the first quarter of 2020

It is assumed that the risk-free interest rate remains constant and equal to its last value in the data set (April 1, 2020). This allows us to calculate the price of call and put options with strike prices being equal to the current underlying prices.

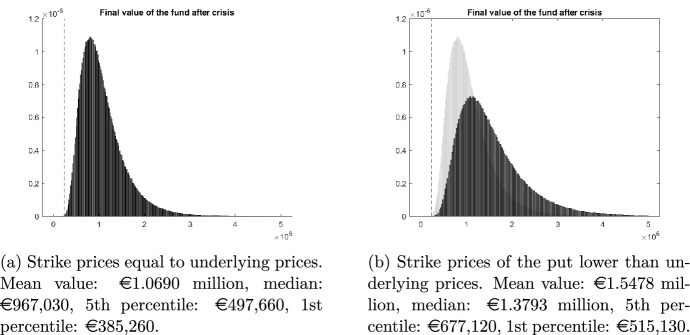
Figure 1a displays the histogram of this baseline scenario with one million random draws. The average value of the insurance strategy across draws is equal to €1.069 million, while the median is €967,030. $95\%$ of the simulated paths deliver a final value above €497,660 and $99\%$ of these provide a value higher than €385,260. In comparison, if the firm sets-up reserves, with return equal to the risk-free rate, it is only able to amass a €235,730 buffer to face the 2031 pandemic crisis, a level higher than the long–short strategy with a probability of only 0.0077. The efficiency gap between these two strategies would be even greater if the €20,000 yearly investment in the option portfolio were considered as a tax-deductible expense by the tax authority, contrary to standard allocations to reserves. In that case, the yearly net cost of the option-based insurance strategy would be $20,000(1-{\tau }_c)$, where ${\tau }_c$ is the corporate income tax. A yearly allocation to reserves, with equivalent cost to shareholders, would lead to cumulated reserves $(1-{\tau }_c)\times$ €235, 730 at the outbreak of the 2031 pandemic.

Fig. 1.

Liquidation value of the two-fund portfolio, with change in option strike prices

It is worth considering how put and call option parameters affect the liquidation value of the two-fund portfolio. More particularly, in the previous simulations, the option strike prices were taken as equal to the spot underlying prices, but other assumptions are of course possible. For illustrative purposes, Fig. 1b represents the distribution of the liquidation value, under the same assumptions as in Fig. 1a, except for put options, which have strike prices equal to $80\%$ of the underlying’s current prices. Since a lower strike price increases leverage, the resulting distribution is more spread out with a higher mean and median, at €1.5478 million and €1.3793 million, respectively. In the case considered here, the first and fifth percentiles are also higher at €677,120 and €515,130, respectively.

We have considered so far that a new pandemic crisis would occur in 2031. However, the timing of the pandemic is itself a random variable which affects the liquidation value of the proposed financial strategy. Figure 2 represents the evolution of the two-fund portfolio’s liquidation value as a function of the year of the pandemic event, maintaining the other assumptions of the scenario constant. The full line represents the expected payoff, while the dotted lines represent the ninety-fifth and fifth percentiles of the simulated distributions. The cross marks correspond to the risk-free strategy payoff, and the crossed circles to the payoff of a risk-free strategy subject to a corporate income tax ${\tau }_c=0.30$. For any stock return trajectory, the liquidation value of the two-fund strategy increases non-linearly with time. Delivering a significant payoff therefore requires some time for the fund to build potential value, but it is comforting to observe that the fifth percentile of the distribution is above the risk-free strategy payoff at all horizons.

Fig. 2.

Liquidation value of the two-fund portfolio at different pandemic horizons

Conclusion

In many countries, including the U.S. and Europe, the COVID-19 crisis has highlighted inadequate preparation for pandemics, and the current state of business interruption insurance is illustrative of this deficiency. Pandemic risk presents features that differ profoundly from those of other insurance risks: it affects simultaneously a large fraction of businesses, which makes risk mutualization unfeasible and, in addition, it is systemic in nature, since it goes hand in hand with a severe worldwide economic downturn. Instead of considering that government involvement is the only possible option, we have explored how capitalization and portfolio management may help solving the pandemic insurance problem. We have considered the case of a small or medium-sized risk-averse firm that cannot directly trade with outside investors. Corporate insurance consists either in following a long–short strategy in the stock market, or in investing in stock options. The logic behind this strategy is to take advantage of the downturn in the stocks that are most exposed to pandemics and, where possible, of the stimulus given to specific sectors, in order to generate substantial gains in the event of a pandemic, while hedging the risks associated with the bearish or bullish nature of the stock market in non-pandemic states. Simulations using data from the French stock market have illustrated the potential benefits of this approach in putting a corporate pandemic insurance in place.

We limited our analysis to the basic principles of such a self-funded insurance scheme, and a deeper exploration of this approach would require further studies in various directions. These may include the factors behind the insured firm’s risk aversion, and the design of the insurance mechanism. For example, if the firm’s risk aversion results from an investment crowding-out mechanism, as in the Froot et al. (1993) approach, or if it reflects bankruptcy costs, then a committed capital facility, in the form of contingent debt or equity, could meet the firm’s needs more effectively, than merely covering the cash flow losses by selling its financial assets. Another issue is related to complementary guarantees that the insurer could provide to the insured firm, in order to reduce the uncertainty on the post-pandemic value of assets. This may be through the securitization of the residual risk, which corresponds to the difference between a guaranteed rate of return and the post-pandemic return on assets. Pandemic cat bonds, issued by insurers, may be the right instrument to make such a guarantee feasible, by transferring the residual risk to dedicated investors. This suggests that the self-funded insurance mechanism that we have examined and the more traditional risk transfer through cat bonds or other instruments may have complementary roles in the coverage of the pandemic risk.16

Appendix

Multi-period setting

Let us extend the results of Section 2 to an infinite horizon model, where time periods are indexed by $t=0,1...$, and the firm can transfer financial resources across time periods. The notations are adapted from the one-period setting as follows. At each period t, the total value of the firm’s initial assets is equal to $A_t$, allocated between productive assets $K_t$ (including investment made at the beginning of period t) and financial reserves $A_t-K_t$. Productive assets provide cash flows $f(K_t)$, with $f^{\prime }>0,f^{″}\le 0$, available at the end of period t . We still assume that three states $s\in \{u,d,p\}$ may occur at each period t, with probability ${\pi }_s$ equal to ${\alpha }_u(1-\pi ),{\alpha }_d(1-\pi )$ and $\pi$, respectively, and that the firm incurs loss L in the pandemic state p. The probability distributions of states are assumed to be independent between periods. Financial reserves are allocated between securities $i=0,1$ and 2 with return $r_{\mathit{si}}$ in state s as specified in Table 1. We denote $x_{\mathit{ti}}$ the value of security i held by the firm at period t. Since the firm’s assets are allocated between productive and financial assets at the beginning of each period, we have

$$\begin{array}{c}\hfill A_t=K_t+\sum _{i\in \{0,1,2\}}{x}_{\mathit{ti}}\text{.}\end{array}$$

The total cash flows come from productive and financial assets, and are allocated either to the owner’s consumption (through the distribution of a dividend) or to corporate investment, i.e., to the increase in the value of the firm’s assets. This allocation of cash flows depends on the state prevailing during the period. Let $c_{\mathit{st}}$ denote the consumption level in state s at period t, and let $A_{t+1,s}$ be the value of the firm’s assets at the beginning of period $t+1$ when state s prevails at period t , hence with total investment $A_{t+1,s}-A_t$. The cash flows coming from productive and financial assets, possibly reduced by loss L, are equal to the sum of consumption and investment, and thus we have

$$\begin{array}{cc}\hfill c_{\mathit{ts}}+A_{t+1,s}-A_t=& f(K_t)+\sum _{i\in \{0,1,2\}}(1+r_{\mathit{si}})x_{\mathit{ti}}\text{if}s\in \{u,d\},\hfill \end{array}$$ 28

$$\begin{array}{cc}\hfill c_{\mathit{tp}}+A_{t+1,p}-A_t=& f(K_t)+\sum _{i\in \{0,1,2\}}(1+r_{\mathit{pi}})x_{\mathit{ti}}-L\text{.}\hfill \end{array}$$ 29

The firm chooses its portfolio of financial assets $(x_{t0},x_{t1},x_{t2})$ and its state-contingent investment level $A_{t+1,s}-A_t$, in order to maximize the discounted sum of consumption expected utility

$$\begin{array}{c}\hfill \sum _{t=0}^{\infty }{\delta }^t\sum _{s_t\in \{u,d,p\}}{\pi }_{s_t}u(c_{t{s}_t}),\end{array}$$

where $\delta$ is the discount factor, such that $\delta <1$, and $s_t$ is the state at period t.

The intertemporal strategy of the firm is characterized by functions $A_t(h_t)$ and $x_{\mathit{ti}}(h_t)$ for all $t\ge 0$ and all $i\in \{0,1,2\}$ , where $h_t=(s_0,s_1,...,s_{t-1})\in H_t\equiv {\{u,d,p\}}^t$ denotes the sequence of states from period 0 to period $t-1$ if $t\ge 1$ and $h_0\in \varnothing$. Let ${\mathrm{\Pi }}_t(h_t)$ be the probability of sequence $h_t$ when $t\ge 1$, with ${\sum }_{h_t\in H_t}{\mathrm{\Pi }}_t(h_t)=1$. For notational consistency, we denote ${\mathrm{\Pi }}_0(h_0)=1$. In words, $A_t(h_t)$ is the value of the firm’s assets at the beginning of period t, with the constraint $A_0(h_0)\equiv A_0$ imposed by the value of initial assets, and thus $A_{t+1}(h_{t+1})-A_t(h_t)$ is its investment at period t, while $(x_{t0}(h_t),x_{t1}(h_t),x_{t2}(h_t))$ is its portfolio of financial assets held during period t. The firm maximizes its discounted expected utility

$$\begin{array}{cc}\hfill & \sum _{t=0}^{\infty }{\delta }^t[\sum _{h_t\in H_t}{\mathrm{\Pi }}_t(h_t)\sum _{s_t\in \{u,d,p\}}{\pi }_{s_t}u(f(A_t(h_t)-\sum _{i\in \{0,1,2\}}{x}_{\mathit{ti}}(h_t))\hfill \\ \hfill & +\sum _{i\in \{0,1,2\}}(1+r_{s_{t}i})x_{\mathit{ti}}(h_t)+A_t(h_t)-A_{t+1}(h_t,s_t)-\mathbb{1}(s_t=p)L)],\hfill \end{array}$$

with respect to $A_t(.):H_t\to R_{+}$ for all $t\ge 1$ and $x_{\mathit{ti}}(.):H_t\to R$ for $i\in \{0,1,2\}$ and all $t\ge 0$. Let $v(A_0)$ be the optimal discounted expected utility level as a function of initial assets $A_0$, with $v^{\prime }(A_0)>0$ and $v^{″}(A_0)<0$.17 At period $t=0$, the firm chooses its portfolio $(x_{00},x_{01},x_{02})$ and its state-dependent investment level $A_1(s_0)-A_0$ in order to maximize

$$\begin{array}{cc}\hfill & \sum _{s_0\in \{u,d,p\}}{\pi }_{s_0}[u(f(A_0-\sum _{i\in \{0,1,2\}}{x}_{0i})+\sum _{i\in \{0,1,2\}}(1+r_{s_{0}i})x_{0i}\hfill \\ \hfill & +A_0-A_1(s_0)-\mathbb{1}(s_0=p)L)+\delta v(A_1(s_0))],\hfill \end{array}$$

where the effect of current decisions on the discounted expected utility in subsequent periods goes through the last term $\delta v(A_1(s_0))$. Conditionally on state $s_0$, the future assets $A_1(s_0)$ are chosen so as to maximize the discounted expected utility

$$\begin{array}{cc}\hfill & u(f(A_0-\sum _{i\in \{0,1,2\}}{x}_{0i})+\sum _{i\in \{0,1,2\}}(1+r_{s_{0}i})x_{0i}\hfill \\ \hfill & +A_0-A_1(s_0)-\mathbb{1}(s_0=p)L)+\delta v(A_1(s_0)).\hfill \end{array}$$

Hence, the portfolio $(x_{00},x_{01},x_{02})$ maximizes

$$\begin{array}{c}\hfill \sum _{s_0\in \{u,d,p\}}{\pi }_{s_0}\overline{u}(f(A_0-\sum _{i\in \{0,1,2\}}{x}_{0i})+\sum _{i\in \{0,1,2\}}(1+r_{s_{0}i})x_{0i}-\mathbb{1}(s_0=p)L),\end{array}$$

where indirect utility function $\overline{u}(.)$ is defined by

$$\begin{array}{c}\hfill \overline{u}(w)\equiv \underset{A_1}{max}\{u(w+A_0-A_1)+\delta v(A_1)\},\end{array}$$

with ${\overline{u}}^{\prime }>0$ and ${\overline{u}}^{″}<0$.18 Hence, in this multi-period setting, the optimal portfolio is the solution to an optimization problem deduced from the one-period problem by replacing utility function u by the indirect utility function $\overline{u}$. The concavity of function $\overline{u}$ allows us to conclude that the results obtained in the one-period setting are also valid in this multi-period setting, with unchanged qualitative conclusions.

Proofs

Proof of Lemma 1

A portfolio $\{x_{0u,}{x}_{1u},x_{2u}\}$ pays one unit of numeraire in state u and zero otherwise, if

$$\begin{array}{cc}\hfill & x_{0u}(1+r_f)+x_{1u}(1+R_1+h)+x_{2u}(1+R_2+h)=1,\hfill \\ \hfill & x_{0u}(1+r_f)+x_{1u}(1+R_1-h^{\prime })+x_{2u}(1+R_2-h^{\prime })=0,\hfill \\ \hfill & x_{0u}(1+r_f)+x_{1u}(1+R_1+H)+x_{2u}(1+R_2-H^{\prime })=0.\hfill \end{array}$$

Solving this system of three equations with three unknown yields

$$\begin{array}{cc}\hfill x_{0u}=& \frac{(h^{\prime }-1)(H+H^{\prime })+(h^{\prime }-H^{\prime })R_1-(H+h^{\prime })R_2}{(1+r_f)(h+h^{\prime })(H+H^{\prime })},\hfill \end{array}$$ 30

$$\begin{array}{cc}\hfill x_{1u}=& \frac{H^{\prime }-h^{\prime }}{(h+h^{\prime })(H+H^{\prime })},\hfill \end{array}$$ 31

$$\begin{array}{cc}\hfill x_{2u}=& \frac{H+h^{\prime }}{(h+h^{\prime })(H+H^{\prime })},\hfill \end{array}$$ 32

which gives

$$\begin{array}{cc}\hfill q_u=& x_{0u}+x_{1u}+x_{2u}\hfill \\ \hfill =& \frac{(H+H^{\prime })(r_f+h^{\prime })-(H^{\prime }-h^{\prime })R_1-(H+h^{\prime })R_2}{(1+r_f)(h+h^{\prime })(H+H^{\prime })}.\hfill \end{array}$$ 33

When there are risk-neutral investors, using ${\alpha }_u=h^{\prime }/(h+h^{\prime })$ yields

$$\begin{array}{c}\hfill q_u=\frac{{\alpha }_u(1-\pi )}{1+r_f}.\end{array}$$ 34

Straightforward calculations with similar notations for states d and p yield

$$\begin{array}{cc}\hfill x_{0d}=& \frac{(1+h)(H+H^{\prime })+(H^{\prime }+h)R_1+(H-h)R_2}{(1+r_f)(h+h^{\prime })(H+H^{\prime })},\hfill \end{array}$$ 35

$$\begin{array}{cc}\hfill x_{1d}=& \frac{-(H^{\prime }+h)}{(h+h^{\prime })(H+H^{\prime })},\hfill \end{array}$$ 36

$$\begin{array}{cc}\hfill x_{2d}=& \frac{h-H}{(h+h^{\prime })(H+H^{\prime })},\hfill \end{array}$$ 37

and

$$\begin{array}{cc}\hfill x_{0p}=& \frac{R_2-R_1}{(1+r_f)(H+H^{\prime })},\hfill \end{array}$$ 38

$$\begin{array}{cc}\hfill x_{1p}=& -x_{2p}=\frac{1}{H+H^{\prime }},\hfill \end{array}$$ 39

which gives

$$\begin{array}{cc}\hfill q_d=& x_{0d}+x_{1d}+x_{2d}\hfill \\ \hfill =& \frac{(H+H^{\prime })(h-r_f)+(H^{\prime }+h)R_1+(H-h)R_2}{(1+r_f)(h+h^{\prime })(H+H^{\prime })},\hfill \end{array}$$ 40

$$\begin{array}{cc}\hfill q_p=& x_{0p}+x_{1p}+x_{2p}\hfill \\ \hfill =& \frac{R_2-R_1}{(1+r_f)(H+H^{\prime })}.\hfill \end{array}$$ 41

In particular, when there are risk-neutral investors, we have

$$\begin{array}{cc}\hfill q_d=& \frac{{\alpha }_d(1-\pi )}{1+r_f},\hfill \end{array}$$ 42

$$\begin{array}{cc}\hfill q_p=& \frac{\pi }{1+r_f},\hfill \end{array}$$ 43

when there are risk-neutral investors.

If (3) holds, then (34),(42), and (43) give (5). If (4) holds, then (33) and (40) give (6). Furthermore, using (7),(40), (41), and ${\alpha }_d=h/(h+h^{\prime })$ yield (8).

Proof of Proposition 1

The first-order optimality conditions for the maximization of

$$\begin{array}{cc}\hfill & \mathbb{E}u\equiv (1-\pi ){\alpha }_{u}u(f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_u)\hfill \\ \hfill & +(1-\pi ){\alpha }_{d}u(f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_d)\hfill \\ \hfill & +\pi u(f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_p-L),\hfill \end{array}$$

with respect to $y_u,y_d$ and $y_p$ are written as

$$\begin{array}{cc}\hfill (1-\pi ){\alpha }_u{u}^{\prime }(w_u)=& q_u{f}^{\prime }(K)\mathbb{E}{u}^{\prime },\hfill \end{array}$$ 44

$$\begin{array}{cc}\hfill (1-\pi ){\alpha }_d{u}^{\prime }(w_d)=& q_d{f}^{\prime }(K)\mathbb{E}{u}^{\prime },\hfill \end{array}$$ 45

$$\begin{array}{cc}\hfill \pi u^{\prime }(w_p)=& q_p{f}^{\prime }(K)\mathbb{E}{u}^{\prime },\hfill \end{array}$$ 46

with $K=A-q_u{y}_u-q_d{y}_d-q_p{y}_p$, and where we denote

$$\begin{array}{c}\hfill \mathbb{E}{u}^{\prime }=(1-\pi )[{\alpha }_u{u}^{\prime }(w_u)+{\alpha }_d{u}^{\prime }(w_d)]+\pi u^{\prime }(w_p).\end{array}$$

Assume first that there are risk-neutral investors, i.e., (3) holds. In that case, (5) and (44–46) give (11), and (9), (10) show that there exists y such that

$$\begin{array}{c}\hfill y=y_u=y_d=y_p-L.\end{array}$$ 47

We have

$$\begin{array}{c}\hfill x_i=(x_{\mathit{iu}}+x_{\mathit{id}})y+x_{\mathit{ip}}(y+L)\text{for}i=0,1,2,\end{array}$$

which gives (12),(13), and

$$\begin{array}{c}\hfill x_0=\frac{y(H+H^{\prime })+(R_2-R_1)L}{(1+r_f)(H+H^{\prime })}=\frac{y+\pi L}{1+r_f}.\end{array}$$ 48

We have $K=A-I=A-x_0-x_1-x_2$. Maximizing the (state-independent) final cash flow of the firm

$$\begin{array}{c}\hfill f(A-x_0-x_1-x_2)+y=f\left(A,-,\frac{y+\pi L}{1+r_f}\right)+y,\end{array}$$

w.r.t. y gives (18).

Assume now that investors are risk-averse, i.e., (6) and (8) hold. In that case, (44–46) give (14) and

$$\begin{array}{c}\hfill y_p-L<y_d<y_u.\end{array}$$ 49

Thus, we may write

$$\begin{array}{cc}\hfill y_d=& y_u-{\mathrm{\Delta }}_d,\hfill \\ \hfill y_p=& y_u+L-{\mathrm{\Delta }}_p,\hfill \end{array}$$

with $0<{\mathrm{\Delta }}_d<{\mathrm{\Delta }}_p$. Using $y_u-y_d=(x_1+x_2)(h+h^{\prime }){\mathrm{\Delta }}_d>0$ and (9) gives (16), and thus (15). Using $y_p-L<y_d$ and (16) yields

$$\begin{array}{c}\hfill x_{1}H-x_2{H}^{\prime }-L<-h^{\prime }(x_1+x_2)<0,\end{array}$$

and thus

$$\begin{array}{c}\hfill L>x_{1}H-x_2{H}^{\prime }>-x_2(H+H^{\prime }),\end{array}$$

which gives (17). Furthermore, maximizing the firm’s expected utility

$$\begin{array}{cc}\hfill \mathbb{E}u\equiv & (1-\pi ){\alpha }_{u}u(f(A-\frac{y_u}{1+r_f}+q_d{\mathrm{\Delta }}_d+q_p({\mathrm{\Delta }}_p-L))+y_u)\hfill \\ \hfill & +(1-\pi ){\alpha }_{d}u(f(A-\frac{y_u}{1+r_f}+q_d{\mathrm{\Delta }}_d+q_p({\mathrm{\Delta }}_p-L))+y_u-{\mathrm{\Delta }}_d)\hfill \\ \hfill & +\pi u(f(A-\frac{y_u}{1+r_f}+q_d{\mathrm{\Delta }}_d+q_p({\mathrm{\Delta }}_p-L))+y_u-{\mathrm{\Delta }}_p),\hfill \end{array}$$

w.r.t. $y_u$, for ${\mathrm{\Delta }}_d$ and ${\mathrm{\Delta }}_p$ given, yields (18), with

$$\begin{array}{c}\hfill K=A-\frac{y_u}{1+r_f}+q_d{\mathrm{\Delta }}_d+q_p({\mathrm{\Delta }}_p-L)=K^{\ast }.\end{array}$$

Proof of Proposition 2

The first-order optimality conditions for the maximization of

$$\begin{array}{cc}\hfill \mathbb{E}u\equiv & (1-\pi ){\alpha }_{u}u(f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_u)\hfill \\ \hfill & +(1-\pi ){\alpha }_{d}u(f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_d)\hfill \\ \hfill & +\pi \mathbb{E}[u(f(A-q_u{y}_u-q_d{y}_d-q_p{y}_p)+y_p-\tilde{L}),\hfill \end{array}$$

with respect to $y_u,y_d$ and $y_p$ are written as

$$\begin{array}{cc}\hfill (1-\pi ){\alpha }_u{u}^{\prime }(w_u)=& q_u\mathbb{E}{u}^{\prime },\hfill \end{array}$$ 50

$$\begin{array}{cc}\hfill (1-\pi ){\alpha }_d{u}^{\prime }(w_d)=& q_d\mathbb{E}{u}^{\prime },\hfill \end{array}$$ 51

$$\begin{array}{cc}\hfill \pi \mathbb{E}{u}^{\prime }({\tilde{w}}_p)=& q_p\mathbb{E}{u}^{\prime },\hfill \end{array}$$ 52

where we denote

$$\begin{array}{c}\hfill \mathbb{E}{u}^{\prime }=(1-\pi )[{\alpha }_u{u}^{\prime }(w_u)+{\alpha }_d{u}^{\prime }(w_d)]+\pi \mathbb{E}{u}^{\prime }({\tilde{w}}_p).\end{array}$$

Using $u^{″\prime }>0$ gives

$$\begin{array}{c}\hfill \mathbb{E}{u}^{\prime }({\tilde{w}}_p)>u^{\prime }({\overline{w}}_p),\end{array}$$

and thus, using $u^{″}<0$, we deduce that there exists $\gamma >0$ such that

$$\begin{array}{c}\hfill \mathbb{E}{u}^{\prime }({\tilde{w}}_p)=u^{\prime }({\overline{w}}_p-\gamma ).\end{array}$$

Comparing with the optimality conditions of Proposition 1 shows that the optimal portfolio choices correspond to the case of deterministic losses $L=\overline{L}+\gamma$. In particular, in the case of risk-neutral investors, the long–short positions allow the firm to cover the loss $L>\overline{L}$.

Proof of Proposition 3

We still denote $y_u$ and $y_d$ the firm’s portfolio payoff in states u and d, respectively. Let ${\overline{y}}_p$ denote the expected portfolio payoff in state p. The state-contingent expected payoffs $y_u,y_d$ and ${\overline{y}}_p$ can be obtained through portfolio choices

$$\begin{array}{c}\hfill x_i=x_{\mathit{iu}}{y}_u+x_{\mathit{id}}{y}_d+x_{\mathit{ip}}{\overline{y}}_p,\end{array}$$ 53

with $i\in \{0,1,2\}$, where $x_{\mathit{is}}$ is defined as in the proof of Proposition 1 for all i, s. Choosing $x_0,x_1$ and $x_2$ is equivalent to choosing $y_u,y_d$ and ${\overline{y}}_p$, with financial investment cost

$$\begin{array}{c}\hfill I=q_u{y}_u+q_d{y}_d+q_p{\overline{y}}_p,\end{array}$$ 54

where $q_u,q_d$ and $q_p$ correspond to the Arrow–Debreu security prices of the complete market model (i.e., when ${\epsilon }_1\equiv {\epsilon }_2\equiv 0$), and are given by (33), (40) and (41). The firm chooses $y_u,y_d$ and ${\overline{y}}_p$ in order to maximize its expected utility

$$\begin{array}{c}\hfill \mathbb{E}u={\sum }_{s=u,p}{\pi }_{s}u(w_s)+{\pi }_p\mathbb{E}u({\tilde{w}}_p),\end{array}$$

where

$$\begin{array}{cc}\hfill w_s=& f(A-I)+y_s\text{for}s=u\text{and}d,\hfill \\ \hfill {\tilde{w}}_p=& f(A-I)+x_1{\epsilon }_1+x_2{\epsilon }_2+{\overline{y}}_p-L,\hfill \end{array}$$

with $(x_1,x_2)$ and I given by (53) and (54), respectively. First-order optimality conditions are written as

$$\begin{array}{cc}\hfill \frac{\partial \mathbb{E}u}{\partial y_s}=& {\pi }_s{u}^{\prime }(w_s)-q_s{f}^{\prime }\mathbb{E}{u}^{\prime }+{\pi }_p\mathbb{E}\{(x_{1s}{\epsilon }_1+x_{2s}{\epsilon }_2)u^{\prime }({\tilde{w}}_p)\}=0\hfill \\ \hfill & \text{for}s=u,d,\hfill \end{array}$$ 55

$$\begin{array}{cc}\hfill \frac{\partial \mathbb{E}u}{\partial {\overline{y}}_p}=& {\pi }_p\mathbb{E}{u}^{\prime }({\tilde{w}}_p)-q_p{f}^{\prime }\mathbb{E}{u}^{\prime }+{\pi }_p\mathbb{E}\{(x_{1p}{\epsilon }_1+x_{2p}{\epsilon }_2)u^{\prime }({\tilde{w}}_p)\}=0,\hfill \end{array}$$ 56

where

$$\begin{array}{c}\hfill \mathbb{E}{u}^{\prime }={\sum }_{s=u,d}{\pi }_s{u}^{\prime }(w_s)+{\pi }_p\mathbb{E}{u}^{\prime }({\tilde{w}}_p).\end{array}$$

Summing (55) and (56), and using

$$\begin{array}{c}\hfill x_{1u}+x_{1d}+x_{1p}=x_{2u}+x_{2d}+x_{2p}=0,\end{array}$$

and

$$\begin{array}{c}\hfill q_u+q_d+q_p=\frac{1}{1+r_f},\end{array}$$

yields

$$\begin{array}{c}\hfill f^{\prime }(A-I)=1+r_f,\end{array}$$ 57

i.e.,

$$\begin{array}{c}\hfill K=A-I=K^{\ast }.\end{array}$$

When investors are risk-neutral, equations (53) and (54) give

$$\begin{array}{cc}\hfill u^{\prime }(w_u)=& \mathbb{E}{u}^{\prime }-\frac{\pi }{{\alpha }_u(1-\pi )}\mathbb{E}\left\{\left[\frac{(H^{\prime }-h^{\prime }){\epsilon }_1+(H+h^{\prime }){\epsilon }_2}{(H+H^{\prime })(h+h^{\prime })}\right],u^{\prime },({\tilde{w}}_p)\right\},\hfill \end{array}$$ 58

$$\begin{array}{cc}\hfill u^{\prime }(w_d)=& \mathbb{E}{u}^{\prime }-\frac{\pi }{{\alpha }_d(1-\pi )}\mathbb{E}\left\{\left[\frac{-(H^{\prime }+h){\epsilon }_1+(h-H){\epsilon }_2}{(H+H^{\prime })(h+h^{\prime })}\right],u^{\prime },({\tilde{w}}_p)\right\},\hfill \end{array}$$ 59

$$\begin{array}{cc}\hfill \mathbb{E}{u}^{\prime }({\tilde{w}}_p)=& \mathbb{E}{u}^{\prime }-\mathbb{E}\left\{\left[\frac{{\epsilon }_1-{\epsilon }_2}{H+H^{\prime }}\right],u^{\prime },({\tilde{w}}_p)\right\}.\hfill \end{array}$$ 60

When the supports of ${\epsilon }_1$ and ${\epsilon }_2$ are not too large, we have $x_1>0$ and $x_2<0$ at an optimal solution, because $x_1=-x_2=L/(H+H^{\prime })>0$ when ${\epsilon }_1\equiv {\epsilon }_2\equiv 0$. Hence ${\tilde{w}}_p$ is increasing w.r.t. ${\epsilon }_1$ and decreasing w.r.t. ${\epsilon }_2$. Using $u^{″}<0$ then gives

$$\begin{array}{cc}\hfill \mathbb{E}[{\epsilon }_1{u}^{\prime }({\tilde{w}}_p)]=& cov[{\epsilon }_1,u^{\prime }({\tilde{w}}_p)]<0,\hfill \end{array}$$ 61

$$\begin{array}{cc}\hfill \mathbb{E}[{\epsilon }_2{u}^{\prime }({\tilde{w}}_p)]=& cov[{\epsilon }_2,u^{\prime }({\tilde{w}}_p)]>0.\hfill \end{array}$$ 62

Assume ${\alpha }_u={\alpha }_d=1/2,h^{\prime }=h$ and $H=0$. In that case, (58) and (59) are written as

$$\begin{array}{cc}\hfill u^{\prime }(w_u)=& \mathbb{E}{u}^{\prime }-\frac{\pi }{1-\pi }\mathbb{E}\left\{\left[\frac{(H^{\prime }-h){\epsilon }_1+h{\epsilon }_2}{h{H}^{\prime }}\right],u^{\prime },({\tilde{w}}_p)\right\},\hfill \end{array}$$ 63

$$\begin{array}{cc}\hfill u^{\prime }(w_d)=& \mathbb{E}{u}^{\prime }-\frac{\pi }{1-\pi }\mathbb{E}\left\{\left[\frac{-(H^{\prime }+h){\epsilon }_1+h{\epsilon }_2}{h{H}^{\prime }}\right],u^{\prime },({\tilde{w}}_p)\right\}.\hfill \end{array}$$ 64

This gives

$$\begin{array}{c}\hfill u^{\prime }(w_u)-u^{\prime }(w_d)=-\frac{2\pi }{h(1-\pi )}\mathbb{E}[{\epsilon }_1{u}^{\prime }({\tilde{w}}_p)]>0,\end{array}$$

which implies $w_u<w_d$, and thus $x_1+x_2<0$.

Let us further assume that u(.) is quadratic, and written as $u(w)=-a{w}^2/2+bw$, with $a,b>0$ and $w<b/a$ for all relevant values. Since ${\epsilon }_1$ and ${\epsilon }_2$ are independently distributed, (60) and (63) give

$$\begin{array}{cc}\hfill w_u=& \overline{w}+\frac{\pi }{h{H}^{\prime }(1-\pi )}[(H^{\prime }-h)x_1{\sigma }_1^2+h{x}_2{\sigma }_2^2],\hfill \\ \hfill {\overline{w}}_p=& \overline{w}+\frac{1}{H^{\prime }}[x_1{\sigma }_1^2-x_2{\sigma }_2^2],\hfill \end{array}$$

where ${\overline{w}}_p=\mathbb{E}{\tilde{w}}_p$ and $\overline{w}=(1-\pi )(w_u+w_p)/2+\pi {\overline{w}}_p$. This yields

$$\begin{array}{c}\hfill {\overline{w}}_p-w_u=\frac{x_1{\sigma }_1^2(h-\pi H^{\prime }){\sigma }_1^2-x_{2}h{\sigma }_2^2}{h{H}^{\prime }(1-\pi )}.\end{array}$$

Hence, $\pi H^{\prime }<h$ is a sufficient condition for ${\overline{w}}_p>w_u$.

Author contributions

The authors contributed equally to the paper.

Funding

The authors declare no funding.

Data availability

All data used is from open-source providers. More specific information is available from the authors upon request.

Declarations

Conflict of interest

The authors declare that their contribution is free from any conflicts of interest, including all financial and non-financial interests and relationships.