OBLIQUE RANDOM SURVIVAL FORESTS

Abstract

We introduce and evaluate the oblique random survival forest (ORSF). The ORSF is an ensemble method for right-censored survival data that uses linear combinations of input variables to recursively partition a set of training data. Regularized Cox proportional hazard models are used to identify linear combinations of input variables in each recursive partitioning step. Benchmark results using simulated and real data indicate that the ORSF’s predicted risk function has high prognostic value in comparison to random survival forests, conditional inference forests, regression, and boosting. In an application to data from the Jackson Heart Study, we demonstrate variable and partial dependence using the ORSF and highlight characteristics of its 10-year predicted risk function for atherosclerotic cardiovascular disease events (ASCVD; stroke, coronary heart disease). We present visualizations comparing variable and partial effect estimation according to the ORSF, the conditional inference forest, and the Pooled Cohort Risk equations. The obliqueRSF R package, which provides functions to fit the ORSF and create variable and partial dependence plots, is available on the comprehensive R archive network (CRAN).

1. Introduction.

Since Breiman (2001) introduced the random forest (RF), it has become recognized as a flexible and accurate tool for classification, regression, and right-censored time-to-event (i.e., survival) analysis (Strobl, Malley and Tutz, 2009). RFs are characterized by an ensemble of decision trees, each of which are grown through recursive partioning (Breiman, 1984). Recursive partitioning is performed in steps, where each step involves splitting a set of data into two descendant subsets, beginning with the full set. The data are split based on an input variable X and a splitting value c such that one descendant set contains observations in the current data with X < c and the other set contains observations in the current data with X ≥ c. The splitting variable and value are chosen to maximize the difference between the descendant sets in an outcome variable, and the splitting variable can be either a single input variable or a linear combination of input variables (LCIVs). Descendant data sets that are split into smaller sets are referred to as ‘non-terminal nodes’ in the tree. Descendant data sets that are too small to split further (i.e., data sets with less than a pre-specified minimum number of unique observations or events) are not split any further and are referred to as ‘terminal nodes’ (i.e., leaves) of the tree.¹ Predictions for a single test observation are computed by determining which terminal node the observation falls to and then aggregating the outcomes of participants in the training data who were mapped to the same node.

Breiman (2001) showed that RFs often achieve lower generalization error when LCIVs are used instead of a single variable (i.e., oblique splitting versus axis-based splitting) to split the training data in each recursive partitioning step. Hothorn and Lausen (2003) incorporated LCIVs by applying linear discriminant analysis to out-of-bag data and using predicted values from the discriminant model for in-bag data as a candidate splitting variable. Menze et al. (2011) introduced oblique RFs, and showed that Breiman’s method of constructing LCIVs could be improved by fitting regularized regression models (Friedman, Hastie and Tibshirani, 2001, Sec. 3.4) to the data in non-terminal nodes and synthesizing a splitting variable using the model’s predictions. Zhu, Zeng and Kosorok (2015) proposed to construct LCIVs using the most important K variables, which they identified by fitting ensembles of extremely randomized trees (Geurts, Ernst and Wehenkel, 2006) to the data in each non-terminal node. For classification and regression problems, RFs with LCIVs have achieved excellent generalization error (Breiman, 2001, Sec. 5) for several data sets in public repositories (Dheeru and Karra Taniskidou, 2017).

Random survival forests (RSFs) (Ishwaran et al., 2008) and conditional inference forests (CIF) (Hothorn, Hornik and Zeileis, 2006) extend Breiman’s RF to right-censored survival data, but neither of these recursive partitioning algorithms incorporate LCIVs. Additionally, to our knowledge, there are no studies examining the use of LCIVs for recursive partitioning in the context of right-censored survival outcomes (Bou-Hamad et al., 2011). Therefore, we developed and evaluated a method to incorporate LCIVs in binary decision trees for right-censored survival data. Zhu (2013) found that extremely randomized survival trees did not produce optimal multiplicative coefficients for LCIVs. Thus, we extended the approach of Menze et al. (2011) by using regularized (Zou and Hastie, 2005) Cox proportional hazards (PH) (Cox, 1992; Simon et al., 2011) models to identify multiplicative coefficients for LCIVs in each recursive partitioning step. Following the notation of Menze et al. (2011), we refer to our method as the oblique RSF (ORSF).

The purpose of this article is to describe the ORSF and assess the prognostic value of its predicted risk fucntion. After a brief summary of RSFs and CIFs in Section 2, ORSFs are described in Section 3. Simulated and real data are used in Sections 4 and 5, respectively, to assess performance of the ORSF in comparison to the RSF, CIF, gradient boosted decision trees, and Cox PH models. Performance and mean time required for computation over the entire collection of data from Sections 4 and 5 is assessed in Section 6. In Section 7, we apply the obliqueRSF R package to conduct exploratory analyses using data from participants in the Jackson Heart Study (JHS). Our analysis of the JHS data focuses on atherosclerotic cardiovascular disease (ASCVD) and its dependence on four key variables: age, systolic blood pressure, estimated glomerular filtration rate, and left ventricular mass. We conclude with a summary and discussion of our results in Section 8.

2. Ensemble tree methods for right-censored survival data.

Here we summarize two separate implementations of ensemble tree methods for right-censored survival data:

1. Random survival forest (RSF) (Ishwaran et al., 2008).

2. Conditional inference forest (CIF) (Hothorn, Hornik and Zeileis, 2006).

We present an ad-hoc summary of the steps taken to grow ensembles of binary decision trees for right-censored survival data (i.e., survival trees) in Section 2.1. Section 2.2 contains notation to describe the framework of survival ensembles. Last, we present summaries of the RSF and CIF in Sections 2.3 and 2.4, respectively.

2.1. How to grow ensembles of survival trees.

• Step 1 Draw B subsamples² from the data: {D₁, …, D_B}

• Step 2 For b = 1, …, B, grow a survival tree using D_b:

  1. Initiate 𝒩_G = {D_b}, the set of ‘nodes to grow.’
  2. If 𝒩_G = ∅, go to (c). Otherwise, for each node in 𝒩_G, do the following:

     1. Define the set of candidate splitting variables for the current node by selecting a random subset of the available predictor variables.³
     2. ⁴If there is no evidence of statistical association between the survival outcome and any of the candidate splitting variables, then (1) remove the current node from 𝒩_G, (2) label the current node as ‘terminal’, and (3) skip steps (iii) and (iv) below.
     3. Split the current node into descendant nodes,⁵ A₁ and A₂, using the candidate splitting variable that maximizes a log-rank statistic comparing survival outcomes between A₁ and A₂.
     4. Remove the current node from 𝒩_G. If A₁ has at least a minimum number of unique observations (i.e., minsplit or nodesize), add A₁ to 𝒩_G. Otherwise, label A₁ as ‘terminal’. Do the same for A₂.
  3. Define a predicted survival or cumulative hazard function for each terminal node based on the observed survival times in the node.

• Step 3 Aggregate predicted survival⁶ or cumulative hazard functions from the B survival trees to compute ensemble predictions.

2.2. Notation.

Consider right-censored survival data from N participants: (y₁, x₁, δ₁), …, (y_N, x_N, δ_N). For participant i, 1 ≤ i ≤ N, y_i represents survival time if δ_i = 1 and time to censoring if δ_i = 0, x_i is a length p vector of predictors: (x_i,1, …, x_i,p). Denote the j^th column of the matrix x = [x₁, …, x_N]′ as x_(j). Let t₁ < … < t_m denote the m unique event times (assume there are no ties). Denote the b^th survival tree as 𝒯_b, let 𝒯_b(x_i) identify the terminal node in 𝒯_b participant i is mapped to, and let c_ib denote the number of times the data from participant i occurs in the b^th bootstrap sample. Following the counting process notation of Andersen et al. (2012), define

$$N_i(s)=I\left(y_i\le s,{\delta }_i=1\right);Y_i(s)=I\left(y_i>s\right)$$ (2.1)

where 0 ≤ s ≤ t_m and I(·) is the indicator function. Define

$$N_b^{\ast }(s,\mathit{x})=\sum _{i=1}^N{c}_{ib}\cdot I\left({\mathit{x}}_i\in {𝒯}_b(\mathit{x})\right)\cdot N_i(s)$$ (2.2)

and

$$Y_b^{\ast }(s,\mathit{x})=\sum _{i=1}^N{c}_{ib}\cdot I\left({\mathit{x}}_i\in {𝒯}_b(\mathit{x})\right)\cdot Y_i(s)$$ (2.3)

as the number of uncensored events prior to and number of participants at risk at time s, respectively, in 𝒯_b(x).

2.3. Random survival forests (RSF).

The RSF extends the prescription described by Breiman and Cutler (2003) to the context of survival analyses. The log-rank statistic (Segal, 1988, Sec. 3.2) is applied to determine which candidate variable and cut-point should be used. A Nelson-Aalen estimator of the cumulative hazard function is formed in each terminal node based on the survival times of observations in the node:

$${\widehat{H}}_b(t\mid \mathit{x})={\int }_0^t\frac{N_b^{\ast }(ds,\mathit{x})}{Y_b^{\ast }(s,\mathit{x})}.$$ (2.4)

In turn, the ensemble survival function is

$${\widehat{S}}_{\text{RSF}}(t\mid \mathit{x})=\text{exp}\left[-\frac{1}{B}\sum _{i=1}^B{\widehat{H}}_b(t\mid \mathit{x})\right]$$ (2.5)

2.4. Conditional inference forests (CIF).

The CIF avoids variable selection bias (Breiman, 1984, pg. 42) by applying permutation tests (Strasser and Weber, 1999) to compare candidate splitting variables. During each recursive partitioning step, if there is no evidence of association between any of the candidate variables and the response, the current node is not split and is labeled terminal. For ensemble prediction, the CIF applies a weighted Kaplan-Meier estimate (Hothorn et al., 2004) based on all training observations in the B leaves containing the new observation:

$${\widehat{S}}_{\text{CIF}}(t\mid \mathit{x})=\prod _{s\le t}\left[1-\frac{{\sum }_{b=1}^B{N}_b^{\ast }(ds,\mathit{x})}{{\sum }_{b=1}^B{Y}_b^{\ast }(s,\mathit{x})}\right].$$ (2.6)

3. The oblique random survival forest (ORSF).

Here we describe the ORSF, beginning with the use of regularized Cox PH models (Section 3.1) and synthesis of candidate splitting variables using regularized Cox PH models (Section 3.2). Additional details related to sampling and prediction are provided in Section 3.3.

3.1. Regularized Cox PH models.

The ORSF embeds regularized Cox PH models into the non-terminal nodes of its survival trees. Suppose there are K observations in the current non-terminal node. The embedded Cox PH model assumes a semi-parametric form for the hazard:

$$h_k(t)=h_0(t)e^{{\mathit{x}}_k^T\mathit{\beta }}$$ (3.1)

where k = 1, …, K, h_k(t) is the hazard for observation k at time t, h₀(t) is the baseline hazard function, and β is a vector of mtry ≤ p coefficients, where mtry is the number of randomly selected predictor variables for the current node and p is the total number of predictor variable. Estimation of β is carried out using the partial likelihood,

$$L(\mathit{\beta })=\prod _{i=1}^m\frac{e^{{\mathit{x}}_{j(i)}^T\mathit{\beta }}}{{\sum }_{j\in R_i}{e}^{{\mathit{x}}_j^T\mathit{\beta }}},$$ (3.2)

where R_i is the set of indices, j, with y_j ≥ t_i (i.e., those still at risk at time t_i), and j(i) is the index of the observation for which an event occurred at time t_i. Simon et al. (2011) proposed to maximize (3.2) subject to the elastic net penalty (Zou and Hastie, 2005):

$$\alpha \sum _{i=1}^p\left|{\beta }_i\right|+(1-\alpha )\sum _{i=1}^p{\beta }_i^2\le s,$$ (3.3)

where s ≥ 0 is a constant that controls shrinkage and has one-to-one correspondence with the complexity parameter, λ ≥ 0. Setting α = 1 and α = 0 in (3.3) results in the classic ‘Ridge’ and ‘Lasso’ penalties, respectively (Friedman, Hastie and Tibshirani, 2001, Sec. 3.4). Each pair of values for α and λ corresponds to a different solution for β. Notably, with a ridge penalty, every node will develop a solution for β with non-zero regression coefficients for all mtry randomly selected predictor variables. On the other hand, a lasso penalty will usually identify sparse solutions that set most of the mtry coefficients in β to zero.

3.2. Linear combinations of input variables (LCIVs).

LCIVs are synthesized using embedded Cox PH models and used as splitting variables for internal nodes in the ORSF. The LCIVs are synthesized using ${\mathit{x}}^T\widehat{\mathit{\beta }}$, where ${\mathit{x}}^T=\left\{{\mathit{x}}_1^T,\dots {\mathit{x}}_{\mathit{K}}^T\right\}$ is the stacked matrix of input vectors and $\widehat{\mathit{\beta }}$ is selected from a number of candidate solutions given by the embedded Cox PH model. The maximum number of predictor variables with non-zero regression coefficients in these candidate solutions is mtry. The process that identifies candidate solutions for $\widehat{\mathit{\beta }}$ is governed by (1) whether cross-validation is applied, and (2) the value of α.

If cross-validation is applied (use.cv=TRUE in the ORSF function), then 5-fold cross-validation will be used in each non-terminal node to identify the following λ values:

• λ_CV: The value of λ maximizing cross-validated partial likelihood (van Houwelingen et al., 2006).

• λ_SE: The highest value of λ within one standard error of λ_CV.

The choice of α affects the candidate solutions identified by λ_CV and λ_SE. For example, when α = 1, both λ_CV and λ_SE identify solutions that use all of the randomly selected candidate splitting variables; however, the solution identified by λ_SE will impose a stronger penalty on regression coefficients. If α is set at a value close but not equal to 1, e.g. 0.90, then λ_CV and λ_SE will both identify ‘ridge-like’ solutions that estimate non-zero regression coefficients for nearly all of the candidate splitting variables.

If the analyst chooses not to use cross-validation, a regularization path is fitted to the current node’s data to identify λ₁, …, λ_mtry, where λ_i is the maximum value of lambda such that the model has i effective degrees of freedom (Efron et al., 2004). To ensure these values of λ can be found, we require α < 1 when cross-validation is not used. In this context, the choice of α affects how quickly the regularization path transitions from a minimally to maximally complex solution. For example, when α is close to 0, the regularization path will be ‘lasso-like’ and identify more solutions with a small number of non-zero regression coefficients compared to a ‘ridge-like’ regularization path, where all or nearly all solutions have non-zero regression coefficients for all candidate variables.

Regardless of whether or not cross-validation is used, each candidate solution for $\widehat{\mathit{\beta }}$ is evaluated as follows:

1. $\widehat{\mathit{\eta }}={\mathit{x}}^T\widehat{\mathit{\beta }}$ is computed for each observation in the current node.

2. nsplit candidate cut-points, c₁ …, c_nsplit are selected at random from the unique values of $\widehat{\mathit{\eta }}$.

3. For i = 1, …, nsplit, a log-rank statistic comparing survival curves between observations with ${\mathit{x}}_k^T\widehat{\mathit{\beta }}\le c_i$ and observations with ${\mathit{x}}_k^T\widehat{\mathit{\beta }}>c_i$ is computed.

When cross-validation is not applied, log-rank statistics are penalized by a scaling factor of (1+γ · df), where γ > 0 is a tuning parameter and df is the effective degrees of freedom of the model that generated the candidate LCIV. Larger values of γ will result in selection of less complex LCIVs with fewer variables. Setting γ = 0 imposes no penalty on the complexity of LCIVs and will result in selection of LCIVs with a larger number of variables. If the maximal log-rank statistic does not exceed a pre-specified threshold, early stopping is applied (i.e., the node is not split and is labeled terminal). Otherwise, the cut-point and candidate solution maximizing the log-rank statistic are used to split the node.

3.3. Additional details.

The ORSF applies subsampling rather than bootstrap sampling with replacement. Ensemble predictions from an ORSF are formed using the same weighted aggregation scheme as in the CIF.

4. Simulation Study.

Here we describe and summarize results from a simulation study following the protocol described by Morris, White and Crowther (2017). The primary aim of the simulation is to compare the prognostic value of the ORSF’s predicted risk function with a variety of competing learning algorithms in three general settings. Data generating mechanisms are summarized in Section 4.1. The primary estimands of the simulation study are described in Section 4.3. Competing learning algorithms and their corresponding hyper-parameter settings are introduced in Section 4.2. Tabular summaries of results are presented in Section 4.5. Computational strategies are reported in Section 4.4. Source codes for the current simulation study are available from the first author’s GitHub site and supplemental material Jaeger et al. (2019).

4.1. Data generating mechanisms.

We generated right-censored survival data from three scenarios using a training sample of N = 500 and a testing sample of M = 1000. The number of predictor variables used to generate survival outcomes, p, was set at 25 and 50 for each scenario. For i = 1, …, N + M, x_i = (x_i,1, …, x_i,p) was generated from a zero mean, unit variance multivariate normal distribution with cov(x_i,u, x_i,v) = (1/3)^|u−v|. Multiplicative coefficient vectors (i.e., β) for variables 1 through p were generated as a uniform sequence of length p, beginning from −1 and ending at +1. The three scenarios were as follows:

1. The length p vector β contained one effect for each predictor. Simulated outcomes followed a Weibull distribution.

2. The length 2p vector β contained one main effect for each predictor and, additionally, each predictor was used in two bi-variate interaction terms. The multiplicative coefficients for interaction variables were generated as a uniform sequence of length p, beginning from −1 and ending at +1.⁷ Simulated outcomes followed the same distribution as in scenario A.

3. The same β vector was used as described scenario B, and each (y_i, δ_i) followed one of three distinct Weibull distributions, depending on the value of x_iβ.

Scenario A is designed to favor the PH model, whereas scenario B will favor survival tree ensembles. Scenario C is of particular interest as the proportional hazards assumption does not hold.

4.2. Competing methods and tuning parameters.

4.2.1. Decision tree ensembles.

ORSF, RSF, and CIF ensembles were composed of 1000 survival trees. The minimum number of unique observations needed to split a node (i.e., minsplit or nodesize) was 10. For the ORSF and RSF, the minimum number of events per terminal node was 1, splitting values were selected by comparing 25 randomly selected cut-points, and the number of variables tried at each node (i.e., mtry) was set to the smallest integer ≥ $\sqrt{p}$. The CIF used tuning parameters consistent with an unbiased recursive partitioning framework (Strobl et al., 2007; Hothorn et al., 2010, 2019). Two ORSF models were fitted as follows:

• ORSF: The ORSF algorithm is applied with α = 0.50 and without using cross-validation to synthesize candidate splitting variables (i.e., setting use.cv=FALSE as described in Section 3.2).

• ORSF_CV: The ORSF algorithm is applied with α = 0.05 (a ridge-like penalty) and using cross-validation to synthesize candidate splitting variables (i.e., setting use.cv=TRUE as described in Section 3.2).

Gradient boosted decision trees were fitted using cross-validation to determine (1) the optimal number of boosting steps and (2) an optimal set of hyper-parameter values (Chen and Guestrin, 2016; Friedman, 2001). For (2), we generated 10 sets of hyper-parameter values randomly (i.e., values for tree depth, column subsampling, row subsampling, minimum child weight, and minimum loss reduction required to make a further partition on a leaf node). The hyper-parameter set that maximized cross-validated partial log-likelihood was used to fit an ensemble of gradient boosted decision trees to the training data.

4.2.2. Cox proportional hazards (PH) models.

Regularized Cox PH models were fitted using Lasso-like (α = 0.90) and Ridge-like (α = 0.10) penalties, and using the value of λ that maximized cross-validated partial likelihood (Friedman, Hastie and Tibshirani, 2010a). Unregularized Cox PH models were fitted using stepwise variable selection based on Akaike’s information criteria (Burnham and Anderson, 2004). Boosted Cox PH models were fitted using cross-validation to determine the optimal number of boosting steps and penalized score statistics to determine parameter updates in each boosting step (Tutz and Binder, 2007).

4.3. Prediction Error.

Predicted risk for right-censored survival outcomes can be assessed using the time dependent concordance index and Brier score (Gerds et al., 2013; Graf et al., 1999). For t > 0, the inverse probability of censoring weighted concordance index and Brier score are estimated using

$$\widehat{\text{C}}(t)=\frac{{\sum }_{i=1}^M{\sum }_{j=1}^{M}I\left(t_i<t_j\right)\cdot I\left(\widehat{S}\left(t\mid {\mathit{x}}_i\right)>\widehat{S}\left(t\mid {\mathit{x}}_j\right)\right)\cdot I\left(t_i<t\right)\cdot {\delta }_i\cdot {\widehat{W}}_{ij}^{-1}}{{\sum }_{i=1}^M{\sum }_{j=1}^{M}I\left(t_i<t_j\right)\cdot I\left(t_i<t\right)\cdot {\delta }_i\cdot {\widehat{W}}_{ij}^{-1}},$$

and

$$\widehat{\text{BS}}(t)=\frac{1}{M}\sum _{i=1}^M\{\widehat{S}{\left(t\mid {\mathit{x}}_i\right)}^2\cdot I\left(y_i<t,{\delta }_i=1\right)\cdot \widehat{G}{\left(y_i\mid {\mathit{x}}_i\right)}^{-1}+{\left[1-\widehat{S}\left(t\mid {\mathit{x}}_i\right)\right]}^2\cdot I\left(y_i>t\right)\cdot \widehat{G}{\left(y_i\mid {\mathit{x}}_i\right)}^{-1}\}$$

respectively, where for participant i in the testing data, $\widehat{S}\left(t\mid {\mathit{x}}_i\right)$ is the estimated probability of survival at time t, x_i is the input information, and $\widehat{G}\left(y_i\mid {\mathit{x}}_i\right)$ is the estimated probability of censoring. Additionally, ${\widehat{W}}_{ij}=\widehat{G}\left(y_i\mid {\mathit{x}}_j\right)\cdot \widehat{G}\left(y_i-\mid {\mathit{x}}_i\right)$ defines the probability of censoring weights for concordance.

The concordance index measures the probability at time t that a randomly selected participant who has experienced an event has a higher model-based prediction than a randomly selected subject who has not experienced an event. Concordance indices of 1.00 and 0.50 correspond to perfect and worthless discrimination, respectively. Gerds et al. (2013) demonstrated asymptotic bias of the concordance index introduced by Harrell et al. (1982) and proposed a method to estimate a time-dependent concordance index for models with covariate dependent censoring (i.e., $\widehat{\text{C}}(t)$). Additionally, Blanche, Kattan and Gerds (2018) showed that the time dependent area under the receiver operating characteristic curve rather than the concordance index introduced by Harrell et al. (1982) should be used to assess t-year predicted risk.

For a single observation at time t, the Brier score is the squared difference between observed survival status (e.g., 1 = alive at time t and 0 = dead at time t) and a model-based prediction of survival at time t. The expected Brier score of a prediction model which ignores all predictor variables (i.e. the Kaplan-Meier estimate of survival calculated with all training samples) is a reference value that can be used as a benchmark Brier score for prediction models. For clarity and ease of interpretation, we tabulate both the unscaled and scaled Brier score estimates, where the scaled Brier score is computed as 1 minus the ratio of the unscaled Brier score to the reference Brier score. Similar to the R² statistic, a scaled Brier score of 1 and 0 indicate a perfect and worthless model, respectively.

4.3.1. Summary measures of prediction error.

The concordance index proposed by Gerds et al. (2013) uses survival time as response and differs conceptually from the the time-dependent receiver-operator characteristic curve proposed by Heagerty, Lumley and Pepe (2000). The latter incident statistic measures a prediction model’s ability to classify survival status at a given time point, while the former cumulative statistic measures a prediction model’s ability to order the survival times. Heagerty and Zheng (2005) have established a formal relationship between these two measures. Following the precedent of Ishwaran et al. (2008), we define concordance error as ${\widehat{\text{C}}}_e(t)=1-\widehat{\text{C}}(t)$.

As $\widehat{\text{BS}}(t)$ is time dependent, integration from baseline to a specified follow-up time provides a summary measure of performance that can be tabulated for direct comparisons between competing learning methods. The integrated BS is defined as

$$\widehat{ℬ𝒮}(T)=\frac{1}{T}{\int }_0^T\widehat{\text{BS}}(t)dt$$ (4.1)

where T is the specified follow-up time. In our results, we set T equal to the median event time in the testing data. We also present values of $\widehat{ℬ𝒮}(T)$ and ${\widehat{\text{C}}}_e(t)$ that are scaled by a factor of 100 to avoid an unnecessary amount of leading zero’s (i.e., we present 0.5 instead of 0.005).

4.4. Computational notes and software.

All analyses were performed in R version 3.5.0. Right-censored survival outcomes were generated using the simsurv R package (Brilleman, 2018). We used the RandomForestSRC (Ishwaran and Kogalur, 2019), party (Hothorn et al., 2010), and obliqueRSF (Jaeger, 2018) R packages to fit RSFs, CIFs, and ORSFs, respectively, the xgboost (Chen et al., 2019) package to fit gradient boosted decision trees, the glmnet (Friedman, Hastie and Tibshirani, 2010b) package to fit regularized Cox PH models, the survival (Therneau, 2015) package to fit classical Cox PH models, the MASS (Venables and Ripley, 2002) package to perform forward stepwise selection using Akaike’s information criteria, and the CoxBoost package to fit boosted Cox PH models (Binder, 2013). To compute $\widehat{ℬ𝒮}(T)$ and $\widehat{\text{C}}(t)$, we used the pec package (Mogensen, Ishwaran and Gerds, 2012). Unadjusted Kaplan-Meier estimates were used to estimate inverse probability of censoring weights throughout (Mogensen, Ishwaran and Gerds, 2012, Sec. 6.2).

4.5. Results.

The mean rankings according to ${\widehat{\text{C}}}_e(t)$ for ORSF_CV and ORSF were 2.17 and 2.67, respectively, out of the 9 learning algorithms we applied (Table 1). As expected, the ORSF and ORSF_CV provided the lowest values of ${\widehat{\text{C}}}_e(t)$ in scenario B. Notably, the ORSF and ORSF_CV also provided the lowest values of ${\widehat{\text{C}}}_e(t)$ in scenario C, despite the invalidity of the PH assumption. In comparison to the RSF and CIF, both the ORSF and ORSF_CV provided lower values of ${\widehat{\text{C}}}_e(t)$ in each of the six simulated analyses. The absolute (percent) reduction in the mean value of ${\widehat{\text{C}}}_e(t)$ from using the ORSF_CV instead of the RSF and using the ORSF_CV instead of the CIF was 3.13 (9.62%) and 0.52 (1.58%), respectively.

Table 1.

Mean concordance errors for competing learning methods, aggregated over 100 simulations in three scenarios. The minimum concordance error for each simulated analysis is written in bold text.

		Ensemble Survival Trees§					Proportional Hazards
Scenario†	p ‡	ORSF	ORSFCV	CIF	RSF	Xgboost	CoxBoost	Lasso	Ridge	Step
Concordance error: 100 · ${\widehat{C}}_e(t)$
A	25	30.79	30.69	31.45	33.90	31.32	30.35	30.31	30.13	30.68
B	25	31.32	31.14	31.92	35.69	32.41	31.65	31.32	30.90	32.10
C	25	29.88	29.86	30.49	32.52	30.64	31.87	31.87	31.63	32.35
A	50	31.00	30.97	31.33	34.06	31.60	33.06	32.90	32.43	33.64
B	50	35.13	35.20	35.71	37.75	36.02	38.35	38.39	38.01	38.98
C	50	37.36	37.39	37.44	40.11	38.15	39.71	39.80	39.14	40.49
Monte-Carlo Standard Error of 100 · ${\widehat{C}}_e(t)$
A	25	0.103	0.106	0.107	0.103	0.106	0.116	0.118	0.119	0.111
B	25	0.098	0.102	0.104	0.093	0.104	0.115	0.118	0.114	0.108
C	25	0.057	0.063	0.068	0.072	0.097	0.081	0.077	0.081	0.080
A	50	0.099	0.087	0.082	0.090	0.100	0.091	0.092	0.096	0.088
B	50	0.085	0.088	0.081	0.061	0.098	0.093	0.093	0.096	0.088
C	50	0.069	0.070	0.063	0.095	0.076	0.101	0.096	0.086	0.104
Percent increase in ${\widehat{C}}_e(t)$, relative to minimum (0.00)
A	25	2.2	1.9	4.4	12.5	4.0	0.8	0.6	0.0	1.8
B	25	1.4	0.8	3.3	15.5	4.9	2.4	1.4	0.0	3.9
C	25	0.0	0.0	2.1	8.9	2.6	6.7	6.7	5.9	8.3
A	50	0.1	0.0	1.2	10.0	2.0	6.7	6.2	4.7	8.6
B	50	0.0	0.2	1.7	7.5	2.5	9.2	9.3	8.2	11.0
C	50	0.0	0.1	0.2	7.4	2.1	6.3	6.5	4.8	8.4
Rankings based on ${\widehat{C}}_e(t)$
A	25	6	5	8	9	7	3	2	1	4
B	25	4	2	6	9	8	5	3	1	7
C	25	2	1	3	9	4	6	7	5	8
A	50	2	1	3	9	4	7	6	5	8
B	50	1	2	3	5	4	7	8	6	9
C	50	1	2	3	8	4	6	7	5	9
		2.67	2.17	4.33	8.17	5.17	5.67	5.50	3.83	7.50

^†Descriptions of Scenarios A, B, and C are provided in Section 4.1.

^‡p represents the number of predictor variables in each simulated data set.

^§RSF = random survival forest; CIF = conditional inference forest; ORSF = oblique random survival forest; ORSF_CV = oblique random survival forest with internal cross-validation (see Section 3.2).

^‡Apparent ties in concordance errors are a result of rounding errors.

The mean rankings according to $\widehat{ℬ𝒮}(T)$ for ORSF_CV and ORSF were 4.67 and 4.17, respectively, out of the 9 learning algorithms we applied (Table 2). In comparison to the RSF and CIF, both the ORSF and ORSF_CV recorded lower mean values of $\widehat{ℬ𝒮}(T)$ in each of the 6 simulated analyses. The absolute (percent) increase in the mean scaled value (see Section 4.3) of $\widehat{ℬ𝒮}\left(T\right)$ using the ORSF_CV instead of the RSF and using the ORSF_CV instead of the CIF were 1.57 (42.39%) and 0.45 (9.37%), respectively.

Table 2.

Mean integrated Brier scores for competing learning methods, aggregated over 100 simulations in three scenarios. The minimum Brier score for each simulated analysis is written in bold text.

Scenario†	p ‡	Ensemble Survival Trees§					Proportional Hazards				Reference*
		ORSF	ORSFCV	CIF	RSF Xgboost		CoxBoost	Lasso	Ridge	Step
Integrated Brier score: 100 · $\widehat{ℬ𝒮}(T)$
A	25	8.89	8.89	8.93	9.07	8.82	8.73	8.73	8.71	8.78	9.48
B	25	8.93	8.93	9.02	9.17	8.87	8.81	8.78	8.74	8.93	9.43
C	25	8.91	8.92	8.96	9.00	8.78	8.93	8.93	8.94	8.95	9.67
A	50	9.15	9.16	9.24	9.27	8.99	9.13	9.11	9.09	9.22	9.73
B	50	11.15	11.16	11.16	11.31	11.14	11.32	11.33	11.31	11.37	11.61
C	50	11.38	11.39	11.40	11.58	11.38	11.47	11.48	11.45	11.61	11.68
Monte Carlo Standard Error of 100 · $\widehat{ℬ𝒮}(T)$
A	25	0.014	0.014	0.015	0.012	0.012	0.011	0.010	0.010	0.009	0.016
B	25	0.008	0.008	0.008	0.007	0.008	0.008	0.008	0.008	0.009	0.010
C	25	0.012	0.012	0.012	0.011	0.013	0.013	0.012	0.012	0.013	0.014
A	50	0.019	0.019	0.020	0.018	0.018	0.019	0.019	0.019	0.018	0.021
B	50	0.017	0.017	0.017	0.016	0.016	0.017	0.018	0.018	0.018	0.018
C	50	0.016	0.016	0.016	0.014	0.014	0.017	0.017	0.016	0.016	0.017
Scaled $\widehat{ℬ𝒮}(T)$ values: 100 · [1 − $\widehat{ℬ𝒮}(T)$/Reference]
A	25	6.26	6.28	5.80	4.37	6.93	7.88	7.91	8.07	7.35	0.00
B	25	5.31	5.35	4.42	2.84	5.97	6.61	6.94	7.33	5.38	0.00
C	25	7.91	7.81	7.35	6.92	9.24	7.64	7.65	7.61	7.45	0.00
A	50	5.96	5.85	5.05	4.71	7.62	6.17	6.40	6.62	5.30	0.00
B	50	3.95	3.85	3.85	2.54	4.03	2.45	2.42	2.53	2.04	0.00
C	50	2.60	2.50	2.46	0.84	2.61	1.78	1.74	1.96	0.65	0.00
Rankings based on $\widehat{ℬ𝒮}(T)$
A	25	7	6	8	9	5	3	2	1	4	10
B	25	7	6	8	9	4	3	2	1	5	10
C	25	2	3	8	9	1	5	4	6	7	10
A	50	5	6	8	9	1	4	3	2	7	10
B	50	2	4	3	5	1	7	8	6	9	10
C	50	2	3	4	8	1	6	7	5	9	10
		4.17	4.67	6.50	8.17	2.17	4.67	4.33	3.50	6.83	10.00

^†Descriptions of Scenarios A, B, and C are provided in Section 4.1.

^‡p represents the number of predictor variables in each simulated data set.

^§RSF = random survival forest; CIF = conditional inference forest; ORSF = oblique random survival forest; ORSF_CV = oblique random survival forest with internal cross-validation (see Section 3.2).

^*The reference values are expected Brier scores of a prediction model that ignores all predictor variables, i.e., the Kaplan-Meier estimate calculated using the training data.

^‡Apparent ties in Brier scores are a result of rounding errors.

5. Application to Real Data.

Here we describe and summarize results from a resampling experiment using data from six independent studies. We summarize each study, separately, in Section 5.1. We describe tuning parameters and the resampling procedure we applied in Sections 5.2 and 5.3, respectively. We present and summarize results in Section 5.5.

5.1. Data Sets.

For each of the data sets described in the following sections, study participants who were lost to follow-up or died from causes unrelated to the primary event(s) were censored at time of last contact or time of death, respectively. Characteristics (e.g., number of participants, number of predictors, percent censored) of each data set are tabulated and presented alongside the characteristics of simulated datasets in Table 3.

Table 3.

Data set summary

		Follow-up times§
Data	Event Type	25%	50%	75%	% Censored	N	M	p
A25	Simulated	3.9	10.0	10.0	55.4	500	1000	25
B25	Simulated	3.9	10.0	10.0	57.5	500	1000	25
C25	Simulated	2.8	10.0	10.0	50.6	500	1000	25
A50	Simulated	3.8	10.0	10.0	55.2	500	1000	50
B50	Simulated	3.5	10.0	10.0	56.2	500	1000	50
C50	Simulated	2.6	10.0	10.0	49.5	500	1000	50
PBC	Death	3.0	4.7	7.2	61.5	209	209	17
GBSG2	Death or relapse	1.6	3.0	4.6	56.4	342	342	8
GEBC	Death or relapse	1.8	2.8	4.1	78.2	307	307	1690
MBC	Death or relapse	2.3	5.3	8.8	56.4	39	39	4707
JHS1	CHD or stroke	10.8	11.7	12.6	90.8	915	914	58
JHS2	Heart Failure	9.2	10.0	10.0	93.8	904	904	58
JHS3	Death	13.0	13.9	14.7	81.3	944	943	58
REGARDS1	CHD or stroke	5.2	8.1	9.9	92.2	4485	4485	67
REGARDS2	Heart Failure	5.0	8.1	9.9	97.3	4485	4484	67
REGARDS3	Death	6.0	8.4	10.0	87.2	4485	4485	67

^§All follow-up times are in years.

5.1.1. Primary biliary cirrhosis (PBC) data.

The PBC data and their description are taken from Appendix D of Fleming and Harrington (2011). PBC of the liver is a rare and fatal disease of unknown cause. These data were collected for the Mayo Clinic trial in PBC of the liver conducted between January 1974 and May 1984 comparing the drug D-penicillamine with a placebo.

5.1.2. German breast cancer study group (GBSG2) data.

The GBSG2 data and their description are taken from Schumacher et al. (1994). In 1984, the GBSG2 started a multicenter randomized clinical trial to compare the effectiveness of three versus six cycles of 500 mg/m² cyclophosphamide, 40 mg/m² methotrexate, and 600 mg/m² fluorouracil on day 1 and 8 starting perioperatively with or without tamoxifen (3 × 10 mg/d for 2 years).

5.1.3. Gene expression breast cancer (GEBC) data.

The GEBC data and their description are taken from Gene Expression Omnibus database and the analysis by Ternès et al. (2017), respectively. to identify treatment-effect modifiers in 614 breast cancer patients (Hatzis et al., 2011; Desmedt et al., 2011) receiving anthracycline-based adjuvant chemotherapy with (n = 507) or without (n = 107) taxane. For the current analysis, we use pre-processed data from Ternès et al. (2017), who applied frozen robust multiarray (McCall, Bolstad and Irizarry, 2010) and cross-platform normalization (Shabalin et al., 2008), and standardized the remaining 1689 genes.

5.1.4. Microarray breast cancer (MBC) data.

The MBC data and their description are taken from (Van’t Veer et al., 2002). Gene expression profiling was conducted on 78 sporadic lymph-node-negative patients to search for a prognostic signature in their gene expression profiles. Forty-four patients remained free of breast cancer after their initial diagnosis for an interval of at least 5 years (good prognosis group, mean follow-up of 8.7 years), and 34 patients developed distant metastases within 5 years (poor prognosis group, mean time to metastases 2.5 years).

5.1.5. Jackson Heart Study (JHS) data.

The JHS is a population-based prospective cohort study designed to examine the etiology of cardiovascular disease (CVD) (e.g., stroke, coronary heart disease, heart failure) and related risk factors among African Americans.(Taylor Jr et al., 2005) In brief, 5,306 non-institutionalized African-American participants aged ≥ 20 years were recruited from the Jackson, Mississippi, metropolitan area between 2000 and 2004. For the current analyses, we incorporated data from JHS participants who provided complete records of age, sex, anthropometric measures, alcohol/smoking/dietary/exercise habits, medication use, zip code, blood pressure, diabetes, cholesterol, high and low density lipoproteins, triglycerides, electrocardiograms, estimated glomerular filtration rate (eGFR) (Levey et al., 2009), insurance, and history of CVD at baseline. We conducted three separate analyses using these data; JHS1 considered composite events of stroke or coronary heart disease, JHS2 considered heart failure events, and JHS3 considered all-cause mortality events.

5.1.6. The REasons for Geographic And Racial Differences in Stroke (REGARDS) Study.

The REGARDS study was designed to investigate reasons underlying the higher rate of stroke mortality among blacks compared with whites, and among residents of the Southeastern US compared with other US regions (Howard et al., 2005). A total of 30,239 adults from the 48 contiguous US states and the District of Columbia were enrolled between January 2003 and October 2007. For the current analysis, we incorporated data from 8,970 participants who provided complete records of age, sex, race, anthropomorphic measures, alcohol/smoking/dietary/exercise habits, quality of life, self-reported history of CVD, echocardiogram, medication use, blood measures, blood pressure, urine albumin and creatinine, and eGFR. We conducted three separate analyses using these data; REGARDS1 considered composite events of stroke or coronary heart disease (Safford et al., 2012), REGARDS2 considered heart failure events , and REGARDS3 considered all-cause mortality events.

5.2. Tuning Parameters.

We applied the same learning algorithms and corresponding tuning parameter specifications as described in Section 4.2.

5.3. Resampling.

Results from the current resampling experiment are based on 250 replicates of bootstrap cross-validation (Mogensen, Ishwaran and Gerds, 2012, Sec. 4.2). In each replicate, for each analysis (e.g., PBC, GBSG2, JHS1, etc.), we

1. randomly allocated roughly one half of the data to a training set, and used the rest of the data for testing.

2. trained each competing method using the training data set.

3. computed $\widehat{ℬ𝒮}(T)$ and ${\widehat{\text{C}}}_e(t)$ using each method’s predicted survival curves for observations in the testing data.

5.4. Monte-Carlo Error Relative to Forest Size.

Using the PBC data, we assessed the Monte-Carlo error (seed effect) of the predicted survival curves relative to the number of trees in the ORSF. We first identified three classes of patients using the protoclust package Bien and Tibshirani (2019). We identified one prototype patient in each class, and used these three patients as a hold-out set. We developed an ORSF with 10, 100, and 1000 trees, and then predicted survival curves for patients in the hold-out set. We replicated this step 250 times and plotted each survival curve to visualize Monte-Carlo error for the three separate forest sizes.

5.5. Results.

The three methods that achieved the lowest values of ${\widehat{\text{C}}}_e(t)$ were the ORSF_CV, the ORSF, and the CIF (mean ranks of 1.70, 1.80 and 3.20, respectively) (Table 4). Distributions of ${\widehat{\text{C}}}_e(t)$ were consistent among competing learning methods with the exception of the penalized Cox PH models, which had higher variability of ${\widehat{\text{C}}}_e(t)$ in analyses of JHS and REGARDS data (Figure 1). The difference in ${\widehat{\text{C}}}_e(t)$ between the ORSF_CV and the RSF was minimal in the GBSG2 analysis (27.86 and 28.71, respectively) and maximal in the GEBC analysis (25.08 and 31.19, respectively). The absolute (percent) increase in the mean value of ${\widehat{\text{C}}}_e\left(t\right)$ from using the RSF instead of the ORSF_CV or the CIF instead of the ORSF_CV was 1.79 (9.08%) and 0.16 (0.82%), respectively. The variability and overall shape of time-dependent trajectories of ${\widehat{\text{C}}}_e(t)$ were similar among the RSF, CIF, and ORSF (Figure 3).

Table 4.

Mean concordance index error for competing learning methods, aggregated over 100 replicates of bootstrap cross-validation in five independent data sets. The minimum concordance error value for each analysis is written in bold text.

	Ensemble Survival Trees§					Proportional Hazards
Scenario†	ORSF	ORSFCV	CIF	RSF	Xgboost	CoxBoost	Lasso	Ridge	Step
Concordance error: 100 · ${\widehat{C}}_e(t)$
GEBC	24.98	25.08	25.79	31.19	27.08	28.62	28.59	26.47	–
GBSG2	28.10	27.86	28.40	28.71	28.09	30.24	30.30	29.99	29.88
JHS1	17.67	17.58	17.74	19.31	17.84	18.69	18.68	18.37	18.74
JHS3	17.61	17.57	17.91	18.40	17.63	18.54	18.90	19.66	18.07
JHS2	13.13	13.16	13.42	13.45	13.61	17.51	18.86	14.43	14.83
PBC	12.25	12.29	12.80	13.90	12.87	13.53	13.72	12.82	15.15
REGARDS1	21.81	21.83	21.84	22.69	22.15	22.68	22.57	22.35	24.58
REGARDS3	18.69	18.80	18.82	19.01	18.55	19.27	20.33	30.62	19.32
REGARDS2	13.91	13.86	14.21	16.08	14.01	15.64	17.87	29.38	16.93
MBC	29.41	29.27	27.99	32.47	31.28	40.62	39.79	35.14	–
Percent increase in ${\widehat{C}}_e(t)$, relative to minimum (0.00)
GEBC	0.0	0.4	3.3	24.9	8.4	14.6	14.5	6.0	–
GBSG2	0.9	0.0	1.9	3.0	0.8	8.5	8.7	7.6	7.2
JHS1	0.5	0.0	0.9	9.8	1.5	6.3	6.3	4.5	6.6
JHS3	0.2	0.0	1.9	4.7	0.3	5.5	7.5	11.9	2.8
JHS2	0.0	0.2	2.2	2.5	3.7	33.4	43.7	10.0	13.0
PBC	0.0	0.3	4.5	13.5	5.1	10.5	12.0	4.7	23.7
REGARDS1	0.0	0.1	0.1	4.1	1.6	4.0	3.5	2.5	12.7
REGARDS3	0.7	1.4	1.5	2.5	0.0	3.9	9.6	65.0	4.2
REGARDS2	0.4	0.0	2.6	16.1	1.1	12.8	29.0	112.0	22.2
MBC	5.1	4.6	0.0	16.0	11.7	45.1	42.2	25.5	–
Rankings based on ${\widehat{C}}_e(t)$
GEBC	1	2	3	8	5	7	6	4	–
GBSG2	3	1	4	5	2	8	9	7	6
JHS1	2	1	3	9	4	7	6	5	8
JHS3	2	1	4	6	3	7	8	9	5
JHS2	1	2	3	4	5	8	9	6	7
PBC	1	2	3	8	5	6	7	4	9
REGARDS1	1	2	3	8	4	7	6	5	9
REGARDS3	2	3	4	5	1	6	8	9	7
REGARDS2	2	1	4	6	3	5	8	9	7
MBC	3	2	1	5	4	8	7	6	–
Mean	1.80	1.70	3.20	6.40	3.60	6.90	7.40	6.40	7.25

^§RSF = random survival forest; CIF = conditional inference forest; ORSF = oblique random survival forest; ORSF_CV = oblique random survival forest with internal cross-validation (see Section 3.2).

^†GEBC = gene expression breast cancer; MBC = microarray breast cancer; GBSG2 = German breast cancer study group; PBC = primary biliary cirrhosis; JHS = Jackson heart study; REGARDS = REasons for Geographic And Racial Differences in Stroke.

^‡Apparent ties in concordance errors are a result of rounding errors.

Fig 1.

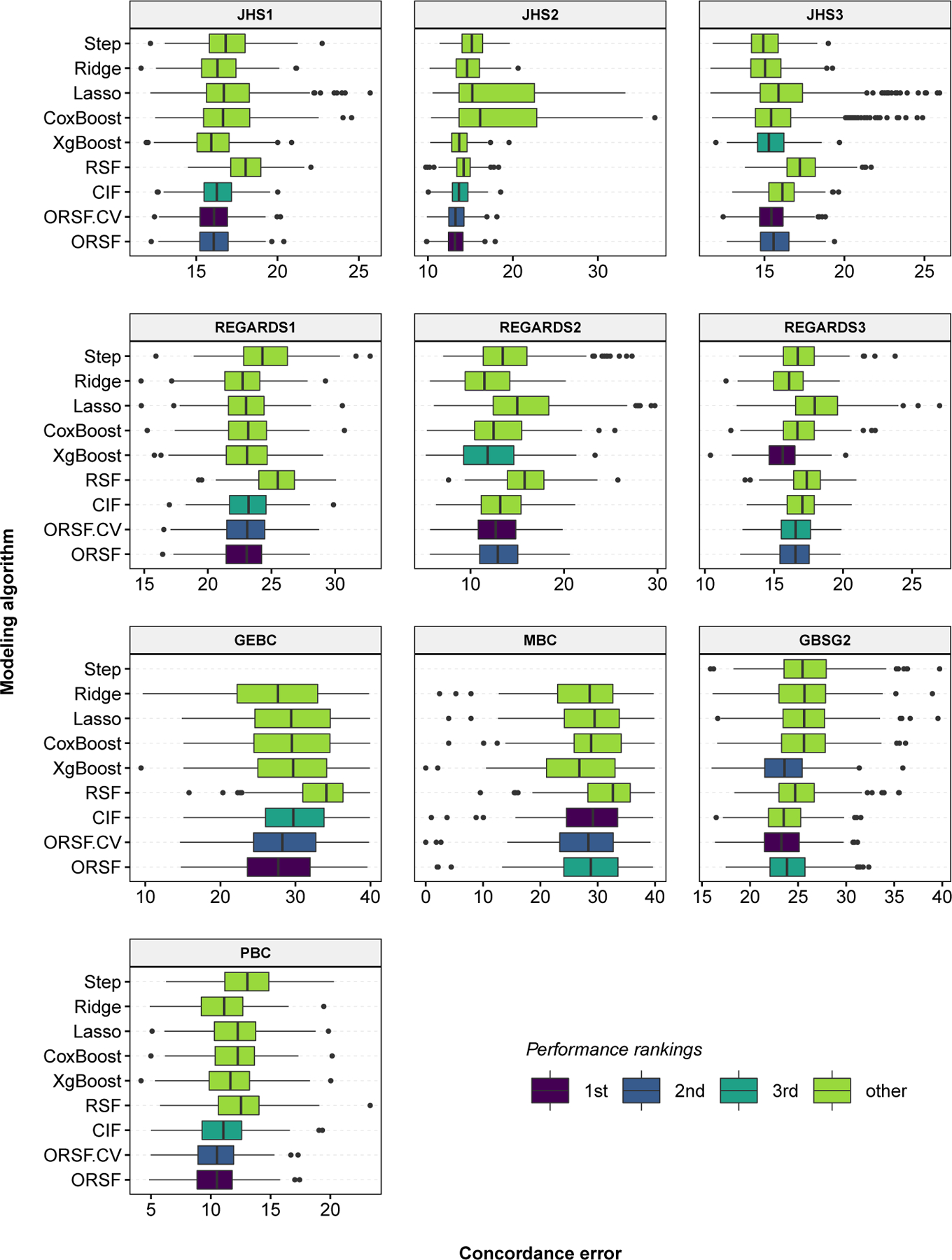
Concordance error values, aggregated over 250 replications of bootstrap cross-validation, for competing methods in 10 analyses of data with right-censored time-to-event outcomes.

Fig 3.

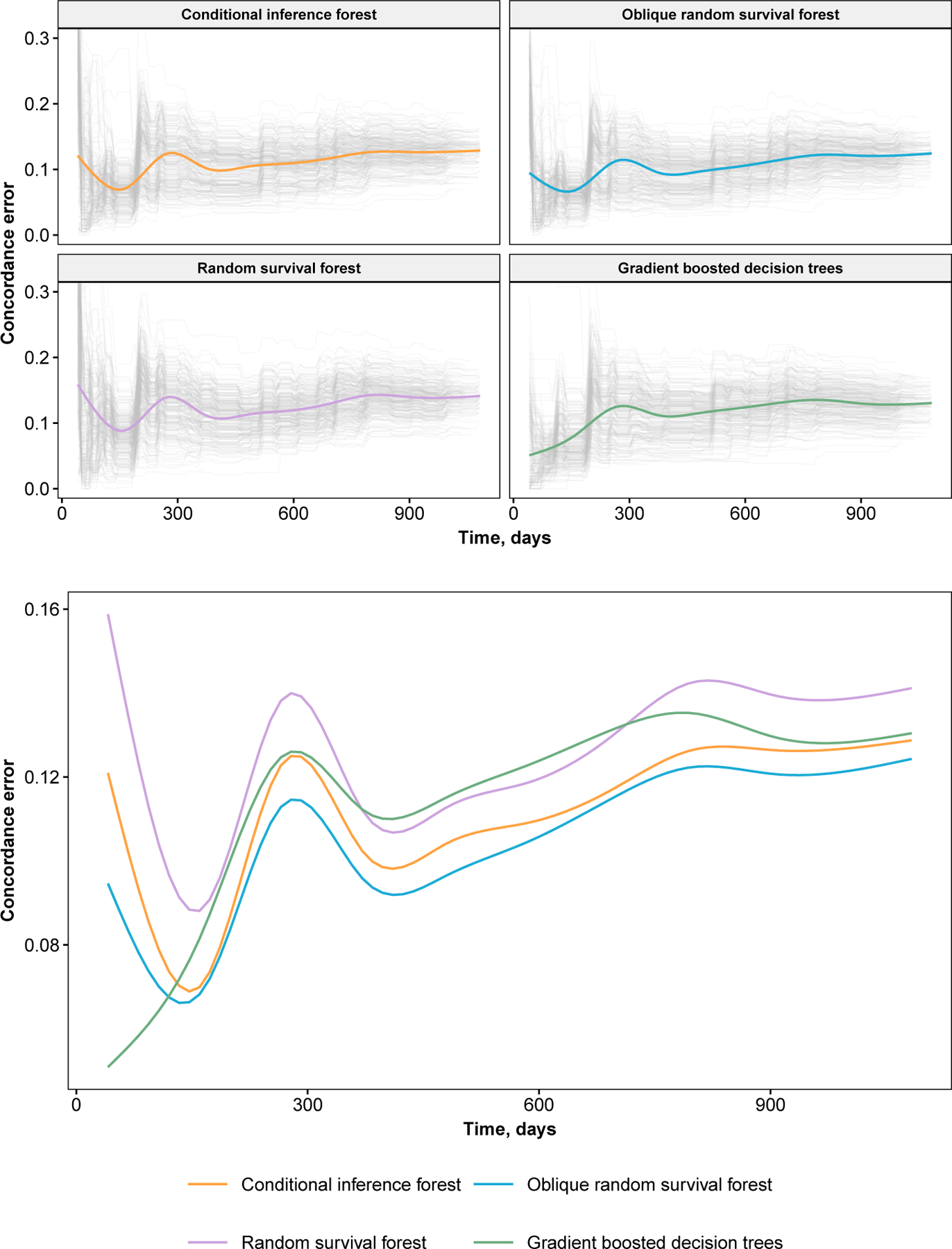
Concordance error values for the primary biliary cirrhosis analysis. Results from individual replications of bootstrap cross-validation are shown as grey trajectories. Smoothed estimates of average values are colored. Error values are plotted from baseline to median event time.

The three methods that achieved the lowest values of $\widehat{ℬ𝒮}(T)$ were the ORSF, gradient boosted decision trees, and the ORSF_CV (mean ranks of 2.30, 2.50 and 3.90, respectively) (Table 5). Distributions of $\widehat{ℬ𝒮}(T)$ were consistent among the competing learning methods with the exception of the penalized Cox PH models, which had higher variability of $\widehat{ℬ𝒮}(T)$ in analyses of JHS and REGARDS data (Figure 2). The difference in $\widehat{ℬ𝒮}(T)$ between the ORSF and the RSF was minimal in the JHS3 analysis (3.228 and 3.232, respectively) and maximal in the GEBC analysis (4.20 and 4.44, respectively). The absolute (percent) increase in the mean scaled value (see Section 4.3) of $\widehat{ℬ𝒮}(T)$ using the ORSF instead of the RSF or instead of the CIF was 1.54 (21.67%) and 0.77 (9.79%), respectively.

Table 5.

Mean integrated Brier scores for competing learning methods, aggregated over 100 replicates of bootstrap cross-validation in five independent data sets. The minimum Brier score for each analysis is written in bold text.

Scenario†	Ensemble Survival Trees§					Proportional Hazards				Reference
	ORSF	ORSFCV	CIF	RSF	Xgboost	CoxBoost	Lasso	Ridge	Step
Integrated Brier score: 100 · $\widehat{ℬ𝒮}(T)$
GEBC	4.20	4.20	4.23	4.44	4.25	4.27	4.27	4.22	–	4.36
GBSG2	7.10	7.12	7.10	7.21	7.20	7.51	7.51	7.49	7.47	7.77
JHS1	2.31	2.31	2.33	2.32	2.31	2.35	2.36	2.34	2.35	2.49
JHS3	3.23	3.23	3.28	3.23	3.15	3.20	3.23	3.20	3.17	3.67
JHS2	2.30	2.30	2.33	2.29	2.31	2.41	2.41	2.37	2.38	2.55
PBC	5.71	5.82	5.79	5.77	5.73	6.08	6.12	5.92	6.45	8.09
REGARDS1	1.69	1.69	1.69	1.70	1.68	1.70	1.70	1.70	1.73	1.76
REGARDS3	2.21	2.22	2.23	2.20	2.16	2.18	2.21	2.26	2.21	2.43
REGARDS2	0.63	0.63	0.64	0.64	0.63	0.64	0.64	0.64	0.66	0.66
MBC	9.07	9.08	9.11	9.62	9.16	9.65	9.67	9.33	–	8.91
Scaled $\widehat{ℬ𝒮}(T)$ values: 100 · [1 − $\widehat{ℬ𝒮}(T)$/Reference]
GEBC	3.58	3.53	3.03	−1.94	2.51	1.96	1.95	3.20	–	0.00
GBSG2	8.60	8.36	8.68	7.18	7.33	3.40	3.29	3.55	3.82	0.00
JHS1	7.46	7.37	6.75	6.84	7.46	5.67	5.53	6.21	5.59	0.00
JHS3	12.12	12.05	10.79	12.01	14.27	12.84	12.10	12.95	13.80	0.00
JHS2	9.95	9.74	8.54	10.39	9.40	5.45	5.33	7.01	6.63	0.00
PBC	29.40	28.03	28.42	28.59	29.10	24.81	24.29	26.83	20.28	0.00
REGARDS1	3.99	3.79	3.58	3.11	4.27	3.20	3.23	3.43	1.41	0.00
REGARDS3	8.93	8.50	7.85	9.16	11.04	10.24	8.86	6.63	8.88	0.00
REGARDS2	4.38	4.14	3.55	3.78	5.31	3.74	2.97	2.47	0.76	0.00
MBC	−1.76	−1.85	−2.27	−7.90	−2.73	−8.22	−8.49	−4.66	–	0.00
Ranks in each data set of competing methods based on $\widehat{ℬ𝒮}(T)$
GEBC	1	2	4	9	5	6	7	3	–	8
GBSG2	2	3	1	5	4	8	9	7	6	10
JHS1	2	3	5	4	1	7	9	6	8	10
JHS3	5	7	9	8	1	4	6	3	2	10
JHS2	2	3	5	1	4	8	9	6	7	10
PBC	1	5	4	3	2	7	8	6	9	10
REGARDS1	2	3	4	8	1	7	6	5	9	10
REGARDS3	4	7	8	3	1	2	6	9	5	10
REGARDS2	2	3	6	4	1	5	7	8	9	10
MBC	2	3	4	7	5	8	9	6	–	1
Mean	2.30	3.90	5.00	5.20	2.50	6.20	7.60	5.90	6.88	8.90

^§RSF = random survival forest; CIF = conditional inference forest; ORSF = oblique random survival forest; ORSF_CV = oblique random survival forest with internal cross-validation (see Section 3.2).

^†GEBC = gene expression breast cancer; MBC = microarray breast cancer; GBSG2 = German breast cancer study group; PBC = primary biliary cirrhosis; JHS = Jackson heart study; REGARDS = REasons for Geographic And Racial Differences in Stroke.

^*The reference values are expected Brier scores of a prediction model that ignores all predictor variables, i.e., the Kaplan-Meier estimate calculated using the training data.

^‡Apparent ties in Brier scores are a result of rounding errors.

Fig 2.

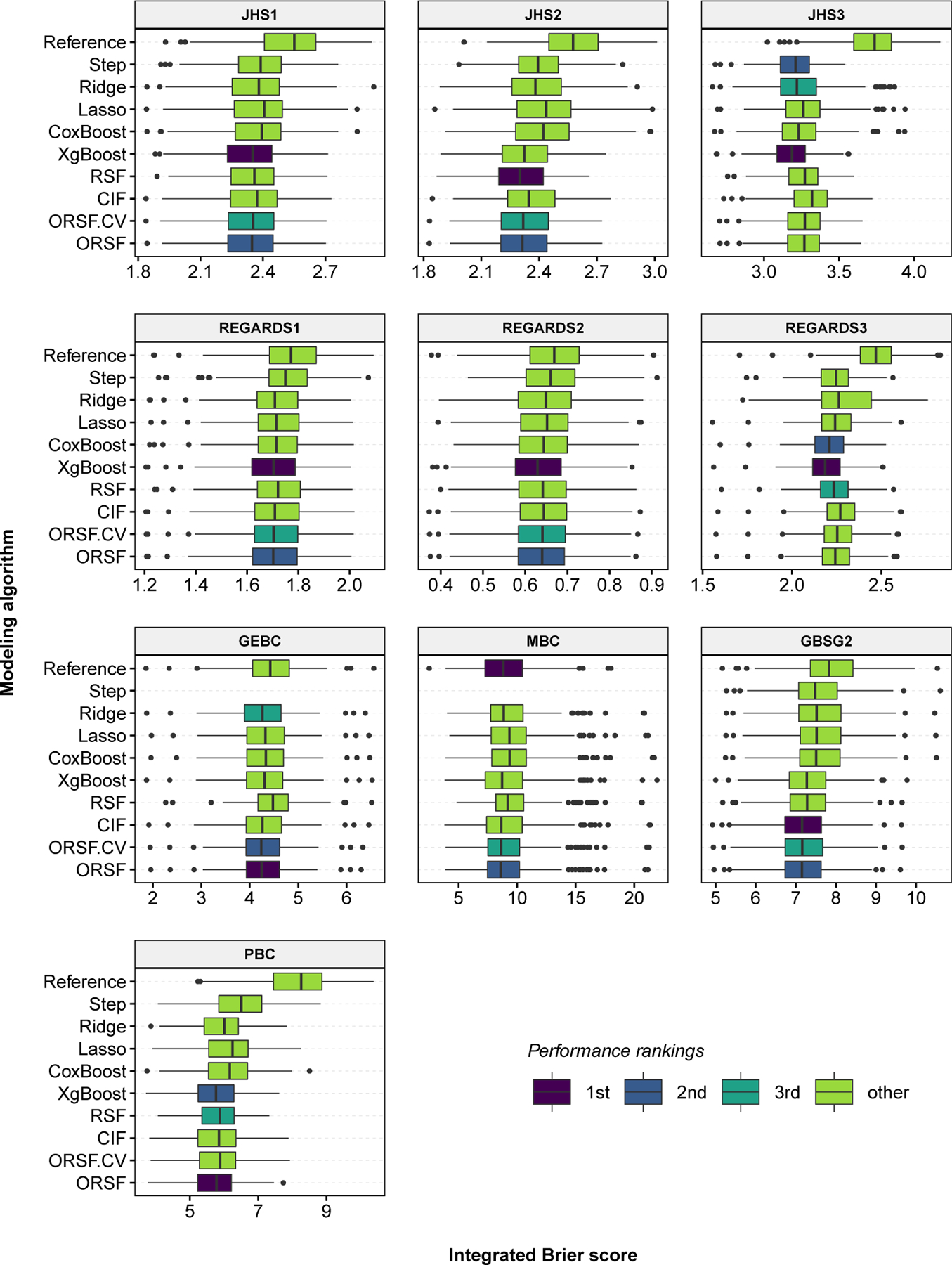
Integrated Brier score values, aggregated over 250 replications of bootstrap cross-validation, for competing methods in 10 analyses of data with right-censored time-to-event outcomes.

Monte-Carlo error was adequate when 1000 trees were used to fit the ORSF (Figure 4). The variability in predicted survival curves was noticeably higher when 10 or 100 trees were used to fit an ORSF.

Fig 4.

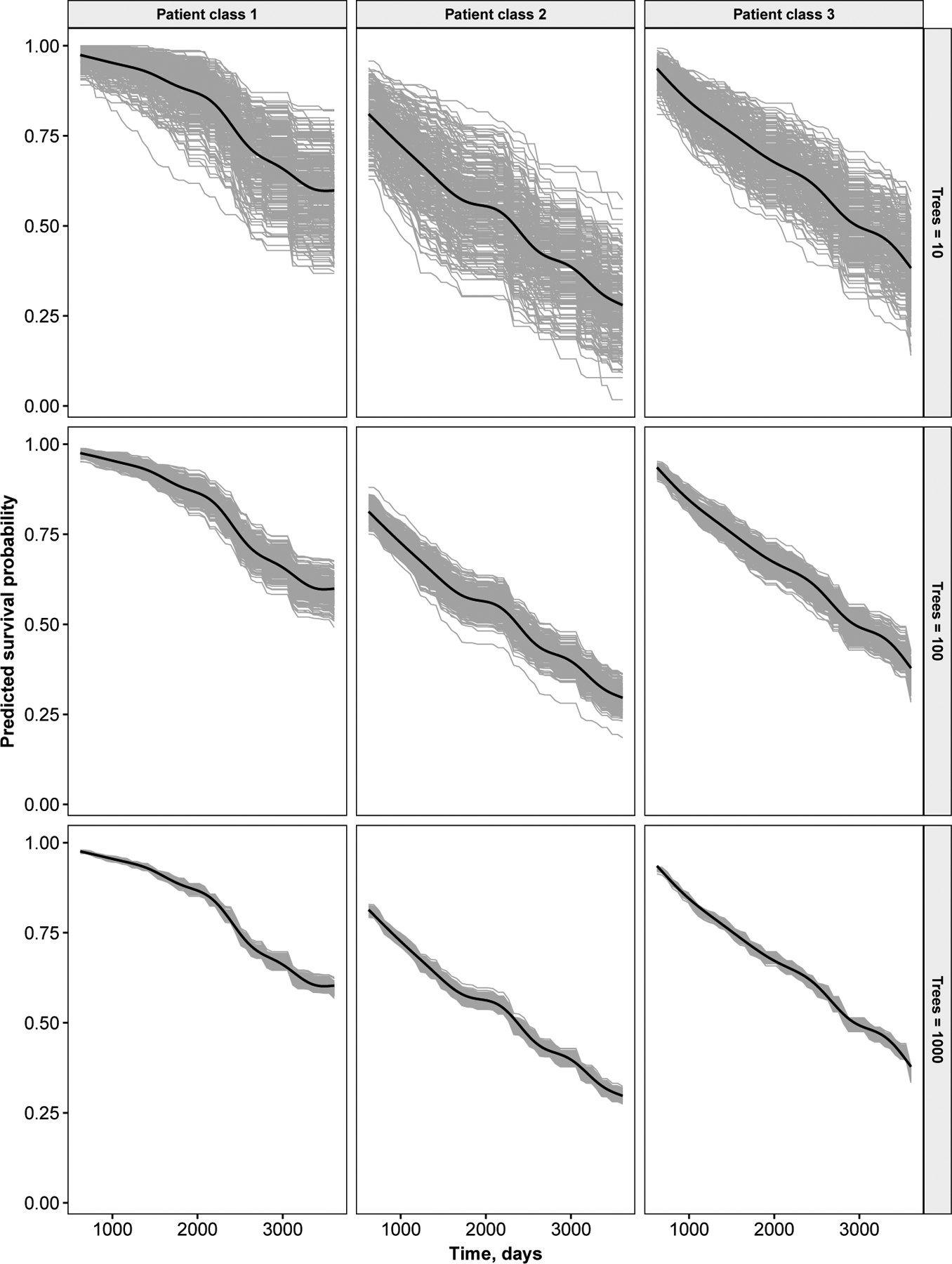
Monte-Carlo error (seed effect) for the primary biliary cirrhosis analysis. Results are shown for three prototypical patients. Grey curves are individual predictions from an individual forest. Smoothed estimates of average values are drawn as black curves.

6. Overall Performance Comparisons.

Here we describe a formal comparison of the performance and computational requirements of each method that was applied in Section 5, incorporating results from each of the real data sets described. To assess the relative performance of each method, we ranked the methods in each data set, separately, giving a rank of 1 to the method with the lowest error, a rank of 2 to the method with the second lowest error, and so on. We recorded the rankings in this manner using both ${\widehat{\text{C}}}_e(t)$ and $\widehat{ℬ𝒮}(T)$ as the metric for error. In Section 6.1, we describe the procedure used to draw inferences from these rankings. We summarize performance of the learning algorithms in Section 6.2 and the computational resources required to run each algorithm in Section 6.3.

6.1. Statistical comparisons of ranks.

We applied a modification of Friedman’s non-parametric rank test (Friedman, 1937), which compares the average ranks among a set of classifiers over a collection of data sets. Let $r_i^j$ be the rank of the j^th of k classifiers on the i^th of D datasets. Friedman’s test compares the average ranks of the competing classifiers, $R_j=\frac{1}{D}\sum _{i=1}^D{r}_i^j$. Under the null hypothesis of equivalent performance, each classifier will have a mean rank of (k + 1)/2, with variance (k² − 1)/(12D) and

$$F_F=\frac{(D-1){\chi }_F^2}{D(k-1)-{\chi }_F^2}~F_{k-1,(k-1)(D-1)}$$ (6.1)

where F_p,q denotes an F distribution with p and q numerator and denominator degrees of freedom, respectively, and

$${\chi }_F^2=\frac{12D}{k(k+1)}\left[\left(\sum _{j=1}^k{R}_j^2\right)-\frac{k{(k+1)}^2}{4}\right].$$ (6.2)

Iman and Davenport (1980) derived F_F to correct the overly conservative ${\chi }_F^2$ statistic (Demšar, 2006). If the null hypothesis of overall equivalent performance is rejected, post-hoc pairwise comparisons can be conducted using

$$z=\frac{R_i-R_j}{\sqrt{k(k+1)/(6D)}}$$ (6.3)

to compare the average ranking of the i^th and j^th classifiers.

6.2. Results.

Among the nine learning algorithms we compared, the hypothesis of equivalence in performance was rejected (F_F = 74.1 [p < 0.001] and 17.2 [p < 0.001] for concordance error and integrated Brier scores, respectively) using the overall F_F test statistic proposed by Iman and Davenport (1980). Figure 5 shows a color-coded comparison matrix. Diagonal cells are split in two, with the mean rank according to $\widehat{ℬ𝒮}(T)$ printed in the upper left and the mean rank according to ${\widehat{\text{C}}}_e(t)$ printed in the lower right. The upper left and lower right sections of the matrix show two sided p-values corresponding to pairwise comparisons of the mean ranks between two methods using the rankings according to $\widehat{ℬ𝒮}(T)$ and ${\widehat{\text{C}}}_e(t)$, respectively. For example, the mean rankings according to ${\widehat{\text{C}}}_e(t)$ of the ORSF_CV and the CIF were 1.70 and 3.20, respectively, and the p-value corresponding to a test of rank equivalence between these two methods was 0.121.

Fig 5.

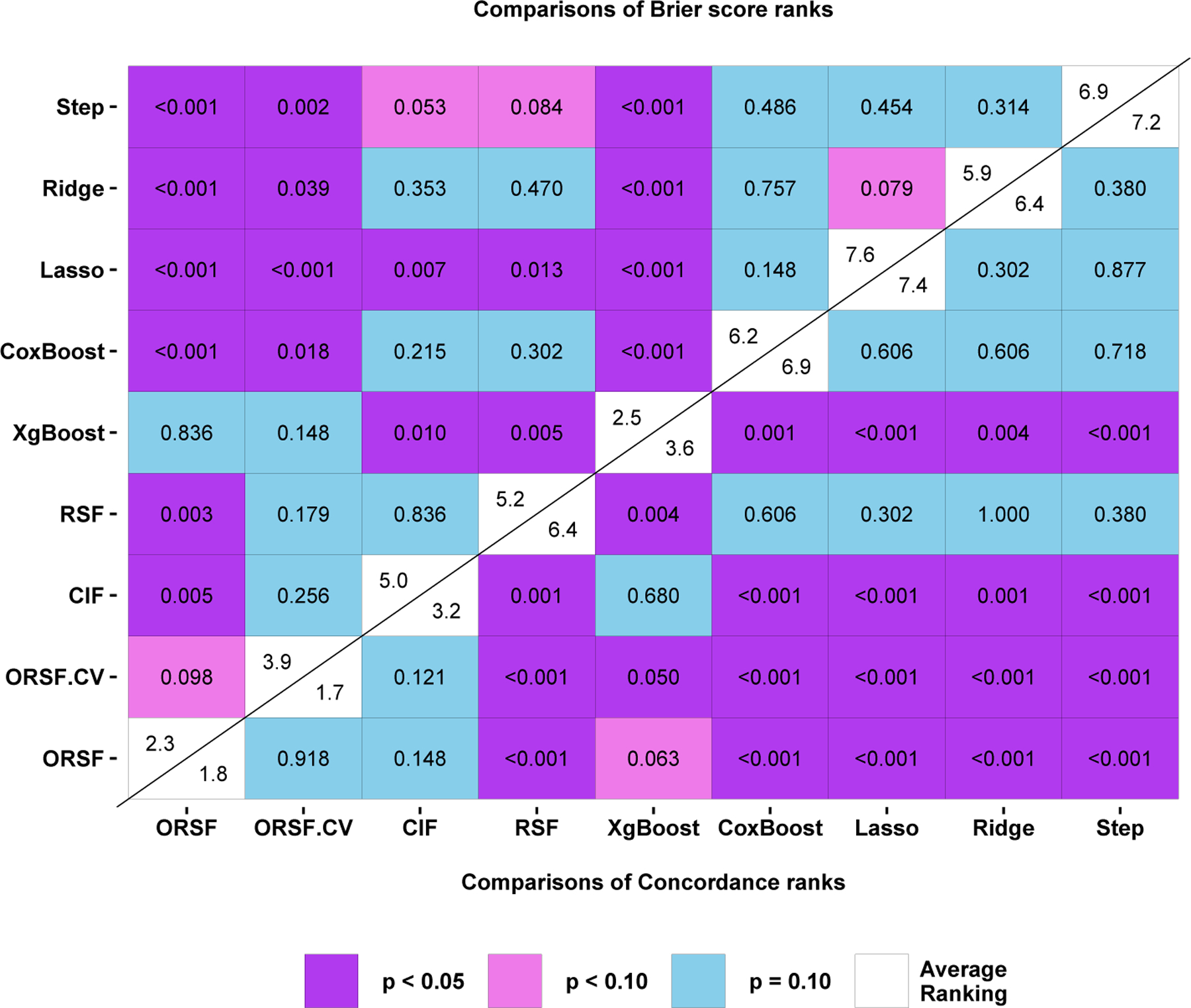
Overall performance comparison between oblique random survival forests and competing learning methods for prediction of the data described in Sections 4 and 5.

After ranking each method in each analysis according to ${\widehat{\text{C}}}_e(t)$, the ORSF_CV had the lowest mean ranking: 1.70. The ORSF and CIF had the second and third lowest mean rankings, 1.80 and 3.20, respectively. For all pairwise comparisons involving ${\widehat{\text{C}}}_e(t)$ for the ORSF_CV, excluding comparison with the ORSF (p = 0.918) and CIF, a statistically significant (p < 0.05) difference in mean rankings was observed.

After ranking each method in each analysis according to $\widehat{ℬ𝒮}(T)$, the ORSF had the lowest mean ranking (2.30) followed by gradient boosted decision trees (mean rank of 2.50) and the ORSF_CV (mean rank of 3.90). For all pairwise comparisons involving $\widehat{ℬ𝒮}(T)$ for the ORSF, excluding comparisons with the ORSF_CV (p = 0.098) and gradient boosted decision trees (p = 0.836), a statistically significant (p < 0.05) difference in mean rankings was observed.

6.3. Computing time.

We recorded the mean amount of time required to fit each learning algorithm in each analysis using real and simulated data (Table 6). As fitting an ORSF requires fitting regularized Cox PH models in each non-terminal node, the mean time of computation for the ORSF was roughly 192 and 32 times that of the RSF and CIF, respectively. When nested cross-validation was used, the mean time of computation for the ORSF was roughly 605 and 102 times that of the RSF and CIF, respectively.

Table 6.

Mean computation time, in seconds, required to fit each learning algorithm in each analysis

Analysis	ORSF	ORSF.CV	CIF	RSF	Xgboost	CoxBoost	Lasso	Ridge	Step
GEBC	1265.7	5848.1	9.8	6.5	275.1	126.3	20.0	14.4	0.0
GBSG2	401.6	1033.3	6.0	1.9	234.4	24.9	0.3	0.3	0.8
PBC	204.0	693.1	2.1	0.8	276.5	8.2	0.2	0.3	4.2
MBC	101.8	291.9	19.2	0.8	316.7	27.7	3.7	4.0	0.0
JHS1	1621.8	5005.0	56.3	6.4	293.6	203.0	3.3	3.5	41.5
JHS3	2556.5	7592.1	62.2	10.6	431.6	413.3	2.9	3.1	49.5
JHS2	1291.9	4385.3	50.5	5.4	265.3	159.3	3.3	3.3	36.4
REGARDS1	1852.3	5142.9	132.4	11.8	533.6	267.7	8.4	8.0	52.6
REGARDS3	2655.5	6873.5	140.6	19.1	525.7	476.2	4.7	5.1	67.5
REGARDS2	909.3	3127.5	120.1	6.3	342.7	109.5	16.2	12.8	48.9
SIM3.25	1448.9	4316.8	8.5	7.1	239.7	79.8	0.3	0.3	5.6
SIM3.50	1593.7	5123.4	7.9	7.7	191.1	92.9	0.4	0.4	15.0
SIM2.25	1084.2	3605.3	6.7	4.4	158.1	56.8	0.3	0.3	6.1
SIM2.50	1311.2	4360.8	7.8	6.6	199.7	82.5	0.4	0.5	28.3
SIM1.25	1176.6	3735.7	7.8	5.8	242.5	68.7	0.3	0.3	9.6
SIM1.50	1342.1	4583.2	8.3	7.5	313.8	87.0	0.5	0.5	30.7
Overall	1301.1	4107.4	40.4	6.8	302.5	142.7	4.1	3.6	24.8

7. Application to Jackson Heart Study.

Here we apply the ORSF and the CIF in a comparative example using data from the Jackson Heart Study (JHS). A description of the JHS is given in Section 5.1.5. In the current example, we included 5126 JHS participants who consented to provide follow-up information on ASCVD events. We randomly split the baseline data from these JHS participants into a training set (N = 3000) and a testing set (M = 2126). We imputed missing values in both sets, separately, using a k-nearest neighbors algorithm (Kowarik and Templ, 2016). Using the training data, we developed prediction rules based on the ORSF and CIF, separately. These prediction rules were applied to compute 10-year predicted risk of ASCVD events for JHS participants in the testing data. Using these values of predicted risk, we created variable dependence and partial dependence plots (Section 7.1) that directly compare expected predictions from the ORSF and CIF without and with adjustment for confounding effects, respectively (Friedman, 2001). For variable dependence plots, we included 10-year predicted risk of ASCVD events according to the Pooled Cohort risk equations, a well-known risk prediction equation that is recommended by Whelton et al. (2018) for clinical assessment of 10-year predicted risk for ASCVD events. Last, we compared predicted risk curves according to the ORSF and CIF for four individual JHS participants from the testing data.

7.1. Variable dependence and partial dependence.

Variable dependence plots render the expected value of an outcome (y-axis) relative to the observed values of an input variable (x-axis), using the unaltered training data. Although variable dependence plots illustrate observed relationships, they do not account for variation in covariates of interest apart from the input variable. Partial dependence plots show predicted risk as a function of the variables in a designated subset of input variables by averaging effects of the designated variables over the observed distribution of variables not in the designated set. Let

$${\mathit{z}}_{\left\{r\right\}}=\left\{{\mathit{z}}_{(1)},\dots ,{\mathit{z}}_{(r)}\right\}\subset \left\{{\mathit{x}}_{(1)},\dots ,{\mathit{x}}_{(p)}\right\}$$

denote the designated subset of r < p predictor variables. Define the complement set of predictor variables z_{s} such that

$${\mathit{z}}_{\left\{r\right\}}\cup {\mathit{z}}_{\left\{s\right\}}=\left\{{\mathit{x}}_{(1)},\dots ,{\mathit{x}}_{(p)}\right\}.$$

The predicted risk function, $\widehat{F}(\mathit{x})$, depends on variables in both subsets. Friedman (2001) shows that conditioning on the variables in z_{s} allows $\widehat{F}(\mathit{x})$ to be considered as a function of only the variables chosen in z_{r}. Moreover, the partial dependence of $\widehat{F}(\mathit{x})$ on variables in z_{r} can be computed by averaging over the observed values of z_{s}, i.e.

$$\overline{F}\left({\mathit{z}}_{\left\{r\right\}}\right)=E\left[\widehat{F}\left(\mathit{x}\mid {\mathit{z}}_{\left\{s\right\}}\right)\right]=\int \widehat{F}(\mathit{x})P\left({\mathit{z}}_{\left\{s\right\}}\right)d{\mathit{z}}_{\left\{s\right\}}$$

7.2. Results.

We identified four explanatory variables to analyze for the current application of the ORSF and CIF to data from the JHS: (1) left ventricular mass (LVM) in g/m^2.7, (2) age in years, (3) estimated glomerular filtration rate (eGFR) (Levey et al., 2009) in ml/min/1.73m², and (4) systolic blood pressure (SBP) in mm Hg, measured in a clinical setting. We performed routine descriptive analyses of these variables in the training and testing datasets, separately (Table 7 and Figure 6).

Table 7.

Descriptive statistics for four variables in the Jackson Heart Study.

Summary measures§		Percentile
	Min.	25%	50%	75%	Max.	Mean	SD
Testing data
Age, years	20.60	45.10	55.20	64.40	93.10	55.04	12.77
eGFR, ml/min/1.73 m2	4.29	81.48	96.90	110.25	153.46	94.94	22.24
Left ventricular mass, g/m2	20.84	59.55	69.17	81.33	215.50	72.88	20.27
Systolic blood pressure, mm Hg	77.98	115.58	125.66	136.67	228.36	127.35	16.91
Training data
Age, years	21.00	45.70	56.10	65.20	95.50	55.58	12.93
eGFR, ml/min/1.73 m2	4.14	80.47	95.24	109.09	151.88	93.59	21.81
Left ventricular mass, g/m2	5.28	60.16	69.26	82.56	225.45	73.30	20.10
Systolic blood pressure, mm Hg	86.24	116.26	125.66	136.67	221.02	127.60	16.90

^§Min = minimum; Max = maximum; SD = standard deviation.

Fig 6.

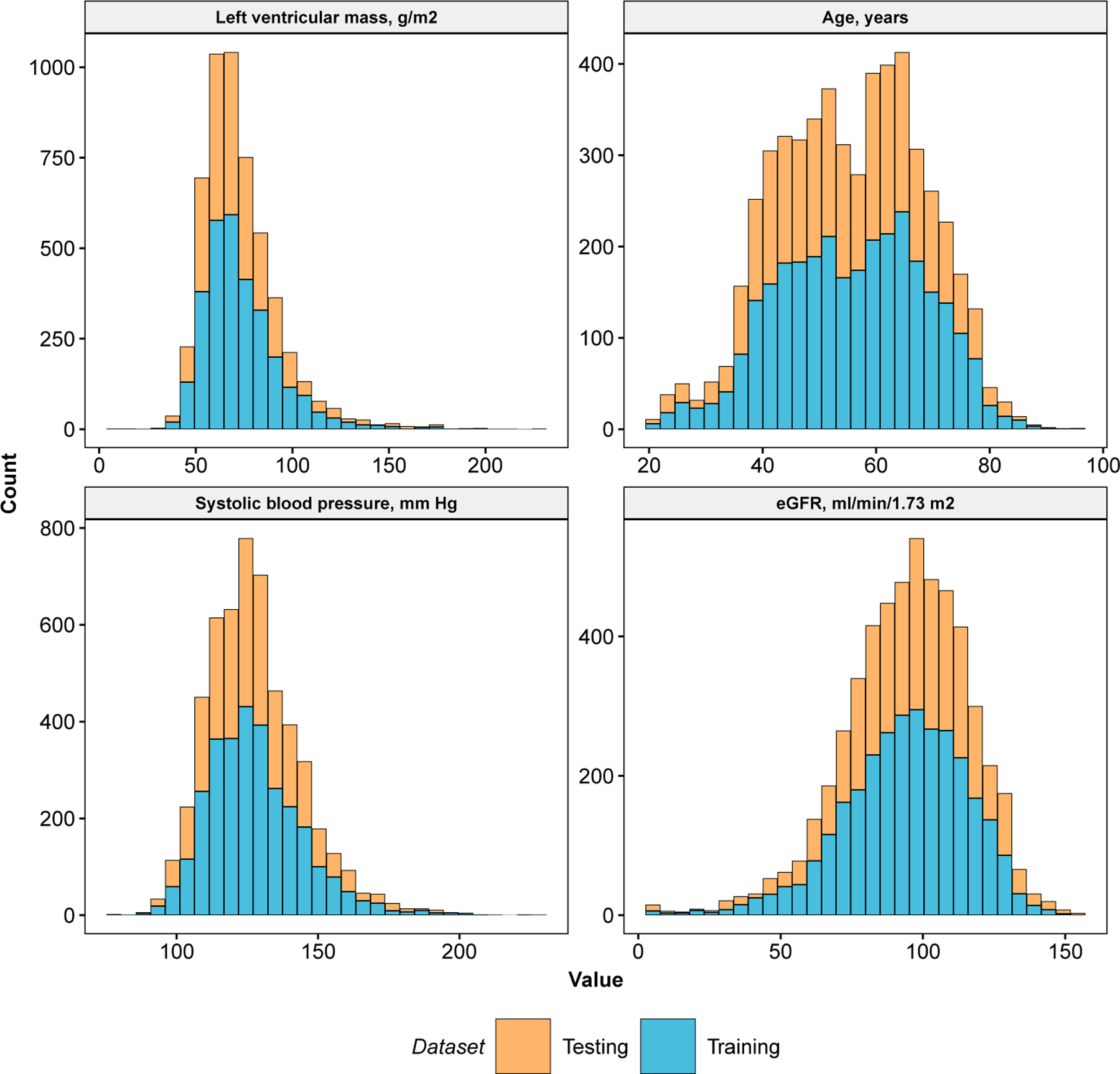
Descriptive summary of left ventricular mass, age, systolic blood pressure, and estimated glomerular filtration rate. Data are from the Jackson Heart Study.

We created variable and partial dependence plots for each explanatory variable and ASCVD risk, separately, using the ORSF and the CIF. Variable dependence plots indicated that predictions from the ORSF demonstrate stronger alignment than the CIF with the Pooled Cohort Risk equations (Figure 7). Partial dependence plots show that the ORSF’s predicted risk function generally differs from the CIF in the upper or lower range of values for each explanatory variable (Figure 8). This pattern of difference in predicted risk may explain the observed differences (Figure 9; top row) and lack of differences (Figure 9; bottom row) in survival curves for four JHS participants in the testing data.

Fig 7.

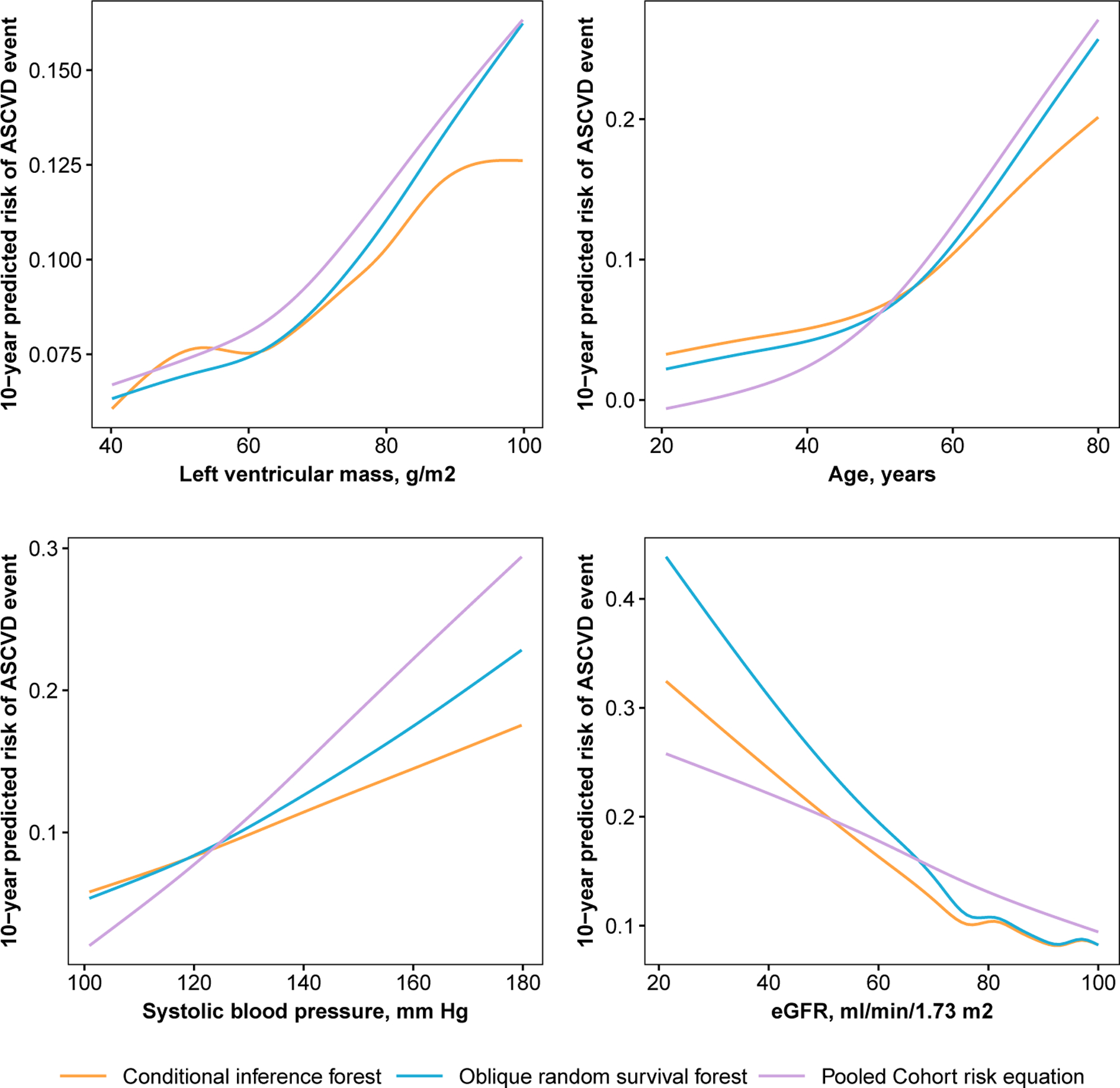
Variable dependence plots for 10-year risk of stroke or coronary heart disease as a function of left ventricular mass, age, systolic blood pressure, and estimated glomerular filtration rate, separately, according to data from participants in the Jackson Heart Study.

Fig 8.

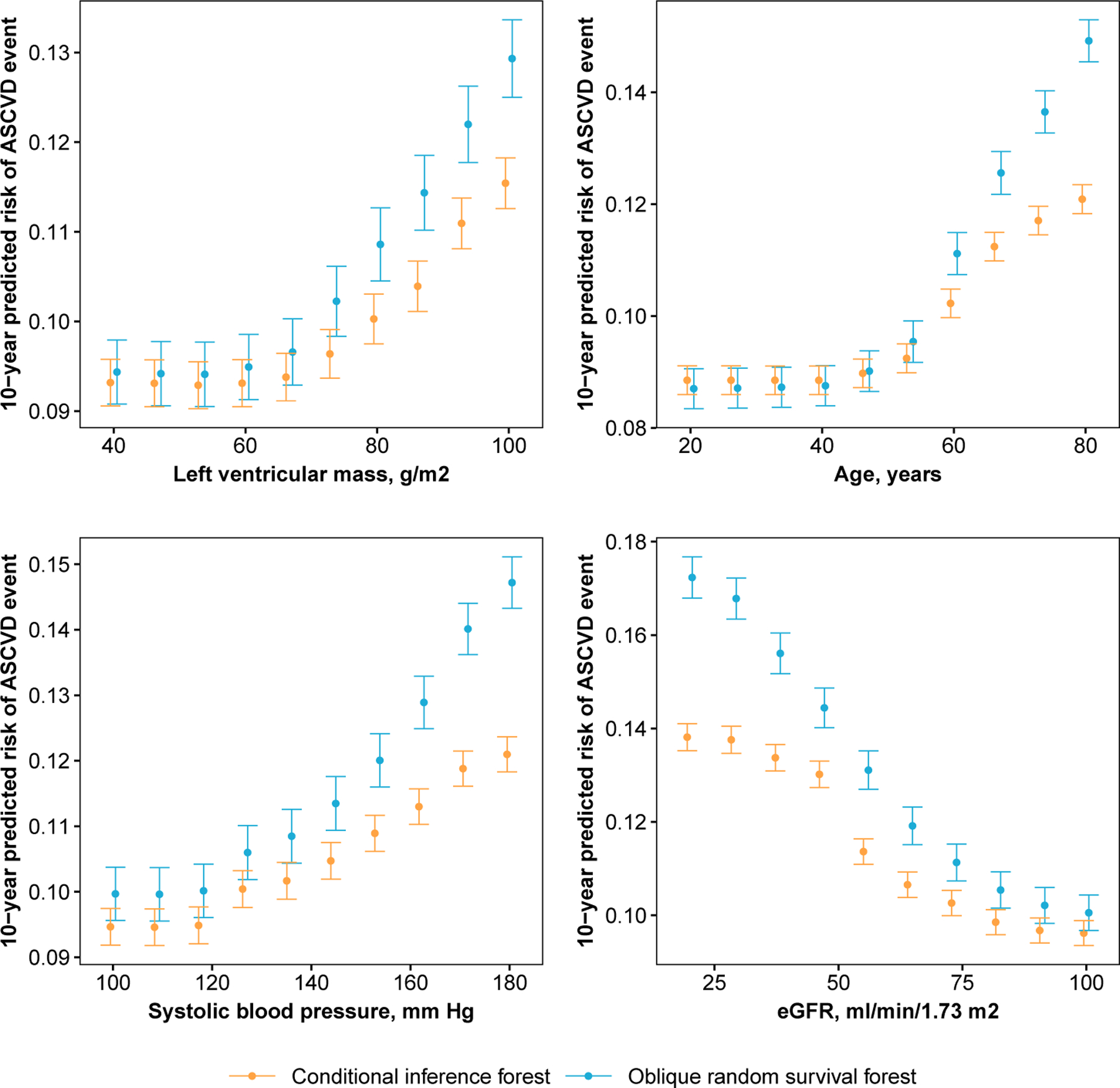
Partial dependence plots for 10-year risk of stroke or coronary heart disease as a function of left ventricular mass, age, systolic blood pressure, and estimated glomerular filtration rate, separately, according to data from participants in the Jackson Heart Study.

Fig 9.

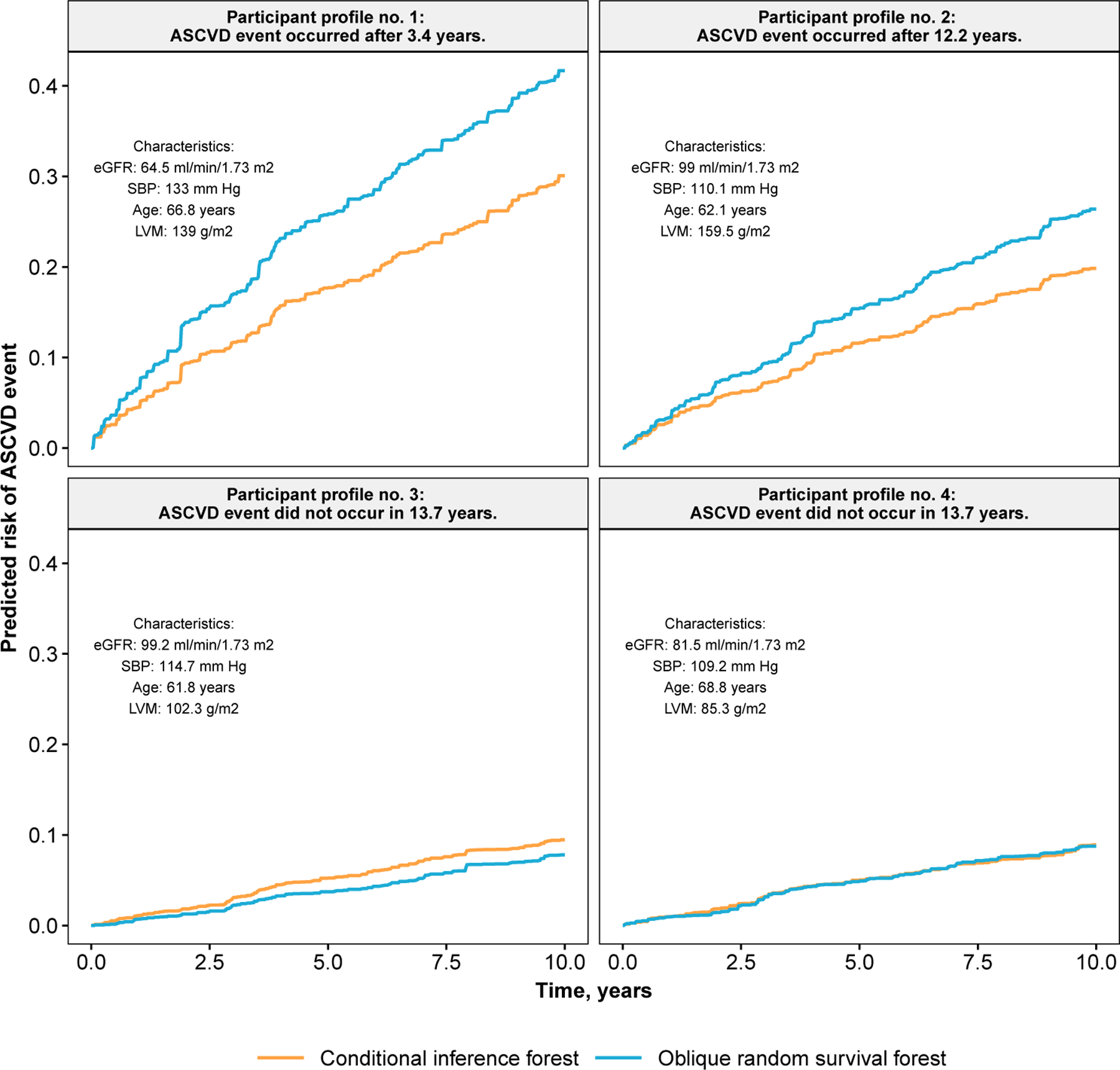
Predicted survival curves for four JHS participants in the testing data.

8. Discussion.

8.1. Summary.

In this article, we have introduced the ORSF and assessed its predictive accuracy. The ORSF extends current implementations of ensemble methods for right-censored time-to-event analyses by applying a recursive partitioning algorithm that can incorporate LCIVs. Our results indicated that the ORSF may provide substantial improvement in discrimination (i.e., lower concordance error) and minor improvement in Brier scores compared to state-of-the-art learning algorithms. Using data from participants in the JHS, we compared dependence plots from the ORSF and CIF using four explanatory variables, separately, for 10-year predicted risk of ASCVD events. Our results demonstrated differences between predicted risk for ASCVD according to the ORSF and CIF. Results also showed that, according to the four variables we analyzed, the ORSF’s predicted risk function had stronger alignment with the Pooled Cohort Risk equations compared to the CIF.

8.2. Why the ORSF works (and when it doesn’t).

In our application to real data, we found that the ORSF’s predicted risk function may substantially lower concordance error compared to the RSF and Brier score compared to the CIF. Given the similarity in these three algorithms, the most likely explanation for the differences we observed is the use of LCIVs, which has been shown to result in additional accuracy and diversity of individual trees in the ensemble (Rainforth and Wood, 2015; Menze et al., 2011; Breiman, 2001). As an informal demonstration (not a comprehensive comparison), we computed predicted survival curves for one observation generated from Scenario C in our simulation study using the ORSF and RSF. Figure 10 illustrates predicted survival curves for this observation from each survival tree in the fitted ORSF and RSF ensembles, separately. In the RSF, many trees give nearly identical survival curves for this participant. On the other hand, there are many more types of survival curves in the ORSF ensemble (diversity). Additionally, survival curves in the ORSF tend to be more aligned with the true survival curve (accuracy). This figure shows one instance where predictions from trees in the ORSF exhibit a clear increase in diversity and accuracy compared to survival trees in the RSF ensemble. However, this is clearly not a claim that this pattern holds in general.

Fig 10.

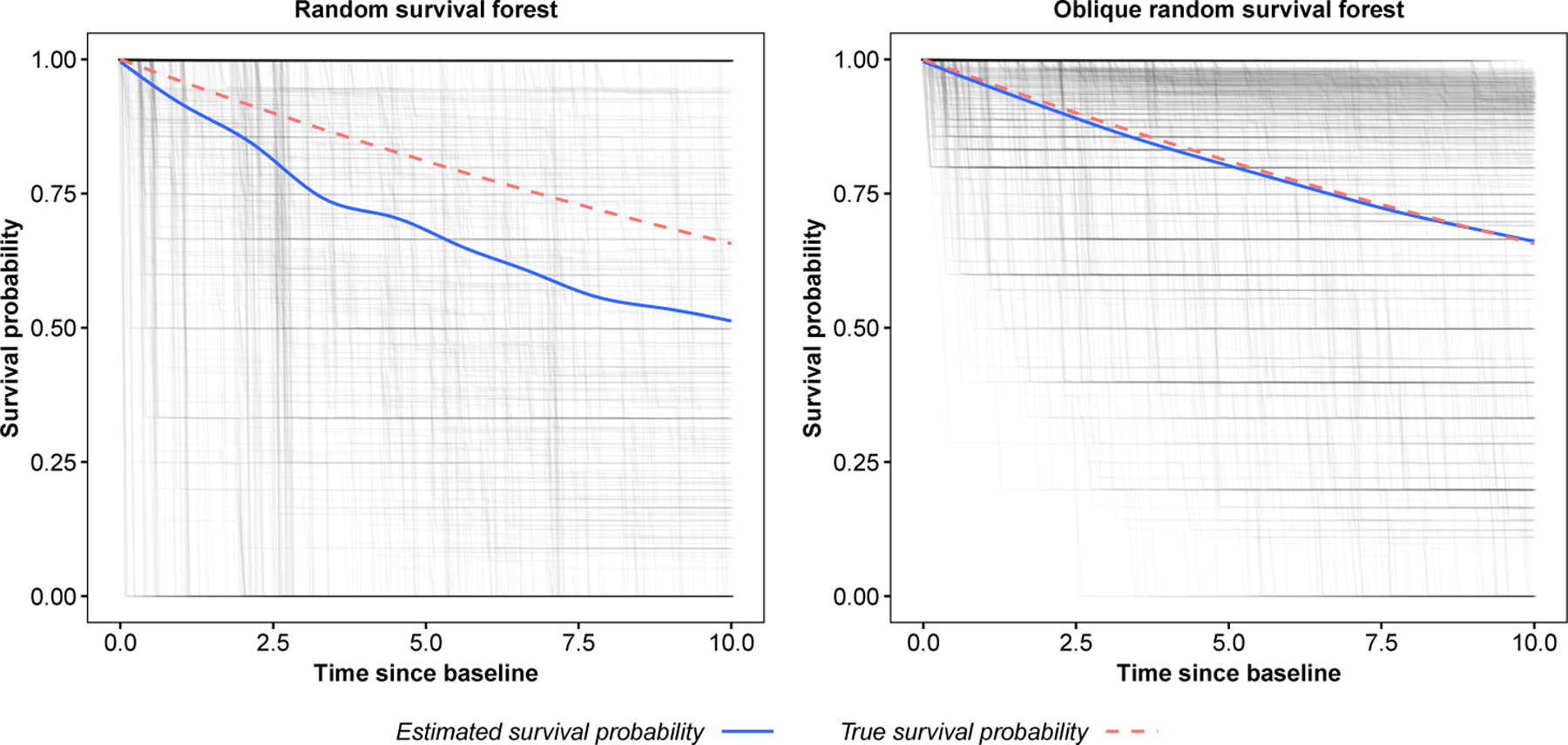
Tree and ensemble predicted survival functions for a single observation from simulated data (Scenario C with p = 50; see Section 4.1). Estimates are from the random survival forest (left) and oblique random survival forest (right).

In our simulated trials, the ORSF recorded higher Brier scores than gradient boosted decision trees. However, this pattern was reversed in the analysis of real data. This is likely due to the invalidity of the proportional hazards assumption in many of the real data problems we considered. These results suggest that in analyses where the proportional hazards assumption is entirely valid, the ORSF and other implementations of RFs for survival analyses may not be able to compete with gradient boosted decision trees or penalized Cox PH models.

In addition to LCIVs, early stopping and class-specific shrinkage of categorical predictors are important components of the ORSF that are based on the CIF (Nasejje et al., 2017). The protocol described by Breiman (1984) is known to result in overfitting and a selection bias towards covariates with many possible splits (i.e., unordered categorical variables) (Hothorn, Hornik and Zeileis, 2006). The ORSF and CIF each apply a mechanism for early stopping if a certain level of statistical association is not measured, and this may explain why both the ORSF and the CIF provided relatively low concordance error. We speculate that early stopping prevents these ensembles from growing decision trees that overfit the training data. However, the ORSF and CIF also provided relatively unimpressive Brier scores in our simulation study and real data analysis compared to gradient boosted decision trees. Therefore, we speculate that early stopping may also prevent decision trees from partitioning a training with a granularity that estimates survival probability as accurately as gradient boosting, especially when the proportional hazard assumption is entirely valid (i.e., scenarios A and B in our simulation study).

8.3. Limitations and Future research.

The additional computational resources required by the ORSF are a clear limitation. While future development and optimization of the C++ routines in the obliqueRSF package may alleviate this limitation, there are several additional topics of interest. For example, the ORSF could be extended to assess the importance of individual variables or clusters of variables. Multiple imputation could be incorporated into the ORSF by imputing missing values separately for each tree in the ensemble using a shared imputation model or a shared set of imputation models. To generate additional diversity in the ensemble, a stochastic error term could be added to the imputation model’s predictions. Predictions from the the ORSF could also be linked to programs that operate on the predicted values of a tree-based ensemble learning algorithm, such as the method of conducting statistical inference introduced by Mentch and Hooker (2016) or the efficient method to compute Shapley additive explanatory values discussed in Lundberg, Erion and Lee (2018). Last, a hybrid algorithm for ORSF that applies cross-validation conditional on sufficient sample size in the current node could be developed. In summary, the obliqueRSF R package offers a powerful learning algorithm, the ORSF (and optionally, the ORSFCV), which may exceed the performance of state-of-the-art learning methods for right-censored time-to-event analyses.