Obtaining the soliton solutions of local M-fractional magneto-electro-elastic media

Abstract

In this research paper, the generalized projective Riccati equations method (GPREM) is applied successfully to procure the soliton solutions of the local M-fractional longitudinal wave equation (LWE) arising in mathematical physics with dispersion caused by the transverse Poisson's effect in a magneto-electro-elastic circular rod (MEECR). Applying a wave transformation to the local M-fractional LWE, the equation can be turned into a set of algebraic equations. Solving the algebraic equation system, we procure the soliton solutions of the local M-fractional LWE. Both the obtained solution functions in the study and the graphical simulations depicted for these functions. It will assist researchers working in this field in the physical interpretation of this equation. Moreover, the reported solutions propose a rich platform to examine the local M-fractional LWE.

1. Introduction

As is well known, the term “soliton” was first introduced to the literature by American physicists Norman J. Zabusky and Martin D. Kruskal in 1965. The study of integrability of nonlinear partial differential equations involving functions of a spatial variable as well as a temporal variable by Kruskal in the 1960s actually has an important key role. These studies first started with a computer simulation of a nonlinear equation known as the Korteweg-de Vries (KdV) equation in the literature by Zabusky and Kruskal. Although the KdV equation is an asymptotic model of the propagation of nonlinear dispersed waves, Zabusky and Kruskal in some sense explored the “solitary wave” solution of the KdV equation, which propagates without dispersion and even regains its physical properties (shape) after interaction (collision) with other such waves. Because of its particle-like properties for such a wave, Zabusky and Kruskal called it “soliton” to describe it precisely. Many researches (Kruskal, Zabusky, Miura, Gardner, Zakharov, Shabat, Zakharov, Mikhailov, Ablowitz, Newell, Segur, Kaup, Manakov, and other distinguished scientists) have been carried out in fields such as nonlinear wave dynamics, nonlinear optics, solid state, plasma, and quantum physics, atmosphere, ocean engineering and planetary sciences due to both the introduction of the soliton concept into the literature and the integrability of nonlinear equations and the development of computer-aided symbolic software. Especially in the last two decades, new concepts, theories, and models related to nonlinearity have been developed and most of them have been supported by experimental studies [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30]. Due to the increase in studies on solitons, the orientation of many researchers to this field. In particular, the modeling of many physical events in nature and obtaining soliton solutions, and nonlinear equations have gained a unique field and importance. Such studies have naturally introduced specific approaches and methods to some fields, and some new solution methods have been developed. For example, in biomedical applications, a heating-free reprogrammable magnetization technique [31], an improved generic carrier-based PWM solution [32], the systematic analysis method [33], finite element analysis based partial differential equation systems solution application (COMSOL multiphysics) [34], a combination of single crystal and powder X-ray diffraction (XRD) using the positional parameters [35], finite control set model-predictive control (FCS-MPC) [36], the Wavesip method [37], amended water strider algorithm [38], Lagrangian relaxation algorithm [39]. Rods (or elastic rods) are one of the best-selected materials for solving nonlinear problems. The study of non-linear wave behavior in rods both theoretically and experimentally and the results obtained in technology have made the studies of wave propagation in rods more widespread. In mechanics, a rod is generally defined as a deformable solid with a finite rigidity in tension, torsion, and bending, which geometrically has two dimensions smaller than its third dimension. One type of wave propagation in rods is LW propagation. The most common model for LW propagation is the Bernoulli model. In this model, while defining the longitudinal vibrations of the rod, it is possible to neglect the potential energy of the shear strain and the kinetic energy of the transverse motion of the particles. According to Bernoulli's theory, linear waves in rods propagate with the velocity $c_0=\sqrt{E/\rho }$, where E is known as Young's modulus and ρ is the density of the material, respectively. In this model, velocity does not depend on the frequency and it is impossible to describe the geometric dispersion of LWs. This point, which is the biggest shortcoming of Bernoulli's model, was later eliminated with the mathematical models proposed by Rayleigh, Love, Bishop, Mindlin, and Hermann.

Many studies have been performed to model wave propagation in a finite elastic rod. Assuming that the cross-section of the rod is circular and constant, and accepting some assumptions to use the Lagrangian material definition with the cylindrical coordinates among these, the Euler equation modeling the nonlinear wave equation of the elastic rod with finite deformation is obtained by using the Hamilton variation principle with the kinetic energy approach [40] as follows:

$$\frac{{\partial }^{2}U}{\partial t^2}-\frac{E}{\rho }\frac{\partial }{\partial x}\left(\frac{\partial U}{\partial x}\right)=\frac{1}{2\rho }\frac{\partial }{\partial x}[3E{\left(\frac{\partial U}{\partial x}\right)}^2+E{\left(\frac{\partial U}{\partial x}\right)}^3+\rho {\nu }^2{R}^2\frac{\partial }{\partial x}\left(\frac{{\partial }^{2}U}{\partial t^2}\right)-\mu {\nu }^2{R}^2\frac{\partial }{\partial x}\left(\frac{{\partial }^{2}U}{\partial x^2}\right)],$$ (1)

where $S=\pi R^2$ is the cross-sectional area of the circular rod with radius r, ν and ρ are the Poisson's ratio and density of the elastic material, respectively. U is the longitudinal displacement, and t is the time variable. Eq. (1) is a wave equation of double nonlinearities and double dispersions of the circular-rod waveguide, which includes both lateral inertia and lateral shear simultaneously. Another study related to the elastic rod is the equation below, which models the nonlinear wave propagation in a standard elastic rod, based on the equations of motion in an elastic rod, again with cylindrical coordinates and assuming that the extended tractions on the lateral boundary of the rod should be zero. This form is also the form of the equation that is the subject of the study within the scope of the article and is given as follows [41]:

$$\frac{{\partial }^{2}u}{\partial t^2}-c_0^2\frac{{\partial }^{2}u}{\partial x^2}=\frac{{\partial }^2}{\partial x^2}(\frac{c_0^2}{2}{u}^2+N\frac{{\partial }^{2}u}{\partial t^2}),$$ (2)

in which $c_0$ is the velocity of the linear longitudinal wave, N is the dispersion parameter, x is the spatial axis according to the longitudinal geometry of the rod, and t is the time variable. Eq. (2) is a nonlinear wave equation with dispersion caused by the transverse Poisson's effect. In addition to these mentioned studies, one of the models in this field is the model developed from the most studied and known Korteweg-de Vries equation. The equation is given [42]:

$${\mathrm{\Psi }}_t+6\mathrm{\Psi }{\mathrm{\Psi }}_x+{\mathrm{\Psi }}_{xxx}=0,$$ (3)

in which $\mathrm{\Psi }={\mathrm{\Omega }}_x$ and Eq. (3) describes the nonlinear LWs in rods under certain conditions. This equation is the well-known Korteweg–de Vries (KDV) equation. Here, Ω is the longitudinal displacement of the particles, and $x,t$ are the dimensionless spatial and temporal coordinates, respectively. Many studies have been done and models have been explored (such as Rayleigh–Love, Bishop, and Mindlin–Hermann, Winkler–Pasternak, Bernoulli–Euler) on the LW propagation in the rod in relation to the KDV equation [43], [44], [45], [46], [47], [48], [49], [50], [51], [52], [53], [54].

The aim of this investigation is to scrutinize the local M-fractional longitudinal wave equation emerging in a magneto-electro-elastic circular rod given by [55]:

$${\mathcal{D}}_{M,t}^{2\alpha ,\beta }\psi (x,t)-c_0^2{\mathcal{D}}_{M,x}^{2\alpha ,\beta }\psi (x,t)-{\mathcal{D}}_{M,x}^{2\alpha ,\beta }[\frac{c_0^2}{2}{\psi }^2(x,t)-p{\mathcal{D}}_{M,t}^{2\alpha ,\beta }\psi (x,t)]=0.$$ (4)

In Eq. (4) ${\mathcal{D}}_{M,t}^{2\alpha ,\beta }\psi (x,t)$ is M derivative of order α of $\psi (x,t)$ with respect to t, p presents the coefficient of dispersion term, and $c_0$ states the linear longitudinal wave velocity for a MEECR. Moreover, all of them hinge on the geometry of the rod and the material characteristics.

Few new exact schemes have been introduced to derive get the soliton solutions of the LWE arising in a MEECR. Yang and Xu acquired the new solutions to the LWE model by using direct integration with boundary conditions and symmetry conditions in [56]. Baskonus and Gomez-Aguilar applied the Bernoulli sub-equation function method to obtain different soliton solutions of the LWE in [55]. The extended sinh-Gordon equation expansion method was applied to get various soliton solutions of LWE by Bulut et al. in [57]. Nur Alam and Tunc solved the LWE using the novel generalized (G'/G)-expansion method in [58]. Younis and Ali considered the ansatz method to construct soliton solutions of the LWE in [59]. Alderremy et al. explored the analytical and semi-analytical wave solutions in [60]. Ilhan et al. examined the analytical solution of the LWE utilizing the powerful sine-Gordon expansion method in [61]. Seadawy and Manafian examined different soliton solutions of the LWE utilizing the extended trial equation method in [62].

This paper is detailed as: In Section 2, the general features of the local M-fractional derivative are presented. The GPREM is detailed in Section 3. The presented method is applied to the local M-fractional LWE to procure several soliton solutions in Section 4. The resulting solutions are detailed in Section 5. Conclusions are presented in the last section.

2. The basics of the truncated M-fractional derivative

This section presents the basic definition and known basic properties of the t-MFD.

Definition 2.0.1

The truncated Mittag-Leffler function is expressed by [63]:

$${}_{i}E_{\beta }(z)=\sum _{k=0}^l\frac{z^k}{\mathrm{\Gamma }(\beta k+1)},$$

where $\beta >0$ and $z\in C$.

Definition 2.0.2

Assume that $h:[0,\infty )\to \mathbb{R}$ be a function, the t-MFD for p of order $\alpha \in (0,1)$, with respect to t is defined by [22]:

$${\mathcal{D}}_{M,t}^{\alpha ,\beta }p(t)=\underset{\epsilon \to 0}{\lim }\frac{p\left(t{}_{i}E_{\beta }\left(\epsilon t^{-\alpha }\right)\right)-p(t)}{\epsilon },$$

where $\beta ,t>0$ and ${}_{i}E_{\beta }(\cdot )$ states Mittag-Leffler function.

Theorem 2.0.1

Suppose that $h(t)$ is a function that has derivatives of order α when $t_0>0$ for $\alpha \in (0,1]$ and $\beta >0$ . Then, $h(t)$ is continuous at $t_0$ [63] .

Theorem 2.0.2

Let $0<\alpha \le 1,\beta >0,a,b\in \mathbb{R}$ and suppose that $p,q$ are α-differentiable at any $t>0$ . Then,

• 1. ${\mathcal{D}}_{M,t}^{\alpha ,\beta }(ap+bq)(t)=a{\mathcal{D}}_{M,t}^{\alpha ,\beta }p(t)+b{\mathcal{D}}_{M,t}^{\alpha ,\beta }q(t)$ , $p,q$ are real values,
• 2. ${\mathcal{D}}_{M,t}^{\alpha ,\beta }(pq)(t)=p(t){\mathcal{D}}_{M,t}^{\alpha ,\beta }q(t)+q(t){\mathcal{D}}_{M,t}^{\alpha ,\beta }p(t)$ ,
• 3. ${\mathcal{D}}_{M,t}^{\alpha ,\beta }\left(\frac{p}{q}\right)(t)=\frac{q(t){\mathcal{D}}_{M,t}^{\alpha ,\beta }p(t)-p(t){\mathcal{D}}_{M,t}^{\alpha ,\beta }q(t)}{q{(t)}^2}$ ,
• 4. If p is differentiable, then ${\mathcal{D}}_{M,t}^{\alpha ,\beta }(p)(t)=\frac{t^{1-\alpha }}{\mathrm{\Gamma }(\beta +1)}\frac{dp(t)}{dt}$ .

3. Description of the GPREM

This part clarifies the basics of the GPREM.

Assume that any NLPDE is expressed as:

$$P(\psi ,D_t\psi ,D_x\psi ,D_{xx}\psi ,D_{tt}\psi ,D_x{D}_t\psi ,...)=0,$$ (5)

in which the parameters x and t are two independent variables, and subscripts represent partial derivatives with respect to x and y.

Step 1: Let's define the wave transformation equation given below:

$$\psi (x,t)=u(\zeta ),\zeta =(x\pm \upsilon t),$$ (6)

where ζ is a new variable, υ symbolizes the soliton's velocity. Eq. (5) takes to the following nonlinear ordinary differential equation form:

$$P(u,u^{\prime },u^{″},\dots )=0,$$ (7)

in which $u^{\prime }=\frac{du}{d\zeta },u^{″}=\frac{d^{2}u}{d{\zeta }^2}$.

Step 2: Consider that Eq. (7) accepts the following solution:

$$u(\zeta )=A_0+\sum _{k=1}^N\sigma {(\zeta )}^{k-1}[A_k\sigma (\zeta )+B_k\rho (\zeta )],$$ (8)

in which $A_0,A_k$ and $B_k$ are real coefficients to be calculated. $\sigma (\zeta )$ and $\rho (\zeta )$ satisfy the following ODEs:

$${\sigma }^{\prime }(\zeta )=ϵ\sigma (\zeta )\rho (\zeta ),$$ (9)

$${\rho }^{\prime }(\zeta )=\chi +ϵ\rho {(\zeta )}^2-\mu \sigma (\zeta ),ϵ=\pm 1,$$ (10)

where

$$\rho {(\zeta )}^2=-ϵ(\chi -2\mu \sigma (\zeta )+\frac{{\mu }^2+r}{\chi }\sigma {(\zeta )}^2).$$ (11)

Herein, μ and χ are nonzero real values. If $\mu =\chi =0$, then Eq. (7) admits the given formula as a solution:

$$u(\zeta )=\sum _{k=1}^N{A}_k{\rho }^k,$$ (12)

in which $\rho (\zeta )$ satisfies the following ODE given by Eq. (13):

$${\rho }^{\prime }(\zeta )=\rho {(\zeta )}^2.$$ (13)

Step 3: In Eq. (8) and Eq. (12), N is a positive integer which is calculated utilizing the classical balancing rule in Eq. (7).

Step 4: Inserting Eq. (8) along with Eqs. (9)–(11) into Eq. (7), then, gathering all terms of the identical order of ${\sigma }^k(\zeta ){\rho }^l(\zeta )$ $(k,l=0,1,2,\dots N)$ and taking each to zero, we procure set of a system whose solutions yield the parameters of $A_0,A_k,B_k,\mu ,r,\chi$.

Step 5: Eq. (9) and Eq. (10) produce the given conditional solutions:

Family 1: When $ϵ=-1,r=-1,\chi >0$, we get,

$${\sigma }_1(\zeta )=\frac{\chi sech\left(\sqrt{\chi }\zeta \right)}{\mu sech\left(\sqrt{\chi }\zeta \right)+1},{\rho }_1(\zeta )=\frac{\sqrt{\chi }tanh\left(\sqrt{\chi }\zeta \right)}{\mu sech\left(\sqrt{\chi }\zeta \right)+1}.$$ (14)

Family 2: If $ϵ=-1,r=1,\chi >0$, we get,

$${\sigma }_2(\zeta )=\frac{\chi csch\left(\sqrt{\chi }\zeta \right)}{\mu csch\left(\sqrt{\chi }\zeta \right)+1},{\rho }_2(\zeta )=\frac{\sqrt{\chi }coth\left(\sqrt{\chi }\zeta \right)}{\mu csch\left(\sqrt{\chi }\zeta \right)+1}.$$ (15)

Family 3: If $ϵ=1,r=-1,\chi >0$, we get,

$${\sigma }_3(\zeta )=\frac{\chi sec\left(\sqrt{\chi }\zeta \right)}{\mu sec\left(\sqrt{\chi }\zeta \right)+1},{\rho }_3(\zeta )=\frac{\sqrt{\chi }tan\left(\sqrt{\chi }\zeta \right)}{\mu sec\left(\sqrt{\chi }\zeta \right)+1},$$ (16)

$${\sigma }_4(\zeta )=\frac{\chi csc\left(\sqrt{\chi }\zeta \right)}{\mu csc\left(\sqrt{\chi }\zeta \right)+1},{\rho }_4(\zeta )=-\frac{\sqrt{\chi }cot\left(\sqrt{\chi }\zeta \right)}{\mu csc\left(\sqrt{\chi }\zeta \right)+1}.$$ (17)

Family 4: If $\mu =\chi =0$, we get,

$${\sigma }_5(\zeta )=\frac{K}{\zeta },{\rho }_5(\zeta )=\frac{1}{ϵ\zeta },$$ (18)

where K is a nonzero real value.

Step 6: Utilizing the parameters of $A_0,A_k,B_k,\mu ,r,\chi$ and Eqs. (14)-(18), by considering the Eq. (6) and Eq. (8) the solutions of Eq. (5) are acquired.

4. Governing model

In this segment, the GPREM has been applied to the proposed local M-fractional LWE to have soliton solutions.

We use the following transformations:

$$\psi =\psi (x,t)=\psi (\zeta ),\zeta =\frac{\lambda }{\alpha }\wp (1+\beta )(x^{\alpha }+\omega t^{\alpha }),$$ (19)

in which $\lambda ,\omega$ are nonzero real values, $0<\alpha \le 1$. Inserting the wave transformation Eq. (19) into Eq. (4), we acquire:

$$2{\lambda }^2{\omega }^{2}p{\psi }^{″}-2{\omega }^2\psi +2c_0^2\psi +c_0^2{\psi }^2=0.$$ (20)

If we utilize the balancing rule in Eq. (20) between the terms ${\mathrm{\Psi }}^{″}and{\mathrm{\Psi }}^2$, we get the balancing constant as $N=2$. So, Eq. (8) takes the following structure:

$$u(\zeta )=A_0+\sum _{k=1}^2\sigma {(\zeta )}^{k-1}[A_k\sigma (\zeta )+B_k\rho (\zeta )].$$ (21)

Combining the Eq. (21) with Eq. (9) and Eq. (10), together, then, collecting all the coefficients of ${\sigma }^k(\zeta ){\rho }^l(\zeta )$ $(k,l=0,1,2,\dots )$ then equating to zero, algebraic system is obtained.

${\mathit{\sigma }}^4(\mathit{\zeta })$coefficient:

$$(c_0^2\chi A_2^2-\left(12{\lambda }^2{\omega }^{2}p{ϵ}^3{A}_{2}r\right)({\mu }^2+1)-\left(c_0^2{B}_2^2ϵ\right)({\mu }^2+r))=0,$$ (22)

${\mathit{\sigma }}^3(\mathit{\zeta })\mathit{\rho }(\mathit{\zeta })$coefficient:

$$(2c_0^2\chi A_2{B}_2-\left(12{\lambda }^2{\omega }^{2}p{ϵ}^3{B}_2\right)({\mu }^2+r))=0,$$ (23)

${\mathit{\sigma }}^3(\mathit{\zeta })$coefficient:

$$(2c_0^2(R{A}_1{A}_2-B_1ϵB_2({\mu }^2+r+B_2^2ϵ\mu R))+{\lambda }^2{\omega }^2ϵp(4R\mu A_2(6{ϵ}^2-1)-4{ϵ}^2{\mu }^2{A}_1(1+r)))=0,$$ (24)

${\mathit{\sigma }}^2(\mathit{\zeta })\mathit{\rho }(\mathit{\zeta })$coefficient:

$$(-4{\lambda }^2{\omega }^{2}p{ϵ}^3{B}_1({\mu }^2+r)+2c_0^2\chi (A_1{B}_2-B_1{A}_2{\chi }^2)+2{\lambda }^2{\omega }^{2}pϵ\mu \chi (10{ϵ}^2-4B_2))+(c_0^2{B}_1ϵ(4B_2\mu \chi -B_{1}r)r+4{\lambda }^2{\omega }^{2}pϵ\chi (A_2\chi +2{ϵ}^2{A}_1\mu ))=0,$$ (25)

${\mathit{\sigma }}^2(\mathit{\zeta })$coefficient:

$$c_0^2\chi (2A_0{A}_2-B_2^2ϵ\chi -A_1^2)-2\chi A_2(c_0^2-{\omega }^2)-c_0^2{B}_1^2ϵ{\mu }^2-2{\lambda }^2{\omega }^{2}pϵ\chi (A_1\mu +6{ϵ}^2{A}_2\chi )-c_0^2{B}_1^2ϵr+4{\lambda }^2{\omega }^{2}pϵ\chi (\chi A_2+{ϵ}^2{A}_1\mu )+4c_0^2{B}_1ϵB_2\mu \chi =0,$$ (26)

$\mathit{\sigma }(\mathit{\zeta })\mathit{\rho }(\mathit{\zeta })$coefficient:

$$\left(2{\lambda }^2{\omega }^{2}pϵB_2\chi \right)(3-4{ϵ}^2)-2{\omega }^2{B}_2+2c_0^2(A_1{B}_1+B_2)+2{\lambda }^2{\omega }^{2}pϵB_1\mu (2{ϵ}^2-1)+2c_0^2{A}_0{B}_2=0,$$ (27)

$\mathit{\sigma }(\mathit{\zeta })$coefficient:

$$(2{\omega }^2{A}_1({\lambda }^{2}pϵ\chi -1)+2c_0^2{A}_1(A_0+1)+2c_0^2ϵB_1(B_1\mu -B_2\chi )-4{\lambda }^2{\omega }^{2}p{ϵ}^3{A}_1\chi )=0,$$ (28)

$\mathit{\rho }(\mathit{\zeta })$coefficient:

$$(-2{\omega }^2{B}_1+\left(2c_0^2{A}_0{B}_1\right)(A_0+1))=0,$$ (29)

${\mathit{\sigma }}^0(\mathit{\zeta })$coefficient:

$$(-c_0^2{B}_1^2ϵ\chi +c_0^2{A}_0^2-2{\omega }^2{A}_0+2c_0^2{A}_0)=0.$$ (30)

Solving this system which is consisting Eq. (22)-Eq. (30) via a suitable algorithm and the aid of Maple, some of the obtained sets are as follows:

Family 1: Taking $ϵ=-1$ and $r=\mp 1$ in Eqs. (8), (9), (10), (20) and related obtained functions then solving the obtained system gives the following sets in Eq. (31), Eq. (33) and Eq. (35).

$$\chi =\frac{{c_0}^2-{\omega }^2}{p{\lambda }^2{\omega }^2},A_0=\frac{2({c_0}^2-{\omega }^2)}{{c_0}^2},A_2=-\frac{6p^4{\lambda }^4{\omega }^4({\mu }^2-1)}{{c_0}^2({c_0}^2-{\omega }^2)},B_1=0,B_2=-\frac{\sqrt{({c_0}^2-{\omega }^2)p({\mu }^2-1)}{\lambda }^3{\omega }^{3}p}{{c_0}^2({c_0}^2-{\omega }^2)},$$ (31)

and we procure the following solution with

$${\psi }_1(x,t)=2\frac{{\omega }^2-{c_0}^2}{{c_0}^2}+\frac{6\mu ({c_0}^2-{\omega }^2)\text{sech}\left({\mathrm{\Phi }}_N\right)}{{c_0}^2(\mu \text{ sech}\left({\mathrm{\Phi }}_N\right)+1)}+({c_0}^2-{\omega }^2)\text{sech}\left({\mathrm{\Phi }}_N\right)\times {\mathrm{\Phi }}_{NM},$$ (32)

where

$${\mathrm{\Phi }}_N=\frac{\sqrt{\frac{-{\omega }^2+{c_0}^2}{p{\lambda }^2{\omega }^2}}\lambda \mathrm{\Gamma }(1+\beta )(x^{\alpha }+\omega t^{\alpha })}{\alpha },$$

$${\mathrm{\Phi }}_{NM}=\frac{(-\frac{6p{\lambda }^2{\omega }^2({\mu }^2-1)\text{sech}\left({\mathrm{\Phi }}_N\right)}{{c_0}^2(\mu \text{ sech}\left({\mathrm{\Phi }}_N\right)+1)}-\frac{6p{\lambda }^3{\omega }^3\sqrt{\frac{{(c_0-{\omega }^2)}^2({\mu }^2-1)}{{\lambda }^2{\omega }^2}}\text{tanh}\left({\mathrm{\Phi }}_N\right)}{{c_0}^2({c_0}^2-{\omega }^2)(\mu \text{ sech}\left({\mathrm{\Phi }}_N\right)+1)})}{p{\lambda }^2{\omega }^2\text{sech}\left({\mathrm{\Phi }}_N\right)}.$$

Family 2: Taking $ϵ=\mp 1$ and $r=1$ in Eqs. (8), (9), (10), (20) and solution of the system algebraically gives the following solutions:

$$\chi =\frac{{c_0}^2-{\omega }^2}{p{\lambda }^2{\omega }^2},A_0=\frac{-2({c_0}^2-{\omega }^2)}{{c_0}^2},A_1=\frac{6\mu p{\lambda }^2{\omega }^2}{{c_0}^2},A_2=-\frac{6p^2{\lambda }^4{\omega }^4({\mu }^2+1)}{{c_0}^2({c_0}^2-{\omega }^2)},B_1=0,B_2=-\frac{\sqrt{({c_0}^2-{\omega }^2)p({\mu }^2+1)}{\lambda }^3{\omega }^{3}p}{{c_0}^2({c_0}^2-{\omega }^2)},$$ (33)

and we procure the following solution with

$${\psi }_2(x,t)=2\frac{{\omega }^2-{c_0}^2}{{c_0}^2}+\frac{6\mu ({c_0}^2-{\omega }^2)\text{csch}\left({\mathrm{\Phi }}_G\right)}{{c_0}^2(\mu \text{ csch}\left({\mathrm{\Phi }}_G\right)+1)}+({c_0}^2-{\omega }^2)\text{csch}\left({\mathrm{\Phi }}_G\right)\times {\mathrm{\Phi }}_{GH},$$ (34)

where

$${\mathrm{\Phi }}_G=\frac{\sqrt{\frac{-{\omega }^2+{c_0}^2}{p{\lambda }^2{\omega }^2}}\lambda \mathrm{\Gamma }(1+\beta )(x^{\alpha }+\omega t^{\alpha })}{\alpha },$$

$${\mathrm{\Phi }}_H=(-\frac{6p{\lambda }^2{\omega }^2({\mu }^2-1)\text{csch}\left({\mathrm{\Phi }}_G\right)}{{c_0}^2(\mu \text{ csch}\left({\mathrm{\Phi }}_G\right)+1)}-\frac{6p{\lambda }^3{\omega }^3\sqrt{\frac{{(c_0-{\omega }^2)}^2({\mu }^2-1)}{{\lambda }^2{\omega }^2}}\text{tanh}\left({\mathrm{\Phi }}_G\right)}{{c_0}^2({c_0}^2-{\omega }^2)(\mu \text{ csch}\left({\mathrm{\Phi }}_G\right)+1)}),{\mathrm{\Phi }}_{GH}=\frac{{\mathrm{\Phi }}_H}{p{\lambda }^2{\omega }^2\text{csch}\left({\mathrm{\Phi }}_G\right)}.$$

Family 3: Taking $ϵ=\mp 1$ and $r=-1$ in Eqs. (8), (9), (10), (20) and resolving the system of the algebraic equations, we get the following values:

$$c_0=\omega \sqrt{-\chi {\lambda }^{2}p+1},A_0=-\frac{2\chi {\lambda }^{2}p}{\chi {\lambda }^{2}p-1},A_1=\frac{6{\lambda }^{2}p\mu }{\chi {\lambda }^{2}p-1},A_2=-\frac{6{\lambda }^{2}p({\mu }^2-1)}{R(R{\lambda }^{2}p-1)},B_1=0,B_2=-\frac{6\sqrt{-\chi ({\mu }^2-1)}{\lambda }^{2}p}{\chi (\chi {\lambda }^{2}p-1)},$$ (35)

and we procure the following solutions given in Eq. (36) and Eq. (37) as follows:

$${\psi }_{3,1}(x,t)=-\frac{2\chi {\lambda }^{2}p}{\chi {\lambda }^{2}p-1}+\frac{6{\lambda }^2\mu p\chi \text{sec}\left({\mathrm{\Upsilon }}_Z\right)}{(\chi {\lambda }^{2}p-1)(\mu \text{sec}\left({\mathrm{\Upsilon }}_Z\right)+1)}+\frac{\chi \text{sec}\left({\mathrm{\Upsilon }}_Z\right)}{(\mu \text{sec}\left({\mathrm{\Upsilon }}_Z\right)+1)}\times {\mathrm{\Upsilon }}_{ZX},$$ (36)

and

$${\psi }_{3,2}(x,t)=-\frac{2\chi {\lambda }^{2}p}{\chi {\lambda }^{2}p-1}+\frac{6{\lambda }^2\mu p\chi \text{csc}({\mathrm{\Upsilon }}_Z)}{(\chi {\lambda }^{2}p-1)(\mu \text{csc}\left({\mathrm{\Upsilon }}_Z\right)+1)}+\frac{\chi \text{csc}\left({\mathrm{\Upsilon }}_Z\right)}{(\mu \text{csc}\left({\mathrm{\Upsilon }}_Z\right)+1)}\times {\mathrm{\Upsilon }}_{ZY},$$ (37)

where

$${\mathrm{\Upsilon }}_{ZX}=(-\frac{6{\lambda }^{2}p({\mu }^2-1)\text{sec}\left({\mathrm{\Upsilon }}_Z\right)}{(\chi {\lambda }^{2}p-1)(\mu \text{sec}\left({\mathrm{\Upsilon }}_Z\right)+1)}-\frac{6\sqrt{-\chi ({\mu }^2-1)}p{\lambda }^2\text{tan}\left({\mathrm{\Upsilon }}_Y\right)}{\sqrt{\chi }(\chi {\lambda }^{2}p-1)(\mu \text{sec}\left({\mathrm{\Upsilon }}_Z\right)+1)}),{\mathrm{\Upsilon }}_{ZY}=(-\frac{6{\lambda }^{2}p({\mu }^2-1)\text{csc}\left({\mathrm{\Upsilon }}_Z\right)}{(\chi {\lambda }^{2}p-1)(\mu \text{csc}\left({\mathrm{\Upsilon }}_Z\right)+1)}-\frac{6\sqrt{-\chi ({\mu }^2-1)}p{\lambda }^2\text{cot}\left({\mathrm{\Upsilon }}_Z\right)}{\sqrt{\chi }(\chi {\lambda }^{2}p-1)(\mu \text{csc}\left({\mathrm{\Upsilon }}_Y\right)+1)}),{\mathrm{\Upsilon }}_Z=\frac{\sqrt{\chi }\lambda \wp (1+\beta )(x^{\alpha }+\omega t^{\alpha })}{\alpha }\mathrm{\text{and}}{\mathrm{\Upsilon }}_Y=\frac{\sqrt{R}\lambda \wp (1+\beta )(x^{\alpha }+\omega t^{\alpha })}{\alpha }.$$

5. Result and discussion

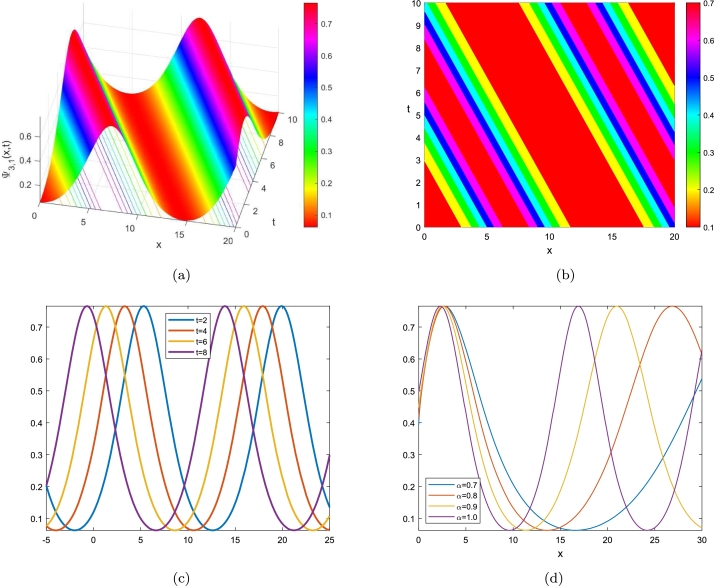
In this section, the achieved results are declared. We acquire bright, dark, and periodic soliton solutions for the LWE in a MEECR with local M-derivative. Figure 1, Figure 2, Figure 3, Figure 4 demonstrate some of the acquired solutions. These solutions provide critical contributions to the interpretation of some physical problems. Fig. 1 is the graphical simulation of ${\psi }_1(x,t)$ given by Eq. (32). Fig. 1-(a) is the 3D, Fig. 1-(b) is the contour views. 3D graph demonstrates the bright soliton in Fig. 1-(a) for $\lambda =1,\omega =-0.5,c_0=2,p=4,\mu =3$ and $\beta =0.95$. Fig. 1-(c) represents 2D soliton profile for $t=2,t=4$, and $t=6$. It can be seen that the amplitude and the shape of the bright soliton remain during the propagation. Furthermore, as t increases, soliton travels to the right. Fig. 1-(d) is the 2D graphical depiction to show the effect of the α when taking the values as 0.7, 0.8, 0.9, and 1.0, respectively. Soliton keeps its bright soliton view but if we pay attention to the peaks of the soliton as if the soliton moves to the right. Since the Fig. (1d) reflects the 2D graphs of different values, we can interpret this situation as the different forms of the soliton depending on the fractional orders.

Figure 1.

The views in 3D, 2D, contour of ψ₁(x,t) for λ = 1,ω = −0.5,c₀ = 2,p = 4,μ = 3, β = 0.95.

Figure 2.

The plots in 3D, 2D, contour of ψ₁(x,t) for λ = 1,ω = −1.1,c₀ = −1,p = −1,μ = 1, β = 0.95.

Figure 3.

3D, contour, 2D depictions of ψ₂(x,t) for λ = 1,ω = −1.1,c₀ = 2,p = 4,μ = 0.5 and β = 0.99.

Figure 4.

The graphics in 3D, contour, 2D of ψ_3,1(x,t) for λ = −0.5,ω = 1,χ = 0.8,p = 1,μ = 5, β = 0.90.

Fig. 2 is also graph of ${\psi }_1(x,t)$ given by Eq. (32). Fig. 2-(a) depicts 3D while Fig. 2-(b) shows the contour projection. Fig. 2-(a) demonstrates the dark soliton view in 3D for $\lambda =1,\omega =-1.5,c_0=-1,p=-1,\mu =1$ and $\beta =0.95$. Fig. 2(c) represents the 2D soliton profile for $t=2,t=4$ and $t=6$. It can be seen that the amplitude and the shape of the dark soliton remain during the propagation. Furthermore, as t increases, soliton travels to the right. A similar examination was made on dark soliton with Fig. 2-(d). When α takes the values as 0.80, 0.85, 0.90, and 1.0, although the soliton behaves similarly to the previous one, the peak of the soliton stays on the horizontal axis, and the wings of the soliton open upwards depending on the increasing values of α (blue to purple lines).

Fig. 3 belongs to ${\psi }_2(x,t)$ which is given in Eq. (34). 3D graph demonstrates the bright soliton in Fig. 3-(a), contour in Fig. 3-(b), 2D in Fig. 3-(c) for various t values. For values of parameters $\lambda =1,\omega =-1.1,c_0=2,p=4,\mu =0.5$ and $\beta =0.99$. Moreover, Fig. 3-(c) presents the 2D soliton profile for $t=2,t=4,t=6$ and $t=8$. It can be seen that the amplitude and the shape of the bright soliton remain during the propagation. Furthermore, as t increases, soliton travels to the right. Similarly, the effect of on the bright soliton for 0.7, 0.8, 0.9, 1.0 values was investigated in Fig. 3-(d). As can be seen from the graph, the skirts of the soliton shrink downwards depending on the increasing α values. This effect is observed less on the left side and more prominent on the right side. At the same time, the apex of the soliton shifts to the left in a sense.

Fig. 4 depicts the some views of ${\psi }_{3,1}(x,t)$ given in Eq. (36). Fig. 4-(a), Fig. 4-(b) and Fig. 4-(c) belong to 3D, contour and 2D simulations, respectively. 3D graph demonstrates the periodic soliton solution in Fig. 4-(a) for values of parameters $\lambda =-0.5,\omega =1,\chi =0.8,p=1,\mu =5$ and $\beta =0.90$. Moreover, Fig. 4-(c) represents the 2D soliton profile for $t=2,t=4,t=6$, and $t=8$. It can be observed from Fig. 4-(a) that amplitude of the soliton decreases while the order of fractional derivative increases. Furthermore, as t increases, soliton travels to the right. The Fig. 4-(d) is another graph showing the effect of α when α takes 0.7, 0.8, 0.9, and 1.0. In the bright soliton representation of the graph for $0<x<5$, different behavior is observed on the left and right-hand sides. In the representation, which is less obvious on the left, growth is observed due to the increasing values of α, and on the right, shrinkage is observed. As the spatial value of x increases, this effect manifests itself in a more prominent periodic appearance $(x>10)$.

We would also like to emphasize the following points here. There are many studies on the LWE equation in the literature. This shows that the models constructed with LWE have an effective importance in clarifying many physical phenomena, and the studies performed with LWE are still current and show the necessity of making new remarks in this field. In this context, the results obtained will be a drop in an ocean in terms of both the soliton behavior and the applicability of the method chosen for such problems. In order to present graphical presentations of the resulted solution functions, selections were made by paying attention to the requirements of both the considered problem and the proposed method in the parameter selections. The real formation of $u(\zeta )$ for the solution function resulting from the selected parameter values is one of these sensitivities. All resulted solution functions provide the main equation for the selected sets. In this respect, the solution functions and graphical expressions obtained within the scope of the article coincide with the studies and generally accepted concepts, examinations, techniques and findings in the literature.

6. Conclusion

In this paper, the importance of studying the local M-fractional LWE stems from its always an attractive topic in physics and has a wide range of applications since few studies have been done on the LWE in the literature. Therefore, there are very few exact solutions to the LWE. This conclusion has motivated us to examine different types of solutions, utilizing the GPREM, which contributes a very efficacious and robust mathematical tool for solving nonlinear problems in mathematical physics and natural sciences. Consequently, some exact solutions for LWE have been accomplished in Section 4. Some solutions are also graphically depicted to comprehend the dynamic behavior of the results. These solutions provide critical contributions to the interpretation of some physical problems.

CRediT authorship contribution statement

Neslihan Ozdemir: Conceived and designed the experiments; Analyzed and interpreted the data; Performed the experiments; Wrote the paper. Aydin Secer: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper. Muslum Ozisik: Conceived and designed the experiments; Analyzed and interpreted the data; Performed the experiments; Wrote the paper. Mustafa Bayram: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Declaration of Competing Interest

The authors declare no conflict of interest.

Data availability

No data was used for the research described in the article.