Coordinate Translator for Learning Deformable Medical Image Registration

Abstract

The majority of deep learning (DL) based deformable image registration methods use convolutional neural networks (CNNs) to estimate displacement fields from pairs of moving and fixed images. This, however, requires the convolutional kernels in the CNN to not only extract intensity features from the inputs but also understand image coordinate systems. We argue that the latter task is challenging for traditional CNNs, limiting their performance in registration tasks. To tackle this problem, we first introduce Coordinate Translator, a differentiable module that identifies matched features between the fixed and moving image and outputs their coordinate correspondences without the need for training. It unloads the burden of understanding image coordinate systems for CNNs, allowing them to focus on feature extraction. We then propose a novel deformable registration network, im2grid, that uses multiple Coordinate Translator’s with the hierarchical features extracted from a CNN encoder and outputs a deformation field in a coarse-to-fine fashion. We compared im2grid with the state-of-the-art DL and non-DL methods for unsupervised 3D magnetic resonance image registration. Our experiments show that im2grid outperforms these methods both qualitatively and quantitatively.

1. Introduction

Deformable registration is of fundamental importance in medical image analysis. Given a pair of images, one fixed and one moving, deformable registration warps the moving image by optimizing the parameters of a nonlinear transformation so that the underlying anatomies of the two images are aligned according to an image dissimilarity function [11,16,32,34,37]. Recent deep learning (DL) methods use convolutional neural networks (CNNs) whose parameters are optimized during training; at test time, a dense displacement field that represents the deformable transformation is generated in a single forward pass.

Although CNN-based methods for segmentation and classification are better than traditional methods in both speed and accuracy, DL-based deformable registration methods are faster but usually not more accurate [4,8,13,15,39]. Using a CNN for registration requires learning coordinate correspondences between image pairs, which has been thought to be fundamentally different from other CNN applications because it involves both extracting and matching features [14,25]. However, the majority of existing works simply rely on CNNs to implicitly learn the displacement between the fixed and moving images [4,13,15].

Registration involves both feature extraction and feature matching, but to produce a displacement field, matched features need to be translated to coordinate correspondences. We argue that using convolutional kernels for the latter two tasks is not optimal. To tackle this problem, we introduce Coordinate Translator, a differentiable module that matches features between the fixed and moving images and identifies feature matches as precise coordinate correspondences without the need for training. The proposed registration network, named im2grid, uses multiple Coordinate Translator’s with multi-scale feature maps. These produce multi-scale sampling grids representing coordinate correspondences, which are then composed in a coarse-to-fine manner to warp the moving image. im2grid explicitly handles the task of matching features and establishing coordinate correspondence using Coordinate Translator’s, leaving only feature extraction to our CNN encoder.

Throughout this paper, we use unsupervised 3D magnetic resonance (MR) image registration as our example task and demonstrate that the proposed method outperforms the state-of-the-art methods in terms of registration accuracy. We think it is important to note that because producing a coordinate location is such a common task in both medical image analysis and computer vision, the proposed method can be impactful on a board range of applications.

2. Related Works

Traditional registration methods solve an optimization problem for every pair of fixed, I_f, and moving, I_m, images. Let ϕ denote a transformation and let the best transformation $\widehat{\varphi }$ be found from

$$\widehat{\varphi }=\underset{\varphi }{\text{arg\hspace{0.17em}min\hspace{0.17em}}}{L}_{\text{sim}}\left(I_f,I_m\circ \varphi \right)+\lambda L_{\text{smooth}}(\varphi ),$$ (1)

where I_m ○ ϕ yields the warped image I_w. The first term focuses on the similarity between I_f and I_m ○ ϕ whereas the second term—weighted by the hyper-parameter λ—regularizes ϕ. The choice of L_sim is application-specific. Popular methods using this framework include spline-based free-form deformable models [32], elastic warping methods [11,27], biomechanical models [16], and Demons [34,37]. Alternatively, learning-based methods have also been used to estimate the transformation parameters [9,19].

Recently, deep learning (DL) methods, especially CNNs, have been used for solving deformable registration problems. In these methods, ϕ is typically represented as a map of displacement vectors that specify the voxel-level spatial offsets between I_f and I_m; the CNN is trained to output ϕ with or without supervision [4,6,13,15,20]. In the unsupervised setting, the displacement field is converted to a sampling grid and the warped image is produced by using a grid sampler [26] with the moving image and the sampling grid as input. The grid sampler performs differentiable sampling of an image (or a multi-channel feature map) using a sampling grid; it allows the dissimilarity loss computed between the warped and fixed images to be back-propagated so the CNN can be trained end-to-end. In past work, [4] used a U-shaped network to output the dense displacement; [12,13] used an encoder network to produce a sparse map of control points and generated the dense displacement field by interpolation; and [8] replaced the bottleneck of a U-Net [31] with a transformer structure [36]. Several deep learning methods also demonstrate the possibility of using a velocity-based transformation representation to enforce a diffeomorphism [10,39].

Our method represents the transformation using a sampling grid G, which can be directly used by the grid sampler. For N-dimensional images (N = 3 in this paper), G is represented by an N-channel map. Specifically, for a voxel coordinate $\mathit{\text{x}}\in {\mathbb{D}}^N$ (where ${\mathbb{D}}^N$ contains all the voxel coordinates in I_f), G(x) should ideally hold a coordinate such that the two values I_f(x) and I_m(G(x)) represent the same anatomy. Note that the displacement field representation commonly used by other methods can be found as G − G_I, where G_I is the identity grid G_I(x) = x.

3. Method

For the image pair I_f and I_m, the proposed method produces a sampling grid G₀ that can be used by the grid sampler to warp I_m to match I_f. Similar to previous DL methods, we use a CNN encoder to extract multi-level feature maps from I_f and I_m. Instead of directly producing a single displacement field from the CNN, G₀ is the composition of multi-level sampling grids, generated from the multi-level feature maps with the proposed Coordinate Translator’s.

3.1. Coordinate Translator

Let F and M denote the multi-channel feature maps that are individually extracted from I_f and I_m, respectively. The goal of a Coordinate Translator is to take as input both F and M, and produce a sampling grid G that aligns M interpolated at coordinate G(x) with F(x) for all $\mathit{\text{x}}\in {\mathbb{D}}^N$.

As the first step, for every x, cross-correlation is calculated between F(x) and M(c_i) along the feature dimension, where ${\mathit{\text{c}}}_i\in {\mathbb{D}}^N$ for i ∈ [1,K] are a set of candidate coordinates. The results are a K-element vector of matching scores between F(x) and every M(c_i): >

$$\text{Matching Score}\left(\mathit{\text{x}}\right)=\left(F{(\mathit{\text{x}})}^{T}M\left({\mathit{\text{c}}}_1\right),\dots ,F{(\mathit{\text{x}})}^{T}M\left({\mathit{\text{c}}}_K\right)\right).$$ (2)

The choice of c_i’s determines the search region for the match. For example, defining c_i to be every coordinates in ${\mathbb{D}}^N$ will compare F(x) against every location in M; these matches can also be restricted within the 3 × 3 × 3 neighborhood of x. We outline our choices of c_i’s in Sect. 4. The matching scores are normalized using a softmax function to produce a matching probability p_i,

$$p_i=\frac{\text{exp}\left(F{(\mathit{\text{x}})}^{T}M\left({\mathit{\text{c}}}_i\right)\right)}{{\sum }_j\text{exp}\left(F{(\mathit{\text{x}})}^{T}M\left({\mathit{\text{c}}}_j\right)\right)}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}every\hspace{0.17em}\hspace{0.17em}}{\mathit{\text{c}}}_i.$$ (3)

We interpret the matching probabilities as the strength of attraction between F(x) and the M(c_i)’s. Importantly, we can calculate a weighted sum of c_i’s to produce a coordinate ${\mathit{\text{x}}}^{\prime }\in {\mathbb{R}}^N$, i.e., ${\mathit{\text{x}}}^{\prime }={\sum }_{i=1}^K{p}_i\cdot {\mathit{\text{c}}}_i$, which represents the correspondence of x in the moving image I_m. This is conceptually similar to the combined force in the Demons algorithm [34]. For every $\mathit{\text{x}}\in {\mathbb{D}}^N$ the corresponding x′ forms the Coordinate Translator output, G.

Coordinate Translator can be efficiently implemented as the Scaled Dot-Product Attention introduced in the Transformer [36] using matrix operations. For 3D images with spatial dimension H × W × S and C feature channels, we reshape F and M to ${\mathbb{R}}^{(H\times W\times S)\times C}$ and the identity grid G_I to ${\mathbb{R}}^{(H\times W\times S)\times 3}$. Thus Coordinate Translator with $\left\{{\mathit{\text{c}}}_1,\dots {\mathit{\text{c}}}_K\right\}={\mathbb{D}}^N$ can be readily computed from,

$$\text{Coordinate Translator}\left(F,M\right)=\text{Softmax}\left(F{M}^T\right)G_I\text{,}$$ (4)

with the softmax operating on the rows of FM^T.

Positional Encoding Layer.

In learning transformations, it is a common practice to initialize from (or close to) an identity transformation [4,8,26]. As shown in Fig. 1, we propose a positional encoding layer that combines position information with F and M such that the initial output of Coordinate Translator is an identity grid. Inside a positional encoding layer, for every x = (x₁,… ,x_N) with x_i’s on an integer grid (x_i ∈ {0,…,d_i−1}), we add a positional embedding (PE),

$$\text{PE}(\mathit{\text{x}})=\left(\text{cos}\frac{x_1\pi }{d_1-1},\text{sin}\frac{x_1\pi }{d_1-1},\cdots ,\text{cos}\frac{x_N\pi }{d_N-1},\text{sin}\frac{x_N\pi }{d_N-1}\right),$$

to the input feature map, where d_i is the pixel dimension along the i^th axis. Trigonometric identities give the cross-correlation of PEs at x₁ and x₂ as

$$\text{PE}{\left({\mathit{\text{x}}}_1\right)}^T\text{PE}\left({\mathit{\text{x}}}_2\right)=\sum _{i=1}^N\text{cos}\left(\frac{\Delta x_i\pi }{d_i-1}\right),$$

where Δx_i is the difference in the i ^th components of x₁ and x₂. This has maximum value when x₁ = x₂ and decreases with the L₁ distance between the two coordinates. We initialize the convolutional layer to have zero weights and bias and the learnable parameter α = 1 (see Fig. 1) such that only the PEs are considered by Coordinate Translator at the beginning of training. As a result, among all ${\mathit{\text{c}}}_i\in {\mathbb{D}}^N$, M(x) will have the highest matching score with F(x), thus producing G_I as the initial output. Coordinate Translator also benefits from incorporating the position information as it allows the relative distance between c_i and x to contribute to the matching scores, similar as the positional embedding in the Transformer [36].

Fig. 1.

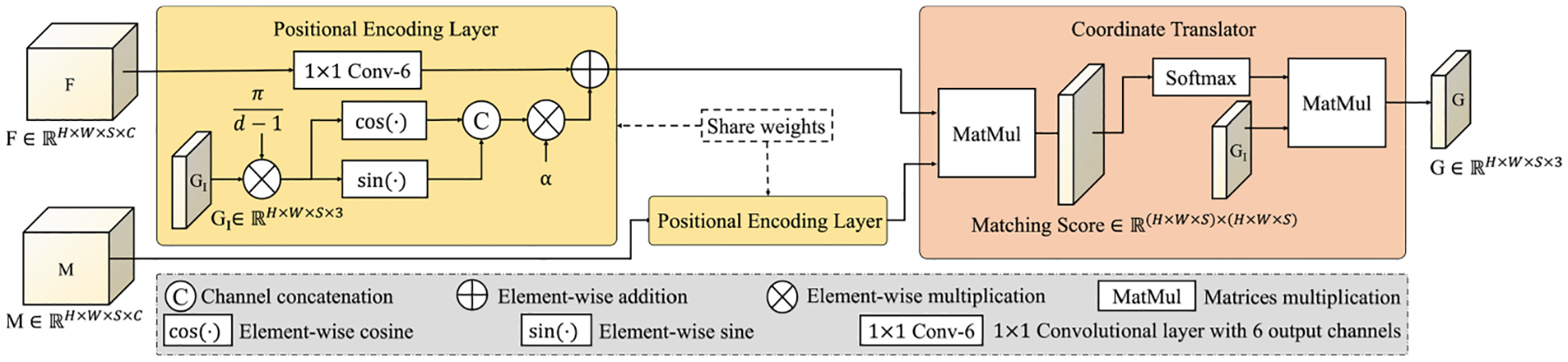
Structure of the proposed positional encoding layer and Coordinate Translator.

3.2. im2grid Network Architecture

The proposed im2grid network is shown in Fig. 2. Similar to previous methods, im2grid produces a sampling grid to warp I_m to I_w. Our CNN encoder uses multiple pooling layers to extract hierarchical features from the intensity images. In the context of intra-modal registration, it is used as a Siamese network that processes I_f and I_m separately. For clarity, Fig. 2 only shows a three level im2grid model with three level feature maps F₁/F₂/F₃ and M₁/M₂/M₃ for I_f and I_m, respectively. In our experiment, we used a five level structure. Our grid decoder uses the common coarse-to-fine strategy in registration. Firstly, coarse features F₃ and M₃ are matched and translated to a coarse sampling grid G₃ using a Coordinate Translator. Because of the pooling layers, this can be interpreted as matching downsampled versions of I_f and I_m, producing a coarse displacement field. G₃ is then used to warp M₂, resolving the coarse deformation between M₂ and F₂ so that the Coordinate Translator at the second level can capture more detailed displacements with a smaller search region. Similarly, M₁ is warped by the composed transformation of G₃ and G₂ and finally the moving image is warped by the composition of the transformations from all levels. A visualization of a five-level version of our multi-scale sampling grids is provided in Fig. 3. In contrast to previous methods that use CNNs to directly output displacements, our CNN encoder only needs to extract similar features for corresponding anatomies in I_f and I_m and the exact coordinate correspondences are obtained by Coordinate Translator’s. Because our CNN encoder processes I_f and I_m separately, it is guaranteed that our CNN encoder only performs feature extraction.

Fig. 2.

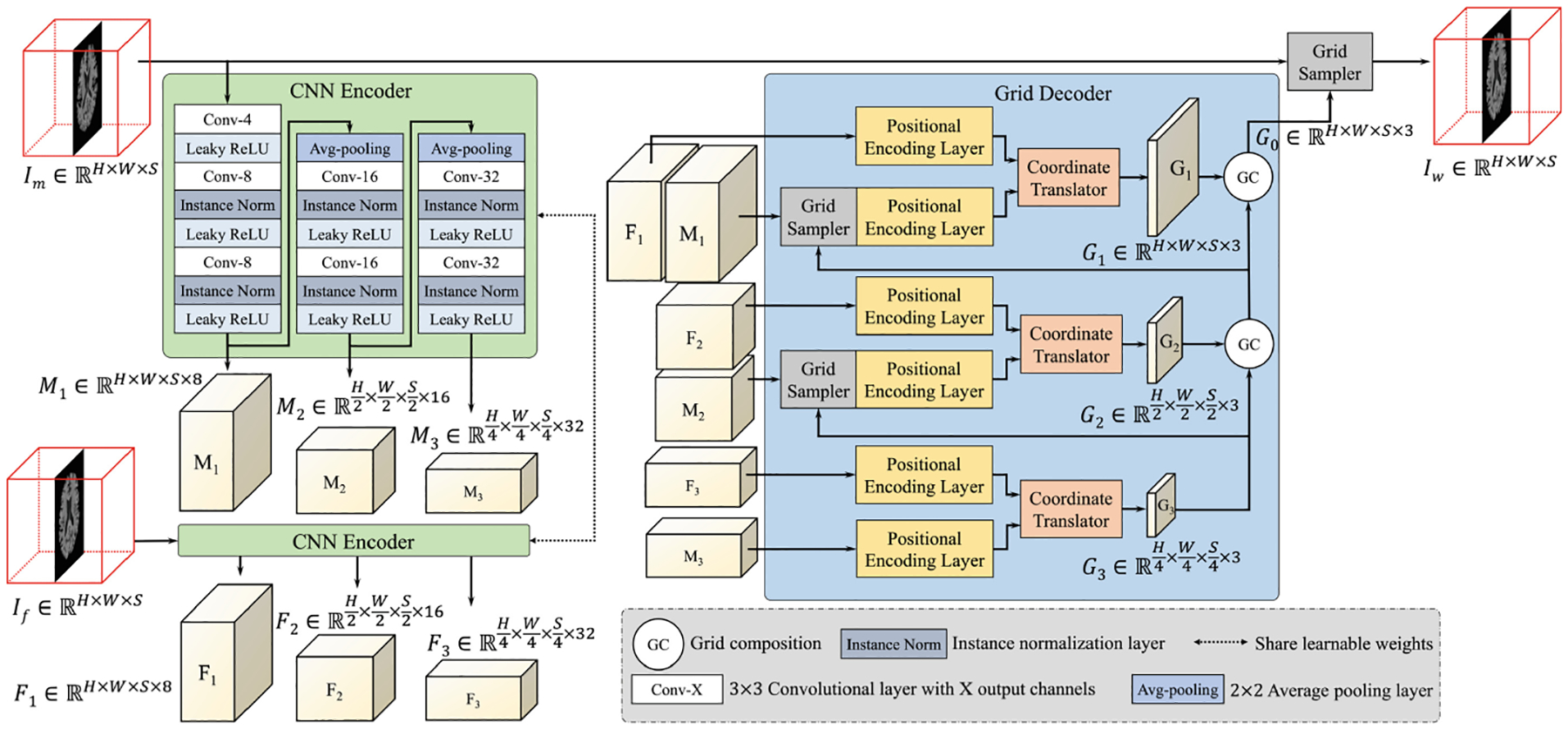
Example of the proposed im2grid network structure with a 3-level CNN encoder. The grid composition operation can be implemented using the grid sampler with two grids as input.

Fig. 3.

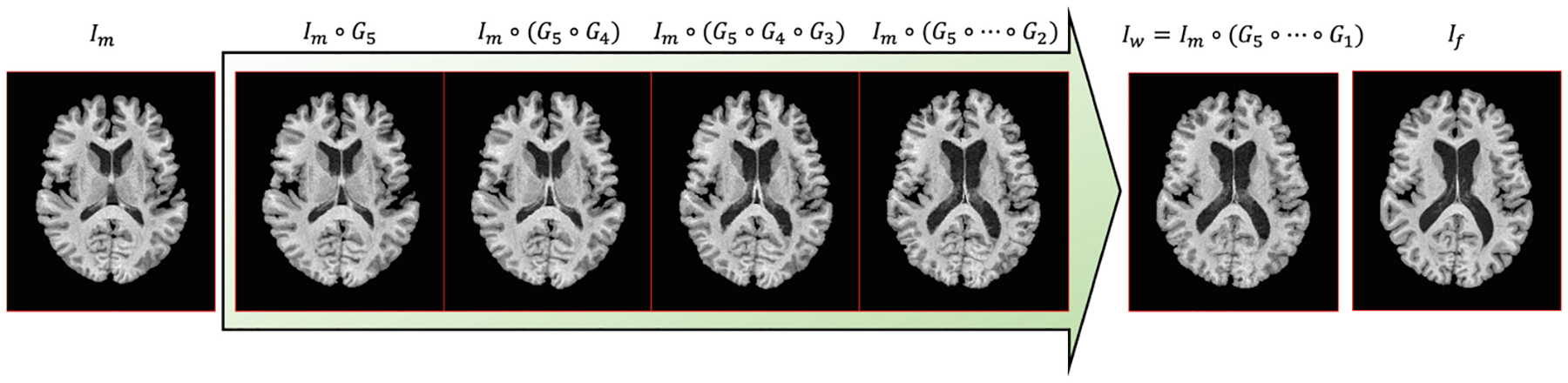
Visualization of the multi-scale sampling grids by sequentially applying finer grids to the moving image. Here we used a five-level CNN encoder and G₅,…,G₁ are coarse to fine sampling grids produced from the five-level feature maps.

The proposed network is trained using the mean squared difference between I_f and I_w(= I_m ○ϕ) and a smoothness loss that regularizes the spatial variations of the G’s at every level,

$$ℒ=\frac{1}{\left|{\mathbb{D}}^N\right|}\sum _{\mathit{\text{x}}\in {\mathbb{D}}^N}{\left(I_f(\mathit{\text{x}})-I_w(\mathit{\text{x}})\right)}^2+\lambda \sum _i\sum _{\mathit{\text{x}}\in {\mathbb{D}}^N}{\Vert \nabla \left(G_i(\mathit{\text{x}})-G_I(\mathit{\text{x}})\right)\Vert }^2,$$ (5)

where $\left|{\mathbb{D}}^N\right|$ is the cardinality of ${\mathbb{D}}^N$ and all G_i’s and G_I are normalized to [−1, 1].

4. Experiments

Datasets.

We used the publicly available OASIS3 [28] and IXI [1] datasets in our experiments. 200, 40, and 100 T1-weighted (T1w) MR images of the human brain from the OASIS3 dataset were used for training, validation, and testing, respectively. During training, two scans were randomly selected as I_f and I_m, while validation and testing used 20 and 50 pre-assigned image pairs, respectively. For the IXI dataset, we used 200 scans for training, 20 and 40 pairs for validation and testing, respectively. All scans underwent N4 inhomogeneity correction [35], and were rigidly registered to MNI space [18] with 1 mm³ (for IXI) or 0.8 mm³ (for OASIS3) isotropic resolution. A white matter peak normalization [30] was applied to standardize the MR intensity scale.

Evaluation Metrics.

First, we calculated the Dice similarity coefficient (DSC) between segmentation labels of I_f and the warped labels of I_m. An accurate transformation should align the structures of the fixed and moving images and produces a high DSC. We obtained a whole brain segmentation for the fixed and moving images using SLANT [24] and combined the SLANT labels (133 labels) to TOADS labels (9 labels) [5]. The warped labels were produced by applying each methods deformation field to the moving image labels. Second, we measured the regularity of the transformations by computing the determinant of the Jacobian matrix, which should be globally positive for a diffeomorphic transformation.

Implementation Details.

Our method was implemented using PyTorch and trained using the Adam optimizer with a learning rate of 3 ×10⁻⁴, a weight decay of 1 × 10⁻⁹, and a batch size of 1. Random flipping of the input volumes along the three axes were used as data augmentation. We used a five-level structure and tested different choices of c_i’s for each Coordinate Translator. We found that given the hierarchical structure, a small search region at each level is sufficient to capture displacements presented in our data. Therefore, we implemented two versions of our method: 1) im2grid which used a 3 × 3 search window in the axial plane for producing G₁ and a 3 × 3 ×3 search window at other levels; and 2) im2grid-Lite which is identical to im2grid except that the finest grid G₁ is not used.

Baseline Methods:

We compared our method with several state-of-the-art DL and non-DL registration methods: 1) SyN: Symmetric image normalization method [2], implemented in the Advanced Normalization Tools (ANTs) [3]; 2) voxelmorph: A deep learning based unsupervised method trained with the mean squared error loss [4]; 3) ViT-V-Net: A transformer [36] based network structure proposed in [8].

For SyN, a wide range of hyper-parameters were tested on the OASIS3 validation set and the best performing parameters were used for generating the final results. For voxelmorph and ViT-V-Net, we adopted the same training strategies as the proposed method, including the loss function and data augmentation. We optimize the parameters of each method for performance on the OASIS3 validation set and then used those parameters in testing on both datasets.

Results.

For both OASIS3 and IXI test datasets, we registered the moving to the fixed image and report the averaged DSC for all labels in Table 1. In both datasets, the proposed methods outperform the comparison methods for DSC. For each individual anatomic label, we also conducted a paired, two-sided Wilcoxon signed rank test (null hypothesis: the difference between paired values comes from a distribution with zero median, α = 10⁻³) between our methods and the comparison methods. Both proposed methods show significant DSC improvements for seven of nine labels and comparable DSC performance to the best comparison method for the remaining two labels (thalamus and putamen). Visual examples on OASIS3 data are shown in Fig. 4. It can be seen, especially from the highlighted regions, that the warped image produced by the proposed methods have a better agreement with the fixed image.

Table 1.

The Dice coefficient (DSC), the average number of voxels with negative determinant of Jacobian (# of |J_ϕ| < 0) and the percentage of voxels with negative determinant of Jacobian (%) for affine transformation, SyN, Voxelmorph, ViT-V-Net, and the proposed methods. The results of the initial alignment by the preprocessing steps are also included. Bold numbers indicate the best DSC for each dataset.

	OASIS3			IXI
	DSC	# of |Jϕ| < 0	%	DSC	# of |Jϕ| < 0	%
Initial	0.651 ± 0.094	–	0%	0.668 ± 0.107	–	0%
Affine	0.725 ± 0.068	–	0%	0.748 ± 0.052	–	0%
SyN [2]	0.866 ± 0.029	223	<0.002%	0.845 ± 0.035	613	0.008%
Voxelmorph [4]	0.883 ± 0.040	85892	<0.7%	0.842 ± 0.068	21574	<0.3%
ViT-V-Net [8]	0.872 ± 0.042	110128	<0.9%	0.845 ± 0.068	21298	<0.2%
im2grid-Lite	0.909 ± 0.021	38915	<0.4%	0.870 ± 0.043	14917	<0.2%
im2grid	0.908 ± 0.023	11880	<0.1%	0.865 ± 0.050	3235	<0.04%

Fig. 4.

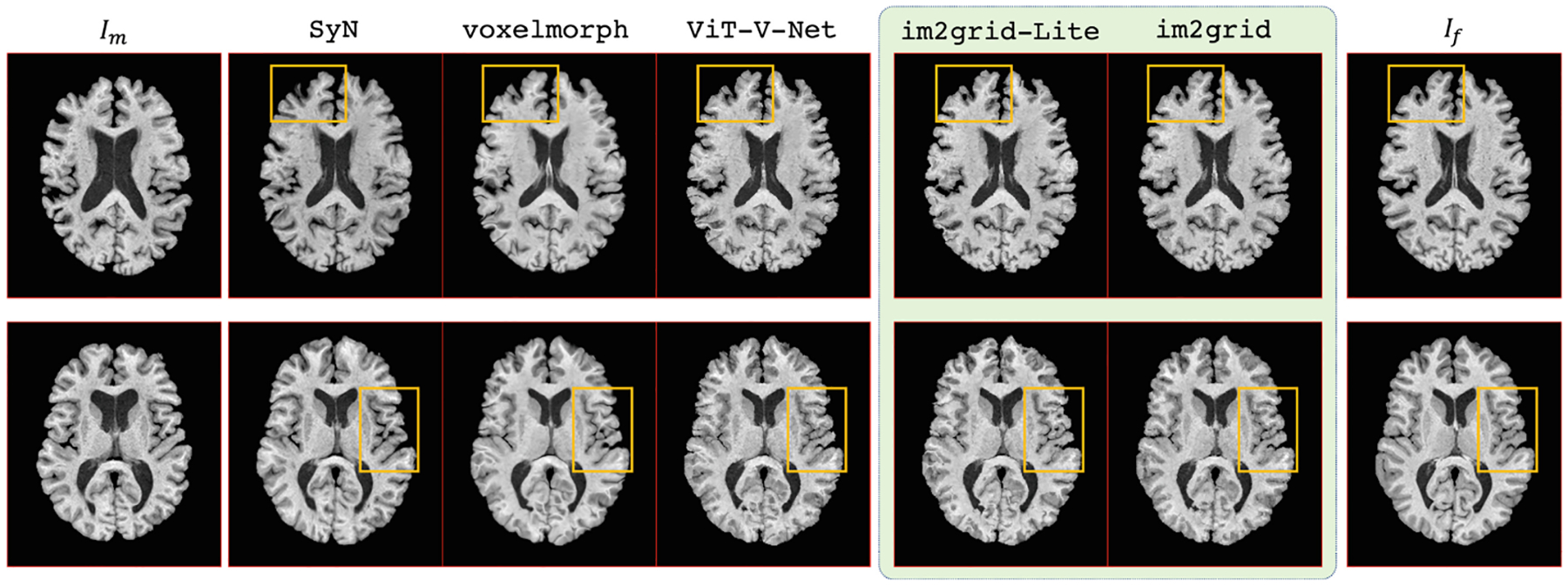
Examples of registering the moving image (the first column) to the fixed image (the last column) using SyN, voxelmorph, ViT-V-Net, and our proposed methods.

Evaluation on Learn2Reg Validation Dataset.

We also test the proposed method on the inter-subject brain MRI registration task from the Learn2Reg challenge [22] (L2R 2021 Task 3). All scans from the challenge have been pre-processed following [23], and for evaluation purpose segmentation maps of 35 labels were generated using FreeSurfer [17]. We choose the im2grid-Lite version for this task because the challenge evaluation is done on the ×2 downsampled images. During training, two scans were randomly selected from the training set and used as input to the proposed method. The performance is evaluated by comparing the warped segmentation of the moving image and the segmentation of the fixed image. The results are summarized in Table 2, where the DSC represents the average Dice coefficient of all segmented labels; DSC30 is the lowest 30% DSC among all cases, which measures the robustness of the methods; SDlogJ is the standard deviation of the log of the Jacobian determinant of the deformation field; and HD95 represents the 95% percentile of Hausdorff distance of segmentations. The results of several state-of-the-art methods from the challenge leaderboard are also included. The proposed method shows better accuracy as well as robustness among the comparison methods. Although adopting the instance-specific optimization as described in [4] can potential boost the performance on the validation set, our method only used the training set because we assume that such fine tuning process is not available during deployment.

Table 2.

Results of the proposed method and several state-of-the-art methods on the Learn2Reg 2021 Task 3 validation dataset.

	DSC	DSC30	SDlogJ	HD95
im2grid-Lite	0.8729 ± 0.0142	0.8714	0.1983	1.3786
TransMorph [7]	0.8691 ± 0.0145	0.8663	0.0945	1.3969
ConvexAdam [33]	0.8464 ± 0.0159	0.8460	0.0668	1.5003
Han et al. [21]	0.8410 ± 0.0139	0.8355	0.0796	1.6595
Lv et al. [29]	0.8271 ± 0.0131	0.8199	0.1206	1.7220

5. Discussion

In this paper, we proposed Coordinate Translator for producing coordinate correspondences from two feature maps. Additionally, we proposed the im2grid network that uses Coordinate Translator’s for deformable image registration. For unsupervised 3D magnetic resonance registration, im2grid outperforms the state-of-the-art methods in accuracy with a similar training and testing speed as other deep learning based registration methods. Although im2grid has no explicit guarantee of being diffeomorphic, the deformation fields it generated contains fewer voxels with negative determinant of Jacobian compared with other deep learning methods that output deformation fields directly from feature maps. We believe this comes from our design decision to restrict the candidate voxels to the immediate neighborhood of a voxel, which yields a locally smooth deformation field at each scale. We note that even a diffeomorphic algorithm with theoretical guarantees (e.g., SyN) can produce non-diffeomorphic transformations because of errors introduced during interpolation [38].

For registration, we demonstrated that using Coordinate Translator for matching features and establishing coordinate correspondences together with the convolutional networks for feature extraction can significantly boost the performance. Coordinate Translator is a general module that can be incorporated in many existing network structures and therefore is not limited to the registration task. We believe that many tasks that involve image input and coordinate output can benefit from the use of the Coordinate Translator module.