Abstract
目的
提出一个深度学习模型实现呼吸运动各个方向一体化的建模预测。
方法
将不同方向的呼吸运动信号分别输入由LSTM组成的顺序嵌入层去捕获历史运动状态的顺序依赖,得到顺序嵌入表示。顺序嵌入表示通过自注意力机制实现各个方向的关联嵌入,得到关联嵌入表示。将顺序嵌入表示和关联嵌入表示进行拼接输入由全连接神经网络组成的预测层生成非线性预测分量,并于平行于上述结构的自回归模块生成的线性预测分量相加生成最终的预测。模型的训练采用“预训练+微调”的模式。在我们的实验中,304例呼吸运动轨迹被使用进行模型预训练,7例测评样本被使用进行模型的测试。
结果
所提出预测模型相比于其他比较方法取得更准确的预测效果,在7例测评样本不同延迟时间上的3D方向绝对偏差减小平均达70%以上。
结论
提出模型在解决精准放疗过程中的系统延迟问题有很大的应用价值,能提供精准的位置预测。
Keywords: 放射治疗, 呼吸运动, 深度学习, 顺序嵌入, 关联嵌入
Abstract
Objective
To propose a deep learning model for modeling and prediction of the integration of respiratory motion in all directions.
Methods
The respiratory motion signals in different directions were input into the sequential embedding layer composed of LSTM to capture the sequential dependence of the historical motion state and obtain the sequential embedding representation, which enabled relational embedding in all directions through the self-attention mechanism to obtain the relational embedding representation. The sequential embedding representation and the relational embedding representation were concatenated and input into a prediction layer consisting of a fully connected neural network to generate nonlinear prediction components, which were added to the linear prediction components generated by the autoregressive module parallel to the above structure to generate the final prediction. The model was trained using a 'pre-training + fine-tuning' approach. In the validation experiments, 304 respiratory motion trajectories were used for model pre-training, and 7 evaluation samples were used for model testing.
Results
The proposed prediction model achieved more accurate prediction results than other methods. For the 7 evaluation samples with different delay time, the proposed prediction model achieved a reduction of absolute deviations in the 3D directions by over 70%.
Conclusion
The proposed model is capable of accurate prediction of respiratory motion and can thus help to reduce system delay in precise radiotherapy.
Keywords: radiotherapy, respiratory motion, deep learning, sequential embedding, relational embedding
在胸腹部肿瘤放射治疗过程中,呼吸运动的存在可能会导致射线束照射位置偏离原定计划靶区位置[1-3]。克服呼吸运动的影响,临床上最先进的方法为自适应运动补偿[4-8]。然而,在跟踪肿瘤治疗过程中,加速器放疗系统的复杂性使其不可避免的在检测到内部肿瘤运动到治疗射线束做出调整反应的过程中存在特定的延迟。为了保证治疗射束与运动靶区相对不变的空间位置,可以通过追踪体表替代运动信号和肿瘤内部植入物的运动信号进行运动建模,从而预测相应延迟时间后的肿瘤位置[9-11]。
目前学者已经提出了各种呼吸运动预测算法。其中基于回归分析的算法通过历史数据的线性组合进行计算[12],不能对复杂的非线性很好的建模预测。支持向量回归法对大规模训练样本难以实施[13]。Ramrath等[14]使用扩展的卡尔曼滤波模型预测,该算法相对复杂,且预测结果并未更优。记忆学习法[15]在小样本、长延时的条件下会出现“病态矩阵”,导致误差过大。近几年来随着深度学习的发展,专门用于序列分析建模的循环神经网络(RNN)以及其变体长短记忆神经网络(LSTM)受到很大的关注[16-20]。使用LSTM进行呼吸运动预测,并取得了不错的效果[21]。同时卷积神经网络(CNN)也被应用于呼吸运动预测,有学者提出CNN-driven的预测模型[22]。呼吸运动信号是一个包含前后(AP),上下(SI)和左右(LR)的多元时间序列,然而,现存的方法是各个方向独立进行建模,分别进行预测,并未考虑不同方向的关联,预测准确性有待提高。
本文提出基于顺序嵌入结合关联嵌入的深度学习模型,首次把各个方向运动作为一个整体,通过长短记忆神经网络(LSTM)和自注意力模块(Self-Attention)[23-25]充分挖掘运动序列的时间依赖和空间关联,各个方向共同进行建模预测,进一步提高了预测准确性。
1. 方法
图 1为对本文提出的模型框架示意图,包括顺序嵌入层、关联嵌入层、预测层和自回归模块。每层的具体结构在以下被阐明。将给定长度的包含上下、左右和前后的呼吸运动信号输入训练好的网络模型,便可得到位置预测。
1.

模型结构
Structure of the prediction model for respiratory motion. A: Overall structure of the network model. B: Long Short-Term Memory neural network. C: Self-attention structure.
1.1. 顺序嵌入层
在呼吸运动预测任务中,由于每个方向都存在特定时间动态模式,因此每个方向的历史运动状态对于未来的预测是极为重要的。在这里,我们使用一个顺序嵌入层去捕获历史运动状态的顺序依赖。具体的,我们使用循环神经网络的变体长短记忆神经网络(LSTM)[26],如(图 1B)所示,去捕获历史运动状态的顺序依赖。LSTM能够保持对过去更长期的记忆,同时克服长序列训练的梯度消失和梯度爆炸问题。我们把单个方向的历史运动状态序列分别输入LSTM,使用最后一个隐藏状态作为这个方向顺序嵌入表示,这个过程称为顺序嵌入。
LSTM的功能通过遗忘门,输入门和输出门来实现,各个控制门主要由一个sigmoid函数和点乘操作组成,决定信息传递与丢弃。其过程可以通过以下公式表示
遗忘门:选择忘掉过去某些信息
 |
1 |
输入门:记忆现在的某些信息
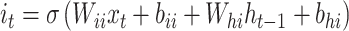 |
2 |
 |
3 |
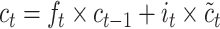 |
4 |
输出门:进行输出
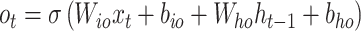 |
5 |
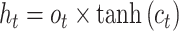 |
6 |
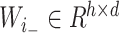 ,
, 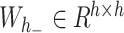 ,
,  代表需要在训练中更新的权重矩阵和偏差向量,其中d和h代表分别代表输入维度和隐藏状态输出维度,σ代表sigmoid激活函数。ft、it和ot分别代表遗忘门、输入门和输出门。ct和ht分别代表不同时间步胞体状态向量和隐藏状态向量。得益于门控设置和中间记忆状态,LSTM具有捕获时间序列长依赖的能力。
代表需要在训练中更新的权重矩阵和偏差向量,其中d和h代表分别代表输入维度和隐藏状态输出维度,σ代表sigmoid激活函数。ft、it和ot分别代表遗忘门、输入门和输出门。ct和ht分别代表不同时间步胞体状态向量和隐藏状态向量。得益于门控设置和中间记忆状态,LSTM具有捕获时间序列长依赖的能力。
1.2. 关联嵌入层
我们通过自注意力机制[23],如(图 1C)所示,实现关联嵌入,其基本思想是每个方向的顺序嵌入表示会和自身以及其他方向的顺序嵌入表示生成注意力值,最后根据这些注意力值进行加权求和,得到的每个方向表示聚合了不同方向的信息,称为关联嵌入表示。自注意力的实现由以下公式表示。
 |
7 |
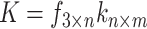 |
8 |
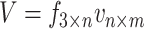 |
9 |
 |
10 |
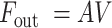 |
11 |
f3×n表示3个方向的顺序嵌入表示组成的矩阵,n表示嵌入表示的维度。对f3×n进行线性变换得到Q、K、V三个矩阵。A是注意力矩阵,(a)i, j表示第i个方向和第j个方向的关联权值。
1.3. 预测层与自回归模块
预测层由非线性预测分量和线性预测分量两部分组成。将顺序嵌入层得到的顺序嵌入表示和关联嵌入层得到的关联嵌入表示进行串联拼接,通过全连接层生成非线性预测分量。自回归模块平行于整个结构,由全连接层构成,历史运动信号直接输入该模块得到线性预测分量,使输出对输入值的尺度变化更敏感,增加整体预测的鲁棒性。线性预测分量和非线性预测分量直接相加得到最终的预测。
自回归模块是通过对历史信号的各个时间状态进行加权求和,是一个线性输出的过程,因此会随输入尺度的变化而明显变化,可由以下公式表示:
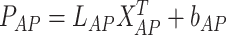 |
12 |
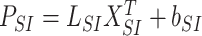 |
13 |
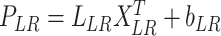 |
14 |
PAP, PSI, PLR分别代表各个方向的线性预测分量。L AP,LSI,LLR分别代表各个方向历史信号状态。XAPT,XSIT,XLRT代表施加各个方向权重向量。bAP,bSI,bLR代表各个方向的偏置。
1.4. 实验设计
1.4.1. 实验数据和平台
数据采用德国吕贝克大学机器人与认知系统研究所[4](Institute for Robotics and Cognitive System, University of Lubeck, Germany),提供的在线数据(signals.rob.uni-luebeck.de)。数据包括在CyberKnife治疗期间被记录的304例呼吸运动轨迹,每例呼吸运动信号平均有60 min的数据采集量。同时还包括对7位志愿者分别进行5~6 min的体内运动信号采集,采样频率为20 Hz。本研究实验利用python进行编程实现,使用pytorch[27]进行模型的构建。
1.4.2. 模型训练和测试
数据预处理阶段我们使用已经获得的在线数据,将各个方向的运动信号分别减去对应的基线值,即运动范围的中值。我们使用“模型预训练+微调”的训练模式,使得当针对具体病人时能够适应其特有的运动模式和空间关联。我们使用CyberKnife治疗期间被记录的304例呼吸运动轨迹作为模型预训练的数据集,使用滑动窗口获得训练数据对,包括给定长度的历史运动信号和对应延迟间隔的值,进行模型的预训练。我们使用在线数据提供的7位志愿者呼吸运动信号作为测评样例数据。如图 2,每一位志愿者呼吸运动信号的前4/5被用来进行模型微调,其余的部分进行测试。历史运动信号长度是一个超参数,其选择要在一半的周期长度到1个周期长度之间,呼吸周期一般在3 s左右。在我们的实验中选择历史运动信号长度选为32个采样点,即1.6 s,每个志愿者以20 HZ频率进行5~6 min的信号采样,对于每一个志愿者可获得大约4800对训练数据进行预训练模型微调,1200对数据进行测试。使用训练数据进行模型的训练,采用小批量随机梯度下降,使用adam优化器,学习率设置为0.0001,使用MSE损失函数。
2.

滑动窗口获得数据对及数据划分
Data partitioning of the respiratory signals. T represents the signal history length, YT the historical respiratory motion signal, l the length of the delay interval, and yT+l the value of the motion signal at the delay interval.
1.4.3. 评价指标
为了评估模型的性能,本研究采用了不同的呼吸运动预测方法进行比较,分别为线性回归法、支持向量回归法和长短记忆神经网络。延迟时间设置为150、300、450 ms的几种情况。
使用平均绝对误差和相对平方误差作为本实验的评价指标。
平均绝对误差(MAE)
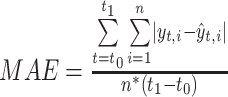 |
15 |
相对平方误差(RSE)
 |
16 |
在公式(15)和(16)中t0和t1分别代表当前测评样本测试数据的起始和结束。n表示数据的维度,在这里指的是呼吸运行信号的3个方向,n为3。
2. 结果
2.1. 呼吸运动预测曲线
我们分别选择两个代表性样例进行SI、AP和LR方向预测曲线展示,图 3中样例1是呼吸运动不规律的代表,受抖动影响较为明显。从图 3可以看出我们的模型在延迟时间300 ms时,依旧能够很好地拟合真实呼吸运动轨迹。图 4中样例3是呼吸运动较为平稳的代表。图 4可以看出我们的模型在延迟时间300 ms时,基本完美的拟合了真实呼吸运动曲线。
3.

样例1在延迟时间为300 ms时,SI、AP和LR方向的预测曲线
Prediction curves of SI (A), AP (B) and LR (C) directions of sample 1 with a delay time of 300 ms.
4.

样例3在延迟时间为300 ms时,SI、AP和LR方向的预测曲线
Prediction curves of SI (A), AP (B) and LR (C) directions of sample 3 with a delay time of 300 ms.
2.2. 延迟偏差定量分析
我们分别计算7例样本在施加预测和无预测的情况下不同延迟时间各个方向的平均绝对偏差,同时计算出其在3D方向的偏差,以及3D偏差减小百分比。如表 1所示,我们的模型在各个方向中均能减小延迟偏差。在所有7例样本不同延迟时间中,最大3D方向偏差减小百分比为80.85%,最小为50.79%,平均为70%。
1.
在无预测和预测情况下各个方向的平均绝对偏差
Mean absolute deviation in all directions (mm)
| Sample | No-prediction | Prediction | 3D deviation reduction (3DNo-3DPre)/3DNo |
||||||||
| Delay | SI | LR | AP | 3D | SI | LR | AP | 3D | |||
| Sample 1 | 150 ms | 0.0501 | 0.5138 | 0.4363 | 0.6759 | 0.0419 | 0.2599 | 0.2033 | 0.3326 | 50.79% | |
| 300 ms | 0.0780 | 0.9940 | 0.8468 | 1.3081 | 0.0524 | 0.4009 | 0.3258 | 0.5192 | 60.30% | ||
| 450 ms | 0.1026 | 1.4422 | 1.2275 | 1.8966 | 0.0661 | 0.6352 | 0.4950 | 0.8080 | 57.40% | ||
| Sample 2 | 150 ms | 0.0436 | 0.4601 | 0.3986 | 0.6103 | 0.0333 | 0.1496 | 0.1140 | 0.1910 | 68.70% | |
| 300 ms | 0.0690 | 0.8821 | 0.7748 | 1.1761 | 0.0429 | 0.2744 | 0.2127 | 0.3498 | 70.25% | ||
| 450 ms | 0.0890 | 1.2865 | 1.1310 | 1.7153 | 0.0456 | 0.4290 | 0.3131 | 0.5330 | 68.93% | ||
| Sample 3 | 150 ms | 0.1260 | 0.2560 | 0.6857 | 0.7427 | 0.0384 | 0.0632 | 0.1223 | 0.1429 | 80.75% | |
| 300 ms | 0.2446 | 0.5055 | 1.3592 | 1.4707 | 0.0543 | 0.0958 | 0.2592 | 0.2817 | 80.85% | ||
| 450 ms | 0.3619 | 0.7485 | 2.0178 | 2.1824 | 0.0890 | 0.1953 | 0.4356 | 0.4856 | 77.75% | ||
| Sample 4 | 150 ms | 0.1496 | 0.7768 | 0.7204 | 1.0699 | 0.0926 | 0.2071 | 0.2558 | 0.3419 | 68.04% | |
| 300 ms | 0.2377 | 1.5273 | 1.3953 | 2.0823 | 0.1106 | 0.3528 | 0.3877 | 0.5358 | 74.27% | ||
| 450 ms | 0.3413 | 2.2626 | 2.0587 | 3.0780 | 0.1270 | 0.5632 | 0.6172 | 0.8452 | 72.54% | ||
| Sample 5 | 150 ms | 0.1079 | 0.3664 | 0.4080 | 0.5589 | 0.0486 | 0.0916 | 0.1450 | 0.1783 | 68.10% | |
| 300 ms | 0.1881 | 0.7237 | 0.7904 | 1.0881 | 0.0551 | 0.1674 | 0.2332 | 0.2923 | 73.13% | ||
| 450 ms | 0.2803 | 1.0807 | 1.1769 | 1.6222 | 0.0796 | 0.2219 | 0.3359 | 0.4104 | 74.70% | ||
| Sample 6 | 150 ms | 0.0806 | 0.2482 | 0.6385 | 0.6897 | 0.0388 | 0.0830 | 0.1561 | 0.1810 | 73.76% | |
| 300 ms | 0.1281 | 0.4809 | 1.2376 | 1.3340 | 0.0891 | 0.1971 | 0.2918 | 0.3633 | 72.77% | ||
| 450 ms | 0.1883 | 0.6999 | 1.7999 | 1.9404 | 0.0843 | 0.3231 | 0.5217 | 0.6194 | 68.08% | ||
| Sample 7 | 150 ms | 0.1247 | 0.3508 | 0.5295 | 0.6473 | 0.0469 | 0.1009 | 0.1663 | 0.2001 | 69.09% | |
| 300 ms | 0.2399 | 0.6901 | 1.0301 | 1.2630 | 0.0754 | 0.1898 | 0.2879 | 0.3530 | 72.05% | ||
| 450 ms | 0.3531 | 1.0170 | 1.5150 | 1.8586 | 0.1119 | 0.2921 | 0.4305 | 0.5321 | 71.37% | ||
2.3. 对应不同延迟时间的预测效果比较
使用在线数据集提供的7例数据的内部运动信号,分别进行线性回归法[12]、支持向量回归法(SVR)[13]、CNN-driven[22]、Dsanet[28]、LSTM[21]和我们方法的预测,延迟时间分别设为150、300、450 ms。计算上述预测算法预测结果的MAE和RSE。由表 2和表 3可以看出,所有的方法都能实现比无预测时更小偏差。
2.
不同预测方法在不同延迟时间测试的MAE值
Mean absolute deviations (MAEs) tested by different prediction methods at different delay times
| MAE | No-prediction | Linear regression | SVR | CNN-driven | Dsanet | LSTM | OUR | |
| Sample 1 | 150 ms | 0.3334 | 0.2131 | 0.1810 | 0.1762 | 0.2057 | 0.1750 | 0.1684 |
| 300 ms | 0.6396 | 0.3396 | 0.2677 | 0.3014 | 0.3343 | 0.3001 | 0.2597 | |
| 450 ms | 0.9241 | 0.4712 | 0.3492 | 0.4419 | 0.4607 | 0.4350 | 0.3988 | |
| Sample 2 | 150 ms | 0.3008 | 0.1682 | 0.1215 | 0.1219 | 0.1523 | 0.1157 | 0.0990 |
| 300 ms | 0.5753 | 0.3278 | 0.2061 | 0.2270 | 0.2903 | 0.1915 | 0.1766 | |
| 450 ms | 0.8355 | 0.5142 | 0.2932 | 0.3067 | 0.4520 | 0.3097 | 0.2625 | |
| Sample 3 | 150 ms | 0.3559 | 0.1523 | 0.1228 | 0.1010 | 0.1168 | 0.0839 | 0.0746 |
| 300 ms | 0.7031 | 0.2708 | 0.1819 | 0.1829 | 0.2582 | 0.1557 | 0.1365 | |
| 450 ms | 1.0427 | 0.4146 | 0.2558 | 0.2528 | 0.4058 | 0.2462 | 0.2399 | |
| Sample 4 | 150 ms | 0.5489 | 0.2626 | 0.3295 | 0.1989 | 0.2344 | 0.1917 | 0.1852 |
| 300 ms | 1.0534 | 0.4994 | 0.4389 | 0.2947 | 0.4578 | 0.3258 | 0.2837 | |
| 450 ms | 1.5542 | 0.8086 | 0.5614 | 0.4424 | 0.7012 | 0.4644 | 0.4358 | |
| Sample 5 | 150 ms | 0.2941 | 0.1480 | 0.1046 | 0.1346 | 0.1238 | 0.1231 | 0.0951 |
| 300 ms | 0.5674 | 0.2496 | 0.1560 | 0.1582 | 0.2249 | 0.1643 | 0.1519 | |
| 450 ms | 0.8459 | 0.3793 | 0.2236 | 0.2487 | 0.3499 | 0.2391 | 0.2125 | |
| Sample 6 | 150 ms | 0.3224 | 0.1991 | 0.2172 | 0.1203 | 0.1588 | 0.1202 | 0.0926 |
| 300 ms | 0.6155 | 0.4548 | 0.2887 | 0.2391 | 0.2921 | 0.2128 | 0.1927 | |
| 450 ms | 0.8960 | 0.6839 | 0.3668 | 0.3448 | 0.4667 | 0.3408 | 0.3097 | |
| Sample 7 | 150 ms | 0.3350 | 0.1856 | 0.1160 | 0.1142 | 0.1660 | 0.1117 | 0.1047 |
| 300 ms | 0.6534 | 0.3499 | 0.1884 | 0.1985 | 0.3105 | 0.1951 | 0.1844 | |
| 450 ms | 0.9617 | 0.5050 | 0.2671 | 0.3009 | 0.4866 | 0.2812 | 0.2484 |
3.
不同预测方法在不同延迟时间测试的RSE值
RSEs tested by different prediction methods at different delay time
| RSE | No-prediction | Linear regression | SVR | CNN-driven | CNN-driven | LSTM | OUR | |
| Sample 1 | 150 ms | 0.1099 | 0.0541 | 0.0411 | 0.0384 | 0.0511 | 0.0373 | 0.0371 |
| 300 ms | 0.3683 | 0.1271 | 0.0878 | 0.1036 | 0.1219 | 0.1055 | 0.0868 | |
| 450 ms | 0.7489 | 0.2327 | 0.1498 | 0.2096 | 0.2167 | 0.2178 | 0.2002 | |
| Sample 2 | 150 ms | 0.0776 | 0.0259 | 0.0140 | 0.0128 | 0.0217 | 0.0116 | 0.0096 |
| 300 ms | 0.2835 | 0.0980 | 0.0468 | 0.0462 | 0.0796 | 0.0353 | 0.0347 | |
| 450 ms | 0.5959 | 0.2327 | 0.1004 | 0.0936 | 0.1917 | 0.0998 | 0.0801 | |
| Sample 3 | 150 ms | 0.0351 | 0.0080 | 0.0064 | 0.0028 | 0.0045 | 0.0021 | 0.0017 |
| 300 ms | 0.1355 | 0.0231 | 0.0152 | 0.0108 | 0.0198 | 0.0093 | 0.0075 | |
| 450 ms | 0.2948 | 0.0496 | 0.0304 | 0.0220 | 0.0446 | 0.0235 | 0.0218 | |
| Sample 4 | 150 ms | 0.0302 | 0.0060 | 0.0169 | 0.0035 | 0.0047 | 0.0035 | 0.0034 |
| 300 ms | 0.1140 | 0.0207 | 0.0259 | 0.0086 | 0.0178 | 0.0124 | 0.0082 | |
| 450 ms | 0.2482 | 0.0520 | 0.0405 | 0.0188 | 0.0399 | 0.0279 | 0.0244 | |
| Sample 5 | 150 ms | 0.0116 | 0.0031 | 0.0017 | 0.0024 | 0.0021 | 0.0019 | 0.0014 |
| 300 ms | 0.0444 | 0.0087 | 0.0042 | 0.0041 | 0.0072 | 0.0045 | 0.0039 | |
| 450 ms | 0.0980 | 0.0194 | 0.0091 | 0.0093 | 0.0169 | 0.0102 | 0.0084 | |
| Sample 6 | 150 ms | 0.0772 | 0.0243 | 0.0383 | 0.0089 | 0.0169 | 0.0087 | 0.0062 |
| 300 ms | 0.2912 | 0.1100 | 0.0629 | 0.0397 | 0.0638 | 0.0327 | 0.0279 | |
| 450 ms | 0.6154 | 0.2344 | 0.1040 | 0.0940 | 0.1453 | 0.0814 | 0.0801 | |
| Sample 7 | 150 ms | 0.0778 | 0.0245 | 0.0105 | 0.0105 | 0.0195 | 0.0105 | 0.0086 |
| 300 ms | 0.2880 | 0.0832 | 0.0316 | 0.0333 | 0.0624 | 0.0358 | 0.0308 | |
| 450 ms | 0.6052 | 0.1665 | 0.0694 | 0.0786 | 0.1558 | 0.0806 | 0.0598 |
2.4. 微调数据量对预测的影响
在比较实验中我们的微调数据和测试数据之比设置为8∶2。为了进一步表明微调数据量对预测的影响,我们分别设置微调数据和测试数据比为7∶3和6∶4,进行训练预测。计算其在响应时间为300 ms下预测结果的MAE和RSE(表 4、5)。
4.
不同比例在响应时间为300 ms时测试的MAE值
MAEs tested at different scales with a response time of 300 ms
| MAE | Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | Sample 6 | Sample 7 |
| 06:04 | 0.2775 | 0.2829 | 0.1681 | 0.3296 | 0.2128 | 0.2402 | 0.1933 |
| 07:03 | 0.2743 | 0.2045 | 0.16 | 0.294 | 0.2017 | 0.2054 | 0.1847 |
| 08:02 | 0.2597 | 0.1766 | 0.1365 | 0.2837 | 0.1519 | 0.1927 | 0.1844 |
5.
不同比例在响应时间为300 ms时测试的RSE值
RSEs tested at different scales with a response time of 300 ms
| RSE | Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | Sample 6 | Sample 7 |
| 06:04 | 0.0884 | 0.0610 | 0.0085 | 0.0133 | 0.0086 | 0.0457 | 0.0375 |
| 07:03 | 0.0828 | 0.0389 | 0.0097 | 0.0109 | 0.0083 | 0.0387 | 0.0300 |
| 08:02 | 0.0868 | 0.0347 | 0.0075 | 0.0082 | 0.0039 | 0.0279 | 0.0308 |
3. 讨论
传统的方法以及近些年提出的深度学习相关的呼吸运动预测方法,都独立地预测呼吸运动的各个方向,需要针对不同方向依次进行运动曲线拟合或者模型的训练,这样不仅需要额外的任务负担,同时忽略了不同方向的空间相关,预测准确性有待提高。在我们的研究中,把单个病人不同方向的运动信号看作一个整体,通过LSTM实现顺序嵌入,通过自注意力实现关联嵌入,充分捕获呼吸运动信号的时间依赖和空间相关性,实现各个方向一体化建模预测,减小了延迟偏差。
Ernst等[12]提出使用基于小波的多尺度自回归模型进行呼吸运动预测,并于其他基于自回归基础的模型进行比较。在他们的实验中分别进行模拟数据和真实数据测试,模式数据是多个正弦模型的拟合其非常平滑和规则,真实数据受抖动及测量噪声的影响其信号不规则和不平滑。他们的实验结果表明,在模拟数据中基于自回归的方法能取得理想的预测效果,但是用于真实数据时要先进行数据的平滑处理,得到的效果也不理想,并且提出的基于小波的多尺度自回归模型相比于其他的自回归模型并没有很大的提升。我们的方法直接应用于真实数据,如图 3所示,样例1的呼吸运动信号极为不规律,抖动极为明显。我们的模型依旧能够很好的拟合各个方向的运动轨迹,同时从表 1看出样例1的3D偏差减小百分比在响应时间为150、300、450 ms时分别为50.79%、60.30%、57.40%,有较好减少位置偏差的效果。从表 2和表 3可以看出在不同样本不同响应时间中我们的模型的评价指标也是远好于AR。Ernst等[13]又再次提出使用支持向量回归进行呼吸运动预测,并证明其效果优于先前的基于自回归的方法。然而Ernst F等指出支持向量回归的参数选择是困难的,其包含核函数和对应参数的选择、惩罚因子的选择、错误不敏感水平选择和信号历史长度选择等,并且参数的选择对实验结果有较大的影响。我们的模型需要考虑的参数仅仅是LSTM隐藏层的维度,并且相对固定,在我们的实验中设置为36。在我们的实验中,支持向量回归使用高斯核,其他参数选择默认设置。通过表 2和表 3看出我的模型预测效果同样也优于支持向量回归。近年来随着深度学习的发展,大量深度学习相关的肿瘤运动预测模式被提出。Zhou D等提出CNN-driven[22]预测模型,利用CNN强大的特征挖掘能力,对运动信号的时间模式特征进行充分挖掘,进行肿瘤运动预测。由于CNN存在平移不变性以及没有记忆功能,对于预测过程中存在的呼吸运动基线变化无法做出正确的响应,因此在实际肿瘤预测中是不可靠的。Lin等[21]首次提出使用LSTM进行呼吸运动预测,各个方向独立预测,并取得较好的预测效果。我们的模型是在LSTM基础上加入自注意力模块引入空间关联,加入自回归模块克服LSTM对输入尺度变化不敏感的问题,实现各个方向一体化进行预测。通过表 2和表 3可以看出我们的模型预测效果优于LSTM,证明引入空间关联和线性成分对于提升预测效果有一定的作用,同时通过表 1可以看出各个方向的误差均有减小,3D偏差减少百分比达到70%以上,我们的模型对于多方向的呼吸运动预测具有良好性能。
在我们的模型中LSTM隐藏层的维度是最主要的超参数,直接决定模型的复杂度。隐藏层的维度设置过大,模型复杂度增大,计算负担重,收敛变慢。其设置小,模型复杂度变小,特征挖掘和学习能力下降。在我们的实验中隐藏层的维度设置为36,在保持学习能力下,又能保证快速的收敛,是一个轻量级网络,有仅6万多参数量。在使用GUP的情况下,使用当前治疗病人3 min左右的采样数据量,在预训练模型上进行微调,1-2 min内便可收敛,同时网络生成预测过程在20 ms之内,因此能够很好的适用于实际放疗过程。我们的模型训练使用“预训练+微调”的模式,这种模式在最近的深度学习相关的肿瘤运动预测模型[22]被使用。不同的病人呼吸运动信号的运动模式和空间关联都有一定不同,对预训练模式的微调能够使得模型适应当前病人具体的呼吸运动特性。由表 4和表 5可以看出,提供更多具体病人的运动数据进行微调能够提高预测准确性。同时在长时间治疗过程中,病人可能出现运动模式的渐变过程,可以进行实时在线微调,使其能够适应治疗过程中呼吸运动模式的变化。
综上,本研究提出的深度学习模型相比于线性回归,支持向量回归,CNN-driven和LSTM模型能够实现更准确的预测效果,并且各个方向一体化建模预测,在解决精确放疗中系统延迟问题有很大的应用价值。在实际放疗追踪中,我们的深度学习预测模型可与内-外关联模型[29-31]联合使用,通过预测-关联实现外部替代信号到内部肿瘤位置的预测,可以在实际放疗追踪中得到很好的应用。
Biography
张昆鹏,在读硕士研究生,E-mail: 2733422685@qq.com
Funding Statement
国家自然科学基金(61871208)
Supported by National Natural Science Foundation of China (61871208)
Contributor Information
张 昆鹏 (Kunpeng ZHANG), Email: 2733422685@qq.com.
张 华 (Hua ZHANG), Email: xinsier@smu.edu.cn.
References
- 1.Piruzan E, Vosoughi N, Mahdavi SR, et al. Target motion management in breast cancer radiation therapy. Radiol Oncol. 2021;55(4):393–408. doi: 10.2478/raon-2021-0040. [Piruzan E, Vosoughi N, Mahdavi SR, et al. Target motion management in breast cancer radiation therapy[J]. Radiol Oncol, 2021, 55(4): 393-408.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brandner ED, Chetty IJ, Giaddui TG, et al. Motion management strategies and technical issues associated with stereotactic body radiotherapy of thoracic and upper abdominal tumors: a review from NRG oncology. Med Phys. 2017;44(6):2595–612. doi: 10.1002/mp.12227. [Brandner ED, Chetty IJ, Giaddui TG, et al. Motion management strategies and technical issues associated with stereotactic body radiotherapy of thoracic and upper abdominal tumors: a review from NRG oncology[J]. Med Phys, 2017, 44(6): 2595-612.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Boda-Heggemann J, Knopf AC, Simeonova-Chergou A, et al. Deep inspiration breath hold-based radiation therapy: a clinical review. Int J Radiat Oncol Biol Phys. 2016;94(3):478–92. doi: 10.1016/j.ijrobp.2015.11.049. [Boda-Heggemann J, Knopf AC, Simeonova-Chergou A, et al. Deep inspiration breath hold-based radiation therapy: a clinical review[J]. Int J Radiat Oncol Biol Phys, 2016, 94(3): 478-92.] [DOI] [PubMed] [Google Scholar]
- 4.Ernst F. Compensating for Quasi-periodic Motion in Robotic Radiosurgery. New York, NY: Springer New York; 2012. [Ernst F. Compensating for Quasi-periodic Motion in Robotic Radiosurgery[M]. New York, NY: Springer New York, 2012.] [Google Scholar]
- 5.Ipsen S, Bruder R, O'Brien R, et al. Online 4D ultrasound guidance for real-time motion compensation by MLC tracking. Med Phys. 2016;43(10):5695. doi: 10.1118/1.4962932. [Ipsen S, Bruder R, O'Brien R, et al. Online 4D ultrasound guidance for real-time motion compensation by MLC tracking[J]. Med Phys, 2016, 43(10): 5695.] [DOI] [PubMed] [Google Scholar]
- 6.Archibald-Heeren BR, Byrne MV, Hu YF, et al. Robust optimization of VMAT for lung cancer: Dosimetric implications of motion compensation techniques. J Appl Clin Med Phys. 2017;18(5):104–16. doi: 10.1002/acm2.12142. [Archibald-Heeren BR, Byrne MV, Hu YF, et al. Robust optimization of VMAT for lung cancer: Dosimetric implications of motion compensation techniques[J]. J Appl Clin Med Phys, 2017, 18(5): 104-16.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sakata Y, Hirai R, Kobuna K, et al. A machine learning-based realtime tumor tracking system for fluoroscopic gating of lung radiotherapy. Phys Med Biol. 2020;65(8):085014. doi: 10.1088/1361-6560/ab79c5. [Sakata Y, Hirai R, Kobuna K, et al. A machine learning-based realtime tumor tracking system for fluoroscopic gating of lung radiotherapy[J]. Phys Med Biol, 2020, 65(8): 085014.] [DOI] [PubMed] [Google Scholar]
- 8.Wu VWC, Ng APL, Cheung EKW. Intrafractional motion management in external beam radiotherapy. J Xray Sci Technol. 2019;27(6):1071–86. doi: 10.3233/XST-180472. [Wu VWC, Ng APL, Cheung EKW. Intrafractional motion management in external beam radiotherapy[J]. J Xray Sci Technol, 2019, 27(6): 1071-86.] [DOI] [PubMed] [Google Scholar]
- 9.Cai J. 4D modeling and estimation of respiratory motion for radiation therapy. Med Phys. 2015;42(4):2098. doi: 10.1118/1.4915250. [Cai J. 4D modeling and estimation of respiratory motion for radiation therapy[J]. Med Phys, 2015, 42(4): 2098.] [DOI] [Google Scholar]
- 10.Lin H, Zou W, Li TR, et al. A super-learner model for tumor motion prediction and management in radiation therapy: development and feasibility evaluation. Sci Rep. 2019;9(1):14868. doi: 10.1038/s41598-019-51338-y. [Lin H, Zou W, Li TR, et al. A super-learner model for tumor motion prediction and management in radiation therapy: development and feasibility evaluation[J]. Sci Rep, 2019, 9(1): 14868.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jöhl A, Ehrbar S, Guckenberger M, et al. Performance comparison of prediction filters for respiratory motion tracking in radiotherapy. Med Phys. 2020;47(2):643–50. doi: 10.1002/mp.13929. [Jöhl A, Ehrbar S, Guckenberger M, et al. Performance comparison of prediction filters for respiratory motion tracking in radiotherapy[J]. Med Phys, 2020, 47(2): 643-50.] [DOI] [PubMed] [Google Scholar]
- 12.Ernst F, Schlaefer A, Schweikard A. Prediction of respiratory motion with wavelet-based multiscale autoregression. Med Image Comput ComputAssist Interv. 2007;10(Pt 2):668–75. doi: 10.1007/978-3-540-75759-7_81. [Ernst F, Schlaefer A, Schweikard A. Prediction of respiratory motion with wavelet-based multiscale autoregression[J]. Med Image Comput ComputAssist Interv, 2007, 10(Pt 2): 668-75.] [DOI] [PubMed] [Google Scholar]
- 13.Ernst F, Schweikard A. Forecasting respiratory motion with accurate online support vector regression (SVRpred) Int J Comput Assist Radiol Surg. 2009;4(5):439–47. doi: 10.1007/s11548-009-0355-5. [Ernst F, Schweikard A. Forecasting respiratory motion with accurate online support vector regression (SVRpred)[J]. Int J Comput Assist Radiol Surg, 2009, 4(5): 439-47.] [DOI] [PubMed] [Google Scholar]
- 14.Ramrath L, Schlaefer A, Ernst F, et al. Prediction of respiratory motion with a multi-frequency based extended kalman filter. Int J ComputAssist Radiol Surg. 2007;2:S56–8. [Ramrath L, Schlaefer A, Ernst F, et al. Prediction of respiratory motion with a multi-frequency based extended kalman filter[J]. Int J ComputAssist Radiol Surg, 2007, 2: S56-8.] [Google Scholar]
- 15.Li RJ, Lewis JH, Berbeco RI, et al. Real-time tumor motion estimation using respiratory surrogate via memory-based learning. Phys Med Biol. 2012;57(15):4771–86. doi: 10.1088/0031-9155/57/15/4771. [Li RJ, Lewis JH, Berbeco RI, et al. Real-time tumor motion estimation using respiratory surrogate via memory-based learning[J]. Phys Med Biol, 2012, 57(15): 4771-86.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sherstinsky A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys D Nonlinear Phenom. 2020;404(10):132306. [Sherstinsky A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network[J]. Phys D Nonlinear Phenom, 2020, 404(10): 132306.] [Google Scholar]
- 17.Sahoo BB, Jha R, Singh A, et al. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019;67(5):1471–81. doi: 10.1007/s11600-019-00330-1. [Sahoo BB, Jha R, Singh A, et al. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting[J]. Acta Geophys, 2019, 67(5): 1471-81.] [DOI] [Google Scholar]
- 18.Wang GY, Li ZB, Li GJ, et al. Real-time liver tracking algorithm based on LSTM and SVR networks for use in surface-guided radiation therapy. Radiat Oncol. 2021;16(1):13. doi: 10.1186/s13014-020-01729-7. [Wang GY, Li ZB, Li GJ, et al. Real-time liver tracking algorithm based on LSTM and SVR networks for use in surface-guided radiation therapy[J]. Radiat Oncol, 2021, 16(1): 13.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang R, Liang XK, Zhu XY, et al. A feasibility of respiration prediction based on deep Bi-LSTM for real-time tumor tracking. IEEEAccess. 2019;12(6):51262–8. [Wang R, Liang XK, Zhu XY, et al. A feasibility of respiration prediction based on deep Bi-LSTM for real-time tumor tracking[J]. IEEEAccess, 2019, 12(6): 51262-8.] [Google Scholar]
- 20.Yu SM, Wang JT, Liu JG, et al. Rapid prediction of respiratory motion based on bidirectional gated recurrent unit network. IEEE Access. 2019;12(8):49424–35. [Yu SM, Wang JT, Liu JG, et al. Rapid prediction of respiratory motion based on bidirectional gated recurrent unit network[J]. IEEE Access, 2019, 12(8): 49424-35.] [Google Scholar]
- 21.Lin H, Shi CY, Wang B, et al. Towards real-time respiratory motion prediction based on long short-term memory neural networks. Phys Med Biol. 2019;64(8):085010. doi: 10.1088/1361-6560/ab13fa. [Lin H, Shi CY, Wang B, et al. Towards real-time respiratory motion prediction based on long short-term memory neural networks[J]. Phys Med Biol, 2019, 64(8): 085010.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhou DJ, Nakamura M, Mukumoto N, et al. Development of AIdriven prediction models to realize real-time tumor tracking during radiotherapy. Radiat Oncol. 2022;17(1):42. doi: 10.1186/s13014-022-02012-7. [Zhou DJ, Nakamura M, Mukumoto N, et al. Development of AIdriven prediction models to realize real-time tumor tracking during radiotherapy[J]. Radiat Oncol, 2022, 17(1): 42.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]. in NIPS, Long Beach, California, USA, 2017.
- 24.Xiao YT, Yin HS, Zhang YD, et al. A dual-stage attention-based Conv-LSTM network for spatio-temporal correlation and multivariate time series prediction. Int J Intell Syst. 2021;36(5):2036–57. doi: 10.1002/int.22370. [Xiao YT, Yin HS, Zhang YD, et al. A dual-stage attention-based Conv-LSTM network for spatio-temporal correlation and multivariate time series prediction[J]. Int J Intell Syst, 2021, 36(5): 2036-57.] [DOI] [Google Scholar]
- 25.Shih SY, Sun FK, Lee HY. Temporal pattern attention for multivariate time series forecasting. Mach Learn. 2019;108(8/9):1421–41. [Shih SY, Sun FK, Lee HY. Temporal pattern attention for multivariate time series forecasting[J]. Mach Learn, 2019, 108(8/9): 1421-41.] [Google Scholar]
- 26.van Houdt G, Mosquera C, Nápoles G. A review on the long shortterm memory model. Artif Intell Rev. 2020;53(8):5929–55. doi: 10.1007/s10462-020-09838-1. [van Houdt G, Mosquera C, Nápoles G. A review on the long shortterm memory model[J]. Artif Intell Rev, 2020, 53(8): 5929-55.] [DOI] [Google Scholar]
- 27.Paszke A, Gross S, Massa F, et al. Pytorch: An imperative style, highperformance deep learning library. Adv Neural Inf Process Syst. 2019;18(1):32. [Paszke A, Gross S, Massa F, et al. Pytorch: An imperative style, highperformance deep learning library[J]. Adv Neural Inf Process Syst, 2019, 18(1): 32.] [Google Scholar]
- 28.Huang ST, Wang DL, Wu XH, et al. DSANet: dual self-attention network for multivariate time series forecasting[C]//CIKM'19: Proceedings of the 28th ACM International Conference on Information and Knowledge Management. 2019: 2129-32.
- 29.Bertholet J, Knopf A, Eiben B, et al. Real-time intrafraction motion monitoring in external beam radiotherapy. Phys Med Biol. 2019;64(15):15T. doi: 10.1088/1361-6560/ab2ba8. [Bertholet J, Knopf A, Eiben B, et al. Real-time intrafraction motion monitoring in external beam radiotherapy[J]. Phys Med Biol, 2019, 64(15): 15TR01.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang JT, Sun RC, Yu SM, et al. An improved correlation model for respiration tracking in robotic radiosurgery using essential skin surface motion. IEEE RoboticsAutom Lett. 2021;6(4):7885–92. [Wang JT, Sun RC, Yu SM, et al. An improved correlation model for respiration tracking in robotic radiosurgery using essential skin surface motion[J]. IEEE RoboticsAutom Lett, 2021, 6(4): 7885-92.] [Google Scholar]
- 31.Yu SM, Hou PC, Sun RC, et al. Correlated skin surface and tumor motion modeling for treatment planning in robotic radiosurgery. Front Neurorobot. 2020;14(2):582385. doi: 10.3389/fnbot.2020.582385. [Yu SM, Hou PC, Sun RC, et al. Correlated skin surface and tumor motion modeling for treatment planning in robotic radiosurgery[J]. Front Neurorobot, 2020, 14(2): 582385.] [DOI] [PMC free article] [PubMed] [Google Scholar]


