Abstract

The phase equilibria for the quaternary system Li+, Rb+, Mg2+//SO42– – H2O at 273.2 K were studied by the isothermal dissolution equilibrium method. Based on the measured data, the space diagram, stable phase diagram, water content diagram, and the diagram of density vs composition are plotted. The stable phase diagram in the system consists of four quaternary invariant points, nine univariate curves, and six crystallization zones. For the invariant points, E1 and E4 belong to the commensurate type, and E2 and E3 belong to the incommensurate type. The order of the crystallization area is Rb2SO4·MgSO4·6H2O > 3Li2SO4·Rb2SO4·2H2O > Li2SO4·Rb2SO4 > MgSO4·7H2O > Li2SO4·H2O > Rb2SO4. The density of the equilibrium liquid changed regularly with the content of Rb2SO4 in the solution. By comparing the stable phase diagram of the partial ternary subsystems at T = 273.2 K and T = 298.2 K, it is found that the crystallization regions of Rb2SO4 increases with the decrease in temperature, which indicates that cooling is conducive to the crystallization of Rb2SO4. By comparing the stable phase diagram of the system at T = 273.2 K and T = 308.2 K, it was found that the system was composed of four invariant points, nine univariate curves, and six crystal regions. The double salt 3Li2SO4·Rb2SO4·2H2O is converted to 3Li2SO4·Rb2SO4. The crystallization region of single salt MgSO4·7H2O, Rb2SO4 and double salt Li2SO4·Rb2SO4 decreased obviously.
1. Introduction
Lithium and rubidium are extremely important to dilute alkali metals.1 With the rapid development of strategic industries such as high-tech industries and new energy, lithium and rubidium are widely used in aerospace, batteries, semiconductors, special glass, and other fields, showing great scientific value.2,3
Generally, rubidium is unable to exist as an independent deposit in nature but for two ways: one is symbiotic with solid minerals of other metals and the other exists in liquid minerals in the form of ions, such as salt lake brine.4,5 The world contains a high amount of lithium resources, and brine-type lithium resources account for the vast majority of its reserves. For example, the Qinghai-Tibet Plateau in China is rich in liquid mineral resources, such as salt lake brine, underground brine, etc. Among them, the Qaidam Basin, known as the “treasure basin”, possesses a large amount of lithium and rubidium, achieving a content of 262— and 10.8 mg·L–1, respectively.6−8 It is estimated that the lithium reserves (as LiCl) are as high as more than 15 million tons, and the Rb2O in the Qaidam Salt Lake alone is at least 625,500 tons. However, rubidium and lithium are difficult to separate due to their similar chemical properties. In brine, rubidium is often symbiotic with lithium preferring to form solid solution or double salt under the interaction.9
The theory of the water–salt system phase diagram can effectively guide the further development and utilization of salt lake brine resources.10,11 Therefore, it is very necessary to carry out research on the phase equilibrium of lithium- and rubidium-related water–salt systems to obtain the phase equilibrium data, which is of great significance for industrial extraction of lithium and rubidium brine resources. The salt lake brine in the Qaidam Basin is mostly magnesium sulfate subtype, containing a high content of magnesium content.12 To support the comprehensive development and utilization of lithium, rubidium, and other resources, combined with the environmental characteristics of the Qaidam Basin, this paper intends to carry out a study on the stable phase equilibrium of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K.
A lot of studies had been done in the water–salt system containing lithium or rubidium. The ternary system Li+, Mg2+//SO42––H2O at 273.2, 288.15, 298.2, and 308.15 K demonstrated that a simple system is likely been formed rather than a double system.13−16 The research on the phase equilibrium of the ternary system Li+, Rb+//SO42––H2O 298 K has been reported in many articles in the 20th century.17−19 Some scholars have studied the quaternary systems Li+, K+, Rb+//SO42––H2O, Li+, Na+, Rb+//SO42––H2O. Our research group has also completed the following research work: ternary system Li+, Rb+//SO42––H2O at 298.2 K, Rb+, Mg2+//SO42––H2O at 298.2 K,20,21 quaternary system Rb+, Cs+, Mg2+//SO42––H2O at 298.2 K, and Li+, Cs+, Mg2+//SO42––H2O at 298.2 K.22,23 Owing to the low annual average temperature(near 0 degrees) in the Qaidam Basin,24 it is necessary to determine a stable phase equilibrium of the sulfate system with lithium, rubidium, and magnesium coexistence at 273.2 K, which has not been reported yet. The isothermal dissolution method was used in this work to carry out a study on the phase equilibrium of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K. It provides solubility data for the separation and extraction of lithium and rubidium resources in brine.
2. Experimental Section
2.1. Reagents and Apparatus
The deionized water used for the preparation of experimental samples and experimental analysis in this experiment was prepared by a UPT water purification system, and its conductivity was less than κ ≤ 1 × 10–4 S·m–1. The inorganic reagents used in this experiment are listed in Table 1. Table 2 lists the instruments used in the experiments.
Table 1. Reagents Description Table.
| chemical reagents | CAS no. | initial purity w(w %) | recrystallization | final purity w(w %) | source |
|---|---|---|---|---|---|
| Li2SO4·H2O | 10102-25-7 | ≥99.0% | Chengdu Kelong Chemical Reagent Plant, China | ||
| Rb2SO4 | 7488-54-2 | ≥99.0% | dried in an oven at 393.2 K | ≥99.5% | Shanghai Dingli Chemical Co., Ltd., China |
| MgSO4·7H2O | 10034-99-8 | ≥99.0% | ≥99.5% | Chengdu Kelong Chemical Reagent Plant, China |
Table 2. Instruments Description Table.
| instruments | type | precision | source |
|---|---|---|---|
| electronic analytical balance | BSA-124S | ± 0.0002 g | Sartorius Scientific Instruments Co., Ltd., China |
| X-ray diffractometer | DX-2700 | a | Dandong Fangyuan Instrument Co., Ltd., China |
| flame atomic absorption spectrometer | iCE-3300 | a | Thermo fisher Technology Co., Ltd., China |
| low-temperature constant temperature and humidity thermostat | SDH-001 | ±0.2 K | Chongqing Inbo Experimental Instrument Co., Ltd., China |
Not detected.
2.2. Experimental Method
The quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K phase equilibrium was studied by the isothermal dissolution equilibrium method.25 The initial solution was prepared based on the solubility data of the ternary invariant point, and another new salt was gradually added according to a certain gradient to obtain a series of sample solutions with different compositions. For example, according to the invariant point data of the ternary system Li+, Rb+//SO42––H2O at 273.2 K, the initial solution was configured and then different amounts of MgSO4·7H2O were added according to a certain gradient. The sample was placed in the SDH-001 type thermostat, and the temperature was kept at (273 ± 0.2) K. The supernatant liquid of the sample was periodically taken for analysis, and the system was considered to be in equilibrium when its density and composition did not change. After reaching equilibrium, the system should be allowed to stand until the sample was clarified and the solid–liquid were separated. The liquid phase was used for chemical composition analysis, and the density (ρ) was determined by the gravity bottle method.26 The corresponding solid phase was analyzed by X-ray powder diffractometry.
2.3. Analytical Methods
The SO42– concentration was determined by the alizarin red titration and subtraction method, and the standard uncertainty was 0.006.27 The Mg2+ concentration was determined by the ethylenediaminetetraacetic acid volumetric method with a standard uncertainty of 0.005.27 Li+ concentrations were determined using a Thermo Fisher iCE-3000 atomic absorption spectrometer. Rb+ combined with the sodium tetraphenylborate–cetyltrimethylammonium bromide back-titration method and assisted with an atomic absorption spectrometer, with a standard uncertainty of 0.0061.27
3. Results and Discussions
The quaternary system Li+, Rb+, Mg2+//SO42––H2O contains three binary subsystems and three ternary subsystems. Among them, the stable phase equilibria Li+, Rb+//SO42––H2O and Rb+, Mg2+//SO42––H2O were completed by our research group. Other binary and ternary invariant point data at 273.2 K obtained by literature review14,28 are compared with the invariant point data obtained in this paper, which are listed in Table 3.14,28 It can be seen from Table 3, the invariant point data obtained in this paper are basically consistent with the literature data, which indicates that the data obtained by using the same experimental method is reliable.
Table 3. Invariant of the Binary and Ternary Subsystem in the Quaternary System Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K and Pressure P = 94.77 kPaa.
| system | composition
of solution, w(B) × 102 |
equilibrated solid phase | source | |||
|---|---|---|---|---|---|---|
| w(Li2SO4) | w(Rb2SO4) | w(MgSO4) | w(H2O) | |||
| Li+//SO42––H2O | 26.59 | 0.00 | 0.00 | 73.41 | LSH | ref14 |
| 26.88 | 0.00 | 0.00 | 73.12 | LSH | this work | |
| Rb+//SO42––H2O | 0.00 | 26.42 | 0.00 | 73.58 | RS | ref28 |
| 0.00 | 27.36 | 0.00 | 72.64 | RS | this work | |
| Mg2+//SO42––H2O | 0.00 | 0.00 | 21.03 | 78.97 | M7 | ref14 |
| 0.00 | 0.00 | 21.06 | 78.94 | M7 | this work | |
| Li+, Mg2+//SO42––H2O | 19.31 | 0.00 | 10.98 | 69.71 | LSH + M7 | ref14 |
| 19.38 | 0.00 | 10.81 | 69.81 | LSH + M7 | this work | |
Standard uncertainties u are u(T) = 0.20 K; u(Li+) = 0.005; u(Rb+) = 0.0061; u(Mg2+) = 0.005; u(SO42–) = 0.0060; w(B) is the mass fraction of B; LSH: Li2SO4·H2O; RS: Rb2SO4; and M7: MgSO4·7H2O.
Table 4 shows the invariant point composition data of the quaternary system Li+, Rb+, Mg2+//SO42––H2O and the binary and ternary subsystems at 273.2 K. The density and solubility data of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K are shown in Table 5. In Table 5, w(B) is the mass fraction and Jänecke index J(B) (B = Li2SO4, Rb2SO4, and MgSO4) is the percentage of dry basis.23 The calculation formula is as follows:
Table 4. Experimental Data Corresponding to the Invariant Points of the Binary and Ternary Subsystems in the Quaternary System Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K and Pressure P = 94.77 kPaa.
| no. | system | composition of solution, w(B) × 102 |
Jänecke
index of dry salt |
equilibrated solid phase | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| J(Li2SO4) + J(Rb2SO4) + J(MgSO4) = 100 | ||||||||||
| w(Li2SO4) | w(Rb2SO4) | w(MgSO4) | w(H2O) | J(Li2SO4) | J(Rb2SO4) | J(MgSO4) | J(H2O) | |||
| a | Li+//SO42––H2O | 26.88 | 0.00 | 0.00 | 73.12 | 100.00 | 0.00 | 0.00 | 284.62 | LSH |
| b | Rb+//SO42––H2O | 0.00 | 27.27 | 0.00 | 72.73 | 0.00 | 100.00 | 0.00 | 266.70 | RS |
| c | Mg2+//SO42––H2O | 0.00 | 0.00 | 21.03 | 78.97 | 0.00 | 0.00 | 100.00 | 375.51 | MSH |
| A | Li+, Rb+//SO42––H2O | 23.06 | 1.36 | 0.00 | 75.58 | 94.43 | 5.57 | 0.00 | 309.50 | LSH + LRH |
| B | 17.72 | 11.94 | 0.00 | 70.34 | 71.67 | 28.33 | 0.00 | 237.15 | LRH + LR | |
| C | 9.67 | 24.67 | 0.00 | 65.66 | 28.16 | 71.84 | 0.00 | 191.21 | LR + RS | |
| D | Li+, Mg2+//SO42––H2O | 19.38 | 0.00 | 10.81 | 69.81 | 64.49 | 0.00 | 35.81 | 231.24 | LSH + M7 |
| E | Rb+, Mg2+//SO42––H2O | 0.00 | 2.47 | 20.56 | 76.97 | 0.00 | 10.73 | 89.27 | 334.22 | RMH + M7 |
| F | 0.00 | 26.92 | 0.23 | 72.85 | 0.00 | 99.15 | 0.85 | 268.32 | M7 + RS | |
| E1 | LLi+, Rb+, Mg2+//SO42––H2O | 18.60 | 1.06 | 11.50 | 68.85 | 59.70 | 3.39 | 36.91 | 220.99 | LRH + LSH + M7 |
| E2 | 13.92 | 2.30 | 14.81 | 68.97 | 44.87 | 7.40 | 47.73 | 222.22 | LRH + LR + M7 | |
| E3 | 8.93 | 2.69 | 16.96 | 71.42 | 31.24 | 9.43 | 59.34 | 249.87 | LR + RMH + M7 | |
| E4 | 10.93 | 18.43 | 0.46 | 70.19 | 36.64 | 61.82 | 1.54 | 235.40 | RMH + LR + RS | |
w(M) is the mass fraction of M; standard uncertainties u are u(T) = 0.20 K; u(Li+) = 0.005; u(Rb+) = 0.0061; u(Mg2+) = 0.005; u(SO42–) = 0.0060; LRH: 3Li2SO4·Rb2SO4·2H2O; RMH: Rb2SO4·MgSO4·6H2O; LR: Li2SO4·Rb2SO4; M7: MgSO4·7H2O; LSH: Li2SO4·H2O; and RS: Rb2SO4.
Table 5. Solubilities and Densities for the Quaternary System Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K and Pressure P = 94.77 kPaa.
| No. | density ρ/g·cm–3 | composition of solution, w(B) × 102 |
Jänecke
index of dry salt |
equilibrated solid phase | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| J(Li2SO4) + J(Rb2SO4) + J(MgSO4) = 100 | ||||||||||
| w(Li2SO4) | w(Rb2SO4) | w(MgSO4) | w(H2O) | J(Li2SO4) | J(Rb2SO4) | J(MgSO4) | J(H2O) | |||
| 1, G | 1.3347 | 19.31 | 0.00 | 10.98 | 69.71 | 63.75 | 0.00 | 36.25 | 230.14 | LSH + M7 |
| 2 | 1.2870 | 19.47 | 0.66 | 11.66 | 68.21 | 61.25 | 2.09 | 36.66 | 214.54 | LSH + M7 |
| 3, E1 | 1.3056 | 18.60 | 1.06 | 11.50 | 68.85 | 59.70 | 3.39 | 36.91 | 220.99 | LSH + M7 + LRH |
| 4, K | 1.2829 | 0.00 | 2.47 | 20.56 | 76.97 | 0.00 | 10.73 | 89.27 | 334.22 | M7 + RMH |
| 5 | 1.2484 | 1.18 | 2.39 | 20.43 | 76.00 | 4.90 | 9.97 | 85.12 | 316.62 | M7 + RMH |
| 6 | 1.2575 | 2.76 | 2.38 | 20.28 | 74.58 | 10.84 | 9.37 | 79.79 | 293.41 | M7 + RMH |
| 7 | 1.2751 | 4.49 | 2.28 | 20.02 | 73.21 | 16.77 | 8.50 | 74.72 | 273.21 | M7 + RMH |
| 8 | 1.2812 | 7.10 | 2.26 | 17.88 | 72.76 | 26.07 | 8.28 | 65.64 | 267.08 | M7 + RMH |
| 9, E3 | 1.2739 | 8.93 | 2.69 | 16.96 | 71.42 | 31.24 | 9.43 | 59.34 | 249.87 | M7 + RMH + LR |
| 10 | 1.2905 | 10.49 | 2.35 | 16.38 | 70.78 | 35.90 | 8.05 | 56.05 | 242.26 | M7 + LR |
| 11 | 1.3027 | 12.53 | 2.13 | 15.18 | 70.16 | 41.99 | 7.13 | 50.88 | 235.12 | M7 + LR |
| 12, E2 | 1.3187 | 13.92 | 2.30 | 14.81 | 68.97 | 44.87 | 7.40 | 47.73 | 222.22 | M7 + LR + LRH |
| 13 | 1.3156 | 13.98 | 2.06 | 14.33 | 69.63 | 46.04 | 6.77 | 47.19 | 229.31 | LRH + M7 |
| 14 | 1.3044 | 15.90 | 1.80 | 11.83 | 70.47 | 53.83 | 6.10 | 40.06 | 238.63 | LRH + M7 |
| 15 | 1.3072 | 16.81 | 1.55 | 11.60 | 70.03 | 56.10 | 5.18 | 38.72 | 233.64 | LRH + M7 |
| 16 | 1.2940 | 17.85 | 1.59 | 11.85 | 68.70 | 57.04 | 5.09 | 37.87 | 219.50 | LRH + M7 |
| 17, E1 | 1.3056 | 18.60 | 1.06 | 11.50 | 68.85 | 59.70 | 3.39 | 36.91 | 220.99 | LSH + LRH + M7 |
| 18 | 1.3755 | 9.67 | 24.67 | 0.00 | 65.66 | 28.16 | 71.84 | 0.00 | 191.21 | RS + LR |
| 19 | 1.3318 | 10.22 | 19.89 | 0.29 | 69.59 | 33.62 | 65.43 | 0.95 | 228.86 | RS + LR |
| 20 | 1.3148 | 10.48 | 17.86 | 0.33 | 71.32 | 36.55 | 62.29 | 1.15 | 248.69 | RS + LR |
| 21, E4 | 1.3112 | 10.93 | 18.43 | 0.46 | 70.19 | 36.64 | 61.82 | 1.54 | 235.40 | RS + LR + RMH |
| 22 | 1.2807 | 10.86 | 15.47 | 0.39 | 73.29 | 40.65 | 57.91 | 1.44 | 274.44 | LR + RMH |
| 23 | 1.2333 | 11.07 | 11.42 | 0.78 | 76.73 | 47.58 | 49.07 | 3.35 | 329.67 | LR + RMH |
| 24 | 1.2053 | 11.23 | 7.55 | 1.87 | 79.35 | 54.38 | 36.56 | 9.05 | 384.16 | LR + RMH |
| 25 | 1.1983 | 11.05 | 5.25 | 4.18 | 79.52 | 53.94 | 25.65 | 20.41 | 388.24 | LR + RMH |
| 26 | 1.2103 | 10.21 | 4.75 | 6.98 | 78.06 | 46.52 | 21.65 | 31.83 | 355.86 | LR + RMH |
| 27 | 1.2357 | 10.36 | 4.05 | 9.54 | 76.06 | 43.27 | 16.90 | 39.83 | 317.64 | LR + RMH |
| 28 | 1.2456 | 9.86 | 2.97 | 12.67 | 74.49 | 38.65 | 11.66 | 49.69 | 292.05 | LR + RMH |
| 29 | 1.2527 | 9.66 | 2.81 | 13.29 | 74.24 | 37.52 | 10.90 | 51.59 | 288.23 | LR + RMH |
| 30 | 1.2565 | 9.33 | 2.77 | 14.22 | 73.68 | 35.43 | 10.54 | 54.03 | 279.93 | LR + RMH |
| 31 | 1.2685 | 9.05 | 2.72 | 16.39 | 71.85 | 32.13 | 9.67 | 58.20 | 255.18 | LR + RMH |
| 32, E3 | 1.2739 | 8.93 | 2.69 | 16.96 | 71.42 | 31.24 | 9.43 | 59.34 | 249.87 | LR + RMH + M7 |
| 33 | 1.3056 | 17.72 | 11.94 | 0.00 | 70.34 | 59.74 | 40.26 | 0.00 | 237.15 | LRH + LR |
| 34 | 1.2823 | 18.31 | 10.02 | 0.99 | 70.69 | 62.47 | 34.17 | 3.36 | 241.14 | LRH + LR |
| 35 | 1.2750 | 18.31 | 8.02 | 1.48 | 72.19 | 65.83 | 28.86 | 5.31 | 259.62 | LRH + LR |
| 36 | 1.2589 | 18.12 | 5.87 | 3.07 | 72.94 | 66.97 | 21.70 | 11.33 | 269.62 | LRH + LR |
| 37 | 1.2652 | 17.78 | 4.41 | 5.37 | 72.44 | 64.51 | 15.99 | 19.50 | 262.89 | LRH + LR |
| 38 | 1.2743 | 16.51 | 3.56 | 8.14 | 71.80 | 58.53 | 12.62 | 28.85 | 254.60 | LRH + LR |
| 39 | 1.2797 | 15.75 | 3.11 | 10.26 | 70.87 | 54.08 | 10.69 | 35.23 | 243.28 | LRH + LR |
| 40 | 1.2840 | 15.30 | 2.78 | 12.55 | 69.38 | 49.95 | 9.08 | 40.97 | 226.54 | LRH + LR |
| 41 | 1.3089 | 14.25 | 2.54 | 13.09 | 70.12 | 47.69 | 8.50 | 43.81 | 234.69 | LRH + LR |
| 42, E2 | 1.3187 | 13.92 | 2.30 | 14.81 | 68.97 | 44.87 | 7.40 | 47.73 | 222.22 | LRH + LR + M7 |
| 43 | 1.2365 | 23.06 | 1.36 | 0.00 | 75.58 | 94.43 | 5.57 | 0.00 | 309.50 | LSH + LRH |
| 44 | 1.2315 | 22.90 | 1.49 | 1.35 | 74.26 | 88.96 | 5.78 | 5.26 | 288.50 | LSH + LRH |
| 45 | 1.2408 | 22.05 | 1.38 | 2.71 | 73.86 | 84.36 | 5.27 | 10.37 | 282.63 | LSH + LRH |
| 46 | 1.2611 | 20.94 | 1.28 | 5.15 | 72.64 | 76.53 | 4.66 | 18.81 | 265.52 | LSH + LRH |
| 47 | 1.2796 | 19.41 | 1.16 | 7.37 | 72.06 | 69.47 | 4.14 | 26.39 | 257.92 | LSH + LRH |
| 48 | 1.2877 | 18.84 | 1.03 | 9.20 | 70.93 | 64.80 | 3.56 | 31.64 | 244.03 | LSH + LRH |
| 49 | 1.2929 | 18.36 | 0.99 | 10.33 | 70.32 | 61.85 | 3.32 | 34.82 | 236.93 | LSH + LRH |
| 50 | 1.2994 | 17.97 | 0.99 | 10.90 | 70.13 | 60.18 | 3.31 | 36.51 | 234.83 | LSH + LRH |
| 51, E1 | 1.3056 | 18.60 | 1.06 | 11.50 | 68.85 | 59.70 | 3.39 | 36.91 | 220.99 | LSH + LRH + M7 |
| 52 | 1.2838 | 0.00 | 21.61 | 0.23 | 78.16 | 0.00 | 98.95 | 1.05 | 357.88 | RS + RMH |
| 53 | 1.2525 | 1.51 | 21.32 | 0.52 | 76.65 | 6.47 | 91.30 | 2.22 | 328.31 | RS + RMH |
| 54 | 1.2736 | 3.64 | 21.20 | 0.50 | 74.66 | 14.37 | 83.64 | 1.99 | 294.59 | RS + RMH |
| 55 | 1.2980 | 6.04 | 20.97 | 0.49 | 72.51 | 21.97 | 76.26 | 1.77 | 263.73 | RS + RMH |
| 56 | 1.3130 | 8.66 | 19.31 | 0.45 | 71.58 | 30.46 | 67.95 | 1.58 | 251.84 | RS + RMH |
| 57 | 1.2960 | 9.95 | 19.62 | 0.48 | 69.95 | 33.12 | 65.30 | 1.59 | 232.77 | RS + RMH |
| 58, E4 | 1.3112 | 10.93 | 18.43 | 0.46 | 70.19 | 36.64 | 61.82 | 1.54 | 235.40 | RS + RMH + LR |
w(M) is the mass fraction of M; standard uncertainties u are u(T) = 0.20 K; u(Li+) = 0.0050; u(Rb+) = 0.0061; u(Mg2+) = 0.0050; u(SO42–) = 0.0060; LRH: 3Li2SO4·Rb2SO4·2H2O; RMH: Rb2SO4·MgSO4·6H2O; LR: Li2SO4·Rb2SO4; M7: MgSO4·7H2O; LSH: Li2SO4·H2O; and RS: Rb2SO4.
3.1. Quaternary System Li+, Rb+, Mg2+//SO42––H2O 273.2 K Space Diagram
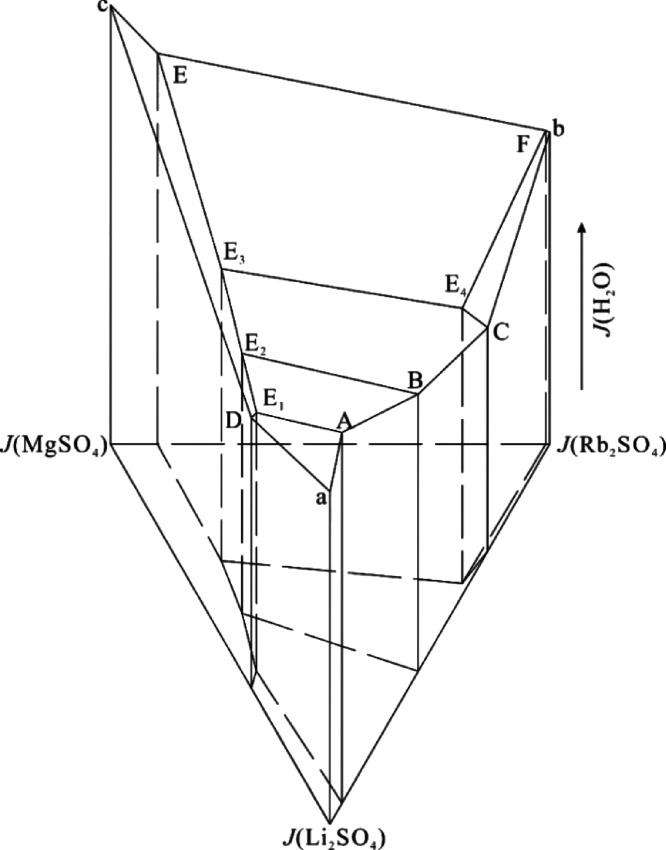
According to the binary and ternary invariant point data of the system in Table 4, the space diagram as shown in Figure 1 is drawn.
Figure 1.
Space diagram of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K.
In Figure 1, the meanings of each point and line are as follows: The lateral prisms of points A, B, and C, respectively, represent the three binary systems Li2SO4–H2O, Rb2SO4–H2O, and MgSO4–H2O. A, B, C, D, E, and F represent the invariant points of ternary system Li+, Rb+//SO42––H2O, Li+, Mg2+//SO42––H2O and Rb+, Mg2+//SO42––H2O at 273.2 K, respectively. E1, E2, E3, and E4 represent the invariant points of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K. The equilateral triangle on the bottom of the space phase diagram represents the dry base stable phase diagram of Li+, Rb+, Mg2+//SO42––H2O at 273.2 K, and the distance to the bottom of any point in the space phase diagram is the Jänecke index of H2O at that point.
3.2. Quaternary System Li+, Rb+, Mg2+//SO42––H2O 273.2 K Stable Phase Diagram
The stable phase diagram of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K was drawn based on the data of Jänecke index J(B) in Table 5, as shown in Figure 2. The meanings of the dots, lines, and areas in Figure 2 are as follows:
-
(1)
E1, E2, E3, and E4 represent invariant points of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K. Each point corresponds to three equilibrium solid phases and one equilibrium liquid phase, which are composed as follows:
Point E1: The mass fraction of solution is w(Li2SO4) = 18.60%, w(Rb2SO4) = 1.06%, and w(MgSO4) = 11.50%. The X-ray powder crystal diffraction analysis (Figure 3) shows that the equilibrium solid phase salt is composed of MgSO4·7H2O, Li2SO4·H2O, and double salt 3Li2SO4·Rb2SO4·2H2O.
Point E2: The mass fraction of solution is w(Li2SO4) = 13.92%, w(Rb2SO4) = 2.30%, and w(MgSO4) = 14.81%. The X-ray powder crystal diffraction analysis (Figure 4) shows that the equilibrium solid phase salt is composed of MgSO4·7H2O and double salts Li2SO4·Rb2SO4 and 3Li2SO4·Rb2SO4·2H2O.
Point E3: The mass fraction of solution is w(Li2SO4) = 8.93%, w(Rb2SO4) = 2.69%, and w(MgSO4) = 16.96%. The X-ray powder crystal diffraction analysis (Figure 5) shows that the equilibrium solid phase salt is composed of MgSO4·7H2O and double salts Li2SO4·Rb2SO4 and Rb2SO4·MgSO4·6H2O.
Point E4: The mass fraction of solution is w(Li2SO4) = 10.93%, w(Rb2SO4) = 18.43%, and w(MgSO4) = 0.46%. The X-ray powder crystal diffraction analysis (Figure 6) shows that the equilibrium solid phase salt is composed of Rb2SO4 and double salts Li2SO4·Rb2SO4 and Rb2SO4·MgSO4·6H2O.
Figure 2.
Stable phase diagram of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K.
Figure 3.
X-ray diffraction patterns of the solid phases corresponding to the invariant point E1.
Figure 4.
X-ray diffraction patterns of the solid phases corresponding to the invariant point E2.
Figure 5.
X-ray diffraction patterns of the solid phases corresponding to the invariant point E3.
Figure 6.
X-ray diffraction patterns of the solid phases corresponding to the invariant point E4.
According to the phase equilibrium theory of the water–salt phase diagram, the invariant point of the quaternary system has three solids and one liquid coexisting, which is the intersection of the isothermal saturation surfaces of the three solid-phase salts. According to the judgment rule of commensurate invariant point and incommensurate invariant point, in a quaternary system, if the invariant point is within or on the edge of the triangle formed by its corresponding three solid-phase salts, it is the commensurate invariant point.25 Otherwise, it is an incommensurate invariant point. For the quaternary system in this paper, the equilibrium solid phase salts corresponding to the invariant point E1 are MgSO4·7H2O, Li2SO4·H2O, and 3Li2SO4·Rb2SO4·2H2O, and E1 is located in the triangle formed by these three salts, so E1 is the commensurate invariant point. Similarly, E4 is also a commensurate invariant point. The equilibrium solid phase salts corresponding to the invariant point E2 are MgSO4·7H2O, Li2SO4·Rb2SO4, and 3Li2SO4·Rb2SO4·2H2O. E2 is located outside the triangle formed by these three salts, so the E2 position is not commensurate with the invariant point. Similarly, E3 is also called the incommensurate invariant point.
The temperature may have an influence on the amount of water of crystal contained in hydrate. Previous studies have shown that when T > 342.89 K,29 the crystalline form of magnesium sulfate is MgSO4·H2O. 322.53 K < T < 342.89 K, the crystalline form of magnesium sulfate is MgSO4 6H2O. 272.53 K < T < 322.64 K The crystalline form of magnesium sulfate is MgSO4 7H2O. At T < 272.53 K, the crystalline form of magnesium sulfate is MgSO4·11H2O. At 273.2 K, the crystalline form of magnesium sulfate formed in this paper is MgSO4·7H2O, which is consistent with previous studies.
-
(2)
There are nine univariant curves, namely, the two-solid-one-liquid invariant curve, the form of the solid phase precipitated on the curve is as follows:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
-
(3)
The system has six crystalline regions, namely, Li2SO4·H2O, Rb2SO4, MgSO4·7H2O, 3Li2SO4·Rb2SO4·2H2O, Li2SO4·Rb2SO4, and Rb2SO4·MgSO4·6H2O. Among them, the double salt Rb2SO4·MgSO4·6H2O has the largest crystallization area, indicating the smallest solubility and the easiest crystallization in the system. The crystal area of the single salt Rb2SO4 is the smallest, indicating the largest solubility and the most difficult to precipitate in the system. Therefore, at 273.2 K, the double salt Rb2SO4·MgSO4·6H2O is easier to crystallize from the mixed solution than the single salt Rb2SO4. In the actual production process, the rubidium–magnesium double salt can be preferentially separated, and then the rubidium–magnesium can be separated to obtain the pure salt Rb2SO4.
3.3. Quaternary System Li+, Rb+, Mg2+//SO42––H2O 273.2 K Water Content-Composition Diagram
From the analysis of the crystallization area of the single salt Rb2SO4, it can be seen that the crystallization area of the salt is the smallest, which indicates that the solubility of the single salt Rb2SO4 is the largest among the six salts in this system. Therefore, the change of the content of Rb2SO4 in the solution will greatly affect the change of the water content and density of the solution. From this, the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K water content-composition diagram was drawn with J(Rb2SO4) as the abscissa and J(H2O) as the ordinate (Figure 7).
Figure 7.
Water content diagram of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K.
It can be seen from Figure 7 that on the univariate curves IE2 and E3E4, as J(Rb2SO4) increases, J(H2O) first increases and then decreases. On the univariate curves JE1, KE3, and E2E3, with the increase of J(Rb2SO4), J(H2O) showed an increasing trend. On the univariate curves GE1 and HE4, with the increase of J(Rb2SO4), J(H2O) showed a downward trend. The variation of water content in this system is very diverse, which may be due to the precipitation of various hydrated salts in this system: Li2SO4·H2O, MgSO4·7H2O, 3Li2SO4·Rb2SO4·2H2O, and Rb2SO4·MgSO4·6H2O.
3.4. Quaternary System Li+, Rb+, Mg2+//SO42––H2O at 273.2 K Density-Composition Diagram
According to the experimental data in Table 4, with J(Rb2SO4) as the abscissa and the corresponding density data as the ordinate, the corresponding density-composition diagram was drawn (Figure 8). It can be seen from Figure 8 that on the univariate curve HE4, as J(Rb2SO4) increases, the density of the equilibrium solution also increases. On the univariate curves JE1 and E2E3, as J(Rb2SO4) increases, the equilibrium solution density decreases. On the univariate curves IE2 and E3E4, with the increase of J(Rb2SO4), the equilibrium solution density decreased first and then increased.
Figure 8.
Density vs composition diagram of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K.
3.5. Multi-Temperature Comparison of Partial Ternary Subsystems
The invariant point composition data of the ternary systems Li+, Rb+//SO42––H2O and Rb+, Mg2+//SO42––H2O at 273.2 and 298.2 K20,21 are listed in Table 6. Figures 9 and 10 show the multi-temperature phase diagram of the ternary subsystem Li+, Rb+//SO42––H2O and Rb+, Mg2+//SO42––H2O. As shown in Figures 9 and 10, with the increase of temperature, the crystallization area of Rb2SO4·MgSO4·6H2O, Li2SO4·H2O, and Li2SO4·Rb2SO4 increases, while the crystallization area of Rb2SO4 decreases. The results indicated that the temperature drop was beneficial to the crystallization of Rb2SO4.
Table 6. Invariant Points of the Subsystems of the Quaternary System Li+, Rb+, Mg2+//SO42––H2O at 273.2 and 298.2 K and Pressure P = 94.77 kPaa.
| system | temperature T/(K) | composition of solution w(B) × 102 |
Jänecke index of
dry salt, J(B)
(g/100 g S) |
equilibrated solid phase | source | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| J(Li2SO4) + J(Rb2SO4) + J(MgSO4) = 100 | |||||||||||
| w(Li2SO4) | w(Rb2SO4) | w(MgSO4) | w(H2O) | J(Li2SO4) | J(Rb2SO4) | J(MgSO4) | J(H2O) | ||||
| Li+, Rb+//SO42––H2O | 273.2 | 23.06 | 1.36 | 0.00 | 75.58 | 94.43 | 5.57 | 0.00 | 309.50 | LSH + LRH | this work |
| 17.72 | 11.94 | 0.00 | 70.34 | 71.67 | 28.33 | 0.00 | 1401.5 | LRH + LR | |||
| 9.67 | 24.67 | 0.00 | 65.66 | 28.16 | 71.84 | 0.00 | 191.21 | LR + RS | |||
| 298.2 | 22.86 | 3.38 | 0.00 | 73.76 | 87.12 | 12.88 | 0.00 | 281.10 | LSH + LRH | ref.20 | |
| 17.02 | 14.33 | 0.00 | 68.65 | 54.29 | 45.71 | 0.00 | 218.98 | LRH + LR | |||
| 6.28 | 31.11 | 0.00 | 62.61 | 16.80 | 83.20 | 0.00 | 167.45 | LR + RS | |||
| Rb+, Mg2+//SO42––H2O | 273.2 | 0 | 2.47 | 20.56 | 76.97 | 0 | 5.14 | 94.86 | 334.22 | M7 + RM | this work |
| 0 | 26.92 | 0.23 | 72.85 | 0 | 98.15 | 1.85 | 268.32 | RM + RS | |||
| 298.2 | 0 | 4.31 | 26.75 | 68.94 | 0 | 6.77 | 93.23 | 221.96 | M7 + RM | ref. 21 | |
| 0 | 31.69 | 0.63 | 67.68 | 0 | 95.80 | 4.20 | 209.41 | RM + RS | |||
w(M) is the mass fraction of M; standard uncertainties u are u(T) = 0.20 K; u(Li+) = 0.0050; u(Rb+) = 0.0061; u(Mg2+) = 0.0050; u(SO42–) = 0.0060; LRH: 3Li2SO4·Rb2SO4·2H2O; RM: Rb2SO4·MgSO4·6H2O; LR: Li2SO4·Rb2SO4; M7: MgSO4·7H2O; LSH: Li2SO4·H2O; and RS: Rb2SO4.
Figure 9.
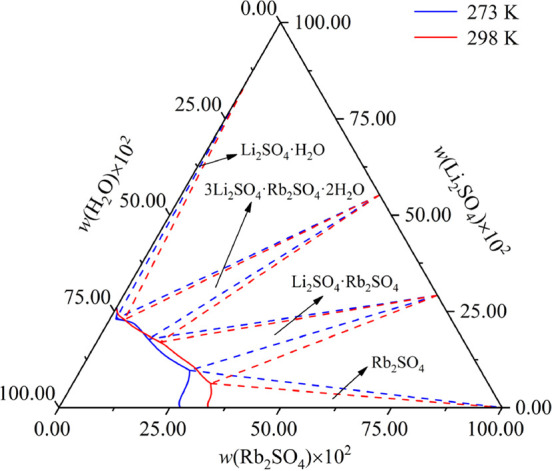
Stable phase diagram of ternary systems Li+, Rb+//SO42––H2O multi-temperature comparison.
Figure 10.

Stable phase diagram of ternary systems Rb+, Mg2+//SO42––H2O multi-temperature comparison.
3.6. Multi-Temperature Comparison of the Stable Phase Diagram of the Quaternary System Li+, Rb+, Mg2+//SO42––H2O
In order to more intuitively compare the influence of temperature on the stable phase diagram of the quaternary system Li+, Rb+, Mg2+//SO42––H2O, combined with the previous studies at 298.2 and 308.2 K,30 we drew the comparative phase diagram of the system at two temperatures. In Figure 11, the system is composed of four invariant points, nine univariate curves, and six solid phase crystallization zones at two different temperatures, all of which belong to complex systems with double salt generation. The area of solid crystal and the form of double salt crystal change obviously with the increase of temperature. The double salt 3Li2SO4·Rb2SO4·2H2O is converted to 3Li2SO4·Rb2SO4. The crystallization area of single salt MgSO4·7H2O, Rb2SO4 and double salt Li2SO4·Rb2SO4 decreased. Therefore, in actual production, cooling is conducive to the crystallization precipitation of MgSO4·7H2O and Rb2SO4.
Figure 11.
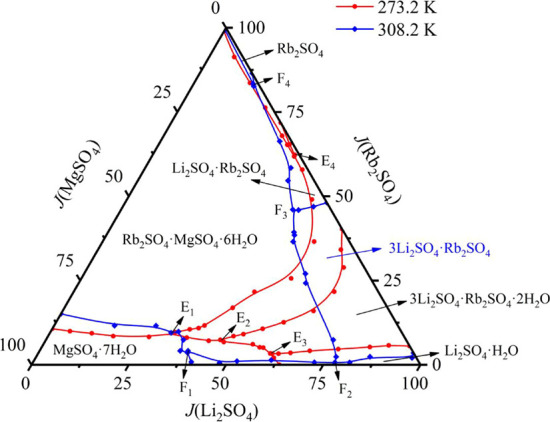
Stable phase diagram of quaternary system Li+, Rb+, Mg2+//SO42––H2O multi-temperature comparison.
4. Conclusions
In this paper, the stable phase equilibrium relationship of the quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K was determined using the isothermal dissolution method. The stable phase diagram, space phase diagram, water diagram, and density-composition diagram of the system are derived from the experimental data. Meanwhile, the stable phase diagrams of the subsystems at T = 273.2 K and T = 298.2 K, and the stable phase diagram of the system measured at T = 273.2 K and T = 308.2 K are compared. Specific outcomes from this paper include the following:
-
(1)
The quaternary system Li+, Rb+, Mg2+//SO42––H2O at 273.2 K stable phase diagram is composed of four invariant points, nine univariate curves, and six crystallization regions, with double salt formation, belonging to a complex system. The six crystalline phase regions correspond to Li2SO4·H2O, Rb2SO4, MgSO4·7H2O, 3Li2SO4·Rb2SO4·2H2O, Li2SO4·Rb2SO4, and Rb2SO4·MgSO4·6H2O, respectively. The crystallization area is determined by the following order: Rb2SO4·MgSO4·6H2O > 3Li2SO4·Rb2SO4·2H2O > Li2SO4·Rb2SO4 > MgSO4·7H2O > Li2SO4·H2O > Rb2SO4. Among them, a largest crystallization area of the double salt Rb2SO4·MgSO4·6H2O was observed, indicating the larger possibility of crystallization in this system. The area of the Rb2SO4 crystalline region is the smallest, indicating that the salt has the highest solubility among the six salts.
-
(2)
Comparing the phase diagrams of the ternary systems Li+, Rb+//SO42––H2O (Figure 9) and Rb+, Mg2+//SO42––H2O (Figure 10)at T = 273.2 K and T = 298.2 K, as the temperature decreases, the crystalline regions of Rb2SO4 increase. It shows that the cooling is conducive to the precipitation of Rb2SO4 crystallization.
-
(3)
By comparing the stable phase diagram of the quaternion system Li+, Rb+, Mg2+//SO42––H2O at T = 273.2 K and T = 308.2 K(Figure 11), the crystalline form of compound salt 3Li2SO4·Rb2SO4·2H2O changes to 3Li2SO4·Rb2SO4 with the increase of temperature. The crystallization area of single salt MgSO4·7H2O, Rb2SO4 and double salt Li2SO4·Rb2SO4 decreased obviously.
Acknowledgments
This project was supported by the National Natural Science Foundation of China. (Nos. U21A2017 and U1607121).
The authors declare no competing financial interest.
References
- Li J.; Li T.; Ma Y.; Chen F. Distribution and origin of brine-type Li - Rb mineralization in the Qaidam Basin NW China. Sci. China Earth 2022, 65, 477–489. 10.1007/s11430-021-9855-6. [DOI] [Google Scholar]
- Ouyang S.; Zheng K.; Huang Q.; Liu Y.; Boccaccini A. R. Synthesis and characterization of rubidium-containing bioactive glass nanoparticles. Mater. Lett. 2020, 273, 127920 10.1016/j.matlet.2020.127920. [DOI] [Google Scholar]
- Cui L.; Jiang K.; Wang J.; Dong K.; Zhang X.; Cheng F. Role of ionic liquids in the efficient transfer of lithium by Cyanex 923 in solvent extraction system. AIChE J. 2019, 65, e16606 10.1002/aic.16606. [DOI] [Google Scholar]
- Guo X. H.; Zheng M. P.; Liu X.; Nie Z.; Pu L. Z. Saline Cesium Resource and Prospect of its Exploitation and Utilization in Tibet. J. Salt Sci. Chem. Ind. 2008, 8–13. [Google Scholar]
- Zhu C.; Dong Y.; Yun Z.; Hao Y.; Wang C.; Dong N.; Li W. Study of lithium exploitation from carbonate subtype and sulfate type salt-lakes of Tibet. Hydrometallurgy 2014, 149, 143–147. 10.1016/j.hydromet.2014.07.006. [DOI] [Google Scholar]
- Wang B.; Ji Y. H.; Zhang J. P.; Liu C.; Lu X. H. Reseach progress on separations of Rubidium and Cesium from saline. J. Nanjing Univ. Technol. 2008, 05, 104–110. [Google Scholar]
- Sang S. H.; Yin H. A.; Ni S. J.; Zhang C. J. Metastable equilibrium solublities of solutions in the quaternary system of K2B4O7 - Na2B4O7 - Li2B4O7 - H2O at 273 K. Acta Phys.-Chim. Sin. 2007, 1285–1287. [Google Scholar]
- Liu Z. M.; Yang G. S. Development, utilization and sustainable development of salt lake resources in China. Bull. Mineral., Petrol. Geochem. 1999, 59–61. [Google Scholar]
- Jiang Y. C.; Yun T.; Gao S. Y.; Xia S. P. Progress of Separation and Analysis Methods for Rare Alkali Metals Rubidium and Cesium. Chin. J. Rare Met. 2002, 04, 299–303. [Google Scholar]
- Song P. S.; Li W.; Sun B.; Nie Z.; Pu L. Z.; Wang Y. S. Recent Development on Comprehensive Utilization of Salt Lake Resources. Inorg. Chem. Ind. 2011, 27, 801–815. [Google Scholar]
- Song P. S. The phase diagram of salt-water systems and utilization of salt lake resources. J. Salt Lake Res. 2016, 24, 35–49. [Google Scholar]
- Gao D.; Yu X.; Guo Y.; Wang S.; Liu M.; Deng T.; Chen Y.; Belzile N. Extraction of lithium from salt lake brine with triisobutyl phosphate in ionic liquid and kerosene. Chem. Res. Chin. Univ. 2015, 31, 621–626. 10.1007/s40242-015-4376-z. [DOI] [Google Scholar]
- Li B.; Wang Q. Z.; Li J.; Fang C. H.; Song P. S. A study on the ternary systems Li+, K+ // SO42– - H2O and Li+, Mg2+ // SO42– - H2O at 25 °C. Acta Phys.-Chim. Sin 1994, 536–542. [Google Scholar]
- Zhou H.; Zeng D.; Han H.; Dong O.; Li D.; Yao Y. Solubility isotherm of the system Li2SO4 – K2SO4 – MgSO4 – H2O at 273. 15 K. J. Chem. Eng. Data 2013, 58, 1692–1696. 10.1021/je4001125. [DOI] [Google Scholar]
- Wang S.; Shi C.; Yuan F.; Guo Y.; Deng T. Experimental and Thermodynamic Modeling Study of the Quaternary System Containing Lithium, Potassium, Magnesium, and Sulfate at 288. 15 K. J. Chem. Eng. Data 2020, 65, 49–55. 10.1021/acs.jced.9b00731. [DOI] [Google Scholar]
- Wang S.; Deng T. (Solid + liquid) isothermal evaporation phase equilibria in the aqueous ternary system (Li2SO4 + MgSO4 + H2O) at T = 308. 15 K. J. Chem. Thermodyn 2008, 40, 1007–1011. 10.1016/j.jct.2008.02.008. [DOI] [Google Scholar]
- Shevchuk V. G. Solubility in the system Li2SO4-Rb2SO4-H2O at 35°C. Zh. Neorg. Khim. 1962, 7, 2463–2465. [Google Scholar]
- Kuznetsova G. P.; Plyushchev V. E.; Oboznenko Y. U. The solubility of solid phase of the Li2SO4-Rb2SO4-H2O system. Izv. Vysshikh Uchebn. Zavedenii. Khim. i Khim. Tekhnol. 1964, 7, 355–359. [Google Scholar]
- Pina C. M.; Fernandez Dıaz L.; Molins E.; et al. Growth and characterization of the new double sulphate, Li3Rb(SO4)2·H2O. Z. Kristallogr. 1998, 213, 635. 10.1524/zkri.1998.213.12.635. [DOI] [Google Scholar]
- Huang P.; Zeng Y.; Wu L. X.; Chen P. J.; Deng S. J.; Li L. G.; Yu X. D. Stable Phase Equilibrium in Ternary System Li+, Rb+ // SO42– - H2O at 298. 2 K. Ind. Miner. Process 2018, 47, 10–13. [Google Scholar]
- Chen Y.; Sun H. B.; Zeng Y.; Yu X. D.; Li L. G. Stable Phase Equilibrium in the Ternary System Rb+, Mg2+ // SO42– - H2O at 298 K. Conserv. Util. Min. Resour. 2019, 39, 73–77. 10.13779/j.cnki.issn1001-0076.2019.01.015. [DOI] [Google Scholar]
- Liu X.; Zeng Y.; Liu J.; Yu X.; Sun H. Stable Phase Equilibrium of the Quaternary System Li2SO4 + Cs2SO4 + MgSO4 + H2O at 298.2 K. J. Chem. Eng. Data 2019, 64, 2774–2779. 10.1021/acs.jced.9b00162. [DOI] [Google Scholar]
- Zeng Y.; Chen P. J.; Yu X. D. Phase equilibria for quaternary system Rb+, Cs+, Mg2+ // SO42–- H2O at 2982 K. J. Chem. Ind. Eng. 2020, 71, 3460–3468. 10.11949/0438-1157.20200159. [DOI] [Google Scholar]
- Ren X. J.; Huang X. L. Phase equilibria in the quatemary system of Li+, Mg2+ // Cl–, SO42– -H2O at 273.15 K. Inorg. Chem. Ind. 2016, 48, 13–15. [Google Scholar]
- Niu Z. D.; Cheng F. Q.; Li B. C.; et al. Salt-Water System Phase Diagrams and Applications; Tianjin University Press: Tianjin, 2002; pp. 84–85. [Google Scholar]
- Chen H. Y.; Chen H.. Chemical reagent - General method for the Bdetermination of density (GB/T 611–2006); Sciences Press: Beijing, 2007. [Google Scholar]
- Shang C. S.; An L. Y.; Hu Z. W. ICP - OES Determination of Rubidium in Bitter. Chem. Res. Appl. 2012, 24, 642–645. [Google Scholar]
- Li M.; Gao S.; Xia S.; Yue T. Solubility of the Rb2SO4 - C2H5OH - H2O Ternary System. Chin. J. Rare Met. 2003, 27, 238–241. [Google Scholar]
- Li D.; Zeng D.; Yin X.; Gao D. Phase diagrams and thermochemical modeling of salt lake brine systems. III. Li2SO4 + H2O, Na2SO4 + H2O, K2SO4 + H2O, MgSO4 + H2O and CaSO4 + H2O systems. Calphad 2018, 60, 163–176. 10.1016/j.calphad.2018.01.002. [DOI] [Google Scholar]
- Shevchuk V. G. The Li2SO4-MgSO4-Rb2SO4 system at 35°C. Russ. J. Inorg. Chem. 1963, 8, 1021–1023. [Google Scholar]