Magnetic Anisotropy of Individual Nanomagnets Embedded in Biological Systems Determined by Axi-asymmetric X-ray Transmission Microscopy

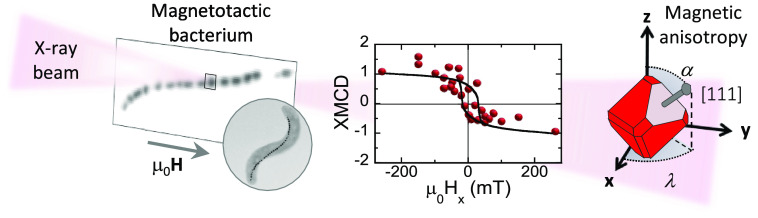
Abstract

Over the past few years, the use of nanomagnets in biomedical applications has increased. Among others, magnetic nanostructures can be used as diagnostic and therapeutic agents in cardiovascular diseases, to locally destroy cancer cells, to deliver drugs at specific positions, and to guide (and track) stem cells to damaged body locations in regenerative medicine and tissue engineering. All these applications rely on the magnetic properties of the nanomagnets which are mostly determined by their magnetic anisotropy. Despite its importance, the magnetic anisotropy of the individual magnetic nanostructures is unknown. Currently available magnetic sensitive microscopic methods are either limited in spatial resolution or in magnetic field strength or, more relevant, do not allow one to measure magnetic signals of nanomagnets embedded in biological systems. Hence, the use of nanomagnets in biomedical applications must rely on mean values obtained after averaging samples containing thousands of dissimilar entities. Here we present a hybrid experimental/theoretical method capable of working out the magnetic anisotropy constant and the magnetic easy axis of individual magnetic nanostructures embedded in biological systems. The method combines scanning transmission X-ray microscopy using an axi-asymmetric magnetic field with theoretical simulations based on the Stoner–Wohlfarth model. The validity of the method is demonstrated by determining the magnetic anisotropy constant and magnetic easy axis direction of 15 intracellular magnetite nanoparticles (50 nm in size) biosynthesized inside a magnetotactic bacterium.

The last century has faced a fundamental need to develop nanotechnology-based pathways to achieve relevant performance for technological, biomedical, and environmental purposes aiming to overcome the emerging social challenges. In this regard, nanomagnets offer interesting physical properties showing the potential to fulfill such demands.^1,2 The rapid advances in nanofabrication achieved in the last decades have enabled the exploration of a great variety of magnetic nanostructures for a myriad of applications ranging from magnetic recording^3,4 to clinical applications. In the particular case of biomedical applications, the suitability of nanomagnets lies in two main facts. First, their reduced size (from few nanometers to tens of nanometers) is comparable to those of proteins, nucleic acids, or viruses, allowing promising interaction with biological systems. Second, the magnetic nature of the nanostructures grants their manipulation by external magnetic fields. All of this makes magnetic nanostructures excellent candidates to be used as diagnosis agents in cardiovascular diseases, to locally heat and destroy cancer cells in hyperthermia cancer treatment, or for targeted magnetic cell delivery in regenerative medicine.⁵⁻¹⁰

A successful implementation in biomedicine of the designed magnetic nanostructure relies on its underlying physical properties at the nanoscale within the biological entity. In particular, the role of magnetic anisotropy arises as an overriding question.¹¹ Indeed, the magnetic anisotropy has a strong influence on the magnetic response of the nanomagnets. For example, it determines the stabilization of the magnetization of the magnetic nanostructure, its superparamagnetic size limit, the magnetization reversal mechanism, and the coercive and saturation fields, among others. All of them are determining parameters in the efficiency of the nanomagnet for its subsequent medical applications.¹²⁻²⁰ However, the access to this type of information is restricted to mean values obtained by means of macroscopic techniques which average over a large number of nanomagnets to get a measurable signal. This impedes obtaining reliable information toward the design of customized nanomaterials for specific applications.

Despite the existence of several space-resolved magnetic sensitive techniques capable of characterizing individual nanomagnets within natural systems, the information that can be obtained is limited. For example, off-axis electron holography in the transmission electron microscope^21,22 gives information about the field lines generated by the magnetic nanostructures, but it cannot directly image their magnetization. Similarly, nitrogen-vacancy optical magnetic imaging,²³ a more recent technique, presents a rather poor spatial resolution of about 400 nm. Finally, magnetic force microscopy²⁴⁻²⁷ provides a high spatial resolution (typically 50 nm) and the ability to work in variable applied magnetic fields, but the information this technique provides is mostly qualitative.

On the other hand, synchrotron radiation techniques such as X-ray photoemission electron microscopy (XPEEM) and scanning transmission X-ray microscopy (STXM) possess comparative advantages since they provide a high spatial resolution (down to tens of nanometers) combined with element specificity and magnetic sensitivity. XPEEM has shown the possibility to obtain, by means of X-ray magnetic circular dichroism (XMCD) contrast,²⁸ magnetic hysteresis loops of individual magnetic nanoparticles down to 18 nm.²⁹ However, it presents certain drawbacks when it comes to studying nanomagnets within biological entities. Its surface sensitivity stands out as a main obstacle. This is due to the fact that the XMCD signal is detected via collection of generated low-kinetic energy secondary photoelectrons upon illumination with synchrotron radiation. These photoelectrons originate within the topmost 2–3 nm surface region.³⁰ Therefore, XPEEM cannot be used for the characterization of magnetic nanostructures embedded in biological systems as the biological wrap attenuates the signal originating from the nanomagnet surface. Furthermore, XPEEM allows application of only moderate magnetic fields (up to ≈20 mT²⁹) due to the magnetic field induced change of trajectory of emitted photoelectrons, hindering the measurement of hysteresis loops of nanosystems with high coercive fields. In this respect, STXM is a more flexible technique. The XMCD signal is obtained by measuring the transmitted photon intensity through the specimen. Thus, STXM is a bulk sensitive technique capable of gaining magnetic information on intracellular magnetic nanostructures. Last but not least, as STXM measures photons, there is no limitation in terms of magnetic fields.³¹

Here we report on a hybrid method combining experimental data acquisition with a theoretical modeling to obtain quantitative information on the effective magnetic anisotropy (magnetic anisotropy constant and magnetic easy axis direction) of individual nanomagnets. The method relies on a magnetic imaging technique with nanometric spatial resolution (e.g., XPEEM or STXM) under axi-asymmetric magnetic fields and fitting of the experimental data on a model based on the Stoner–Wohlfarth formalism. The axi-asymmetric magnetic field leads to asymmetric hysteresis loops which allow removal of the degeneracy on the angular orientation of the magnetic easy axis. It facilitates the theoretical analysis because it reduces the correlations between the parameters involved, thus improving the accuracy of the results.

To highlight the full potential of the proposed method, this approach has been tested over a model system consisting of magnetic nanoparticles embedded in a biological system, i.e., a magnetotactic bacterium with ≈50 nm size magnetite nanoparticles biosynthesized in its interior. Magnetotactic bacteria are microorganisms that have the ability to synthesize internally membrane-enclosed single-domain magnetic nanoparticles called magnetosomes. Within the bacterium, magnetosomes are aligned, forming an internal magnetic chain which behaves as a large permanent magnetic dipole causing their orientation along the geomagnetic field lines.³²⁻³⁶ Previous works have demonstrated the superiority of STXM-XMCD over XPEEM for magnetic imaging of intracellular magnetosomes.³⁷⁻⁴²

Results and Discussion

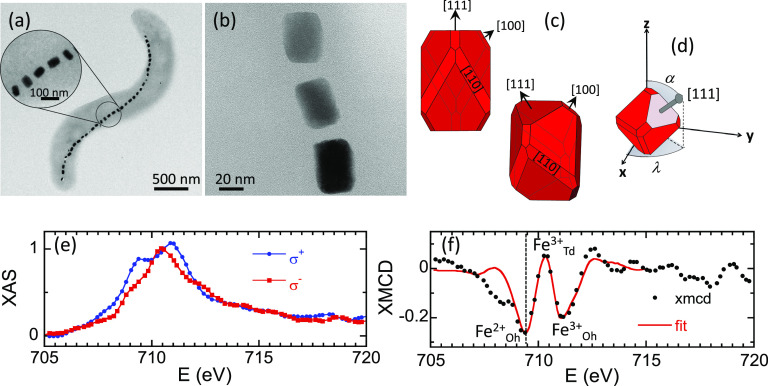
Figure 1a depicts a TEM image of magnetotactic bacterium Magnetovibrio blakemorei strain MV-1, employed in this work. MV-1 cells possess a single magnetosome chain containing a variable number of truncated hexa-octahedral magnetite (Fe₃O₄) magnetosomes with approximate dimensions 35 × 35 × 65 nm³ (refs (36) and (43)) (Figure 1b,c) and single magnetic domains with a high magnetic moment stable at room temperature.^22,44 Magnetosomes in the chain are aligned closely parallel to their axis of elongation, a ⟨111⟩ crystallographic direction of magnetite (Figure 1c), along the axis of motility of the cell,^43,45−48 although important deviations are sometimes observed (see Figure 1a). The elongation along the ⟨111⟩ direction (the [111] direction in Figure 1c), which coincides in this system with a magnetocrystalline easy axis, yields a strong effective uniaxial magnetic anisotropy of the magnetosomes along that direction.^49,50 As a consequence, the nanoparticles biosynthesized by M. blakemorei are uniaxial single magnetic domains whose magnetization process can be described by a modified Stoner–Wohlfarth model,⁵¹⁻⁵⁴ as will be shown in the following.

Figure 1.

TEM imaging and XMCD analysis of M. blakemorei. (a) TEM image of a M. blakemorei MV-1 bacterium. The enlarged region shows a section of the chain with magnetosomes whose long axes are deviated from the chain axis. (b) Zoom-in of three magnetosomes of the chain. (c) Schematic representations of a truncated hexa-octahedron, which is the crystal habit of magnetosomes from the strain MV-1, showing the different facets.⁴³ (d) Spherical coordinates (α, λ) of the [111] elongated direction of the magnetosomes in the xyz reference system used in the simulations (Figure 2). (e) Fe L₃-edge transmission X-ray absorption spectra with the incoming beam right-polarized under an external positive/negative saturating magnetic field (σ^±) obtained from a collection of randomly distributed M. blakemorei cells. Spectra have been normalized by the peak intensity at the L₃-edge of the nonmagnetic contribution of the X-ray absorption (XAS = σ⁺ + σ^–). Computing σ^– – σ⁺ gives the XMCD signal (f), where the best linear combination fit has been added (continuous red line). The vertical dotted line in (f) marks the energy at which the STXM images were recorded (E = 709.3 eV).

The chemical purity of the batch to which the investigated bacterium belongs to, has been characterized by means of XMCD on a macroscopic sample composed of a collection of randomly distributed cells (ALICE station, beamline PM3, Helmholtz-Zentrum Berlin). The absorption spectra have been measured in transmission geometry across the Fe L₃-edge for incoming circular polarized radiation with right helicity and an external positive/negative saturating magnetic field (σ^±) applied parallel to the beam direction (see Figure 1e). The resultant XMCD signal, computed as σ^– – σ⁺, presented in Figure 1f, depicts three major peaks centered at 709.3, 710.3, and 711.1 eV. These spectroscopic signatures within the XMCD are characteristic of the inverse spinel structure of magnetite and attributed to Fe²⁺ at octahedral (Oh) sites and Fe³⁺ occupying tetrahedral (Td) and octahedral positions, respectively.^55,56 XMCD is proportional to the projection of the magnetization along the propagation direction of the incoming beam. Hence, the opposite XMCD sign between the 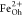and 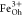peaks as compared to that of the 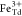peak highlights the expected antiferromagnetic alignment between the Fe cations in Oh and Td sites. We note the presence within the XMCD of an additional spectroscopic feature which shows up as a shoulder at the low energy side of the peak. This structure appears due to saturation or thickness effects inherent to transmission experiments.⁵⁷ It can be shown that its presence does not substantially affect the size of the XMCD features associated with 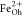, , 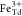and 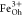so that the XMCD can be fit by a linear combination of the theoretical spectra of each individual Fe component between 705 and 715 eV.⁵⁸ Our fit yields a 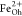::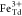 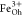ratio of 1.06(7):1.00(8):1.18(9) (red curve in Figure 1f), in good agreement with stoichiometric magnetite (1:1:1). Comparable XAS and XMCD spectra were obtained by means of STXM on a single intracellular magnetosome chain (see the Supporting Information).

Figure 2a,b shows schematically the configuration used for the STXM-XMCD measurements carried out using the MAXYMUS microscope at the UE46-PGM2 beamline at the Helmholtz-Zentrum Berlin.⁵⁹ An axi-asymmetric external magnetic field was generated by four rod NdFeB permanent magnets which can be rotated independently.³¹ The magnetic field at the sample location is mostly oriented along the x-direction and can be varied between μ₀H_x = ± 260 mT. The μ₀H_y,z components of the applied field are shown in Figure 2c as a function of μ₀H_x. While the μ₀H_y and μ₀H_z components reach much lower maximum values than the μ₀H_x component, these are enough to impose an asymmetry to the applied field that will be the key point to define the magnetic anisotropy of each individual magnetosome (see the Supporting Information).

Figure 2.

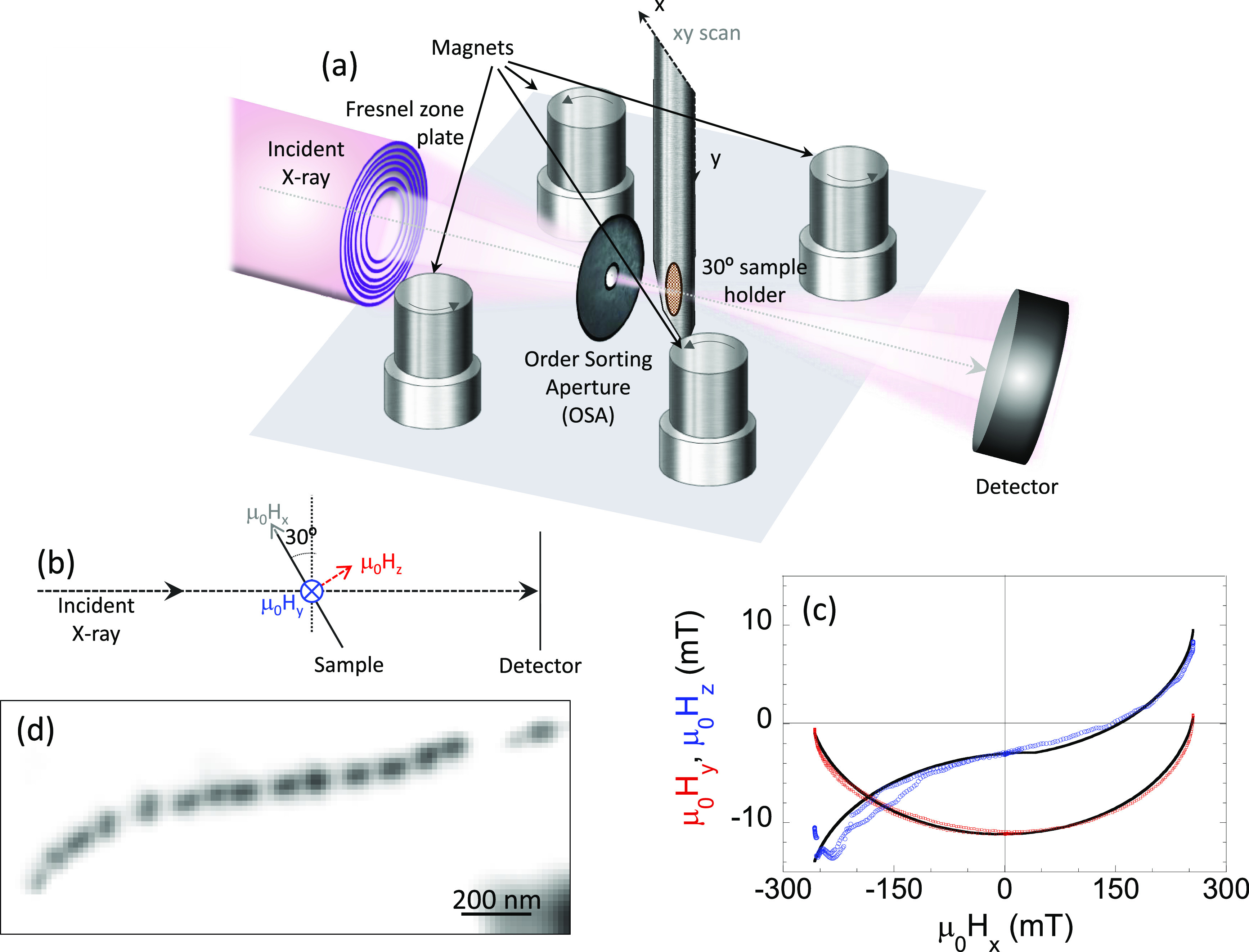
Schematic representation of the axi-asymmetric STXM-XMCD experiment. (a,b) Schematic setup of the STXM microscope and magnet system implemented for the XAS and STXM-XMCD measurements. (c) μ₀H_y,z magnetic field components as a function of μ₀H_x. The continuous lines are fits to the experimental calibration points whose analytical expression has been used in the theoretical models (see the Supporting Information). (d) Space-resolved XAS image of the 15-magnetosome intracellular chain we measure collected at the Fe L₃-edge resonance energy.

Aimed to analyze the magnetization process of individual magnetosomes within an intact magnetotactic bacterium, we selected a cell containing a 15-magnetosome chain. Figure 2d depicts the XAS image of the selected bacterium for the experiment. The image has been obtained by averaging σ⁺ and σ^– images obtained at the Fe L₃-edge resonance energy.

The space-resolved STXM-XMCD signal was recorded at E = 709.3 eV (maximum XMCD signal) while cycling the external magnetic field μ₀H_x between ±260 mT. As previously mentioned, there exist μ₀H_y,z components associated with μ₀H_x (Figure 2c). Figure 3 (central panel) illustrates the dependence of the normalized XMCD signal on μ₀H_x. Figure 3a–g shows selected space-resolved images of the XMCD at specific values of μ₀H_x. A movie showing the field-dependent STXM-XMCD image sequence of every single point in the loop can be found in the Supporting Information. The XMCD signal is proportional to the projection of the magnetic moment along the propagation direction of the X-ray beam, so that red or blue color in the XMCD images indicates opposite direction of the projection of the magnetic moment. During the process, the color of each magnetosome is either completely red or blue (with some exceptions, attributed to the signal noise), confirming that magnetosomes are magnetic single domains whose magnetic moments rotate coherently toward the applied field. Therefore, starting from a state of magnetic saturation (μ₀H_x=+260 mT), all magnetosomes are aligned showing a negative XMCD signal (all magnetosomes red, panel a). As μ₀H_x decreases, the XMCD signal remains almost constant until μ₀H_x around −10 to −20 mT (panel c) when the XMCD sign of leftmost magnetosomes changes sign, and hence its magnetic orientation, as their magnetic moment reorients toward the magnetic field direction. A further decrease of μ₀H_x leads to a sequential rotation of the rest of magnetosomes which is completed at μ₀H_x = −50 mT (all magnetosomes blue, panel e). Similar results were obtained when ramping the magnetic fields from μ₀H_x = −260 mT to +260 mT (panels e–g). Main panel of Figure 4 shows the space-resolved 2D map of the coercive field (μ₀H_c) computed from the XMCD signal vs μ₀H_x (see Methods). Accordingly, with the magnetization process described, here it can be seen that |μ₀H_c| increases in magnitude from 17 to 25 mT for magnetosomes 1–5 and 9–10 through 30 mT for magnetosomes 6–8 until 45–50 mT for the rightmost magnetosomes (11–15). According to the Stoner–Wohlfarth model, being magnetosomes with stable uniaxial magnetic single domains, these differences in μ₀H_c suggest differences in the effective magnetic anisotropy values and/or orientation of the magnetosomes [111] easy axes with the applied field.⁵¹ Indeed, the hysteresis loops of the particles, shown in Figure 4 for selected magnetosomes, display different profiles, from square-shaped such as that of magnetosome 15 to nearly anhysteretic as for magnetosome 1.

Figure 3.

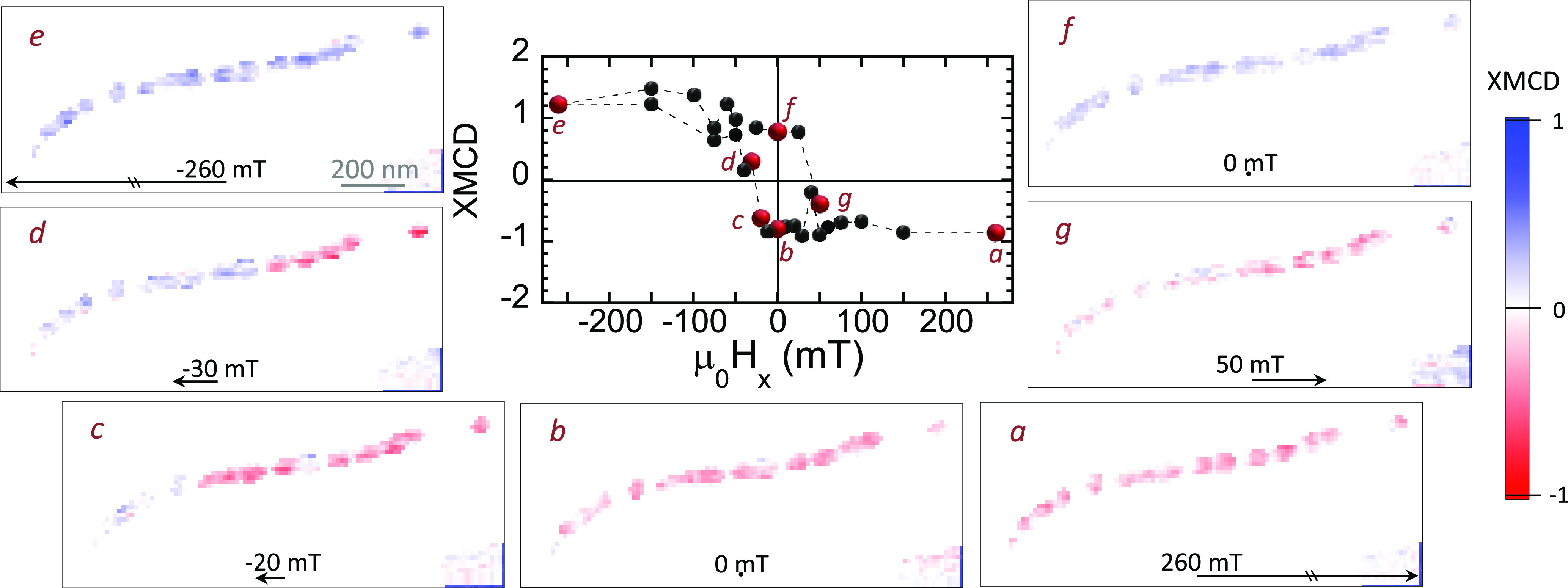
Magnetization process of an intracellular magnetosome chain. (Central panel) Hysteresis loop of the whole chain. (a–g) Space-resolved STXM-XMCD images of the 15-magnetosome intracellular chain collected at the Fe L₃-edge resonance energy (709.3 eV) at selected values of the applied magnetic field μ₀H_x. Red and blue colors represent the normalized XMCD signal varying between ±1. Opposite color indicates opposite direction of the projection of the magnetic moment. A movie showing the field-dependent STXM-XMCD image sequence of the whole chain can be found in the Supporting Information.

Figure 4.

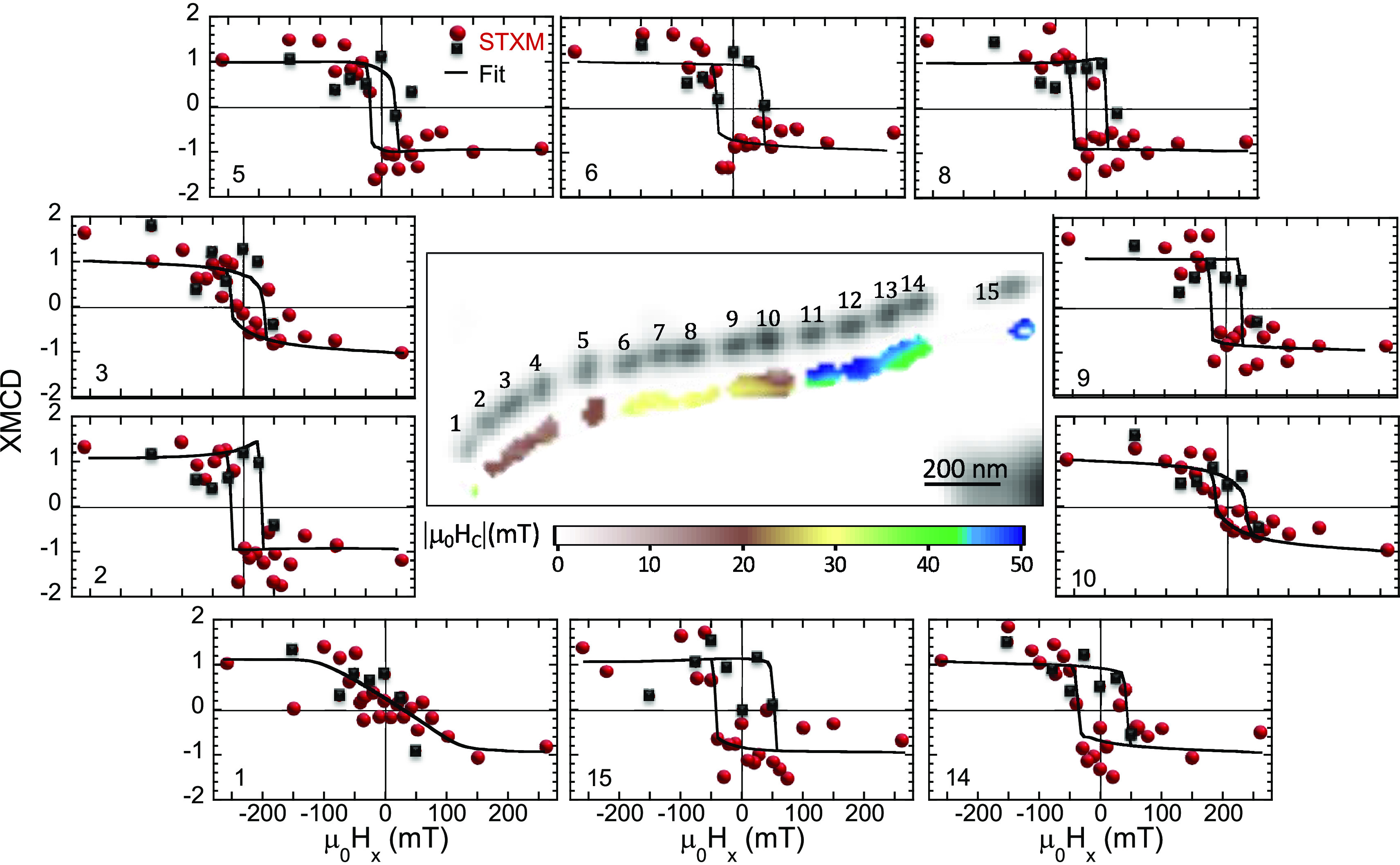
Hysteresis loops of individual magnetosomes: experiment vs model. Center: Space-resolved XAS image of the intracellular 15-magnetosome chain collected at the Fe L₃-edge resonance energy (709.3 eV) displayed in Figure 2. The color map below corresponds to the coercive field, |μ₀H_c| map, that is, the μ₀H_x value at which the interpolated dichroic signal of the first branch of the hysteresis loop (μ₀H_x from 260 to −260 mT) becomes null. Figures around the previous one represent the space-resolved hysteresis loops obtained for selected magnetosomes of the chain. Red spheres correspond to the decreasing field branch (+ to −) and black squares to the increasing field branch (− to + ). Continuous lines correspond to the simulated hysteresis loops considering the optimal values found for the anisotropy constant (K) and polar (α) and azimuthal (λ) angles shown in Figure 5.

Quantitative information on the magnetic anisotropy constant and orientation of the magnetic easy axis of each individual magnetosome has been gathered from the theoretical modeling of the hysteresis loops. According to the Stoner–Wohlfarth model⁵¹ for uniaxial magnetic single domains, the equilibrium magnetic orientation of each magnetosome’s magnetic moment can be determined by minimizing the single dipole energy density, given by the sum of an effective uniaxial anisotropy contribution along the [111] direction and the Zeeman energy:

1

Here, vectors are referred to the xyz reference system shown in Figure 2a. K is the effective uniaxial anisotropy constant, û_m is the magnetic moment unit vector defined by the polar and azimuthal angles θ and φ, respectively, and û₁₁₁ is the unit vector along the direction of the effective magnetic easy axis, namely, the [111] direction defined by the polar and azimuthal angles α and λ, respectively (Figure 1d). Here we assume that the uniaxial shape anisotropy plays a dominant role compared to the weak cubic magnetocrystalline anisotropy of magnetite.^49,50 This is evidenced in the zero-field energy surfaces constructed considering both contributions (see Figure S3 in the Supporting Information), where it is shown that the overall anisotropy remains uniaxial along the [111] long axis regardless of the cubic contribution. In addition, taking into account the coherent rotation of neighboring magnetosomes’ magnetic moments as suggested by the STXM imaging, the magnetic interactions between nearest neighbors are expressed in the same way as a uniaxial anisotropy energy,⁶⁰ thus the effective anisotropy term accounts for the competition between both contributions: shape anisotropy and dipolar interactions between nearest neighbors, and a minor contribution from the cubic magnetocrystalline anisotropy. Finally, in the Zeeman term, û_H represents the 3D applied magnetic field unit vector and M_s is the spontaneous magnetization, set to that of magnetite M_s = 48 × 10⁴A/m. The analytical expression used for the field H⃗ has been obtained from the fit to the experimental calibration points (Figure 2c).

For a given function E(θ, φ), hysteresis loops have been simulated assuming a dynamical approach that accounts for the thermal fluctuations of the magnetization, as described elsewhere.⁵²⁻⁵⁴ For each magnetosome, we have calculated a collection of hysteresis loops considering combinations of the three variables K, α, and λ, where K ∈ [10 kJ/m³, 30 kJ/m³], α ∈ [44°, 136°], and λ ∈ [−90°, 90°]. For each combination (K, α, λ), the goodness of the fit is evaluated by calculating the root-mean-square deviation (RMSD) between the experimental and calculated hysteresis loops following the expression shown in the Methods. The best agreement between the experimental and calculated hysteresis loops corresponds to the combination (K, α, λ) that minimizes the RMSD (asterisks in Figure 5a–c).

Figure 5.

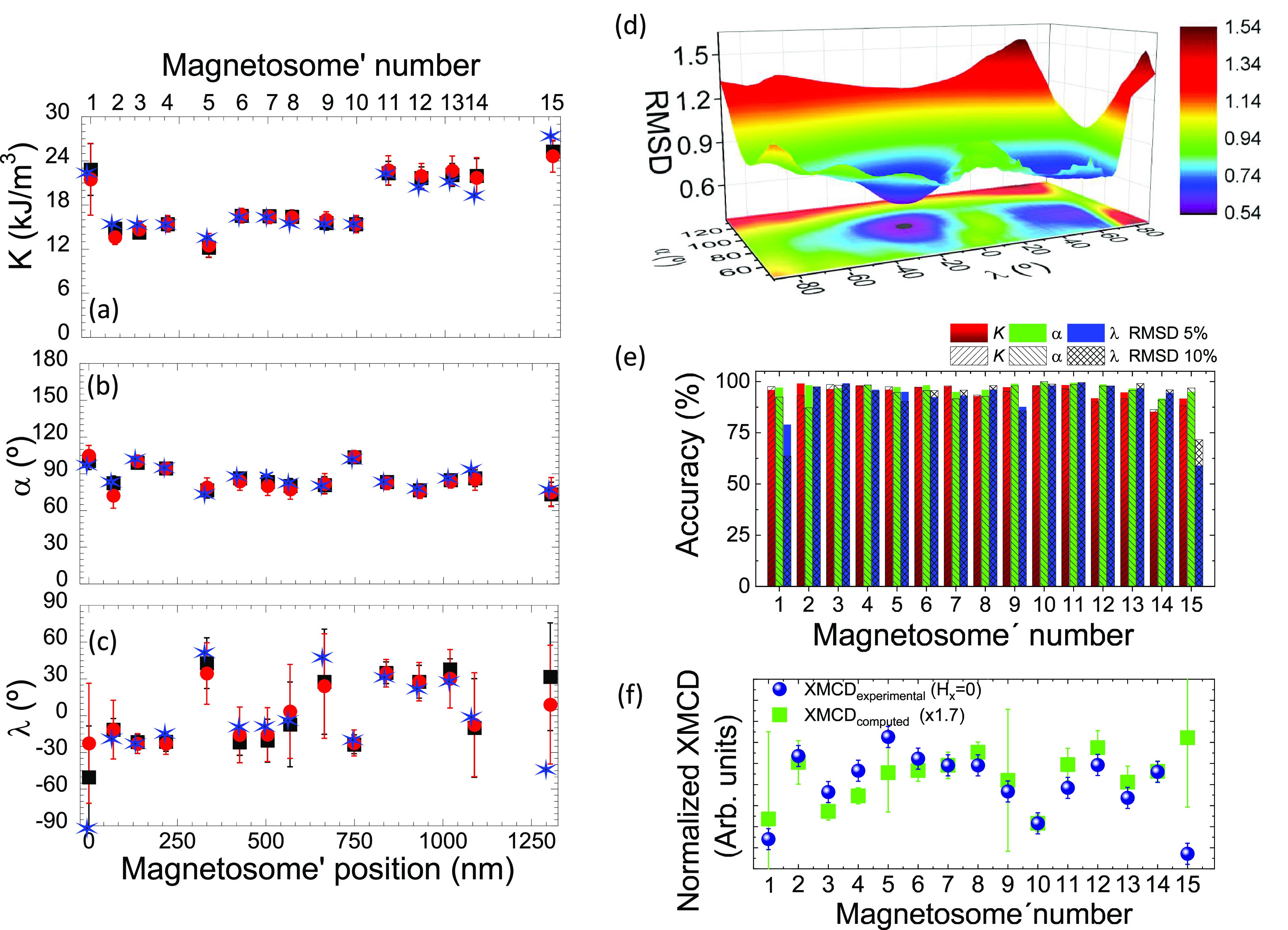
Magnetic anisotropy constant and orientation of the magnetic easy axis of individual magnetosomes. (a) Effective uniaxial anisotropy constant (K) and (b) polar (α) and (c) azimuthal (λ) angles extracted from the fit of the STXM hysteresis loops of the uniaxial anisotropy axis of the magnetosomes. Blue asterisks represent the best theoretical-experimental match (minimum root-mean-square deviation, RMSD) used for the simulations in Figure 4. Black squares and red spheres represent the mean value of the RMSD distributions within a confidence interval of 5% and 10% with respect to RMSD_min. The error bars represent the standard deviations of the distributions. (d) 3D distribution and contour plot of the RMSD as a function of α and λ obtained for magnetosome 2 considering an effective anisotropy constant value K = 15 kJ/m³. (e) Accuracy of the fitted variables K, α, or λ for each of the magnetosomes for a confidence limit of 5% (full bars) and 10% (dashed bars) of the RMSD. (f) Comparison between experimental XMCD dependence on magnetosome number obtained at H_x = 0 (blue dots) and the expected (computed) XMCD for an easy axis oriented along the direction defined by the α and λ values of panels b and c considering a RMSD confidence of 5% (green squares). The XMCD_experimental has been obtained from the data depicted in Figure 4 by averaging the absolute value of the XMCD at H_x = 0 for the increasing and decreasing field branches. Error bars for XMCD_experimental have been set to ±0.1 based on the XMCD signal dispersion measured experimentally. The error bars for XMCD_computed have been calculated from the 5% RMSD reported errors for α and λ.

In Figure 4, we have included the best fit curves for ten selected magnetosomes. The curves reproduce satisfactorily the experimental hysteresis loops. Consistently, the coercive field values obtained experimentally for the 260 to −260 mT branch (see Figure 4) are comparable to the ones obtained from the fit to our model. Note, however, that the hysteresis loops are not symmetric with respect to μ₀H_x; see, for example, loops corresponding to magnetosomes 3 and 6. This is due to the experimentally imposed axi-asymmetric magnetic field. This characteristic applied magnetic field introduces an asymmetry in the system which is essential to determine the 3D orientation of the magnetization easy axis. A magnetic field purely directed through the x direction would not allow to accurately determine the orientation of the easy axis due to a degeneracy in the model which makes +λ and –λ indistinguishable (see Figure S4 in the Supporting Information). This degeneracy is removed with axi-asymmetric fields (see the Supporting Information). Moreover, the field asymmetry reduces the correlations between the three adjustable parameters, improving the robustness of the simulations. Likewise, the geometry imposed on the experimental system also favors to discern slight changes in the orientation of the magnetosomes (particularly, α). Since the dichroic signal recorded by STXM is proportional to the projection of the magnetic moment along the beam direction, and not to the direction of the applied field, small changes of ±10° in α change drastically the profile of the hysteresis loops (see the Supporting Information, Figure S5). Such large differences simplify the fitting process.

The best-fit values for the three adjusted parameters for each one of the 15 magnetosomes are marked with blue asterisks in Figure 5a–c.

The values obtained for the effective uniaxial anisotropy constant range from K = 12 kJ/m³ (magnetosome 5) to K = 27 kJ/m³ (magnetosome 15) (Figure 5a). As indicated previously, the effective anisotropy constant includes the contributions of the particle shape anisotropy and the dipolar interactions between particles plus a minor contribution from the magnetocrystalline anisotropy.

An estimation of the shape anisotropy constant can be gathered from the calculation of the shape anisotropy energy landscape of a truncated hexa-octahedron morphology using a model based on finite element method⁶¹ (more details can be found in the Supporting Information). As expected, the model confirms that for this geometry there is only one absolute energy minimum along the elongated direction parallel to the ⟨111⟩ crystallographic axis. The energy barrier between the minima and maxima, and hence the shape anisotropy of the hexa-octahedral magnetosomes, depends on their elongation degree (width/length, W/L). For an average magnetosome of MV-1 with W/L = 0.72,⁶² the model yields K_shape = 22 kJ/m³, of the same order as the values obtained from the fits. The differences in K observed among the magnetosomes can thus be ascribed to either changes in the W/L ratio and/or the dipolar interactions between magnetosomes.

Regarding the orientation of the magnetic easy axis ([111] elongated direction) of the magnetosomes, Figure 5b and c shows the results obtained for α and λ for the 15 magnetosomes.

The polar angle, α, is a parameter that can be determined with great accuracy, as later evidenced by the small indetermination of the results. α, that is, the inclination of the easy axis with respect to the sample plane, is expected to be close to 90° because the bacterium lies on the substrate plane and so magnetosomes are also expected to rest on this very same plane. Indeed, we found that the α distribution for all the magnetosomes is centered at 90° albeit with some dispersion of ±15.

On the other hand, λ ranges between ±90°. For instance, the magnetic easy axis of magnetosome 1 is mostly perpendicular to the μ₀H_x field direction, which agrees with the anhysteretic hysteresis loop observed for this nanoparticle in Figure 4.

For the sake of proving the accuracy of the values obtained for the three variables (K, α, and λ) by the minimization of the RMSD and for determining their uncertainties, we have performed a statistical analysis of all fitted curves by assessing the dispersion and asymmetry of the parameter space close to the minima. To illustrate this, Figure 5d shows an example of the 3D representation of the RMSD as a function of the variables α and λ for magnetosome 2, where the absolute minimum RMSD_min is well observed. We have calculated the probability distribution of each variable by considering the simulations that give a RMSD that lies below a certain confidence limit. Here we have considered two confidence limits: 5% and 10% above RMSD_min; see the Supporting Information (section S6) for more details. The values obtained from the fit (blue asterisks in Figure 5a–c) are considered to be accurate if they are similar to those obtained by averaging the values from the statistical distributions within their respective confidence limits (black squares and red spheres for 5% and 10% confidence limits, respectively). The standard deviations of the distributions have been taken as a measure of the uncertainty of the corresponding variable and are represented by black (5%) and red (10%) error bars in Figure 5a–c. As depicted in panels (a)–(c) of Figure 5, the values determined from the fit (blue asterisks) and those determined from the statistical analysis (black squares and red dots) are alike in most of the cases. We have defined the accuracy on the determination of a given variable (K, α, or λ) as accuracy = 100 × ((1 – |V_fit – V_stat.|/ΔV) where V_fit and V_stat are the values of that variable obtained from the fit and from the statistical analysis (confidence of 5% and 10%), respectively. ΔV is the range over which the variable has been explored (20 kJ/m³ for K, 92° for α and 180° for λ). As shown in Figure 5e, while the average accuracy of λ is ≈92%, the accuracy on the determination of both α and K is even higher and reaches 95% on average.

Besides the fact that the obtained fit variables fall within expectation and possess statistical significance, we can further asses the robustness of the proposed method by comparing the outcome of the fits with the experimental data. By making use of the α and λ fitted variables, defining the [111] magnetic easy axis for each magnetosome, and by taking into account the geometry of the experiment (see Methods) we can compute the expected XMCD at H = 0. Indeed, in the absence of any external magnetic field, the magnetization direction for each nanomagnet is expected to lay along its own magnetic easy axis. The computed XMCD (for H = 0) is depicted in Figure 5f by green squares. For the sake of comparison we show with blue dots the XMCD measured experimentally at H_x = 0. We consider that the y and z components (for H_x = 0) are not strong enough to significantly drag the magnetization away from its easy axis direction. We also note that the fits leading to the K, α, and λ values reported in Figure 5a–c assigned the same weight to all XMCD data points (see Figure 4) obtained for different magnetic fields. That is, the XMCD measured at H_x = 0 has no special influence in the outcome of the fit. Although evident, this information is relevant because it ensures that we can compare the outcome of the fit, that is, the fitted [111] direction of the magnetic easy axis, with an specific XMCD image which signal is determined by the orientation of the experimental [111] magnetic easy axis. As shown in Figure 5f, there is very good agreement between the experimental and computed XMCDs. We note that this resemblance is not just restricted to a comparison between computed and experimental data on a magnetosome by magnetosome basis. The computed curve does also reproduce the variation of XMCD in between magnetosomes. Such a difference, solely due to the different orientations of their [111] magnetic axes, is fully reproduced by the computed curve. This proves, not only that the α and λ fit variables (resulting from 15 independent fits) are within experimental error similar to the experimental ones, but also that the method here proposed is self-consistent and yields reliable results capable of capturing the physics of the system.

Conclusions

In summary, here we have demonstrated the potential of a combined experimental–theoretical approach to obtain relevant quantitative magnetic information on nanomagnets. Selecting the proper magnetic imaging technique allows using this approach even for encapsulated systems, in particular it is suitable for nanoparticles embedded in biological entities. The method has been applied to magnetotactic bacterium M. blakemorei strain MV-1. First, space-resolved magnetic hysteresis loops with nanometric resolution are obtained by means of axi-asymmetric STXM-XMCD. Subsequently, the experimental magnetic hysteresis loops are fitted by means of a Stoner–Wohlfarth-based approach allowing obtaining relevant quantitative magnetic information in terms of the magnetic anisotropy constant and orientation of the magnetic easy axis. The asymmetry of the applied field allows an accurate theoretical modeling of the experimental hysteresis loops removing degeneracies inherent to symmetric magnetic field configurations.

In conclusion, we present an experimental and theoretical approach to explore in an element-specific way the magnetic properties of anisotropic magnetic nanostructures. We show that this method can be applied to nanomagnets embedded in biological entities including systems based on isolated magnetic nanoparticles for biomedical applications. Although it is true that the application of the presented method requires access to a large scale facility, recent progress in laser-driven X-ray sources suggests that this might change. Indeed, these so-called betatron-type plasma X-ray sources, with dimensions orders of magnitude smaller than those of synchrotron radiation facilities, can deliver X-ray radiation with tunable polarization, high spatial coherence, and a peak brightness similar to that of third-generation synchrotrons.⁶³⁻⁶⁶ Hence, it is not unreasonable to expect that, in a not too distant future, compact laser-driven plasma X-ray sources will allow the here presented method to become a standard laboratory technique.

Methods

Bacterial Strain and Growth Conditions

Magnetovibrio blakemorei strain MV-1 (DSM 18854) was grown anaerobically at 30 °C in liquid medium containing per liter of artificial seawater (ASW): 41.8 mM sodium succinate and 2.4 mM sodium acetate as carbon sources, 0.33% (wt/vol) casamino acids, 33.4 mL modified Wolfe’s mineral solution and iron quinate (100 μM) as iron source to enhance magnetosome formation. The medium was distributed into Hungate tubes and fluxed with nitrous oxide (N₂O) for 20 min prior to autoclaving (15 min, 121 °C). Finally, after the media was cooled to room temperature, 0.58 mM cysteine was added.⁶⁷ After 144 h of incubation, when well-formed magnetosomes were observed, the cells were harvested by centrifugation, washed three times in mQ water, and fixed in 2% glutaraldehyde.

Subsequent measurements were performed on unstained cells adsorbed onto 300 mesh carbon-coated copper grids. A 5 μL drop of MV-1 in concentration 10⁹ cell/mL was deposited onto Cu grids. To obtain homogeneous samples, infrared radiation was used during the deposition aimed at accelerating the drying and minimizing the surface tension.

Transmission Electron Microscopy

TEM images were acquired with a PHILIPS EM208S electron microscope at an accelerating voltage of 120 kV.

X-ray Magnetic Circular Dichroism (XMCD)

Room temperature XMCD experiments were carried out using ALICE station^68,69 at the PM3 beamline of synchrotron BESSY II in Berlin, Germany. Data acquisition was done in transmission mode. X-ray radiation (circularly polarized, right helicity, beam size 100 × 200 μm²) impinged the sample surface at normal incidence. X-ray absorption spectra (XAS) were obtained across the Fe L₃-edge with a step size of 0.2 eV with an applied magnetic field parallel to the X-ray beam of +0.35 T (σ⁺) and −0.35 T (σ^–). Six spectra were acquired and averaged to improve the signal-to-noise ratio. XMCD, defined as σ^– – σ⁺, is proportional to the projection of the magnetization along the beam propagation direction. Under the described experimental conditions, the normalized XMCD would only depend on the magnetic orientation of the magnetization for each magnetosome (defined by α and λ, see Figure 1) so that XMCD = ctt(sin 30 sin α cos λ + cos 30 cos α), where ctt is a constant common to all magnetosomes.

Scanning Transmission X-ray Microscopy (STXM)

Magnetic imaging of individual magnetosome chains within M. blakemorei was performed at room temperature by means of scanning transmission electron microscopy (STXM) using X-ray magnetic circular dichroism (XMCD) as a magnetic contrast mechanism. Measurements were carried out at the MAXYMUS end station at HZB BESSY II, Berlin.

The Cu grid, with the sample deposited on it, defines the xy-plane. The beam impinged the sample surface at 30° from its normal, a standard configuration of the STXM system allowing a nonzero projection of the magnetization for in-plane magnetized systems along the beam propagation direction. A system based on four rotatable permanent magnets³¹ produces an axi-asymmetric magnetic field where the intensity and direction of the y and z components depend on the μ₀H_x (ranging between ±260 mT); see Figure 2.

Magnetic imaging was performed as a function of μ₀H_x which was cycled from +260 mT to −260 mT and vice versa. The 110 × 45 pixel images correspond to a field of view of 1100 × 450 nm². The space-resolved transmission was recorded by scanning the beam position in 10 nm steps. At each magnetic field point we obtained images at the Fe L₃ resonance (709.3 eV) for incoming circularly polarized radiation with σ⁺ and σ^– helicity, respectively. The integration time was set to 20 ms. Each image was normalized to a bright field image and drift corrected to a reference image. The XMCD images were computed as σ^– – σ⁺. This process was repeated twice to improve signal-to-noise ratio. Magnetic hysteresis loops of individual magnetosomes displayed in Figure 4 were obtained by integrating the XMCD signal over their position as a function of μ₀H_x. The hysteresis loop displayed in Figure 3 has been obtained by averaging the XMCD over the whole magnetosome chain.

For the sake of enhancing the magnetic contrast, and thus the visualization of the XMCD, Figure 3 shows XMCD images obtained after multiplication of the original XMCD signal by the X-ray absorption image (XAS = σ^– + σ⁺) after background subtraction.

The 2D map of |μ₀H_c| displayed in Figure 4 was obtained by smoothing and interpolating the XMCD vs μ₀H_x signal obtained for the positive branch (from +260 to −260 mT) at each pixel of the image. The local coercive field was defined to be that corresponding to the μ₀H_x value for which XMCD crossed zero.

Hysteresis Loop Simulation and Fitting Procedure

For a given function E(θ, φ), the hysteresis loops have been modeled assuming a dynamical approach described elsewhere.⁵²⁻⁵⁴ A collection of more than 85 500 hysteresis loops were simulated considering different values of K, α, and λ. K was varied from 10 to 30 kJ/m³ in steps of 1 kJ/m³, α was ranged between 44° and 136° on steps of 2°, and λ was varied between −90° and 90° in steps of 2°.

The hysteresis loops have been computed by considering the axi-asymmetric magnetic field and the geometry used for the experiments. Note that following the geometry of the experiment, described in Figure 2, the y axis of the simulated hysteresis loop corresponds to the projection of the magnetization vector along the beam direction, that is, 120° off the xy sample plane. It explains that a saturating positive field gives a negative magnetization and vice versa.

Each simulation was compared with the experimental hysteresis loops obtained for each individual magnetosome aiming to find the best fit. Thus, the three variable parameters associated with the magnetic anisotropy constant and the orientation of the magnetic easy axes (K, α, and λ) have been adjusted to minimize for each magnetosome the root-mean-square deviation (RMSD):

2

where i represents the number of experimental points acquired in the experiment, 28 in our case, and d is the number of degrees of freedom defined as the number of experimental data minus the number of parameters computed, three in this particular problem: K, α, and λ.

In order to double check the goodness of the fit, we have carried out a statistical analysis by analyzing the RMSD distribution obtained for each single magnetosome. Thus, considering an interval of confidence of 5% and 10%, we represent the probability distribution of K, α, and λ whose RMSD values are within the defined interval (RMSD_min and RMSD_min + 5/10% RMSD_min). In this way, K, α, and λ are defined as the mean value of the probability distribution while its associated error is obtained as the standard deviation of the obtained distribution.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.1c09559.

• STXM-XAS as a function of energy (MOV)

• Magnetization process of an intracellular magnetosome chain (MOV)

• Macro- and microscopic XAS and XMCD spectroscopy, analytical expression of the axi-asymmetric magnetic field, calculation of the shape magnetic anisotropy using finite elements method, influence of the cubic magnetocrystalline anisotropy of magnetite in the energy of the system, influence of the axi-asymmetric magnetic field and geometry of the experimental system on the profile of the hysteresis loops, statistical analysis of the RMSD distribution (PDF)

Author Contributions

S.V., M.L.F., L.M, A.G.P., A.M., and A.G.A. conceived and designed the research. L.G. cultivated Magnetovibrio blakemorei cells and prepared the samples. L.M., L.G., D.G., and A.G.P. collected the XMCD data with the help of R.A., M.W., and S.V. The XMCD data were analyzed by L.M., D.G., and S.V. L.M. and I.O. adapted the Stoner–Wohlfarth model to the experimental setup. I.O. was in charge of the theoretical modeling and software development. L.M. compared experimental results with theoretical modeling. D.G. was in charge of finite element calculations. L.M., A.G.P., S.V., M.L.F., and I.O. wrote the manuscript with contributions of all authors.

The authors declare no competing financial interest.