Abstract
Background: DNA replication plays an indispensable role in the transmission of genetic information. It is considered to be the basis of biological inheritance and the most fundamental process in all biological life. Considering that DNA replication initiates with a special location, namely the origin of replication, a better and accurate prediction of the origins of replication sites (ORIs) is essential to gain insight into the relationship with gene expression.
Objective: In this study, we have developed an efficient predictor called iORI-LAVT for ORIs identification.
Methods: This work focuses on extracting feature information from three aspects, including mono-nucleotide encoding, k-mer and ring-function-hydrogen-chemical properties. Subsequently, least absolute shrinkage and selection operator (LASSO) as a feature selection is applied to select the optimal features. Comparing the different combined soft voting classifiers results, the soft voting classifier based on GaussianNB and Logistic Regression is employed as the final classifier.
Results: Based on 10-fold cross-validation test, the prediction accuracies of two benchmark datasets are 90.39% and 95.96%, respectively. As for the independent dataset, our method achieves high accuracy of 91.3%.
Conclusion: Compared with previous predictors, iORI-LAVT outperforms the existing methods. It is believed that iORI-LAVT predictor is a promising alternative for further research on identifying ORIs.
Keywords: Origin of replication sites, multi-feature, LASSO, voting classifier, DNA replication, dimensional feature
1. INTRODUCTION
DNA replication is considered as the basis of biological inheritance and always occurs in all organisms in which DNA is the genetic material. This biological process plays an important role in maintaining the stability of genetic information of biological species. Based on one of the originally double-stranded molecules as a template, it generates two exactly the same DNA molecules [1]. DNA replication includes three stages: initiation, extension and formation. In the initial stage, the replication initiation site is selected, the pre-replication complex (pre RC) is assembled, and then the activation of pre RC and the initiation of DNA replication are completed. In the extension phase, a variety of DNA polymerases work together to complete the DNA synthesis. In the termination step, the protein recognizes and binds to the replication termination site to prevent DNA replication and prevent the progress of the replication fork, resulting in DNA replication termination.
In the whole process of DNA replication, the effective prediction and identification of replication initiation sites ensure the authenticity of the DNA replication. The genes of parents can be effectively inherited by the offspring to ensure biological stability inheritance, which is of great significance to reproduction and biological evolution. Although the replication machinery differs between species, they also share some commonalities, such as the origin of replication [2, 3]. Therefore, the valid prediction of the origins of replication sites is important for a further understanding of gene expression and regulation during cell division. To some extent, it could also accelerate the development process of specific drugs for diseases due to genome duplication problems [4-6].
For this purpose, some laboratory methods, including chromatin immunoprecipitation (ChIP), ChIP-sequencing, DNase I footprinting technique, and electrophoretic mobility shift assays, have been employed to identify ORIs [2, 7]. Subsequently, to understand the genomic information more effectively, some biological sequence data modeling [8, 9] methods have begun to be applied to the construction of genome data, thus obtaining a large amount of biological data. They can also provide a large amount of data basis for many researchers later. However, considering the explosive growth of biological sequences and the time-consuming and expensive defects of traditional laboratory methods, traditional experimental methods are not suitable for predicting ORIs. In this context, some computational tools have been developed and applied to the recognition of ORIs. For prokaryotic ORIs, an Ori-Finder system based on Z-curve method is constructed by Gao et al. [10, 11] to identify ORIs in bacterial and archaea genomes. Subsequently, a method based on motif [12] was proposed to identify the ORIs in Gammaproteobacteria. Based on the accumulation of experimental biological data, a recent review has summarized the development of computational methods for the identification of eukaryotic ORIs [13]. Although these computational tools can identify ORIs, they can only predict the ORIs of positive samples. Thus, faster and more valid computational methods are urgently needed to identify ORIs.
To overcome the defects of above models, some new computational methods have been proposed to identify ORIs. Chen et al. [14] established the first predictor based on DNA structural properties and support vector machine (SVM). Then, Type-I PseKNC [15] and Type-II PseKNC [16] were proposed using pseudo k-tuple nucleotide composition and SVM. Soon afterwards, Xing et al. [17] designed a predictor using seven feature extraction methods and SVM. Subsequently, Do et al. [18] constructed a predictor using extreme gradient boosting (XGBoost), FastText and PseKNC. Recently, a model named iORI-Euk [19] was proposed by Dao et al., which is based on sequence binary encoding and SVM. Furthermore, there are still some relevant researches focused on identifying ORIs, such as those of Manavalan et al. [20], Wei et al. [21], and iORI-ENST [22].
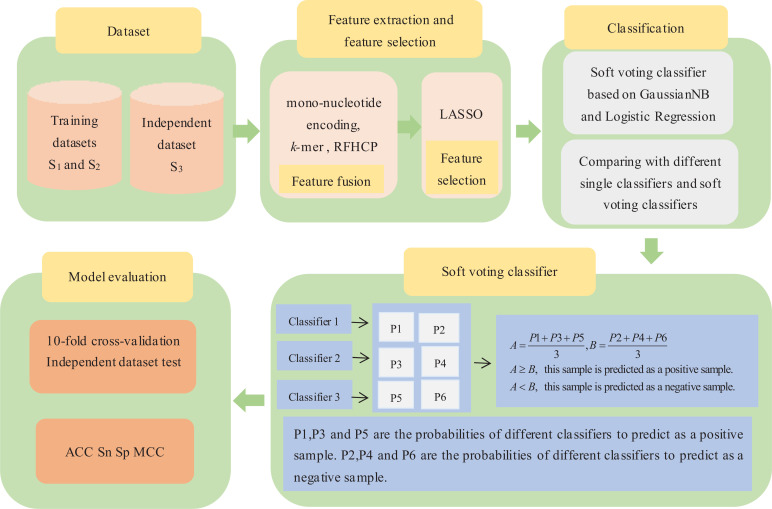
Although there exist some methods to identify ORIs, their prediction performance is not ideal. Driven by previous predictors, a new and powerful model named iORI-LAVT has been developed for predicting ORIs. Firstly, mono-nucleotide encoding, k-mer and ring-function-hydrogen-chemical properties are used to extract sequence information. Secondly, LASSO is employed as a feature selection to choose the optimal feature set. Finally, the soft voting classifier based on GaussianNB and Logistic Regression is selected as the final classifier to identify ORIs. After that, 10-fold cross-validation test and independent dataset test are carried out to evaluate the feasibility of our model. In order to facilitate the understanding of the readers regarding our article, Fig. (1) shows the flow-chart diagram of iORI-LAVT.
Fig. (1).
The flow-chart diagram of iORI-LAVT.
2. MATERIALS AND METHODS
2.1. Dataset
To establish a statistical predictor, the key step is to select reliable datasets for the experiment. In this paper, three datasets are used to validate our model. Within three datasets, S1 and S2 are training datasets, and S3 is an independent dataset. S1 is a dataset constructed by Li et al. [15], which belongs to the Saccharomyces cerevisiae (S.cerevisiae) genome. The first 704 S.cerevisiae ORI sequences were derived from the database OriDB (http://www.oridb.org/). To ensure that the constructed dataset was reliable, we removed those suspected ORI sequences and kept only the “confirmed” 410 ORI sequences. Then, CD-HIT software [23] was used to eliminate samples with more than 75% redundancy and bias. Finally, 405 ORI sequences were obtained and 406 non-ORI sequences have been obtained in the same way. S2 and S3 are derived from Arabidopsis thaliana (A. thaliana) genome and have been created by Dao et al. [19]. The experimental samples were taken from the database Deori (http://origin.tubic.org/deori/ . Moreover, CD-HIT software [23] was used to eliminate samples with more than 80% redundancy and bias. S2 contains 1015 ORI sequences and 1015 non-ORI sequences, and S3 is made of 500 ORI sequences and 500 non-ORI sequences. In addition, to retain the information as much as possible and reduce the noise of different lengths, the length of all the given DNA sequences is 300bp. Table 1 presents the composition of the experimental dataset.
Table 1.
The composition of the experimental dataset.
| Dataset | ORI Sequences | Non-ORI Sequences | Total |
|---|---|---|---|
| S1 | 405 | 406 | 811 |
| S2 | 1050 | 1050 | 2030 |
| S3 | 500 | 500 | 1000 |
2.2. Feature Extraction
Feature extraction is an important step in constructing effective predictors. In this process, it converts the original biological sequences into digital vectors which can be processed by a computer. In addition, with the development of bioinformatics, some multi-feature extraction methods have been widely applied to various pattern recognitions. Many studies have also shown that multi-feature can not only extract more complete sequence information but also improve the performance of the model. In this study, three feature extraction methods, including mono-nucleotide encoding, k-mer and ring-function-hydrogen-chemical properties, have been employed to extract the sequence information.
2.2.1. Mono-nucleotide Encoding
Mono-nucleotide encoding is an efficient and popular feature extraction method, which can convert the four single nucleotides of DNA into a 4-dimensional 0/1 vector, respectively. In this way, A is encoded as (1,0,0,0), C is encoded as (0,1,0,0), G is encoded as (0,0,1,0) and T is encoded as (0,0,0,1). For example, given a DNA sequence ‘AACGT’, it can be transformed into [1,0,0,0,1,0,0,0,0,1,0,0,0,0,1, 0,0,0,0,1]. In this way, a DNA sequence with the length of 300 bp is transformed into a 300 * 4 = 1200-dimensional feature [24].
2.2.2. K-mer
K-mer [25, 26] is a common and valid feature representation method, which represents the local sequence information and is widely used in many fields of bioinformatics. Given a sequence, k-mer is the occurrence frequency of all possible k-tuple nucleotides in the sequence. When the value of k is determined, the feature of k-mer is obtained with the dimension of 4k.
Suppose a DNA sequence with the length of L, the feature can be obtained by the following formula:
where, 
represents the occurrence frequency of the ith k-tuple nucleotides in the sequence. And is defined as:
where, 
is the occurrence number of the ith k-tuple nucleotides in the sequence.
For example, when k=2, the feature of 2-mer is:
where, 
is the occurrence frequency of 
in the given DNA sequence and then the feature of 2-mer is obtained with the dimension of 16. Likewise, 3-mer and 4-mer are obtained using this way. However, with the increase of k, the dimension of k-mer feature is also gradually increasing, thus leading to distorted dimension. Therefore, the value of k is set as 2, 3 and 4 in this study. Eventually, each DNA sequence is transformed into 42 + 43 + 44 = 336 dimensional vectors.
2.2.3. Ring-function-hydrogen-chemical Properties (RFHCP)
Any DNA sequence consists of four basic nucleotides: adenine (A), cytosine (C), guanine (G) and thymine (T). Some studies have shown that the four nucleotides of DNA have significant chemical property differences in ring structure, hydrogen bond strength and functional group [27-31]. As far as ring structure is concerned, there are two rings in A and G, while one ring is formed in C and T. Based on the strength of the hydrogen bond, four basic nucleotides can be divided into two groups: A and T, C and G. Considering the different functional groups, A and C are amino groups while G and T are ketone groups. On the basis of these properties, every nucleotide is transformed into 
:
In brief, the four basic nucleotides A, C, G, and T are transformed as (1,1,1), (0,0,1), (1,0,0), and (0,1,0), respectively.
Considering the relevance of a single nucleotide within the DNA sequence, a density method is designed by evaluating the importance of frequency and position:
where, L is the length of the given DNA sequence, 
is the length of the ith string 
in the given DNA sequence, and 
is the occurrence number of 
from starting nucleotide to the 
nucleotide. In this way, a nucleotide is expressed as 
.
For example, a sequence of ‘AACT’ can be transformed into [[1,1,1,1], [1,1,1,1], [0,0,1,0.33], [0,1,0,0.25]]. Finally, a 1200-dimensional feature is obtained.
2.3. Least Absolute Shrinkage and Selection Operator
Least absolute shrinkage and selection operator (LASSO) proposed by Robert Tibshirani is a compressive estimation method [32, 33]. By constructing an L1 penalty function, a more refined model is obtained, which compresses some regression coefficients and set some regression coefficients to 0. Therefore, it retains the advantage of subset contraction and is a biased estimation for processing complex linear data.
is a given dataset. 
is a data sample, 
is a class label, 
is the dimension of the sample and m is the number of the dataset. We refined a simple linear regression model with the square error as a loss function. The optimization goal is:
where, 
data matrix, 
is a column matrix consisting of labels, and ω is the weight coefficient. Therefore, the problem has an analytical solution:
If d > m, it is not full rank and there will be infinite solutions. We are not sure which is the optimal solution, so it is easy for the problem of overfitting to occur. In addition, for an ordinary linear model, its complexity is related to the number of variables. And the more the variables, the more likely for overfitting to occur. Therefore, we need filter variables to obtain a better performing parameter and reduce the complexity of the model. Lasso is a common method, which invovles L1 penalty function:
where, ω is the weight coefficient, λis the regularization parameter, and m is the number of samples. It is equivalent to the following formula:
where, C corresponds to a constant. In other words, we restrict the model space by limiting the size of the norm, thus avoiding overfitting to some extent. Based on the advantage, LASSO is widely used in the field of pattern recognition [34, 35].
2.4. Soft Voting Classifier
Soft voting classifier is an important type of ensemble learning, which predicts the probability of different classifiers for a certain class, and then compare their average values to select the category of their maximum value as the final result. Compared to the traditional single classifier, soft voting classifier model is more stable and accurate. Therefore, the soft voting classifier is also beneficial in constructing predictors. In this paper, these classifiers are used to test the model, including Logistics Regression [36], GaussianNB [37], eXtreme Gradient Boosting [38], Support Vector Machine [39] and Random Forest [40]. Through a series of analyses and comparisons in section 3.3, a soft voting classifier based on GaussianNB and Logistics Regression is established for identifying ORIs.
2.4.1. GaussianNB
GaussianNB [37] is a probability method that can make predictions based on sample data. The algorithm's essence is to classify the given classification items by determining the probability of each category under this condition. Finally, it is estimated as to which category has the highest probability of occurrence.
is a given dataset, where d is the dimension of the feature and m is the number of the dataset. 
dataset matrix, 
is a column matrix consisting of labels. Assuming that 
is a category to be classified, then 
is the sample x of feature and d is the dimension of sample x. While 
is the possible category of prediction for the dataset, where l is the number of all possible categories. The detailed algorithm steps are as follows:
(I). Calculate the probabilities of different categories in the total samples:
(II). Calculate the conditional probabilities that x belongs to each category in turn:
where, 
are respectively the mean value and variance of feature item 
in the training sample category 
.
(III). Comparing all the conditional probabilities in (II), the category of its maximum value is the prediction classification result:
2.4.2. Logistic Regression
Logistic regression [36], also known as logistic regression analysis, is a generalized linear regression analysis model. It is widely used in the fields of data mining, automatic diagnosis of diseases and economic prediction. Compared to common linear regression, it adds a sigmoid function and is often used in classification problems. The algorithm principle of logistic regression is as follows:
a) Constructing a prediction function (a sigmoid function), the expression of the function is
where the optimum parameter is 
data matrix, m is the number of samples, and d is the dimension of samples.
b) Establish the loss function of Logistic Regression:
where, 
is a column matrix consisting of labels.
c) Solve the minimum value of loss function using gradient descent method:
Finally, the parameter update formula is:
2.5. Performance Evaluation
To further illustrate the feasibility and rationality of our model, 10-fold cross-validation test and independent dataset testing were adopted to evaluate our model. Here, we have analyzed our model with the following four indicators: accuracy (ACC), sensitivity (Sn), specificity (Sp) and Matthew’s correlation coefficient (MCC) [41-54]. The calculation formulas of these four evaluation indexes are as follows:
where, 
is the total number of ORI sequences, 
is the total number of non-ORI sequences. 
represents non-ORI sequences incorrectly predicted as ORI sequences, while 
represents ORI sequences incorrectly predicted as non-ORI sequences.
3. RESULTS AND DISCUSSION
3.1. Comparison of Feature Representation Methods
To a great extent, the determination of feature extraction methods plays a decisive role in the quality of a prediction model. Furthermore, to achieve better results for experimental model, we have carried out three experiments. They are MEK, RFHCP, and combined features of MEK and RFHCP. MEK is the combination of mono-nucleotide encoding and k-mer. Mono-nucleotide encoding represents the location information of four single nucleotides in a sequence. K-mer is the frequency information of the occurrence of all possible K-tuple nucleotides in a sequence. Finally, we can obtain a 1536-dimensional feature vector by MEK. RFHCP involves the information of ring-function-hydrogen-chemical properties and the relevant information of a single nucleotide within a sequence. The feature of RFHCP is obtained with a 1200-dimensional feature vector. The feature of ‘MEK+RFHCP’ comprises the combined features of MEK and RFHCP, and it is a 2736-dimensional feature vector. To facilitate the readers’ understanding of the observation results, Figs. (2 and 3) have been provided that compare the performance of combined feature extraction and single feature extraction representation on S1 and S2 datasets, respectively. It can be clearly seen that the performance of the method combining MEK and RFHCP is superior to the single feature representation method. It indicates that the combined feature of MEK and RFHCP can not only obtain more DNA sequence information but also improve the prediction result of the model.
Fig. (2).
The performance comparison of different feature representation methods on S1.
Fig. (3).
The performance comparison of different feature representation methods on S2.
3.2. Comparison Among Various Feature Selection Methods
Feature selection is a crucial step in the process of modeling. In this work, we have tried to use Principal Component Analysis (PCA) [55], mutual_info_classif (MIC), Light Gradient Boosting Machine (LGBM) and LASSO [32, 33] to reduce the dimension of the model. PCA is a statistical method, which transforms a set of variables that may be correlated to a set of linearly unrelated variables through orthogonal transformation. The parameters of PCA are n-components=150 in S1 and n_components=100 in S2. MIC is a filtering method that is used to capture the arbitrary relationship (including linear and nonlinear relationship) between each feature and the label. The parameter of MIC is n_neighbors=3. LGBM is a method of feature selection by calculating the importance of each feature through information gain, and the parameter of LGBM is n-estimators =100. Fig. (4) shows the experimental results of different feature selections. It can be seen from Fig. (4) that LASSO has an advantage over other three feature selection methods in both S1 and S2 datasets. Therefore, LASSO is chosen to reduce the dimension of the feature. In addition, the optimal parameters are searched from 0.001 to 0.1 with an interval of 0.001.
Fig. (4).
Comparison of accuracy of different feature selection methods.
3.3. Comparison of Multiple Classifiers
There are various methods of machine learning, and each method has its own advantage. In order to select a more suitable classifier for our model, we first tested the familiar classification methods, including Logistic Regression (LR) [36], GaussianNB [37], eXtreme Gradient Boosting (XGB) [38], Support Vector Machine (SVM) [39] and Random Forest (RF) [40]. The parameters of LR are penalty='l2' and C=1; The parameters of GaussianNB are priors=None and var_smoothing=1e-09; the parameter of XGB is n-estimators =100; The parameters of SVM are C = 1 and gamma = ‘scale’; the parameter of RF is n-estimators =100. The experimental results of each classifier on S1 and S2 datasets have been compared, as shown in Fig. (5). It can be seen from Fig. (5) that LR, GaussianNB and SVM perform well in predicting ORIs. These three classifiers exhibited 88.29%, 89.65% and 87.92% performance metrics on S1 dataset, and 93.69%, 95.71% and 95.91% on S2 dataset.
Fig. (5).
Comparison of accuracy of single classifier with the voting classifier.
Considering that the combined effect of multiple classifiers may be better than a single classifier, we carried out soft voting on the three classifiers, which are LR, GaussianNB and SVM. Then, we put three outstanding classifiers into different soft voting combinations. Table 2 provides the four performance metrics of different soft voting classifiers. Synthesizing the results of S1 and S2 in various soft voting classifiers, the soft voting effect of GaussianNB and LR combination was found to be better than other combinations. In this voting classifier, the four performance metrics of our model accounted for 90.39%, 89.65%, 91.13% and 81.02% on S1, and 95.96%, 96.25%, 95.67% and 91.93% on S2.
Table 2.
The performance of different soft voting classifiers on S1 and S2.
| Dataset | Classifier | ACC(%) | Sn(%) | Sp(%) | MCC(%) |
|---|---|---|---|---|---|
| S1 | GaussianNB+LR | 90.39 | 89.65 | 91.13 | 81.02 |
| GaussianNB+SVM | 89.77 | 88.17 | 91.36 | 79.80 | |
| LR+SVM | 89.03 | 88.65 | 89.42 | 78.29 | |
| GaussianNB+LR+SVM | 89.89 | 89.90 | 89.90 | 79.98 | |
| S2 | GaussianNB+LR | 95.96 | 96.25 | 95.67 | 91.93 |
| GaussianNB+SVM | 95.81 | 95.86 | 95.76 | 91.63 | |
| LR+SVM | 94.43 | 94.37 | 94.48 | 88.93 | |
| GaussianNB+LR+SVM | 95.86 | 96.25 | 95.47 | 91.75 |
To judge whether the experimental model is superior to a single classifier, the accuracy comparison between the soft voting classifier combined with GaussianNB and LR and different single classifiers is also shown in Fig. (5). It has been proved that the soft voting combination of multiple classifiers is indeed better than the single classifier.
3.4. Comparison with Previous Excellent Predictors
In previous studies, many predictors [14-19] have been used to predict the origin of DNA replication, but their prediction results are not satisfactory, including Bendability+cleavage intensity [14], Type-I PseKNC [15], Type-II PseKNC [16], those proposed by Xing et al. [17], Do et al. [18], and iORI-Euk [19]. In this paper, iORI-LAVT has been improved on the basis of previous research. Table 3 shows the performance comparison between iORI-LAVT and the existing predictors on S1 and S2. On the S1 dataset, the four performance metrics were estimated as 90.39%, 89.65%, 91.13% and 81.02%, respectively. The observed improvements in ACC, Sn and MCC accounted for 0.88%, 0.02%, and 1.71%, respectively, for S1 dataset. On the S2 dataset, our model exhibited 95.96%, 96.25%, 95.67% and 91.93% of ACC, Sn, Sp and MCC, respectively, with the improvement estimated at 2.17%, 1.47%, 2.86% and 4.33% in terms of ACC, Sn, Sp and MCC, respectively. Compared to previous methods, the results show iORI-LAVT as superior to the existing predictors. To test whether the model is overfitted, employing an independent dataset test also constitutes an important step. Based on S2, S3 served as an independent dataset to verify the mobility of our model. In addition, Table 4 shows the comparison results of iORI-LAVT with previous predictors on the independent dataset S3. The four metrics of iORI-LAVT were estimated at 91.30%, 94.2%, 88.40% and 82.74%, respectively. Thus, it can be observed that it outperforms other indicators well on the basis of four performance metrics and improves ACC, Sn, Sp and MCC by 3.3%,2.6%,4%, and 6.54%, respectively.
Table 3.
The comparison results of iORI-LAVT with previous predictors on S1 and S2.
| Dataset | Method | ACC (%) | Sn (%) | Sp (%) | MCC(%) |
|---|---|---|---|---|---|
| S1 | Bendability+cleavage intensity [14] | 80.76 | 81.23 | 80.3 | 61.53 |
| Type-I PseKNC [15] | 83.72 | 84.69 | 82.76 | 67.46 | |
| Type-II PseKNC [16] | 87.79 | 89.63 | 85.96 | 75.64 | |
| Do et al. [18] | 89.51 | 85.19 | 93.83 | 79.31 | |
| iORI-LAVT | 90.39 | 89.65 | 91.13 | 81.02 | |
| S2 | Xing et al. [17] | 89.9 | 90.64 | 89.16 | 79.81 |
| iORI-Euk [19] | 93.79 | 94.78 | 92.81 | 87.60 | |
| iORI-LAVT | 95.96 | 96.25 | 95.67 | 91.93 |
Table 4.
Comparison with previous predictors on independent dataset S3.
| Method | ACC (%) | Sn (%) | Sp (%) | MCC(%) |
|---|---|---|---|---|
| iORI-Euk [17] | 88.00 | 91.60 | 84.40 | 76.20 |
| iORI-LAVT | 91.30 | 94.2 | 88.40 | 82.74 |
CONCLUSION
Efficient prediction of origin of DNA replication sites is important for further understanding gene expression and regulation during cell division. Although there are models for identifying the origin of replication sites, the effect is still suboptimal. In this study, we have established a new predictor called iORI-LAVT for identifying the origin of replication sites, which is based on LASSO selection and soft voting classifier. In addition, extraction methods, including mono-nucleotide encoding, k-mer and ring-function-hydrogen-chemical properties, are utilized to represent sequence information. Furthermore, 10-fold cross-validation test and independent dataset test are employed to evaluate our model performance. After 10-fold cross-validation test, the prediction accuracies of S1 and S2 have been observed as 90.39% and 95.96%, respectively. As for the independent dataset S3, our method achieves high accuracy of 91.3%. In contrast with other models, our model proves to be an effective tool for prediction of the origin of replication sites.
ACKNOWLEDGEMENTS
Declared none.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No animals/humans were used for studies that are the basis of this research.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data supporting the findings of the article are available in the datasets at: https://github.com/YingyingYao/ iORI-LAVT.
FUNDING
This work was supported by the National Natural Science Foundation of China (No. 12101480), the Natural Science Basic Research Program of Shaanxi (No. 2021JM-115), and the Fundamental Research Funds for the Central Universities (No. JB210715).
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
REFERENCES
- 1.Halazonetis T.D. Conservative DNA replication. Nat. Rev. Mol. Cell Biol. 2014;15(5):300. doi: 10.1038/nrm3784. [DOI] [PubMed] [Google Scholar]
- 2.Song C., Zhang S., Huang H. Choosing a suitable method for the identification of replication origins in microbial genomes. Front. Microbiol. 2015;6:1049. doi: 10.3389/fmicb.2015.01049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Waga S., Stillman B. The DNA replication fork in eukaryotic cells. Annu. Rev. Biochem. 1998;67:721–751. doi: 10.1146/annurev.biochem.67.1.721. [DOI] [PubMed] [Google Scholar]
- 4.Raghu Ram E.V., Kumar A., Biswas S., Kumar A., Chaubey S., Siddiqi M.I., Habib S. Nuclear gyrB encodes a functional subunit of the Plasmodium falciparum gyrase that is involved in apicoplast DNA replication. Mol. Biochem. Parasitol. 2007;154(1):30–39. doi: 10.1016/j.molbiopara.2007.04.001. [DOI] [PubMed] [Google Scholar]
- 5.McFadden G.I., Roos D.S. Apicomplexan plastids as drug targets. Trends Microbiol. 1999;7(8):328–333. doi: 10.1016/S0966-842X(99)01547-4. [DOI] [PubMed] [Google Scholar]
- 6.Soldati D. The apicoplast as a potential therapeutic target in and other apicomplexan parasites. Parasitol. Today. 1999;15(1):5–7. doi: 10.1016/S0169-4758(98)01363-5. [DOI] [PubMed] [Google Scholar]
- 7.Lubelsky Y., MacAlpine H.K., MacAlpine D.M. Genome-wide localization of replication factors. Methods. 2012;57(2):187–195. doi: 10.1016/j.ymeth.2012.03.022. [DOI] [PubMed] [Google Scholar]
- 8.Chen J.Y., Carlis J.V. Genomic data modeling. Inf. Syst. 2003;28(4):287–310. doi: 10.1016/S0306-4379(02)00071-6. [DOI] [Google Scholar]
- 9.Griffith M., Griffith O.L., Smith S.M., Ramu A., Callaway M.B., Brummett A.M., Kiwala M.J., Coffman A.C., Regier A.A., Oberkfell B.J., Sanderson G.E., Mooney T.P., Nutter N.G., Belter E.A., Du F., Long R.L., Abbott T.E., Ferguson I.T., Morton D.L., Burnett M.M., Weible J.V., Peck J.B., Dukes A., McMichael J.F., Lolofie J.T., Derickson B.R., Hundal J., Skidmore Z.L., Ainscough B.J., Dees N.D., Schierding W.S., Kandoth C., Kim K.H., Lu C., Harris C.C., Maher N., Maher C.A., Magrini V.J., Abbott B.S., Chen K., Clark E., Das I., Fan X., Hawkins A.E., Hepler T.G., Wylie T.N., Leonard S.M., Schroeder W.E., Shi X., Carmichael L.K., Weil M.R., Wohlstadter R.W., Stiehr G., McLellan M.D., Pohl C.S., Miller C.A., Koboldt D.C., Walker J.R., Eldred J.M., Larson D.E., Dooling D.J., Ding L., Mardis E.R., Wilson R.K. Genome modeling system: A knowledge management platform for genomics. PLOS Comput. Biol. 2015;11(7):e1004274. doi: 10.1371/journal.pcbi.1004274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gao F., Zhang C.T. Ori-Finder: A web-based system for finding oriCs in unannotated bacterial genomes. BMC Bioinformatics. 2008;9:79. doi: 10.1186/1471-2105-9-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Luo H., Zhang C.T., Gao F. Ori-Finder 2, an integrated tool to predict replication origins in the archaeal genomes. Front. Microbiol. 2014;5:482. doi: 10.3389/fmicb.2014.00482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sperlea T. Muth, L.; Martin, R γ BOriS: Identification of origins of replication in Gammaproteobacteria using motifbased. BioRxiv. 2019 doi: 10.1101/597070. [DOI] [PMC free article] [PubMed]
- 13.Dao F.Y., Lv H., Wang F., Ding H. Recent advances on the machine learning methods in identifying DNA replication origins in eukaryotic genomics. Front. Genet. 2018;9:613. doi: 10.3389/fgene.2018.00613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen W., Feng P., Lin H. Prediction of replication origins by calculating DNA structural properties. FEBS Lett. 2012;586(6):934–938. doi: 10.1016/j.febslet.2012.02.034. [DOI] [PubMed] [Google Scholar]
- 15.Li W.C., Deng E.Z., Ding H., Chen W., Lin H. iORI-PseKNC: A predictor for identifying origin of replication with pseudo k-tuple nucleotide composition. Chemom. Intell. Lab. Syst. 2015;141:100–106. doi: 10.1016/j.chemolab.2014.12.011. [DOI] [Google Scholar]
- 16.Dao F.Y., Lv H., Wang F., Feng C.Q., Ding H., Chen W., Lin H. Identify origin of replication in Saccharomyces cerevisiae using two-step feature selection technique. Bioinformatics. 2019;35(12):2075–2083. doi: 10.1093/bioinformatics/bty943. [DOI] [PubMed] [Google Scholar]
- 17.Xing Y.Q., Liu G.Q., Zhao X.J., Zhao H.Y., Cai L. Genome-wide characterization and prediction of Arabidopsis thaliana replication origins. Biosystems. 2014;124:1–6. doi: 10.1016/j.biosystems.2014.07.001. [DOI] [PubMed] [Google Scholar]
- 18.Do D.T., Le N.Q.K. Using extreme gradient boosting to identify origin of replication in Saccharomyces cerevisiae via hybrid features. Genomics. 2020;112(3):2445–2451. doi: 10.1016/j.ygeno.2020.01.017. [DOI] [PubMed] [Google Scholar]
- 19.Dao F.Y., Lv H., Zulfiqar H., Yang H., Su W., Gao H., Ding H., Lin H. A computational platform to identify origins of replication sites in eukaryotes. Brief. Bioinform. 2021;22(2):1940–1950. doi: 10.1093/bib/bbaa017. [DOI] [PubMed] [Google Scholar]
- 20.Manavalan B., Basith S., Shin T., Lee G. Computational prediction of species-specific yeast DNA replication origin via iterative feature representation. Brief. Bioinform. 2020;22(4):bbaa304. doi: 10.1093/bib/bbaa304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wei L., He W., Malik A., Su R., Cui L., Manavalan B. Computational prediction and interpretation of cell-specific replication origin sites from multiple eukaryotes by exploiting stacking framework. Brief. Bioinform. 2020;22(4):bbaa275. doi: 10.1093/bib/bbaa275. [DOI] [PubMed] [Google Scholar]
- 22.Yao Y., Zhang S., Liang Y. iORI-ENST: Identifying origin of replication sites based on elastic net and stacking learning. SAR QSAR Environ. Res. 2021;32(4):317–331. doi: 10.1080/1062936X.2021.1895884. [DOI] [PubMed] [Google Scholar]
- 23.Li W., Godzik A. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics. 2006;22(13):1658–1659. doi: 10.1093/bioinformatics/btl158. [DOI] [PubMed] [Google Scholar]
- 24.Chen Z., Zhao P., Li F., Marquez-Lago T.T., Leier A., Revote J., Zhu Y., Powell D.R., Akutsu T., Webb G.I., Chou K.C., Smith A.I., Daly R.J., Li J., Song J. iLearn: An integrated platform and meta-learner for feature engineering, machine-learning analysis and modeling of DNA, RNA and protein sequence data. Brief. Bioinform. 2020;21(3):1047–1057. doi: 10.1093/bib/bbz041. [DOI] [PubMed] [Google Scholar]
- 25.Zhang Z.Y., Yang Y.H., Ding H., Wang D., Chen W., Lin H. Design powerful predictor for mRNA subcellular location prediction in Homo sapiens. Brief. Bioinform. 2020 doi: 10.1093/bib/bbz177. [DOI] [PubMed] [Google Scholar]
- 26.Yang H., Yang W., Dao F.Y., Lv H., Ding H., Chen W., Lin H. A comparison and assessment of computational method for identifying recombination hotspots in Saccharomyces cerevisiae. Brief. Bioinform. 2020;21(5):1568–1580. doi: 10.1093/bib/bbz123. [DOI] [PubMed] [Google Scholar]
- 27.Bari A.T.M.G., Reaz M.R., Choi H.J., Jeong B.S. In: Database Systems for Advanced Applications. Hong B., Meng X., Chen L., Winiwarter W., Song W., editors. Berlin, Heidelberg: Springer; 2013. DNA encoding for splice site prediction in large DNA sequence. pp. 46–58. [DOI] [Google Scholar]
- 28.Chen W., Feng P., Tang H., Ding H., Lin H. Identifying 2-O-methylationation sites by integrating nucleotide chemical properties and nucleotide compositions. Genomics. 2016;107(6):255–258. doi: 10.1016/j.ygeno.2016.05.003. [DOI] [PubMed] [Google Scholar]
- 29.Chen W., Yang H., Feng P., Ding H., Lin H. iDNA4mC: Identifying DNA N4-methylcytosine sites based on nucleotide chemical properties. Bioinformatics. 2017;33(22):3518–3523. doi: 10.1093/bioinformatics/btx479. [DOI] [PubMed] [Google Scholar]
- 30.Wei L., Chen H., Su R. M6APred-EL: A sequence-based predictor for identifying N6-methyladenosine sites using ensemble learning. Mol. Ther. Nucleic Acids. 2018;12:635–644. doi: 10.1016/j.omtn.2018.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wei L., Su R., Luan S., Liao Z., Manavalan B., Zou Q., Shi X. Iterative feature representations improve N4-methylcytosine site prediction. Bioinformatics. 2019;35(23):4930–4937. doi: 10.1093/bioinformatics/btz408. [DOI] [PubMed] [Google Scholar]
- 32.Tibshirani R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B. 1996;58:267–288. doi: 10.1111/j.2517-6161.1996.tb02080.x. [DOI] [Google Scholar]
- 33.Lee T.F., Chao P.J., Ting H.M., Chang L., Huang Y.J., Wu J.M., Wang H.Y., Horng M.F., Chang C.M., Lan J.H., Huang Y.Y., Fang F.M., Leung S.W. Using multivariate regression model with least absolute shrinkage and selection operator (LASSO) to predict the incidence of Xerostomia after intensity-modulated radiotherapy for head and neck cancer. PLoS One. 2014;9(2):e89700. doi: 10.1371/journal.pone.0089700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang S., Duan Z., Yang W., Qian C., You Y. iDHS-DASTS: Identifying DNase I hypersensitive sites based on LASSO and stacking learning. Mol. Omics. 2021;17(1):130–141. doi: 10.1039/D0MO00115E. [DOI] [PubMed] [Google Scholar]
- 35.Zhang S., Zhu F., Yu Q., Zhu X. Identifying DNA-binding proteins based on multi-features and LASSO feature selection. Biopolymers. 2021;112(2):e23419. doi: 10.1002/bip.23419. [DOI] [PubMed] [Google Scholar]
- 36.Yu H.F., Huang F.L., Lin C.J. Dual coordinate descent methods for logistic regression and maximum entropy models. Mach. Learn. 2011;85(1-2):41–75. doi: 10.1007/s10994-010-5221-8. [DOI] [Google Scholar]
- 37.Friedman N., Geiger D., Pazzanzi M. Bayesian network classifiers. Mach. Learn. 1997;2:131–163. doi: 10.1023/A:1007465528199. [DOI] [Google Scholar]
- 38.Chen T., Guestrin C. XGBoost: A Scalable Tree Boosting System.; Proceeding of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Aug New York, NY, USA. 2016. pp. 785–794. [Google Scholar]
- 39.Vapnik V.N. Statistical Learning Theory. New York: John Wiley & Sons; 1998. pp. 1–768. [Google Scholar]
- 40.Breiman L. Random forest. Mach. Learn. 2001;45:5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- 41.Zhang S.L., Li X.J. Pep-CNN: An improved convolutional neural network for predicting therapeutic peptides. Chemom. Intell. Lab. Syst. 2022;221:104490. doi: 10.1016/j.chemolab.2022.104490. [DOI] [Google Scholar]
- 42.Alam M., Ali S.D., Tayara H., Chong K.T. A CNN-based RNA N6-methyladenosine site predictor for multiple species using heterogeneous features representation. IEEE Access. 2020;8:138203–138209. doi: 10.1109/ACCESS.2020.3002995. [DOI] [Google Scholar]
- 43.Tahir M., Hayat M., Chong K.T. Prediction of N6-methyladenosine sites using convolution neural network model based on distributed feature representations. Neural Netw. 2020;129:385–391. doi: 10.1016/j.neunet.2020.05.027. [DOI] [PubMed] [Google Scholar]
- 44.Su R., Hu J., Zou Q., Manavalan B., Wei L. Empirical comparison and analysis of web-based cell-penetrating peptide prediction tools. Brief. Bioinform. 2020;21(2):408–420. doi: 10.1093/bib/bby124. [DOI] [PubMed] [Google Scholar]
- 45.Zhou C., Liu S., Zhang S. Identification of amyloidogenic peptides via optimized integrated features space based on physicochemical properties and PSSM. Anal. Biochem. 2019;583:113362. doi: 10.1016/j.ab.2019.113362. [DOI] [PubMed] [Google Scholar]
- 46.Zhang S., Yang K., Lei Y., Song K. iRSpot-DTS: Predict recombination spots by incorporating the dinucleotide-based spare-cross covariance information into Chou’s pseudo components. Genomics. 2019;111(6):1760–1770. doi: 10.1016/j.ygeno.2018.11.031. [DOI] [PubMed] [Google Scholar]
- 47.Zhang S., Qiao H. KD-KLNMF: Identification of lncRNAs subcellular localization with multiple features and nonnegative matrix factorization. Anal. Biochem. 2020;610:113995. doi: 10.1016/j.ab.2020.113995. [DOI] [PubMed] [Google Scholar]
- 48.Wang J.S., Zhang S.L. PA-PseU: An incremental passive-aggressive based method for identifying RNA pseudouridine sites via Chou’s 5-steps rule. Chemom. Intell. Lab. Syst. 2021;210:104250. doi: 10.1016/j.chemolab.2021.104250. [DOI] [Google Scholar]
- 49.Lv Z., Zhang J., Ding H., Zou Q. RF-Pse U: A random forest predictor for RNA pseudouridine sites. Front. Bioeng. Biotechnol. 2020;8:134. doi: 10.3389/fbioe.2020.00134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Feng P., Yang H., Ding H., Lin H., Chen W., Chou K.C. iDNA6mA-PseKNC: Identifying DNA N6-methyladenosine sites by incorporating nucleotide physicochemical properties into PseKNC. Genomics. 2019;111(1):96–102. doi: 10.1016/j.ygeno.2018.01.005. [DOI] [PubMed] [Google Scholar]
- 51.Liu B., Yang F., Huang D.S., Chou K.C. iPromoter-2L: A two-layer predictor for identifying promoters and their types by multi-window-based PseKNC. Bioinformatics. 2018;34(1):33–40. doi: 10.1093/bioinformatics/btx579. [DOI] [PubMed] [Google Scholar]
- 52.Chen W., Feng P.M., Lin H., Chou K.C. iRSpot-PseDNC: Identify recombination spots with pseudo dinucleotide composition. Nucleic Acids Res. 2013;41(6):e68–e68. doi: 10.1093/nar/gks1450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lin H., Deng E.Z., Ding H., Chen W., Chou K.C. iPro54-PseKNC: A sequence-based predictor for identifying sigma-54 promoters in prokaryote with pseudo k-tuple nucleotide composition. Nucleic Acids Res. 2014;42(21):12961–12972. doi: 10.1093/nar/gku1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ehsan A., Mahmood K., Khan Y.D., Khan S.A., Chou K.C. A novel modeling in mathematical biology for classification of signal peptides. Sci. Rep. 2018;8(1):1039. doi: 10.1038/s41598-018-19491-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hotelling H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933;24(6):417-441. doi: 10.1037/h0071325. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data supporting the findings of the article are available in the datasets at: https://github.com/YingyingYao/ iORI-LAVT.