Novel gas exchange analysis in COVID-19 lung disease

The study by Harbut et al. [1] reported in this issue of the European Respiratory Journal analyses gas exchange in patients with acute coronavirus disease 2019 (COVID-19) lung disease; arterial oxygen and carbon dioxide tension (P_O2 and P_CO2) and the mean (or mixed) value for alveolar (A̅) P_O2 and P_CO2 (not an “ideal” [2] but the actual value) were measured, when patients (and healthy controls) were breathing air. From the mean alveolar to arterial P_O2 and arterial to mean alveolar P_CO2 gradients (A̅aP_O2 and aA̅P_CO2), the authors computed intrapulmonary shunt and alveolar dead space using the classical three compartment model of Riley and Cournand [2] (but, with important differences: see later). Harbut et al. [1] argued that intrapulmonary shunt should be a marker for alveolar consolidation, as in lobar pneumonia, but at a more microscopic level; alveolar dead space, on the other hand, should be a surrogate for pulmonary microvascular obstruction and thrombosis, e.g. following severe endothelial injury.

Short abstract

A new method of measuring mean alveolar P_O2 and P_CO2 (as opposed to the classical ideal alveolar air analysis) with arterial P_O2 and P_CO2, is applied to patients with COVID-19 lung disease, acutely and after recovery https://bit.ly/3Tuaffb

Intrapulmonary shunt and alveolar dead space in COVID–19 pneumonitis

The study by Harbut et al. [1] reported in this issue of the European Respiratory Journal analyses gas exchange in patients with acute coronavirus disease 2019 (COVID-19) lung disease; arterial oxygen and carbon dioxide tension (P_O2 and P_CO2) and the mean (or mixed) value for alveolar (A̅) P_O2 and P_CO2 (not an “ideal” [2] but the actual value) were measured, when patients (and healthy controls) were breathing air. From the mean alveolar to arterial P_O2 and arterial to mean alveolar P_CO2 gradients (A̅aP_O2 and aA̅P_CO2), the authors computed intrapulmonary shunt and alveolar dead space using the classical three compartment model of Riley and Cournand [2] (but, with important differences: see later). Harbut et al. [1] argued that intrapulmonary shunt should be a marker for alveolar consolidation, as in lobar pneumonia, but at a more microscopic level; alveolar dead space, on the other hand, should be a surrogate for pulmonary microvascular obstruction and thrombosis, e.g. following severe endothelial injury.

30 patients were studied, initially 3–15 days from the start of COVID-19 symptoms, and subsequently during recovery [1]. They had mild to moderate hypoxaemia (P_aO2 mean 68.3 mmHg, range 52–106 mmHg); 18 (60%) received supplemental oxygen. 24 out of 30 became in-patients, but only one was admitted to intensive care (and recovered). 18 of 30 patients had elevated shunt plus elevated dead space (versus healthy controls); five had a raised shunt only, and three had just a raised dead space. At recovery, only two patients had continuing (but minimally elevated) shunt (down from 23), but eight still had high alveolar dead space (down from 21). The authors [1] claim that their method, which is applicable at the bedside, can distinguish intravascular pathology (most likely at a microvascular level) from alveolar and epithelial injury leading to airspace flooding/consolidation and intrapulmonary shunt.

These results represent a significant step forward in the analysis of gas exchange in a clinical setting. The methodology (see below) gives a more accurate assessment of intrapulmonary shunt and alveolar dead space from arterial and mean alveolar measurements of O₂ and CO₂ than the well-established analysis of V̇_A/Q̇ mismatch using the ideal alveolar air approach [2]. This method, and its validation, recently published [3], will be the focus of the remainder of this editorial.

A new analysis of O₂ and CO₂ exchange

The paper of Wagner et al. [3] “Using pulmonary gas exchange to estimate shunt and deadspace in lung disease…” has two sections: theory and practice. Theoretically, gas exchange across the blood–gas barrier is governed by two factors: solubility (λ) in blood for gas_x, and the ratio of ventilation to perfusion (V̇_A/Q̇); the latter may vary from unit to unit of gas exchange such that in any one unit_y:

P_A/P_v̅ ~ P_c/P_v̅ = λ/(λ + V̇_A/Q̇)   (1)

where A and c are the mixed alveolar gas and mixed capillary blood components of any unit of gas exchange (instantaneous partial pressure equilibration between them is assumed), v̅ is the mixed venous blood (common to all units), and λ is the blood solubility of gas_x (essentially, for O₂ and CO₂, λ is the tangent to the blood dissociation curve ΔC/ΔP, where C is O₂ or CO₂ content (mL·mL⁻¹) and P is partial pressure at a particular instantaneous point on the curve). Wagner et al. [4] used this relationship (equation 1) in their multiple inert gas elimination technique (MIGET) in which six inert gases of different solubilities (λ range of 10⁴-fold) were infused until a steady state was achieved; from their individual retention (P_A/P_v̅) and excretion (P_E̅/P_v̅), where E̅ is mixed expired gas, V̇_A or Q̇ could be plotted against V̇_A/Q̇ for a lung of 50 notional compartments.

In the more recent paper, Wagner et al. [3] had a two compartment model, either 1) 50% of blood flow (Q̇) shunted (zero V̇_A/Q̇), and 50% with normal ventilation and V̇_A/Q̇; or 2) 50% of ventilation V̇_A) unperfused with V̇_A/Q̇ of infinity, and 50% with normal blood flow and V̇_A/Q̇. The authors showed (in their figure 2) that the relative A̅–a or a–A̅ partial pressure gradient was about ×3 greater for O₂ versus CO₂ in the shunt model, and ×1.7 greater for CO₂ versus O₂ in the dead space model, i.e. shunt is more dominated by A̅aP_O2 and alveolar dead space by aA̅P_CO2. They attributed this to the approximately 10-fold greater solubility (λ) of CO₂ in blood versus O₂ over the physiological range of partial pressures. Nevertheless, in their figure 3, where they had models with a mixture of shunt and dead space (in essence, three compartments), the value of AaP_O2 was influenced by the value of aAP_CO2 and vice versa. Thus, it becomes essential to measure the gradient for CO₂ as well as O₂ to apportion shunt and dead space correctly when both are present. This is where the analysis of Wagner et al. [3] differs from that of Riley and Cournand [2].

The ideal alveolar air analysis of Riley and Cournand [2]

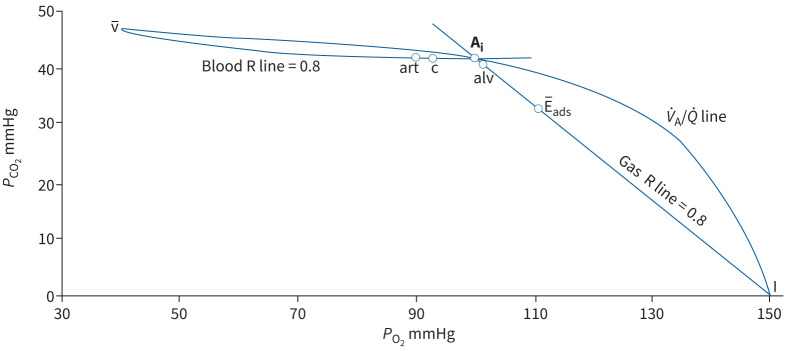
Rapid response O₂ and CO₂ gas analysers were not available in 1949, and there were doubts about the accuracy of end-expired samples for defining mean alveolar P_O2 and P_CO2. Riley and Cournand [2] found an ingenious solution, using the P_O2–P_CO2 diagram of Fenn et al. [5], and proposed that in the steady state the ratio of oxygen uptake to CO₂ production (the respiratory quotient (RQ) or respiratory exchange ratio (R)), normally around 0.8, must be the same for the lung as for the body as a whole (figure 1). Thus, mean P_AO2 and P_ACO2 must lie along a line, in a plot of P_CO2 (y-axis) against P_O2 (x-axis), with a slope (P_CO2/P_O2) of 0.8, starting from the inspired point (P_O2 ~150 and P_CO2 0 mmHg). Similarly, mean capillary (c) P_O2 and P_CO2, in partial pressure equilibrium with mean alveolar gas tensions, must lie along a line starting from the mixed venous point (v̅), with a slope (which, in terms of concentrations, is linear) for the blood content ratios (C_v̅CO2 − C_cCO2)/(C_cO2 − C_v̅O2) also equalling 0.8. When the slope of blood content ratio line of 0.8 is re-expressed in terms of P_O2 and P_CO2 (the blood R line in figure 1), the intersection of blood and gas R lines defines the alveolar P_O2 and P_CO2 for an ideal lung with a single V̇_A/Q̇ ratio (∼0.86) appropriate for an RQ (or R) of 0.8. The ideal alveolar air concept is more easily understood graphically, as portrayed in figure 1.

FIGURE 1.

Graphical analysis of the calculation of ideal alveolar air (A_i; ideal point) modified from Riley and Cournand [2]. Blood or gas carbon dioxide tension (P_CO2) is plotted against oxygen tension (P_O2) (in mmHg) with the gas inspired (I; air) set at P_O2 150 and P_CO2 0 mmHg (see text). Curved line joining point I to point v̅ (the P_CO2–P_O2 of mixed venous blood) is the V̇_A/Q̇ line, reflecting all possible alveolar P_CO2 and P_O2 values for V̇_A/Q̇ ratios from zero (at v̅) to infinity (at I) at a lung and body respiratory quotient (RQ or R) of 0.8. Gas and blood R lines, constructed for R=0.8, intersect at the “ideal” point. “art” is the P_CO2–P_O2 of mixed arterial blood in a healthy subject, “c” is the composition of mixed blood leaving alveolar capillaries (arterial minus anatomic shunt), alv of mixed alveolar gas, and E̅_ads of mixed expired air corrected for apparatus dead space.

Defining the “ideal” point in practice, and dead space to tidal volume ratio (V_D/V_T)

The blood RQ line (figure 1) becomes flat as it approaches the gas R line. Therefore, Riley and Cournand [2] proposed, reasonably, that the arterial P_CO2,which is positioned on the flat part of the curve, could define the intersection of the gas and blood R lines and, thus, the ideal alveolar P_O2 and P_CO2. The ideal alveolar P_O2 could be calculated (approximately) as inspired P_O2 minus P_aCO2 divided by the gas R slope (0.8). This way of calculating the AaP_O2 gradient has been used in respiratory physiology and medicine for the past 72 years!

Dead space as a fraction of tidal volume (V_D/V_T) is calculated from the gas R line (figure 1) as the ratio (A_i − E̅_ads)/(A_i − I), or in terms of P_CO2 as (P_aCO2 − P_E̅CO2)/(P_aCO2 − P_ICO2); since P_ICO2 is zero, this simplifies to (P_aCO2 − P_E̅CO2)/P_aCO2. In the analysis of Wagner et al. [3], alveolar dead space equals (P_aCO2 − P_A̅CO2)/P_aCO2, where A̅ equals alv in figure 1.

Why the “ideal” point and V_D/V_T are not the optimal solutions

In lung disease, P_aCO2 cannot be relied on to predict mixed or mean P_AO2. In intrapulmonary shunt, P_aCO2 will be greater than P_AO2, by 2.3 mmHg for a 30% shunt alone and by 9.0 mmHg for 30% alveolar dead space alone (table 1); thus, the ideal alveolar air analysis [2] will underestimate the true mixed or mean alveolar to arterial (A̅aP_O2) gradient. Although 2.3 mmHg aA̅P_CO2 gradient (A in table 1) is not a big difference (and the effect on the shunt calculation would be small), the error would be much greater if there was a combination of increased shunt and increased dead space (table 1). Figure 4 in Wagner et al. [3] shows a complex interaction between the A̅aP_O2 and the aA̅P_CO2 gradients, which means that both need to be defined for intrapulmonary shunt and dead space fractions to be measured accurately.

TABLE 1.

Mean (or mixed) alveolar to arterial gradients for oxygen (A̅aP_O2) and arterial to mean alveolar gradients for CO₂ (aA̅P_CO2) in mmHg, intrapulmonary shunt (as % of total pulmonary blood flow) and alveolar dead space (as % of total alveolar ventilation) for different combinations of shunt and alveolar dead space

		A̅aPO2 mmHg	aA̅PCO2 mmHg	Shunt % total blood flow	Dead space % total ventilation
A	Shunt only	48	2.3	30	0
B	Dead space only	13	9.2	0	30
C	Mixed: shunt = dead space	63	11.3	30	30
D	Mixed: shunt >> dead space	63	7.5	44	10
E	Mixed: dead space >> shunt	26	7.5	5	23

Calculated from figure 3b in Wagner et al. [3].

The V_D/V_T of Riley and Cournand [2] includes the anatomic dead space (∼33% of total in a resting healthy subject); this significantly reduces its sensitivity.

The A̅aP_O2 and aA̅P_CO2 gradients in table 1 show that shunt and dead space affect O₂ and CO₂ exchange independently, differing from the Riley and Cournand [2] analysis portrayed in figure 1. For example, in A there is a small aA̅P_CO2 gradient even when there is no alveolar dead space, and in B an A̅aP_O2 gradient exists in the presence of zero shunt. In C and D, the A̅aP_O2 gradients are the same despite a 14% difference in shunt, but there is a 20% difference in dead space. There are similar aA̅P_CO2 gradients in D and E, despite different alveolar dead spaces, because of a 39% difference in shunt. In E, a substantial A̅aP_O2 exists (26 mmHg) with a small shunt (5%) because there is a significant dead space (23%). In other words, A̅aP_O2 is not an accurate reflection of intrapulmonary shunt (formerly called “venous admixture”) and aA̅P_CO2 is not a true representation of alveolar dead space.

The analysis of Wagner et al. [3]: practical matters

Computerisation

The older, graphical approach cannot be expected to cope with the complexity of the blood dissociation curves for O₂ and CO₂, and their interaction. Body temperature, hydrogen ion concentration, haemoglobin and P50 all need to be taken into account. With the advent of digital computers, and expert programming, these complexities became manageable. The pioneers in this field, in the late 1960s, were Kelman [6] and West [7].

Expired gas analysis

Measurements of inspired and expired P_O2 and P_CO2 and tidal volume need to be made, in a controlled way over 3–5 min, using a noseclip and mouthpiece. This type of monitoring is now routine in cardiopulmonary exercise testing. A steady state, as judged by a stable end-tidal P_CO2, a constant respiratory rate and adequate tidal volume are needed for the calculation of inspired and expired ventilation, and oxygen consumption (from which cardiac output and P_v̅O2 are computed). During this monitoring period, radial artery blood is sampled over several breaths. Details can be found in the article by Harbut et al. [1]. The calculation (and its justification) of mean alveolar tensions from the expired P_O2 and P_CO2 profiles is described in detail in Wagner et al. [3].

Conclusion

Wagner et al. [3] have shown, by their theoretical analysis and practical approach, that mean (or mixed) alveolar (A̅)–arterial P_O2 and P_CO2 gradients (and intrapulmonary shunt and alveolar dead space) can be measured with greater accuracy than with the classical ideal alveolar air approach [2], particularly in disease when substantial shunt and dead space co-exist (as they usually will). This is a big step forward in gas exchange pathophysiology. Harbut et al. [1] have used this method and analysis to show that shunt and alveolar dead space, representing different pathological processes, may be present together in patients with COVID-19 lung disease. The time has come to extend this analysis to other pulmonary conditions.

Shareable PDF

This one-page PDF can be shared freely online.

Shareable PDF ERJ-01962-2022.Shareable ^{(229.8KB, pdf)}