Multiple Facets of Modeling Electronic Absorption Spectra of Systems in Solution

Abstract

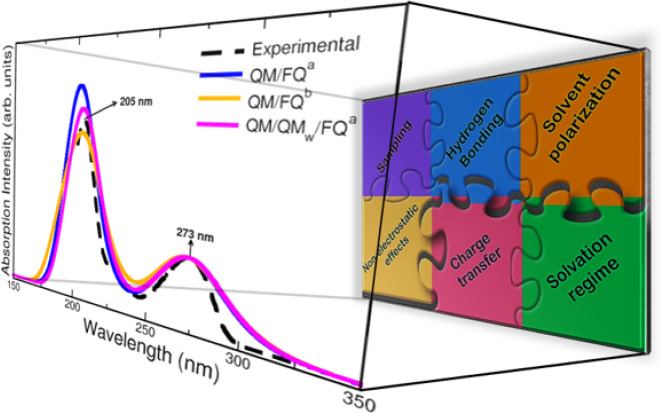
In this Perspective, we outline the essential physicochemical aspects that need to be considered when building a reliable approach to describe absorption properties of solvated systems. In particular, we focus on how to properly model the complexity of the solvation phenomenon, arising from dynamical aspects and specific, strong solute–solvent interactions. To this end, conformational and configurational sampling techniques, such as Molecular Dynamics, have to be coupled to accurate fully atomistic Quantum Mechanical/Molecular Mechanics (QM/MM) methodologies. By exploiting different illustrative applications, we show that an effective reproduction of experimental spectral signals can be achieved by delicately balancing exhaustive sampling, hydrogen bonding, mutual polarization, and nonelectrostatic effects.

1. Introduction

How can we create an accurate atomistic model to simulate absorption spectra of systems in solution? The advances in theoretical and computational chemistry have led to the definition of reliable protocols for the reproduction of many experimental data of molecules in the gas-phase. However, when dealing with solvated molecules, the complexity of the problem increases and the definition of a unique, robust protocol still remains challenging.^1,2 In most of the leading reports, indeed, the simulation of spectral properties is usually performed by using a simplistic representation of the molecular system, where often a single or a limited number of conformations are taken into account for the solute, while the environment is reduced to an unsophisticated nonrealistic view usually mimicked by dielectric constants as in the implicit cases³ or recreated by a few molecules.^4,5 The reason for such choices is that the complexity of the system constrains its faithful description since that ideal implies high computational costs, becoming almost unattainable for the most part.

However, in the last years, fully atomistic approaches based on a multiscale partitioning of the systems have become more and more diffuse, because they provide a physicochemical consistent portrayal of the solvent, and because their capability to accurately sample the conformational degrees of freedom of the solute–solvent phase-space. All these characteristics are highly desirable features when it comes to spectroscopy.

By retaining the atomistic nature of the whole system, quantum-mechanics/molecular mechanics (QM/MM) approaches⁶ for solvation are defined. Depending on the coupling between the QM and MM portions, different approaches can be formulated, ranging from the electrostatic embedding,⁷ in which the MM part polarizes the QM part, but not viceversa, to polarizable embedding (PE), where mutual solute–solvent polarization effects are recovered;^1,8,9 clearly, PE gives the most physically consistent picture of the solvation phenomenon. Among the PE approaches that have been developed so far, in this Perspective the focus is on QM/Fluctuating Charges (FQ)¹⁰ and QM/Fluctuating Charges and Fluctuating Dipoles (FQFμ),¹¹ which have been developed and extended to calculate spectroscopic and response properties of molecules in solution.¹²⁻¹⁵

It has amply been reported in the literature that electronic absorption arising from the solute is affected by the surrounding solvent.¹⁶⁻¹⁹ A typical example are solvatochromic shifts,^{14,17,19−21} and more generally the solvent can assist or slow down the common n → π* and π → π* electronic transitions, which results in changes in the appearance, position, intensity, and width of absorption bands.^2,22−24 Hence, the initial question to answer when building a model for solvation is how the solvent interacts with the solute and how these interactions must be meticulously inserted in the model to obtain a detailed description of absorption spectra. To address this problem, PE approaches are the most suitable when coupled to molecular dynamics (MD) simulations, which allow for a correct sampling of the solute solvent phase-space.¹ In this way, the dynamical aspects of the solvation phenomena, and a reliable description of strong, specific solute–solvent interactions can be achieved.

As it is clear from the previous paragraphs, the definition of a model that successfully reproduces experimental findings would open the door to reliable predictions of spectra for substances or systems whose UV–vis measurements are hard to be performed in the laboratory.^1,25 As in the experiments, many aspects underlie the acquisition of computed absorption spectra and some of them remain critically important. The sampling, the role of the solvent polarization, the hydration patterns commonly via hydrogen bonding, and the inclusion of nonelectrostatic and charge transfer terms are all ingredients of a proper computational modeling and are analyzed and reported in this Perspective. To highlight the role of all the aforementioned elements, we select different established applications, which are used to show the strengths and flaws of the current models. This can also provide options for improving the existing models in order to treat more complex systems and phenomena.

2. Theoretical Modeling of Absorption Phenomena

The reliable calculation of absorption properties of molecular systems embedded in an external environment (e.g., a solvent) is challenging. In fact, models need to coherently take into account the various physicochemical aspects of solvation, and how they influence absorption phenomena. Among them, of paramount importance is the accounting for dynamical aspects, which implies an accurate sampling of the solute–solvent phase-space, through the correct identification of all possible conformational minima.¹ Also, depending on the nature of the molecule-environment couple, a reliable model needs to account for the directionality of specific interactions, such as hydrogen bonding.²⁶ In parallel, a physically consistent description of the spectral signal, i.e., of the electronic properties of the molecular system as perturbed by the environment, is required.¹ Both aspects (i.e., the phase-space sampling and the simulation of the spectral signal) equally contribute to obtain a physically consistent modeling and therefore need to be coherently integrated into the computational protocol. Peculiar aspects related to the phase sampling and specific interactions are discussed in detail in the following sections by resorting to illustrative examples. In this section, the attention is focused on the calculation of the spectral absorption signal.

Multiscale approaches, and QM/MM methods in particular, have recently proven to reliably describe absorption spectra of systems embedded in an external environment.¹ In such models when specified to solutions, the target (i.e., the solute) is described at the QM level, whereas the solvent is atomistically treated at the classical level by means of a parametrized force field (FF).⁶ The total energy of the system can therefore be written as⁶

1

where E_QM and E_MM are QM and MM energies and E_QM/MM^int is the interaction energy, which may be decomposed as follows:

2

where electrostatic (E_QM/MM^ele), polarization (E_QM/MM), repulsion (E_QM/MM^rep), dispersion (E_QM/MM), and charge transfer (CT, E_QM/MM^CT) contributions are highlighted.

The various QM/MM approaches differ in the way E_QM/MM^int is defined. In principle, the most physically reliable description of the electronic properties of the solvated system may only be achieved if all QM/MM interactions are described. However, while electrostatic and polarization effects can be consistently defined within a classical modeling of the solvent layer, repulsion, dispersion, and CT contributions originate from the quantum nature of the electronic degrees of freedom.²⁷ For this reason, most QM/MM approaches limit the description of QM/MM interactions to electrostatics, yielding the so-called electrostatic embedding,⁷ and only in a few cases mutual solute–solvent polarization effects are considered (polarizable embedding).¹ While in electrostatic embedding the interaction term is expressed in terms of a set of MM fixed-value charges, in polarizable QM/MM approaches the interaction term involves a set of electric variables (generally charges and/or dipoles) which are polarized as a response to the QM potential/field, and viceversa.¹⁰ Among the different polarizable QM/MM approaches which have been proposed in the literature, here we concentrate on QM/Fluctuating Charges (QM/FQ) and QM/Fluctuating Charges and Fluctuating Dipoles (QM/FQFμ), which have been developed and amply tested in recent years.¹

2.1. A Brief Sketch of QM/FQ and QM/FQFμ for Computing Absorption Spectra

In QM/FQ, each MM atom is assigned a charge (q) which can vary according to the electronegativity equalization principle (EEP),²⁸ i.e. a charge flow occurs when two atoms have different chemical potential.¹⁰ The FQ force field is defined in terms of two atomic parameters, namely the electronegativity (χ) and the chemical hardness (η).²⁹ Differently, in QM/FQFμ, an additional polarization source is introduced to model the anisotropic nature of noncovalent interactions. It is incorporated in terms of a set of fluctuating dipoles μ, which are assigned to MM atoms and are expressed through the atomic polarizability α.¹¹

If the QM portion is described at the SCF level, the total QM/FQFμ energy reads (QM/FQ is recovered by discarding all terms depending on μ):¹¹

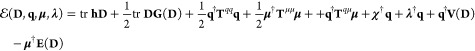3

where h and G are the usual one- and two-electron matrices and D is the density matrix. χ collects atomic electronegativities, whereas T_ij^qq, T_ij, and T_ij^μμ are charge–charge, charge-dipole and dipole–dipole interaction kernels, respectively. Their expressions can be found in refs (11) and (30). q^†V(D) and μ^†E(D) describe the electrostatic interactions between the QM density and the FQs and Fμs, respectively. λ is a set of Lagrangian multipliers that impose specific charge constraints, which may be (i) the entire MM system is constrained to a fixed charge value, thus allowing CT between solvent molecules (the resulting approaches are named QM/FQ_CT and QM/FQFμ_CT); (ii) the charge constrain is imposed to each MM molecule and thus no CT can occur between MM molecules.¹¹

Independently of the charge constraints that are exploited, the effective Fock matrix in the AO basis set {χ_μ} is¹¹

4

Notice that in the nonpolarizable QM/MM, MM charges are fixed, therefore the QM/MM contribution to the Fock matrix 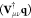does not vary along the SCF procedure. On the contrary, in QM/FQ and QM/FQFμ MM variables (charges and dipoles) explicitly depend on the QM density. As a consequence, their contribution to the Fock matrix has to be computed at each SCF step, thus describing mutual QM/MM polarization effects. Charges and dipoles are computed by imposing the global functional to be stationary with respect to charges, dipoles, and Lagrangian multipliers. This results in the following linear system:¹¹

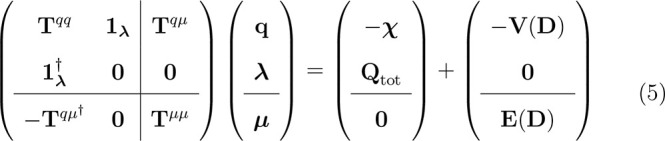5

6

where 1_λ accounts for the Lagrangian blocks, C_Q collects atomic electronegativities and charge constraints, L_λ is the vector containing charges, dipoles, and Lagrangian multipliers, and R(D) represents the QM potential and field. Again, the FQ linear system can be easily recovered from eq 5, by simply discarding rows/columns involving μs and their response. To further extend QM/FQ and QM/FQFμ to the calculation of absorption properties of solvated systems, the modification of the ground state (GS) molecular orbitals (MOs) which results from the SCF procedure is not sufficient. In fact, as a result of the electronic excitation, the solvent degrees of freedom cannot be assumed to be frozen to the solute’s GS equilibrium. Indeed, since the time scales associated with electronic excitations are of the order of femtoseconds, it is generally assumed that the solvent degrees of freedom instantaneously readjust to the solute electronic transition, while the vibrational modes, associated with much lower time scales (picoseconds), are frozen to the GS equilibrium. Thus, the solvent enters a so-called electronic “nonequilibrium” regime.^13,31

Due to presence of nonlinear terms in the Hamiltonian as a result of the use of polarizable approaches (see eq 4), two alternative formalisms can be utilized, namely: (i) all polarization sources linearly respond to the transition density (linear response, LR);^13,32 (ii) they adjust to the excited-state electronic configuration, in a state-specific fashion. The latter treatment may be limited to a first-order correction, giving rise to the so-called corrected linear response (cLR) approach.^13,32

Both LR and cLR formalisms have already been discussed in the literature for polarizable QM/MM approaches.^{10,13,33−39} Here, we briefly recall how Casida’s equations⁴⁰ for the calculation of electronic excitation energies ω are modified:

7

where 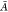and 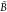matrices read:¹³

8

9

ε indicates MO energies (with the common notation: virtual MOs a, b, ...; occupied MOs i, j, ...), (pq|rs) are two-electron integrals, c_x and c_l are coefficients defining the SCF level (HF: c_x = 1, c_l = 0; pure DFT: c_x = 0, c_l = 1). As specified in eqs 8 and 9, additional terms with respect to the in-vacuo formulation are present for polarizable embedding approaches. In particular, both direct contributions (the C^pol term in eqs 8 and 9) and indirect effects (modifications of GS MO coefficients and energies) appear. C^pol is specified according to the polarizable embedding approach. In case of QM/FQFμ:¹³

10

Here, q^T and μ^T are perturbed FQs and Fμs, which are adjusted to the transition density D_K^T=X_K+Y_K.¹³ They are calculated by solving a modified set of linear equations, explicitly depending on the electric potential and field due to the QM transition density:¹³

11

Notice that, in the case of the electrostatic embedding approach, only the GS MO coefficients and energies are modified, i.e., no direct contributions are included in the equations defining excited state energies.

The first conceptual step of both LR and cLR is the definition o the Kth solute electronic excitation, by keeping the solvent response frozen, i.e. by imposing C^pol = 0 in eqs 8 and 9. Then, MM polarizable variables are adjusted to the K density. In the LR regime, the response to the whole transition densities is considered, so that only the dynamic solute–solvent interactions (some sort of dispersion interactions) are taken into account, while energy differences due to the relaxation of the solute density are not taken into consideration. The latter are considered by the cLR approach, which instead discards the dynamic aspects of solute–solvent interactions. Clearly, the two contributions describe two different physicochemical phenomena, which can be seen as complementary. A model to account for both contributions at the same time, the so-called cLR² approach, has been recently proposed.^41,42

As a side note, to describe the absorption phenomenon, we have presented the extension of polarizable QM/MM approaches to a linear TD-DFT description (see eq 7). It is however known that the choice of the DFT functional might widely affect the electronic response of a molecular system, and should thus be selected based on previous studies reported in the literature.⁴³⁻⁴⁹ To refine such a description, correlated methods, such as Coupled Cluster, can be exploited, though they have not been amply tested in the context of polarizable QM/MM methodologies.⁵⁰⁻⁵³

3. Computational Protocol

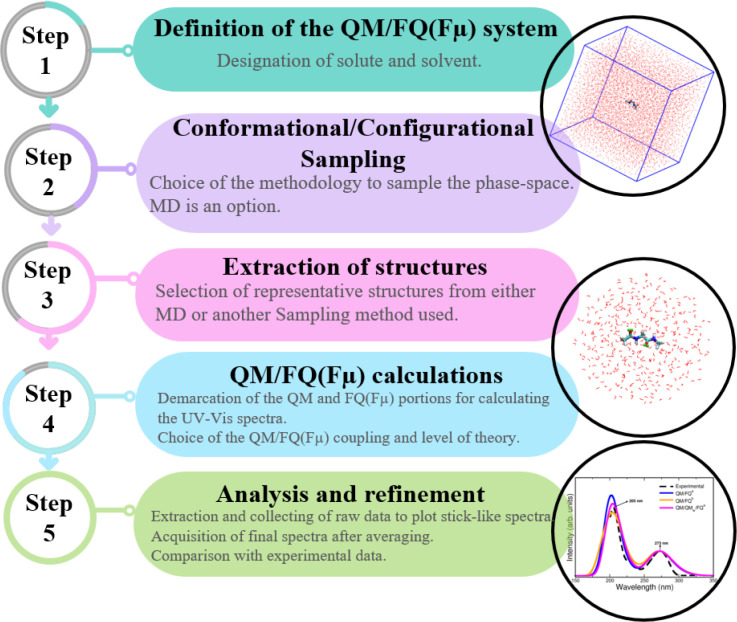
In recent years, we have developed a computational protocol (see Figure 1), which adopts the concepts highlighted in the previous sections and remarkably has successfully been applied to describe absorption properties of solvated systems. Both the direct effect of the environment on UV–vis spectra and the contribution of the spatial arrangement of the solvent to the final spectra are considered when such a procedure is followed. In this Perspective, each one of these steps will be cursorily explained since they have been amply commented elsewhere, along with the “best practices”.^1,9 The first step involves (i) the definition of the system, demarcating the QM (generally the solute) and MM (most often the solvent) portions, with the first being responsible for the spectral property. Then, (ii) a conformational and configurational sampling is performed, by resorting to strategies such as MD simulations, which may also imply a specific reparametrization of the existing FFs. Once the solute–solvent phase space is explored, the computational sample is prepared (iii) by extracting some configurations or representative structures, ensuring no correlation between them. Frequently those snapshots are cut in sphere-shaped droplets and, for absorption spectra, a radius less than 20 Å and just hundreds of them have proven to give excellent results.⁵⁴⁻⁵⁶ Later, (iv) QM/FQ calculations of the target property, here electronic absorption spectroscopy, are carried out on the spherical frames obtained at the previous step, at a given QM computational level, which is chosen according to previous studies on similar properties/systems or based on a thorough benchmarking. The two model variants, QM/FQ and QM/FQFμ may be exploited at this step as well as different sets of parameters for water and for nonaqueous solvents. Nonelectrostatic interactions may also be included in the QM/MM modeling.⁵⁷ Finally, (v) the individual results are extracted, analyzed, and averaged to produce final spectra. At this point, the convergence of the spectra when varying the number of configurations must be assessed. Comparison with experimental data and further refinement of some of the above stages (if needed) sign off the utilization of the protocol.

Figure 1.

Flowchart of the computational protocol followed in the simulation of absorption spectra.

Table 1 lists all systems whose UV–vis absorption spectra or related quantities (solvatochromic shifts, excitation energies) have been simulated via the computational protocol depicted in Figure 1.

Table 1. Record of Different Systems Whose UV–Vis Electronic Absorption Properties or Spectra Have Been Simulated Using the QM/FQ Protocol Depicted in Figure 1^a.

solute	solvent	parametrization	approach	year	ref
formaldehyde	water	A	QM/FQ/PCM	2013	(50)
nicotine	water	A	QM/FQ/PCM	2015	(58)
D3 (polythiophene)	water	A	QM/FQ	2018	(59)
DOX	water	A	QM/FQ	2018	(59)
	water	A	QM/FQ	2019	(55)
	water, DNA	A	DFTB/FQ	2022	(60)
	water	B, C, D	QM/FQ, QM/FQFμ	2022	(54)
7-methoxycoumarin	water	A	QM/FQ	2019	(55)
Bodipy 5-Methylcytidine bimane pyridinium dye	water	A	QM/FQ	2019	(55)
		B, C, D	QM/FQ, QM/FQFμ	2022	(54)
5-aminophthalimide	water	A	QM/FQ	2019	(55)
	water	A	QM/FDE/FQ	2021	(61)
	water	B, C, D	QM/FQ, QM/FQFμ	2022	(54)
Rhodamine 6G	water	A	QM/FQ	2019	(62)
Curcumin KK and EK	water	A	QM/FQ	2019	(63)
PNA	water	B, D	QM/FQ, QM/FQFμ	2019	(13)
	DIO, THF, ACN	E	QM/FQ	2021	(42)
	ETH, MET, WTR
	water	C	CC2-in-MLHF/FQ	2021	(51)
	water	B, C, D	QM/FQ, QM/FQFμ	2022	(54)
pyridine	water	B, D	QM/FQ, QM/FQFμ	2019	(13)
	water	C, D	QM/FQ, QM/FQFμ	2019	(14)
	water	C	CC2-in-MLHF/FQ	2021	(51)
pyrimidine	water	B, D	QM/FQ, QM/FQFμ	2019	(13)
	water	C, D	QM/FQ, QM/FQFμ	2019	(14)
caffeine	water	A, C	QM/FQ	2020	(56)
paraxanthine
theophylline
luteolin	water	A	QM/FQ	2020	(64)
kaempferol
quercetin
myricetin
acrolein	water	C, D	QM/FQ, QM/FQFμ	2019	(14)
	water	C	CC2-in-MLHF/FQ	2021	(51)
	water	A	QM/FDE/FQ	2021	(61)
	water	B, C, D	QM/FQ, QM/FQFμ	2022	(54)
QB	DIO, THF, ACN	E	QM/FQ	2021	(42)
MER	ETH, MET, WTR
BET	water	B, C, D	QM/FQ, QM/FQFμ	2022	(54)
Nitrite	water	A, C	QM/FQ, QM/FQFμ	2021	(65)
acetamide	water	A	QM/FQ	2022	(66)
NMA
DMA
ubiquitin	water	A	DFTB/FQ	2022	(60)
a-Ibu	water	A	QM/FQ	2022	(67)
NAGMA	water	A, C	QM/FQ	2022	(68)
NALMA

^aParametrizations: A: Rick et al.,²⁹ B: Carnimeo et al.,⁶⁹ C: Giovannini et al.,⁷⁰ D (FQFμ): Giovannini et al.,¹³ E: Ambrosetti et al.⁴²

4. Illustrative Applications

In this section, we discuss different aspects that need to be considered for constructing a successful model to correctly reproduce electronic absorption spectra of molecules in solution, and in some cases their solvatochromic shifts, by resorting to a set of selected applications. In all cases, according to the original works, MD simulations are performed at the purely classical level and by imposing periodic boundary conditions (PBC) on cubic boxes.

4.1. Importance of a Comprehensive Sampling

How does the solvent interact with the solute and how are the solute’s conformational degrees of freedom affected? In order to answer these questions, an exhaustive sampling of the phase space is a key stage prior to the calculation of the spectral property. Two main factors ensure a high-quality sampling for the whole system, i.e., (i) the conformational sampling of the solute referred to the orientation of the internal dihedral angles within the molecule that originate from intramolecular interactions (such as weak noncovalent interactions, hydrogen bonds, ...), and (ii) the configurational sampling of the solvent or the distribution and orientation of solvent molecules around the solute.¹

Plenty of methodologies employing both classical and quantum mechanics have shown to be useful for the purpose of sampling conformations/configurations of systems in solution.⁷¹ Conformer generators, stochastic and genetic algorithms, Monte Carlo and MD simulations, among others, form part of the most prosperous techniques proposed in the literature.⁷²⁻⁷⁸ It is worth mentioning that QM/MM calculations (step iv of the protocol, see Figure 1) are regularly performed on structures extracted from MD trajectories, but the procedure can also be extended to motifs coming from other sampling strategies.⁶⁵ When MD is used, the simulations are quite versatile and they can be conducted in a classical, ab initio or combined QM/MM MD way.^71,79−81 The strongest criticism about the choice of a reliable FF might be circumvented by adapting the available FFs to the solute/solvent couple (by means of reparametrization⁸²⁻⁸⁴ as was done in refs (85).⁸⁶,) Hydration patterns and distribution functions are so useful to perceive the diversity of the sampling and many software come in handy to that end.⁸⁷⁻⁸⁹

Regarding spectroscopy, chiral properties (e.g., CD or OR) are usually the most sensitive ones to the system conformation⁹ but there are some cases of UV–vis results where the correct solute–solvent sampling has been a determining factor.^58,64 For example, the effects of a conformational sampling obtained from MD runs are evident in the simulation of the UV–vis study of nicotine⁵⁸ where due to a proper MD sampling it is revealed the formation of complex specific hydrogen bonding networks of water molecules connecting different parts of the solute, that turn out to be pivotal in the reproduction of the experimental data. Figure 2 presents the computed and experimental spectra and representative conformers with one or two bridging water molecules between the nitrogen atoms, that are most frequently sampled during the MD and thus contribute to the final spectra. In this case, the combination of a detailed description of nicotine-water interactions, with directional effects such as hydrogen bonding, offered by the QM/FQ/PCM approach and the conformational sampling resulting from MD provides a great improvement with respect to other modeling strategies.

Figure 2.

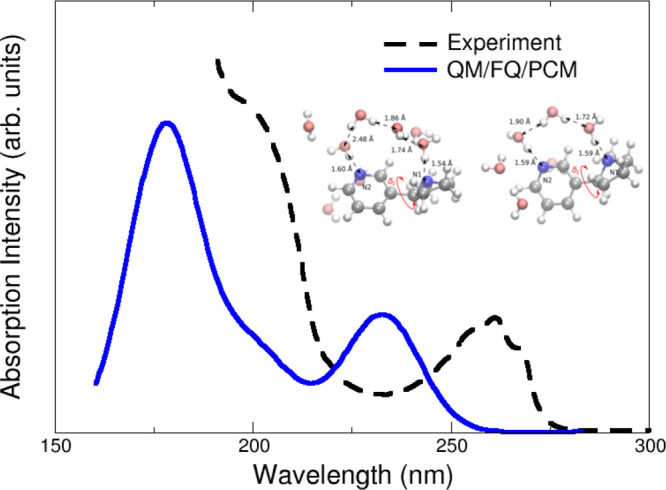
Calculated QM/FQ/PCM absorption spectra of nicotine in aqueous solution. The experimental spectrum (black) taken from ref (58) is given for comparison. Nicotine was freely allowed to move during MD simulations. QM level: CAM-B3LYP/aug-cc-pVDZ. Image adapted from ref (58). Copyright 2015 American Chemical Society.

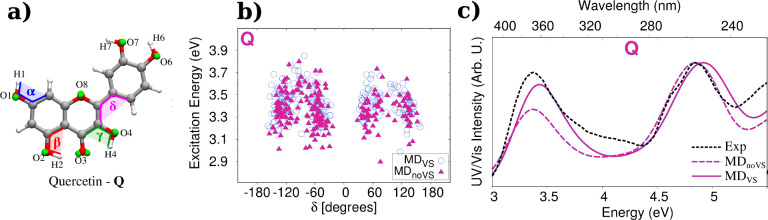
To retain a more accurate description of the directionality of the key O···H–O and N···H–O molecule–water interactions, in some works,^26,64,66,68 additional interaction sites (also known as virtual sites, VS) have been added to the molecular topology of the solutes. An improvement of the agreement between QM/FQ and experimental spectra was reported by Skoko et al.⁶⁴ in the UV–vis study of flavonoids in aqueous solution. For the test cases, the inclusion of VS mainly affects the relative intensity of the two bands and for Kaempferol, Quercetin, and Myricetin, an MD sampling done without VS underestimates the intensity of the first transition with respect to the experimental findings. The presence of explicit water molecules also modifies the conformational distribution and in turn the spreading of excitation energies for the different flavonoids. Individual results for quercetin are presented in Figure 3. Computed excitation energies of the first transition are plotted as a function of the δ dihedral angle in Figure 3b, whereas its corresponding absorption spectra are depicted in Figure 3c. Both these results suggest that a refined modeling of intermolecular interactions through the incorporation of VSs in the oxygen atoms seems to be fundamental to accomplish a rigorous reproduction of the overall spectral shape.

Figure 3.

(a) Definition of dihedral angles and oxygen virtual sites of quercetin.⁶⁴ (b) QM/FQ excitation energies of the first electronic transition of quercetin in water as a function of its δ dihedral angle. (c) Experimental⁹⁰ and computed absorption spectra as calculated with QM/FQ when coupled to both MD_VS and MD_noVS. Quercetin was freely allowed to move during MD simulations. QM level: B3LYP/6-311+G(d, p). Images adapted with permission under a Creative Commons CC BY License from ref (64). Copyright 2020 MDPI.

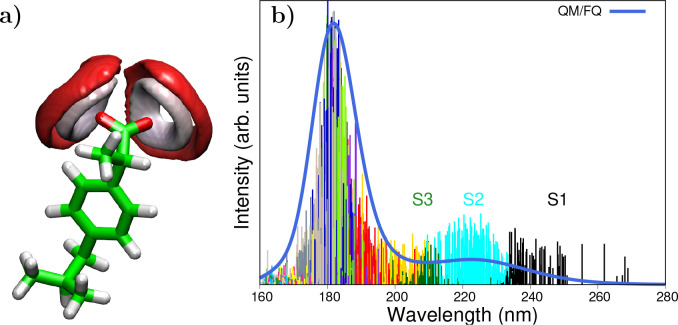
It is important to draw attention to the fact that MD offers some advantages in the long run as a result of the assorted distribution of solvent molecules around the different solute conformations. These merits are especially associated with the natural emerging of the inhomogeneous broadening of the bands in the absorption spectra, which stems from the spreading of the stick spectra of the individual snapshots as can be seen in Figure 4 for the anti-inflammatory drug, Ibuprofen. In addition, sticks can be color-coded to better understand the origin of some bands and choose excited states of interest for subsequent applications as in the case of Resonance Raman spectroscopy.⁶⁷Figure 4 also illustrates that the main band of solvated anionic Ibuprofen (that at 222 nm) appears mainly as a consequence of electronic transitions to states S1, S2, and S3.

Figure 4.

(a) Spatial distribution function of water oxygen (red) and hydrogen (white) atoms around ibuprofen.⁶⁷ (b) Sticks and convoluted QM/FQ UV–vis absorption spectrum of anionic Ibuprofen in aqueous solution. Colored sticks stand for different excited states, from which S1, S2, and S3 are labeled. Ibuprofen was freely allowed to move during MD simulations. QM level: CAM-B3LYP/6-311++G(d, p). Images adapted with permission under a Creative Commons CC BY License from ref (67). Copyright 2022 MDPI.

Note that unsatisfactory reproduction of reference data (e.g., experimental spectra, full QM calculations,...) may be due to the specific methods that are employed in one (or more) of the steps of the computational protocol (see Figure 1). For instance, a potential source of error might follow the so-called “geometry mismatch” problem, which emerges from the combination of classical MD simulations and quantum-chemical calculations.⁹¹⁻⁹⁷ In short, there is no consistency between conformations resulting from classical force fields and those coming from quantum descriptions. This may yield a poor description of spectral features. Some possible solutions to overcome this drawback have been proposed in the literature, among them, resorting to QM/MM MD simulations⁹³ or parametrizing the classical force fields so that they reproduce the QM description.⁸⁵

4.2. Hydrogen-Bonding Description

The way of describing or representing hydrogen bonds (HBs) is crucial in the acquisition of accurate absorption spectra of aqueous systems. As was mentioned before, their correct directionality can be recovered by using VS in the MDs during the sampling stage, however, HBs appear to be also decisive for reproducing specific spectral details, with renowned consequences as shifts of a few nanometers in UV–vis spectra.² Admittedly, it always depends on the nature of solute and solvent, but for polar solvents like water and solutes with potential HB sites, it has been proved that the presence or absence of water molecules determines the molecular conformational distribution and thus, the spectral property at hand.

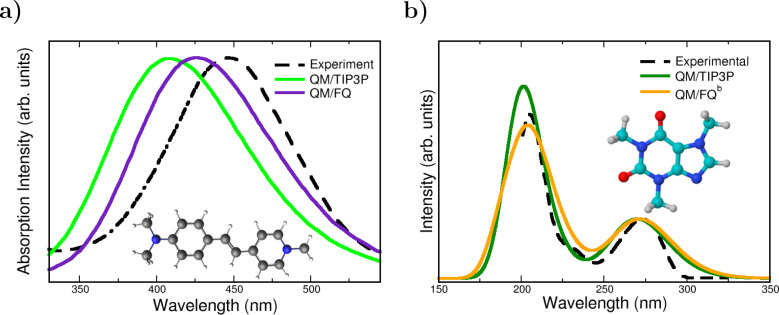
Consequences of using a static QM/continuum approach are known for the case of curcumin, a natural antioxidant, dissolved in aqueous solution.⁶³ The enol–keto (EK) form of curcumin (and other curcuminoids) has been reported⁹⁸ to be the lowest energy isomer and its UV–vis spectrum is experimentally dominated by a single vertical transition placed at about 429 nm.⁹⁹ Such a band is the result of a pure HOMO → LUMO transition, with π – π* character.¹⁰⁰ As can be seen in Figure 5, an implicit treatment of the solvent with the PCM approach makes the absorption maximum to lie at about 381 nm, whereas it is red-shifted toward the experimental value if QM/MM is exploited, lying at 435 nm for QM/FQ. This improvement offered by the atomistic approach coupled with a dynamical description of the solvation phenomenon is rationalized by analyzing the strong HB interactions detected in the radial distribution functions resulting from classical MD simulations. Despite the fact that MD predicts the EK structure to be predominantly planar (it means that just one conformer should be significant akin to the static QM/PCM picture), the arrangement of water molecules around the equilibrium position of curcumin is crucial to correctly account for the variability of the configurations that lead to the emergence of that main band.

Figure 5.

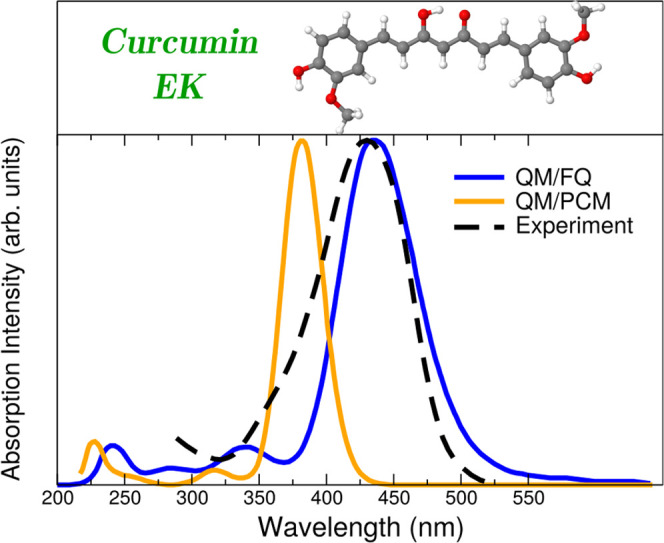
Simulated QM/FQ and QM/PCM absorption spectra for the enol–keto (EK) tautomer of curcumin in aqueous solution.⁶³ Curcumin was freely allowed to move during MD simulations. QM level: M06-2X/def2-TZVP. Experimental data taken from ref (99). Image reproduced and adapted with permission from ref (63). Copyright 2019 Royal Society of Chemistry.

In another case, the impact of the atomistic description of the solvent molecules has been reported by Giovannini et al.,¹⁴ by investigating the n → π* and π → π* vacuo-to-water solvatochromic shifts of acrolein. A hierarchy of solvation approaches for modeling the aqueous environment has been tested and some results are presented in Figure 6. It should be pointed out that since acrolein is free to move along the MD trajectories, solvatochromic shifts reported for it arise from both solute–solvent interactions and also from changes in its internal geometry when passing from vacuum to solution. The effect of hydrogen bonding solute–solvent interactions is immediately perceptible by comparing QM/PCM and QM/FQ (in all its variants) computed results with the experimental blueshift of 0.25 eV and redshift of −0.52 eV reported in ref (101) for n → π* and π → π* transitions, respectively, when going from gas phase to a water solution (sign is just a convention). It is clear that the continuum QM/PCM totally fails at reproducing the experiments. From different papers in the literature,^2,4 it has been suggested that possible refinements can be achieved by adding water molecules near the solute in a cluster-like QM/QM_w model. Figure 6 shows that this approach does not alter the solvatochromic shift of the π → π* transition of acrolein but it enhances the result for the n → π*, although it is still overestimated. That strategy can be extended to the QM/FQ methodology, where explicit water molecules are included in the QM portion in what is called QM/QM_w/FQ.³⁴ Sometimes results achieved in that way have been in better agreement with experiments^55,65,68 or have been taken as reference, but it also happens that the QM/FQ approach is more than enough in the description of the solvent since it outperforms other solvation models at a lower computational cost.⁵⁵

Figure 6.

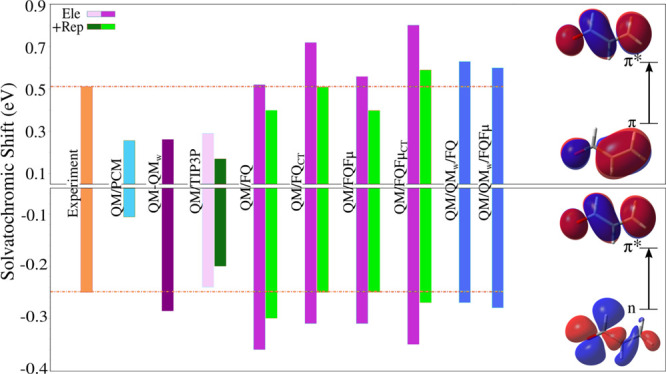
Computed and experimental π → π* (top) and n → π* (bottom) vacuo-to-water solvatochromic shifts of acrolein. Acrolein was freely allowed to move during MD simulations. QM level: CAM-B3LYP/aug-cc-pVDZ. To get a better picture, experimental values taken from ref (101) extend along the whole results. Orbitals involved in both transitions are also included. Image adapted from ref (14). Copyright 2019 American Chemical Society.

Additional evidence of the reliability of the HB description given by QM/FQ coupled to MD sampling is given by Ibuprofen in water solution.⁶⁷ In particular, the strength of HBs around the solute (see the spatial distribution functions, sdfs, in Figure 4) has been quantified by using the stabilization energies provided by the Natural Bond Orbitals (NBO) framework.¹⁰² After comparing NBO results from QM/FQ and from purely QM ibuprofen-water clusters, it appears that when 6 water molecules (plus the rest of the FQ layer) surround the solute, the dominant contributions are due to the same kind of charge transfer and the magnitudes of stabilization energies are similar to those found in microsolvated aggregates.

In light of the above examples, the atomistic, albeit classic, treatment of the QM/FQ model seems to be a major ingredient to reproduce experimental findings.

4.3. Mutual Polarization Effects

The quality of the description of solute–solvent interactions rules the accuracy of computed spectral properties. For this reason, the physics lying behind the QM/MM model definitely matters and it should be able to represent how both layers “feel” each other. Although in the EE approach the MM layer does polarize the QM density, the opposite is not true, disregarding the fact that both solute and solvent are collectively affected by the presence of each other. Polarizable QM/MM approaches overcome this important shortcoming by endowing MM atoms with polarizable sources that vary as a result of the interaction with the QM density, and viceversa.

Different examples of how polarization effects exert influence on molecular response properties have been pointed out in the literature.^23,36,103 In this Perspective, we have picked a select set of them to comment on the relevance of mutual solute–solvent polarization effects. The first case involves acrolein whose solvatochromic shifts for the two lowest-lying electronic transitions are shown in Figure 6. For the n → π* transition, the nonpolarizable QM/TIP3P (which places fixed charges at atomic sites¹⁰⁴) well reproduces the experimental shift, underestimating it by just 4%, while the shift of the π → π* transition is wrongly reproduced, with an error of 44% in absolute value.¹⁴ In contrast, much better results are achieved when exploiting polarizable QM/MM approaches, with a striking 0% and 9% of error for the π → π* transition in the contexts of QM/FQ and QM/FQFμ, respectively.

Polarization effects can be directly observed in the UV–vis spectra of the styrylpyridinium cyanine dye displayed in Figure 7a. For that chromophore, the absorption spectrum in water exhibits an absorption band at 446 nm and another band at a shorter wavelength of 278 nm (not shown in the plot).^44,105 Comparison between QM/FQ and QM/TIP3P spectra indicates that the mutual polarization is crucial to improve the description of experimental data, since QM/TIP3P places the absorption maximum in the furthest position with respect to the other solvation models, thus having the highest error.⁵⁵ This system is another peculiar example in which including explicit water molecules in the QM portion does not alter considerably the spectrum. This is due to the fact that there are no specific solute–solvent interactions according to the radial distribution functions from the MD sampling. Also, for NAGMA and NALMA dipeptides,⁶⁸ a shift toward the experimental results is recovered by using the QM/FQ model rather than QM/TIP3P. Concerning a very popular solute, caffeine, some repercussions are noted too. Caffeine is a xanthine, structurally similar to a purine. Its UV–vis absorption spectrum in water exhibits two bands centered at 205 and 273 nm.¹⁰⁶ Similar to the case of the Cyanine dye, Figure 7b shows that for solvated caffeine (it also applies for paraxanthine),⁵⁶ the accounting for polarization improves the relative intensities between the bands.

Figure 7.

QM/TIP3P, QM/FQ, and experimental UV–vis spectra of (a) pyridinium dye⁵⁵ and (b) caffeine⁵⁶ in aqueous solution. Experimental spectra from refs (105) and (106). The pyridinium dye was rigid whereas Caffeine was freely allowed to move during MD simulations. QM level: CAM-B3LYP/6-311++G(d, p) and B3LYP/6-311++G(d, p) for pyridinium dye and caffeine, respectively. Image (a) reproduced and adapted from ref (55). Copyright 2019 John Wiley & Sons publications. Image (b) reproduced and adapted with permission from ref (56). Copyright 2020 Royal Society of Chemistry.

4.3.1. Different Treatments of Solvent Polarization: From QM/FQ to QM/FQFμ

At this point, it should be clear that a correct inclusion of mutual solute–solvent polarization and a detailed description of solute–solvent interactions (e.g., HBs) both need to be appropriately modeled to guarantee high-quality computed absorption spectra. Undoubtedly, polarizable QM/MM approaches are proper choices, but spectra can vary as a function of the chosen PE model. Basically, the alternatives differ in how the QM/MM coupling term is inserted in the QM Hamiltonian¹ and in the polarization sources under consideration. While charges rule polarization effects QM/FQ, charges and dipoles play that role in QM/FQFμ. Therefore, when QM/FQFμ is used, each MM atom is assigned a charge and a dipole which can vary according to the external electric potential and electric field. QM/FQFμ introduces a better description than QM/FQ of short-range electrostatics and out-of-plane polarization effects.^13,42 Within the absorption spectroscopy scenario, the most notorious implications of using QM/FQFμ have been the shifting of the absorption bands and a more spread distribution of raw spectral data (sticks). Indeed, the application of QM/FQFμ has granted the calculation of accurate vacuo-to-water solvatochromic shifts not only in sign but also in value.^13,14

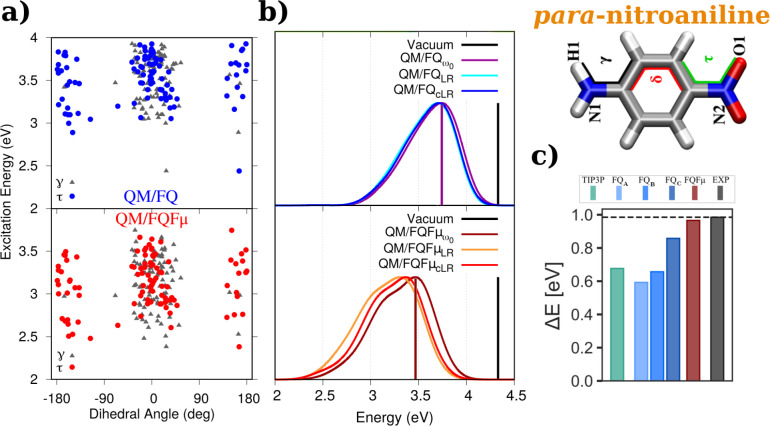
Data for para-nitroaniline (PNA) are shown in Figure 8. Known for its solvatochromicity, PNA is typically used as a probe in the assessment of the quality of computational models for spectroscopy.^13,42,51,54 The effect of the conformational wealth on excitation energies of PNA is reported in Figure 8a. Small discrepancies between QM/FQ and QM/FQFμ vertical excitation energies are identified. The corresponding UV–vis spectra for PNA aqueous solutions are shown in Figure 8b. A few important points are immediately drawn: first, QM/FQFμ convoluted spectra show a larger in-homogeneous broadening with respect to QM/FQ, due to a broader distribution of the sticks. Second, the different description of electrostatic interactions given by QM/FQ and QM/FQFμ leads to a diverse value of solvatochromic shifts for the π → π* transition of PNA (see the position of the vertical bars in Figure 8b). Experiments^107,108 suggest that the solvatochromic shift of PNA is 0.99 eV, which is a value better achieved in the case of the QM/FQFμ approach.^13,54

Figure 8.

QM/FQ (top) and QM/FQFμ (bottom) (a) cLR excitation energies of PNA in aqueous solution as a function of selected dihedral angles and (b) ω₀, LR, and cLR spectra. Vertical bars mark the position of excitation energies in vacuum and those obtained with ω₀, i.e., the frozen density approximation.¹³ c) PNA vacuo-to-water solvatochromic shifts, ΔE = E^solv – E^vac, in water⁵⁴ computed with QM/EE and different QM/FQ parametrizations. PNA was freely allowed to move during MD simulations. QM level: CAM-B3LYP/aug-cc-pVDZ and CAMY-B3LYP/TZ2P. Images (a) and (b) reproduced and adapted from ref (13), with the permission of AIP Publishing, Copyright 2019 AIP Publishing. Image (c) reproduced and adapted with permission under a Creative Commons Attribution 4.0 International (CC BY 4.0) from ref (54). Copyright 2022 arXiv.

Still commenting on PNA, it is well-known that a correct definition of the solvation regime, i.e., how to reliably describe the environment response following the electronic transition, is crucial to compute accurate excitation energies in solution. Specifically, here we focus on the LR and cLR approaches, which have already been extended to both QM/FQ and QM/FQFμ.¹³ In brief, cLR, unlike LR, is able to catch the relaxation of the environment (the solvent in this case) as a response to the charge equilibration of the QM density to the specific excited state. Therefore, cLR is the most appropriate method when dealing with excitations that involve large density rearrangements.^32,109Figure 8b shows computed excitation energies of solvated PNA¹³ obtained either with LR or cLR regimes. In this specific case, LR and cLR excitation energies are similar, thus indicating that the LR scheme, where the response of the MM portion is adjusted to the QM transition density, is sufficient in the treatment of the excitation of this molecule. That is not always the case: in ref (42), it has been shown that relevant discrepancies between LR and cLR excitation energies might occur, for instance for 1-methyl-4-[(oxocyclohexadienylidene)ethylidene]-1,4-dihydropyridine (MER) and 2,6-diphenyl-4-(2,4,6-triphenylpyridin-1-ium-1- yl)phenolate (BET) and to a lesser extent for 1-methyl-8-oxy-quinolinium betaine (QB) when dissolved in different solvents (1,4-dioxane (DIO), tetrahydrofuran (THF), acetonitrile (ACN), ethanol (ETH), methanol (MET) and water (WAT)). Computed values are listed in Table 2.

Table 2. QM/FQ LR and cLR Excitation Energies (in eV) of QB, MER, and BET in Different Solvents^a.

	QB		MER		BET
solvent	LR	cLR	LR	cLR	LR	cLR
DIO	2.62	2.55			2.43	2.22
THF	2.57	2.51	2.63	2.85
ACN	2.78	2.74	2.83	2.98	2.94	2.79
MET	3.26	3.17			3.55	3.30
ETH			2.98	3.19
WTR	3.41	3.35	3.18	3.33	3.88	3.71

^aData taken from Ref (42). QB, MER, and BET were kept frozen in their minimum energy structure during MD simulations.

4.3.2. How the Results Depend on the FQ Parametrization

In QM/MM approaches, the simulation of specific environments requires specific MM parametrization. As stated before, there is a list of predefined parameters that are used in the calculations to define the solvent’s response. They are electronegativities and chemical hardnesses (and atomic polarizabilities) for QM/FQ (and QM/FQFμ). The hearth of the parametrization procedure is the fitting of calculated values of selected observables, such as interaction or total energies, with respect to reference data sets that can be obtained from full ab initio calculations on representative structures. Water or water–solute clusters of different molecularities have been often employed to find parameters for polarizable force fields. In this way, QM/FQ has been parametrized by Rick et al.,²⁹ Carnimeo et al.,⁶⁹ Giovannini et al.,⁸⁵ and lately by Ambrosetti et al.,⁴² increasingly trying to refine computed spectral properties. QM/FQFμ parameters have been proposed once.¹¹ Many works have greatly benefited from one or another parametrization as can be read in Table 1. Overall, changing parameters improves the description of the position of the absorption bands⁶⁸ or relative intensities.⁵⁶ It is worth recalling here that what is changing when varying parameters is the degree of polarization that the solute can induce on the surrounding solvent molecules, thus directly affecting the solute’s spectral response.¹

Recently, the performance of different QM/MM embedding models and parametrizations to compute vacuo-to-water solvatochromic shifts has been investigated by Nicoli et al.⁵⁴ For PNA, those results are collected in Figure 8c. In that work, for QM/FQ calculations, three sets of parameters, namely, QM/FQ A,²⁹ QM/FQ B,⁶⁹ and QM/FQ C,⁷⁰ are reviewed. In all cases, the sign is correctly reproduced and after refinement, the solvatochromic shift moves toward the experimental value. Notwithstanding, QM/FQFμ outperforms the other models for this particular system and, although it is not the emphasis of this section, the shift given by the nonpolarizable QM/TIP3P method compares somewhat poorly to the experimental value.

To conclude this section, we refer interested readers to a recent assessment of the performance of different polarizable embedding approaches, ranging from QM/FQ to QM/Discrete Reaction Field (QM/DRF) and QM/FQFμ, in the reproduction of solvatochromic shifts of several dyes dissolved in aqueous solution.⁵⁴

4.4. Inclusion of Nonelectrostatic Terms

As stated in section 2, most QM/MM approaches limit the QM/MM interaction term in eq 2 to electrostatic and polarization contributions. Nonelectrostatic interactions (repulsion and dispersion) are commonly included through parametric functions, such as the Lennard-Jones potential, which does not depend on the QM density. As a consequence, nonelectrostatic terms modify neither the GS nor the excited state QM density and only indirectly affect the final numerical values. The difficulty in treating QM/MM nonelectrostatic interactions stands in the fact that, since the MM part is classical, ad hoc models need to be constructed to properly model interactions of a purely quantum nature.

Here, we focus on how Pauli repulsion E_QM/MM^rep can affect absorption properties of solvated systems, by exploiting a method which has been developed in our group and is general enough to be applied to any kind of environment and QM/MM method.^14,15,57,70 The approach is rather simple: each MM molecule is endowed with a set of functions mimicking the QM density of the MM portion ρ_MM, and E_QM/MM is written as the opposite of an exchange integral, i.e.:^110,111

12

The specific definition of the MM density ρ_MM for the case of water can be found elsewhere.⁵⁷ Here, it is worth remarking that the QM/MM repulsion energy is calculated as a two-electron integral, in which the MM density remains constant during the SCF cycles. As a consequence, E_QM/MM^rep results in a one-electron contribution to the QM Hamiltonian, thus leading to a modification of the MO coefficients and energies. Therefore, Pauli repulsion gives an indirect contribution to excited state properties. Cases studied in the literature introducing these also-called quantum confinement effects include solvatochromic shifts evaluated with different levels of theory: nonpolarizable fixed-charges QM/TIP3P model, polarizable QM/FQ and QM/FQFμ models, and both polarizable models with the addition of repulsion forces.¹⁴ To showcase how nonelectrostatics can affect absorption properties, we focus on the well-known case of vacuo-to-water solvatochromic shifts of acrolein.^14,20

Some authors have become aware of the role of those effects when observing that solvatochromic shifts change by treating a few solvent molecules surrounding the solute at the QM level.²⁰ Of course the criticism/disadvantage of doing so lies in the expensiveness of the selection process of the solvent molecules (how many, where to put them) and the calculation itself. By using our approach, it is no longer necessary to take care of explicit water molecules to account for nonelectrostatic effects. By going back to Figure 6, we see that when the Pauli repulsion contribution between the QM solute and water molecules is considered (green bars) in addition to the electrostatic coupling, the solvatochromic shift for the n → π* transition reduces and approaches the experiment. The same does not apply to the π → π* transition, which requires the further consideration of charge exchange between water molecules to be perfectly simulated (see also section 2).¹⁴ Similar conclusions can be drawn after including repulsion in the modeling of the UV–vis spectra of solvated nitrite.⁶⁵ These findings also reveal that nonelectrostatic effects in absorption spectroscopy are indeed not uniform, and nonobvious predictions can be made a priori.

Nonelectrostatic contributions may also be modeled by resorting to multiple-layer methods. In this scenario, excitation energies of solvated acrolein have been studied by using a multilayer polarizable embedding approach with frozen density embedding (FDE), QM/FDE/FQ,⁶¹ or by coupling different quantum-embedding approaches with a third FQ layer.⁵¹ In these approaches, the environment’s density is retained, thus quantum forces are automatically included, without the need of resorting to specific parametrizations of the environment.

4.5. Brief Note on the Influence of Charge Transfer

Charge transfer (CT) effects can occur within the same molecule (intrasolute or intramolecular), between solute and solvent, and between solvent molecules. In the intrasolute case, excitations of CT character refer to transitions associated with significant movements of the electron density. The degree to which CT takes place can be assessed by means of different descriptors, such as the D_CT index based on the difference between the unrelaxed (or relaxed) excited-state density and ground-state density.¹¹² This spatial index indicates the charge displacement which is associated with the transition and has been exploited in connection to polarizable QM/MM approaches in various works.^13,55,56,59

QM/FQ and QM/FQFμ can allow intermolecular solvent–solvent CT, i.e., the charge transfer between MM molecules (see section 2). Such effects have been evaluated for acrolein, pyridine, and pyrimidine in ref (14), and Figure 6 shows that, for acrolein, QM/FQ_CT and QM/FQFμ_CT give solvatochromic shifts in almost perfect agreement with experiments when coupled to nonelectrostatic effects.

As for solute–solvent CT, neither QM/FQ nor QM/FQFμ (and none of the available QM/MM approaches) allows the exchange of charge between the two portions. When strong charge transfer occurs between solute and solvent, the orbitals involved in the transitions belong not only to the solute but also to the nearest solvent molecules. This happens in the case of nitrite⁶⁵ (see one of the molecular orbitals in Figure 9a), where it is necessary to add the first, second, and third solvation shells in the QM portion—turning into QM/QM_w/FQ—in order to recover the experimental position of the main band in the UV–vis spectrum. Distributions of D_CT indexes for the 12 transitions of NO₂^– along the 200 snapshots (12 × 200 sticks) analyzed by Uribe et al.⁶⁵ are reported in Figure 9b. Clearly, the two distributions peak in different values, and the addition of water molecules to the QM portion makes the distribution flat, at the same time moving the main maximum to ≈2.9 Å, which confers to some excitations the feature of being of charge transfer nature. The need to include solute ↔ solvent charge transfer effects for a correct description of experimental spectra of small anions in aqueous solution^65,113 shows that even those apparently simple molecules hide a complex electronic structure that entails n → π*, π → π* transitions and charge transfer states.

Figure 9.

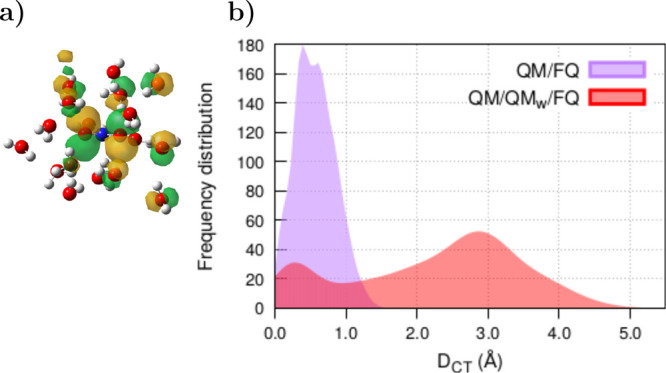
(a) Picture of one of the molecular orbitals involved in the UV–vis transitions of NO₂^– in water, obtained with the QM/QM_w/FQ approach. FQ water molecules are omitted. (b) Distribution of D_CT indices computed with QM/FQ and QM/QM_w/FQ on 200 snapshots extracted from MD trajectories of solvated NO₂^–. Twelve excited states are taken into account in each snapshot. NO₂^– was freely allowed to move during MD simulations. QM level: CAM-B3LYP/6-311++G(d, p). Numerical results are taken from ref (65).

Some attempts to describe the charge transfer in multiscale simulations have been done by Lin et al.^114−116 who proposed a model with a flexible boundary characterized by on-the-fly exchanges of partial charges and atoms between the QM and MM subsystems. However, to the best of our knowledge, such an approach has only been applied to the description of ground state properties.

4.6. Toward Nonaqueous Media

Until now, we have focused on the specific case of aqueous systems. QM/FQ has recently been extended to nonaqueous solvents of various polarity and hydrogen-bonding capability,⁴² namely, 1,4-dioxane, tetrahydrofuran, acetonitrile, ethanol, and methanol. This implies the specification of the values of atomic electronegativities and chemical hardnesses, which are independent of the solute and/or the spectral observable but only depend on the solvent, which ultimately makes the parametrization transferable. Detailed results for PNA are reported in Figure 10, which shows that excitation energies and, in turn, solvatochromic shifts increase with the polarity of the solvent. QM/FQ excitation energies are almost in line with the experimental trends, giving excellent values and in some cases exhibiting outstanding agreement with experimental data. Conversely, QM/EE strongly underestimates experimentally measured shifts, thus revealing once again the relevance of the solute–solvent polarization as highlighted in a previous section and in ref (42). Finally, it is worth noting that, for low-polar solvents, both QM/EE and QM/FQ fail at reproducing the experimental trends. This might be due to the lack of nonelectrostatic interactions in our modeling,^14,15,57,70 which may be particularly relevant in these cases.

Figure 10.

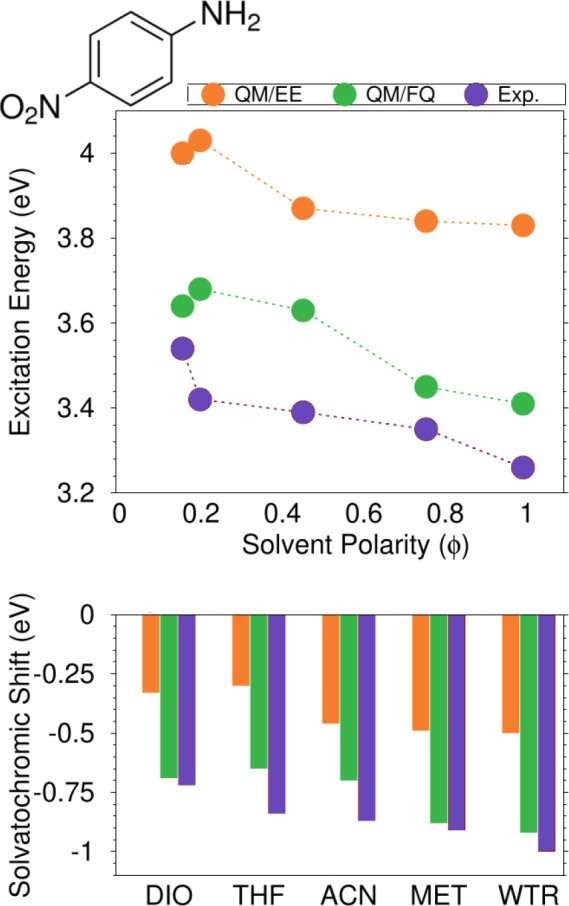
Top panel: QM/EE, QM/FQ, and experimental PNA excitation energies as a function of the solvent polarity. Bottom panel: solvatochromic shifts in diverse solvents, computed with respect to gas-phase.⁴² PNA was kept frozen in its minimum energy structure during MD simulations. QM level: CAM-B3LYP/aug-cc-pVDZ. Image adapted from ref (42). Copyright 2021 American Chemical Society.

5. Concluding Remarks

In this Perspective, we have shown, by means of clear-cut examples, the crucial role of diverse aspects in the simulation of electronic absorption spectra of solvated systems. Thus, a model intended to obtain a reliable description of experimental data and to have predictive power should be able to integrate essential elements, such as the phase-space sampling, solvation effects, and a physically sound calculation of the spectral signal. The dynamical aspects of the solvation phenomenon can be considered by resorting to classical MD simulations, whereas the computation of spectral properties can be performed by using multiscale QM/MM methodologies. As expected, spectral features depend on the reliability of the force fields used in MD and QM/MM calculations. For the latter, QM/FQ has proven to be particularly advantageous because of its flexibility to integrate the various effects in place in the solvated sample, thus treating all solute–solvent interactions that are meaningful for the generation of the spectroscopic response. Mutual polarization effects, nonelectrostatic contributions, relaxation effects in the solvent response, and even vibronic effects can be properly included. Broadly speaking, when QM/FQ in any of its flavors—QM/FQ or QM/FQFμ—has been challenged to reproduce absorption spectra or solvatochromic shifts of systems in solution, results have found better agreement with experimental data than continuum solvation and electrostatic embedding approaches.

Despite their success, further improvements for QM/FQ and QM/FQFμ can be foreseen. The first development line is their extensive parametrization for diverse environments, which will allow treating more and more complex systems, up to biological environments. The parametrization effort also extends to quantum repulsion, and eventually, quantum dispersion, which up to now have been only challenged for aqueous systems. In addition, dealing with large systems implies the immediate use of enhanced MD sampling techniques and a careful choice of the partitioning of the system. Also, in order to make the computational approach entirely coherent with the physics of the absorption phenomenon, charge transfer interactions (both between QM/MM or MM/MM moieties) would need to be included. However, universal protocols for treating such effects are not available yet, making it an interesting topic for future investigations. We finally note that, in the above discussion, effects arising from the electronic-nuclear coupling, which also affect the spectral shape, have not been emphasized. More extensive investigations, in line with recent studies,¹¹⁷ would contribute to increase the quality of the description of experimental spectra.

Author Contributions

CRediT: Sara Gomez data curation (lead), writing-original draft (lead); Tommaso Giovannini data curation (supporting), software (lead), writing-original draft (supporting); Chiara Cappelli conceptualization (lead), funding acquisition (lead), resources (lead), supervision (lead), writing-review & editing (lead).

The authors declare no competing financial interest.