Effects of spatial fMRI resolution on the classification of naturalistic movies

Abstract

Studies involving multivariate pattern analysis (MVPA) of BOLD fMRI data generally attribute the success of the information-theoretic approach to BOLD signal contrast on the fine spatial scale of millimeters facilitating the classification or decoding of perceptual stimuli. However, to date MVPA studies that have actually explored fMRI resolutions at less than 2 mm voxel size are rare and limited to small sets of unnatural stimuli (like visual gratings) as well as specific sub-regions of the brain, notably the primary somatosensory cortices. To investigate what spatial scale best supports high information extraction under more general conditions this study combined naturalistic movie stimuli with high-resolution fMRI at 7 T and linear discriminant analysis (LDA) of global and local BOLD signal patterns.

Contrary to predictions, LDA and similar classifiers reached a maximum in classification accuracy (CA) at a smoothed resolution close to 3 mm, well above the 1.2 mm voxel size of the fMRI acquisition. Maximal CAs around 90% were contingent upon global fMRI signal patterns comprising 4 k–16 k of the most reactive voxels distributed sparsely throughout the occipital and ventro-temporal cortices. A Searchlight analysis of local fMRI patterns largely confirmed the global results, but also revealed a small subset of brain regions in early visual cortex showing limited increases in CA with higher resolution. Principal component analysis of the global and local fMRI signal patterns suggested that reproducible neuronal contributions were spatially auto-correlated and smooth, while other components of higher spatial frequency were likely related to physiological noise and responsible for the reduced CA at higher resolution. Systematic differences between experiments and subjects suggested that higher CA was significantly correlated with more consistent behavior revealed by eye tracking. Thus, the optimal resolution of fMRI data for MVPA was mainly limited by physiological noise of high spatial frequency as well as behavioral (in-)consistency.

1. Introduction

In the field of functional magnetic resonance imaging (fMRI), data-driven machine-learning classification methods, often referred to as multivariate pattern analysis (MVPA), have gained popularity as they promise to overcome certain limitations of traditional univariate fMRI analysis (Kriegeskorte et al., 2006; Norman et al., 2006; Pereira et al., 2009). Unlike the well-established statistical parametric mapping (SPM) technique (Friston et al., 1995), these alternative, information-theoretic methods do not depend on an explicit general linear model (GLM) of the BOLD signal, nor do they require strong a-priori assumptions about the relevant stimulus features and the hemodynamic response function (HRF) of the cortex. Based on multivariate statistics, MVPA methods like Linear Discriminant Analysis (LDA) can more efficiently exploit spatial correlations of the fMRI signal in order to gain sensitivity for the detection of small effects. fMRI data analysis by means of non-parametric, model-free machine-learning methods is particularly interesting in conjunction with naturalistic stimuli like photographs or movies that evoke complex perceptual processes, for which adequate fMRI signal models are lacking despite some unique efforts in the field (Horikawa et al., 2013; Nishimoto et al., 2011). These advantages make MVPA methods particularly useful for the kind of single-subject and single-trial analyses required for diagnostic applications, neuro-feedback (BCI) and unrepeatable cognitive processes like learning.

Many MVPA studies have loosely attributed the success of multivariate classification methods to fMRI contrast on a “fine” spatial scale (Alink et al., 2013; Emmerling et al., 2016; Guntupalli et al., 2016; Haxby et al., 2014). Indeed high-resolution (HR) fMRI studies in humans and animals have demonstrated fMRI contrast on a spatial scale of <1 mm (Menon and Goodyear, 1999; Olman et al., 2012; Yacoub et al., 2008). Such information would typically be lost to partial-volume effects and low statistical power in conventional fMRI analysis with low-resolution (LR) acquisitions (>2 mm) and additional smoothing (>3–8 mm FWHM) aimed at detecting significant deviations in the regional mean signal of voxel clusters (Kriegeskorte et al., 2006). MVPA methods, by contrast, are designed to take advantage of a spatially diverse (high-dimensional) fMRI signal (of high resolution), given sufficient SNR to make activation patterns distinct and reproducible (Chaimow et al., 2017). However, experimental evidence in support of this premise is scarce in the literature:

A majority of MVPA studies, even those ostensibly concerned with fMRI signal patterns “on a fine spatial scale”, have relied on acquisitions far from the resolution limits of fMRI, especially at high field (!3 T) (Alink et al., 2013; Guntupalli et al., 2016). Sacrificing fMRI resolution in the inevitable trade-off for SNR, TR and (whole-brain) coverage makes perfect sense in the context of traditional fMRI analysis, which relies on spatial smoothing to justify statistical assumptions and to overcome the limitations of anatomical co-registration procedures. The few studies that have actually applied MVPA to HR fMRI data were limited to small sets of artificial stimuli like oriented gratings as well as small cortical sub-regions like V1 (Emmerling et al., 2016; Gardumi et al., 2016; Sengupta et al., 2017; Swisher et al., 2010). Such HR fMRI experiments have successfully detected patterns of cortical orientation columns only 0.7 mm in diameter. However, MVPA studies that used a voxel size much larger than these cortical structures have demonstrated an equal or better ability to discriminate similar orientation stimuli (Haynes and Rees, 2005; Kamitani and Tong, 2005). This apparent conundrum triggered an ongoing debate about “fMRI hyperacuity”, or mechanisms by which the fMRI signal from cortical columns might transcend to the spatial scale of voxels (Chaimow et al., 2017; Kamitani and Sawahata, 2010; Kriegeskorte et al., 2010; Op de Beeck, 2010), although similar information on different spatial scales could also be supported by independent physiological processes.

This paper is not a contribution to the hyperacuity debate regarding the discrimination of stimuli (oriented gratings) specifically tailored to elicit predictable changes in the neuronal response on a sub-millimeter scale. Instead we address the question whether or not high-resolution fMRI at 7 T in practice increases the discriminability of a wide range of naturalistic (visual) stimuli by MVPA classification methods. Some MVPA studies that have used naturalistic stimuli like movies indicate that smoothing may increase CA contrary to expectations (Haxby et al., 2011). But fMRI resolutions of <2 mm in voxel size were not explored. More recent studies have actually compared MVPA at resolutions as high as 0.8–1.1 mm but were limited to primary visual and auditory brain regions as well as small sets of highly tailored and very similar stimuli (gratings, vowels) (Gardumi et al., 2016; Sengupta et al., 2017; Swisher et al., 2010) – quite the opposite of our naturalistic stimuli expected to elicit strong fMRI contrast across a range of spatial scales. Even so, aforementioned studies tentatively corroborate a maximum in classification accuracy at a moderate fMRI resolution of 2–3 mm, although results were somewhat mixed and exhibited a substantial amount of variability above all.

In principle, high-field MRI systems (≥7 T) show promise for functional brain imaging in humans as they facilitate fMRI scans with higher spatial and temporal resolution thanks to both increased SNR and functional (T2*-weighted) BOLD contrast. It has been argued, however, that the co-amplification of physiological noise and the lack of precise inter-subject alignment methods limit the gains of higher field strength in many practical applications (Krüger and Glover, 2001; Triantafyllou et al., 2005). Focused on the tSNR of single voxels in resting-state fMRI these studies neglect the spatially correlated fMRI signal evoked by stimulation, which is the basis of MVPA. Ultimately, the spatial band-width and relative amplitude of BOLD signal and noise components must determine the optimal resolution for information extraction by SPM or MVPA. In other words, the available spatial bandwidth of the BOLD signal must overcompensate inevitable losses in instrumental SNR as well as any interference due to “physiological noise” in order to achieve a net gain in information as a result of higher fMRI resolution.

In light of these mixed results, the purpose of this study is to determine whether or not MVPA profits from HR fMRI at 7 T in practice – specifically whether the accuracy of common classifiers like LDA increases with fMRI resolution. In preparation for this study, we recently published a comparison of common classification algorithms demonstrating that comparisons between data sets are largely independent of the choice of classifier (Mandelkow et al., 2016). However, results will likely have some dependence on the type of stimuli as well as the targeted brain region. Aiming for results that would generalize across a wide range of (visual) stimuli, we chose short clips from (naturalistic) action movies (L. Wachowski and A. Wachowski, 1999), which are popular in the field for a number of reasons: Unlike abstract stimuli like moving dots or gratings, movies of human actions and environments have ecological validity for human subjects and are certain to evoke a broad range of natural cognitive processes. Such processes are of great interest in cognitive neuroscience, but challenging to analyze by traditional (GLM-based) fMRI methods, because investigators are forced to speculate on the (many) relevant stimulus features and their relative contributions to the evoked BOLD signal (Huth et al., 2012; Naselaris et al., 2015). From a practical point of view, movies are easy to deliver with precise timing in the MRI scanner and they are known to evoke a strong and reproducible BOLD fMRI response in large parts of the brain, especially if they are engaging, i.e. attracting a subject’s attention (Golland et al., 2007; Hasson et al., 2008; Jääskeläinen et al., 2008).

2. Methods

Briefly, the following experiments were designed to compare the relative information content of high- and low-resolution fMRI data based on the classification accuracy (CA) achieved by multivariate machine-learning classifiers trained to discriminate BOLD activation patterns evoked by a variety of visual stimuli presented as a movie. The fMRI resolution was varied primarily by acquiring data at two different voxel sizes, 1.2 mm and 2 mm isotropic, and additionally by applying various amounts of Gaussian smoothing. In contrast to Gardumi et al. (2016). we opted for separate fMRI acquisitions at two representative spatial resolutions in order to account for the theoretical SNR advantage of low-resolution acquisitions as well as any other effects that may have an influence in practice (e.g. sensitivity to motion and physiological noise, parallel imaging g-factor, shimming, readout bandwidth, etc.) (Buxton, 2009; Kasper et al., 2014; Krüger and Glover, 2001; Triantafyllou et al., 2006).

2.1. fMRI experiments

Four subjects (age 24 ± 1.2 years, 2 male) each gave written informed consent in accordance with institutional guidelines at the NIH (IRB-approved protocol 00-N-0082) to undergo a series of repeated fMRI experiments at 7 T. During each fMRI experiment the subject was asked to watch one of two 5-min scenes from a popular action movie presented without audio. For the purpose of eye tracker calibration, the movie stimulus was immediately preceded and followed by a 30-s sequence of 9 fixation dots. Subjects were instructed to pursue the fixation dots visually and to watch the video attentively and in a natural fashion. This kind of naturalistic stimulus was chosen to elicit a broad range of cognitive processes and in turn a highly diverse BOLD response suitable for machine-learning classification. Experiments were repeated over 5 to 6 scan sessions spread over six months until each subject had completed 16 viewings of the same video stimuli, 8 experiments at each resolution.

2.2. fMRI data acquisition

For the assessment of resolution effects fMRI data were acquired with a TR of 2 s and either a high or a low isotropic resolution of 1.2 mm and 2 mm respectively (8 scans each). The low-resolution (LR) scans had about twice as much temporal SNR and spatial coverage (max. tSNR 1⁄4 100–150, 35 slices) as the high-resolution (HR) scans (max. tSNR 1⁄4 50–80, 24 slices), but the data analysis below is restricted to the overlapping FOV covering inferior temporal cortex and most of the occipital lobe. T2*-weighted single-shot EPI images in transversal orientation were acquired on a 7 T MRI scanner (Siemens, Erlangen, Germany) with 70 mT/m @ 200 T/m/s gradients and a combined quadrature transmit 32-channel receive head coil (Nova Medical, Wilmington, USA). The imaging parameters for both sequences (HR/LR) were typical for fMRI including: TR 1⁄4 2 s, TE 1⁄4 26/28 ms, FA 1⁄4 68/63, BW 1⁄4 227/192 kHz, matrix 1⁄4 1602/962, GRAPPA 1⁄4 3. As an anatomical reference for the within-subject co-alignment of fMRI time series a whole-brain volume of T2*-weighted images was acquired at 1 mm isotropic resolution by a GRE sequence (TR/TE 1⁄4 3 s/24 ms; FA 1⁄4 80; BW 1⁄4 230 Hz/pixel; matrix 1⁄4 256 192).

A 3 cm gap between the outer transmit and inner receive coil accommodated a mirror and a small MR-compatible CCD camera (MRC Systems GmbH, Heidelberg, Germany) to allow both the projection of visual stimuli and video recording of the subject’s eye movements using eye-tracking software by Arrington Research, Inc. (USA). A separate computer running the Psychophysics Toolbox in Matlab (http://psychtoolbox.org/) (Brainard, 1997) served to play the digital video stimuli in synchrony with MRI acquisition triggers and the eye tracker. In addition, each subject’s cardiac and respiratory signals were recorded by pulse-oximetry and a chest belt.

2.3. Eye tracking

At 30 Hz the eye-tracking signal was sampled much faster than the fMRI, but it was fraught with variability from technical sources mostly due to eye closure (blinking) and head motion. This resulted in outliers and baseline drifts, which were corrected by removing samples of extreme amplitude or slope and by computing a linear baseline correction based on calibration measurements directly before and after each movie stimulus presentation. The prevalence of outliers due to eye closures and the Pearson correlation between the corrected gaze trajectories from different experiments provided information on each subjects perceptual consistency and attention to the movie viewing task. Median correlation coefficients of 40–60% attested to high reproducibility in each subject’s free-viewing behavior, but systematic differences between subjects were noticeable and reflected in the fMRI data as discussed below. Significant (Pearson) correlation coefficients (r) were assessed via the common transform to a t-statistic with (n-2) degrees of freedom:

$$t_{n-2}~r\sqrt{\left(n-2\right)/\left(1-r^2\right)}$$

All analyses were implemented in house using Matlab.

2.4. fMRI data pre-processing

Pre-processing and analysis of the fMRI data was performed using custom code written in MATLAB (http://www.mathworks.com) and supplemented by tools from AFNI (http://afni.nimh.nih.gov) (Cox, 1996) and FSL (http://fsl.fmrib.ox.ac.uk) (Smith et al., 2004). The effective resolution of time-resolved fMRI data generally depends as much on the data acquisition as on the interpolation blurring incurred in the pre-processing required for data analysis. An isotropic resolution during MRI acquisition was crucial to minimize blurring by realignment for motion correction. Also, the realignment within and between scans of the same subject was implemented in a single interpolation step (7-point sinc). The subsequent within-subject analysis deliberately excluded any transformation to an anatomical standard space in order to preserve the original resolution of the data as much as possible.

fMRI data from all experimental runs first underwent slice-timing and motion realignment, they were simultaneously aligned to each subject’s individual T2-weighted anatomical scan, resampled to a common isotropic resolution of 1.2 mm and cropped to the FOV shared across scans (Sup. Fig. 12). Note that up-sampling the LR data to a higher nominal resolution did not change its intrinsic smoothness (see Fig. 2). To mimic lower resolutions, smoothing by a Gaussian kernel of 2–12 mm FWHM was applied after all geometric alignment steps. Note that in terms of image SNR post-hoc smoothing is inferior to fMRI acquisitions at a lower resolution, hence the dual-acquisition approach taken in this study. Motion parameters, their derivatives, as well as linear and quadratic trends were regressed out before converting each voxel’s time series to a z-score by subtracting the mean and normalizing the variance over time. Motion correction and motion parameter regression was particularly important in light of the fact that HR fMRI data exhibited a much stronger linear drift in the phase encoding direction than LR data, commonly due to increased gradient duty cycle and heating. An average voxel displacement metric (root-mean-square voxel displacement aver-aged over volumes and time) was computed from the motion correction parameters of each scan (as part of the FSL-mcflirt algorithm) in order to assess the potential influence of subject motion on the results of the classification analysis below.

Fig. 2.

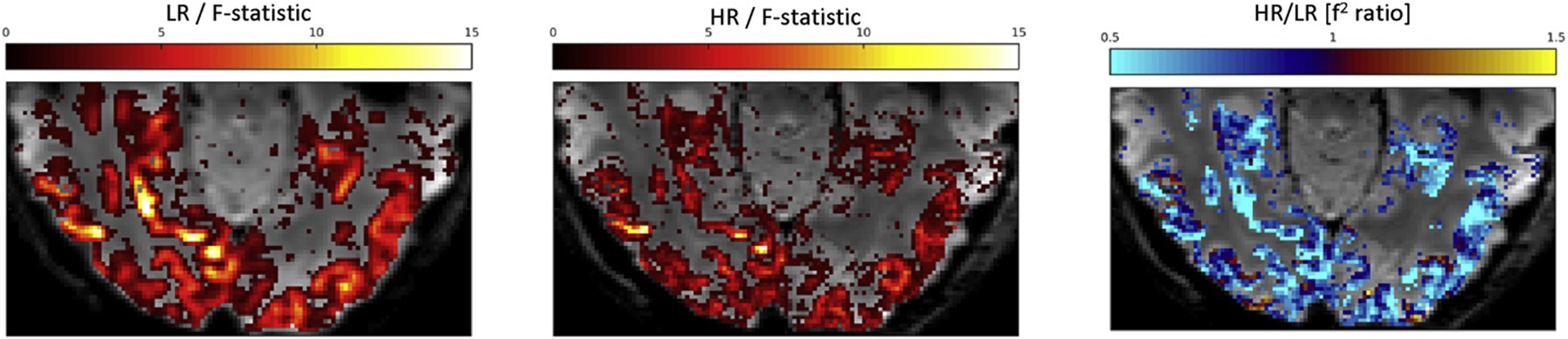
F-statistic maps and effect size ratio HR/LR. An example of F-statistic maps for low- and high-resolution data (LR/HR 1⁄4 left/middle) cut off at p<1% (uncorrected) show more extensive and larger fMRI contrast in the former (LR) (left). Right: A voxel-wise comparison by way of the effect size ratio (HR/LR) confirms that LR > HR almost everywhere. Background: mean EPI of the posterior half of a representative axial slice transecting the occipital and inferior temporal lobes.

2.5. Classification accuracy (CA)

For its main purpose of quantifying differences in the information content of HR and LR fMRI data this study relied on the intra-subject CA achieved by machine-learning classifiers as a proxy. The present work was preceded by a comparative study of classification algorithms to demonstrate the suitability and equivalence of various classifiers and to serve as a more detailed description of the methodology summarized below (Mandelkow et al., 2016): In concrete terms CA was the percentage of individual fMRI volumes in a set of validation data that the classifier correctly assigned to the class representing all fMRI volumes in the training data that were acquired at the same time point (n*TR) during the movie stimulus. Thus, the classification problem featured 150 separate classes corresponding to the number of fMRI volumes acquired during the movie stimulus in each experiment; and the number of samples in each class was equal to the number of repeated experiments – eight per subject and fMRI resolution.

2.6. Cross-validation

The stratified cross-validation scheme used one entire experimental run at a time as validation data – 150 fMRI volumes acquired in one scan. The training data comprised all other experiments in the same subject, acquired with the same fMRI resolution (and movie stimulus), but with the important exception of any other scans that were acquired during the same scan session as the validation data. Without this provision systematic differences between scan sessions (due to shimming, coil loading etc.) would frequently outweigh the stimulated fMRI response and lead to biased CA results (Sup. Fig. 2 in (Mandelkow et al., 2016)).

2.7. Feature selection (fROI)

Because feature selection and input dimensionality had the largest influence on CA results, this direction in parameter space was scanned by varying the number of input features i.e. voxels in the functional ROI (fROI). Between 16 and 216 voxels were included in the order of decreasing stimulus response as assessed by a univariate ANOVA that treated stimulus time points (1…T) as independent groups and experimental runs (1…R) as repetitions. The resulting F-statistic has T*(R-1) and (T-1) degrees of freedom and is proportional to Cohen’s f2 effect size, essentially a (squared) contrast-to-noise ratio (CNR2). It can also be viewed as a measure of BOLD response reproducibility. By construction the variably sized fROIs were not contiguous but naturally clustered in visual areas of the occipital and posterior temporal cortex (Fig. 1). Also, noting the (artefactual) stimulus-correlated signal from the moving eyes and the common susceptibility artefacts surrounding the paranasal sinuses we decided to restrict all further classification analyses to the posterior half of the FOV (Sup. Fig. 12). This measure significantly reduced the computational burden (memory) and was not likely to influence the resolution effects described here. Fig. 2 compares “reproducibility” maps for HR and LR data from one representative subject. These F-statistic maps and resulting fROIs were not recomputed but kept the same for the analysis of smoothed data (Fig. 3).

Fig. 1.

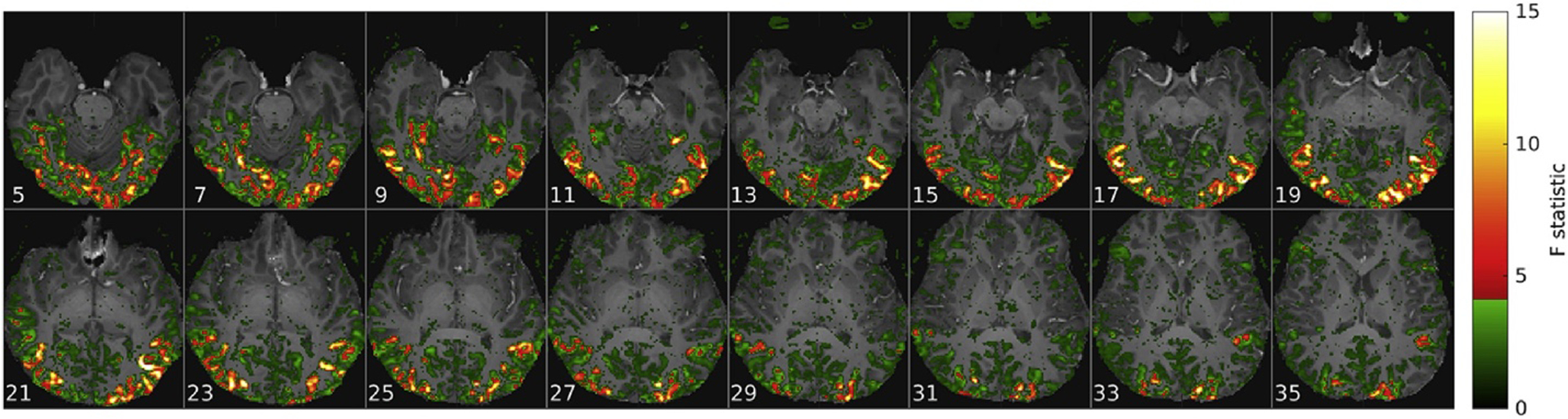
Movie stimuli elicited reproducible fMRI responses across the brain. Example of a voxel-wise ANOVA F-statistic map (threshold p<1%, uncorrected) superimposed on the T1-weighted anatomical MRI of one representative subject (16 axial slices in radiological convention). Stimulus-correlated fMRI activity (colors) was widespread in the occipital and ventral temporal cortices, consistent with their established involvement in visual perception. Red-yellow colors mark the top 214 voxel features that maximized classification accuracy (Fig. 3). The less stimulated frontal regions including the artifactual fMRI signal in the moving eyeballs were excluded from further analysis.

Fig. 3.

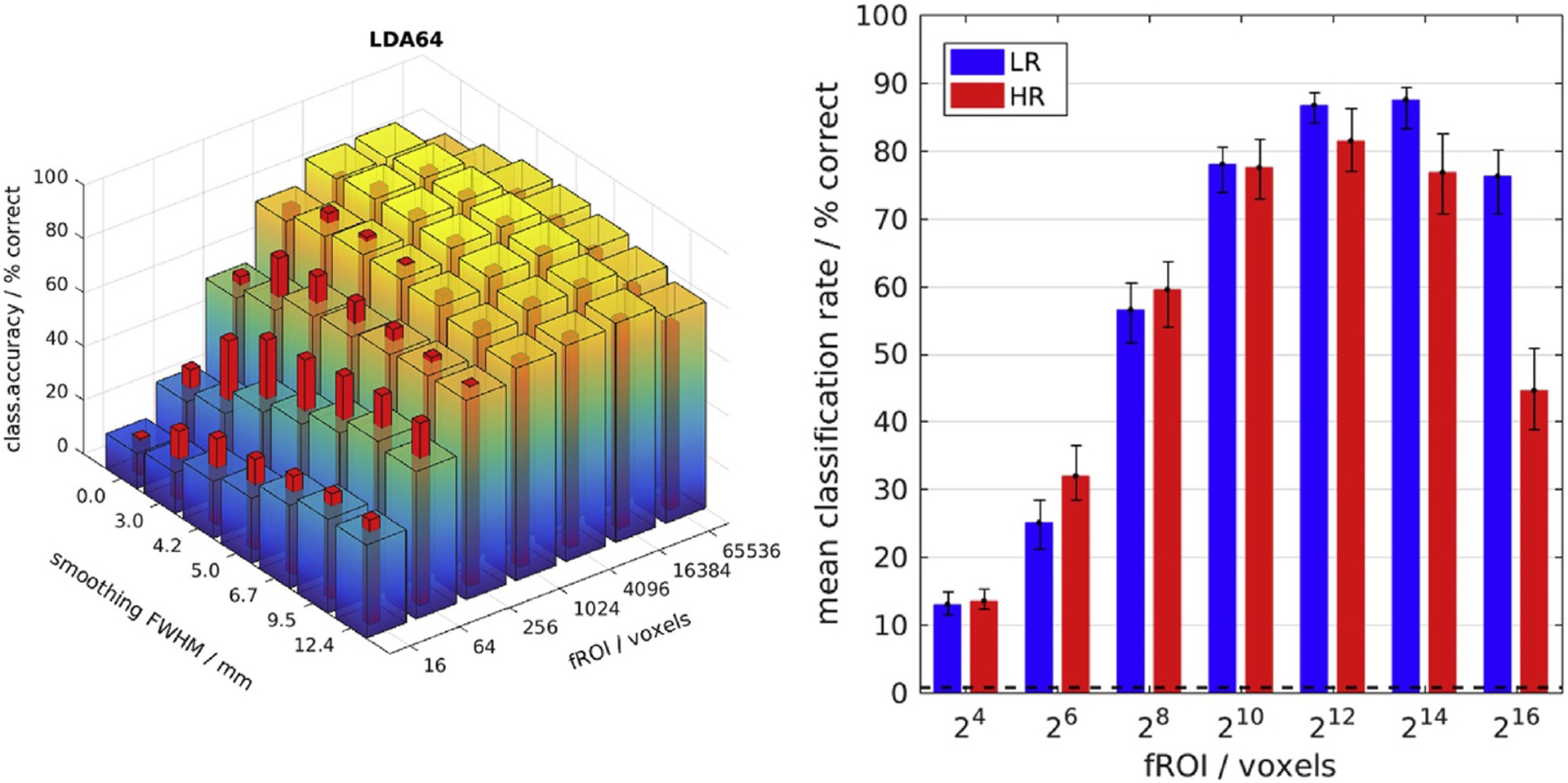
Maximal classification accuracy for widespread global patterns at 3 mm resolution. Left: Classification accuracy (CA) as a function of fMRI resolution (HR/LR 1⁄4 red/blue-yellow bars), smoothing and fROI size: The LDA classifier reached a maximum in CA for LR data smoothed to 3 mm FWHM and a large fROI size of 214 voxels. HR data yielded higher CA than LR data only for small (sub-optimal) fROI sizes (1024) and in conjunction with higher levels of smoothing. Right: CA without smoothing - the error bars span a 95% confidence interval around the mean computed by 100-fold bootstrap.

2.8. Classification algorithm

A majority of MVPA studies to date have focused on the linear support-vector machine (SVM) as the classifier of choice. However, this binary classifier was ill suited to our data, which divides into many more classes (time points) than repetitions (experimental runs). This study primarily relied on PCA-regularized Linear Discriminant Analysis (LDA) for its main purpose of quantifying the relative information content of HR and LR fMRI data. Regularized LDA, based on the Mahalanobis distance after dimensionality reduction by PCA, offered the highest classification accuracy in a preceding comparison of nearest-neighbour classifiers (Mandelkow et al., 2016). By way of extending our previous work, a number of alternative classifiers were also considered and found to be similarly suitable for detecting consistent differences in CA (Sup. Fig. 9). However, the effects of fROI size and smoothing on CA were more pronounced and demonstrable in nearest-neighbour classifiers based on the simpler correlation distance metric, which unlike LDA had a maximum CA well below 100% “saturation” and were less “robust” to (excessive) smoothing of the data (Fig. 5 and Sup. Fig. 13). The weighting of input features by the inverse noise covariance matrix in conjunction with the necessary regularization (i.e. dimensionality reduction) by PCA made the LDA classifier computationally more expensive, but conferred a large increase in CA as well as a greater robustness to changes in resolution (Sup. Fig. 9) and smoothing of the fMRI data (Fig. 5). Table 1 lists classifiers referred to in the results. More comparisons and information can be found in the supplemental materials and in (Mandelkow et al., 2016).

Fig. 5.

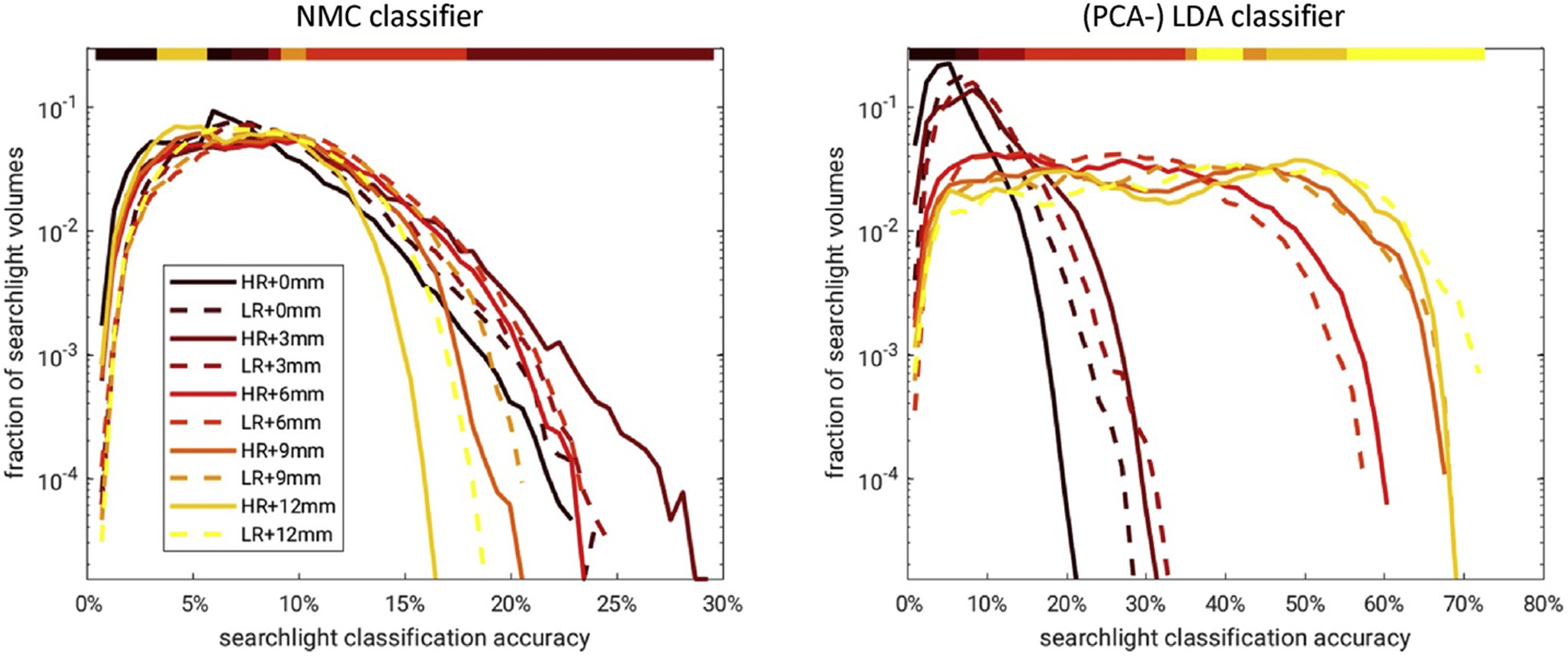
Smoothing shifted the distribution of searchlight CA. Left: A family of histograms was used to summarize the effect of smoothing on SL CA across SL locations and subjects. A log-scale helps resolve the right tail corresponding to SL locations of high CA, which are of particular interest. The color bar above denotes the highest curve for any given SL CA: 3 mm smoothing yielded the most SL locations with CA>20% for HR and LR data analyzed by the NMC classifier using a 8.4 mm SL diameter. Right: Analogous to the smoothing analysis of small global fROIs (Fig. 3), the PCA-regularized LDA classifier profited from much larger amounts of smoothing up to 12 mm FWHM.

Table 1 -.

Glossary of nearest-neighbour classifiers.

NNC	Nearest-neighbour (NN) by correlation distance
NMC	Nearest-mean (NM) by correlation distance
LDA64	Linear Discriminant Analysis (NM by Mahalanobis distance) using 64 PCs

2.9. Searchlight analysis

Instead of global BOLD signal distributions many MVPA studies have focused on small compact fROIs in order to probe and compare the information content of specific brain regions and to limit classifier input dimensionality. One popular variant of this approach is Searchlight analysis (Kriegeskorte et al., 2006), which in our (simplified) implementation (using Matlab) involved successively computing the CA for small cubic (not spherical) searchlight ROIs, e.g. 5 5 5 voxels surrounding every voxel location in the brain. Searchlight analysis thus yielded a spatial CA map representing local information density (Fig. 4). To boost sensitivity (CA) without increasing SL volume any misclassification of ±1 TR was counted as correct, as these were very likely to occur due to hemodynamic lag – See Fig. 3 in (Mandelkow et al., 2016).

Fig. 4.

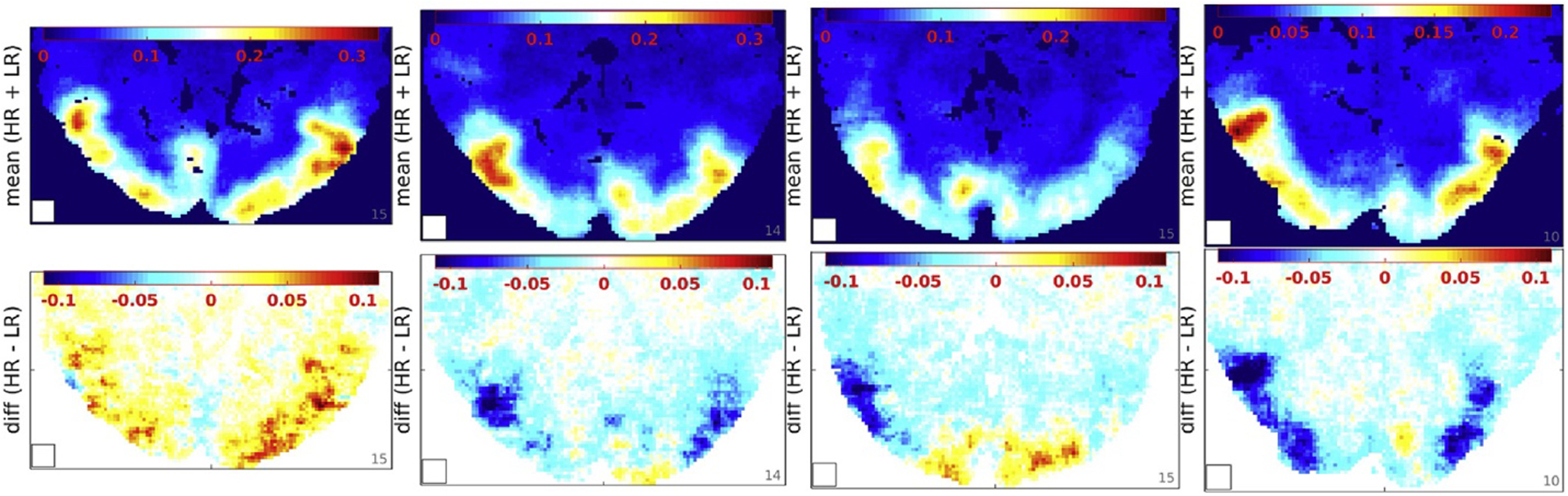
Positive differences in searchlight CA (HR ¡ LR) were found in early visual areas. Top/Bottom: Mean (HR þ LR)/2 and difference (HR LR) in searchlight classification accuracy by the NMC classifier, one exemplary slice exhibiting the largest spread (HR LR) in each of the four subjects (left-right). The white square (bottom left) represents the searchlight volume of 73 voxels (8.4 mm)3. (Slight differences in image geometry reflect differences in the FOV cropped to each individual subject.)

In analogy to the global fROI size (Fig. 3) we varied the searchlight ROI volume between (6 mm)3 and (18 mm)3 to assess its influence on the spatial distribution of SL CA for HR and LR data (Sup. Fig. 10). Based on those results we evaluated the effect of different smoothing levels on SL CA using an intermediate volume of (8.4 mm)3. The results were summarized by plotting the empirical distribution of SL CA across voxels and subjects as a family of histograms in Fig. 5.

3. Results

3.1. Functional activation maps

The F-statistic (reproducibility) maps computed from HR and LR data in each subject clearly delineated corresponding regions in the occipital and ventral temporal cortices (Fig. 1). These areas including the lingual, parahippocampal and fusiform gyri are commonly associated with the ventral stream of high-level visual processing (Grill-Spector and Weiner, 2014). For the comparison of resolution effects all following classification analyses were restricted to the posterior half of the field of view, in order to exclude regions of poor image quality around the paranasal sinuses and, above all, the artefactual fMRI signal modulation in the moving eyeballs. Thus, the following results pertain to the aforementioned bulk of visual brain areas at the focus of our attention. The comparison of F-statistic maps cut off at a common statistical threshold of (p<1%, uncorrected) showed significant effects in an area that was more confined for HR than for LR data (Fig. 2A and B). However, CNR maps proportional to the F-statistic were more suitable for a voxel-wise comparison of effect size: In Fig. 2C a CNR ratio (HR/LR) of less than one (blue) indicates that LR data yielded a higher CNR almost everywhere in the brain. This limited the number of (red) voxels that might be interpreted as showing a positive partial volume effect as a result of HR scanning. However, this comparison of voxel-wise univariate statistics did not obviate the following analysis of information content extractable by MVPA.

3.2. Classification accuracy

Consistent with previous work, machine-learning classifiers like the LDA and GNB proved to be highly effective in discriminating diverse naturalistic visual stimuli presented as movies (Chen et al., 2015; Haxby et al., 2011; Mandelkow et al., 2016).

Fig. 3 shows how global CA depended on fROI size, fMRI resolution and smoothing. The highest CA of about 90% was achieved by the LDA classifier, nota bene, applied to LR data (2 mm, blue-yellow bars) with 3 mm FWHM of additional smoothing and a large fROI comprising 4 k–16 k of the most strongly modulated voxels (Fig. 3B, note the log-scale). In all subjects this maximum was broad, meaning its position was not very sensitive to the exact number of voxel features in the fROI covering between 5% and 50% of all significantly activated voxels within the analyzed posterior-half FOV (Fig. 1 and Sup. Fig. 12).

Only for small fROI sizes well below 1000 voxels did HR data (1.2 mm, red bars) yield consistently higher CA than LR, albeit well below the global maximum (Fig. 3A and Sup. Fig. 13). Nevertheless, this suggests that some advantages of reduced partial volume effects may be realized by HR data at least in a small selection of voxels. Curiously, however, this positive effect of higher resolution was not reduced but amplified by smoothing. In fact, the largest difference in CA was observed between HR and LR data after smoothing both to 3 mm FWHM.

Note that all observed classification accuracies were well above the theoretical chance level of 1/150 (0.7%). As a control, cross-classification between quasi-identical experiments differing only in the stimulus movie presented yielded classification rates within 1% of the chance level (Sup. Fig. 14). This control was all the more relevant, since a stimulation paradigm without randomization implies a potential vulnerability to systematic trends like the observed pseudo-motion due to gradient heating.

It is worth mentioning that the LDA classifier exhibited a strong interaction between fROI size and smoothing levels: The peak in CA as a function of smoothing shifted from 3 mm to 9 mm FWHM as the fROI size was decreased to a small number of voxels (e.g. 64) far below the maximum. For small fROIs (e.g. 64 voxels), well below the maximum (at 216 voxels), the peak CA as a function of smoothing shifted from 3 mm to 9 mm FWHM (Fig. 3A). This effect appeared to be mediated by the PCA regularization of the LDA classifier, since it was reproduced in the related GNB classifier, but only in conjunction with dimensionality reduction by PCA. A possible explanation is the indirect expansion of the fROI by smoothing, which redistributes signal from beyond its borders. At any rate smoothing seemed to affect the relative strength of signal and noise components extracted by PCA. In the same vein, one may note that extensive smoothing up to 12 mm FWHM degraded stimulus classification performance by less than 20% for the PCA-regularized LDA classifier. The GNB classifier was similarly robust against smoothing, but only with the same regularization. Without PCA it lost more than 50% in CA. By way of explanation, one may point to the fact that the temporal PCs of highest variance remained similar with or without smoothing.

3.3. Searchlight analysis

The results presented thus far focused on global BOLD signal distributions over large parts of the brain. They showed that fMRI resolution was less relevant than spatial coverage and smoothing for the reliable discrimination of global BOLD signal patterns. However, this tradeoff could be different when considering small local ROIs as most classification studies have done in the past. Indeed a searchlight analysis using a moving cubic ROI of (8.4 mm)3 revealed that some brain regions, mostly in early visual cortex, did support higher classification rates with HR data (Fig. 4). Besides that, the SL analysis mostly mirrored the global classification results: SL CA increased with SL volume and was almost ubiquitously higher for LR than for HR data, with exceptions only for small searchlight ROIs (<18 mm)3 (Sup. Fig. 10). For very small searchlight ROIs (<6 mm)3 classification accuracies dropped close to chance level making their interpretation questionable.

Mean searchlight CA (HR þ LR) and optimal resolution (HR LR) varied across brain regions and subjects (Fig. 4). Fig. 5 shows how smoothing altered the empirical distribution of SL CA across brain regions and subjects. A log-scale was used to resolve the right tail corresponding to SL locations of high CA, which were of particular interest. As indicated by the color bar on top, 3 mm smoothing yielded the most SL locations with CA>20%. Higher (and lower) smoothing factors dominated for CA<20%. At least this was the case for HR and LR data analyzed by the NMC classifier using a SL volume of (8.4 mm)3. However, analogous to the smoothing analysis of global fROIs (Fig. 3), the PCA-regularized LDA classifier engendered a divergent smoothing response showing continually strong increases in CA up to 12 mm of smoothing.

3.4. PCA

Regularized LDA based on the Mahalanobis distance after dimensionality reduction by PCA achieved the highest CA both for global and local (SL) classification experiments. The spatial eigenvectors computed by PCA can be viewed as weight maps revealing fMRI signal correlation patterns (Fig. 6): The eight leading spatial PCs accounting for most of the signal variance in each subject revealed a segregation of spatially smooth components, on the one hand, and distinctly more “granular” ones, on the other hand. The former were highly reproducible across experiments of both resolutions (HR/LR) and similar between subjects. The latter, by contrast, were prominent only in HR data and exhibited relatively low inter-experimental reproducibility (F-statistic, colored numbers). The fact that such PCs of low reproducibility still contributed substantially to the mean fMRI signal (averaged across experiments) suggests that they were prominent in few experiments only. PCA on local searchlight ROIs revealed a similar segregation of components. The comparison of PCs from searchlight ROIs in locations with large differences in CA between HR and LR data (HR LR) (Fig. 7) suggested that the presence and relative variance contribution of such high-spatial-frequency PCs determined the “optimal” resolution for local searchlight classification. This hypothesis was supported by a significant correlation between search-light CA and local fMRI signal smoothness quantified simply as the fraction of power in the lower half of the spatial spectrum (Fig. 7, blue bars) (Sup. Fig. 11).

Fig. 6.

Functional connectivity patterns revealed by the 8 leading principal components. Five representative slices (rows) representing projections of the 8 highest-variance PCs (columns) in one representative subject. LR data (top panel) and HR data (bottom panel) share the spatially smooth leading components, but HR data also exhibit noise components (PC#7) of high spatial frequency and low reproducibility judging by the low F-statistic (colored numbers).

Fig. 7.

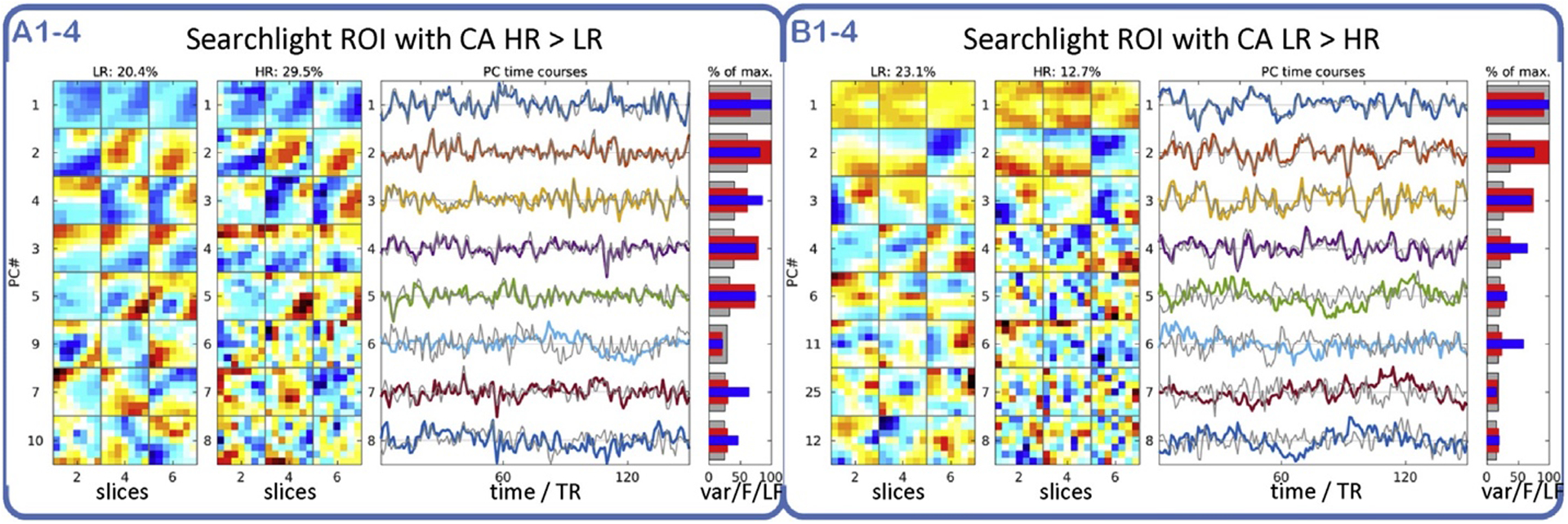
PCA in two representative searchlight ROIs with CA of HR > LR and LR > HR. Panel A: Searchlight ROI representative of locations where HR fMRI yielded higher CA than LR data (29.5% > 20.4%): The leading PCs (1–5) are smooth and similar between HR and LR data (sub-panels A1þA2, rows 1–5, 3 slices 1⁄4 columns per PC). Panel B: Same experiments, different searchlight ROI, where CA of HR < LR (12.7% < 23.1%): Fewer of the leading PCs (1–4) are smooth and agree between HR and LR data, others are less reproducible (red bars) and smooth (blue bars). Colored/gray lines 1⁄4 average PC time courses for HR/LR data. PCs are sorted by % variance contribution in HR data (gray bars). Red bars show PC reproducibility (F-statistic normalized by maximum) in HR data. As a measure of spatial PC smoothness blue bars represent low-frequency over total spatial spectral power in the HR data.

3.5. Variability across experiments

According to the above results LR data supported higher classification rates than HR data on average and under most experimental conditions. However, the results revealed some systematic variations across brain regions and across subjects (Figs. 4 and 8A). The spatial variations may well be rooted in functional neuroanatomy, as HR data seems to yield higher classification rates primarily in early visual areas. However, the systematic differences between subjects reproduced across 16 experimental runs were not easily dismissed as noise and begged for an explanation. Based on the available data we considered motion parameters and eye tracking signals as explanatory variables.

Fig. 8.

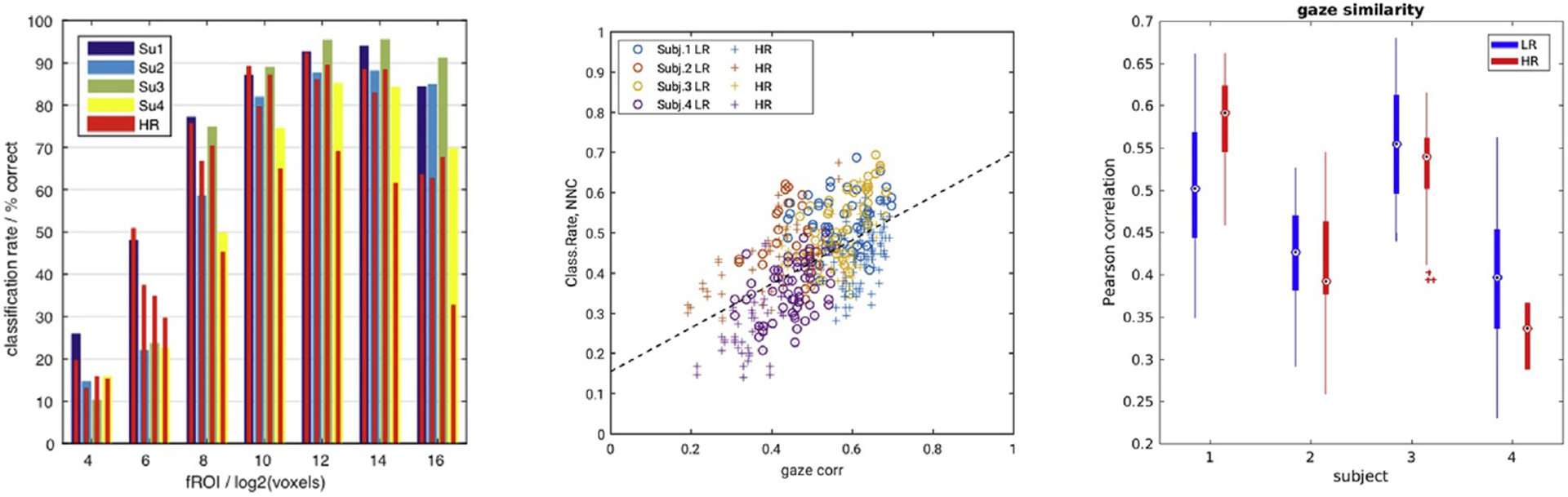
Differences in CA correlated with gaze similarity. Left: The 4 subjects (Su1–4) showed systematic differences in average global CA by LDA both for LR and HR data (wide blue-yellow/thin red bars). Middle: Inter-experimental gaze similarity (x-axis) correlated significantly with CA based on the NNC classifier (y-axis) for each pair of experiments (t-test p(t1122)≪1010) (colors 1⁄4 four separate subjects, markers ○/þ 1⁄4 LR/HR data). Right: The median inter-experimental gaze correlations for each of the four subjects also correlated with the mean CA on the left (t-test p(t82)<1%).

The motion parameters estimated during motion correction were naturally variable between experiments and subjects. However, correlations between the average voxel displacement metric (FSL, mcflirt) and CA were inconsistent and weak across experiments, therefore not likely to explain much of the observed differences in CA (Sup. Fig. 15). Nevertheless, a negative correlation between increased subject motion and decreased classification rates was observable in isolated scans.

The eye tracking data from repeated experimental runs in multiple subjects showed very similar gaze trajectories with inter-experimental cross-correlation coefficients above 40% on average (Fig. 8B). This confirmed a high degree of reproducibility in the way subjects viewed the movie stimulus. Indeed, a cluster analysis of gaze positions for every point in stimulus time made it obvious that there was rarely more than one focus of attention in any given scene of the movie. Nevertheless, pairwise Pearson correlations between gaze trajectories from different experimental runs in each subject revealed markedly higher gaze pattern similarity i.e. behavioral consistency in those experiments and subjects that also accounted for the highest global CA by pairwise NNC (t-test p(t1122)≪1010) (Fig. 8B). Here the degrees of freedom were estimated conservatively as 112 1⁄4 binomial coefficient (8, 2) * 4 subjects. The correlation was also significant for the comparison of mean CA with mean gaze similarity (t-test p(t82)<1%) (Fig. 8A and C). By the same token, the spurious group differences in gaze correlations between HR and LR experiments (in the same subject) (Fig. 8C) might account for stronger positive/negative resolution effects (HR LR) in subjects 1/4 (Figs. 8A and 4).

4. Discussion

The present study demonstrates how spatial resolution affects the information content of the BOLD fMRI signal extractable by MVPA classification methods. It does so by quantifying the classification accuracy in discriminating a large set of naturalistic stimuli presented as a movie.

Contrary to the initial hypothesis, both the global and local (search-light) CA achieved by LDA as well as a number of related classifiers peaked around a smoothed resolution of 3 mm, well above the 1.2 mm voxel size of the HR fMRI acquisitions in this study. This result is not inconsistent with previous classification studies that have shown peaks in CA at 2–8 mm of smoothing, although it is difficult to assess the effective resolution resulting from the data acquisition and preprocessing in any given study (Alink et al., 2013; Haxby et al., 2011; Op de Beeck, 2010). But none of these classification studies explored fMRI data at high-resolution (<2 mm), and those that have were limited to small sets of specialized stimuli (Gardumi et al., 2016; Sengupta et al., 2017; Swisher et al., 2010).

Our results were unexpected in light of HR fMRI studies at high field (>3 T) that have demonstrated the existence of BOLD contrast at a spatial scale below 1 mm (Menon and Goodyear, 1999; Yacoub et al., 2008). However, that work is largely confined to primary somatosensory cortices and carefully tailored experimental conditions involving highly immobile subjects (bite bars etc.) and extensive signal averaging over repeated experiments. Under more general conditions such results are hard to obtain, as local BOLD contrast is reduced by various sources of spatial correlations, not least short- and long-range neuronal connections, but also (micro-)vascular dispersion and large draining veins, not to mention physiological artifacts due to cardiac pulsation, respiration, motion etc. (Liu, 2016; Turner, 2002).

According to basic information theory, the discriminability of stimuli (CA) would depend on the tradeoff between CNR and the spatial bandwidth (resolution) of the BOLD signal. On the face of it, smaller voxels would increase the available spatial information, but only if the BOLD signal is sufficiently uncorrelated and reproducible and only at the expense of simultaneously decreasing SNR due to thermal (instrumental) noise. Since our experiments with increased fMRI resolution yielded mostly negative returns in CA, it stands to reason that the fMRI signal at high spatial frequency carried insufficient extra information to outweigh the additional noise and (physiological) artifacts incurred.

By itself the linear relationship between MRI voxel size and SNR would not explain the observed loss of information. However, PCA and the smoothing analysis point to an explanation based on the local correlation structure (or spatial spectrum) of both the BOLD signal and confounding (physiological) noise components:

Most of the leading high-variance PCs shared between HR and LR data were spatially smooth and exhibited high reproducibility (F-scores). But HR data also revealed some markedly different PCs: Their granular spatial structure was strongly suggestive of residual motion or physiological artifacts to which HR acquisitions were most sensitive. Comparatively, low F-scores indicate that these components had relatively high inter-experimental variability and were unlikely to increase CA. On the contrary, they were more prominent and accounted for a higher variance contribution in global PCs from HR data (Fig. 6B) and in local PCs from SL locations exhibiting a large difference in CA between HR and LR data (HR < LR) (Fig. 7B, Sup. Fig. 11). In other words, the more reproducible (neurogenic) fMRI signal was spatially smooth, much unlike the less reproducible signal components, which represent (physiological) noise and artifacts most likely. (This observation primarily pertains to the relevant PCs of highest variance, not to exclude less significant signal and noise contributions of high or low spatial frequency.) It is therefore plausible that spatial smoothing improved CNR and classification rates by suppressing spatially uncorrelated artifacts and noise. The positive effects of smoothing for small fROIs and SL volumes in particular may also include their effective expansion resulting from the redistribution of signal from beyond their borders. This effect may be amplified by k-space filters that cause more widespread spectral leakage i.e. ringing in the image domain. The apparent segregation of signal and artifact components by PCA would furthermore explain why LDA (and GNB) classifiers achieved the highest classification rates by taking the noise covariance into account.

4.1. Experimental variability

A limitation of this study is the small number of four subjects, which resulted from our emphasis on a larger number of experimental repetitions. This makes it difficult to appraise inter-subject variations (Fig. 8A), which were nonetheless systematic and warranted some inquiry into possible causes. Subject head motion was, of course, the prime suspect, but correlations between CA and several summary metrics calculated from the motion correction parameters for each experiment revealed mostly weak and insignificant associations. Clearly increased subject motion did have a negative effect on CA, but only in isolated experiments – not enough to establish a trend.

By contrast, the correlation analysis of gaze trajectories strongly suggested that subjects with more similar (reproducible) gaze patterns that were correlated between experiments exhibited higher classification rates (Fig. 8B). One might speculate that perceptual inconsistency translated into spatial blurring of the BOLD fMRI signal. This might seem trivially plausible in brain areas with somatotopic organization like V1, but studies of attentional effects do suggest more complex interactions between attention and cortical representations: E.g. a recent study by Çukur et al. finds that attention increases the spatial extent of the BOLD signal (Çukur et al., 2013).

The observed spatial variability in the SL difference maps likely is influenced by the local tortuosity of the cortex, its functional topography and vascularization, all of which determine the spatial distribution of BOLD signal sources on the scale of voxels (Kriegeskorte et al., 2010). Following this rationale, it does not seem implausible that (optically heterogeneous) visual stimuli show a higher CA with HR data foremost in the retinotopically organized visual cortex V1–4 (Fig. 4). The well-known spatial distribution of afferent signals in somatotopic somatosensory areas has been exploited in a number of MVPA decoding studies, e.g. (Gardumi et al., 2016; Kay et al., 2008; Miyawaki et al., 2008).

Finally, the subject-wise comparison of SL difference maps and average gaze correlations (Figs. 4 and 8C) also hints at a link between consistent behavior (or attention) and the optimal resolution for SL classification: Subjects with higher gaze similarity tended to have higher SL CA in the HR data. Specifically, the most positive SL difference maps in subject #1 (Fig. 4) might well be explained by that subject’s positive difference in median gaze correlations (HR LR) (Fig. 8C). This bias in behavior between two (small) groups of experiments from the same subject is almost certainly spurious, but the systematic inter-subject differences observed support the prospect of developing cognitive bio-markers based on the fMRI response to naturalistic stimuli (Hasson et al., 2009).

For technical reasons, this study covered a majority but not all brain regions that can be stimulated by movie viewing (Jääskeläinen et al., 2008). Likewise, it does not investigate the possible influence of different kinds of movie stimuli (Hasson et al., 2010). Such endeavors were beyond the scope of this study but should be pursued by those expecting to find significantly different resolution effects.

5. Conclusions

The high-resolution fMRI experiments at 7 T did not reveal a general increase in CA as a result of increasing fMRI resolution from 2 mm to 1.2 mm. Both for global and local (SL) fMRI signal patterns CA was found to peak broadly around a smoothed resolution of 3 mm FWHM, a voxel size well within the technical limits of high-field fMRI. PCA points to the explanation that the stimulated neuronal components of the fMRI signal were predominantly smooth and locally correlated, while the dominant (physiological) noise components exhibited higher spatial frequencies possibly related to cardiac, respiratory or residual subject motion artifacts, prevalent in HR data.

The experiments revealed systematic variability between brain regions and subjects, which would explain mixed results in the literature. Consistent with previous work, the SL analysis showed some increase in CA with resolution in retinotopically organized early visual areas. Across subjects higher CA was correlated with more consistent behavior as indicated by reproducible gaze patterns and possibly mediated by attention.

For reliable fMRI signal classification spatial resolution was less relevant than spatial coverage and fMRI contrast (CNR) aided by high-SNR acquisitions and averaging across experiments. This is consistent with the notion that reproducible (neuronal) fMRI signal components are locally auto-correlated and have a sparse global distribution, which can be undersampled without loss of information. By contrast, the most prominent (physiological) noise components of higher spatial frequency were effectively suppressed by smoothing and by LDA taking the multivariate noise covariance matrix into account.

In light of these results, one might recommend fMRI acquisitions at a relatively low isotropic resolution of 2–3 mm, which facilitates a large FOV (whole-brain coverage) plus high SNR, thus yielding the most reliable classification of global fMRI signal patterns evoked by naturalistic stimuli. After interpolation for motion correction and geometric alignment the optimal resolution of 3–4 mm can be achieved by additional smoothing.

Abbreviations:

BOLD

blood oxygenation level dependent (fMRI)

BW

(readout) bandwidth (MRI parameter)

CA

classification accuracy

CNR

contrast-to-noise ratio

FA

flip angle (MRI parameter)

fMRI

functional MRI

fROI

functional ROI (1⁄4 voxels/features)

FSL

FMRIB Software Library

FWHM

full width at half maximum

GLM

general linear model

GNB

Gaussian Naïve Bayes (classifier)

GRAPPA

(MRI parallel imaging technique)

HR

high-resolution (fMRI)

HRF

hemodynamic response function

LDA

Linear Discriminant Analysis (classifier)

LR

low-resolution (fMRI)

Mcflirt

FSL motion correction software

MRI

magnetic resonance imaging

MVPA

multivariate pattern analysis

NIH

National Institutes of Health

NN

nearest-neighbour (classifier)

NM

nearest-mean (classifier)

PC

principal component

PCA

principal component analysis

ROI

region of interest

SL

searchlight

SNR

signal-to-noise ratio

SVD

singular value decomposition

SVM

support vector machine

TE

echo time (MRI parameter)

TR

(volume) repetition time (MRI)