Abstract
Motivation
Tumor purity and ploidy have a substantial impact on next-gen sequence analyses of tumor samples and may alter the biological and clinical interpretation of results. Despite the existence of several computational methods that are dedicated to estimate tumor purity and/or ploidy from The Cancer Genome Atlas (TCGA) tumor-normal whole-genome-sequencing (WGS) data, an accurate, fast and fully-automated method that works in a wide range of sequencing coverage, level of tumor purity and level of intra-tumor heterogeneity, is still missing.
Results
We describe a computational method called Accurity that infers tumor purity, tumor cell ploidy and absolute allelic copy numbers for somatic copy number alterations (SCNAs) from tumor-normal WGS data by jointly modelling SCNAs and heterozygous germline single-nucleotide-variants (HGSNVs). Results from both in silico and real sequencing data demonstrated that Accurity is highly accurate and robust, even in low-purity, high-ploidy and low-coverage settings in which several existing methods perform poorly. Accounting for tumor purity and ploidy, Accurity significantly increased signal/noise gaps between different copy numbers. We are hopeful that Accurity is of clinical use for identifying cancer diagnostic biomarkers.
Availability and implementation
Accurity is implemented in C++/Rust, available at http://www.yfish.org/software/.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Cancer is a group of heterogeneous diseases that each bears its own biological signature. Uncovering these biological signatures may yield highly informative markers and targets for cancer therapeutics (Bild et al., 2006; Potti et al., 2006; Roychowdhury and Chinnaiyan, 2014; Sabbah et al., 2008). Recently, next-generation sequencing (NGS) have enabled scientists to search for these cancer signatures on a genome-wide scale (Cronin and Ross, 2011; Hanahan and Weinberg, 2011; Ross and Cronin, 2011). However, tumor purity, measured as the fraction of cancer cells in a heterogeneous tumor sample, and tumor cell ploidy, the average copy number of a cancer genome, have a substantial impact on NGS analyses of tumor samples and may alter the biological and clinical interpretation of results (Aran et al., 2015; Elloumi et al., 2011; Yadav and De, 2015). In this article, we made a distinction between tumor cell ploidy (short as tumor ploidy) and tumor sample ploidy (average between normal and cancer cells in a tumor sample as described in Methods). Traditionally, a pathologist is tasked to estimate tumor purity and ploidy by visually inspecting a tumor sample. The progression of genomic technologies in the past decade has opened the door to computationally infer tumor purity and ploidy from genomic data. Recently, tumor-normal pair sequencing has gained significant traction among researchers in profiling cancer genomes for its improved statistical power over tumor-only sequencing (Garofalo et al., 2016; Mwenifumbo and Marra, 2013). The Cancer Genome Atlas (TCGA) contains close to a thousand tumor-normal pair samples profiled by high-coverage (>30×) whole-genome-sequencing (WGS) and another thousand profiled by low-coverage (6–8×) WGS. A plethora of computational methods (Andor et al., 2014; Carter et al., 2012; Gusnanto et al., 2012; Larson and Fridley, 2013; Li and Xie, 2014; Mayrhofer et al., 2013; Oesper et al., 2013; Su et al., 2012; Yu et al., 2014) have been developed to infer tumor purity and ploidy from tumor-normal pair WGS data.
Estimating tumor purity and ploidy relies on statistical signals that can differentiate tumor cells from normal cells in a tumor sample. Statistical differentiation in the tumor NGS data comes mainly from two types of genetic variants. One type of event is somatic copy number alterations (SCNAs). Comparing sequencing coverage at SCNA loci of a tumor sample against that of its matching normal sample constitutes a statistical differentiation. The second type is single nucleotide variants (SNVs). Comparing allelic sequencing coverage at SNV loci of a tumor sample against that of its matching normal sample constitutes a second statistical differentiation. Based on how coverage information of these two types of events are utilized in estimating tumor purity and ploidy, existing computational methods can be broadly grouped into three categories. Category one utilizes coverage information of SCNAs only (Gusnanto et al., 2012; Oesper et al., 2013). Category two utilizes coverage information of SNVs only (Larson and Fridley, 2013; Su et al., 2012). Category three utilizes both information (Li and Xie, 2014; Yu et al., 2014).
One issue shadowing methods of category one and two is the identifiability issue, where different combinations of tumor purity and tumor cell ploidy can explain the observed data equally well (Carter et al., 2012; Oesper et al., 2013). For a method that utilizes coverage information of SCNAs only, a combination of (30%, 3), tumor purity = 30% and tumor cell ploidy = 3, can explain the sequencing coverage of this tumor sample equally well as a combination of (15%, 4) (and many others combinations) because these combinations result in the same tumor sample ploidy = 2.3, according to Equation 1. Similarly, a method that only utilizes coverage information of SNVs suffers the same issue (Equation 17). To circumvent the identifiability issue, these methods made explicit or implicit assumptions that help to narrow candidates down to one solution. For example, PurityEst (Su et al., 2012), a method that uses B-allele frequencies (BAFs) at somatic mutations (one type of SNVs) to estimate tumor purity, effectively assumes tumor cell ploidy is equal to 2. CNAnorm (Gusnanto et al., 2012) prefers a solution closest to diploid. ABSOLUTE (Carter et al., 2012) incorporates karyotype data in addition to coverage information of SCNAs. Oesper et al. (2013) outputs all optimal solutions or limits to solutions with a baseline copy number of the clonal tumor population.
As in basic algebra that two equations are required to solve a two-variable system, by combining coverage information of SCNAs and SNVs, methods in category three can fundamentally solve this identifiability issue (Favero et al., 2015; Li and Xie, 2014; Yu et al., 2014). Some of these methods, i.e. MixClone (Favero et al., 2015), even take intra-tumor heterogeneity (IRH) (Navin et al., 2011) into account. As demonstrated by direct comparisons with these methods (Fig. 4 and Supplementary Fig. S5), Accurity differentiates from them by its accuracy, robustness and speed.
The idea of Accurity is based on recent cancer biology research (Wang et al., 2014), cancer subclones evolve from a common ancestral cancer clone and thus a significant portion of their cancer genomes inherits a common copy number profile. We use one hypothetical cancer genome to represent all cancer cells in a tumor sample and there will be two types of genomic regions in this cancer genome. At genomic regions of the first type, all cancer subclones have the same integral copy number. These regions are inherited from the ancestral clone and no new SCNA has been introduced at these regions since divergence from the ancestral clone. We call these regions clonal. At genomic regions of the second type, new SCNAs have occurred in some cancer subclones during their course of divergence from the ancestral clone. The copy number at such a region varies among different subclones and its copy number representation as a weighted average is non-integral. We call these regions subclonal. Based on this understanding, Accurity first used an autocorrelation-based algorithm to separate the integral-copy-number clonal regions from the non-integral-copy-number subclonal ones. During the second stage of analysis, Accurity used a Hierarchical Gaussian Mixture (HGM) model to fit coverage information of SCNAs and heterozygous germline single-nucleotide-variants (HGSNVs) at clonal regions to estimate tumor purity and ploidy (Fig. 1).
Fig. 1.
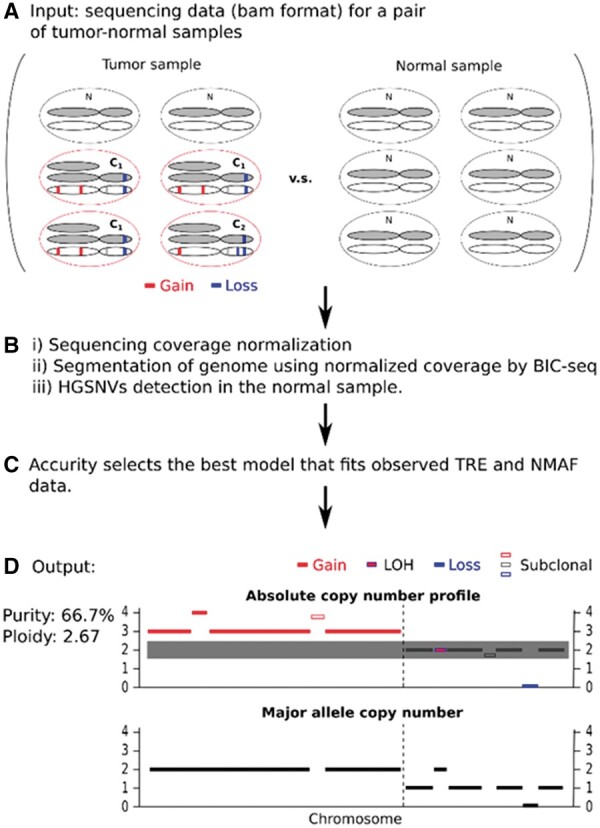
Workflow of Accurity. (A) DNA from a pair of matching tumor-normal samples is extracted and profiled using a WGS technology. In the tumor sample, about 2/3 of all cells are cancerous. About ¾ of all cancer cells belong to clone C1 and the rest belong to clone C2. Clone C1 and C2 share substantial SCNAs as they evolve from a single ancestral clone. (B) We i) normalize the sequencing coverage data to correct the GC bias; ii) use BIC-seq to partition the 22 autosomes of the cancer genome into segments according to sequencing coverage; iii) call heterozygous germline single nucleotide variants (HGSNVs) for the normal sample using our approximate variant caller. We calculate tumor read enrichment (TRE) for all cancer genome segments in bins of 500 bp and the normalized major allele fraction (NMAF) of all HGSNVs. (C) Accurity conducts an autocorrelation analysis on the TRE distribution to derive an initial periodicity estimate and fits a joint Hierarchical Gaussian Mixture (HGM) model on TRE and NMAF data according to Bayesian Information Criterion (BIC). (D) Accurity outputs tumor purity and tumor cell ploidy estimates, an absolute copy number profile and a major allele copy number profile for the cancer genome. Clonal segments are assigned with integers (solid bars) and subclonal segments are assigned with non-integers (hollow bars)
Knowledge of tumor purity and ploidy can have a significant impact on the detection of SCNAs, which are important to cancer progression (Beroukhim et al., 2010; Shah et al., 2012; Zack et al., 2013). Power to detect SCNAs is highly dependent on the tumor purity. In a low-purity tumor sample, a large fraction of copy-neutral DNA from non-cancerous cells significantly decreases the signal/noise ratio of SCNAs. A tumor-purity-agnostic SCNA caller, assuming 100% tumor purity, is almost certain to be underpowered (Alkodsi et al., 2015; Liu et al., 2013; Yadav and De, 2015). Knowledge of tumor ploidy is also crucial to detect SCNAs. Ploidy of some aneuploidy cancer samples could be far from two. Methods that use the genome-wide average copy number as a baseline could call copy-neutral regions as deletions and amplifications as normal. Inversely, when tumor ploidy is low, such methods could call copy-neutral regions as amplifications and intermediate deletions as normal.
We applied Accurity (Fig. 1) to simulated data and demonstrated that Accurity can produce accurate and robust estimates under a wide variety of settings: focal SCNAs or chromosomal SCNAs or whole-genome duplications (WGDs), low-coverage or high-coverage. We also applied Accurity to real sequencing data from dozens of TCGA samples. Purity estimates by Accurity were highly concordant with histological estimates. Accounting for tumor purity and ploidy, Accurity significantly increased signal/noise gaps between different copy numbers and can help to identify complex SCNAs, which is of keen interest to cancer diagnostic community.
2 Materials and methods
2.1 Tumor purity and ploidy
We define the fraction of cancer cells in a tumor sample as the tumor purity and the fraction of normal cells is . We assume that the ploidy of normal cells is two and denote the ploidy of cancer cells as (tumor cell ploidy). Tumor sample ploidy is a weighted average of that of normal and cancer cells, expressed in and as follows:
| (1) |
We denote the copy number of a chromosomal segment in cancer cells as (tumor cell copy number). Similarly, the copy number of segment for the entire tumor sample (tumor sample copy number) is as follows:
| (2) |
Note the difference between tumor cell ploidy and tumor sample ploidy. The latter includes ploidy contribution from normal cells in a tumor sample while the former is only about tumor cells. The two are identical for a 100% pure tumor. Similarly, the tumor cell copy number of a segment is different from tumor sample copy number of the same segment. The observed sequencing coverage of a tumor sample is directly proportional to the tumor sample ploidy, thus dependent on tumor purity and tumor cell ploidy.
2.2 GC-correction for sequencing coverage
Dependency between GC content in a region and its coverage from Illumina sequencing data is widely documented (Benjamini and Speed, 2012; Boeva et al., 2014). As observed in Benjamini and Speed (2012), the GC effect for human genomes is largely unimodal. In AT-rich (GC-fraction < 0.5) regions, coverage increases with increasing GC. In GC-rich (GC-fraction > 0.5) regions, coverage decreases with increasing GC. The peak coverage can be different for different samples and bin sizes, but is usually located between 0.4 and 0.55 GC-fraction. We adopted the full-fragment model from Benjamini and Speed (2012) and chose a bin size of 500 bp to match the usual fragment length in NGS sequencing. For each sample, Accurity calculates GC fraction for every bin, and fits a loess model to the coverage data (smoothness parameter of 0.3, R package loess). The normalized coverage for one bin is as follows:
| (22) |
where is the normalized coverage, is the observed coverage, is the predicted coverage given observed GC-fraction of this bin, and is the genome-wide average of coverage. In calculating coverage , Accurity requires: (i) read mapping quality larger than or equal to 30, (ii) reads properly paired and their mates mapped, (iii) more than half of the fragment (its length inferred by the alignment algorithm) to be in the bin. The bin size 500 bp is adjustable by a user in a configuration file. We suggest the bin size to be the median fragment length of the sequencing library.
After the binned sequencing coverage data is normalized, segmentation of the tumor genome is achieved by applying BIC-seq to the normalized coverage data, step B of Figure 1. Accurity then calculates TRE for all bins and conducts model selection.
2.3 Tumor Read Enrichment (TRE) for a chromosomal segment bin
Denote the number of reads covering a genomic segment bin for a tumor sample and its matching normal sample as and , respectively, and a total number of and reads for a tumor sample and its matching normal sample. The Tumor Read Enrichment (TRE) for segment bin , , is defined as follows:
| (3) |
TRE is a normalized read enrichment of a chromosomal segment bin in a tumor sample relative to its matching normal sample. Factors that influence both tumor and normal samples, such as read mappability and GC bias, are canceled out.
2.4 Expected TRE and Normal TRE (NTRE) and their relationship with tumor purity and ploidy
For a chromosomal segment bin , assuming independence between local and global coverage, the expected TRE of segment bin can be approximated as follows:
| (4) |
We define a few nuisance parameters to illustrate the further derivation of , during which all these nuisance parameters will cancel out. The length of segment bin is denoted as . The length of the reference genome, which is roughly three billions, is . The genome-wide average sequencing coverage is for tumor sample and for its matching normal sample . The average sequencing coverage for segment bin from a tumor sample is , which adds a sequence-specific factor to the genome-wide sequencing coverage. The average sequencing coverage for segment bin from the matching normal sample is . There is an implicit assumption that is the same in both tumor and normal samples, which is well approximated because identical normalization procedures (correcting GC-bias, etc. details in GC-correction section) are applied to both samples. With all these definitions, we can derive the expected TRE, , as a statistic only dependent on tumor purity, , tumor cell ploidy, and the copy number of the segment bin in cancer cell, :
| (5) |
All bins inside each segment (output of BIC-seq) are assumed to have the same copy number, and thus the same expected TRE based on the equation above. It is also clear that if a tumor sample is 100% pure and tumor cell ploidy is 2, for a cancer cell segment with copy-number = 2, its expected TRE, . We drop subscript of and add superscript to denote the expected TRE for all segments with copy number as :
| (6) |
For all segments with copy number the corresponding is
| (7) |
Forms of and can explain the periodicity we observed from a GC-corrected TRE histogram. We define periodicity P of a TRE histogram as the interval between two copy numbers (Fig. 2) and its expected value is
| (8) |
Fig. 2.
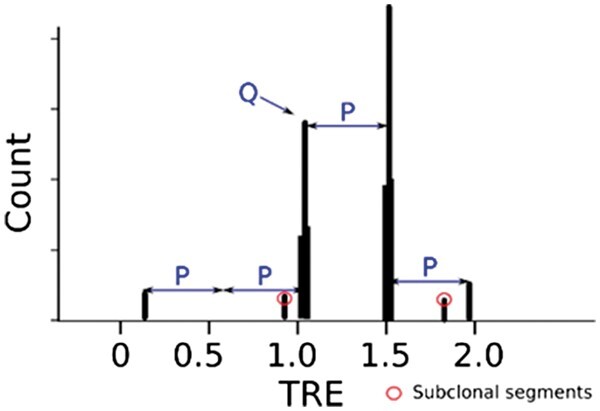
The histogram of tumor read enrichment (TRE) from the example in Figure 1. Auto-correlation analysis can identify periodicity P as the interval between neighboring major peaks and Q is the TRE value corresponding to copy-number-two segments. Two minor peaks with circles are subclonal segments. Subclonal segments are excluded during model fitting and selection because our HGM model is designed for clonal segments
In a histogram of TREs (Fig. 2), periodicity is the interval between two adjacent major peaks. Each major peak in a TRE histogram represents one group of clonal segments with the same integral copy number. Usually periodicity of a tumor sample decreases with low purity or high ploidy.
Further, we define a Normal TRE (NTRE) , as the TRE corresponding to segments of copy number 2, then
| (9) |
Solving equation 8 and 9 above rewrites tumor sample purity and tumor cell ploidy in terms of and .
| (10) |
| (11) |
2.5 Normalized major allele fraction (NMAF) for HGSNVs
A read with a non-reference allele is less likely to be mapped correctly to the reference genome than a reference-allele read because a non-reference allele introduces a mismatch (Degner et al., 2009). This allelic mapping bias causes the non-reference allele to have less read coverage than the reference allele. Denote , , and as the read counts for a reference allele (R) and an alternative allele (A) in a tumor (t) and normal (n) sample. For each allele of a tumor sample, we normalize its read count by dividing it with its corresponding read count of the matching normal sample to minimize the allelic mapping bias.
| (12) |
| (13) |
The normalized allele fraction for each allele is as follows:
| (14) |
| (15) |
The NMAF of an HGSNV is the larger number of and .
| (16) |
HGSNVs are called using our approximate HGSNV calling method. Our approximate method does not strive for accuracy, but get good summary information for HGSNVs over the whole genome. It starts from a candidate set of 44 million SNPs from the 1000 Genomes project. At any locus, if (i) the normal sample is covered by eight or more reads, (ii) the minor allele is covered by 3 or more reads and (iii) the tumor sample is covered by four or more reads, one HGSNV is called. HGSNVs are discovered from a normal sample but its NMAF contains information from both normal and tumor sample.
2.6 Expected NMAF
Given a segment of copy number , purity and major allele copy number , the expected NMAF is
| (17) |
where and for an HGSNV in a normal sample.
2.7 An HGM Model for TRE and NMAF and its BIC score
We designed a two-level HGM model: the first level of Gaussian mixture models modelling coverage data of SCNAs (including normal copy number regions) shared by all cancer cells (clonal segments); the second one modelling major-allele coverage data of all HGSNVs within clonal segments. Each first-level Gaussian distribution models segments with the same copy number and acts as a parent distribution to a set of second-level Gaussian distributions which model HGSNVs that fall inside these segments but are of different major allele copy numbers (Fig. 1). Given a pair value of tumor purity and ploidy , for all segment bins with the same copy number , we calculate their expected TRE and for all HGSNVs that fall inside these segments and have the same major allele copy number , we calculate their expected NMAF . Then the likelihood functions for observed TRE data and major-allele fraction data are
| (18) |
| (19) |
where and are the standard deviations of and respectively, is the mixture weight of each first-level Gaussian distribution, is the mixture weight of each second-level Gaussian distribution, is the number of first-level Gaussian distributions, is the number of second-level Gaussian distributions (approximately ), is the number of 500 bp (size adjustable by user) bins from all clonal segments, and is the number of HGSNVs within all clonal segments. We use 500 bp segment bins to account for the size variation of segments (information from long segments will be underrepresented if every segment is treated as a single data point).
We use Bayesian Information Criterion (BIC) to gauge model fitness and select the best model that fits the data. BIC strikes a balance between model fitness and model complexity by adding a term of to one log likelihood function, where is the number of parameters in the model and is the number of data points. In our case, the BIC score is
| (20) |
The best estimates of purity and ploidy are obtained by minimizing the BIC score:
| (21) |
In our tests without BIC, using the pure likelihood score alone tends to prefer models with more first-level Gaussian clusters (more parameters), which leads to a smaller-than-truth periodicity estimate and an inflated tumor ploidy estimate. This is why ABSOLUTE (not using BIC) tends to overestimate the ploidy and the number of WGD events in our simulation study. We observed that adoption of BIC greatly reduced the occurrences of model overfitting.
2.8 Grid search over P and Q to find optimal tumor purity and ploidy
Instead of calculating the BIC score for every possible tumor purity and tumor cell ploidy , which are infinite, Accurity grid search starts from a limited range of P and Q that are interchangeable with and according to Equations 10 and 11. The search ranges of P and Q can be extracted from a TRE histogram via an autocorrelation analysis. Autocorrelation analysis is ideal to discover periodic patterns in a TRE histogram.
Before an autocorrelation analysis is conducted, Accurity applies a GC correction methodology to normalize read coverage and calculates TREs for every segment bin, and applies a kernel smoothing method to the TRE histogram. A real-life TRE histogram still displays substantial noise after GC-correction. To reduce the effect of noise on initial periodicity inference, Accurity smooths the TRE histogram by a 1D Gaussian kernel (variation of mean TRE is the width).
Accurity then calculates an auto-correlation function for a TRE histogram. The non-zero lag at which the auto-correlation function achieves its maximum value becomes the initial periodicity estimate . Accurity further identifies major peaks in the TRE histogram that are apart, which represent clonal segments of integral copy numbers, and filters out segments that do not belong to any major peak, which are classified as subclonal segments (Fig. 1). TRE and NMAF data of clonal segments from major peaks are then used to calculate the BIC score. The search range of is in step of , where is the variance of estimated by autocorrelation analysis.
The search range for NTRE Q are the TRE values of all the major peaks identified through the autocorrelation analysis. The major peaks correspond to clonal segments of integral copy numbers. Without knowing which one corresponds to clonal segments of copy number two, we include all of them in the search range of Q.
Once the search ranges of P and Q are obtained, we employ a grid search strategy to find optimal . After finding optimal and , Accurity converts them to tumor purity and ploidy estimates and .
2.9 Generate in silico tumor normal sequencing data
To compare Accurity with ABSOLUTE, and CNAnorm, we generated in silico tumor-normal WGS data using NGS simulation software Eagle (https://github.com/sequencing/EAGLE) at three coverage settings: high coverage (30×), low coverage (5×) and high coverage (30×) with two cancer subclones. For each coverage setting, we simulated three CNA profiles: focal CNAs of length 5MB, mixture of focal and chromosomal (whole-chromosome) CNAs, and mixture of focal, chromosomal, and WGD CNAs. In WGD simulation, we randomly choose 10MB genomic segments that in total cover about half of the genome and set their copy numbers at two, and the rest of genome at three. We used 1.5 million heterozygous SNPs from the 1000Genome project as HGSNVs in all simulations unless otherwise stated. For each coverage and CNA setting, we generated nine samples with purity ranging from 10 to 90%.
Additionally, we generated nine 10× tumor sequencing data with purity from 10 to 90% by mixing different amounts of HCC1187 cell line data with its matched normal data. The Illumina whole genome sequencing data of the tumor HCC1187 and its matched normal HCC1187BL cell lines was downloaded from Illumina BaseSpace (https://basespace.illumina.com). HCC1187 is at 104× coverage and HCC1187BL is at 54× coverage. We first downsampled the matched normal to generate a normal sample at 10×. By mixing different amounts of reads from the pure tumor sample (HCC1187) and the normal sample, a series of mixed tumor samples were created at 10× coverage with 10, 20, 30, 40, 50, 60, 70, 80 and 90% of tumor DNA.
3 Results
3.1 Evaluation of Accurity on in silico data
We tested Accurity in a wide spectrum of simulation settings which cover three different types of SCNAs: focal amplifications and deletions, chromosome-level amplifications and deletions, and whole-genome duplication events (WGD or polyploidy), and two levels of sequencing coverage: 30× (high-coverage) and 5× (low-coverage). Further details are in Methods section. Figure 3 shows that Accurity estimates are highly concordant with the true values in all scenarios. The mean squared errors (MSEs) between estimates and the true values are 0.01 in the high-coverage single-clone and two-clone simulation settings (Fig. 3A and C). This showed that Accurity successfully distinguished clonal regions from subclonal regions. In the low-coverage setting, Accurity deteriorates but manages to produce respectable estimates with an MSE of 0.041 (Fig. 3B). Accurity had equally good results with different types of SCNAs, indicating that it is highly robust to different levels of disruption to a cancer genome (Fig. 4). Accurity has also performed well on nine pairs of mixed HCC1187 cell line data (Supplementary Fig. S7).
Fig. 3.
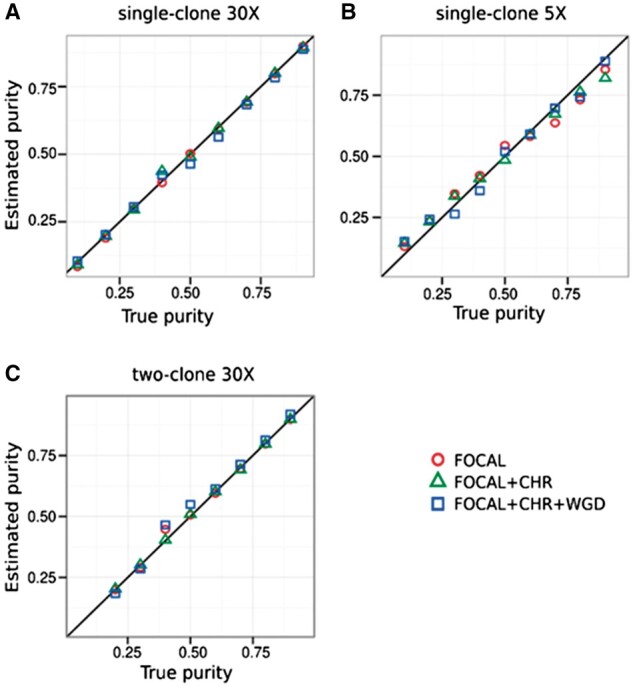
Performance of Accurity on (A) single-clone high-coverage 30×, (B) single-clone low-coverage 5×, (C) two-clone 30×. FOCAL: focal amplifications and deletions. CHR: whole-chromosome amplifications and deletions. WGD: whole genome duplications
Fig. 4.
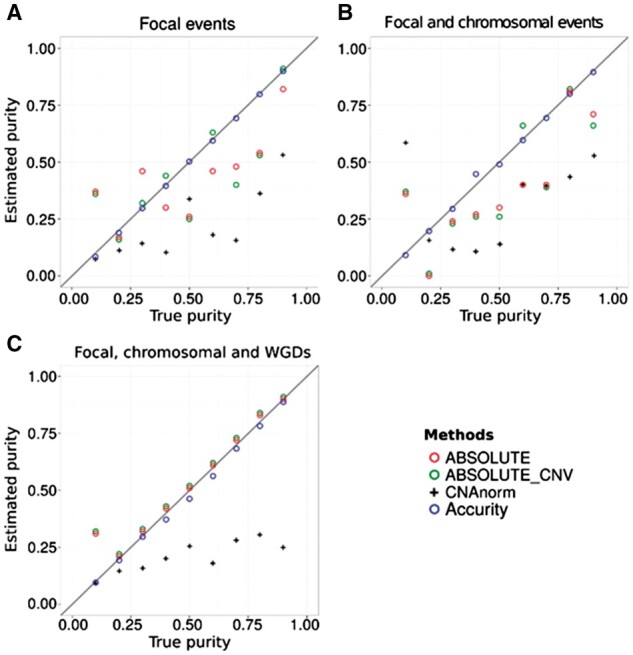
Comparison of true and estimated tumor purity by Accurity, ABSOLUTE, ABSOLUTE_CNV and CNAnorm on a simulated tumor sample (single-clone, 30× coverage) and its matching normal sample. ABSOLUTE estimates purity by combining the SCNA data with a predefined karyotype prior distribution (default option). ABSOLUTE_CNV estimates purity from SCNA data alone. The diagonal straight line indicates Estimated purity = True purity. (A) Only focal SCNAs were present. (B) Focal and chromosomal SCNAs were present. (C) Focal and chromosomal SCNAs and WGDs were present
We also ran ABSOLUTE (Carter et al., 2012), ABSOLUTE_CNV (ABSOLUTE without using karyotype prior information) and CNAnorm (Gusnanto et al., 2012) on the single-clone high-coverage in silico WGS data to estimate tumor purity and ploidy (Fig. 4). ABSOLUTE performed poorly if no WGD event is introduced to the cancer genome, which suggests that ABSOLUTE was designed for big SCNA events such as WGDs. For several ABSOLUTE-low-performing samples in Figure 4A and B, ABSOLUTE_CNV had slightly better results than ABSOLUTE, suggesting that incorporating extra karyotype information could adversely affect tumor purity inference when only focal or chromosomal SCNAs disrupt a cancer genome. CNAnorm performed poorly in most cases, indicating that read count data alone is not sufficient for accurate tumor purity and ploidy inference.
For ploidy inference, Accurity estimates were consistently within 10% of the true ploidy level in all settings. Ploidy estimates by ABSOLUTE were often much higher than the truth. It also tended to predict many false WGD events. It predicted 14 WGD events out of 17 WGD-free samples, which translates to a false positive rate of 82.3%. We suspect the lack of a robust model selection criterion such as BIC causes ABSOLUTE to fit data with models more complex than the truth and hence the very high rate of WGD false positives (further discussed in Methods). Overall, utilizing a greater amount of information from both SCNAs and HGSNVs and robust modelling enables Accurity to outperform other methods in tumor purity and ploidy inference.
3.2 Purity and ploidy estimates for TCGA samples by Accurity
We applied Accurity to 172 pairs of TCGA tumor-normal samples. For 61 samples, the TRE histogram were so noisy that no valid period could be detected by Accurity. As a result, Accurity succeeded for 111 samples, with 32 high-coverage (coverage > 10), 49 medium coverage (5–10), 30 in low coverage (<5). We compared Accurity estimates with those of ABSOLUTE, ESTIMATE and LUMP, as reported in Aran et al. (2015) (Supplementary Table S1). The overall performance of Accurity (spearman correlation ρ = 0.328 n = 111) (Fig. 5) is on par with ABSOLUTE (ρ = 0.368 n = 153, ρ = 0.315 if restricted to the 111 samples that Accurity succeeded in). Both outperformed ESTIMATE and LUMP substantially.
Fig. 5.
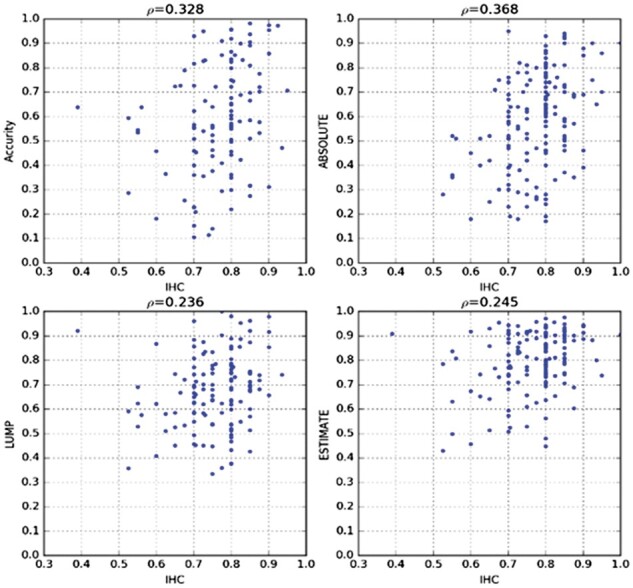
Tumor purity estimates by Accurity on TCGA samples versus other methods. ABSOLUTE ρ is 0.315 if restricted to the 111 samples that Accurity succeeded in
There is a performance decline for Accurity once coverage is below 10. In high coverage (coverage > 10) samples (Supplementary Table S2), Accurity is on par with ABSOLUTE, outperforming the other two. In lower-coverage (<10) samples, the Accurity performance declined. With coverage 5–10, Accurity (ρ = 0.187) did not compare favorably with the other methods. With coverage below 5, Accurity performed similarly as coverage 5–10, with slight improvement, (ρ = 0.291) and outperformed the other three by a big margin since ABSOLUTE, ESTIMATE and LUMP all performed quite poorly.
We further confirmed the dependency of Accurity’s performance on coverage using more simulation data (Supplementary Fig. S8). The deviation of the Accurity estimate from the true purity level increased to more than 0.1 once coverage is below 10. Although the Accurity performance declined in samples of lower coverage (<10), its performance in respectable, esp. in samples of coverage below 5. This validates our idea of leveraging the periodicity in the TRE histogram to estimate purity. As long as a clear period in TRE histogram can be detected, Accurity can produce a reasonable estimate.
3.3 Enhanced SCNA detection after accounting for purity and ploidy
Each Gaussian distribution in the first level of the Accurity HGM model corresponds to a certain copy number. Once Accurity infers the best tumor purity and ploidy estimates, the copy number of each segment is determined through its peak membership in Figure 2, in which every peak corresponds to a copy number. This is by no means a perfect solution. A complete probabilistic model for copy number assignments is lacking. We use an example (Fig. 6) to illustrate the potential power of Accurity in calling copy numbers.
Fig. 6.
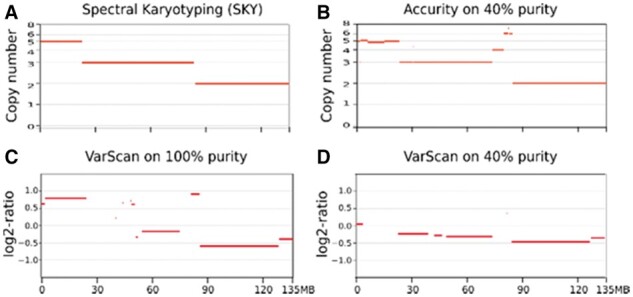
Improvement in power to detect SCNAs. Each panel is a copy number profile of chromosome 10 for HCC1187. X-axis is the chromosomal position. Horizontal red bars in each plot are chromosomal segments. Y-axis is copy number in A and B, log2-ratio in C and D. (A) Copy number profile on HCC1187 (100% purity) by spectral karyotyping (SKY), regarded as the ground truth. (B) Copy number profile on 40% purity HCC1187 by Accurity. (C) Copy number profile on 100% purity HCC1187 by VarScan. (D) Copy number profile on 40% purity HCC1187 by VarScan
The ability to incorporate tumor purity and ploidy in calling SCNAs gives Accurity an advantage over purity-ploidy-agnostic CNA callers that effectively assume tumor purity to be 100% and tumor ploidy close to 2. The advantage of Accurity is especially clear in analyzing tumor samples of low purity or high ploidy. Figure 6 is a comparison of copy number profiles generated by a widely used software VarScan (Koboldt et al., 2012) and Accurity, using a mixed HCC1187 sample (Methods). The SKY (spectral karyotyping) result of HCC1187 (Fig. 6A) is regarded as the ground truth showing that chromosome 10 contains three segments of copy number 2, 3 and 5, respectively. SKY also determines HCC1187 to be a triploid (ploidy close to 3). In an unmixed (purity = 100%) sample (Fig. 6C) VarScan failed to call copy number in some segments but the overall picture is good. It correctly inferred the greater signal separation between copy number 3 and 5 than the separation between 2 and 3. However, its signal/noise separation completely collapsed in a 40% mixed HCC1187 sample (Fig. 6D). Accurity, on the other hand, produced the same copy number profile on a 40% mixed HCC1187 (Fig. 6B) as that on the unmixed HCC1187. It also infers the ploidy of HCC1187 to be around 2.67. Even with its good signal/noise separation in the unmixed HCC1187, VarScan has difficulty in translating log2-ratio to copy numbers because the elevated ploidy (∼2.67) of HCC1187 moved the usual baseline (copy number = 2) log2-ratio away from 0 to below 0 in this case (Fig. 6C). By comprehensively modelling both tumor purity and ploidy, Accurity significantly increased the signal/noise gap between different copy numbers and was able to call more SCNAs (Fig. 6B).
3.4 Implementation and performance
Accurity is implemented in C++ and RUST and can be built for virtually all Linux distributions. In theory, it can be compiled and run on the Windows and Mac platforms but we have not tested. Average runtime of Accurity is about 45 min for a 5× tumor/normal matched pair; about three hours for a 30× tumor/normal matched pair on a single core of Intel(R) Xeon(R) CPU E5-2670 v3 @ 2.30 GHz; with a peak RAM consumption of under 4 GB. Owing to its C++/RUST implementation, Accurity is faster than tested methods and occupies less memory.
We provided all methods with the same tumor-normal pair of bam files. We ran all programs with default parameters (versions as downloaded on August 15, 2016) and the same computational environment as stated above.
4 Discussion
In this article, we describe Accurity, an accurate, fast and fully automated method that infers tumor purity and ploidy from tumor-normal WGS data. Accurity is accurate because its HGM model is based on the most up-to-date knowledge about cancer biology, i.e. IRH, and encompasses SCNAs and HGSNVs, both highly abundant in a tumor sample. The second factor contributing to its accuracy is its adoption of noise reduction techniques from the signal processing field and a robust statistical evaluation criteria, Bayesian Information Criteria. Accurity is fast because of its two-stage optimal-search algorithm. During the first guiding stage, Accurity uses auto-correlation analysis to obtain rough estimates of tumor purity and ploidy. In the second refining stage, Accurity refines the rough estimates through a rigorous statistical search. Accurity is fully automated, does not require user input on the likely range of tumor purity and ploidy, and works under a wide range of settings because the noise reduction and auto-correlation techniques from the first guiding stage can significantly enhance statistical signals to estimate tumor purity and ploidy, even in noisy low-coverage settings. Through in silico experiments, we demonstrated its ability to infer purity and ploidy accurately even at low-purity (10%) and low-coverage (5×) and its superior performance over two other methods, ABSOLUTE (Carter et al., 2012) and CNAnorm (Gusnanto et al., 2012). Analysis on TCGA samples shows that Accurity purity estimates are highly concordant with TCGA histological estimates. Accurity is also fast and finishes analyzing one sample in a few minutes.
For tumor samples harboring so few SCNAs that the periodic pattern in the coverage data cannot be confidently recognized through autocorrelation analysis, Accurity would fail to yield purity and ploidy estimates. Another hypothetical factor that could cause Accurity to fail is an extremely high level of intra-tumor heterogeneity, which can reduce the fraction of clonal segments to such a low degree that there are not enough clonal segments for Accurity to infer purity and ploidy.
Many studies have shown that taking tumor purity into account can impact genomic analyses significantly (Aran et al., 2015; Yoshihara et al., 2013). We demonstrated that accounting for tumor purity and ploidy, Accurity has the potential of revealing SCNAs that are missed by methods assuming 100% tumor purity and near-normal tumor ploidy, which can benefit the broad cancer research community to uncover cancer driving amplifications and deletions. However, its statistical model for copy numbers is incomplete and comprehensive power comparison is lacking. Our handling of subclonal segments, assigning a copy number averaged across all cancer subclones, suffices for producing a crude tumor genome-wide copy number profile, but is far from satisfactory to understand clonal evolution during tumor progression. Next iteration of Accurity will focus on disentangling subclonal segments to reconstruct tumor subclonal structure.
Funding
This work was supported by China Thousand-Talent program, Chinese Academy of Sciences Hundred-Talent program Y6G7011018, ‘Personalized Medicines – Molecular Signature-based Drug Discovery and Development’ Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA12050202) awarded to YSH.
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Zhihui Luo, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai, China.
Xinping Fan, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai, China; University of Chinese Academy of Sciences, No.19A Yuquan Road, Beijing, China.
Yao Su, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai, China.
Yu S Huang, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai, China; University of Chinese Academy of Sciences, No.19A Yuquan Road, Beijing, China.
References
- Alkodsi A. et al. (2015) Comparative analysis of methods for identifying somatic copy number alterations from deep sequencing data. Brief. Bioinf., 16, 242–254. [DOI] [PubMed] [Google Scholar]
- Andor N. et al. (2014) EXPANDS: expanding ploidy and allele frequency on nested subpopulations. Bioinformatics, 30, 50–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aran D. et al. (2015) Systematic pan-cancer analysis of tumour purity. Nat. Commun., 6, 8971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Speed T.P. (2012) Summarizing and correcting the GC content bias in high-throughput sequencing. Nucleic Acids Res., 40, e72.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beroukhim R. et al. (2010) The landscape of somatic copy-number alteration across human cancers. Nature, 463, 899–905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bild A.H. et al. (2006) Linking oncogenic pathways with therapeutic opportunities. Nat. Rev. Cancer, 6, 735–741. [DOI] [PubMed] [Google Scholar]
- Boeva V. et al. (2014) Multi-factor data normalization enables the detection of copy number aberrations in amplicon sequencing data. Bioinformatics, 30, 3443–3450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter S.L. et al. (2012) Absolute quantification of somatic DNA alterations in human cancer. Nat. Biotechnol., 30, 413–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cronin M., Ross J.S. (2011) Comprehensive next-generation cancer genome sequencing in the era of targeted therapy and personalized oncology. Biomark. Med., 5, 293–305. [DOI] [PubMed] [Google Scholar]
- Degner J.F. et al. (2009) Effect of read-mapping biases on detecting allele-specific expression from RNA-sequencing data. Bioinformatics, 25, 3207–3212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elloumi F. et al. (2011) Systematic bias in genomic classification due to contaminating non-neoplastic tissue in breast tumor samples. BMC Med. Genomics, 4, 54.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Favero F. et al. (2015) Sequenza: allele-specific copy number and mutation profiles from tumor sequencing data. Ann. Oncol. Off. J. Eur. Soc. Med. Oncol., 26, 64–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garofalo A. et al. (2016) The impact of tumor profiling approaches and genomic data strategies for cancer precision medicine. Genome Med., 8, 79.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusnanto A. et al. (2012) Correcting for cancer genome size and tumour cell content enables better estimation of copy number alterations from next-generation sequence data. Bioinformatics, 28, 40–47. [DOI] [PubMed] [Google Scholar]
- Hanahan D., Weinberg R.A. (2011) Hallmarks of cancer: the next generation. Cell, 144, 646–674. [DOI] [PubMed] [Google Scholar]
- Koboldt D.C. et al. (2012) VarScan 2: somatic mutation and copy number alteration discovery in cancer by exome sequencing. Genome Res., 22, 568–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson N.B., Fridley B.L. (2013) PurBayes: estimating tumor cellularity and subclonality in next-generation sequencing data. Bioinformatics, 29, 1888–1889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Xie X. (2014) Deconvolving tumor purity and ploidy by integrating copy number alterations and loss of heterozygosity. Bioinformatics, 30, 2121–2129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu B. et al. (2013) Computational methods for detecting copy number variations in cancer genome using next generation sequencing: principles and challenges. Oncotarget, 4, 1868–1881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayrhofer M. et al. (2013) Patchwork: allele-specific copy number analysis of whole-genome sequenced tumor tissue. Genome Biol., 14, R24.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mwenifumbo J.C., Marra M.A. (2013) Cancer genome-sequencing study design. Nat. Rev. Genet., 14, 321–332. [DOI] [PubMed] [Google Scholar]
- Navin N. et al. (2011) Tumour evolution inferred by single-cell sequencing. Nature, 472, 90–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oesper L. et al. (2013) THetA: inferring intra-tumor heterogeneity from high-throughput DNA sequencing data. Genome Biol., 14, R80.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potti A. et al. (2006) A genomic strategy to refine prognosis in early-stage non-small-cell lung cancer. N. Engl. J. Med., 355, 570–580. [DOI] [PubMed] [Google Scholar]
- Ross J.S., Cronin M. (2011) Whole cancer genome sequencing by next-generation methods. Am. J. Clin. Pathol., 136, 527–539. [DOI] [PubMed] [Google Scholar]
- Roychowdhury S., Chinnaiyan A.M. (2014) Translating genomics for precision cancer medicine. Annu. Rev. Genomics Hum. Genet., 15, 395–415. [DOI] [PubMed] [Google Scholar]
- Sabbah M. et al. (2008) Molecular signature and therapeutic perspective of the epithelial-to-mesenchymal transitions in epithelial cancers. Drug Resistance Updates Rev. Comment. Antimicrob. Anticancer Chemother., 11, 123–151. [DOI] [PubMed] [Google Scholar]
- Shah S.P. et al. (2012) The clonal and mutational evolution spectrum of primary triple-negative breast cancers. Nature, 486, 395–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su X. et al. (2012) PurityEst: estimating purity of human tumor samples using next-generation sequencing data. Bioinformatics, 28, 2265–2266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y. et al. (2014) Clonal evolution in breast cancer revealed by single nucleus genome sequencing. Nature, 512, 155–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadav V.K., De S. (2015) An assessment of computational methods for estimating purity and clonality using genomic data derived from heterogeneous tumor tissue samples. Brief. Bioinf., 16, 232–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshihara K. et al. (2013) Inferring tumour purity and stromal and immune cell admixture from expression data. Nat. Commun., 4, 2612.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Z. et al. (2014) CLImAT: accurate detection of copy number alteration and loss of heterozygosity in impure and aneuploid tumor samples using whole-genome sequencing data. Bioinformatics, 30, 2576–2583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zack T.I. et al. (2013) Pan-cancer patterns of somatic copy number alteration. Nat. Genet., 45, 1134–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


