BundleWarp, streamline-based nonlinear registration of white matter tracts

Abstract

Nonlinear registration plays a central role in most neuroimage analysis methods and pipelines, such as in tractography-based individual and group-level analysis methods. However, nonlinear registration is a non-trivial task, especially when dealing with tractography data that digitally represent the underlying anatomy of the brain’s white matter. Furthermore, such process often changes the structure of the data, causing artifacts that can suppress the underlying anatomical and structural details. In this paper, we introduce BundleWarp, a novel and robust streamline-based nonlinear registration method for the registration of white matter tracts. BundleWarp intelligently warps two bundles while preserving the bundles’ crucial topological features. BundleWarp has two main steps. The first step involves the solution of an assignment problem that matches corresponding streamlines from the two bundles (iterLAP step). The second step introduces streamline-specific point-based deformations while keeping the topology of the bundle intact (mlCPD step).

We provide comparisons against streamline-based linear registration and image-based nonlinear registration methods. BundleWarp quantitatively and qualitatively outperforms both, and we show that BundleWarp can deform and, at the same time, preserve important characteristics of the original anatomical shape of the bundles. Results are shown on 1,728 pairs of bundle registrations across 27 different bundle types. In addition, we present an application of BundleWarp for quantifying bundle shape differences using the generated deformation fields.

1. Introduction

Medical image analysis would be incomplete without registration methods. Image registration is the backbone of numerous methods and pipelines in the neuroimaging field. Many pre-, intermediate-, and post-processing methods rely on registration such as motion/eddy (Jenkinson and Smith, 2001; Leemans and Jones, 2009; Rohde et al., 2004; Mohammadi et al., 2010; Rohde et al., 2004) and susceptibility correction (Graham et al., 2017), white matter segmentation (Garyfallidis et al., 2017; Chandio et al., 2020; Wasserthal et al., 2018), template creation (O’Donnell et al., 2012; Zhang and Arfanakis, 2018; Yeh et al., 2018; Hansen et al., 2021), and disease vs health group analysis (Smith et al., 2006; Bach et al., 2014; Chandio et al., 2020; Yeatman et al., 2012). One of the primary applications of brain MRI is to perform group analysis to find significant group differences in healthy controls and patients with any underlying disease (Smith et al., 2006; Chandio et al., 2020; Dayan et al., 2015; Cousineau et al., 2017). MRI scans come from different scanners and subjects. Each subject’s MRI is in the native coordinate space. It is important to align MRI data from different subjects and scanners to the same standard space to find correspondences among the same brain areas across subjects. Those corresponding/overlapping areas are then analyzed to find differences between subjects or groups (Smith et al., 2006). With this goal, many image-based linear and nonlinear registration methods have been developed such as ANTs (Avants et al., 2009), AIR (Woods et al., 1998), FAIR (Andersson et al., 2007), FNIRT (Andersson et al., 2007), and Elastix (Klein et al., 2009).

One of the most used and explored MRI modalities in recent decades is diffusion-weighted MRI (dMRI) (Basser et al., 1994; Le Bihan et al., 2001) that allows for the reconstruction of white matter fibers and connectivity in vivo. White matter fibers of the brain are computationally reconstructed from dMRI (Basser et al., 1994; Le Bihan et al., 2001; Alexander et al., 2007) by means of tractography methods (Farquharson et al., 2013; Catani and De Schotten, 2008; Gong et al., 2008; Mori and Van Zijl, 2002). A whole-brain tractography comprised of millions of digitally reconstructed white matter fibers from a single subject is called a tractogram. A single digital white matter fiber pathway is called a streamline, and a set of streamlines that travel together and have similar shapes and geometry is called a tract/bundle. There are several applications of tractography, such as neurosurgical planning or studying the effects of disease on brain connectivity across populations(Chandio et al., 2020; Yeatman et al., 2012; Yendiki et al., 2011). For segmentation of white matter bundles and their inter or intra-group analysis, data need to be aligned to a common reference. Similar to image-based group analysis pipelines (Smith et al., 2006; Bach et al., 2014), streamline-based group analysis pipelines (Chandio et al., 2020; Yeatman et al., 2012; Cousineau et al., 2017; Dayan et al., 2015) also require registration as an intermediate step. Unlike image and voxel-based volumetric white matter tracts (Hansen et al., 2021), streamline-based white matter tracts (Yeh et al., 2018) provide rich details about the brain’s white matter structural connectivity at the sub-millimeter scale as different voxels are integrated to generate streamlines. However, streamline-based registration is much more complicated. Streamline-based registration would require finding correspondences between streamlines of two bundles to map/match those corresponding streamlines and minimize the distance between bundles. Tractography data come with their challenges. Very often, two bundles will have a different number of streamlines in them, and mapping one streamline from moving to one streamline in a static (one-to-one mapping) approach would not work. If the moving bundle has more streamlines than the static bundle, some of the streamlines in the moving bundle will be left unmapped. Moreover, bundles of the same types usually have a similar overall shape, but streamlines within the bundles could have different lengths and geometries. A pure nonlinear streamline-based registration would require producing a warp/transformation matrix specific to each streamline and each point on the streamline. Desired output would be such that it closely aligns two bundles without destroying the original anatomical shape of the bundle or creating spurious streamlines.

The most common approach to aligning tractograms/tracts to a common space is to register the subject’s fractional anisotropy (FA) image to a template FA image and then apply the computed transformations (affine or deformable) to streamlines. Most commonly, ANTs’ nonlinear SyN registration (Avants et al., 2009) is performed on FA images, and resulting affine and warp maps are applied to streamlines. This process is also known as spatial normalization of tractography/streamlines (Greene et al., 2018). However, image-based transformation maps do not consider the finer details of the tractography. Those transformations are derived from images and are not specific to streamlines, i.e., they do not consider neighborhood information on streamlines. Each streamline can have a different number of points and Euclidean length. Every streamline requires a deformation that is based on its geometry. Each point on the streamline needs to be warped in a manner such that the topological order of the points on the streamlines is preserved after the registration. Hence, it is desirable to have a robust streamline-based registration method for aligning tractography data directly in the streamline-space.

Several streamline-based registration methods have been proposed recently. Most of them fall in the category of linear registration (Leemans et al., 2006; Durrleman et al., 2011, 2014; Zvitia et al., 2009; Garyfallidis et al., 2015; O’Donnell et al., 2012). However, literature on nonlinear streamline-based registration methods is scarce, and very few methods are purely streamline-based. For example, (Arsigny et al., 2009) generates scalar volumes from streamlines and then warps those volumes. The resulting transformations are applied to streamlines. Similarly, (Wassermann et al., 2011) uses tract density images to register bundles. Another method(Glozman et al., 2018) implemented a seed point matching strategy to establish correspondences between regions on the bundles, and registration is performed independently on those regions. A deep-learning based method was developed for the registration of diffusion data where tract orientation maps (TOMs) of white matter tracts and whole-brain FA images were used as the training data(Zhang et al., 2021). Each voxel in a TOM file represents the local mean fiber orientation (one peak). While TOM files provide local mean fiber direction (peak), they do not have streamline connectivity information. It does not provide information about which points/peaks are neighbors to which other points/peaks on a streamline. Another recently proposed method for nonlinear streamline registration uses deformation transfer via parallel transport(Lizarraga et al., 2021). It finds and applies transformations in latent space, and after registration, streamlines are reconstructed. The majority of the existing nonlinear registration methods for streamlines are not purely streamline-based. These methods perform registration on a volumetric density map of bundles(Arsigny et al., 2009; Wassermann et al., 2011) and apply generated transforms to streamlines or project streamlines in the latent space where the registration takes place, and streamlines are then reconstructed(Lizarraga et al., 2021) or use a seed point matching strategy to establish correspondences between bundle regions and perform registration separately on regions of the bundles(Glozman et al., 2018). All of these approaches do not take into consideration the streamline topological connectivity in the registration process. However, recently, a nonlinear streamline matching method was proposed(Olivetti et al., 2020) that aims to find nonrigid correspondence between streamlines of two whole-brain tractograms. Although it does not apply a transformation or generate a warp map, it does pave the way for direct streamline-based nonlinear registration of tracts.

In this paper, building on our previous work on the direct alignment of tractograms/tracts in streamline-space(Garyfallidis et al., 2015; Olivetti et al., 2020; Chandio and Garyfallidis, 2020), we introduce a new method, BundleWarp. BundleWarp is a method for streamline-based nonlinear registration of white matter tracts. Given two bundles, static (fixed) and moving bundle (bundle to be registered), BundleWarp first linearly aligns two bundles using streamline-based linear registration (SLR)(Garyfallidis et al., 2015). It then finds pairs of matching streamlines in two bundles to establish correspondence among the streamlines of two bundles using iterLAP. iterLAP is a proposed extension of the rectangular sum of linear assignment problem (rLAP) for many-to-one streamline matching when static and moving bundles do not have the same number of streamlines. Finally, it warps the matching pair of streamlines using proposed memoryless coherent point drift (mlCPD) method(Myronenko et al., 2006; Myronenko and Song, 2010). The velocity field is regularized (Myronenko and Song, 2010; Yuille and Grzywacz, 1989) using motion coherence theory(Yuille and Grzywacz, 1988) to coherently move points on the streamline as a group to maintain the topological structure of the streamlines.

BundleWarp provides users with an option to control the level of deformations in the registration through a single regularization parameter λ. Given two bundles, static (fixed) and moving, BundleWarp can partially deform the moving bundle with a high value of λ or fully deform the moving bundle using a low value of λ. By default, BundleWarp partially deforms the bundle.We show that partially deforming the bundle improves the linear registration and, at the same time, preserves the original anatomical shape of the input bundle. Additionally, we propose quantifying bundle shape differences through the nonlinear displacement field generated by fully deforming the moving bundle to precisely match the static bundle. To the best of our knowledge, BundleWarp is the only streamline-based white matter tract registration method that provides users with an option to control the level of deformations in the registration.

We show results of BundleWarp registration on 1,728 pairs of bundles (including 27 different types of bundles). We compare the BundleWarp method with other streamline-based linear and image-based nonlinear registration methods. We show that BundleWarp outperforms based on qualitative (visual) and three quantitative metrics; bundle-based minimum distance, bundle shape similarity score, and volumetric DICE coefficient. In addition, we use the displacement field generated by BundleWarp to visually and analytically quantify the shape difference between bundles. BundleWarp can be used to aid bundle segmentation(Garyfallidis et al., 2017), bundle atlasing(Romero-Bascones et al., 2022), and tractometry(Chandio et al., 2020).

2. Methods

2.1. Data

Data used in the preparation of this article were obtained from the Parkinson’s Progression Markers Initiative (PPMI)(Marek et al., 2011) database. PPMI diffusion MRI data were acquired using a standardized protocol used on Siemens TIM Trio and Siemens Verio 3 Tesla MRI machines from 32 different international sites. Diffusion-weighted images were acquired along 64 uniformly distributed directions using a b-value of 1000 s/mm² and a single b=0 image. More information on the MRI acquisition and processing can be found online at www.ppmi-info.org. We have processed 64 subjects: 32 controls and 32. We selected subjects in the age range of 39–61. Both groups have 14 females and 16 males.

2.2. Data Preparation

Diffusion MRI data was denoised using the local principal component analysis (LPCA) noise reduction method (Manjón et al., 2013). For brain tissue extraction, the median Otsu algorithm (Yang et al., 2012) was used. The distortions induced by eddy currents and motion were corrected by registering the diffusion-weighted volumes to the b0 volume. An affine transformation was computed to register b0 and non-b0 3D volumes by maximizing normalized mutual information. The optimization strategy used in DIPY is similar to that implemented in ANTs (Avants et al., 2009). The B-matrix (b-vectors) were rotated to preserve the correct orientational information as described in this paper(Leemans and Jones, 2009). The whole-brain tractograms were generated by fitting a constrained spherical deconvolution (CSD) model to get directional information from dMRI data (Tournier et al., 2007), from which a simplified peaks representation was extracted. The obtained peaks were then used as the input to a local tracking algorithm. We performed deterministic tracking (Mori et al., 1999; Basser et al., 2000) using EuDX (Garyfallidis, 2012). The EuDX tracking algorithm was initialized with the following parameters; tracking starts from voxels where fractional anisotropy (FA) > 0.3, number of seeds per voxel = 15, step size = 0.5, angular threshold = 60 degrees, and stopping tracking if FA value drops below 0.1. Each generated tractogram comprised of 5–10 million streamlines. Twenty-seven white matter tracts were extracted from each subject’s whole brain tractogram by deploying auto-calibrated RecoBundles (Garyfallidis et al., 2017; Chandio et al., 2020). Data was processed using DIPY (Garyfallidis et al., 2014). Data derivatives(Chandio, 2020) are publicly available here: https://doi.org/10.35092/yhjc.12033390.v1.

2.3. Tractography Data Representation

A streamline is stored as an ordered sequence of 3D vector points. The collection of streamlines is called tractogram/tracts. Let S_i be a streamline in a whole-brain tractogram/tract T.

T = {S₁, S₂, …, S_n}, S_i ∈ T, S_i = {s₁, s₂, …, s_k}, where s_i is a 3D vector point. Streamlines in T can have different different number of points (k) and different lengths. Here, length of a streamline implies its Euclidean length in millimeters. Since each streamline is a set of 3D vectors, it can be considered a point-set.

2.4. BundleWarp Registration

Given two bundles, a static bundle (often referred to as fixed in most registration methods) and a moving bundle (bundle to be registered), BundleWarp performs a two-step streamline-based registration to align the moving bundle with the static bundle.

In the first part, we linearly align two bundles using streamline-based linear registration (SLR)(Garyfallidis et al., 2015).

The SLR can be summarized in the following steps:

1. Set all streamlines from both static and moving bundles to have the same number of points K per streamline

2. Minimize BMD cost function

3. Apply the transformation to the moving bundle to align it with the static bundle.

Where BMD stands for bundle-based minimum distance(Garyfallidis et al., 2015) described in Appendix A.1.2.

After streamlines are roughly aligned and are in the same space, we start the deformation process. In the deformation step, every streamline and every point on a streamline gets a nonlinear transformation map (warp map) specific to it, unlike linear registration, where all streamlines share one global transformation map. We create streamline correspondences between streamlines in moving and static bundles so that we can warp one streamline from moving to one streamline in static. However, static and moving bundles often do not have the same number of streamlines, and one-to-one mapping would not suffice in that case. Therefore, we design a many-to-one pairwise streamline correspondence approach based on the rectangular Linear Assignment Problem (rLAP) (Olivetti et al., 2020; Kuhn, 1955) for bundles with a varying number of streamlines that we call iterLAP.

The linear assignment problem (LAP)(Kuhn, 1955) is also known as minimum weight matching in bipartite graphs. The problem is described by a cost matrix C, where each C[i, j] element is the cost of matching a vertex (streamline) i of the first partite set (moving bundle) with a vertex (streamline) j of the second set (static bundle). The goal is to find a complete assignment of moving bundle’s streamlines to static bundle’s streamlines that results in minimal cost. Where LAP can be written as

$$\text{min}\sum _i\sum _j{C}_{i,j}{X}_{i,j}$$

Here, X is a boolean matrix and if X[i, j] is equal to 1 then moving bundle’s i^th streamline is assigned/matched to j^th streamline of static bundle. In classic LAP, cost matrix C is a square matrix. The method can be extended to rectangular LAP (rLAP) to have a rectangular cost function when two sets do not have the same number of elements. However, both LAP and rLAP result in one-to-one matching/assignment. In rLAP, when there are more rows than columns in C_m×n, it only assigns n rows to n columns.

In order to get many-to-one correspondence of streamlines when m > n, we design many-to-one rectangular LAP (iterLAP).

We start by calculating the MDF distance between each streamline of moving bundle with every streamline of static bundle, populating an m × n MDF distance matrix as shown in Fig. 1C. Here, the MDF distance matrix becomes the cost matrix C. Next, we feed m×n MDF distance matrix to rLAP. rLAP returns n matched pairs. We are left with m − n streamlines in the moving bundle and need to be matched with streamlines in static. We run rLAP again on the sub-matrix $\widehat{C}$ of MDF distance matrix C. Where, $\widehat{C}$ is a (m − n) × n. We rerun rLAP using $\widehat{C}$ as a cost matrix. If (m − n) > n and still some moving bundle’s streamlines are unmatched, we repeat the process until all streamlines have found a corresponding streamline in the static bundle. iterLAP can be summarized as follows:

1. Calculate m × n MDF distance matrix C from moving and static bundles’ streamlines

2. While all streamlines in moving are not matched

   1. Run rLAP on C to get pairwise streamline correspondences
   2. k = m − n
   3. if k < n :

      1. $\begin{array}{ll}\widehat{C}=k\times n\text{sub}-\text{matrix}\text{of}C\hfill & ▹\widehat{C}\text{has}\text{the}\text{distance}\text{between}\text{unmatched}\text{k}\text{streamlines}\text{in}\text{moving}\text{bundle}\text{and}\text{all}\text{n}\text{streamlines}\text{in}\text{static}\text{bundle}\hfill \end{array}$
      2. $C=\widehat{C}$

3. matched pairs is a list of m elements. Each element is a tuple (i, j). Where i is the moving bundle’s streamline index and j is the index of it’s corresponding streamline in static bundle.

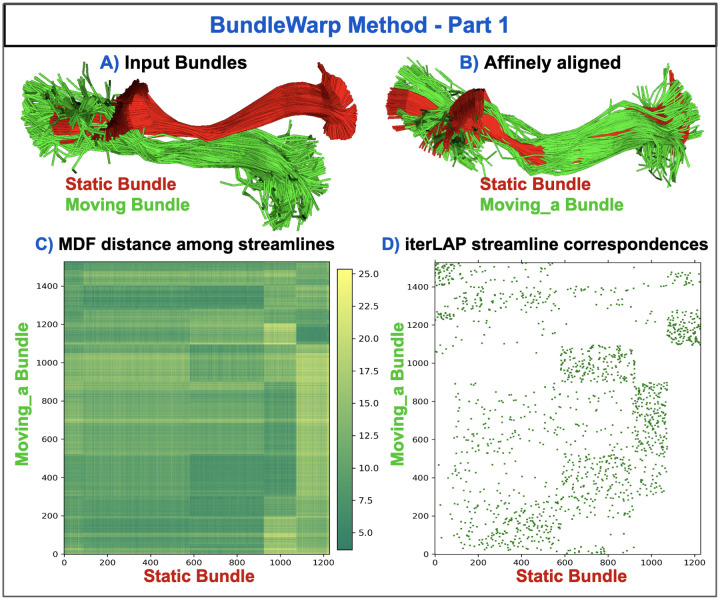
Figure 1.

Steps A-D in BundleWarp (BW) method. A) Input static (red) and moving (green) IFOF L bundles. B) Moving bundle is affinely aligned with the static bundle. C) MDF distance is calculated among streamlines of affinely moved (moving a) bundle and static bundle. D) Using distance matrix from (C), many-to-one rectangular linear assignment problem (iterLAP) is applied to find streamline correspondence in two bundles. In (D), green pixels show correspondence between the x-axis (static bundle’s streamlines) and y-axis (moving a bundle’s streamlines). The pixel size has been enlarged for visibility. See Fig 2 for the next steps in BW.

In the second part, after we have built the correspondences among streamlines of moving and static bundles, we start to warp them (find nonlinear transformations) using proposed memoryless Coherent Point Drift (mlCPD) registration method for bundle of streamlines. In mlCPD, for each pair of corresponding streamlines in matched pairs, we perform deformable point-cloud registration using the Coherent Point Drift (CPD) method(Myronenko et al., 2006; Myronenko and Song, 2010). Here, we iterate and apply CPD registration separately on each pair of streamlines. Since a single streamline is an ordered set of points, it can be treated as a point-cloud set (Fig. 2E). Through iteratively applying CPD, (1) we move the points on the same streamline together taking into account the local neighborhood information/connectivity, and (2) we save memory and computational power since we work with small point-clouds of two streamlines instead of entire bundles. Dealing with large number of point-clouds could become computationally extensive task and one large point-cloud representing entire bundle would lose the streamline connectivity information. Moreover, the original CPD method if applied to the full bundles would fail due to large memory allocation requests. Hence, we propose mlCPD to overcome above mentioned limitations. mlCPD does require the initial matching of pair streamlines by iterLAP (see above). iterLAP is calculated once and mlCPD is calculated as many times as the number of streamlines in the moving bundle.

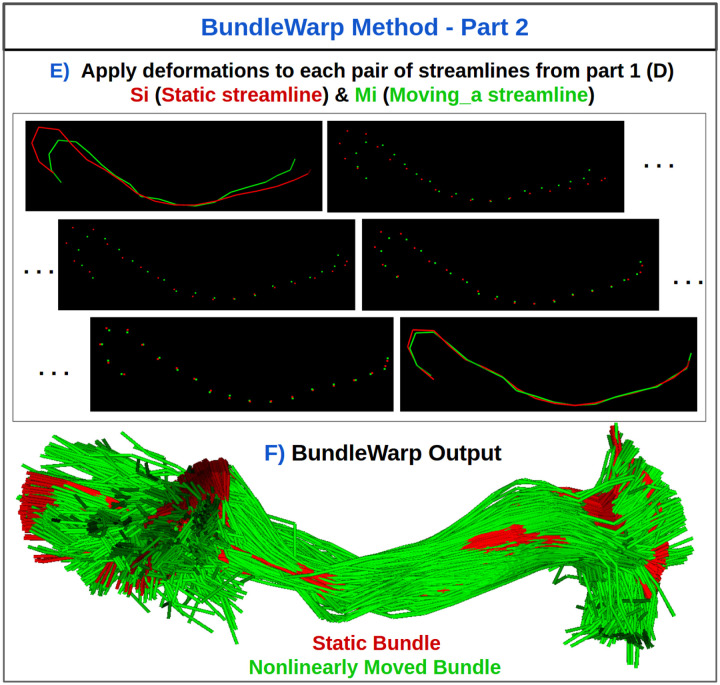
Figure 2.

Steps E and F in BundleWarp (BW) method. Iterate over matched pairs of streamlines from Fig. 1.D and deform moving a streamline. (E) Streamlines are considered point-set clouds and each streamline is deformed independently. (F) The final output of the BundleWarp method with λ=0.3.

The mlCPD algorithm takes a probabilistic approach to align two point-sets. Registration is formulated as a maximum likelihood (ML) estimation problem using the Gaussian Mixture Models (GMMs) method. The points in the moving set Y are considered as the GMM centroids, while the static point-set X represents the data points generated by the GMM. The GMM centroids from the Y point-set are fitted to the X point-set by maximizing the likelihood. When the two point-sets are optimally aligned, the correspondence is the maximum of the GMM posterior probability for a given data point. To preserve the topological structure of the point-sets (streamlines), the GMM centroids are forced to move coherently as a group. The expectation-maximization (EM) algorithm is used to optimize the cost function. It concurrently finds the nonrigid transformation and the correspondence amongst point-sets of two streamlines. It regularizes the velocity field such that points move coherently using motion coherence theory(Yuille and Grzywacz, 1988, 1989).

Here, Y = (y₁, y₂, …, y_m)^T is a moving streamline represented as a m × 3 matrix. m is number of points in the moving streamline. X = (x₁, x₂, …, x_n)^T is a static streamline represented as a n × 3 matrix. n is number of points in the static streamline. Points in Y are considered as the centroids of a GMM, and are fitted to the data points X by maximizing the likelihood function. The GMM probability density function is written as

$$p(x)=\sum _{i=1}^m\frac{1}{m}p(x\mid i)\hspace{1em}\text{with}\hspace{1em}x\mid i~N\left(y_i,{\sigma }^2{I}_D\right)$$

Where D is the dimensions of the centroids (D = 3 in our case).

Let Y_o be the initial centroid values, G_m×m a square symmetric Gram matrix with elements

$$g_{ij}=G\left(y_i,y_j\right)=e^{-\frac{1}{2}{\Vert \frac{y_i-y_j}{\beta }\Vert }^2}$$

W_m×m = (w₁, w₂, …, w_m)^T is a Gaussian kernel weights, I is identity matrix, and 1 is a column vector of all ones. The estimated velocity field v represents the underlying non-rigid transformation. Free parameters λ represents the trade-off between data fitting and smoothness regularization and β represents the strength of the interaction between points. σ captures the range for each Gaussian mixture component. α is the annealing rate. In the M-step of EM algorithm, system of nonlinear equations is solved for W. mlCPD algorithm for streamlines can be summarized as follows.

For each pair of streamlines in matched pairs:

1. Initialize parameters λ > 0, β > 0, and σ.

2. Construct G matrix, initialize Y = Y_o. Where Y_o is a moving streamline and X is a static streamline.

3. Deterministic annealing:

   • EM optimization:

     • E-step: Compute posterior probabilities matrix P
     • M-step: solve for W: (diag(P1)G + λσ²I)W = PX − diag(P1)Y_o
     • update Y = Y_o + GW
   • Anneal σ = ασ

4. Compute the velocity field v(z) = G(z,.)W

5. Get correspondence from posterior probabilities P

Where, P_m×n is a posterior probability matrix of GMM with:

$$p_{ij}=\frac{e^{-\frac{1}{2}{\Vert \frac{y_i^{old}-x_j}{\sigma }\Vert }^2}}{{\sum }_{i=1}^m{e}^{-\frac{1}{2}{\Vert \frac{y_i^{old}-x_j}{\sigma }\Vert }^2}}$$

Regularization is imposed using Gaussian kernel which takes a similar regularization form as the one in motion coherence theory(Myronenko and Song, 2010; Yuille and Grzywacz, 1988, 1989). This way we regularize the deformation field to be smooth and coherently move points on the same streamline to preserve its topology.

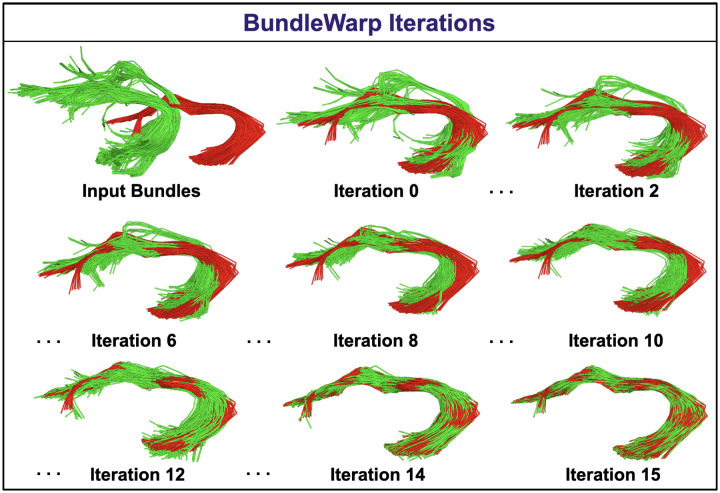
BundleWarp method’s registration iterations are visualized in Fig. 3. Here, iteration 0 implies linear registration that could be affine or rigid (we keep affine by default). In the rest of the iterations, the moving bundle is deformed. BundleWarp converges within 15 iterations. For the purpose of showing how quickly and accurately BundleWarp converges and fully deforms the moving bundle, we selected the regularization parameter λ = 0.001. However, the level of deformations can be controlled by increasing the value of λ. See section 2.5 and 4 for detailed discussion on the selection of λ.

Figure 3.

BundleWarp (BW) method iterations. Where red is the static and green is the moving bundle. Iteration 0 means affine registration. The rest of the iterations show a deformable registration process in BW. BW converges in 15 iterations.

2.5. Parameter Selection

The optimal expected output of nonlinear tract registration is non-trivial to decide. The same type of white matter bundle can have different shapes and sizes for different subjects. Deforming the original topological/anatomical shape of the bundle is not necessarily ideal as it can lose the characteristics needed in the analysis. For example, a patient with a tumor will have some pathways missing from the area of tumor location. Deforming the shape of the bundle too much, in this case, can lead to the nonrecognition of abnormalities/tumors in the analysis.

BundleWarp provides users with an option to control the level of deformations needed in the output. To the best of our knowledge, BundleWarp is the first nonlinear registration method for tractography data that provides the functionality to either partially or fully deform a bundle.

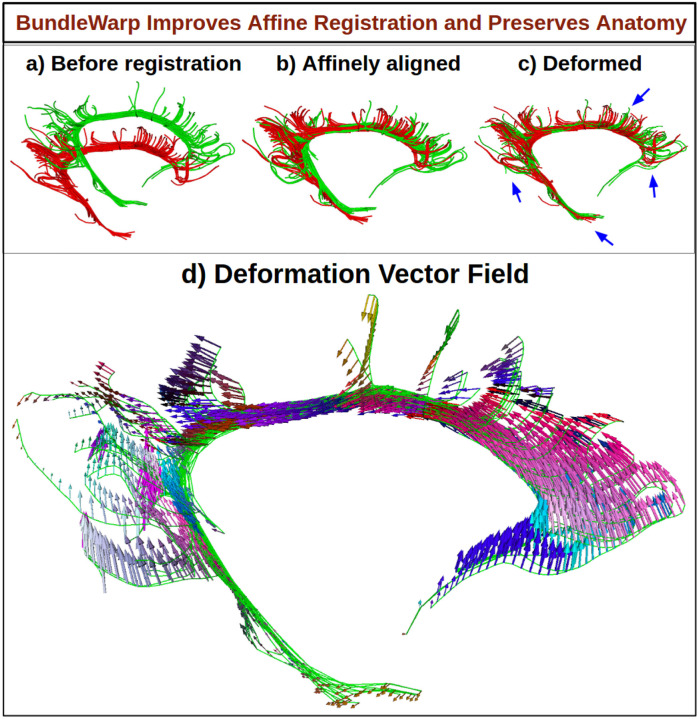
Users can decide how much they want to deform the bundle by providing the values of λ and β, where λ controls the trade-off between regularizing the deformation and having points match very closely. The lower the value of λ, the more closely the bundles would match. β controls the smoothness of the deformation. β represents the width of the smoothing Gaussian filter. By default, we set β to be 20 for all bundles except when the Euclidean length of the bundle is shorter than 50 mm. In the case of small bundles with length < 50mm, β is set to 10. A low value of β contributes to generating locally smooth transformations. A higher value of β will make the model produce more of a translation transformation. λ regularizes the velocity field. Setting λ to a relatively higher value, such as 0.3, we include fewer deformations in the model, and the moving bundle is partially deformed. The output will be an improvement over linear registration, yet the bundle will retain its original topological/anatomical shape, as shown in Fig. 4. In Fig. 4, we show partially deformable BundleWarp registration. Here, (a) moving Cingulum bundle (in red color) is registered to static/fixed bundle (in green color) with λ = 0.3 and β = 10 (because the length of the cingulum bundle is less than 50mm) to improve linear registration (b) and, at the same time, preserve the original anatomical structure of the moving Cingulum bundle (c). In Fig. 4d, we visualize the vector field of deformations over an affinely registered moving bundle. Vector field arrows show how much and in which direction BundleWarp adds deformations after linear registration. Additionally, blue arrows in (c) point towards areas that are deformed and add significant improvement over the linear alignment of two bundles, yet the moving bundle retains its original characteristics. Here, a smooth and coherent vector field (d) indicates a smooth mapping of the streamlines, as we can see the structure of the Cingulum bundle in the vector field.

Figure 4.

The BundleWarp method improves the linear registration by adding smooth deformations where needed and at the same time preserving the topological structure of the bundle. a) Shows input Cingulum static (red) and moving (green) bundles. b) Shows moving bundle affinely registered to static bundle. c) Shows deformations introduced by BundleWarp. Blue arrows indicate where deformations improved the output of affine registration. d) Shows a smooth velocity vector field visualized over affinely registered bundle shown in b.

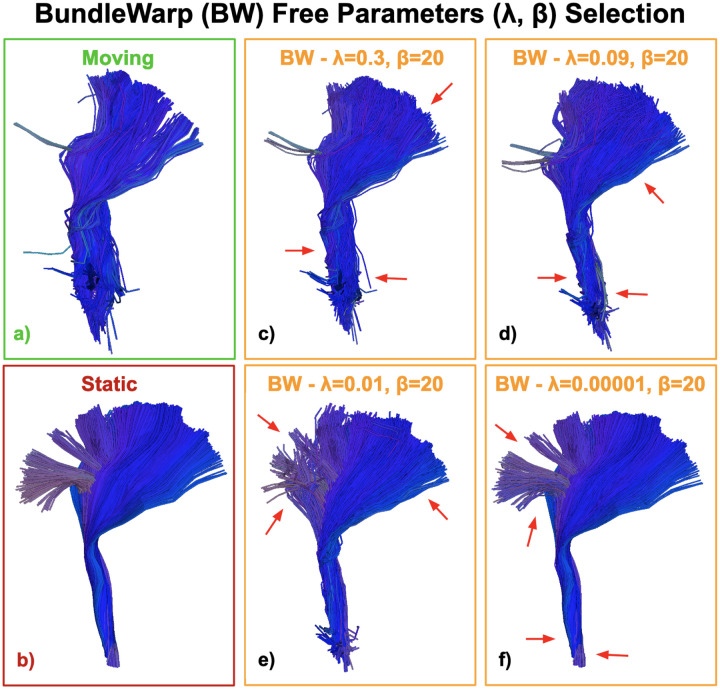
In Fig. 5, we explore different values of λ on Corticospinal tract in left hemisphere (CST L). Here, (a) is the moving bundle (to be registered) and (b) is the static (fixed) bundle. As we decrease the value of λ (c-f), we see the moving bundle is deformed more by the BundleWarp method and starts to look more like the static bundle. A lower value of λ will yield results such that the moving bundle will be completely deformed to look exactly like the static bundle, as seen in Fig: 5f. We kept the value of β to 20 for spatially smooth transformation.

Figure 5.

BundleWarp free parameter selection. Here, (a) is the moving bundle (to be registered) and (b) is the static (fixed) bundle. We show the warped bundle (output of BundleWarp) with different values of λ and β parameters. λ represents the trade-off between the goodness of maximum likelihood fit and regularization. A higher value of λ penalizes the velocity field more and the moving bundle is partially deformed (c-d). A smaller value of λ will force streamlines to fully deform and look exactly like the static bundle (e-f). As we decrease the value of λ (e-f), we see the moving bundle is deformed more and starts to look more like the static bundle.

2.6. Quantifying Bundle Shape Differences

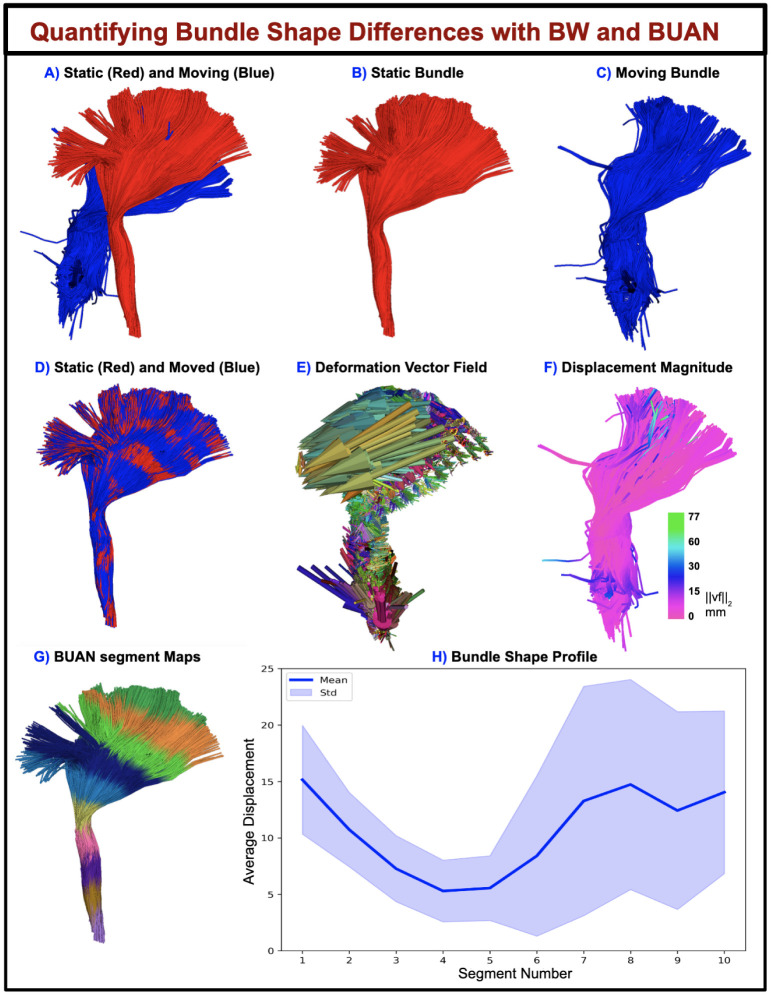
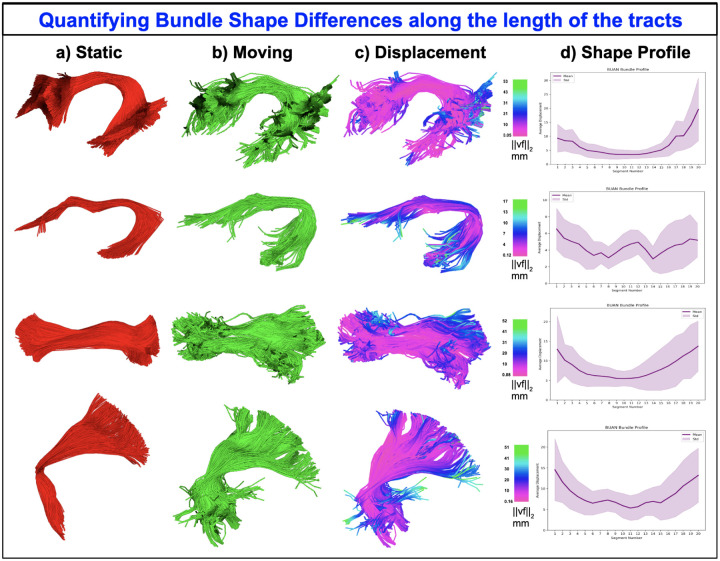
Apart from registering/aligning two bundles, the displacement vector field derived from fully deformable BundleWarp registration can be used to quantify bundle shape differences. We propose bundle shape differences analysis using the BundleWarp method when λ is set to a low value such as λ = 0.00001. The overview of the proposed approach is visualized in Fig. 6. In Fig. 6, static (red) and moving (blue) corticospinal tracts in the left hemisphere of the brain (CST L) are visualized before registration is applied to them (A). Static (B) and moving (C) bundles are visualized individually. Fully deformable BundleWarp registration is applied with λ = 0.00001 and β = 20. The output of the BundleWarp registration is shown in (D), where static (red) and moved (registered moving bundle) bundles are seen completely overlapping (showing perfect fully deformable registration).

Figure 6.

Quantifying bundle shape differences using the displacement field generated by BundleWarp (BW) and projecting it along the length of the bundle with BUAN. A) shows input static and moving bundles overlapped before registration. B) static bundle, C) moving bundle. D) shows static and moved (deformed) bundle overlapping after BW registration is applied. E) shows the deformation vector field generated by BW. F) displacement magnitude of the vector field has been visualized over the moved bundle. G) 10 segment maps created on moved bundle using BUAN. H) Mean displacement in mm is quantified along the length of the bundle with BUAN tractometry.

When the moving bundle is completely deformed (D), one can compute the displacement vector field vf as the difference between the streamline points on the affinely moved bundle (ap) and the corresponding points after deformation (dp): vf = dp − ap.

This vector field provides information about the quantity and the direction of the deformation applied to every streamline point and can be used to quantify shape differences between two bundles.

The displacement vector field (vf) of the fully deformed bundle is visualized in Fig. 6E. Here, Fig. 6F. shows the magnitude of the displacement field in mm projected on the deformed bundle. Here green color shows areas on the bundle that were deformed the most. Hence the areas with the most shape differences (as they required extreme deformations). We show a novel use of along the length quantification of bundle shape differences with displacement field using BUAN(Chandio et al., 2020) tractometry. Fig. 6G. shows ten segments created along the length of the deformed bundle. The displacement magnitude of all the points belonging to the i^th segment was averaged, and the bundle profile was created as shown in Fig. 6H. Here, the x-axis has the segment number along the length of the CST L bundle, and the y-axis has the average displacement in millimeters. We can visually (E and F) and analytically (H) quantify from the BundleWarp displacement field that static and moving bundles have the most shape differences at the extremities, specifically the fanning part of the CST L as those areas require more deformations for two bundles to match completely.

2.7. Quantitative Quality Assessment of the Registration

To quantitatively assess the performance of registration, we calculate two streamline-based metrics, bundle-based minimum distance (BMD)(Garyfallidis et al., 2015) and bundle shape similarity score (SM)(Garyfallidis et al., 2012; Chandio et al., 2020) between static and moved bundles. See Appendix 1. for mathematical definitions of these metrics. BMD tells us the distance between two bundles in millimeters; hence lower BMD means bundles are closely aligned. SM calculates the overall shape similarity of two bundles given they are in the same space(Chandio et al., 2020). SM ranges from 0–1, 0 when there is no similarity in two bundles, and 1 when they are identical. SM requires a threshold for how closely we want bundles to match. The threshold was set to 5mm, which requires bundles to be very similar in shape to get a higher SM value. We also use the volumetric dice similarity metric to evaluate the overlap between static and moved bundles. We create binary fiber density maps of static and moved bundles and use them to calculate volumetric dice similarity. Dice score ranges from 0–1, 0 when there is no overlap between two bundles, and 1 when they are identical/completely overlap.

3. Results

3.1. Influence of λ on BundleWarp registration

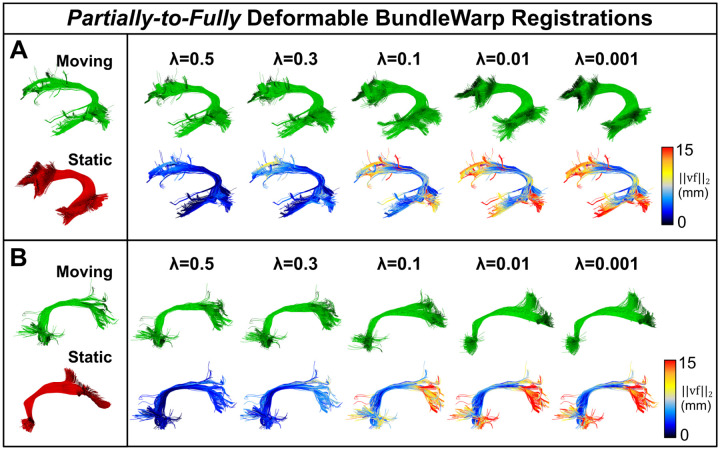
BundleWarp is capable of deforming bundles either partially or fully depending on the regularization parameter λ. BundleWarp provides users with a free regularization parameter λ that can be tuned to get the desired level of deformations in the registration. In Fig. 7, we explore different values of λ and show its effect on the BundleWarp registration output. The top panel in Fig. 7 shows static (red) and moving (green) arcuate fasciculus (AF L) bundles in the left hemisphere of the brain. The bottom panel in Fig. 7 shows static (red) and moving (green) arcuate fasciculus (AF R) bundles in the right hemisphere of the brain. In both panels, the output of the BundleWarp registration with varying values of λ is shown in the first row, and the second row visualizes the displacement magnitude in mm over the moving bundle. β was set to 20. Yellow-red colors on the bundle indicate a higher amount of displacement introduced in the deformation step of the BundleWarp registration. Note that we only visualize the displacement generated by the deformation step (after affine registration) of BundleWarp as each point on the streamlines get its warp map, unlike linear registration where the same affine map is applied to all the points and streamlines. As we move from the left (λ = 0.5) to the right (λ = 0.001), we observe that the moving bundle is deformed more to match the static bundle. λ in range of [0.3–0.5] partially deforms the moving bundle. These values of λ warp the moving bundle to better align with the static bundle (compared to linear registration) and preserve the bundle’s original shape. λ in range of [0.001–0.1] or λ < 0.001 fully deforms the moving bundle. These values of λ try to deform the moving bundle to completely overlap with the static bundle, and in achieving such registration, the moving bundle loses its original shape. From the second rows in both panels, we can see that the extremities of the AF L and AF R needed more deformations than the middle part of the bundles to match the static bundles.

Figure 7.

The effect of BundleWarp (BW) regularization free parameter λ on the registration. Arcuate fasciculus (green) in the left (top panel) and right (bottom panel) hemispheres of the brain are shown to be registered to a static bundle (red). Each panel shows BW registration output (first row in both panels) with varying values of the λ. As we move from left to right (higher value to a lower value of λ), more deformations are introduced in the registration. The second rows in both panels show displacement vector field magnitude visualized on the affinely aligned bundle. Here, yellow-to-red colors indicate areas on the bundles that were deformed the most. Areas that required higher deformations were the areas with the most shape differences in static and moving bundles.

3.2. Method Comparisons

We performed BundleWarp registrations on 1,728 pairs of bundles. We extracted 27 white matter tracts from whole-brain tractograms of 64 subjects (a total of 1,728 tracts were extracted, 27 different types of bundles, 64 bundles per type). We used 27 atlas bundles (model/template bundles) from the HCP-842 template (Yeh et al., 2018) atlas as static bundles, and extracted bundles from 64 subjects were considered moving bundles (bundles to be registered to static bundle’s space). Static bundles were always kept the same coming from the HCP-842 atlas. Moving bundles come from different subjects. The same type of extracted bundles were registered to the same type of atlas bundle. For example, each subject’s arcuate fasciculus bundle was registered to the atlas arcuate fasciculus bundle. Names of the 27 tracts are listed in bottom panel of Fig. 9, 10, and 11. For BundleWarp registration of all the bundles, we kept λ = 0.3 and β = 20. NOTE: We kept a higher value of regularization, which means we introduce fewer deformations and do not completely deform the moving bundle. For comparisons with other registration methods, we selected streamline-based linear registration (SLR) (Garyfallidis et al., 2015) and Advanced Normalization Tools (ANTs) (Avants et al., 2009) methods. SLR provides direct streamline-based affine registration of white matter tracts. ANTs provides nonlinear registration of images. We registered each subject’s FA image to FSL’s(Jenkinson et al., 2012) FMRIB58 FA template(https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FMRIB58_FA) using ANTs SyN registration using ANTspy(Avants et al., 2009; Tustison et al., 2021). The HCP-842 bundle template (Yeh et al., 2018) is in the same space as the FMRIB58 FA template. The generic affine and warp map produced by ANTs SyN registration of two FA images were used to apply transformations to that subject’s 27 bundles using scilpy(https://github.com/scilus/scilpy).

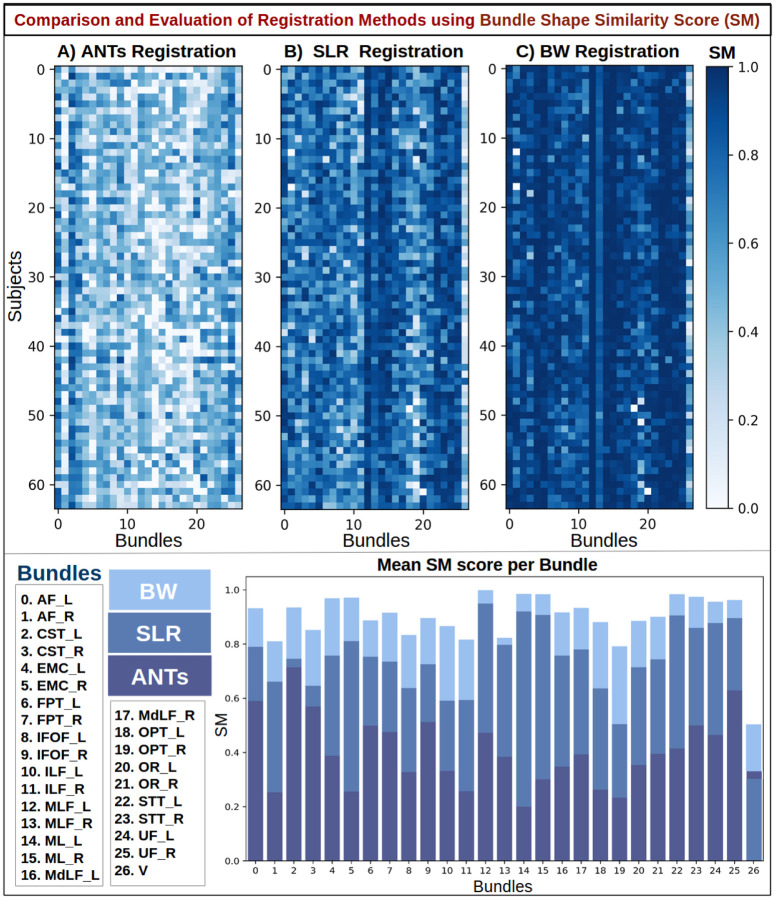
Figure 9.

Quantitative results using bundle shape similarity metric (SM) to compare Ants, SLR, and BundleWarp (BW) methods. The top panel shows three SM matrices for three registration methods. 27 bundles extracted from 64 subjects (1,728 total bundles) were registered to 27 atlas bundles of the same type. Here, rows represent subject and columns represent bundle type. Each pixel in the matrices indicates the SM score among the atlas bundle and registered bundle (static and moved). Darker blue means higher shape similarity, hence better registration performance. The bottom panel shows the mean SM score per bundle for each method and bundle names. BW method has the highest SM score for all bundles.

Figure 10.

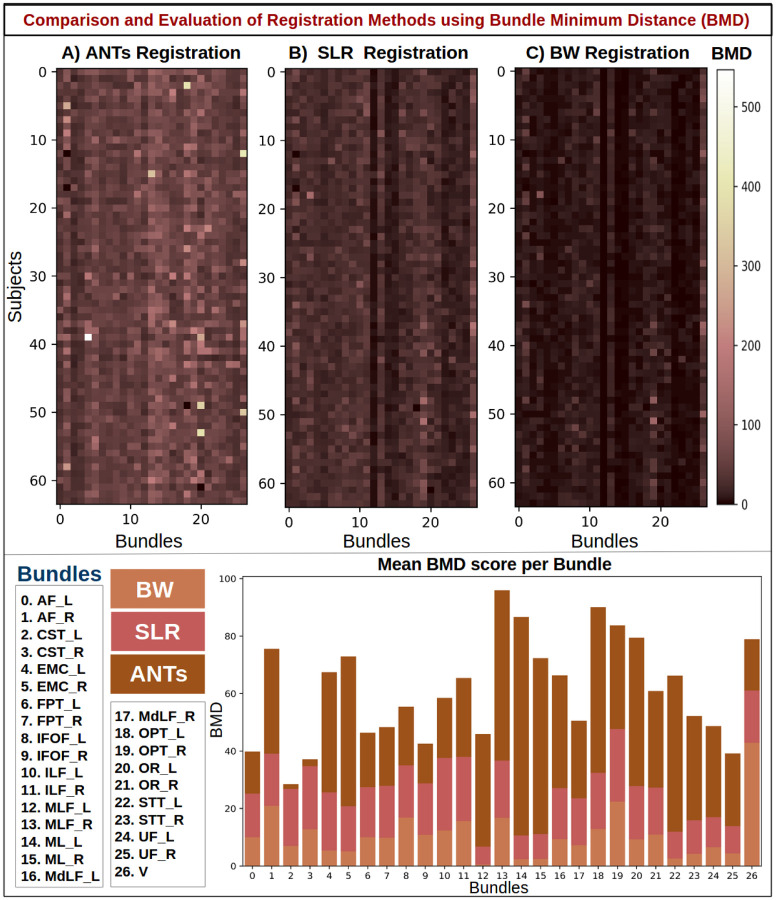
Quantitative results using bundle-based minimum distance (BMD) to compare Ants, SLR, and BundleWarp (BW) methods. The top panel shows three BMD matrices for three registration methods. 27 bundles extracted from 64 subjects (1,728 total bundles) were registered to 27 atlas bundles of the same type. Here, rows represent subject and columns represent bundle type. Each pixel in the matrices indicates BMD distance among the atlas bundle and registered bundle (static and moved). Darker brown means lower bundle distances, hence better registration performance. The bottom panel shows the mean BMD distance per bundle for each method and bundle names. BW method has the smallest BMD for all bundles.

Figure 11.

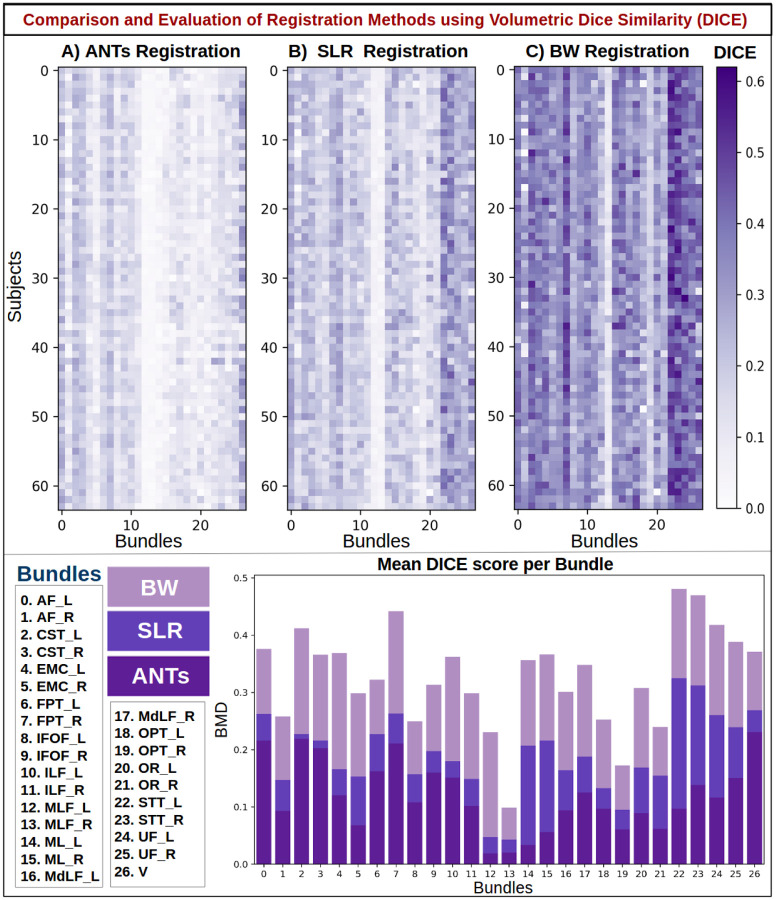
Quantitative results using volumetric dice similarity score (DICE) to compare Ants, SLR, and BundleWarp (BW) methods. The top panel shows three DICE matrices for three registration methods. 27 bundles extracted from 64 subjects (1,728 total bundles) were registered to 27 atlas bundles of the same type. Density maps of atlas bundles and registered bundles were created and used for calculating the volumetric DICE score. Here, rows represent subject and columns represent bundle type. Each pixel in the matrices indicates the DICE score among the atlas bundle and registered bundle (static and moved). Darker purple means a higher DICE score, hence better registration performance. The bottom panel shows the mean DICE score per bundle for each method and bundle names. BW method has the highest DICE for all bundles.

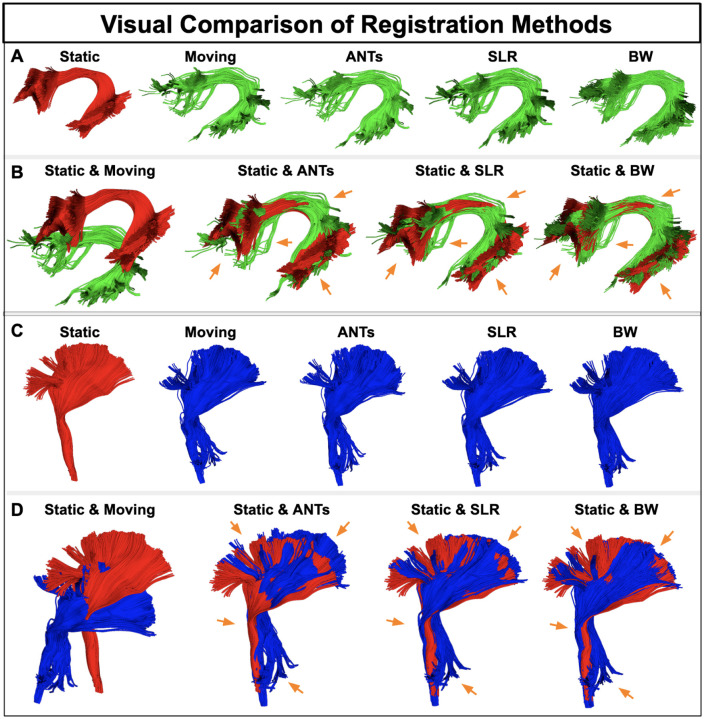
This section presents qualitative and quantitative comparisons of three registration methods: BundleWarp (BW), SLR, and ANTs. Fig. 8 shows qualitative/visual results and comparisons of the three methods. Here, we show visual results on the arcuate fasciculus (AF L) and corticospinal tract (CST L) in the brain’s left hemisphere selected randomly from one subject. In Fig. 8, In panels, A and C, static and moving bundles are visualized, followed by registered bundles by ANTs, SLR, and BW methods. In B and D panels, the overlap of the static bundle with the moving bundle and the registration output of the three methods is visualized.

Figure 8.

Visual comparison of BundleWarp (BW) with streamline-based linear registration method SLR, and image-based nonlinear registration method ANTs. (A and C) static, moving, ANTs output, SLR output, and BW output. (B and D) the static bundle is visualized with moving, ANTs output, SLR output, and BW output bundles. Orange arrows point at areas that are most affected by registration. BW produces the best registration results. λ was set to 0.3 in the BW method.

Panel A shows results on AF L bundle, whereas panel B shows results on CST L bundle. Here, orange arrows point toward the areas that are improved by registration methods. We can see that BW yields the best registration results for both bundles. We find that streamline-based direct registration of white matter tracts (even just a linear registration such as SLR) performs better than image-based transformations applied to streamlines. This result is also reported in the SLR paper (Garyfallidis et al., 2015). This is anticipated as direct streamline registration is more specific to streamline structure and shape.

For quantitative results, we used two streamline-based metrics, bundle shape similarity metric (SM) and bundle-based minimum distance (BMD). We also used the volumetric dice similarity metric (DICE) to compare the overlap of fiber density images of tracts. Fig. 9, Fig. 10, and Fig. 11 present quantitative comparison of methods SM, BMD and DICE. The top panels in all three figures show three matrices of the respective metric for three registration methods, ANTs, SLR, and BW. 27 bundles extracted from 64 subjects (1,728 total bundles) were registered to 27 atlas bundles of the same type. Three metrics were calculated between static and moved (registered) bundles. Here, rows represent subjects, and columns represent bundle types. Each pixel in the matrices indicates the respective metric’s score among the atlas bundle and registered bundle (static and moved).

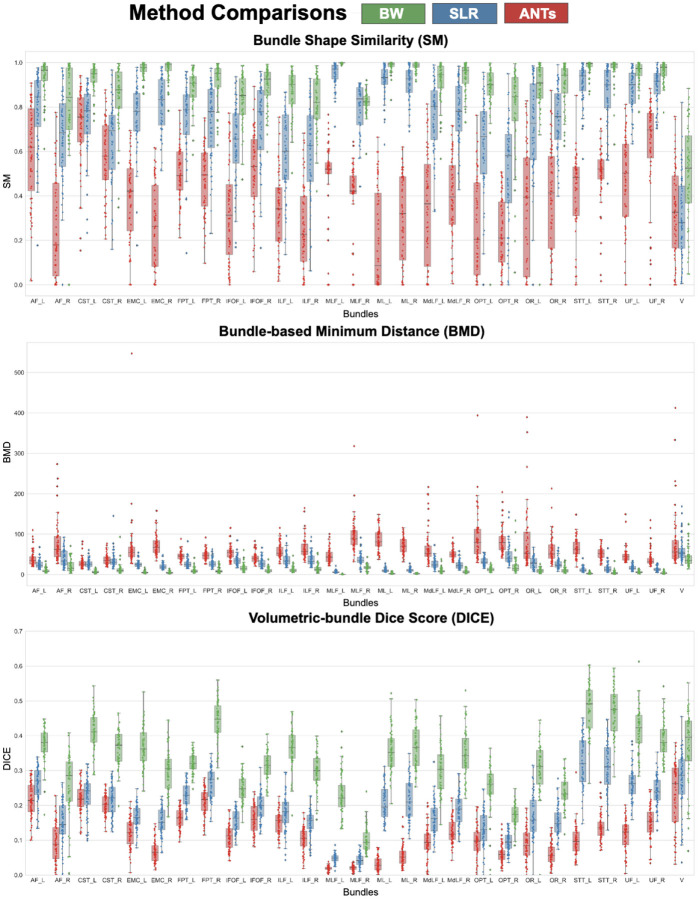
In Fig. 9, results are presented for the SM metric, which is a bounded metric and ranges between 0 and 1. Darker blue (closer to 1) means higher shape similarity, implying better registration performance. Conversely, white or light blue color implies a lower value of SM and lower shape similarity between bundles. The bottom panel shows the mean SM score per bundle for each method. Twenty-seven bundle names are listed on the left of the bottom panel. BW method has the highest SM score for all bundles. SLR performs second best for all bundles except for Verma (V) bundle, while ANTs registration has the lowest bundle shape similarity.

In Fig. 10, results are presented for the BMD metric, which represents the distance between two bundles. Lower distance indicates two bundles are closely aligned, and higher distance means two bundles are far from each other. In the BMD matrices, darker brown color signifies lower distance, hence better registration performance. In contrast, lighter brown color signifies a higher BMD distance between bundles. The bottom panel shows the mean BMD score per bundle for each method. BW method has the lowest BMD score for all bundles (which is desirable). SLR performs second best for all bundles and has the second lowest BMD score. ANTs registration has the highest BMD score implying comparatively suboptimal alignment of bundles.

In Fig. 11, results are presented for the DICE metric, which is a bounded metric and ranges between 0 and 1. Darker purple color (closer to 1) means a higher DICE score, hence better registration performance. White or light purple color implies a lower value of DICE and lower volumetric overlap between static and moved bundles. The bottom panel shows the mean DICE score per bundle for each method. BW method has the highest DICE score for all bundles. SLR performs second best. ANTs registration has the lowest dice similarity.

Fig. 12 presents boxplots summarizing the quantitative comparisons of ANTs (red), SLR (blue), and BW (green) methods using SM, BMD, and DICE metrics. Three panels (a,b,c) show boxplots of three metrics, respectively. The results of each metric type and populated matrices per method are described above and visualized in Fig. 9, 10, and 11. Each panel has boxplots for a metric (y-axis) for 27 bundles (x-axis). Fig. 12a, shows SM results. BW has the highest SM score. Fig. 12b, shows BMD results. BW has the lowest BMD score (desirable). Fig. 12c, shows DICE results. BW has the highest DICE score.

Figure 12.

Quantitative comparisons of ANTs (red), SLR (blue), and BundleWarp (BW) (green) methods using Shape Similarity Score (SM), Bundle-based Minimum Distance (BMD), and DICE coefficient metrics. Three panels (a,b,c) show boxplots of three metrics respectively. These metrics were calculated for 64 subjects’ 27 bundles registered to 27 atlas bundles of the same type (total of 1,728 bundles, 64 of each type) to evaluate the registration. Each panel has grouped boxplots for a metric (y-axis) for 27 bundles (x-axis). a) Shows SM results (the higher the better). BW has the highest SM score . b) Shows BMD results(the lower the better). BW has the lowest BMD score . c) Shows DICE results (the higher the better). BW has the highest DICE score.

We show with qualitative and quantitative methods that BundleWarp outperforms every other method in comparison. While SLR performed second best, and ANTs registration was placed at the end. Although SLR is a linear registration method, it still performs better than ANTs nonlinear registration. However, BundleWarp and SLR are direct streamline registration methods. While we applied ANTs SyN registration to FA images, the resulting affine and warp maps were used to transform streamlines. Direct streamline registration methods consider streamline geometry and shape, while image-based registration cannot incorporate streamline shape, size, and geometry into its method. We show that direct streamline registration is beneficial and outperforms image-based registration for streamlines.

Note that we kept the regularization term relatively high λ = 0.3. This means we introduced minimal deformations in the BundleWarp registration or, as we call it, partially deformed. If we set λ to a low value such as λ = 0.00001, BundleWarp would completely deform the moving bundle to look like the static bundle. See Fig. 5 for impact of λ on the registration. If we fully deform the bundle, we would get a perfect SM and DICE scores of 1 and 0 BMD between the static and moved bundle. However, this is not advised and would completely change the shape and anatomy of the original bundles. Staying close to the original anatomy helps with statistical correspondence across the length of the bundles.

3.3. Bundle Shape Difference Analysis

We performed bundle shape difference analysis using displacement field generated by fully deformable BundleWarp. We visualize displacement magnitude on the moving bundle and analytically quantify bundle shape differences along the length of the tract using BUAN tractometry. This is an example of individual-level analysis. Fig. 13 shows bundle shape analysis of one of the subjects selected randomly. Four rows for four bundles, AF L, UF L, ILF L, and OPT L, respectively. Each column shows (a) static and (b) moving bundles. Fully deformable BundleWarp registration is applied (λ < 0.001), and the generated displacement field’s magnitude is visualized over the moving bundle that has been affinely registered to the static bundle (c). The blue-green color represents the higher displacement of those streamlines/areas. Bundle shape differences profile is created using BUAN (d). Each row (bundle) has a different min and max displacement magnitude/y-axis (c-d) values. We can see that in most cases, the extremities of the bundles require higher displacement (deformations) to match the static bundle implying higher shape differences in those areas of the bundles.

Figure 13.

Quantifying bundle shape differences along the length of the tracts using displacement fields generated by BundleWarp. Four rows for four bundles, AF L, UF L, ILF L, and OPT L respectively. Each column shows (a) static, and (b) moving bundles. Fully deformable BundleWarp registration is applied and the generated displacement field’s magnitude is visualized on the moving bundle (c). Bundle shape differences profile is created using BUAN (d).

4. Discussion

Nonlinear registration of any data, in general, is a non-trivial task. When dealing with medical data, a question arises, what is a perfect registration? From a mathematical point of view, a perfect registration should fully map moving data to be completely overlapped and look precisely like static/reference data. However, from a medical point of view, a perfect registration would be such that it aligns moving data to be in the same space as the static, and the overlap between them is higher than before. At the same time, moving data should not lose their original anatomical shape and characteristics. And from technical point of view, a desired method should not be memory or computation heavy. Most registration methods aim at completely deforming input data to look precisely like static/template data. For example, in the case of image registration, structure and intensity values are often changed in moving images to match that of the static/fixed image. Neuroimaging data are widely used to understand the disease and find significant group differences between patient data and healthy controls. Most group analysis pipelines rely on nonlinear registration to align data and find differences among the corresponding areas. This could generate artifacts and/or remove the actual effects of the disease from the data(Rohlfing, 2006; Tsang et al., 2010) if registration completely changes the moving data to match the static data.

White matter bundles extracted from whole-brain tractograms of patient and control groups are analyzed using tractometry pipelines to find significant group differences along the length of the tracts. Like image-based group analysis methods, tractometry methods rely on linear or nonlinear registration of white matter tracts or tractograms. Due to the lack of nonlinear streamline-based methods, most tractometry pipelines rely on image-based registration(Yeatman et al., 2012; Yendiki et al., 2011; Cousineau et al., 2017; Dayan et al., 2015; Colby et al., 2012). While some tractometry pipelines (Chandio et al., 2020; Chandio, 2022) have also utilized streamline-based linear registration. Hence, there is a need for a nonlinear streamline-based registration method. However, nonlinear registration of tractograms/tracts needs careful evaluation. For example, if we fully deform a moving bundle to look exactly like a static bundle, we lose all the anatomical information specific to that subject. Moreover, if registration is sub-optimal and it does not deform properly, it could make streamlines of the moving bundle spurious and introduce unnecessary artifacts.

We introduced a novel and robust method for partially-to-fully deformable registration of white matter tracts in the streamline-space. We created a method keeping in mind how important it is to preserve the anatomical structure of the tracts during nonlinear registration. By default, BundleWarp partially deforms the moving bundle and preserves anatomical characteristics of the bundle. However, we provide a free regularization parameter λ that can control the level of deformations needed in the registration. λ decides the trade-off between regularizing the deformations and moving the bundle to match exactly like the static bundle. Using BundleWarp, a user can partially deform the bundle by setting a higher value of λ such as in the range of [0.2–1] or they can fully deform the moving bundle by setting a low value of λ such as in the range of [0.1–0.00001]. There is another regularization parameter for smoothing, β. β determines the width of the Gaussian kernel. β decides the neighborhood of points on the streamline to consider when applying the topological constraint. Points closer to each other on the streamline will be moved as a group to preserve the topological structure of the tracts. For most of the bundles with an average length greater than 50 mm, β = 20 is sufficient and generates smooth transformations. For smaller bundles such as the Cingulum bundle with an average length of less than 50 mm, β = 10 yields the best results. To the best of our knowledge, BundleWarp is the only streamline-specific method for white matter tract registration that provides this capability. BundleWarp is fast converges within 15 iterations of mlCPDs. For a typical size of a bundle with streamline count in the range of [200–4000], BundleWarp execution time would be less than a minute or at most a minute. See Appendix A.2 for detailed discussion on BundleWarp execution time depending on static and moving bundle sizes. BundleWarp returns the deformations and a pairwise MDF distance matrix with MDF distances among all the streamlines of static and moving bundles. It also returns many-to-one streamline correspondences among moving and static bundles. Pairwise distances and streamline correspondence can be further utilized in other methods such as clustering and streamline filtering (Chandio et al., 2021).

4.1. Advantages

Direct nonlinear alignment of the tracts in the streamline space has the main advantage of taking into account the topological connectivity of streamlines as opposed to voxel or volumetric based representation of white matter tracts. Voxel-based representation and registration of tracts do not provide adequate precision because the tract size and shape vary considerably among subjects (Wassermann et al., 2011). Therefore, it cannot ensure that a given voxel corresponds to the same tract across different subjects. For this reason, voxel/image based registration methods when applied to streamlines, would not be able to accurately align tracts(Garyfallidis et al., 2015).

In our experiments, we compare BundleWarp with image-based nonlinear registration, Advanced Normalization Tools, ANTs SyN(Avants et al., 2009), and streamline-based linear registration, SLR(Garyfallidis et al., 2015). We show qualitatively and quantitatively that BundleWarp outperforms linear and nonlinear methods for the registration of white matter tracts. Even the linear streamline-based method SLR performs better than nonlinear ANTs normalization applied to streamlines. These outcomes are expected as ANTs registration is image-based and cannot take into account the geometrical shape and structure of individual streamlines. A single streamline travels through many voxels and integrates information across long regions. Hence, applying image-based affine and warp maps to streamlines results in sub-optimal alignment of the tracts. Whereas BundleWarp takes into account the streamlines’ topological connectivity and shape differences by constraining the optimization solution and making the algorithm more robust to outliers. In our experiments, we show that partially deformable BundleWarp registration with λ = 0.03. Fig. 4d shows a smooth deformation vector field over an affinely moved Cingulum bundle. It shows that deformations added by BundleWarp after linear registration are coherent and smooth, as we can see in the structure of the Cingulum bundle in the vector field.

4.2. Preserving Anatomical Structure

Every subject is different and has unique white matter structural fingerprints. Most white matter bundles have a known shape, structure, function, and location in the brain that defines them. However, the same type of bundle can still have different shapes and sizes for different subjects. Deforming the original anatomical shape of the bundle is not necessarily ideal as it can lose the characteristics needed in the analysis. For example, a patient with brain injury, a tumor, or atrophies in the brain due to a neurodegenerative disease will have some pathways missing from the affected areas in the brain. Deforming the shape of the bundle too much, in these cases, can remove the disease/pathology effects, which are crucial to individual or group level analysis. If every subject’s bundles start to look the same, we will lose the disease effects when dealing with groups of patients and healthy controls. Hence, it is of utmost importance to preserve most of the original anatomical structure of bundles in the registration process. BundleWarp preserves the core characteristics of the bundles as shown in Fig. 4.

4.3. Recommended Parameter Values

BundleWarp is a powerful method that can fully deform the moving bundle to look exactly like the static bundle. However, it should not be used for completely deforming the bundle. By default, BundleWarp will only partially deforms the moving bundle to align better with the static bundle. We recommend λ = 0.3 (or higher) and 0.3 is the default value of λ in the BundleWarp method. Since λ is not scale-dependent (scale of bundles) and controls the fluidity of the data points, we kept it the same for all bundles regardless of their shapes and sizes. In case a user sets λ to the value such as λ < 0.2, a warning will be displayed on the console explaining and making the user aware of the effects of setting a lower value of λ on the data. We have kept the default value of β depending on the average length of the bundle. β = 10 when bundle length < 50 mm and β = 20 for bundles with length > 50 mm. BundleWarp converges within 15 iterations, and the default number of maximum iterations is set to 15 as well.

In machine learning approaches, the regularization term λ is often selected using a cross-validation approach to find an optimal value of λ. For example, the Mean Squared Error (MSE) is minimized in the cross-validation method, and the λ with minimal MSE is selected. We could use MSE or replace it with a shape similarity score or bundle-based distance metric for selecting an optimal λ value in BundleWarp registration. However, as discussed earlier in the manuscript, defining an optimal registration output is non-trivial. Similarly, it is hard to define the optimal value of the cost function that is being minimized by the cross-validation method. For example, an optimal shape similarity score would be 1, or an optimal BMD would be 0 for λ to be selected. However, that would completely change the shape of the bundles in the registration, which is undesirable. Hence, we empirically found λ in the range of [0.3–0.5] to generate optimal and desirable registration output. All comparison results used λ = 0.3.

4.4. Applications of BundleWarp

BundleWarp can be added in several other tractography-based methods, such as bundle segmentation, bundle atlasing, and tractometry. In this paper, we proposed a novel use of the displacement vector field generated by fully deformable BundleWarp registration for quantifying bundle shape differences. The method is tested here with human brain data, but in theory, it is not specific to a species. Therefore, this is applicable to all types of other animal brains. Furthermore, the method only requires input streamlines; therefore, it could find use in other fields of science that use similar data structures (e.g., odometry, fluid dynamics, etc.).

4.4.1. Bundle Shape Analysis

We propose a novel approach for quantifying bundle shape differences using fully deformable BundleWarp registration. We project and examine the displacement field magnitudes as they change along the length of the tracts using BUAN tractometry. We show an example of how the deformation field can be used to learn bundle shape differences. This is an exceptional application where we do recommend fully deforming the moving bundle by using λ < 0.001 for accurately quantifying bundle shape differences. When the moving bundle is completely deformed to look exactly like the static bundle, the deformation field can be visualized to show how much the points on streamlines were moved/deformed to match the static bundle, as explained and shown in Fig. 6 and Fig. 13.

However, the displacement field has been used before to quantify bundle shape differences. For example, the authors of the paper(Glozman et al., 2018) used a seed point matching strategy to establish correspondences between bundle regions to perform registration and compute shape differences. In contrast, BundleWarp uses a streamline-matching, and deformations are added, taking into account the entire streamline/bundle. Furthermore, we add an additional step in which local deformations are averaged along the length of the bundle. In this paper, we only analyzed bundle shape differences at individual subject-level. This idea will be further explored and tested on larger populations to find bundle shape differences among them, such as in longitudinal and aging studies.

4.4.2. Bundle Segmentation

BundleWarp can be integrated into the RecoBundles (RB)(Garyfallidis et al., 2017) method for improved bundle segmentation. RB requires an input tractogram and a set of model bundles. By default, RecoBundles uses SLR registration to align model bundles with the input tractogram. We can add an option to include partially deformable BundleWarp registration to find better corresponding model bundle streamlines in the input tractogram. BundleWarp could also be used in other deep learning-based bundle segmentation methods(Wasserthal et al., 2018; Gupta et al., 2018; Xue et al., 2022). Where bundles are extracted by experts first creating a training dataset. Bundles from the training dataset can be nonlinearly aligned using BundleWarp so that they are in the same space. This could help achieve better model accuracy. However, this needs to be tested, and we will explore this direction in our future work.

4.4.3. Tractometry

BundleWarp can be incorporated into our BUAN tractometry(Chandio et al., 2020) pipeline. BUAN extracts bundles from populations and analyzes the microstructural measures (e.g., FA) projected onto the bundles along the length of the tracts to find significant group differences. BUAN creates horizontal segments along the length of the tracts to be analyzed. Horizontal segments are created based on points on the streamlines belonging to the closest model bundle centroid point. Here, a partially deformable BundleWarp can be added to nonlinearly align subjects’ bundles with model bundles to find better segment correspondences among populations. BundleWarp could also be utilized similarly in other tractometry pipelines(Yeatman et al., 2012; Yendiki et al., 2011).

4.4.4. Bundle Atlasing

BundleAtlasing(Romero-Bascones et al., 2022) is a recently proposed method for building population-and-bundlespecific streamline atlases. It relies on two main steps: unbiased registration and bundle combination (Romero-Bascones et al., 2022). The registration step is currently performed by SLR and would benefit from adding a partially deformable BundleWarp as a nonlinear registration step. In this way, bundles would be matched more accurately, and obtained atlases could better represent the underlying anatomy of the group under study.

4.5. Limitations and Future Work

BundleWarp is designed for nonlinear registration of individual white matter tracts and has small execution time. Theoretically, it could be applied to whole brain tractograms as well but the execution time will increase drastically as it calculates pairwise MDF distances to find streamline correspondences. Future work will explore recently proposed methods for fast streamline distance calculation(St-Onge et al., 2021; Wang, 2022). We will also explore clustering whole-brain tractogram first and aligning individual clusters(Olivetti et al., 2020) with BundleWarp for whole-brain tractogram registration. Where each cluster can be independently registered in parallel, reducing the time and memory complexity of the problem. However, in this work we focused on specific bundles which we think is of higher interest due to the increased interest in tractometric studies(Yeatman et al., 2012; Chandio et al., 2020; Cousineau et al., 2017; Yendiki et al., 2011).

5. Conclusion

BundleWarp, is an efficient and robust streamline-based nonlinear registration method for white matter tracts. It provides warping fields that preserve the crucial anatomical structures of streamlines/bundles. In addition, BundleWarp has the capability to either partially or fully deform bundles by tuning a single regularization parameter depending on the desired output. We show qualitatively and quantitatively that Bundlewarp outperforms other streamline-based and image-based registration methods for white matter tracts. We also show that bundle shape differences can be visually and analytically quantified using the displacement field generated by the BundleWarp method along the length of the tracts using BUAN tractometry. Therefore, BundleWarp can facilitate a series of processing steps such as bundle segmentation, bundle-specific atlas creation, bundle shape analysis, and overall improve the performance of tractometry studies.

Code and Data availability

Code and tutorials for BundleWarp are publicly available in GitHub and can be found here https://github.com/BramshQamar/BundleWarp. BundleWarp will also be made publicly available through DIPY(Garyfallidiset al., 2014) at dipy.org. Data(Chandio, 2020) used in the experiments can be found here https://doi.org/10.35092/yhjc.12033390.v1.