Abstract
Spinning thermal radiation is a unique phenomenon observed in condensed astronomical objects, including the Wolf-Rayet star EZ-CMa and the red degenerate star G99-47, due to the existence of strong magnetic fields. Here, by designing symmetry-broken metasurfaces, we demonstrate that spinning thermal radiation with a nonvanishing optical helicity can be realized even without applying a magnetic field. We design nonvanishing optical helicity by engineering a dispersionless band that emits omnidirectional spinning thermal radiation, where our design reaches 39% of the fundamental limit. Our results firmly suggest that metasurfaces can impart spin coherence in the incoherent radiation excited by thermal fluctuations. The symmetry-based design strategy also provides a general pathway for controlling thermal radiation in its temporal and spin coherence.
Thermal radiation with unique photon spin textures is observed in symmetry-broken metasurfaces.
INTRODUCTION
Thermal radiation describes the universal phenomenon that all objects at nonzero temperatures emit infrared electromagnetic energy (1–3). Notable research progress has been made so far in tailoring its temporal coherence, i.e., spectrum (4–6), and the spatial coherence, i.e., directivity (7–9). However, the photon spin, another crucial characteristic of electromagnetic radiation, is commonly ignored, since most thermal emitters show weak to zero spin angular momentum (SAM) in the emitted waves. Unexpectedly, the thermal radiation reaching the earth from many astronomical objects has substantial circular polarization. The unique phenomenon provides strong evidence for the presence of a magnetic field around stars (10–12) or reveals the existence of chiral organic molecules (13). Recent studies also show that circular polarization can be a possible sign of life (14). Therefore, revealing photon spin characteristics in thermal radiation is of fundamental interest as it contains unique information regarding the emitters.
In analogy with celestial observations, it has recently come to light that the application of an external magnetic field or intrinsic nonreciprocity in generic bianisotropic media also leads to circularly polarized thermal emission characteristics. This is true for magneto-optical materials (15), topological Weyl semimetals (16, 17), and topological insulators (18, 19). This phenomenon of spinning thermal radiation is yet to be observed because of material constraints and the requirement of magnetic fields. When time-reversal symmetry is preserved such as in hyperbolic materials (20), the circularly polarized thermal radiation is predicted at specific angles (20), but the overall purity is very small (19). Also, in the hyperbolic case, the thermo-optic helicity, which is the summation of the projected SAM over the far-field hemisphere, is always zero/near zero. We note that recent studies have experimentally demonstrated spinning thermal radiation using mechanisms such as the optical Rashba effect (21) and integrated waveplate (22). However, the spinning thermal radiation is limited to the surface-normal direction with integrated waveplate (22). In the optical Rashba effect, the spinning thermal radiation is only generated in oblique directions away from the surface normal (21). The mirror symmetry guarantees that the left-handed circular-polarized heat radiation (LCP) and right-handed circular-polarized heat radiation (RCP) appear in pairs, which causes the net optical helicity to be zero.
Here, we show that photon spin introduces an additional degree of freedom for tailoring thermal radiation (Fig. 1, A to D). Although spectrally and angularly tailored thermal radiative sources based on plasmon/phonon polaritons (23–25), bound states in the continuum (26), epsilon-near-zero resonances (27), hyperbolic materials (28, 29), photonic crystals (30), and quantum wells (31) have received extensive attention, an omnidirectional circularly polarized light source is still not accessible, especially in the mid-infrared region. Our thermal metasurface approach is compact so large benchtop light sources and bulky optical components (waveplates and polarizers) are not required.
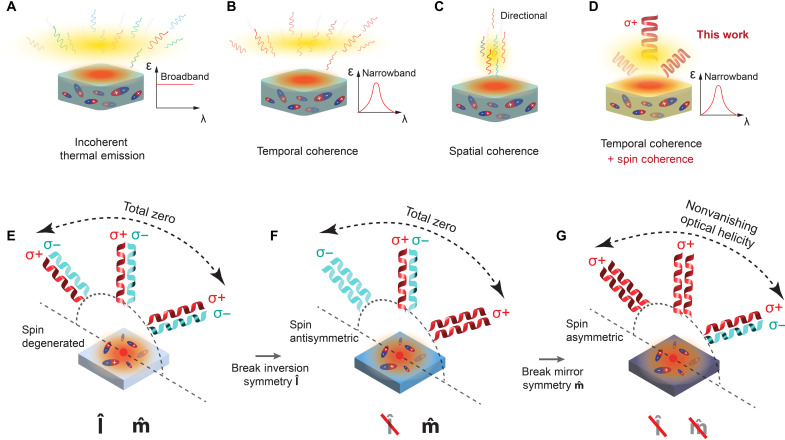
Fig. 1. Symmetry-based optical spin control of thermal radiation.
(A) Thermal radiation originates from fluctuating dipoles and is thus considered an incoherent signal. It is naturally broadband and omnidirectional and carries no SAM. (B and C) Recent research efforts aim to impart temporal (B) and spatial (C) coherence in thermal radiation, where narrow-band and directional thermal radiation are demonstrated. (D) In this work, by imparting spin coherence, we achieve effective tailoring of thermal emission in its spectral and spin properties. (E) Schematic demonstrates that the photon spin characteristics are governed by the symmetries in the 2D system. When both inversion (î) and mirror () symmetries are preserved, the photon spin of thermally radiated photons is degenerate in energy-momentum space. Thus, the spin and helicity both vanish. (F) When inversion symmetry is broken, spinning thermal radiation arises at oblique angles. However, the antisymmetric spin pattern guarantees the spin degeneracy at surface normal and a total-zero optical helicity. (G) In this work, we show that photon spin arises in an asymmetric pattern when both inversion and mirror symmetries are broken, and the nonvanishing optical helicity is observed.
We note that extensive efforts have been made so far to generate spin-selective absorption from microwave to visible frequencies (32–42). Our work provides a direct experimental demonstration proving that spin selectivity can be realized in the radiation excited by incoherent thermal fluctuations. In addition, the efforts on spin selectivity are mainly limited to the surface-normal direction. In contrast, the nonvanishing optical helicity demonstrated here extends the effort to control the angular distribution of photon spin with symmetry-based designs. Although recent numerical studies have proposed omnidirectional spin-selective absorption (42), the experimental realization is obstructed because of the complicated three-dimensional (3D) architecture. Our 2D planar design is compatible with the well-established nano/microfabrication techniques, making it practical for future energy applications.
Our nonmagnetic approach is summarized in Fig. 1 (E to G). For conventional materials when both inversion and mirror symmetries are preserved, photon spin of thermal photons is degenerate in energy and momentum space, and zero circularly polarized heat radiation is generated (Fig. 1E). Breaking inversion symmetry can lead to spin characteristics in oblique directions away from the surface normal, as shown in the extrinsic chirality (43, 44) and the optical Rashba effect (21). However, the antisymmetric spin pattern causes the net helicity to vanish once again (Fig. 1F). To overcome these limitations, in this work, we show that the simultaneous breaking of mirror symmetry and inversion symmetry releases all the constraints. We obtain an asymmetric spin pattern and nonvanishing optical helicity in the radiation excited by thermal fluctuations (Fig. 1G). We point out that nonvanishing optical helicity only requires the breaking of mirror symmetry. The simultaneous breaking of mirror and inversion symmetries is required to obtain an asymmetric pattern of spinning thermal radiation. The complete symmetry breaking in our design also provides freedom to introduce symmetries. We demonstrate three examples of symmetry-based thermal engineering with mirror, inversion, and fourfold rotational (C4) symmetries and show that incoherent thermal fluctuations can be substantially altered by these symmetries. With this symmetry-based approach, we also suggest a general and effective pathway to engineering the spectral and spin characteristics of thermal radiation.
RESULTS
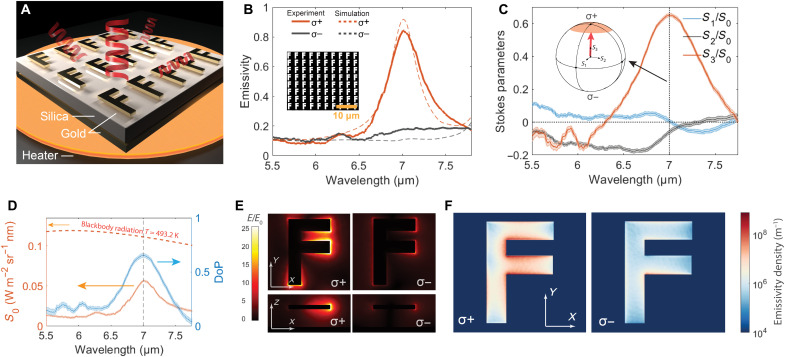
To generate nonvanishing optical helicity, we start by designing a symmetry-broken metasurface that lifts spin degeneracy. A schematic of the metasurface is shown in Fig. 2A, where a rectangular array of F-shape meta-atoms is patterned on a silicon dioxide (SiO2) dielectric layer with a gold (Au) backplane. Our “F” meta-atoms are designed to break both inversion and mirror symmetry in this quasi-2D system. Our designed structure also provides a large parameter space for optimizing the spectrum and energy-momentum-spin band structure of the thermal emission. As shown in Fig. 2B, the measured emissivity of LCP is more than four times larger than the emissivity of RCP at the surface-normal direction. In Fig. 2C, we show a complete characterization of the polarization state of thermal radiation based on Stokes parameters, where S3/S0 indicates the purity of the circular polarization. S3/S0 is equivalent to the widely adopted metric “degree of circular polarization (DoCP),” which is expressed as (σ+ − σ−)/(σ+ + σ−), and σ+ and σ− are the emissivities of LCP and RCP, respectively. We represent the radiation state emanating from incoherent thermal fluctuations in the metasurface by a circular area that is centered close to the north pole of the Poincaré sphere (inset of Fig. 2C). We emphasize that the near-zero S1 and S2 at 7 μm indicate that the relatively limited DoCP is actually from the limited coherence of the thermal emission signal. In Fig. 2D, we plot S0 and the degree of polarization (DoP) to demonstrate the total intensity and the polarization purity of the thermal radiation from our metasurface.
Fig. 2. Spinning thermal radiation and microscopic mechanisms.
(A) Schematic of the designed metasurface with F-shape meta-atoms, where both the inversion and mirror symmetries are broken in the pseudo-2D system. (B) The measured LCP (σ+) and RCP (σ−) emissivity (solid) of the fabricated devices. They show good agreement with the simulation results (dashed). Inset: Scanning electron microscopy imaging of the fabricated device. Scale bar, 10 μm. The results directly demonstrate that spin degeneracy is removed, and the symmetry-broken metasurface imparts spin coherence in the incoherent thermal fluctuations. (C) Stokes parameters show the full polarization state (shaded areas represent the SD values of the measurements). The fabricated device presents a high S3 peak at 7 μm, while the S1 and S2 are close to zero. Inset: Representation of the polarization state in the Poincaré sphere. (D) S0 and DoP demonstrate the total intensity and the polarization purity of the thermal radiation signal (shaded areas represent the SD values of the measurements). S0 is compared with the blackbody radiation spectrum (dashed) at the measurement temperature (492.3 K). (E) The time-averaged electric field strength (normalized by the field E0 of incident waves) at 7 μm under LCP (left) and RCP (right) excitations. The fields are plotted along the XY (top) and XZ (bottom) planes, respectively. (F) Local emissivity density of LCP (left) and RCP radiation (right) in the meta-atom. Evident enhancement is observed for LCP radiation. (F) indicates that the spinning thermal radiation arises from the intrinsic local chirality of the metasurface.
To show the microscopic mechanisms of the circular polarization and nonvanishing optical helicity, we investigate the near-field electromagnetic response of the metasurface. The major mechanisms of spin degeneracy removal in photonic systems can be divided into two categories. On the one hand, the Pancharatnam-Berry phase generated by a geometric gradient can lead to spin-dependent photon behaviors (45–48). On the other hand, the phenomenon can also originate from the intrinsic local chirality in the meta-atoms (49–51). We reveal that the strong intrinsic local chirality of our F-shape plasmonic meta-atoms is the origin of the observed circular-polarized thermal radiation in the far field. To show this, we simulate the electric field strength at 7 μm under LCP and RCP excitations (Fig. 2E). We calculate the local absorption cross-sectional density , where ε(r′, ω) is the permittivity at point r′and frequency ω, E(l)(r′, ω) is the (l)-polarized local electric field, and is the incident plane wave. According to the local Kirchhoff law (52), the local emissivity density is equal to the local absorption cross-sectional density. We map the local emissivity density of LCP and RCP radiation in the meta-atom in Fig. 2F. An evident resonant enhancement can be observed for LCP radiation near the region of the two horizontal lines of F, while the enhancement is clearly absent for RCP. The strong spin-selective local dissipation/emission in the meta-atoms is the direct reason for the strong LCP emission peak at 7 μm. We note that the F-shape meta-atoms can also be seen as perturbed resonators (see fig. S19). The symmetry breaking introduced by the perturbative segments lifts the spin degeneracy in the resonators and thus results in spinning thermal radiation. The perturbation also provides a “knob” to effectively tune the temporal and spin coherence of thermal radiation (26, 39).
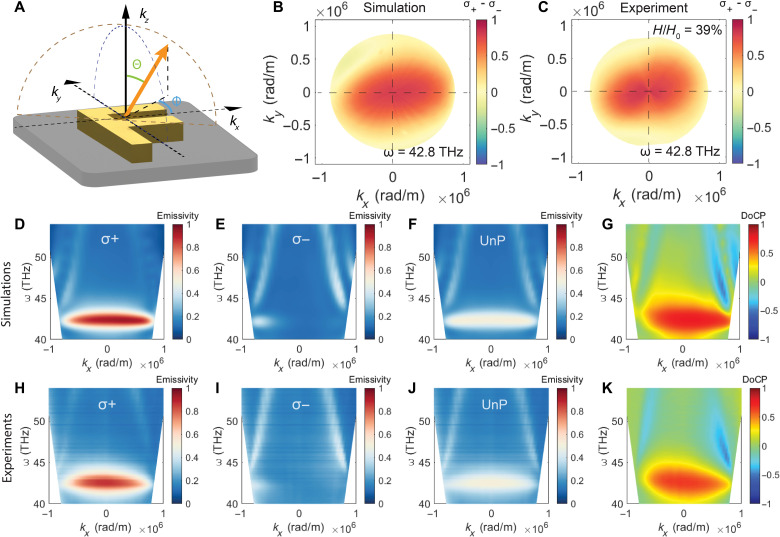
To demonstrate the nonvanishing optical helicity and map the energy-momentum (E-k) dispersion of thermal radiation, we establish a unique spin-polarized angle-resolved thermal emission spectroscopy (SPARTES) system. The system allows us to characterize the spectral and polarimetric properties of thermal radiation signals at various deflection (θ) and azimuth angles (ϕ) over the far-field hemisphere as shown in Fig. 3A (detailed description of the SPARTES system can be found in Materials and Methods; additional thermal emission spectroscopy data can be found in the Supplementary Materials). We now consider the experimental data of thermal photons with momentum along the x axis, i.e., along kx for our discussion (ky = 0). The measured spectra are plotted in Fig. 3 (H to K) and show an excellent agreement with simulations (Fig. 3, D to G). A strong contrast between the emissivity of LCP and RCP is observed, which is a direct manifestation of the spin degeneracy removal.
Fig. 3. Spin-polarized angle-resolved thermal emission spectroscopy.
(A) Schematic of the coordinate system. SPARTES collects thermal radiation signals at different deflection (θ) and azimuth angles (ϕ) over the far-field hemisphere. (B and C) Calculated (B) and experimentally measured (C) differential emissivity at 7 μm. The thermal radiation is predominantly LCP over the entire hemisphere. The total optical helicity, which is proportional to the integral of the differential emissivity in the k-space, is nonzero. It reaches more than one-third of the fundamental limits (H/H0 = 39%). (D to K) Simulated (top) and measured (bottom) angle-resolved thermal radiation spectra in the energy-momentum space (ky = 0) show excellent agreements. The LCP emissivity (D and H), RCP emissivity (E and I), unpolarized emissivity (F and J), and DoCP (G and K) are plotted for comparison. A unique spin-polarized dispersionless band and spin asymmetry are obtained in our fabricated symmetry-broken metasurface.
First, we note that the LCP and RCP emissivities (σ+, σ−) are not only distinct (Fig. 3, D, E, H, and I) but also asymmetric in momentum space (+k and −k). However, there is a clear symmetric pattern in the energy-momentum space of the averaged emissivity defined as σavg = σ+/2 + σ−/2 (Fig. 3, F and J). This is because the averaged emissivity is proportional to the total radiative power, and the symmetric total radiation in k-space is fundamentally guaranteed by the reciprocity in this magnetic field–free system. The asymmetric LCP and RCP emissivity also leads to a unique DoCP pattern, which is neither symmetric nor antisymmetric. We point out that this spin asymmetry in k-space is from the complete symmetry breaking of our F structure, where neither the 2D inversion symmetry nor the mirror symmetry is preserved.
To achieve net nonzero helicity, it is necessary to obtain spin asymmetry for a large solid angle beyond the normal emission. We demonstrate this strong effect at 7 μm by engineering a dispersionless energy band along kx. To reveal the thermal radiation characteristics in this dispersionless energy band, we plot the differential circular-polarized emissivity (σ+ − σ−) at 7 μm on the far-field hemisphere (projected onto the kxy plane). As evidently illustrated in Fig. 3 (B and C), the thermal radiation is predominantly left-handed circularly polarized in all directions. The total optical helicity H is nonzero and is defined as (53)
| (1) |
where nk,σ+ and nk,σ− are the photon numbers of LCP and RCP associated with the wave vector k. We note that total SAM associated with the radiation can be characterized by optical helicity and its vectorial counterpart optical spin (53). However, optical helicity is more well suited for describing the efficiency of imparting SAM through far-field thermal radiation (see fig. S15).
To explore the fundamental limit, we normalize the optical helicity H of our device by the optical helicity H0 of a perfect omnidirectional LCP thermal emitter (where the differential emissivity σ0+ − σ0− = 1). We show that our design reaches 39% of the fundamental limit at 7 μm from the experimental results, i.e., H/H0∣λ = 7 μm = ∑k (σ+ − σ−)/∑k (σ0+ − σ0−)∣λ = 7 μm = 39%. This is in strong contrast with previous demonstrations where the optical helicity is identically zero (21) since the spin characteristics are antisymmetric in k-space (nk,σ+ = n−k,σ−).
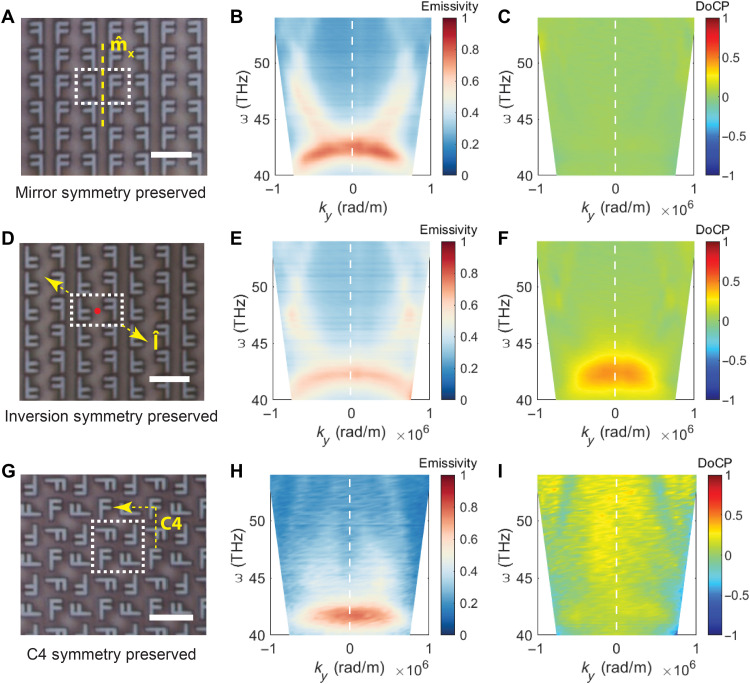
Now, we show that the spin characteristics of thermal photons can be tailored by the symmetries of the metasurface. We design the F structure to have complete symmetry breaking, i.e., none of the mirror symmetry, inversion symmetry, or high-order rotational symmetries are present in the meta-atoms themselves. Therefore, by introducing additional symmetries at a larger length scale than the meta-atoms, we demonstrate effective control of thermal radiation in its spectral and spin properties. To show this, in Fig. 4, we present the E-k dispersion where thermal photon momentum is along the y axis (ky ≠ 0, kx = 0). The experimentally measured averaged emissivity and the corresponding DoCP in three different metasurfaces with mirror, inversion, and fourfold rotational symmetries (C4) are shown. We point out three interesting features in the obtained thermal emission spectra. In Fig. 4C, by introducing mirror symmetry along the real-space y axis, the DoCP is made to vanish. In the second row, we show that the DoCP of thermal radiation in the inversion-symmetric device becomes symmetric in energy-momentum space (Fig. 4F), which is in strong contrast to the “single-F” metasurface where the DoCP is asymmetric (Fig. 3, G and K). Third, we design a C4 device that also has inversion symmetry (equivalent to C2 in this 2D case). Here, distinctive spectral, spatial, and spin features are present as a manifestation of the additional rotation symmetry in this C4 symmetric thermal metasurface (Fig. 4G) as compared to the C2 symmetric structure (Fig. 4D). We note that the near-zero DoCP originates from the coupling between the four F meta-atoms in a unit cell and can be explained through a geometric phase mechanism (54) (see fig. S7). We emphasize that all averaged emissivity plots (Fig. 4, B, E, and H) show symmetric patterns in k-space irrespective of spatial symmetries, which arise from the requirement of reciprocity.
Fig. 4. Symmetry-broken metasurfaces for thermal radiation engineering.
(A to I) The optical images (left; scale bar, 5 μm), averaged emissivity spectra (middle), and DoCP (right) are plotted for devices with mirror symmetry (A to C), inversion symmetry (D to F), and fourfold rotational symmetry (G to I), respectively. The average emissivity is symmetric along k = 0 in all three cases, which is a manifestation of the reciprocity. The DoCP is zero for the mirror-symmetric device and symmetric for the inversion and C4 devices. The results demonstrate that the intertwined spectral and spin properties of thermal radiation can be effectively tailored through symmetry engineering.
DISCUSSION
Last, we discuss the impact and potential applications of our results. The observed nonvanishing optical helicity indicates that highly omnidirectional and even broadband circularly polarized thermal emitters can be realized through metasurfaces. Our demonstrated devices here can be directly applied as a wide-angle, narrow-band circular-polarized mid-infrared light source, for applications including optical gas sensing (55) and infrared imaging (56). We highlight that the metasurface-based device can be integrated into on-chip systems to achieve compact functional devices. Moreover, considering the field of near-field heat transfer, we expect that a thermal emitter with nonvanishing optical helicity will have the unique ability to transfer net angular momentum and torque through heat (15, 18). Exploration in this direction may facilitate the discovery of thermal spin torque phenomena at the nanoscale and eventually benefit the development of thermal energy devices including near-field spin thermophotovoltaics. In addition, the unique spectral-spatial-spin feature of the engineered thermal emission can be exploited as high-contrast infrared beacons in outdoor environments, as the background thermal emission from other natural objects is highly incoherent without any spin textures. Last, our metasurface-based strategy for controlling optical spin introduces an additional degree of freedom of thermal radiation engineering, providing a general approach to tailoring thermal radiation for future energy applications.
MATERIALS AND METHODS
Device fabrication
The devices shown in this work consist of rectangular arrays of gold meta-atoms patterned on thin films of silicon dioxide (SiO2). To fabricate the device, we first deposited a 180-nm gold (Au) layer on a silicon (Si) wafer. The Au layer prevents the thermal radiation of the heater and the Si substrate from being measured. Then, an 820-nm SiO2 layer was deposited on the Au layer. We note that 10-nm titanium (Ti) layers were also used at the Si/Au and the Au/SiO2 interfaces to increase adhesion. The F-shape meta-atoms were first written to the spin-coated PMMA 950 A4 resist using a 100-keV electron beam lithography system (JEOL JBX-8100FS). After the resist was developed, a 120-nm Au was deposited on the patterned resist using an e-beam evaporator. Last, the metasurface was created in the lift-off process, where the excess resist was removed with acetone. The area of the fabricated metasurface was 5 mm × 5 mm, relaxing the alignment requirements for angle-resolved measurements.
Spin-polarized angle-resolved thermal emission spectroscopy
We used a two-axis rotary sample stage in the SPARTES setup to characterize the thermal emission along different directions over the far-field hemisphere (see figs. S3 and S4). For sample heating, a 88.9mm ring heater controlled through a programmable power supply was used. A thin tungsten sheet was attached to the ring heater to cut off the thermal emission from the heater. Tungsten was chosen here because of its low emissivity, good thermal conductivity, and high-temperature stability. The thermal radiation signal from a sample was first collected and collimated through a parabolic mirror. Then, a waveplate and a linear polarizer were used to extract the spin properties of the thermal radiation. A Fourier transform infrared spectrometer (Thermo Fisher Scientific, is50 Nicolet) with a liquid nitrogen–cooled mercury-cadmium-telluride detector was used for spectral analysis. The entire system was in a nitrogen-purged environment to eliminate the atmospheric absorption of the mid-infrared thermal radiation signal.
Polarimetric analysis
To characterize the Stokes parameters of thermal radiation signal, we used a retardation waveplate followed by a linear polarizer (see fig. S5). Assuming that the transmission axis of the polarizer is at an angle α to the x axis, the fast axis of the waveplate is at an angle β to the x axis, and the phase difference between the fast and slow axis of the waveplate is δ, the transmitted light intensity for incident radiation with Stokes parameters (S0, S1, S2, S3) is (57, 58)
| (2) |
The Stokes parameters S0, S1, S2, and S3 of the input radiation were characterized by measuring the transmitted light intensity for certain combinations of (α, β) as
| (3) |
| (4) |
| (5) |
| (6) |
and the DoP was calculated by
| (7) |
We note that the equation for S3 is general and can be applied to characterize S3 using a waveplate with arbitrary phase retardation δ. When a perfect quarter-waveplate δ = 90∘ is adopted, the equation reduces to the conventional form S3 = I(45∘,0∘) − I(135∘,0∘).
All the signals for the Stokes parameter measurement were collected at a sample temperature of T = 493.2 K. A quarter-waveplate rated at 7 μm was used in the SPARTES system. Since we were interested in the polarimetric properties in a relatively broad spectral range (5.5 to 7.7 μm), the wavelength dependence of the phase retardation δ was taken into account, and the general form of the equation was applied to evaluate S3 accurately.
To obtain the wavelength-dependent retardation δλ, the waveplate was placed between two parallel polarizers. The transmitted light spectra were collected when rotating the waveplate to different angles θ. Using the Jones matrix formalism, the transmittance Tλ can be expressed as
| (8) |
where Tp is the transmittance of the linear polarizers (along the transmission axis). Then, δλ ∈(0∘,180∘) was obtained at each wavelength λ by
| (9) |
The measured wavelength-dependent retardation δλ of the waveplate is shown in fig. S6. The waveplate has quarter-wave retardation around 7 μm, and a linear dispersion of retardance can be seen in the spectral region of 5.5 to 7.7 μm.
Moreover, the signal intensity of left-handed thermal radiation SLCP and right-handed thermal radiation SRCP was characterized on the basis of the relations that S0 = SLCP + SRCP and S3 = SLCP − SRCP, i.e.
| (10) |
| (11) |
System calibration
To calibrate both the spectral responsivity and the background noise (environmental radiation) and extract thermal emissivity, a blackbody source (IR-518/301 Blackbody, Infrared Systems) with a known thermal radiation spectrum was used. Instead of using a single-temperature measurement, we implemented a more accurate multitemperature calibration. To elaborate, the collected total signal in the experiment included the emission from the sample, the environmental thermal radiation, and the dark counts of the detector itself. Assuming a sample α, at a temperature T and angle θ, the collected total signal can be expressed by
| (12) |
where denotes the wavenumber, is the responsivity of our detector, is the temperature-independent spectral emissivity of the sample, is the blackbody radiation spectrum, is the environment radiation, and is the dark counts of the detector.
In the calibration, we used a blackbody source (). Thus
| (13) |
We were only left with two unknown factors and . We measured the signal spectrum at a series of temperature T and made a linear least-square fitting of as a function of at each wave number, where the slope of the fitting was , and the y intercept was , as
| (14) |
| (15) |
After the calibration, the emissivity profile for any unknown sample was obtained by taking the differential thermal emission spectra at two different temperatures T1 and T2 as
| (16) |
We note that this multitemperature calibration approach requires the emissivity to be temperature independent. To show this temperature independence and validate our methods, raw thermal radiation signals at different temperatures are provided in figs. S8 and S9.
Acknowledgments
We thank F. Kalhor, R. Starko-Bowes, and C. Khandekar for useful discussions. We thank A. Jishi for experimental assistance.
Funding: This work was supported by the Defense Advanced Research Projects Agency (DARPA) Nascent Light-Matter Interactions (NLM) program.
Author contributions: X.W., T.S., and S.K.R. performed the device fabrication and experimental characterization. X.W., S.B., and Z.J. contributed to the theoretical aspects of the work. X.W., Y.W., L.Q., and D.J. performed the numerical simulations. X.W. and Z.J. wrote the manuscript. Z.J. supervised the research.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Figs. S1 to S19
Supplementary Text
REFERENCES AND NOTES
- 1.D. G. Baranov, Y. Xiao, I. A. Nechepurenko, A. Krasnok, A. Alù, M. A. Kats, Nanophotonic engineering of far-field thermal emitters. Nat. Mater. 18, 920–930 (2019). [DOI] [PubMed] [Google Scholar]
- 2.Y. Li, W. Li, T. Han, X. Zheng, J. Li, B. Li, S. Fan, C.-W. Qiu, Transforming heat transfer with thermal metamaterials and devices. Nat. Rev. Mater. 6, 488–507 (2021). [Google Scholar]
- 3.S. Fan, Thermal photonics and energy applications. Joule 1, 264–273 (2017). [Google Scholar]
- 4.J.-J. Greffet, R. Carminati, K. Joulain, J.-P. Mulet, S. Mainguy, Y. Chen, Coherent emission of light by thermal sources. Nature 416, 61–64 (2002). [DOI] [PubMed] [Google Scholar]
- 5.X. Liu, T. Tyler, T. Starr, A. F. Starr, N. M. Jokerst, W. J. Padilla, Taming the blackbody with infrared metamaterials as selective thermal emitters. Phys. Rev. Lett. 107, 045901 (2011). [DOI] [PubMed] [Google Scholar]
- 6.T. Asano, M. Suemitsu, K. Hashimoto, M. De Zoysa, T. Shibahara, T. Tsutsumi, S. Noda, Near-infrared–to–visible highly selective thermal emitters based on an intrinsic semiconductor. Sci. Adv. 2, e1600499 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.J. Xu, J. Mandal, A. P. Raman, Broadband directional control of thermal emission. Science 372, 393–397 (2021). [DOI] [PubMed] [Google Scholar]
- 8.J. H. Park, S. E. Han, P. Nagpal, D. J. Norris, Observation of thermal beaming from tungsten and molybdenum bull’s eyes. ACS Photonics 3, 494–500 (2016). [Google Scholar]
- 9.M. Zhou, E. Khoram, D. Liu, B. Liu, S. Fan, M. L. Povinelli, Z. Yu, Self-focused thermal emission and holography realized by mesoscopic thermal emitters. ACS Photonics 8, 497–504 (2021). [Google Scholar]
- 10.J. R. P. Angel, J. D. Landstreet, Discovery of circular polarization in the red degenerate star G99-47. Astrophys. J. 178, L21 (1972). [Google Scholar]
- 11.A. De la Chevrotiere, N. St-Louis, A. Moffat; MiMeS Collaboration , Search for a magnetic field via circular polarization in the Wolf–Rayet star EZ CMa. Astrophys. J. 764, 171 (2013). [Google Scholar]
- 12.S. De, H. Tashiro, Circular polarization of the cmb: A probe of the first stars. Phys. Rev. D 92, 123506 (2015). [Google Scholar]
- 13.J. Bailey, A. Chrysostomou, J. Hough, T. Gledhill, A. McCall, S. Clark, F. Ménard, M. Tamura, Circular polarization in star-formation regions: Implications for biomolecular homochirality. Science 281, 672–674 (1998). [PubMed] [Google Scholar]
- 14.W. Sparks, J. H. Hough, T. A. Germer, F. Robb, L. Kolokolova, Remote sensing of chiral signatures on mars. Planet. Space Sci. 72, 111–115 (2012). [Google Scholar]
- 15.A. Ott, P. Ben-Abdallah, S.-A. Biehs, Circular heat and momentum flux radiated by magneto-optical nanoparticles. Phys. Rev. B 97, 205414 (2018). [Google Scholar]
- 16.Y. Wang, C. Khandekar, X. Gao, T. Li, D. Jiao, Z. Jacob, Broadband circularly polarized thermal radiation from magnetic Weyl semimetals. Opt. Mater. Express 11, 3880–3895 (2021). [Google Scholar]
- 17.B. Zhao, C. Guo, C. A. Garcia, P. Narang, S. Fan, Axion-field-enabled nonreciprocal thermal radiation in weyl semimetals. Nano Lett. 20, 1923–1927 (2020). [DOI] [PubMed] [Google Scholar]
- 18.M. F. Maghrebi, A. Gorshkov, J. Sau, Fluctuation-induced torque on a topological insulator out of thermal equilibrium. Phys. Rev. Lett. 123, 055901 (2019). [DOI] [PubMed] [Google Scholar]
- 19.E. Khan, E. E. Narimanov, Spinning radiation from a topological insulator. Phys. Rev. B 100, 081408 (2019). [Google Scholar]
- 20.C. Khandekar, F. Khosravi, Z. Li, Z. Jacob, New spin-resolved thermal radiation laws for nonreciprocal bianisotropic media. New J. Phys. 22, 123005 (2020). [Google Scholar]
- 21.N. Shitrit, I. Yulevich, E. Maguid, D. Ozeri, D. Veksler, V. Kleiner, E. Hasman, Spin-optical metamaterial route to spin-controlled photonics. Science 340, 724–726 (2013). [DOI] [PubMed] [Google Scholar]
- 22.S. L. Wadsworth, P. G. Clem, E. D. Branson, G. D. Boreman, Broadband circularly-polarized infrared emission from multilayer metamaterials. Opt. Mater. Express 1, 466–479 (2011). [Google Scholar]
- 23.B. Zhao, L. Wang, Y. Shuai, Z. M. Zhang, Thermophotovoltaic emitters based on a two-dimensional grating/thin-film nanostructure. Int. J. Heat Mass Transf. 67, 637–645 (2013). [Google Scholar]
- 24.J. Park, J.-H. Kang, X. Liu, S. J. Maddox, K. Tang, P. C. McIntyre, S. R. Bank, M. L. Brongersma, Dynamic thermal emission control with inas-based plasmonic metasurfaces. Sci. Adv. 4, eaat3163 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.B. Ma, Y. Huang, W. Zha, B. Qin, R. Qin, P. Ghosh, S. Kaur, M. Qiu, Q. Li, Narrowband diffuse thermal emitter based on surface phonon polaritons. Nanophotonics 11, 4115–4122 (2022). [Google Scholar]
- 26.A. C. Overvig, S. A. Mann, A. Alù, Thermal metasurfaces: Complete emission control by combining local and nonlocal light-matter interactions. Phys. Rev. X 11, 021050 (2021). [Google Scholar]
- 27.I. Liberal, N. Engheta, Manipulating thermal emission with spatially static fluctuating fields in arbitrarily shaped epsilon-near-zero bodies. Proc. Natl. Acad. Sci. U.S.A. 115, 2878–2883 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.S. S. Kruk, Z. J. Wong, E. Pshenay-Severin, K. O’brien, D. N. Neshev, Y. S. Kivshar, X. Zhang, Magnetic hyperbolic optical metamaterials. Nat. Commun. 7, 11329 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.P. N. Dyachenko, S. Molesky, A. Y. Petrov, M. Störmer, T. Krekeler, S. Lang, M. Ritter, Z. Jacob, M. Eich, Controlling thermal emission with refractory epsilon-near-zero metamaterials via topological transitions. Nat. Commun. 7, 11809 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Y. X. Yeng, M. Ghebrebrhan, P. Bermel, W. R. Chan, J. D. Joannopoulos, M. Soljačić, I. Celanovic, Enabling high-temperature nanophotonics for energy applications. Proc. Natl. Acad. Sci. U.S.A. 109, 2280–2285 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.M. De Zoysa, T. Asano, K. Mochizuki, A. Oskooi, T. Inoue, S. Noda, Conversion of broadband to narrowband thermal emission through energy recycling. Nat. Photonics 6, 535–539 (2012). [Google Scholar]
- 32.W. Li, Z. J. Coppens, L. V. Besteiro, W. Wang, A. O. Govorov, J. Valentine, Circularly polarized light detection with hot electrons in chiral plasmonic metamaterials. Nat. Commun. 6, 8379 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.L. Kang, S. P. Rodrigues, M. Taghinejad, S. Lan, K.-T. Lee, Y. Liu, D. H. Werner, A. Urbas, W. Cai, Preserving spin states upon reflection: Linear and nonlinear responses of a chiral meta-mirror. Nano Lett. 17, 7102–7109 (2017). [DOI] [PubMed] [Google Scholar]
- 34.L. Ouyang, W. Wang, D. Rosenmann, D. A. Czaplewski, J. Gao, X. Yang, Near-infrared chiral plasmonic metasurface absorbers. Opt. Express 26, 31484–31489 (2018). [DOI] [PubMed] [Google Scholar]
- 35.M. S. Mahmud, D. Rosenmann, D. A. Czaplewski, J. Gao, X. Yang, Plasmon-phonon coupling between mid-infrared chiral metasurfaces and molecular vibrations. Opt. Express 28, 21192–21201 (2020). [DOI] [PubMed] [Google Scholar]
- 36.M. S. Mahmud, D. Rosenmann, D. A. Czaplewski, J. Gao, X. Yang, Chiral plasmonic metasurface absorbers in the mid-infrared wavelength range. Opt. Lett. 45, 5372–5375 (2020). [DOI] [PubMed] [Google Scholar]
- 37.B. Tang, Z. Li, E. Palacios, Z. Liu, S. Butun, K. Aydin, Chiral-selective plasmonic metasurface absorbers operating at visible frequencies. IEEE Photon. Technol. Lett. 29, 295–298 (2017). [Google Scholar]
- 38.E. Plum, N. I. Zheludev, Chiral mirrors. Appl. Phys. Lett. 106, 221901 (2015). [Google Scholar]
- 39.Z. Shen, X. Fang, S. Li, W. Yin, L. Zhang, X. Chen, Terahertz spin-selective perfect absorption enabled by quasi-bound states in the continuum. Opt. Lett. 47, 505–508 (2022). [DOI] [PubMed] [Google Scholar]
- 40.H. Tang, D. Rosenmann, D. A. Czaplewski, X. Yang, J. Gao, Dual-band selective circular dichroism in mid-infrared chiral metasurfaces. Opt. Express 30, 20063–20075 (2022). [DOI] [PubMed] [Google Scholar]
- 41.M. Li, L. Guo, J. Dong, H. Yang, An ultra-thin chiral metamaterial absorber with high selectivity for lcp and rcp waves. J. Phys. D 47, 185102 (2014). [Google Scholar]
- 42.Z. Wang, H. Jia, K. Yao, W. Cai, H. Chen, Y. Liu, Circular dichroism metamirrors with near-perfect extinction. ACS Photonics 3, 2096–2101 (2016). [Google Scholar]
- 43.E. Plum, V. A. Fedotov, N. I. Zheludev, Optical activity in extrinsically chiral metamaterial. Appl. Phys. Lett. 93, 191911 (2008). [Google Scholar]
- 44.A. Y. Zhu, W. T. Chen, A. Zaidi, Y.-W. Huang, M. Khorasaninejad, V. Sanjeev, C.-W. Qiu, F. Capasso, Giant intrinsic chiro-optical activity in planar dielectric nanostructures. Light Sci. Appl. 7, 17158 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.X. Yin, Z. Ye, J. Rho, Y. Wang, X. Zhang, Photonic spin hall effect at metasurfaces. Science 339, 1405–1407 (2013). [DOI] [PubMed] [Google Scholar]
- 46.B. Desiatov, N. Mazurski, Y. Fainman, U. Levy, Polarization selective beam shaping using nanoscale dielectric metasurfaces. Opt. Express 23, 22611–22618 (2015). [DOI] [PubMed] [Google Scholar]
- 47.E. Maguid, I. Yulevich, D. Veksler, V. Kleiner, M. L. Brongersma, E. Hasman, Photonic spin-controlled multifunctional shared-aperture antenna array. Science 352, 1202–1206 (2016). [DOI] [PubMed] [Google Scholar]
- 48.Y. Yuan, K. Zhang, B. Ratni, Q. Song, X. Ding, Q. Wu, S. N. Burokur, P. Genevet, Independent phase modulation for quadruplex polarization channels enabled by chirality-assisted geometric-phase metasurfaces. Nat. Commun. 11, 4186 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.M. Hentschel, M. Schäferling, X. Duan, H. Giessen, N. Liu, Chiral plasmonics. Sci. Adv. 3, e1602735 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.E. Hendry, T. Carpy, J. Johnston, M. Popland, R. V. Mikhaylovskiy, A. J. Lapthorn, S. Kelly, L. D. Barron, N. Gadegaard, M. Kadodwala, Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 5, 783–787 (2010). [DOI] [PubMed] [Google Scholar]
- 51.J. K. Gansel, M. Thiel, M. S. Rill, M. Decker, K. Bade, V. Saile, G. von Freymann, S. Linden, M. Wegener, Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009). [DOI] [PubMed] [Google Scholar]
- 52.J.-J. Greffet, P. Bouchon, G. Brucoli, F. Marquier, Light emission by nonequilibrium bodies: Local Kirchhoff law. Phys. Rev. X 8, 021008 (2018). [Google Scholar]
- 53.R. P. Cameron, S. M. Barnett, A. M. Yao, Optical helicity, optical spin and related quantities in electromagnetic theory. New J. Phys. 14, 053050 (2012). [Google Scholar]
- 54.X. Xie, M. Pu, J. Jin, M. Xu, Y. Guo, X. Li, P. Gao, X. Ma, X. Luo, Generalized pancharatnam-berry phase in rotationally symmetric meta-atoms. Phys. Rev. Lett. 126, 183902 (2021). [DOI] [PubMed] [Google Scholar]
- 55.A. Lochbaum, Y. Fedoryshyn, A. Dorodnyy, U. Koch, C. Hafner, J. Leuthold, On-chip narrowband thermal emitter for mid-ir optical gas sensing. ACS Photonics 4, 1371–1380 (2017). [Google Scholar]
- 56.F. Huth, M. Schnell, J. Wittborn, N. Ocelic, R. Hillenbrand, Infrared-spectroscopic nanoimaging with a thermal source. Nat. Mater. 10, 352–356 (2011). [DOI] [PubMed] [Google Scholar]
- 57.H. G. Berry, G. Gabrielse, A. Livingston, Measurement of the stokes parameters of light. Appl. Optics 16, 3200–3205 (1977). [DOI] [PubMed] [Google Scholar]
- 58.T. Kihara, Measurement method of stokes parameters using a quarter-wave plate with phase difference errors. Appl. Optics 50, 2582–2587 (2011). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs. S1 to S19
Supplementary Text