A permutation-based approach to inference for weighted sum regression with correlated chemical mixtures

Abstract

There is a growing demand for methods to determine the effects that chemical mixtures have on human health. One statistical challenge is identifying true “bad actors” from a mixture of highly correlated predictors, a setting in which standard approaches such as linear regression become highly variable. Weighted Quantile Sum (WQS) regression has been proposed to address this problem, through a two-step process where mixture component weights are estimated using bootstrap aggregation in a training dataset and inference on the overall mixture effect occurs in a held-out test set. WQS is popular in applied papers, but the reliance on data splitting is suboptimal, and analysts who use the same data for both steps risk inflation of the nominal Type I error rate. We therefore propose a modification of WQS that uses a permutation test for inference, which allows for weight estimation using the entire dataset and preserves Type I error. To minimize computational burden, we propose replacing the bootstrap with L1 or L2 penalization and describe how to choose the appropriate penalty given expert knowledge about a mixture of interest. We apply our method to a national pregnancy cohort study of prenatal phthalate exposure and child health outcomes.

Introduction

A growing number of U.S. federal agencies have called for research on chemical mixtures and how they affect human health^1–3. Such mixtures have applications throughout environmental epidemiology, from air pollution to phthalates, a family of endocrine-disrupting chemicals found in plastics⁴. The concept of a multi-pollutant approach is relatively new⁵, as is the idea of an exposome, a complement to the genome that is defined as the totality of a person’s environmental and lifestyle exposures from the prenatal period onward⁶. Thus, there is a need for novel statistical methods to evaluate the health impacts of mixtures of individual exposures. An additional goal of mixture analysis is to identify “bad actors,” that is, the most harmful components, which can inform regulatory decisions, as it may be impractical to ban an entire class of compounds.

Statistical difficulties arise because environmental exposures are often highly correlated. We have observed this problem firsthand in data from The Infant Development and Environment Study (TIDES), a national, multicenter pregnancy cohort study focused on prenatal phthalate exposure and child health outcomes. In TIDES, pairwise correlations between log-transformed urinary phthalate metabolites range from 0.04 to 0.98. Previous analyses with the TIDES data have dealt with this by fitting separate models for each phthalate metabolite, a common approach in the phthalate literature ^7,8. This method avoids the problem of unexpected sign changes in coefficients due to collinearity, but clearly, considering chemicals one at a time cannot lead to conclusions about simultaneous exposure or potential interactions, and results could still be spurious if one chemical is serving as a proxy for another. More sophisticated variable selection methods are also challenged in the presence of collinearity. The least absolute shrinkage and selection operator (lasso), for example, tends to select one representative component at random from a correlated mixture, while the elastic net will select all or none of the correlated components⁹.

Several methods have been proposed for variable selection and effect estimation in the context of multiple chemical exposures^10,11. One popular choice in applied papers is Weighted Quantile Sum (WQS) regression, which has been cited more than 150 times since its publication in 2014¹², in journals such as Nature¹³ and JAMA¹⁴. In WQS, the linear predictor is reformulated as a weighted sum of exposures, where a variable is selected if its estimated weight surpasses a pre-determined threshold. To prevent over-fitting, weights are estimated repeatedly via maximum likelihood in bootstrap datasets, then averaged in such a way that the bootstrap datasets with higher signal have more influence on the final estimates. Ideally, this occurs in a training dataset, and significance testing of the overall mixture effect is performed on a held-out test set. The WQS framework is appealing and flexible, but this reliance on data splitting can be suboptimal as it necessarily reduces the sample size for both estimation and testing. This is why, in practice, analysts often perform both estimation and testing on a single dataset^14,15, which inflates the Type I error rate. Clearly, analysts working with chemical mixtures could benefit from a method that is similar to WQS in form but does not require data to be split for valid inference.

In this paper, we introduce a modified version of WQS regression that allows for the entire dataset to be used both when estimating mixture component weights and when testing the overall mixture effect. We show via simulation studies that, by replacing the standard t-test for the overall mixture coefficient with a permutation test, one can preserve Type I error across a variety of predictor correlation settings. To offset the added computational burden of a permutation test, we replace the WQS bootstrap with optional L1 or L2 penalization and leave the choice of penalty (L1 versus L2) in the hands of the researcher, who can use her expert knowledge about a particular chemical mixture to decide. The L1 penalty is generally optimal when only a few of the mixture components are bad actors, while L2 penalization performs better when many or all of the mixture components are associated with the outcome. We conduct extensive simulation studies to compare our method with WQS and standard linear regression on metrics such as sensitivity and specificity of variable selection, empirical Type I error rates, estimation bias, and precision. We apply our method to the TIDES dataset in an analysis of first-trimester maternal phthalate concentrations and anogenital distance in male infants.

Methods

Notation and preliminaries

For i = 1, …, n, let y_i be a continuous outcome, x_i a p × 1 vector of chemical exposures from a mixture of interest, and z_i an m × 1 vector of non-mixture covariates. Our mean model, which comes from Weighted Quantile Sum (WQS) regression¹², is

$${\mu }_i={\beta }_0+{\beta }_1\sum _{j=1}^p{w}_j{x}_{ij}+\sum _{k=1}^m{\psi }_k{z}_{ik},$$ (1)

where μ_i = E(y_i|x_i, z_i), β₀ is the intercept, β₁ is the overall mixture effect, and w_j is the weight of component j in the mixture, such that 0 ≤ w_j ≤ 1, j = 1, …, p, and ${\sum }_{j=1}^p{w}_j=1$. For the covariate vector z_i, ψ is the vector of corresponding coefficients, which are unconstrained. Parameters in this model can be estimated using constrained least-squares or constrained maximum likelihood, provided one is willing to make a distributional assumption for y_i|x_i, z_i. Note that this model is a reformulation of the multivariable linear regression model, $E\left(y_i\mid x_i,z_i\right)={\beta }_0+{\sum }_{j=1}^p{\beta }_j^{\star }{x}_{ij}+{\sum }_{k=1}^m{\psi }_k{z}_{ik}$, where ${\beta }_1={\sum }_{j=1}^p{\beta }_j^{\star },w_j={\beta }_j^{\star }/{\sum }_{j=1}^p{\beta }_j^{\star }$, and the ${\beta }_j^{\star }$ are constrained to all be either nonnegative or nonpositive, for j = 1, …, p. In chemical mixtures analysis, this sign is generally assumed to be that of harmful effect, i.e., all components are either toxic or harmless, but not beneficial.

If mixture component distributions are skewed, x_ij may be recoded to represent quantiles of the measured exposures. For example, in WQS¹², if quartiles are desired, x_ij is set to 0, 1, 2, or 3 to indicate that the jth mixture component of the ith individual is in the first, second, third, or fourth quartile, respectively, of that component’s distribution, so that β₁ represents the change in average outcome for a one-quartile increase in all mixture components. If influential points are less of a concern, the components are standardized, e.g., by their standard deviation, so that β₁ represents the change in average outcome for a one-standard-deviation increase in all mixture components.

Our method relies heavily on the fitting approaches of WQS regression, the lasso, and ridge regression. Therefore, these methods are briefly outlined here.

For WQS¹², data are first split into training and test sets. B bootstrap samples are drawn from the training set, and for each bootstrap dataset, parameters are estimated via constrained maximum likelihood. WQS requires that a sign for β₁ be pre-specified, and in practice, researchers applying WQS will either fit the unidirectional model that is of interest a priori¹⁶ or fit the model with both signs and present both sets of results¹⁷. In a process similar to bootstrap aggregation (referred to as bagging), the estimate for w_j is ${\overline{w}}_j=\frac{1}{B}{\sum }_{b=1}^B{w}_{j(b)}f\left({\widehat{\beta }}_{1(b)}\right)$, where w_j(b) is the weight for the jth component using the bth bootstrap sample and $f\left({\widehat{\beta }}_{1(b)}\right)$ is a pre-specified signal function that assigns greater importance to bootstrap samples with stronger signals. The default signal function in version 3.0.0 of the gWQS R package is a scaled t-statistic for β₁ from bootstrap dataset b; in earlier applications, $f\left({\widehat{\beta }}_{1(b)}\right)$ was set to 1¹⁸. Once weights are determined, a linear regression is fit to data from the held-out test set that includes the weighted sum, i.e., ${\sum }_{j=1}^p{\overline{w}}_j{x}_{ij}$, as a predictor. However, in practice, analysts will often do significance testing with the same data used to estimate the weights^14,15.

The lasso and ridge regression are shrinkage estimators, meaning coefficients are reduced by imposing a penalty on their size. For the lasso, this penalty is an upper bound on the L1 norm of the coefficients, i.e., the sum of their absolute values:

$${\widehat{\beta }}^{\text{lasso }}=\underset{\beta }{\text{argmin}}\left\{\frac{1}{2}\sum _{i=1}^n{\left(y_i-{\beta }_0-\sum _{j=1}^p{\beta }_j{x}_{ij}\right)}^2+\lambda \sum _{j=1}^p\left|{\beta }_j\right|\right\}$$ (2)

For ridge regression, this penalty is an upper bound on the squared L2 norm of the coefficients, i.e., the sum of squares:

$${\widehat{\beta }}^{\text{ridge }}=\underset{\beta }{\text{argmin}}\left\{\frac{1}{2}\sum _{i=1}^n{\left(y_i-{\beta }_0-\sum _{j=1}^p{\beta }_j{x}_{ij}\right)}^2+\lambda \sum _{j=1}^p{\beta }_j^2\right\}$$ (3)

For both the lasso and ridge regression, a growing number of coefficients are shrunk toward zero as the tuning parameter, λ, increases, and coefficients are generally not constrained to be either nonnegative or nonpositive. The λ parameter is generally chosen to minimize or nearly minimize mean squared prediction error, which is estimated via cross-validation¹⁹. A hallmark of the lasso is that for sufficiently large λ, coefficients can be shrunk to exactly zero.

All three methods promote regularization, but through different mechanisms. In WQS, weights can be estimated at exactly zero in a single bootstrap dataset, but the bagging process necessarily pushes weights away from zero and toward equality as nonnegative estimates are averaged across bootstrap datasets. That is, WQS works to avoid overfitting by limiting sparsity in the weights. In contrast, the lasso shrinks coefficients toward zero to offset λ and works to avoid overfitting by increasing parsimony. Ridge regression does a little of both, as coefficients are shrunk toward zero and toward each other with increasing λ¹⁹. If, however, coefficients are constrained to be nonnegative or nonpositive, L2 penalization can also result in sparsity, as we will subsequently see.

Model fitting

Our method involves a two-step fitting process. First, component weights are estimated through optimization of a loss function that involves either L1 or L2 penalization, depending on the analyst’s knowledge and assumptions about the mixture of interest. Second, we refit the model via ordinary least squares (OLS), where one of the predictors is a weighted sum of mixture components using the estimated weights, as in WQS. The use of penalization instead of the bootstrap for regularization makes hypothesis testing with a permutation test computationally feasible, and the permutation test in turn allows the analyst to use the complete data to estimate the weights, if desired.

Step 1: Weight estimation

For the first step of model fitting, mixture variables are centered and scaled. We then minimize a modified lasso/ridge loss function, excluding non-mixture covariates from the penalization and adding the constraint that mixture component coefficients are either all nonnegative or all nonpositive. That is,

$$\left({\widehat{\beta }}^{\star }\widehat{\psi }\right)=\underset{{\beta }^{\star },\psi }{\text{argmin}}\{\begin{array}{c}\frac{1}{2}{\sum }_{i=1}^n{\left(y_i-{\beta }_0^{\star }-{\sum }_{j=1}^p{\beta }_j^{\star }{x}_{ij}-{\sum }_{k=1}^m{\psi }_k{z}_{ik}\right)}^2+\lambda {\sum }_{j=1}^p\left(L_1{\beta }_j^{\star }+L_2{\left({\beta }_j^{\star }\right)}^2\right)\\ \text{ s}.\text{t}.{\beta }_j^{\star }\ge 0,j=1,\dots ,p\\ \frac{1}{2}{\sum }_{i=1}^n{\left(y_i-{\beta }_0^{\star }-{\sum }_{j=1}^p{\beta }_j^{\star }{x}_{ij}-{\sum }_{k=1}^m{\psi }_k{z}_{ik}\right)}^2-\lambda {\sum }_{j=1}^p\left(L_1{\beta }_j^{\star }-L_2{\left({\beta }_j^{\star }\right)}^2\right)\\ \text{ s}.\text{t}.{\beta }_j^{\star }\le 0,j=1,\dots ,p\end{array}$$ (4)

where L₁ is an indicator of choosing to apply the L1 penalty and L₂ is an indicator of choosing the L2. A researcher should choose the penalty that best fits the chemical mixture and research question of interest. L1 penalization is well-suited to identifying a few bad actors when many mixture components have little to no association with the outcome (i.e., true weights of zero), while L2 penalization is better when many components are similarly associated with the outcome (i.e., true weights closer to equality). The reasons and intuition for this are detailed in the next section.

Given the chosen penalty, we minimize each version of Equation 4 — once with the positive constraint and once with the negative — and select the sign that yields a smaller sum of squared errors.

The minimizer ${\widehat{\beta }}^{\star }$ depends on the choice of λ, which is tuned through 10-fold cross-validation, where the model is repeatedly fit along a log-scale path of 100 possible values of λ and the mean cross-validated error, given the chosen sign constraint, is computed for each. We implement minimization efficiently with the cyclical coordinate descent algorithm of the R package glmnet²⁰. λ_MAX is set to the smallest value of λ such that all ${\widehat{\beta }}_j^{\star }$, j = 1, …, p, are set to zero; the path begins with λ_MIN = 0.001 × λ_MAX. For optimal sensitivity, we recommend choosing the λ that minimizes mean cross-validated error, i.e., “lambda.min” in glmnet, and use this λ for all simulation studies and our applied example.

Once λ is selected, ${\widehat{\beta }}^{\star }$ is fully determined, and ${\widehat{w}}_j={\widehat{\beta }}_j^{\star }/{\sum }_{j=1}^p{\widehat{\beta }}_j^{\star }$, j = 1, …, p. If using L1 penalization and the chosen λ sets all coefficients to zero, β₁ becomes unidentifiable in the second step, so we instead tune λ to the next lowest value on the path. This adjustment results in the selection of at least one mixture component.

Step 2: Hypothesis testing

In the second step of model fitting, the outcome y_i is regressed on the estimated weighted sum, ${\sum }_{j=1}^p{\widehat{w}}_j{x}_{ij}$, in a linear regression controlling for desired non-mixture covariates. This regression could use data from a held-out test set, in which case the usual least-squares inference applies, with $\left({\widehat{\beta }}_1-{\beta }_1\right)/SE\left({\widehat{\beta }}_1\right)~t(\text{df}=n-m-2)$. If data splitting is not desirable, the same data can be used for weight estimation and the subsequent linear regression, but significance testing requires an alternative approach to avoid inflation of the Type I error rate.

We propose a permutation test as an alternative approach. To generate the distribution of ${\widehat{\beta }}_1$ under H₀ : β₁ = 0 in a model lacking non-mixture covariates (i.e., z_i does not exist), our two-step method is repeatedly fit on the outcome vector y = (y₁…y_n) and a random permutation of x_i, i = 1, …, n. The subsequent ${\widehat{\beta }}_1\text{s}$ form a null distribution because the random pairing of y_i and x_i ensures no remaining association between the outcome and predictors. Data are not split into training and test sets for any iteration. In each iteration, λ is adaptively chosen in the same manner as in the original fitting (e.g., always set to “lambda.min”), and the same penalty (L1 or L2) is always used. At the conclusion of a large number of iterations, such as 1000, an empirical two-sided p-value is computed with the formula (r+1)/(N+1), where r is the number of test statistics $\left({\widehat{\beta }}_1\text{s}\right)$ with absolute values greater than or equal to the absolute value of the original test statistic, and N is the number of iterations performed²¹. In this paper, N is always set to 1000.

When the model includes non-mixture covariates z_i, i = 1, …, n, the permutation test follows a slightly different procedure. First, the outcome and mixture variables are each regressed on the set of non-mixture covariates in separate linear regressions to obtain the n × 1 residual vector y_z and n × p residual matrix X_z. We note here that given λ, the ${\beta }_j^{\star }$ estimates for j = 1, …, p are equivalent whether our method is fit to (1) the original outcome variable, mixture variables, and non-mixture covariates, or (2) y_z and X_z. The appendix contains a detailed proof of this property, known as the Frisch-Waugh-Lovell theorem^22,23. Therefore, we can conduct the permutation test as before, with y_z as the outcome vector and random permutations of the rows of X_z. This breaks the association between the outcome and the mixture without breaking the association between the outcome and the non-mixture covariates, simulating the desired null distribution. In simulation studies, we show that this test preserves Type I error across a range of signals and predictor correlation settings.

Implications of L1 versus L2 penalization

In this section, we discuss the intuitive differences between L1 and L2 penalization, and we prove, under certain assumptions, the properties discussed earlier: As the tuning parameter, λ, increases, L1 penalization shrinks some weights toward zero and others toward 1, while L2 penalization pushes weights closer to each other. Without loss of generality, we consider the case when the estimators of β^⋆ are constrained to be nonnegative.

Figure 1 illustrates the impact of choosing the L1 versus the L2 penalty when the nonnegativity constraint is applied to two parameters. The contours of the log likelihood, centered at the ordinary least squares solution, are shown for a normally distributed outcome with two positively correlated predictors. The solutions to Equation 4 occur at the intersections of this log likelihood with the shaded feasibility regions for the two possible penalties, and we can see that the L2-penalized solution is nearer to the line ${\beta }_1^{\star }={\beta }_2^{\star }$. In other words, the L2 penalty pushes coefficients, and therefore weights, closer to equality. Note that, unlike with unconstrained lasso and ridge regression, either penalty could result in coefficients estimated at exactly zero, because the feasibility regions created by the nonnegativity constraints have hard edges. That is, if the OLS solution were in the second quadrant and the intersection of the log likelihood with the L2 feasibility region was along the y axis, ${\beta }_1^{\star }$ would be estimated at exactly zero.

Figure 1.

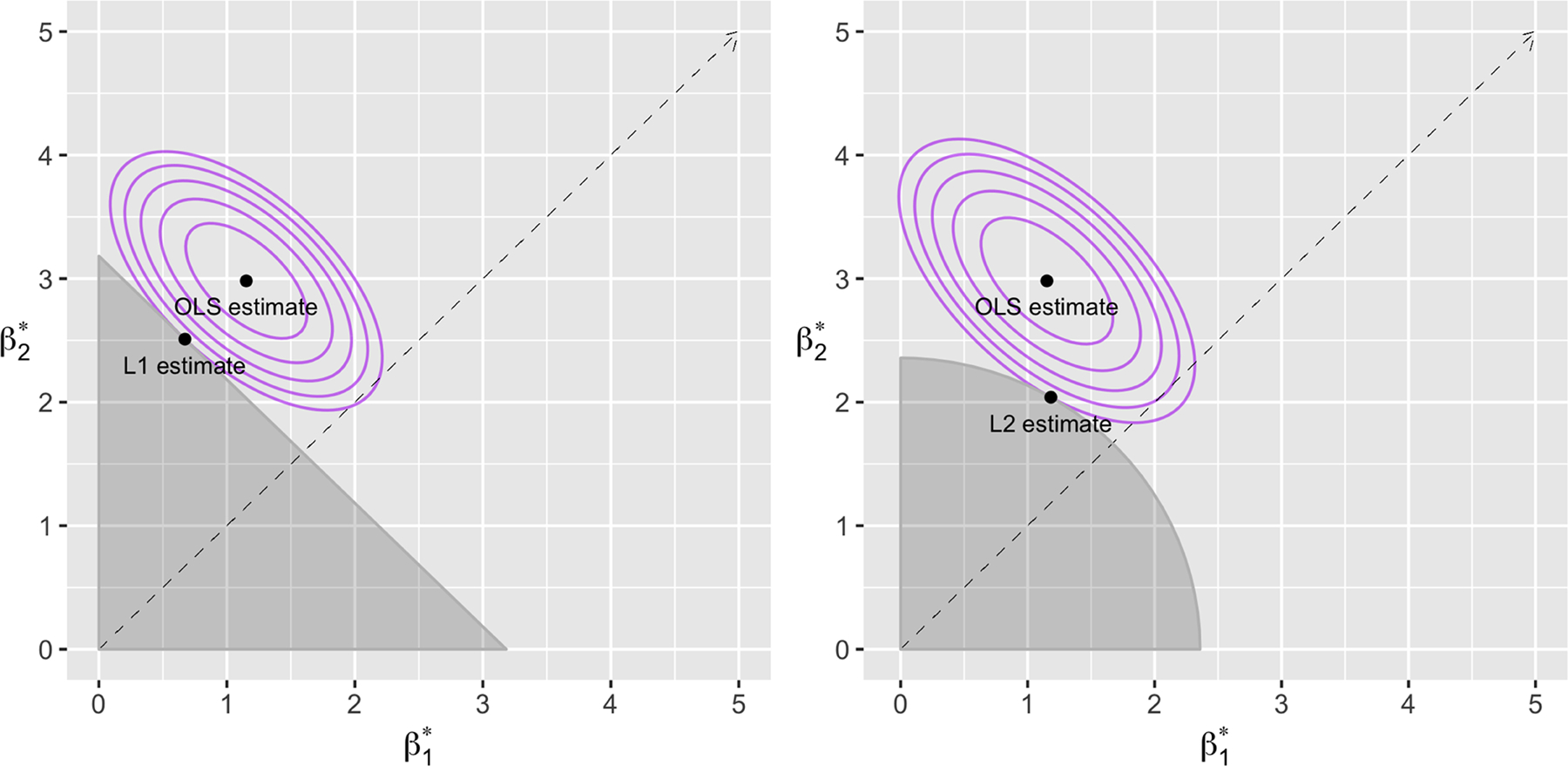
Illustration of how the L2 penalty moves coefficients and therefore weights closer to equality, in a simulated setting with two positive coefficients for two positively correlated predictors. The intersection of the contours of the normal log likelihood with the shaded feasibility region for an L2-penalized regression with nonnegativity constraints (right) is closer to the dotted line of equality than the intersection with the L1 feasibility region (left). The ordinary least squares (OLS) estimator is also shown, as the minimizer of the log likelihood. Lambda was chosen by the one-standard-error rule.

We now briefly outline the proofs of these properties. For this paragraph and the subsequent paragraph only, restrict x_i and β^⋆ to the subsets of x_i and β^⋆ that correspond to the k nonzero components of the nonnegative least-squares solution, ${\widehat{\beta }}_{\text{NNLS}}^{\star }$. For λ close to zero, the L1-penalized solution is ${\widehat{\beta }}_{\text{L}1}^{\star }={\left({\sum }_{i=1}^n{x}_i{x}_i{}^T\right)}^{-1}\left({\sum }_{i=1}^n{y}_i{x}_i-\lambda 1_k\right)={\widehat{\beta }}_{\text{NNLS}}^{\star }-{\left({\sum }_{i=1}^n{x}_i{x}_i{}^T\right)}^{-1}\lambda 1_k$, where 1_k is a k × 1 vector of 1s. For centered and standardized x_i, ${\sum }_{i=1}^n{x}_{\text{i}}{x_{\text{i}}}^T=(n-1)\widehat{R}$, where $\widehat{R}$ is the sample predictor correlation matrix, which we assume to be positive exchangeable for illustrative purposes. Therefore, ${\sum }_{i=1}^n{x}_i{x}_i{}^T$ and ${\left({\sum }_{i=1}^n{x}_i{x}_i{}^T\right)}^{-1}$ are both compound symmetric, implying ${\left({\sum }_{i=1}^n{x}_i{x}_i{}^T\right)}^{-1}\lambda 1_k=c{1}_k$. That is, ${\widehat{\beta }}_{\text{L}1}^{\star }$ equals the nonnegative least-squares solution with every element reduced by the constant c, an increasing function of λ. As λ increases, weights corresponding to least-squares coefficients of larger magnitude (i.e., l such that ${\widehat{\beta }}_{\text{NNLS},l}^{\star }>\frac{1}{k}{\sum }_{j=1}^k{\widehat{\beta }}_{\text{NNLS},j}^{\star }$) move toward 1 and weights corresponding to smaller coefficients (i.e., s such that ${\widehat{\beta }}_{\text{NNLS},s}^{\star }<\frac{1}{k}{\sum }_{j=1}^k{\widehat{\beta }}_{\text{NNLS},j}^{\star }$) shrink toward zero, because $\frac{{\widehat{\beta }}_{\text{NNLS},l}^{\star }-c}{{\sum }_{j=1}^k{\widehat{\beta }}_{\text{NNLS},j}^{\star }-kc}>\frac{{\widehat{\beta }}_{\text{NNLS},l}^{\star }}{{\sum }_{j=1}^k{\widehat{\beta }}_{\text{NNLS},j}^{\star }}$ and $\frac{{\widehat{\beta }}_{\text{NNLS},s}^{\star }-c}{{\sum }_{j=1}^k{\widehat{\beta }}_{\text{NNLS},j}^{\star }-kc}<\frac{{\widehat{\beta }}_{\text{NNLS},s}^{\star }}{{\sum }_{j=1}^k{\widehat{\beta }}_{\text{NNLS},j}^{\star }}$.

To show that the L2-penalized solution pushes weights toward equality under the same conditions, first note that ${\widehat{\beta }}_{\text{NNLS},j}^{\star }={(n-1)}^{-1}{\widehat{R}}_j^{-1}{\sum }_{i=1}^n{y}_i{x}_i=\frac{1+ak-2a}{(1-a)(1+ak-a)}\left({\widehat{\beta }}_{\text{SLR},j}^{\star }-\frac{a}{1+ak-2a}{\sum }_{l\ne j}{\widehat{\beta }}_{\text{SLR},l}^{\star }\right)$, where ${\widehat{R}}_j^{-1}$ is the jth row of ${\widehat{R}}^{-1}$, a is the off-diagonal correlation in $\widehat{R}$, and ${\widehat{\beta }}_{\text{SLR},j}^{\star }$ is the estimated slope from the simple linear regression of centered y on the jth mixture component (details in the appendix). For λ close to zero, the L2-penalized solution is ${\widehat{\beta }}_{\text{L}2}^{\star }={\left({\sum }_{i=1}^n{x}_i{x}_i{}^T+\lambda I_k\right)}^{-1}{\sum }_{i=1}^n{y}_i{x}_i={\left((n-1)\widehat{R}+\lambda I_k\right)}^{-1}{\sum }_{i=1}^n{y}_i{x}_i={\left(1+\frac{\lambda }{n-1}\right)}^{-1}{(n-1)}^{-1}{B}^{-1}{\sum }_{i=1}^n{y}_i{x}_i$, where I_k is the k × k identity matrix and B is also an exchangeable correlation matrix with off-diagonals $b=\frac{a}{1+\frac{\lambda }{n-1}}$. Then, similar to ${\widehat{\beta }}_{\text{NNLS},j}^{\star }$, we can write

${\widehat{\beta }}_{\text{L}2,j}^{\star }={\left(1+\frac{\lambda }{n-1}\right)}^{-1}\frac{1+bk-2b}{(1-b)(1+bk-b)}\left({\widehat{\beta }}_{\text{SLR},j}^{\star }-\frac{b}{1+bk-2b}{\sum }_{l\ne j}{\widehat{\beta }}_{\text{SLR},l}^{\star }\right)\propto {\widehat{\beta }}_{\text{NNLS},j}^{\star }+\frac{1+ak-2a}{(1-a)(1+ak-a)}\left(\frac{a}{1+ak-2a}-\frac{b}{1+bk-2b}\right){\sum }_{l\ne j}{\widehat{\beta }}_{\text{SLR},l}^{\star }.$

The L2-penalized weights are therefore:

$${\widehat{w}}_{\text{L}2,j}=\frac{{\widehat{\beta }}_{\text{L}2,\text{j}}^{\star }}{{\sum }_{m=1}^k{\widehat{\beta }}_{\text{L}2, \text{m}}^{\star }}=\frac{{\widehat{\beta }}_{\text{NNLS},j}^{\star }+\frac{1+ak-2a}{(1-a)(1+ak-a)}\left(\frac{a}{1+ak-2a}-\frac{b}{1+bk-2b}\right){\sum }_{l\ne j}{\widehat{\beta }}_{\text{SLR},l}^{\star }}{{\sum }_{m=1}^k{\widehat{\beta }}_{\text{NNLS},m}^{\star }+\frac{1+ak-2a}{(1-a)(1+ak-a)}\left(\frac{a}{1+ak-2a}-\frac{b}{1+bk-2b}\right){\sum }_{l\ne m}{\widehat{\beta }}_{\text{SLR},l}^{\star }}$$ (5)

It is straightforward to show $\frac{a}{1+ak-2a}$ is increasing in a and ${\widehat{\beta }}_{\text{NNLS},j}^{\star }>0\Rightarrow {\widehat{\beta }}_{\text{SLR},j}^{\star }>0$; therefore, the second term in the numerator of (5) is positive. It is also straightforward to show that the rank order of ${\widehat{\beta }}_{\text{NNLS}}^{\star }$ matches the rank order of $\left\{{\widehat{\beta }}_{\text{SLR},j}^{\star },j=1,\dots ,k\right\}$, so that this term is larger for the least-squares coefficients of smaller magnitude and smaller for coefficients of larger magnitude. Thus, as λ increases, b decreases and the k nonzero weights are increasingly moved toward 1/k.

Although for ease of exposition we showed these results assuming a positive exchangeable correlation between mixture components, we would expect the general conclusions to hold for correlated mixtures such as those encountered in environmental epidemiology. In our simulation studies, we apply our method both to positive exchangeable predictor correlation matrices and to the predictor correlation matrix observed in the TIDES dataset.

Simulation studies

We assessed the properties of our method in four simulation studies across a range of predictor correlation matrices and degrees of mixture-outcome association. In the first simulation study, the outcome was random noise to assess empirical Type I error rates. We generated a mixture of nine predictors for four cases: three with exchangeable predictor correlation ρ (0.2, 0.5, or 0.8) and one with observed predictor correlation matrix Σ from the log-transformed phthalate metabolite concentrations in TIDES (Supplemental Material 1); the outcome was sampled from a N(10, 2) distribution. In the three remaining studies (Scenarios 1 to 3), the outcome was a linear combination of mixture variables with normally distributed error ϵ_i. Scenario 1 involved a mixture of 20 components, 10 of which were true predictors, with $y_i=10+{\sum }_{j=1}^{10}3x_{ij}+{ϵ}_i$. In Scenario 2, the mixture had 10 components, two of which were true predictors, with y_i = 10 + 5x_i1 + 3x_i2 +ϵ_i. In both Scenarios 1 and 2, we considered four cases, with two values of R² (0.1 [“low signal”], 0.6 [“high signal”]), which determined the error variance, and two values of pairwise correlation ρ (0.2 [“low correlation”], 0.8 [“high correlation”]). Scenario 3 involved nine mixture components generated with the TIDES correlation matrix Σ, all of which were true predictors, with $y_i=10+{\sum }_{j=1}^{9}3x_{ij}+{ϵ}_i$ and the two possible values of R². In all cases, predictors were distributed N(10, 1), the sample size was 300, and 1000 datasets were simulated.

Eight methods were fit to each simulated dataset. We applied our method with both penalties (L1 and L2) and two approaches to significance testing: (1) estimating weights with a training dataset and using a separate test set for inference (“data splitting”) and (2) estimating weights with the entire dataset and doing a permutation test for inference (“permutation test”). We also fit two versions of WQS, one in which weights were estimated using training data and a test set was used for inference (“data splitting”) and one in which the same data were used to estimate the weights and test the overall mixture effect (“no data splitting”). For a given simulated dataset, data-splitting methods used the same training and test sets, with 60% of observations in the test set. Finally, we considered a single linear regression model (“all in one”) and separate linear regressions for each mixture component (“one at a time”). For all methods, predictors were divided by their standard deviation, and quantiles were not used, given that a well-trained analyst would likely be able to identify the predictors as normally distributed. For tables on sensitivity and specificity, selection was defined as weights ≥ 0.05 (the threshold set in the original WQS paper for similar data-generating mechanisms) or p-values < 0.05. All analyses were completed in R version 3.6.0.

Empirical Type I error rates were estimated as the proportion of times the null hypothesis of no association between mixture and outcome was rejected, with nominal α = 0.05. For “all in one”, we performed an F-test comparing the full model to an intercept-only model; for “one at a time”, we took the minimum p-value from coefficient t-tests, as this is the result that, in practice, might be used to identify a chemical mixture as potentially harmful. All of our methods preserved the nominal Type I error rate, as did “all in one” and WQS with data splitting (Table 1). However, the Type I error rate was inflated for WQS without data splitting, with the greatest violations occurring for lower predictor pairwise correlations. The “one at a time” minimum p-value approach also inflated Type I error rates, due to multiple testing.

Table 1.

Empirical Type I error rates (95% CI) in hypothesis tests of overall mixture effect, for three exchangeable predictor correlations ρ and observed correlation Σ in TIDES phthalate metabolites

Method	ρ = 0.2	ρ = 0.5	ρ = 0.8	Observed Σ
Nominal α	0.05	0.05	0.05	0.05
Preserved Type I error
All in one	0.05 (0.04, 0.06)	0.05 (0.04, 0.07)	0.05 (0.04, 0.07)	0.05 (0.03, 0.06)
WQS - data splitting	0.05 (0.03, 0.06)	0.04 (0.03, 0.05)	0.05 (0.04, 0.07)	0.04 (0.03, 0.05)
Modified WQS
L1 - data splitting	0.05 (0.03, 0.06)	0.05 (0.04, 0.07)	0.06 (0.04, 0.07)	0.04 (0.03, 0.06)
L1 - permutation test	0.06 (0.04, 0.07)	0.04 (0.03, 0.05)	0.05 (0.03, 0.06)	0.04 (0.02, 0.05)
L2 - data splitting	0.05 (0.04, 0.07)	0.05 (0.03, 0.06)	0.05 (0.04, 0.07)	0.04 (0.03, 0.05)
L2 - permutation test	0.05 (0.03, 0.06)	0.04 (0.03, 0.05)	0.05 (0.04, 0.06)	0.04 (0.03, 0.06)
Inflated Type I error
WQS - no data splitting	0.25 (0.22, 0.27)	0.15 (0.13, 0.17)	0.10 (0.08, 0.12)	0.15 (0.12, 0.17)
One at a time - min p	0.37 (0.34, 0.40)	0.27 (0.24, 0.30)	0.19 (0.16, 0.21)	0.24 (0.21, 0.27)

Selection accuracy is summarized in Tables 2 and 3. In general, all of the weighted sum regressions were improved by use of the complete dataset instead of a training set for weight estimation; these implementations had better sensitivity (more variables correctly selected) and better specificity (fewer variables incorrectly selected). Among methods with the same approach to data splitting, the optimal implementation was highly dependent on the scenario and case. In Scenario 1 (10 true predictors out of 20), our L2-penalized methods had better sensitivity than WQS, while the L1 methods had better specificity. In Scenario 2 (two true predictors out of 10), the L1 methods had the best specificity again and equally good sensitivity in all but the low-signal, high-correlation case. In Scenario 3, the L2 methods were consistently the most sensitive. Clearly, the choice of penalty should reflect the true data-generating mechanism, as well as the importance to the researcher of sensitivity versus specificity. The “one at a time” linear regressions had good sensitivity but poor specificity, generally selecting all variables, and the “all in one” regression had the opposite, with poor sensitivity except in Scenario 2 or in cases with high signal and low correlation.

Table 2.

Median (IQR) number of predictors correctly and incorrectly selected in simulation scenarios with low signal (R² = 0.1)

Method	Scenario 1, ρ = 0.2		Scenario 1, ρ = 0.8		Scenario 2, ρ = 0.2		Scenario 2, ρ = 0.8		Scenario 3
	# correct	# incorrect	# correct	# incorrect	# correct	# incorrect	# correct	# incorrect	# correct
TRUTH	10	0	10	0	2	0	2	0	9
Preserved Type I error
All in one	1 (1, 2)	0 (0, 1)	0 (0, 1)	0 (0, 1)	2 (1, 2)	0 (0, 1)	1 (0, 1)	0 (0, 1)	1 (0, 1)
WQS - data splitting	5 (4, 6)	2 (2, 3)	3 (2, 4)	3 (2, 4)	2 (2, 2)	3 (2, 4)	2 (1, 2)	3 (3, 4)	6 (5, 6)
Modified WQS
L1 - data splitting	3 (2, 4)	1 (1, 2)	2 (1, 2)	1 (1, 2)	2 (1, 2)	1 (0, 2)	1 (1, 1)	2 (1, 2)	3 (2, 4)
L1 - permutation test	5 (4, 6)	2 (1, 2.25)	2 (2, 3)	2 (1, 2)	2 (2, 2)	1 (0, 2)	1 (1, 2)	2 (1, 2)	4 (4, 5)
L2 - data splitting	6 (5, 6)	3 (2, 4)	4 (3, 6)	4 (2, 5)	2 (2, 2)	3 (2, 4)	2 (1, 2)	4 (2, 6)	7 (6, 8)
L2 - permutation test	6 (5, 7)	3 (2, 4)	5 (3, 6)	4 (2, 5)	2 (2, 2)	2 (1, 3)	2 (1, 2)	3 (2, 6)	7 (6, 8)
Inflated Type I error
WQS - no data splitting	6 (5, 6)	2 (1, 3)	4 (3, 4)	3 (2, 3)	2 (2, 2)	2 (2, 3)	2 (1, 2)	3 (2, 4)	6 (5, 7)
One at a time	9 (7, 10)	6 (4, 7)	10 (10, 10)	10 (10, 10)	2 (2, 2)	2 (1, 3)	2 (2, 2)	8 (8, 8)	8 (8, 9)

Note: Scenario 1 involved a mixture of 20 components, 10 of which were equally associated with the outcome. Scenario 2 had 10 mixture components, two of which were associated with the outcome, one more than the other. Scenario 3 had nine components, all equally associated with the outcome and generated using the observed correlation matrix from the applied example. Selection was defined as weights ≥ 0.05 for the weighted sum regressions and p-values < 0.05 for the linear regressions.

Table 3.

Median (IQR) number of predictors correctly and incorrectly selected in simulation scenarios with high signal (R² = 0.6)

Method	Scenario 1, ρ = 0.2		Scenario 1, ρ = 0.8		Scenario 2, ρ = 0.2		Scenario 2, ρ = 0.8		Scenario 3
	# correct	# incorrect	# correct	# incorrect	# correct	# incorrect	# correct	# incorrect	# correct
TRUTH	10	0	10	0	2	0	2	0	9
Preserved Type I error
All in one	9 (9, 10)	0 (0, 1)	2 (1, 2)	0 (0, 1)	2 (2, 2)	0 (0, 1)	2 (2, 2)	0 (0, 1)	5 (4, 5)
WQS - data splitting	8 (7, 8)	1 (0, 1)	5 (4, 5)	2 (1, 3)	2 (2, 2)	1 (0, 1)	2 (2, 2)	2 (1, 3)	7 (7, 8)
Modified WQS
L1 - data splitting	8 (7, 9)	1 (0, 1)	4 (4, 5)	2 (1, 3)	2 (2, 2)	1 (0, 1)	2 (2, 2)	1 (1, 2)	7 (6, 7)
L1 - permutation test	9 (9, 10)	0 (0, 0)	6 (5, 6)	2 (1, 3)	2 (2, 2)	0 (0, 1)	2 (2, 2)	1 (0, 2)	8 (7, 8)
L2 - data splitting	8 (8, 9)	1 (0, 2)	6 (5, 7)	3 (2, 4)	2 (2, 2)	1 (1, 2)	2 (2, 2)	2 (2, 3)	8 (8, 9)
L2 - permutation test	10 (9, 10)	0 (0, 0)	7 (6, 8)	3 (2, 4)	2 (2, 2)	0 (0, 1)	2 (2, 2)	2 (2, 3)	9 (8, 9)
Inflated Type I error
WQS - no data splitting	9 (9, 10)	0 (0, 0)	6 (5, 6)	2 (1, 3)	2 (2, 2)	0 (0, 1)	2 (2, 2)	1 (0, 2)	8 (7, 8)
One at a time	10 (10, 10)	10 (10, 10)	10 (10, 10)	10 (10, 10)	2 (2, 2)	8 (7, 8)	2 (2, 2)	8 (8, 8)	9 (9, 9)

Note: Scenario 1 involved a mixture of 20 components, 10 of which were equally associated with the outcome. Scenario 2 had 10 mixture components, two of which were associated with the outcome, one more than the other. Scenario 3 had nine components, all equally associated with the outcome and generated using the observed correlation matrix from the applied example. Selection was defined as weights ≥ 0.05 for the weighted sum regressions and p-values < 0.05 for the linear regressions.

In practice, a researcher using these methods will probably be more interested in the magnitude of the weights than their relation to an arbitrary cutoff. Therefore, Figures 2 and 3 illustrate the estimated weight distributions for three of the methods fit to Scenarios 1 and 2: WQS with training data, as this is the version that preserves Type I error, and our method with full data and either an L1 or L2 penalty. We show results only for the low-signal settings, as the differences between the methods are more obvious in these more challenging cases. In Figure 2, the L1-penalized method displays near-perfect specificity, almost always setting weights of incorrect variables to zero. But, this method can also underestimate weights for true predictors, especially in a high-correlation setting. The L2-penalized method, on the other hand, estimates weights that are more similar to those of WQS and is evidently better than WQS at distinguishing between correct and incorrect predictors in the high-correlation setting. In Figure 3, both WQS and the L2-penalized method assign too much weight to irrelevant predictors and therefore underestimate the weights of the two true predictors. The L1-penalized method, on the other hand, generally sets irrelevant weights to zero and is therefore much more accurate in weight estimation for the two true predictors.

Figure 2.

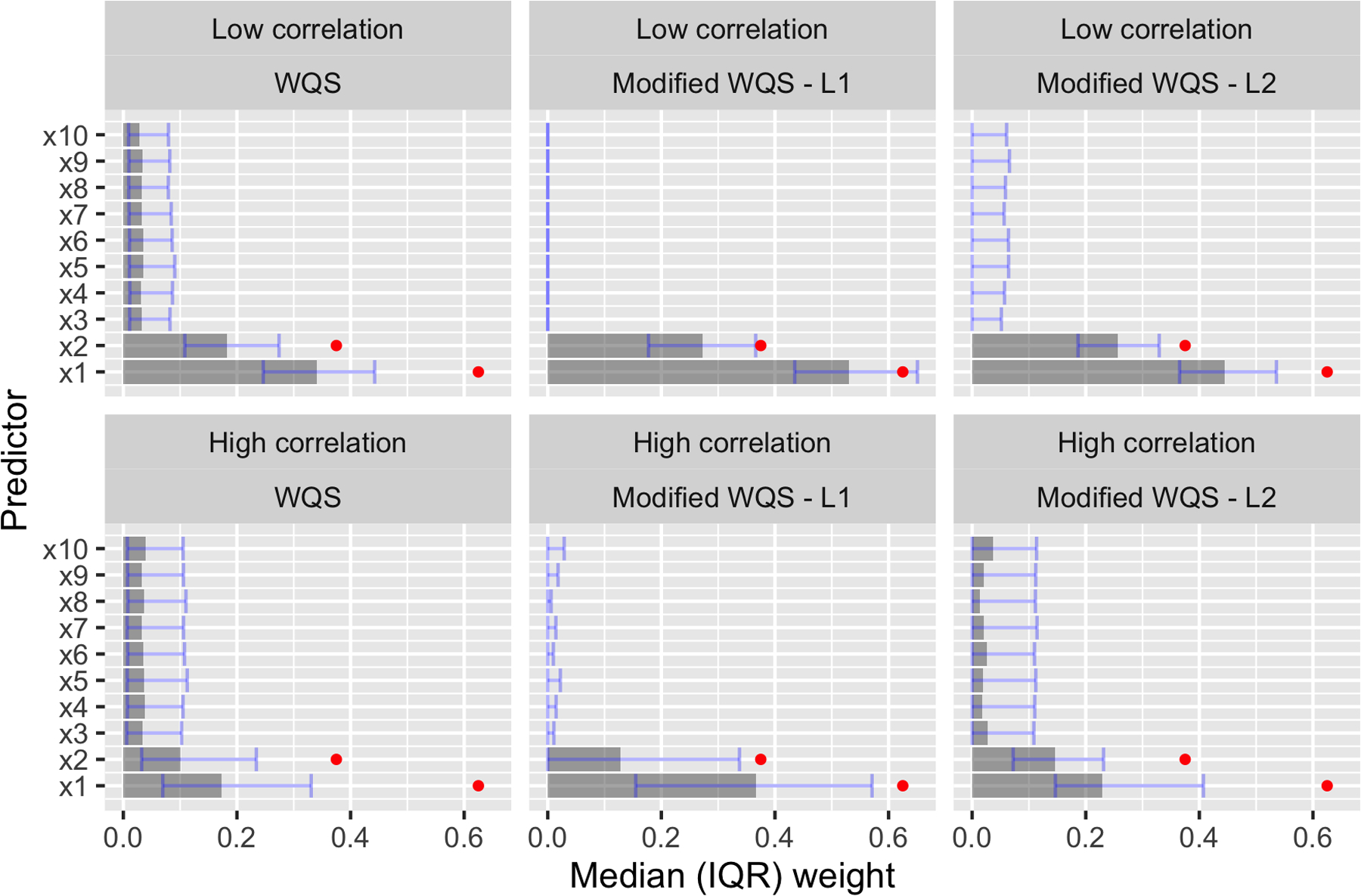
Scenario 1, R² = 0.1: Median estimated weights with bars from the 25th to the 75th percentile. Weights were estimated using training data for WQS and full data for our method. True weights are shown in red.

Figure 3.

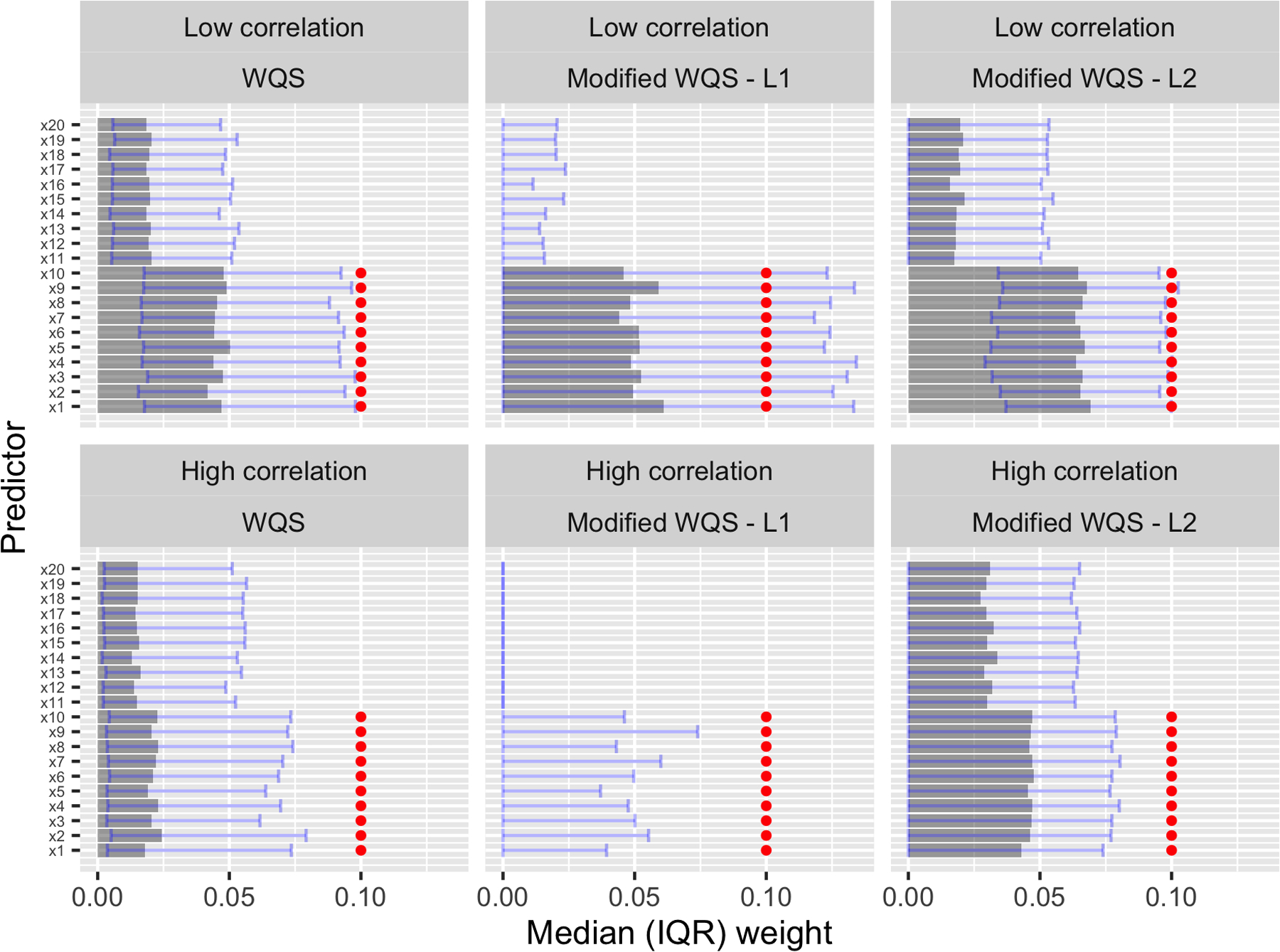
Scenario 2, R² = 0.1: Median estimated weights with bars from the 25th to the 75th percentile. Weights were estimated using training data for WQS and full data for our method. True weights are shown in red.

We also considered bias, variance, and power in estimation of the overall mixture effect, with results for the low-signal settings shown in Tables 4 and 5 (bias was minimal for all methods in the high-signal settings, and power was perfect). In general, the methods that used data splitting were slightly biased downward, and those that used the full data were slightly biased upward. Of the full-data methods, ours was less biased than WQS, and the bias was smaller in high-correlation or observed-correlation settings. In Scenario 1 with ρ = 0.2, the “L1 - data splitting” version of our method underestimated the overall mixture effect more than other methods and had the lowest observed power (0.826), indicating a different method may be preferable in this case. Variance was comparable between all methods that used the same sample size for inference, and power to identify the overall mixture effect as significant (p < 0.05) was always higher in the methods that used a larger sample size. Of the methods that preserved Type I error, the permutation-test versions of our method had higher power than WQS in all cases.

Table 4.

Mean (SD) of overall mixture effect estimators in simulation scenarios with low signal (R² = 0.1)

Method	Scenario 1		Scenario 2		Scenario 3
	ρ = 0.2	ρ = 0.8	ρ = 0.2	p = 0.8	Observed Σ
TRUTH	30	30	8	8	27
Preserved Type I error
WQS - data splitting	25.9 (6.7)	29.1 (6.8)	8.6 (2.4)	7.9 (1.9)	24.7 (6.4)
Modified WQS
L1 - data splitting	17.6 (7.9)	27.2 (6.7)	7.0 (2.5)	7.5 (1.9)	20.8 (6.6)
L1 - permutation test	32.0 (5.9)	32.0 (5.2)	9.0 (1.8)	8.5 (1.5)	27.2 (5.4)
L2 - data splitting	26.3 (7.0)	29.0 (6.9)	8.3 (2.4)	7.9 (1.9)	24.2 (6.3)
L2 - permutation test	34.5 (5.0)	32.0 (5.2)	9.8 (1.7)	8.6 (1.5)	27.7 (4.9)
Inflated Type I error
WQS - no data splitting	34.5 (5.0)	32.3 (5.2)	10.0 (1.7)	8.6 (1.5)	28.6 (4.8)

Table 5.

Estimated power to identify overall mixture effect as significant (p < 0.05) in simulation scenarios with low signal (R² = 0.1)

Method	Scenario 1		Scenario 2		Scenario 3
	ρ = 0.2	ρ = 0.8	ρ = 0.2	ρ = 0.8	Observed Σ
Preserved Type I error
WQS - data splitting	0.968	0.989	0.954	0.981	0.976
Modified WQS
L1 - data splitting	0.826	0.983	0.919	0.978	0.952
L1 - permutation test	0.989	1	0.985	1	0.998
L2 - data splitting	0.970	0.991	0.942	0.983	0.98
L2 - permutation test	1	1	0.988	1	1
Inflated Type I error
WQS - no data splitting	1	1	1	1	1

Note: Scenario 1 had 20 mixture components, 10 of which were equally associated with the outcome. Scenario 2 had 10 mixture components, two of which were associated with the outcome, one more than the other. Scenario 3 had nine components, all equally associated with the outcome and generated using the observed correlation matrix from the applied example.

Applied example

Phthalates are a family of chemicals used to increase flexibility of plastics, including food and beverage containers, hygiene and beauty products, and plastic packaging. Exposure to phthalates can occur through ingestion, inhalation, or skin absorption, after which phthalates are metabolized and leave the body primarily through urine^4,24. Two phthalates, DEHP and DBP, can cause birth defects in male rats in what is known as the “phthalate syndrome”²⁵, and in human cohort studies, these and other phthalates have been linked to adverse reproductive, neurodevelopmental, metabolic, and respiratory outcomes^26–31.

The Infant Development and Environment Study (TIDES) is a prospective pregnancy cohort study focused on prenatal phthalate exposure and child development. In each trimester, participants gave urine samples for measurement of phthalate metabolite concentrations. Swan et al.⁷ analyzed associations between the first-trimester concentrations and infant anogenital distance (AGD), a sensitive marker of prenatal disruption in the genital tract. Short male AGD has been associated with poorer semen quality, reduced testosterone, and infertility³². In separate multivariable linear regressions for each first-trimester metabolite (the “one at a time” approach), Swan et al.⁷ observed significant inverse relations between infant anoscrotal distance (AGD_AS) and three of four metabolites of DEHP: MEHP, MEOHP, and MEHHP, adjusting for infant age at birth exam, weight-for-length Z-score, gestational age at birth, study center, time of day of urine collection, and maternal age. The fourth metabolite of DEHP, MECPP, was not significantly associated with AGD_AS. Five other metabolites, each pertaining to one parent phthalate, were also examined: MEP, MBzP, MBP, MiBP, and MCPP. In separate covariate-adjusted models, none were associated with AGD_AS.

We were interested in assessing the relation between first-trimester phthalate metabolites and infant AGD_AS with both WQS (with data splitting) and our method (with data splitting or a permutation test) and comparing the results with the original Swan, et al.⁷ analysis. We also fit a linear regression including all nine metabolites and tested overall mixture significance with an F-test (“all in one”). Phthalate concentrations were adjusted for urinary specific gravity³³, log₁₀-transformed, and divided by their sample standard deviations, so that β₁ is the expected change in AGD_AS, measured in mm, when all metabolites increase by one standard deviation. All methods adjusted for the same non-mixture covariates that were included in Swan et al.⁷; when fitting our method, these terms were not penalized. Given the existing research on DEHP and DBP, which correspond to five of the nine metabolites, we chose an L2 penalty for our method. WQS was applied with negative β₁, 100 bootstraps, and t-statistic bootstrap weights (the default in the gWQS package). As there was no evidence of influential points in the metabolite distributions, quantiles were not used. The same training and test sets were used for WQS and our method, with 60% of data in the test set. AGD_AS was available for 366 male infants.

Estimated weights and coefficients are shown in Table 6. We include the most significant “one at a time” result for comparison with the tests of overall mixture effect, as this is the finding that, in practice, could flag a mixture as potentially harmful. No metabolites were selected in the “all in one” approach, and coefficients that had been similar in the original analysis took on opposing signs, likely due to collinearity. In terms of weight estimation, WQS placed 66 percent of the weight on the DEHP metabolites, 20 percent on MBP, and 5 percent or less on each of the other metabolites. Our method placed more weight on the DEHP metabolites: 81 percent when training data were used to estimate the weights and 74 percent when the complete data were used. Our method also allocated about 15 percent of the weight to MBP. The overall mixture effect was stronger for our method, with ${\widehat{\beta }}_1=-0.80$ and −0.71 compared to −0.52 for WQS; this was significant only for our method with data splitting.

Table 6.

Association of first-trimester maternal phthalate exposure and anogenital distance in male infants in TIDES

	Estimated metabolite weights $\widehat{w}$ and coefficients $\widehat{\beta }$ for phthalate metabolites									Mixture overall
	MEHP	MEOHP	MEHHP	MECPP	MEP	MBzP	MBP	MiBP	MCPP	${\widehat{\beta }}_1$	P-value
All in one ($\widehat{\beta }$)	0.00	−1.86	0.39	0.78	−0.19	0.48	−0.35	0.23	0.30	—	0.07
One at a time ($\widehat{\beta }$)	−0.45*	−0.58*	−0.54*	−0.35	−0.19	0.07	−0.35	−0.17	0.10	—	0.01
WQS ($\widehat{w}$)	0.26	0.22	0.11	0.07	0.05	0.06	0.20	0.02	0.01	−0.52	0.17
Modified WQS
L2 - data splitting ($\widehat{w}$)	0.19	0.23	0.21	0.18	0.00	0.03	0.15	0.00	0.00	−0.80	0.03
L2 - permutation test ($\widehat{w}$)	0.18	0.25	0.22	0.09	0.11	0.00	0.14	0.02	0.00	−0.71	0.13

Note: The asterisk indicates a significant (p < 0.05) coefficient in the linear regressions.

In summary, our method was able to detect a stronger signal from the mixture overall than WQS, perhaps due to the larger amount of weight placed on the DEHP metabolites. Multiple weights were set to zero or near zero for our method, while WQS distributed weight more equally, possibly to spurious predictors. Ultimately, our method with data splitting was the only one to find a significant overall mixture effect, which was somewhat surprising, as the permutation test uses a larger sample size and had slightly higher power in simulation studies. One takeaway from this result may be the importance of applying our method both with data splitting and with the permutation test for comparison. Evidently, our method has potential benefits beyond enabling analysts to use the same data in weight estimation and inference.

Conclusion

The identification of bad actors is an important and challenging aspect of chemical mixtures analysis. Our simulations imply that two common approaches in this field — separate “one at a time” regressions and WQS without data splitting — can be suboptimal, due to inflation of Type I error rates to unacceptable levels (up to 0.25 for a nominal α of 0.05). We have also shown that data splitting can increase the variance of estimated overall mixture effects, reduce power, increase bias, and harm sensitivity and specificity of variable selection. These challenges motivate our modified weighted sum regression in which a permutation test is used to perform inference on the same data used to estimate the weights. To offset the computational burden of a permutation test, we propose that weights be regularized using L1 or L2 penalization instead of bootstrap aggregation. Our method allows for all data to be used in all steps of the analysis, while preserving the desired Type I error rate. Although this paper focuses primarily on hypothesis testing to characterize variability of the overall mixture effect, a confidence interval could also be computed, for example using the nonparametric bootstrap. Code to fit our method and run the simulation studies is available at https://github.com/glyden/Modified-WQS.

Our method is sensitive to the choice of L1 versus L2 penalization, and we recommend that researchers use their underlying philosophy about or experience with the chemical mixture in question to decide. For example, if a mixture has many chemicals that are all known to be somewhat associated with the outcome, i.e., the true weights are not sparse, the L2 penalty will be more sensitive and more powerful than the L1. If, on the other hand, a mixture has only one or two bad actors that a researcher wishes to identify, the L1 penalty will be more accurate in weight estimation and less likely to assign weight to spurious predictors. In simulation studies, our method with a permutation test was able to match or beat the selection accuracy of WQS with data splitting in all but one case, given the appropriate choice of penalty. Even in that case (Scenario 1, R² = 0.1, ρ = 0.8), the L1 version of our method had better specificity than WQS and the L2 version had better sensitivity. The choice of penalty matters less when there is a strong association between the mixture and the outcome. In high-signal simulations, both versions of our method (L1 and L2) had superior sensitivity and specificity compared to WQS with data splitting, across all cases.

One limitation of our method is the slight upward bias that results from using the same data twice: first to estimate the weights and then to estimate and test the overall mixture effect. This is a fundamental problem in machine learning and data-adaptive methods, which is often addressed by using methods of cross-validation or data splitting, as in WQS. WQS with data splitting, however, suffered from downward bias in our simulations, which may be less acceptable to analysts working with chemical mixtures than upward bias, as there may be greater ramifications to underestimating a truly harmful effect. The bias of our method was small to negligible in clinically relevant settings (i.e., those with higher predictor correlation) and consistently smaller than the bias of WQS without data splitting, which also fails to preserve Type I error. In exchange for a small amount of upward bias, our method allows analysts to use their full study dataset for both estimation and testing, increasing power and selection accuracy while preserving Type I error.

In conclusion, we have introduced a new approach to weight estimation and inference modeled on Weighted Quantile Sum regression that does not require data splitting for valid inference on the overall mixture effect. We have observed that shrinkage methods can be tailored for chemical mixtures analysis by adding nonnegativity or nonpositivity constraints, and we encourage the use of a priori knowledge about specific chemical mixtures and their potential effects on human health to select between L1 or L2 penalization. Our method is a new option for researchers who wish to evaluate the overall health impact of a chemical mixture while simultaneously identifying bad actors for policy and regulatory purposes.

Appendix

Proof of the Frisch-Waugh-Lovell theorem for constrained penalized regression

Let Z be the n × m matrix of non-mixture covariates, X be the n × p matrix of mixture variables, and x_j be the jth column of X. Assume a vector of 1s corresponding to an intercept is included in Z. Let H_Z be the hat matrix for Z, i.e., Z(Z^TZ)⁻¹Z^T, and let Q_Z = I_n − H_Z, so that Q_Zy represents the residual vector from a linear regression of y on Z and Q_ZX represents the matrix of residuals from linear regressions of the columns of X on Z. Note that both H_Z and Q_Z are orthogonal projections and therefore by definition symmetric and idempotent.

Consider two minimization problems:

$$(\widehat{\beta }\widehat{\psi })=\underset{\beta \in {ℝ}^p,\psi \in {ℝ}^m}{\text{argmin}}\frac{1}{2}\Vert y-Z\psi -X\beta {\Vert }_2^2+\lambda \Vert \beta {\Vert }_1,{\beta }_j\ge 0,j=1,\dots ,p$$ (6)

$$\tilde{\beta }=\underset{\beta \in {ℝ}^p,\alpha \in ℝ}{\text{argmin}}\frac{1}{2}{\Vert Q_{Z}y-\alpha 1_n-Q_{Z}X\beta \Vert }_2^2+\lambda \Vert \beta {\Vert }_1,{\beta }_j\ge 0,j=1,\dots ,p$$ (7)

We wish to show $\widehat{\beta }=\tilde{\beta }$. Without loss of generality, we consider the case when β is constrained to be nonnegative and the L1 penalty is used; the proof for nonpositive β or with L2 penalization is similar.

Components of $\widehat{\psi }$ are not constrained. Therefore, the following will always hold:

$$\frac{d}{d\psi }\left\{\frac{1}{2}\Vert y-Z\psi -X\beta {\Vert }_2^2+\lambda \Vert \beta {\Vert }_1\right\}=-Z^T(y-Z\psi -X\beta )\Rightarrow Z^T(y-Z\widehat{\psi }-X\widehat{\beta })=0$$ (8)

$$\Rightarrow \widehat{\psi }={\left(Z^{T}Z\right)}^{-1}{Z}^T(y-X\widehat{\beta })$$ (9)

Meanwhile, the derivative of the minimand in 6 w.r.t. β_j will equal zero at the minimizer for all j such that ${\widehat{\beta }}_j>0$, i.e.:

$$\frac{d}{d{\beta }_j}\left\{\frac{1}{2}\Vert y-Z\psi -X\beta {\Vert }_2^2+\lambda \Vert \beta {\Vert }_1\right\}=-x_j^T(y-Z\psi -X\beta )+\lambda$$ (10)

$$\Rightarrow x_j^T(y-Z\widehat{\psi }-X\widehat{\beta })-\lambda =0\forall j\text{ s}.\text{t}.{\widehat{\beta }}_j>0;\text{ else, }{\widehat{\beta }}_j=0$$ (11)

Continuing to 7, the same holds for all j such that ${\tilde{\beta }}_j>0$:

$$\frac{d}{d{\beta }_j}\left\{\frac{1}{2}{\Vert Q_{Z}y-\alpha 1_n-Q_{Z}X\beta \Vert }_2^2+\lambda \Vert \beta {\Vert }_1\right\}=-x_j^T{Q}_Z^T\left(Q_{Z}y-\alpha 1_n-Q_{Z}X\beta \right)+\lambda$$ (12)

$$\Rightarrow x_j^T\left(Q_{Z}y-Q_{Z}X\tilde{\beta }\right)-\lambda =0\forall j\text{ s}.\text{t}.{\tilde{\beta }}_j>0\text{; else, }{\tilde{\beta }}_j=0\text{, }$$ (13)

where we have used the facts $Q_Z^T=Q_Z,Q_Z{Q}_Z=Q_Z$, and $\alpha Q_Z^T{1}_n=0$ because 1_n ∈ R(Z) and Q_Z is the projection matrix onto the space orthogonal to R(Z).

Substituting 9 into 11, we find:

$$x_j^T(y-Z\widehat{\psi }-X\widehat{\beta })-\lambda =x_j^T\left(y-Z{\left(Z^{T}Z\right)}^{-1}{Z}^T(y-X\widehat{\beta })-X\widehat{\beta }\right)-\lambda$$ (14)

$$=x_j^T\left(y-H_{Z}y+H_{Z}X\widehat{\beta }-X\widehat{\beta }\right)-\lambda$$ (15)

$$=x_j^T\left(\left(I_n-H_Z\right)y-\left(I_n-H_Z\right)X\widehat{\beta }\right)-\lambda$$ (16)

$$=x_j^T\left(Q_{Z}y-Q_{Z}X\widehat{\beta }\right)-\lambda =0\forall j\text{ s}.\text{t}.{\widehat{\beta }}_j>0;\text{ else, }{\widehat{\beta }}_j=0\text{, }$$ (17)

which matches 13. Therefore, the minimization problems are equivalent, and $\widehat{\beta }=\tilde{\beta }$.

Implications of L1 versus L2 penalization, continued: Technical details

We now provide the details that justify the following result from the Implications of L1 versus L2 penalization section: ${\widehat{\beta }}_{\text{NNLS},j}^{\star }={(n-1)}^{-1}{\widehat{R}}_j^{-1}{\sum }_{i=1}^n{y}_i{x}_i=\frac{1+ak-2a}{(1-a)(1+ak-a)}\left({\widehat{\beta }}_{\text{SLR},j}^{\star }-\frac{a}{1+ak-2a}{\sum }_{l\ne j}{\widehat{\beta }}_{\text{SLR},l}^{\star }\right)$.

First, note that ${\widehat{\beta }}_{\text{SLR},j}^{\star }=\frac{{\sum }_{i=1}^n{x}_{ij}{y}_i}{{\sum }_{i=1}^n{x}_{ij}^2}=\frac{{\sum }_{i=1}^n{x}_{ij}{y}_i}{n-1}$, because x_j is centered and standardized. Therefore, ${\widehat{\beta }}_{\text{NNLS},j}^{\star }={(n-1)}^{-1}{\widehat{R}}_j^{-1}{\sum }_{i=1}^n{y}_i{x}_i={\widehat{R}}_j^{-1}{\widehat{\beta }}_{\text{SLR}}^{\star }$, where ${\widehat{\beta }}_{\text{SLR}}^{\star }$ is the vector of slopes from the k simple linear regressions.

Second, recall that $\widehat{R}$ is a compound symmetric matrix, such that the diagonals of $\widehat{R}$ are 1 and the off-diagonals are a. Thus, $\widehat{R}=\left((1-a)I_k+a{1}_k{1}_k^T\right)$, which implies ${\widehat{R}}^{-1}=\frac{1}{1-a}{I}_k-\frac{\frac{a}{{(1-a)}^2}{1}_k{1}_k^T}{1+\frac{a}{1-a}{1}_k^T{1}_k}$ by the Sherman-Morrison formula. It is then straightforward to show that the diagonals of ${\widehat{R}}^{-1}$ are $\frac{1+ak-2a}{(1-a)(1+ak-a)}$ and the off-diagonals are $\frac{-a}{(1-a)(1+ak-a)}$, proving the desired result.