A 6G meta-device for 3D varifocal

Abstract

The sixth-generation (6G) communication technology is being developed in full swing and is expected to be faster and better than the fifth generation. The precise information transfer directivity and the concentration of signal strength are the key topics of 6G technology. We report the synthetic phase design of rotary doublet Airy beam and triplet Gaussian beam varifocal meta-devices to fully control the terahertz beam’s propagation direction and coverage area. The focusing spot can be delivered to arbitrary positions in a two-dimensional plane or a three-dimensional space. The highly concentrated signal can be delivered to a specific position, and the transmission direction can be adjusted freely to enable secure, flexible, and high-directivity 6G communication systems. This technology avoids the high costs associated with extensive use of active components. 6G communication systems, wireless power transfer, zoom imaging, and remote sensing will benefit from large-scale adoption of such a technology.

The rotary meta-device offers possibilities of security, flexibility, and high directivity for future 6G communication systems.

INTRODUCTION

Fifth-generation (5G) wireless communication technology is taking off and is being widely commercialized worldwide. The starting gun for the technology research and development of the sixth-generation (6G) communication network has been fired (1). All spectra will be fully explored in the future 6G mobile communication system to provide a higher data rate, including optical frequency bands, terahertz (THz), millimeter wave, and sub-6 GHz (2). Compared with the optical frequency bands, the THz band can penetrate partial occlusions and realize high-precision imaging and perception in nonvisual scenes. The THz band technology has abundant spectrum resources to support the 100 Gbps and even Tbps level ultrahigh-speed data rate in wireless communications. It is hundreds to thousands of times higher than the transmission data rate of the millimeter wave in 5G. According to these advantages, it is essential to develop the THz technology based on the future 6G requirement (3). In conventional THz systems, bulky and heavy dielectric lenses and reflectors are the two most common devices. They can collimate waves from the THz source in transmitters or focus incident waves to the detector in receivers (4). The THz waves can only be guided to a fixed transmitter or detector (5) or transmitted to a single receiver located at a fixed position or covering a limited area. Although there are traditional lenses that realize off-axis focusing, the requirements of tilting need extra space, and the tilting stage hinders its compact integration. These disadvantages hinder the development of the future 6G application with a high precision positioning and concentrated signal strength. For example, indoor communication scenarios with dense users/receivers in a small space require high resolution and flexible tunability (6). Otherwise, the signals may cover the receivers nearby the target. It is crucial to allow the signal to distinguish, focus on, and track the specific users/receivers without wasting power on the nearby receivers and impairing privacy. The technology of 6G applications requires a tunable THz device with adjustable directivity and highly concentrated signal transmission in an arbitrary two-dimensional (2D) plane and 3D space.

In recent years, planar metasurface-based devices have been developed and potentially replaced conventional bulky devices (7–12). The metasurface is composed of subwavelength artificial meta-antennas (13–17), and it can accurately manipulate the wavefront of electromagnetic waves in subwavelength resolution (18–23). Meta-devices are easy to be integrated because of the advantages of being flat, ultrathin, and compact (24–27). Nowadays, various designs and functionalities, impracticable to be implemented in conventional bulky devices, are realized in metasurfaces, such as achromatic meta-lens (28), achromatic meta-lens array (29), meta-lens multiphoton quantum source (30), and beam steering devices in optical (31), THz, and microwave bands (32, 33). Beam steering devices are important for wireless communication systems, especially for 6G communication. Meta-devices that can flexibly control the radiation direction and coverage area of beams are attractive topics (34). In optical band, varifocal meta-lenses have been demonstrated through various methods, for example, integrating a liquid crystal (LC) layer (35, 36), using phase change material (37, 38), adopting stretchable elastic substrates (39), utilizing the polarization freedom (40), and controlling the lateral or rotational displacement of meta-lens doublet (41). In microwave bands, beam scanning of the metasurfaces can be achieved by integrating active transistors, such as Positive-intrinsic-negative (PIN) diodes (42–44), varactor (45, 46), and Micro Electromechanical System (MEMS) (47). Some active materials, such as LC, graphene, and VO₂, are explored to achieve beam steering and projection in the THz band (48). However, the THz beam can only be steered in a single direction or be focused in limited specified areas via these methods. The proposed function may be achieved with extensive use of active components (e.g., PIN diodes and varactor diodes). However, the high costs and complexity in making these devices suitable to operate in the THz regime will impair their large-scale deployment in future 6G communication systems and other relevant application scenarios (49). Here, we propose a rotary metasurface technology to fully control the THz beam’s radiation direction and coverage area based on the 6G communication requirement. The focusing spot of the THz wave can be projected into an arbitrary spot in a 2D plane or even a 3D space. Only the user/detector in the specific spot could receive the signal, and the highly concentrated signal can be flexibly switched to other users/detectors. This will increase the directivity, security, and flexibility in future 6G communication. Besides the proposed technology, several methods have been demonstrated to fulfill the requirements of the future 6G technology. For example, the graphene metasurface is used to steer two or three beams at three different angles (50). The reconfigurable intelligent surface is another critical way (51). It uses the active components to realize the dynamic beam steering. The LC-based reflectarray metasurface could have a scanning range of ±40° (52). However, these methods either cannot cover the full 3D space, have complex configuration, or only provide nonconcentration signals.

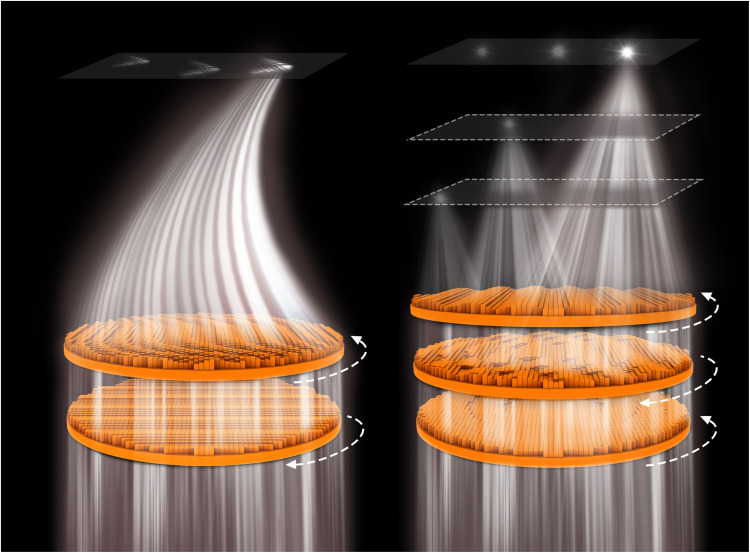
This article reports an approach to creating varifocal THz meta-devices with a fully tunable range of focal spots. We make the varifocal meta-devices by reasonably incorporating and rotating several phase profiles, i.e., the cubic phase, gradient phases, and focusing phases, performing various projections within two or three metasurfaces. By exploiting the transmission phase within the meta-antenna of the corresponding position, the meta-devices can work as efficient projectors, steering the focal spot in a 2D plane or even a 3D space. As a proof of concept, we demonstrated two kinds of varifocal meta-devices to verify the ability to manipulate the wavefront and focus arbitrarily. The doublet meta-device is designed for steering the Airy beam focusing in a 2D plane. The triplet meta-device is developed for focal spot manipulation in 3D space. The schematic diagrams of these two meta-devices are shown in Fig. 1. The various configurations for the meta-devices allow the focal spot to be reconfigured to access different transmitters or detectors, offering possibilities for a flexible, high-directivity, high–signal concentration, and secure 6G communication system in the future. Besides the arbitrary manipulation of the focal spot, the diffraction-free, self-healing, self-accelerating properties of Airy beams can improve signal transmission stability and security in wireless communication (53). In a nutshell, diffraction-free characteristics mean that signals can be transmitted consistently over longer distances. The self-healing feature facilitates rapid signal recovery after disruption; self-accelerating performance gives the signal the ability to avoid eavesdroppers.

Fig. 1. The schematics of the varifocal meta-devices.

The proposed technology contributes to the development of the WEAF Mnecosystem, i.e., the Water, Earth, Air, and Fire Micro/Nanotechnologies Ecosystem, by combining three key-enabling technologies (KETs) of 6G and future networks, which are THz communications, metasurfaces, and 3D printing (54). In particular, the Airy beams fit the WEAF Mnecosystem well for its diffraction-free, self-recovery, and self-accelerating properties (55). The proposed technology lies within a broader scenario of KETs, expected to become more crucial in the future. These breakthroughs will contribute to the development of 6G communication, making it more robust and reliable.

RESULTS

Design and fabrication

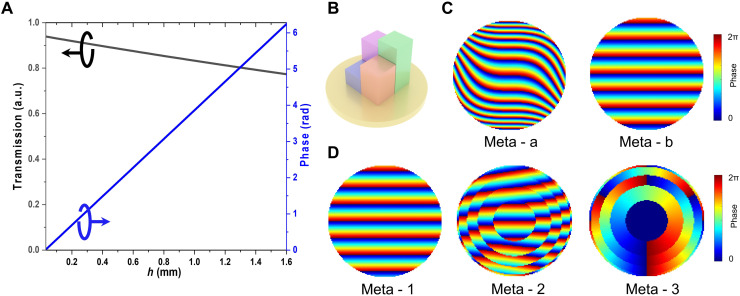
To design a metasurface with a 30-mm diameter, we developed a 3D printing method for easy, large-scale, and low-cost fabrication for practical 6G applications (see Materials and Methods for the detailed fabrication process). The material selected for the 3D-printed metasurface is a high-temperature resin with a refractive index of 1.631 + 0.009i at the working wavelength, λ = 1 mm, retrieved by time-domain spectroscopy measurement (15). The accuracy of our fabrication method is 0.085λ in the horizontal direction and 0.025λ in the vertical direction. It allows us to perform high-precision wavefront tailoring. The wave number and the transmission distance can characterize the phase of the THz wave. After the THz wave with an initial phase ϕ₀ passes through the dielectric pillar with a thickness of d and a wave number of k_0, its phase ϕ gradually accumulates to ϕ = ϕ₀ + k₀d. Therefore, changing the dielectric pillar’s thickness and hence the wave’s propagation distance can modulate the transmission phase accordingly. Combining this principle with our manufacturing methods, we set the unit cell period to 0.25λ, while the meta-antenna height h varies from 0 to 1.59λ with a total of 63-level discrete phase states, as shown in Fig. 2 (A and B). The unit-cell electromagnetic design simulation is performed by the COMSOL Multiphysics commercial simulation tool.

Fig. 2. The working principles of varifocal meta-devices.

(A) The simulated transmission and phase characteristics as a function of height h. a.u., arbitrary units. (B) The schematic of the nanorods. (C) Phase profiles of the meta-device for varifocal Airy beam. (D) Phase profiles of the meta-device for manipulating the focal spot in 3D space.

As a first demonstrating example, we design the meta-device for the varifocal Airy beam, using the cubic phase profile ϕ₁ to generate it (56, 57)

$${\mathrm{\varphi }}_1=\frac{1}{3}{(2\pi a)}^3(x^3+y^3)$$ (1)

where a = −x₀/(λf) is a constant, with the half-power beamwidth being 1.6x₀, while (x, y) are the coordinates of the metasurface pixel elements. The Airy beam will be shifted away from the zero-order diffraction by introducing two additional independent gradient phases. The relative rotation of the two identical gradient phases ϕ₂ and ϕ₃ will generate different gradient phases with different magnitudes and directions, and

$${\mathrm{\varphi }}_2={\mathrm{\varphi }}_3=-bx$$ (2)

where b is a constant. Then, for each gradient metasurface, the beam deflection in the x direction of a normal incident beam can be calculated by the generalized law of refraction

$$\sin ({\mathrm{\theta }}_t)n_t-\sin ({\mathrm{\theta }}_i)n_i=\frac{\mathrm{\lambda }}{2\pi }\frac{d(-bx)}{dx}$$ (3)

where θ_i and θ_t are the incident and refraction angles, respectively, while n_i and n_t are the refractive indices of the two media. In our case, θ_i = 90°, n_i = n_t = 1, and λ = 1 mm, and then θ_t can be expressed as

$${\mathrm{\theta }}_t=\arcsin \left(\frac{-b}{2\pi }\right)$$ (4)

Each gradient metasurface will deflect the incident beam with a fixed refraction angle; thus, combining these two independent rotational gradient phase profiles can create a newly flexible gradient phase profile. Here, we assume that the rotation angle of gradient phases, ϕ₁, is θ/2, and the other gradient phases, ϕ₂, is −θ/2. By adding the two gradient phase profiles together, we get the new flexible gradient phase profile, ψ as

$$\begin{array}{rl}\mathrm{\psi }& =-b[x\cos (\mathrm{\theta }/2)+y\sin (\mathrm{\theta }/2)]-b[x\cos (-\mathrm{\theta }/2)\\ & +y\sin (-\mathrm{\theta }/2)]=-2bx\cos (\mathrm{\theta }/2)\end{array}$$ (5)

The beam deflection angle θ_t in the direction of x at a normal incident wave can be expressed as

$${\mathrm{\theta }}_t=\arcsin \left[\frac{-b\cos (\mathrm{\theta }/2)}{\pi }\right]$$ (6)

The focus scanning range in the x direction swings from 0 to a particular maximum value depending on the constant b of the original gradient phase. Notably, it could cover all directions in the plane when rotating the two metasurfaces together. Thus, the Airy beam focal spot can be transferred to any point in a 2D plane. An obvious and direct method is fabricating three metasurfaces with the cubic phase and two gradient phases to realize such a design. Here, we combine the cubic phase and one of the gradient phase profiles into one single metasurface, named “meta - a” (fig. S1), to simplify the fabrication process and increase transmission efficiency. The other gradient phase profile is denoted as “meta - b”. In this way, the fabrication process is simplified, and the size and complexity of the meta-device are reduced. At the same time, the two gradient phases remain independent. Rotating meta - a will induce the rotation of the sidelobe of the Airy beam, which will further help verify our design. Figure 2C shows the phase profiles of meta - a and meta - b.

To design the meta-device for focal spot manipulation in 3D space, we use two identical gradient phases (ϕ₂ and ϕ₃) to tune the position of the focal spot in the transversal plane (x, y: plane). As for controlling the focal spot projection along the longitudinal direction (z axis), we introduce two focusing phase profiles ϕ₄ and ϕ₅

$$\begin{array}{rl}{\mathrm{\varphi }}_4& =-\mathrm{round}[\frac{1}{\mathrm{\lambda }{f}_0}(x^2+y^2)]\\ \\ {\mathrm{\varphi }}_5& =\mathrm{round}[\frac{1}{\mathrm{\lambda }{f}_0}(x^2+y_2)]\end{array}$$ (7)

where f₀ is the focal length, and the round function is used for rounding a higher integer number in each phase profile. It is to avoid errors brought by the rotation of these two phase profiles (58). Here, we show how the relative rotation will affect the focal length. Assume that the rotation angle of the phase profile ϕ₄ and ϕ₅ is θ₁ and θ₂, respectively. The total phase of the two focusing phases becomes

$${\mathrm{\varphi }}_{\mathrm{total}}={\mathrm{\varphi }}_4(x,y){\mathrm{\theta }}_1+{\mathrm{\varphi }}_5(x,y){\mathrm{\theta }}_2={\mathrm{\varphi }}_5(x,y)({\mathrm{\theta }}_2-{\mathrm{\theta }}_1)$$ (8)

and the focal length f will be (59)

$$f=\frac{\pi }{{\mathrm{\theta }}_2-{\mathrm{\theta }}_1}{f}_0$$ (9)

For example, when the angle difference changes from 1.5π to π, the focal length will gradually shift from f₀/1.5 to f₀. Thus, the focal spot can be fully tuned in 3D space. Similar to the above case, we combine one of the gradient phases and one of the focusing phase profiles to reduce the fabrication complexity and meta-device size (fig. S1). The three phase profiles encoded on metasurfaces are shown in Fig. 2D.

Experimental setup and results

For experimental verification purposes, we set a = 0.059 and b = 1.4 in the meta-device for varifocal Airy beam. These parameters are optimized through the Fresnel diffraction method. These phase profiles collectively provide the Airy beam up to 60-mm transmission distance, and the beam steering range covers areas with a diameter of 60 mm at 0.3 THz. In the meta-device for focal spot manipulation in 3D space, we set b = 1.4 and f₀ = 60 mm. The accessible range will be from 40 to 60 mm (fig. S2). Thus, the covered volume of the THz signal will be a conical frustum space.

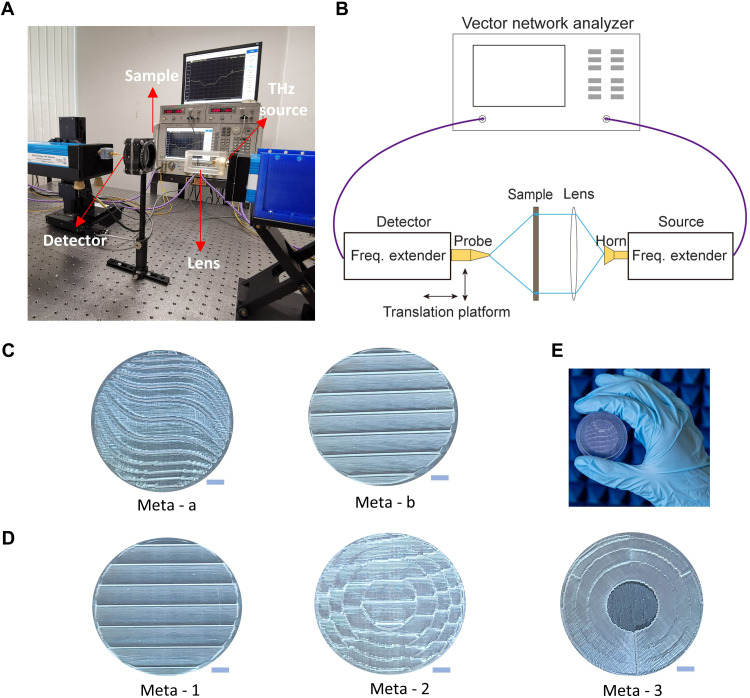
As shown in Fig. 3A, a custom-developed THz near-field measurement configuration is built to test the performance of the dynamic varifocal systems. Figure 3B shows the block diagram of the experimental setup. We adopt the vector network analyzer (Agilent N5245A) with a pair of frequency extenders (OML V03VNA2-T/R) powered by a pair of dc power sources. The extender on the left-hand side is used to measure the THz field from the receiving probe. It is fixed on the three-axis translational stage and is controlled by a computer. The extender on the right-hand side is connected to our proposed varifocal system fed by a horn antenna. The dielectric lens converts the spherical wave from the feed horn into a plane wave. The extenders and translational stage are placed on an optical table with vibration control (Newport S-2000 Stabilizer). The fabricated samples for measurement are shown in Fig. 3 (C and D, respectively). Figure 3E shows the hand-held view of the fabricated sample.

Fig. 3. Experimental validation for the varifocal meta-device.

(A) Experimental setup for characterization of the varifocal meta-device. (B) The block diagram of the experimental setup. (C) Fabricated samples of the meta-device for varifocal Airy beam. (D) Fabricated samples of the meta-device for manipulating the focal spot in 3D space. (E) View of the hand-held meta-device. Scale bars, 5 mm (C and D).

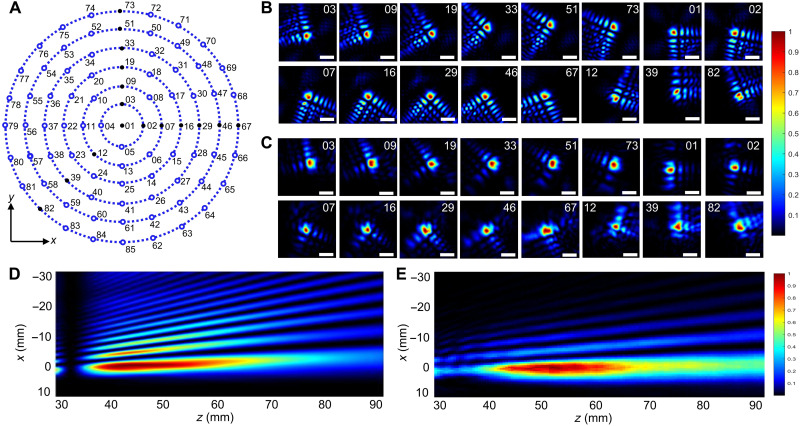
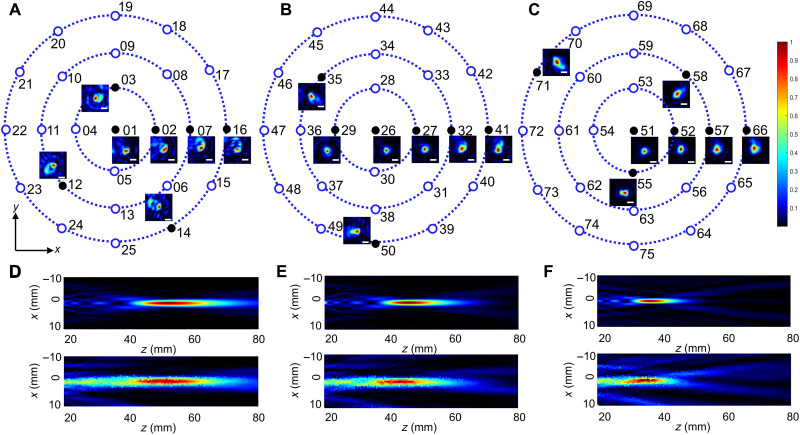
Figure 4 describes the experimental results for arbitrary Airy beam focal spots in the 2D plane. We arbitrarily select six concentric circles and equally spaced points among them to demonstrate the tuning ability. For each focusing case, we calculate the theoretical focus position and the corresponding rotation angles for meta - a and meta - b. The data are shown in table S1. Without loss of generality, 16 points (the solid black points in Fig. 4A) from three different radii are experimentally demonstrated. Figure 4B shows the theoretically calculated results (see Materials and Methods for the detailed calculation). The rotation of the side lobe comes from the rotation of the cubic phase profile. Figure 4C shows the experimental results. Both the focal spot and the distribution of the side lobe agree well with the theoretically predicted ones. Figure 4 (D and E) describes the theoretically calculated and experimental Airy beams in the xz plane, taking the case where the focus is in the center. The Airy beam focal spot in the longitudinal direction extends by approximately 25λ, demonstrating the diffraction-free property of the generated Airy beam. We also verify the self-healing property of the generated Airy beam (fig. S3) and the broadband property of the Airy beam varifocal meta-device (fig. S4A).

Fig. 4. Experimental demonstration of the performance of the meta-device for varifocal Airy beam generation.

(A) Illustration of the modulation range of the focal spot. All dots are numerically calculated on the basis of the theoretical analysis (see the database for the position of the spot and the corresponding rotation angle of each metasurface in table S1). The solid dots are verified in experiments. (B) Theoretical and (C) experimental results of the varifocal Airy beam in the xy plane. Scale bars, 10 mm. (D) Theoretical and (E) experimental results of the varifocal Airy beam in the xz plane. The direction of incidence is toward the positive z axis.

Figure 5 describes the performance of the meta-device for THz wave manipulation in 3D space. As discussed in fig. S2, the accessible range of the THz signal can be tuned continuously from 40 to 60 mm. Here, we choose the minimum (40 mm), the maximum (60 mm), and a value in between (50 mm) of the range to demonstrate the ability to arbitrarily manipulate the beam direction and coverage area. Figure 5 (A to C) illustrates the measured field intensity on the three planes. The inserts shows the measured intensity at the nearby solid black points. We could find that well-defined spots can be formed in the whole plane. For each focusing case, we calculate the theoretical position and the corresponding rotation angles for “meta - 1,” “meta - 2,” and “meta - 3.” The data are shown in table S2. The theoretical and measured results are summarized in fig. S5. We also take the case of the spot being in the center as an example to verify the design in the longitudinal direction. Figure 5 (D and E) shows the theoretical (top) and measured (bottom) intensity distributions in the xz plane when the accessible distance is set to 40, 50, and 60 mm, respectively. The experimental results match well with the theoretical ones. We also demonstrate the broadband property of the varifocal meta-devices (fig. S4B and Fig. 3, C and D).

Fig. 5. Experimental demonstration of the performance of the meta-device for focal spot manipulation in 3D space.

(A to C) Illustration of the modulation range and the measured intensity distributions in the xy plane when the accessible distance is set to (A) 60, (B) 50, and (C) 40 mm. All dots are numerically calculated on the basis of the theoretical analysis (see the database for the position of the spot and the corresponding rotation angle of each metasurface in table S2). The solid dots are verified in experiments. Scale bars, 5 mm. (D to F) Measured (top) and theoretical (bottom) intensity distributions in the xz plane when the accessible distance is set to (D) 60, (E) 50, and (F) 40 mm. The direction of incidence is toward the positive z axis.

DISCUSSION

We demonstrate the full manipulating capacity of the THz beam’s propagation direction and coverage area via rotary doublet and triplet varifocal meta-devices. The THz wave can be projected into an arbitrary spot in a 2D plane or even a 3D space. The synthetics of meta-device design phase profiles enable the compact tunable meta-devices for the THz band. The 3D-printing method is used for the THz meta-device fabrication. It is a promising fabrication method for 6G communication industrial-level components. The doublet meta-device shows the beam steering ability of the Airy beam in a 2D plane. The diffraction-free, self-healing, self-accelerating properties of Airy beams are demonstrated to enable signal transmission stability and security in wireless communication. The triplet meta-device is used to focus the THz wave to arbitrary positions in 3D space. Unlike the traditional telescopic lens, which requires extra space for the telescopic and tilting stage, our triple meta-device can adjust the focus position by rotating without an additional space requirement. Advances in piezoelectric ceramic technology enable accurate rotation of meta-devices, allowing for ultrafast dynamic control of the focal spots. Piezoelectricity can be used to induce mechanical deformation to tune the properties of the meta-devices. Piezoelectricity will rotate the metasurfaces to a specific angle in real time, according to the intended positions of the focal spot. This further supports the tunability and flexibility of our meta-devices. This opens new possibilities for the coming 6G communication systems with multiple transmitters or detectors. The highly concentrated signal can be delivered to a specific user/detector and flexibly adjust the transmission direction. We offer possibilities for secure, flexible, high-directivity, and high–signal concentration future communication systems. We trust that 6G communication, wireless power transfer, zoom imaging, and remote sensing will benefit from this THz-tunable meta-device in the future.

MATERIALS AND METHODS

Unit cell design of the meta-device

For the unit cell electromagnetic design simulation, we use the COMSOL Multiphysics commercial simulation tool to perform the 3D structure simulation. The geometry of the proposed structure is cuboid. The length and width of a cuboid are set as 0.25λ, in which λ is the working band. The height of a cuboid, h, is varied from 0 to 1.59λ with a total of 63-level discrete phase states. The boundary is set as the periodic boundary condition in the x- and γ-directions and the perfect match layer in the z-direction. The uniform mesh size of 20 μm (x-, y-, and z-directions) is generated within a unit cell.

Fresnel diffraction algorithm

The THz wave transmission is described in fig. S7. Here, u₀(x₀, y₀, z₀) defines the incident plane, and u(x, y, z) is the plane of emergence. This process satisfies the Fresnel diffraction integral formula, which is

$$\begin{gathered} u(x,y,z)=\frac{\exp [\mathrm{i}k(z-z_0)]\cdot \exp [\frac{\mathrm{i}k}{2(z-z_0)}(x^2+y^2)]}{i\mathrm{\lambda }(z-z_0)} \\ \times {\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}{u}_0(x_0,y_0,z_0)\exp \left\{\frac{\mathrm{i}k}{2(z-z_0)}[k{(x-x_0)}^2+{(y-y_0)}^2]\right\}\mathrm{d}{x}_0\mathrm{d}{y}_0 \end{gathered}$$ (10)

We will use the matrix product theory to solve the integral formula. The multiplication of a matrix (M_a)_m×p and a matrix (M_b)_p×n will generate a new matrix (M)_m×n. The elements of row i and column j are the multiplication of row i of (M_a)_m×p and column j of (M_b)_p×n. In this way, a single multiplication process can achieve 1 × n cycles of summation. Therefore, we rewrite Eq. 10 to separate the variables for the integration term. Then, the integral formula turns to

$$\begin{gathered} u(x,y,z)=\frac{\exp [\mathrm{i}k(z-z_0)]\cdot \exp [\frac{\mathrm{i}k}{2(z-z_0)}(x^2+y^2)]}{\mathrm{i}\mathrm{\lambda }(z-z_0)} \\ \times {\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\exp \left(\frac{-\mathrm{i}k}{z-z_0}{x}_{0}x\right)u_0(x_0,y_0,z_0) \\ \times \exp [\frac{\mathrm{i}k}{2(z-z_0)}(x_0^2+y_0^2)]\exp \left(\frac{-\mathrm{i}k}{z-z_0}{y}_{0}y\right)\mathrm{d}{x}_0\mathrm{d}{y}_0 \end{gathered}$$ (11)

By discretizing the integral term of Eq. 11 and transforming it into the product of several matrices, all the loops can be summed up at once, thus substantially improving the efficiency of the operation. Assuming that the number of the sampling points of the plane of incidence and the plane of emergence are N₀ × N₀ and N × N, the discretized coordinate values would be

$$\begin{gathered} \{\begin{array}{rl}& x_0=x_0^1,x_0^2,x_0^3\dots ,x_0^{N_0}\\ & y_0=y_0^1,y_0^2,y_0^3\dots ,y_0^{N_0}\end{array} \\ ,\{\begin{array}{rl}& x=x^1,x^2,x^3\dots ,x^{N_0}\\ & y=y^1,y^2,y^3\dots ,y^{N_0}\end{array} \end{gathered}$$ (12)

Updating the integral formula, Eq. 11 turns to

$$u(x,y,z)=\frac{\exp [\mathrm{i}k(z-z_0)]\cdot \exp [\frac{\mathrm{i}k}{2(z-z_0)}(x^2+y^2)]}{\mathrm{i}\mathrm{\lambda }(z-z_0)}{M}_x\times M\times M_y$$ (13)

where

$$\{\begin{array}{rl}{M}_x& =\exp (-\frac{\mathrm{i}k}{z-z_0}\cdot x^T\cdot x_0)\\ M_y& =\exp (-\frac{\mathrm{i}k}{z-z_0}\cdot y_0\cdot y^T)\\ M& =u_0(x_0,y_0,z_0)\exp [\frac{\mathrm{i}k}{2(z-z_0)}({x_0^{\mathrm{\prime }}}^2+{y_0^{\mathrm{\prime }}}^2)]\end{array}$$ (14)

and

$$\{\begin{array}{c}{x}_0^{\mathrm{\prime }}=\left[\begin{array}{c}{x}_0\\ x_0\\ \dots \\ x_0\end{array}\right]=\left[\begin{array}{cccc}{x}_0^1& x_0^2& \dots & x_0^{N_0}\\ x_0^1& x_0^2& \dots & x_0^{N_0}\\ \dots & \dots & \dots & \dots \\ x_0^1& x_0^2& \dots & x_0^{N_0}\end{array}\right]\hfill \\ y_0^{\mathrm{\prime }}=[\begin{array}{cccc}{y}_0& y_0& \dots & y_0\end{array}]=\left[\begin{array}{cccc}{y}_0^1& y_0^1& \dots & y_0^1\\ y_0^2& y_0^1& \dots & y_0^1\\ \dots & \dots & \dots & \dots \\ y_0^{N_0}& y_0^{N_0}& \dots & y_0^{N_0}\end{array}\right]\end{array}$$ (15)

Therefore, the THz wave intensity distribution of the emergence plane will be

$$I={\mid u(x,y,z)\mid }^2$$ (16)

3D-print technology

The dielectric meta-devices are manufactured by 3D printing technology using a stereolithography-based 3D printer, i.e., Form3 from Formlabs (15). The 3D printer has a laser spot size of 85 μm and the most accurate axis resolution of 25 μm. The high-temperature resin with a measured refractive index of 1.631 + 0.009i at 0.3 THz is chosen as the printing material for its high resistance to scratching and deformation. The available layer thicknesses of the high-temperature resin for printing are 25, 50, and 100 μm. For the THz devices, 25-μm layer thickness is chosen here for the highest resolution. We added the supports for connecting the platform and the meta-lens in the fabrication process, as shown in fig. S6. Supports are needed to withstand the weight of the meta-lens during the printing process, and they can also mitigate the deformation of the printed structure. The 3D printer uses a laser to cure solid isotropic parts of a liquid photopolymer resin. After releasing the printed devices from the building platform, the support was removed from the meta-device by hand.

Supplementary Materials

This PDF file includes:

Notes S1 to S4

Figs. S1 to S9

Tables S1 to S4

References