Mapping the Patient-Reported Outcomes Measurement Information System (PROMIS-29) to EQ-5D-5L

Abstract

Background and Objective

The Patient-Reported Outcomes Measurement Information System (PROMIS-29) is gaining popularity as healthcare system funders increasingly seek value-based care. However, it is limited in its ability to estimate utilities and thus inform economic evaluations. This study develops the first mapping algorithm for estimating EuroQol 5-Dimension 5-Level (EQ-5D-5L) utilities from PROMIS-29 responses using a large dataset and through extensive comparisons between econometric models.

Methods

An online survey was conducted to collect responses to PROMIS-29 and EQ-5D-5L from the general Australian population (N = 3013). Direct and indirect mapping methods were explored, including linear regression, Tobit, generalised linear model, censored regression model, beta regression (Betamix), the adjusted limited dependent variable mixture model (ALDVMM) and generalised ordered logit. The most robust model was selected by assessing the performance based on average ten-fold cross-validation geometric mean absolute error and geometric mean squared error, the predicted mean, maximum and minimum utilities, as well as the fitting across the entire distribution.

Results

The direct approach using ALDVMM was considered the preferred model based on lowest geometric mean absolute error and geometric mean squared error in cross-validation (0.0882, 0.0299) and its superiority in predicting the actual observed mean, full health states and lower utility extremes. The robustness and precision in prediction across the entire distribution of utilities with ALDVMM suggest it is an accurate and valid mapping algorithm. Moreover, the suggested mapping algorithm outperformed previously published algorithms using Australian data, indicating the validity of this model for economic evaluations.

Conclusions

This study developed a robust algorithm to estimate EQ-5D-5L utilities from PROMIS-29. Consistent with the recent literature, the ALDVMM outperformed all other econometric models considered in this study, suggesting that the mixture models have relatively better performance and are an ideal candidate model for mapping.

Supplementary Information

The online version contains supplementary material available at 10.1007/s40273-022-01157-3.

Key Points for Decision Makers

The Patient-Reported Outcomes Measurement Information System (PROMIS-29) is a validated and widely used measure of health-related quality of life in clinical settings, and it has an accompanying value set to calculate utilities. However, it is of limited use in economic evaluations as EuroQol 5-Dimension 5-Level (EQ-5D-5L) is the common measure of interest in economic evaluations.

This study compares a wide range of direct and indirect mapping approaches, including finite mixtures of beta regression (Betamix) and an adjusted limited dependent variable mixture model (ALDVMM) to map PROMIS-29 to EQ-5D-5L.

This study finds mixture models to have relatively better performance and ideal candidate models for mapping.

This study generates a mapping algorithm for transforming PROMIS-29 scores to EQ-5D-5L utilities.

Introduction

Healthcare system funders are increasingly seeking value-based care making patient-reported outcome measures suitable to estimate the impact of health interventions on health status, and track patients’ health changes over time. One of the popular patient-reported outcome measures is the Patient-Reported Outcomes Measurement Information System (PROMIS^®), developed by the National Institutes of Health in the USA in 2004. The PROMIS^® consists of an item bank of questions that can be administered using standardised or custom short forms, profiles and computer adaptive tests [1]. The item bank questions are calibrated using psychometric techniques such as item response theory [2], which ensures they can be administered flexibly while remaining comparable.

One of the standardised instruments under the PROMIS^® is the PROMIS-29 (Profile V2.1) which measures seven domains, i.e. depression, anxiety, physical function, pain interference, fatigue, sleep disturbance, and the ability to participate in social roles and activities. Each domain includes an item bank, assessed with four questions ranked by patients on a five-point numeric scale. Higher scores indicate worse outcomes for anxiety, depression, fatigue, ability to participate in social roles and activities, and pain interference domains, and lower scores reflect worse outcomes for physical function and sleep disturbances domains. All domains refer to the previous 7 days except physical function, which has no time frame. In addition, there is also a question on pain intensity on an 11-point rating scale (0–10) [3].

To facilitate interpretation, the output from PROMIS^® domains can be presented as a T-score, which is a standardised score developed using a representative sample of the population. It is centred around a score of 50, and 10 is equal to one standard deviation from the reference population (usually the US general population) [4]. Thus, a T-score of 70 is two standard deviations above or below (depending on the wording of the question) the average of the reference population.

The construct validity and sensitivity of PROMIS-29 (Profile V2.1, V2.0) to changes in health status have been confirmed by several studies on patients with musculoskeletal pain [5], systemic sclerosis [6] and multiple chronic conditions [7], as well as kidney transplant recipients [8]. It has been translated into numerous languages and has been culturally adapted to several nations, which has led to its extensive adoption internationally [9–11].

Economic evaluation regulatory agencies such as the National Institute for Health and Care Excellence (NICE) in the UK, and the Pharmaceutical Benefits Advisory Committee (PBAC) and Medical Services Advisory Committee (MSAC) in Australia recommend using quality-adjusted life-years (QALYs) as the standard metric of health benefits when conducting economic evaluations of health technologies [12–15]. Health-state utility values (henceforth utilities) are typically estimated using a multi-attribute utility instrument [16]. Patients complete a questionnaire describing their health states, upon which a preference-based algorithm is applied to estimate utilities. The EuroQol five dimensions measure (EQ-5D) is the multi-attribute utility instrument most widely used to measure utilities in clinical trials and related studies and is the National Institute for Health and Care Excellence’s (NICE) preferred instrument for cost-utility evaluations in health technology assessments [12, 17]. The EQ-5D is the most widely used generic, preference-based, health outcome measure [18]. This popularity can be attributed to its format, worldwide validated translations and available value sets. The EQ-5D has been used globally in patients with various health conditions; this allows the comparisons of its utility values across different diseases and populations. The EQ-5D is simple to administer and score and has been proven to yield psychometric properties comparable to more comprehensive instruments [19]. The older version of this instrument has three levels, with a range from no problems to extreme problems. However, the newer version of the instrument (EQ-5D-5L) was introduced recently to increase the sensitivity of the instrument and to address the ceiling effect, leading to 5⁵ or 3125 possible health states [20].

One approach to estimate utilities is to conduct valuations whereby people express their preferences for different health states, thus utilities, described by the PROMIS^® using a time trade-off, standard gamble or discrete-choice experiment study [21]. Two such valuation studies have been conducted to date [22, 23], both in the USA. Dewitt et al. developed the PROMIS-Preference (PROPr) scoring system for valuations using standard gamble and seven domains of PROMIS^® [22], including cognition, depression, physical function, pain interference, fatigue, sleep disturbance, and the ability to participate in social roles and activities. However, PROPr includes a cognition domain that is not included in PROMIS-29 and needs to be estimated from other PROMIS 29 domains [24]. Craig et al. developed a value set based on PROMIS-29 (Profile V1.0) using a discrete-choice experiment approach [23]. However, this value set resulted in much lower utility estimates than those produced by other health instruments—the mean was only 0.16 in a sample drawn from the US general population [25]. Moreover, this version of PROMIS-29 is now retired and is substantially different from its newer versions in the domain of “social roles and activities”. Hartman and Craig identified this underestimation as a rescaling issue and proposed an algorithm to convert PROMIS-29 utilities to EQ-5D-3L utilities [26].

The other approach to utility estimation is to develop a “mapping” algorithm from PROMIS-29 scores to utilities [27]. Guidelines from decision-making authorities recommend using mapping to estimate utilities in the absence of direct utility measures [14, 28, 29]. A review of National Institute for Health and Care Excellence (NICE) health technology appraisals found that mapping was adopted in over a quarter of submissions between the years 2004 and 2008 [30]. Mapping can be ‘direct’ whereby utilities are directly estimated from explanatory variables, or ‘indirect’ whereby the probabilities for each response are predicted, and the relevant tariff is used to estimate utilities. The resulting algorithm can be applied to the PROM data collected in the study or clinical trial to estimate the associated utilities and quality-adjusted life-years [31].

There are three studies that map PROMIS-29 to utility measures [32]. Revicki et al. conducted the first mapping study, predicting EQ-5D-3L utilities (US valuation) from PROMIS-29 responses using data from 1658 people in the USA [33]. The algorithm was developed using ordinary least squares (OLS) and the best-performing model accounted for 57% of the variance in the EQ-5D-3L utilities. Hays et al. predicted Health Utilities Index Mark 3 utilities (Canadian valuation) from PROMIS-29 (Profile V2.0) responses, using data from 3000 people recruited in the USA [25]. The algorithm was developed using OLS and linear equating and the best-performing model accounted for 64% of the variance in the Health Utilities Index Mark 3 utilities. Klapproth et al. predicted EQ-5D-5L crosswalk utilities from PROMIS-29 responses using data from people recruited in the UK (n = 1509), France (n = 1501) and Germany (n = 1502) [34]. The EQ-5D-5L crosswalk utilities (using the 3L value sets for health states described by the 5L version) were used because the value set for the 5L version was not available for all three countries. The mapping algorithms were estimated using stepwise OLS with backward selection, starting with full models that incorporated linear, quadratic and cubic functional forms. The authors found that the use of polynomials improved the predictive performance, particularly for poorer health states. However, the study did not explore other regression models. While OLS is one of the most widely adopted direct approaches, it can suffer from poor accuracy as utilities are often highly skewed and bounded at one [35–38]. Moreover, the use of EQ-5D-5L crosswalk utilities introduces an additional level of uncertainty in the prediction.

The primary aim of this study is to develop the first mapping algorithm to predict EQ-5D-5L (non-crosswalk) utilities from PROMIS-29 responses. A value set for the 5L version is adopted to avoid the potential bias caused by using the crosswalk utilities. In previous research, in the absence of a value set for the 5L version, the value set for the 3L version has been used to predict the 5L utilities (crosswalk utilities). The secondary aim is to explore and compare various mapping approaches, including a range of regression models and direct and indirect (response) mapping. Several advanced methods such as finite mixtures of beta regression (Betamix) and the adjusted limited dependent variable mixture model (ALDVMM) are considered [39, 40].

Methodology

An online survey was conducted in June 2020 using the PureProfile online panel provider to collect responses from 3013 Australians representative of the general population. Respondents completed the PROMIS-29 (Profile V2.1), EQ-5D-5L and the Charlson Comorbidity Index (CCI) questionnaires [3, 17, 41]. Information on age, sex, state of residence and postcode was also collected.

Source and Target Measures

Source Measure: PROMIS-29 (Profile V2.1)

The PROMIS-29 (Profile V2.1) consists of 29 questions measuring seven domains of health, including depression, anxiety, physical function, pain interference, fatigue, sleep disturbance, and the ability to participate in social roles and activities [3]. Respondents rate each question based on the degree of severity or impairment in a given symptom or function. The PROMIS-29 (Profile V2.1) also assesses pain intensity using a single numeric rating item where the severity level ranges from 0 (no pain) to 10 (worst possible pain).

Target Measure: EQ-5D-5L

Our target measure was the five-level EQ-5D version, EQ-5D-5L, which was introduced in 2009 in an attempt to improve the instrument sensitivity and to address ceiling effects, as compared to the previous three-level version EQ-5D-3L [20]. This new version consists of five questions about mobility, self-care, usual activities, pain/discomfort and anxiety/depression. Each dimension comprises five levels, with a range from having no problems to having extreme problems [17]. The EQ-5D-5L utilities were estimated by applying an Australian valuation set developed using a discrete-choice experiment approach [42] (see Table 4, Approach 5 of their paper)1.

Table 4.

Ranking the performance of models

Models	GMAE	Rank in GMAE	GMSE	Rank in GMSE	Predicted mean	Rank in predicting mean	Predicted minimum	Rank in predicting minimum	Predicted maximum	Rank in predicting maximum	Average ranking
Direct mapping (using explanatory variable set 5)
OLS	0.0889	4	0.0242	3	0.8280	4	−0.2914	5	1	1	3.4
Tobit	0.0897	6	0.0245	4	0.8201	5	−0.1071	8	0.9532	8	6.2
GLM	0.0883	2	0.0240	2	0.8279	1	−0.3335	1	0.9971	5	2.2
CLAD	0.0911	7	0.0251	6	0.8371	7	−0.2941	4	1	1	5.0
Betamix	0.0888	3	0.0245	5	0.8279	1	−0.2911	6	0.9970	6	4.2
ALDVMM-2 part	0.0882	1	0.0229	1	0.8279	1	−0.3246	2	0.9972	4	1.8
ALDVMM-3 part	0.0893	5	0.0256	7	0.8301	6	−0.2954	3	0.9958	7	5.6
Indirect mapping
GLOGIT	0.1010	8	0.0346	8	0.8413	8	−0.2520	7	1	1	6.4

All the reported statistics are after truncation

Explanatory variables for set 5: the PROMIS-29 (as categorical variables), age, age squared and sex

ALDVMM Adjusted Limited Dependent Variable Mixture Model, ALDVMM-2 part ALDVMM model with two components, ALDVMM-3: part ALDVMM model with three components, Betamix Mixture beta regression model, CLAD censored least absolute deviation, GLM generalised linear model, GLOGIT generalised logistic regression, GMAE geometric mean absolute error, GMSE geometric mean squared error, OLS ordinary least square

Charlson Comorbidity Index

The self-reported CCI was also included in the questionnaire as a potential predictor in the mapping model. The index consists of questions about the presence of 12 defined medical conditions, whether receiving treatment for the problem or not, and whether the medical condition has limited the respondent’s activities. An individual can receive a maximum of 3 points for each medical condition: 1 point for the presence of the condition, 1 for receiving treatment and an additional 1 point if the condition affects their usual activities[41].

Estimation and Validation Samples

In-sample cross-validation was performed for model comparisons using a ten-fold technique as there was no access to an external validation sample [43]. The dataset was divided randomly into ten subsamples, and nine subsamples were utilised as the “estimation sample”, and the remaining data were considered the “validation sample”. This process was repeated ten times, with each of the ten subsamples used once as the validation data.

Statistical Analysis

This mapping study explored a wide range of regression models for the best-performing algorithm. All statistical analyses were conducted in STATA 16. Methodological guidance recommended by the Mapping onto Preference-Based Measures Reporting Standards checklist [44], and reporting standards guidance outlined in the 2017 International Society for Pharmacoeconomics and Outcomes Research Task Force report were followed [31] (see Tables A1 and A2 in the Electronic Supplementary Material [ESM]).

Modelling Approach

The direct mapping approaches predict utilities directly by regressing EQ-5D-5L utilities on the PROMIS-29 domains or items. In estimation with direct mapping, five sets of explanatory variables were considered as initial candidate predictors. The final predictors were selected using the forward stepwise selection (at the 5% significance level). Set 1 was based on the Revicki et al. study, which predicted EQ-5D-3L utilities from PROMIS-29 domains’ T-scores [33]. Set 2 was based on Klapproth et al., which considered T-scores (in a linear, quadratic or cubic functional form) as well as age and sex as predictors [34]. The other three sets of explanatory variables were based on PROMIS-29 domains and items of raw responses:

• Set 3: each of the seven domains of PROMIS-29 (raw scores) plus pain intensity, sex, age and age squared.

• Set 4: each of the PROMIS-29 items as a continuous variable, plus sex, age and age squared.

• Set 5: each of the PROMIS-29 items as a categorical variable, plus sex, age and age squared.

The direct approach considered a range of regression methods including OLS, Tobit, generalised linear model (GLM), censored least absolute deviation (CLAD) model, Betamix and ALDVMM.

The OLS method has several limitations, as mentioned previously [35–38]. Alternative econometric methods including Tobit, GLM and CLAD were therefore adopted to overcome these limitations [45–47]. The Tobit model accounts for utilities bounded at one, while the GLM approach can account for the non-normal distribution of utilities and better handles skewed data than linear regression [48]. The CLAD approach uses median values instead of a mean value, which is more robust to outliers and beneficial when a ceiling effect is present [45, 46, 49].

The mixture models, ALDVMM and Betamix, were also considered because of their flexibility and ability to accommodate multimodality [39, 40]. The ALDVMM prevents prediction outside the feasible range by limiting the dependent variable. It also accounts for the unfeasible gap between full health and the next possible health state [50]. The ALDVMM accounts for multimodality by modelling utilities as a mixture of multiple components, each representing a cluster of respondents with similar utility scores. Here, the estimated models consisted of two and three components. Betamix was used for its ability to model skewed and multimodal data measured on a zero to one interval [51, 52].

In the GLM estimation, the modified Park test identified a Poisson family distribution for the EQ-5D-5L utilities [53], and the Pregibon Link test and the modified Hosmer–Lemeshow test identified a power function with a power of 0.50 as the link function [54, 55]. In the estimation of ALDVMM2, two to four components were considered but the model with four components failed to converge. The predicted utilities were trucated at one if they were higher than one.

For indirect mapping, the responses to each EQ-5D-5L question were the dependent variables, and then the predicted responses were combined to predict utilities. As each question was modelled separately, each mapping algorithm consisted of five separate models. One set of explanatory variables was considered in indirect mapping, including PROMIS-29 items (as categorical variables), age, age squared and sex. We considered the generalised ordered logit (GLOGIT) model, which first predicts responses, and then utilities [46, 56, 57]. Monte Carlo simulations were used to generate the predicted responses to each dimension of the EQ-5D-5L within the GLOGIT approach.

The robustness of both direct and indirect method results was examined by considering two additional sets of explanatory variables:

• Set 6: each of the PROMIS-29 items as a categorical variable, plus CCI, age and age squared.

• Set 7: each of the PROMIS-29 items as a categorical variable, plus the interaction between CCI and age (including age squared).

Measures of Predictive Accuracy

The predictive accuracy of the models was compared using a number of metrics, including the geometric mean absolute error (GMAE)3 and the geometric mean squared error (GMSE)4 across ten-fold cross-validation. The geometric mean, instead of the arithmetic mean, was adopted because the former is less affected by outliers [58]. The other metrics adopted were focused on the accuracy in predicting the mean, minimum and maximum utilities of the sample. An overall ranking of the models was produced to accommodate all the criteria. Moreover, the distribution of the observed utilities was plotted against the predicted utilities to visually assess each method’s performance.

Results

Descriptive Statistics

The survey was completed by 3013 respondents. The average age of respondents was 47 years, and 51% of the sample were female. Respondent characteristics were representative of the Australian population across sex, age and jurisdictional location. Table 1 provides descriptive statistics of the study sample. The average EQ-5D-5L utility was 0.83 (standard deviation = 0.25). In the entire sample, 25% of the respondents had a utility equal to 1 (full health), and 2.5% had a utility of less than zero (poorest health state).

Table 1.

Descriptive statistics

Variables	General population survey
No. of observations	3013
Age, (years)
Mean (SD)	46.92 (17.67)
Range	18–90
Female, n (%)	1531 (50.81%)
PROMIS-29 domains scores, mean (SD)
Physical function	18.08 (3.30)
Anxiety	8.43 (3.89)
Depression	7.80 (4.18)
Fatigue	9.54 (4.38)
Sleep disturbance	10.91 (3.89)
Ability to participate in social roles and activities	15.27 (4.03)
Pain interference	7.65 (4.33)
Pain intensity (0–10 scale)	3.09 (2.76)
PROMIS-29 domains T-scores, mean (SD)
Physical function	50.59 (8.27)
Anxiety	54.49 (10.12)
Depression	52.24 (10.27)
Fatigue	50.48 (10.89)
Sleep disturbance	51.62 (8.71)
Ability to participate in social roles and activities	51.74 (9.19)
Pain interference	51.70 (9.55)
EQ-5D-5L utilities
Mean (SD)	0.828 (0.25)
Range	−0.38 to 1
Utilities < 0, n (%)	75 (2.49%)
Utilities = 1, n (%)	752 (24.96%)
Utilities > 0.9, n (%)	1724 (57.22%)

PROMIS domain scores range from 4 to 20. A higher score reflects better functioning for the physical function domain and the ability to participate in the social roles and activities domain, while a lower score indicates a better health status for the other domains

PROMIS-29 Patient-Reported Outcomes Measurement Information System, SD standard deviation

The correlations between PROMIS-29 domains and EQ-5D-5L utilities and its dimensions (measured by Spearman’s ρ) are presented in Table 2, suggesting strong and statistically significant correlations between the EQ-5D-5L utilities and PROMIS-29 domains [Spearman’s rho (ρ) = 0.69 to −0.38; p = 0.000, 95% confidence interval]. High correlations are desirable as the accuracy of a mapping algorithm depends on the magnitude of overlap between the source and target measures [59]. The highest correlation was between the EQ-5D-5L utilities and the physical function domain of PROMIS-29 (ρ = 0.69), closely followed by the pain interference domain (ρ = −0.67). The lowest correlation was between the EQ-5D-5L utilities and the sleep disturbance domain (ρ = −0.38). The correlations between EQ-5D-5L dimensions and PROMIS-29 domains were overall statistically significant, except those between the mobility dimension of EQ-5D-5L and the anxiety, depression, fatigue and sleep disturbance domains of PROMIS-29. The highest correlation existed between the physical function domain of PROMIS-29 and the mobility dimension of EQ-5D-5L, likely owing to the fact that both instruments have similar questions regarding mobility and physical functions.

Table 2.

Correlations between Patient-Reported Outcomes Measurement Information System (PROMIS-29) domains and EuroQol 5-Dimension 5-Level (EQ-5D-5L) dimensions

PROMIS-29 domains	EQ-5D-5L dimensions
	Mobility	Self-care	Usual activities	Pain/discomfort	Anxiety/depression	EQ-5D-5L utilities
Physical function	−0.75*	−0.60*	−0.70*	−0.58*	−0.27*	0.69*
Anxiety	0.21	0.25*	0.31*	0.27*	0.72*	−0.44*
Depression	0.25	0.29*	0.34*	0.28*	0.73*	−0.48*
Fatigue	0.34	0.32*	0.43*	0.39*	0.58*	−0.50*
Sleep disturbance	0.26	0.23*	0.31*	0.34*	0.45*	−0.38*
Ability to participate in social roles and activities	−0.49*	−0.42*	−0.58*	−0.47*	−0.51*	0.58*
Pain interference	0.63*	0.52*	0.65*	0.70*	0.36*	−0.67*

*Indicates statistical significance at the 5% level

Model Comparison

Table 3 presents the performance of each model for all metrics. For the direct mapping, models using predictors set 5 consistently performed better than those using sets 1–4, which is sensible because the ordinal nature of PROMIS-29 responses was not considered in the four sets. Set 2, which included polynomial forms of PROMIS-29 domains T-scores, performed better than sets 1, 3 and 4 in predicting lower utilities. This is consistent with Klapproth et al.’s finding that accounting for the non-linearity improves the prediction performance for poorer health states [34]. Only models using set 5 were discussed below and considered in the formal ranking.

Table 3.

Predictive performance of models results from ten-fold cross-validation

Models	GMAE	GMSE	Mean	Minimum	Maximum
Actual			0.8279	−0.3770	1
Direct mapping
Explanatory variable set 1
OLS	0.1087	0.0290	0.8239	0.1714	1
Tobit	0.1153	0.0307	0.8221	0.0121	0.9521
GLM	0.1063	0.2766	0.8254	−0.0919	0.9931
CLAD	0.1298	0.0296	0.8371	0.1087	1
Betamix	0.1107	0.0283	0.8243	−0.1218	0.9843
ALDVMM-2 part	0.1074	0.0275	0.8257	−0.1873	0.9935
ALDVMM-3 part	0.1102	0.0288	0.8240	−0.1241	0.9914
Explanatory variable set 2
OLS	0.0991	0.0236	0.8132	−0.1984	1
Tobit	0.0998	0.0261	0.8101	−0.1005	0.9412
GLM	0.0989	0.0234	0.8204	−0.2003	0.9941
CLAD	0.0995	0.0253	0.8282	−0.1210	1
Betamix	0.1176	0.0234	0.8250	−0.1996	0.9876
ALDVMM-2 part	0.0904	0.0235	0.8232	−0.2138	0.9880
ALDVMM-3 part	0.0914	0.0252	0.8211	−0.2023	0.9861
Explanatory variable set 3
OLS	0.0965	0.0239	0.8240	0.1991	1
Tobit	0.1105	0.0249	0.8158	0.0021	0.9631
GLM	0.0900	0.0232	0.8271	−0.1267	0.9961
CLAD	0.1231	0.0215	0.8304	0.1279	1
Betamix	0.0987	0.0232	0.8259	−0.1098	0.9941
ALDVMM-2 part	0.0995	0.0241	0.8269	−0.1098	0.9972
ALDVMM-3 part	0.0989	0.0261	0.8248	−0.1011	0.9925
Explanatory variable set 4
OLS	0.0980	0.0272	0.8273	0.1052	1
Tobit	0.0989	0.0279	0.8175	0.0175	0.9438
GLM	0.0988	0.0263	0.8201	−0.1950	0.9962
CLAD	0.1000	0.0280	0.8383	−0.0720	1
Betamix	0.0986	0.0273	0.8264	−0.1983	0.9960
ALDVMM-2 part	0.0984	0.0257	0.8270	−0.1996	0.9966
ALDVMM-3 part	0.0988	0.0277	0.8252	−0.1967	0.9950
Explanatory variable set 5
OLS	0.0889	0.0242	0.8280	−0.2914	1
Tobit	0.0897	0.0249	0.8201	−0.1071	0.9532
GLM	0.0883	0.0240	0.8279	−0.3335	0.9971
CLAD	0.0911	0.0251	0.8371	−0.2941	1
Betamix	0.0888	0.0248	0.8279	−0.2911	0.9970
ALDVMM-2 part	0.0882	0.0229	0.8279	−0.3246	0.9972
ALDVMM-3 part	0.0893	0.0256	0.8301	−0.2954	0.9958
Indirect (response) mapping
GLOGIT	0.1010	0.0346	0.8413	−0.2520	1

GMAE and GMSE were obtained from ten-fold cross-validation. Predicted utilities over one were truncated at one. Explanatory variables for set 1: seven PROMIS-29 domains T-scores, set 2: polynomial forms of seven PROMIS-29 domains T-scores, age and sex, set 3: seven domains of PROMIS-29 (as continuous variables), age, age squared and sex, set 4: the PROMIS-29 items, age, age squared and sex, set 5: the PROMIS-29 (as categorical variables), age, age squared and sex

ALDVMM adjusted limited dependent variable mixture model, ALDVMM-2 part ALDVMM model with two components, ALDVMM-3 part ALDVMM model with three components, Betamix Mixture beta regression model, GLM generalised linear model, CLAD censored least absolute deviation, GLOGIT generalised logistic regression, GMAE geometric mean absolute error, GMSE geometric mean squared error, OLS ordinary least square

The reported GMAE, GMSE, mean and maximum are after truncation

The ALDVMM-2 part model and GLM resulted in the lowest geometric mean absolute error scores 0.0882 and 0.0883, respectively. The former also clearly outperformed the other models by producing the lowest geometric mean squared error. GLM, Betamix and ALDVMM-2 part were able to correctly predict the observed mean (0.8279). Whilst none of the models accurately predicted the observed minimum utility (−0.3770), GLM (−0.3335) and ALDVMM-2 part (−0.3246) dominated the other models. The ALDVMM performance was not improved by adding another component and the ALDVMM-2 part outperformed the ALDVMM-3 part. OLS and CLAD, after truncation, were able to recover the maximum utility. For the indirect mapping, GLOGIT performed poorly for almost all the metrics, but it did predict the maximum utility correctly.

Table 4 ranks the models’ performances for each of the five criteria and reports the average of the five ranking scores. The ALDVMM-2 part model was the clear winner with a score of 1.8, followed by GLM with a score of 2.2. The two worst-performing models were GLOGIT (6.4) and Tobit (6.2).

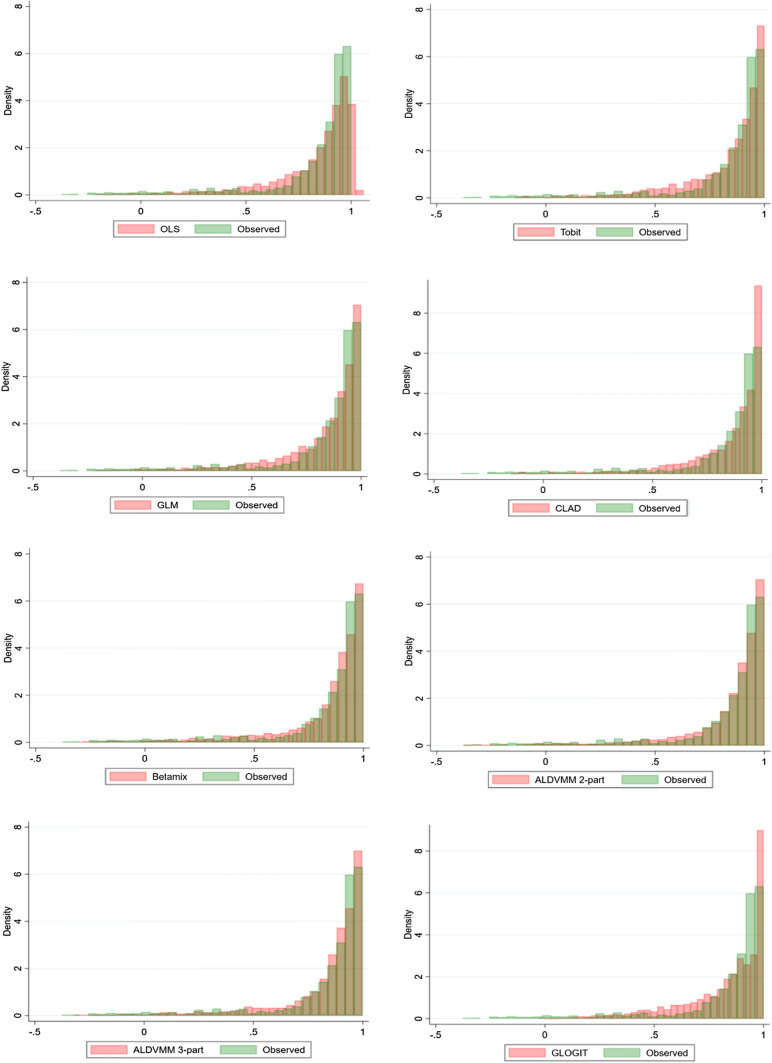
Figure 1 compares the distribution of predicted utilities using explanatory variables set 5 with the observed distribution of the EQ-5D-5L utilities. This helps visually assess the performance of models across the whole distribution. The three mixture models overall fitted better, particularly towards both ends of the distribution. The scatterplots between observed and estimated utilities using explanatory variables set 5 are also generated to assess the predictive performance regarding how close each estimated utility is to its corresponding observed EQ-5D-5L utility (presented in Fig. A1 of the ESM). While it clearly demonstrates the poor predictive performance of GLOGIT, it is somewhat difficult to differentiate the performances of the other models.

Fig. 1.

Distribution of the observed versus predicted utilities for direct and indirect methods. Results were obtained using the explanatory variables set 5: the Patient-Reported Outcomes Measurement Information System (PROMIS-29) [as categorical variables], age, age squared and sex. ALDVMM adjusted limited dependent variable mixture model, Betamix: Mixture beta regression, CLAD censored least absolute deviation, GLM generalised linear model, GLOGIT generalised logistic regression, OLS ordinary least square

As previously mentioned, predictors set 6 and 7 were also considered to test the robustness of models. The results were consistent with those using set 5. Adding the CCI improved predictions, particularly for lower utilities, which was expected as the CCI is a measure of comorbidities and thus severity of a respondent’s health state. However, the models using the CCI as a predictor are not suitable for producing mapping algorithms as CCI data are not always available.

Mapping Function

The ALDVMM-2 part model using the explanatory variables set 5 was considered the best-performing model. The mapping algorithm based on this model using the full dataset is presented in Table A4 of the ESM. The variance covariance matrix is provided in the ESM, which enables researchers to conduct a probabilistic sensitivity analysis in future cost-effectiveness analyses.

Comparison to Other Studies

We further compared the predictive performance between our mapping algorithm and the other two published mapping algorithms [33, 34]. The detail of this comparison is presented in Table A5 of the ESM.

Discussion

This paper develops the first algorithm mapping PROMIS-29 responses to the EQ-5D-5L (non-crosswalk) utilities using a large Australian dataset representative of the population. This algorithm predicted utilities with high precision. In particular, the mapping algorithm performed well in predicting lower health utilities, which previous studies struggled to achieve [33, 34]. This is particularly important as PROMIS-29 is often used for the population with multiple chronic conditions, who might have lower health utilities.

Although the differences in GMAE and GMSE appear small, these differences are more pronounced when the observed and predicted utilities are compared. For example, the estimated utility of a patient responding to the EQ-5D-5L with mobility = 1, self-care = 2, usual activity = 3, pain and discomfort = 2, and anxiety and depression = 3 is 0.7508. Using the OLS with the set 4 mapping algorithm predicts this utility to be between 0.6105 and 0.8638 (mean = 0.7865) depending on patient characteristics such as age and sex. Our best-performing model ALDVMM predicts these utilities to be between 0.6663 and 0.8314 (mean = 0.7612). This difference in utilities can make a substantial difference to the results of economic evaluations.

The mapping algorithm was developed through a rigorous process. We considered a large number of econometric models, including direct and indirect mapping as well as different model specifications and functional forms of the predictors. We also adopted five different metrics for comparison and produced ranking scores accommodating all the metrics. A distribution plot of the predicted and observed utilities was further generated for visual assessment. The ALDVMM-2 part model outperformed all the other models, including OLS adopted by the two previous mapping studies from PROMIS to EQ-5D [31–34]. Our results suggest that using models that accommodate multimodality may achieve superior performance; this has also been found in other mapping studies [60–66]. In our study, this superiority was particularly pronounced by the models’ accuracy in predicting utilities with a range from 0.4 to 0.8. While OLS is the most commonly used method for mapping, and it is easy to execute [35], its shortcomings may lead to a biased estimation of utilities and therefore suboptimal resource allocation.

We also explored different types of predictors. In addition to PROMIS-29 domains and their T-scores considered in Revicki et al. and Klapproth et al. [33, 34], we considered PROMIS-29 item raw scores, which accounts for the extra information at the individual question level. Moreover, the T-scores were calculated for the US general population and may not be appropriate for the other population. Another key difference to the former studies is that we included the PROMIS-29 pain intensity question, which was left out in previous studies.

Our study will enable the estimation of utilities from the PROMIS-29 in Australia for the first time. This is important as PROMIS-29 is one of the critical measures of health outcomes in Australia [67]. Previous mapping studies using PROMIS-29 were conducted in the USA and Europe [33, 34], and Klapproth et al. found limited generalisability of mapping algorithms across the countries [34].

There have been a few attempts to generate utilities directly by valuing PROMIS-29 [22, 23]. However, these studies are often subject to limitations. Craig et al. developed a value set that produced significantly lower utilities than expected [23]. The Dewitt et al. valuation set was developed based on the PROPr form, which uses a cognition domain not included in PROMIS-29 [22]. This has made it difficult to calculate a PROPr utility score when a PROMIS profile instrument is used. To further explore the valuation method for direct utility estimation is warranted.

There are several limitations in the study. First, the participants in this study were from an online panel. They had a similar distribution of age, sex and jurisdiction location to the Australian general population; however, self-selection bias might have occurred. Second, only internal cross-validation was used given the unavailability of external datasets containing PROMIS-29 and EQ-5D-5L, which is similar to the existing literature. Third, the analyses were based on only a single dataset. As with all mapping studies, there is uncertainty around the results and the differences in the measures of model performance. Future research using different datasets, sample sizes and types of respondents would further validate the proposed mapping algorithm.

Conclusions

This study developed an algorithm to map the PROMIS-29 to EQ-5D-5L utilities in Australia. The robustness and prediction precision of ALDVMM confirmed it as a superior mapping approach compared with other regression methods. With this algorithm, PROMIS-29 can be translated to quality-adjusted life-years for use in economic evaluations. This study extends the usefulness of PROMIS-29 from measuring patient outcomes in a clinical setting to a broader economic evaluation tool that can enable more efficient, healthcare resource allocation decisions.

Supplementary Information

Below is the link to the electronic supplementary material.

Declarations

Funding

Open Access funding enabled and organized by CAUL and its Member Institutions. This project was funded by the Agency for Clinical Innovation, Sydney, NSW, Australia.

Conflicts of interest/competing interests

All authors have no conflicts of interest that are directly relevant to the contents of this study.

Ethics approval

Ethical approval for this study was obtained from the Macquarie University Ethics Committee on 28 May, 2020 (Reference number: 52020674715853).

Consent to participate

Informed consent was obtained from all individual participants included in the study.

Consent for publication

Not available.

Availability of data and material

Because of ethical concerns associated with sensitive data, supporting data are not available.

Code availability statement

The codes are available upon request to the corresponding author.

Author contributions

MA, YG, KS, BP, RS and HC contributed to the conception and design of this mapping study. MA conducted the statistical analysis. All the authors contributed to the interpretation of data, drafting the article, revising it critically for the intellectual content and final approval of the version to be published.