Abstract
Quantification of brain oxygenation and metabolism, both of which are indicators of the level of brain activity, plays a vital role in understanding the cerebral perfusion and the pathophysiology of brain disorders. Magnetic resonance imaging (MRI), a widely used clinical imaging technique, which is very sensitive to magnetic susceptibility, has the possibility of substituting positron emission tomography (PET) in measuring oxygen metabolism. This review mainly focuses on the quantitative blood oxygenation level-dependent (qBOLD) method for the evaluation of oxygen extraction fraction (OEF) in the brain. Here, we review the theoretic basis of qBOLD, as well as existing acquisition and quantification methods. Some published clinical studies are also presented, and the pros and cons of qBOLD method are discussed as well.
Keywords: Quantitative BOLD, Oxygen extraction fraction, Static dephasing regime, Brain diseases
Introduction
Oxygen extraction fraction (OEF), the ratio of oxygen consumed as it diffuses from blood to tissues through the capillary network, is a specific biomarker that is under extensive research in clinical practice for evaluating tissue viability, cerebral tumors (Brown and Giaccia 1998; Ito et al. 1982), stroke (Derdeyn et al. 2002, 1998; Gupta et al. 2012), and the treatment of Alzheimer’s disease (Iadecola 2004; Ishii et al. 1996). In the absence of adequate cerebral blood flow (CBF), the elevation of OEF is considered to be a compensatory mechanism (Jordan and DeBaun 2018). From the 1980s onwards, quantitative research of cerebral blood oxygen has been carried out progressively with positron emission tomography (PET) using 15O-radiotracers, and the method for measuring OEF was established (Mintun et al. 1984). The PET results showed that the value of OEF ranged from 40% to 44% in the different cortical areas (Nakane et al. 1998; Yamauchi et al. 1996). However, due to the low spatial resolution and high radiation dose, the utility of PET-based methods was inhibited. With lower price and higher availability compared to PET, magnetic resonance blood oxygenation level-dependent (BOLD) contrast imaging may provide cerebral hemodynamic information related to oxygen metabolism, indicating that monitoring cerebral OEF using magnetic resonance imaging (MRI) would be of great value of clinical applications and more flexibility for research (Yablonskiy et al. 2013).
With the advancements in magnetic resonance (MR) technology and essential physiological models, several non-invasive MRI-based methods for OEF measurements have been cultivated and developed rapidly. These approaches can be divided into three main categories including phased-based measurement (Fan et al. 2012; Fernández-Seara et al. 2006; Jain et al. 2010; Wehrli et al. 2017), intravascular T2-based quantification (Golay et al. 2001; Oja et al. 1999), and extravascular T2'-based measurement integrating the BOLD effect (An and Lin 2000, 2003; He and Yablonskiy 2007; Xie et al. 2011; Yin et al. 2018). All three methods presuppose that deoxygenated blood modulates the MR signal, and thus, indirectly reflects the change of blood oxygen metabolizing in the brain.
The first class of method utilizes phase image to examine susceptibility difference between venous blood (i.e., the sagittal sinus) and the surrounding tissues (Jain et al. 2010). Initially, the global estimation of brain oxygenation by targeting the draining veins is the primary concern of this type of technology, known as susceptibility-based oximetry. With the emergence of quantitative susceptibility mapping (QSM), it becomes possible to derive absolute value of susceptibility at the voxel level (de Rochefort et al. 2010; Liu et al. 2012), and the phase-based measurement can be extended to small cortical veins (Fan et al. 2019; Lu et al. 2021; Probst et al. 2021), so as to obtain the regional values of OEF. However, it is still difficult to quantify the parenchymal OEF and generate voxel-wise mapping based on QSM data, unless vasoconstrictive challenge (Zhang et al. 2015, 2017) or time-consuming optimization methods are used (Cho et al. 2018, 2020a, 2021, b). But these methods are not conducive to clinical application and also need more tests.
The second class of method obtains intravascular T2 relaxation time, which can be converted to venous oxygen saturation (Yv) with a calibration plot (van Zijl et al. 1998). OEF can then be calculated as,
| 1 |
where Ya is the arterial oxygenation close to 100% under normal conditions (Ross et al. 2013). In order to overcome the partial volume effects and obtain a completely isolated venous blood signal, only large veins were generally targeted (Golay et al. 2001; Oja et al. 1999), but this remained difficult to achieve due to the spatial resolution limitation until the introduced arterial spin labeling (ASL) technique (Alsop et al. 2015). A pulsed-ASL-based technique, T2-Relaxation-Under-Spin-Tagging (TRUST) proposed by Lu and Ge (2008), labels distal veins and the signal contribution from static tissue, and cerebrospinal fluid (CSF) is eliminated via simple control-label subtraction. However, similar to other T2-based approaches, TRUST can only measure the blood oxygen saturation in large venous vessels and estimate global OEF value (Lu et al. 2012). The quantitative imaging of extraction of oxygen and tissue consumption (QUIXOTIC) technique is another representative intravascular T2-based approach that applies the velocity-selective spin labeling (VSSL) module to eliminate the signal above a preset cutoff velocity, leaving the voxel signal to come exclusively from the contribution of venous blood, enabling voxel-wise OEF mapping (Bolar et al. 2011). However, the cutoff velocity, as well as the setting of the inversion pulse time used to suppress the arterial signal, depends on the physiological blood velocity distribution and the empirical value of blood T1 (Bolar et al. 2011), making it challenging for QUIXOTIC technology to cope with the complex and variable clinical manifestations of cerebrovascular disease.
The third class of method generally refers to the quantitative BOLD (qBOLD), which is the main topic of this review. Ever since the analytical tissue model was proposed by Yablonskiy and Haacke (1994), qBOLD has been greatly enriched and thrived as one of the MRI-based approaches for the measurement of OEF. Quantitative BOLD is quite different from the first two types of methods. As the name implies, the qBOLD approaches are a typical application of hemodynamics in the brain utilizing the widely recognized BOLD effect in functional MRI (Bandettini et al. 1992; Frahm et al. 1993; Kwong et al. 1992; Ogawa et al. 1992). These methods are based on the signal attenuation model, which is capable of describing signal changes induced by the presence of deoxyhemoglobin (dHb) at different echo times, and a set of parameters related to cerebral blood oxygen activity in the model would be obtained by means of fitting the experimental curve to deduce the theoretical OEF value (An and Lin 2000, 2003; He and Yablonskiy 2007). Before the year of 2010, the qBOLD approaches showed more prospects compared to the phase-based and T2-based quantification because such techniques were independent of blood vessel geometry and only considered the statistical characteristics of blood vessel distribution in the brain. Therefore, quantitative BOLD is essentially a method capable of quantifying the tissue OEF and thus producing a voxel-wise mapping. Moreover, qBOLD approaches have been put into clinical trials for a long time (An et al. 2001, 2009, 2015; Lee et al. 2003; Wang et al. 2021b; Xie et al. 2011; Yu et al. 2013) and have been used to access OEF fluctuation during the functional stimulation (Yang et al. 2019; Yin et al. 2018).
Of course, the qBOLD approaches also present some problems. As a model-based and modified gradient recalled echo (GRE) technology, the estimation errors of OEF are attributed to two factors, one being the model’s premise assumptions and the other being the complex indeterminate relationships between the parameters. Therefore, some studies have combined qBOLD with intravascular T2-based methods to extract information on venous hemodynamics using the VSSL module (Lee et al. 2018), thus removing the coupling between hemodynamic parameters and OEF. Alternatively, qBOLD can also be adapted in combination with phase-based methods to remove unrealistic assumption such as constant non-blood tissue susceptibility in the whole brain, using the QSM susceptibility information for better dealing with the detailed tissue microstructure (Cho et al. 2018). It can be assumed that the quantification of qBOLD may be further improved if both susceptibility and hemodynamic information are obtained simultaneously (Lee and Wehrli 2022), and the fact is that the qBOLD technology itself is constantly being developed and improved all these years.
In this review, we focus only on the qBOLD technique and purpose to introduce the basic technical methodology of qBOLD and the clinical work, which have been carried out to have a general overview of the current status and development foreground of this research area. Specifically, we start with an overview of the most representative theoretical models, followed by some specific details and extensions of the methodology, and finally the application of the qBOLD technique in brain diseases.
Theory for qBOLD
Simplistic Model
The simplistic model is actually very similar to water in a phantom (He and Yablonskiy 2007). This one-component structure cannot describe the actual brain structure, but the abstracted model, which has been widely used in OEF estimation and studies of cerebrovascular diseases, could improve the generalization, and it is reasonably acceptable (An et al. 2015; Lee et al. 2003; Wang et al. 2021b; Xie et al. 2011; Yin et al. 2018; Yu et al. 2013).
The fundamental assumption of the qBOLD model is that the blood vessels in each voxel are uniformly and randomly distributed (An and Lin 2000; An et al. 2001). Relaxation rate constant is sensitive to mesoscopic scale magnetic field gradients (Stone and Blockley 2017), and in general the relationship between and OEF is described in the following analytical form (An and Lin 2000; He and Yablonskiy 2007),
| 2 |
where γ in Eq. 2 is the hydrogen nucleus spin magnetic ratio, which takes the value of ; Hct is the hematocrit, in the large blood vessels, with a typical value in human body of 0.42 (Lu et al. 2004), and the Hct ratio of tissue to large blood vessels is about 0.85 (Eichling et al. 1975) so that the small-vessel hematocrit can be calculated as 0.357; is the susceptibility difference between completely deoxygenated and oxygenated red blood cells, which is generally taken as 0.27 ppm per unit Hct (Spees et al. 2001); is the dHb-induced frequency shift, and DBV is deoxygenated blood volume, mainly contributed by veins; is the main magnetic field, and generally the experiments based on qBOLD to calculate OEF are done at 3 T.
The theory describing the evolution of MR signals in biological tissues under static magnetic field inhomogeneities, called static dephasing regime, is also the basis of qBOLD model (Yablonskiy and Haacke 1994). In the static dephasing regime, the characteristic dephasing time caused by static magnetic field inhomogeneities is much shorter than the characteristic diffusion time. The effect of water diffusion on signal attenuation of free induction decay (FID) is therefore ignored in the simplistic model. Only considering the extravascular tissue compartment, MR signal acquisition around the spin echo (SE) can be achieved by Gradient Echo Sampling of Spin Echo (GESSE), which is an early implementation of qBOLD quantitative imaging sequence (An and Lin 2000). is the signal amplitude with the spin-echo as the time origin and the signal from brain tissue, decays as an exponential form:
| 3 |
| 4 |
Here the relaxation rate is a constant for brain tissue, is the zero-order Bessel function. The characteristic time is given by:
| 5 |
According to the asymptotic properties of Bessel functions, the variation of -weighted signal can be divided into two time regimes, a short time and a long time scale (An and Lin 2000). The characteristic time, is generally considered to be the boundary between these two regimes (An and Lin 2000; He and Yablonskiy 2007; Yin et al. 2018). For the times greater than , the one-component signal, , is linearly exponential. For shorter time, the signal decay profile is quadratically dependent on time:
| 6 |
| 7 |
It is clear that the acquired signal with around the spin echo can be distinguished by Eq. 7 for the two relaxation components and . Logarithmic transformation on both sides of Eq. 7, the relaxation rate can be quickly quantified by linear fitting (An and Lin 2000; Yin et al. 2018). This is the most important step in quantifying OEF using the qBOLD method, which will be discussed in detail in “Parameter Quantification”.
Multicomponent Tissue Model
Fujita et al. have demonstrated that the measurement of is correlated with the spin echo time in the GESSE sequence (Fujita et al. 2003). That’s because the brain tissue is a multi-component structure, and each component has a different T2 relaxation constant. Thus, there will be different weights on the acquired images for different spin echo times. The correct brain tissue model, consequently, should consider with the multi-component structure to get more accurate estimation (Fujita et al. 2003). He and Yablonskiy proposed a modified qBOLD model, in which the signal strength was contributed mainly from three components, intravascular, extravascular tissue and finally extracellular fluid, including CSF and interstitial fluid (ISF) (He and Yablonskiy 2007). For the multi-component qBOLD model, the normalized signal forms of these three components were represented as and . Hence, the Eq. 3 should be rewritten as follows (He et al. 2008; Yablonskiy et al. 2013):
| 8 |
where parameters and were the fractions of signal from brain parenchyma and CSF/ISF at the spin echo, which depended on the relaxation rate constants of brain tissue components, the relative spin densities of the tissue components and the pulse sequence details. The signal profile of brain parenchyma was unified with the simplistic model (see Eq. 3), and the function represents the macroscopic field inhomogeneities.
This model assumed that the extracellular fluid signal, had the frequency and phase shifts relative to the extravascular tissue component on account of the different protein and lipid content between the CSF/ISF and brain cellular tissue:
| 9 |
For intravascular signals, given the assumption that random orientation distribution of vessels in each voxel, the frequency was also considered to be uniformly distributed, and the normalized signal can be presented in the form (Sukstanskii and Yablonskiy 2001):
| 10 |
where function and are the Fresnel integral functions, is a sign function (+ 1 for positive arguments and − 1 for negative arguments), and is the characteristic frequency shift as defined in Eq. 5. The multi-component model introduces a very large number of parameters, such as , , , etc. Most of the newly introduced parameters are simultaneously obtained by curve fitting except for the relaxation rate of blood , which is based on empirical assumptions under different field strengths (He and Yablonskiy 2007; He et al. 2008).
In fact, it is also a simplification to divide the brain roughly into three components, but the relatively long exchange times give this model a certain feasibility (Yablonskiy et al. 2013). Due to the cumbersome post-processing steps and the large number of parameters to be fitted, however, this model has not been widely used in human studies at present. Numerical simulation results showed that (Wang et al. 2013), although the multi-component tissue model could more accurately describe the brain structure, additional parameters were introduced accounting for ISF/CSF signals, which also increases the relative errors. Conversely, the relative errors of fitting would be decreased if the model considered the intravascular contribution. And the simulation also indicated that there was a minimum value of relative errors when the echo time located in the long-time regime, as shown in Fig. 1, which might provide some references for the optimization of MRI protocols and pulse sequence parameters.
Fig. 1.
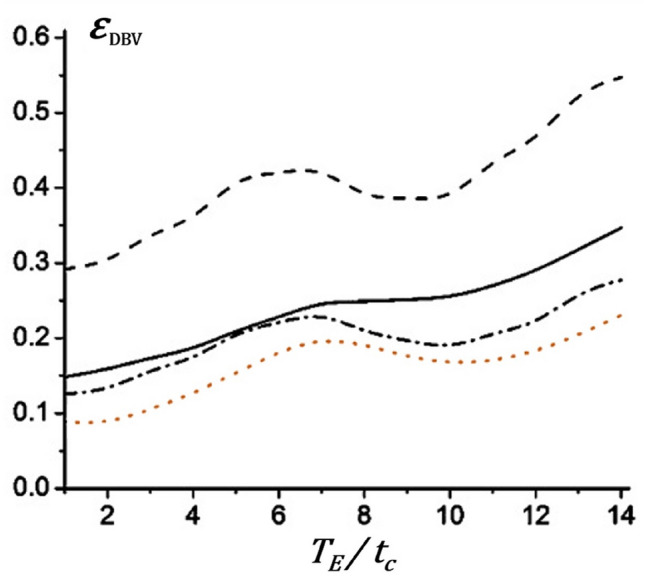
The comparison of the relative errors as functions of echo time (TE). Solid lines: one-compartment model; dashed lines: two-compartment model (i) tissue and ISF/CSF; dotted lines: two-compartment model (ii) tissue and blood; dash–dotted lines: three-compartment model (iii) tissue, CSI/CSF, and blood [Adapted from Wang et al. (2013) with permission]
However, also because of the multi-component model and more detailed description of the qBOLD theory proposed by He and Yablonskiy (2007), the qBOLD technique gradually gained the attention of the academic community. The subsequent theoretical work and clinical promotion of qBOLD were greatly influenced by their work.
Diffusion qBOLD
The multi-component tissue model proposed by He and Yablonskiy could implement the OEF quantification, but the value of DBV and T2 were underestimated (He and Yablonskiy 2007). It is suggested that if the model considered the diffusion effect, the T2 estimates would be improved (Kiselev and Posse 1999a, b). As mentioned above, the primary multi-component model was built on the static dephasing regime where the diffusion was negligible. Based on this assumption, it can be known that the attenuation of MR signal is independent of vessel radius. However, the phantom studies showed that the diffusion of water had a marked impact on the capillaries (Schröder et al. 2006). Sohlin and Schad (2011) expected that diffusion might be significant where the radius distribution of the capillary network was in the range of 20–4 µm in vivo, and the dynamic averaging effect would be extended to larger vessels at longer echo times in a spin echo experiment. Thus Dickson and colleagues suggested to replace the traditional static model with the diffusion dephasing model to obtain the more accurate and reliable tissue parameters by fitting the signal intensity of multiple echoes (Dickson et al. 2010).
Unlike the first two models, it is difficult for the diffusion dephasing model to establish an intuitive physical equation to fit the real signal in such a complex system that takes diffusion effects into account. Actually, the modeling of diffusion qBOLD signal, as well as the quantitative approach, is more like a form of MR Fingerprinting (MRF) (Ma et al. 2013). This means that for diffusion qBOLD, it is crucial to correctly simulate the motion of protons in the diffusion dephasing system so that an accurate dictionary consisting of quantitative parameters, such as OEF, DBV, etc. can be constructed.
The most important step in diffusion qBOLD was to generate the vascular system with a homogenous vessel density constrained within a sphere of radius , as shown in Fig. 2. And then Monte Carlo simulation was used to simulate the protons random walk in such vascular network. At each step of the random walk, the random shift of the protons in each direction followed a normal distribution . Given the diffusion coefficient and the time interval , the standard deviation could be written as (Stone et al. 2019b):
| 11 |
Fig. 2.
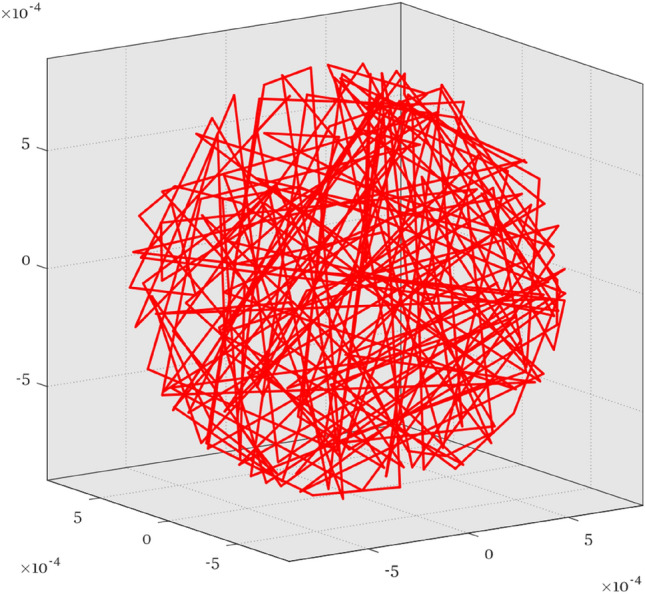
The simulation diagram of vessel system. RS = 900 μm, Number of vessels = 100
If it was further assumed that all these vessels had a uniform susceptibility (Dickson et al. 2010), the phase accumulation of the proton arising from the vascular network could be linearly correlated with OEF (Boxerman et al. 1995).
Assuming that the final phase accumulation of each proton was , then the decay of the signal was the collective contribution of these M protons,
| 12 |
The more details can be referred to the numerical simulation work of Dickson et al. (2010) and Stone et al. (2019b).
In order to match the collected real signals with the parameters of interest for the qBOLD approach, as mentioned in the very beginning of this section, it is necessary to construct a look-up table containing parameters, such as OEF, DBV, and diffusion coefficient D, varied at equal intervals by Monte Carlo simulations. As the value of D can be obtained from diffusion weighted imaging (DWI), we need only to estimate the same number of parameters by fitting a 4D b-spline in the look-up table for the diffusion qBOLD. Dickson et al. (2010) had shown that the simulated results were in good agreement with the multi-component tissue model when the diffusion coefficient was set to zero. However, due to the diffusion effect, the magnetic field before and after the refocusing pulse were not equivalent, and the protons couldn’t be entirely re-phased at the spin echo (Dickson et al. 2010). Therefore, the peak point in the diffusion dephasing regime appeared earlier than in the static dephasing regime, and the amplitude was somewhat reduced.
As we can see, the diffusion qBOLD clearly has a great similarity with the static dephasing model of the vascular network. Blood vessels are modeled as random distributed, infinitely long cylinders with uniform blood oxygenation, and the DBV controls the physical details of the network geometry. The only difference was that the diffusion effect was taken into account in the random walk of protons through the vascular network.
Methodological considerations for qBOLD
Parameter quantification
Quantifying OEF based on the qBOLD theoretical model is essentially a non-linear process. But for the simplistic model, each physiological parameter is obtained step by step, and the fitting process is only reflected in the quantification of (An and Lin 2000; Yin et al. 2018). The stepwise quantification approach may introduce error propagation. In contrast, the multi-component tissue model as well as the diffusion model are quantified simultaneously for all parameters, which can overcome this problem (Cherukara et al. 2019).
He and colleagues first validated the accuracy of quantifying OEF using the multi-component tissue model in twelve male rats, and the experiment showed that the qBOLD results were in high agreement with pulse oximetry under two different anesthesia methods (He et al. 2008). Meanwhile, the diffusion qBOLD was proposed to test for the sources of quantitative error in parameters such as DBV and OEF in vivo (Dickson et al. 2010), as shown in Fig. 3.
Fig. 3.
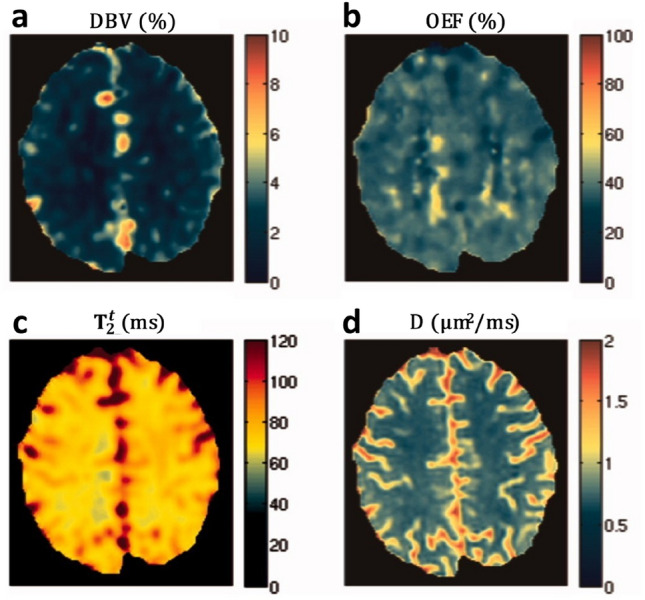
Parameter maps from the diffusive qBOLD; a DBV, b OEF, c , d D values from a co-registered DWI. [Adapted from Dickson et al. (2010) with permission]
A total of eight subjects were studied and the higher OEF was obtained in absolute value, with the average OEF value around 38% and smaller variance compared to the static dephasing model without considering diffusion (Dickson et al. 2010). The tissue T2 fitted by the diffusion qBOLD was indeed improved compared to the multi-component model, which was about 80.5 ms in gray matter and 71.3 ms in white matter (Dickson et al. 2010). However, the gray matter T2 was still lower compared to the results obtained from other relaxation parameters quantitative experiment (Spees et al. 2001). Moreover, similar to the multi-component tissue model, diffusion qBOLD still systematically underestimated DBV, suggesting that the effect of diffusion was not the main source of error in the DBV analysis (Dickson et al. 2010).
The multi-component model and diffusion qBOLD can theoretically reflect the real physiological tissue structure of the brain or delineate a relatively realistic proton trajectory. We can hardly deny that these modified models are more reliable in quantifying OEF than the simplistic model. However, due to the complexity of the model and the time-consuming Monte Carlo simulations, these methods are not easy to analyze, and the excessive parameters introduced by CSF compartments will increase the relative error during the post-processing fitting process, which will affect the accuracy of parameter quantification (Dickson et al. 2010; Wang et al. 2013). Thus, for the present, in some studies, the intravascular signal was suppressed by providing a flow dephasing gradient (An and Lin 2003; Wang et al. 2016a), and the signal from the extravascular fluid compartments, such as CSF, was eliminated using FLuid Attenuated Inversion Recovery (FLAIR) preparation pulses (Stone and Blockley 2017; Stone et al. 2019a), i.e., inversion pulses thus allowing the analysis of the qBOLD signal consistent with the assumptions of the simplistic model. On the basis of such an idea, several protocols have been proposed, and a unified post-processing process has been established. In the next part of this section, we will elaborate on the detailed steps of the simplistic model to calculate OEF based on a set of gradient echo signals acquired by the conventional GESSE, which can be easily extended to other acquisition methods.
The value of OEF can be obtained directly from the linear relationship defined by Eq. 2, so DBV and are calculated first. In order to remove the effect on the signal from Eqs. 6 and 7, a pair of echoes on either side of the spin-echo is then calculated:
| 13 |
TE is the echo time of the spin-echo, and τ is the time interval between the spin echo and the acquired gradient echoes. In order to improve the accuracy of , more symmetric gradient echoes can be used to calculate (An and Lin 2000). After obtaining , the effect is removed from the original signal according to Eqs. 6 and 7, and take the logarithm of both sides of the equations. represents the time interval between the ith gradient echo and the spin echo, rewriting the above two equations:
| 14 |
| 15 |
We will find that is linearly dependent on , using linear least squares to fit the curve of Eq. 15, and the slope is . We should pay attention to whether the selected gradient-echo moment is in the long-time scale, which directly indicates the value of . The value of DBV can be derived by dividing Eq. 7 by Eq. 6 with the following relationship:
| 16 |
where the first term is obtained by extrapolation and the second is the true signal value at the spin-echo moment, as shown in Fig. 4.
Fig. 4.
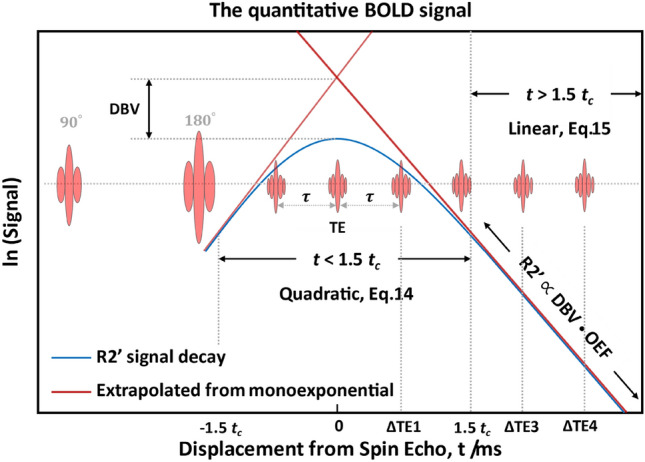
Schematic of the qBOLD model describing the transverse MR signal decay in the presence of a blood vessel network. is inferred from the long-term regime, and DBV is inferred from the mismatch between the linear intercept of this fit and spin echo signal (t = 0 ms). [Modified from Stone and Blockley (2017)]
After determining , and DBV, the value of OEF can be directly calculated by Eq. 2. The design of the echo time in the sequence parameters is very important, especially the choice of τ, which directly determines the accuracy of estimation and thus affects the accuracy of , ultimately affecting the OEF. By the verification of error analysis (An and Lin 2000). An and Lin (2000) proposed that, the time interval, satisfying this criterion , would quantify more accurately and thus can better quantify the OEF.
What’s more, one point worth emphasizing is that whatever model we choose, it is important to recognize that a high signal-to-noise ratio (SNR) of the data is essential to obtain reliable fitting results (He and Yablonskiy 2007; Sedlacik and Reichenbach 2010; Yablonskiy 1998). The GESSE simulation results also showed that OEF could only be well estimated when a high SNR, greater than 500, was achieved (Sohlin and Schad 2009). Bayesian approach might be a good choice, combing the prior information of physiological parameters and giving the parameter uncertainties (Cherukara et al. 2019; Wang et al. 2013). In addition to this, another optional and relatively simple method was proposed to quantify OEF using separate measurements, called multi-parametric qBOLD (see Multi-parametric qBOLD) (Christen et al. 2012).
Sequence Design for qBOLD Signal Acquisition
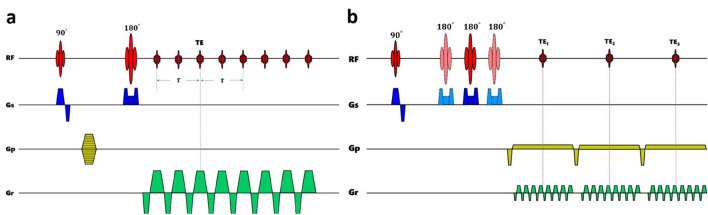
The acquisition of qBOLD signal is generally based on two main sequences, GESSE and asymmetric spin echo (ASE). As shown in Fig. 5, at first glance, the overall structure of both is remarkably similar. There will be an array of gradient echoes on the left and right of the spin echo. The GESSE sequence has a fixed spin-echo moment and changes the gradient echo time. In contrast, the ASE sequence has a fixed gradient-echo time, and changes the spin-echo moment by shifting the position of the 180° pulse. Through this way, the magnetic field fluctuation due to the changes in susceptibility can be evaluated (An and Lin 2003; Stone et al. 2019b).
Fig. 5.
Sequence diagram of the qBOLD approach sequence; a two-dimensional, multi-echo gradient and spin echo sequence, b two-dimensional three-echo asymmetric SE echo-planar imaging (EPI) sequence
Gradient Echo Sampling of Spin Echo
GESSE sequence acquires a set of gradient echoes around the spin echo. To ensure a good SNR for each echo data, the TE should not be longer than T2, so the echo spacing should be shortened and the bandwidth should be increased (Yablonskiy 1998). Of course, the use of 3D readout can also improve the SNR and reduce signal distortion due to macroscopic field inhomogeneities (He et al. 2008), but it may further increase the scan time. The first detailed analysis using the GESSE sequence was performed based on a rigorous phantom design to assess the feasibility of qBOLD theory in terms of volume fraction and relaxation parameter quantification, and it was concluded that the GESSE method had the ability to separate mesoscopic magnetic field inhomogeneity effects to extract tissue-specific physiological information (Yablonskiy 1998). This work was an important theoretical support for the qBOLD method based on GESSE acquisition toward in vivo experiments. Subsequently, this method was rapidly applied to healthy subjects using 2D acquisition, and the OEF value was in high agreement with PET results (An and Lin 2000; An et al. 2001; Lammertsma et al. 1983). It was also found that macroscopic magnetic field inhomogeneities could induce DBV overestimation, and additional acquisition of field maps was essential for quantitative correction of parameters (An and Lin 2002; He and Yablonskiy 2007).
However, the relatively long data acquisition time of GESSE makes it difficult to control the scan time to be clinically acceptable, even if the echo spacing is controlled at 1.5 ms (Xie et al. 2011). This question makes it challenging to perform whole brain high-resolution OEF imaging in clinical settings, not to mention the additional field maps to be acquired. In practice, the phase data of GESSE actually can be used directly to calculate the macroscopic field inhomogeneities, removing their contribution to the estimate (Dickson et al. 2010; Liu et al. 2020). The idea of using GRE phase information for correction is also reflected in the research of mapping (Baudrexel et al. 2009; Sedlacik et al. 2014). In addition, the introduced CSF/ISF compartment in the qBOLD model would also affect the fitting precision. Simon et al. (2016) proposed FLAIR-GESSE sequence with inversion time (TI) set at 1.38 s to suppress the CSF signal, thus raising the stability of OEF quantification.
Asymmetric Spin Echo EPI Approach
Due to the fixed echo time TE in the ASE sequence, the effect of T2 can be considered as a constant weighting in the signal (Blockley et al. 2013). Therefore, using single-echo acquisition, ASE can directly estimate without the need for image acquisition, which is close to the spin echo in the GESSE (Blockley and Stone 2016), and it could also minimize the TE-dependent diffusion effects (An and Lin 2003). The ASE sequence combined with the EPI readout compresses scanning time compared to GESSE, overcoming the problem of motion sensitivity due to the long acquisition (An and Lin 2003). It is the reason why ASE is more widely used in clinical research than GESSE, and it is more feasible in whole-brain OEF estimation. Houston et al. were early to observe the changes in MR signal relative to baseline under hypoxic conditions using the ASE method only with a fixed time offset (Houston et al. 2000). Nevertheless, there were no quantitative studies based on the ASE method before the firstly proposed ASE-EPI-based method, and the images were acquired with different time offset to quantify OEF in normal subjects and the relatively homogeneous results throughout the brain were obtained (An and Lin 2003). The flow dephasing gradient was also applied to suppress the intravascular signal, and the results showed that the lower b value (b = 13 s/mm2) was sufficient to do this (An and Lin 2003).
As with GESSE, correction of macroscopic field inhomogeneities is also essential for ASE method, but the difference is that this cannot be done with standard ASE data alone (Blockley et al. 2013). The acquisition of separate field maps is necessary, which in turn increases the scanning time. In order to solve this problem, Blockley and Stone (2016) combined Gradient-Echo Slice Excitation Profile Imaging (GESEPI) technique with the ASE sequence, called GASE. GASE essentially oversampled in the slice direction (z-direction), and the z-direction maximum phase encoding value determined how much magnetic field gradient through slice can be compensated (Yang et al. 1998). This correction process was implemented directly through the GASE sequence, making the post-processing step much simpler (Blockley and Stone 2016). Based on their previous work, they later proposed the FLAIR-GASE sequence, which further simplified the application of qBOLD and improved the robustness of the resultant OEF mapping after suppressing the CSF signal (Stone and Blockley 2017). In general, because of the flexibility of ASE sequence, the shorter acquisition time, the relative ease of post-processing, and the great operability of sequence optimization, the qBOLD method using ASE to generate brain oxygenation mapping has quickly gained traction in clinical applications (An et al. 2015, 2012; Chang et al. 2016; Fields et al. 2018; Guilliams et al. 2018; Sen et al. 2016; Stone et al. 2019a; Zhang et al. 2013).
Multi-parametric qBOLD
As mentioned in “Parameter Quantification”, the qBOLD method for multiparameter quantification such as OEF using GESSE or ASE single experiment relies heavily on high SNR to produce accurate results through fitting procedures (Ulrich and Yablonskiy 2016). Moreover, Sedlacik and Reichenbach's phantom study showed that if OEF and DBV were quantified simultaneously, this approach could lead to large variations due to their interdependent effects on the BOLD signal, whereas if one value was fixed first, the other parameter could be estimated more correctly (Sedlacik and Reichenbach 2010). Based on this idea, Christen et al. (2011) for the first time converted the multi-parameter fitting problem into a very direct univariate fitting task by measuring blood volume and relaxation parameters separately, and then tested this approach on healthy rats, which was correlated well with the direct measurements (Bouzat et al. 2008; Christen et al. 2011). This study was the origin of the multi-parametric qBOLD (MqBOLD).
On the basis of animal studies, Christen and colleagues continued to translate this approach into clinical studies, further simplifying post-processing steps, and determined the specific standard scanning protocol of MqBOLD in vivo (Christen et al. 2012). Most of the subsequent MqBOLD-based studies have inherited this specification (Hirsch et al. 2014; Kaczmarz et al. 2020) and used concise formulas to generate OEF mapping, rewriting Eq. 2 to Eq. 17:
| 17 |
The only difference between these two equations is that cerebral blood volume (CBV) here represents the average contribution of arterial and venous blood instead of the original DBV, so strictly speaking, it is not entirely the effect of deoxyhemoglobin on the BOLD signal (Christen et al. 2011, 2012). Using the MqBOLD approach, we need to use three independent experiments, multi-echo GRE, multi-echo SE, and dynamic susceptibility contrast perfusion-weighted imaging (DSC-PWI), to determine , , and CBV, respectively (Christen et al. 2012; Hirsch et al. 2014), as shown in Fig. 6. The correction of macroscopic field inhomogeneities is mainly reflected in the generation of mapping (Baudrexel et al. 2009).
Fig. 6.
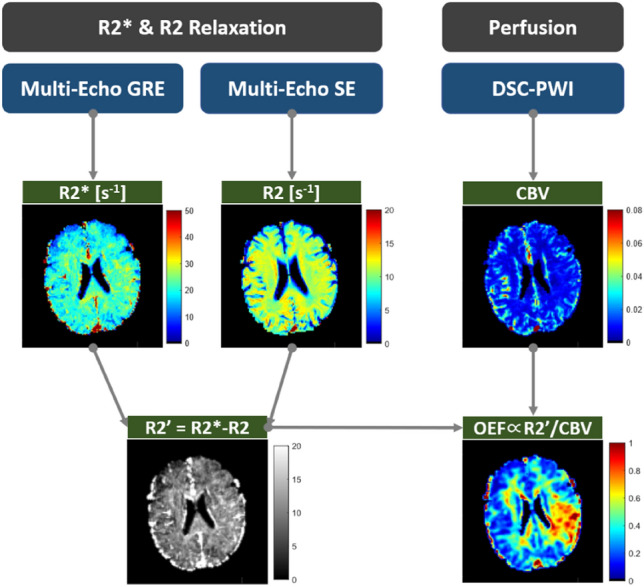
Overview of MqBOLD sequences and derived parameters. Representative images of a 72-year-old male patient with acute ischemic stroke (2 h post-onset case)
As can be seen, quantification of OEF with MqBOLD actually translates to choose the appropriate scanning sequences, or post-processing methods, to accurately estimate these three parameters, including how to solve the challenge of DSC absolute quantification (Wirestam et al. 2007). Hirsch and colleagues conducted a very comprehensive evaluation of the MqBOLD validity from the technology standpoint (Hirsch et al. 2014). They argued that the OEF results were reasonable using GESSE and the simplistic model without considering diffusion effects, but this was not necessarily true for MqBOLD. Because the multi-echo SE for mapping compensated for the diffusion effects (Carr and Purcell 1954), which led to a mismatch of diffusion effects between and from separate measurements and might cause large errors (Hirsch et al. 2014). But at the same time, they also confirmed the robustness of DSC for voxel-wise CBV calculation (Nguyen et al. 2015) and believed that the variation in OEF produced by the MqBOLD approach would be of a great clinical marker even for semi-quantitation. Later, a more detailed study was carried out on the analysis of T2-related biases in MqBOLD (Kaczmarz et al. 2020), and the experiments showed that the overestimation of OEF in MqBOLD could be overcome by applying 3D GRAdient and Spin Echo (GRASE) imaging sequences (Kaczmarz et al. 2020). Unlike 2D acquisition, which requires the consideration of slice-selection pulse imperfections (Prasloski et al. 2012), quantification using 3D-GRASE imaging was not affected by stimulated echoes (Hennig 1988; Kaczmarz et al. 2020).
Compared to ASE and GESSE, MqBOLD doesn’t require additional development of MRI sequences, and overcomes the dependence of high SNR, allowing for acquiring relatively high spatial resolution images, making it a simpler and more convenient MRI-based method for clinical OEF determination (Christen et al. 2012). However, MqBOLD is clearly an invasive measurement because of the need of accurate CBV, which requires the injection of a gadolinium-based contrast agent into the patient. But fortunately, considering that DSC is a routine sequence for MRI examination in patients with brain tumors and stroke (Willats and Calamante 2013), MqBOLD approach is acceptable in clinical studies and even makes better use of perfusion information.
Clinical Applications
There are many clinically applicable MR imaging approaches to assess brain oxygenation, but in this section, we only discuss clinical studies that utilize the qBOLD method of brain diseases.
Cerebrovascular Disease
Elevated OEF can predict the occurrence of hypoxia–ischemia and identify at-risk patients with cerebrovascular disease (Fan et al. 2020; Kang et al. 2022). At the same time, this physiological phenomenon, as a metabolic reserve (Heiss and Podreka 1993), can be regarded as an important biomarker for assessing salvageable tissue (Fan et al. 2019). The clinical research based on qBOLD was first applied in acute ischemic stroke (AIS) by Lee et al. (2003). This validation study found that the threshold of tissue viability, obtained by the GESSE approach for monitoring changes in cerebral oxygen metabolism relative to the contralateral hemisphere, was very consistent with previous PET results (Touzani et al. 1997). It should be mentioned that this study is the first attempt to quantify oxygen metabolism using MRI for cerebrovascular disease, letting alone the validation of qBOLD for clinical uses. An et al. (2015) correlated the ASE and DSC measurements in AIS patients with larger sample size and defined the product of OEF and CBF as oxygen metabolic index (OMI). This index was further used to derive the threshold of the ischemic penumbra (Fig. 7).
Fig. 7.
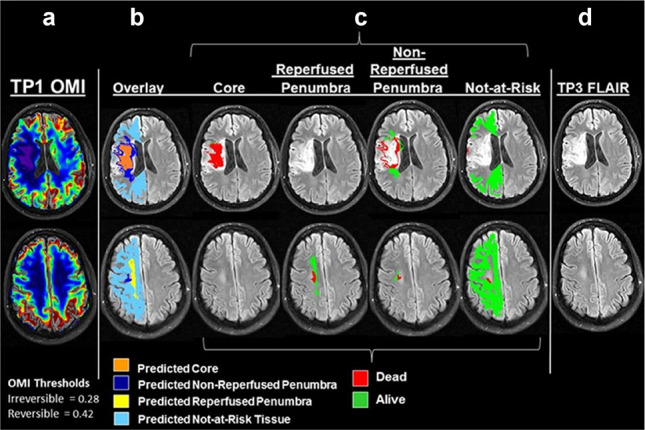
An example from a patient with a right middle cerebral artery stroke. The OMI map two hours after onset was in column (a), with an OMI threshold of 0.28 to differentiate infarct core from penumbra, and 0.4 to differentiate the penumbra from tissue not-at-risk. The second MRI scan, six hours after onset, further subdivided the penumbra (b). Survived (green) or died (red) tissues in column (c) were determined by FLAIR imaging after 1 month (d). [Adapted from An et al. (2015) with permission]
In the study of severe unilateral internal carotid artery (ICA) or middle cerebral artery (MCA) atherosclerosis, the increased OEF was observed to be associated with decreased CBF in hemispheres ipsilateral to the vascular lesions (Xie et al. 2011). This compensatory mechanism, also known as stage two hemodynamic compromise (Derdeyn et al. 2002), was also found in cerebral small vessel disease (cSVD), which is accompanied by the increase of white matter hyperintensities (WMH) density and prolonged disease duration (Ford et al. 2020; Kang et al. 2022). For cSVD, Kang et al. first used ASE approach to obtain the whole-brain OEF mapping but paid more attention to the changes of OEF in watershed region during subsequent analysis (Kang et al. 2022). Indeed, elevated watershed OEF was found to correlate with microstructural damage and greater WMH burden, which might mean that the OEF variation leading the WMH growth (Kang et al. 2022).
Sickle Cell Disease
Sickle cell disease (SCD) is a group of inherited hemoglobinopathies (Jordan and DeBaun 2017; Piel et al. 2013), the most severe form of which is sickle cell anemia (SCA). Autosomal recessive mutation in the β-globin gene results in reduced oxygen carrying capacity of erythrocytes and the induced chronic anemia, which leads to microvascular obstruction and tissue ischemia (Fields et al. 2018; Ware et al. 2017). Although SCD patients can present stroke-like symptoms, unlike cerebrovascular disease, the most immediate change in hemodynamics of SCD is the decrease in arterial oxygen content (CaO2), resulting in an inadequate oxygen delivery (Guilliams et al. 2018; Hurlet-Jensen et al. 1994; Oguz et al. 2003). A global elevation in CBF and OEF is therefore necessary to meet the cerebral oxygen metabolic demand, and such elevations can be detected (Jordan et al. 2016; Wang et al. 2021b). However, as the density of deep white matter silent infarcts increases, CBF in this region would still be reduced (Ford et al. 2018), and information about regional OEF becomes more important in SCD, highlighting the advantage of qBOLD as a quantitative method of OEF at the voxel level (Fields et al. 2018).
In the study of pediatric SCD, it was found that the peak OEF region in white matter often corresponded to lower CBF relative to total white matter volume, and the peak OEF region was coincided with highest infarct density region (Fields et al. 2018). At the same time, the occurrence of infarction was observed within internal border zone, which invalidated compensatory mechanisms and left tissue oxygen metabolism demands unmet, increasing the future stroke risk (Fields et al. 2018). By comparing OEF and CBF before and after chronic transfusion therapy (CTT), researchers found that the physiology of blood transfusion for stroke prevention in children with SCA perhaps was related to the global and regional reduction of OEF and CBF with concomitant increase in CaO2 (Guilliams et al. 2018). The volume of peak OEF within the border zone also gradually diminished after transfusions (Fig. 8) (Guilliams et al. 2018).
Fig. 8.
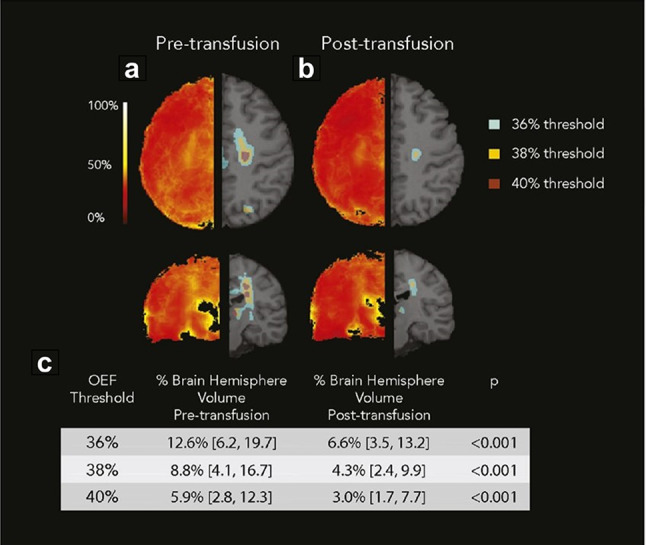
Averaged OEF maps before (a), and after (b) CTT. Left side indicates the averaged maps. Right side shows the regions above the OEF thresholds. The median proportion of hemispheric volume above the OEF threshold decreased after transfusion (c). [Adapted from Guilliams et al. (2018) with permission]
A similar approach was applied by Fields et al. (2019) in their following work. They later evaluated the neuroprotective efficacy of hydroxyurea (HU) in younger SCA patients, aged five to twenty five, and found that HU and CTT had a similar but different degrees of cerebral oxygen metabolic stress regulation (Fields et al. 2019). Wang et al. (2021b) also analyzed the correlation between OEF and diffusion tensor imaging (DTI) parameters in SCD, and their results suggested that microstructural damage may precede the development of cerebral infarctions (Wang et al. 2021b), consistent with the findings in non-SCD cSVD studies (Kang et al. 2022).
Brain Tumors
Hypoxia is a hallmark of malignancies implicated in several aspects of neo-angiogenesis, tumorigenesis, and tumor progression (Jensen 2009). For brain tumors, especially in highly aggressive glioblastomas (GBM), hypoxic niches contribute to a more malignant tumor phenotype (Huang et al. 2016), resistant to chemo- and radiation therapy (Harrison et al. 2002). As a consequence, imaging of tumor hypoxic regions (Tóth et al. 2013), detection of tumor microenvironment (TME) (Stadlbauer et al. 2019a), and accurate tumor classification (Stadlbauer et al. 2016), play a key role in the treatment of brain tumors (Omuro and DeAngelis 2013; Schatten 2018). As we mentioned in Multi-parametric qBOLD, DSC-PWI is the most commonly used examination for brain tumor perfusion MRI, which is an important support for the clinical application of MqBOLD approach in brain tumors (Boxerman et al. 2020).
Tóth et al. (2013) first measured the whole-brain OEF of 45 glioma patients based on MqBOLD. Within the tumorous areas, the regions with OEF value one standard deviation above the mean were defined as ‘hypoxic tumor’ and the protocol was collectively referred to as hypoxia imaging (Tóth et al. 2013). The heterogeneity of glioma was well illustrated in this prospective trial, where they found that high-grade tumors still exhibited higher OEF, despite higher CBV, than lower-grade tumors, and the volume of high OEF increased with the malignancy of the tumor tissue. The feasibility of the MqBOLD method to identify hypoxic regions in high-grade tumors was initially confirmed (Tóth et al. 2013). Much everer hypoxia in response to OEF elevation could also serve as a signature to differentiate glioma patients with epidermal growth factor receptor amplification, but it might not be an independent predictor of overall survival (Oughourlian et al. 2021).
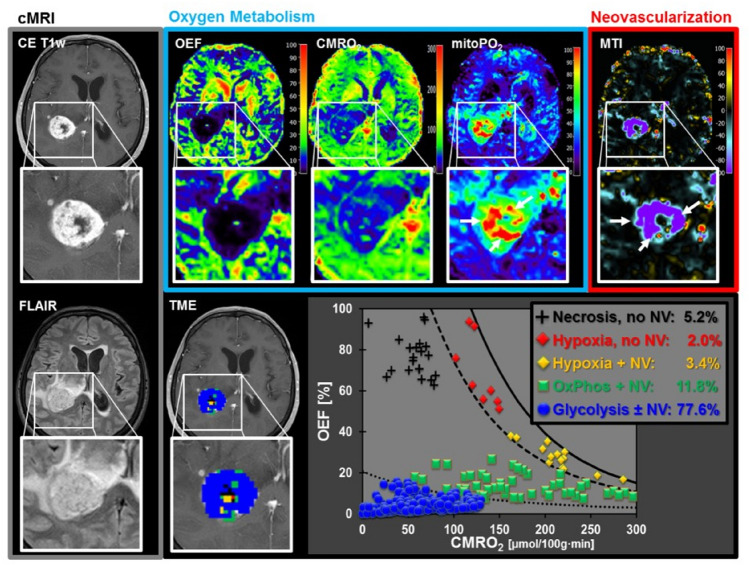
In addition, abnormal angiogenesis is also essential for tumor growth and metastasis (Bielenberg and Zetter 2015). Thus, establishing the relationship between tumor vascularization and hypoxia could provide more information on pathophysiological mechanisms of drug therapy and further follow up on the prognosis of cancer patients (Stadlbauer et al. 2019a). A recent study has proposed a novel physiological MRI method named TME mapping, combining MqBOLD and vascular architecture mapping (VAM) to achieve the classification of different TME compartments (Stadlbauer et al. 2018). They determined that iso-citrate dehydrogenase 1 (IDH1) wild-type glioblastomas had two distinct phenotypes, one dominated by hypoxic necrosis, and the other by glycolysis, the latter with a high proportion of functional neo-vasculature (Fig. 9). This method can also be used in glioma grading and IDH gene mutation detection (Stadlbauer et al. 2016), and prospective studies suggest that the MqBOLD-based TME mapping may also be feasible in breast cancer (Bennani-Baiti et al. 2020; Stadlbauer et al. 2019b).
Fig. 9.
A patient with a glioblastoma IDH1 wt showing features of the glycolytic dominated phenotype. The large areas of the lesions with both very high mitochondrial oxygen tension (mitoPO2) and very high micro-vessel type indicator (MTI) values, representing the presence of glycolysis, and proliferation of functional neovascularization, respectively. [Adapted from Stadlbauer et al. (2018) with permission]
Discussion
There are a few issues need to be addressed to understand the technical limitations in this review, as well to properly interpret the qBOLD results and choose the appropriate application scenarios.
First, the qBOLD analytical model introduces several physical or physiological parameters, such as hematocrit, Hct. The current qBOLD-based studies set it to a constant of 0.42, but under pathological conditions of cerebral ischemia, there is a certain degree of Hct reduction in local small vessels (Yamauchi et al. 1998), which may cause an underestimation of OEF if empirical values are still used. Apart from that, arterial oxygen saturation, Ya is assumed to be an absolute value of 100% during post-processing quantification. In most cases, it is an acceptable assumption but a study based on near-infrared spectroscopy suggests that hypoxia may induce a decrease in arterial oxygen saturation (McCormick et al. 1991), which is exactly what MqBOLD has focused on in brain tumors. In addition, the magnetic field strength may also affect these parameters, especially if the multi-component tissue model is adopted, the relationship between blood T2 and OEF may need further verification, and the frequency offset of CSF/ISF may have to take into account phase wrapping.
Second, the qBOLD technique is hardly able to account for the effect of non-BOLD contributions to the quantification of relaxation parameters. Therefore, it is a fact that myelin, hemosiderin, non-heme iron accumulation, etc. may all contribute to potential errors in the final OEF estimation (Ni et al. 2015), narrowing the clinical applications in patients with cerebrovascular diseases, such as intracerebral hemorrhage. Combined with QSM, qBOLD has the potential to break through this limitation utilizing both phase and magnitude gradient echo data (Cho et al. 2018, 2020a, b,2021). Furthermore, measurement protocol may also be a sensitive issue for relaxation parameters quantification (Ni et al. 2015), particularly for MqBOLD approach (Ulrich and Yablonskiy 2016). The GRE and SE experiments have different weightings of brain tissue compartments, and if maps are acquired from multi-echo SE experiment, which usually requires long TR and SE times, long T2 compartments may dominate the MR signal. This is also the case in maps, where components of short T1 and short T2, like myelin water can generate a high weighting in the map, and thus the value of would not really reflect the true BOLD response (Ulrich and Yablonskiy 2016).
Finally, although the focus of this article is primarily cerebral OEF measurements, it should also be noted that qBOLD method is being used for other organs with increasing frequency, particularly the kidney (Wang et al. 2016a, b, 2021a). Because imaging is performed in abdominal organs, fast acquisition of ASE-EPI is required, as well as respiratory triggering (Wang et al. 2021a).
Conclusion
OEF, as a biomarker of both normal and pathological brain function, contributes significantly to systematic monitoring the disease progression and exploring the pathogenesis. The qBOLD technique, meanwhile, as one of the powerful MRI tools for quantifying OEF, has evolved from feasibility to practical utility over the past two decades. Concomitant with the proposed more precise quantitative methods (Cherukara et al. 2019), more optimized MRI sequences (Stone and Blockley 2017), and the solution of limited SNR (Christen et al. 2012), clinical applications of qBOLD have been gaining increasing attention from researchers. Now that a consensus on the qBOLD imaging strategy and analysis methods is needed, only then may it become an increasingly valuable tool in MRI brain imaging so that it can be used in multicenter large-sample studies.
Abbreviations
- OEF
Oxygen extraction fraction
- MRI
Magnetic resonance imaging
- qBOLD
Quantitative blood oxygenation level-dependent
- MqBOLD
Multi-parametric qBOLD
- Yv
Venous oxygen saturation
- Ya
Arterial oxygen saturation
- DBV
Deoxygenated blood volume
- CBV
Cerebral blood volume
- CBF
Cerebral blood flow
- CaO2
Arterial oxygen content
- SE
Spin echo
- GRE
Gradient recalled echo
- EPI
Echo-planar imaging
- ASE
Asymmetric spin echo
- GESSE
Gradient echo sampling of spin echo
- DSC
Dynamic susceptibility contrast
- FLAIR
Fluid attenuated inversion recovery
- PET
Positron emission tomography
- ASL
Arterial spin labeling
- VSSL
Velocity-selective spin labeling
- TRUST
T2-Relaxation-Under-Spin-Tagging
- QSM
Quantitative susceptibility mapping
- QUIXOTIC
Quantitative imaging of extraction of oxygen and tissue consumption
- CSF
Cerebrospinal fluid
- ISF
Interstitial fluid
- SCD
Sickle cell disease
- AIS
Acute ischemic stroke
- cSVD
Cerebral small vessel disease
Authors’ Contributions
HWL drafted the paper, made critical revisions, and approved the final version. CYW gave important suggestions for the structure of this review and made critical revisions. YL and XCY supported in gathering clinical data and made critical revisions. HW made critical revisions and approved the final version.
Funding
This work was supported by the National Natural Science Foundation of China (No. 81971583), National Key R&D Program of China (No. 2018YFC1312900), Shanghai Natural Science Foundation (No. 20ZR1406400), Shanghai Municipal Science and Technology Major Project (No.2017SHZDZX01, No.2018SHZDZX01) and ZJLab.
Data Availability
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Code Availability
Not applicable.
Declarations
Conflict of Interest
The authors declare there is no conflicts of interest regarding the publication of this paper.
Ethical Approval
Not applicable.
Consent to Participate
Not applicable.
References
- Alsop DC, Detre JA, Golay X, Günther M, Hendrikse J, Hernandez-Garcia L, Lu H, MacIntosh BJ, Parkes LM, Smits M, van Osch MJP, Wang DJJ, Wong EC, Zaharchuk G. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn Resonance Med. 2015;73(1):102–116. doi: 10.1002/mrm.25197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- An H, Lin W. Quantitative measurements of cerebral blood oxygen saturation using magnetic resonance imaging. J Cereb Blood Flow Metab. 2000;20(8):1225–1236. doi: 10.1097/00004647-200008000-00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- An H, Lin W. Cerebral oxygen extraction fraction and cerebral venous blood volume measurements using MRI: effects of magnetic field variation. Magn Resonance Med. 2002;47(5):958–966. doi: 10.1002/mrm.10148. [DOI] [PubMed] [Google Scholar]
- An H, Lin W. Impact of intravascular signal on quantitative measures of cerebral oxygen extraction and blood volume under normo- and hypercapnic conditions using an asymmetric spin echo approach. Magn Resonance Med. 2003;50(4):708–716. doi: 10.1002/mrm.10576. [DOI] [PubMed] [Google Scholar]
- An H, Lin W, Celik A, Lee YZ. Quantitative measurements of cerebral metabolic rate of oxygen utilization using MRI: a volunteer study. NMR Biomed. 2001;14(7–8):441–447. doi: 10.1002/nbm.717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- An H, Liu Q, Chen Y, Lin W. Evaluation of MR-derived cerebral oxygen metabolic index in experimental hyperoxic hypercapnia, hypoxia, and ischemia. Stroke. 2009;40(6):2165–2172. doi: 10.1161/STROKEAHA.108.540864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- An H, Sen S, Chen Y, Powers WJ, Lin W. Noninvasive measurements of cerebral blood flow, oxygen extraction fraction, and oxygen metabolic index in human with inhalation of air and carbogen using magnetic resonance imaging. Transl Stroke Res. 2012;3(2):246–254. doi: 10.1007/s12975-011-0142-9. [DOI] [PubMed] [Google Scholar]
- An H, Ford AL, Chen Y, Zhu H, Ponisio R, Kumar G, Shanechi AM, Khoury N, Vo KD, Williams J, Derdeyn CP, Diringer MN, Panagos P, Powers WJ, Lee J-M, Lin W. Defining the ischemic penumbra using magnetic resonance oxygen metabolic index. Stroke. 2015;46(4):982–988. doi: 10.1161/STROKEAHA.114.008154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magn Resonance Med. 1992;25(2):390–397. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
- Baudrexel S, Volz S, Preibisch C, Klein JC, Steinmetz H, Hilker R, Deichmann R. Rapid single-scan T-mapping using exponential excitation pulses and image-based correction for linear background gradients. Magn Resonance Med. 2009;62(1):263–268. doi: 10.1002/mrm.21971. [DOI] [PubMed] [Google Scholar]
- Bennani-Baiti B, Pinker K, Zimmermann M, Helbich TH, Baltzer PA, Clauser P, Kapetas P, Bago-Horvath Z, Stadlbauer A. Non-invasive assessment of hypoxia and neovascularization with MRI for identification of aggressive breast cancer. Cancers. 2020 doi: 10.3390/cancers12082024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bielenberg DR, Zetter BR. The contribution of angiogenesis to the process of metastasis. Cancer J. 2015;21(4):26–273. doi: 10.1097/PPO.0000000000000138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blockley NP, Stone AJ. Improving the specificity of R2′ to the deoxyhaemoglobin content of brain tissue: prospective correction of macroscopic magnetic field gradients. Neuroimage. 2016;135:253–260. doi: 10.1016/j.neuroimage.2016.04.013. [DOI] [PubMed] [Google Scholar]
- Blockley NP, Griffeth VEM, Simon AB, Buxton RB. A review of calibrated blood oxygenation level-dependent (BOLD) methods for the measurement of task-induced changes in brain oxygen metabolism. NMR Biomed. 2013;26(8):987–1003. doi: 10.1002/nbm.2847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolar DS, Rosen BR, Sorensen AG, Adalsteinsson E. QUantitative Imaging of eXtraction of oxygen and TIssue consumption (QUIXOTIC) using venular-targeted velocity-selective spin labeling. Magn Reson Med. 2011;66(6):1550–1562. doi: 10.1002/mrm.22946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouzat P, Christen T, Thomas SD, Pannetier N, Rémy C, Payen J-F, Barbier EL (2011) Evaluation of a new quantitative BOLD approach to map local blood oxygen saturation in healthy rat. In: Proceedings of the 19th annual meeting of ISMRM. Montreal, Quebec, Canada
- Boxerman JL, Hamberg LM, Rosen BR, Weisskoff RM. Mr contrast due to intravascular magnetic susceptibility perturbations. Magn Reson Med. 1995;34(4):555–566. doi: 10.1002/mrm.1910340412. [DOI] [PubMed] [Google Scholar]
- Boxerman JL, Quarles CC, Hu LS, Erickson BJ, Gerstner ER, Smits M, Kaufmann TJ, Barboriak DP, Huang RH, Wick W, Weller M, Galanis E, Kalpathy-Cramer J, Shankar L, Jacobs P, Chung C, van den Bent MJ, Chang S, Al Yung WK, Cloughesy TF, Wen PY, Gilbert MR, Rosen BR, Ellingson BM, Schmainda KM, Jumpstarting Brain Tumor Drug Development Coalition Imaging Standardization Steering C Consensus recommendations for a dynamic susceptibility contrast MRI protocol for use in high-grade gliomas. Neuro Oncol. 2020;22(9):1262–1275. doi: 10.1093/neuonc/noaa141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JM, Giaccia AJ. The unique physiology of solid tumors: opportunities (and problems) for cancer therapy. Can Res. 1998;58(7):1408. [PubMed] [Google Scholar]
- Carr HY, Purcell EM. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys Rev. 1954;94(3):630–638. doi: 10.1103/PhysRev.94.630. [DOI] [Google Scholar]
- Chang F-Y, Xiao J-X, Xie S, Yu L, Zhang Z-X, Wang W, Luo J, Zhang Z-P, Guo H. Determination of oxygen extraction fraction using magnetic resonance imaging in canine models with internal carotid artery occlusion. Sci Rep. 2016;6(1):30332. doi: 10.1038/srep30332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cherukara MT, Stone AJ, Chappell MA, Blockley NP. Model-based Bayesian inference of brain oxygenation using quantitative BOLD. Neuroimage. 2019;202:116106. doi: 10.1016/j.neuroimage.2019.116106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho J, Kee Y, Spincemaille P, Nguyen TD, Zhang J, Gupta A, Zhang S, Wang Y. Cerebral metabolic rate of oxygen (CMRO2) mapping by combining quantitative susceptibility mapping (QSM) and quantitative blood oxygenation level-dependent imaging (qBOLD) Magn Reson Med. 2018;80(4):1595–1604. doi: 10.1002/mrm.27135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho J, Spincemaille P, Nguyen TD, Gupta A, Wang Y. Temporal clustering, tissue composition, and total variation for mapping oxygen extraction fraction using QSM and quantitative BOLD. Magn Reson Med. 2021;86(5):2635–2646. doi: 10.1002/mrm.28875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho J, Lee J, An H, Goyal MS, Su Y, Wang Y. Cerebral oxygen extraction fraction (OEF): Comparison of challenge-free gradient echo QSM+qBOLD (QQ) with 15O PET in healthy adults. J Cereb Blood Flow Metab. 2020;41(7):1658–1668. doi: 10.1177/0271678X20973951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho J, Zhang S, Kee Y, Spincemaille P, Nguyen TD, Hubertus S, Gupta A, Wang Y. Cluster analysis of time evolution (CAT) for quantitative susceptibility mapping (QSM) and quantitative blood oxygen level-dependent magnitude (qBOLD)-based oxygen extraction fraction (OEF) and cerebral metabolic rate of oxygen (CMRO2) mapping. Magn Reson Med. 2020;83(3):844–857. doi: 10.1002/mrm.27967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christen T, Lemasson B, Pannetier N, Farion R, Segebarth C, Rémy C, Barbier EL. Evaluation of a quantitative blood oxygenation level-dependent (qBOLD) approach to map local blood oxygen saturation. NMR Biomed. 2011;24(4):393–403. doi: 10.1002/nbm.1603. [DOI] [PubMed] [Google Scholar]
- Christen T, Schmiedeskamp H, Straka M, Bammer R, Zaharchuk G. Measuring brain oxygenation in humans using a multiparametric quantitative blood oxygenation level dependent MRI approach. Magn Reson Med. 2012;68(3):905–911. doi: 10.1002/mrm.23283. [DOI] [PubMed] [Google Scholar]
- de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu J, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn Reson Med. 2010;63(1):194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- Derdeyn CP, Videen TO, Yundt KD, Fritsch SM, Carpenter DA, Grubb RL, Powers WJ. Variability of cerebral blood volume and oxygen extraction: stages of cerebral haemodynamic impairment revisited. Brain. 2002;125(3):595–607. doi: 10.1093/brain/awf047. [DOI] [PubMed] [Google Scholar]
- Derdeyn CP, Yundt KD, Videen TO, Carpenter DA, Grubb RL, Powers WJ. Increased oxygen extraction fraction is associated with prior ischemic events in patients with carotid occlusion. Stroke. 1998;29(4):754–758. doi: 10.1161/01.STR.29.4.754. [DOI] [PubMed] [Google Scholar]
- Dickson JD, Ash TWJ, Williams GB, Harding SG, Carpenter TA, Menon DK, Ansorge RE. Quantitative BOLD: the effect of diffusion. J Magn Reson Imaging. 2010;32(4):953–961. doi: 10.1002/jmri.22151. [DOI] [PubMed] [Google Scholar]
- Eichling JO, Raichle ME, Grubb RL, Larson KB, Ter-Pogossian MM. In vivo determination of cerebral blood volume with radioactive oxygen-15 in the monkey. Circ Res. 1975;37(6):707–714. doi: 10.1161/01.RES.37.6.707. [DOI] [PubMed] [Google Scholar]
- Fan AP, An H, Moradi F, Rosenberg J, Ishii Y, Nariai T, Okazawa H, Zaharchuk G. Quantification of brain oxygen extraction and metabolism with [15O]-gas PET: a technical review in the era of PET/MRI. Neuroimage. 2020;220:117136. doi: 10.1016/j.neuroimage.2020.117136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan AP, Benner T, Bolar DS, Rosen BR, Adalsteinsson E. Phase-based regional oxygen metabolism (PROM) using MRI. Magn Reson Med. 2012;67(3):669–678. doi: 10.1002/mrm.23050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan AP, Khalil AA, Fiebach JB, Zaharchuk G, Villringer A, Villringer K, Gauthier CJ. Elevated brain oxygen extraction fraction measured by MRI susceptibility relates to perfusion status in acute ischemic stroke. J Cereb Blood Flow Metab. 2019;40(3):539–551. doi: 10.1177/0271678X19827944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández-Seara MA, Techawiboonwong A, Detre JA, Wehrli FW. MR susceptometry for measuring global brain oxygen extraction. Magn Reson Med. 2006;55(5):967–973. doi: 10.1002/mrm.20892. [DOI] [PubMed] [Google Scholar]
- Fields ME, Guilliams KP, Ragan D, Binkley MM, Mirro A, Fellah S, Hulbert ML, Blinder M, Eldeniz C, Vo K, Shimony JS, Chen Y, McKinstry RC, An H, Lee J-M, Ford AL. Hydroxyurea reduces cerebral metabolic stress in patients with sickle cell anemia. Blood. 2019;133(22):2436–2444. doi: 10.1182/blood-2018-09-876318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fields ME, Guilliams KP, Ragan DK, Binkley MM, Eldeniz C, Chen Y, Hulbert ML, McKinstry RC, Shimony JS, Vo KD, Doctor A, An H, Ford AL, Lee J-M. Regional oxygen extraction predicts border zone vulnerability to stroke in sickle cell disease. Neurology. 2018;90(13):e1134. doi: 10.1212/WNL.0000000000005194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ford AL, Chin VW, Fellah S, Binkley MM, Bodin AM, Balasetti V, Taiwo Y, Kang P, Lin D, Jen JC, Grand MG, Bogacki M, Liszewski MK, Hourcade D, Chen Y, Hassenstab J, Lee J-M, An H, Miner JJ, Atkinson JP. Lesion evolution and neurodegeneration in RVCL-S. Neurology. 2020;95(14):e1918. doi: 10.1212/WNL.0000000000010659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ford AL, Ragan DK, Fellah S, Binkley MM, Fields ME, Guilliams KP, An H, Jordan LC, McKinstry RC, Lee J-M, DeBaun MR. Silent infarcts in sickle cell disease occur in the border zone region and are associated with low cerebral blood flow. Blood. 2018;132(16):1714–1723. doi: 10.1182/blood-2018-04-841247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frahm J, Merboldt K-D, Hänicke W. Functional MRI of human brain activation at high spatial resolution. Magn Reson Med. 1993;29(1):139–144. doi: 10.1002/mrm.1910290126. [DOI] [PubMed] [Google Scholar]
- Fujita N, Shinohara M, Tanaka H, Yutani K, Nakamura H, Murase K. Quantitative mapping of cerebral deoxyhemoglobin content using MR imaging. Neuroimage. 2003;20(4):2071–2083. doi: 10.1016/j.neuroimage.2003.06.002. [DOI] [PubMed] [Google Scholar]
- Golay X, Silvennoinen MJ, Zhou J, Clingman CS, Kauppinen RA, Pekar JJ, van Zij PCM. Measurement of tissue oxygen extraction ratios from venous blood T2: increased precision and validation of principle. Magn Reson Med. 2001;46(2):282–291. doi: 10.1002/mrm.1189. [DOI] [PubMed] [Google Scholar]
- Guilliams KP, Fields ME, Ragan DK, Eldeniz C, Binkley MM, Chen Y, Comiskey LS, Doctor A, Hulbert ML, Shimony JS, Vo KD, McKinstry RC, An H, Lee J-M, Ford AL. Red cell exchange transfusions lower cerebral blood flow and oxygen extraction fraction in pediatric sickle cell anemia. Blood. 2018;131(9):1012–1021. doi: 10.1182/blood-2017-06-789842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta A, Chazen JL, Hartman M, Delgado D, Anumula N, Shao H, Mazumdar M, Segal AZ, Kamel H, Leifer D, Sanelli PC. Cerebrovascular reserve and stroke risk in patients with carotid stenosis or occlusion. Stroke. 2012;43(11):2884–2891. doi: 10.1161/STROKEAHA.112.663716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison LB, Chadha M, Hill RJ, Hu K, Shasha D. Impact of tumor hypoxia and anemia on radiation therapy outcomes. Oncologist. 2002;7(6):492–508. doi: 10.1634/theoncologist.7-6-492. [DOI] [PubMed] [Google Scholar]
- He X, Yablonskiy DA. Quantitative BOLD: mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: default state. Magn Reson Med. 2007;57(1):115–126. doi: 10.1002/mrm.21108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Zhu M, Yablonskiy DA. Validation of oxygen extraction fraction measurement by qBOLD technique. Magn Reson Med. 2008;60(4):882–888. doi: 10.1002/mrm.21719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heiss WD, Podreka I. Role of PET and SPECT in the assessment of ischemic cerebrovascular disease. Cerebrovasc Brain Metab Rev. 1993;5(4):235–263. [PubMed] [Google Scholar]
- Hennig J. Multiecho imaging sequences with low refocusing flip angles. J Magn Reson (1969) 1988;78(3):397–407. doi: 10.1016/0022-2364(88)90128-X. [DOI] [Google Scholar]
- Hirsch NM, Toth V, Förschler A, Kooijman H, Zimmer C, Preibisch C. Technical considerations on the validity of blood oxygenation level-dependent-based MR assessment of vascular deoxygenation. NMR Biomed. 2014;27(7):853–862. doi: 10.1002/nbm.3131. [DOI] [PubMed] [Google Scholar]
- Houston GC, Papadakis NG, Carpenter TA, Hall LD, Mukherjee B, James MF, Huang CLH. Mapping of the cerebral response to hypoxia measured using graded asymmetric spin echo EPI. Magn Reson Imaging. 2000;18(9):1043–1054. doi: 10.1016/S0730-725X(00)00196-X. [DOI] [PubMed] [Google Scholar]
- Huang WJ, Chen WW, Zhang X. Glioblastoma multiforme: effect of hypoxia and hypoxia inducible factors on therapeutic approaches (Review) Oncol Lett. 2016;12(4):2283–2288. doi: 10.3892/ol.2016.4952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurlet-Jensen AM, Prohovnik I, Pavlakis SG, Piomelli S. Effects of total hemoglobin and hemoglobin S concentration on cerebral blood flow during transfusion therapy to prevent stroke in sickle cell disease. Stroke. 1994;25(8):1688–1692. doi: 10.1161/01.STR.25.8.1688. [DOI] [PubMed] [Google Scholar]
- Iadecola C. Neurovascular regulation in the normal brain and in Alzheimer's disease. Nat Rev Neurosci. 2004;5(5):347–360. doi: 10.1038/nrn1387. [DOI] [PubMed] [Google Scholar]
- Ishii K, Kitagaki H, Kono M, Mori E. Decreased medial temporal oxygen metabolism in Alzheimer's disease shown by PET. J Nucl Med. 1996;37(7):1159. [PubMed] [Google Scholar]
- Ito M, Lammertsma AA, Wise RJS, Bernardi S, Frackowiak RSJ, Heather JD, McKenzie CG, Thomas DGT, Jones T. Measurement of regional cerebral blood flow and oxygen utilisation in patients with cerebral tumours using 15O and positron emission tomography: analytical techniques and preliminary results. Neuroradiology. 1982;23(2):63–74. doi: 10.1007/BF00367239. [DOI] [PubMed] [Google Scholar]
- Jain V, Langham MC, Wehrli FW. MRI estimation of global brain oxygen consumption rate. J Cereb Blood Flow Metab. 2010;30(9):1598–1607. doi: 10.1038/jcbfm.2010.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen RL. Brain tumor hypoxia: tumorigenesis, angiogenesis, imaging, pseudoprogression, and as a therapeutic target. J Neurooncol. 2009;92(3):317–335. doi: 10.1007/s11060-009-9827-2. [DOI] [PubMed] [Google Scholar]
- Jordan LC, DeBaun MR. Cerebral hemodynamic assessment and neuroimaging across the lifespan in sickle cell disease. J Cereb Blood Flow Metab. 2017;38(9):1438–1448. doi: 10.1177/0271678X17701763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan LC, DeBaun MR. Cerebral hemodynamic assessment and neuroimaging across the lifespan in sickle cell disease. J Cereb Blood Flow Metab. 2018;38(9):1438–1448. doi: 10.1177/0271678X17701763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan LC, Gindville MC, Scott AO, Juttukonda MR, Strother MK, Kassim AA, Chen S-C, Lu H, Pruthi S, Shyr Y, Donahue MJ. Non-invasive imaging of oxygen extraction fraction in adults with sickle cell anaemia. Brain. 2016;139(3):738–750. doi: 10.1093/brain/awv397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaczmarz S, Hyder F, Preibisch C. Oxygen extraction fraction mapping with multi-parametric quantitative BOLD MRI: reduced transverse relaxation bias using 3D-GraSE imaging. Neuroimage. 2020;220:117095. doi: 10.1016/j.neuroimage.2020.117095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang P, Ying C, Chen Y, Ford AL, An H, Lee J-M. Oxygen metabolic stress and white matter injury in patients with cerebral small vessel disease. Stroke. 2022;53(5):1570–1579. doi: 10.1161/STROKEAHA.121.035674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiselev VG, Posse S. Analytical model of susceptibility-induced MR signal dephasing: effect of diffusion in a microvascular network. Magn Reson Med. 1999;41(3):499–509. doi: 10.1002/(SICI)1522-2594(199903)41:3<499::AID-MRM12>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- Kiselev VG, Posse S. Erratum: analytical theory of susceptibility induced NMR Signal dephasing in a cerebrovascular network [Phys. Rev. Lett. 81, 5696 (1998)] Phys Rev Lett. 1999;83(7):1487–1487. doi: 10.1103/PhysRevLett.83.1487. [DOI] [Google Scholar]
- Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, et al. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci U S A. 1992;89(12):5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lammertsma AA, Wise RJS, Heather JD, Gibbs JM, Leenders KL, Frackowiak RSJ, Rhodes CG, Jones T. Correction for the presence of intravascular oxygen-15 in the steady-state technique for measuring regional oxygen extraction ratio in the brain: 2. Results in normal subjects and brain tumour and stroke patients. J Cereb Blood Flow Metab. 1983;3(4):425–431. doi: 10.1038/jcbfm.1983.68. [DOI] [PubMed] [Google Scholar]
- Lee H, Englund EK, Wehrli FW. Interleaved quantitative BOLD: combining extravascular R2ʹ - and intravascular R2-measurements for estimation of deoxygenated blood volume and hemoglobin oxygen saturation. Neuroimage. 2018;174:420–431. doi: 10.1016/j.neuroimage.2018.03.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H, Wehrli FW. Whole-brain 3D mapping of oxygen metabolism using constrained quantitative BOLD. Neuroimage. 2022;250:118952. doi: 10.1016/j.neuroimage.2022.118952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J-M, Vo KD, An H, Celik A, Lee Y, Hsu CY, Lin W. Magnetic resonance cerebral metabolic rate of oxygen utilization in hyperacute stroke patients. Ann Neurol. 2003;53(2):227–232. doi: 10.1002/ana.10433. [DOI] [PubMed] [Google Scholar]
- Liu EY, Guo J, Simon AB, Haist F, Dubowitz DJ, Buxton RB. The potential for gas-free measurements of absolute oxygen metabolism during both baseline and activation states in the human brain. Neuroimage. 2020;207:116342. doi: 10.1016/j.neuroimage.2019.116342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Liu T, de Rochefort L, Ledoux J, Khalidov I, Chen W, Tsiouris AJ, Wisnieff C, Spincemaille P, Prince MR, Wang Y. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. Neuroimage. 2012;59(3):2560–2568. doi: 10.1016/j.neuroimage.2011.08.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu H, Ge Y. Quantitative evaluation of oxygenation in venous vessels using T2-Relaxation-Under-Spin-Tagging MRI. Magn Reson Med. 2008;60(2):357–363. doi: 10.1002/mrm.21627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu H, Clingman C, Golay X, van Zijl PCM. Determining the longitudinal relaxation time (T1) of blood at 3.0 Tesla. Magn Reson Med. 2004;52(3):679–682. doi: 10.1002/mrm.20178. [DOI] [PubMed] [Google Scholar]
- Lu H, Xu F, Grgac K, Liu P, Qin Q, van Zijl P. Calibration and validation of TRUST MRI for the estimation of cerebral blood oxygenation. Magn Reson Med. 2012;67(1):42–49. doi: 10.1002/mrm.22970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X, Luo Y, Fawaz M, Zhu C, Chai C, Wu G, Wang H, Liu J, Zou Y, Gong Y, Haacke EM, Xia S. Dynamic changes of asymmetric cortical veins relate to neurologic prognosis in acute ischemic stroke. Radiology. 2021;301(3):672–681. doi: 10.1148/radiol.2021210201. [DOI] [PubMed] [Google Scholar]
- Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187–192. doi: 10.1038/nature11971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick PW, Stewart M, Goetting MG, Balakrishnan G. Regional cerebrovascular oxygen saturation measured by optical spectroscopy in humans. Stroke. 1991;22(5):596–602. doi: 10.1161/01.STR.22.5.596. [DOI] [PubMed] [Google Scholar]
- Mintun MA, Raichle ME, Martin WRW, Herscovitch P. Brain oxygen utilization measured with O-15 radiotracers and positron emission tomography. J Nucl Med. 1984;25(2):177. [PubMed] [Google Scholar]
- Nakane H, Ibayashi S, Fujii K, Sadoshima S, Irie K, Kitazono T, Fujishima M. Cerebral blood flow and metabolism in patients with silent brain infarction: occult misery perfusion in the cerebral cortex. J Neurol Neurosurg Psychiatry. 1998;65(3):317–321. doi: 10.1136/jnnp.65.3.317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen TB, Cron GO, Perdrizet K, Bezzina K, Torres CH, Chakraborty S, Woulfe J, Jansen GH, Sinclair J, Thornhill RE, Foottit C, Zanette B, Cameron IG. Comparison of the diagnostic accuracy of DSC- and dynamic contrast-enhanced MRI in the preoperative grading of astrocytomas. Am J Neuroradiol. 2015;36(11):2017. doi: 10.3174/ajnr.A4398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni W, Christen T, Zun Z, Zaharchuk G. Comparison of R2′ measurement methods in the normal brain at 3 tesla. Magn Reson Med. 2015;73(3):1228–1236. doi: 10.1002/mrm.25232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Tank DW, Menon R, Ellermann JM, Kim SG, Merkle H, Ugurbil K. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci. 1992;89(13):5951. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oguz KK, Golay X, Pizzini FB, Freer CA, Winrow N, Ichord R, Casella JF, van Zijl PCM, Melhem ER. Sickle cell disease: continuous arterial spin-labeling perfusion MR imaging in children. Radiology. 2003;227(2):567–574. doi: 10.1148/radiol.2272020903. [DOI] [PubMed] [Google Scholar]
- Oja JME, Gillen JS, Kauppinen RA, Kraut M, van Zijl PCM. Determination of oxygen extraction ratios by magnetic resonance imaging. J Cereb Blood Flow Metab. 1999;19(12):1289–1295. doi: 10.1097/00004647-199912000-00001. [DOI] [PubMed] [Google Scholar]
- Omuro A, DeAngelis LM. Glioblastoma and other malignant gliomas: a clinical review. JAMA. 2013;310(17):1842–1850. doi: 10.1001/jama.2013.280319. [DOI] [PubMed] [Google Scholar]
- Oughourlian TC, Yao J, Hagiwara A, Nathanson DA, Raymond C, Pope WB, Salamon N, Lai A, Ji M, Nghiemphu PL, Liau LM, Cloughesy TF, Ellingson BM. Relative oxygen extraction fraction (rOEF) MR imaging reveals higher hypoxia in human epidermal growth factor receptor (EGFR) amplified compared with non-amplified gliomas. Neuroradiology. 2021;63(6):857–868. doi: 10.1007/s00234-020-02585-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piel FB, Hay SI, Gupta S, Weatherall DJ, Williams TN. Global burden of sickle cell anaemia in children under five, 2010–2050: modelling based on demographics, excess mortality, and interventions. PLoS Med. 2013;10(7):e1001484. doi: 10.1371/journal.pmed.1001484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prasloski T, Mädler B, Xiang Q-S, MacKay A, Jones C. Applications of stimulated echo correction to multicomponent T2 analysis. Magn Reson Med. 2012;67(6):1803–1814. doi: 10.1002/mrm.23157. [DOI] [PubMed] [Google Scholar]
- Probst J, Rohner M, Zahn M, Piccirelli M, Pangalu A, Luft A, Deistung A, Klohs J, Wegener S. Quantitative susceptibility mapping in ischemic stroke patients after successful recanalization. Sci Rep. 2021;11(1):16038. doi: 10.1038/s41598-021-95265-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross EM, Matteucci MJ, Shepherd M, Barker M, Orr L. Measuring arterial oxygenation in a high altitude field environment: comparing portable pulse oximetry with blood gas analysis. Wilderness Environ Med. 2013;24(2):112–117. doi: 10.1016/j.wem.2012.11.009. [DOI] [PubMed] [Google Scholar]
- Schatten H. Brief overview of prostate cancer statistics, grading, diagnosis and treatment strategies. In: Schatten H, editor. Cell & Molecular biology of prostate cancer: updates, insights and new frontiers. Cham: Springer International Publishing; 2018. pp. 1–14. [DOI] [PubMed] [Google Scholar]
- Schröder H, Bongers A, Schad LR. Validierung von Modellannahmen einer MR-Sauerstoffextraktionsbildgebung mittels einer Phantomstudie. Z Med Phys. 2006;16(4):275–284. doi: 10.1078/0939-3889-00326. [DOI] [PubMed] [Google Scholar]
- Sedlacik J, Boelmans K, Löbel U, Holst B, Siemonsen S, Fiehler J. Reversible, irreversible and effective transverse relaxation rates in normal aging brain at 3T. Neuroimage. 2014;84:1032–1041. doi: 10.1016/j.neuroimage.2013.08.051. [DOI] [PubMed] [Google Scholar]
- Sedlacik J, Reichenbach JR. Validation of quantitative estimation of tissue oxygen extraction fraction and deoxygenated blood volume fraction in phantom and in vivo experiments by using MRI. Magn Reson Med. 2010;63(4):910–921. doi: 10.1002/mrm.22274. [DOI] [PubMed] [Google Scholar]
- Sen S, An H, Menezes P, Oakes J, Eron J, Lin W, Robertson K, Powers W. Increased cortical cerebral blood flow in asymptomatic human immunodeficiency virus-infected subjects. J Stroke Cerebrovasc Dis. 2016;25(8):1891–1895. doi: 10.1016/j.jstrokecerebrovasdis.2016.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon AB, Dubowitz DJ, Blockley NP, Buxton RB. A novel Bayesian approach to accounting for uncertainty in fMRI-derived estimates of cerebral oxygen metabolism fluctuations. Neuroimage. 2016;129:198–213. doi: 10.1016/j.neuroimage.2016.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohlin MC, Schad LR (2009) Theoretical prediction of parameter stability in quantitative BOLD MRI: dependence on SNR and sequence parameters. In: Proceedings of the 18th annual meeting ISMRM. Honolulu, HI, USA
- Sohlin MC, Schad LR. Susceptibility-related MR signal dephasing under nonstatic conditions: experimental verification and consequences for qBOLD measurements. J Magn Reson Imag. 2011;33(2):417–425. doi: 10.1002/jmri.22423. [DOI] [PubMed] [Google Scholar]
- Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJH. Water proton MR properties of human blood at 1.5 Tesla: magnetic susceptibility, T1, T2, T, and non-Lorentzian signal behavior. Magn Reson Med. 2001;45(4):533–542. doi: 10.1002/mrm.1072. [DOI] [PubMed] [Google Scholar]
- Stadlbauer A, Roessler K, Zimmermann M, Buchfelder M, Kleindienst A, Doerfler A, Heinz G, Oberndorfer S. Predicting glioblastoma response to bevacizumab through MRI biomarkers of the tumor microenvironment. Mol Imag Biol. 2019;21(4):747–757. doi: 10.1007/s11307-018-1289-5. [DOI] [PubMed] [Google Scholar]
- Stadlbauer A, Zimmermann M, Bennani-Baiti B, Helbich TH, Baltzer P, Clauser P, Kapetas P, Bago-Horvath Z, Pinker K. Development of a non-invasive assessment of hypoxia and neovascularization with magnetic resonance imaging in benign and malignant breast tumors: initial results. Mol Imag Biol. 2019;21(4):758–770. doi: 10.1007/s11307-018-1298-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadlbauer A, Zimmermann M, Doerfler A, Oberndorfer S, Buchfelder M, Coras R, Kitzwögerer M, Roessler K. Intratumoral heterogeneity of oxygen metabolism and neovascularization uncovers 2 survival-relevant subgroups of IDH1 wild-type glioblastoma. Neuro Oncol. 2018;20(11):1536–1546. doi: 10.1093/neuonc/noy066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadlbauer A, Zimmermann M, Kitzwögerer M, Oberndorfer S, Rössler K, Dörfler A, Buchfelder M, Heinz G. MR Imaging–derived oxygen metabolism and neovascularization characterization for grading and IDH gene mutation detection of gliomas. Radiology. 2016;283(3):799–809. doi: 10.1148/radiol.2016161422. [DOI] [PubMed] [Google Scholar]
- Stone AJ, Blockley NP. A streamlined acquisition for mapping baseline brain oxygenation using quantitative BOLD. Neuroimage. 2017;147:79–88. doi: 10.1016/j.neuroimage.2016.11.057. [DOI] [PubMed] [Google Scholar]
- Stone AJ, Harston GWJ, Carone D, Okell TW, Kennedy J, Blockley NP. Prospects for investigating brain oxygenation in acute stroke: Experience with a non-contrast quantitative BOLD based approach. Hum Brain Mapp. 2019;40(10):2853–2866. doi: 10.1002/hbm.24564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone AJ, Holland NC, Berman AJL, Blockley NP. Simulations of the effect of diffusion on asymmetric spin echo based quantitative BOLD: an investigation of the origin of deoxygenated blood volume overestimation. Neuroimage. 2019;201:116035. doi: 10.1016/j.neuroimage.2019.116035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukstanskii AL, Yablonskiy DA. Theory of FID NMR signal dephasing induced by mesoscopic magnetic field inhomogeneities in biological systems. J Magn Reson. 2001;151(1):107–117. doi: 10.1006/jmre.2001.2363. [DOI] [PubMed] [Google Scholar]
- Tóth V, Förschler A, Hirsch NM, den Hollander J, Kooijman H, Gempt J, Ringel F, Schlegel J, Zimmer C, Preibisch C. MR-based hypoxia measures in human glioma. J Neurooncol. 2013;115(2):197–207. doi: 10.1007/s11060-013-1210-7. [DOI] [PubMed] [Google Scholar]
- Touzani O, Young AR, Derlon J-M, Baron J-C, MacKenzie ET. Progressive impairment of brain oxidative metabolism reversed by reperfusion following middle cerebral artery occlusion in anaesthetized baboons. Brain Res. 1997;767(1):17–25. doi: 10.1016/S0006-8993(97)00515-5. [DOI] [PubMed] [Google Scholar]
- Ulrich X, Yablonskiy DA. Separation of cellular and BOLD contributions to T2* signal relaxation. Magn Reson Med. 2016;75(2):606–615. doi: 10.1002/mrm.25610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Zijl PCM, Eleff SM, Ulatowski JA, Oja JME, Uluǧ AM, Traystman RJ, Kauppinen RA. Quantitative assessment of blood flow, blood volume and blood oxygenation effects in functional magnetic resonance imaging. Nat Med. 1998;4(2):159–167. doi: 10.1038/nm0298-159. [DOI] [PubMed] [Google Scholar]
- Wang C, Zhang R, Wang R, Jiang L, Zhang X, Wang H, Zhao K, Jin L, Zhang J, Wang X, Fang J. Noninvasive measurement of renal oxygen extraction fraction under the influence of respiratory challenge. J Magn Reson Imaging. 2016;44(1):230–237. doi: 10.1002/jmri.25163. [DOI] [PubMed] [Google Scholar]
- Wang C, Zhao K, Zhang R, Jiang L, Wang R, Zhang X, Wang H, Jin L, Zhang J, Wang X, Fang J. Evaluation of renal oxygenation change under the influence of carbogen breathing using a dynamic R2, R2′ and R2* quantification approach. NMR Biomed. 2016;29(11):1601–1607. doi: 10.1002/nbm.3625. [DOI] [PubMed] [Google Scholar]
- Wang R, Lin Z, Yang X, Zhao K, Wang S, Sui X, Su T, Wang X. Noninvasive evaluation of renal hypoxia by multiparametric functional MRI in early diabetic kidney disease. J Magn Reson Imaging. 2021 doi: 10.1002/jmri.27814. [DOI] [PubMed] [Google Scholar]
- Wang X, Sukstanskii AL, Yablonskiy DA. Optimization strategies for evaluation of brain hemodynamic parameters with qBOLD technique. Magn Reson Med. 2013;69(4):1034–1043. doi: 10.1002/mrm.24338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Fellah S, Fields ME, Guilliams KP, Binkley MM, Eldeniz C, Shimony JS, Reis M, Vo KD, Chen Y, Lee J-M, An H, Ford AL. Cerebral oxygen metabolic stress, microstructural injury, and infarction in adults with sickle cell disease. Neurology. 2021;97(9):e902–e912. doi: 10.1212/WNL.0000000000012404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ware RE, de Montalembert M, Tshilolo L, Abboud MR. Sickle cell disease. The Lancet. 2017;390(10091):311–323. doi: 10.1016/S0140-6736(17)30193-9. [DOI] [PubMed] [Google Scholar]
- Wehrli FW, Fan AP, Rodgers ZB, Englund EK, Langham MC. Susceptibility-based time-resolved whole-organ and regional tissue oximetry. NMR Biomed. 2017;30(4):e3495. doi: 10.1002/nbm.3495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willats L, Calamante F. The 39 steps: evading error and deciphering the secrets for accurate dynamic susceptibility contrast MRI. NMR Biomed. 2013;26(8):913–931. doi: 10.1002/nbm.2833. [DOI] [PubMed] [Google Scholar]
- Wirestam R, Knutsson L, Risberg J, Börjesson S, Larsson EM, Gustafson L, Passant U, Ståhlberg F. Attempts to improve absolute quantification of cerebral blood flow in dynamic susceptibility contrast magnetic resonance imaging: a simplified T1-weighted steady-state cerebral blood volume approach. Acta Radiol. 2007;48(5):550–556. doi: 10.1080/02841850701280825. [DOI] [PubMed] [Google Scholar]
- Xie S, Hui LH, Xiao JX, Zhang XD, Peng Q. Detecting misery perfusion in unilateral steno-occlusive disease of the internal carotid artery or middle cerebral artery by MR imaging. AJNR Am J Neuroradiol. 2011;32(8):1504–1509. doi: 10.3174/ajnr.a2523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy DA. Quantitation of intrinsic magnetic susceptibility-related effects in a tissue matrix. Phantom study. Magn Reson Med. 1998;39(3):417–428. doi: 10.1002/mrm.1910390312. [DOI] [PubMed] [Google Scholar]
- Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn Reson Med. 1994;32(6):749–763. doi: 10.1002/mrm.1910320610. [DOI] [PubMed] [Google Scholar]
- Yablonskiy DA, Sukstanskii AL, He X. Blood oxygenation level-dependent (BOLD)-based techniques for the quantification of brain hemodynamic and metabolic properties – theoretical models and experimental approaches. NMR Biomed. 2013;26(8):963–986. doi: 10.1002/nbm.2839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamauchi H, Fukuyama H, Nagahama Y, Katsumi Y, Okazawa H. Cerebral hematocrit decreases with hemodynamic compromise in carotid artery occlusion. Stroke. 1998;29(1):98–103. doi: 10.1161/01.STR.29.1.98. [DOI] [PubMed] [Google Scholar]
- Yamauchi H, Fukuyama H, Nagahama Y, Nabatame H, Nakamura K, Yamamoto Y, Yonekura Y, Konishi J, Kimura J. Evidence of misery perfusion and risk for recurrent stroke in major cerebral arterial occlusive diseases from PET. J Neurol Neurosurg Psychiatry. 1996;61(1):18–25. doi: 10.1136/jnnp.61.1.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang QX, Williams GD, Demeure RJ, Mosher TJ, Smith MB. Removal of local field gradient artifacts in T2*-weighted images at high fields by gradient-echo slice excitation profile imaging. Magn Reson Med. 1998;39(3):402–409. doi: 10.1002/mrm.1910390310. [DOI] [PubMed] [Google Scholar]
- Yang Y, Yin Y, Lu J, Zou Q, Gao J-H. Detecting resting-state brain activity using OEF-weighted imaging. Neuroimage. 2019;200:101–120. doi: 10.1016/j.neuroimage.2019.06.038. [DOI] [PubMed] [Google Scholar]
- Yin Y, Zhang Y, Gao J-H. Dynamic measurement of oxygen extraction fraction using a multiecho asymmetric spin echo (MASE) pulse sequence. Magn Reson Med. 2018;80(3):1118–1124. doi: 10.1002/mrm.27078. [DOI] [PubMed] [Google Scholar]
- Yu L, Xie S, Xiao J, Wang Z, Zhang X. Quantitative measurement of cerebral oxygen extraction fraction using MRI in patients with MELAS. PLoS ONE. 2013;8(11):e79859–e79859. doi: 10.1371/journal.pone.0079859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Liu T, Gupta A, Spincemaille P, Nguyen TD, Wang Y. Quantitative mapping of cerebral metabolic rate of oxygen (CMRO2) using quantitative susceptibility mapping (QSM) Magn Reson Med. 2015;74(4):945–952. doi: 10.1002/mrm.25463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Zhou D, Nguyen TD, Spincemaille P, Gupta A, Wang Y. Cerebral metabolic rate of oxygen (CMRO2) mapping with hyperventilation challenge using quantitative susceptibility mapping (QSM) Magn Reson Med. 2017;77(5):1762–1773. doi: 10.1002/mrm.26253. [DOI] [PubMed] [Google Scholar]
- Zhang X, Zhang Y, Yang X, Wang X, An H, Zhang J, Fang J. Feasibility of noninvasive quantitative measurements of intrarenal R2′ in humans using an asymmetric spin echo echo planar imaging sequence. NMR Biomed. 2013;26(1):91–97. doi: 10.1002/nbm.2823. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Not applicable.