Abstract
目的
基于深度学习研发腰椎稳定性自动诊断工具,并验证其诊断精度。
方法
收集153例腰椎疾病患者术前腰椎过屈、过伸位X线片,由3名骨科医师标注5个关键点,分别为L4后下角、前下角以及L5后上角、前上角、后下角,共获得3套标注结果。将306张腰椎X线片按照3∶1∶2比例随机分为训练集(n=156)、验证集(n=50)和测试集(n=100)。提出一种新的神经网络结构Swin-PGNet,使用已标注的X线片图像对其进行训练,使其能自动定位腰椎椎体关键点,并通过关键点测算L4、5椎间Cobb角和L4椎体滑移距离。对于关键点定位、Cobb角测量和椎体滑移距离测量,以平均误差、组内相关系数(intra-class correlation coefficient,ICC)比较医师标注与Swin-PGNet之间的差异。椎间Cobb角变化超过11° 作为腰椎不稳判断标准,腰椎滑移距离超过3 mm作为腰椎滑脱判断标准,比较医师和Swin-PGNet判断腰椎稳定性的准确率。
结果
① Swin-PGNet关键点定位平均误差为(1.407 0.939)mm,医师间平均误差为(3.034±2.612)mm。 ② Cobb角标注:Swin-PGNet平均误差为(2.062
0.939)mm,医师间平均误差为(3.034±2.612)mm。 ② Cobb角标注:Swin-PGNet平均误差为(2.062 1.352)°,医师间平均误差为(3.580
1.352)°,医师间平均误差为(3.580 2.338)°;Swin-PGNet与3名医师间误差比较,差异均无统计学意义(P>0.05),但不同医师间误差比较差异有统计学意义(P<0.05)。③ 椎体滑移距离:Swin-PGNet平均误差为(1.656
2.338)°;Swin-PGNet与3名医师间误差比较,差异均无统计学意义(P>0.05),但不同医师间误差比较差异有统计学意义(P<0.05)。③ 椎体滑移距离:Swin-PGNet平均误差为(1.656 0.878)mm,医师标注平均误差为(1.884
0.878)mm,医师标注平均误差为(1.884 1.612)mm;Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异均无统计学意义(P>0.05)。Swin-PGNet腰椎不稳判断准确率为84.0%、医师为75.3%,腰椎滑脱判断准确率分别为71.3%、70.7%,Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异均无统计学意义(P>0.05)。④ 腰椎稳定性判定一致性分析:3名医师标注椎间Cobb角的ICC为0.913 [95%CI(0.898,0.934)] (P<0.05),椎体滑移距离为0.741 [95%CI(0.729,0.796)] (P<0.05),说明3名医师间标注具有一致性。Swin-PGNet-所有医师间椎间Cobb角ICC为0.922 [95%CI(0.891,0.938)] (P<0.05),椎体滑移距离为0.748 [95%CI(0.726,0.783)](P<0.05),说明Swin-PGNet与医师标注具有一致性。
1.612)mm;Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异均无统计学意义(P>0.05)。Swin-PGNet腰椎不稳判断准确率为84.0%、医师为75.3%,腰椎滑脱判断准确率分别为71.3%、70.7%,Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异均无统计学意义(P>0.05)。④ 腰椎稳定性判定一致性分析:3名医师标注椎间Cobb角的ICC为0.913 [95%CI(0.898,0.934)] (P<0.05),椎体滑移距离为0.741 [95%CI(0.729,0.796)] (P<0.05),说明3名医师间标注具有一致性。Swin-PGNet-所有医师间椎间Cobb角ICC为0.922 [95%CI(0.891,0.938)] (P<0.05),椎体滑移距离为0.748 [95%CI(0.726,0.783)](P<0.05),说明Swin-PGNet与医师标注具有一致性。
结论
基于深度学习构建的腰椎稳定性自动诊断工具Swin-PGNet实现了腰椎不稳与滑脱的准确、便捷自动识别,可辅助临床进行诊断。
Keywords: 人工智能, 医学图像处理, 关键点定位, 腰椎不稳, 辅助诊断
Abstract
Objective
To develop an automatic diagnostic tool based on deep learning for lumbar spine stability and validate diagnostic accuracy.
Methods
Preoperative lumbar hyper-flexion and hyper-extension X-ray films were collected from 153 patients with lumbar disease. The following 5 key points were marked by 3 orthopedic surgeons: L4 posteroinferior, anterior inferior angles as well as L5 posterosuperior, anterior superior, and posterior inferior angles. The labeling results of each surgeon were preserved independently, and a total of three sets of labeling results were obtained. A total of 306 lumbar X-ray films were randomly divided into training (n=156), validation (n=50), and test (n=100) sets in a ratio of 3∶1∶2. A new neural network architecture, Swin-PGNet was proposed, which was trained using annotated radiograph images to automatically locate the lumbar vertebral key points and calculate L4, 5 intervertebral Cobb angle and L4 lumbar sliding distance through the predicted key points. The mean error and intra-class correlation coefficient (ICC) were used as an evaluation index, to compare the differences between surgeons’ annotations and Swin-PGNet on the three tasks (key point positioning, Cobb angle measurement, and lumbar sliding distance measurement). Meanwhile, the change of Cobb angle more than 11° was taken as the criterion of lumbar instability, and the lumbar sliding distance more than 3 mm was taken as the criterion of lumbar spondylolisthesis. The accuracy of surgeon annotation and Swin-PGNet in judging lumbar instability was compared.
Results
① Key point: The mean error of key point location by Swin-PGNet was (1.407±0.939) mm, and by different surgeons was (3.034±2.612) mm. ② Cobb angle: The mean error of Swin-PGNet was (2.062±1.352)° and the mean error of surgeons was (3.580±2.338)°. There was no significant difference between Swin-PGNet and surgeons (P>0.05), but there was a significant difference between different surgeons (P<0.05). ③ Lumbar sliding distance: The mean error of Swin-PGNet was (1.656±0.878) mm and the mean error of surgeons was (1.884±1.612) mm. There was no significant difference between Swin-PGNet and surgeons and between different surgeons (P>0.05). The accuracy of lumbar instability diagnosed by surgeons and Swin-PGNet was 75.3% and 84.0%, respectively. The accuracy of lumbar spondylolisthesis diagnosed by surgeons and Swin-PGNet was 70.7% and 71.3%, respectively. There was no significant difference between Swin-PGNet and surgeons, as well as between different surgeons (P>0.05). ④ Consistency of lumbar stability diagnosis: The ICC of Cobb angle among different surgeons was 0.913 [95%CI (0.898, 0.934)] (P<0.05), and the ICC of lumbar sliding distance was 0.741 [95%CI (0.729, 0.796)] (P<0.05). The result showed that the annotating of the three surgeons were consistent. The ICC of Cobb angle between Swin-PGNet and surgeons was 0.922 [95%CI (0.891, 0.938)] (P<0.05), and the ICC of lumbar sliding distance was 0.748 [95%CI(0.726, 0.783)] (P<0.05). The result showed that the annotating of Swin-PGNet were consistent with those of surgeons.
Conclusion
The automatic diagnostic tool for lumbar instability constructed based on deep learning can realize the automatic identification of lumbar instability and spondylolisthesis accurately and conveniently, which can effectively assist clinical diagnosis.
Keywords: Artificial intelligence, medical image processing, key point location, lumbar instability, auxiliary diagnosis
腰椎稳定性是判断腰椎退变性疾病患者是否需要进行融合手术的关键指标,与患者腰背疼痛程度、生活质量具有紧密联系[1-3],因此准确判断腰椎稳定性对于评估腰椎疾病状态、术前规划及术中决策至关重要[4]。目前,临床通常以过屈、过伸位X线片上椎间Cobb角变化以及椎体滑移距离作为腰椎稳定性判断标准,如椎间Cobb 角变化超过11° 即诊断为腰椎不稳,椎体滑移距离超过3 mm即诊断为腰椎滑脱[5]。椎间Cobb 角和椎体滑移距离测量主要由医师手工或利用PACS系统测量工具完成,相关X线片测量参考点的选择受医师主观影响较大,不同医师间的测量一致性及稳定性较差,且耗时费力[6-11]。因此,开发一种客观、稳定、可靠的脊柱稳定性判断工具,对于构建腰椎退变性疾病标准化诊疗体系具有重要意义。
近年来,深度学习已成功应用于医学图像处理领域,在脊柱领域也有相关研究[12-18]。例如,Alukaev等[12]结合目标检测和图像分割,实现了Cobb角3.42° 的平均预测误差;Wang等[13]提出结合冠状面和矢状面腰椎X线片预测Cobb角,实现了6.26° 的平均预测误差;Fu等[14]使用编码-解码结构分割椎体,同时共享其权重用于回归椎体4个角的坐标,将Cobb角平均预测误差降至3.15°;Zhao等[15]提出一种U型结构网络,上采样中加入通道注意力机制,跳接模块中加入残差块,在最深特征层提出卷积块注意模块,最终得到Cobb角平均预测误差2.45° 的优秀性能。基于既往研究中的基础算法,我们提出一种新的神经网络Swin-PGNet,该网络使用Swin-Transformer(ST)[19]与Resnet34 [20]共同对图像进行下采样,并利用局部-全局融合模块(patch-global fusion block,PGFB)对不同深度特征进行融合,通过二阶段方法直接对椎体关键点进行定位预测,从而自动测量患者过伸、过屈位X线片椎间Cobb角以及椎体滑移距离,判断患者脊柱稳定性。报告如下。
1. 材料与方法
1.1. 腰椎X线片图像数据库的建立及标注
以2013年10月—2020年3月在四川大学华西医院骨科因腰椎疾病接受经侧前方L4、5椎间融合术的患者为研究对象,收集术前腰椎过伸、过屈位X线片(DICOM格式),采用自行编写的脱敏工具对患者姓名、住院号、身份证号、联系电话等敏感字段进行删除脱敏。共153例患者306张X线片纳入研究。
采用四川大学华西医院研发的影像标注工具AI-Tutor,由3名骨科医师(2名副主任医师,1名主治医师)对图像进行人工标注。于每例患者过伸、过屈位X线片标注5个关键点,分别为L4后下角(A点)、前下角(B点)以及L5后上角(C点)、前上角(D点)、后下角(E点),见图1。AI-Tutor工具可在标注后自动导出图像以及与之对应的点坐标,训练时图像数据转换为png格式,坐标信息保存在txt文件中。将306张X线片按照3∶1∶2比例,随机分为训练集(n=156)、验证集(n=50)和测试集(n=100)。
图 1.
Key points on hyper-flexion and hyper-extension X-ray films
过屈、过伸位X线片关键点
1.2. 神经网络结构与训练
1.2.1. 神经网络结构
Swin-PGNet网络结构总体类似U-net[21]的编码-解码结构,网络输出图像和输入图像尺寸一致(图2)。采用一种基于ST[19]和Resnet34[20]的双编码结构对图像进行编码。同时,两条编码分支用PGFB模块融合信息,将卷积神经网络不同深度的局部特征加入到ST编码过程中,在解码时两条编码分支深度相同的特征被拼接以后进行上采样,一直到特征图大小与原图一致。
图 2.

Swin-PGNet network structure
Swin-PGNet网络结构
ST模块由两部分组成,第1部分为窗口多头自注意力机制(window multi-head self-attention,W-MSA)、第2部分为移动W-MSA(shift W-MSA,SW-MSA),前者的输出是后者的输入(图3)。图像首先平均分成16块,然后线性投射,在模块内部依次经过线性归一化层、多头自注意力层、残差连接和具有高斯误差线性单元的多层感知机(multi-layer perceptron,MLP)。从上到下每个特征层的ST模块堆叠数为 [2,2,6,2],多头自注意力头数为 [4,8,16,32],线性嵌入维度为96,窗口尺寸为8,每轮训练时随机选择神经网络中20%路径不参与学习。其中,每个ST模块中两次窗口自注意力对图像区域的选取如图4所示,L层将特征图分为4块,并在每一块内部计算其中元素相互之间的关联程度;在L+1层中将特征层分为9块,计算每一块内部元素相互之间的关联程度。ST模块内部计算公式如下:
图 3.
ST module and PGFB module
ST模块及PGFB模块
图 4.
Calculated picture area of shift window
移动窗口计算的图片区域
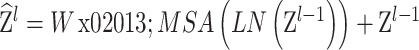 |
1 |
 |
2 |
 |
3 |
 |
4 |
其中, 和
和 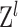 分别表示第
分别表示第 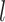 个(S)W-MSA模块的MLP输出。参考既往研究[22-23]自注意力计算公式如下:
个(S)W-MSA模块的MLP输出。参考既往研究[22-23]自注意力计算公式如下:
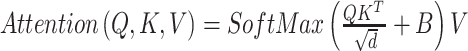 |
5 |
其中,Q、K、 分别表示查询、键和值的矩阵。
分别表示查询、键和值的矩阵。 表示窗口中的分块数量,
表示窗口中的分块数量, 表示查询或键的维度。此外,
表示查询或键的维度。此外,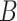 中的值来自于偏置矩阵
中的值来自于偏置矩阵 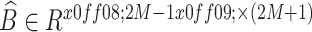 。
。
ST模块下采样过程中,图像首先经过分块层将 的图片转化成
的图片转化成 的维度,线性投射层将其通道数转化为预设的96,并且将其前两个维度拉伸之后送入ST模块。分块融合层对特征图两倍下采样,并将其原有通道数翻倍,具体方法为将特征图均分4块,然后在通道维度上拼接起来。
的维度,线性投射层将其通道数转化为预设的96,并且将其前两个维度拉伸之后送入ST模块。分块融合层对特征图两倍下采样,并将其原有通道数翻倍,具体方法为将特征图均分4块,然后在通道维度上拼接起来。
卷积神经网络是经典的Resnet34,每一层通道数设置为 [32,32,64,128,256],每一个卷积之后都有一个批归一化层和一个ReLU激活函数。将卷积编码器 维度的特征和ST编码器
维度的特征和ST编码器 维度的特征一并输入PGFB模块中,
维度的特征一并输入PGFB模块中,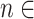 [2,4,6]。
[2,4,6]。
PGFB模块中,卷积网络输入维度为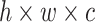 ,ST模块输入维度为
,ST模块输入维度为 。对于卷积网络的输入,首先经过
。对于卷积网络的输入,首先经过 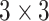 的卷积层、批归一化层以及ReLU层,再进入线性嵌入层,输出维度为
的卷积层、批归一化层以及ReLU层,再进入线性嵌入层,输出维度为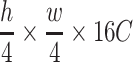 ,再通过
,再通过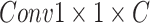 将其通道数和ST模块输入统一为C。将卷积层与ST模块两种特征图做注意力机制后与ST模块原本特征图矩阵点乘后输出。
将其通道数和ST模块输入统一为C。将卷积层与ST模块两种特征图做注意力机制后与ST模块原本特征图矩阵点乘后输出。
跳接块用于将来自ST编码器、卷积编码器相同深度特征层特征以及更深一层的跳接块输出特征在通道维度上进行拼接,三者拼接完成后使用上采样将特征尺寸翻倍,再通过 将其通道数与Resnet当前深度的通道数统一,并将其输出到下一个跳接块中。最后的特征经过
将其通道数与Resnet当前深度的通道数统一,并将其输出到下一个跳接块中。最后的特征经过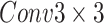 和
和 将输出维度设置为3,分别代表热力图、x方向偏移图和y方向偏移图。
将输出维度设置为3,分别代表热力图、x方向偏移图和y方向偏移图。
1.2.2. 标签设置以及坐标计算
将热力图制定为分类问题,具体步骤为将真实关键点坐标距离25以内的像素点设置为1,其余为0,具体公式如下:
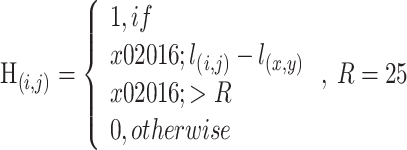 |
6 |
最终偏移图和热力图联合计算关键点坐标方法和人体检测普遍使用方法[24]类似:
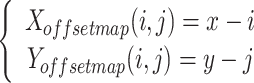 |
7 |
 |
8 |
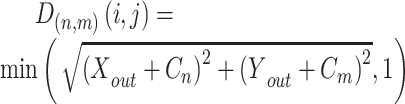 |
9 |
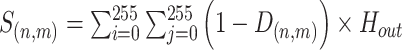 |
10 |
 |
11 |
其中,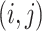 和
和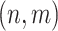 是图上坐标,
是图上坐标, 是真实关键点坐标。
是真实关键点坐标。 指热力图标签,
指热力图标签,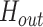 是网络输出的热力图,
是网络输出的热力图,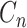 和
和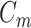 是x和y方向的修正图,offsetmap指偏移图,
是x和y方向的修正图,offsetmap指偏移图,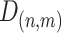 是
是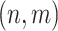 的距离图,
的距离图,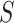 是分数图,
是分数图,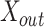 和
和 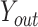 是网络输出的偏移图,
是网络输出的偏移图,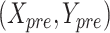 最终预测坐标。
最终预测坐标。
1.2.3. 神经网络的训练
Swin-PGNet是二阶段方法,第1阶段进行粗定位,找出L4和L5区域;第2阶段在前一阶段得到的坐标周围 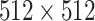 区域中对关键点精确定位。
区域中对关键点精确定位。
第1阶段将X线片像素空间值统一为0.1 mm/pixel,然后用0像素值将图像填充至长宽比为1∶1,最后放缩至 256×256作为模型输入;对关键点进行粗定位,定位L4和L5大致位置,以预测坐标为中心点取大小为512×512的区域,放缩图像尺寸至256×256作为第2阶段模型的输入。第2阶段训练集制作,通过在关键点真实坐标半径为50像素距离中随机选取一点,以此点为中心截取大小为512×512 的局部图像。每个点的预测均单独进行,分为训练粗定位和精细定位两个阶段模型,每次输入图片均为单通道灰度图。
使用随机梯度下降优化器训练网络,初始学习率为0.001,训练批量为4。在第4、6和8个时期将学习率缩小1/10。使用python库imgaug实现数据增强。图像在x和y方向随机平移最多10个像素;所有像素强度随机缩放为0.5~1.0;放大或缩小图像,使其在原始比例的 0.95~1.05 之间;将图像逆时针或顺时针旋转最多 3°;最后对每个图像进行弹性变换。ST模块和卷积神经网络均在ImageNet训练集的预训练权重上进行,在整个训练集上训练20个轮次,选择验证集上效果最好模型作为最终模型。负责输出预测热力图的通道结果会通过一个sigmoid函数,并且对它使用交叉熵损失函数定义为 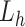 。为训练偏移回归头,惩罚预测偏移和真实偏移之间的差异,相应损失为:
。为训练偏移回归头,惩罚预测偏移和真实偏移之间的差异,相应损失为:
 |
12 |
其中,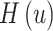 是Huber Robust损失,
是Huber Robust损失,  是真实关键点坐标位置,
是真实关键点坐标位置,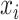 是真实关键点坐标位置
是真实关键点坐标位置 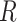 范围内的点。最终损失函数表示如下:
范围内的点。最终损失函数表示如下:
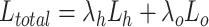 |
13 |
其中,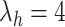 而
而 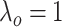 ,这样可以平衡两项损失。
,这样可以平衡两项损失。
1.3. 神经网络的评估
在100张腰椎X线片(50例患者过伸、过屈位腰椎X线片)测试集上对Swin-PGNet的预测结果进行评估,比较Swin-PGNet和医师标注的关键点定位、L4、5椎间Cobb角、L4椎体滑移距离。评价指标包括关键点定位平均误差、椎间Cobb角测量平均误差、椎体滑移距离测量平均误差,腰椎不稳及腰椎滑脱判断准确率。
1.3.1. 误差定义
① 关键点定位误差定义如下:
 |
14 |
其中, 表示关键点定位误差(mm);
表示关键点定位误差(mm); 和
和  是关键点在图像中的标注坐标,
是关键点在图像中的标注坐标,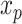 和
和  是关键点在图像中的预测坐标;
是关键点在图像中的预测坐标;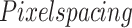 是图像中像素点对应的真实物理空间距离,预处理中统一成0.1 mm/pixel。
是图像中像素点对应的真实物理空间距离,预处理中统一成0.1 mm/pixel。
② 椎间Cobb角测量误差定义如下:
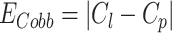 |
15 |
其中, 表示椎间Cobb角测量误差,
表示椎间Cobb角测量误差,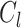 表示医师标注椎间Cobb角度,
表示医师标注椎间Cobb角度, 表示 Swin-PGNet预测椎间Cobb角度。
表示 Swin-PGNet预测椎间Cobb角度。
③ 椎体滑移距离测量误差定义如下:
 |
16 |
其中, 表示椎体滑移距离测量误差,
表示椎体滑移距离测量误差,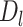 表示医师标注椎体滑移距离,
表示医师标注椎体滑移距离,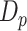 表示 Swin-PGNet预测椎体滑移距离。
表示 Swin-PGNet预测椎体滑移距离。
1.3.2. 临床判断分析
椎间Cobb角及椎体滑移距离测量方法:Cobb角为L4椎体下终板直线与L5椎体上终板直线夹角;过上位椎体后下角(A点)作下椎体后上角(C点)与后下角(E点)形成直线的平行线,两条线距离即为椎体滑移距离。见图5。以同一患者过伸、过屈位X线片上,椎间Cobb角变化超过11° 判定为腰椎不稳,椎体滑移距离超过3 mm判定为腰椎滑脱。
图 5.
Diagram for measuring Cobb angle and sliding distance of lumbar vertebrae based on hyper-flexion and hyper-extension X-rayfilms
基于腰椎过屈、过伸位X线片测量腰椎Cobb角以及椎体滑移距离示意图
a、b. Cobb角;c、d. 椎体滑移距离
a, b. Cobb angle; c, d. Sliding distance
对于关键点定位平均误差、椎间Cobb角测量平均误差和椎体滑移距离测量平均误差3个评价指标,将每名医师的标注单独作为金标准分别对Swin-PGNet进行训练,计算Swin-PGNet与该医师标注的误差,取Swin-PGNet与3名医师标注误差的平均值,得到Swin-PGNet平均误差。同时,计算每 2 名医师间误差,取3组误差的平均值作为医师间平均误差。最后,比较Swin-PGNet与医师间的平均误差,验证Swin-PGNet在定位和测量任务中的精度是否超过医师。
对于腰椎不稳、腰椎滑脱判断准确率2个评价指标,同样将每名医师的标注单独作为金标准对Swin-PGNet进行训练,并根据临床标准判断患者是否存在腰椎不稳和腰椎滑脱,当Swin-PGNet测量结果与医师一致时认为判断正确,否则判断错误,计算Swin-PGNet在3名医师标签上的平均准确率。同时,将每 2 名医师的标注互相比较,对同一患者腰椎不稳/腰椎滑脱判断一致则认为判断正确,否则判断错误,统计3个比较组的平均准确率。最后比较Swin-PGNet和医师间对腰椎不稳以及腰椎滑脱判断的准确率,验证Swin-PGNet的诊断水平是否超过医师水平。
1.4. 统计学方法
采用Python软件中的numpy包进行统计分析。计量资料经正态性检验均符合正态分布,数据以均数±标准差表示,组间比较采用方差分析,两两比较采用SNK检验;计数资料以率表示,组间比较采用χ2检验。
采用组内相关系数(intra-class correlation coefficient,ICC)分析不同医师间以及Swin-PGNet与医师测量一致性。检验水准α=0.05。
2. 结果
2.1. 关键点定位误差分析
Swin-PGNet关键点定位平均误差为(1.407±0.939)mm,Swin-PGNet与医师在各关键点定位误差的比较结果详见表1。医师间平均误差为(3.034±2.612)mm,其中医师1-2为(3.049±2.681)mm,医师1-3为(3.207±2.783)mm,医师2-3为(2.846±2.373)mm。
表 1.
Comparison of Swin-PGNet with surgeons in key points localization (n=100,  , mm)
, mm)
Swin-PGNet与医师在关键点定位的比较(n=100, ,mm)
,mm)
| 关键点 Key point |
Swin-PGNet-医师1 Swin-PGNet-surgeon 1 |
Swin-PGNet-医师2 Swin-PGNet-surgeon 2 |
Swin-PGNet-医师3 Swin-PGNet-surgeon 3 |
平均值 Average value |
| A | 1.155±0.753 | 1.104±0.760 | 1.095±0.739 | 1.118±0.751 |
| B | 1.418±0.988 | 1.035±0.776 | 1.377±0.925 | 1.277±0.896 |
| C | 1.812±1.330 | 1.584±0.948 | 1.704±1.134 | 1.700±1.137 |
| D | 1.388±0.895 | 1.308±0.713 | 1.435±0.940 | 1.377±0.849 |
| E | 1.693±1.288 | 1.488±0.857 | 1.502±1.037 | 1.561±1.061 |
| 平均值 Average value |
1.493±1.051 | 1.304±0.811 | 1.423±0.955 | 1.407±0.939 |
2.2. 临床判断分析
2.2.1. 腰椎稳定性分析
① Cobb角:Swin-PGNet平均误差为(2.062 1.352)°,医师间平均误差为(3.580
1.352)°,医师间平均误差为(3.580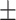 2.338)°;Swin-PGNet与3名医师间误差比较,差异均无统计学意义(P>0.05),但不同医师间误差比较差异有统计学意义(P<0.05),说明Swin-PGNet对医师在Cobb角上的标注学习成功,但3名医师在该任务上存在明显差异。
2.338)°;Swin-PGNet与3名医师间误差比较,差异均无统计学意义(P>0.05),但不同医师间误差比较差异有统计学意义(P<0.05),说明Swin-PGNet对医师在Cobb角上的标注学习成功,但3名医师在该任务上存在明显差异。
② 椎体滑移距离:Swin-PGNet平均误差为(1.656 0.878)mm,医师标注平均误差为(1.884
0.878)mm,医师标注平均误差为(1.884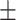 1.612)mm,Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异均无统计学意义(P>0.05),说明Swin-PGNet对医师在椎体滑移距离上的标注学习成功,且3名医师在该任务上无明显差异。
1.612)mm,Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异均无统计学意义(P>0.05),说明Swin-PGNet对医师在椎体滑移距离上的标注学习成功,且3名医师在该任务上无明显差异。
Swin-PGNet腰椎不稳判断准确率为84.0%,医师为75.3%,Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异无统计学意义(P>0.05);Swin-PGNet腰椎滑脱判断准确率为71.3%,医师为70.7%, Swin-PGNet与3名医师间误差比较以及不同医师间误差比较,差异均无统计学意义(P>0.05),见表2。
表 2.
Comparison of lumbar stability judgments (n=50)
腰椎稳定性判断比较(n=50)
| 指标 Index |
Swin-PGNet-医师1 Swin-PGNet-surgeon 1 |
Swin-PGNet-医师2 Swin-PGNet-surgeon 2 |
Swin-PGNet-医师3 Swin-PGNet-surgeon 3 |
统计值 Statistic |
平均值 Average value |
| 椎间Cobb角(°) | 2.163
|
1.978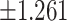
|
2.045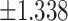
|
F=8.996 P=0.229 |
2.062 1.352 1.352 |
| 椎体滑移距离(mm) | 1.533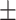 0.918 0.918 |
1.686 0.754 0.754 |
1.748 0.962 0.962 |
F=0.083 P=0.847 |
1.656 0.878 0.878 |
| 腰椎不稳判断准确率(%) | 84 | 80 | 88 |
χ2=2.413 P=0.299 |
84.0 |
| 腰椎滑脱判断准确率(%) | 76 | 70 | 68 |
χ2=2.135 P=0.344 |
71.3 |
| 指标 Index |
医师1-2 Surgeon 1-2 |
医师1-3 Surgeon 1-3 |
医师2-3 Surgeon 2-3 |
统计值 Statistic |
平均值 Average value |
| 椎间Cobb角(°) | 3.654 2.257 2.257 |
3.833 2.640 2.640 |
3.254 2.116 2.116 |
F=11.447 P=0.001 |
3.580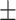 2.338 2.338 |
| 椎体滑移距离(mm) | 1.830 1.343 1.343 |
2.076 1.785 1.785 |
1.746
|
F=0.104 P=0.901 |
1.884 1.612 1.612 |
| 腰椎不稳判断准确率(%) | 74 | 72 | 80 |
χ2=2.380 P=0.123 |
75.3 |
| 腰椎滑脱判断准确率(%) | 70 | 66 | 76 |
χ2=1.051 P=0.305 |
70.7 |
2.2.2. 腰椎稳定性指标测量一致性分析
3名医师标注椎间Cobb角的ICC为0.913 [95%CI(0.898,0.934)](P<0.05),椎体滑移距离为0.741 [95%CI(0.729,0.796)] (P<0.05) ,说明3名医师间标注具有一致性。Swin-PGNet-所有医师间椎间Cobb角ICC为0.922 [95%CI(0.891,0.938)] (P<0.05),椎体滑移距离为0.748 [95%CI(0.726,0.783)](P<0.05),说明Swin-PGNet标注结果与医师标注具有一致性。见表3及图6。
表 3.
Comparison of consistency of lumbar stability judgment
腰椎稳定性判断一致性比较
| 组别 Group |
Cobb角 Cobb angle |
椎体滑移距离 Lumbar sliding distance |
|||
| ICC(95%CI) | 统计值 Statistic |
ICC(95%CI) | 统计值 Statistic |
||
| 不同医师间 | 0.913(0.898,0.934) | P<0.001 | 0.741(0.729,0.796) | P<0.001 | |
| Swin-PGNet-医师1 | 0.907(0.870,0.924) | P<0.001 | 0.720(0.705,0.741) | P<0.001 | |
| Swin-PGNet-医师2 | 0.916(0.885,0.931) | P<0.001 | 0.741(0.726,0.775) | P<0.001 | |
| Swin-PGNet-医师3 | 0.950(0.936,0.954) | P<0.001 | 0.786(0.759,0.808) | P<0.001 | |
| Swin-PGNet-所有医师 | 0.922(0.891,0.938) | P<0.001 | 0.748(0.726,0.783) | P<0.001 | |
图 6.
A 68-year-old female patient with L4, 5 intervertebral disc herniation with spinal stenosis, Swin-PGNet judged L4 lumbar spondylolisthesis without segmental instability, which was the same as the surgeon’s judgment
患者,女,68岁,L4、 5椎间盘突出伴椎管狭窄,Swin-PGNet判断为L4腰椎滑脱不伴节段性不稳,与医师判断相同
绿色为Swin-PGNet自动定位,蓝色为人工标注;上为过屈位X线片,下为过伸位X线片 a. 关键点定位 ;b. Cobb角;c. 椎体滑移距离
Green for automatic location by Swin-PGNet, blue for manual marking; upper for hyper-flexion X-ray films, lower for hyper-extension X-ray films a. Key points location; b. Cobb angle; c. Sliding distance
3. 讨论
人工智能在医学影像分析中有着广泛应用,如胸部CT肺结节定位、识别,其精度已超过影像学医师,且随着数据积累,算法可自我迭代,以获取更加优异表现。本研究采用的新的神经网络Swin-PGNet,是结合ST [19]与Resnet34[20]算法共同对图像进行下采样,创新性地提出一种新的PGFB模块,对不同深度特征进行融合,通过二阶段方法直接对椎体关键点进行定位预测,从而实现了椎间Cobb角及椎体滑移距离的自动测量,并基于此对患者脊柱稳定性进行自动判断。
Swin-PGNet采用了ST和Resnet的双编码结构来提取腰椎图像特征,传统卷积神经网络擅长提取局部特征,而ST擅长获取全局的长语义关系,使图像每个像素点交互学习彼此语义信息。与此同时,使用PGFB模块将卷积分支提取的局部特征加入到SW分支中,进一步提升网络对关键点定位精度。在解码过程中,网络将两个编码器相同尺度的特征在通道方向上拼接后上采样,融合图像的全局信息和局部信息,进而将不同深度特征融合在一起,网络可以学习到不同深度下局部特征相互之间的全局关系,降低定位误差。
本研究算法采用了感兴趣区域提取-关键点精细化定位的二阶段流程。如果使用单阶段直接预测,由于腰椎X线片尺寸大,无法输入原尺寸图片进入网络训练,因GPU显存不足需要将图片缩小后进行预测,预测结果按照缩放比例还原,存在不可避免的系统误差。使用二阶段方法可以在第一阶段通过粗定位找出目标椎体的位置,提取出该位置附近的原始尺寸图片放入第二阶段进行精确定位,以减小甚至消除系统误差。
我们对L4后下角、前下角以及L5后上角、前上角、后下角进行自动关键点定位,发现网络在L4后下角、前下角以及L5前上角的定位效果较好,而在L5后上角、后下角的定位效果较差。这可能是前者在图像中的形态更清晰,而后者由于髂嵴和椎弓影像的影响增大了关键点定位的难度。尽管如此,Swin-PGNet关键点定位平均误差远小于不同医师间的平均误差。这一点也反映在椎间Cobb角测量上,Swin-PGNet在椎间Cobb角测量任务中取得了(2.062±1.352)° 的平均误差,而医师间平均误差为(3.580±2.338)°,说明Swin-PGNet在椎间Cobb角自动测量这一任务上表现优秀,进而在判断腰椎不稳准确率上取得了84.0%的满意结果,明显优于人工测量的75.3%。在腰椎滑移距离测量任务上,Swin-PGNet仅稍好于人工测量,进而体现在对腰椎滑脱判断的准确率(71.3% vs 70.7%),尤其在医师3的标签中,Swin-PGNet判断准确率(68%)较人工测量(76%)降低了8%。我们分析这可能与本研究使用Quinnell法[25-26]计算腰椎椎体滑移距离有关。该测算方法是以L5后上角、后下角和L4后下角作为参考点,而Swin-PGNet对L5后上角、后下角关键点定位误差较大。与此同时,我们从实例中观察到Swin-PGNet对于腰椎上、下终板垂直方向的误差小于水平方向的误差,提示其学习到了关键点位置与椎体终板水平方向的关系,使定位误差对于Cobb角测量的影响较小,但对采用Quinnell法测量椎体滑移距离中L5后上角与后下角连线方向影响较大。
统计分析结果显示,Swin-PGNet在椎间Cobb角、椎体滑移距离测量以及腰椎不稳、椎体滑脱判断方面与医师标注无明显差异(P>0.05),充分说明网络对于任务的学习成功。3名医师在Cobb角标注中存在差异性(P<0.05),但在腰椎不稳判断上无明显差异(P>0.05)。我们分析发现主要标注差异是椎间Cobb角平均值,这与标注Cobb角时医师标注习惯不同有关。其中2名医师倾向于椎体终板平行线末端,1名医师倾向于椎体终板拐角最外侧点。虽然椎间Cobb角标注存在差异,但腰椎不稳判断是由患者过伸位和过屈位X线片上椎间Cobb角变化值决定的,医师在两个不同体位X线片中以同样标准标注椎体角点,最终计算出的角度变化值相近。因此,关于腰椎不稳的判断,3名医师标注无明显差异。此外,在Cobb角测量中,不同医师间ICC为0.913(P<0.05),Swin-PGNet-所有医师为0.922(P<0.05),而在椎体滑移距离任务中这两项结果分别是0.741(P<0.05)和0.748(P<0.05),说明本研究采用的Cobb角测量方法较为可靠,而Quinnell法测量椎体滑移距离的方式本身可能存在系统误差。
综上述,本研究基于深度学习研发的腰椎稳定性自动诊断工具,在腰椎X线片关键点定位任务、Cobb角测量以及腰椎不稳判断任务中优于医师;在腰椎椎体滑移距离测量和腰椎滑脱判断任务中,与医师标注结果接近。该方法可以辅助临床医师进行诊断,同时提高工作效率。
利益冲突 在课题研究和文章撰写过程中不存在利益冲突;经费支持没有影响文章观点和对研究数据客观结果的统计分析及其报道
伦理声明 研究方案经四川大学华西医院生物医学伦理审查委员会批准[2020年审(554)号]
作者贡献声明 胡厚民:算法设计、研究实施及撰写文章;王贤帝:临床分析及指导文章写作;杨恒:患者数据采集和数据预处理;张劲:实验思路指导;李康、曾建成:课题总体设计及文章审阅
Funding Statement
国家重点研发计划项目(2020YFB1711500);四川大学华西医院学科卓越发展1·3·5工程项目(ZYYC21004)
National Key Research & Development Projects (2020YFB1711500); Sichuan University West China Hospital Discipline Excellence Development 1 · 3 · 5 Project (ZYYC21004)
Contributor Information
康 李 (Kang LI), Email: likang@wchscu.cn.
建成 曾 (Jiancheng ZENG), Email: tomzeng5@vip.163.com.
References
- 1.Schwab JH Global sagittal alignment. Skeletal Radiology. 2017;(46):1613–1614. doi: 10.1007/s00256-017-2752-0. [DOI] [PubMed] [Google Scholar]
- 2.Duval-Beaupère G, Schmidt C, Cosson P A Barycentremetric study of the sagittal shape of spine and pelvis: the conditions required for an economic standing position. Ann Biomed Eng. 1992;20(4):451–462. doi: 10.1007/BF02368136. [DOI] [PubMed] [Google Scholar]
- 3.Diebo BG, Varghese JJ, Lafage R, et al. Sagittal alignment of the spine: What do you need to know? Clin Neurol Neurosurg, 2015, 139: 295-301.
- 4.Berven S, Wadhwa R Sagittal alignment of the lumbar spine. Neurosurg Clin N Am. 2018;29(3):331–339. doi: 10.1016/j.nec.2018.03.009. [DOI] [PubMed] [Google Scholar]
- 5.Vrtovec T, Pernus F, Likar B A review of methods for quantitative evaluation of spinal curvature. Eur Spine J. 2009;18(5):593–607. doi: 10.1007/s00586-009-0913-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang J, Li H, Lv L, et al. Computer-aided Cobb measurement based on automatic detection of vertebral slopes using deep neural network. Int J Biomed Imaging, 2017, 2017: 9083916. doi: 10.1155/2017/9083916.
- 7.Smith JS, Shaffrey CI, Ames CP, et al Treatment of adult thoracolumbar spinal deformity: past, present, and future. J Neurosurg Spine. 2019;30(5):551–567. doi: 10.3171/2019.1.SPINE181494. [DOI] [PubMed] [Google Scholar]
- 8.Lafage R, Ferrero E, Henry JK, et al Validation of a new computer-assisted tool to measure spino-pelvic parameters. Spine J. 2015;15(12):2493–2502. doi: 10.1016/j.spinee.2015.08.067. [DOI] [PubMed] [Google Scholar]
- 9.Sun H, Zhen X, Bailey C, et al. Direct estimation of spinal Cobb angles by structured multi-output regression//International Conference on Information Processing in Medical Imaging. Cham: Springer, 2017.
- 10.Langensiepen S, Semler O, Sobottke R, et al Measuring procedures to determine the Cobb angle in idiopathic scoliosis: a systematic review. Eur Spine J. 2013;22(11):2360–2371. doi: 10.1007/s00586-013-2693-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang J, Lou E, Le LH, et al Automatic Cobb measurement of scoliosis based on fuzzy Hough Transform with vertebral shape prior. J Digit Imaging. 2009;22(5):463–472. doi: 10.1007/s10278-008-9127-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alukaev D, Kiselev S, Mustafaev T, et al A deep learning framework for vertebral morphometry and Cobb angle measurement with external validation. Eur Spine J. 2022;31(8):2115–2124. doi: 10.1007/s00586-022-07245-4. [DOI] [PubMed] [Google Scholar]
- 13.Wang L, Xu Q, Leung S, et al. Accurate automated Cobb angles estimation using multi-view extrapolation net. Med Image Anal, 2019, 58: 101542. doi: 10.1016/j.media.2019.101542.
- 14.Fu X, Yang G, Zhang K, et al An automated estimator for Cobb angel measurement using multi-task networks. Neural Computing and Applications. 2021;33:4755–4761. doi: 10.1007/s00521-020-05533-y. [DOI] [Google Scholar]
- 15.Zhao Y, Zhang J, Li H, et al Automatic Cobb angle measurement method based on vertebra segmentation by deep learning. Med Biol Eng Comput. 2022;60(8):2257–2269. doi: 10.1007/s11517-022-02563-7. [DOI] [PubMed] [Google Scholar]
- 16.Sun Y, Xing Y, Zhao Z, et al Comparison of manual versus automated measurement of Cobb angle in idiopathic scoliosis based on a deep learning keypoint detection technology. Eur Spine J. 2022;31(8):1969–1978. doi: 10.1007/s00586-021-07025-6. [DOI] [PubMed] [Google Scholar]
- 17.Pan Y, Chen Q, Chen T, et al Evaluation of a computer-aided method for measuring the Cobb angle on chest X-rays. Eur Spine J. 2019;28(12):3035–3043. doi: 10.1007/s00586-019-06115-w. [DOI] [PubMed] [Google Scholar]
- 18.Liu J, Yuan C, Sun X, et al The measurement of Cobb angle based on spine X-ray images using multi-scale convolutional neural network. Phys Eng Sci Med. 2021;44(3):809–821. doi: 10.1007/s13246-021-01032-z. [DOI] [PubMed] [Google Scholar]
- 19.Liu Z, Lin Y, Cao Y, et al. Swin transformer: Hierarchical vision transformer using shifted windows//2021 IEEE/CVF International Conference on Computer Vision (ICCV). USA: IEEE, 2021.
- 20.He K, Zhang X, Ren S, et al. Deep residual learning for image recognition//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) . USA: IEEE, 2016.
- 21.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015. Cham: Springer, 2015.
- 22.Hu H, Gu J, Zhang Z, et al. Relation networks for object detection//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. USA: IEEE, 2018.
- 23.Hu H, Zhang Z, Xie Z, et al. Local relation networks for image recognition//2019 IEEE/CVF International Conference on Computer Vision (ICCV). USA: IEEE, 2019.
- 24.Papandreou G, Zhu T, Kanazawa N, et al. Towards accurate multi-person pose estimation in the wild//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). USA: IEEE, 2017.
- 25.Boden SD, Wiesel SW Lumbosacral segmental motion in normal individuals. Have we been measuring instability properly? Spine (Phila Pa 1976) 1990;15(6):571–576. doi: 10.1097/00007632-199006000-00026. [DOI] [PubMed] [Google Scholar]
- 26.Quinnell RC, Stockdale HR Flexion and extension radiography of the lumbar spine: a comparison with lumbar discography. Clin Radiol. 1983;34(4):405–411. doi: 10.1016/S0009-9260(83)80224-4. [DOI] [PubMed] [Google Scholar]







