Abstract
Motivation
Multi-omics approaches offer the opportunity to reconstruct a more complete picture of the molecular events associated with human diseases, but pose challenges in data analysis. Network-based methods for the analysis of multi-omics leverage the complex web of macromolecular interactions occurring within cells to extract significant patterns of molecular alterations. Existing network-based approaches typically address specific combinations of omics and are limited in terms of the number of layers that can be jointly analysed. In this study, we investigate the application of network diffusion to quantify gene relevance on the basis of multiple evidences (layers).
Results
We introduce a gene score (mND) that quantifies the relevance of a gene in a biological process taking into account the network proximity of the gene and its first neighbours to other altered genes. We show that mND has a better performance over existing methods in finding altered genes in network proximity in one or more layers. We also report good performances in recovering known cancer genes. The pipeline described in this article is broadly applicable, because it can handle different types of inputs: in addition to multi-omics datasets, datasets that are stratified in many classes (e.g., cell clusters emerging from single cell analyses) or a combination of the two scenarios.
Availability and implementation
The R package ‘mND’ is available at URL: https://www.itb.cnr.it/mnd.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Current omics technologies are capable of generating data relative to different types of molecular entities (DNA, RNA, proteins, etc.). The resulting heterogeneous datasets can be analysed to reconstruct a more complete picture of the molecular events underlying human diseases. The analysis of such datasets is a challenging problem in bioinformatics, due to differences in terms of information type, coverage, data distribution type, noise, just to mention a few and, last but not least, research questions that can be addressed (Ahmad and Fröhlich, 2016; Huang et al., 2017; Ritchie et al., 2015).
Knowledge about the complex web of direct and indirect interactions among macromolecules at genome scale is a powerful resource for explaining multiple omics measurements, highlighting the molecular mechanisms underlying diseases (Kristensen et al., 2014). Indeed, the emergence of a disease can be explained as a combinatorial problem in which different molecular alterations affect a series of pathways that result in a similar phenotype (Barabasi et al., 2011).
In this view, network-based methods exploit known interactions in finding meaningful patterns in omics datasets—such as coherent variations of several functionally related genes (Bersanelli et al., 2016a,b)—and help explain the heterogeneity of alterations detected at gene-level, as the intra-tumour genetic heterogeneity, in terms of interacting genes (e.g. disease modules (Barabasi et al., 2011)). In this last decade, the principle of network diffusion (ND)—also referred to as network propagation—has been proposed to solve several problems in biological data analysis, thanks to its ability to quantify network proximity considering simultaneously all the possible network paths between query network nodes (e.g. genes) (Cowen et al., 2017).
Several studies focused on the integrative analysis of multiple omics datasets using ND. The method TieDIE (Paull et al., 2013) applies ND for identifying a subnetwork that links a source gene set carrying genomic alterations to a target set of differentially expressed genes on the same network. There is evidence that ND is useful in predicting ‘silent’ players in cancer (Ruffalo et al., 2015), using different combinations of diffusion scores (e.g. dot product, Spearman correlation) obtained from two types of initial statistics (mutation frequency and differential expression). More recently, NetICS (Dimitrakopoulos et al., 2018), which uses ND on directed graphs, has been proposed to integrate aberration events [somatic mutations (SMs), copy number variations, methylation and miRNA expression data] with differential expressions to prioritize cancer genes. In general, existing methods are usually relevant only to two types of omics or specific combinations of them.
In this article, we present a gene-score, named ‘mND’, to assess gene relevance on the basis of gene position in a genome-scale network in relation to one or more types of biological evidences (‘layers’ hereafter) (Fig. 1). Genes are ranked considering their relevance within each layer (e.g. number of mutations, P-values from differential expression analysis), their network proximity to other relevant genes as well as the layer-specific relevance of their neighbours. Statistical significance of the gene scores defined by mND (mND scores) is assessed by dataset permutations. To help unravel the role of a gene in each layer, in addition to producing a global gene ranking, mND classifies each gene as a member of a module of high scoring genes, linker of high scoring genes or, lastly, high scoring but isolated gene. Unlike current methods, mND can be used in integrative analysis of different types of omics (e.g. mutation, CNV and expression changes) or multiple samples of same omic type (e.g. patient-level mutational analysis), without particular constraints on the number of layers and layer type. We show that, taking into account ND scores of neighbouring genes, mND has a better ability in finding high scoring genes in network proximity over multiple layers. Furthermore, we account for good performances in recovering known cancer genes in four cancer types, using two types of omics and a single type of omics at patient-level. We show that the application of mND to rank genes based on mutations and expression changes in breast cancer points to relevant pathways underlying the disease, providing a more complete picture than each individual omics on its own. Lastly, layer-specific gene classification suggests functional roles and offers mechanistic insights in relation to the datasets studied.
Fig. 1.
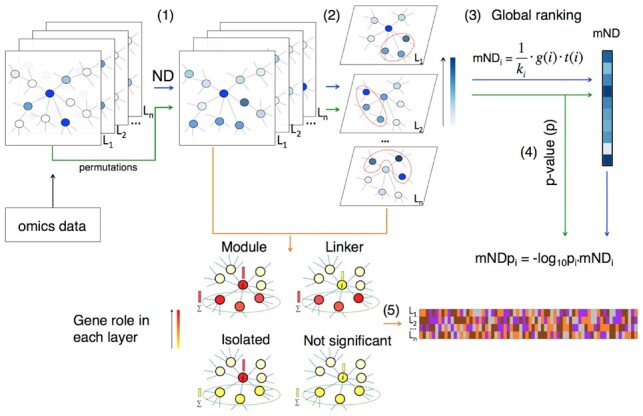
Flowchart of the analysis pipeline with mND. (1) Network-diffusion is applied to the original dataset, composed of multiple layers L1, L2, …, Ln (e.g. different types of omics or multiple samples of same omic type); (2) identification of the top k neighbours for each gene in each layer; (3) calculation of mND score; (4) empirical P-value assessment; (5) classification of genes across layers
2 Materials and methods
2.1 mND
The calculation of mND score requires an undirected interaction network G and a matrix of initial scores , in which each column (representing a layer) is a score vector over all vertices of G.
The computation of mND consists of five steps (Fig. 1).
Network diffusion. Input scores () are smoothed by ND, obtaining the corresponding network-constrained scores , using the following iterative procedure, where the subscript indicates the current iteration and
| (1) |
where is a scalar that weights the relative importance of topology and input scores, and W is the symmetric normalized form of the adjacency matrix A:
| (2) |
where are the elements of the adjacency matrix, are the degrees of the corresponding genes. The final matrix Xss is the matrix that satisfies the termination criterion . Parameter α was set to 0.7, a value that represents a good trade-off between diffusion rate and computational cost, and determined consistent results in previous studies (Bersanelli et al., 2016a, b; Hofree et al., 2013; Mosca et al., 2014, 2017; Vanunu et al., 2010). We estimated the sensitivity of mND to α and found that varying α by ±10% resulted in highly correlated mND scores and only a few different genes (6–8%) among the top 100 (Supplementary Fig. S1 and Table S1). To enable direct multiplication of values belonging to different layers, Xss is column-wise normalized by the maximum of each column, obtaining the matrix .
Neighbours selection. For each gene i, the top first neighbours with the highest diffusion scores in each layer l are selected as representatives of the network proximity of the neighbourhood of i to the original scores in layer l, and their ND scores are summed:
| (3) |
where with is the network-constrained value of j-th gene in l-th layer ), is the set of all -subsets of , and .
We explored the performance of mND at varying k and found k = 3 to be a reasonable choice (see Section 3). Further, we evaluated the sensitivity of mND to the value of k and found that varying k of one unit had only minor effects on mND scores, which are highly correlated and indeed differ of only a few (∼4–6) genes among the top 100 (Supplementary Fig. S2 and Table S2). An opportunity to further optimize the value of k relies in selecting a value that yields connected networks enriched in initial scores (Supplementary Methods).
Integration. At this point, the mND score for gene i is calculated as the product between the sum of its network constrained scores (term ) and the sum of the contributions of its top k first neighbours (term ):
| (4) |
where L is the total number of layers and .
Significance assessment. The corresponding values of , obtained with permuted versions of , are used to calculate empirical P-values, i.e. the fraction of times . The product of and
| (5) |
provides a gene score weighted by its estimated statistical significance, as previously described (Bersanelli et al., 2016b; Xiao et al., 2014).
Classification. Lastly, a gene i is classified by evaluating the membership of the gene in two gene sets Hl and Nl which define, respectively, the high scoring genes according to original data () and neighbour information (T). The gene set Hl is composed of the high scoring genes in layer l of , defined using a layer-specific criterion (e.g. the differentially expressed genes at P < 0.05). The gene set Nl is composed of the genes with the highest
| (6) |
where is the empirical P-value calculated comparing T to T†, the latter obtained with permuted X. The use of empirical P-value to scale T overcomes the issue of ties due to genes with equal values of T. The cardinality of Nl can be defined several ways: considering an ad hoc number of top values (e.g. in proportion to |Hl|), on the basis of or a combination of the two criteria. The gene i is ISOLATED if it is in Hl but its neighbourhood is not in Nl. If both the gene and its neighbourhood are in, respectively, Hl and Nl the gene is part of a high scoring module and therefore termed MODULE. If the gene is not in Hl but its neighbourhood is in Nl, then it is named as LINKER.
The computational cost of mND depends on interactome size (number of nodes and links), number of layers and number of permutations used in significant assessment. In particular, ND is the rate-limiting step, which is repeated several times during significance assessment. For example, the computation of ND using STRING (11 796 genes and 309 850 links) on two layers of initial scores required approximately 30 s on a server with dual Intel(R) Xeon(R) CPU E5-2697 v3 @ 2.60 GHz, 64GB DDR4 2133 MHz memory and disk storage on Lustre Filesystem; the whole analysis, involving 1000 permutations, took about 1 h and 50 min on 4 cores. See Supplementary Table S3 for additional details and further examples.
2.2 Macromolecular interactions
Three sources of interactions were considered, abbreviated as STRING (11 796 genes; 309 850 interactions) (Szklarczyk et al., 2015), GH (13 244; 138 045) (Ghiassian et al., 2015) and WU (6016; 128 150) (Wu et al., 2010). Native identifiers were mapped to Entrez Gene (Brown et al., 2015) identifiers using the R package ‘org.Hs.eg.db’ (Carlson, 2018).
2.3 Analysis of somatic mutations and gene expression variations
SMs and gene expression (GE) data from matched tumour-normal samples (blood for SM and solid tissue for GE) were collected from The Cancer Genome Atlas (TCGA) (Tomczak et al., 2015) for breast invasive carcinoma (BC), lung squamous cell carcinoma (LUSC), prostate adenocarcinoma (PRAD) and thyroid carcinoma (THCA), using the R packages TCGAbiolinks (Colaprico et al., 2016) and isma (Di Nanni et al., 2019) and considering the human genome version 38 (hg38).
Mutation Annotation Format files were obtained from four pipelines: Muse (Fan et al., 2016), Mutect2 (Cibulskis et al., 2013), SomaticSniper (Larson et al., 2012) and Varscan2 (Koboldt et al., 2012). Only mutation sites detected by at least two variant callers were considered. Gene mutation frequencies were calculated as the fraction of subjects in which a gene was associated with at least one mutation. Gene expression data were obtained using the TCGA workflow ‘HTSeq-Counts’. The R package limma (Ritchie et al., 2015) was used to normalize and quantify differential expression in matched tumour-normal samples, yielding log-fold changes, the corresponding P-values and FDRs (BH method).
The four cancer datasets were considered in two tasks: the analysis of two types of omics, mutations and expression changes, and the analysis of mutation profiles of multiple patients. In the first task, was defined as gene mutation frequencies while as –log10 (FDR). In the second task, each layer was represented by mutation profiles of subjects, defined as the number of mutation sites in each gene. In all analysis, empirical P-values were calculated on a total of 1000 permutations (the input matrix and 999 random permutations of it).
In the joint analysis of mutations and expression changes in BC, the two sets of high scoring genes (H1, H2) were defined considering, respectively, all genes with at least one mutation (1238 genes) and the top 1200 differentially expressed genes (FDR < 10−7). We observed that k = 3 was a reasonable choice to obtain connected gene networks enriched in genes with the highest mutation frequencies and expression variations (Supplementary Methods and Fig. S3).
2.4 Signal assignment to gene modules and performance assessment in finding significant genes that lie in network proximity
Each gene module was defined as the largest connected component obtained considering the genes associated with a biological pathway (from KEGG database (Kanehisa et al., 2017)) and all interactions among them in GH interactome (Supplementary Fig. S4). The highest and lowest values of gene mutation frequencies (x1) and fold changes (x2) calculated from BC data (see above) were used to define, respectively, high scoring genes and low scoring genes (Supplementary Fig. S5). High scoring values were randomly assigned to genes of each module independently for and , in thus to obtain a specific percentage (e.g. 10%) of high scoring genes within the module in each layer. Unused high scoring values were assigned to genes outside the module and, lastly, low scoring values were assigned to the remaining genes within and outside the module. Recall was defined as the fraction of module genes ranked (by the assessed method) among the top M genes, where M is the module size. Recall was assessed using, beyond mND score, the product of ND scores (‘NDPROD’) between the two layers (as in Ruffalo et al. (2015)), the minimum of ND scores (‘NDMIN’) between the two layers (as in TieDIE, Paull et al., 2013) and the rank product (‘RP’) of initial scores.
2.5 Evaluating performance in recovering known cancer genes
The partial area under the ROC curve (pAUC) was used to quantify the performance of methods in recovering known cancer genes at low false positive rates. This measure accounts for the number of true positives that score higher than the n-th highest scoring negative, measured for all value from 1 to n:
| (7) |
where TP is the total number of known cancer genes and TPi is the number of true positives that score higher than the i-th highest scoring negative (Scott and Burton, 2007). We calculated pAUCn to evaluate which method had low false positive rates in prioritizing genes whose mutation or differential expression was associated with the considered cancer. Genes mutations associated with cancer were collected from COSMIC (Tate et al., 2019) and previous studies (Kandoth et al., 2013; in Lawrence et al., 2014). Differentially expressed genes were derived from Bioexpress (Dingerdissen et al., 2018), considering log2-fold change between matched primary tumour-normal samples greater than or equal to 1 and FDR < 0.05. NetICS was downloaded from https://github.com/cbg-ethz/netics.
2.6 Pathway analysis
Pathways were downloaded from the KEGG database (Kanehisa et al., 2017). A total of 331 human pathways with at least five genes were considered. The number of genes prioritized in each pathway by mND, by gene expression (, ND scores of gene mutation frequencies () and gene expression ( (Supplementary Table S4A–D, respectively), were quantified for different numbers of top ranking genes (n ={50, 100, 150, 250, 300}). For each pathway and value of n, the difference DP(n) between the number of genes (D) found by mND and the best of the other approaches was quantified as (Supplementary Table S4E):
| (8) |
3 Results
Following is the presentation of the performance of mND in the general problem of locating significant genes that lie in network proximity, using random permutations of real omics data on gene modules representing biological pathways. The assessment of its ability in recovering known cancer genes, a problem considered by recent network-based multi-omics methods (Dimitrakopoulos et al., 2018; Paull et al., 2013; Ruffalo et al., 2015). Lastly, the description of the results obtained applying mND on gene mutations and GE changes observed in BC.
3.1 Finding significant genes that lie in network proximity
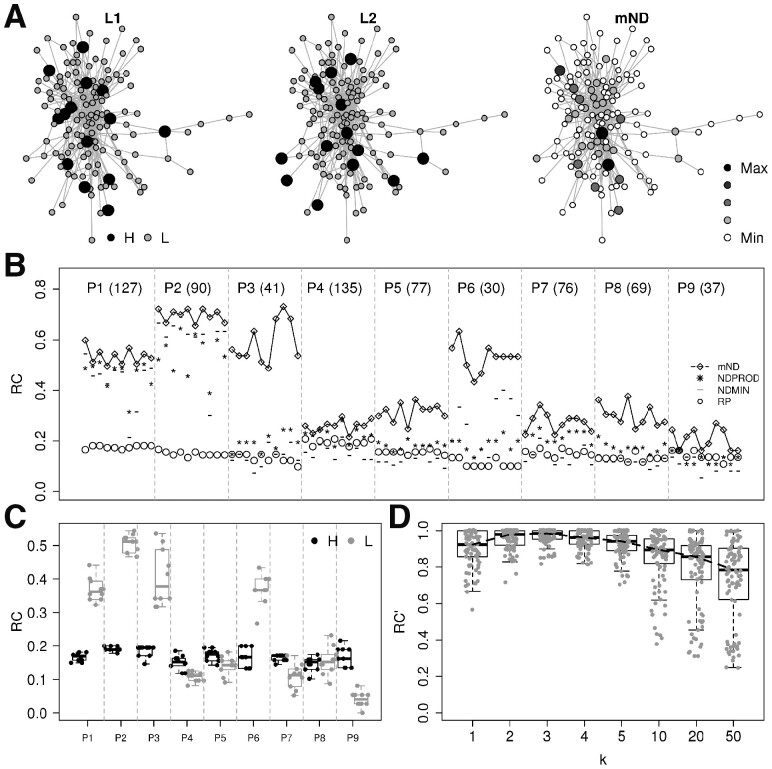
To assess the ability of mND in finding high scoring genes in network proximity across multiple layers, we assigned two types of real signal (gene mutation frequencies and log-fold changes) to gene modules of different size and modularity, corresponding to real pathways (Fig. 2A, Supplementary Figs S4 and S5).
Fig. 2.
Performance in ranking high scoring genes in network proximity. (A) Example of a gene module with its high scoring genes (H, black) in each of the two layers and the resulting mND score; only genes belonging to the module and links occurring among such genes are reported. (B) Recall values for 10 signal permutations for each of the nine modules (P1, P2, …, P9), using mND score and other methods; the number between parentheses after module id is module size. (C) Recall values, shown separately for high scoring genes and other genes in each module. (D) Recall values normalized by the highest recall found for each input configuration at varying number of neighbours (k). (A–D) These results were obtained using interactome GH
In each of the resulting configurations, we compared the recall values (see Materials and methods) obtained by mND to those obtained by other methods. The rank product (RP) was successful in identifying genes with high scoring values in at least one of the two layers (Fig. 2B), but typically missed other module genes with lower values. NDPROD, a multi-omic approach described in Ruffalo et al. (2015) and corresponding to using only the term in Equation (4), led to better performance than RP in more than half of the cases, and equal or even low performance in others, indicating the failure to identify high scoring genes in favour of genes in network proximity to the module, but outside of it (Fig. 2B). Similarly, NDMIN, the multilayer combination strategy underlying TieDIE method (Paull et al., 2013), yielded recall values that are higher or lower than RP depending on gene module and signal distribution. Instead, mND determined the highest recall in almost all cases. This result underlines the importance of using gene neighbourhoods, i.e. the term in Equation (4) (Fig. 2B). Importantly, the performance of mND is the result of spotting both high scoring genes (almost all) plus other module genes with low score, but relevant topological position (Fig. 2C).
Overall, a small number of neighbours (parameter k in Equation (4)) was sufficient to guarantee the highest performances (Fig. 2D), which were observed around k = 3. We observed a similar trend when finding significant genes lying in network proximity over three layers (Supplementary Fig. S6).
To assess whether the results obtained in ranking high scoring genes lying in network proximity (Fig. 2) were limited to the interactome in use (GH), we repeated the same analyses using a different interactome (STRING). We observed the same patterns in terms of mND performance, types of genes found and the relation between performance and k parameter (Supplementary Fig. S7).
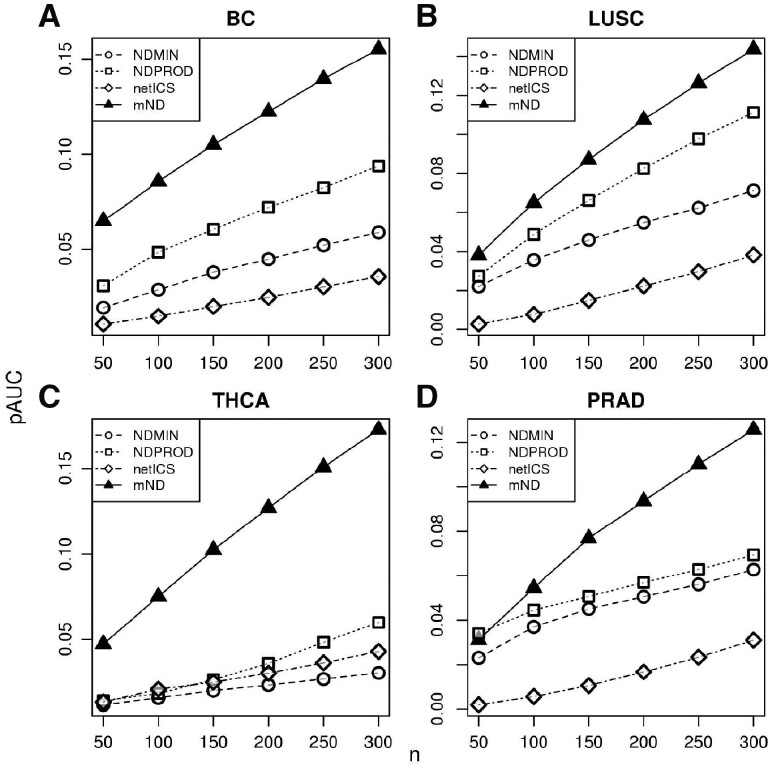
3.2 Recovering known cancer genes
We evaluated the performance of mND in the problem of recovering known cancer genes in four cancer types. Considering mutations and expression changes as input, mND reported higher pAUC than other network-based methods in all four cancer types considered (Fig. 3). We also studied the performance using mutational profiles only as input. In this case, mND reported better performance than other methods in three out of four datasets in recovering genes whose mutations are associated with cancer (Supplementary Fig. S8), while it was the best method in using mutation profiles to recover both mutated and differentially expressed genes involved in cancer (Supplementary Fig. S9).
Fig. 3.
Performance in recovering known cancer genes. Partial AUC (pAUC) at varying number of top false positive ranking genes (n) in the analysis of mutations and expression changes in four cancer types. (A–D) These results were generated using interactome WU
3.3 Gene networks enriched in mutations and expression changes in BC
As a proof of principle, we applied mND to find functionally related genes on the basis of gene mutation frequency (layer 1, L1) and GE variation (layer 2, L2) in BC. Genes highly ranked by mND (Fig. 4A) include those that were relevant according to initial scores in both layers (Fig. 4B, e.g. CCNB1, TOP2A), as well as those that were high scoring in one of them (Fig. 4B, e.g. EGFR and PIK3CA), and linker genes (Fig. 4B, red circles), which have low initial values, but lie in relevant network proximity to significantly altered genes. Interestingly, top scoring linker genes include genes already known to be involved in BC, such as CDC42 and BRCA1 (Fig. 4B and C). To assess whether genes highly ranked by mND are in significant network proximity, we used network resampling (Bersanelli et al., 2016b): this computational approach calculates a network score considering top ranking genes and shows to which extent such network score is expected if links among genes are shuffled (keeping the same degree distribution). This procedure confirmed that genes highly ranked by mND are in significant network proximity (Supplementary Fig. S10): in particular, a dense module of 123 genes was identified (Fig. 4D).
Fig. 4.
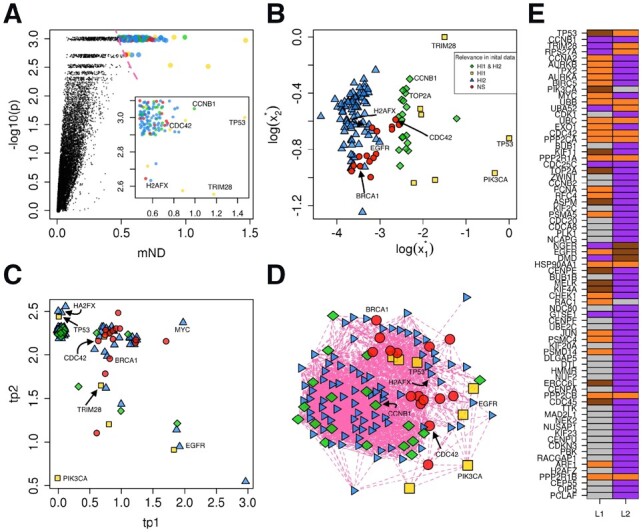
Analysis of mutations and expression changes in BC. (A) mND score and empirical P-value; the red dashed line indicates the top 123 genes (subplot); colours and shapes have the same meaning of panel B. (B) Gene diffusion scores of the top 123 genes ranked by mND. (C) tp values (Equation 6) for the two layers. (D) Gene network composed of the top 123 genes ranked by mND; colours and shapes have the same meaning as in panel B. (E) Classification of genes across layers (only the top 75 ranked genes are shown for clarity); brown: isolated; orange: linker; purple: module; grey: not significant. (A–D) Layer 1 (L1): mutations; Layer 2 (L2): expression variations. H1, H2: sets of genes with high initial scores in respectively L1 and L2. NS: not significant, genes not belonging to H1 and H2. Green rhombuses: genes belonging to H1 and H2; blue triangles: genes belonging only to H1; yellow rectangles: genes belonging only to H2; red shapes: genes neither in H1 nor in H2. These results were generated using interactome STRING
Gene classification underlined gene roles in each layer, which suggest possible underlying molecular mechanisms (Fig. 4E). For instance, TP53 is classified as ‘isolated’ according to mutations and ‘linker’ on the basis of GE, because it is highly mutated and its interacting partners are mainly differentially expressed rather than mutated. CDC42 is classified as linker in both layers: it neither carries a relevant amount of mutations nor is among the top differentially expressed genes, but its interacting partners are highly enriched in both mutations and differential expression. Interestingly, CDC42 is an important molecule in luminal BC, with prognostic significance (Chrysanthou et al., 2017). Among genes highlighted as modules, we found PIK3CA (a highly mutated gene in BC (Mukohara, 2015)), highly ranked on the basis of mutations.
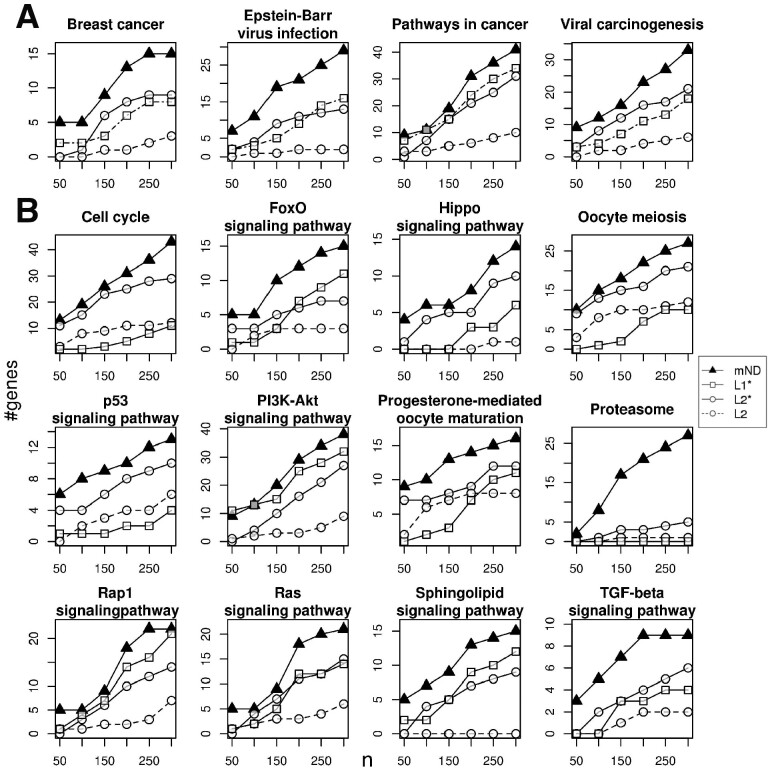
We characterized the genes prioritized by mND in terms of biological pathways. Interestingly, among the pathways in which mND found relatively more genes than each omics considered independently, we found KEGG ‘Breast Cancer’ and signal transduction ways known to have a relevant role in BC (Fig. 5), like ‘Cell Cycle’ (Liu et al., 2008), ‘Hippo signalling pathways’ (Wei et al., 2018), ‘FoxO Signalling pathways’ (Farhan et al., 2017), ‘p53 Signalling pathways’ (Gasco et al., 2002), ‘PI3K-Akt signalling’ (Paplomata and Regan, 2014) and ‘Proteasome’ (Mani and Gelmann, 2005).
Fig. 5.
Pathways enriched in mutated genes and/or differentially expressed genes in BC. Number of genes found by mND and single omics analyses (L1*, L2* and L2) in each pathway at varying number of top ranking genes considered (horizontal axis, n); L1: mutations; L2: gene expression variations; the asterisk distinguishes between gene ranking by original data and the corresponding network diffusion scores. (A) Disease pathways; (B) other pathways. (A and B) Pathways from KEGG database
4 Discussion
Multi-omics analyses, patient-level analyses and multi-classes analyses (e.g. multiple cell clusters) demand methods to highlight the importance of altered genes considering, respectively, different types of summary information across subjects or subject-specific molecular profiles. At the same time, to explain complex patterns in these datasets (e.g. the heterogeneity of mutation profiles of tumour samples) it is important to consider the complex web of macromolecular interactions, which provides known relations among the variables (e.g. genes) under analysis. Recently, the use of first neighbours has been proposed in network-based methods for the analysis of single omics (Gwinner et al., 2017; Horn et al., 2018) and recommended for multi-omics analyses (Modos et al., 2017).
The approach described in this work (mND) highlights genes with a significant network position considering multiple types of biological evidence. Importantly, since mND relies on the mathematical machinery of ND, it prioritizes genes considering their own importance (in proportion to original evidences) and the importance of their network location. ND scores are used to quantify the topological relevance of a gene in the context of the distribution of the considered evidences throughout the entire network and, in particular, mND uses layer-specific highly ‘informative’ first neighbours.
We have shown that mND has a good performance in the general problem of locating significant genes in network proximity using multiple evidences. This problem is involved in several applications in which multi-omics datasets are explained relying on the architecture of intracellular circuits, underlying ‘hot’ gene modules (e.g. disease modules) supported by multiple layers of information.
In the analysis of mutations and differential expression in BC—two types of omics with relevant differences for data analysis in terms of distribution and sparsity—mND prioritized genes carrying both types of alterations, genes associated with one type of alteration and linkers genes, extracting knowledge from both layers. If this should not be the case, a simple solution could be to add the appropriate coefficients in the two sums of Equation (4), in order to weight each layer in relation to the research questions under investigation. The joint analysis of the two omics led to enrichment in relevant pathways, compared to single omics on its own, a result that underlies the added value of combining multiple evidences with mND.
Beyond gene global ranking, mND classifies genes in each layer as members of a module, linkers or isolated genes, on the basis of the amount of signal found in the genes themselves and their neighbours. Complementing the global ranking with layer-by-layer information on gene positions, such classification helps clarifying genes role in the context of the alterations detected. For instance, TP53 clearly emerges as a gene with primary role in BC, not only because of its mutation, but also because its functional partners are differentially expressed (it is classified as linker in GE layer); CDC42 is considered important in the molecular mechanisms underlying BC (Chrysanthou et al., 2017), despite being not reported as significantly altered in the considered dataset: indeed, its functional partners include both mutated genes and differentially expressed genes; other genes play a role according to one type of alteration only, like CDCA8 (Phan et al., 2018), which emerged as being involved specifically in terms of differential expression, being a member of a differential expression module. In the analysis of mutation profiles at single patient level, gene classification underlined the presence of several linkers with a relevant role in BC (Supplementary Fig. S11). For instance, the deletion of HIC-1, never found mutated in the dataset under analysis but spotted as linker in 15 subjects, has been demonstrated to promote BC (Cheng et al., 2014; Wang et al., 2018); FYN has been proposed as a prognostic marker in ER+ BC (Elias and Ditzel, 2015) and promotes mesenchymal phenotypes of basal types BC cells (Lee et al., 2018).
mND introduces an important advance in the class of multi-omics methods: the applicability of the approach is broad in terms of data types and experimental designs. Indeed, mND works on a general gene-by-sample input matrix, where each column is a vector of scores representing different data types (e.g. genomics, transcriptomics) or the same type (e.g. fold changes or P-values from single cell clusters).
Interestingly, we reported good performance also in recovering known cancer genes, a problem addressed by recent network-based methods for the analysis of multi-omics datasets.
In conclusion, the results described in this article support the use of mND for global ranking of genes considering multiple evidences. The results generated by mND can be further processed with other existing tools, for example to characterize the top ranking genes using current annotations (e.g. pathways) or network theory (e.g. centrality measures). At present, mND applies to an interactome with a fixed topology and without edge directions. The generalization of mND pipeline to include layers with different topologies as well as the inclusion of edge directions are interesting opportunities for future developments. However, the latter information is currently lacking for most PPIs and would imply a significant reduction of coverage in terms of the genes studied. As all network-based methods, the performance of mND is bounded by the reliability of current models that describe intracellular circuits. As the data about macromolecular interactions will become more and more available and reliable, network-based analyses will be less affected by the lack of a reference human interactome (Luck et al., 2017). In this context, the impact of tools like mND in molecular biology will presumably increase.
Supplementary Material
Acknowledgements
We would like to thank John Hatton (CNR-ITB) for proofreading the manuscript.
Funding
This work has been supported by the Italian Ministry of Education, University and Research [Flagship InterOmics PB05, PRIN 2015 20157ATSLF, PON ELIXIR CNR-BIOmics PIR01_00017]; Italian Ministry of Health [GR-2016-02363997]; Fondazione Regionale per la Ricerca Biomedica (Regione Lombardia) [LYRA 2015 0010, FindingMS ERAPERMED2018-233 GA 779282]; and the European Union’s Horizon 2020 research and innovation programme [GEMMA 825033].
Conflict of Interest: none declared.
Contributor Information
Noemi Di Nanni, Department of Biomedical Sciences, Institute of Biomedical Technologies, National Research Council, 20090 Segrate (MI), Italy; Department of Industrial and Information Engineering, University of Pavia, Italy.
Matteo Gnocchi, Department of Biomedical Sciences, Institute of Biomedical Technologies, National Research Council, 20090 Segrate (MI), Italy.
Marco Moscatelli, Department of Biomedical Sciences, Institute of Biomedical Technologies, National Research Council, 20090 Segrate (MI), Italy.
Luciano Milanesi, Department of Biomedical Sciences, Institute of Biomedical Technologies, National Research Council, 20090 Segrate (MI), Italy.
Ettore Mosca, Department of Biomedical Sciences, Institute of Biomedical Technologies, National Research Council, 20090 Segrate (MI), Italy.
References
- Ahmad A., Fröhlich H. (2016) Integrating heterogeneous omics data via statistical inference and learning techniques. Genomics Comput. Biol., 2, 32. [Google Scholar]
- Barabasi A.L. et al. (2011) Network medicine: a network-based approach to human disease. Nat. Rev. Genet., 12, 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bersanelli M. et al. (2016a) Methods for the integration of multi-omics data: mathematical aspects. BMC Bioinformatics, 17 (Suppl 2): 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bersanelli M. et al. (2016b) Network diffusion-based analysis of high-throughput data for the detection of differentially enriched modules. Sci. Rep., 6, 34841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown G.R. et al. (2015) Gene: a gene-centered information resource at NCBI. Nucleic Acids Res., 43, D36–D42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson M. (2018) org.Hs.eg.db: Genome wide annotation for human. R package version 3.7.0.
- Cheng G. et al. (2014) HIC1 silencing in triple-negative breast cancer drives progression through misregulation of LCN2. Cancer Res., 74, 862–872. [DOI] [PubMed] [Google Scholar]
- Chrysanthou E. et al. (2017) Phenotypic characterisation of breast cancer: the role of CDC42. Breast Cancer Res. Treat., 164, 317–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cibulskis K. et al. (2013) Sensitive detection of somatic point mutations in impure and heterogeneous cancer samples. Nat. Biotechnol., 31, 213–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colaprico A. et al. (2016) TCGAbiolinks: an R/Bioconductor package for integrative analysis of TCGA data. Nucleic Acids Res., 44, e71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowen L. et al. (2017) Network propagation: a universal amplifier of genetic associations. Nat. Rev. Genet., 18, 551–562. [DOI] [PubMed] [Google Scholar]
- Dingerdissen H. et al. (2018) BioMuta and BioXpress: mutation and expression knowledgebases for cancer biomarker discovery. Nucleic Acids Res., 46, D1128–D1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimitrakopoulos C. et al. (2018) Network-based integration of multi-omics data for prioritizing cancer genes. Bioinformatics, 34, 2441–2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Nanni N. et al. (2019) isma: an R package for the integrative analysis of mutations detected by multiple pipelines. BMC Bioinformatics, 20, 107.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elias D., Ditzel H.J. (2015) Fyn is an important molecule in cancer pathogenesis and drug resistance. Pharmacol. Res., 100, 250–254. [DOI] [PubMed] [Google Scholar]
- Fan Y. et al. (2016) MuSE: accounting for tumor heterogeneity using a sample-specific error model improves sensitivity and specificity in mutation calling from sequencing data. Genome Biol., 17, 178.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farhan M. et al. (2017) FOXO signaling pathways as therapeutic targets in cancer. Int. J. Biol. Sci., 13, 815–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasco M. et al. (2002) The p53 pathway in breast cancer. Breast Cancer Res., 4, 70–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghiassian S. et al. (2015) A disease module detection (diamond) algorithm derived from a systematic analysis. PLoS Comput. Biol., 11, e1004120.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gwinner F. et al. (2017) Network-based analysis of omics data: the LEAN method. Bioinformatics, 33, 701–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofree M. et al. (2013) Network-based stratification of tumor mutations. Nat. Methods, 10, 1108–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn H. et al. (2018) Netsig: network-based discovery from cancer genomes. Nat. Methods, 15, 61–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S. et al. (2017) More is better: recent progress in multi-omics data integration methods. Front. Genet., 8, 84.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandoth C. et al. (2013) Mutational landscape and significance across 12 major cancer types. Nature, 502, 333–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M. et al. (2017) KEGG: new perspectives on genomes, pathways, diseases and drugs. Nucleic Acids Res., 45, D353–D361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koboldt D. et al. (2012) VarScan 2: somatic mutation and copy number alteration discovery in cancer by exome sequencing. Genome Res., 22, 568–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristensen V. et al. (2014) Principles and methods of integrative genomic analyses in cancer. Nat. Rev. Cancer, 15, 299–313. [DOI] [PubMed] [Google Scholar]
- Larson D.E. et al. (2012) SomaticSniper: identification of somatic point mutations in whole genome sequencing data. Bioinformatics, 28, 311–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence M.S. et al. (2014) Discovery and saturation analysis of cancer genes across 21 tumour types. Nature, 505, 495–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee G.H. et al. (2018) FYN promotes mesenchymal phenotypes of basal type breast cancer cells through STAT5/NOTCH2 signaling node. Oncogene, 37, 1857–1868. [DOI] [PubMed] [Google Scholar]
- Liu J. et al. (2008) Identification of a gene signature in cell cycle pathway for breast cancer prognosis using gene expression profiling data. BMC Med. Genomics, 1, 39.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luck K. et al. (2017) Proteome-scale human interactomics. Trends Biochem. Sci., 42, 342–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mani A., Gelmann E. (2005) The ubiquitin-proteasome pathway and its role in cancer. Clin. Oncol., 23, 4776–4789. [DOI] [PubMed] [Google Scholar]
- Modos D. et al. (2017) Neighbours of cancer-related proteins have key influence on pathogenesis and could increase the drug target space for anticancer therapies. NPJ Syst. Biol. Appl., 3, 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosca E. et al. (2014) Diffusion of information throughout the host interactome reveals gene expression variations in network proximity to target proteins of hepatitis C virus. PLoS One, 9, e113660.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosca E. et al. (2017) Network diffusion-based prioritization of autism risk genes identifies significantly connected gene modules. Front. Genet., 8, 129.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukohara T. (2015) PI3K mutations in breast cancer: prognostic and therapeutic implications. Breast Cancer, 7, 111–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paplomata E., Regan R. (2014) The PI3K/AKT/mTOR pathway in breast cancer: targets, trials and biomarkers. Ther. Adv. Med. Oncol., 6, 154–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paull E.O. et al. (2013) Discovering causal pathways linking genomic events to transcriptional states using tied diffusion through interacting events (TieDIE). Bioinformatics, 29, 2757–2764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phan N.N. et al. (2018) Distinct expression of CDCA3, CDCA5, and CDCA8 leads to shorter relapse free survival in breast cancer patient. Oncotarget, 9, 6977–6992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie M.D. et al. (2015) Methods of integrating data to uncover genotype–phenotype interactions. Nat. Rev. Genet., 16, 85–97. [DOI] [PubMed] [Google Scholar]
- Ritchie M.E. et al. (2015) limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res., 43, e47.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruffalo M. et al. (2015) Network-based integration of disparate omic data to identify “silent players” in cancer. PLoS Comput. Biol., 11, e1004595.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott M.S., Burton G.J. (2007) Probabilistic prediction and ranking of human protein-protein interactions. BMC Bioinformatics, 8, 239.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szklarczyk D. et al. (2015) String v10: protein-protein interaction networks, integrated over the tree of life. Nucleic Acids Res., 43, D447–D452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tate J.G. et al. (2019) COSMIC: the Catalogue Of Somatic Mutations in Cancer. Nucleic Acids Res., 47:D941–D947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomczak K. et al. (2015) The Cancer Genome Atlas (TCGA): an immeasurable source of knowledge. Contemp. Oncol. (Pozn), 19(1A), A68–A77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanunu O. et al. (2010) Associating genes and protein complexes with disease via network propagation. PLoS Comput. Biol., 6, e1000641.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y. et al. (2018) HIC1 deletion promotes breast cancer progression by activating tumor cell/fibroblast crosstalk. J. Clin. Invest., 128, 5235–5250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei C. et al. (2018) The role of Hippo signal pathway in breast cancer metastasis. Onco Targets Ther., 11, 2185–2193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu G. et al. (2010) A human functional protein interaction network and its application to cancer data analysis. Genome Biol., 11, R53.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao Y. et al. (2014) A novel significance score for gene selection and ranking. Bioinformatics, 30, 801–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.