Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jan 10;127(3):623–633. doi: 10.1021/acs.jpcb.2c06546

Allosteric Signaling in PDZ Energetic Networks: Embedding Error Analysis

Benjamin S Cowan †,∥, David L Beveridge ‡,§, Kelly M Thayer †,‡,§,∥,*
PMCID: PMC9884075  PMID: 36626697

Abstract

graphic file with name jp2c06546_0008.jpg

Allosteric signaling in proteins has been known for some half a century, yet how the signal traverses the protein remains an active area of research. Recently, the importance of electrostatics to achieve long-range signaling has become increasingly appreciated. Our laboratory has been working on developing network approaches to capture such interactions. In this study, we turn our attention to the well-studied allosteric model protein, PDZ. We study the allosteric dynamics on a per-residue basis in key constructs involving the PDZ domain, its allosteric effector, and its peptide ligand. We utilize molecular dynamics trajectories to create the networks for the constructs to explore the allosteric effect by plotting the heat kernel results onto axes defined by principal components. We introduce a new metric to quantitate the volume sampled by a residue in the latent space. We relate our findings to PDZ and the greater field of allostery.

Introduction

One of the most important characteristics of protein function implicated in interaction domain regulation is protein’s capacity for allosteric dynamics. Allostery or “different shape” is an important set of intermolecular interactions characterized by the coupling of conformational changes in tertiary and quaternary structures upon ligand binding between distinct interaction sites wherein the binding interactions of a ligand at a distal site increase or decrease the affinity of a protein’s active site toward a target ligand. Since its original articulation by Monod et al. over 50 years ago,1 experimental and computational studies have expanded the operational scope of allosteric phenomenon beyond pure changes in the conformational landscape of the protein toward protein’s free energy landscape dynamics.2−4 Thus, allosteric effector binding and the presence in protein interactions result in equilibrium shifts toward more energetically favorable preexisting ensemble state populations in the free energy landscape, which is observably different from the dominant population of states present in that effector’s absence.3,4 In such a model, population shift modulates the dominant population of preexisting residue interaction pathways operative in strain energy propagation across conformation upon allosteric perturbation. These allosteric strain-energy propagation pathways (referred to as allosteric networks) are composed of residues dynamically coupled with one another. The forms of interaction between these residues can involve combinations of both enthalpic and entropic components of residue’s interactions.3 This is observed as the transmission of an allosteric signal across coupled residue interactions to target sites that disrupt, enhance, and modulate substrate binding.5

The role of nonbonded energetic interactions and, particularly, side-chain electrostatic interactions has been demonstrated to be significant to protein function,6 folding stability,7 catalysis,8 and allostery.9 Moreover, recent studies have reported redistributions in electrostatic networks to energetically couple residue’s ligand-binding interactions to distal regions in enthalpy-driven allostery10 with such long-range electrostatic redistributions being a potentially universal process underlying allosteric signal propagation both with and without significant conformational change.10 As such, investigating the energetic and electrostatic basis underlying redistributions in long-range residue interaction pathways may prove to be crucial in understanding the nature of population shift both in enthalpically and entropically driven forms of allostery.

Although the existence of allostery has been known for about half a century, how the allosteric signal propagates across the protein remains difficult to ascertain. While analyzing the structure based on its natural xyz coordinates is a natural and obvious choice, it is difficult to differentiate small meaningful changes from thermal fluctuations. To complicate matters, the structures must first be aligned. This implies that changes furthest from the center of mass will be of larger magnitude because of the radial effect. This can be overcome by making local alignments in the area of interest, but how that should be chosen may largely affect the results obtained and often is not straightforward to choose.

Problems in linear algebra regularly deal with transformations of vectors in one basis set to another. This study postulates the idea that taking such a mindset and applying it to the protein structure may perhaps be a useful vantage from which to consider complex long-range dynamical structural properties such as allostery. Kernels embody one such transformation procedure, and the heat kernel in particular lends itself to this study with the flow of the allosteric signal being similar to the flow of heat in coupled bodies as one would encounter in physics problems. We thus chose to adapt this approach to our studies. In essence, the procedure seeks to iteratively guess a transformation operator that maximizes the variance of the data when projected into some basis set. We surmised that this may be useful to understand the complex dynamics of proteins.

To perform the studies, a small well-studied PDZ model system was chosen. One interaction domain family, the postsynaptic density-95/discs large/zonula occludens 1 (PDZ) domain, is considered to be the most studied system for understanding single-domain allostery.10−15 PDZ domains are crucial for organizing a great diversity of signaling pathways16,17 and implicated in clustering proteins into functional complexes at the plasma membrane18 in addition to sorting, assembling, and anchoring multidomain interaction complexes.19 Various studies on several PDZ domains, including normal mode analysis,20 statistical coupling analysis,12,21,22 NMR relaxation,23 and site-directed mutational analysis,14,24,25 have demonstrated PDZ’s capacity for allosteric behavior. Structurally, PDZ domains are approximately 80–100 amino acid residues long. They typically adopt a topologically similar compact globular structure that consists of six β-strands (β1−β6), a short α-helix (α1), and a long α-helix (α2) (Figure 1). Typically, PDZ domains recognize specific amino acids in the C-terminal ends of peptide or protein motifs through a highly conserved carboxylate binding motif sequence n-terminal to the β2 strand with the ligand binding occurring in PDZ’s hydrophobic core between β2 and α2.

Figure 1.

Figure 1

Open in a new tab

Molecular structure and key features of CRIB-Par6 and its PDZ domain. PDZ is comprised of five β-sheets (blue) and two α-helices (purple). PDZ-domain ligand-binding pocket region is highlighted in purple, while the semiCRIB motif region is highlighted in yellow. PDB ID 1NF3.

The CRIB-Par6 protein provides a particularly interesting model system for investigating the interplay of structural rearrangements and the role of energetic communication pathways contributing to PDZ domain ligand affinity allostery. Par6’s PDZ2 domain functions as a key colocalizing adaptor, whose binding to Par3’s PDZ3 domain and atypical protein kinases (aPKCs) forms the Par3-Par6-aPKC complex at apical cell junction sites, which is responsible for maturation of cell-membrane junction sites through allosteric signal transduction pathways underlying Par6’s binding dynamics and interactions.26,27 When the PDZ is bound by its Cdc42 allosteric effector, the structurally ordered CRIB motif (β0) becomes dynamically coupled with the residues in alpha helix 1 (α1) mediated by a dipeptide switch. This β1−β2 loop switch transmits an allosteric activation switch to the ligand binding pocket.28 This results in a 10-fold increase in binding affinity of PDZ for its peptide ligand.13

As of now, Par6’s allosteric control mechanism involving interdomain communication in which a flexible extra-domain sequence (CRIB) upon effector binding regulates an intra-domain process (PDZ ligand binding) is the only PDZ-domain family protein wherein the carboxylate binding pocket is remodeled from a deviant conformation to a recovered high-affinity conformation in order to regulate C-terminal ligand binding.29 Par6 allosteric dynamics therefore represent a strikingly important evolutionary departure from known PDZ domain functionality and allosteric mechanism, a functional consequence of which could be shifting of a conformational equilibrium of Par6 from high association with an internal ligand to regulator C-terminal ligands, altering the activity and localization of the par complex as a whole.13,30 Despite being a prototypical example of functional communication between domains, the basis of CRIB-Par6’s transmission of GTPase binding signal28 and its ligand-selective nature29 remains unexplained.

Rather than protein structure networks (PSNs) and contact-networks, which merely encode edge presence between nodes by a specified geometric distance threshold, we construct locally-thresholded electrostatic interaction networks,31,32 which embed residues (nodes) connected by weighted edges representing the level of electrostatic interaction between residues. Such a methodology enables investigations into longer-range forms of residue connectivity beyond covalent-bond distance thresholds alone.33 As the allosteric dynamics of residue interactions are implicated in the redistribution of electrostatic interaction energy between distinct interaction states, we investigate how each residue’s electrostatic interactions are redistributed between distinct CRIB-Par6 ensemble states. Through our analysis, we demonstrate that an allosteric shift toward CRIB-Par6’s high-affinity conformation is associated with structure-wide redistributions in residues’ electrostatic network interactions functionally implicated in PDZ-ligand binding.

In this study, we investigate the allosteric dynamics of residues’ electrostatic interactions and their energetic redistributions between CRIB-Par6 effector and ligand-binding interaction states through a network theoretic approach. Four constructs representing all liganded CRIB-Par6 interaction states produced in previously published work34 were analyzed in this study. These states include the unbound (P), Cdc42 effector-bound (AP), VKESLV ligand-bound (PL), and effector and ligand-bound (APL) states (Supplementary Figure 1). Through such approaches, proteomic interactions are formalized into graph-based models wherein dynamic fluctuations are mapped into a graph data structure with nodes representing amino-acids and edges representing weights of the measured dynamic properties.35 Across a variety of studies, applications of network-based methodologies toward investigating allosteric dynamics have been capable of quantifying global functional changes in protein structure,36−38 key functional centers, and significant communication pathways.39−42 Moreover, molecular dynamics studies investigating allosteric communication pathways in terms of side chain energetic correlations18,43 and noncovalent energetic interaction networks33 of other PDZ domain proteins indicate an energetic basis to PDZ’s allosteric coupling of incoming binding signals between upstream regions proximal to the C-terminal ligand recognition motif to distal regions.10 This further demonstrated a “hidden” electrostatic basis for the internal redistributions and the rewiring of pairwise energetic interactions across PDZ structure, providing the basis of PDZ dynamic allostery governing population shift. As such, the role of electrostatic long-range communication and stability in PDZ signal propagation events appears increasingly evident. Thus, understanding the nature of energetic rearrangements, particularly redistributions in long-range networks of electrostatically coupled residues across Par6 structure upon Cdc42-CRIB interactions involved with PDZ ligand selectivity, provides an important point of investigating Par6 allosterism.

Methods

Generation of Interaction State Constructs and MD Simulations

MD-simulations were run on four proteomic states accounting as a representative selection of ensemble structures corresponding to different states of CRIB-Par6’s possible effector and ligand interactions. These four CRIB-Par6 states include the unbound 123 residue PDZ protein (P), Cdc42 allosteric effector-bound (AP), VKESLV peptide ligand-bound (PL), and allosteric-effector and ligand-bound (APL) states. Genetic assays of carboxy-terminal peptide libraries demonstrate that the intrinsic affinity of Par6 for this VKESLV peptide ligand is significantly enhanced by the addition of Cdc42.13 As such, the Cdc42-dependent manner of Par6 and VKESLV interactions models the allosteric dependent manner for Par6-PDZ ligand interactions. The four interaction state constructs were modeled based upon the crystal structure of PDBID 1NF3 and the NMR structure PDBID 1RZX. The details of construct modeling have been previously published.34 Simulation data utilized in this study were derived from a previous study conducted by Thayer et al. on a Markov state modeling (MSM) analysis of all-atom MD simulations performed on these four Par6 constructs.34 Each of the four MD simulations was carried out for a total of 0.4 μs using AMBER12.44 Details on design of constructs, force field parameters, equilibration process, and simulation stability and convergence analysis have been previously published34 and have been described in detail in the Supplementary Information.

Locally Thresholded Interaction Networks

The pairwise interaction energy network32,45 is a method adopted to create representations of protein systems at the energetic level. The nodes of such networks represent the residues of the protein with edges representing the electrostatic interaction between each residue pair. The degree of each node in the network is equal to N – 1 where N denotes the total number of residues within the protein. The weight of each edge between each residue pair is calculated as the sum of all electrostatic potential interaction energies between the pairs of atoms in each residue. To quantify the magnitude of pairwise interactions, we take the absolute value of each of these interaction weights. Depending on the strength of the computed electrostatic interaction energy, different edges will have varying edge weights, with higher edge weights representing a higher degree of energetic interactions between residues.

Due to the computationally intensive nature of computing the pairwise interaction energy network for every frame of a simulation, we analyze the pairwise energies for a selected subset of frames from each trajectory. For each interaction state construct’s 400 ns-long trajectory with 5050 frames, one frame out of every 100 frames starting from the first frame is extracted at a regular interval. The collected samples were then concatenated into a new trajectory consisting of 51 frames, serving as the trajectory’s representation.

We were concerned that no precedent exists as to what sampling frequency would be appropriate for the study and to what extent the results may depend on this choice. To address this, we also repeated the analysis at double the frequency (0.5 frames per ns equivalent to 100 snapshots per residue per trajectory) and quadruple the frequency (0.25 frames per ns), and for comparison, the purposely undersampled two frames per ns with just 25 snapshots. This extended data set can be found in the Supplementary Information Spreadsheet. We discovered that the results were largely invariant to this choice at least for this system. Thus we chose to focus on the 51-frame sampling frequency in our main report as a reasonable compromise between computational time and resolution of results backed by the confidence instilled by this experiment.

Each of these concatenated trajectories is subsequentially fed through the energy analysis protocol from CPPTRAJ. The electrostatic interaction energy between every pair of CRIB-Par6’s 123 residues is computed using a bash script that performed the CPPTRAJ energy command with each pair of residues. Subsequently, Python scripts were written to parse the CPPTRAJ outputs into tensors of shape (T, (N, N)) where T is the number of frames in the trajectory (T = 51) and N is the number of residues (N = 123). Subsequently, the pairwise interaction edge weights undergo a localized-normalization and thresholding protocol.32 This procedure sparsifies the electrostatic network by normalizing the pairwise edge weights on a per-node basis and picking all nodes above the threshold. This process prunes edges where the local energetic environment affects a residue’s energetic interactions less, simultaneously emphasizing network regions where such environmental energetic contributions significantly occur.31

Generation of Heat Kernels from Locally Thresholded Interaction Networks

For each of the CRIB-Par6 interaction state constructs, we compute the heat kernel of each 51 locally thresholded electrostatic interaction networks through a protocol developed by the Thayer lab.31 The heat kernels of each construct are stored as a (T, (N × N)) tensor object. The heat kernel of a network46 is a function simulating the diffusion of heat and/or information across the network over a time parameter, measuring how information tends to “flow” within different communities of nodes and weighting significant topological features of network structure. Calculating the (N × N) heat kernel matrix of a (N × N) weighted network46 biases the topological properties encoded by the network’s edge weights to further emphasize node connectivities, interactions, and the structure of the network at both local and global scales.

Principal Component Analysis (PCA) on the Heat Kernels

As embedding graph data in lower dimensional space has proven to be a useful means toward graph characterization,31 we perform PCA on the heat kernels to capture the most significant variations among nodes’ connectivities across the heat kernels. To perform the PCA, each interaction state construct’s 51 heat kernels are projected onto a shared set of eigenbasis vectors. Thus, each construct’s 123 residues across all sampled trajectory frames are represented by 51 node embeddings in the shared PCA space, yielding 123 × 51 = 6273 total embeddings. We choose to project the heat-kernel embeddings of each interaction state’s electrostatic networks into R3 space across the top three eigenvectors with the highest eigenvalues (Principal Components: PC1, PC2, and PC3) as they account for the most significant variances in heat-kernel values and thus network topology. The PCA heat kernel embedding projections of all 123 residues across 51 frames are stored in a tensor of shape ((N × T), D), where D equals the number of PC dimensions (D = 3). Thus, embedding each residue’s electrostatic dynamics with other residues across simulation time into this shared low-dimensional space provides insight toward the dynamics of node clusters and associations in the context of residue’s energetic interactions over the course of the simulation.

Calculation of Embedding Error

Once the heat kernels for each system are embedded in PCA space, we perform embedding error analysis on their node embeddings across combinations of the four CRIB-Par6 interaction state constructs. Embedding error analysis seeks to quantify how different each residue’s electrostatic interactions as embedded across the heat-kernel PCA projections of one CRIB-Par6 interaction state are to that residue’s interactions in a different state. To calculate the embedding error for each residue between two systems, we employ a calculation of the Wasserstein distance metric implemented by the SciPy package (Scipy.org). This metric, also referred to as the earth mover’s distance, describes the minimum amount of “work” required to transform one distribution U into another distribution V where “work” is quantified as the amount of distribution weight that must be moved and multiplied by the distance it must be moved. For the set of samples composing distributions, x1, x2, ..., xn ∈ U and y1, y2, ..., yn ∈ V, the Wasserstein metric can be formalized as:

graphic file with name jp2c06546_m001.jpg

where Γ(U, V) is the set of distributions on 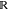Inline graphic × Inline graphic, whose marginal distributions are U and V.(47) The Wasserstein distance metric between two distinct constructs’ positional node embedding distributions of a particular residue is calculated across each of the three eigenbasis axes (PC1, PC2, and PC3) and summed together, resulting in an “embedding error score” for that residue. Thus, the larger a residue’s embedding error score between two systems, the more distinct that residue’s electrostatic interactions as organized over the temporal dynamics of one CRIB-Par6 state are from its interactions in another state. This process is iteratively performed on each residue, resulting in a (1 × N) distribution of each residue’s embedding error score between the two compared constructs. Calculation of this embedding error score distribution across all CRIB-Par6 residues between a pair of interaction states forms the foundation of the explored pairwise and maximal embedding error analyses, which are detailed in the Results section.

Code Development

Algorithms implemented in the methodologies were generated in Python 3.748 through Jupyter Notebooks.49 See Supplementary Documentation for more information on implementation.

Results

Locally Thresholded Electrostatic Networks

To capture residues’ electrostatic interactions across simulation time, we generate locally-thresholded energetic networks for each trajectory frame. Each of these pairwise interaction energy networks45 encodes residues as nodes and the edge between every pair of residues as the electrostatic interaction energy between them. Due to the computational cost of calculating these energetic networks for all simulation frames, we generate the networks for a subset of 51 frames sampled regularly across each interaction state construct’s trajectory. The MD simulations are reported elsewhere and consist of 550 ns of all atom solvated molecular dynamics simulation carried out in the AMBER simulation package (REF Bharat). The edges are weighted to account for the effect of each residue’s local energetic environment on its interaction with every other residue and thresholded to increase network sparsity. To visually analyze each interaction state’s networks, we can sum over the edge weights for all 51 frames to generate a single network representation. We visualize the locally-thresholded electrostatic network for all constructs utilizing the Gephi software package50 (Figure 2). Nodes are colored and scaled by degree where higher degree nodes are larger and more yellow-shifted, while lower degree nodes are smaller and purple-shifted. The degree of a node quantifies the number of connections (i.e., significant electrostatic interactions with other residues) to other nodes/residues within the network. Thus, residues with higher degree node embeddings display a more “hub-like” relation to other nodes in the electrostatic network. Edges between nodes are colored and scaled by the magnitude of their edge weights. Noticeably, higher degree residues tend to display edges with more significant electrostatic interaction energy weights.

Figure 2.

Figure 2

Open in a new tab

Electrostatic interaction networks from PDZ MD simulations. Pairwise electrostatic interaction networks obtained for the P (a), AP (b), PL (c), and APL (d) interaction state constructs were generated. Nodes are labeled by their corresponding residue index and proportionally scaled according to their number of incoming connections with highly connected nodes being larger and more yellow-shifted. An edge between two nodes is scaled larger and red-shifted as correlated with the magnitude of its corresponding electrostatic interaction weight value.

Projection of Electrostatic Network Heat Kernels for Embedding Analysis

By projecting each of the 51 sampled trajectory frames’ electrostatic network heat kernels onto a set of R3 eigenbasis vectors, we obtain an interpretable low-dimensional representation of how residues’ electrostatic interactions as embedded by the kernels are dynamically structured across simulation time for each CRIB-Par6 interaction state construct. We generate a plot of the PCA-embedded heat kernels across C1 and PC3 for each of the four constructs, P, AP, PL, and APL (Figure 3). Each plot contains 123 × 51 = 6273 unique node embeddings, with each embedding corresponding to a single residue’s electrostatic interactions at a sampled frame. The shared PCA plots of the electrostatic heat kernels are populated by node embeddings, which are colored by each node’s degree in the electrostatic network system. The level of compactness in node embedding clusters within the shared PCA space reveals information about the strength of the energetic relationships between node embeddings and the residues they represent both across each frame’s electrostatic interaction networks and the networks across simulation time.

Figure 3.

Figure 3

Open in a new tab

Electrostatic kernel projections. The projection consists of 51 × 123 embedded node values where each residue has 51 individual node embeddings mapped to PC1 and PC3. In total, there are 6273 embedded points. Color mapping represents the degree of node connectivity in the protein system. The more yellow a node embedding, the higher that node embedding’s degree of connectivity. Embeddings at other sampling frequencies can be found in the Supplementary Information. The heat kernel projections for the P (a), AP (b), PL (c), and APL (d) interaction state constructs.

Pairwise Embedding Error Analysis (PEEA)

The primary aim of PEEA on the heat kernel projections is toward extracting insight concerning both the time-evolving dynamics of each residue’s electrostatic interactions in an interpretable low-dimensional embedding of the electrostatic networks and how those interactions differ between distinct CRIB-Par6 interaction states. The average embedding error, in other words, is a way to measure the extent of change of the network, as projected in the R3 PCA space, across all residues in the graph. As such, we seek toward understanding the degree by which each residue’s local and global electrostatic interactions are restructured by different conditions of CRIB-Par6’s interaction with its effector and ligand-binding partners. In PEEA, we utilize an embedding error metric to quantify how different each residue’s 51 node embeddings in one interaction state construct are from its embeddings in other distinct constructs.

To perform PEEA, an embedding error score value between each possible pair of the four CRIB-Par6 systems, unbound (P), AP, PL, and APL was calculated for each of the 123 residues. As such, for each residue, there are Inline graphic different embedding error score values resulting from the first Wasserstein distance metric calculation between each combination of CRIB-Par6 systems. For reference throughout the following results, the embedding error comparison/distribution between two distinct interaction state constructs “A” and “B” is represented as “A_B”.

The embedding error distributions between both the three possible pairs of CRIB-Par6 bound-to-unbound states (AP_P, PL_P, and APL_P) and the three possible pairs of CRIB-Par6 bound-to-bound states (AP_PL, APL_PL, and AP_APL) are calculated across all 123 residues of CRIB-Par6 (Figure 4a). Moreover, we determined the top 10 residues with the highest embedding error scores for each of the bound-to-unbound CRIB-Par6 pairwise comparisons (Supplementary Figures 2–7).

Figure 4.

Figure 4

Open in a new tab

Pairwise embedding error analysis. (a) Distributions of residue embedding error score values for each of the six pairwise embedding error comparisons between CRIB-Par6 interaction states. The x-axis represents the residue number, and y-axis represents the embedding error score between the positional embeddings of the compared interaction states. CRIB-Par6 secondary structural elements corresponding to residue positions are visualized with a line representation under the x-axis. (b) Average embedding error score values (shown above bars) across all residues for each pairwise embedding error comparisons averaged across different sampling interval (SI) trials (SI = 25, 50, 100, and 200) with standard error bars displayed. Colors of bar graphs are as in (a).

Subsequentially, the average embedding error score of all CRIB-Par6 residues for each of these residue-wise embedding error distributions is calculated (Figure 4b). Calculation of the average embedding error for each pairwise comparison quantifies the level by which the structure of electrostatic network interactions across the entire CRIB-Par6 protein is reorganized by differences in binding-conditions. The three embedding error comparisons yielding the highest average embedding error scores across all residues include APL_PL (0.055), AP_PL (0.048), and APL_P (0.0422). Comparatively, those pairwise embedding error distributions yielding the three lowest average residue embedding error scores across CRIB-Par6 are the comparisons between the effector-bound and unbound states (AP_P, 0.0346), effector-bound and effector and ligand-bound states (AP_APL, 0.0267), and the purely ligand-bound and unbound states (PL_P, 0.0228).

Applying Maximum to Embedding Error Analysis to Assign Maximum Interaction State Embedding Error Categories

While performing maximal embedding error analysis (MEEA), a single distribution consisting of the maximal embedding error score of each residue across all the six pairwise system embedding error comparisons was created to identify the two CRIB-Par6 interaction states, which yield the maximal difference in each residue’s electrostatic network embeddings (Figure 5a). A graph displaying the percent composition of residue membership into each of these maximal embedding error-scoring state comparisons is displayed in Figure 5b and Table S1. Noticeably, the maximal embedding error scores for 80.5% of all CRIB-Par6 residues is contributed from the embedding error distribution calculated between the Cdc42 effector-bound and VKESLV ligand-bound states (APL_PL). The residues from this APL_PL maximal embedding error group are distributed globally across Par6’s structure (Figure 6a), including those in structural elements such as the semiCRIB motif, the α1 and α2 helices, and the PLGF peptide recognition site (P38-F41). The second largest set of residues whose maximum embedding error scores between interaction states is that between the purely effector-bound and ligand-bound states (AP_PL), accounting for 17.1% of all residues’ maximal embedding error values. Notably, approximately 48% of the residues from this AP_PL maximum embedding error group occupy a localization in the PDZ ligand binding region with a noticeably contiguous occupation of residues 31–37 from this group occurring within the β1−β2 loop region (Figure 6b). The last embedding error comparison accounting for the remaining 2.4% of all residues’ maximal electrostatic heat kernel PCA embedding scores occurs between the Cdc42 effector-bound and Cdc42 effector-bound and VKESLV ligand-bound states (APL_AP) with two of these three residues occupying the α1 helix.

Figure 5.

Figure 5

Open in a new tab

Maximal embedding error analysis. (a) Maximum of embedding error score values taken from Figure 4a. The x-axis represents residue number, and y-axis represents embedding error score value between the positional embeddings of the compared interaction states. The maximum embedding error score of each residue is color-coded as in Figure 4. Out of six possible interaction state embedding error categories, only three were maximal. CRIB-Par6 secondary structural elements are visualized under the x-axis. (b) Percent residue composition of constructs from panel a. Coloration follows from panel a.

Figure 6.

Figure 6

Open in a new tab

Mapping of maximal embedding error designation onto CRIB-Par6 structure. (a) Global distribution of maximal embedding error groups across the protein. (b) Maximal embedding error group AP_PL dominates the β1−β2 loop region, which connects the β1 and β2 strands labeled in Figure 1.

Discussion

Through the pairwise and maximal embedding error analyses, we aimed to investigate the extent by which differences between interaction states reorganize the electrostatic network interactions between residues. By determining the specific pairwise embedding comparison yielding the maximal embedding error score for each residue, we aimed to identify distinct sets of residues whose electrostatic network dynamics are most restructured by those. Residues of the same maximal embedding error group share the property of being most reorganized in their electrostatic network interactions by the same functional differences between two specific states.

The results of the pairwise and maximal embedding analyses indicate that the vast majority of residues are electrostatically modulated in their ligand binding interactions by the presence of an allosteric effector. The residue composition (>80% of CRIB-Par6 residues) attributed to the APL_PL category is the highest of the three comparison groups, distributing globally across CRIB-Par6’s structure (Figure 6a). Moreover, the APL_PL embedding error comparison yields the highest average embedding error score across all pairwise comparisons (Figure 4b), indicating that the two constructs with the most characteristically distinct organization of CRIB-Par’s electrostatic network interactions from one another occur between two ligand-bound states differing by Cdc42-allosteric activation.

In the PDZ system, which was chosen in part because of its conveniently small size, a study of the embeddings based upon a battery of sampling frequencies (Sampling Interval Trial Study and Supplementary Figures 8–13) revealed that at least in this case, the result was fairly robust, even with as few as 25 snapshots per residue across the whole trajectory. We suspect that a sampling frequency of one frame per nanosecond across a converged trajectory, the level we chose to focus on, will also be appropriate for other systems but of course remains to be seen as other systems are explored. Repeating the analysis at different sampling levels illustrates an approach for honing an appropriate sampling level in subsequent studies that may involve other biomolecular systems, particularly those of larger size.

Compared to other PDZ-containing proteins, Par6 is rather unique that its PDZ binding domain assumes a low ligand-binding affinity conformational substate when unbound. As the difference in embedding is measured between the purely ligand-bound (PL) and effector and ligand-bound constructs (APL), the rather structure-wide occupation of residues with maximal embedding difference between these two states may imply an important role of Cdc42’s capacity to regulate the electrostatics of ligand-bound interactions across the entirety of the protein structure. Specifically, the rather global effect that this difference has across CRIB-Par6 residues indicates that the most significant electrostatic difference across all interaction states is that between when the Cdc42 effector is and is not present in ligand binding interactions. Such findings are corroborated by evidence that Par6’s allosteric Cdc42 effector-bound state structurally aligns much more similarly to the majority of known PDZ structures than its unbound state.51 CRIB-Par6 is also unique among PDZ-domain containing proteins as extra-domain interactions between CRIB and the effector GTPase control CRIB’s allosteric regulation of PDZ’s affinity for C-peptide binding28 and as such, PDZ’s capacity to allosterically propagate a ligand-binding signal.

Moreover, the role of CRIB interactions in the effector-bound complex on increasing Par6-PDZ2’s ligand-affinity mirrors the role of a3 in studies of PSD95-PDZ3.10,24 Removal of the distal a3 helix region has been demonstrated to lower the ligand-binding affinity of the PDZ3 domain, with more recent studies attributing the ligand-binding allostery of a3-containing PSD95 as mechanistically controlled by long-range redistributions in side-chain electrostatic interactions.10 Similarly, our analyses evidence that CRIB-PDZ interactions enable the long-range reorganizations in electrostatic network interactions across the PDZ domain, which facilitate ligand-binding. Thus, understanding allosteric signal propagation as a process of redistributions in long-range electrostatic interactions establishes a common mechanistic basis between PDZ2 and PDZ3 ligand-binding activity. As such, the overwhelming residue composition attributed to the APL_PL maximal embedding error class evidence a structure-wide electrostatic-basis for Cdc42’s role in causing an allosteric transition from a deviant weakly-interacting PDZ conformation to a “restored” active conformation that increases peptide-affinity by ∼10-fold.13

In contrast to the APL_PL maximal embedding error group, the set of residues whose maximal embedding error occurs between the effector-bound and effector and ligand-bound states (AP_APL) is composed of only 2.4% of all residues (Figure 5b), the lowest residue occupancy of all three maximum embedding error groups. As the maximum embedding error score for these residues occurs between two allosterically bound states where the ligand is and is not present, the distinctively low percent residue composition of the APL_PL group indicates that ligand presence or absence has a very minimal impact on the electrostatic dynamics of the already effector-bound complex. In the effector-unbound complex, ligand presence has an even lower impact on redistributing the electrostatic landscape of CRIB-Par6. This is evidenced by findings that across all six possible pairwise embedding comparisons, the lowest average difference in the electrostatic network embeddings of all residues occurs between the PL and P states (PL_P) with the average embedding error between the APL and AP states (APL_AP) being the second lowest (Figure 4b). Thus, rather than ligand presence or absence being the determining factor in whether the electrostatic dynamics of CRIB-Par6 residue interactions are restructured, differences in effector presence appear most significant.

At the outset of the project, we posited the idea of considering the embedding error with PCA and heat kernels as a new approach for obtaining information about allosteric signaling in proteins, which we have tested for the PDZ system. This methodology affords insight into which residues are involved in significant electrostatic changes between the constructs. The results of the embedding error analysis between the APL and PL systems are perhaps of greatest interest as they most clearly address the question of Cdc42’s allosteric effect: how does the protein binding to the ligand by itself differ from the protein binding to the ligand with the assistance of the allosteric effector? Note that in our methodology, each pairwise analysis between states had been given equal opportunity to become the most prominent and that this was found to be the greatest by maximal embedding error falls out of the calculation directly. This suggests to us that the method provides meaningful results in a way unimpeded by the radial importance bias inherent to a global root mean square distance-based measure, nor is it affected by experimenter’s choice of residues for local alignment. Furthermore, we observe that the residues from the APL_PL maximal embedding distribute across the Par6 structure (Figure 6a) connecting key structural elements known to have functional importance, namely, the semiCRIB motif, the α1 and α2 helices, and the PLGF peptide recognition site (P38-F41). Connection with these previously described key elements further corroborates the utility of our method. It suggests that the signal traverses from the allosteric effector via the helices to the peptide recognition site via electrostatic communication.

Residues whose maximal embedding error was contributed by embedding differences between the effector-bound and ligand-bound states (AP_PL) display a characteristically localized region of occupancy across the conformationally dynamic β1−β2 loop and β2−β3 structural elements proximal to the ligand-binding site (Figure 6b). The functional importance of these regions to Par6 allostery is well established. Structuring of the CRIB domain upon Cdc42 binding leads to significant dynamical changes among β1−β2 loop residues, restricting the loop region to a set of conformations more suitable for binding to C-terminal ligands and thereby lowering the entropic cost of association.29,30,52 Moreover, rearrangements of β2−β3 regions C-terminal to the ligand binding site are implicated in PDZ ligand-binding specificity of class I C-terminal peptides53 such as VKESLV. While yielding the second highest percent residue composition of the three maximal embedding error groups (17.1%), meaningful interpretation of how the distribution of residues from the AP_PL maximal embedding error category cannot be interpreted as the effect of either Cdc42-binding interactions or ligand-binding interactions alone. The AP and PL interaction states differ by both effector (A) and ligand (L) presence rather than the presence or absence of one or the other in complex with CRIB-Par6 (P). Rather than communicating the effect of a single binding partner on redistributing residues’ electrostatic dynamics in an already occupied state, these findings seem to address Par6’s allosteric transition from the low-affinity to high-affinity state consequent of Cdc42-binding effects on ligand-binding effects. Thus, alike to the PDZ3 domain protein, the electrostatic redistributions between these AP and PL states evidence ligand-binding allostery of CRIB-Par6’s PDZ2 domain as viewed in terms of a population shift6 of specific electrostatic interactions toward a high-affinity (effector-bound) state over a low affinity state.

A theme in the allostery literature is to debate whether an observed phenomenon is a cause or an effect. Considering our results on the electrostatic networks, we can observe PDZ in the allosterically activated free (AP) and allosterically activated bound (APL) states, and nonactivated states, free (P), and bound (PL). While the networks correlate with the allosteric signaling, the constructs themselves are not sufficient to prove that the signaling was caused by the electrostatics of the protein nor can we rule out that it does. Ascertaining such information from experiments will be exceedingly difficult, and therefore, we believe computationalists have a unique vantage to provide the insight into plausible means to test hypotheses. Nonequilibrium dynamics simulation techniques may provide insight.

Conclusions

In this study, we investigated the dynamics of residues’ energetic interactions between distinct CRIB-Par6 interaction states to understand the role of energetic forces in PDZ allostery. By employing an embedding error methodology to quantify differences between residues’ energetic network embeddings, we investigated how effector and ligand-binding interactions allosterically restructure and redistribute residue–residue interactions across CRIB-Par6’s protein structure. The pairwise embedding and maximal embedding error analyses provide new insight both into the importance of the electrostatic network and the mechanism by which it occurs. We observed that distinct differences in binding-state interaction reorganize different sets of residues’ electrostatic interactions most significantly. Our findings evidence that the impact of Cdc42 allosteric activation on ligand-bound dynamics results in the most substantial redistribution in residues’ electrostatic interactions across all binding-state differences, which we have been able to enumerate at the residue level. The most substantial difference between any two interaction states in how residue’s electrostatic interactions are dynamically organized is that between ligand-bound states differing by the presence or absence of the Cdc42 effector. Furthermore, our analyses implicate the important functional role of electrostatic redistributions in conformationally dynamic regions for facilitating population shift during allosteric transitions from low to high affinity states, again which we have been able to pinpoint to the electrostatic term and report at the residue level. Importantly, our findings point toward an electrostatic basis underlying how residues’ dynamics may be functionally reorganized to facilitate changes in ligand-binding affinity as we have shown in Figure 6. Such findings may implicate viewing allosteric phenomena through long-range electrostatic redistributions as providing an essential framework through which allosteric dynamics can be understood as redistributions in the energetic landscape rather than purely entropic or enthalpic mechanisms alone.

Acknowledgments

The authors gratefully acknowledge the Molecules to Medicine consortium, especially Michael P. Weir, In Sub Mark Han, Abhilash Jayaraj, Dylan Abramson, and Theodore Sternlieb, for fruitful discussion. Bharat Lakhani generously shared PDZ trajectories. Ishita Mukerji provided useful feedback on early versions of the manuscript. We gratefully acknowledge Henk Meij’s administration of Wesleyan’s High Performance Computing facility. This work was supported by the NIH R15 GM128102-02 to K.M.T., the NIH R15 GM144870-01 to D.L.B., and NSF grants CNS-0619508 and CNS-095985 to Wesleyan University for high performance computing facilities.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.2c06546.

  • Figure S1: Constructs used in this study; Figures S2–S7: Supporting figures to PEEA analysis; Figures S8–S13: Sampling interval trial study; Table S1: Maximal embedding error groups (PDF)

  • Excel spreadsheet containing complete data set for trial of sampling frequency (XLSX)

  • Supplementary Material Method Calculations.docx: a file containing more detailed information regarding the calculation methodologies (PDF)

  • Input file for running the AMBER cpptraj program (TXT)

  • Code for generation of the tensor (PDF)

  • Code for the generation of the heat kernel (PDF)

  • Code for the generation of the Wasserstein distances (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp2c06546_si_001.pdf (1.6MB, pdf)
jp2c06546_si_003.xlsx (67.2KB, xlsx)
jp2c06546_si_004.pdf (109.7KB, pdf)
jp2c06546_si_005.txt (582B, txt)
jp2c06546_si_006.pdf (119.4KB, pdf)
jp2c06546_si_007.pdf (184.8KB, pdf)
jp2c06546_si_008.pdf (138.7KB, pdf)

References

  1. Monod J.; Wyman J.; Changeux J. P. On the Nature of Allosteric Transitions: A Plausible Model. J. Mol. Biol. 1965, 12, 88–118. 10.1016/S0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
  2. Cooper A.; Dryden D. T. Allostery without conformational change. A plausible model. Eur. Biophys. J. 1984, 11, 103–109. 10.1007/BF00276625. [DOI] [PubMed] [Google Scholar]
  3. Tsai C.-J.; del Sol A.; Nussinov R. Allostery: absence of a change in shape does not imply that allostery is not at play. J. Mol. Biol. 2008, 378, 1–11. 10.1016/j.jmb.2008.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Tsai C.-J.; Nussinov R. A Unified View of “How Allostery Works”. PLoS Comput. Biol. 2014, 10, e1003394 10.1371/journal.pcbi.1003394. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. del Sol A.; Tsai C.-J.; Ma B.; Nussinov R. The origin of allosteric functional modulation: multiple pre-existing pathways. Structure 2009, 17, 1042–1050. 10.1016/j.str.2009.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Liu J.; Nussinov R. Energetic redistribution in allostery to execute protein function. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 7480–7482. 10.1073/pnas.1709071114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Zhou H. X.; Pang X. Electrostatic Interactions in Protein Structure, Folding, Binding, and Condensation. Chem. Rev. 2018, 118, 1691–1741. 10.1021/acs.chemrev.7b00305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Warshel A. Electrostatic basis of structure-function correlation in proteins. Acc. Chem. Res. 1981, 14, 284–290. 10.1021/ar00069a004. [DOI] [Google Scholar]
  9. Perutz M. F. Electrostatic effects in proteins. Science 1978, 201, 1187–1191. 10.1126/science.694508. [DOI] [PubMed] [Google Scholar]
  10. Kumawat A.; Chakrabarty S. Hidden electrostatic basis of dynamic allostery in a PDZ domain. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E5825–E5834. 10.1073/pnas.1705311114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ho B. K.; Agard D. A. Probing the flexibility of large conformational changes in protein structures through local perturbations. PLoS Comput. Biol. 2009, 5, e1000343 10.1371/journal.pcbi.1000343. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lockless Steve W.; Ranganathan R. Evolutionarily Conserved Pathways of Energetic Connectivity in Protein Families. Science 1999, 286, 295–299. 10.1126/science.286.5438.295. [DOI] [PubMed] [Google Scholar]
  13. Peterson F. C.; Penkert R. R.; Volkman B. F.; Prehoda K. E. Cdc42 regulates the Par-6 PDZ domain through an allosteric CRIB-PDZ transition. Mol. Cell 2004, 13, 665–676. 10.1016/S1097-2765(04)00086-3. [DOI] [PubMed] [Google Scholar]
  14. Fuentes E. J.; Der C. J.; Lee A. L. Ligand-dependent dynamics and intramolecular signaling in a PDZ domain. J. Mol. Biol. 2004, 335, 1105. 10.1016/j.jmb.2003.11.010. [DOI] [PubMed] [Google Scholar]
  15. Gianni S.; Walma T.; Arcovito A.; Calosci N.; Bellelli A.; Engström A.; Travaglini-Allocatelli C.; Brunori M.; Jemth P.; Vuister G. W. Demonstration of long-range interactions in a PDZ domain by NMR, kinetics, and protein engineering. Structure 2006, 14, 1801. 10.1016/j.str.2006.10.010. [DOI] [PubMed] [Google Scholar]
  16. Harris B. Z.; Lim W. A. Mechanism and role of PDZ domains in signaling complex assembly. J. Cell Sci. 2001, 114, 3219–3231. 10.1242/jcs.114.18.3219. [DOI] [PubMed] [Google Scholar]
  17. Fan J. S.; Zhang M. Signaling complex organization by PDZ domain proteins. Neurosignals 2002, 11, 315–321. 10.1159/000068256. [DOI] [PubMed] [Google Scholar]
  18. Kong Y.; Karplus M. Signaling pathways of PDZ2 domain: a molecular dynamics interaction correlation analysis. Proteins 2009, 74, 145–154. 10.1002/prot.22139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Van den Berk L. C.; van Ham M. A.; te Lindert M. M.; Walma T.; Aelen J.; Vuister G. W.; Hendriks W. J. The interaction of PTP-BL PDZ domains with RIL: an enigmatic role for the RIL LIM domain. Mol. Biol. Rep. 2004, 31, 203–215. 10.1007/s11033-005-1407-8. [DOI] [PubMed] [Google Scholar]
  20. Gerek Z. N.; Ozkan S. B. Change in Allosteric Network Affects Binding Affinities of PDZ Domains: Analysis through Perturbation Response Scanning. PLoS Comput. Biol. 2011, 7, e1002154 10.1371/journal.pcbi.1002154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lee J.; Natarajan M.; Nashine V. C.; Socolich M.; Vo T.; Russ W. P.; Benkovic S. J.; Ranganathan R. Surface Sites for Engineering Allosteric Control in Proteins. Science 2008, 322, 438–442. 10.1126/science.1159052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lakhani B.; Thayer K. M.; Black E.; Beveridge D. L. Spectral analysis of molecular dynamics simulations on PDZ: MD sectors. J. Biomol. Struct. Dyn. 2020, 38, 781–790. 10.1080/07391102.2019.1588169. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Zhang J.; Sapienza P. J.; Ke H.; Chang A.; Hengel S. R.; Wang H.; Phillips G. N.; Lee A. L. Crystallographic and Nuclear Magnetic Resonance Evaluation of the Impact of Peptide Binding to the Second PDZ Domain of Protein Tyrosine Phosphatase 1E. Biochemistry 2010, 49, 9280–9291. 10.1021/bi101131f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Petit C. M.; Zhang J.; Sapienza P. J.; Fuentes E. J.; Lee A. L. Hidden Dynamic Allostery in a PDZ Domain. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 18249–18254. 10.1073/pnas.0904492106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Fuentes E. J.; Gilmore S. A.; Mauldin R. V.; Lee A. L. Evaluation of Energetic and Dynamic Coupling Networks in a PDZ Domain Protein. J. Mol. Biol. 2006, 364, 337–351. 10.1016/j.jmb.2006.08.076. [DOI] [PubMed] [Google Scholar]
  26. Horikoshi Y.; Suzuki A.; Yamanaka T.; Sasaki K.; Mizuno K.; Sawada H.; Yonemura S.; Ohno S. Interaction between PAR-3 and the aPKC–PAR-6 complex is indispensable for apical domain development of epithelial cells. J. Cell Sci. 2009, 122, 1595–1606. 10.1242/jcs.043174. [DOI] [PubMed] [Google Scholar]
  27. Chen J.; Zhang M. The Par3/Par6/aPKC complex and epithelial cell polarity. Exp. Cell Res. 2013, 319, 1357–1364. 10.1016/j.yexcr.2013.03.021. [DOI] [PubMed] [Google Scholar]
  28. Whitney D. S.; Peterson F. C.; Volkman B. F. A Conformational Switch in the CRIB-PDZ Module of Par-6. Structure 2011, 19, 1711–1722. 10.1016/j.str.2011.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Whitney D. S.; Peterson F. C.; Kovrigin E. L.; Volkman B. F. Allosteric Activation of the Par-6 PDZ via a Partial Unfolding Transition. J. Am. Chem. Soc. 2013, 135, 9377–9383. 10.1021/ja400092a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Whitney D. S.; Peterson F. C.; Kittell A. W.; Egner J. M.; Prehoda K. E.; Volkman B. F. Binding of Crumbs to the Par-6 CRIB-PDZ Module Is Regulated by Cdc42. Biochemistry 2016, 55, 1455–1461. 10.1021/acs.biochem.5b01342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Abramson D. I.The Colors of a Protein: Protein Dynamics Through the Lens of Spectral Graph Theory; Honors Thesis; Wesleyan University: Middletown, Connecticut, 2021. [Google Scholar]
  32. Han I. S. M.; Abramson D.; Thayer K. M. Insights into Rational Design of a New Class of Allosteric Effectors with Molecular Dynamics Markov State Models and Network Theory. ACS Omega 2022, 7, 2831–2841. 10.1021/acsomega.1c05624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vijayabaskar M. S.; Vishveshwara S. Interaction energy based protein structure networks. Biophys. J. 2010, 99, 3704–3715. 10.1016/j.bpj.2010.08.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Thayer K. M.; Lakhani B.; Beveridge D. L. Molecular Dynamics–Markov State Model of Protein Ligand Binding and Allostery in CRIB-PDZ: Conformational Selection and Induced Fit. J. Phys. Chem. B 2017, 121, 5509–5514. 10.1021/acs.jpcb.7b02083. [DOI] [PubMed] [Google Scholar]
  35. Verkhivker G. M.; Agajanian S.; Hu G.; Tao P. Allosteric Regulation at the Crossroads of New Technologies: Multiscale Modeling, Networks, and Machine Learning. Front. Mol. Biosci. 2020, 7, 136. 10.3389/fmolb.2020.00136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ballester P. J.; Mitchell J. B. O. A machine learning approach to predicting protein–ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. 10.1093/bioinformatics/btq112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Brinda K. V.; Vishveshwara S. A Network Representation of Protein Structures: Implications for Protein Stability. Biophys. J. 2005, 89, 4159–4170. 10.1529/biophysj.105.064485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ghosh A.; Vishveshwara S. Variations in clique and community patterns in protein structures during allosteric communication: investigation of dynamically equilibrated structures of methionyl tRNA synthetase complexes. Biochemistry 2008, 47, 11398–11407. 10.1021/bi8007559. [DOI] [PubMed] [Google Scholar]
  39. Del Sol A.; O’Meara P. Small-world network approach to identify key residues in protein-protein interaction. Proteins 2005, 58, 672–682. 10.1002/prot.20348. [DOI] [PubMed] [Google Scholar]
  40. Ricci C. G.; Silveira R. L.; Rivalta I.; Batista V. S.; Skaf M. S. Allosteric Pathways in the PPARγ-RXRα nuclear receptor complex. Sci. Rep. 2016, 6, 19940. 10.1038/srep19940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Rivalta I.; Sultan M. M.; Lee N.-S.; Manley G. A.; Loria J. P.; Batista V. Allosteric pathways in imidazole glycerol phosphate synthase. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, E1428–E1436. 10.1073/pnas.1120536109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Hertig S.; Latorraca N. R.; Dror R. O. Revealing Atomic-Level Mechanisms of Protein Allostery with Molecular Dynamics Simulations. PLoS Comput. Biol. 2016, 12, e1004746 10.1371/journal.pcbi.1004746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Liu Z.; Chen J.; Thirumalai D. On the accuracy of inferring energetic coupling between distant sites in protein families from evolutionary imprints: Illustrations using lattice model. Proteins 2009, 77, 823–831. 10.1002/prot.22498. [DOI] [PubMed] [Google Scholar]
  44. Case D. A.; Cheatham T. E. 3rd.; Darden T.; Gohlke H.; Luo R.; Merz K. M. Jr.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Ma C.; Chung D. J.; Abramson D.; Langley D. R.; Thayer K. M. Mutagenic Activation of Glutathione Peroxidase-4: Approaches toward Rational Design of Allosteric Drugs. ACS Omega 2022, 7, 29587. 10.1021/acsomega.2c01289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. ElGhawalby H.; Hancock E. R. Heat Kernel Embeddings, Differential Geometry and Graph Structure. Axioms 2015, 4, 275–293. 10.3390/axioms4030275. [DOI] [Google Scholar]
  47. Ramdas A.; Garcia N.; Cuturi M. On Wasserstein Two Sample Testing and Related Families of Nonparametric Tests. Entropy 2017, 19, 47. 10.3390/e1902004. [DOI] [Google Scholar]
  48. Van Rossum G.; Drake F. L.. Python 3 Reference Manual; CreateSpace, 2009. [Google Scholar]
  49. Kluyver T.; Ragan-Kelley B.; Pérez F.; Granger B.; Bussonnier M.; Frederic J.; Kelley K.; Hamrick J.; Grout J.; Corlay S.; Ivanov P.; Avila D.; Abdalla S.; Willing C. In Jupyter Notebooks – a publishing format for reproducible computational workflows; Loizides F.; Schmidt B., Eds.; IOS Press, 2016; pp 87–90. [Google Scholar]
  50. Bastian M.; Heymann S.; Jacomy M.. Gephi: An Open Source Software for Exploring and Manipulating Networks, 2009.
  51. Doyle D. A.; Lee A.; Lewis J.; Kim E.; Sheng M.; MacKinnon R. Crystal structures of a complexed and peptide-free membrane protein-binding domain: molecular basis of peptide recognition by PDZ. Cell 1996, 85, 1067–1076. 10.1016/S0092-8674(00)81307-0. [DOI] [PubMed] [Google Scholar]
  52. Joberty G.; Petersen C.; Gao L.; Macara I. G. The cell-polarity protein Par6 links Par3 and atypical protein kinase C to Cdc42. Nat. Cell Biol. 2000, 2, 531–539. 10.1038/35019573. [DOI] [PubMed] [Google Scholar]
  53. Gerek Z. N.; Keskin O.; Ozkan S. B. Identification of specificity and promiscuity of PDZ domain interactions through their dynamic behavior. Proteins 2009, 77, 796–811. 10.1002/prot.22492. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp2c06546_si_001.pdf (1.6MB, pdf)
jp2c06546_si_003.xlsx (67.2KB, xlsx)
jp2c06546_si_004.pdf (109.7KB, pdf)
jp2c06546_si_005.txt (582B, txt)
jp2c06546_si_006.pdf (119.4KB, pdf)
jp2c06546_si_007.pdf (184.8KB, pdf)
jp2c06546_si_008.pdf (138.7KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES