Reproducing the Ensemble Average Polar Solvation Energy of a Protein from a Single Structure: Gaussian-Based Smooth Dielectric Function for Macromolecular Modeling

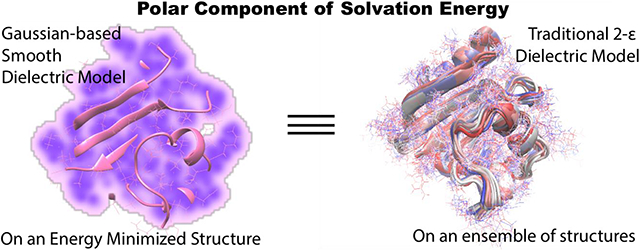
Abstract

Typically, the ensemble average polar component of solvation energy $(\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}})$ of a macromolecule is computed using molecular dynamics (MD) or Monte Carlo (MC) simulations to generate conformational ensemble and then single/rigid conformation solvation energy calculation is performed on each of snapshots. The primary objective of this work is to demonstrate that Poisson-Boltzmann (PB) based approach using a Gaussian-based smooth dielectric function for macromolecular modeling previously developed by us (Li et al. J Chem Theory Comput 2013, 9 (4), 2126-2136) can reproduce the ensemble average $(\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}})$ of a protein from a single structure. We show that the Gaussian-based dielectric model reproduces the ensemble average $\Delta G_{polar}^{solv}\left(\langle \Delta G_{polar}^{solv}\rangle \right)$ from an energy minimized structure of a protein regardless of the minimization environment (structure minimized in vacuo, implicit or explicit waters or crystal structure), the best case, however, is when it is paired with an in vacuo minimized structure. In other minimization environments (implicit or explicit waters or crystal structure) the traditional two-dielectric model can still be selected with which the model produces correct solvation energies. Our observations from this work reflect how the ability to appropriately mimic the motion of residues, especially the salt-bridges residues, influences a dielectric model’s ability to reproduce the ensemble average value of polar solvation free energy from a single in vacuo minimized structure.

Graphical Abstract

Introduction:

Implicit solvent models provide time-efficient alternatives to the explicit models for calculating solvation energy of biological macromolecules. By “integrating out” the solvent degrees of freedom present in the explicit solvent setup, they describe the solvent as a continuum structure-less phase with a high dielectric constant¹, while the solute region is assigned a lower dielectric constant value. As a result, these models can gain much higher speed than the explicit models depending on the phenomena under consideration, the design of the system and the nature of the implicit solvent model². In addition, numerous published works have shown that the results delivered by implicit models are very similar to that from the explicit models^3-9. Ranging from protein design and structure prediction^10-11, pH-based simulations^12-13 and pK_a predictions^14-15 to being able to model electrostatic contribution to binding^16-18, folding^19-20 and solvation^21-23 of macromolecules and several other examples²⁴, the implicit models have proven to be an indispensable tool for computational research in biology and chemistry. Implicit solvent models have also been shown to bypass the sensitivity issue concerning free energy calculations with different explicit water models²⁵.

In implicit solvent models, the biological macromolecule is represented with atomistic level of details while water phase is a continuum medium as opposed to the completely explicit models (the solute and water are treated explicitly). The solvation energy (the polar component only) in the implicit solvent models is calculated via Poisson-Boltzmann (PB) or Generalized Born (GB) approaches. These approaches, in particular PB, were shown to deliver almost identical polar solvation energy as the expensive thermodynamic integration (TI)^6-7 or Free energy perturbation (FEP)^4-5 when the macromolecule was kept rigid (single solute conformation). However, macromolecules are not rigid objects and they undergo small or large conformational changes while being transferred from one medium to another. Disregarding this can cause severe errors in predictions of solvation free energies²⁶.

Currently, a popular approach in the community to compute the average solvation energy has been to carry out a molecular dynamics (MD)/Monte Carlo(MC) simulation and obtain a representative ensemble of structures (snapshots) and then perform TI, FEP or Bennett Acceptance Ratio (BAR) calculations on each of the snapshots (while keeping each of them rigid)^{3, 5, 8}. But these methods are extremely demanding of computational time and resources, since a typical ensemble may consist hundreds or thousands of snapshots. One can, alternatively, also subject these snapshots to PB modeling and obtain the corresponding polar solvation energy (as mentioned above). The calculated polar solvation energies together with non-polar solvation energies delivered from surface area/volume of individual snapshots are expected to represent an experimentally measured solvation energy. Such an approach is an essential component of energy calculations employing molecular mechanics Poisson-Boltzmann surface area (MM/PBSA)²⁷ and molecular mechanics Generalized Born surface area (MM/GBSA)²⁸ methods. However, the bottleneck of MM/PBSA and MM/GBSA approaches is the generation of representative ensemble of structures, which is very expensive computationally, especially if applied for large scale modeling.

As an alternative to explicit modeling of conformational changes, one can also mimic the effect of these changes on the solvation energy via appropriate dielectric constant of the macromolecule. Dielectric distributions affect the structure-energy relations via screening of the electrostatic interactions within the solute and between the solute and solvent^29-30. However, as mentioned above, biological macromolecules are not rigid bodies and experimentally observable quantities are ensemble averaged. The traditional two-dielectric PB calculations cannot mimic these conformational changes within an ensemble because it uses homogeneous dielectric constant for macromolecule and water phase. This drawback has motivated the idea and usage of heterogeneous dielectric distributions^31-36. They have shown to yield better predictions for protein folding¹⁹ and binding free energies¹⁶ when benchmarked against experimental data while at the same time, they can also reveal the effects of mutations on these processes³⁷.

With the objective of mimicking conformational flexibility via dielectric properties of macromolecules, Li et al.³⁸ developed a Gaussian-based smooth dielectric model and implemented this in the popular PB-equation solver DelPhi³⁹. This model delivers a smooth and heterogeneous dielectric distribution in the solvated system which accounts not only for the conformational flexibility of the solute but also the differential dielectric properties of the solvent phase in the proximity of solute. The necessity of such a differential treatment of the solvent is evident from the works of Ref.^40-41 that show that the water molecules which lie close to the solute “boundary” and in the cavities within the solute feature different dielectric responses and dynamics than those far out in the bulk region. This model has yielded successful predictions for pK_a of protein and nucleic acid residues¹⁵ and solvation energies of small molecules²³, agreeable with corresponding experimental measurements while also reproducing the average dielectric distribution of proteins as observed from molecular dynamics (MD) simulations³⁴. A recent work has also enabled the Gaussian-based model to incorporate the effects of mobile ions despite the absence of strict solute-solvent boundaries⁴² (a necessity intrinsic to the implementation of the traditional 2-dielectric PB models).

In this work, we have carried out an extensive investigation of the ability of the Gaussian-based smooth dielectric function to mimic the conformational flexibility, and as a result, deliver the average polar component of solvation energy of a protein from a single structure, determined otherwise from gathering an ensemble of thermodynamically weighted structures via MD/MC simulations and performing individual snapshot calculations^{28, 43-44}. The latter is a time-consuming process regardless of the solvent model being used. The primary goal was to be able to render this average computationally, by incorporating the effects of the aforementioned dynamics while still preserving the time efficacy of the implicit solvent models, and thus to serve as a starting point for developing a fast and efficient single structure MM/PBSA method. For this purpose, 74 representative proteins from the Protein Data Bank (PDB)⁴⁵ were used and a set of protocols were rigorously tested to ascertain the best way to achieve the goal. A detailed study of the model and the underlying physical principles reveals that the Gaussian-based method in conjunction with an energy minimized structure of a protein (regardless of the minimization environment) can reproduce its ensemble average polar solvation energy obtained from explicit water MD. In contrast, the traditional method can do so only if the crystal structure or a solvent-minimized structure is used. But there are some demerits associated with it. The outcome of this work provides a convenient option enabling computation of the average polar contribution to the solvation energy which can circumvent the time-consuming ensemble-based calculations.

Methods:

Set of representative proteins:

Protein structures for this work were obtained from the PDB⁴⁵. To obtain a dataset of reasonable size that can be managed in parallel with extensive MD simulations data, the resolution of the structures was limited between 0.8 and 0.99 Å with at most 200 amino acids. Besides we required the structures to be monomeric. The proteins retrieved were required to have at most 30% sequence similarity. In addition, it was ensured that these structures did not contain a ligand or modified residue. This search yielded 74 globular proteins from the PDB (as of April 29, 2017). These proteins were used as representatives for our investigation and their PDB IDS are listed in the Supporting information (SI).

Structure preparation:

The protein structures were prepared for MD simulations using GROMACS v5.0.5⁴⁶ with atomic parameters of the AMBER99SSB⁴⁷ force field. All the titratable residues were kept in their charged states. To build the explicit water solvated systems, these structures were solvated using TIP3P water molecules⁴⁸ and ions were added wherever neutralization was needed.

Energy minimization in explicit water, implicit solvent and in vacuo environments:

The explicit water solvated systems were subjected to 10,000 steps of steepest descent (SD) energy minimization using GROMACS v5.0.5⁴⁶. The heavy atoms were harmonically restrained to their original positions with a force of 1000 kJ mol⁻¹nm⁻¹ while everything else in the system was set free to move.

Two other minimizations, involving only the protein structures, were also carried out. These were performed in vacuo and Generalized Born Implicit Solvent (GBIS)⁴⁹ environments. Only 5000 SD steps were used since the system size was drastically smaller than the explicit water systems. For both of these cases, cutoffs for the non-bonded interactions were lifted but all the heavy atom harmonic restraints were retained. For GBIS minimization, the external dielectric was set at 80.0 (emulating water environment) and that for in vacuo was 1.0. The parameters for minimizations are provided in Supporting Information (SI).

MD simulations:

Post energy minimization, only the explicit water solvated systems were subjected to 3 independent MD simulations for 20ns each (with different initial atomic velocities) to allow versatility in the resulting ensemble of structures. Prior to production phase of the MD, they were equilibrated under constant volume-temperature (NVT) conditions for 500ps (with heavy atoms harmonically restrained) followed by 2000ps (=2ns) of constant pressure-temperature (NPT) equilibration at 300K temperature and 1 atm pressure (with the same restraints). In the 20ns MD that followed, the restraints were lifted. The initial 10ns of was discarded as they were considered to not have equilibrated yet. The structures for analysis were sampled from the last 10ns at every 10ps. This yielded 1000 snapshots per MD run, all of which were subjected to PB based solvation free energy calculation after stripping off the explicit water molecules (and ions for neutralization wherever present). For all the equilibrations and MD, particle mesh Ewald (PME)⁵⁰ based electrostatic calculations were invoked in conjunction with periodic boundary conditions. The parameter configurations for equilibration and MD are provided in the Supporting information (SI).

Ensemble average polar solvation energy via PB based calculations vs alchemical MD methods.

Three independent MD simulations in explicit water rendered 3000 thermodynamically weighted configurations per protein⁴³, which we shall refer to as its ensemble. For each member of the ensemble, the polar component of the solvation free energy $(\Delta G_{polar}^{solv})$ was computed to obtain ensemble average^{28, 51-52}. The method used for this purpose requires an explanation, which is provided below.

Ideally to compute the $\Delta G_{polar}^{solv}$ for a molecule, alchemical free energy calculation methods in explicit solvent setups are preferred. Thermodynamic integration based molecular dynamics (TI-MD) is an example of such a method. Authors of Ref.^6-7 have calculated the polar component of the solvation free energy of 19 proteins using TI-MD. These values were computed by fixing the protein’s structure in space and coupling the partial atomic charges to a coupling parameter ‘λ’ which was varied from 0 to 1. As the protein’s electrostatic properties traverses a set of alchemical intermediate states due to λ, the energy cost associated with it in the presence of explicit water molecules is calculated and eventually summed up to render the total solvation energy (polar + non-polar component). Should the protein structure be allowed to move, the resultant energy cost would include effects of protein molecular mechanical energies which cannot be resolved to get the exclusive polar solvation energy. This procedure can be iteratively applied on each “snapshot” of an ensemble (from MD/ Monte Carlo) to determine the ensemble solvation energy. However, as mentioned in Introduction section, this can be very time consuming.

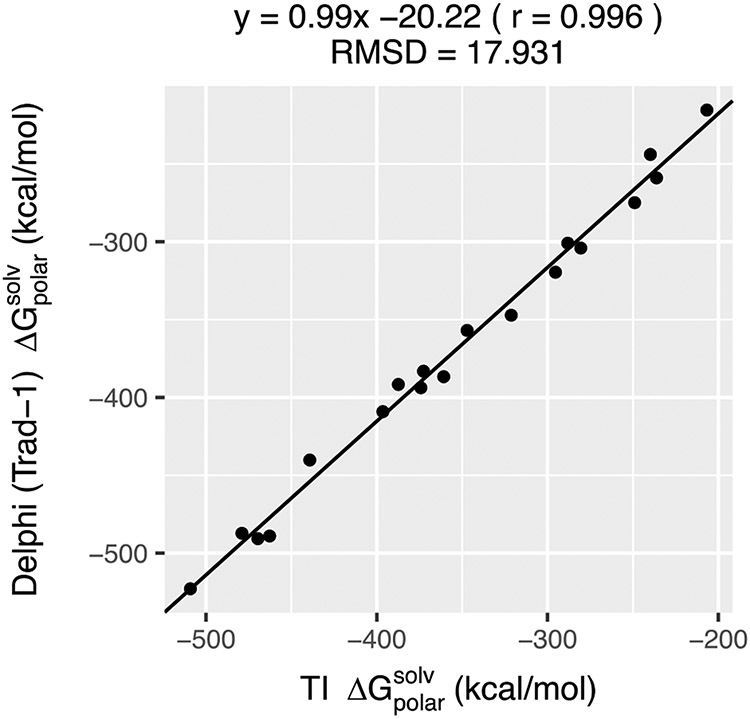
Delphi³⁹ calculates and outputs the polar component of solvation energy of a “snapshot”, which is termed “reaction field energy” (for the sake of completeness, in the Supporting information (SI) we demonstrate that DelPhi reaction field energy delivers polar solvation energy which matches the analytical Born Approximation for simple ions, see Figure S1) . To examine if the PB-based calculations provide similar or identical polar solvation energies as TI-MD, we computed the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ for the 19 proteins used by the authors of the aforementioned work^6-7 while preserving the structural coordinates, charges and radii the way they were used by them. A scale of 2.0 grids/Å, a ‘perfil’ of 70 and the traditional 2-dielectric method was used while setting the protein internal dielectric to 1.0 and solvent dielectric to 80.0. The $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ values from both methods are compared (Figure 1). It is evident that Delphi is able to yield $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ almost precisely identical to that obtained by TI-MD in explicit water (correlation = 0.99 and RMSD = 17.93 kcal/mol). This reinforces our claim that, provided the structures are rigid, PB calculations with Delphi (with protein internal dielectric=1 and solvent dielectric = 80) can deliver $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ that would otherwise require a much longer TI-MD runs. Therefore, by using Delphi with the above protocols to calculate $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ for each “snapshot”, the ensemble polar solvation energy was calculated in a manageable time.

Figure 1:

The comparison of the polar solvation energies of 19 net-neutral proteins obtained from explicit solvent thermodynamic integration (TI) simulations and implicit solvent Poisson-Boltzmann (PB) calculations using the traditional 2-dielectric model with Delphi. For both the cases, the corresponding structures were kept rigid. The TI simulations were performed by the authors of Ref^6-7. The Pearson correlation (r) and RMSD (in kcal/mol) of the comparison are also mentioned.

Polar Solvation energy of energy minimized structures:

For each of the protein energy minimized (EM) structures (minimized in 3 different environments), $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ was computed using the traditional 2-dielectric model as well the Gaussian-based smooth dielectric model38. With a scale of 2.0 grids/Å, a ‘perfil’ of 70 was used for the former and that of 50 was used for the latter. For the Gaussian-model, a ‘sigma’ = 0.93 was applied. The meaning of these parameters and the use of the aforementioned specific values can be found in the Delphi user-manual(compbio.clemson.edu/downloadDir/delphi/delphi_manual.pdf). For all the calculations, the probe radius was set at 1.4 Å with zero electrolyte concentration and the external dielectric constant was set to 80 (emulating water environment). The boundary potentials were determined using the dipole method (refer to the Delphi Manual).

In the rest of the manuscript, all the PB calculations performed using the traditional 2-dielectric method will carry a label ‘TRAD-x’ and that for the Gaussian-based smooth dielectric method will carry a label ‘GAUSS-x’. ‘x’ in these labels indicate the protein internal dielectric constant. For instance, ‘TRAD-1’ and ‘GAUSS-1’ will identify as the corresponding methods with protein internal dielectric set at 1.

Modified Gaussian-based smooth dielectric model in Delphi:

A modification was incorporated in the algorithm that computes the polar solvation energy (frequently referred as the reaction field energy) using the Gaussian-based smooth dielectric function in Delphi. The key idea of the Gaussian-based approach is that a strict surface doesn’t separate the solute interior from the external medium, as is assumed in the traditional 2-dielectric models. Using the 3D distribution of the atomic packing densities (modeled as Gaussian, and hence the name), a Gaussian-based smooth dielectric function is derived using the formula:

$$\epsilon (\mathbf{r})={\epsilon }_{\text{ref}}({\rho }_{\text{in}})+{\epsilon }_{\text{solv}}(1-{\rho }_{\text{in}})$$ (1)

This delivers a position-dependent dielectric distribution (ε(r)) when the solute is present in a medium of dielectric constant ‘ε_solv.’ The atomic packing density (ρ_in) is normalized to 1; it is 1 at the atom centers and fades to zero in farther regions. The internal reference dielectric value ϵ_ref is used to assign an inhomogeneous dielectric distribution unlike the traditional 2-dielectric model. This details can be found in our previous work³⁸.

In the original implementation of the Gaussian-based model in Delphi, the polar component of solvation energy is calculated by taking the difference of the grid energies obtained from modeling a solute in (i) external solvent medium (medium-1) and (ii) medium with dielectric constant same as the internal dielectric constant (medium-2). However, this requires building a surface between solute and medium-2, a surface that does not exist in surface-free approach of the Gaussian-based model and therefore is artificially drawn when calculating grid energies in medium-2. For that a user-specified dielectric value is used to delineate the surface (‘SRFCUT’ in Delphi input).

In this work, we make two-fold modifications. First, the “surface” is drawn not based on a dielectric value but on the atomic density value (ρ_SF). This is done to fix the solute “volume” regardless of the ϵ_ref value of the internal reference dielectric constant since different ‘ε_ref’ can influence the position of the dielectric-based surface but not that of a density-based surface. In this work, we used the atomic density value of 0.759, which corresponds to a dielectric of 20 for ϵ_ref = 1. Second, we model a smoother transition from this “surface” to the external region for medium-2 using an exponential function. By fixing the medium-2 as vacuum (ϵ₂ = 1), the smoothing term secures the surface-less approach of the Gaussian-based model to a great extent. This results in the following dielectric distribution when the external medium is vacuum:

$$\begin{gathered} if{\rho }_{in}(\mathit{r})\ge {\rho }_{SF}:{\epsilon }^{\prime }(\mathbf{r})=\epsilon (\mathbf{r}) \\ if{\rho }_{in}(\mathit{r})<{\rho }_{SF}:{\epsilon }^{\prime }(\mathbf{r})=1+(\epsilon (\mathbf{r})-1)e^{-({\rho }_{in}(\mathit{r})-{\rho }_{SF})({\epsilon }_{ref}-{\epsilon }_{solv})} \end{gathered}$$ (2)

Here, ε’(r) is the dielectric value of a 3D point when the solute is present in vacuum and ε(r) is the dielectric value assigned to that point when the protein’s presence in solvent was modelled (refer to equation 1). This form ensures that far away from the surface, the dielectric value is close to 1 and near the surface, it is close to the value that corresponds to ρ_SF. The above schematic is shown as supporting information (see Figure S2) for an arbitrary placement of atoms along a single dimension. This density based surface cut off option is now available in DelPhi http://compbio.clemson.edu/delphi.

Results and Discussion:

In this work, we investigate the ability of a single structure (subjected to various energy minimization protocols) in conjunction with different dielectric models to reproduce the ensemble average polar component of solvation energy. We show that the ability to mimic fluctuation of residues, especially the charged ones that form salt-bridges, plays a significant role in providing a particular dielectric model an advantage over the other. We provide a justification for our observations and eventually discuss their physical underpinnings. Based on these observations and physical understandings, we finally suggest the best set of protocols to capture the effects of dynamics through implicit solvent modeling using a single structure to deliver polar component of solvation energy.

In Vacuo energy minimized structure paired with Gaussian-based smooth dielectric distribution can best reproduce the ensemble $\langle \Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}\rangle$

The $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ of the protein structures obtained after minimization in three different environments - in vacuo, Generalized Born Implicit Solvent (GBIS) and explicit water (TIP3P), were compared with the ensemble average polar solvation energy, $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ (procedure outlined in the Methods). For the sake of completeness, the crystal structure of the proteins was also subjected to this comparison. The crystal structures were, first protonated and then energy minimized while its heavy atoms were heavily restrained (force constant of 1e6 KJ mol⁻¹nm⁻²) to keep the backbone atoms positions unchanged. We shall refer to these structures as optimized crystal structures in the paper.

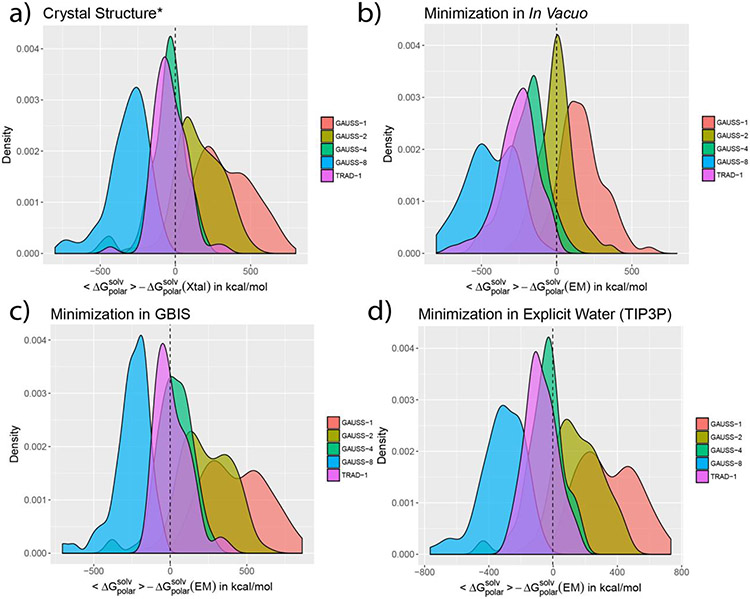
The results of these comparisons are shown in terms of probability distribution of the differences of ensemble average $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ and the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ of the EM and optimized crystal structures (Figure 2). In the figure, the difference $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle -\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)$, extends to both negative and positive values. Since both $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)$ and $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ are negative, it is vital to understand how these differences should be interpreted. A negative difference implies $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle <\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)$, depicting that the ensemble average is more negative than the polar solvation energy of the EM structure. In terms of magnitudes, the EM structure $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ is smaller than the $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ (underestimation). On the other hand, a positive difference implies $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle >\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)$, i.e. the ensemble average is less negative than the corresponding polar solvation energy form the EM structure. Magnitude wise, the EM structure $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ is larger than the $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ (overestimation). Therefore, if $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle -\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)\approx 0$, such a case successfully reproduces ensemble average using a EM structure alone. With this, we now turn to describing the trends observed in Figure 2.

Figure 2:

The density distribution of the difference $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle -\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)$ are shown for a) crystal (aka. Xtal) structure (* added protons are optimized) and structures minimized b) In Vacuo c) in GBIS and d) in explicit solvent (TIP3P). The labels ‘TRAD-x’ and ‘GAUSS-x’ indicate the traditional 2-dielectric and Gaussian-based smooth dielectric distributions, respectively. ‘x’ is the protein’s internal dielectric value. The dashed vertical line is at the zero mark in each plot.

Both, Gaussian-based (GAUSS) and traditional (TRAD) dielectric models were used with the optimized crystal and EM structures to compare with $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$. For the former, values of 1, 2, 4 and 8 were used as internal reference dielectric constant. For the latter, only a single value (=1) was used because values larger than 1 resulted in highly underestimated $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ with respect to the ensemble averaged $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$. In Figure 2, a visual inspection reveals that the traditional dielectric model (TRAD-1) has a very similar degree of agreement with the $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ when paired with the optimized crystal structure (Figure 2a) and structures optimized in solvent (Figure 2c, 2d). With the in vacuo optimized structure, the trend is conspicuously different (Figure 2b). Quantitatively, when expressed in terms of the mean relative unsigned error, the best agreement is attained by the GBIS minimized structures, followed by the optimized crystal structure and structure minimized in explicit solvent (see Table 1). It can, therefore, be tempting to use the GBIS minimized structure of a protein with the traditional model (internal ϵ) to obtain its ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$. However, it must be done with caution. This is because the low relative mean error value is a statistical result and when it comes to individual proteins, as the plots suggest, some of them feature an underestimation of $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle (\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle -\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)<0$; left of the black lines in Figure 2). To attain a better agreement, these cases demand that the internal ϵ be less than 1. Such a modification is physically unreasonable. In fact, such an underestimation is true for the majority of proteins regardless of the environment of optimization (see Table 2).

Table 1:

Average relative error and average absolute error from the ensemble average polar solvation energy, $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$, of that from the optimized crystal and energy minimized structures.

Minimization Environment	Dielectric distribution model
	TRAD-1	GAUSS-1	GAUSS-2	GAUSS-4	GAUSS-8
Crystal Structure *	5.59% a (90.90) b	19.34% (338.14)	10.35% (180.00)	5.31% (94.06)	18.09% (312.99)
In Vacuo	15.26% (262.13)	10.55% (179.48)	5.13% (85.01)	11.52% (206.69)	25.76% (449.86)
GBIS	5.14 % (85.71)	24.82 % (432.90)	14.41% (248.53)	5.16% (92.97)	14.50% (250.07)
Explicit Water (TIP3P)	6.21% (101.12)	20.07% (348.26)	10.16% (174.61)	5.30% (92.72)	18.18% (315.74)

^*After optimizing the added hydrogens while restraining the heavy atoms in the crystal structure with a force constant of 1e6 KJ mol⁻¹nm⁻².

^aMean relative unsigned error

^bIn the parentheses, average absolute error (in kcal mol⁻¹).

Table 2:

The percentage of cases (out of the 74 proteins) where the difference in the ensemble average polar solvation energy and polar solvation energy of optimized crystal and EM structure obtained using TRAD-1 dielectric method is negative. The difference is expressed as $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle -\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)$. These cases would require decreasing the protein internal dielectric below 1 to correct for the error incurred by the TRAD-1 model, which is physically invalid.

Minimization Environment	% cases where $\mid \langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle \mid >\mid \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(EM)\mid$
Crystal Structure	66.22 %
In Vacuo	100.00 %
GBIS	54.05%
Explicit Water (TIP3P)	78.34 %

At the same time, the Gaussian-based dielectric model reveals a better agreement with the ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$. This is also inferable visually from the figure, owing to the close placement of the peaks of the error distribution plots to the zero line. Unlike the traditional method, the Gaussian-based model offers a good match regardless of the minimization protocol. Quantitatively, the mean relative unsigned error varies depending on the ϵ_ref value used for a particular Gaussian-based model but there is always a case for all of the optimization environments where the mean relative unsigned error ≈ 5% (Table 1). For instance, GAUSS-4 has an error comparable to and better than what the TRAD-1 incurs for the optimized crystal structure and structures optimized in solvent. GAUSS-2 with in vacuo minimized structures, moreover, not only offers a better agreement with $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ than the TRAD-1 model but it offers the best agreement amongst all the cases (lowest mean relative unsigned error; 5.13%). Furthermore, with minor adjustments of the input parameters for the Gaussian-based model in Delphi (see Delphi Manual), one can tune the degree of agreement. This circumvents the problem of having to use unreasonable dielectric values for proteins, unlike the traditional method. Therefore, the in vacuo minimized structure, when paired with the Gaussian-based dielectric model, can offer the best approximation to the ensemble average polar solvation energy.

Before delving into extensive analyses of the factors that influence the performance of the dielectric models, it is important that we address some of these trends observed for the traditional and Gaussian-based dielectric models in detail.

Observations in Figure 2 indicates differences in the behavior of the traditional dielectric model (ϵ_in = 1; ϵ_out = 80) when used with differently optimized structures. From the traditional model, the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ of the optimized crystal or solvent-minimized structures is in good agreement with the $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ but that from the in vacuo EM structure is significantly underestimated. This can be understood as follows.

Upon a pairwise comparison of $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ from TRAD-1 model, the following trend was observed:

$$\Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}(\mathit{In}\mathit{Vacuo})>\left(\Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}(\mathit{Xtal})\approx \Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}(\mathit{TIP}3\mathit{P})>\Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}(\mathit{GBIS})\right)\approx \langle \Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}\rangle$$ (3)

When these comparisons were extended to protein coulombic energies, the following was seen (protein dielectric = 1.0).

$${\mathit{U}}_{\mathit{coul}}(\mathit{In}\mathit{Vacuo})<\left({\mathit{U}}_{\mathit{coul}}(\mathit{Xtal})\approx {\mathit{U}}_{\mathit{coul}}(\mathit{TIP}3\mathit{P})<{\mathit{U}}_{\mathit{coul}}(\mathit{GBIS})\right)\approx \langle {\mathit{U}}_{\mathit{coul}}\rangle$$ (4)

A clear reversal of the trend in Equation 3 is seen in Equation 4. Furthermore, Figure S4 illustrates this comparison qualitatively as well as quantitatively. One can notice the differences of U_coul and $\Delta G_{polar}^{solv}$ of solvent-minimized (and optimized crystal) structures calculated w.r.t the in vacuo minimized structure. The opposite trends of comparison for these energy terms are evident. This is because a molecular structure with a high negative value of coulombic energy almost certainly contains oppositely charged particles placed more closely than in a structure with a less negative U_coul. The former stabilizes the packing in the gas phase, but reduces interactions with water. This loss in favorability towards solvation comes from the closely placed charges of opposite polarities forming a very small dipole. The smaller dipole consequently “annihilates” the atomic charges, thus compromising the favorable electrostatic interaction that could have existed with the polar solvent. As a result, the solvation is unfavorable relative to a configuration with a higher (less negative) U_coul. The less favorability of solvation of smaller dipoles can be conjectured from simple spherical models. For instance in Figure S1c of the supporting information, smaller separation of opposite charges (2 Å) has a less negative $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ than a larger one (3 Å) regardless of the cavity dielectric. Since the in vacuo EM structures are likely to have oppositely charged atoms (or residues) placed more closely due primarily to the absence of any de-solvation, they feature more negative U_coul and therefore, relatively less favorable $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$. The other configurations incur the effects of the solvent and consequently have a less negative U_coul but a more favorable $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$. This validates the good agreement that structures minimized in solvent have with the ensemble average, in terms of $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ computed using traditional dielectric model. This is because the ensemble comprises of configurations generated in an explicit solvent environment (see Methods).

The inherent heterogeneity of the dielectric distribution underlying the Gaussian-based model complicates the above analysis provided for the traditional method. Not only does the formulations for the coulombic energy become non-trivial, it is practically difficult to exactly pinpoint a surface that segregates the solute region from the solvent due to its surface-free nature³⁸. This precludes a simple interpretation of the trends of $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ obtained from the Gaussian model. Nonetheless, the Gaussian model preserves the general trend of the effects of dielectric constant on the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$, i.e. increasing the solute dielectric decreases the latter’s absolute value. This is apparent from the density plots in Figure 2 where increasing the ϵ_ref of the Gaussian model shifts the peak to the left of the zero-mark, indicating that the deviation from the ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ increases, or that the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ becomes less negative. These trends are separately depicted in the Figure S3 in SI, that compare how the solute internal dielectric affects $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ for the two dielectric models. This inverse relation of the solute dielectric and $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ prevails in systems as simple as a dipole embedded in a spherical cavity where the increase of the cavity dielectric decreases $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ value (Figure S1c, S1d). Underlying this relationship is the fact that an increased solute dielectric increases the screening of the interaction of solute dipoles with water phase, thus making solvation less favorable.

Figure 2 also indicates that using the same value for GAUSS’s ϵ_ref and TRAD’s ϵ_in yields a more negative value for the former. This is because the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ calculated with Gaussian-based smooth dielectric model (as implemented in Delphi) depends not only on the reference value of internal dielectric constant (ϵ_ref), but also on the “surface” that separates the solute from the external medium. The numerical demarcation of this “surface”, drawn based on a cut-off of effective dielectric value (iso-dielectric surface, SURFCUT)³⁸ or effective atomic density (iso-density surface, ρ_SF) results in solute-solvent (solute-vacuum) interface being places, in some regions, slightly inside the traditional molecule surface. This decreases its effective size of the solute thus making the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ more negative than what the traditional 2-dielectric model would deliver.

In the next sections, we discuss various structural factors that mostly influence the ability of the two dielectric models to reproduce ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ from a single structure. Since the objective of this work was to render a method that will incur the least error in this process, GAUSS-2 (with in vacuo EM structure) model will be of primary focus. We will compare its outputs with that of the traditional method and elaborate on their differences.

Differences in the population of salt-bridges (SBs) directly affect the differences in $\Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}$ using traditional method across different EM structures of a protein.

Our results indicate that a Gaussian-based smooth dielectric distribution (GAUSS-2) in conjunction with in vacuo minimized structure reproduces the ensemble average, $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$, with smallest mean relative unsigned error (Table 1). They also indicate that $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ for optimized crystal or EM structures obtained with different dielectric models exhibit different but reasonably good agreements when compared with ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$. To determine the causes for these differences, we tested and compared several structural properties of the minimized structures that correlate with it. Note that since the solvation properties of optimized crystal structure and the structure minimized in explicit solvent are almost identical, any observation associated with the latter applies to the former equally well.

It is well known that constant breaking and forming of salt bridges is a salient feature of protein dynamics^53-55 and their dynamics affects the dielectric distribution of the protein interior^{34, 56}. For our purposes, the fluctuation between the closed/open forms of a SB is quantified in terms of occupancy. Occupancy is defined as the percent of the 3000 configurations (of the host protein) wherein the SBs were closed (O-N distance < 3.4 Å). Therefore, a SB with a 100% occupancy is never found to be broken in the ensemble while one with 0% occupancy is only identified in the minimized structure but never in the ensemble. Anything in between should be interpreted likewise. That the SB pairs identified across all the 74 proteins featured fluctuations, is evident from the histogram of occupancies in Figure S5 in SI, where occupancies pervade all the values from 0-100%.

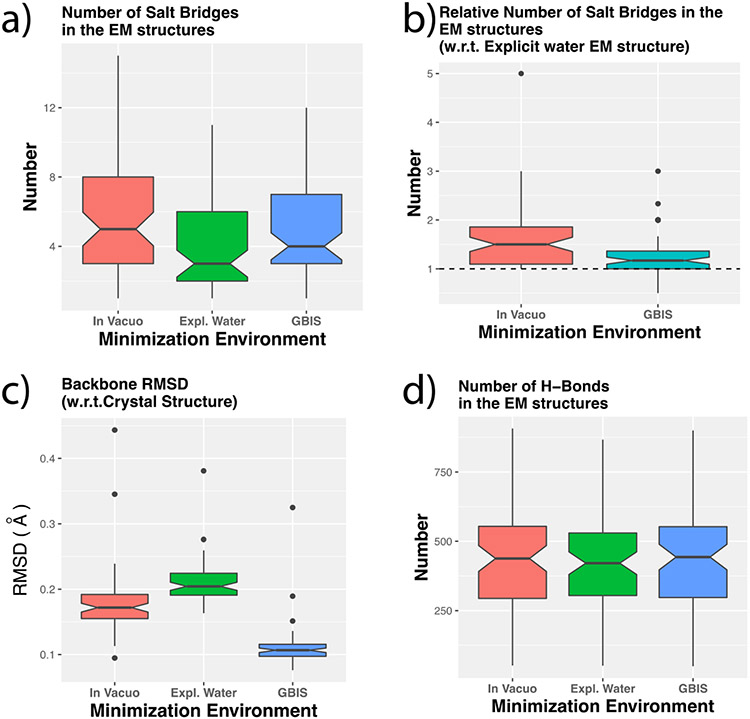
We found that the population of the charged/titratable residues forming SBs is a clear cause that differentiates the abilities of minimized structures to reproduce the ensemble averages. The comparison of the population of salt bridges (in closed conformation) after minimization shows that the in vacuo protein EM structures have a high number of these than the EM structures from the other two environments (Figure 3a). This has been further demonstrated by computing relative number of SBs using the number in the corresponding EM structure from explicit water environment for normalization (Figure 3b). From that, the in vacuo structures clearly exhibit a high population of salt bridges while the number of salt bridges in GBIS based minimized structures are slightly larger than the explicit water ones. In fact, more than 90% of the in vacuo structures have more SBs than the corresponding explicit water based EM structures. This indicates that incorporating solvent effects in any form (implicit or explicit) can have a similar influence on the salt bridge formation. Such an influence can be ascribed to the screening of coulombic forces due to higher solvent dielectric and the desolvation energy due to partial burial of the SB forming titratable groups when they form a salt bridge. At the same time, the absence of these effects in vacuum allows the residue pairs to orient their side chains in a manner that would allow them to stay bonded via a stable SB (a closed salt-bridge). This argument also seconds the trend of coulombic energy of various configurations of a protein described in the preceding section.

Figure 3:

Boxplots showing (a) the distribution of the number of SBs in the energy minimized (EM) structures from the three environments, (b) the number of SBs for in vacuo and GBIS EM structures relative to that from explicit water environment, (c) the backbone structural RMSD of the structures relative to the crystal structure after minimization in the corresponding environment, (d) the number of intra-protein hydrogen bonds in the EM structures after minimization in different environments. The dotted horizontal line in (b) indicates the unity mark.

The significance of the number of charged residues and their ability to form salt bridges becomes more prominent upon examining how other structural features such as structural backbone RMSD and intra-protein hydrogen bond network vary after minimization in different environments. Energy minimization protocol is not expected to cause a significant change of a protein’s conformation, especially the backbone conformation, but it may result in different hydrogen positions. To verify, we calculated the structural RMSD of the backbone and number of intra-protein hydrogen bonds (hydrogen bonds within the atoms of a protein) after minimization, with respect to the corresponding crystal structure. The comparison for structural RMSD is shown in Figure 3c. We noticed that large backbone changes did not occur post minimization regardless of the environment. Essentially, the backbone atomic positions were preserved. The RMSDs in all the cases were less than 0.5 Å. In the same way, Figure 3d illustrates the comparison for the number of intra-protein hydrogen bonds. It is evident that all of the three environments yielded similar numbers after minimization. The above analysis indicates that EM in different environments results is very similar backbone structures and intra-protein hydrogen bonds and therefore, cannot be the reason for the differences in the polar solvation energies. However, the number of closed SBs in the EM structures bear a qualitative correlation to the differences in their polar solvation energies.

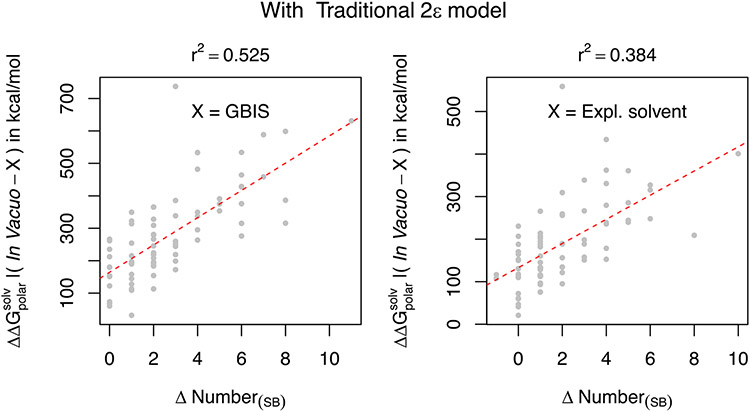
Seeking to find a quantitative association of the change in polar solvation energy $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ and the number of SBs formed or lost upon solvation, we plot the difference of $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ (computed using the traditional method and expressed as $\Delta \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$) of the in vacuo minimized structure and the GBIS/Explicit solvent minimized structure against the difference in the number of SBs (ΔNumber_(SB)) in the two structures (Figure 4). As one can infer from the reasonably high r² values (0.525 and 0.884 for GBIS and Explicit Solvent, respectively) that a linear relation is evident. This is a clear indicative of how the solvent can affect the number of SBs and subsequently alter the polar solvation free energy. Moreover, since the ordinate in the plots is the true difference $\left(\Delta \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}=\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(InVacuo)-\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(insolvent)\right)$, a greater loss of the SBs yields a more favorable solvation ($\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ is more negative). This is a direct consequence of the antagonistic relation between $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ and the coulombic energy U_coul.

Figure 4:

The difference of the $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$, computed using the traditional 2ε dielectric model $\left(\Delta \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\right)$ of the in vacuo and solvent minimized structures is plotted as a function of the difference of the number of salt-bridges in those structures. Left plot corresponds to GBIS and the right plot corresponds to explicit solvent (TIP3P). The quality of the linear fit (dotted red line) is quantified by the square of Pearson coefficient (r²).

The above quantitative association of SBs and the polar solvation energy have further implications when the dynamics of the proteins are considered. In the next section, we draw more weight onto these inferences and demonstrate how the breaking and forming of SBs in MD simulations is well mimicked by the Gaussian-model but not the traditional one. This, we show, influences the success or failure of a dielectric distribution model to reproduce ensemble average.

Gaussian-based smooth dielectric model reproduces ensemble $\langle \Delta {\mathbf{G}}_{\mathbf{polar}}^{\mathbf{solv}}\rangle$ as it can mimic the fluctuations of the SBs.

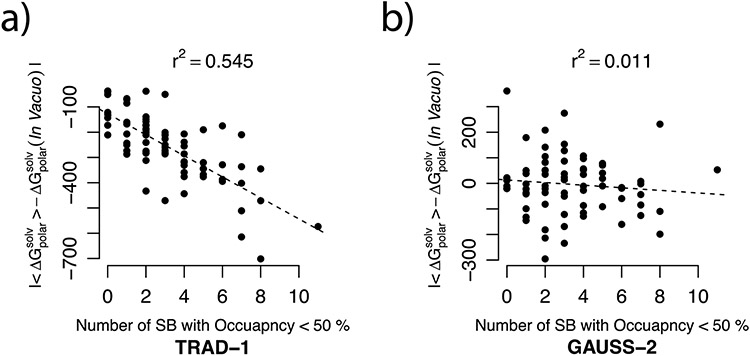
To assess the implication of the fluctuation of the SBs on the ability of the either dielectric model to reproduce ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$, the relation of the error of $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ from these models (for in vacuo EM structure) with occupancies of the SBs was sought. We plotted the error $(\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle -\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(InVacuo))$ against the number of SBs with occupancy < 50% (see Figure 5). The plot indicates if the error incurred by a dielectric distribution model deteriorates as more of the SBs present in the EM structure break during the MD. One can notice, from the linear trend in Figure 5a, that it is indeed the case with the traditional model. At the same time from Figure 5b, the error of the GAUSS-2 method is not only smaller than that of the TRAD-1 method but is independent of the occupancy of the salt-bridges.

Figure 5.

The error in $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ from using (a) traditional 2-dielectric method and (b) the Gaussian-based smooth dielectric model with in vacuo minimized structures with respect to the ensemble average (expressed as $\mid \langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle -\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}(InVacuo)\mid$) are plotted as a function of the population of the salt bridges which were present for more than 50% of the frames in its MD generated ensemble (occupancy > 50%). The solid black lines depict the linear model fits to these comparisons and the r² value is mentioned for each of these linear fits. All energy units are kcal/mol.

This indicates that as more of the SBs, extant in the EM structure, have a tendency to break and stay ‘broken’ during the MD, the traditional 2-dielectric method fails to reproduce the $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ (r² = 0.545). This can also imply that the ability of a dielectric model to capture ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ from a single structure significantly depends on its ability to mimic or capture the effect of fluctuations of the salt-bridges. This demonstrates that the Gaussian-based dielectric model (GAUSS-2) is able to capture SB fluctuations effect resulting in smaller error (than the TRAD method) and calculated polar solvation energy has no dependence on the occupancy of the SBs (r² = 0.011).

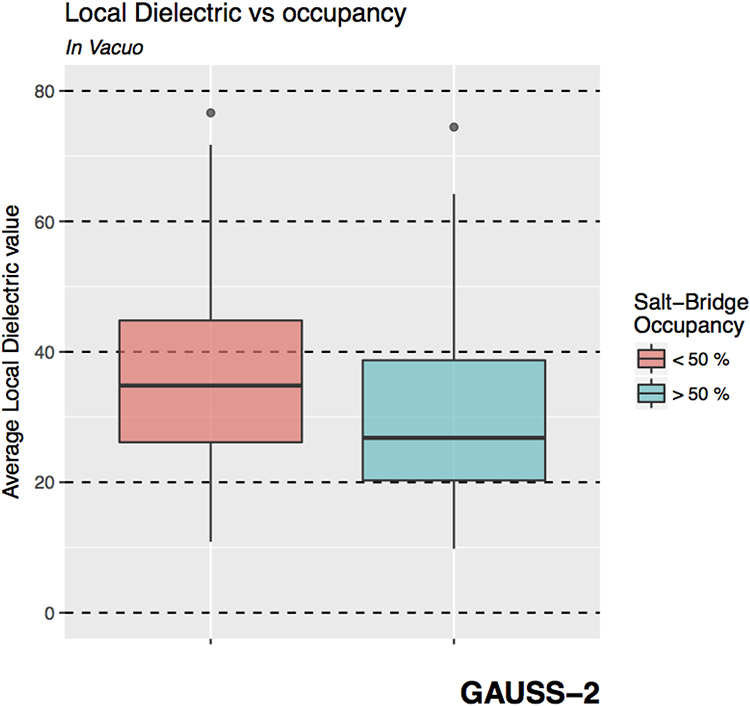
This can be attributed to the very basis of the Gaussian-based model. As is described in Ref.³⁸ and elaborated in the Methods section, the dielectric assigned to a region depends on the local atomic density, i.e., a region with lower atomic density is assigned a higher dielectric value and vice-versa. Consequently, the less dense regions will also have more room for motion owing to lesser likelihood for steric clashes with other solute atoms. As a result, the Gaussian-method would assign regions of potentially high mobility a higher dielectric constant. Therefore, if the Gaussian-method yields a good agreement with the ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$, it must be able to capture the SB fluctuations appropriately. Thus it is expected that it should assign relatively higher dielectric constant in the vicinity of those SBs which a lower occupancy (more room for fluctuation) than around those which have a higher occupancy (due to spatial restrictions arising from higher atomic density). To assess if that is indeed true, the local dielectric around the O-N atom pairs of the SBs identified in the in vacuo EM structure are computed to determine its relation with SB occupancy. The results are depicted in Figure 6.

Figure 6.

Boxplots showing the distribution of the average dielectric constant assigned by the Gaussian-based smooth dielectric model in the locality of the salt-bridges (SBs) which have an occupancy < 50%(red) and > 50% (blue).

In fact, the SBs with lower occupancies (< 50%) have a higher local dielectric constant on an average compared to the SBs that have an occupancy of more than 50%. This ratio is significant provided that regions populated with salt-bridges have, in general, a higher average dielectric constant than the buried regions rich in non-polar and polar residues³⁸ (see Figure S6).

Therefore, being able to capture the effects of fluctuation of the salt-bridge residues plays pivotal to the success of a dielectric distribution in reproducing the ensemble average solvation energy.

The ϵ_ref of a Gaussian-based dielectric distribution that best reproduces the ensemble average from a structure depends on the strength of salt-bridge interactions in it.

It is evident from Figure 3a that these structures have more SBs than the corresponding GBIS/explicit solvent minimized structures. Going back to Figure 2, one can also see that for a fixed value of ϵ_ref of the Gaussian-based model, $\Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}$ of an in vacuo minimized structure is smaller in absolute value than that of the crystal or a solvent-minimized structure. Both of these observations concede, i.e. the increased number of SBs in the in vacuo minimized structure is the reason its less favorable solvation energy (as explained above). When solvated, these structures tend to lose some of these salt-bridges (Figure 5). In the MD generated ensemble, these SBs have variable occupancies (Figure S5). This is indicative of the natural fluctuation of the SBs between open (broken) and closed (formed) states, occurring due to the interplay of the coulombic energy (favorable when closed) and solvation energy (favorable when open). The presence of both of these states in the ensemble indicate that their contribution to the overall energy of the solvated system in non-trivial (an example is shown in Figure 7a-d).

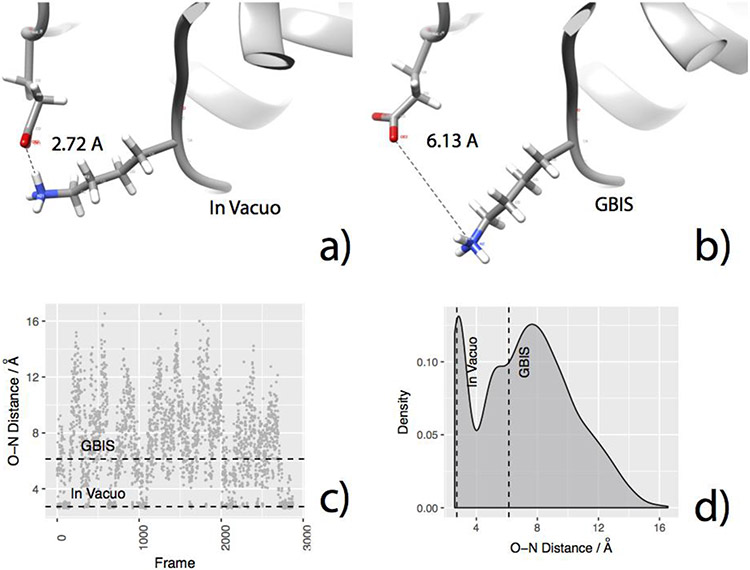
Figure 7.

For an example protein 1TQG, the plots show how the initial O-N distances for a SB forming residue pair may exist in a closed (formed) or open (broken) configurations in the ensemble. The figures indicate a) O-N distance of GLU32 and LYS79 in ITQG in the in vacuo EM structure, b) GBIS EM structure, c) The O-N distance observed in the MD generated ensemble (horizontal broken lines indicate the corresponding distance in vacuo EM and GBIS EM structures, respectively), d) the distribution of the O-N distance in MD generated ensemble (vertical broken lines indicate the corresponding distance in vacuo EM and GBIS EM structures, respectively).

Figure 7 shows an example of a salt bridge that fluctuates between open and closed forms in MD simulations; it is closed/formed (O-N distance = 2.72 Å implying stronger interaction, Figure 7a) in the vacuum minimized structure but open/broken (O-N distance = 6.13 Å implying a weaker interaction Figure 7b) in the GBIS minimized structure of its host protein. In the MD generated ensemble, the salt bridge appears to have sampled both - the closed and open conformations (Figure 7c, d), with very similar probabilities. However, there is significant difference in how the Gaussian-based dielectric function treats closed versus open salt bridges. A schematic is shown in Figure 8.

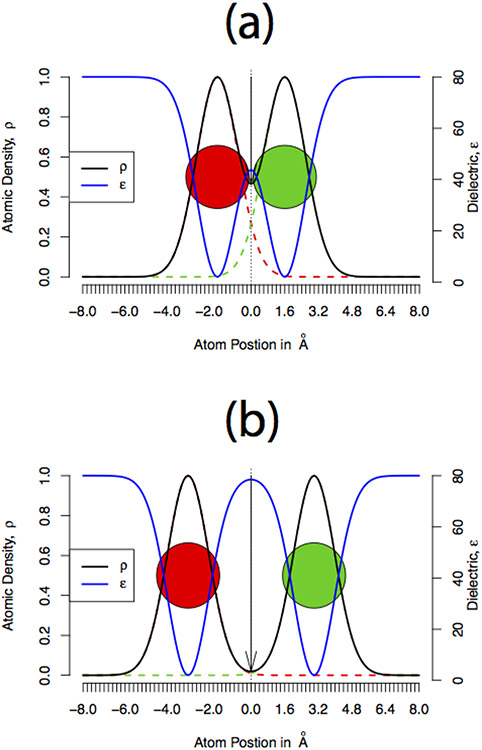
Figure 8.

Plots showing cartoon representations of the atomic density and the corresponding dielectric distribution assigned using Gaussian-based dielectric model when the atoms are separated at (a) smaller and (b) larger distance.

The average local dielectric value in the vicinity of a closed salt bridge is smaller compared (Figure 8a) to that around an open salt bridge (Figure 8b), simply because the atoms are more packed in the former. From point of view of the polar solvation energy, a small electric dipole (closed salt bridge) will have a weaker interaction with a polar solvent (water here) relative to a large electric dipole (open salt bridge). This will result is more favorable polar solvation energy obtained with structures with open salt-bridges (GBIS minimized structures) versus structures with closed salt-bridges (in vacuo minimized structures). Therefore, the inequality $\mid \Delta G_{polar}^{solv}(Gaus{s}^{Vac})\mid <\mid \Delta G_{polar}^{solv}(Gaus{s}^{GBIS})\mid$ for a fixed value of ϵ_ref, should explain why GAUSS-2 performs well with the in vacuo minimized structures but a higher ϵ_ref (GAUSS-4) performs well with the crystal or solvent-minimized structures. This is simply because the solvent-minimized structures have more open salt-bridges (Figure 3a) than the corresponding in vacuo minimized structures and hence they require more screening of their interactions with solvent phase (higher dielectric) to reproduce ensemble average polar solvation energy.

Conclusions:

The primary objective was to ascertain if the Gaussian-based smooth dielectric distribution (as implemented in DelPhi) for modeling the dielectric distribution can mimic the natural dynamics of a protein and therefore, yield its ensemble average polar solvation energy using a single structure alone. The Gaussian-based model, in parallel with the traditional 2-dielectric model, was paired with structures minimized in different environments (in vacuo, GBIS and explicit water) and crystal structure of 74 proteins to study its ability to approximate the ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$. Our study shows that the traditional dielectric model is able to reproduce a protein’s $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ only with its crystal structure or a structure minimized in solvent. However, for most of the proteins, one would have to decrease the dielectric internal dielectric (ε_in) to below 1, in order to achieve better approximations. This unreasonable modification can be circumvented by the use of Gaussian-based dielectric model. Not only does it yield a better agreement with the ensemble $\langle \Delta {\mathrm{G}}_{\text{polar}}^{\text{solv}}\rangle$ for physically valid internal dielectric values (known as ε_ref), its performance is appreciable regardless of the minimization environment. In fact, for most of the cases, Gaussian-based dielectric model performs better than the traditional model, even if subtly. Upon comparing the overall results, we show and therefore, suggest that the use of Gaussian-based dielectric model with ϵ_ref = 2, paired with a protein’s in vacuo minimized structure, is best suited for reproducing its ensemble average polar solvation energy.

A detailed analysis revealed the reasons for the aforementioned differences in performance and other solvation energy trends. We found that the conformational states of SBs (open/closed) in a protein’s minimized structure play an important role in offering one dielectric model an advantage over the other in terms of reproducing its ensemble average polar solvation energy. This means that a dielectric model, that best mimics the flexibility of the SB forming residues from their configuration in the EM structure, is better at reproducing the ensemble average polar solvation free energy. The Gaussian-based dielectric model is shown to accomplish this and therefore is capable of generating ensemble average polar solvation energy of a protein from its in vacuo energy minimized structure. Our findings can henceforth, serve as a starting point for developing a time-inexpensive single structure MM/PBSA method.