Automated quantification and statistical assessment of proliferating cardiomyocyte rates in embryonic hearts

Abstract

The use of digital image analysis and count regression models contributes to the reproducibility and rigor of histological studies in cardiovascular research. The use of formalized computer-based quantification strategies of histological images essentially removes potential researcher bias, allows for higher analysis throughput, and enables easy sharing of formalized quantification tools, contributing to research transparency, and data transferability. Moreover, the use of count regression models rather than ratios in statistical analysis of cell population data incorporates the extent of sampling into analysis and acknowledges the non-Gaussian nature of count distributions. Using quantification of proliferating cardiomyocytes in embryonic murine hearts as an example, we describe how these improvements can be implemented using open-source artificial intelligence-based image analysis tools and novel count regression models to efficiently analyze real-life data.

INTRODUCTION

Retrieval and analysis of quantitative readouts from histological images have become an increasingly important component of cardiovascular research. Quantitative histology heavily relies on computer-aided image analysis, resulting in increased transparency and reproducibility of generated data due to machine-based formalized quantification and increased throughput (1–3). Identification and quantification of specific cardiac cell populations according to their developmental origins (4), activated signaling pathways (5), or cellular processes (6) is achieved using quantitative analysis of histological images. In most cases, the scientific readout is not absolute cell counts but the relative frequency of studied cells, obtained by dividing the number of cells of interest by the total cell count. For example, the rate of 5-ethynyl-2′-deoxyuridine (EdU) positive cardiomyocytes/total number of cardiomyocytes is used to assess cardiomyocyte proliferation in embryonic hearts (6). The statistical analysis of those data is directed to determine how experimental factor(s) and a combination thereof affect these processes. The rigor of such analyses depends on the magnitude of the denominator, in other words, how many cells are screened in total. Consider 20% EdU⁺ cardiomyocytes rates obtained from three measurements: 2/10, 20/100, and 200/1,000. Although the rate is the same in all three measurements, one would consider 200/1,000 as the most robust estimate. However, the magnitude of denominator is often left for a scientist to choose arbitrarily and is not included in the statistical analysis framework, as data are transformed into ratio variables by calculating the rate; obtained rates are then analyzed by t test-based statistical methods or their nonparametric counterparts. We propose to improve quality of such analyses by quantifying the whole population of identifiable cells per section/biological replicate using formalized machine learning-based image analysis algorithms, and analyzing nontransformed data using statistical methods tailored explicitly for count and rate data. The ultimate goal of obtaining rates of proliferating cardiomyocytes can be divided into two primary tasks: 1) identifying all cells and 2) classifying them into proliferating EdU⁺ cardiomyocytes, EdU⁻ cardiomyocytes, and the rest of the cardiac cells. Below we provide a concise description of such improved pipeline, using quantification of EdU⁺ positive cardiomyocytes in embryonic murine hearts as an example.

DATASET DESCRIPTION

Previously analyzed and published data set (7) consists of control and Prdm16 cardiomyocyte-specific knockout animal (cKO) heart sections collected at embryonic days E13.5 and E15.5. Edu was administered to pregnant females 2 h before embryo harvesting, and incorporation was detected via Alexa Fluor 647 azide coupling using commercially available click chemistry-based assay, followed by NKX2-5 and DNA staining. Prepared slides were imaged using an Olympus FluoView FV1000 confocal microscope.

IMAGE QUANTIFICATION

Image Segmentation

Nuclear EdU signal is considered a marker of proliferation in embryonic cardiomyocytes, and the positive NKX2-5 signal is used to identify cardiomyocytes. As those markers are detected in nucleus, we choose nuclei as objects of interest, for instance, segmentation, which in embryonic hearts corresponds to cardiomyocyte number because of developmental mononuclearity. Technically, identification of nuclei involves instance segmentation, a process to delineate distinct objects of interest in an image. In our work, we have achieved the best results in segmenting densely packed DAPI-stained nuclei in embryonic heart sections using the deep learning-based Stardist algorithm (8) on ZeroCostDL4Mic, a freely available platform for image analysis based on Google Drive and Google Colab (9, 10). DAPI channel images and pretrained Stardist model (11) were uploaded via Google Drive and processed with Stardist (2-D) yupyter notebook maintained at ZeroCostDL4Mic. However, segmentation using pretrained model was not satisfactory, with a significant portion of nuclei missing an assigned mask. Therefore, misclassified regions and corresponding masks were cropped in Fiji (12) and manually adjusted using LabKit (13). Manually curated image-mask pairs were used as training material to finetune the initial classification model (Fig. 1A). Once a reasonable level of nuclei segmentation was achieved, the DAPI images of the whole data set were automatically segmented.

Figure 1.

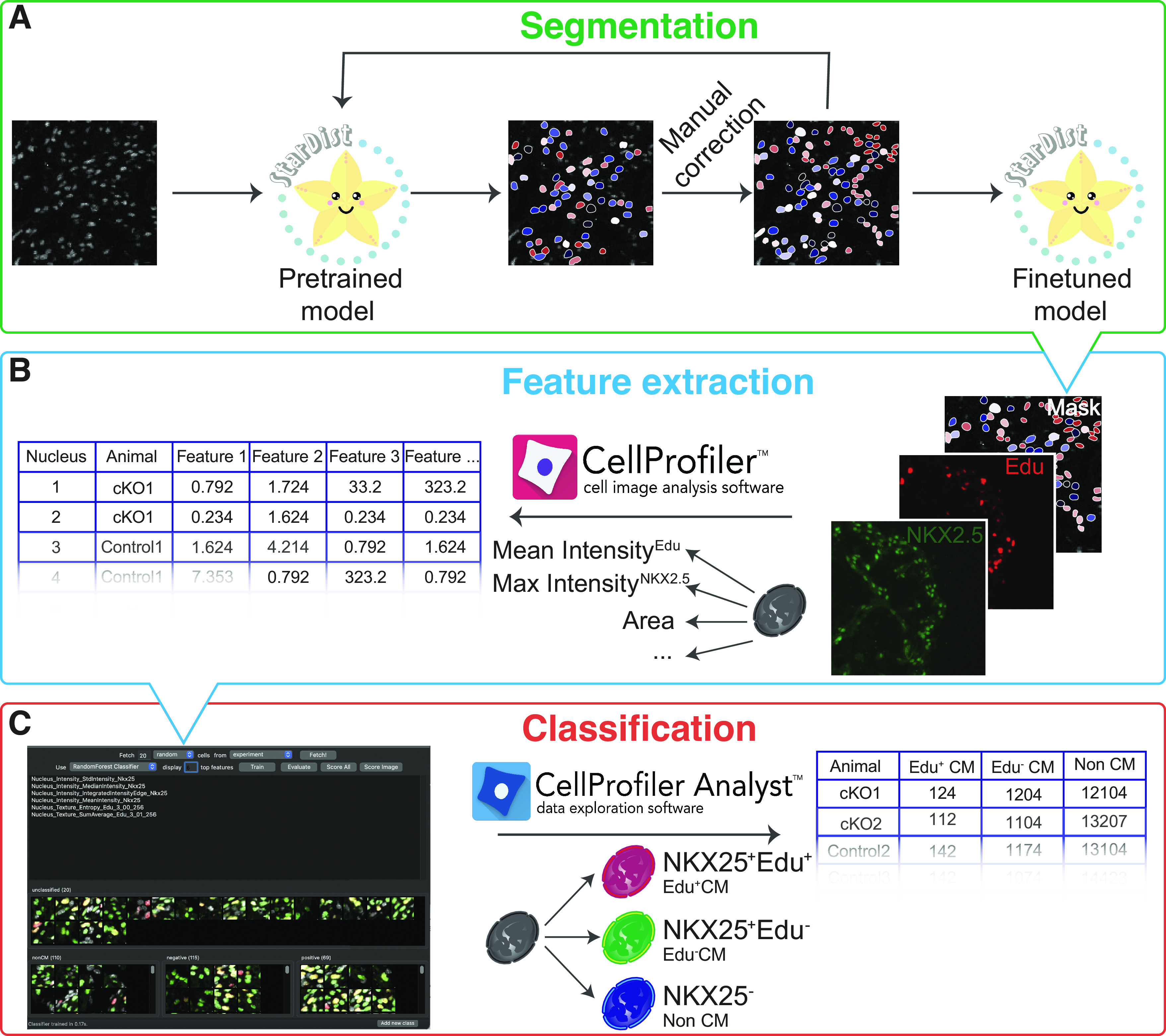
Pipeline for automated quantification of cardiomyocyte proliferation rates. Images of DAPI-stained embryonic heart nuclei are segmented using Stardist with finetuned model. Pretrained Stardist model is finetuned by retraining on manually corrected masks (A). DAPI (nuclei), EdU (proliferation), NKX2-5 (cardiomyocytes) signals, and nuclear borders obtained by segmenting DAPI channel with Stardist are used as inputs for CellProfiler to extract features for each individual nucleus (B). Obtained feature vectors and snapshots of each object are used to build a classifier and to classify every identified nucleus into EdU⁺ (class positive), EdU⁻ cardiomyocytes (class negative), and noncardiomyocytes (class non-CM) in CellProfiler Analyst (C).

Feature Extraction

The classification task can be subdivided into two subtasks: feature extraction and classification itself. Nuclei borders identified with Stardist were used as frames to measure different parameters of DAPI, EdU, and NKX2-5 signals. This subtask is achieved using CellProfiler, a free, open-source software for measuring and analyzing cell images (14). CellProfiler converts visual information from the images of single nuclei into a row of different extracted features for each identified nucleus (Fig. 1B). Set of object intensity, intensity distribution, and texture parameters was measured for Edu, DAPI, and NKX2.5 channel, as well as shape and size parameters of the mask. Although simple classification tasks can be performed in CellProfiler, we found that more complex, multifeature, machine learning-based classification models are required to achieve satisfactory classification accuracy. Therefore, the classification of nuclei into those from EdU⁺ cardiomyocytes, EdU⁻ cardiomyocytes, and noncardiomyocytes was performed in CellProfiler-Analyst (15) using extracted feature database generated by CellProfiler. CellProfiler-Analyst provides object tiles, and snapshots of single nuclei from their original images for the researcher to manually sort into classification bins to form an annotated set. Based on these provided examples, the software builds a classifier using CellProfiler extracted features and one of the available machine learning algorithms. The researcher can provide more object examples and vary the machine learning model and the number of features used for classification to achieve optimal classification accuracy, as assessed by evaluating the obtained confusion matrix (Fig. 1B). To classify nuclei from our studied data set, we trained a random forest classifier by manually assigning more than 70 nuclei to each class. Once classifier achieved >95% recall and precision for each class the whole data set was scored. Noteworthy, Edu and NKX2-5 signal texture and not the intensity parameters were the key features in classifier distinguishing between EdU⁺ cardiomyocytes, EdU⁻ cardiomyocytes, and noncardiomyocytes. The training data set and the classifier were saved and exported for data reproducibility and transparency purposes.

STATISTICAL ANALYSIS

The numerical outcome of such analysis is the count data: numbers of EdU⁺ cardiomyocytes, EdU⁻ cardiomyocytes, and noncardiomyocytes. The statistical analysis of such data aims to evaluate how and if experimental factors and their combinations affect these counts. This can be achieved by performing regression analysis for count data. Poisson regression serves as a classic tool to model and assess the association between the count response variable and explanatory variables. In Poisson regression, an occurrence count recorded for a particular measurement window is modeled. If counts are recorded at different measurement windows, an adjustment called an offset must be introduced in the regression equation, and thus the rate or the count per measurement unit is modeled. In the presented example, number of proliferating cardiomyocytes is offset by a total number of all cardiomyocytes counted. However, applicability of Poisson regression is limited because of the assumption of data equidispersion, rooted in the nature of the Poisson distribution, which is often violated in real count data that express variance higher (overdispersion) or lower (underdispersion) than a mean. Mean-parametrized Conway-Maxwell Poisson (COM-Poisson) regression does not require the equidispersion assumption and can be used to efficiently model data with under- or overdispersion (16, 17), whereas negative binomial regression can be used for overdispersed data (18). The studied data set consists of nuclei numbers quantified from 53 slides, prepared from the heart sections of 25 embryos (EmbryoID), harvested at two embryonic stages (E13.5 and E15.5), and belonging to control or knockout groups (Fig. 2A). In this analysis, we did not sum nuclei counts from different microscopic slides from a single sectioned heart, therefore, to avoid pseudoreplication (19, 20) and honor the hierarchical nature of this study design, we treated embryo as a random factor (EmbryoID), whereas embryonic stage and genotype were analyzed as fixed experimental factors. This statistical analysis aims to assess whether genotype, embryonic stage, and their combination affect counts of proliferating CMs. To answer this question, we modeled rates of EdU⁺ cardiomyocytes (positive) as a linear combination of experimental (stage, group) and random (1 | EmbryoID) factors and the offset {offset[log(offset)]} parameter (Fig. 2B). Offset variable is total number of counted cardiomyocytes. We used glmmTMB package in R to perform COM-Poisson regression (21). Calling function summary on Regression object outputs table with information on how experimental factors affect EdU⁺ cardiomyocyte counts. When compared with reference genotype category control, cKO animals have 23% [exp(−0.25713) = 0.77 times, or 23%] statistically significantly (P value = 1.32e-06) lower EdU⁺ cardiomyocyte counts. Analogically, compared with E13.5, proliferation rates increased by 15% (exp(0.13947)) at E15.5 and the interaction of both factors was significant (P value = 0.00557). Although we obtained statistically significant effect of experimental factors on rates of proliferating CMs, it is necessary to assess that observed differences are coming from the model that fits well-studied data set. The quality of regression model was studied using DHAMRa package in R (22). DHARMa simulates new values from the fitted model for each observation and creates readily interpretable standardized residuals, that can be intuitively interpreted as residuals from linear regression, which allow us to evaluate how well-generated model fits the studied data set (Fig. 2C). Residuals are simulated by calling function to simulate residuals for generated regression model Regression and statistically assessed by plotting the output of this function. The most common issue with the count regression models is over/underdispersion, which means that residual variance is larger or smaller than expected under used model. Overdispersion causes inflation of type I error, whereas underdispersion leads to loss of test power. The unaccounted over/underdispersion would cause deviation of DHARMa residuals. More formally over/underdispersion could be checked in DHARMa package by calling test dispersion function on simulated residuals, which would statistically compare the dispersion of simulated residuals to the observed residuals. Quantile-quantile plot and corresponding statistical tests performed on generated COM-Poisson regression model indicate that residuals are normally distributed, and the residuals calculated for individual genotypes are normally distributed and have comparable variance. Taken together, model quality assessment indicates that obtained regression model accurately fits studied data set and provides robust statistical estimates. Alternatively to DHARMa, model diagnostics could be performed using performance or easystats collection of packages (23, 24).

Figure 2.

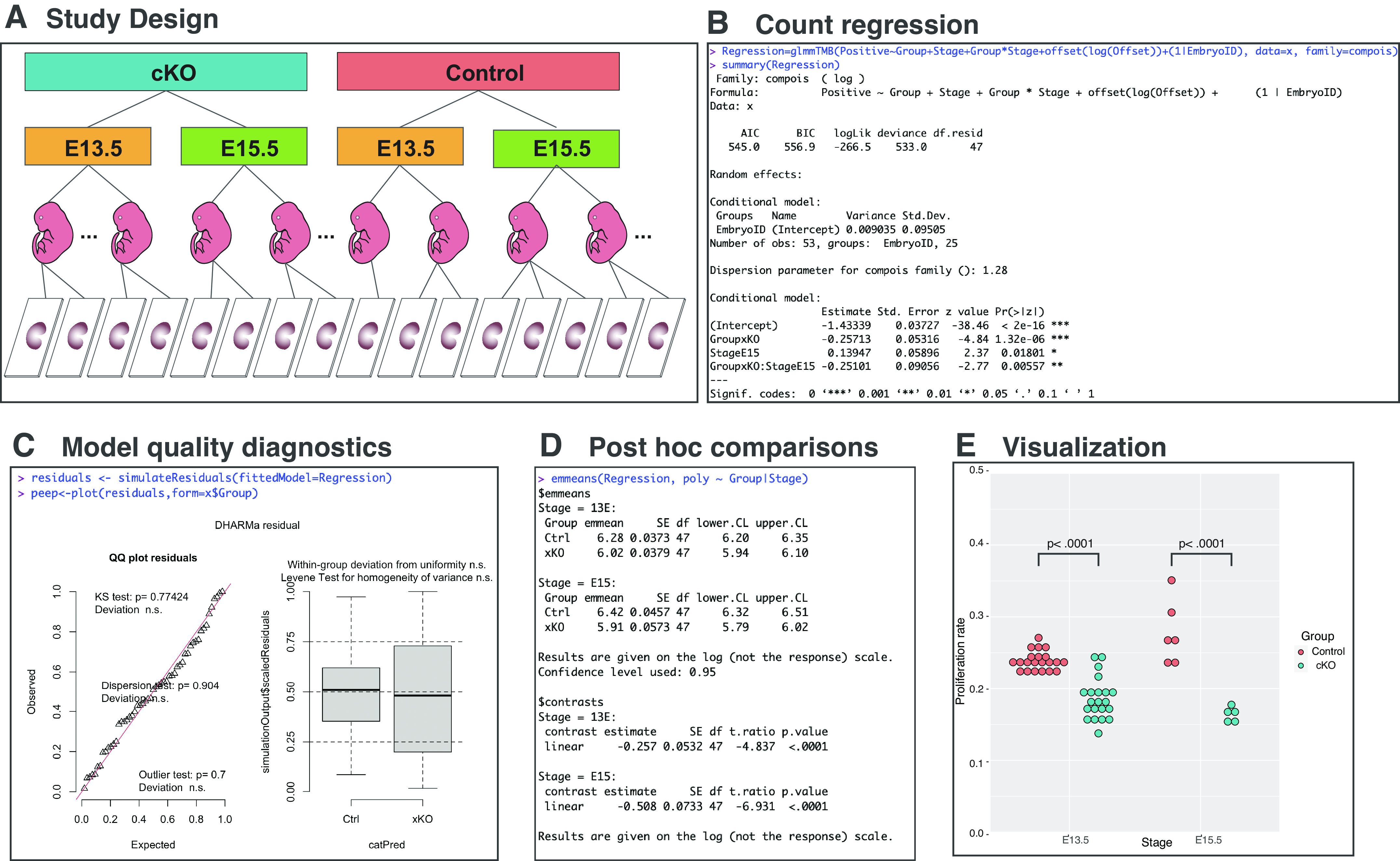
Statistical analysis of cardiomyocyte proliferation data set. Counts of total and proliferating cardiomyocytes were retrieved from 53 microscopy slides from 25 embryonic hearts harvested at 2 embryonic stages (E13.5 and E15.5) belonging to 2 genotypes (control and cKO) (A). Rates of Edu⁺ cardiomyocytes were modeled using COM-Poisson regression as combination of experimental factors, random factor, and offset using glmmTMB package in R (B). The suitability of produced regression model was assessed with DHARMa by evaluating the variance and distribution of residuals (C). Post hoc comparison of proliferating cardiomyocyte rates between genotypes within each embryonic stage was performed using estimated marginal means package emmeans (D) and data visualized using ggplot2 (E). cKO, cardiomyocyte-specific knockout animal; COM, Conway-Maxwell.

Post hoc comparisons for data analyzed using count regression can be performed by assessing estimated marginal means and calculating contrasts. Several packages, including marginaleffects and modelbased from easystats (24) bundle or emmeans (25) can be used to perform post hoc analysis on count regression models. We have chosen emmeans, as it provides a more straightforward and intuitive application programming interface than easystats, especially for specifying contrasts. Post hoc analysis wastargeted toward comparing the differences between genotypes (Group) within individual embryonic stages (Stage), by calling function emmeans, for regression object regression, and specifying the contrast of interest (poly ∼ group | stage). The function output provided estimated marginal means and confidence intervals for each experimental group as well as contrasts. Obtained results indicate that at both studied developmental stages knockout mice have lower CM proliferation rates, by 23% [1 − exp(−0.257)] at E13.5 and by 40% at E15.5 [1 − exp(−0.508)] when compared with control. Finally, obtained results were plotted using ggplot2 (26) in R (Fig. 2E). Obtained results are in excellent agreement with published manual analysis of studied data set (7).

DISCUSSION

Here we present a pipeline for automated quantification and statistical assessment of differences in rates of proliferating cardiomyocytes in embryonic murine hearts. To improve reproducibility and rigor of such studies, we propose two interconnected improvements. First, we use computer-aided quantification of proliferating cardiomyocytes. Computer rather than human-lead quantification of proliferating cardiomyocytes offers several advantages. Use of formalized methods allows researchers to export, save, and share algorithms and parameters used in every step of the pipeline, thus making analysis process transparent, transferable, and reproducible. Moreover, once parameters and algorithms are optimized, complete images/sections can be quantified in an unbiased way, rather than performing manual quantification in arbitrarily selected area or number of nuclei. Second, we use statistical methods tailored for the count and rate data. It has been reported that count and rate data should not be analyzed after transformation, but instead models based on Poisson distribution should be used (27–30). This approach not only acknowledges non-Gaussian distribution of count data but as well takes into consideration of denominator in rate data. However, often distribution of real-life data does not meet core assumption of equidispersion required for Poisson regression. To overcome this limitation, we use a COM-Poisson regression that can model data with both under- and over-dispersion (16). Alternatively, negative binomial regression can be used to model overdispersed data (18). Researchers can perform count regressions using alternative model structures and distributions implemented in glmmTMB and choose the best model for studied data set based on outcome of aforementioned diagnostic tests and complimentary model comparisons implemented in performance package from easystats bundle. Not only proliferation but also other various cellular processes or signaling pathways can be visualized by nuclear fluorescence. Moreover, nuclear signal can facilitate segmentation of cells (31). Therefore, our pipeline can be easily customized and adapted for quantifying other various experimental readouts.

GRANTS

J. Chen is funded by National Heart, Lung, and Blood Institute Grants HL155826, HL157119, and HL153032. Microscopy work was performed at the University of California–San Diego Neuroscience Microscopy Shared Facility and was supported by the National Institute of Neurological Disorders and Stroke Grant P30NS047101.

DISCLOSURES

J.C. holds an American Heart Association Endowed Chair in Cardiovascular Research. J.B. is a consultant for Rocket Pharmaceuticals on image analysis. None of the other authors has any conflicts of interest, financial or otherwise, to disclose.

AUTHOR CONTRIBUTIONS

J.B., Z.Z., and J.C. conceived and designed research; J.B., Z.Z., and T.W. performed experiments; J.B., T.W., and J.C. analyzed data; J.B., T.W., and J.C. interpreted results of experiments; J.B. prepared figures; J.B. drafted manuscript; J.B., Z.Z., T.W., and J.C. edited and revised manuscript; J.B., Z.Z., T.W., and J.C. approved final version of manuscript.