The optimal allocation of Covid-19 vaccines

Abstract

We develop a simple model of vaccine prioritization for a potential pandemic. We illustrate how the model applies to the case of Covid-19, using an early 2020 primitive estimate of occupation-based exposure risks and age-based infection fatality rates. Even based on primitive estimates the vaccine distribution strongly emphasizes age-based mortality risk rather than occupation-based exposure risk. Among others, our result suggests that 50-year-old food-processing workers and 60-year-old financial advisors should have been equally prioritized. We also find that the priorities minimally change when certain populations’ exposure risks are altered by targeted stay-at-home orders or call-up of essential workers.

1. Introduction

The severe acute respiratory syndrome–coronavirus 2 (SARS-CoV-2) pandemic claimed many lives and paralyzed economic activity. Vaccination has always been considered the principal strategy for containing the pandemic. With vaccines initially in limited supply, establishing priorities for their allocation was subject to substantial debate in the U.S. While there was little disagreement that front-line healthcare workers and nursing home residents should be in the very first group for vaccination, individual states implemented different prioritization schemes for other population groups. For instance, in Missouri, the population aged 65 and older was prioritized over teachers and workers in the food industry, while in California these three groups had the same priority.

We develop a simple model of vaccine prioritization and illustrate how it applies to the case of Covid-19 using early estimates of Covid-19 infection and mortality rates. The model recognizes that people face different infection risks depending on their occupations and that, conditional on being infected, the risk of death depends on their ages. The vaccine is assumed to be effective only to some extent and is in limited supply relative to the entire population. We set aside whether vaccinations prevent the transmission of the coronavirus.1 We solve a simple linear program that considers the cost an individual expects to incur if infected and the economic benefit of returning to her workplace. Our procedure allows us to derive the optimal vaccine distribution based on occupation and age among all allocations. This enables us to address who should get the vaccine earlier than others: young meatpacking plant workers or elderly school teachers?

We estimate occupation-based exposure risks (i.e., infection rates) and use estimates of age-based infection mortality rates to assign priorities over populations with different occupations and ages. The infection mortality rates vary across ages far more than the estimated infection rates across occupations. Accordingly, our model suggests a vaccine distribution that emphasizes age-based mortality risk more than occupation-based exposure risk. This insight is robust to supplementing the vaccine distribution with a stay-at-home mandate for targeted occupations and age groups. If some professions can work from home, the vaccines can be given to younger individuals who need to return to their workplaces. However, if the vaccine supply is scarcer, occupation-based exposure risks become more relevant as we distribute vaccines to individuals in relatively lower-risk occupations only at very advanced ages.

The allocation of vaccines has also been analyzed in the context of SEIR modeling framework (Bubar et al., 2021, Chen et al., 2020, Matrajt et al., 2021). However, these papers propose allocations solely based on age. Mulberry et al. (2021) focuses on prioritizing essential workers only. Pathak et al. (2020) also discusses the allocation of scarce resources, including vaccines, during a pandemic. While we focus on which groups to prioritize, Pathak et al. (2020) studies the implementation of a given proportional prioritization (i.e., vaccine reserves for different groups). To illustrate, if the population is partitioned into healthcare vs. non-healthcare workers, and old vs. young, our model assigns priorities among young healthcare workers and elderly non-healthcare workers based on occupation-related exposure and age-based infection mortality. In contrast, Pathak et al. (2020) takes a certain priority structure in the form of reserves for, e.g., healthcare workers and the elderly, as given. Their primary question is how to implement vaccine distribution under the given priorities.2 By considering vaccine allocations that take into account the disruption of wealth we complement the work of Arteaga-Garavito et al. (2020), who show that the diffusion of the virus in a pandemic crisis is an important risk factor for equities.

2. The model

We develop a simple model to identify priority groups for vaccination based on occupations and ages. For this, we partition the population into groups by occupations $I$ and ages $J$. The population distribution over occupations and age groups is $P\in {\mathbb{R}}_{+}^{I\times J}$ such that each element $p_{ij}$ denotes the number of people with certain occupation $i$ and in an age-group $j$. Each person in occupation $i$ faces a risk of infection denoted by $r_i\in (0,1)$. Associated with each person in an age group $j$ is a cost of infection $c_j>0$.

A policy consists of a distribution of a limited supply of vaccines and a targeted stay-at-home order. A vaccine distribution $V\in {\mathbb{R}}_{+}^{I\times J}$ specifies the number of people, $v_{ij}$, in occupation $i$ and age-group $j$ that receive a vaccine. The vaccine distribution satisfies a supply-side budget constraint ${\sum }_{i,j}{v}_{ij}\le b$, where $b$ represents the quantity of vaccine initially available, which is assumed to be less than the total population ${\sum }_{ij}{p}_{ij}$. The vaccine allocation policy can be supplemented by a targeted stay-at-home order $H\in {\mathbb{R}}_{+}^{I\times J}$ with $h_{ij}$ representing the number of people in occupation $i$ and age-group $j$ that cannot return to their workplace. Overall, $V+H\le P$.

A vaccine recipient becomes immune to the virus with probability $\gamma$, which captures the vaccine’s effectiveness. It is worth noting that our model does not distinguish whether the vaccine prevents infections or only reduces the risk of severe illness (captured by the cost of infection). Thus, each dose of the vaccine allocated to group $(i,j)$ reduces $r_i{c}_j$ by the effectiveness rate, $\gamma$. A vaccination policy $V$, together with a stay-at-home order $H$, can decrease the population affected by the virus by $\gamma V+H$ across different occupations and age groups. In particular, for each group $(i,j)$, the policy saves costs $(\gamma v_{ij}+h_{ij})r_i{c}_j$.

The stay-at-home policy $H$ comes with the suspension of economic activities. Let $F\in {\mathbb{R}}_{+}^{I\times J}$ denote the values of economic activities that accrue to individuals. In particular, each $f_{ij}$ denotes the value of the economic activity $i$ undertaken by an individual in the age group $j$. Thus, the total loss in value from stay-at-home for the group $(i,j)$ is $f_{ij}{h}_{ij}$, unless the occupation $i$ can be worked at home, which we allow in one of our specifications.

The goal is to find a policy $(V,H)$ that minimizes the loss of lives and the economic burden from a stay-at-home order. In particular, the planner solves the following linear program:

$$(\text{LP; }\gamma ,b,\theta )\underset{V,H}{min}\sum _{i,j}(\gamma v_{ij}+h_{ij})r_i{c}_j-f_{ij}{h}_{ij},\text{subject to}\left(i\right)\sum _{i,j}{v}_{ij}\le b\text{(budget constraint)}\left(ii\right)v_{ij}+h_{ij}\le p_{ij}\text{(feasibility)}\left(iii\right)\sum _{i,j}{r}_i{d}_j(p_{ij}-\gamma v_{ij}-h_{ij})\le \theta \sum _{i,j}{p}_{ij},\text{(measured fatalities)}$$

where $d_j$ is the infection fatality rate that an individual in age group $j$ faces. Constraint ($iii$) in this program allows us to derive the optimal policy $(V,H)$ such that the (unconditional) fatality rate expected to occur in the population is capped, given vaccine effectiveness of $\gamma$. Alternatively, constraint ($iii$) can inform us about the minimum vaccine effectiveness required to cap the (aggregate) fatality rate at $\theta$, if a stay-at-home order is not possible. Depending on the values assumed for the parameter $\theta$, constraint ($iii$) need not be binding.

3. Data and estimation strategy

We track 8 age groups for the 2017 U.S. population, 16–19, 20–29, 30–39, …, and $80+$, distributed over 454 occupations, aggregated at the 3-digit Census OCC code. We obtain the number of people for each age group employed in a given occupation from the 2017 American Community Survey (ACS). Our sample is representative of 60% of the U.S. population.

To proxy for the benefit $f_{ij}$ that an individual in age group $j$ generates from participating in economic activity by occupation $i$, we use the average yearly wage for each age group and occupation, also provided by the 2017 ACS. From an economics perspective, the wage captures a worker’s contribution to the production of total output as measured by GDP, or equivalently the GDP loss if a worker is unable to work due to a stay-at-home order (Hulten, 1978, Baqaee et al., 2020). We recognize that wages need not be a perfect proxy, with the value of some occupations for the economy potentially being underestimated. To overcome this limitation we designate certain occupations as essential. This is equivalent to assuming that workers in an essential occupation generate a very large value from participating in economic activity, regardless of their age.

For an age group $j$, the average cost $c_j$ of infection depends on the infection fatality rate $d_j$ and the value of statistical life (VSL) of the age group. In particular, the cost of infection is given by

$$c_j=d_j\times {\text{Value of statistical life}}_j.$$

As Table 1 indicates, using VSL for each age group is similar to using standard expected years of life lost (SEYLL), as Emanuel et al. (2020) suggests. For the infection fatality rate – the number of deceased among the infected people – we use the primitive estimates provided by Salje et al. (2020) who jointly analyze French hospital data with the results of a detailed outbreak investigation aboard the Diamond Princess cruise ship.3 For the VSL, we use the estimates provided by Greenstone and Nigam (2020) who update the estimates of Murphy and Topel (2006) to 2015. The details are reported in Table 1.

Table 1.

The Value of Statistical Life (VSL) and Infection Fatality Rate by age groups.

Age group	EU population	Infection fatality rate (%)	VSL in mil. USD	The cost of infection in USD
$<$ 19	0.215	0.001	15.3	153
20–29	0.12	0.005	16.1	805
30–39	0.135	0.02	15.8	3,160
40–49	0.14	0.05	13.8	6,900
50–59	0.135	0.2	10.3	20,600
60–69	0.115	0.7	6.7	46,900
70–79	0.09	1.9	3.7	70,300
$80+$	0.05	8.3	1.5	124,500

Note: for the age group 16–19, we used VSL of the ages 10–19.

The remaining variable that we need to estimate in the model is the infection rate $r_i$, associated with each occupation $i$, for which the data is not directly available. To circumvent the lack of data, we proceed in two steps. First, we infer the infection rate for each occupation group based on the coronavirus-related deaths by occupation that occurred between March 9th and May 25th, 2020, as reported by the U.K. Office for National Statistics (ONS). ONS reports the age-standardized death rate per 100,000 of each minor occupation $i$ by gender for those aged 20 to 64 years. This death rate is unconditional on infection and based on the 2013 E.U. standard population distribution. We use the employment-weighted average of the death rates by gender and construct the death rate, $D_i$, per 100,000 people for each U.K. minor occupation. Given the infection fatality rate $d_j$ for the age group $j$ provided by Salje et al. (2020), we obtain the infection rate for each U.K. minor occupation per 100,000 people as

$$r_i=\frac{D_i}{\sum _j{q}_j{d}_j},$$ (1)

where $q_j\in [0,1]$ denotes the fraction of age-group $j$ according to the E.U. standard population distribution.4 Our maintained assumption is that exposure to the virus depends on occupation, but the infection fatality rate depends on patients’ ages.

Next, we impute infection rates for U.S. occupations. We consider that the main explanatory factor for differences in infection rates across occupations is physical proximity.In an occupation with a higher physical proximity score, workers have to interact more closely with other people, such as co-workers or clients. Thus, presumably, the virus transmission rate is higher in occupations that require a higher degree of physical proximity, and consequently, this will be reflected in the death rates. Even as various social distancing measures are observed, we expect that occupations with a higher degree of physical proximity will still entail a higher infection risk than ones with a lower degree of physical proximity.

We estimate a fractional probit model (Papke and Wooldridge, 1996) using the infection rates $r_i$ corresponding to each U.K. minor occupation we have derived based on (1) and physical proximity measures that are also provided by ONS. A worker employed in occupation $i$ with a degree of physical proximity $x_i\in [0,100]$ is going to be infected over two months with a probability

$$P\left[\text{Infection}\right|x_i]=\frac{r_i}{100,000}=\Phi (\alpha +\beta x_i),$$

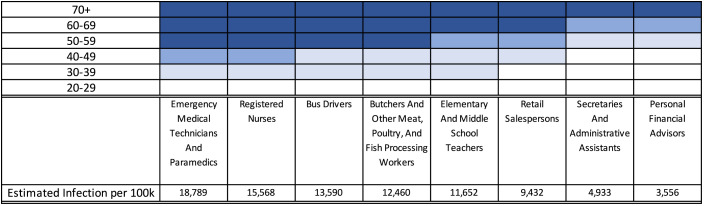
where $\Phi$ is the cumulative distribution function of the standard normal distribution. The estimates we obtain are $\hat{\alpha }=-2.116021$ (CI [−2.592531, −1.639511]) and $\hat{\beta }=0.0128009$ (CI [0.004813, 0.0207889]), which are statistically significant at 0.05 level. The resulting infection rates are thus increasing with the degree of physical proximity, ranging from 2638 (for logging workers) to 20,160 (for physical therapists) per 100,000 people. Estimated infection rates over a two-month period for selected occupations are shown in Fig. 2.

Fig. 2.

Priorities among some selected age–occupation groups. The groups with the top priority are marked in the darkest blue, and they receive vaccines even when the supply is 30 million doses. Lighter blues mark the groups with the second and the third priority, and they will get vaccines when the supply is, respectively, 60 million and 100 million doses. The rest groups with the lowest priorities are marked in white. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We then impute the infection rate for each U.S. occupation based on these estimates.5 In particular, we construct the infection rate per 100,000 people over two months for each U.S. occupation $i$ with proximity score $x_i\in [0,100]$ as

$${\hat{r}}_i=100,000\ast \Phi (\hat{\alpha }+\hat{\beta }{x}_i).$$

We use the proximity score developed by Mongey et al. (2020) who calculate the employment-weighted average of survey-based job characteristics for each 3-digit OCC occupation code based on O*NET data.

For robustness, we estimate the model using mortality rates for ages $20+$. For this, we calculate age-standardized mortality rates by occupation, including the number of deaths of those aged $65+$ that ONS provides for each occupation. In this case, the parameter estimates from the fractional probit regression are $\hat{\alpha }=-1.152288$ and $\hat{\beta }=0.0037667$. Including all ages yields a lower estimate of $\hat{\beta }$, which implies that the infection rates estimated for U.S. occupations will be less responsive to proximity scores, i.e., more homogeneous infection rates across occupations. In this case, our main finding – vaccines are distributed mostly by age rather than occupation – becomes even stronger (Fig. A.5 in Supplemental Appendix). Nevertheless, we are cautious about these estimates, as the death rate for the $65+$ age category is bound to be less precise due to the small sample size of the elderly employed in each occupation.

4. Results

We undertake three exercises. First, we find the optimal vaccine distribution under the assumption that there is no stay-at-home order, and everyone returns to work regardless of whether they have received a vaccine or not. Second, we derive the optimal vaccine distribution when a targeted stay-at-home order is implemented, and the individuals who are unable to return to work produce no output.6 That is, everyone who cannot return to work receives no wage for the stay-at-home order duration. Third, we derive the optimal vaccine distribution when a targeted stay-at-home order is implemented, but for some occupations, employees can work from home. In this case, individuals who can work from home receive the same wages as if they were to return to work, while individuals who cannot work from home produce no output and receive no wages during the stay-at-home order. For the last two exercises, 121 occupations deemed to be essential are exempt from the stay-at-home order. We assume that the length of the stay-at-home order is two months (Abbasi, 2020) to reflect the expected time lag until a vaccine becomes widely available and scale the yearly wage loss accordingly. We also cautiously assume that the initial supply of the vaccine is allocated to employed people above the age of 16 is 60mil doses, covering approximately one-third of the employed workforce. Similarly, we assume that the vaccine effectiveness is 50% (Food and Drug Administration, 2020). We initially derive the optimal vaccination and stay-at-home policy when the constraint on the fraction of coronavirus fatalities is lax.

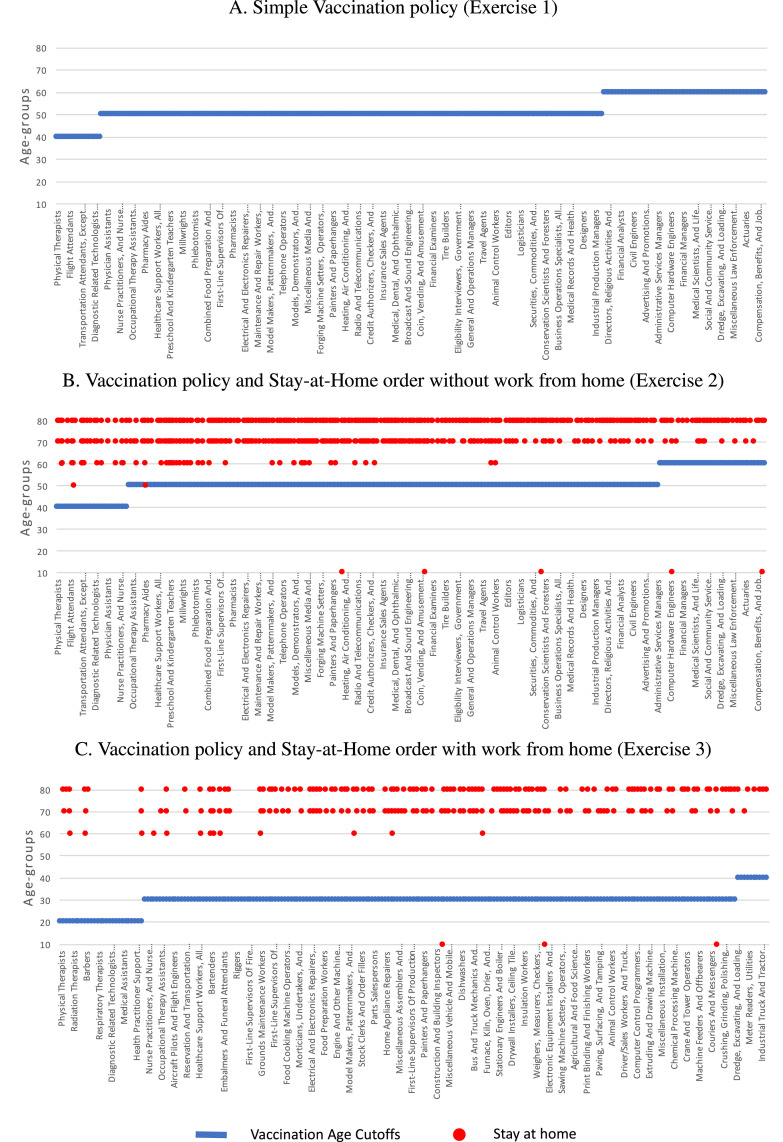
The overall vaccine policy is presented in Fig. 1. We order occupations based on their infection risk and show how the vaccine distribution policy and stay-at-home mandate depend on occupations and ages. The main insight from all three exercises is that age is more important than an occupation’s infection risk when allocating vaccines optimally. The largest volume of vaccines is allocated to the populations of age 50–59, followed by age 60–69 in exercises 1 and 2, or age 30–39 in exercise 3. The loss in economic benefits (proxied by wages) from being out of work plays a role in allocating vaccines only when a stay-at-home order is also used as a policy tool (as in exercises 2 and 3).

Fig. 1.

Age cutoffs for vaccinations and age groups staying at home. Occupations on the $x$-axis are ordered based on their infection risk. (A) The optimal vaccination policy showing the youngest age for each occupation that is eligible to receive the vaccine. (B) The optimal vaccination policy showing the youngest age for each occupation that is eligible to receive the vaccine, together with the occupation–age groups that are mandated to stay at home. (C) The optimal vaccination policy showing the youngest age for each occupation which cannot be done from home that is eligible to receive the vaccine, together with the occupation–age groups that are mandated to stay at home. Occupations that can be done from home do not receive a vaccine.

When we derive the optimal vaccine allocation absent of a stay-at-home order, all employed people above age 60 receive the vaccine (Fig. 1A). Some occupations, such as paramedics and flight attendants, are eligible to receive the vaccine if they are at least 40 years old. For many other occupations, including most other healthcare workers, the eligibility threshold for receiving the vaccine is age 50. There is naturally a trade-off between the infection risk associated with occupation and the risk of death related to age. For instance, food processing workers above age 50 receive a vaccine, while financial advisors only receive it if they are above 60 years old.

When a stay-at-home order complements the vaccination policy, most employees who are at least 80 years old and some in their 70 s are mandated to stay at home (Fig. 1B). For the $80+$ age group, the risk of death is so substantial that a 50% effective vaccine is insufficient to overcome the loss in wages for the duration of the stay-at-home order. For a few occupations, such as textile-related, the stay-at-home order targets teenagers as well. While the infection fatality rate for their age group is meager, the economic value of practicing their occupation, given the corresponding infection rate does not justify the risk. In turn, the stay-at-home order allows nurses as young as 40 to receive vaccines.

Once we take into account that for some occupations, employees can work from home without any loss in wages, then the supply of the vaccine can be distributed only to those occupations in which employees need to be present at their workplace. Allocating vaccines across fewer occupations implies that younger people, for instance, as young as 20 for nurses and food preparation workers, are now eligible to receive the vaccine (Fig. 1C).

We illustrate how priorities are assigned across different age groups for some selected occupations in Fig. 2. The top priority groups are shaded in the darkest blue, and the groups with the next priorities are in lighter blues. The top priority groups consist of high-risk populations in high-exposure occupations, consistent with an emerging consensus. They receive vaccines even under a very limited supply (30 million doses). The following priority groups receive vaccines when the supply increases to 60 million doses or 100 million doses. Young healthcare workers such as paramedics and nurses at age $30+$ (or $40+$) have about the same priorities as financial advisors at age $50+$ (or, respectively, $60+$). A scarcer supply of the vaccine (30 million doses) emphasizes occupational risk, with nurses, for instance, being prioritized at the age of $50$, while retail salespersons are eligible only at the age of $60$.

Supplemental Appendix contains additional results. Designating occupations as essential affects the optimal allocation of the vaccine only when a targeted stay-at-home order is also used (Fig. A.2). In designating, for instance, food processing workers as essential, we ensure that individuals over 50 years old in this occupation receive vaccines. Otherwise, if food processing workers can be subject to the stay-at-home order, only the population under 70 years old, representing 99.3% of the workforce, can return to their workplace, with individuals over 50 years old (in exercise 2) or over 20 years old (in exercise 3) receiving the vaccine. Finally, our model allows us to assess two margins: increasing the effectiveness and increasing the vaccine supply. An increase in the vaccine effectiveness to, say, 70% does not change the vaccine allocation (Fig. A.1). However, as the supply of the vaccine increases to, say, 100mil doses, the age of the youngest eligible recipients decreases (Fig. A.3 and Fig. A.4), even with vaccine effectiveness of 50%.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

We refer to Supplemental Appendix for details on the data of occupation proximity scores, which determine infection rates of occupations, and how to categorize occupations as essential and can be worked from home. The appendix also contains additional results on vaccine allocations for various vaccine supplies and effectiveness.

Data availability

Data will be made available on request.