Optimization of institutional incentives for cooperation in structured populations

Abstract

The application of incentives, such as reward and punishment, is a frequently applied way for promoting cooperation among interacting individuals in structured populations. However, how to properly use the incentives is still a challenging problem for incentive-providing institutions. In particular, since the implementation of incentive is costly, to explore the optimal incentive protocol, which ensures the desired collective goal at a minimal cost, is worthy of study. In this work, we consider the positive and negative incentives for a structured population of individuals whose conflicting interactions are characterized by a Prisoner’s Dilemma game. We establish an index function for quantifying the cumulative cost during the process of incentive implementation, and theoretically derive the optimal positive and negative incentive protocols for cooperation on regular networks. We find that both types of optimal incentive protocols are identical and time-invariant. Moreover, we compare the optimal rewarding and punishing schemes concerning implementation cost and provide a rigorous basis for the usage of incentives in the game-theoretical framework. We further perform computer simulations to support our theoretical results and explore their robustness for different types of population structures, including regular, random, small-world and scale-free networks.

1. Introduction

Cooperation is of vital importance in the contemporary era [1]. However, its evolution and emergence conflict with the immediate self-interest of interacting individuals [2]. Evolutionary game theory provides a common mathematical framework to depict how agents interact with each other in a dynamical process and to predict how cooperative action evolves from a population level [3]. As a representative paradigm, the Prisoner’s Dilemma game has received considerable attention for studying the problem of cooperation in a population of interacting individuals [4].

When individuals play the evolutionary Prisoner’s Dilemma game in a large well-mixed population, in which all are equally likely to interact, cooperation cannot emerge. However, the real-world population structures are not well-mixed but relatively complicated, and the interactions among individuals are limited to a set of neighbours in a structured population [5]. Inspired by the fast progress of network science, several interaction topologies have been tested, including small-world [6] and scale-free networks [7]. Features of these networks can influence the evolutionary dynamics of cooperation significantly [8–14]. Beside network topology, another crucial determinant of the evolution of cooperation is the strategy update rule, which determines the microscopic update procedure [15–18]. For instance, cooperation can be favoured under the so-called death–birth (DB) strategy update rule if the benefit-to-cost ratio in the Prisoner’s Dilemma game exceeds the average degree of the specific interaction network [15–17]. In contrast, it cannot emerge under the alternative birth–death (BD) strategy update rule [15].

Overall, situations abound when cooperation cannot emerge in structured populations when no additional regulation mechanisms or moral nudges are incorporated [15,19,20]. In these unfavourable environments, prosocial incentives can be used to sustain cooperation among unrelated and competing agents [21–29]. Specifically, cooperators can be rewarded for their positive acts, or defectors are punished for their sweepingly negative impact. At the individual level, cooperation can be favoured whenever the amount of incentive exceeds the pay-off difference between cooperating and defecting, no matter whether the incentive is positive or negative. However, in a given unfavourable environment for the emergence of cooperation, it is still unclear how intensive positive or negative incentive is needed to drive the population toward the desired direction. Furthermore, applying incentives is always costly [30–34]. Previous related works assume that, when used, the incentive amount is fixed at a certain value [30,32]. In those circumstances, the obtained incentive protocol is not necessarily the one with the minimal cumulative cost [33]. Therefore, finding the optimal time-varying incentive protocol is vital to ensure effective interventions that drive populations towards a productive and cooperative state at a minimal execution cost.

Our work addresses how much incentive is needed for cooperation to emerge and explores the optimal incentive protocols in a game-theoretical framework, where time-varying institutional positive or negative incentives are provided for a structured population of individuals playing the Prisoner’s Dilemma game. We establish an index function for quantifying the executing cumulative cost. We systematically survey all relevant strategy update rules, including DB, BD, imitation (IM) and pairwise-comparison (PC) updating [15–17,35]. Using optimal control theory, we obtain the dynamical incentive protocol under each strategy update rule leading to the minimal cumulative cost for the emergence of cooperation. Interestingly, we find that the optimal negative and positive incentive protocols are identical and time-invariant for each given strategy update rule. However, applying punishment can induce a lower cumulative cost than the usage of reward if the initial cooperation level is larger than the difference between the full cooperation state and the desired cooperation state. Otherwise, applying reward requires a lower cost. Beside analytical calculations, we perform computer simulations confirming that our results are valid in a broad class of population structures.

2. Results

We start with a structured population of N individuals who interact in a regular network of degree k > 2. In this graph, vertices represent interacting agents and the edges determine who interacts with whom. Each individual i plays the Prisoner’s Dilemma game with its neighbours. An agent can choose either to be a cooperator (C), which confers a benefit b to its opponent at a cost c to itself, or to be a defector (D), which is costless and does not distribute any benefits. After playing the game with one neighbour, if institutional positive incentives are in place, the agent is rewarded an amount μ_R of incentive for choosing C. When negative institutional incentives are implemented, it is fined by an amount μ_P for choosing D. The agent collects an accumulated payoff π_i by interacting with all neighbours. We set the fitness, f_i, of individual i, chiefly the reproductive rate, as 1 − ω + ωπ_i, where ω (0 ≤ ω ≤ 1) measures the strength of selection [36]. In this work, we concentrate on the effects of weak selection, meaning that 0 < ω ≪ 1. Four different fitness-dependent strategy update rules are considered separately, and the details are given in the Model and methods section. In addition, in order to help readers intuitively understand the evolutionary process in networked Prisoner’s Dilemma game with institutional reward or punishment, we present an illustration figure as shown in figure 1.

Figure 1.

Evolutionary Prisoner’s Dilemma game on a graph with institutional reward or punishment. (a) The pairwise interaction between two connected neighbours in a network. (b,c) How incentives are implemented for the two connected agents who played the game when positive (negative) incentives from the incentive-providing institution are applied. (d) The illustration of the four strategy update rules, depicting how agents update their strategies after obtaining payoffs from the pairwise interactions with neighbours and the incentive-providing institution.

2.1. Theoretical predictions for optimal incentive protocols

In this section, we, respectively, explore the incentive protocols under four alternative strategy update rules, including DB, BD, IM and PC updating. The details of these calculations are described in the electronic supplementary material, and here we only summarize the pair approximation approach for our dynamical system with positive or negative incentive in the weak selection limit.

Using the pair approximation approach (see electronic supplementary material, section S1), we get the dynamical equation of the fraction of cooperators under DB rule with positive or negative incentive as

$$\begin{array}{rl}\frac{\mathrm{d}{p}_C}{\mathrm{d}t}& =F_{\mathrm{DB}}(p_C,{\mu }_v,t)\\ & =\frac{\omega (k-2)}{k-1}[b+k({\mu }_v-c)]p_C(1-p_C)+o({\omega }^2),\end{array}$$ 2.1

where p_C is the fraction of cooperators in the whole population and μ_v is the amount of positive incentive that one cooperator receives from an incentive-providing institution or the amount of negative incentive imposed on a defector by a central institution (note that such incentive is applied for every interaction as explained in the Model and methods section). Equation (2.1) has two equilibria, one at p_C = 0 and the other at p_C = 1. If μ_v > c − b/k, the first is unstable and the second stable, indicating that cooperators prevail over defectors (further details are presented in electronic supplementary material, section S1). Notably, in the absence of incentives, i.e. μ_v = 0, we get back the previously identified b/c > k condition for the evolution of cooperation [15,16].

Using the Hamilton–Jacobi–Bellman (HJB) equation [37–39], in the condition of μ_v > c − b/k > 0, we obtain analytically the optimal protocol μ*_v = 2(ck − b)/k both for reward and punishment (see electronic supplementary material, section S1 for details). The optimal rewarding and optimal punishing protocols are both time-invariant and the optimal incentive levels for punishment and reward are identical, namely, μ*_v = μ*_R = μ*_P. Accordingly, with the optimal rewarding or punishing protocol, the dynamical system described by equation (2.1) can be solved and its solution is $p_C=1/[1+\hspace{0.17em}{\mathrm{e}}^{-{\beta }_{\mathrm{DB}}t}(1-p_0)/\hspace{0.17em}{p}_0]$, where β_DB = ω(k − 2)(ck − b)/(k − 1) and p₀ = p_C(0) > 0 denotes the initial fraction of cooperators in the population.

The cumulative cost produced by the rewarding protocol μ*_R for the dynamical system to reach the expected terminal state p_C(t_f) from the initial state p₀ is

$$\begin{array}{rl}{J}_R^{\ast }& ={\int }_0^{t_{\hspace{0.17em}f}}\frac{{(kN{p}_C{\mu }_R^{\ast })}^2}{2}\hspace{0.17em}\mathrm{d}t\\ & =\frac{{(kN{\mu }_R^{\ast })}^2}{2{\beta }_{\mathrm{DB}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-p_0}{\delta }\right)],\end{array}$$ 2.2

and, similarly, the cumulative cost produced by the punishing protocol μ*_P becomes

$$\begin{array}{rl}{J}_P^{\ast }& ={\int }_0^{t_{\hspace{0.17em}f}}\frac{{(kN{p}_D{\mu }_P^{\ast })}^2}{2}\hspace{0.17em}\mathrm{d}t\\ & =\frac{{(kN{\mu }_P^{\ast })}^2}{2{\beta }_{\mathrm{DB}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-\delta }{p_0}\right)].\end{array}$$ 2.3

We further find that J*_R > J*_P if p₀ > δ and J*_R < J*_P if p₀ < δ (see electronic supplementary material, section S1 for details).

For BD updating, the dynamical equation is

$$\begin{array}{rl}\frac{\mathrm{d}{p}_C}{\mathrm{d}t}& =F_{\mathrm{BD}}(p_C,{\mu }_v,t)\\ & =\frac{\omega k(k-2)}{k-1}({\mu }_v-c)p_C(1-p_C)+o({\omega }^2).\end{array}$$ 2.4

We prove that when μ_v > c, the system can reach the stable full cooperation state. Naturally, in the absence of incentives we get back the results of Ohtsuki et al. [15,16]. By solving the HJB equation, the optimal incentive protocol is μ*_v = 2c both for reward and punishment. The solution of equation (2.4) is $p_C=1/[1+\hspace{0.17em}{\mathrm{e}}^{-{\beta }_{\mathrm{BD}}t}(1-p_0)/\hspace{0.17em}{p}_0]$, where β_BD = ωk(k − 2)c/(k − 1) (see electronic supplementary material, section S2). Consequently, the cumulative cost to reach the expected terminal state in the case of the optimal rewarding protocol is

$$J_R^{\ast }=\frac{{(kN{\mu }_R^{\ast })}^2}{2{\beta }_{\mathrm{BD}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-p_0}{\delta }\right)],$$ 2.5

while for the optimal punishing protocol it is

$$J_P^{\ast }=\frac{{(kN{\mu }_P^{\ast })}^2}{2{\beta }_{\mathrm{BD}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-\delta }{p_0}\right)].$$ 2.6

In the case of IM updating, the dynamical equation becomes

$$\begin{array}{rl}\frac{\mathrm{d}{p}_C}{\mathrm{d}t}& =F_{\mathrm{IM}}(p_C,{\mu }_v,t)\\ & =\frac{\omega k^2(k-2)}{{(k+1)}^2(k-1)}[b+({\mu }_v-c)(k+2)]p_C(1-p_C)\\ & +o({\omega }^2),\end{array}$$ 2.7

which indicates that the system evolves to the full cooperation state if μ_v > c − b/(k + 2). The solution of HJB for the optimal incentive protocol gives μ*_v = 2[c(k + 2) − b]/(k + 2) both for reward and punishment (see electronic supplementary material, section S3). The solution of equation (2.7) is $p_C=1/[1+\hspace{0.17em}{\mathrm{e}}^{-{\beta }_{\mathrm{IM}}t}(1-p_0)/\hspace{0.17em}{p}_0]$, where β_IM = ωk²(k − 2)[c(k + 2) − b]/[(k + 1)²(k − 1)]. The cumulative cost required for the optimal rewarding protocol is

$$J_R^{\ast }=\frac{{(kN{\mu }_R^{\ast })}^2}{2{\beta }_{\mathrm{IM}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-p_0}{\delta }\right)],$$ 2.8

while for the optimal punishing protocol it becomes

$$J_P^{\ast }=\frac{{(kN{\mu }_P^{\ast })}^2}{2{\beta }_{\mathrm{IM}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-\delta }{p_0}\right)].$$ 2.9

When PC updating is applied, the dynamical equation is given by

$$\begin{array}{rl}\frac{\mathrm{d}{p}_C}{\mathrm{d}t}& =F_{\mathrm{PC}}(p_C,{\mu }_v,t)\\ & =\frac{\omega k(k-2)}{2(k-1)}({\mu }_v-c)p_C(1-p_C)+o({\omega }^2),\end{array}$$ 2.10

from which we find that when μ_v > c is satisfied, the stable full cooperation state can be reached (see electronic supplementary material, section S4). For the optimal incentive protocol, we get μ*_v = μ*_R = μ*_P = 2c. The solution of equation (2.10) is $p_C=1/[1+\hspace{0.17em}{\mathrm{e}}^{-{\beta }_{\mathrm{PC}}t}(1-p_0)/\hspace{0.17em}{p}_0]$, where β_PC = ωk(k − 2)c/[2(k − 1)]. Consequently, the cumulative cost for the optimal rewarding protocol is

$$J_R^{\ast }=\frac{{(kN{\mu }_R^{\ast })}^2}{2{\beta }_{\mathrm{PC}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-p_0}{\delta }\right)],$$ 2.11

while it is

$$J_P^{\ast }=\frac{{(kN{\mu }_P^{\ast })}^2}{2{\beta }_{\mathrm{PC}}}[\hspace{0.17em}{p}_0+\delta -1+\ln \left(\frac{1-\delta }{p_0}\right)],$$ 2.12

for the optimal punishing protocol.

Note that for each update rule, the governing equation in the weak selection limit always has two equilibrium points, which are the full defection and full cooperation states, respectively. Accordingly, we can obtain the minimal amounts of incentive needed for the evolution of cooperation, as summarized in figure 2. Independently of the applied update rule, the optimal incentive protocols are time-invariant and equal both for reward and punishment. Hence, μ*_v = μ*_R = μ*_P for each update rule. The optimal protocols are summarized in figure 2. We further present the cumulative cost for the optimal reward and punishment protocols for each update rule in figure 2.

Figure 2.

Optimization of institutional incentives for cooperation for different strategy update rules. Here, the minimal μ_R (μ_P) means the minimal amount of positive (negative) incentive needed for the evolution of cooperation for different strategy update rules. μ*_R (μ*_P) represents the optimal positive (negative) incentive protocol for different strategy update rules. $J_R^{\ast }$ ($J_P^{\ast }$) means the cumulative cost produced by the optimal rewarding (punishing) protocol μ*_R (μ*_P) for the dynamical system to reach the expected terminal state 1 − δ from the initial state p₀. In addition, N denotes the population size and k the degree of the regular network. b represents the benefit of cooperation and c the cost of cooperation. The parameters β_DB = ω(k − 2)(ck − b)/(k − 1) under DB updating, β_BD = ωk(k − 2)c/(k − 1) under BD updating, β_IM = ωk²(k − 2)[c(k + 2) − b]/[(k + 1)²(k − 1)] under IM updating, and β_PC = ωk(k − 2)c/[2(k − 1)] under PC updating.

2.2. Numerical calculations and computer simulations for optimal incentive protocols

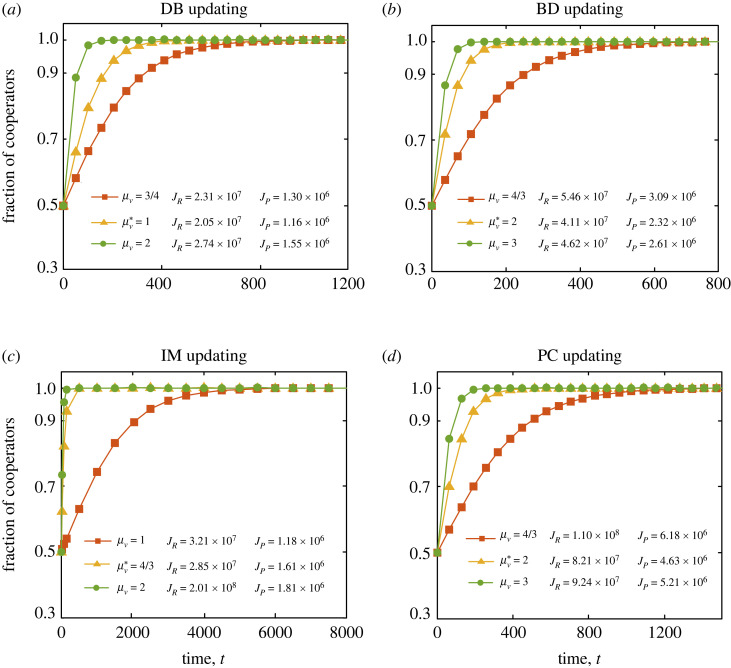
In the following, we validate our analytical results for μ*_v (v ∈ {R, P}) by means of numerical calculations and computer simulations. Figure 3 illustrates the fraction of cooperators p_C as a function of time t for the optimal μ*_v and two other incentive schemes under four strategy update rules we considered. First, we note that our system always reaches the expected terminal state p_C(t_f) = 0.99 when we launch the evolution from a random p₀ = 0.5 state for each update rule. However, reaching this state requires significantly different costs for the incentive-providing institution, and this value is the lowest for μ*_v , no matter whether we apply reward or punishment. Notably, the optimal incentive protocol does not produce the fastest relaxation.

Figure 3.

Time evolution of the fraction of cooperators for positive and negative incentives under different strategy update rules. Each panel shows the results derived from numerical calculations based on the obtained dynamical equation at different levels of incentives for reward (R) or punishment (P). The optimal incentive level is marked by asterisk (*). For comparison we have also marked the J_R and J_P amounts of cumulative cost to reach the desired terminal state for each incentive protocol. Parameters: N = 100, b = 2, c = 1, δ = 0.01, ω = 0.01, p₀ = 0.5 and k = 4.

Moreover, we present the results of Monte Carlo simulations when positive or negative incentives are applied for each update rule (electronic supplementary material, figures S1–S4). We can find that for different update rules the usage of optimal incentive protocol does not result in the fastest relaxation to the desired cooperation state, but it always leads to the smallest cumulative cost for the institution. We must stress that our findings are not limited to regular networks, but they remain valid for a broad range of interaction graphs from irregular random networks to small-world networks and scale-free networks. Our numerical calculations and simulations results coincide with the analytical predictions, and they illustrate that the cumulative cost is the lowest under the optimal incentive protocol.

2.3. Comparison between optimal reward and punishment protocols

Through theoretical analysis presented in the electronic supplementary material, we can conclude that the execution of optimal punishing scheme requires a lower cumulative cost, compared with the optimal rewarding scheme for each update rule, if the initial cooperation level is larger than the difference between the full and desired cooperation states. Otherwise, the usage of optimal rewarding scheme requires a lower cumulative cost. In order to verify such theoretical prediction and have an intuitive comparison, we show the cumulative cost values induced by the optimal punishing and rewarding protocols when the initial fraction p₀ of cooperators is adjustable. By assuming the optimal protocols of incentives, the requested cumulative cost can be determined by numerically integrating or by using Monte Carlo simulations.

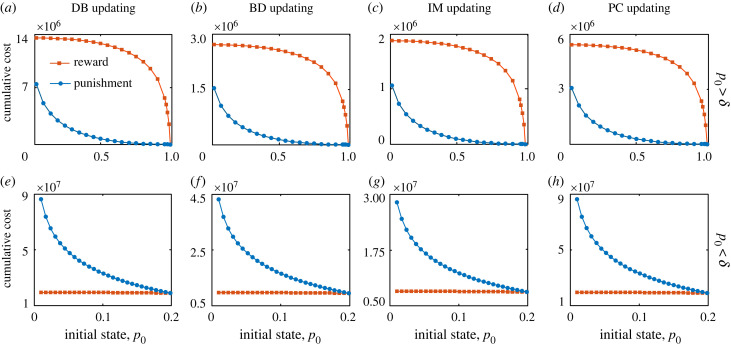
Our numerical results are summarized in figure 4 for each update rule. From the top row of figure 4, we observe that when the initial cooperation level is larger than the difference between the full cooperation and desired terminal states (with a set tolerance for defection, δ), the institution needs to spend less cumulative cost to reach the expected cooperation state by means of punishing. On the contrary, from the bottom row of figure 4, we see that when the initial cooperation level is less than the difference between the full cooperation and desired terminal states, the institution needs to spend less cumulative cost to reach the expected cooperation state by means of rewarding. However, in these different cases, no matter whether the optimal rewarding or punishing protocol is applied, the corresponding cumulative cost value decreases as the initial cooperation level p₀ increases. In addition, our simulations results presented in figure S5 of the electronic supplementary material also support our theoretical analysis, which provides a rigorous basis for the usage of incentives under different initial conditions in the context of evolutionary Prisoner’s Dilemmas game in structured populations.

Figure 4.

Cumulative cost needed for reaching the expected terminal state in dependence of the p₀ initial portion of cooperators for the optimal rewarding and punishing protocols for different strategy update rules. Each column of panels represents a strategy update rule as indicated. Top row represents the results of numerical calculations based on the obtained dynamical equation in the condition of p₀ > δ = 0.01, while bottom row represents the results of numerical calculations in the condition of p₀ < δ = 0.2. Other parameters: N = 100, b = 2, c = 1, ω = 0.01 and k = 4.

3. Discussion

In human society, prosocial incentives are an essential means of avoiding the ‘tragedy of the commons’ [21,22,40]. For incentive-providing institutions, however, the choice of incentives is mainly based on two aspects. One of them is knowing how much incentive is needed to promote the evolution of cooperation (potentially under different update rules) in structured populations. The other is whether the applied incentive scheme is an optimal time-dependent protocol requiring the minimal cost for the institution.

In order to investigate the above-mentioned tasks, we establish a game-theoretical framework. Namely, we consider the positive or negative incentive into the networked Prisoner’s Dilemma game with four different strategy update rules, respectively. For a given update rule, we obtain the theoretical conditions of the minimal amounts of incentives needed for the evolution of cooperation. By establishing an index function for quantifying the executing cost, we derive the optimal positive and negative incentive protocols for each strategy update rule, respectively, by means of the approach of HJB equation. We find that these optimal incentive protocols are time-invariant for all the considered update rules. In addition, the optimal incentive protocols are identical both for negative and positive incentives. However, applying the punishing scheme requires a lower cumulative cost for the incentive-providing institution when the initial cooperation level is relatively high; otherwise, applying the rewarding scheme is cheaper. We further perform computer simulations, which confirm that our results are valid in different types of interaction topologies described by regular, random, small-world and scale-free networks and thus demonstrate the general robustness of the findings.

In this work, we have quantified how much incentive is needed for the evolution of cooperation under each update rule we considered. However, when prosocial incentives are provided, the game structure may be changed. In particular, when the incentive amount μ_v > c, the Prisoner’s Dilemma game will be transformed into the harmony game, where cooperators dominate defectors naturally [9]. Interestingly, we note that if μ_v > c − b/k under DB updating and if μ_v > c − b/(k + 2) under IM updating, cooperation is favoured. This implies that under DB and IM rule, the μ_v value can be smaller than the cost c, which guarantees that the game structure is not changed. For BD and PC updating, however, the incentive amount needed for the evolution of cooperation must completely outweigh the cost of cooperation. Hence the effectiveness of interventions might shed some light on which update type can best capture population behaviours.

Here, we stress that the obtained optimal incentive protocols are time-invariant by solving the optimal control problems we formulated. More strikingly, the obtained optimal negative incentive protocol for each update rule is the same as the optimal positive incentive protocol. Thus, these optimal incentive protocols are state-independent. Then the institution does not need to monitor the population state from time to time for optimal incentive implementation and can save monitoring costs since monitoring is generally costly. In addition, the optimal incentive level for DB and IM updating can guarantee that the dilemma faced by individuals is still a Prisoner’s Dilemma. Accordingly, our work reflects that the incentive-based control protocols we obtained under DB and IM updating are simple and effective for promoting the evolution of cooperation in structured populations.

Incentives can be used as controlling tools to regulate the decision-making behaviours of individuals [28]. However, there are significant preference differences in the usage of punishment and reward for the evolution of cooperation from the perspectives of individuals and incentive-providing institutions [41]. It has been suggested that punishment is often not preferred since the usage of punishment leads to a low total income or a low average payoff in repeated games [23,24]. By contrast, incentive-providing institutions prefer to use punishments more frequently. This is because punishment incurs a lower cost of implementing incentives for the promotion of cooperation [30,41]. Here, we consider the top-down-like incentive mechanism under which cooperators can be rewarded or defectors can be punished directly by the external centralized institution, which has existed and works stably. In this framework, we strictly compare the rewarding and punishing schemes concerning implementation cost and show how the best choice depends on the initial cooperation level, providing a rigorous basis for the usage of incentives in the context of the Prisoner’s Dilemma game and where it might apply in human society.

Extensions of our work are plentiful, especially in analytical terms. We would like to point out that we use the pair approximation approach to obtain our analytical results and this approach is used mainly for regular networks [15]. Indeed, this approach can be extended for other types of complex networks when the properties of these networks are additionally considered [42,43]. Along this line, hence it is worth analytically investigating the low-cost incentive policy for the evolution of cooperation by fully considering spatial properties of the underlying population structures. Furthermore, our theoretical analysis could be extended by resorting to methods relying on calculating the coalescence times of random walks [11]. These methods might be particularly constructive when interventions at the topology level are at stake since they create a tighter link between the outcome and the network. In addition, we obtain our theoretical results in the limit of weak selection. Numerical analysis in other contexts has shown that due to relevant factors from the environment, the intensity of selection can change the game dynamics no matter the population is well-mixed or structured, and plays a crucial role in the determination of cost-efficient institutional incentive [44–47]. Hence, a natural question arising here is whether our theoretical results are still valid when selection is not weak [48]. Indeed, analytical calculations for strong selection remain tractable for some structures with high symmetry. Thus, there is potential to identify the theoretical conditions of how much incentive is needed to promote cooperation and to explore the optimal incentive protocols for these population structures.

In addition, our work focuses on minimizing the incentive costs up to a set level of cooperation in a population, irrespectively of how long that takes. Further research is required for situations in which the rate at which the transition happens can be important and a time-varying protocol might be the solution. We consider our research in the framework of the Prisoner’s Dilemma game, which is a paradigm for studying the evolution of cooperation. There are other prototypical two-person dilemmas, e.g. snowdrift game [49] and stag-hunt game [50]. A promising extension of this work is to consider these mentioned games for future study as well as group interactions or higher-order interactions [51–55]. Furthermore, we design the cost-efficient incentive protocols by considering the global information (i.e. the fraction of cooperators in the whole population), but the local neighbourhood properties on a structured network, such as how many cooperators are there in a neighbourhood, affect the final evolutionary outcomes [56–58]. Hence, it would be important to take into account this local information for optimal incentive protocols with minimal cost in the future work. Finally, other prosocial behaviours, such as honesty [59] or trust and trustworthiness [60], are also fundamental for cooperation, and hence it is a meaningful extension to study the optimization problems of incentives for promoting the evolution of these behaviours.

4. Model and methods

4.1. Prisoner’s Dilemma game

We consider that a population of individuals are distributed on the nodes of an interaction graph. At each round, each individual plays the evolutionary Prisoner’s Dilemma game with its neighbours and can choose to cooperate (C) or defect (D). We consider the payoff matrix for the game as

$$\begin{array}{ll}& \hspace{0.17em}\begin{array}{cc}C& D\end{array}\\ & \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}b-c& -c\\ b& 0\end{array}\right)\end{array},$$ 4.1

where b represents the benefit of cooperation and c (0 < c < b) represents the cost of cooperation. After engaging in the pairwise interactions with all the adjacent neighbours, each individual collects its payoff based on the payoff matrix.

4.2. Institutional incentives

Furthermore, prosocial incentives provided by incentive-providing institutions can be used to reward cooperators or punish defectors after they play the game with their neighbours. Here, we consider both types of incentives, i.e. positive and negative incentives, respectively. If positive incentives are used, then a cooperator in the game is rewarded with a μ_R amount received from a central institution when interacting with a neighbour [24,28]. If negative incentives are used, then a defector is fined by a μ_P amount for each interaction [23]. Consequently, when positive incentives are used, the modified payoff matrix becomes

$$\begin{array}{ll}& \hspace{0.17em}\begin{array}{cc}C& D\end{array}\\ & \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}b-c+{\mu }_R& -c+{\mu }_R\\ b& 0\end{array}\right),\end{array}$$ 4.2

and when negative incentives are used, the modified payoff matrix becomes

$$\begin{array}{ll}& \hspace{0.17em}\begin{array}{cc}C& D\end{array}\\ & \begin{array}{c}C\\ D\end{array}\left(\begin{array}{cc}b-c& -c\\ b-{\mu }_P& -{\mu }_P\end{array}\right).\end{array}$$ 4.3

As a result, based on the above payoff matrices each individual collects its total payoff, which is derived from the pairwise interactions with neighbours and the incentive-providing institution.

4.3. Strategy update rules

According to the evolutionary selection principle, players update their strategies from time to time, but the way how to do it may influence the evolutionary outcome significantly [9,15]. In agreement with previous works [15,16], we here consider four major strategy update rules, describing DB, BD, IM and PC updating. Specifically, for DB updating, at each time step a random individual from the entire population is chosen to die; subsequently the neighbours compete for the empty site with probability proportional to their fitness. For BD updating, at each time step an individual is chosen for reproduction from the entire population with probability proportional to fitness; the offspring of this individual replaces a randomly selected neighbour. For IM updating, at each time step a random individual from the entire population is chosen to update its strategy; it will either stay with its own strategy or imitate one of the neighbours’ strategies with probability proportional to their fitness. For PC updating, at each time step a random individual is chosen to update its strategy, and it compares its own fitness with a randomly chosen neighbour. The focal individual either keeps its current strategy or adopts the neighbour’s strategy with a probability that depends on the fitness difference.

4.4. Optimizing incentives

Since providing incentives is costly for institutions, it has a paramount importance to find the optimal ${\mu }_v^{\ast }$, which requires the minimal effort but is still capable of supporting cooperation effectively. To reach this goal, we first establish an index function for quantifying the executing cumulative cost, which is expressed as

$$J_v={\int }_{t_0}^{t_{\hspace{0.17em}f}}\frac{{(kN{p}_i{\mu }_v)}^2}{2}\hspace{0.17em}\mathrm{d}t,$$ 4.4

where p_i = p_C if v = R, which means that positive incentives are applied, otherwise p_i = p_D, which means that negative incentives are applied. Here t₀ is the initial time and is set to 0 in this work, and t_f is the terminal time for the system. Based on the above description, we then explore the optimal incentive protocol during the evolutionary period between 0 and t_f by using optimal control theory [37–39]. It is a crucial assumption that t_f is not fixed, but we monitor the evolution until the fraction of cooperators reaches the target level p_C(t_f) at t_f. Here, we suppose that p_C(t_f) = 1 − δ > p₀, where p₀ (p₀ > 0) is the initial cooperation level and δ is the parameter determining the expected cooperation level at t_f, satisfying 0 ≤ δ < 1 − p₀.

Accordingly, we formulate the optimal control problem for reward or punishment given as

$$\begin{array}{rl}& min{J}_v={\displaystyle {\int }_0^{t_{\hspace{0.17em}f}}\frac{{(kN{p}_i{\mu }_v)}^2}{2}\hspace{0.17em}\mathrm{d}t,}\\ & \text{s.t.}\{\begin{array}{c}\frac{\mathrm{d}{p}_C}{\mathrm{d}t}=F_{\hspace{0.17em}j}(p_C,{\mu }_v,t),j=\mathrm{DB},\hspace{0.17em}\mathrm{BD},\hspace{0.17em}\mathrm{IM},\hspace{0.17em}\mathrm{or}\hspace{0.17em}\mathrm{PC},\\ p_C(0)=p_0,\\ p_C(t_{\hspace{0.17em}f})=1-\delta .\end{array}\end{array}$$ 4.5

Here the cost function J_v characterizes the cumulative cost on average during the period [0, t_f] for the dynamical system to reach the terminal state 1 − δ from the initial state p₀. Thus the quantity min J_v can work as the objective of calculating the optimal incentive protocol ${\mu }_v^{\ast }$ with the minimal executing cost. The details of solving the optimal control problems can be found in sections S1–S4 of the electronic supplementary material.

4.5. Monte Carlo simulations

During a full Monte Carlo step, on average each player has a chance to update its strategy. The applied four different update rules are specified above. Besides, we have tested alternative interaction topologies, including regular networks generated by using a two-dimensional square lattice of size N = L × L [4] and scale-free networks obtained by using preferential-attachment model [7] starting from m₀ = 6, where at every time step each new node is connected to m = 2 existing nodes fulfilling the standard power-law distribution. Alternatively, Erdös–Rényi random graph model [5] and small-world networks of Watts–Strogatz model with p = 0.1 rewiring parameter [6] are considered. These simulation results are summarized in figures S1–S5 of the electronic supplementary material.

Data accessibility

The data are provided in the electronic supplementary material [61].

Authors' contributions

S.W.: conceptualization, formal analysis, investigation, writing—original draft, writing—review and editing; X.C.: conceptualization, formal analysis, funding acquisition, supervision, writing—original draft, writing—review and editing; Z.X.: data curation, formal analysis, investigation; A.S.: conceptualization, formal analysis, writing—original draft, writing—review and editing; V.V.V.: conceptualization, formal analysis, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

This research was supported by the National Natural Science Foundation of China (grant nos. 61976048 and 62036002) and the Fundamental Research Funds of the Central Universities of China. S.W. acknowledges the support from China Scholarship Council (grant no. 202006070122). A.S. was supported by the National Research, Development and Innovation Office (NKFIH) under grant no. K142948. V.V.V. acknowledges funding from the Computational Science Lab—Informatics Institute of the University of Amsterdam.