Skip to main content
PMC home page
Cerebral Cortex (New York, NY) logoLink to Cerebral Cortex (New York, NY)
. 2022 Mar 11;33(3):729–739. doi: 10.1093/cercor/bhac096

Simultaneous relaxometry and morphometry of human brain structures with 3D magnetic resonance fingerprinting: a multicenter, multiplatform, multifield-strength study

Shohei Fujita 1,2,✉, Matteo Cencini 3,4, Guido Buonincontri 5,6, Naoyuki Takei 7, Rolf F Schulte 8, Issei Fukunaga 9, Wataru Uchida 10, Akifumi Hagiwara 11, Koji Kamagata 12, Yasuhiro Hagiwara 13, Yutaka Matsuyama 14, Osamu Abe 15, Michela Tosetti 16,17, Shigeki Aoki 18
PMCID: PMC9890456  PMID: 35271703

Abstract

Relaxation times and morphological information are fundamental magnetic resonance imaging-derived metrics of the human brain that reflect the status of the underlying tissue. Magnetic resonance fingerprinting (MRF) enables simultaneous acquisition of T1 and T2 maps inherently aligned to the anatomy, allowing whole-brain relaxometry and morphometry in a single scan. In this study, we revealed the feasibility of 3D MRF for simultaneous brain structure-wise morphometry and relaxometry. Comprehensive test–retest scan analyses using five 1.5-T and three 3.0-T systems from a single vendor including different scanner types across 3 institutions demonstrated that 3D MRF-derived morphological information and relaxation times are highly repeatable at both 1.5 T and 3.0 T. Regional cortical thickness and subcortical volume values showed high agreement and low bias across different field strengths. The ability to acquire a set of regional T1, T2, thickness, and volume measurements of neuroanatomical structures with high repeatability and reproducibility facilitates the ability of longitudinal multicenter imaging studies to quantitatively monitor changes associated with underlying pathologies, disease progression, and treatments.

Keywords: quantitative MRI, relaxation times, T1, T2, thickness, volume

Introduction

Relaxation times and morphological information are fundamental magnetic resonance imaging (MRI)-derived metrics of the human brain. Longitudinal (T1) and transverse (T2) relaxation times are the dominating factors of MRI signals and are intrinsic tissue-specific parameters that may relate to pathologic conditions at the cellular level (Seiberlich et al. n.d., online resource; Tofts 2003). Brain morphological parameters such as the cortical thickness and volumes of brain structures are fundamental properties of the human brain, which reflect pathologic conditions at the tissue-organ level. Changes in the relaxation time, cortical thickness, and volume of brain structures have specific patterns during development, aging, and various neurological and neuropsychiatric disorders (Vrenken et al. 2006; Sabuncu et al. 2016; Hagiwara et al. 2021): for instance, temporal epilepsy is characterized by the volume loss and T2 elongation of the hippocampus, and Alzheimer’s disease is characterized by volume losses in the temporal and parietal lobes. Detecting these patterns in neuroanatomically meaningful brain regions enables objective characterization of the subject.

Tissue-specific relaxation times and morphological information individually reflect the status of the underlying tissue; however, their combination can help improve patient assessment. While the combined analysis of relaxometry and morphometry has been applied to tasks including automatic detection and quantification of lesions and regional brain structures (Pell et al. 2004; Knight et al. 2019), relaxometry and structural imaging are usually acquired independently. Multiple separate scans require longer imaging times, unavoidably leading to problems such as misalignment.

Magnetic resonance fingerprinting (MRF) is a new framework that rapidly and simultaneously acquires T1 and T2 maps (Ma et al. 2013). The maps are pattern-matched using time-efficient frameworks performed in a single scan rather than performing separate scans for each relaxation map. These quantitative maps can be used to calculate images with different contrast, including structural T1-weighted images. Because all relaxation time maps and images are acquired from a single scan, the information regarding the relaxation times is inherently aligned to the anatomy, eliminating misregistration. Furthermore, 3D whole-brain scans can now be performed within 10 min, thus enabling it to be performed in a clinically acceptable time (Cao et al. 2019; Ma et al. 2019; Gómez et al. 2020). In addition to the inherently aligned maps, whole-brain MRF scans in high-resolution and 3D can provide relaxation times and morphological information in a single scan.

The repeatability and reproducibility of quantitative imaging techniques necessitate evaluation, as quantitative imaging relies on the acquisition of data using multiple scanners across multiple institutions that can be subsequently pooled for analysis. Hence, for multicenter studies, it is critical to determine the device-related variations in detecting meaningful biological changes. Previous studies have shown that 2D MRF provides relaxation maps with high repeatability and reproducibility in both phantoms (Jiang et al. 2017; Buonincontri et al. 2019; Kato et al. 2019; Korzdorfer, Kirsch, et al. 2019; Shridhar Konar et al. 2021) and the human brain (Buonincontri et al. 2019; Korzdorfer, Kirsch, et al. 2019). However, studies focusing on the repeatability and reproducibility of MRF have been mainly performed in a voxel-wise manner or a limited number of regions of interest. Few studies have analyzed the brain structure-wise morphometry and relaxometry using MRF, despite their importance (Korzdorfer, Kirsch, et al. 2019; Fujita et al. 2020).

This study aimed to demonstrate the feasibility of 3D MRF-based simultaneous relaxometry and morphometry of the human brain structures. The repeatability and reproducibility of these parameters in various regions of the brain were evaluated in healthy volunteers using scan–rescan tests on different scanners across multiple institutions with different magnetic field strengths.

Materials and methods

This is a secondary analysis of the data prospectively collected for an international multicenter study (Buonincontri et al. 2020). The previous article dealt with the relaxation times in a voxel-wise manner, whereas in this manuscript, we expand on this by performing segmentation-based relaxometry and morphometry. All data from the previous article were used. This study was approved by the institutional review board at each institution. Written informed consent was obtained from all participants prior to the scan.

Study design

Healthy volunteers underwent 3D MRF test–retest sessions at 8 sites between September and October 2019. Data were obtained using five 1.5-T and three 3.0-T scanners with different platforms across 3 institutions (Table 1). Each “x” in Table 1 indicates a test–retest session. For each site, the participants were removed from the scanner after the first 3D MRF scan and repositioned before the 3D MRF rescan. The pulse sequence and reconstruction pipeline were the same for all acquisitions.

Table 1.

Matrix of participants and scanning devices.

Scanner no. 1 2 3 4 5 6 7 8
Scanner type MR750 Signa Artist HDxt HDxt MR450 MR450w MR750 Signa Artist
Field strength 3.0 T 1.5 T 3.0 T 1.5 T 1.5 T 1.5 T 3.0 T 1.5 T
Head channels 8 12 8 8 12 12 12 12
Subject 1 x x
Subject 2 x x x x x x x x
Subject 3 x x x x x x x x
Subject 4 x x x x
Subject 5 x x x x
Subject 6 x x
Subject 7 x x x x x x x x
Subject 8 x x x x
Subject 9 x x x x x x x x
Subject 10 x x
Subject 11 x x x x
Subject 12 x x x x
Open in a new tab

Note: All scanners were manufactured by GE healthcare.

MRF acquisition and reconstruction

We used inversion-prepared 3D steady-state free precession MRF implementation (Jiang et al. 2015; Gómez et al. 2020) with a variable flip angle schedule for T1 and T2 quantification (see Supplementary Fig. E1a). This acquisition was previously validated in phantoms against gold standard references and is reported in detail by Gómez et al. (2020). The flip angle schedule consisted of an ascending and descending ramp with a 70° maximum flip angle (see Supplementary Fig. E1b). Echo time (0.5 ms) and repetition time (11 ms) were kept constant during the acquisition. The k-space sampling was performed using a 3D spiral projection trajectory (Cao et al. 2019) with a single interleave for each frame. Each frame included a spoiler gradient along the z-axis, achieving a 4-π dephasing across a voxel. The other trajectory parameters were as follows: field of view, 225 × 225 × 225 mm; matrix size, 200 × 200 × 200; spatial resolution, 1.125-mm isotropic (voxel resolution); and acquisition time, 9 min 3 s for both 1.5 T and 3.0 T.

The data were reconstructed as follows: the k-space data were initially compressed using singular-value decomposition as proposed by (McGivney et al. 2014), retaining the first 10 subspace coefficients. Subsequently, singular-value decomposition-compressed images were obtained for each coil by nonuniform Fourier transform (Fessler 2007). The first subspace coefficient for each coil was used to estimate the coil sensitivity profiles as described by (Walsh et al. 2000). Lastly, data from each coil were combined, and T1 and T2 quantitative maps were retrieved by inner-product pattern matching (Ma et al. 2013) with a precomputed dictionary of signal evolutions. Dictionary entries were generated using the extended phase graph formalism (Weigel 2015), with T1 values ranging from 20 to 3000 ms (10-ms steps) and 3000 to 5000 ms (200-ms steps) and T2 values ranging from 10 to 300 ms (2-ms steps) and 300 to 500 ms (50-ms step). MRF-derived quantitative maps were postprocessed voxel-wise to generate synthetic contrast-weighted images using the following equations:

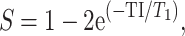graphic file with name DmEquation1.gif

where S is the output signal of T1-weighted image, T1 is the T1 value obtained using MRF, and TI is the inversion time virtually set to 1,300 ms.

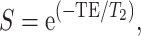graphic file with name DmEquation2.gif

where S is the output signal of T2-weighted image, T2 is the T2 value obtained using MRF, and TE is the echo time virtually set to 100 ms.

The effects of transmitter inhomogeneities (B1+) were not included in the model. All maps and contrast-weighted images were reviewed by an experienced radiologist to identify any possible brain abnormality, truncation, ringing, aliasing, and chemical shift artifacts or any other image quality degradation such as spike noise, signal nonuniformity, banding, and blurring (Zhuo and Gullapalli 2006).

Structural parcellation and calculation of regional quantitative metrics

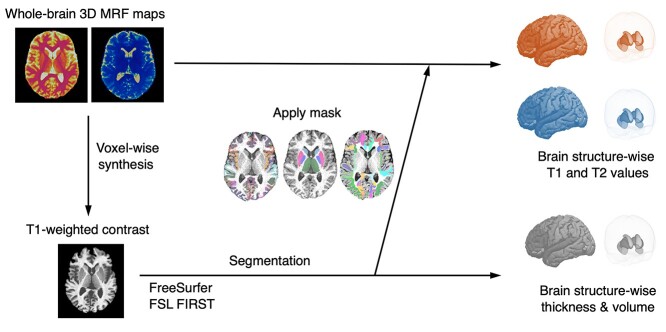
The main postprocessing steps are illustrated in Fig. 1. The MRF-derived T1-weighted images were imported into an automated brain parcellation software generating subject-specific neuroanatomical parcellation. We did not perform any MRF-based tissue segmentations. For cortical and white matter structures, FreeSurfer (version 6.0) (Fischl 2012) was used to determine the regional cortical thickness for each representative neuroanatomical region in the Desikan–Killiany atlas (Desikan et al. 2006). Subcortical structures were parcellated using FSL FIRST (version 6.0.0) (Patenaude et al. 2011) due to a previous study demonstrating the unreliability of FreeSurfer when parcellating subcortical structures (Dale et al. 1999). FreeSurfer and FIRST were chosen because these are the most widely accepted software solutions to parcellate neuroanatomical regions from brain MRI scans. The output mask of FreeSurfer, initially in the Talairach space, was processed using the mri_label2vol (https://surfer.nmr.mgh.harvard.edu/fswiki/FsAnat-to-NativeAnat) function to recoordinate to the individual subject space. The output masks of the FSL FIRST are in the individual subject space without any postprocessing. These subject-specific parcellation binary masks were directly applied to T1 and T2 maps to obtain median relaxation times for each corresponding neuroanatomical region. Following the evaluation procedure of a previous study (Korzdorfer, Kirsch, et al. 2019), median values were used here to mitigate the effect of outliers due to minor missegmentation. Although visual inspections for major missegmentations were performed, perfect segmentation was difficult, given the complex structure of the cortex. Small missegmentations—especially in the cortical structures—will lead to the inclusion of extremely large T1 and T2 values originating from the CSF in the VOI, resulting in outliers, which will hinder the evaluation. Bilateral regional values were first averaged for each scan and then used for subsequent analysis.

Fig. 1.

Fig. 1

Open in a new tab

Schematic showing the postprocessing to calculate brain structure-wise T1, T2, cortical thickness, and subcortical volume values from 3D MRF maps. MRF-derived T1 maps are postprocessed voxel-wise to generate synthetic T1-weighted images (left). These MRF-derived T1-weighted images are imported into the automated brain parcellation software to generate subject-specific neuroanatomical parcellation (bottom). These subject-specific parcellation masks are directly applied to the T1 and T2 maps to obtain median relaxation times for each corresponding neuroanatomical region (top).

Statistical analysis

Repeatability and reproducibility variations were estimated using the within-subject coefficient of variation (wCV, standard deviation [SD] of T1 or T2 measures divided by their mean) at 1.5 T and 3.0 T. To evaluate the scan-rescan intrascanner repeatability, wCV was calculated in each brain region between the test and retest, for each scanner and subject. To evaluate the interscanner reproducibility, wCV was calculated in each brain region between the test scans across scanners (rescan data were discarded because in clinical settings, only a single scan is available) for each subject. Lower wCVs indicate less variance and thus, higher performance. Bland–Altman plots were used to demonstrate intrascanner repeatability and interscanner reproducibility by evaluating agreement and bias between scans (Bland and Altman 1986). For morphological metrics (i.e. cortical thickness and subcortical volume), interfield-strength reproducibility was also assessed using wCV and Bland–Altman plots. Since relaxation times depend on the static magnetic field strength, no comparison between the fields was performed. The wCV was calculated for each brain region for each subject using the average value across sites for each magnetic field strength. The limit of agreement (LOA) was defined as the mean ± 1.96 × SD. The LOA with the mean, assessing the agreement with the mean among multiple observers, was calculated for interscanner data. Intraclass correlation coefficients were not used since the study population was homogeneous.

Given the interscanner SD of measurement error, sample size calculations can be conducted to estimate the required sample size (number of subjects) needed to detect a desired difference between the subject groups. The number of subjects needed to detect a 10% difference in measurement was calculated assuming a statistical power of 0.9 with a 1-sided significance level of 0.05 (Machin et al. 2009). A 10% effect size, typical for this type of study, was chosen based on a previous study by (Thompson et al. 2003), which compared mean cortical thickness between patients with Alzheimer’s disease and control participants. The sample size analysis was performed using the standard formula implemented online (http://www.hedwig.mgh.harvard.edu/sample_size/size.html).

All other statistical analyses were performed with R v4.0.4 (R Core Team, Vienna, Austria; https://www.R-project.org/) using the package tidyverse.

Results

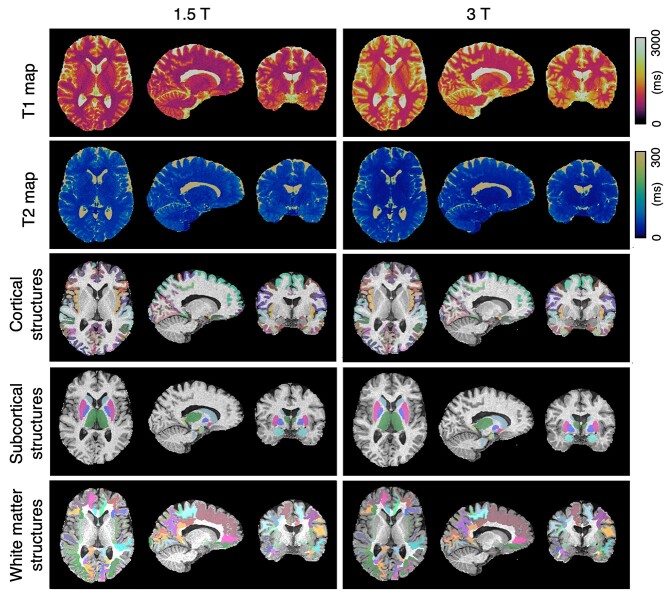
This study included 12 healthy volunteers (10 males and 2 females; age range, 28–43 years). Among the 116 MRF scans, 3 scans exhibited obvious signal nonuniformity, consistent with individuals’ involuntary motions. The remaining 113 scans (97.4%) passed the visual inspection and completed the automated parcellation pipeline without error. No brain abnormality was reported in any of the volunteers. Figure 2 shows an example of a subject’s output of a 3D MRF T1 map, a T2 map, cortical parcellations, and subcortical parcellations for 1.5 T and 3.0 T. Representative contrast-weighted images generated from the quantitative T1 and T2 maps are shown in Supplementary Fig. E2.

Fig. 2.

Fig. 2

Open in a new tab

Representative 3D MRF T1 and T2 maps and neuroanatomical parcellations of 3D MRF-derived T1-weighted images at 1.5 T and 3.0 T. Representative FreeSurfer labels created from automated parcellation of brain regions using 3D MRF-based T1-weighted images. Images and parcellations at 1.5 T (left) and 3.0 T (right). Results of automated brain parcellations are overlaid on the 3D MRF-based T1-weighted images.

Intrascanner repeatability of relaxation times and brain morphology measured with 3D MRF

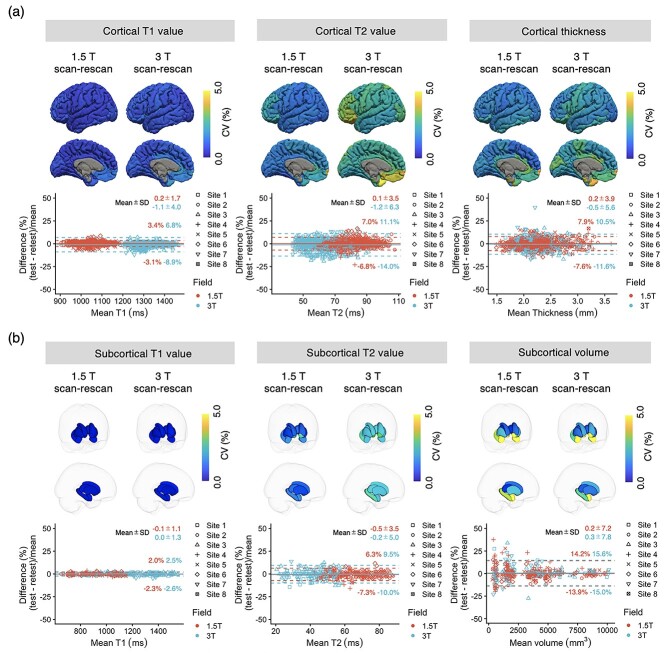
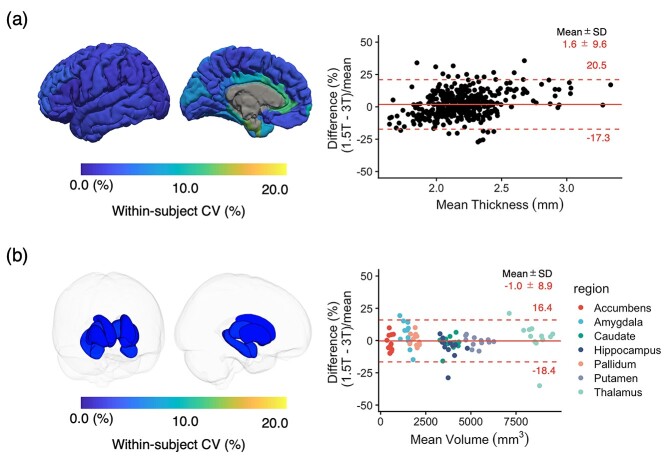
The intrascanner wCVs of regional T1, T2, and thickness across all cortical structures at 1.5 T were 0.8 ± 0.2, 1.7 ± 0.5, and 2.1 ± 0.7%, respectively, whereas those at 3.0 T were 1.1 ± 0.3, 2.9 ± 0.6, and 2.5 ± 0.8%, respectively (Fig. 3a). The wCVs of regional T1, T2, and volume across all subcortical structures at 1.5 T were 0.6 ± 0.2, 1.8 ± 0.5, and 3.3 ± 2.3%, respectively, whereas those at 3.0 T were 0.7 ± 0.2, 2.5 ± 0.3, and 3.1 ± 1.7%, respectively (Fig. 3b). The wCVs of regional T1, T2, and volume across all white matter structures at 1.5 T were 0.7 ± 0.4, 1.6 ± 0.5, and 2.7 ± 1.3%, respectively, whereas those at 3.0 T were 0.8 ± 0.7, 2.7 ± 0.7, and 5.8 ± 3.0%, respectively (Supplementary Fig. E3). The intrascanner wCVs for each cortical, subcortical, and white matter structure are provided in Supplementary Figs. E4–E6, respectively. T2 showed higher wCV values compared with T1 in both cortical and subcortical structures, regardless of the magnetic field strength. Relatively high variations were observed in the T1, T2, and volume of the frontal pole, and volumes of the entorhinal cortex, nucleus accumbens, and amygdala.

Fig. 3.

Fig. 3

Open in a new tab

Intrascanner repeatability. (a) Intrascanner repeatability of T1, T2, and thickness of cortical regions. The scan-rescan within-subject coefficients of variation (wCVs) of relaxation times and thickness of cortical structures acquired with three-dimensional MRF. The scan-rescan wCVs of regional cortical thickness, T1, and T2 values are overlaid on an inflated brain surface. Bland–Altman plots showing scan-rescan variations of T1, T2, and thickness in all cortical structures. (b) Intrascanner repeatability of T1, T2, and volume of subcortical structures. The scan-rescan wCVs of volume and relaxation times on subcortical structures acquired using 3D MRF. Each subcortical structure is colored according to the regional wCV, and the brain surface is transparent for visualization purposes. Bland–Altman plots showing scan-rescan variations of T1, T2, and volume in all subcortical structures. The limits of agreement located at 1.96 × SDs of the distribution are plotted as dashed lines.

Interscanner reproducibility of relaxation times and brain morphology measured with 3D MRF

The interscanner wCVs of regional T1, T2, and thickness of cortical structures across all 1.5-T scanners were 2.1 ± 0.7, 9.8 ± 1.6, and 3.3 ± 0.8%, respectively, whereas those at 3.0 T were 3.1 ± 0.8, 8.7 ± 5.6, and 5.4 ± 2.1%, respectively (Fig. 4a). The interscanner wCVs of regional T1, T2, and volume of subcortical structures across all 1.5-T scanners were 1.6 ± 0.5, 10.5 ± 1.1, and 4.9 ± 2.5%, respectively, whereas those at 3.0 T were 4.4 ± 1.6, 7.2 ± 2.2, and 8.8 ± 6.3%, respectively (Fig. 4b). The interscanner wCVs of regional T1, T2, and volume of white matter structures across all 1.5-T scanners were 1.4 ± 0.4, 10.6 ± 1.3, and 3.5 ± 1.3%, respectively, whereas those at 3.0 T were 6.8 ± 1.3, 7.8 ± 2.9, and 5.85 ± 3.6%, respectively (Supplementary Fig. E7). The interscanner wCVs for each cortical, subcortical, and white matter structure are provided in Supplementary Figs. E8–E10, respectively. The 3.0-T scanners showed higher interscanner wCVs in T1 values of subcortical structures compared with scanners operating at 1.5 T. To detect a 10% change in the relaxation time and brain morphology with 3D MRF using different scanners and assuming a statistical power of 0.9 with a 1-sided significance level of 0.05, a sample size of 1 was required for T1, 8 for T2, 3 for cortical thickness, and 5 for volumes of subcortical structures.

Fig. 4.

Fig. 4

Open in a new tab

Interscanner repeatability. (a) Interscanner reproducibility of T1, T2, and thickness of cortical regions. The wCVs of relaxation times and thickness of cortical structures acquired with 3D MRF. The wCVs of T1, T2, and cortical thickness values are overlaid on an inflated brain surface. Bland–Altman plots showing scan-rescan variations of T1, T2, and thickness in all cortical structures. (b) Interscanner reproducibility of T1, T2, and volume of subcortical structures. The wCVs of relaxation times and volumes of subcortical structures acquired with 3D MRF. Each subcortical structure is colored according to the regional wCV, and the brain surface is transparent for visualization purposes. Bland–Altman plots showing scan-rescan variations of T1, T2, and volume in all subcortical structures. The limits of agreement with the mean are plotted as dashed lines.

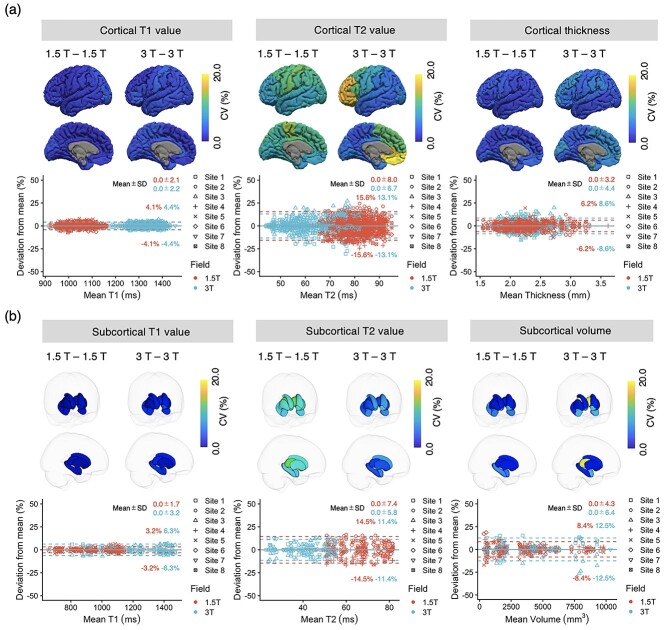
Intrafield-strength reproducibility of cortical thickness and volume of subcortical structures

The wCVs for cortical thickness and volume of subcortical structures across all regions between 1.5 T and 3.0 T were 5.5 ± 2.9 and 4.0 ± 1.6%, respectively (Fig. 5). No bias was observed between measurements derived from scanners operating at different magnetic field strengths.

Fig. 5.

Fig. 5

Open in a new tab

(a) Interfield-strength reproducibility of cortical thickness values. The scan-rescan wCVs of regional cortical thickness, T1, and T2 values are overlaid on an inflated brain surface. (b) Interfield-strength reproducibility of volumes of subcortical structures. Each subcortical structure is colored according to the regional wCV, and the brain surface is transparent for visualization purposes. The limits of agreement located at 1.96 × SD of the distribution are plotted as red dashed lines.

Discussion

Imaging techniques that obtain consistent longitudinal metrics across different scanners have become increasingly important as large numbers of clinical radiology studies move toward quantitative multicenter data. Here, we showed the feasibility of 3D MRF-based simultaneous relaxometry and morphometry of human brain structures and evaluated the repeatability and reproducibility of relaxation times and morphological information on brain structures using test–retest scans using 8 scanners across 3 institutions. While voxel-wise evaluation is a more comprehensive way to assess the variance of a given imaging technique, brain structure-wise evaluation in anatomically meaningful regions, as employed in our study, facilitates clinical decision-making. The brain structure-wise values for T1, T2, cortical thickness, and subcortical volume showed high repeatability at both 1.5 T and 3.0 T, and regional cortical thickness and subcortical volume values showed agreement across magnetic field strengths. The variation found in this study can inform longitudinal and multicenter studies.

In general, the repeatability and reproducibility of T1 and T2 values were in line with the previous studies using 3D MRF (Buonincontri et al. 2020; Fujita et al. 2020). While analysis provided similar results with the previous study based on voxel-wise analysis (Buonincontri et al. 2020), our study focusing on segmentation-based relaxometry and morphometry provides profiles of the brain structures that could be directly used to tackle neuroscientific or clinical questions. For example, CVs are not uniform across brain structures and our result revealed the CV for each brain structure. These results are important in neuroscientific or clinical studies, because in many cases, changes in a specific brain structure is a primary consideration, and the CV of that structure is critical to conduct a longitudinal or large-scale multisite study. Comparing CVs across studies needs caution due to different study designs and cohorts; however, our values are comparable or superior to those of other studies using quantitative mapping techniques (Deoni et al. 2008; Landman et al. 2011). At both 1.5 T and 3.0 T, T2 values showed lower repeatability compared with T1 values. This is consistent with the findings of previous studies that evaluated the repeatability and reproducibility of MRF-derived relaxation times in 3D (Buonincontri et al. 2020) or 2D (Jiang et al. 2017; Buonincontri et al. 2019; Kato et al. 2019; Korzdorfer, Kirsch, et al. 2019). Relatively low T2 reproducibility at 3.0 T compared with that at 1.5 T is consistent with the expected increased sensitivity to B1+ variation at higher field strength. The effect of B1+ field was not included in the model for the present study. Accounting for this effect in the signal model by using an external B1+ map (Ma et al. 2018) or including the B1+ effect directly into the model (Buonincontri and Sawiak 2016; Cloos et al. 2016) could improve the reproducibility of these measurements.

Several neuroanatomical regions, including the temporal pole, entorhinal cortex, and pars orbitalis, showed relatively high variation compared with other regions. This tendency was consistent with a previous 3D MRF report using a single scanner (Fujita et al. 2020). This could be owing to B0 inhomogeneity (these regions are close to the anterior cranial fossa with its apparent B0 inhomogeneity) or region size (small regions are prone to parcellation errors since CV is defined as SD/mean and small structures have large variations in the denominator). In several brain parcellation studies based on conventional structural imaging, inverse relationships between structure size and the relative error of measured cortical thickness were observed (Tustison et al. 2014; Iscan et al. 2015). The range of cortical thickness values (1.1–3.6 mm) obtained with 3D MRF was consistent with both previous 3D T1-weighted imaging and postmortem findings (Desikan et al. 2006; Iscan et al. 2015). The interscanner variability of 3D MRF-derived cortical thickness values and subcortical volumes showed small variances with wCVs of <5%, corresponding to 0.10–0.15, which is in the range reported by Han et al. (Han et al. 2006) for healthy volunteers with average variability values of 0.15 and 0.17 mm for interscanner and cross-field strength (1.5 vs. 3.0 T) comparisons, respectively. For simplicity, cortical volume and surface area were not included in our study; however, Iscan et al. (2015) reported that cortical thickness is more sensitive to site differences than these parameters. Therefore, the repeatability and reproducibility of these metrics are probably similar or better than those of cortical thickness.

The ability to acquire a set of regional T1, T2, thickness, and volume measurements of neuroanatomical structures enhances objective brain evaluations to quantitatively monitor changes related to underlying pathologies, disease progression, and treatments. Whole-brain 3D MRF-based simultaneous relaxometry and morphometry may provide profiles of the brain structures that enable comparisons between patient and control groups. For instance, our results in white matter structures show that 3D MRF requires only 3 subjects to detect elevated T1 values in the normal-appearing white matter of patients with multiple sclerosis (effect size, 6% (Vrenken et al. 2006); statistical power, 0.9; significance level, 1-sided 0.05). With a total imaging time of <10 min for whole-brain 1.125-mm isotropic mapping, our approach serves as a research tool and can be seamlessly integrated into multicenter studies.

Several factors are known to cause variations in quantitative imaging, including the scanner type, operating software, operator, and subject positioning (Bland and Altman 1986; Obuchowski et al. 2015; Hagiwara et al. 2020). This study included scanners from different sites, operating on different software, used by different operators. Each of these factors causes variations in the imaging process, affecting quantitative metrics. One strength of this study is that the data were acquired in settings similar to those used in clinical imaging (such as multiple scanners, different sites, and different operators). Thus, the resulting wCV and bias reflect the overall variation caused by these factors. The platforms used in this study were relatively heterogeneous and included even older scanner types, compared with previous studies that mainly included high-end scanners (Kato et al. 2019; Korzdorfer, Kirsch, et al. 2019).

This study had some limitations. Aged volunteer and patient scans were not included, as is the case with most traveling-subject studies (Korzdorfer, Kirsch, et al. 2019; Leutritz et al. 2020; Hedges et al. 2022). Performing test–retest scans on these individuals across multiple institutions is unfeasible and potentially unethical. Since older individuals and patients have different brain microstructures and metabolic statuses compared with those of young healthy volunteers, our findings in relatively young healthy volunteers may not be directly generalizable to scans obtained from older individuals and patients; however, they could be a starting point of using 3D MRF for obtaining brain regional relaxation values and morphological information. Second, although data were analyzed with 2 major brain segmentation software packages, a comprehensive evaluation of all possible segmentation algorithms and software versions was not feasible. Only parcellation software can provide a comprehensive set of regional values from MRI data. Third, the repeatability and reproducibility of regions containing the cerebrospinal fluid (e.g. ventricles and brain sulci) were not evaluated because the technique used was not designed to measure the parameters of cerebrospinal fluid-filled structures. Furthermore, the acquisition strategy used did not allow system imperfections (Korzdorfer, Jiang, et al. 2019) or magnetization transfer (RP et al. 2020), and we did not use advanced k-space trajectory correction methods (Berzl et al. 2017). The artifacts seen in the 3 scans excluded from this study were consistent with motion artifacts caused by involuntary subject-motion during the acquisitions. Using a motion correction technique may improve the overall robustness and performance of the MRF (Kurzawski et al. 2020). Lastly, all MRI systems in this study were from the same vendor. Therefore, the results should not be blindly extrapolated to pulse sequences and scanners from different vendors.

This study showed the feasibility of 3D MRF for simultaneous brain structure-wise morphometry and relaxometry. Comprehensive test–retest scan analyses demonstrated that 3D MRF-derived morphological information and relaxation times are highly repeatable at both 1.5 T and 3.0 T. Regional cortical thickness and subcortical volume values showed high agreement and low bias across 1.5-T and 3.0-T MRFs. Being able to acquire a set of regional T1, T2, thickness, and volume measurements of neuroanatomical structures with high repeatability and reproducibility facilitates the ability of longitudinal multicenter imaging studies to quantitatively monitor changes related to underlying pathologies, disease progression, and treatments. We hope that our research will enable the translation of simultaneous 3D MRF-based relaxometry and morphometry into clinical applications. Larger multicenter and multivendor studies are required to take full advantage of quantitative imaging to detect pathological changes in the brain.

Supplementary Material

Supplemental_figures_bhac096
Click here for additional data file. (13.8MB, zip)

Acknowledgments

We acknowledge Masahiro Abe for helping with data handling.

Contributor Information

Shohei Fujita, Department of Radiology, Juntendo University, Tokyo, Japan; Department of Radiology, The University of Tokyo, Tokyo, Japan.

Matteo Cencini, Imago7 Foundation, Pisa, Italy; IRCCS Stella Maris, Pisa, Italy.

Guido Buonincontri, Imago7 Foundation, Pisa, Italy; IRCCS Stella Maris, Pisa, Italy.

Naoyuki Takei, GE Healthcare, Tokyo, Japan.

Rolf F Schulte, GE Healthcare, Munich, Germany.

Issei Fukunaga, Department of Radiology, Juntendo University, Tokyo, Japan.

Wataru Uchida, Department of Radiology, Juntendo University, Tokyo, Japan.

Akifumi Hagiwara, Department of Radiology, Juntendo University, Tokyo, Japan.

Koji Kamagata, Department of Radiology, Juntendo University, Tokyo, Japan.

Yasuhiro Hagiwara, Department of Biostatistics, School of Public Health, The University of Tokyo, Tokyo, Japan.

Yutaka Matsuyama, Department of Biostatistics, School of Public Health, The University of Tokyo, Tokyo, Japan.

Osamu Abe, Department of Radiology, The University of Tokyo, Tokyo, Japan.

Michela Tosetti, Imago7 Foundation, Pisa, Italy; IRCCS Stella Maris, Pisa, Italy.

Shigeki Aoki, Department of Radiology, Juntendo University, Tokyo, Japan.

Funding

This work was supported by the Japan Agency for Medical Research and Development (AMED) (grant numbers JP19lk1010025h9902 and JP 20dm0307101h0002); the Japan Society for the Promotion of Science Grants-in-Aid for Scientific Research (JSPS KAKENHI) (grant numbers 19 K17150, 19 K17177, 18H02772, and 18 K07692); Health, Labor and Welfare Policy Research Grants for Research on Region Medical; a Grant-in-Aid for Special Research in Subsidies for ordinary expenses of private schools from The Promotion and Mutual Aid Corporation for Private Schools of Japan; and the Brain/MINDS beyond program from AMED (grant numbers JP19dm0307024 and JP19dm0307101). MC and MT receive research funding from GE Healthcare.

Conflict of interest statement: NT and RFS are currently employed at GE Healthcare; MC and MT receive research funding from GE Healthcare; the other authors have nothing to disclose.

Data availability

The original T1 and T2 maps for each subject used in this study are openly available at (10.5281/ZENODO.3989799).

References

  1. Berzl  M, Pfeil  A, Meyer  C, Campbell-Washburn  A, Körzdörfer  G, Nittka  M, Maier  A, Pfeuffer  J. 2017. Improved spiral trajectory correction using the gradient impulse response function (GIRF) with application to MR Fingerprinting. Paper presented at the Proceeding of the 25th ISMRM.
  2. Bland  JM, Altman  DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986:1(8476):307–310. [PubMed] [Google Scholar]
  3. Buonincontri G, Sawiak SJ. MR fingerprinting with simultaneous B1 estimation. Magn Reson Med. 2016:76(4):1127–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Buonincontri  G, Biagi  L, Retico  A, Cecchi  P, Cosottini  M, Gallagher  FA, Gomez  PA, Graves  MJ, McLean  MA, Riemer  F, et al.  Multi-site repeatability and reproducibility of MR fingerprinting of the healthy brain at 1.5 and 3.0T. NeuroImage. 2019:195:362–372. 10.1016/j.neuroimage.2019.03.047. [DOI] [PubMed] [Google Scholar]
  5. Buonincontri  G, Kurzawski  JW, Kaggie  JD, Matys  T, Gallagher  FA, Cencini  M, Donatelli  G, Cecchi  P, Cosottini  M, Martini  N, et al.  Three dimensional MRF obtains highly repeatable and reproducible multi-parametric estimations in the healthy human brain at 1.5T and 3T. NeuroImage. 2020:226:117573. 10.1016/j.neuroimage.2020.117573. [DOI] [PubMed] [Google Scholar]
  6. Cao  X, Ye  H, Liao  C, Li  Q, He  H, Zhong  J. Fast 3D brain MR fingerprinting based on multi-axis spiral projection trajectory. Magn Reson Med. 2019:82(1):289–301. [DOI] [PubMed] [Google Scholar]
  7. Cloos MA, Knoll F, Zhao T, Block KT, Bruno M, Wiggins GC, Sodickson DK. Multiparametric imaging with heterogeneous radiofrequency fields. Nat Commun. 2016:7:12445. 10.1038/ncomms12445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Dale  AM, Fischl  B, Sereno  MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. NeuroImage. 1999:9(2):179–194. [DOI] [PubMed] [Google Scholar]
  9. Deoni  SCL, Williams  SCR, Jezzard  P, Suckling  J, Murphy  DGM, Jones  DK. Standardized structural magnetic resonance imaging in multicentre studies using quantitative T1 and T2 imaging at 1.5 T. NeuroImage. 2008:40(2):662–671. [DOI] [PubMed] [Google Scholar]
  10. Desikan  RS, Segonne  F, Fischl  B, Quinn  BT, Dickerson  BC, Blacker  D, Buckner  RL, Dale  AM, Maguire  RP, Hyman  BT, et al.  An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage. 2006:31(3):968–980. [DOI] [PubMed] [Google Scholar]
  11. Fessler  JA. On NUFFT-based gridding for non-Cartesian MRI. J Magn Reson. 2007:188(2):191–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fischl  B. FreeSurfer. NeuroImage. 2012:62(2):774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fujita  S, Buonincontri  G, Cencini  M, Fukunaga  I, Takei  N, Schulte  RF, Hagiwara  A, Uchida  W, Hori  M, Kamagata  K, et al.  Repeatability and reproducibility of human brain morphometry using three-dimensional magnetic resonance fingerprinting. Hum Brain Mapp. 2020:42(2):275–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gómez PA, Cencini M, Golbabaee M, Schulte RF, Pirkl C, Horvath I, Buonincontri G.  Rapid three-dimensional multiparametric MRI with quantitative transient-state imaging. Sci Rep. 2020:10(1):13769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hagiwara  A, Fujita  S, Ohno  Y, Aoki  S. Variability and standardization of quantitative imaging: monoparametric to multiparametric quantification, radiomics, and artificial intelligence. Investig Radiol. 2020:55(9):601–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hagiwara  A, Fujimoto  K, Kamagata  K, Murata  S, Irie  R, Kaga  H, Someya  Y, Andica  C, Fujita  S, Kato  S, et al.  Age-related changes in relaxation times, proton density, myelin, and tissue volumes in adult brain analyzed by 2-dimensional quantitative synthetic magnetic resonance imaging. Investig Radiol. 2021:56(3):163–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Han  X, Jovicich  J, Salat  D, van der  Kouwe  A, Quinn  B, Czanner  S, Busa  E, Pacheco  J, Albert  M, Killiany  R, et al.  Reliability of MRI-derived measurements of human cerebral cortical thickness: the effects of field strength, scanner upgrade and manufacturer. NeuroImage. 2006:32(1):180–194. [DOI] [PubMed] [Google Scholar]
  18. Hedges  EP, Dimitrov  M, Zahid  U, Brito Vega  B, Si  S, Dickson  H, McGuire  P, Williams  S, Barker  GJ, Kempton  MJ. Reliability of structural MRI measurements: the effects of scan session, head tilt, inter-scan interval, acquisition sequence, FreeSurfer version and processing stream. NeuroImage. 2022:246:1187517. 10.1016/j.neuroimage.2021.118751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Iscan  Z, Jin  TB, Kendrick  A, Szeglin  B, Lu  H, Trivedi  M, Fava  M, McGrath  PJ, Weissman  M, Kurian  BT, et al.  Test-retest reliability of freesurfer measurements within and between sites: effects of visual approval process. Hum Brain Mapp. 2015:36(9):3472–3485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jiang  Y, Ma  D, Seiberlich  N, Gulani  V, Griswold  MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn Reson Med. 2015:74(6):1621–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Jiang  Y, Ma  D, Keenan  KE, Stupic  KF, Gulani  V, Griswold  MA. Repeatability of magnetic resonance fingerprinting T1 and T2 estimates assessed using the ISMRM/NIST MRI system phantom. Magn Reson Med. 2017:78(4):1452–1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kato  Y, Ichikawa  K, Okudaira  K, Taoka  T, Kawaguchi  H, Murata  K, Maruyama  K, Koerzdoerfer  G, Pfeuffer  J, Nittka  M, et al.  Comprehensive evaluation of B1(+)-corrected FISP-based magnetic resonance fingerprinting: accuracy, repeatability and reproducibility of T1 and T2 relaxation times for ISMRM/NIST system phantom and volunteers. Magn Reson Med Sci. 2019:19(3):168–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Knight  MJ, Wearn  A, Coulthard  E, Kauppinen  RA. T2 relaxometry and diffusion tensor indices of the hippocampus and entorhinal cortex improve sensitivity and specificity of MRI to detect amnestic mild cognitive impairment and Alzheimer’s disease dementia. J Magn Reson Imaging. 2019:49(2):445–455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Korzdorfer  G, Jiang  Y, Speier  P, Pang  J, Ma  D, Pfeuffer  J, Hensel  B, Gulani  V, Griswold  M, Nittka  M. Magnetic resonance field fingerprinting. Magn Reson Med. 2019:81(4):2347–2359. [DOI] [PubMed] [Google Scholar]
  25. Korzdorfer  G, Kirsch  R, Liu  K, Pfeuffer  J, Hensel  B, Jiang  Y, Ma  D, Gratz  M, Bar  P, Bogner  W, et al.  Reproducibility and repeatability of MR fingerprinting relaxometry in the human brain. Radiology. 2019:292(2):429–437. [DOI] [PubMed] [Google Scholar]
  26. Kurzawski  JW, Cencini  M, Peretti  L, Gomez  PA, Schulte  RF, Donatelli  G, Cosottini  M, Cecchi  P, Costagli  M, Retico  A, et al.  Retrospective rigid motion correction of three-dimensional magnetic resonance fingerprinting of the human brain. Magn Reson Med. 2020:84(5):2606–2261. [DOI] [PubMed] [Google Scholar]
  27. Landman  BA, Huang  AJ, Gifford  A, Vikram  DS, Lim  IA, Farrell  JA, Bogovic  JA, Hua  J, Chen  M, Jarso  S, et al.  Multi-parametric neuroimaging reproducibility: a 3-T resource study. NeuroImage. 2011:54(4):2854–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Leutritz  T, Seif  M, Helms  G, Samson  RS, Curt  A, Freund  P, Weiskopf  N. Multiparameter mapping of relaxation (R1, R2*), proton density and magnetization transfer saturation at 3 T: a multicenter dual-vendor reproducibility and repeatability study. Hum Brain Mapp. 2020:41(15):4232–4424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ma  D, Gulani  V, Seiberlich  N, Liu  K, Sunshine  JL, Duerk  JL, Griswold  MA. Magnetic resonance fingerprinting. Nature. 2013:495(7440):187–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Ma  D, Jiang  Y, Chen  Y, McGivney  D, Mehta  B, Gulani  V, Griswold  M. Fast 3D magnetic resonance fingerprinting for a whole-brain coverage. Magn Reson Med. 2018:79(4):2190–2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ma  D, Jones  SE, Deshmane  A, Sakaie  K, Pierre  EY, Larvie  M, McGivney  D, Blumcke  I, Krishnan  B, Lowe  M, et al.  Development of high-resolution 3D MR fingerprinting for detection and characterization of epileptic lesions. J Magn Reson Imaging. 2019:49(5):1333–1346. [DOI] [PubMed] [Google Scholar]
  32. Machin  D, Campell  MJ, Tan  SB, Tan  SH. Sample size tables for clinical studies. 3rd ed. Chichester: Wiley-Blackwell; 2009 [Google Scholar]
  33. McGivney  DF, Pierre  E, Ma  D, Jiang  Y, Saybasili  H, Gulani  V, Griswold  MA. SVD compression for magnetic resonance fingerprinting in the time domain. IEEE Trans Med Imaging. 2014:33(12):2311–2322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Obuchowski  NA, Reeves  AP, Huang  EP, Wang  XF, Buckler  AJ, Kim  HJ, Barnhart  HX, Jackson  EF, Giger  ML, Pennello  G, et al.  Quantitative imaging biomarkers: a review of statistical methods for computer algorithm comparisons. Stat Methods Med Res. 2015:24(1):68–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Patenaude  B, Smith  SM, Kennedy  DN, Jenkinson  M. A Bayesian model of shape and appearance for subcortical brain segmentation. NeuroImage. 2011:56(3):907–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pell  GS, Briellmann  RS, Waites  AB, Abbott  DF, Jackson  GD. Voxel-based relaxometry: a new approach for analysis of T2 relaxometry changes in epilepsy. NeuroImage. 2004:21(2):707–713. [DOI] [PubMed] [Google Scholar]
  37. RP AGT, Neji R, Wood TC, Baburamani AA, Malik SJ, Hajnal JV. Controlled saturation magnetization transfer for reproducible multivendor variable flip angle T1 and T2 mapping. Magn Reson Med. 2020:84(1):221–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Sabuncu  MR, Ge  T, Holmes  AJ, Smoller  JW, Buckner  RL, Fischl  B, Alzheimer's Disease Neuroimaging Initiative . Morphometricity as a measure of the neuroanatomical signature of a trait. Proc Natl Acad Sci U S A. 2016:113(39):E5749–E5756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Seiberlich  N, Gulani  V, Calamante  F, ScienceDirect (Online service). Quantitative magnetic resonance imaging. Advances in magnetic resonance technology and applications. Vol. 1. (pp. 1 online resource). Retrieved from https://yale.idm.oclc.org/login?URL=https://www.sciencedirect.com/science/book/9780128170571. [Google Scholar]
  40. Shridhar Konar  A, Qian  E, Geethanath  S, Buonincontri  G, Obuchowski  NA, Fung  M, Gomez  P, Schulte  R, Cencini  M, Tosetti  M, et al.  Quantitative imaging metrics derived from magnetic resonance fingerprinting using ISMRM/NIST MRI system phantom: an international multicenter repeatability and reproducibility study. Med Phys. 2021:48(5):2438–2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Thompson  PM, Hayashi  KM, de  Zubicaray  G, Janke  AL, Rose  SE, Semple  J, Herman  D, Hong  MS, Dittmer  SS, Doddrell  DM, et al.  Dynamics of gray matter loss in Alzheimer's disease. J Neurosci. 2003:23(3):994–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Tofts  P. Quantitative MRI of the brain: measuring changes caused by disease. In: Wiley, Chichester, West Sussex. Hoboken (NJ): Wiley; 2003 [Google Scholar]
  43. Tustison  NJ, Cook  PA, Klein  A, Song  G, Das  SR, Duda  JT, Kandel  BM, van  Strien  N, Stone  JR, Gee  JC, et al.  Large-scale evaluation of ANTs and FreeSurfer cortical thickness measurements. NeuroImage. 2014:99:166–179. [DOI] [PubMed] [Google Scholar]
  44. Vrenken  H, Geurts  JJ, Knol  DL, van  Dijk  LN, Dattola  V, Jasperse  B, van  Schijndel  RA, Polman  CH, Castelijns  JA, Barkhof  F, et al.  Whole-brain T1 mapping in multiple sclerosis: global changes of normal-appearing gray and white matter. Radiology. 2006:240(3):811–820. [DOI] [PubMed] [Google Scholar]
  45. Walsh  DO, Gmitro  AF, Marcellin  MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med. 2000:43(5):682–690. [DOI] [PubMed] [Google Scholar]
  46. Weigel  M. Extended phase graphs: dephasing, RF pulses, and echoes - pure and simple. J Magn Reson Imaging. 2015:41(2):266–295. [DOI] [PubMed] [Google Scholar]
  47. Zhuo  J, Gullapalli  RP. AAPM/RSNA physics tutorial for residents: MR artifacts, safety, and quality control. Radiographics. 2006:26(1):275–297. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental_figures_bhac096
Click here for additional data file. (13.8MB, zip)

Data Availability Statement

The original T1 and T2 maps for each subject used in this study are openly available at (10.5281/ZENODO.3989799).

Articles from Cerebral Cortex (New York, NY) are provided here courtesy of Oxford University Press

RESOURCES