Abstract
Stress relaxation during plastic deformation has been reported to improve ductility of metallic materials. In this study, the stress relaxation behaviour in pure magnesium is investigated during interrupted uniaxial tensile tests. During intermittent stopping of the machine for relaxation studies, the total strain is expected to remain constant. However, an anomalous non-constancy in total strain is observed in the present work. The total strain increases with relaxation time. Additional in-situ tensile tests indicate that the non-constant total strain is restricted only in the gauge area of the specimen, indicating a likely shear dominated deformation such as grain boundary sliding (GBS) responsible for the anomalous behaviour. The role of GBS during relaxation is studied using the deformation induced evolution of surface inhomogeneity. Determinations of surface profiling step heights at grain boundaries and inclination of grains were used to quantify the effect of GBS. The estimated activation volume of 4.35 b3 further confirms the role of slip induced GBS on the deformation. A new stress relaxation model accommodating GBS is proposed and is found to fit the experimental data accurately.
Keywords: Stress relaxation, Magnesium, Grain boundary sliding
1. Introduction
The use of magnesium alloys in automotive components is highly desirable because their superior strength to weight ratio compared to aluminum alloys. However, potential obstacles to their wide adoption are relatively low stiffness, poor formability especially at low temperatures, and relatively low ductility of engineered components.
Low ductility is an inherent nature of magnesium alloys due to lack of sufficient number of independent slip systems. Efforts are in place to enhance the ductility by reducing grain size and texture modification. However, the underlying mechanism is found to be debatable. The tensile test of pure magnesium single crystals by Yoshinaga and Horiuchi [1] showed that the plastic deformation is due to basal slip. The nonbasal slip had no contribution to plastic deformation. Further, compression tests by Obara et al. [2] confirmed that the dislocation slip on basal planes dominates the room temperature plastic deformation. Creep and stress relaxation study in polycrystalline magnesium in the temperature range of 219 °C to 405 °C showed that the deformation is controlled mainly by thermally activated glide of basal dislocations. The rate determining obstacles were observed to be jogs in screw segments, with lengths greater than or equal to distance between basal planes [3]. On the contrary, ductility improvement in fine grain Mg alloys observed by Koike et al. [4] showed that 40 % of dislocation segments are of non-basal type. With basal dislocation slip not offering sufficient slip systems to satisfy the strain compatibility requirement of plastic yield criteria, ductility improvement is due to compatibility stresses at grain boundaries. At a homologous temperature of 0.32, the possibility of GBS in Mg and its alloys has been explored by various researchers. However the occurrence of GBS at room and lower temperature has been a debatable topic. Observation of GBS in pure Mg at 78 K was first reported by Hauser et al. [5]. Experimental techniques such as mechanically scribed lines [6] and measurement of surface step profile [7, 8] have been used to confirm the GBS in magnesium at room temperature. Based on experimental observation, Mussot et al. [9] showed that GBS occurs as a compatibility requirement for anisotropic plastic strains at grain boundaries. Ando et al. [10], summarized that at low temperature, the plastic strain anisotropy and absorption of lattice dislocations at grain boundaries lead to stress concentrations and GBS. Koike et al. [7] and Valiev and Kaibyshev [11] contended that preferential slip on basal planes in hexagonal close packed (HCP) alloys causes inhomogeneous deformation within grains at room temperature leading to slip induced GBS. However, Gifkins and Langdon [6] in their study concluded that GBS does not occur in Mg and Mg alloys at room temperature and step formation at grain boundaries was explained as zone sliding.
Under isothermal condition, ductility of metallic materials can also be improved mechanically by changing the strain rate to postpone the onset of plastic instability. Recent study with various grades of steel has reported ductility improvement by introducing stress relaxation during uniaxial tensile test [12]. Bong et al. [13] demonstrated the use of stress relaxation in forming ultra thin ferritic stainless steel using a servo press. Similar improvement in ductility has been observed with 316L stainless steel [14, 15], dual phase steel [16] and Ti-6Al-4V titanium alloy [17]. Few studies have proposed the underlying mechanism of stress relaxation which encompasses elucidation of enhancement of ductility [14, 16, 18]. However, the mechanism of dislocation annihilation and stress homogenization through dislocation arrangement during stress relaxation responsible for ductility improvement proposed by Hariharan et al. [14] is probably the only mechanism which has been microstructurally validated [19]. Most of the these studies on ductility improvement due to stress relaxation has been focused on steels where deformation occurs through slip movement and dislocation interaction. The effect of stress relaxation in magnesium where dislocation movement is restricted to limited number of slip planes, to the best of authors’ knowledge, has not been studied before.
Novel mechanical testing methods such as stress relaxation and a robust understanding of the interplay between multiaxial strain behavior and microstructure are needed before these materials can be adopted in key automotive components. The present effort is a step toward achieving this goal. The current study aims and demonstrates that ductility enhancement is possible through the judicious use of stress relaxation methods in magnesium alloys. Although a few magnesium alloys, such as AZ series are being used presently in the automotive industry, the automotive industry still needs both data and validated material models of these alloys before they can be widely used. Alloying elements in magnesium alloys have been found to alter the stress relaxation behavior [20]. In this context, pure magnesium was chosen for the study as it eliminates the complexities associated with the influence of alloying elements on the overall deformation behavior of the material.
1.1. Stress relaxation - prior work and logarithmic model
Stress relaxation, essentially an observation of stress drop with time when a tensile test is intermittently stopped at a fixed strain level, has been used to estimate rate dependent parameters related to thermally activated plastic deformation. Flow stress during plastic deformation is defined as a sum of stresses required to overcome long range obstacles (internal/athermal true stress, σi) and short-range obstacles (effective/thermal true stress, σ*).
As the total true strain (ϵtotal = ϵp + ϵe, where ϵp is the plastic strain and ϵe is the elastic strain) remains constant during a stress relaxation test, the plastic strain rate is, , where and E are the stress rate and Young’s modulus respectively. If the elastic stiffness due to machine structure and other components are not adequately compensated, ‘E’ should be replaced with an effective elastic modulus. Combining the Orowan [21] equation for plastic strain rate, , (ϕ is a constant, ρm is the mobile dislocation density, b is the Burgers vector magnitude and ν is the average dislocation velocity), the stress rate during relaxation is given by:
| (1) |
Considering thermally activated plastic deformation, following the work reported by Dotsenko [22], the rate form of velocity (ν = ν0 exp(−ΔG/kT), where ν0 is a constant relating the average dislocation distance during each activation, ΔG is the activation energy, k is the Boltzmann constant and T is temperature), can be substituted in the above equation, which upon integration leads to the logarithmic model (Appendix Appendix A),
| (2) |
where α and β are the material constants. α = kT/V* and , σ0 refers to the true stress at the beginning of relaxation (t=0) and V* is the activation volume. Modelling stress relaxation using equation 2 assumes constancy of σi and ρm during stress relaxation. Caillard and Martin [23] assumed the internal stress during stress relaxation to vary linearly with plastic strain during relaxation, , where θr is the strain hardening rate of internal stress. Internal stress does not remain constant during stress relaxation [24]. However, this change was considered to be negligible by Varma et al. [15].
From the Orowan equation for plastic strain rate,. Dotsenko [22] in an extensive review of stress relaxation reported that although ρm varies during stress relaxation, was ignored in earlier models (eq.2) of stress relaxation. Analyzing the deviation of experimental results from the analytical model, Okazaki et al. [25] argued that ρm remains constant for only a short period and decreases with increase in hold time during stress relaxation. However, deviation of experimental results could be due to multiple reasons and does not strongly conclude the role of ρm during relaxation. Using a novel repeated relaxation test, Spatig et al. [26] showed that the variation of ρm during relaxation cannot be ignored. Activation energy values obtained with stress relaxation in 99.996 % aluminium was related to recovery process [27]. Takeuchi et al. [28] and Li [29] reported that ρm decreases initially during relaxation and remains constant with hold time in ionic KCl crystals. The significant dislocation annihilation during stress relaxation based on TEM observations reported by Varma et al. [19] in 316L stainless steel and Mohebbi et al. [30] in ultra fine grained aluminium alloy substantiate the importance of accounting for variation of ρm while modelling stress relaxation. The logarithmic model for stress relaxation has been improved by Hariharan et al.[14, 15] to accommodate the variation of σi and ρm in estimating the activation parameters.
Therefore, the objective of the present work is to understand the influence of stress relaxation in magnesium. It will be shown in the following sections that the macroscopic transient response of magnesium is distinctly different from those of other materials. An improved phenomenological model for GBS relaxation in magnesium is proposed and validated with the experimental results.
2. Experimental details
2.1. Initial material
Tensile specimens were prepared by wire EDM (Electric discharge machining) as per the ASTM-E8M standard [31] from commercially pure 99.95 % Mg along the extrusion direction with an average grain size of 32.0 μm ± 4.5 μm.
2.2. Mechanical tests
The standard macro uniaxial tensile and relaxation tests were performed using 30 kN Zwick4 tensile machine equipped with an optical video extensometer. A Kammrath Weiss micro tensile module of 10 kN capacity inside a Tescan scanning electron microscope (SEM) was also used for the in-situ uniaxial tensile tests where the tests were stopped and unloaded at below mentioned strain with and without relaxation hold time. A detailed description of the setup is provided in Appendix Appendix B. Samples for micro tensile tests were polished to mirror finish and etched with 2 % Nital. SEM micrographs were captured at similar magnification intervals for both conditions for comparison post unloading. The tensile sample gauge dimensions were 25 mm × 6 mm × 3 mm and 11 mm × 4 mm × 3 mm for the standard and the micro tensile test respectively. The tests were performed with the following parameters: (a) strain rate of 10−2 s−1, 1.9 % strain and varying hold time of 10 s and 60 s as input parameter. 10 s and 60 s represent the 10 second and 60 second hold time samples, respectively. The 1.9 % strain was chosen because it corresponds to strain at 90 % of tensile strength. The strain was chosen so as to have maximum deformation in the microstructure prior to stress relaxation. Changes in total strain detected in experiments due to the machine stiffness were reported to be negligible for most practical considerations [14]. The uniform elongation was used to calculate the strain corresponding to the ultimate tensile strength. Each test condition was repeated with at least three samples. Unless otherwise stated, the error bars mentioned in the test as “± quantity” represent one standard deviation spread in measured values.
2.3. Surface topography analysis
A separate set of mechanical tests was conducted for surface profiling, where the samples after a tensile pre-strain were unloaded with and without relaxation. Samples for surface profiling were polished to mirror finish and were subsequently etched with 2 % nital. Surface topography of these samples was characterized by a constant-force, contact-type Nanosurf Nanite B atomic force microscope (AFM). A 7 nm tip was used to scan 74 μm × 74 μm surface laterally, with a constant force of 20 nN. AFM results were quantified for measurement of step height at grain boundaries and grain inclination by Gwyddion, a free software for SPM (scanning probe microscopy) data visualization and analysis. Quantification involved measurement on many line profiles extracted from multiple 74 μm × 74 μm AFM scans.
3. Results and Discussion
3.1. Experimental results
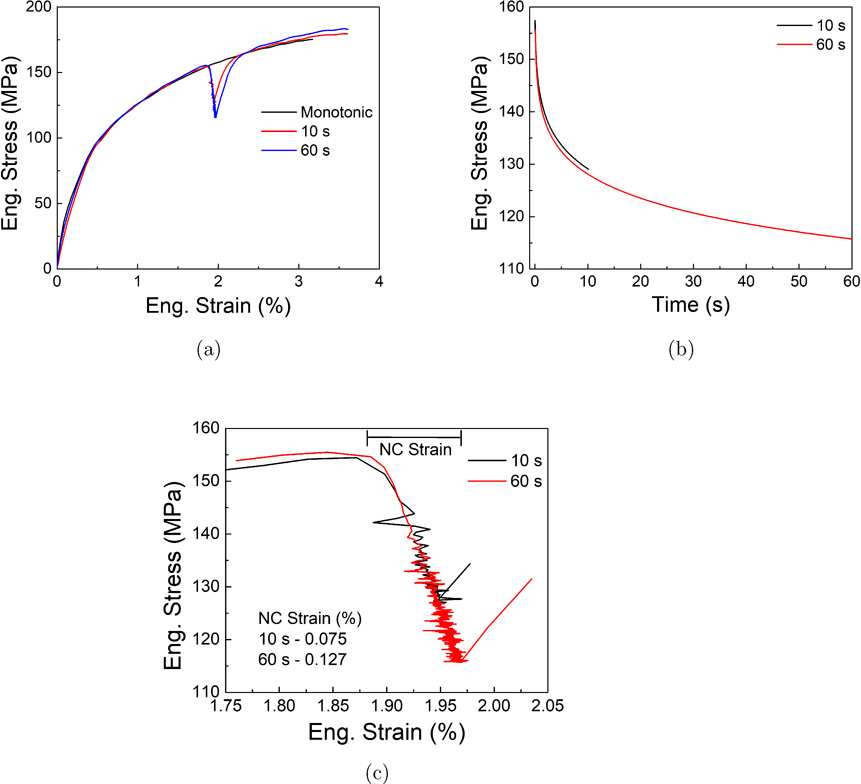
Figure 1a shows a representative stress-strain response of monotonic and relaxation at ϵ = 1.9 % for different hold times (10 s and 60 s) test samples. Ductility improvement of about 15.5 % ± 1.1 % is observed with relaxation tests in comparison to the monotonic test. Stress drop of 28 MPa ± 3.1 MPa and 40 MPa ± 1.9 MPa is observed for 10 s and 60 s hold times, respectively (figure 1b).
Figure 1:
Effect of relaxation on mechanical properties carried out for various hold times at 1.9 % strain and 10−2 s−1 strain rate a)Monotonic and stress relaxation - eng. stress strain curve, b) Stress drop during relaxation and c) Offset: Stress-strain during relaxation
The stress drop during relaxation experiments occurs at a constant total strain. However, in the present work, strain during stress relaxation increases with time and is referred henceforth as non-constant (NC) strain (figure 1c). The NC strain increases from 0.07 % ± 0.01 % for 10 s to 0.127 % ± 0.012 % for 60 s. The specimen constrained between the grips does not move during relaxation, therefore the NC strain during relaxation can be attributed to the occurrence of localized shear displacements in the gauge area. Grain boundary sliding is shear dominant and a plausible mechanism to explain this observation. It may be mentioned here that a similar NC strain was observed in ultra-fine grained Al alloy, although this NC strain was not correlated with the GBS [30]. Therefore, while GBS is indeed a possible mechanism, additional confirmation is needed to correlate the observation uniquely with GBS.
Figure 2 presents optical microscope images of the tensile sample surface post deformation (with full width of the sample in view). Optical micrograph of monotonic tensile test sample shows significant surface undulation over several grains (see arrows in figure 2a). Koike et al. [7] observed enhancement in slip induced GBS and reduction in the surface undulation (stress concentration) with temperature. Intergrain sliding in nanocrystalline nickel is reported during stress relaxation in compression at temperatures between 623 K-673 K [32]. This reduction in surface undulation was also observed with stress relaxation, leading to a uniformly deformed microstructure (figure 2b).
Figure 2:
Effect of relaxation on surface in the gauge section of a polished tensile sample obtained after macro tensile tests a) no relaxation and b) relaxation - 60s hold time. The 60 s hold time sample showed a significant decrease in zone slides (indicated with arrows)
AFM microscopic examination after the mechanical tests shows elevated grain boundary activity in the relaxed sample. Surface profiles of the starting material show an average step height of 45 nm at grain boundaries (figure 3a). Figure 3b and 3c are representative surface profiles of monotonic and 60 s samples. Surface undulation can be due to the inability of the free surface to support the shear stress. However, the pronounced appearance of steps at grain boundaries, inclination of grains along with slip lines and twins indicate that the observed surface undulations are due to GBS. Quantification of step heights and inclinations was conducted on multiple image profiles of slid grains taken at various locations. Figure 4a shows a representative profile ranging over 74 μm. It can be observed that the 60 s hold sample shows sharper changes in profile at the grain boundaries. The no hold sample shows gradual changes to profile at grain boundaries, possibly indicating slide in grain clusters or zone sliding. The no hold and relaxed samples are observed to follow opposite trends with the 60 s relaxation creating more step heights in larger numbers of grain boundaries than that in the no hold sample (figure 4b). A similar observation is made for inclination of grains. The 60 s hold time sample shows higher degree inclinations in comparison to those for the no hold sample (figure 4c). Average step heights observed for no hold and 60 s hold time were 264 nm ± 188 nm and 341 nm ± 214 nm, respectively. Although there is an increase in step height in a larger number of grains for the 60 s hold sample as evident in figure 4b, a macroscopic decrease in surface undulation (as shown in figure 2b) is possible because stress relaxation homogenizes the overall stress field causing a large number of grains to slide.
Figure 3:
Effect of relaxation on tensile sample surface - surface 3D images obtained through AFM after macro tensile tests a) before test, b) no relaxation and c) relaxation - 60s hold time.
Figure 4:
a)Linear step profile - arrows indicate grain boundaries, b) Step height - frequency distribution and c) Inclination of grains - frequency distribution for as received, no hold and 60 s hold condition samples obtained after macro tensile tests. Error bars represent variations in the number of grains showing particular step height range and rotation range respectively.
Additional stress relaxation experiments were carried out with an in-situ micro tensile module in a SEM as described in section 2. Strain measurement in the in-situ experiments was obtained from the displacement of the cross head, in contrast to the use of extensometer in macro experiments. It is evident from Figure 5 that NC strain is not observed in the strain estimated from cross head movement. This further validates that the strain observed during relaxation is limited to gauge length and that the sample is rigidly fixed between the grips. SEM micrographs (figure 6) obtained after unloading the sample from in-situ experiments confirms the observation of relatively higher grain boundary activity for the relaxed sample. Figure 6 compares the effect of relaxation on GBS behavior, where the relaxed sample shows higher deformation at grain boundaries, and even grain separation (figure 6f) in some cases comparison to these features observed for the monotonic tensile sample.
Figure 5:
Engineering stress vs. engineering strain plot showing a comparison of strain evolution between that measured with an extensometer in a macro test and by the movement of cross head in a in-situ stress relaxation test.
Figure 6:
SEM micrographs at obtained after in-situ tensile tests carried out at 10−2 s−1 strain rate show GBS for: (a) 250X, (c) 500X, (e) 1000X magnification for the no relaxation sample and (b) 250X, (d) 500X, (f) 1000X magnification for the 60 s hold time sample unloaded at 1.9 % strain. Grain boundary activity is indicated with arrows.
As discussed earlier, limited results are available on GBS during stress relaxation of HCP alloys. However, there are creep studies at room temperature which can be correlated with stress relaxation using rate equations [33]. Since the underlying mechanism of both creep and stress relaxation under given conditions are similar [34], the results from creep studies of HCP alloys can provide valuable insights on the mechanical behaviour during relaxation. For instance, the authors’ past results showed GBS as primary deformation mechanism during indentation creep at room temperature [35] in pure zinc. Similar room temperature indentation creep study in pure magnesium showed GBS to be the dominating deformation mechanism in the low stress regime in contrast to twinning in the high stress regime [36]. Matsunaga et al. [37] observed only one slip system in pure magnesium to be activated during ambient temperature creep study which in turn leads to dislocation accommodation taking place at the grain boundaries. Extensive transmission electron microscopy work for slip line evolution at grain boundary [38], showed rapid dislocation exhaustion due to interaction of existing slip bands with GB during creep in Ti-6Al alloy at room temperature. AZ31 magnesium alloy was observed to be strain rate sensitive in the strain rate range of 10−5 s−1 to 10−8 s−1. It was found that the deformation mechanism changes from deformation twinning to GBS in the range, with activation volume decreasing from 100 b3 to 15 b3 confirming the change. The authors reasoned that the stress concentration is accommodated by dislocation absorption at the grain boundaries leading to GBS with relatively low thermal assistance [39]. Transmission electron microscopy and X-ray diffraction study following indentation creep and stress relaxation experiments carried out for dislocation density evolution showed an intermixture involving grain boundary diffusion and grain boundary-dislocation annihilation and emission as the dominant deformation mechanism in nanocrystalline Ni [40].
Ductility improvement through stress relaxation was studied and the underlying mechanisms were unearthed primarily in SS316L stainless steel [14, 19]. The studies conveys that two mechanisms a) dislocation annihilation, leading to reduction in mobile dislocation density dominating during the initial period of relaxation and b) stress homogenization through dislocation rearrangement dominating the later part of relaxation, operate simultaneously during relaxation. Following the rationale and discussion related to low temperature creep, since the available slip systems with basal dislocation slip is insufficient, the dislocation annihilation is possible only by dislocation absorption at grain boundaries. Straining the sample leads to increased stress concentration at grain boundaries [8, 39] and manifests in the form of surface undulation and step formation without stress relaxation (figure 7b). Stress relaxation homogenizes the stress concentration sites and reduces surface undulation with increasing the number of grains which experience sliding (figure 7c). It is therefore postulated that stress homogenization dominates relaxation with enhancement in slip induced GBS. In fact, SEM micrographs showing increased grain boundary activity with increase in hold time supports the argument for GBS stress homogenization (figure 6). A schematic illustrating GBS during stress relaxation is presented in figure 7.
Figure 7:
Schematic illustrating the observation of GBS during relaxation a) before mechanical test, b) no stress relaxation and c) post stress relaxation.
GBS strain (ϵGBS) is estimated to be 0.98 % and 1.09 % for no hold and 60 s respectively using proposed method in [41]. The difference of 0.11 % in ϵGBS between the two conditions is 86 % of the NC strain observed for 60 s. It confirms GBS to be the primary deformation mechanism during relaxation.
The observation on NC strain violates the basic relation of constancy in total strain (ϵt = ϵe + ϵp = c) and invalidates the use of eq.1 for developing stress relaxation models. Consequently, it is proposed to extend the logarithmic model for stress relaxation in the following section to accommodate the NC strain due to GBS.
3.2. New model for GBS relaxation
Stress drop (σt), during relaxation can be additively decomposed as,
| (3) |
where, represents the stress drop during relaxation without GBS and the stress drop due to GBS is accommodated through . The variation of σi and ρm during relaxation is described by the first term of the summation in eq. 3 and is given by the modified logarithmic model [14]
| (4) |
where, and are scaled to model internal stress and dislocation density. The transient stress change due to GBS can be derived as follows.
Similar to eq.3, the strain rate change during relaxation can also be represented as [30, 42]
| (5) |
In the absence of GBS , the above equation represents usual stress relaxation where,
Following the approach in [30], the strain rate equation [43] for GBS can be written as;
| (6) |
where, G = shear modulus, d = grain diameter, σ* = thermal stress and DGB = grain boundary diffusion coefficient.
Substituting G = E/2(1 + ν), where ν is the Poisson’s ratio and since all the parameters except σ* remain invariant during relaxation, the above equation can be rewritten as
| (7) |
where, q is a constant.
Integrating eq.7 (Appendix Appendix C) and substituting in eq.3, the transient stress during relaxation including GBS is given as
| (8) |
The stress drop data of the relaxations performed at 1.9 % strain for 10 s and 60 s hold time were fit using the new model. The constants of the model were identified by least square fit of the experimental data using the commercial software, MATLAB. The values obtained for the constants are tabulated in Table 1. Figure 8a provides graphical representation of fitting 60 s hold time stress drop experimental data. It can be observed that both 10 s and 60 s data can be fit using the proposed model with good accuracy (Table 1). Using the method in [14] and the proposed model, the activation volume is estimated to be 4.35 b3. These values compare well to the low activation energy values observed by Koike et al. [7] attributed to slip induced GBS. is dependent on internal stress and activation volume, a lower value observed for magnesium in spite of a small activation volume indicate smaller internal stress. and λ values indicate lower mobile dislocation density prior to stress relaxation and a strong variation of mobile dislocation density with time. The contribution of GBS on the stress drop during relaxation is shown in figure 8. The trend is similar to that predicted by Mohebbi et al. [30].
Table 1:
Model parameters
| Rel. Time | λ | q | σi | R-Square | ||
|---|---|---|---|---|---|---|
|
| ||||||
| 10s 60s |
6.381 | 8.03 | −5.2 × 10−4 | 2.6 × 10−6 | 104 | 0.9993 0.9997 |
Figure 8:
Stress relaxation model prediction for relaxation at ϵ = 1.9 %, , t = 60 s, inset showing contribution of GBS to stress relaxation.
4. Conclusion
Pure Mg subjected to stress relaxation tests showed a 15.5 % ± 1.1 % increase in ductility over monotonic tests. Non-constancy strain of 0.07 % ± 0.01 % and 0.127 % ± 0.012 % were observed during stress relaxation for hold times of 10 s and 60 s, respectively. A separate set of mechanical tests was conducted, where the tensile samples were unloaded with and without relaxation. The 3D surface profiles created with AFM showed significant amounts of step creations at grain boundaries that are characteristic of grain boundary sliding (GBS). The grain boundaries with step height above 500 nm increased during relaxation. Additional in-situ experiments on stress relaxation indicated significant activities and strain incompatibility at grain boundaries suggesting the role of GBS during relaxation. An activation volume of 4.35 b3 estimated from the macroscopic stress relaxation data further corroborates the inference attributed to the role of GBS. A recently proposed stress relaxation model was modified to include the effect of GBS, assuming superposition of rate effects. The model is found to fit the experimental data with sufficient accuracy. It is also observed that GBS contributes to stress drop and stress homogenization. Based on these observations, enhanced GBS is proposed to be the stress homogenization mechanism leading to ductility improvement during relaxation in pure Mg at room temperature.
Highlights.
Stress relaxation induced ductility in pure Magnesium investigated.
Anomalous non-constancy in strain during stress relaxation reported.
Grain boundary sliding (GBS) observed during stress relaxation.
Phenomenological model proposed for GBS during relaxation.
Appendix A. Integration of Equation 2
Combining equation 1, rate form of velocity and σ = σi + σ*, we get
| (A.1) |
where and
Integrating the above equation and applying the boundary condition σ = σ0 at t = 0, we get equation 2,
| (A.2) |
where α and β are the material constants with α = kT/V* and .
Appendix B. Detailed description of in-situ tensile testing setup
Figure B.9 provides a photograph of the In-situ micro tensile setup with individual components marked. The specimen prepared as per drawing (Figure B.10) is griped at the centre. The specimen is strained with help of opposite moving cross heads so that the center of the specimen remains fixed for continuous and uninterrupted observation through SEM. Load on the specimen is measured with a 10 kN load cell. Displacement in the cross head is measured through an encoder.
Figure B.9:
In-situ micro tensile module with individual components marked.
Figure B.10:
In-situ micro tensile specimen drawing.
*Additional: The module is capable of high temperature tensile test. The same is achieved through the heater and cooling of the grip sections.
Appendix C. Integration of the proposed model
The equation for GBS (eq.7) is given as
| (C.1) |
Integrating equation C.1,
| (C.2) |
where, 1/c is the integration constant.
Substituting equation 4 and C.2 in equation 3 and applying boundary condition σt = σ0 at t=0, we obtain equation 8
| (C.3) |
Footnotes
Certain commercial equipment, instruments, software or materials are identified to describe a procedure or concept adequately. Such identification is not intended to imply recommendation, endorsement or implication by NIST that the equipment, instruments, software or materials identified are necessarily the best available for the purpose.
References
- [1].Yoshinaga H, Horiuchi R, On the Nonbasal Slip in Magnesium Crystals, Transactions of the Japan Institute of Metals 5 (1) (1964) 14–21. doi: 10.2320/matertrans1960.5.14. URL https://www.jstage.jst.go.jp/article/matertrans1960/5/1/5{_}1{_}14/{_}article [DOI] [Google Scholar]
- [2].Obara T, Yoshinga H, Morozumi S, Slip system in magnesium, Acta Metallurgica 21 (7) (1973) 845–853. doi: 10.1016/0001-6160(73)90141-7. URL https://linkinghub.elsevier.com/retrieve/pii/0001616073901417 [DOI] [Google Scholar]
- [3].Gibbs GB, Creep and stress relaxation studies with polycrystalline magnesium, The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics 13 (122) (1966) 317–329. doi: 10.1080/14786436608212610. URL https://www.tandfonline.com/doi/full/10.1080/14786436608212610 [DOI] [Google Scholar]
- [4].Koike J, Kobayashi T, Mukai T, Watanabe H, Suzuki M, Maruyama K, Higashi K, The activity of non-basal slip systems and dynamic recovery at room temperature in fine-grained AZ31B magnesium alloys, Acta Materialia 51 (7) (2003) 2055–2065. doi: 10.1016/S1359-6454(03)00005-3. URL https://linkinghub.elsevier.com/retrieve/pii/S1359645403000053 [DOI] [Google Scholar]
- [5].H. F. E, C. D. Starr, T. L. S, D. J. E, Deformation Mechanisms in Polycrystalline Aggregates of Magnesium, Tech. rep, University of California, Berkeley: (1954). [Google Scholar]
- [6].Gifkins RC, Langdon TG, On the question of low-temperature sliding at grain boundaries, J. Inst. Metals 93 (1965) 347–352. [Google Scholar]
- [7].Koike J, Ohyama R, Kobayashi T, Suzuki M, Maruyama K, Grain-Boundary Sliding in AZ31 Magnesium Alloys at Room Temperature to 523 K, MATERIALS TRANSACTIONS 44 (4) (2003) 445–451. doi: 10.2320/matertrans.44.445. URL https://www.jstage.jst.go.jp/article/matertrans/44/4/44{_}4{_}445/{_}article [DOI] [Google Scholar]
- [8].Matsunaga T, Sato E, Estimation of Grain Boundary Sliding During Ambient-Temperature Creep in Hexagonal Close-Packed Metals Using Atomic Force Microscope, in: Scanning Probe Microscopy-Physical Property Characterization at Nanoscale, InTech, 2012. doi: 10.5772/35640. URL http://www.intechopen.com/books/scanning-probe-microscopy-physical-property-characterization-at-nanoscale/estimation-of-grain-boundary-sliding-during-ambient-temperature-creep-in-hcp-metals-using-afm [DOI] [Google Scholar]
- [9].Mussot P, Rey C, Zaoui A, Grain boundary sliding and strain compatibility, Res Mechanica 14 (May) (1985) 69–79. [Google Scholar]
- [10].Ando D, Sutou Y, Koike J, Internal microstructure observation of enhanced grain-boundary sliding at room temperature in AZ31 magnesium alloy, Materials Science and Engineering: A 666 (2016) 94–99. doi: 10.1016/j.msea.2016.04.030. URL https://linkinghub.elsevier.com/retrieve/pii/S0921509316303963 [DOI] [Google Scholar]
- [11].Valiev R, Kaibyshev O, On the quantitative evaluation of superplastic flow mechanisms, Acta Metallurgica 31 (12) (1983) 2121–2128. doi: 10.1016/0001-6160(83)90031-7. URL https://linkinghub.elsevier.com/retrieve/pii/0001616083900317 [DOI] [Google Scholar]
- [12].Hariharan K, Majidi O, Kim C, Lee M, Barlat F, Stress relaxation and its effect on tensile deformation of steels, Materials & Design (1980–2015) 52 (2013) 284–288. doi: 10.1016/j.matdes.2013.05.088. URL https://linkinghub.elsevier.com/retrieve/pii/S0261306913005207 [DOI] [Google Scholar]
- [13].Bong HJ, Barlat F, Lee M-G, Probing Formability Improvement of Ultra-thin Ferritic Stainless Steel Bipolar Plate of PEMFC in Non-conventional Forming Process, Metallurgical and Materials Transactions A 47 (8) (2016) 4160–4174. doi: 10.1007/s11661-016-3561-0. URL http://link.springer.com/10.1007/s11661-016-3561-0 [DOI] [Google Scholar]
- [14].Hariharan K, Dubey P, Jain J, Time dependent ductility improvement of stainless steel SS 316 using stress relaxation, Materials Science and Engineering: A 673 (2016) 250–256. doi: 10.1016/j.msea.2016.07.074. URL https://linkinghub.elsevier.com/retrieve/pii/S0921509316308383 [DOI] [Google Scholar]
- [15].Varma A, Krishnaswamy H, Jain J, Lee M-G, Barlat F, Advanced constitutive model for repeated stress relaxation accounting for transient mobile dislocation density and internal stress, Mechanics of Materials 133 (2019) 138–153. doi: 10.1016/j.mechmat.2019.03.009. URL https://www.sciencedirect.com/science/article/pii/S0167663618308196{#}!https://linkinghub.elsevier.com/retrieve/pii/S0167663618308196 [DOI] [Google Scholar]
- [16].Majidi O, Barlat F, Korkolis YP, Fu J, Lee M-G, Thermal effects on the enhanced ductility in non-monotonic uniaxial tension of DP780 steel sheet, Metals and Materials International 22 (6) (2016) 968–973. doi: 10.1007/s12540-016-6210-7. URL http://link.springer.com/10.1007/s12540-016-6210-7 [DOI] [Google Scholar]
- [17].Prasad K, Krishnaswamy H, Arunachalam N, Investigations on ductility improvement and reloading yielding during stress relaxation of dual phase Ti-6Al-4V titanium alloy, Journal of Alloys and Compounds 828 (2020) 154450. doi: 10.1016/j.jallcom.2020.154450. URL https://linkinghub.elsevier.com/retrieve/pii/S0925838820308136 [DOI] [Google Scholar]
- [18].T. Yamashita H, Ueno H, Nakai H, and Higaki, Technology to Enhance Deep-Drawability by Strain Dispersion Using Stress Relaxation Phenomenon, in: SAE 2015 World Congress & Exhibition (2015-01-0531), 2015. doi: 10.4271/2015-01-053. [DOI] [Google Scholar]
- [19].Varma A, Gokhale A, Jain J, Hariharan K, Cizek P, Barnett M, Investigation of stress relaxation mechanisms for ductility improvement in SS316L, Philosophical Magazine 98 (3) (2018) 165–181. doi: 10.1080/14786435.2017.1398422. URL https://www.tandfonline.com/doi/full/10.1080/14786435.2017.1398422 [DOI] [Google Scholar]
- [20].Blum W, Weidinger P, Watzinger B, Sedláček R, Rösch R, Haldenwanger HG, Time dependent deformation of the magnesium alloys AS21 and AZ91 around 100 °C, Zeitschrift fuer Metallkunde/Materials Research and Advanced Techniques 88 (8) (1997) 636–641. [Google Scholar]
- [21].Orowan E, Problems of plastic gliding, Proceedings of the Physical Society 52 (1) (1940) 8–22. doi: 10.1088/0959-5309/52/1/303. URL https://iopscience.iop.org/article/10.1088/0959-5309/52/1/303 [DOI] [Google Scholar]
- [22].Dotsenko VI, Stress Relaxation in Crystals, Physica Status Solidi (b) 93 (1) (1979) 11–43. doi: 10.1002/pssb.2220930102. URL http://doi.wiley.com/10.1002/pssb.2220930102 [DOI] [Google Scholar]
- [23].Caillard D, Martin JL, Thermally activated mechanisms in crystal plasticity, Pergamon Materials Series, Elsevier Science, 2003. [Google Scholar]
- [24].Povolo F, Tinivella R, Stress relaxation in bending of type AISI 304 and A-286 steels at 773 K, Journal of Materials Science 19 (6) (1984) 1851–1862. doi: 10.1007/BF00550255. [DOI] [Google Scholar]
- [25].Okazaki K, Aono Y, Kagawa M, Mobile dislocations during stress relaxation in an Fe-0.056 at. % Ti alloy, Acta Metallurgica 24 (12) (1976) 1121–1130. doi: 10.1016/0001-6160(76)90029-8. URL https://linkinghub.elsevier.com/retrieve/pii/0001616076900298 [DOI] [Google Scholar]
- [26].Spätig P, Bonneville J, Martin J-L, A new method for activation volume measurements: application to Ni3(Al,Hf), Materials Science and Engineering: A 167 (1–2) (1993) 73–79. doi: 10.1016/0921-5093(93)90339-G. URL https://linkinghub.elsevier.com/retrieve/pii/092150939390339G [DOI] [Google Scholar]
- [27].Butt MZ, Zubair M, Ul-Haq I, Comparative study of the stress relaxation in aged and un-aged high-purity aluminum polycrystals, Journal of Materials Science 35 (24) (2000) 6139–6144. doi: 10.1023/A:1026752404893. [DOI] [Google Scholar]
- [28].Takeuchi N, Ohgaku T, Tomita O, Stress relaxation in KCI single crystals, Journal of Materials Science 16 (9) (1981) 2619–2621. doi: 10.1007/BF01113606. URL http://link.springer.com/10.1007/BF01113606 [DOI] [Google Scholar]
- [29].Li JC, Charged dislocations and plasto-electric effect in ionic crystals, Materials Science and Engineering: A 287 (2) (2000) 265–271. doi: 10.1016/S0921-5093(00)00784-X. URL https://www.sciencedirect.com/science/article/abs/pii/S092150930000784X?via{%}3Dihubhttps://linkinghub.elsevier.com/retrieve/pii/S092150930000784X [DOI] [Google Scholar]
- [30].Mohebbi MS, Akbarzadeh A, Yoon Y-O, Kim S-K, Stress relaxation and flow behavior of ultrafine grained AA 1050, Mechanics of Materials 89 (2015) 23–34. doi: 10.1016/j.mechmat.2015.06.001. URL https://linkinghub.elsevier.com/retrieve/pii/S0167663615001258 [DOI] [Google Scholar]
- [31].A. E. E8M-16a, Standard test methods for tension testing of metallic materials, ASTM International West Consh (PA) (2016). doi: 10.1520/E0008_E0008M-15A. [DOI] [Google Scholar]
- [32].Trusov LI, Khvostantseva TP, Solov’ev VA, Mel’nikova VA, Low temperature stress relaxation of nanocrystalline nickel, Journal of Materials Science 30 (11) (1995) 2956–2961. doi: 10.1007/BF00349669. [DOI] [Google Scholar]
- [33].Solberg J, Thon H, Stress relaxation and creep of some aluminium alloys, Materials Science and Engineering 75 (1–2) (1985) 105–116. doi: 10.1016/0025-5416(85)90182-X. URL https://linkinghub.elsevier.com/retrieve/pii/002554168590182X [DOI] [Google Scholar]
- [34].Gjestland H, Nussbaum G, Regazzoni G, Lohne O, Bauger Ø, Stress-relaxation and creep behaviour of some rapidly solidified magnesium alloys, Materials Science and Engineering: A 134 (1991) 1197–1200. doi: 10.1016/0921-5093(91)90954-L. URL https://linkinghub.elsevier.com/retrieve/pii/092150939190954L [DOI] [Google Scholar]
- [35].Gokhale A, S. R, E.-W. Huang, S. Y. Lee, R. Prasad, S. S. Singh, J. Jain, Quantitative evaluation of grain boundary sliding and its dependence on orientation and temperature in pure Zn, Materials Letters 246 (2019) 24–27. doi: 10.1016/j.matlet.2019.03.025. URL https://linkinghub.elsevier.com/retrieve/pii/S0167577X19303970 [DOI] [Google Scholar]
- [36].Nautiyal P, Jain J, Agarwal A, A comparative study of indentation induced creep in pure magnesium and AZ61 alloy, Materials Science and Engineering: A 630 (2015) 131–138. doi: 10.1016/j.msea.2015.01.075. URL https://linkinghub.elsevier.com/retrieve/pii/S0921509315001033 [DOI] [Google Scholar]
- [37].Matsunaga T, Kameyama T, Takahashi K, Sato E, Intragranular Deformation Mechanisms during Ambient-Temperature Creep in Hexagonal Close-Packed Metals, MATERIALS TRANSACTIONS 50 (12) (2009) 2865–2872. doi: 10.2320/matertrans.M2009224. URL https://www.jstage.jst.go.jp/article/matertrans/50/12/50{_}M2009224/{_}article [DOI] [Google Scholar]
- [38].Neeraj T, Hou D-H, Daehn G, Mills M, Phenomenological and microstructural analysis of room temperature creep in titanium alloys, Acta Materialia 48 (6) (2000) 1225–1238. doi: 10.1016/S1359-6454(99)00426-7. URL https://linkinghub.elsevier.com/retrieve/pii/S1359645499004267 [DOI] [Google Scholar]
- [39].Matsunaga T, Somekawa H, Hongo H, Tabuchi M, Strain-Rate Sensitivity Enhanced by Grain-Boundary Sliding in Creep Condition for AZ31 Magnesium Alloy at Room Temperature, Materials Science Forum 838–839 (2016) 106–109. doi: 10.4028/www.scientific.net/MSF.838-839.106. URL https://www.scientific.net/MSF.838-839.106 [DOI] [Google Scholar]
- [40].Cao Z, Wang L, Hu K, Huang Y, Meng X, Microstructural evolution and its influence on creep and stress relaxation in nanocrystalline Ni, Acta Materialia 60 (19) (2012) 6742–6754. doi: 10.1016/j.actamat.2012.08.047. URL https://linkinghub.elsevier.com/retrieve/pii/S1359645412005964 [DOI] [Google Scholar]
- [41].Bell RL, Langdon TG, An investigation of grain-boundary sliding during creep, Journal of Materials Science 2 (4) (1967) 313–323. doi: 10.1007/BF00572414. URL http://link.springer.com/10.1007/BF00572414 [DOI] [Google Scholar]
- [42].Hariharan K, Jain J, Stress relaxation test: Issues in modelling and interpretation, Manufacturing Letters (oct 2020). doi: 10.1016/j.mfglet.2020.10.003. URL https://linkinghub.elsevier.com/retrieve/pii/S2213846320301607 [DOI] [Google Scholar]
- [43].Lüthy H, White RA, Sherby OD, Grain boundary sliding and deformation mechanism maps, Materials Science and Engineering 39 (2) (1979) 211–216. doi: 10.1016/0025-5416(79)90060-0. URL https://linkinghub.elsevier.com/retrieve/pii/0025541679900600 [DOI] [Google Scholar]