Abstract
In the present analysis, we study the energy transference through engine oil-based Prandtl–Eyring nanofluid flow through a heated stretching surface. The nanofluid is prepared by adding copper (Cu) and titanium dioxide (TiO2) nanoparticles (NPs) to the base fluid engine oil. The flow mechanism and thermal transmission are observed by exposing the nanofluid flow through the heated slippery surface. The influences of permeable surface, radiative flux and heat absorption/generation are also elaborated in this study. The flow of nanofluids has been designed using a PDEs system, which are then transformed into a set of ODEs via resemblance modification. The numerical technique “shooting method” is used to solve the acquired nonlinear set of non – dimensional ODEs. The results are physically exemplified through tables and plots. It has been detected that the accumulation of nanomaterials in the engine oil, reduces the skin friction while accelerating the energy transfer rate. The velocity field significantly decelerates with the encouragement of the porosity factor, and volume fraction of NPs. However, the temperature profile significantly escalates with the encouragement of the porosity factor, and volume fraction of NPs.
In the present analysis, we study the energy transference through engine oil-based Prandtl–Eyring nanofluid flow through a heated stretching surface.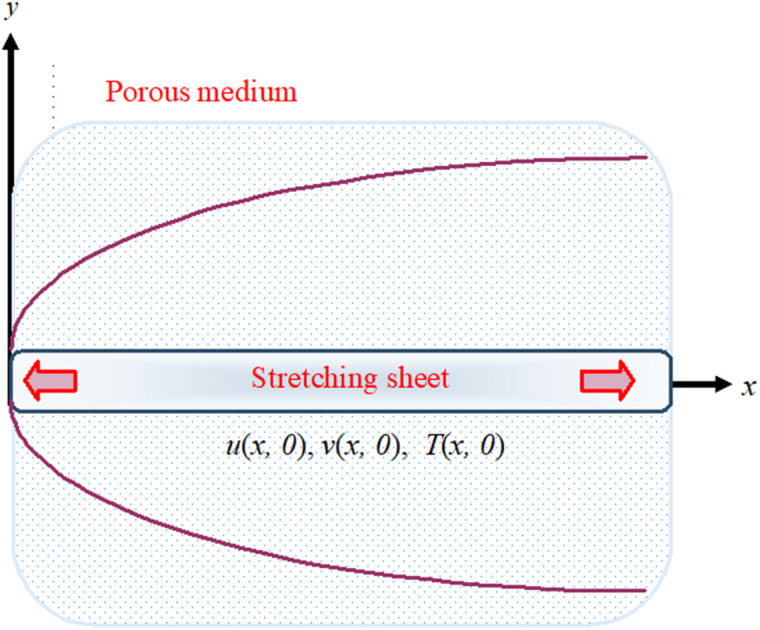
1. Introduction
Base fluids (traditional liquids) play a critical role in transferring heat in industrial operations. In general, the heat transferability of these liquids is poor. To overcome this obstacle, nanoparticles (<100 nm) are inserted to enhance abilities of heat transport. Choi and Eastman1 proposed this idea first. Solid particles conduct thermal heat more efficiently than liquids, which is a widely accepted fact. Therefore, the addition of particles of nanoscale size to conventional fluids significantly enhanced their thermal conductivity. Nanoparticles is the name given to these solid particles. A nanofluid is a fluid that consists of both the nanoparticles and base fluid. Eastman2 claimed in an experimental study that a slight quantity of nanoscale solid substantial particles can enhance the thermal conductivity of normal liquids. This research found that adding Cu NPs or carbon nanotubes (CNTs) at 1% enhanced the thermal efficiency of ethylene glycol (the base fluid) by 40–50% (volume fraction). This is due to nanofluids playing an important part in electromechanical devices, advanced cooling systems, heat exchange, and so on. The stimulus of radiant energy on a hydromagnetic unsteady liquid flow through a leaky stretchable sheet with heat and mass conversion was described by Bilal et al.3 The micro-rotation characteristic was discovered to be caused by the permeability factor. Ghasemi et al.4 revealed the influence of magnetic pitch on nanofluid flow across a stretching sheet at the stagnation point. Furthermore, the outcomes revealed that as the Lewis number upsurges, so does the heat flux of the nanofluid. The magnetohydrodynamic water-based NF flow containing motile microorganisms and nanotubes across a porous vertical floating substrate was investigated by Algehyne et al.5 Increasing heat absorption and production rates were thought to increase the rate of energy transference. Investigators6–11 looked into the thermal properties of nanofluids by incorporating multiple types of nanoparticles into the base fluid.
Recently, hybrid nanofluids (HNF), a more advanced type of nanofluid, have been introduced. The hybrid nanofluids are made up of an ordinary liquid and two or more types of nanoparticles. In terms of heat transport, hybrid nanofluids outperform conventional nanofluids. Suresh et al.12 exercised an experimental two-step method to create a hybrid nanofluid composed of Al2O3–Cu/water. Madhesh et al.13 conducted experiments on a copper–titania (Cu–TiO2) hybrid nanocomposite and copper–titania (Cu–TiO2) HNF flows with volume fraction ranging from 0.1% to 1.0%. The outcomes discovered that for a volume concentration of up to 1%, the heat flux rate is enhanced by 49%. Toghraie et al.14 carried out a research on the mixture of a ZnO–TiO2/EG HNF to illustrate the influences of nanoparticle temperature and concentration on the conduction of the HNF. The outcomes were intriguing, showing that at 50 degrees Celsius, heat radiation was 32% with a volume fraction of 3.5%. In addition to these experimental efforts, scientists have concentrated on theoretical research of hybrid nanoliquid flows. Gul et al.15 compared Yamada–Ota and Hamilton–Crosser HNF models that contained silicon carbide (SiC) and titanium oxide TiO2 nanoparticles (NPs) in diathermic oil. After being stimulated with a magnetic dipole, the flow of the hybrid nanoliquid was predicted to occur over a larger surface. The key findings indicated that the Yamada–Ota model outperformed the Hamilton–Crosser hybrid nanoliquid flow model in terms of heat transfer efficiency. Arif et al.16 studied theoretically ternary hybrid nanoliquid flow with base liquid water between two parallel sheets with various nanoparticle shapes such as cylinders, spheres, and platelets of carbon nanotubes, aluminium oxide, and graphene, respectively. The unsteady fluid flow and energy transmission of a Cu–Al2O3/water-based HNF over an axially impermeable contracting and extending substrate were investigated by Khan et al.17 A hybrid nanofluid (Cu–Al2O3/water) was discovered to accelerate heat transmission when compared to a conventional fluid. Elattar et al.18 explored the flow of a steady electrically charged HNF through an opaque thin flexible sheet using the computational technique PCM. The influence of velocity index and Hall current raises the velocity contour, while changes in particle volume and sheet thickness lower it. Wang et al.19 inspected the influence of a biochemical reaction on a HNF unsteady flow along a texture that was expanding. The presence of the unsteadiness variable has been observed to regulate the transition from laminar to turbulent flow. Alharbi et al.20 characterised the flow of an energy propagating high conductivity ternary HNF that included nanocrystals as well as an extended sheet. When ternary hybrid NPs are varied the base fluid thermal conductivity is greatly improved. Ahmad et al.21 looked into the heat transport properties of engine oil containing nanoparticles like Cu and TiO2. They found that the effectiveness of copper and titanium oxide in engine oil is overlooked.
Prandtl–Eyring nanofluid is a mixed convection flow of nanoparticles with activation energy that is non-linear. As a result, numerous non-Newtonian fluid models have been offered in the literature. The Prandtl–Eyring fluid is one of them. Darji et al.22 described visco-inelastic liquid flow boundary layer similarity solutions. Hayat et al.23 inspected the consequence of magnetohydrodynamics on the flow of a peristaltic dissipative Prandtl–Eyring liquid. According to the results, Akbar24 discovered the convective boundary constraints of Prandtl–Eyring liquid flow with peristatic properties. Khan et al.25 conducted a mathematical computational evaluation of bio convection on PEF. The effects of thermo/phonetic force and Brownian motion on electrically conducting PEF generated by strained shallow were investigated by Abdelmalek et al.26
Because of the numerous implementations in nanofluid mechanics, investigators are developing a wave-based heat transfer methodology rather than a diffusion operation.27–29 Heat transfer is a well-established phenomenon that happens as a consequence of temperature variations between two distinct objects or between components of an identical system. For decades, Fourier's30 fundamental law of heat conduction, has been used to measure heat transfer properties. Later, with concern, it was discovered that this model produces a parabolic energy equation with an initial disruption that lasts across the process. A “paradox of heat conduction” denotes this weakness in the Fourier model. Cattaneo31 addresses this flaw by incorporating a relaxation term into the Fourier approach. Afterward, Christov32 created the Cattaneo-suggested relationship with the Oldroyd upper-convected variant via frame-indifferent alteration. This type of relationship is identified as the Cattaneo–Christov (CC) flux model. Kumar et al.33 used a CC flux model to investigate the features of Dusty fluid of dissolved HNF flows in two phases through an elongated cylinder. The shooting approach with RK–Fehlberg system, were used for numerical results. Ramzan et al.34 used the CC model and MHD impact with heterogeneous reactions adjacent to a stagnation point to calculate the Williamson fluid flow. It should be acknowledged that the fluid parameter has a diametrically opposed influence on velocity and temperature profiles. Shah et al.35 used the CC model to investigate heat transfer in a 2D (two dimensional) flow of Ree–Eyring nanoliquid through a stretching sheet.
The primary goal of this research is to determine how heat absorption and thermal radiation, as well as viscous dissipation and energy transportation, occur in engine oil-based NF flow over a heated elongating surface. Cu and TiO2 nanoparticles are added to engine oil to create the nanofluid. The nanofluid flow was modelled as a system of PDEs, which are then transformed into a set of ODEs via resemblance modification. The numerical technique “shooting method” is used to solve the acquired nonlinear set of non – dimensional ODEs. Local velocity gradient and Nusselt number statistics are estimated and analysed. Despite the fact that the phenomena described in this manuscript have never been attempted before.
2. Mathematical formulation
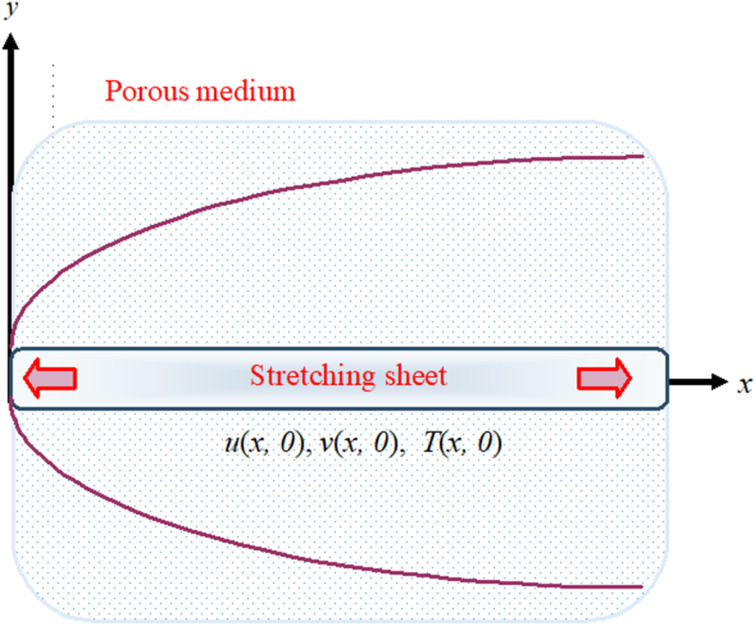
We have assumed the 2D viscous dissipative nanofluid flow over an irregular moving horizontal porous plate. The plate is moving with velocity 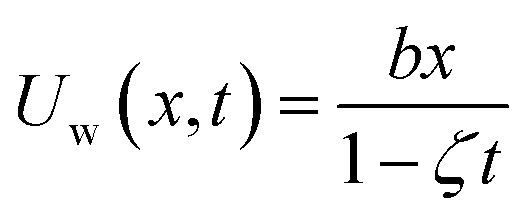 , where b is a stretching rate as shown in Fig. 1. The flow has been investigated in terms of thermal radiation and viscous dissipation. At x = 0 the surface is heated with relation
, where b is a stretching rate as shown in Fig. 1. The flow has been investigated in terms of thermal radiation and viscous dissipation. At x = 0 the surface is heated with relation 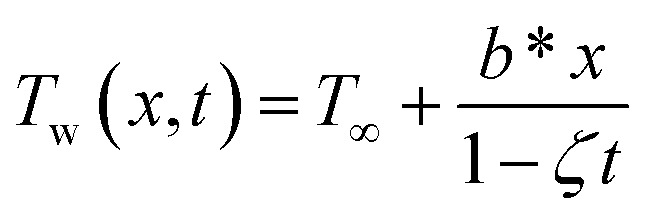 where b* and Tw represents the energy variation, surrounding temperature and surface heat, respectively. The surface of the plate is supposed to be slippery.
where b* and Tw represents the energy variation, surrounding temperature and surface heat, respectively. The surface of the plate is supposed to be slippery.
Fig. 1. The physical representation of flowing fluid across a stretching surface.
2.1. Formal model
The fluid flow model is displayed in Fig. 1 as:
2.2. Governing equations
The constitutive Prandtl–Eyring model33–35 for the nanofluid flow in a porous medium and heat equation with variable temperature, thermal radiation, Cattaneo–Christov heat flux model, and heat source/sink utilizing the approximate boundary-layer are:
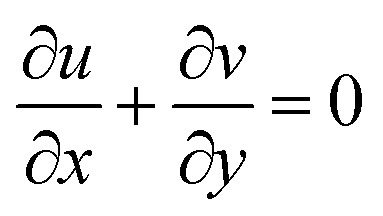 |
1 |
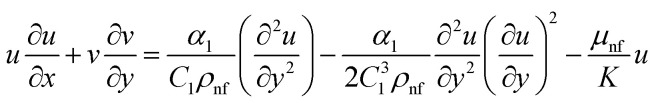 |
2 |
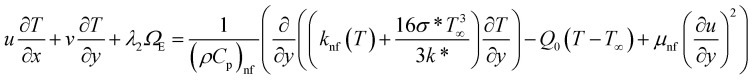 |
3 |
Boundary conditions21
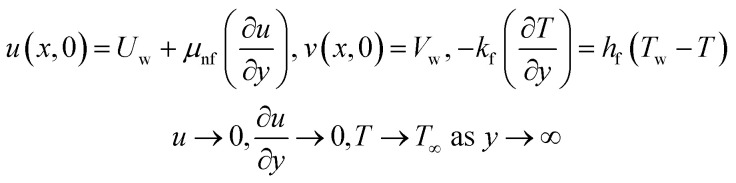 |
4 |
Here, v, and u are the velocity components, α1 and C1 are the fluid parameters, μnf is the dynamic viscosity of nanofluid, ρnf is the density, knf is the thermal conductivity, Q0 is the heat source, hf is the heat transition constant and K is the surface permeability, ΩE is the heat flux for which model equations is
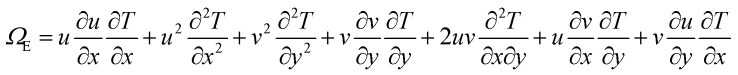 |
5 |
The varying thermal conductivity is classified as:
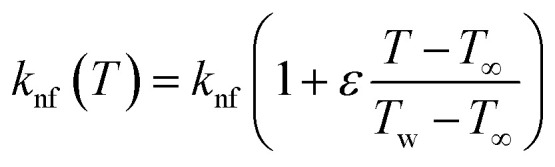 |
6 |
2.3. Thermo-physical material properties of nanofluid and base fluid
Different researchers presented mathematical models that explain the effective characteristics of heat transfer in the nanofluids. These models present physical characteristic of the nanofluid in term of relevant physical characteristics of the solid nanoparticles and base fluid. The density of a ferrofluid (ρff) is related to the density of the fluid (ρf) and that of the solid nanoparticle phase (ρs) as follows:35
| ρnf = (1 − ϕ)ρf + ϕρs | 7 |
Here ϕ is the volume fraction of NPs. Similarly the volume specific heats are correlated as:
| (ρCp)nf = (1 − ϕ)(ρCp)f + ϕ(ρCp)s | 8 |
The dynamic viscosity of the fluid and the nanofluid are given by;
| μnf = (1 − ϕ)−2.5μf | 9 |
To estimate the efficient thermal conductivity of the nanofluid, the Maxwell–Garnetts (MG) model can be utilized:
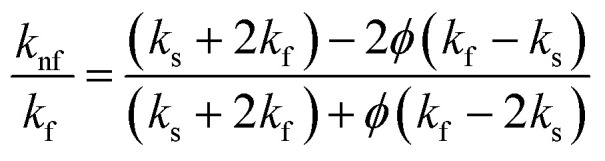 |
10 |
In the present study heat transfer analysis through copper (Cu) and titanium dioxide (TiO2) nanoparticles (NPs) to the base fluid engine oil has been achieved into the account the characteristics using in Table 1.
The experimental values of engine oil, Cu and TiO2 (ref. 21).
| ρ (kg m−3) | C p (j kg−1 K−1) | k (W mK−1) | |
|---|---|---|---|
| Engine oil | 884 | 1910 | 0.1440 |
| Copper Cu | 8933 | 385.0 | 401.0 |
| Titanium dioxide TiO2 | 4250 | 686.20 | 8.9538 |
3. Dimensionless formulations model
Using all assumptions and velocity filed on eqn (1)–(4), eqn (1) hold identically, and the dimensionless process for eqn (2)–(4), the stream functions are expressed as:
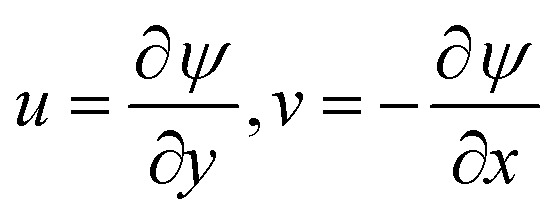 |
11 |
The similarity variables are:
 |
12 |
Using eqn (8) & (9) in eqn (1)–(3), we get the following dimensionless form of a system of ODEs:
 |
13 |
 |
14 |
The transform boundary conditions are:
 |
15 |
where,
 |
16 |
Also
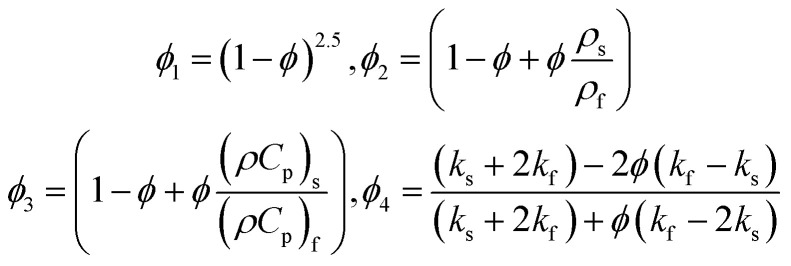 |
17 |
4. Skin friction drag and nusselt number
The physical interest quantities such as the drag force Cf and nusselt number Nu are specify as
 |
18 |
where
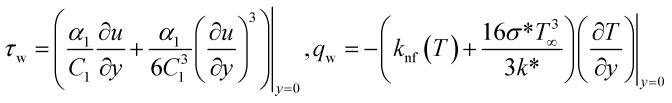 |
19 |
Incorporating eqn (15) in (14), we get:
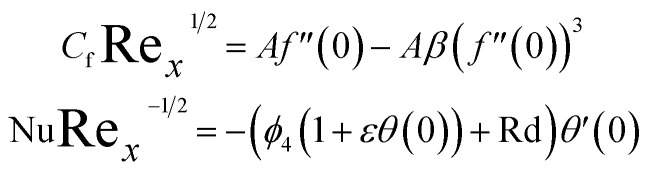 |
20 |
5. Numerical solution
The obtained system of ODEs (eqn (13)–(15)) is further reduced to the 1st order differential equations through the following variables framework:
| f = ¥1, f′ = ¥2, f′′ = ¥3, θ = ¥4, θ′ = ¥5 | 21 |
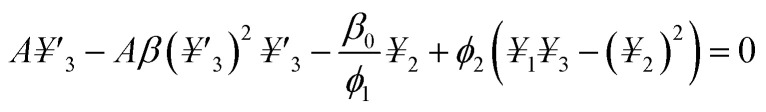 |
22 |
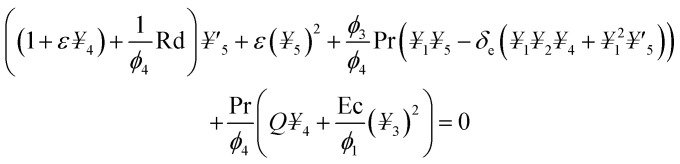 |
23 |
The transform boundary conditions are:
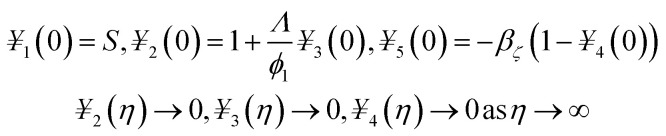 |
24 |
6. Result and discussion
This section explained the physical procedure and trend that underpin each plot and table. The physical sketch of the flow problem was elaborated in Fig. 1. Fig. 2–13 show the behaviour of velocity and energy outlines in relation to various physical constraints.
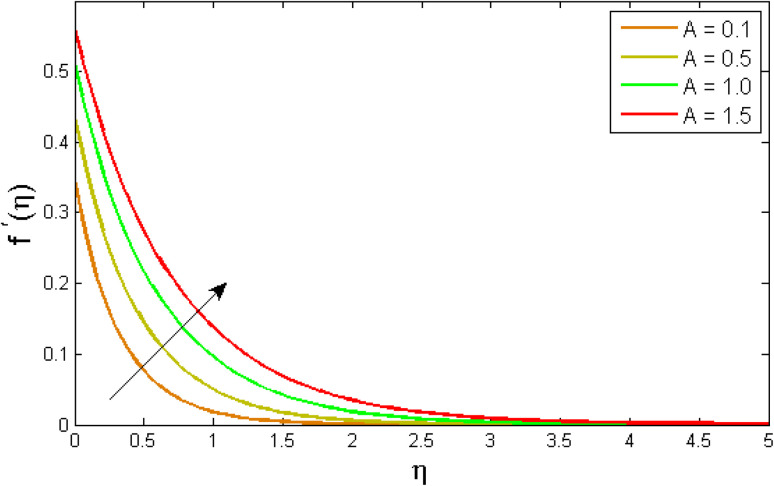
Fig. 2. Variation of velocity outlines f′(η) versus fluid parameter A.
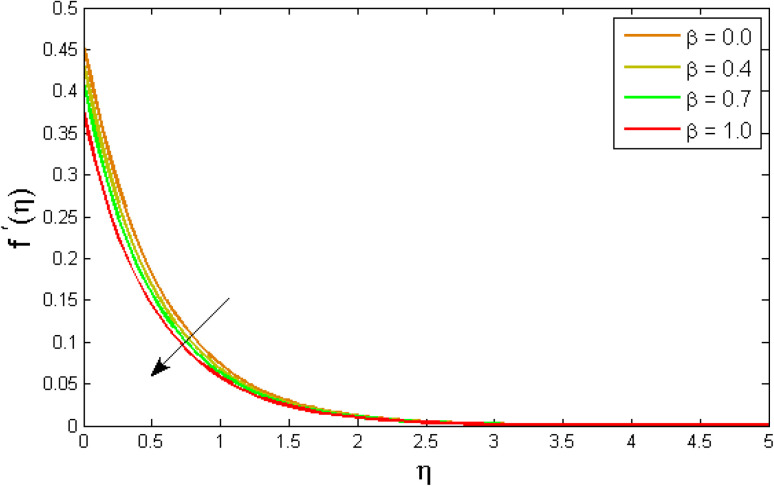
Fig. 3. Variation of velocity outlines f′(η) versus fluid parameter β.
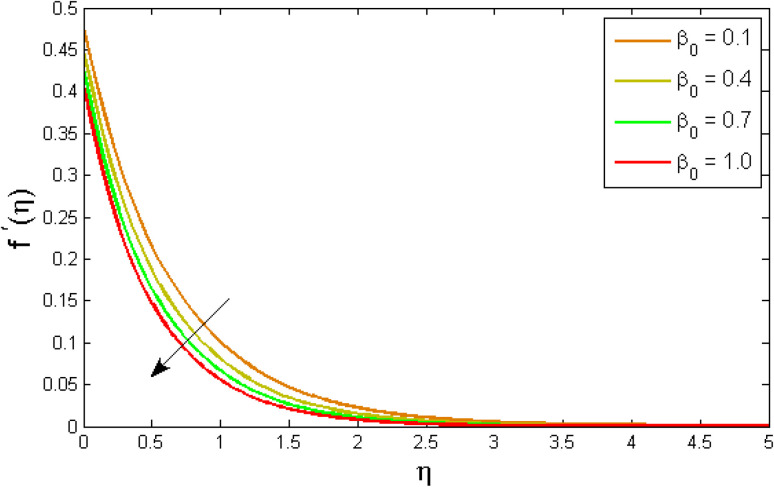
Fig. 4. Variation of velocity outlines f′(η) versus porosity parameter β0.
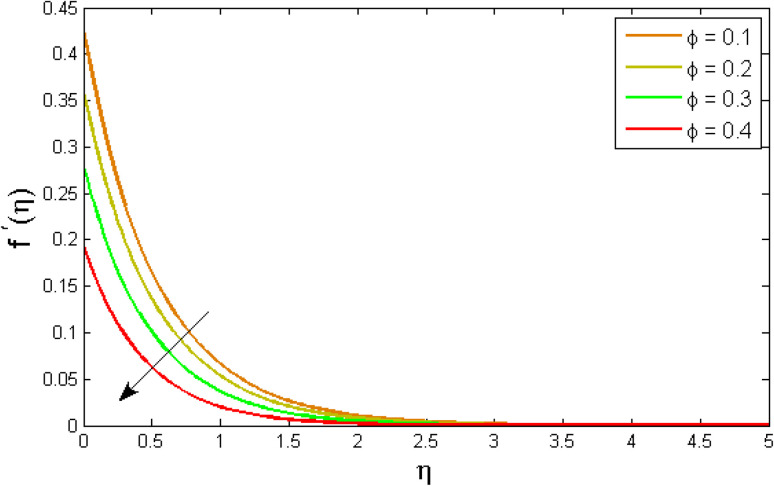
Fig. 5. Variation of velocity outlines f′(η) versus volume fraction parameter ϕ.
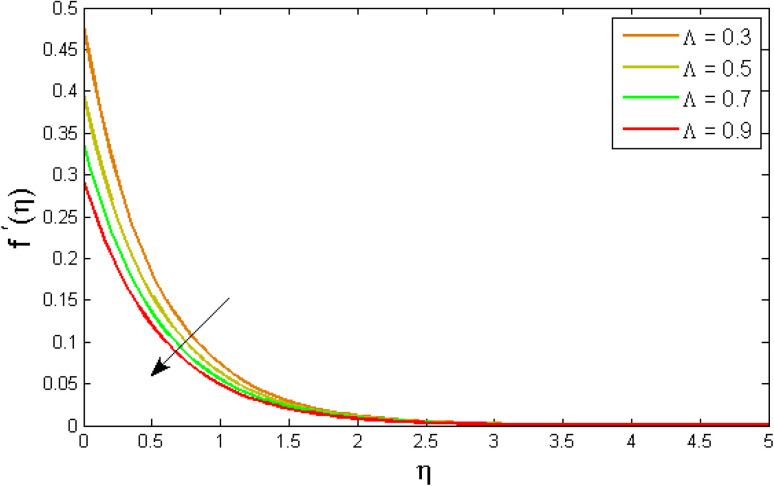
Fig. 6. Variation of velocity outlines f′(η) versus velocity slip parameter Λ.
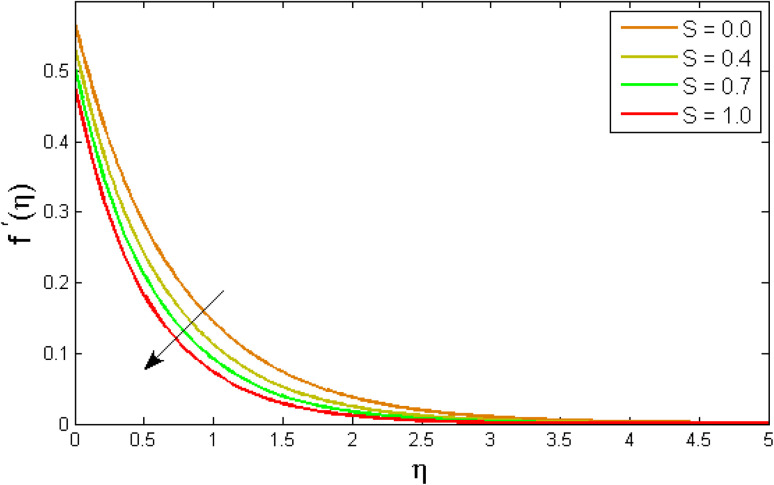
Fig. 7. Variation of a velocity outlines f′(η) versus mass transfer parameter S.
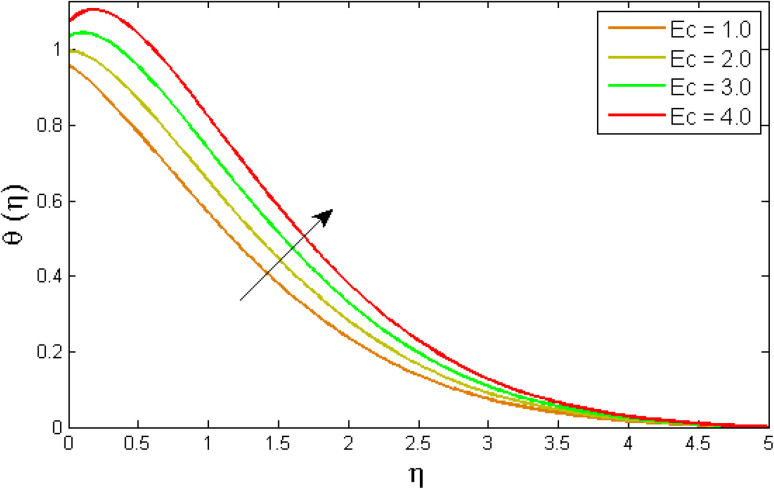
Fig. 8. Variation of temperature outlines θ(η) versus Eckert number Ec.
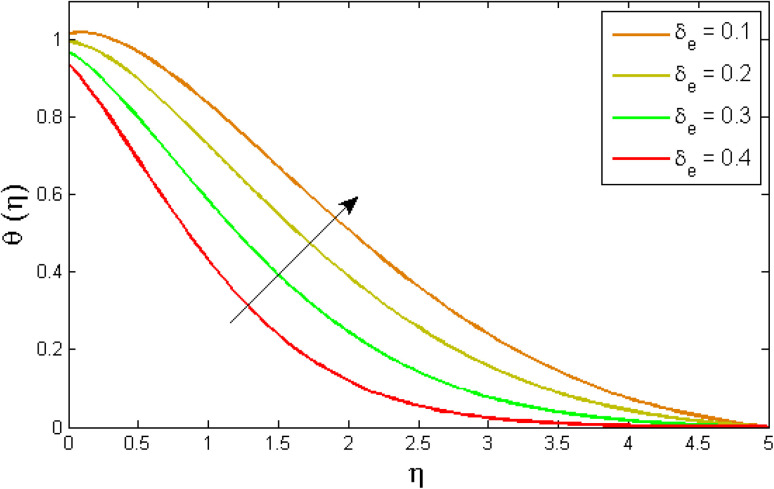
Fig. 9. Variation of temperature outlines θ(η) versus thermal relaxation parameter δe.
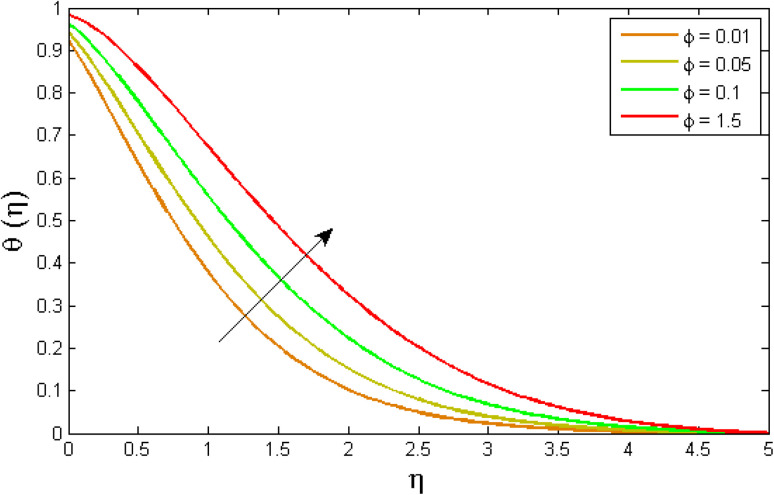
Fig. 10. Variation of temperature outlines θ(η) versus volume fraction parameter ϕ.
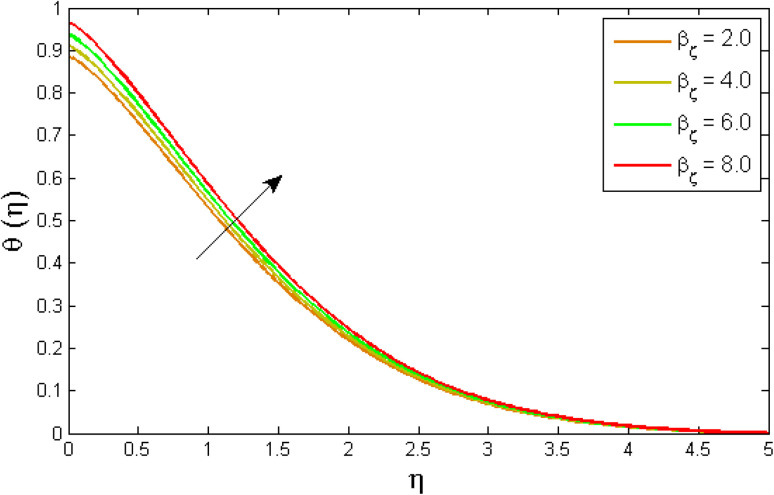
Fig. 11. Variation of temperature outlines θ(η) versus Biot number Bζ.
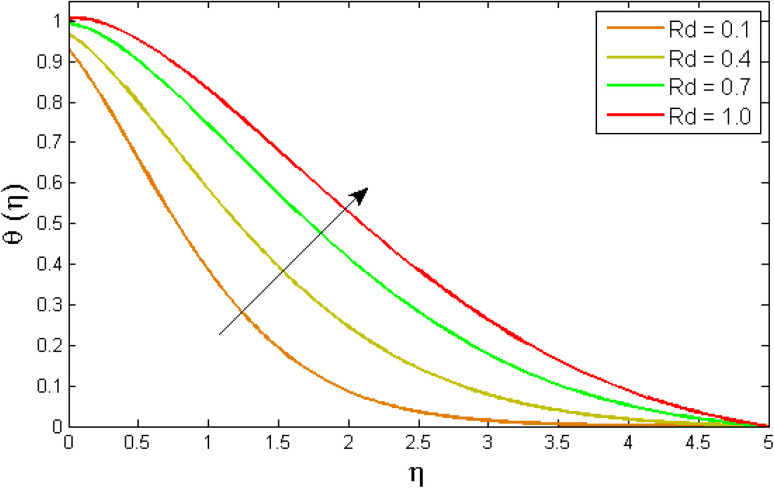
Fig. 12. Variation of temperature outlines θ(η) versus temperature dependent thermal radiation parameter Rd.
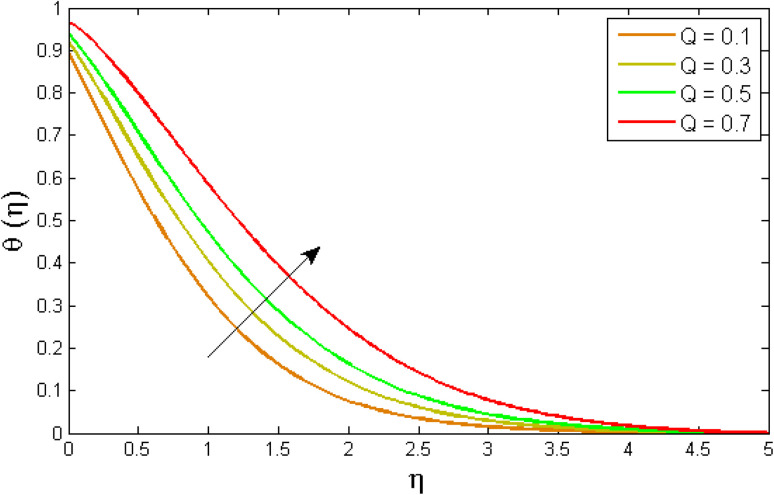
Fig. 13. Variation of temperature outlines θ(η) versus heat generation parameter Q.
6.1. Velocity profile
Fig. 2–7 elucidated the trend of velocity outlines f′(η) versus fluid parameters A & β, porosity parameter β0, velocity slip parameter Λ, volume fraction parameter ϕ, and suction parameter S. Fig. 2 illustrates the effects of fluid parameter A on fluid velocity while the other parameters are held constant. This graph shows that increasing the value of A causes an upsurge in the value of velocity. Because higher values of A tend to reduce viscosity, which overwhelms the resistance offered by the liquid. Fig. 3 depicts how the fluid velocity gradient tends to decrease as fluid parameter β increases. It is physically true because β varies inverse proportion with momentum diffusivity, resulting in a decrease in velocity gradient. Fig. 4 portrays the impacts of the porosity parameter β0 on the velocity distribution. The velocity decreases as β0 increases. Physically, the existence of a porous medium has increased the medium's opposition to fluid flow. Fig. 5 shows how the volumetric concentration ϕ affects the velocity profile f′(η). When the particle volume ϕ fraction is risen, the velocity profile f′(η) reduces. As the volume fraction ϕ of the nanoparticles grows, the fluid thickens, and a conflicting force develops, leading to deceleration. Fig. 6 depicts a graphical representation of the behaviour of velocity profiles f′(η) as a function of the velocity slip parameter Λ. In general, Λ calculates the amount of slip at the cylinder's surface. Here, we examine how fluid velocity decreases as Λ increases. It is because Λ primarily reduce speed of fluid motion, confirming a reduction in net movement of fluid molecules. Because there is less molecular progression, velocity fields decline. Fig. 7 indicates the behaviour of the velocity field for various values of S. Suction is an efficient method for preventing boundary layer separation, as well as controlling velocity and heat energy. The amount of fluid particles is close to the wall after reaching the maximum value of the suction/blowing parameter. Accordingly, the outline of the associated boundary layer becomes thinner over time, and the velocity profiles decelerate as S strength increases.
6.2. Temperature profile
Fig. 8–13 reported the conduct of the energy profile θ(η) versus the thermal relaxation parameter δe, volume fraction parameter ϕ, Biot number Bζ, heat generation constraint Q, thermal radiation term Rd and Eckert number Ec. Fig. 8 depicts that the variation of Eckert number Ec on temperature profile. The stimulus of Eckert number Ec on nanofluid temperature is evident because an increase in Eckert number accelerates advective transport (kinetic energy). As a result, fluid particles interact together more frequently, and these collisions convert kinetic energy (KE) into thermal energy. Accordingly, the temperature profile upsurges. Fig. 9 displays the stimulus of the thermal relaxation parameter on temperature distribution. Temperature distribution decreases as the thermal relaxation parameter δe increases. It is also observed that the thickness of the thermal boundary layer diminutions. This is due to the fact that as δe intensifies, the material particles necessitate more time to transferal heat to their neighbouring droplets. To put it another way, for advanced values of the δe parameter, the material reveals a non-conducting property, which contributes to a narrower temperature distribution. Fig. 10 exposed that the temperature upsurges with the upshot of the volume fraction parameter ϕ. Because of the collision of tiny nanoparticles in the flow field produces thermal energy, which advances the temperature of the fluid. Therefore, the addition of Cu and titanium NPs enhances the energy propagation θ(η). Fig. 11 display the impression of Biot number Bζ on the energy profile. The Biot number is related to the surface's convective boundary constraints. As βζ boosts, so does the temperature profile close to the surface, raising the temperature close to the surface and, consequently, the thickness of the thermal boundary layer, as realized in Fig. 11. Fig. 12 indicates that the variation of thermal radiation Rd on temperature profile. The temperature profile improves as thermal radiation (Rd) values boost. Larger Rd values have dominant impact on conduction. As a result of the radiation, a significant quantity of heat is distributed into the system, raising the temperature. Fig. 13 depicts the encouragement of a heat generation factor Q on fluid temperature. The temperature profile is seen to boost as Q goes up. Heat is generated in the flow regime as a result of positive modifications in the heat generation parameter, causing a rise in fluid temperature.
7. Skin friction and nusselt number
Table 2 and 3 quantitively reported the computational outcomes of skin friction CfRex1/2 and Nusselt number NuRex−1/2versus different physical entities. It has been perceived that the accumulation of NPs to the engine oil, accelerates the skin friction, while reducing the energy transfer rate. Where, the fluid parameter β boost the skin friction, while the variation of porosity parameter dimmish the skin friction as observed in Table 2. It can be noticed from Table 3 that the rising quantity of thermal relaxation parameter, Eckert number and thermal radiation declined the energy transmission rate. In Table 4 the presents results are compared with previous published results, and excellent agreement is noticed in both results.
:Outputs of skin friction versus physical constraints.
| β | β 0 | ϕ | C fRex1/2 for TiO2 | C fRex1/2 for Cu |
|---|---|---|---|---|
| 0.1 | −0.8646406 | −0.9474403 | ||
| 0.3 | −0.7848349 | −0.830342 | ||
| 0.5 | −0.6975074 | −0.6999307 | ||
| 0.1 | −0.8646406 | −0.9474403 | ||
| 0.3 | −0.8748317 | −0.9533525 | ||
| 0.5 | −0.8840958 | −0.9589156 | ||
| 0.1 | −0.8646406 | −0.9474403 | ||
| 0.2 | −0.8034606 | −0.8956594 | ||
| 0.3 | −0.6906621 | −0.7638494 |
Outputs of Nusselt number NuRex−1/2versus physical entities.
| δ e | Ec | ϕ | Rd | NuRex−1/2 for TiO2 | NuRex−1/2 for Cu |
|---|---|---|---|---|---|
| 0.1 | 0.7661464 | 0.6494773 | |||
| 0.3 | 1.007504 | 0.8727002 | |||
| 0.5 | 1.275255 | 1.132698 | |||
| 0.1 | 0.7661464 | 0.6494773 | |||
| 0.3 | 0.686729 | 0.5710788 | |||
| 0.5 | 0.6076494 | 0.4929863 | |||
| 0.1 | 0.7661464 | 0.6494773 | |||
| 0.2 | 0.4552573 | 0.4717461 | |||
| 0.3 | 0.4482464 | 0.3758579 | |||
| 0.1 | 0.7661464 | 0.6494773 | |||
| 0.2 | 0.731588 | 0.6073274 | |||
| 0.3 | 0.6974548 | 0.5682502 |
Comparison of f′′(0) for different values of Λ with literature Ahmad et al.21.
| Λ | f′′(0) for TiO2 | f′′(0) for Cu | f′′(0) for TiO2 | f′′(0) for Cu |
|---|---|---|---|---|
| Present paper | Ahmad et al.21 | |||
| 0.2 | −0.8676146 | −0.9223163 | −0.82123 | −0.92408 |
| 0.4 | −0.6956203 | −0.7309784 | −0.67790 | −0.74650 |
| 0.6 | −0.584262 | −0.6094886 | −0.58010 | −0.62984 |
| 0.8 | −0.5055081 | −0.5246363 | −0.50856 | −0.54659 |
| 1.0 | −0.446524 | −0.4616436 | −0.45368 | −0.48387 |
8. Conclusions
We analyzed the energy transference and entropy generation through nanofluid flow through a heated extending surface. The nanofluid is organized by the accumulation of Cu and TiO2 NPs in the engine oil. The flow of nanofluids has been designed using a PDEs system, which are then transformed into a set of ODEs via resemblance modification. The numerical technique “shooting method” is used to solve the acquired nonlinear set of non – dimensional ODEs. The outcomes are physically exemplified through figures and tables. The key findings are:
• The velocity f′(η) significantly improves with the influence of parameters A, while declining with the effects of parameter β, suction parameter S, slip parameter Λ, porosity factor, and volume fraction of nanoparticles.
• The temperature θ(η) curve boosts with growing values of the thermal relaxation coefficient δe and volume fraction parameter ϕ.
• The temperature θ(η) pointedly boosts with the stimulus of Q, Eckert number Ec, and thermal radiation parameter Rd.
• The accumulation of nanomaterials in the engine oil, speeding up the skin friction, while reduces the energy transfer rate.
• The fluid parameter β boost the skin friction, while the variant in porosity parameter dimmish the skin friction.
• The rising quantity of thermal relaxation parameter, Eckert number and thermal radiation declined the energy transmission rate.
Nomenclature
- Br
Brinkman number
- C p
Specific heat transfer (J/Kg/K)
- c b
Drag force
- Ec
Eckert number
- h f
Heat transition constant
- K
Permeability of porous medium
- k
Thermal conductivity (W m−1 K−1)
- Pr
Prandtl number
- Q 0
Heat generation/absorption
- Rd
Thermal radiation
- T
Temperature of fluid
- T r
Temperature ratio
- u, v
Velocity components (m s−1)
- x, y
Coordinates axis (m)
Greek letter
- α 1, C1
Fluid parameter
- A, β
Dimensionless fluid parameter
- β 0
Porosity parameter
- β ζ
Biot number
- Λ
Velocity slip parameter
- δ e
Thermal relaxation parameter
- ϕ
Volume fraction parameter
- ε
Temperature dependent thermal conductivity parameter
- η
Independent coordinate
- ν
Kinematic viscosity
- μ
Dynamic viscosity
- ρ
Density (kg m−3)
- ρC p
Heat capacitance
- ψ
Stream function (m2 s−1)
Subscripts
- f
Base fluid
- s
Solid nanoparticle
- nf
Nanoparticles
- w
Wall
- ∞
Free-stream
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Author contributions
All authors have equal contributions.
Conflicts of interest
The authors declare that they have no competing interests.
Supplementary Material
References
- Choi S. U. S. Eastman J. A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Int. Mech. Eng. Congr. Expo. 1995:12a–17a. [Google Scholar]
- Eastman J. A. Choi S. U. S. Li S. Yu W. Thompson L. J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001;78:718. doi: 10.1063/1.1341218. [DOI] [Google Scholar]
- Bilal M. Saeed A. Gul T. Kumam W. Mukhtar S. Kumam P. Parametric simulation of micropolar fluid with thermal radiation across a porous stretching surface. Sci. Rep. 2022;12(1):1–11. doi: 10.1038/s41598-021-99269-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghasemi S. E. Mohsenian S. Gouran S. Zolfagharian A. A novel spectral relaxation approach for nanofluid flow past a stretching surface in presence of magnetic field and nonlinear radiation. Results Phys. 2022;32:105141. doi: 10.1016/j.rinp.2021.105141. [DOI] [Google Scholar]
- Algehyne E. A. Alhusayni Y. Y. Tassaddiq A. Saeed A. Bilal M. The study of nanofluid flow with motile microorganism and thermal slip condition across a vertical permeable surface. Waves Random Complex Media. 2022:1–18. [Google Scholar]
- Hafeez M. B. Khan M. S. Qureshi I. H. Alebraheem J. Elmoasry A. Particle rotation effects in Cosserat–Maxwell boundary layer flow with non-Fourier heat transfer using a new novel approach. Sci. Iran. 2021;28:1223–1235. [Google Scholar]
- Hafeez M. B. Amin R. Nisar K. S. Jamshed W. Abdel-Aty A. H. Khashan M. M. Heat transfer enhancement through nanofluids with applications in automobile radiator. Case Stud. Therm. Eng. 2021;27:101192. doi: 10.1016/j.csite.2021.101192. [DOI] [Google Scholar]
- Hafeez M. B. Sumelka W. Nazir U. Ahmad H. Askar S. Mechanism of Solute and Thermal Characteristics in a Casson Hybrid Nanofluid Based with Ethylene Glycol Influenced by Soret and Dufour Effects. Energies. 2021;14:6818. doi: 10.3390/en14206818. [DOI] [Google Scholar]
- Hafeez M. B. Krawczuk M. Shahzad H. An Overview of Heat Transfer Enhancement Based Upon Nanoparticles Influenced By Induced Magnetic Field with Slip Condition via Finite Element Strategy. Acta Mech. Automatica. 2022;16:200–206. doi: 10.2478/ama-2022-0024. [DOI] [Google Scholar]
- Hafeez M. B. Krawczuk M. Nisar K. S. Jamshed W. Pasha A. A. A finite element analysis of thermal energy inclination based on ternary hybrid nanoparticles influenced by induced magnetic field. Int. Commun. Heat Mass Transfer. 2022;135:106074. doi: 10.1016/j.icheatmasstransfer.2022.106074. [DOI] [Google Scholar]
- Hafeez M. B. Krawczuk M. Shahzad H. Pasha A. A. Adil M. Simulation of hybridized nanofluids flowing and heat transfer enhancement via 3-D vertical heated plate using finite element technique. Sci. Rep. 2022;12:1–15. doi: 10.1038/s41598-021-99269-x. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Suresh S. Venkitaraj K. P. Selvakumar P. Chandrasekar M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf., A. 2011;1–3:41–48. doi: 10.1016/j.colsurfa.2011.08.005. [DOI] [Google Scholar]
- Madhesh D. Parameshwaran R. Kalaiselvam S. Experimental investigation on convective heat transfer and rheological characteristics of Cu–TiO2 hybrid nanofluids. Exp. Therm. Fluid Sci. 2014;52:104–115. doi: 10.1016/j.expthermflusci.2013.08.026. [DOI] [Google Scholar]
- Toghraie D. Chaharsoghi V. A. Afrand M. Measurement of thermal conductivity of ZnO–TiO2/EG hybrid nanofluid. J. Therm. Anal. Calorim. 2016;125(1):527–535. doi: 10.1007/s10973-016-5436-4. [DOI] [Google Scholar]
- Gul H. Ramzan M. Nisar K. S. Mohamed R. N. Ghazwani H. A. S. Performance-based comparison of Yamada–Ota and Hamilton–Crosser hybrid nanofluid flow models with magnetic dipole impact past a stretched surface. Sci. Rep. 2022;12:1–11. doi: 10.1038/s41598-021-99269-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arif M. Kumam P. Kumam W. Mostafa Z. Heat transfer analysis of radiator using different shaped nanoparticles water-based ternary hybrid nanofluid with applications: a fractional model. Case Stud. Therm. Eng. 2022;31:101837. doi: 10.1016/j.csite.2022.101837. [DOI] [Google Scholar]
- Khan U. Waini I. Ishak A. Pop I. Unsteady hybrid nanofluid flow over a radially permeable shrinking/stretching surface. J. Mol. Liq. 2021;331:115752. doi: 10.1016/j.molliq.2021.115752. [DOI] [Google Scholar]
- Elattar S. et al., Computational assessment of hybrid nanofluid flow with the influence of hall current and chemical reaction over a slender stretching surface. Alexandria Eng. J. 2022;61:10319–10331. doi: 10.1016/j.aej.2022.03.054. [DOI] [Google Scholar]
- Wang F. Ahmad S. Al Mdallal Q. Alammari M. Khan M. N. Rehman A. Natural bio-convective flow of Maxwell nanofluid over an exponentially stretching surface with slip effect and convective boundary condition. Sci. Rep. 2022;12:1–14. doi: 10.1038/s41598-021-99269-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alharbi K. A. M. et al., Computational Valuation of Darcy Ternary-Hybrid Nanofluid Flow across an Extending Cylinder with Induction Effects. Micromachines. 2022;13:1–15. doi: 10.3390/mi13040588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmad S. et al., Features of Cu and TiO2 in the flow of engine oil subject to thermal jump conditions. Sci. Rep. 2021;11:19592. doi: 10.1038/s41598-021-99045-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darji R. M. Timol M. G. Professor A. Similarity Solutions of Laminar Incompressible Boundary Layer Equations of Non-Newtonian Viscoinelastic Fluids. Int. J. Math. Arch. 2011;2:1395–1404. [Google Scholar]
- Hayat T. Bibi S. Alsaadi F. Rafiq M. Peristaltic Transport of Prandtl–Eyring Liquid in a Convectively Heated Curved Channel. PLoS One. 2016;11:e0156995. doi: 10.1371/journal.pone.0156995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akbar N. S. MHD Eyring–Prandtl Fluid Flow with Convective Boundary Conditions in Small Intestines. Int. J. Biomath. 2013;6:1350034. doi: 10.1142/S1793524513500344. [DOI] [Google Scholar]
- Khan M. Salahuddin T. Malik M. Y. Alqarni M. S. Alqahtani A. M. Numerical modeling and analysis of bioconvection on MHD flow due to an upper paraboloid surface of revolution. Phys. A. 2020;553:124231. doi: 10.1016/j.physa.2020.124231. [DOI] [Google Scholar]
- Abdelmalek Z. Hussain A. Bilal S. Sherif E. S. M. Thounthong P. Brownian motion and thermophoretic diffusion influence on thermophysical aspects of electrically conducting viscoinelastic nanofluid flow over a stretched surface. J. Mater. Res. Technol. 2020;9:11948–11957. doi: 10.1016/j.jmrt.2020.08.014. [DOI] [Google Scholar]
- Molla M. M. Hossain M. A. Taher M. A. Magnetohydrodynamic natural convection flow on a sphere with uniform heat flux in presence of heat generation. Acta Mech. 2006;186:75–86. doi: 10.1007/s00707-006-0373-0. [DOI] [Google Scholar]
- Hassan M. Mohyud-Din S. T. Ramzan M. Study of heat transfer and entropy generation in ferrofluid under low oscillating magnetic field. Indian J. Phys. 2018;93:749–758. doi: 10.1007/s12648-018-1328-8. [DOI] [Google Scholar]
- Molla M. M. Hossain M. A. Paul M. C. Natural convection flow from an isothermal horizontal circular cylinder in presence of heat generation. Int. J. Eng. Sci. 2006;44:949–958. doi: 10.1016/j.ijengsci.2006.05.002. [DOI] [Google Scholar]
- Fourier J. B. J., Théorie analytique de la chaleur, Firmin Didot, 1822, pp. 499–508 [Google Scholar]
- Cattaneo C. Sulla conduzione del calore. Attidel Semin. Mat. e Fis. Univ. di Modena. 1948;3:83–101. [Google Scholar]
- Christov C. I. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009;36:481–486. doi: 10.1016/j.mechrescom.2008.11.003. [DOI] [Google Scholar]
- Varun Kumar R. S. Punith Gowda R. J. Naveen Kumar R. Radhika M. Prasannakumara B. C. Two-phase flow of dusty fluid with suspended hybrid nanoparticles over a stretching cylinder with modified Fourier heat flux. SN Appl. Sci. 2021;3:1–9. [Google Scholar]
- Ramzan M. Bilal M. Chung J. D. MHD stagnation point Cattaneo–Christov heat flux in Williamson fluid flow with homogeneous–heterogeneous reactions and convective boundary condition—a numerical approach. J. Mol. Liq. 2017;225:856–862. doi: 10.1016/j.molliq.2016.10.139. [DOI] [Google Scholar]
- Shah Z. Vrinceanu N. Rooman M. Deebani W. Shutaywi M. M. Mathematical Modelling of Ree–Eyring Nanofluid Using Koo-Kleinstreuer and Cattaneo–Christov Models on Chemically Reactive AA7072-AA7075 Alloys over a Magnetic Dipole Stretching Surface. Coatings. 2022;12:391. doi: 10.3390/coatings12030391. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.