An untrained deep learning method for reconstructing dynamic magnetic resonance images from accelerated model-based data

Abstract

Purpose:

To implement physics-based regularization as a stopping condition in tuning an untrained deep neural network for reconstructing MR images from accelerated data.

Methods:

The ConvDecoder neural network was trained with a physics-based regularization term incorporating the spoiled gradient echo equation that describes variable-flip angle (VFA) data. Fully-sampled VFA k-space data were retrospectively accelerated by factors of R={8,12,18,36} and reconstructed with ConvDecoder (CD), ConvDecoder with the proposed regularization (CD+r), locally low-rank (LR) reconstruction, and compressed sensing with L1-wavelet regularization (L1). Final images from CD+r training were evaluated at the ‘argmin’ of the regularization loss; whereas the CD, LR, and L1 reconstructions were chosen optimally based on ground truth data. The performance measures used were the normalized root-mean square error, the concordance correlation coefficient (CCC), and the structural similarity index (SSIM).

Results:

The CD+r reconstructions, chosen using the stopping condition, yielded SSIMs that were similar to the CD (p=0.47) and LR SSIMs (p=0.95) across R and that were significantly higher than the L1 SSIMs (p=0.04). The CCC values for the CD+r T₁ maps across all R and subjects were greater than those corresponding to the L1 (p=0.15) and LR (p=0.13) T₁ maps, respectively. For R ≥ 12 (≤4.2 minutes scan time), L1 and LR T₁ maps exhibit a loss of spatially refined details compared to CD+r.

Conclusion:

The use of an untrained neural network together with a physics-based regularization loss shows promise as a measure for determining the optimal stopping point in training without relying on fully-sampled ground truth data.

1. INTRODUCTION

MRI exhibits superior tissue contrast compared to other imaging modalities, such as computed tomography (CT)¹. In imaging ischemic stroke patients, for instance, MRI was shown to be substantially more sensitive in detecting lesions (93.5% positivity rate²) compared to CT (85% positivity rate²)³. In breast imaging⁴, for example, MRI has shown greater sensitivity than mammography with recent advancements^5–7. While sensitivity is superior, MRI may lack specificity in some cases compared to other imaging techniques⁴. False positives in general may lead to unnecessary biopsies with concomitant stress to the patient and cost to the healthcare system⁶. Thus, there is substantial effort toward increasing the diagnostic specificity of MRI through the development of quantitative imaging schemes that provide numeric data in addition to standard of care (SOC) images^8,9 for informing patient care.

Quantitative imaging involves fitting MRI data to a known physical model to estimate parameters that represent tissue characteristics¹⁰. For instance, the fast spoiled gradient echo (SPGR) sequence equation is fit to data from a T₁-weighted variable-flip angle (VFA) acquisition to estimate the tissue T₁ values at each voxel¹¹, where T₁ values have been shown to distinguish some pathologies¹². T₁ parameter mapping is also an important component in other quantitative schemes, such as pharmacokinetic analysis of dynamic contrast-enhanced (DCE) MRI in breast cancer imaging¹³ and brain imaging^12,13,14 for diagnosis^13,15 and treatment monitoring^16–19.

Despite the utility of quantitative imaging, scan time constraints remain a barrier to incorporating quantitative imaging schemes into SOC protocols. To combat this issue, many investigators are attempting to reduce scan time necessary for clinical application through model-based, multi-contrast methods. One such example is Magnetic Resonance Fingerprinting (MRF) for collecting multiparametric maps in a single, fast scan using dictionary matching²⁰ with unique, non-clinical sequences²¹. MR multitasking^22–24 is another multiparametric mapping technique that combines different imaging dynamics along multiple orthogonal dimensions that are subsequently resolved as a low-rank tensor²², naturally extending low-rank matrix priors. Echo-planar time-resolved imaging (EPTI) is another promising method for fast quantitative imaging that involves optimally under-sampling k-space along both spatial and temporal dimensions without blurring artifacts from traditional echo-planar imaging^25,26. These are rich multi-contrast acquisitions that incorporate a well-defined physical model with great potential for compatibility with deep learning advancements.

Model-based reconstruction²⁷ via trained deep learning methods^28–30 has shown promise in utilizing deep convolutional neural networks (CNNs) for reconstructing images with sufficient spatial and/or temporal resolution from highly accelerated raw MRI data for successful subsequent analysis with appropriate models. One such method is the Model-Based Deep Learning (MoDL)²⁸ framework by Aggarwal et al., which introduces an end-to-end supervised CNN-based noise estimator as a regularization term. Supervised methods, however, are limited by the availability of sufficiently large, curated training datasets. This is an issue that self-supervised and untrained methods^31–35 circumvent by relaxing the need for fully-sampled ground truth data. The reference-free latent map extraction (RELAX) method³⁶ trains a U-Net³⁷ architecture in a self-supervised manner to map under-sampled data to quantitative parameter maps. While the RELAX method does incorporate physical dynamics, the method still requires a large training set. The Self-Supervision via Data Under-sampling (SSDU) method³⁰ is a self-supervised method that also relies only on a large training set of available under-sampled data that is split into separate sets via multiple masks.

Conversely, untrained generative neural networks – such as Deep Image Prior³⁵, DeepDecoder³², and ConvDecoder³¹ (where the term “untrained” was coined) – do not rely on a training data set. Instead, they operate on a single under-sampled input and are thus scan-specific, relying on the neural network structure for implicit regularization. The ConvDecoder has been shown to substantially outperform conventional methods based on sparsity and low-rank principles and has been shown to perform similarly to trained methods in some cases³¹. Still, these methods neither incorporate the known physical dynamics that further constrain the image reconstruction inverse problem nor include a stopping condition for determining when an optimal solution has been reached; therefore, they are prone to overfitting and can result in image artifacts^27,31,33,35. Yaman et al.³⁸ and, recently, Leynes et al.³⁹ propose regularizations based on data-consistency and statistical properties, respectively, that serve as stopping conditions for scan-specific reconstructions, but these methods do not include the quantitative model.

To address the need for a physics-informed untrained method with a reliable stopping condition for high-resolution dynamic MRI data amendable to quantitative analysis, we previously applied the ConvDecoder (CD)³¹ method with an SPGR-based regularization term (CD+r)⁴⁰ as a proof-of-principle for reconstructing multi-dimensional images from simulated accelerated VFA data. Here, we formalize the CD+r method and apply it to retrospectively accelerated 3D VFA data collected from three healthy subjects. We compare the image reconstruction quality and T₁ map output of fully-sampled VFA data to the output of retrospectively accelerated VFA data reconstructed with CD+r, CD, parallel imaging with locally low-rank regularization (LR)⁴¹, and compressed sensing (L1)⁴². We show that the physics-based regularization term in training CD+r provides a natural stopping condition for reconstruction that is blind to ground truth data, yielding T₁ maps that have a higher agreement with reference T₁ maps compared to T₁ maps derived from the CD, L1, and LR methods with ground truth-informed optimized hyperparameters. CD+r is a promising untrained method that leverages MRI physics for accelerated multi-contrast data acquisition where there is no fully-sampled ground truth as a benchmark for tracking reconstruction performance. Additionally, CD+r is useful for imaging modalities and anatomies with insufficient training examples for supervised and self-supervised methods. While CD+r is evaluated for a specific case (i.e., T₁-mapping), it applies to any quantitative model-based MRI dataset with an appropriate model chosen as the regularization term, making it a useful physics-informed solution to model-based MR image reconstruction from under-sampled data.

2. METHODS

2.1. Definition of the MRI forward operator

We define a sampling mask, M, which is multiplied with fully-sampled k-space, y, data to yield retrospectively under-sampled k-space data, y_u. The sampling mask is combined with the coil sensitivities⁴³, S, and the Fourier transform, F, to arrive at the MRI forward operator, A, defined as

$$\mathit{\text{A}}=\mathit{\text{MFS}}.$$ [1]

For a mask of all ones, corresponding to fully-sampled data, the A operator maps the image, x, to k-space samples, y, through the relationship y = Ax. In the case of accelerated data, y_u, the zero-filled image, x_adj, can be computed as ${\mathit{\text{x}}}_{\mathit{\text{adj}}}\text{=}{\mathit{\text{A}}}^{\mathit{\text{H}}}{\mathit{\text{y}}}_{\mathit{\text{u}}}$, where ${\mathit{\text{A}}}^{\mathit{\text{H}}}$ is the adjoint of A.

2.2. Physics-based model definition and quantitative parameter mapping

While the proposed method in this work is compatible with any quantitative model-based MRI dataset, VFA data were chosen for a proof-of-principle analysis because of the ease of acquiring fully-sampled raw data. Because a T₁ map from VFA data is an important component of other quantitative acquisitions, such as DCE-MRI, demonstrating a speedup with this method already presents a speedup of a quantitative image exam. For a VFA acquisition, the SPGR equation describes the behavior of the image signal intensity (SI) as a function of RF flip angle θ. This equation is defined as follows⁴⁴:

$$SI\left(\theta \right)\text{=} S_o\frac{\sin \left(\text{θ}\right)\text{(1-}{\text{e}}^{-TR\text{/}{T}_{\text{1}}})}{\text{(1-cos}\left(\text{θ}\right){\text{e}}^{\text{-}TR\text{/}{T}_{\text{1}}}\text{)}},$$ [2]

where T₁ is the longitudinal relaxation time, TR is the repetition time, and S_o is the equilibrium signal intensity that is proportional to the spin density. To fit Eq. [2] to signal intensity images, x, collected at multiple flip angles, we implemented dictionary matching²⁰ using 2,000 T₁ values linearly spaced between 50 ms and 4000 ms. The result is a T₁ map, T₁, corresponding to a simulated image defined as x_m, which is the set of VFA images outputted from fitting x to $SI\left(\theta \right)$ via dictionary matching (see Supplemental Methods on dictionary matching).

2.3. Implementation of the proposed deep learning framework

The ConvDecoder³¹, G(w), is a generative CNN with weights w that maps a low-dimensional vector of random noise (Gaussian noise with mean 0 and standard deviation 1) to an image. It is an extension of the original DeepDecoder³² framework with added convolutional operations, where the weights are iteratively optimized on a single dataset as opposed to trained on a collection of training data (i.e. supervised and self-supervised methods).

The cost function, L(G(w)), for training G(w) is defined as follows:

$$L\left(\mathit{\text{G}}\left(w\right)\right)\text{=}\underset{w}{min}{‖y_u\text{-}\mathit{\text{AG}}\left(w\right)‖}_{\text{2}}^{\text{2}}.$$ [3]

This cost function strictly enforces data consistency between the inputted accelerated k-space data, y_u, and the network output, G(w), passed through the forward operator, A (see Eq. [1]). Even though the problem is ill-posed, the CNN provides implicit regularization favoring natural images. The original implementation of the ConvDecoder (CD) architecture (see Supplemental Figure S1 for the network structure) was adapted into DeepInPy⁴⁵, a Python-based framework for training deep learning methods specific to MRI reconstruction problems. Each under-sampled dataset presented to the CD network is reconstructed separately and independently. The network was calibrated using the ISMRM/NIST phantom⁴⁶ scanned with the same equipment and protocol described below in Section 2.4 (see Supplemental Methods for phantom details).

The weights were updated through backpropagation using the Adam optimizer⁴⁷, where a step size of $\delta =0.01$ was empirically chosen based on calibration with the phantom scans. The network was trained for 10,000 training steps. The optimal reconstruction (complex-valued, coil-combined VFA image series) for each CD experiment was chosen by evaluating the argmin of the final normalized root-mean square error (NRMSE) curve as a function of training steps as a “best-case” reconstruction compared to the ground truth. The NRMSE was retrospectively smoothed with the Savitzky-Golay method⁴⁸ prior to finding the argmin (Supplemental Figure S2).

For ConvDecoder with physics-based regularization (CD+r), the CD network structure (Figure S1) and same optimization scheme were used; however, the cost function in Eq. [3] was altered to reflect the regularization term:

$$L(\mathit{\text{G}}(w))=\underset{w}{min}{‖y_u-\mathit{\text{AG}}(w)‖}_2^2+\mu {‖\mathit{\text{G}}(w)-x_m‖}_2^2,$$ [4]

where $\mu$ is the regularization parameter, and x_m is the SPGR model output computed through dictionary matching as described in Section 2.2. The proposed pipeline for CD+r is visually outlined in Figure 1. The model, x_m, was updated from G(w) every j=5 training steps through alternating minimization⁴⁹, where the value of j was empirically optimized (see Supplemental Methods for more detail). Four values of the regularization parameter were selected after investigating many values across scales during hyperparameter optimization: $\mu \in \left\{0.05,0.10,0.50,1.0\right\}$. The regularization loss was retrospectively smoothed with the Savitzky-Golay method⁴⁸ (Supplemental Figure S2), and the optimal reconstruction for each experiment was selected by computing the argmin of the regularization loss (noting that CD+r is blind to the ground truth data).

Figure 1: Overview of the CD+r reconstruction pipeline.

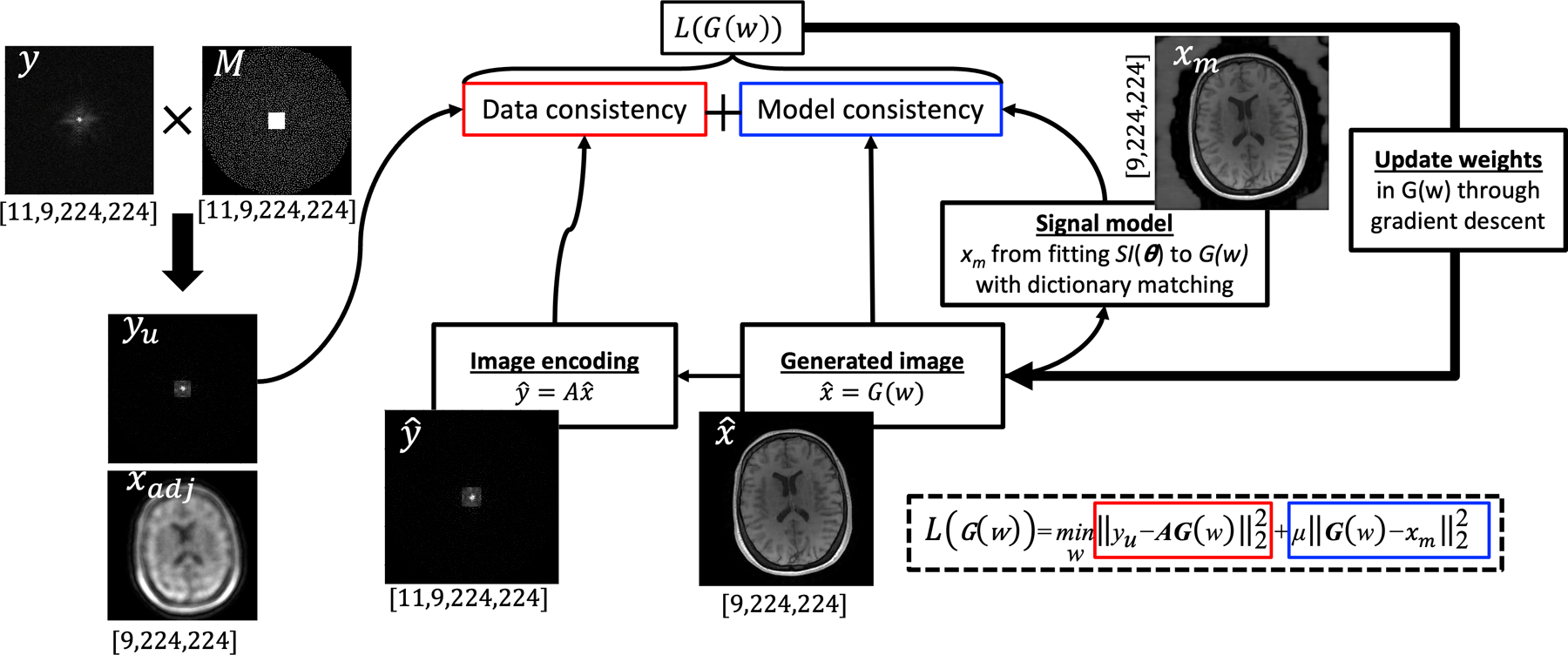
A fully-sampled k-space dataset, y (where the shape is defined below the labelled panel), is multiplied with a Poisson-disc sampling mask (M) to arrive at under-sampled k-space, y_u (the corresponding zero filled image, x_adj, is shown below it). The ConvDecoder takes noise as input and outputs an estimated VFA image series as $\widehat{x}=G\left(w\right)$. Using this estimate, a second VFA image series $x_m$ is computed by dictionary matching the output of $\widehat{x}$ fitted to the signal model, $SI\left(\theta \right)$. These two images are inputted into the model consistency term of the loss function at each training step, which compares y_u to $A\widehat{x}$ and G(w) to$x_m$. The weights of G(w) are updated through gradient descent based on the loss L(G(w)), and a new $\widehat{x}$ is generated. As described in the main text, x_m is updated every five training steps. The size of all k-space data is reported as [# of coils, # of flip angles, X, Y], and the size of all images is reported as [# of flip angles, X, Y].

Reconstruction-based T₁ maps corresponding to the optimal reconstructions outputted from CD and CD+r were a biproduct of dictionary matching in solving for x_m during optimization²⁰. All deep learning experiments were performed on NVIDIA V100 GPUs with 16 GB memory. Code to reproduce our results is available at https://github.com/kslav/cdr_mri.git.

2.4. Data acquisition

Three healthy subjects (denoted S1, S2, and S3) were scanned using a 3T MAGNETOM Vida MRI scanner equipped with a 32-channel head coil array (Siemens, Munich, Germany) under approval of the Institutional Review Board and with informed consent. Fully-sampled VFA data from each subject were collected using a 3D SPGR sequence with an acquisition matrix of 224×224×224 over a (22.4 cm)3 field of view (i.e., 1 mm³ isotropic resolution), TR/TE = 6.10/2.75 ms, and nine flip angles from 4° through 20° and linearly spaced in 2° increments. No parallel imaging was employed so that all k-space samples were collected, which required 50 minutes of scanning per subject.

A representative dynamic slice (as a function of θ) from each dataset was selected for analysis following an inverse Fourier transform along the read-out direction. The magnitudes of the VFA anatomical images at all nine flip angles are displayed in Supplemental Figure S3 (images and data are complex-valued, see Supplemental Methods for more information on data formatting). To eliminate correlated noise across the sensitivity coils, noise pre-whitening was performed on all three datasets using a noise pre-scan and the BART toolbox⁵⁰. Finally, software SVD-based coil compression was applied to the raw k-space datasets^50–52 to shrink the coil space down to 11 signal-contributing virtual coils, thereby eliminating coils contributing less than 1% of the total signal (see Supplemental Figure S4).

2.5. Simulated data generation without model error

To determine how quantitative model error affects the performance of the proposed physics-regularized method, datasets with no model error were first created from the raw data by synthesizing the forward equation. A set of three reference T₁ maps and modelled images were estimated using dictionary matching applied to the three fully-sampled datasets. Each simulated VFA image series was multiplied by coil sensitivity maps (described in Section 2.6 below) to arrive at simulated coil images. The k-space data were subsequently computed by taking the Fourier transform of these coil images. Finally, noise was added to the k-space of each simulated image based on the native SNR of the raw data. The result was a set of three noisy, simulated datasets derived from the three raw datasets without VFA model error.

2.6. Preparation of retrospectively accelerated data

After acquiring and pre-processing the raw k-space and generating simulated data by the methods in Sections 2.4 and 2.5, respectively, the raw and simulated data were subsequently normalized to have a norm of 1,000 (see Supplemental Methods on phantom scans). The coil sensitivities, S, were computed using the ESPIRiT algorithm⁵³ implemented in BART. The coil sensitivity maps corresponding to each raw dataset were used in Section 2.5 for the simulated data as the modelled anatomy remained the same.

Next, the sampling masks, M, were created. A set of unique variable-density 2D Poisson-disc sampling patterns with fully-sampled auto-calibration regions of size 25×25 was generated using BART and stored in a 3D volume of masks matching the VFA data dimensions. We chose acceleration factors of R ∈{8, 12, 18, 36}, corresponding to scan durations of {6.25, 4.17, 2.78, 1.4} minutes; thus, a set of M was generated for each value of R (Figure S4). The three fully-sampled raw and simulated datasets were all retrospectively accelerated by taking the product of M with the fully-sampled k-space. An example set of corresponding zero-filled images is displayed in Supplemental Figure S5.

2.7. Implementation of the baseline methods of reconstruction

Compressed sensing (L1)^42,54 and locally low-rank reconstruction (LR)^41,55, both implemented using BART, were chosen as the baseline methods against which the performance of the proposed method was evaluated. These methods were chosen because they are commonly used, are effective, do not rely on training data, and lack a stopping condition independent of ground truth data.³¹ For each set of raw and simulated data, the optimal reconstructed images from L1 and LR were found by optimizing over the regularization parameter, λ, and the number of iterations, N, (available in Table 1 for the raw data and Supplemental Table S1 for the simulations) through the minimization of the NRMSE computed between the ground truth images and the reconstructions. Reconstruction-based T₁ maps corresponding to the final L1 and LR-reconstructed images were computed using dictionary matching.

Table 1.

Performance measures, (NRMSE, SSIM), for all reconstruction methods applied to raw data. The optimal number of iterations for L1 and LR were 110 and 150, respectively.

R=8
Subject	L1		LR		CD		CD+r (μ = 0.10)
	Performance	Regularization	Performance	Regularization	Performance	Number of steps	Performance	Number of steps
S1	(0.158, 0.862)	0.01	(0.141, 0.904)	0.0079	(0.139,0.894)	1702 (1500)	(0.149,0.883)	1414 (1500)
S2	(0.155, 0.864)	0.01	(0.137, 0.892)	0.0077	(0.134,0.876)	1695 (1500)	(0.136, 0.876)	1934 (2000)
S3	(0.135, 0.885)	0.01	(0.116, 0.921)	0.0073	(0.111, 0.914)	2060 (2000)	(0.111, 0.913)	2196 (2000)
R=12
Subject	L1		LR		CD		CD+r (μ = 0.10)
	Performance	Regularization	Performance	Regularization	Performance	Number of steps	Performance	Number of steps
S1	(0.179, 0.844)	0.01	(0.161, 0.882)	0.0063	(0.149,0.879)	1695 (1500)	(0.163,0.873)	1391 (1500)
S2	(0.177, 0.841)	0.0098	(0.155, 0.869)	0.006	(0.143,0.868)	1645 (1500)	(0.149,0.848)	1485 (1500)
S3	(0.157, 0.864)	0.0091	(0. 131, 0.904)	0.0058	(0.119, 0.907)	2156 (2000)	(0.120, 0.906)	1947 (2000)
R=18
Subject	L1		LR		CD		CD+r (μ = 0.10)
	Performance	Regularization	Performance	Regularization	Performance	Number of steps	Performance	Number of steps
S1	(0.210, 0.811)	0.0078	(0.189, 0.848)	0.0049	(0.162,0.880)	1798 (2000)	(0.198,0.840)	773 (1000)
S2	(0.207, 0.802)	0.0071	(0.182, 0.835)	0.0046	(0.151,0.848)	1728 (1500)	(0.163,0.850)	1440 (1500)
S3	(0.186, 0.836)	0.0065	(0.155, 0.877)	0.0045	(0.13,0.907)	2262 (2500)	(0.130, 0.907)	2967 (3000)
R=36
Subject	L1		LR		CD		CD+r (μ = 0.10)
	Performance	Regularization	Performance	Regularization	Performance	Number of steps	Performance	Number of steps
S1	(0.289, 0.726)	0.0038	(0.256, 0.775)	0.0048	(0.199, 0.837)	2177 (2000)	(0.339, 0.681)	9772 (9999)
S2	(0.277, 0.718)	0.0036	(0.249, 0.752)	0.0051	(0.185, 0.817)	2030 (2000)	(0.307, 0.701)	7660 (7500)
S3	(0.261, 0.756)	0.003	(0.219, 0.810)	0.0038	(0.155, 0.864)	2486 (2500)	(0.156, 0.866)	2551 (2500)

2.8. Performance measures and statistical analysis

The NRMSE, concordance correlation coefficient (CCC)⁵⁶, and structural similarity index (SSIM)⁵⁷ were computed to assess the performance of the proposed framework. We used the fully-sampled raw k-space data as reference ground truth scans and computed the corresponding reference T₁ maps for all three subjects. This allowed us to quantitatively benchmark the performance of the reconstruction schemes (Sections 2.3 and 2.7) against the ground truth image quality. The NRMSE and SSIM were used to quantify the performance of the VFA image series, whereas the NRMSE and CCC were used to measure the agreement between the reference T₁ maps (Section 2.5) and the reconstruction-based T₁ maps. The Wilcoxon rank sum test was used to compute p-values when comparing performance metrics across methods. Generally, average values are accompanied with “(± standard deviation).”

3. RESULTS

Across all methods, acceleration factors, and simulated and raw data, a total of 168 reconstruction experiments were performed. Each CD experiment took 3.16 (±0.24) hours to complete on average, and each CD+r experiments took 5.15 (±0.20) hours to complete.

3.1. Applying the regularization loss as a stopping condition

The suitability of the regularization loss as a stopping condition was evaluated across the CD+r experiments in the simulated and raw data settings at four values of μ and R (Figure 2, Supplemental Figure S6). The NRMSEs, SSIMs, and optimal number of training steps can be found for these experiments for the raw data in Supplemental Table S2 and the simulated data in Supplemental Table S3. Bolded values in Supplemental Tables S2 and S3 indicate the highest performing metrics, which, in Supplemental Table S2, correspond predominantly to μ=0.1 for R≤18 and to μ=1.0 for R=36. In Supplemental Table S3, the highest performing metrics correspond to μ=0.5 and μ=1.0. Figure 2A displays training curves and performance measures for the simulated case for a representative subject (S3) at R = 12. In this figure, the reconstructions for μ = 0.05 and μ = 0.10 both yielded NRMSEs of 0.13. These two results match the NRMSE of the optimal CD reconstruction (μ = 0) (based on the global minima of the NRMSE curve. Similar NRMSE values were found for μ = 0.50 and μ = 1.0.

Figure 2: Regularization loss and NRMSE in a representative dataset for R = 12.

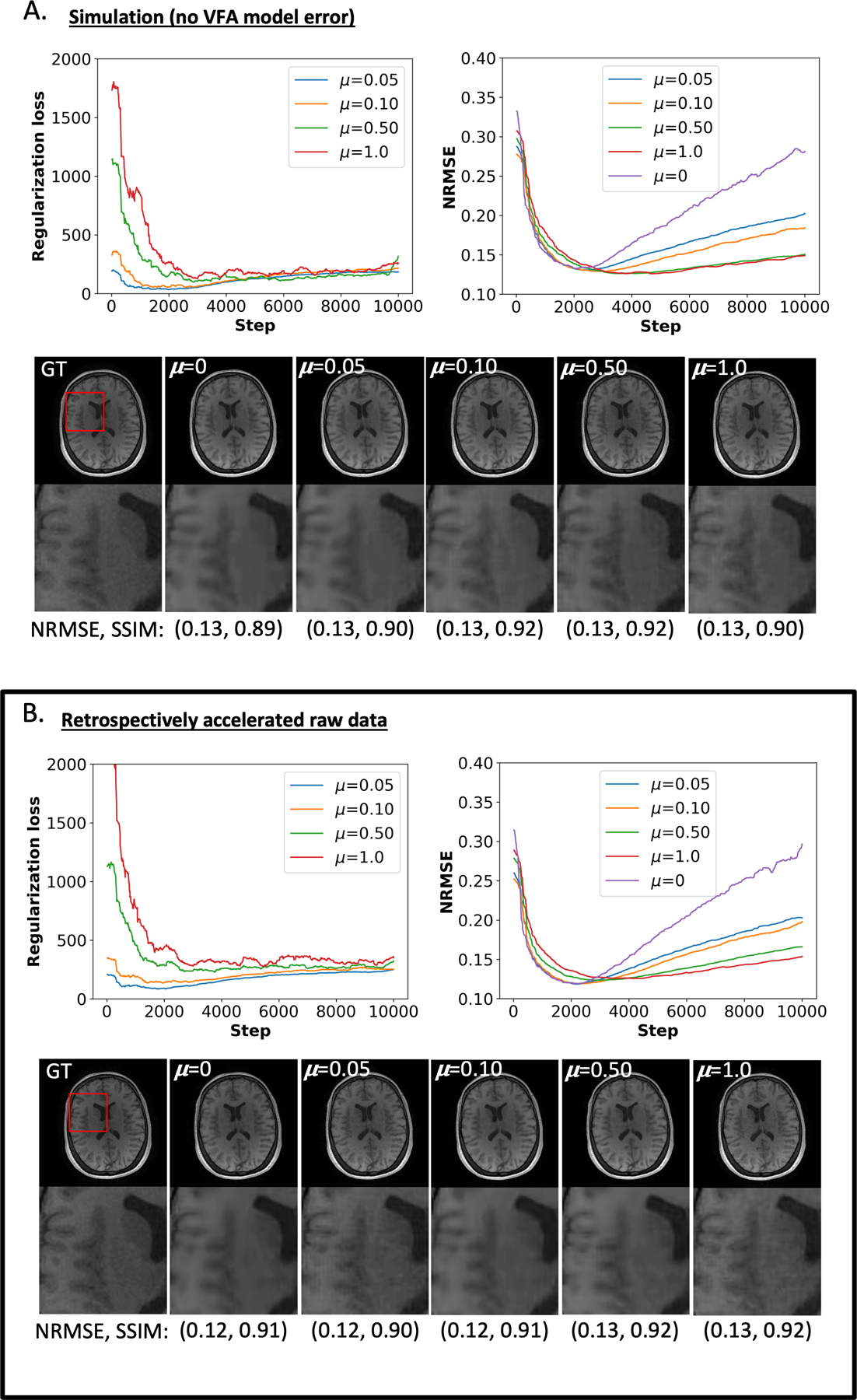
A) The top left and top right plots show the regularization loss and the NRMSE, respectively, as a function of training steps for the simulated data. Below these plots, representative VFA reconstructions at $\theta ={10}^{\circ }$ at four regularization rates, μ, are juxtaposed with the ground truth (GT) image. The numbers in parentheses below the anatomical images inform the NRMSE and SSIM for the optimal reconstruction based on the argmin of the regularization loss (for non-zero μ) and the NRMSE curve (for μ=0). B) Analogous to the information in panel (A) for the raw data analysis. The results in both panels are similar in terms of NRMSE and SSIM; though, more training steps were required to reach the optimal stopping condition for $\mu =0.50$ and 0.10.

The added physics-informed regularization in Figure 2A yielded lower NRMSE values across all four μ’s at later epochs (roughly post 3,000) compared to CD. At the final training step of 9,999 (Figure 2A), the CD reconstruction had a NRMSE of 0.28 compared to 0.20 for the CD+r experiment with the greatest final NRMSE, corresponding to μ = 0.05. The CD+r reconstructions for subject S3 yielded an average NRMSE and SSIM across μ of 0.13 (±0.002) and 0.91 (±0.01), respectively, compared to the CD reconstruction with a NRMSE of 0.13 and a SSIM of 0.89. Averaging over all simulated subject datasets at R=12, the CD+r reconstructions yielded an average NRMSE and SSIM of 0.15 (±0.01) and 0.89 (±0.03), respectively, compared to CD reconstructions with an average NRMSE of 0.15 (±0.01) and an average SSIM of 0.88 (±0.03).

The raw data analysis for subject S3 at R=12 is displayed in Figure 2B. Larger regularization rates of μ = 0.50 and μ = 1.0 corresponded with a greater duration of optimization compared to the simulated results in Figure 2A. Like the NRMSE curves in Figure 2A, the added physics-informed regularization in Figure 2B lowered NRMSEs for all four μ values at later epochs compared to CD in Figure 2B. The CD+r reconstructions for subject S3 yielded an average NRMSE and SSIM across μ of 0.12 (±0.005) and 0.91 (±0.01), respectively, compared to the CD reconstruction with a NRMSE of 0.12 and a SSIM of 0.91. Averaging over all raw subject datasets at R=12, the CD+r reconstructions yielded an average NRMSE and SSIM of 0.17 (±0.04) and 0.86 (±0.04), respectively, compared to CD reconstructions with an average NRMSE of 0.15 (±0.02) and an average SSIM of 0.88 (±0.02).

3.2. Comparing the image reconstructions across the four methods

The SSIM and NRMSE values can be found in Table 1 for the raw data reconstructions (Supplemental Table S1 for the simulated data reconstructions) for all methods and acceleration factors. For display in subsequent figures, greater focus is placed on juxtaposing LR, CD, and CD+r as LR (NRMSE = 0.17 (±0.05), SSIM = 0.86 (±0.05)) performed better on average across subjects and R values than L1 (NRMSE = 0.20 (±0.05), SSIM = 0.82 (±0.06)). Bolded values in Table 1 and Table S1 indicate the highest performing metrics, predominantly corresponding to CD and CD+r for R≥18.

Taking the same representative subject, S3, from Figure 2, Figure 3 compares the L1, LR, CD, and CD+r (with $\mu =0.10$) reconstructions for the simulated dataset (Figure 3A) and the raw dataset (Figure 3B) at R=12. In Figure 3A, L1 yields a higher NRMSE of 0.17 and a lower SSIM of 0.87, compared to NRMSE values of 0.13 for both LR, CD, and CD+r. The difference image in Figure 3A for L1 reveals a higher normalized error in the skull and grey matter regions, qualitatively visible as blurring in the magnified anatomical images. The results from the raw data analysis in Figure 3B are consistent with the results in Figure 3A. Averaged across all three raw datasets at R=12 in Figure 2B, the NRMSE values for the LR, CD, and CD+r reconstructions were 0.15 (±0.02), 0.14 (±0.02), and 0.14 (±0.02), respectively. Similarly, the average SSIM values for the three respective methods were 0.89 (±0.02), 0.88 (±0.03), and 0.88 (±0.03).

Figure 3: Performance of all four methods in a representative dataset for R = 12.

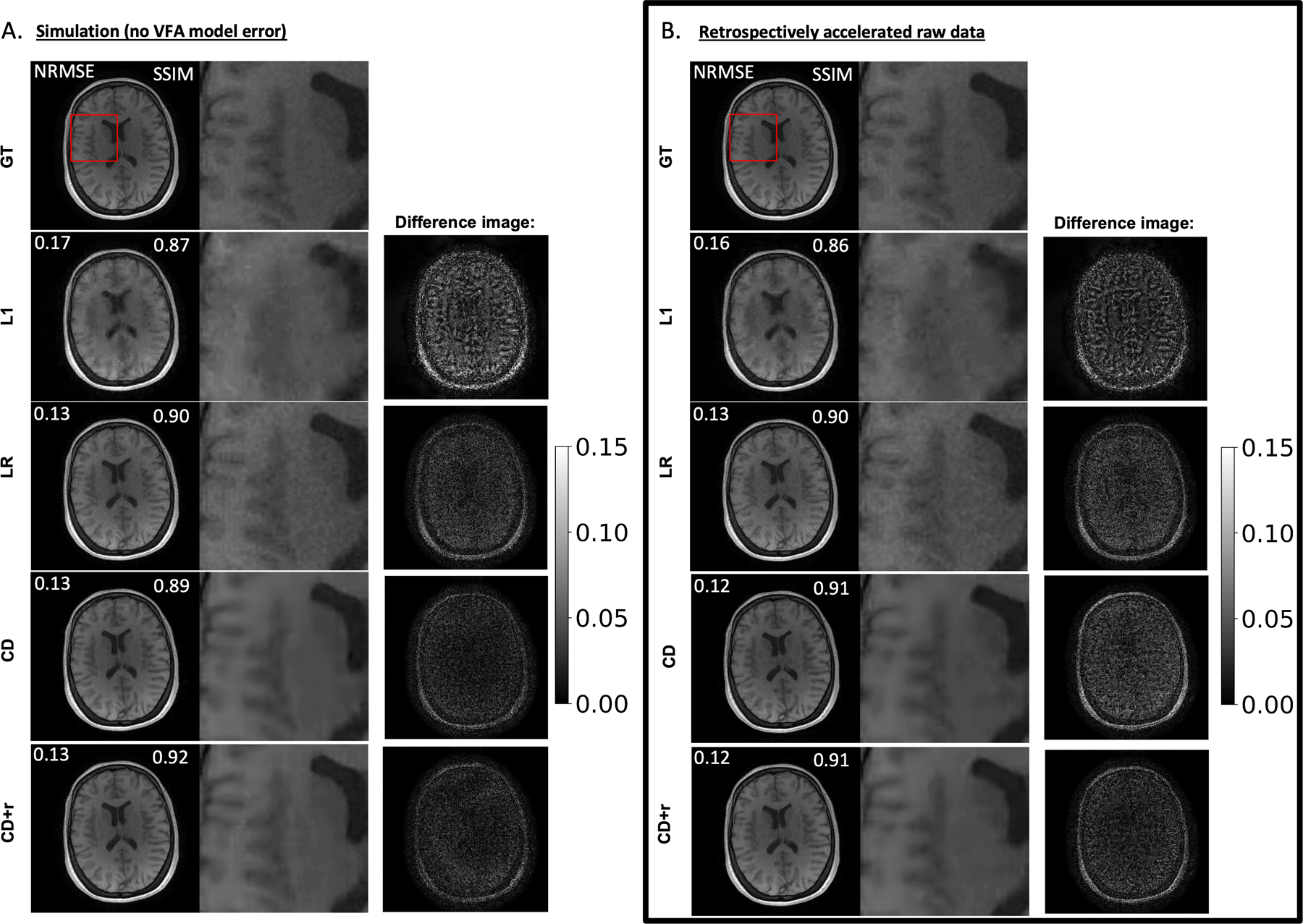
A) Optimal reconstructions of simulated data at $\theta ={10}^{\circ }$ and $\mu =0.10$ for CD+r. The CD+r reconstruction is compared to the results from L1, LR, and CD, where the white numbers overlayed on the images reflect the NRMSE and SSIM, as labeled, computed across all flip angles. The greyscale bar represents fractional error between the ground truth (GT) and each reconstruction. L1 yields a higher NRMSE of 0.17 and a lower SSIM of 0.87, compared to NRMSE values of 0.13 for the remaining methods. This higher error in the L1 reconstruction is evident in the magnified anatomical images, where there is loss of edge information in the grey matter region adjacent to the ventricle. In the absence of VFA model error, CD+r yielded the highest SSIM value among the reconstructions. (B) Analogous to the information in (A) for the raw data analysis. The results from the raw data analysis are consistent with the results in panel A, where all NRMSEs and SSIM values are within 0.1 of their simulation-based counterparts. CD+r performed similarly to CD when model error was no longer accounted for.

To compare the performance of LR, CD, and CD+r across datasets and acceleration factors, the SSIM values for R ∈{8, 12, 18} were plotted in Figure 4A against the flip angle (Supplemental Figure S7 for the simulations). The anatomical image of Subject S2 at $\theta ={10}^{\circ }$ is shown as a representative case in Figure 4B, where LR and CD reconstructions have larger SSIMs (+0.02) compared to CD+r for R=8 and R=12. At R=18, however, all four methods yield the same SSIM. In the SSIM plot for R=18, the CD and CD+r curves closely overlap and are higher than the LR curve for flip angles below 12 ^o. The anatomical images show that LR reconstructions tend to be noisier, which obscures tissue details at higher acceleration factors compared to the smoother reconstructions from CD and CD+r. In the absence of model error, Supplemental Figure S7 shows that CD+r confers an advantage over CD for higher acceleration factors and stronger regularization.

Figure 4. ConvDecoder performance at different R values across all raw datasets.

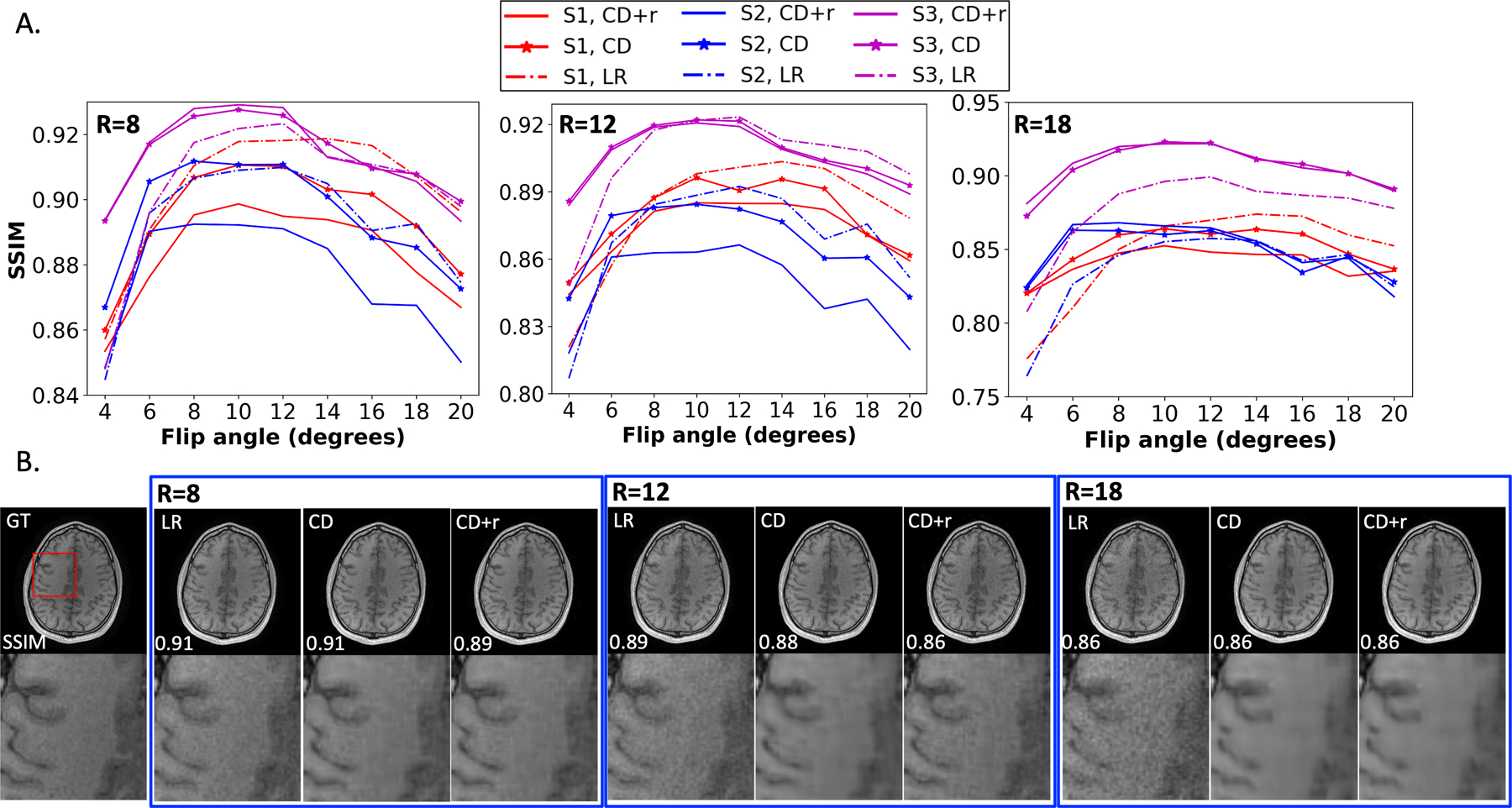
(A) Plots of the SSIM as a function of flip angle for R ∈ {8, 12, 18} for all three subjects. The solid, star, and dashed curves in the SSIM plots correspond to CD+r ($\mu =0.10$), CD, and LR, respectively. (B) Anatomical images for subject S2 from each reconstruction (blue curves in panel (A)) at $\theta ={10}^{\circ }$ for each of the three R values. The SSIM values are overlaid on each anatomical image. While LR and CD have higher SSIM values at the lowest two R values, the three methods match in performance at R=18, where all three blue curves in panel A closely overlap across all flip angles. The dynamic range in SSMI that the curves differ by with respect to one another does not exceed ±0.2 (within two significant figures).

3.3. Comparing the T₁ maps across the four methods

Aside from the reconstructed VFA image series from each of the four methods, we also investigated the quality of the T₁ maps corresponding to each optimal reconstruction. The NRMSEs and CCCs for the T₁ maps corresponding to the reconstructions from all accelerated raw data at all R can be found in Table 2 (simulation results in Supplemental Table S4). Bolded values in Table 2 and Supplemental Table S4 indicate the highest performing metrics, corresponding to CD and CD+r T₁ maps across all R.

Table 2.

Performance measures for T₁ mapping analysis of the raw data. Paired values in parentheses in each field correspond to the (NRMSE, CCC).

R=8
Subject	L1	LR	CD	CD+r (μ = 0.10)
S1	(0.204, 0.921)	(0.207, 0.916)	(0.201,0.928)	(0.202,0.926)
S2	(0.201, 0.918)	(0.206, 0.912)	(0.204,0.920)	(0.194, 0.928)
S3	(0.193, 0.918)	(0.201, 0.910)	(0.185, 0.928)	(0.186, 0.928)
R=12
Subject	L1	LR	CD	CD+r (μ = 0.10)
S1	(0.243, 0.883)	(0.246, 0.878)	(0.219,0.914)	(0.235,0.897)
S2	(0.248, 0.869)	(0.249, 0.867)	(0.220,0.907)	(0.224,0.900)
S3	(0. 230, 0.879)	(0. 234, 0.874)	(0.211, 0.906)	(0.211, 0.905)
R=18
Subject	L1	LR	CD	CD+r (μ = 0.10)
S1	(0.0.287, 0.830)	(0.0.288, 0.827)	(0.254,0.883)	(0.283,0.840)
S2	(0.290, 0.813)	(0.293, 0.807)	(0.249,0.876)	(0.255,0.868)
S3	(0.265, 0.837)	(0.271, 0.828)	(0.235,0.880)	(0.229, 0.889)
R=36
Subject	L1	LR	CD	CD+r (μ = 0.10)
S1	(0.364, 0.703)	(0.374, 0.682)	(0.315, 0.811)	(0.434, 0.633)
S2	(0.38, 0.624)	(0.408, 0.575)	(0.301, 0.813)	(0.417, 0.648)
S3	(0.329, 0.739)	(0.332, 0.730)	(0.280, 0.822)	(0.277, 0.821)

Figure 5 compares the T₁ maps corresponding to the optimal LR, CD, and CD+r reconstructions for R ∈ {8, 12, 18}. Qualitatively, the LR T₁ map showed the least agreement with the ground truth T₁ map across all acceleration factors. For R = 8, 12, 18, respectively, the LR results were CCC = 0.91, 0.87, 0.83 compared to CD results of CCC = 0.93, 0.91, 0.88 and CD+r results of CCC = 0.93, 0.91, 0.89. At R = 36 (1.5 min of scan time), the CD+r T₁ map (CCC = 0.82) and the CD T₁ map (CCC=0.82) showcased similar agreement with the ground truth map.

Figure 5. T₁ maps for a single raw dataset at three accelerations.

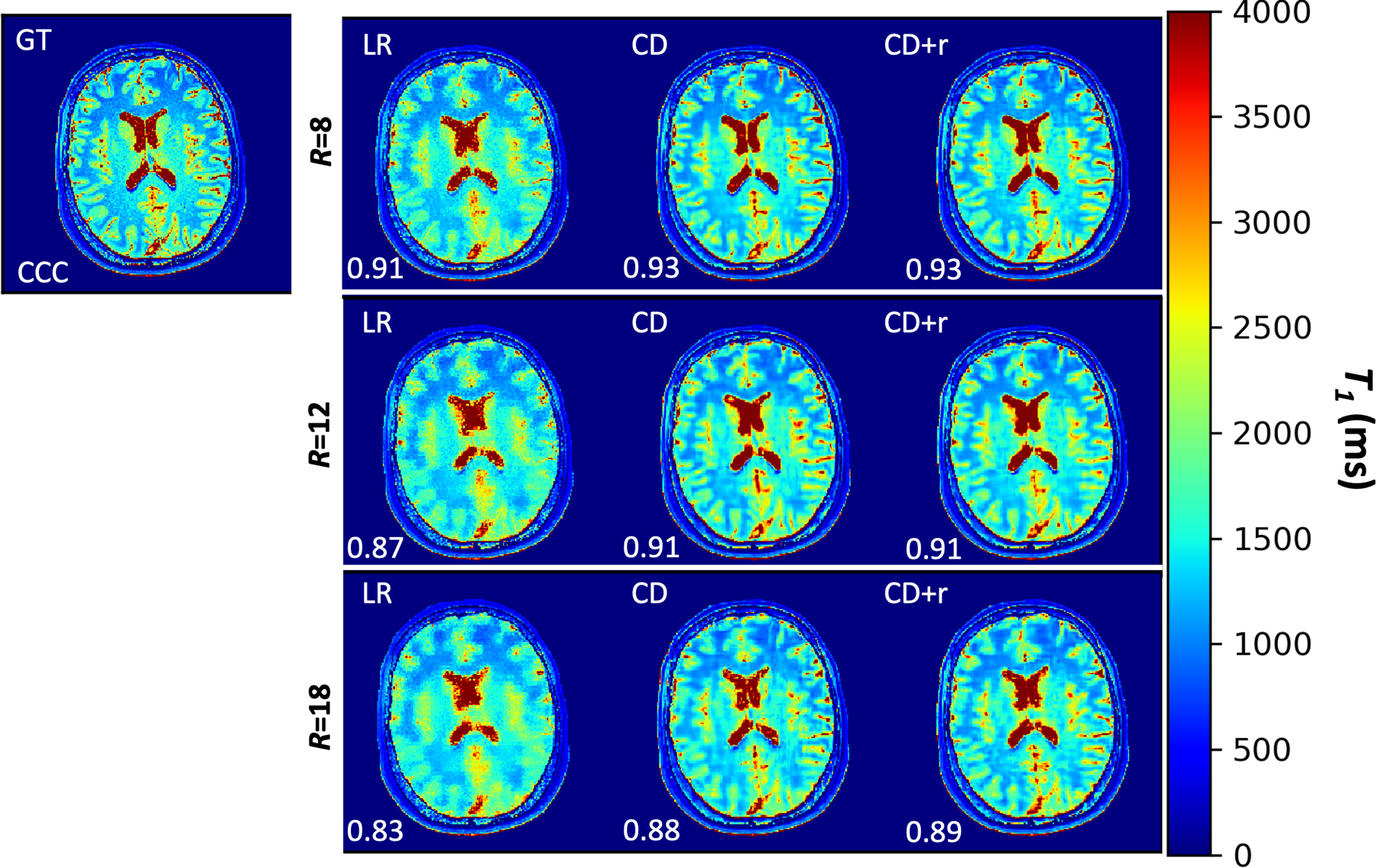
T₁ maps for R ∈ {8, 12, 18} corresponding to mapping the anatomical LR, CD, and CD+r reconstructions. The CD and CD+r ($\mu =0.10$) reconstructions were obtained at the optimal number of training steps listed in Table 1. For all values of R, the LR T1 map has visible blurring in the grey matter folds compared to the CD and CD+r T1 maps. At R=8, the CCC value for the CD+r T₁ map is 2% higher than the CCC value for the L1 T₁ map; this difference is 7% at R=18 with CD+r showing greater agreement to the ground truth T₁ map.

Figure 6 displays the T₁ maps for all three retrospectively accelerated raw datasets at R = 12 (simulation results presented in Supplemental Figure S8). As in Figure 5, the LR T₁ maps lack spatially refinement across the tissue, most evident in the gray matter folds and ventricles that are clearly defined in the ground truth parameter map. Figure 7 compares the CCC and NRMSE values for the LR and CD+r T₁ maps from all subjects and acceleration factors, revealing that the CD+r T₁ maps across all experiments yield smaller NRMSE values (p=0.162) and larger CCC values (p=0.131) than the LR T₁ maps when compared to the reference maps. In the simulated setting, (Supplemental Figures S8 and S9) the CD+r T₁ maps exhibited better agreement with the reference maps than the LR T₁ maps to a statistically significant extent (NRMSE with p=0.015 and CCC with p=0.002).

Figure 6. T₁ maps for all raw datasets at R = 12.

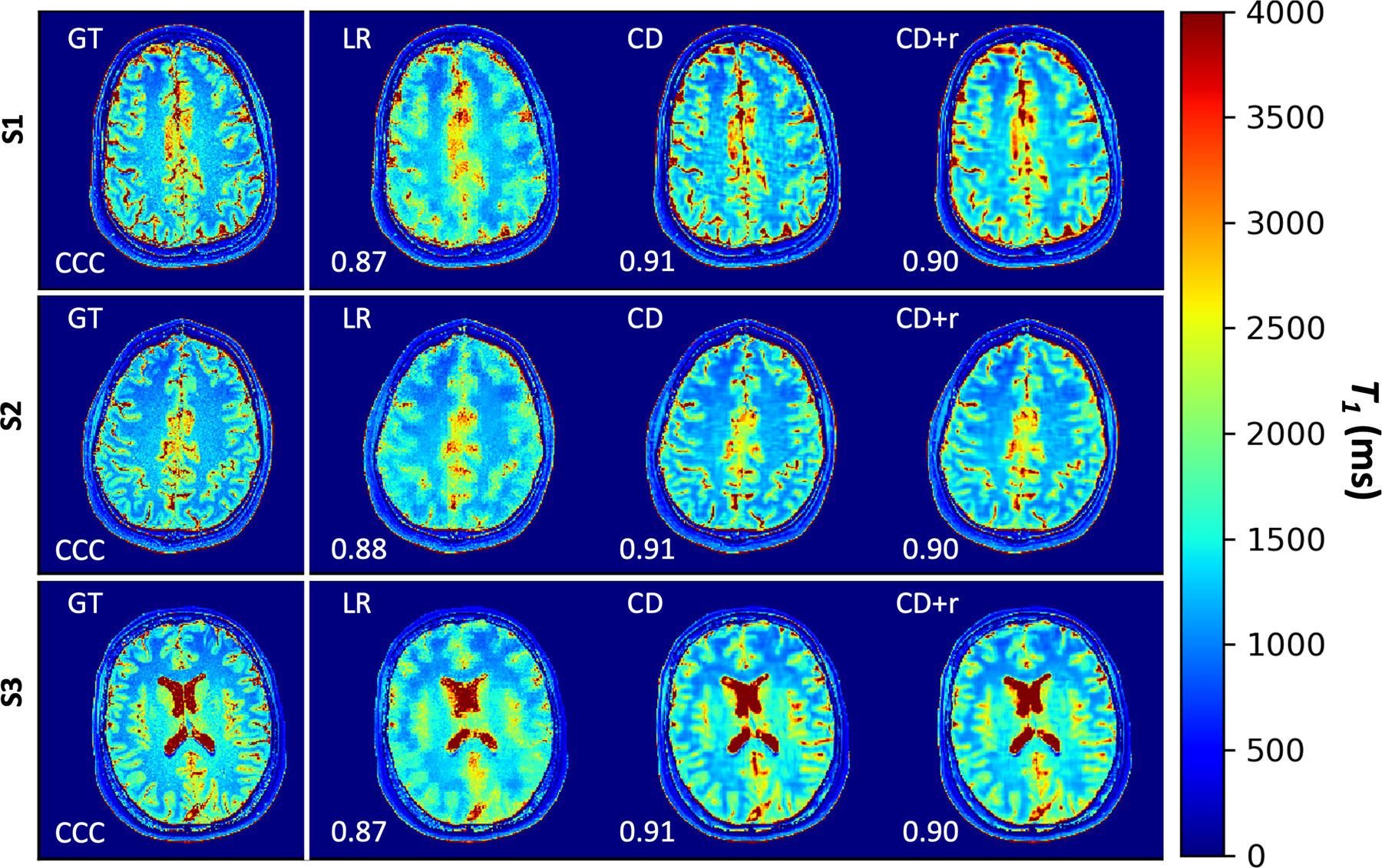
T₁ maps for all three subjects corresponding to mapping the anatomical LR, CD, and CD+r reconstructions. The CD and CD+r ($\mu =0.10$) reconstructions for each subject are displayed after the optimal number of training steps specified in Table 1. For all values of R, the CD and CD+r T₁ maps show less blurring in the grey matter regions as compared to the LR T₁ maps. The CCC values, overlain on each map, are lower for the LR T₁ maps for all subjects (≤0.88) as compared to the CD and CD+r T₁ maps for all subjects (≥ 0.90).

Figure 7: NRMSE and CCC values for all T₁ maps from the raw data analysis.

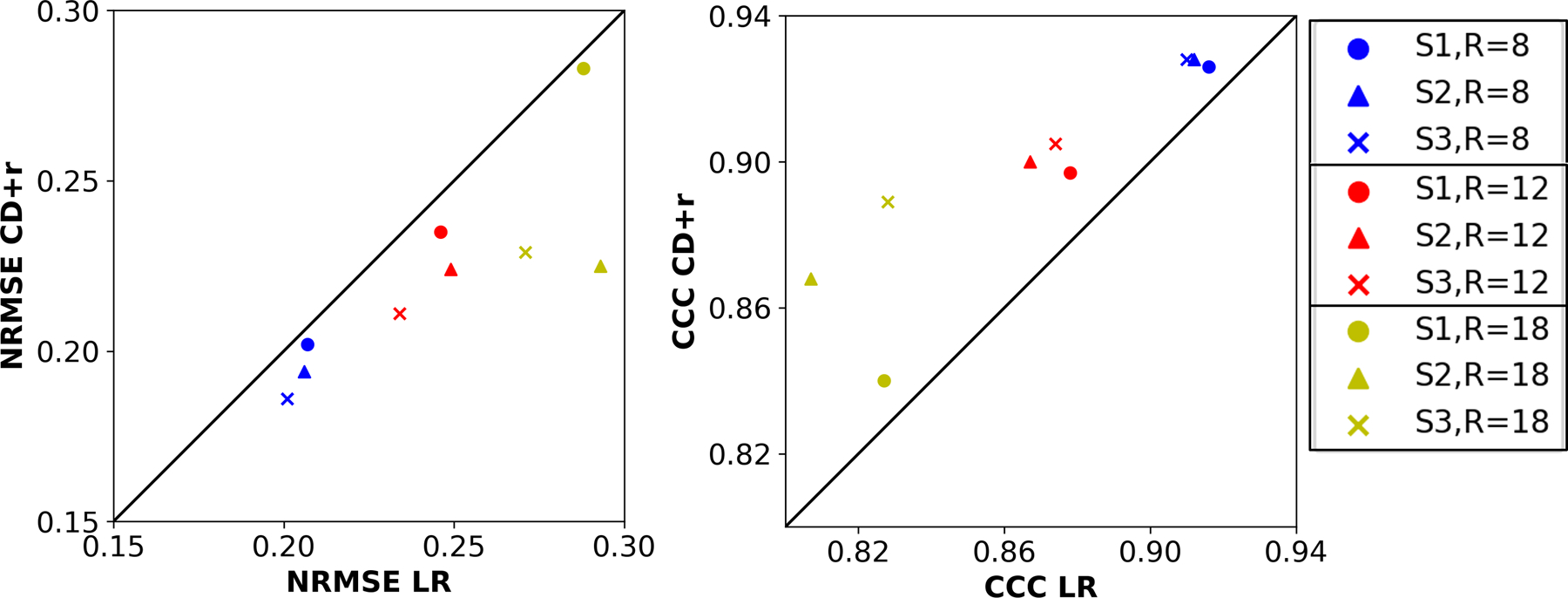
The left plot compares the NRMSEs of the CD+r T₁ maps of all subjects against the NRMSEs of the corresponding LR T₁ maps across three R values. The right plot compares the CCCs of the CD+r T₁ maps of all subjects against the CCCs of the corresponding LR T₁ maps for the same three R values. The legend at left identifies the R values by color (blue: R=8, red: R=12, yellow: R=18) and the subjects by marker shape (circle: S1, triangle: S2, cross: S3). The LR NRMSE values are greater than the CD+r values (p=0.162) across all subjects and R values, and the LR CCC values are lower (p=0.131) in all cases.

4. DISCUSSION

This study is the first to utilize the untrained ConvDecoder method with a physics-based regularization term serving as a stopping condition to reconstruct retrospectively accelerated raw, dynamic MRI data, noting that the original CD architecture was previously only applied to reconstructing 2D static images with no physics-based regularization³¹. It is important to note that the NRMSE curve was known to us due to the retrospective nature of this study that provides access to ground truth data. We therefore used the NRMSE to choose the best stopping condition for L1, LR, and CD in order to provide a “best-case” reconstruction for comparison, noting that this is not achievable in practice. Importantly, CD+r was blind to the ground truth data, yet CD+r was able to perform similarly to the “best-case” result of CD, while outperforming the other two methods. While trained methods typically outperform untrained methods³¹, it can be difficult to acquire ground truth training data for some types of scans, such as dynamic contrast-enhanced MRI and other quantitative imaging schemes that have strict temporal sampling requirements. There is therefore a need for untrained methods that can work with limited data.

A major challenge of using untrained methods is the selection of an appropriate regularization parameter and early stopping condition when ground truth data is not available to benchmark the reconstructions. Importantly, the physics-based regularization proposed in this study demonstrated reliability as a stopping condition that can be computed without access to ground truth data given a suitable value for the regularization parameter. Even when neglecting early stopping and when trained to completion after 10,000 training steps, CD+r yielded reconstructions with substantially lower NRMSEs at the end of training compared to CD across all subjects, acceleration factors, and μ values. Because the optimal value of μ is not known a priori for novel reconstructions, we investigated μ values at different scales and subsequently showed that (i) the NRMSE increases slowly as training continues beyond the known (i.e. optimal) solution and (ii) the automatic stopping condition remains close to the optimal solution. Thus, there is tolerance in the choice of solution based on the stopping condition and regularization parameter.

Another important contribution of the CD+r method is the ability to compute highly detailed quantitative parameter maps simultaneously during reconstruction via the physics-based regularization term. The T₁ maps corresponding to the CD+r reconstructions yielded high agreement with the reference T₁ map across all subjects, achieving CCC > 0.9 for R ≤ 12 (as short as 4-minute of acquisition time), thus outperforming the L1 and LR baselines. Comparing the CD+r T₁ maps with those derived from the baseline LR method (Figures 5 and 6), CD+r yields T₁ maps with more spatial refinement in closer agreement with the reference (GT) T₁ map. The LR T₁ map, however, exhibits greater noise and blurring, particularly in the gray matter region across subjects and acceleration factors. It is important to note that L1, LR, and CD benefited from a priori knowledge of the ground-truth when selecting the regularization parameters, while CD+r did not.

While CD+r compared positively to baseline methods, there are opportunities for further investigation. First, untrained methods are generally slower than trained methods, and CD+r is not excluded from this. Trained methods, while taking ample time and resources to train (particularly for large training datasets with thousands of examples), are fast at inference, outputting a solution after a small number of forward passes through a deep network, whereas untrained methods are iteratively fit to data over many training steps for each independent set of data. As CD+r explicitly solves for the dynamic images, the reconstruction will require more time and memory for datasets with more dynamic points. One solution, proposed by Darestani et al.³¹, is to warmstart the neural network (i.e., load pre-trained weights from a similar anatomy to initiate the network rather than beginning with random weights). Arora et. al. also showed that multiple slices could be reconstructed with a single generative model⁵⁸. In Darestani et al.’s example, it was shown that a ConvDecoder architecture optimized for one set of non-fat suppressed knee MR images is a good initialization for training a ConvDecoder architecture to reconstruct another set of fat-suppressed knee MR images. In the context of this study, an adjacent tissue slice can be used to warmstart the CD+r reconstruction scheme for all subsequent brain reconstructions of the same imaging modality, and we show promising preliminary results for this approach in Supplemental Figure S10. It may also be possible to incorporate computation savings from subspace-based methods⁵⁹. Additionally, because the physics-based regularization term in CD+r informs when the optimal solution is reached, training can be stopped early and would thus save up to one hour of computation (given the computational resources used in this work) compared to CD.

Another drawback to consider is that the current design of CD+r applies only to 2D dynamic data. As such, reconstructing a dynamic 3D volume would necessitate slice-by-slice reconstruction with warmstarting or an updated CD+r architecture that can take as input 4D, perhaps with convolutions along the dynamic dimension for further compression. This approach has successfully been explored in other trained methods for fast image reconstruction^60–62. While we implemented one type of deep image prior, there remains the question of whether other DIPs, such as RARE⁶³ and TD-DIP⁶⁴, may confer a greater advantage. Similarly, the optimal sampling mask remains to be explored for our application. Lastly, as only healthy subjects were available for direct imaging in the research setting, there is the question of the performance of CD+r in the context of diseased tissue. This direction of work would involve close collaboration with radiologists to determine the diagnostic quality of images and with mathematical oncologists to appropriately curate models of disease for regularization.

The analysis in this work indicates that it may be possible to use the unsupervised physics-based regularization term – blind to ground truth data – to determine the optimal stopping point in training while yielding results similar to methods that do reference the ground truth, which is an important real-world consideration when deploying these methods prospectively. These retrospective results indicate that it may be possible to achieve similar performance using the CD+r method given prospectively accelerated data, at least given the Poisson-disc sampling pattern used in this work. A prospective analysis merits further investigation.

While the CD+r method was evaluated using VFA data and the SPGR model, it is generalizable to any MRI modality and corresponding physical model, making it compatible with, for example, MRF, EPTI, and MR multitasking given the reformulation of the ConvDecoder network to output tensor data. In another example, a recent approach to choosing the stopping condition proposed splitting the measurements into three disjoint sets for training, validation, and early stopping, respectively; as this does not exploit the physical model, it could also be combined with the proposed physics-based regularization⁶⁵. To recover high-spatial, high-temporal resolution images from an ultra-fast DCE-MRI acquisition⁴⁴, as another example, the dictionary used for fitting the SPGR model to the VFA data would be replaced with a dictionary storing perfusion model curves, such as those outputted by the Kety-Tofts⁶⁶ model. The structure and training of the network would be optimized for the DCE-MRI inverse problem through hyperparameter optimization of the number of layers, the size of the latent space, and the step size used for gradient descent.

5. CONCLUSION

We have introduced an untrained deep learning-based generative neural network for model-based MRI reconstruction with a physics-based regularization. We demonstrated the utility of the stopping condition provided by the physics-based regularization term in the CD+r training, which was especially powerful in T₁ mapping at high accelerations. The ability to determine the optimal reconstruction without a performance measure requiring ground truth data is integral to the reconstruction of prospectively acquired accelerated MRI data. The success of this method on highly accelerated raw data indicates the potential to incorporate a fast acquisition of dynamic MRI data in the clinical setting for quantitative imaging.

Supplementary Material

supinfo

Figure S1: Modified ConvDecoder architecture for multi-contrast MRI reconstruction. The ConvDecoder architecture consists of six blocks with 128 latent channels. From left to right (denoted by the white arrows) the input of random noise (red tetrahedron of size 64×16×16, Gaussian noise with mean 0 and standard deviation of 1) is operated on by the first layer of the architecture. The output of each layer serves as the input into the next layer until the final complex-valued VFA images (green) are outputted from the final layer of size 9×224×224×2. Each layer (excluding the last) consists of a sequential order of operations as follows: up-sampling operation (white) to increase the size of the input, a convolutional operation (orange) consisting of kernels of size 3×3, a nonlinearity conferred by ReLU activation functions (dark gray), and batch normalization (dark blue). The final layer does not up-sample its input and instead directly convolves the input, passes it through the nonlinearity, performs batch normalization, and outputs an image with the user-specified dimensions. The size of each layer output is as follows: [128×28×28], [128×46×46], [128×78×78], [128×133×133], and [9×224×224×2].

Figure S2: Regularization loss for raw dataset S3 at R = 12 for all regularization parameters. Each plot displays the actual regularization loss (blue) plotted across all 10,000 training steps with the smoothed regularization loss (orange) overlaid after application of the Savitzky-Golay method, which is effectively a low-pass filter. This smoothing method functions by filtering the signal with an n-degree polynomial of a fixed window size, where the polynomial is fit at each point in the signal, using least-squares with derivate of order m, capturing surrounding points within the extent of the window. For smoothing the regularization loss and NRMSE in this work, a window size of 51 was chosen with n = 1 and m = 0.

Figure S3: Ground truth anatomical images from fully-sampled raw data. The T₁-weighted, anatomical images at all nine flip angles are displayed for each subject (S1, S2, S3) for reference. The signal intensity is lower for higher flip angles, and the dynamic range of the contrast is greater for mid-range flip angles.

Figure S4: Data pre-processing steps. The correlation matrix between all 16 original sensitivity coils is shown in the top left panel, demonstrating that there is correlation (non-zero off-diagonal elements of the matrix) between the coils. After noise pre-whitening is applied to each k-space dataset, we see that the off-diagonal correlations have been eliminated (before and after images are shown for completeness). Following noise pre-whitening, software coil compression based on singular value decomposition was applied to solve for 11 signal-contributing virtual coils.

Figure S5: Sampling masks and corresponding accelerated zero-filled images. From the top left to the top right, the Poisson disk sampling masks are displayed for each of the four acceleration factors, R∈{8, 12, 18, 36}, with the corresponding equivalent scan time in minutes in parentheses. The anatomical images spanning from the bottom left to the bottom right of the figure are the corresponding ground-truth (GT) and zero-filled images for a representative scan.

Figure S6: Regularization loss and NRMSE in a representative dataset for R ∈ {8, 18, 36}. A) The left and right plots in each row, separated by a black line, correspond to a particular R value; these plots show the regularization loss (left) and the NRMSE (right) as a function of training step for the simulated data. (B) Analogous to plots in (A) for the raw data. The regularization loss curves corresponding to the two smallest regularization rates of 0.05 and 0.10 are more amendable to qualitative inspection of the minima, especially for R = 36.

Figure S7. CD and CD+r performance at different R values across all simulated datasets. (A) Plots of the SSIM as a function of flip angle for R∈{8, 12, 18} for all three subjects for four regularization rates in CD+r. The solid and dashed curves in the SSIM plots correspond to CD and CD+r, respectively.

Figure S8. T₁ maps for all simulated datasets at R = 12. T₁ maps for all three subjects corresponding to mapping the anatomical LR, CD, and CD+r reconstructions. The CD and CD+r ($\mu =0.10$) reconstructions for each subject were saved at their optimal number of training steps specified in Table 1. For all R’s, CD and CD+r recover more spatially refined T₁ values in the gray matter and ventricles than LR. The CCC values, overlain on each map, are lower for the LR T₁ maps for all subjects (CCC<0.78) as compared to the CD and CD+r T₁ maps for all subjects (CCC>0.82).

Figure S9. NRMSE and CCC values for all T₁ maps from the simulated data analysis. The left plot compares the NRMSEs across R∈{8, 12, 18} of the CD+r T₁ maps of each subject against the NRMSEs of the corresponding LR T₁ maps. The right plot compares the CCCs (for the same R values) of the CD+r T₁ maps of each subject against the CCCs of the three corresponding LR T₁ maps. The legend at left identifies the R values by color (blue: R=8, red: R=12, yellow: R=19) and the subjects by marker shape (circle: S1, triangle: S2, cross: S3). For all subjects and acceleration factors, the CD+r T₁ maps have lower NRMSE (p=0.015) and higher CCC (p=0.002) than the LR T₁ maps.

Figure S10. Warm starting training using a neighboring slice in a representative dataset. (A) Regularization loss for the original reconstruction with randomly initialized weights (blue and orange curves, where the orange curve is a smoothed version of the blue curve) and the warmstarted reconstruction (green and red curves, where the red curve is a smoothed version of the green curve). (B) NRMSE for the randomly initialized (blue) and warmstarted network (green). (C) Optimal reconstructions from the case of no warmstarting (blue-boxed image) at 1,947 optimization steps and with warm starting (orange-boxed figure) at 601 optimization steps. The NRMSE and SSIM of both reconstructions were the same. These results demonstrate the ability to save computation time (324% in this case) by initializing CD+r with the optimal weights saved form reconstructing a neighboring slice in the tissue volume.