Intercellular permeation and cyclosis-mediated transport of a fluorescent probe in Characeae

Abstract

Intercellular communication and transport is the essential prerequisite for the function of multicellular organisms. Simple diffusion as a transport mechanism is often inefficient in sustaining the effective exchange of metabolites, and other active transport mechanisms become involved. In this paper, we use the giant cells of characean algae as a model system to explore the role of advection and diffusion in intercellular transport. Using fluorescent dye as a tracer, we study the kinetics of the permeation of the fluorophore through the plasmodesmata complex in the node of tandem cells and its further distribution across the cell. To explore the role of cytoplasmic streaming and the nodal cell complex in the transport mechanism, we modulate the cytoplasmic streaming using action potential to separate the diffusive permeation from the advective contribution. The results imply that the plasmodesmal transport of fluorescent probe through the central and peripheral cells of the nodal complex is differentially regulated by a physiological signal, the action potential. The passage of the probe through the central cells of the nodal complex ceases transiently after elicitation of the action potential in the internodal cell, whereas the passage through the peripheral cells of the node was retained. A diffusion-advection model is developed to describe the transport kinetics and extract the permeability of the node-internode cell wall from experimental data.

Significance

Intercellular communication is a crucial element of organization in multicellular organisms, determining the exchange of information and metabolites between the constituent cells. Understanding the mechanisms of cell permeability and its control is of fundamental importance for physiology and biophysics. This paper explores the permeation kinetics through the nodal complex and plasmodesmata in a simple model of tandem internodal characean cells using an original noninvasive technique and a simulation model. The results imply that plasmodesmata play an important role in modulating the intercellular signaling pathways involving action potentials. Cell excitation differentially regulates the plasmodesmal transport of fluorescent probe through the central and peripheral cells of the nodal complex.

Introduction

In multicellular organisms, intercellular transport is crucial in distributing resources and information between cells, which is vital for growth and functioning processes, providing a means of communication via signaling molecules. The giant cells of characean algae are an excellent model for studying such transport processes. Due to the large cell size, rather simple optical methods often suffice for studies on a cellular level. Perhaps, for this reason, the observation of such algae led to the discovery of cytoplasmic streaming (cyclosis) as early as the eighteenth century (1). In characean cells, the continuous motion of the endoplasm follows a particularly well-defined flow pattern and reaches extraordinarily high velocity. Such a transport mechanism in characean algae represents active advection.

The structure of the cells and intercellular connections determines the character of the long-distant transport of the metabolites. We employ the characean alga Chara corallina as a model system. Its body consists of large, approximately cylindrical internodal cells connected by nodal complexes (Fig. 1 a and c). Giant internodal cells with a length of up to 10 cm and a diameter around 1 mm (2) make up the stem-like main axis of the thallus (the plant body). Branchlets composed of smaller cells grow in whorls from the nodes of the main axis. The thallus anchors in soil via colorless rhizoidal cells. Adjacent internodal cells are always separated by a node (3,4). The nodal complex consists of chloroplast-rich, spheroidal peripheral cells and clear, flat central cells (5,6). Electron microscopy (4) revealed that, in C. corallina, the shortest path between internodes leads through the flat central nodal cells (7). Throughout the thallus, the cytoplasm is connected via plasmodesmata. These plasma-membrane-lined pores penetrate all internal cell walls, thus facilitating intercellular communication and metabolite exchange. The plasmodesmata are initially cylindrical pores with a diameter of 20–25 nm. As the cells mature, especially node-internode plasmodesmata become highly branched (8). Although there has been some controversy over the presence of a desmotubule in plasmodesmata of C. corallina (4,8), most of the authors support the majority view that the cytoplasmic channels contain desmotubules in C. corallina (9,10,11). The number of pores and the area fraction of plasmodesmata apertures are larger for node-internode than for node-node walls in C. corallina (4).

Figure 1.

(a) Photograph of a C. corallina shoot illustrating the morphology of the thallus. (b) Schematic representation of cytoplasmic streaming in an internodal cell. The thin layer of cytoplasm between the inner side of the chloroplast layer and the vacuole is moving continuously. Indifferent zones separate two bands of opposite flow direction. (c) Micrograph of a tandem cell. To ensure good visibility of the node, branchlet cells are shown instead of main axis cells. To see this figure in color, go online.

Rapid regulation of plasmodesmal permeability is pivotal for plants, but the underlying mechanisms are weakly understood. Tyree (12) concluded from the analysis of transport equations that small solutes diffuse through plasmodesmata. The driving mechanism of intercellular transport, thus, is passive. Modulation of transport is accomplished via dynamic regulation of the permeability of plasmodesmata. The spatial extent of intercellular transport was investigated by Shepherd and Goodwin (6,13), who injected fluorescent tracers into C. corallina to visualize the spreading of substances throughout the thallus. They discovered that the spatial range of transport can be restricted depending on the developmental stage of the algae and the season. More recently, Bulychev (14) studied the transnodal transport of photosynthetic metabolites indirectly using chlorophyll fluorescence measurements. This method enables the determination of the time required for the transport across the node. The transnodal passage of permeable metabolites was examined in the case of a moderate increase in osmolarity (14) or at various concentrations of NaCl and KCl in the medium (15). Those results indicate the existence of specific regulation, presumably mediated by the increase in cytoplasmic ${\text{Ca}}^{2+}$ level during the action potential generation. Nevertheless, the mechanisms of plasmodesmata permeation regulation are still not fully understood.

Intracellular transport is the first and last step in intercellular transport. Especially in the giant cells of characean algae, the transport to and from the cell junctions can be crucial. Understanding how substances are transported over large distances within internodes requires some knowledge about cell morphology. The outermost boundary of a C. corallina cell is a cellulose cell wall (Fig. 1 b). A vacuole situated in the center of the cell occupies the largest fraction of the cell volume (7). Between a plasma membrane at the cell wall and the tonoplast enclosing the vacuole, a thin layer ($\sim 10-20\mu \mathrm{m}$ (2)) of cytoplasm is located. In an internodal cell, the cortical layer of the cytoplasm (the ectoplasm) contains chloroplasts and actin filaments. Other than typical in higher plants, the chloroplasts are immobile (16,17). They are arranged in a pattern of helical rows. The same helical arrangement is found in actin cables underneath the chloroplasts (18). Cargo-carrying myosins moving along the actin filaments induce a flow in the cytosol (19). The motion of the cytoplasm is rotational: Two spiraling bands of molecular motors at the cell periphery drive the cellular fluid up and down in a cyclic fashion (Fig. 1 b). The zones of opposite flow direction are separated by indifferent zones, also called neutral lines, whose position is marked by a lack of chloroplasts (Fig. 1 b and c). The cyclosis flow in C. corallina reaches extraordinary speeds of up to 100 μm s⁻¹ (20,21). A three-dimensional (3D) profile of the cytoplasmic flow was investigated by van de Meent et al. (21), who demonstrated that the shear flow directly transmits through the vacuolar membrane involving the motion in the whole cell. Cyclosis has been hypothesized to mitigate the slowness of diffusive metabolite transport over the distances in the order of centimeters that are typical for C. corallina. Thus, the intercellular transport in characean algae consists of the active advection of substances toward and away from the cellular junction and the diffusive permeation through the plasmodesmata.

To explore the interplay between the active and passive transport processes, the cytoplasmic streaming in C. corallina can be manipulated by temperature variation (22), chemical stimuli (22,23), and electrical stimuli (24). The importance of cyclosis for the intercellular transport between C. corallina internodes was demonstrated by Bostrom and Walker (23). They showed that the transport rate increases significantly with increasing streaming velocity. In agreement with this finding, Ding and Tazawa (22) reported that streaming inhibition in both or either of the adjacent internodes in a tandem cell reduces the amount of substance transported in a specific time interval. The authors argue that advection assists transnodal transport by maintaining a high concentration gradient across the node. A disadvantage of most experiments devoted to the permeation of metabolites through the node is that they require the destruction of the cells and removal of cytoplasm for concentration determination. Therefore, those measurements were neither spatially nor temporally resolved.

This paper reports spatially and temporally resolved studies of the intercellular transport of a fluorescent marker between a pair of internodal C. corallina cells. Using streaming inhibition, we separate advective transport from diffusion. Our approach, assisted by the analysis of the diffusion-advection transport model, allows us to determine the transport parameters. Additionally, we discuss the role of the nodal cells in transnodal transport.

Materials and methods

Experimental

The transnodal transport in C. corallina was investigated using main axis cells. A tandem of internodal cells was harvested at least 12 h but usually more than 24 h before the measurement and stored in artificial pond water (APW), containing 0.1 mM KCl, 1.0 mM NaCl, and 0.1 mM CaCl₂. The pH was adjusted to 7.0 by adding low concentration of NaHCO₃.

The transport through the nodal complex was visualized using fluorescein as a fluorescent tracer. Dye loading was accomplished using a noninvasive ester loading technique to avoid mechanical stress. One of the internodal cells was placed in a solution containing fluorescein diacetate (FDA; Sigma-Aldrich, St. Louis, USA). The solution for loading of cells was prepared by diluting 10 $\mu$L of stock solution (15 mg/mL FDA in acetone) with 10 mL APW immediately before experiments. The final solution then contained 15 $\mu$g/mL FDA and only 0.1% acetone. FDA is a membrane-permeant non-fluorescent substance that diffuses through the plasma membrane into the cytoplasm where esterases facilitate its hydrolysis. When acetate is cleaved off, the fluorescent species fluorescein remains. As fluorescein is less permeant, it accumulates in the cytoplasm.

To investigate the transnodal transport, only one of the internodal cells was loaded with the dye, whereas the other one was dye free in the initial state. To achieve this, one of the internodes was partially submerged in the solution with FDA, whereas a larger part of the tandem was kept in pure APW, as indicated in Fig. 2 a. The APW droplets with and without FDA were spatially separated. Diffusion of FDA into the droplet of pure APW via liquid bridges was prevented by isolating the cells using a grease barrier (medium-viscosity Korasilon paste, Kurt Obermeier, Bad Berleburg, Germany) that also fixed the cells in place. Additionally, a three-chamber setup (see Fig. 2 b) was used to inhibit cyclosis by applying voltage pulses. Pulses with amplitudes ranging from 1 to 4 V were generated by a USB DAQ module (Redlab 1408-FS (Meilhaus Electronic, Alling, Germany) controlled via Labview. Fluorescence microscopy studies were conducted using an inverted microscope Axio Observer.D1 (Carl Zeiss, Oberkochen, Germany) equipped with a mercury lamp HBO 100 (Carl Zeiss, Oberkochen, Germany) as a light source. A 5×-lens EC Plan-NEOFLUAR 0,16 Pol (Carl Zeiss, Oberkochen, Germany) was employed in most measurements. The fluorescence was observed using the excitation filter 450–490 nm and $546\pm 12$ nm emission.

Figure 2.

(a) To study intercellular transport in pairs of internodes of C. corallina, one of the internodal cells was loaded with fluorescent dye. One cell was partially immersed in a drop of artificial pond water (APW) containing fluorescein diacetate (FDA). Pure APW was spatially separated from the solution with FDA. Grease was used to fix the cells and served as a further measure to prevent contact of the droplets. (b) A three-chamber setup was used to apply voltage pulses for triggering APs. In that case, the cell holders separating the chambers were sealed with grease. One of two adjoining internodal cells was loaded with a fluorescent dye. Fluorescent imaging was employed to visualize the spreading of the dye. Voltage pulses can be applied to induce APs and thus inhibit the cytoplasmic streaming in the cells. To see this figure in color, go online.

Images were acquired using a highly sensitive camera Andor iXon Ultra EMCCD (Oxford Instruments, Abingdon, UK) in the high-dynamic-range mode. To avoid bleaching of the fluorescent dye and the light-induced stress reactions in the cells, the samples were illuminated only during the acquisition. For this purpose, the shutter of an optical filter wheel Lambda 10-2 (Sutter Instrument, Novato, USA) and the camera were triggered via Labview using an NI USB-6000 (NI, Austin, USA) multifunctional device (Fig. 2). The acquisition frame rate was around 1 s⁻¹ for a typical exposure time of 21 ms.

To investigate transnodal transport, the fluorescence intensity was monitored in both internodal cells and in the node while one of the internodes was loaded with dye. Note that the dye loading continued throughout the measurement.

Results and discussion

Transnodal transport with cyclosis

Permeation of the dye from one internodal (source) cell into the other (sink) cell consists of diffusive transport across the plasmodesmata in the nodal cell complex. We focus on the transport from the nodal cells into the internode, acting as a sink. The dye collected in the sink cell is further transported by the advective flow (cyclosis) and distributed over the whole cell. The fluorescence in the sink cell is continuously increasing with time. The fluorescence signal exhibits a strong inhomogeneity in the cytoplasm. The permeating dye accumulates in cloud-like patches that are transported by the cytoplasmic flow. Regarding the streaming direction with respect to the nodal complex, a downstream region, where the flow is directed away from the node, and an upstream region, where the streaming is directed toward the node, are distinguished (Fig. 3). Cytoplasmic streams of opposite directions are separated by the indifferent zones. As the patches of dye move in the cytoplasm, they diffuse out, resulting in an additional exchange of the dye between the up- and downstream region. However, in the initial time period, nearly all transported dye is carried with the stream. The fluorescence intensity starts increasing significantly in the downstream region of the junction when the dye-rich patches close one circle around the cell. Measuring fluorescence intensities in the downstream $c_{\mathrm{d}}$ and upstream $c_{\mathrm{u}}$ regions (see Fig. 3 a), we obtain two separate curves shown in Fig. 3 c. The transport process shows only a weak mixing. The advective transport along the cell strongly dominates the diffusion across the indifferent zone. Even after 2 h of acquisition, the dye concentrations in the two regions do not reach equilibrium. The concentration difference increases with time also as a result of non-stationary concentration kinetics in the source cell, a consequence of ongoing dye loading.

Figure 3.

To evaluate fluorescent images of C. corallina cells loaded with fluorescein, fluorescence intensities were spatially averaged over the ROI shown in (a). The nodal concentration $c_{\mathrm{N}}$ and the sink cell up- and downstream concentration $c_{\mathrm{u},\mathrm{d}}$ of fluorescein are assumed to be proportional to the intensities $I_{\mathrm{N}}$ and $I_{\mathrm{u},\mathrm{d}}$ in the respective ROI. Arrows indicate the direction of cytoplasmic streaming in the downstream (green arrow) and upstream region (red arrow) of the sink cell. The lower figures show the evolution of fluorescence intensity after smoothing and interpolation in (b) the node and (c) the up- and downstream region in the internode. (d) Time series of fluorescence images showing the internodal sink cell. In the first frame (top), arrows indicate the streaming direction in the regions separated by the indifferent zone (thick white dashed line). The displacement of patches of dye illustrates the cytoplasmic streaming. To see this figure in color, go online.

Transnodal transport during streaming inhibition

To separate the effect of the advective flow from the diffusion, we used action potential (AP) pulses to temporarily cease the cyclosis. This approach allowed us to gain a deeper insight into the diffusion mechanism. Voltage pulses were applied to the sink cell to trigger the AP and thus stop the cytoplasmic streaming. Streaming inhibition could occur either in the sink cell or in both sink and source cells. Rarely, the streaming in the nodal complex was also affected. Complete streaming recovery required several minutes; however, total cessation of streaming was observed only for a short time interval (Fig. 4 a).

Figure 4.

Influence of an AP on the intercellular dye transport. The red line indicates the moment when an electric stimulus was applied to trigger an AP. (a) The velocity of the streaming cytoplasm, estimated from the displacement of fluorescent patterns. After the AP was triggered, cyclosis stopped momentarily. (b) The fluorescence intensity measured in the vicinity of the node. Two peaks appeared as the streaming recovered, indicating that dye had accumulated in the node-internode contact region in the absence of advection. The inset shows the ROI for the intensity measurement. The direction of cytoplasmic streaming is indicated by the white arrow. To see this figure in color, go online.

In the absence of advection in the sink cell, we would expect the accumulation of the permeating dye in a single patch at the nodal junction. The patch would become visible when the flow recovers and we would expect a single broad peak in the intensity-time curve measured in the downstream region. However, the experiment shows a different picture.

Fig. 4 shows the intensity in the sink cell close to the node. When the streaming recovers, the intensity exhibits a sharp peak, which is followed by a broader peak of lower intensity (Fig. 4). Although the occurrence of intensity peaks supports the hypothesis of strong dye accumulation as a result of cyclosis inhibition, the number of peaks is inconsistent with the notion that dye transport occurs through the whole nodal junction. Instead, dye appears to be transported only through a segment of the node-internode contact area.

The time separation between the centers of the intensity peaks was roughly $\Delta t\approx$ 47 s. The streaming velocity measured from the motion of patches of dye in the period between the occurrence of both peaks was approximately $v\approx$ 19 $\mu$m/s. An estimate of the spatial separation between the peaks is $\Delta t·v=$ 893 $\mu$m, which is comparable with the cell diameter $2r\approx$ 840 $\mu$m. This result implies that only peripheral nodal cells contribute to the dye transport after an AP. The most direct pathway for intercellular transport, leading through the central nodal cells, seems to be blocked. The effective area of the nodal junction is reduced from a disk-shaped region in the unperturbed case to a ring, as indicated in Fig. 8.

Figure 8.

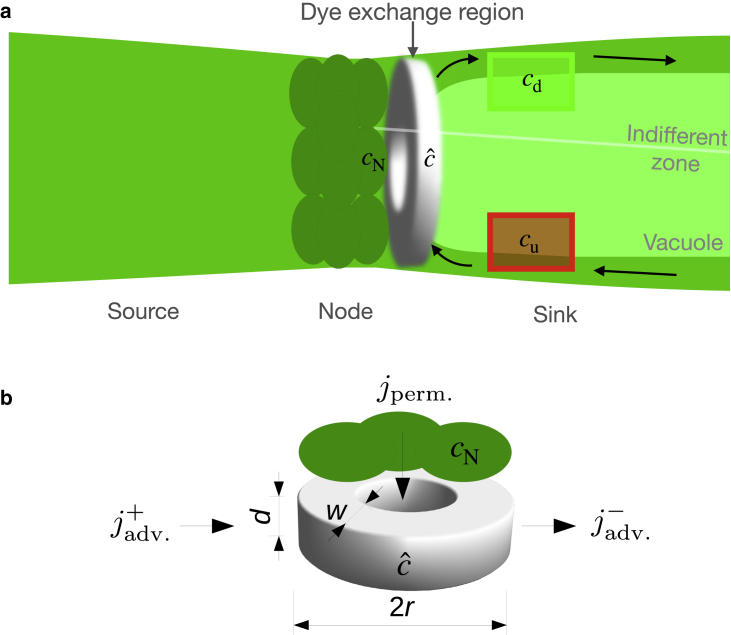
(a) Sketch of a tandem cell consisting of two internodal cells adjoined by a nodal complex. In experiments, the left internode is loaded with dye and acts as the source cell. The right cell (sink) receives dye that permeates through the circular contact area with the node. From the node, dye diffuses into a disk-shaped volume bounded by the nodal cells and the vacuole. The situation shown here illustrates the effect of an AP that inhibits transport through the central part of the node. The effective dye exchange region (shown in white) is then reduced to a ring. The green and red region mark where $c_{\mathrm{d},\mathrm{u}}$ would be measured. Arrows indicate the direction of cytoplasmic streaming. (b) Detailed sketch of the dye exchange region to clarify geometric parameters. The diffusive influx from the node with flux density $j_{\text{perm}.}$ and the advective in- and efflux $j_{\text{adv}.}^{\pm }$ are indicated. To see this figure in color, go online.

Streaming can be inhibited for extended periods of time with pulse sequences. However, complete cessation was observed only for short periods of time of about 10 s. When the streaming is allowed to recover or triggering of APs fails (cells appear to adapt to the stimuli), bright, distinct stripes become visible (see Fig. 5). This observation is another indication that only a ring-shaped segment of the contact area is involved in the dye exchange. If the transport occurs through the total contact area, including the central cells, we would expect the high dye concentration region to appear as an approximately disk-shaped patch in the fluorescence images.

Figure 5.

After application of a sequence of voltage pulses for prolonged streaming inhibition, bright stripes of high dye concentration appear in the downstream region as the streaming recovers. Brackets indicate the position of the stripes and are labeled in order of appearance. The arrow indicates the direction of the flow. To see this figure in color, go online.

Note that, other than in the case with a single AP, the number and separation of stripes are not simply a consequence of the geometry of the contact region for repeated pulse application. Instead, relative positions of stripes are a result of cytoplasm displacement during a temporary failure of streaming inhibition.

The ability of AP to hinder transport through plasmodesmata in C. corallina cells has recently been demonstrated (25). In experiments reported in (25), the amount of permeating metabolites diminished greatly after the AP generation, whereas the time of crossing this barrier was subject to small variations. This agrees with our findings of the ring-shaped pattern of fluorescent probe transported via the nodal complex after AP. The cell excitation causes the stoppage of cytoplasmic streaming due to transient elevation of $\left[{\text{Ca}}^{2+}\right]$ in the cytoplasm. This leads to reduced ATP consumption by the actomyosin complex. The ATP-dependent H⁺ pump of the plasma membrane is also inhibited by increased ${\left[{\text{Ca}}^{2+}\right]}_{\text{cyt}}$ (26). There is evidence that the reduction in ATP level dilates the plasmodesmal aperture, whereas elevation of ATP content in the cytosol restricts the size exclusion limit of plasmodesmata (27). The differences in the excitability of small and big nodal cells may determine uneven permeability changes of their plasmodesmata due to differences in intracellular ATP level.

Theoretical model and evaluation

To determine the transport parameters from the experimental data, we employ a diffusion-advection model. In this model, the fluorescent dye permeates from the node to the sink cell and is further transported with the cytoplasmic flow. Neglecting adsorption of the dye, the governing equation for the dye concentration $c\left(\mathbf{r},t\right)$ in a position $\mathbf{r}$ at a time $t$ can be expressed as

$$\frac{\partial c\left(\mathbf{r},t\right)}{\partial t}=D\Delta c\left(\mathbf{r},t\right)-\mathbf{v}·\nabla c\left(\mathbf{r},t\right)$$ (1)

where $D$ is the diffusion constant in the cytoplasm, $\mathbf{v}$ is the streaming velocity, and $\Delta$ is the Laplace operator.

Taking into account that the transport occurs in a thin layer of cytoplasm, we can consider the motion as quasi-two-dimensional (2D). That is to say, we neglect the variation of the dye concentration across the cytoplasmic layer thickness. We construct a 2D simulation domain as a representative of a 3D slab of thickness $d$ (the cytoplasmic layer thickness) such that the concentrations and fluxes in our model remain 3D quantities.

The solution domain is obtained by unfolding the surface of the internodal cell. As in the experimental system, we distinguish the up- and downstream regions regarding the flow direction with respect to the node. These regions are enclosed by the indifferent zones and are connected at the end of the cell and the nodal complex. Cutting the cell from the end and along the indifferent zones, we map the up- and downstream region onto two connected rectangular domains (Fig. 6). After the unfolding, the velocities in these two subdomains point in the same direction. The magnitude of cyclosis velocity is constant except for a small shear zone close to the indifferent lines (21,28). Rather than simulating hydrodynamic flow, we ignore shear, assuming a velocity inversion across the indifferent zones. To further simplify the geometry, we reduce the end of the internodal cell to the lines bounding the simulation domain, ${\mathcal{L}}_1$ and ${\mathcal{L}}_4$ (Fig. 6). The nodal complex is mapped to the line separating the subdomains. This line is split into two boundaries ${\mathcal{L}}_7^{\prime }$ and ${\mathcal{L}}_7^{″}$, one for each subdomain, to model the influx of dye from the node into both the up- and downstream region of the sink cell.

Figure 6.

(a) Sketch of an internodal cell. (b) Schematic unfolding of an internodal cell surface for a 2D model of transport kinetics. The cytoplasm layer is cut from the end of the cell and unfolded into two domains that are bounded by the indifferent lines and separated by the node. The nodal complex is reduced to a line source perceived as two boundaries ${\mathcal{L}}_7^{\prime }$ and ${\mathcal{L}}_7^{″}$, one for each subdomain. To see this figure in color, go online.

Pairwise, the top and bottom boundaries (Fig. 6) correspond to the same indifferent zone. Thus, the boundary conditions are given by the balance of concentrations and fluxes:

$$c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_2}=c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_3}$$ (2)

$${\mathbf{n}}_{{\mathcal{L}}_{\mathbf{2}}}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_2}=-{\mathbf{n}}_{{\mathcal{L}}_{\mathbf{3}}}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_3}$$ (3)

and

$$c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_5}=c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_6}$$ (4)

$${\mathbf{n}}_{{\mathcal{L}}_{\mathbf{5}}}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_5}=-{\mathbf{n}}_{{\mathcal{L}}_{\mathbf{6}}}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_6}$$ (5)

where $n_{{\mathcal{L}}_i}$ is the outer normal at the boundary ${\mathcal{L}}_i$. Boundaries ${\mathcal{L}}_1$ and ${\mathcal{L}}_4$ stand for the end of the internodal cell, where the up- and downstream region are connected. This junction is represented by periodic boundaries

$$c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_1}=c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_4}$$ (6)

$${\mathbf{n}}_{{\mathcal{L}}_{\mathbf{1}}}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_1}=-{\mathbf{n}}_{{\mathcal{L}}_{\mathbf{4}}}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_4}$$ (7)

The nodal boundary separates both domains and, therefore, can be split into two, ${{\mathcal{L}}_7}^{\prime }$ and ${{\mathcal{L}}_7}^{″}$, as seen from the corresponding subdomains with the outer normals ${\mathbf{n}}_{{\mathcal{L}}_{\mathbf{7}}^{\prime }}$ and ${\mathbf{n}}_{{\mathcal{L}}_{\mathbf{7}}^{″}}$, respectively (Fig. 6). This boundary has two functions: It connects the two domains of the opposite streaming direction, and it connects the sink cell to the node. These functions are expressed in the boundary conditions, which are periodic with a source term:

$$c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_7^{\prime }}=c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_7^{″}}$$ (8)

$$-{\mathbf{n}}_{{\mathcal{L}}_{\mathbf{7}}^{\prime }}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_7^{\prime }}-{\mathbf{n}}_{{\mathcal{L}}_{\mathbf{7}}^{″}}·\left(-D\nabla c\left(\mathbf{r},t\right)+\mathbf{v}c\left(\mathbf{r},t\right)\right){|}_{{\mathcal{L}}_7^{″}}=\kappa \left(c_{\mathrm{N}}\left(t\right)-c\left(\mathbf{r},t\right){|}_{{\mathcal{L}}_7^{\prime },{\mathcal{L}}_7^{″}}\right)$$ (9)

where $c_{\mathrm{N}}$ is the concentration in the node, and $\kappa$ is the effective permeation coefficient. The relation between $\kappa$ and the permeability $P$ can be obtained from the flux balance:

$$\kappa =\frac{A_{\text{node}}}{Hd}P$$ (10)

where $d$ is the thickness of the protoplasmal layer, $A_{\text{node}}$ is the nodal area, and $H$ is the domain width (Fig. 6).

As a characteristic length scale, we choose the length of the sink cell $L$. There are two ways to obtain the characteristic time scale ${\tau }_0$. One way is to use the diffusion time scale ${\tau }_D=L^2/D$. Another way is to use the advective scale ${\tau }_a=L/v$. Fig. 7 shows the simulation of the concentration $c/c_{\mathrm{N}}$ as a function of the dimensionless time with ${\tau }_0={\tau }_a$ for selected values (dimensionless) $\tilde{D}=0.5$, $\tilde{p}=0.1$ in a hypothetical case when the concentration in the node was kept at a constant value $c_{\mathrm{N}}$. Initially, the sink cell was dye free; i.e., $c\left(\mathbf{r},0\right)=0$. The two curves correspond to the concentration dependencies in the neighboring upstream and downstream points. Downstream concentration $c_{\mathrm{d}}$ exhibits a fast growth; at the same time, the upstream concentration is slowly increasing due to a delay needed for the dye to be transported around the cell.

Figure 7.

Numerical simulation using Eq. 1 of the concentration $\tilde{c}=c/c_{\mathrm{N}}$ as a function of the dimensionless time with ${\tau }_0={\tau }_a$ for selected values (dimensionless) $\tilde{D}=0.05$, $\tilde{p}=0.1$ in a hypothetical case when the concentration in the node was kept at a constant value $c_{\mathrm{N}}$. The concentration in the sink cell, where initially $c\left(\mathbf{r},0\right)=0$, was measured in the up- and downstream region close to the node. To see this figure in color, go online.

Typical values of the diffusion constant of the dye in the order of ${10}^{-11}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ and the advection velocity ${10}^{-5}{\text{ms}}^{-1}$ allow us to compare the diffusive and advective time scales. With the Péclet number of $Pe\approx {10}^5$, the advective transport rate far exceeds the diffusive one.

To extract the transport parameters from the experiment, we develop the model further, reducing the full 2D description to an equation for the concentration in a localized region of interest (ROI). We keep symbol $\hat{c}$ for the averaged over ROI concentration, which depends on time $t$. We take into account the geometry of the node-internode junction and describe the advective and permeation flux, neglecting intracellular diffusion.

The dye exchange between the nodal complex and the sink occurs where the nodal cells and internode are in contact. The fluorophore permeates through the node into a portion of internode cytoplasm located at the nodal junction. The lateral dimensions of the dye-receiving volume are determined by the contact area with the node and its thickness is the cytoplasmic layer thickness $d$ (see Fig. 8 a). A cylindrical, disk-like geometry seems a reasonable assumption for the shape of this dye exchange region, since the node-internode contact area is approximately discoidal. However, as discussed previously, the effective dye exchange region appears to be reduced to a ring after an AP, when transport through the central nodal cells is inhibited.

We denote by $\hat{c}\left(t\right)$ the concentration in the dye exchange region. It is altered by the diffusive transport between the node and the sink cells and by the advection (cyclosis) in the sink cell. The direction of the respective fluxes is indicated in Fig. 8 b. The diffusive transport is driven by the concentration gradient across the node. The associated particle number flux density $j_{\text{perm}.}$, can be expressed as

$$j_{\text{perm}.}=P\left(c_{\mathrm{N}}\left(t\right)-\hat{c}\left(t\right)\right)$$ (11)

where $P,\left[P\right]=\mathrm{m}/\mathrm{s}$ is the permeability and $c_{\mathrm{N}}$ the dye concentration in the node. To obtain the permeating particle number flux ${\Phi }_{\text{perm}.},\left[{\Phi }_{\text{perm}.}\right]={\mathrm{s}}^{-1}$, the flux density is integrated over the dye exchange region

$${\Phi }_{\text{perm}.}\left(t\right)\approx AP\left(c_{\mathrm{N}}\left(t\right)-\hat{c}\left(t\right)\right),A=\{\begin{array}{cc}\pi r^2\text{,}& \text{unperturbed}\text{cell}\\ \pi {(r^2-(r-w)}^2)\text{,}& \text{after}\text{action}\text{potential}\end{array}$$ (12)

where $r$ is the disk or outer ring radius and $w$ the ring width/radial thickness (see also Fig. 8 b).

The advection-induced influx of cytosol with a low dye concentration is associated with a flux density

$$j_{\text{adv}.}^{+}\left(t\right)=v{c}_{\mathrm{u}}\left(t\right)$$ (13)

with $c_{\mathrm{u}}\left(t\right)$ the dye concentration in the upstream region of the sink cell, where the flow is directed toward the node. The efflux of dye-rich fluid is described approximately by

$$j_{\text{adv}.}^{-}\left(t\right)=-v\hat{c}\left(t\right)$$ (14)

The effective area for both advective particle number fluxes is a rectangle with the outer diameter of the dye exchange region $2r$ and the cytosol layer thickness as side lengths.

$${\Phi }_{\text{adv}.}\left(t\right)=2rdv\left(c_{\mathrm{u}}\left(t\right)-\hat{c}\left(t\right)\right)$$ (15)

The rate of particle number change in the dye exchange region $\dot{\hat{N}}={\Phi }_{\text{perm}.}+{\Phi }_{\text{adv}.}$ is therefore given by

$$\dot{\hat{N}}\left(t\right)=AP\left(c_{\mathrm{N}}\left(t\right)-\hat{c}\left(t\right)\right)+2rdv\left(c_{\mathrm{u}}\left(t\right)-\hat{c}\left(t\right)\right)$$ (16)

$\hat{N}$ can also be written as a product of the dye concentration and the volume of the region $\hat{N}\left(t\right)=\hat{c}\left(t\right)Ad$. With this expression, Eq. 16 becomes

$$\dot{\hat{c}}\left(t\right)=\frac{P}{d}\left(c_{\mathrm{N}}\left(t\right)-\hat{c}\left(t\right)\right)+\frac{2r}{A}v\left(c_{\mathrm{u}}\left(t\right)-\hat{c}\left(t\right)\right)$$ (17)

or, introducing the permeability coefficient $k=P/d$,

$$\dot{\hat{c}}\left(t\right)=k\left(c_{\mathrm{N}}\left(t\right)-\hat{c}\left(t\right)\right)+\frac{2r}{A}v\left(c_{\mathrm{u}}\left(t\right)-\hat{c}\left(t\right)\right)$$ (18)

The cyclosis in cells of C. corallina stops when an action potential is triggered. In this case $v=0$ and Eq. 18 simplifies to

$$\dot{\hat{c}}\left(t\right)=k\left(c_{\mathrm{N}}\left(t\right)-\hat{c}\left(t\right)\right)$$ (19)

Under the assumption that the nodal cell concentration is constant, $c_{\mathrm{N}}\left(t\right)=c_{\mathrm{N}}^0$, for the short time span of completely inhibited cyclosis, this differential equation can be solved analytically. The solution reads

$$\hat{c}\left(t\right)=c_{\mathrm{N}}^0+\left({\hat{c}}_0-c_{\mathrm{N}}^0\right)e^{-kt}$$ (20)

where ${\hat{c}}_0=\hat{c}\left(0\right)$. This equation can be transformed into the following expression for $k$

$$k=\frac{1}{t}\ln \left(\frac{{\hat{c}}_0-c_{\mathrm{N}}^0}{\hat{c}\left(t\right)-c_{\mathrm{N}}^0}\right)$$ (21)

Analysis of the experimental data: Application of the advection-diffusion model

The fluorescence intensities in the up- and downstream region of the sink cell and in the nodal complex were averaged over rectangular ROIs as indicated in Fig. 3. In the internode, ROIs had to be large enough to minimize fluctuations due to spatial inhomogeneities of fluorescence. At the same time, their lateral dimensions and position were restricted to mitigate the effect of cell curvature. The ROI positions were chosen with care to avoid overlap with regions containing remains of branchlets, which may fluoresce.

The measured intensity curves were smoothed and interpolated (second-order Savitzky-Golay filter, 51-frame window) such that a dataset consisting of 100 equidistant intensity-time data points was obtained. These curves were imported to Mathematica Software (Wolfram) and interpolated to obtain functions for the node intensity $I_{\mathrm{N}}\left(t\right)$ and the upstream intensity $I_{\mathrm{u}}\left(t\right)$. Background correction of the intensity curves was either done by the local background subtraction of an image recorded before loading the cell or by subtracting initial intensity values in loaded cells.

We apply the model equation Eq. 18, which was derived for concentrations, to the intensities, assuming that the average intensity of FDA fluorescence in the ROI is proportional to the fluorophore concentration; i.e., $I_{\mathrm{N},\mathrm{u},\mathrm{d}}\left(t\right)\propto c_{\mathrm{N},\mathrm{u},\mathrm{d}}\left(t\right)$ and $\hat{I}\left(t\right)\propto \hat{c}\left(t\right)$. This approach, however, is valid only for the internodal cells where the thickness of the cytoplasmic layer is nearly constant and the pH dependence of the FDA fluorescence can be neglected. Note that it still has to be clarified whether concentrations measured in this way in the nodal complex and the sink cell are comparable.

The model equation Eq. 18 was solved with Mathematica for different values of the permeability coefficient $k$ with the initial condition $\hat{I}\left(t=0\right)=I_{\mathrm{d}}\left(t=0\right)$, where $t=0$ marks the start of the image acquisition. The velocity $v$ of cytoplasmic streaming was estimated from the motion of fluorescent patterns in the sink cell and the radius $r$ of the dye exchange region was replaced with the internodal cell radius close to the node.

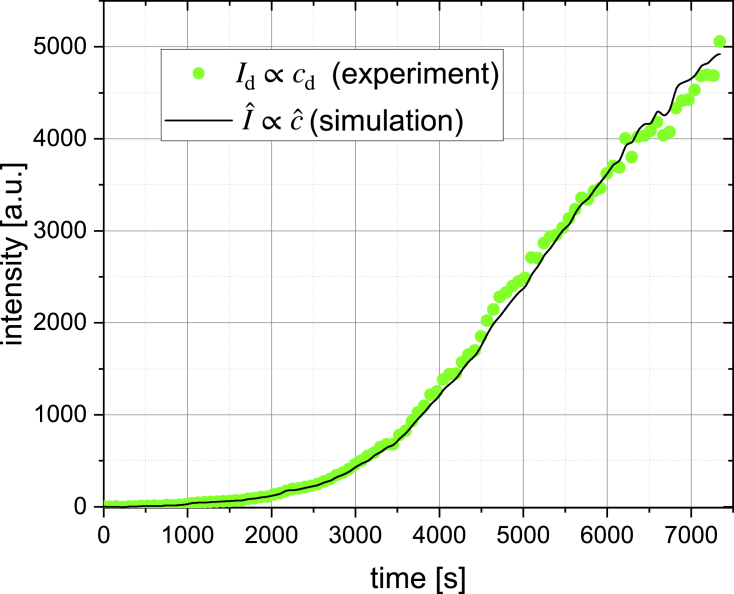
Using the information on the geometry of the dye exchange region, the advection-diffusion model (Eq. 18) can be applied to determine the permeability coefficient from time-resolved measurements of the dye concentrations. Simulation results $\hat{I}\left(t\right)$ were compared with the measured downstream intensity $I_{\mathrm{d}}\left(t\right)$, assuming that the difference between the concentration in the dye exchange region, for which the model was developed, and the downstream region is only a small time delay that is negligible on the long time scale of our experiments. An exemplary result is shown in Fig. 9. Experimental data and simulated concentration curve are in a good agreement over the whole course of the measurement (roughly 2 h). The permeability coefficient was determined from the comparison of the experiment and simulation for five cells, yielding $\overline{k}=1.1·{10}^{-2}{\mathrm{s}}^{-1}$ $\left({\sigma }_k=4·{10}^{-3}{\mathrm{s}}^{-1}\right)$.

Figure 9.

Experimental data for the sink cell downstream fluorescence intensity (green points; see also Fig. 3) is shown together with the result of the advection-diffusion model (black line) for a permeability coefficient of $k=1.3·{10}^{-2}{\mathrm{s}}^{-1}$ that minimizes the residual. To see this figure in color, go online.

Permeability determination for arrested cyclosis

In experiments with repeated application of voltage pulses, the recovery of cyclosis is accompanied by the motion of a sharp, bright dye stripe. The permeability coefficient was calculated using Eq. 21. The required quantities are the concentration in the sink cell at the moment when the streaming stops, ${\hat{c}}_0=\hat{c}\left(0\right)$, and when it begins to recover, $\hat{c}\left(\tau \right)$, the concentration in the node $c_{\mathrm{N}}$, and the duration of the period of total streaming cessation $\tau$. As in the experiments with continuous streaming, dye concentrations are assumed to be proportional to the fluorescence intensities averaged over ROI. In an ideal situation, the concentrations $\hat{c}$, or rather the respective intensities $\hat{I}$, would be measured in the sink at the nodal junction. This area is inaccessible with our methods. We assume that $\hat{I}\left(\tau \right)\propto \hat{c}\left(\tau \right)$ is equal to the dye concentration measured in the bright stripe (Fig. 10) of high dye concentration at the time $t>\tau$ when it enters the downstream region. Note that $\hat{I}\left(\tau \right)$ might be underestimated due to the diffusive spreading of the dye in the stripe. ${\hat{I}}_0\propto {\hat{c}}_0$ is measured before streaming recovery in the ROI defined by the position of the stripe (red region in Fig. 10). The time $\tau$ during which streaming is completely stopped is estimated from the motion of patches of dye in the cytoplasm. For the nodal concentration $c_{\mathrm{N}}$, which was assumed to be constant in the derivation, the temporally and spatially averaged fluorescence intensity measured in an ROI in the nodal complex (blue region in Fig. 10) is plugged into Eq. 21. The average $k$ calculated from four experiments is $\overline{k}=1.6·{10}^{-2}{\mathrm{s}}^{-1}$ $\left({\sigma }_k=5·{10}^{-3}{\mathrm{s}}^{-1}\right)$.

Figure 10.

The repeated application of voltage pulses to a C. corallina cell results in the inhibition of cytoplasmic streaming and strong dye accumulation in the sink cell close to the node. As the streaming begins to recover, a bright stripe becomes visible. The permeability coefficient can be calculated from the intensity measured in the region of the stripe (red) before and after streaming recovery, the time of complete streaming inhibition and the nodal intensity (blue ROI). Brightness and contrast were manipulated to enhance the visibility of structures in the right cell. To see this figure in color, go online.

The deviation of the permeability coefficient obtained in the experiments with and without streaming inhibition is within the range of the standard deviations.

Estimation of the cytoplasmic diffusion coefficient of fluorescein

The diffusion coefficient $D$ of fluorescein in the cytosol of C. corallina can be estimated from the broadening of the bright, dye-rich stripes that form after the application of a sequence of voltage pulses. To evaluate the stripe broadening, a linear ROI is defined along the direction of cytoplasmic streaming. The intensity profile $I\left(x,t\right)$ along this line, where $x$ is the position on the line, is fitted with a Gaussian according to the model

$$I\left(x,t\right)=\alpha \left(t\right)e^{-\frac{(x-\beta (t\left)\right)2}{\gamma \left(t\right)}}+\delta \left(t\right)$$ (22)

$\beta \left(t\right)$ is the position of the concentration maximum and $\gamma \left(t\right)$ is a measure of the stripe width. The advective flow results in a displacement of the maximum with the streaming velocity, and the diffusion leads to the broadening with

$$\gamma \left(t\right)=4Dt$$ (23)

The estimation of the diffusion constant $D$ of fluorescein in the cytosol works only if the stripe can be well resolved shortly after it appears in the downstream region. If rests of branchlets occlude this region or if patches with a high dye concentration are in the vicinity of the stripe, the method fails as fitting the intensity profiles does not work. The temporal evolution of $\gamma$ for a high-concentration stripe is shown exemplary in Fig. 11.

Figure 11.

Temporal evolution of the squared width $\gamma$ of a bright stripe determined by a Gaussian-type fit according to Eq. 22. The diffusion constant $D$ is estimated from the slope of a linear regression (red line). To see this figure in color, go online.

The obtained result for the diffusion constant of fluorescein in the cytoplasm is $D=\left(28\pm 4\right)\mu {\mathrm{m}}^2/\mathrm{s}$ (${\sigma }_D=4\mu {\mathrm{m}}^2/\mathrm{s}$ from two measurements on different cells) where errors were calculated from the 95% certainty interval of the linear regression of $\gamma \left(t\right)$. The diffusion of fluorescein in the cytosol is inhibited in comparison with fluorescein diffusion in aqueous solution where $D=436\mu {\mathrm{m}}^2/\mathrm{s}$ at room temperature (29).

For comparison, the constant of diffusion through plasmodesmata $D_{\mathrm{p},\text{eff}}$ can be estimated from the reduced permeability coefficients $k=P/d$, where $P$ is the permeability coefficient, and $d$ is the thickness of the cytoplasmic layer. The effective diffusion coefficient $D_{\mathrm{p},\text{eff}}$ is given by $D_{\mathrm{p},\text{eff}}=PL$ where $L$ is the effective thickness (length) of the plasmodesmata. Thus, $D_{\mathrm{p},\text{eff}}=kdL$. Averaged over all experiments (with and without streaming inhibition), $\overline{k}=1.3·{10}^{-2}{\mathrm{s}}^{-1}$. Assuming a value of $d=15\mu \mathrm{m}$ for the cytoplasmic layer thickness ($d=10-20\mu \mathrm{m}$ (2)) and $L=$ 300 nm for the thickness of the plasmodesmata (as determined from electron micrographs of Cook (9) by Bulychev (14)), one obtains $D_{\mathrm{p},\text{eff}.}\approx 6·{10}^{-2}\mu {\mathrm{m}}^2/\mathrm{s}$.

This estimation assumes that the transport occurs through the whole area of the dye exchange region. However, only a fraction of the node-internode cell wall is occupied by plasmodesmata and contributes to diffusive permeation. To account for that, the diffusion constant must be corrected: $D_{\mathrm{p}}=D_{\mathrm{p},\text{eff}.}/\epsilon \approx 26\mu {\mathrm{m}}^2/\mathrm{s}$ where $\epsilon =2.29·{10}^{-3}$ is the area fraction of the contact area occupied by plasmodesmata (14). The diffusion constant for permeation appears to be comparable with the diffusivity in the cytoplasm. This is rather unexpected, since the retardation of diffusion in plasmodesmata in comparison to the “free” cytoplasm seems a well-known phenomenon (14). However, the physiological variability of $\epsilon$ is considerable and literature values vary by orders of magnitude (4,14,30). This variation can partially be explained by different definitions of plasmodesmal area, with Bostrom (4) and Fischer (30) inferring it from electron micrographs and Bulychev (14) estimating it from the size exclusion limit. Fischer et al. (30) reported that 15.3% of the common area between central nodal cells and the internode of C. corallina are occupied by plasmodesmata. This would yield a significantly reduced diffusion coefficient of $D_{\mathrm{p}}\approx 3.8·{10}^{-1}\mu {\mathrm{m}}^2/\mathrm{s}$ in the nanopores.

Conclusions

This work provides new insight into the properties and regulation of intercellular channels traversing plant cell walls (plasmodesmata) that play a critical role in long-distance transports of photosynthetic assimilates and signaling substances. The diffusion of a low-molecular-weight fluorescent probe within the plasmodesmal pores is examined using an original noninvasive technique and a simulation model. The noninvasive approach of cell loading with permeable fluorogenic dye to estimate the diffusive characteristics of metabolite permeation through the plasmodesmata avoids mechanical injury or cell destruction. The data obtained contribute to a comparatively short list of reported diffusion coefficients for low-molecular-weight substances passing through intercellular pores. Observations of permeation of the fluorescent dye between internodal cells of C. corallina allow us to determine the kinetic parameters for the permeation and diffusion based on two types of experiments. The cells exhibit very fast cyclosis, which results in the rapid mixing of the dye supplied from the source cell. The transport mechanism is strongly affected by cyclosis. Rapid efflux from the node and redistribution of the dye sustain a large concentration gradient across the node. AP allows us to temporarily suspend the advection in the sink cell, leaving only permeation through the plasmodesmata. Interestingly, the plasmodesmata of peripheral cells do not close during the AP. Owing to the slow diffusion of the dye in the cytoplasm, we can determine the shape of the exchange region, which has a ring shape. The results imply that the plasmodesmal transport of fluorescent probe through the central and peripheral cells of the nodal complex is differentially regulated by a physiological signal, the AP. The passage of the probe through the central cells of the nodal complex ceases transiently after elicitation of the AP in the internodal cell, whereas the passage through the peripheral cells of the node was retained. This indicates that plasmodesmata may play a role in modulating the intercellular signaling pathways involving APs. Plasmodesmata of characean algae as close relatives of higher plants are likely to be homologous to higher-plant plasmodesmata and may provide deeper insight into the evolution of these complex intercellular connections.

Author contributions

F.v.R., conceptualization, investigation, formal analysis, writing – original draft, and writing – review & editing; A.A., conceptualization and writing – original draft; A.B., conceptualization and writing – original draft; A.E., conceptualization, simulations, writing – original draft, and writing – review & editing.

Editor: Dylan Myers Owen.