Elucidating lipid conformations in the ripple phase: Machine learning reveals four lipid populations

Abstract

A new mixed radial-angular, three-particle correlation function method in combination with unsupervised machine learning was applied to examine the emergence of the ripple phase in dipalmitoylphosphatidylcholine (DPPC) lipid bilayers using data from atomistic molecular dynamics simulations of system sizes ranging from 128 to 4096 lipids. Based on the acyl tail conformations, the analysis revealed the presence of four distinct conformational populations of lipids in the ripple phases of the DPPC lipid bilayers. The expected gel-like (ordered; $L_{\mathrm{o}}$) and fluid-like (disordered; $L_{\mathrm{d}}$) lipids are found along with their splayed tail equivalents ($L_{\mathrm{o},\mathrm{s}}$ and $L_{\mathrm{d},\mathrm{s}}$). These lipids differ, based on their gauche distribution and tail packing. The disordered $\left(L_{\mathrm{d}}\right)$ and disordered-splayed $\left(L_{\mathrm{d},\mathrm{s}}\right)$ lipids spatially cluster in the ripple in the groove side, that is, in an asymmetric manner across the bilayer leaflets. The ripple phase does not contain large numbers of $L_{\mathrm{d}}$ lipids; instead they only exist on the interface of the groove side of the undulation. The bulk of the groove side is a complex coexistence of $L_{\mathrm{o}},L_{\mathrm{o},\mathrm{s}}$, and $L_{\mathrm{d},\mathrm{s}}$ lipids. The convex side of the undulation contains predominantly $L_{\mathrm{o}}$ lipids. Thus, the structure of the ripple phase is neither a simple coexistence of ordered and disordered lipids nor a coexistence of ordered interdigitating gel-like $\left(L_{\mathrm{o}}\right)$ and ordered-splayed $\left(L_{\mathrm{o},\mathrm{s}}\right)$ lipids, but instead a coexistence of an ordered phase and a complex mixed phase. Principal component analysis further confirmed the existence of the four lipid groups.

Significance

The lipid membrane is one of the most fundamental structures in biology, surrounding all cells separating the interior from the surrounding environment. Membranes exhibit very complex behaviors. One of the fundamental questions is the change in their structure upon phase transition at the main phase-transition temperature. Above it, the membrane is fluid and below it becomes like a gel. The structure in the gel-like phase can be complex, with the membrane displaying asymmetric ripples. The structure of the lipids in this ripple phase has so far remained debatable. Here we used molecular dynamics simulations and machine learning to reveal the long-sought-after ripple structure and that the ripple consists of four distinct different lipid conformations instead of two, as previously expected.

Introduction

The existence of the asymmetric ripple phase was first discovered by Tardieu et al. almost 50 years ago (1). Much of the details of the ripple phase (often called $P_{{\beta }^{\prime }}$) remained unknown but in a landmark study, Sun et al. (2) analyzed electron density from x-scattering and observed that the sawtooth-shaped ripple has two sides, a major side, often called the major arm, which is gel-like, and a possibly fluid-like minor arm, in accordance with suggestions in the literature at that time. In another study, Sengupta et al. argued that the minor arm cannot be in the fluid, or the so-called $L_{\alpha }$, phase as otherwise the length of the arm would be longer, due to the significantly larger area per lipid in the $L_{\alpha }$ phase (3).

The x-ray scattering study of Akabori and Nagle (4) reported that the lipids in the minor arm are definitely in a fluid-like state but not in registry in the curved area of the ripple and in the minor arm of the ripple. Furthermore, they hypothesized that in addition to the gel-like ordered $\left(L_{\mathrm{o}}\right)$ lipids in the major arm, the minor arm has several different conformational classes of lipids instead of the typical binary classification that only distinguishes ordered and disordered (5). It is also noteworthy that the main phase transition into the ripple phase from the fluid phase, despite being of first order, has long been known to have features of critical behavior (6,7,8). This unusual behavior was first pointed out by Nagle, who called it a 3/2-order transition (9).

Computer simulations and theory have also contributed significantly to this debate. The first observation of the ripple phase in atomistic molecular dynamics (MD) simulations was reported in 2005 by de Vries et al. (10). While the asymmetry was present in their MD simulations, in contrast to Sun et al. (2), de Vries et al. did not find the coexistence of a gel and fluid but instead they wrote “the organization of the lipids in one domain of the ripple is found to be that of a splayed gel; in the other domain the lipids are gel-like and fully interdigitated” (10). A similar conclusion was reached by Lenz and Schmid using a coarse-grained model (11). More recent atomistic MD studies have also reported two-phase coexistence of liquid- and gel-like lipids (5,12). The molecular-level structure and the conformational components that contribute to the ripple remain unresolved.

In this study, we performed atomistic MD simulations using systems of 128, 512 and 4096 dipalmitoylphosphatidylcholine (DPPC) lipids over 16 $\mu$s over a broad temperature range (for details seen materials and methods). We then applied conformational clustering based on a three-particle intramolecular density distribution and unsupervised machine learning (ML) methods from image analysis to identify conformational lipid classes. The analysis showed the existence of four distinct lipid conformations: ordered, disordered, ordered splayed, and disordered splayed. The existence of these classes was then directly verified by analyzing the clusters using principal component analysis (PCA) as well as other methods, and they were used to resolve the structure of the ripple phase. The analysis of the ripple shows that it has a complex asymmetric structure in which the two splayed lipid classes have an important role.

Materials and methods

Simulation methodology

Atomic-scale MD simulations of single-component DPPC lipid bilayers were performed. The systems consisted of 512 DPPC lipids and ≈20,000 TIP3P water molecules (13). The choice of 512 lipids was based on the work by Walters et al. showing that the ripple phase is influenced by finite size effects (14). The Gromacs software package was used in all simulations (15). The initial membrane structures were generated using the CHARMM-GUI Membrane Builder (16). The systems were first energy minimized and pre-equilibrated for 20 ns in the NPT ensemble (p = 1 bar and T = 325 K). The production runs were done using the V-rescale thermostat (17) and the Parrinello-Rahman barostat (18); pressure was controlled semi-isotropically, a 2 fs time step was used, and periodic boundary conditions were applied in all directions. For the Lennard-Jones interactions, a switching function over 1–1.2 nm was used, while the particle-mesh Ewald method (19) with a real-space cutoff of 1.2 nm was employed for electrostatics. The production simulations were ran at 293 K, 298 K, 300 K, 305 K, 310 K, 315 K, 316 K, 317 K, 318 K, 320 K, and 325 K. The temperature range was chosen such that it spanned both the fluid and gel phases. A bilayer system at each temperature was simulated for 500 ns.

Robustness of the results was verified by repeating several of the simulations below $T_{\mathrm{m}}$ using different initial conditions; additionally, size dependence was assessed by simulating systems with 128 and 4096 lipids, and the usual metrics such as thickness and the area per lipid were verified to be in agreement with previous results (12,16,20). The 128-lipid systems were run for 1 $\mu$s each at eight temperatures (295 K, 300 K, 305 K, 310 K, 314 K, 317 K, 318 K, and 320 K). The 4096-lipid systems were run for 500 ns each at three temperatures (313 K, 315 K, and 317 K). The total simulation time was 16 $\mu$s.

VMD (21) was used for visualizations, and data analysis was performed using custom Python codes, MDAnalysis (22), scipy (23), scikit-learn (24), and scikit-image (25) libraries. The PCA of the lipid motion was calculated using PCAlipids (26).

Results

Three-particle correlation function to measure local structure

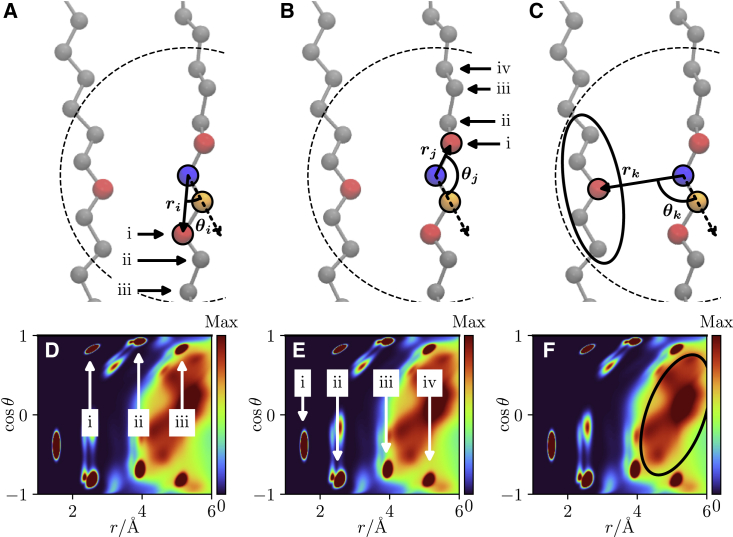
To quantify local structure, we used the mixed, radial-angular, three-particle distribution function, $g_3\equiv g_3\left(r_{BC},{\theta }_{ABC}\right)$, originally introduced by Sukhomlinov and Müser in 2020 in a different context (27,28). In this method, illustrated in Fig. 1, a triplet of atoms is selected: 1) the central atom (blue), $B$; 2) the nearest neighbor to the central atom (orange), $A$; and 3) the other atom within the cutoff (red), $C$. Physically, $g_3$ is proportional to the probability of finding the atom $C$ at a distance of $r$ from the central atom $B$ when the vectors ${\overrightarrow{r}}_{BC}$ and ${\overrightarrow{r}}_{BA}$ form an angle of ${\theta }_{ABC}$. Fig. 1 gives three examples of this using the same central and nearest neighbor atoms in each case.

Figure 1.

Schematic of the mixed angular-radial three-particle correlation function applied to a single carbon in a DPPC acyl chain/lipid tail. A central atom (blue) and its nearest neighbor atom (orange) are selected. The angle formed between the three atoms with the central atom at the apex, $\theta$, and the distances between the central atom and the selected atoms, $r$, are calculated. This is repeated for all target atoms within the cutoff (dashed line). Three key structural contributions are shown here with an example target atom in red. The “same-side” tail (A), “opposite-side” tail (B) and “other” tail (C). Below each diagram the locations of the main contribution to the probability distribution by each of these different tail contributions are indicated (D, E, and F, respectively). The same tail contributions are marked with arrows, labeled showing the peak density and contributing atom (from the central atom shown). The “other” tail is much more diffuse and contributions from single atoms are less resolvable, so this is indicated by the black ellipse showing the contributed region. The same-side contributions are radially offset relative to the opposite side because the nearest neighbor atom is not included. To see this figure in color, go online.

Here, $g_3$ was applied on the carbon atoms of the DPPC molecules in two ways: 1) to calculate the bilayer average including both inter- and intramolecular contributions, and 2) to analyze each DPPC molecule individually, only assessing the intramolecular contributions. Each $g_3$ distribution was time averaged across a 50 ns simulation window to create a short timescale snapshot of the local structure under the assumption that this is less than the characteristic timescale of a lipid conformational transition. For the calculation of $g_3$, 401 radial and 201 angular bins were used with a cutoff of 7 Å. The cutoff was chosen to be greater than the packing distance (29) to capture the salient structural details. Above a critical value capturing the nearby chain contributions, the analysis was not sensitive to the choice of cutoff value. The nearest neighbor distance was determined using a distance-based metric, defined using the minimum of the first peak of the radial distribution function, although other criteria, including direct calculation, can also be used (27).

Fig. 1 shows three structural details specific to the DPPC carbon atoms. Fig. 1, A and B show two cases of bonding within the chosen tail. This is relative to the nearest neighbor; since the nearest neighbor is not included in the distribution, the same-side contributions are shifted. The distinct peaks in the distributions correspond to the atom $n$ bonds away from the central atom on the opposite side and $n+1$ bonds away on the same side. The first peak in both cases picks up the adjacent atom angular component and hence does not split. For $n\ge 2$, in a bonded chain, there are increased degrees of freedom which allow peak splitting. Fig. 1 C shows the packing of other tails. This is the contribution from the carbon atoms in a different lipid tail to the central atom. This could be the other tail of the same lipid or that of a neighboring lipid.

An important benefit of using $g_3$ compared with other metrics is that the important structural differences are emergent rather than requiring a molecule- and system-specific intuition. This allows for a workflow that is independent of the system analyzed and capable of identifying structural changes in any molecules. Many other metrics apply a priori knowledge to the system and therefore provide a less general solution. This workflow only applies the assumption that structural differences exist, not what those specific structural differences might be.

Lipid clustering and lipid similarity

To compare the $g_3$ distributions of individual lipids with each other, the mean structural similarity index metric (SSIM) (30) was applied. SSIM was originally developed as a metric for determining the similarity of images. Here the images are the $g_3$ distribution matrices as computed above for each of the individual lipids. SSIM is unique compared with many other metrics in that it combines three quantities to determine the similarity metric and, in addition, these quantities are evaluated locally.

The three quantities in the original paper were luminance, contrast, and structure (30). In the case of lipid $g_3$ probability distributions, the differences in mean probability, standard deviation, and spatial probability distribution are used. The SSIM can be defined in each of the local windows as

$$\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}\left(x,y\right)=\frac{\left(2{\mu }_x{\mu }_y+c_1\right)\left(2{\sigma }_{xy}+c_2\right)}{\left({\mu }_x^2+{\mu }_y^2+c_1\right)\left({\sigma }_x^2+{\sigma }_y^2+c_2\right)}\text{,}$$ (1)

where $x$ and $y$ refer to the window in each distribution matrix, $\mu$ is the window mean, ${\sigma }^2$ is the variance of the window, ${\sigma }_{xy}$ is the covariance of the two windows, and $c_1$ and $c_2$ are small correction factors to avoid division by zero. The final SSIM is the average over the local windows reducing the two distributions to a scalar value in the range 0–1, with 1 being the result of comparing two identical distributions with the value decreasing the less similar the two distributions are:

$$\text{SSIM}=\frac{1}{N}\sum _{i=1}^N\text{SSIM}\left(x_i,y_i\right)\text{,}$$ (2)

where $x_i$ and $y_i$ are the $i^{\text{th}}$ window in matrices $x$ and $y$, and $N$ is the total number of windows. This was applied to all simulated systems. The data range was set to the maximal density value in all compared $g_3$ distributions. A window size of 7 bins was used. It was verified that the result was independent of the window size.

The $g_3$ distributions from the 11 simulations of 512 lipids each $\left(N_{\text{lipid}}=5632\right)$ were used to sample the conformational phase space. This generated $N_{\text{lipid}}$ features (similarity scores) for each of the lipids in the system. The features were combined into an $N_{\text{lipid}}\times N_{\text{lipid}}$ similarity matrix. For the analysis of all 512 lipid systems, this corresponds to a similarity matrix of size $5632\times 5632$, where each row in the similarity matrix represents a vector containing the SSIM between the lipid and every lipid being analyzed (including itself). When comparing individual lipids with each other the SSIM values were in the range 0.4–1. The difference here compared with other works is that other ML techniques build feature matrices like this by using predefined distances between predefined atoms (5,31,32). Here, the natural length scales emerge spontaneously from the system and its properties via $g_3$.

Unsupervised machine learning

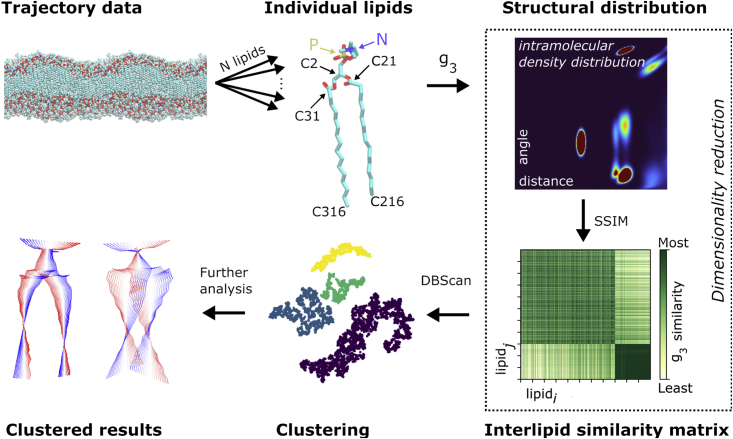
After generating the similarity scores, dimensionality reduction was performed by applying the t-distributed stochastic neighbor embedding (t-SNE) (33) method with a randomized initial embedding to the $5632\times 5632$ similarity matrix. This reduced the similarity matrix to two-dimensional (2D) embedded representation which was scaled to have unit variance. The unsupervised ML clustering algorithm called density-based spatial clustering of applications with noise (DBScan) (34) was applied to the 2D data. DBscan was chosen instead of the commonly used $k$-means (35) clustering, since in DBScan the number of clusters is not predefined but emerges from the data. Second, and very importantly, in contrast to $k$-means, DBScan is able to find clusters that are nonlinearly separable. DBScan needs a neighborhood defined by the parameter $\epsilon$. A value of 0.085 was used here, but this will vary based on the system analyzed. The selection of a suitable $\epsilon$ is key to identifying all the clusters. This value was selected and verified by using the “elbow plots” (34), by visual inspection of the scaled dimensionally reduced data colored according to the clusters, a plot of the similarity matrix reduced to 2D via PCA, and confirmed by examination of the $g_3$ distributions of the lipids. Feature extraction from the clusters was completed by visualizing the $g_3$ distributions within each cluster to determine the locations of density differences. The lipids within each of the clusters were then identified and further analyzed, as will be discussed below. Fig. 2 summarizes the data analysis and clustering process.

Figure 2.

Conformational clustering. First, each lipid (some of the important atoms are marked) is isolated from the trajectory and is calculated to quantify the intramolecular structure. The mean structural similarity index metric (SSIM), Eq. 2, of each lipid $g_3$ distribution is compared with all other lipids. Embedding with t-SNE (33) reduces the matrix of similarity values to a 2D form (from $N_{\text{lipids}}$ dimensions). These 2D data are clustered using DBScan (34) to find similar conformational groupings. This is mapped back onto the bilayer for further analysis. The similarity matrix shows how similar the distribution of row $i$ is with the distribution of row $j$. The distinct difference in the final quarter of the similarity matrix is a result of passing over the phase transition and the large conformation difference this causes. To see this figure in color, go online.

Structural details from $g_3$ analysis and the main phase transition

The particular strength of $g_3$ is that it is able to detect and quantify structural motifs and changes within the DPPC lipid tails without any a priori knowledge of the underlying lipids, structural metrics, or connectivity. The algorithm sees merely the system as a monatomic cloud of atoms. Details such as tail bonding, packing, and conformational properties emerge spontaneously in the distributions; this analysis could be applied to any molecule or system undergoing structural changes and help aid in the determination of system structure without prior knowledge of the structural properties relevant to the molecule. Although not shown in this work, the system sizes in the analysis are not constrained to being the same. Since the lipids are processed and treated individually, through careful treatment to ensure the same normalization, lipids from systems of different sizes can be compared together. Care should be taken to ensure finite size effects do not introduce artificial results.

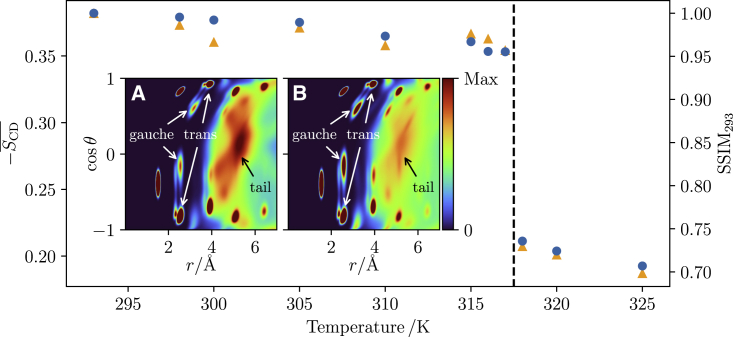
Fig. 3 shows temperature dependence of the conventional deuterium order parameter $\left(S_{\text{CD}}\right)$ and $g_3$ using both intra- and intermolecular contributions. $S_{\text{CD}}$ measures the ensemble average orientation of the C–H bond vector $\left(\theta \right)$ with the bilayer normal ($z$ axis) as $S_{\text{CD}}=\frac{1}{2}⟨3{\cos }^2\theta -1⟩$. The phase-transition temperature detected by these two independent metrics is identical, between 317 K and 318 K. This is slightly above the experimental values of about 314 K (36,37,38) but consistent with other simulations using the CHARMM36 force field (39).

Figure 3.

Phase transition, in simulations of systems containing 512 lipids, detected by the average deuterium order parameter, $\overline{S_{\text{CD}}}$ (orange) and using $g_3$ similarity relative to the 293 K system (blue). Both deuterium order parameter and $g_3$ similarity (SSIM) are able to detect a phase change between 317 K and 318 K. Insets: probability density distributions for $g_3$ of the DPPC carbon atoms of all lipids in the simulation at 317 K (A) and 318 K (B). The dihedral gauche and trans peaks are marked along with the contribution by the other tails. To see this figure in color, go online.

The inset in Fig. 3 shows $g_3$ distributions below (317 K) and above (318 K) the phase transition. The distributions display two key features: firstly, and most obviously, the influence of the other tails on the distribution (see the discussion in connection with Fig. 1). Below the transition the lipid tails are packing in rigid, fixed positions, producing a sharper peak which drops off at larger distances. Above the transition this peak becomes much more diffuse, with lower peak height and spread across a longer distance, reducing the level of dropoff compared with the more ordered lipids.

The second noticeable difference is in the trans/gauche peaks. Below the transition, the gauche peak density is significantly reduced when compared with above. The ordered lipids show less gauche dihedrals in the tails, a well-reported metric for determining the main phase transition. The phase transition can easily be verified even by visual inspection: As the temperature decreases below $T_{\mathrm{m}}$, it switches from a flat, planar bilayer to a kinked one with regions of different thickness and of asymmetric lengths (Fig. 4). This was robust, and all bilayer sizes and system temperatures below $T_{\mathrm{m}}$ adopted a ripple conformation with the exception of one of the 128-lipid systems, which has been noted as a finite size effect (14). The simulations above $T_{\mathrm{m}}$ were consistent with experimental and simulation results for the fluid phase (12,16,20). Below $T_{\mathrm{m}}$, a thorough experimental quantification of a DPPC ripple phase is lacking; however, the major arm gel-like region has a thickness consistent with experimental quantification of a gel-phase lipid bilayer (40), and the minor arm thinning is in qualitative agreement with experimental work on the short-chained dimyristoylphosphatidylcholine (DMPC) lipid in the ripple phase (4). The ripple amplitude, the maximum difference between the average phosphate $z$ position averaged over 10 Å windows parallel to the ripple wavelength, was also consistent with the DMPC ripple phase data (4).

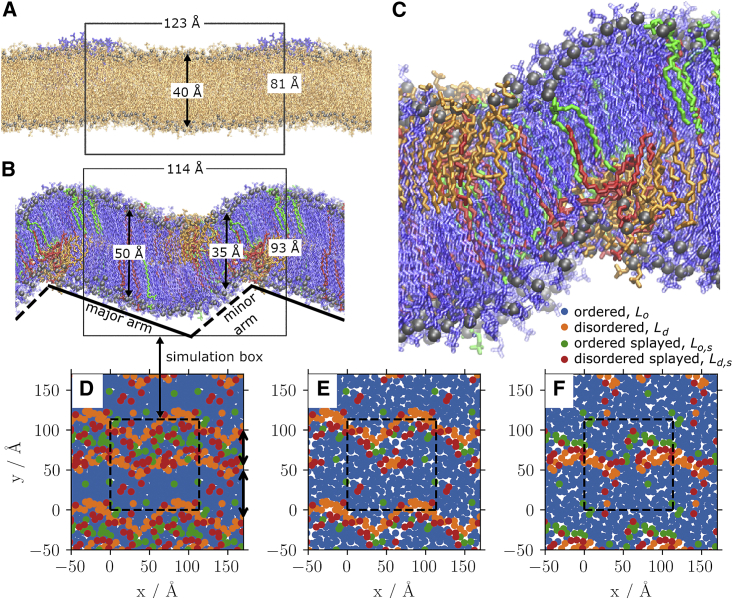
Figure 4.

Side profile snapshots from the 512 lipid simulations at 318 K (A) and 317 K (B), either side of $T_{\mathrm{m}}$ (see Fig. 3). (C) A zoomed-in snapshot of the ripple in the 512 lipid, 317 K system shown in (B). All snapshots are colored according the conformational cluster the lipid has been assigned. The ripple phase features two regions, the major arm (solid line) and the minor arm (dashed line). (D–F) Top views of the 317 K system. (D) The sum of the two leaflets; (E and F) the upper and lower leaflet, respectively. The simulation box is indicated in the figures by the box, and periodic images are included for visual clarity. The ripple has an amplitude of 19.2 Å. For comparison, the thickness perpendicular to the major arm (44 Å) is consistent with experimental values for the DPPC gel phase (40), and the tilt in the major arm is also consistent with experiments using DMPC (4,41). The two arms are asymmetric in length, in agreement with experiments and theory (1,2,42,43). To see this figure in color, go online.

The structure of the ripple phase

While the system-wide $g_3$ is capable of detecting the phase transition on a system-wide scale, the ripple phase is not homogeneous. The structure of the ripple phase can, however, be analyzed by examining the lipid-wise $g_3$ and comparing the interlipid similarity. Importantly, clustering (using DBScan) revealed four distinct conformational motifs for lipids: disordered $\left(L_{\mathrm{d}}\right)$, ordered $\left(L_{\mathrm{o}}\right)$, ordered splayed $\left(L_{\mathrm{o},\mathrm{s}}\right)$, and disordered splayed $\left(L_{\mathrm{d},\mathrm{s}}\right)$. These structural motifs emerged in both the 512-lipid systems and were confirmed in the large 4096-lipid systems but only three of them appeared in the 128-lipid system, with no differentiation between the ordered-splayed and disordered-splayed lipids; as recently pointed out by Walter et al., finite size effects can be significant in lipid systems (14). The 512-lipid systems that we focus on here have a minimal, ripple-forming system size with features consistent with experimental results.

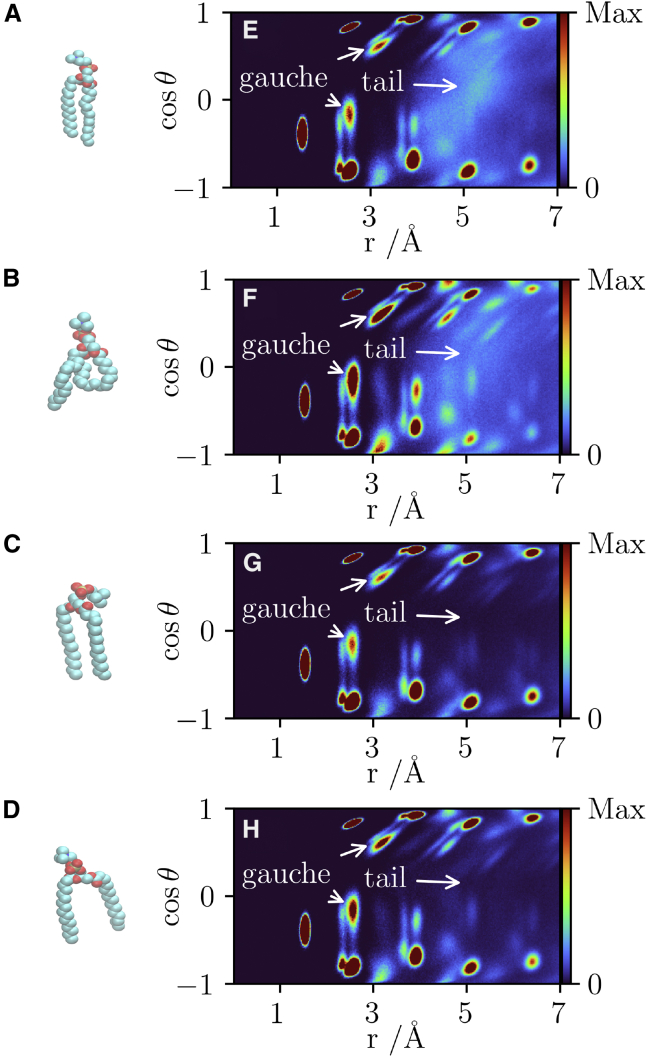
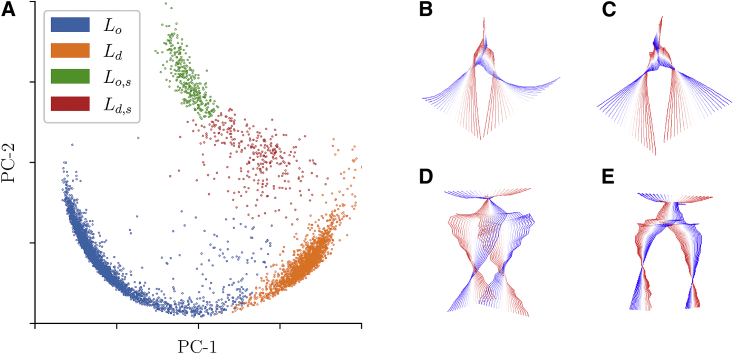
An example of each of these lipid conformations and the $g_3$ distribution of this is shown in Fig. 5. The unsplayed-splayed behavior is captured by the lipid tail contribution and the ordered-disordered behavior by the gauche defects. Quantifying the degree of difference in the splayed and unsplayed lipids, the splay angle of the lipid was calculated. It is defined as the angle between atoms C316, C2, and C216 as labeled in Fig. 2. The most probable value of the splay angle for each of the clusters differs (the maxima of the probability density). The unsplayed lipids, both ordered (13.73° $\pm$ 0.16°) and disordered (16.51° $\pm$ 0.55°) had a significantly smaller splay angle than the splayed-ordered (24.81° $\pm$ 0.19°) and splayed-disordered (26.13° $\pm$ 0.56°) lipids. Standard errors were calculated using the bootstrap algorithm with 9999 resamples (23). The conformational dynamics of each of the lipid clusters was assessed with lipid PCA (26). Fig. 6 shows the main component of each of the lipid clusters. The disordered lipids’ ($L_{\mathrm{d}}$ and $L_{\mathrm{d},\mathrm{s}}$) main motion is a scissoring motion, which has been seen in the fluid-phase DPPC lipids in a range of force fields (26). The ordered ($L_{\mathrm{o}}$ and $L_{\mathrm{o},\mathrm{s}}$) lipids instead have their tails constrained and primarily have a twisting rotational motion. All of the four components are fully distinct.

Figure 5.

Exemplary lipid from each of the identified clusters taken from the 512 lipid, 315 K simulation. A linear-ordered lipid (A), disordered lipid (B), splayed-ordered lipids (C), and splayed-disordered lipids (D). The corresponding $g_3$ distributions of the atoms in these individual lipids are also shown. (E), (F), (G), and (H) correspond to (A), (B), (C), and (D), respectively. The first gauche defect peaks (up and down tail) are marked with arrows, and the contribution of the other tail peak is marked with an arrow for clarity. To see this figure in color, go online.

Figure 6.

(A) Principal component reduction of the lipid similarity SSIM matrix showing the first PC-1 and second PC-2 components. Each of the points represents a lipid from the simulations of 512 lipids and is colored according to the cluster it was assigned to. (Right) The first (most dominant) principal component from the lipid motion principal component analysis for $L_{\mathrm{d}}$ (B), $L_{\mathrm{d},\mathrm{s}}$ (C), $L_{\mathrm{o}}$ (D), and $L_{\mathrm{o},\mathrm{s}}$ (E). The key motion in the disordered conformations (B and C) adopts a similar scissoring/splaying tail motion. In contrast, the ordered conformations (D and E) adopt a twisting rotational motion. The color scheme goes from red to white to blue, showing the conformational change associated with the first principal component of the lipid motion. To see this figure in color, go online.

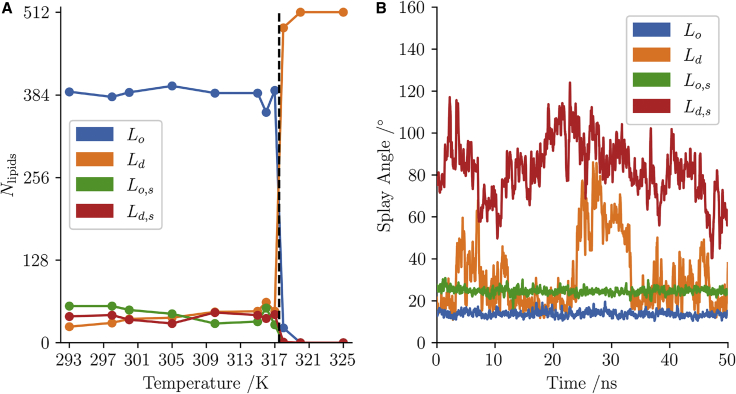
Above $T_{\mathrm{m}}$ the major component is the widely studied disordered lipid. Below $T_{\mathrm{m}}$, however, the complex, heterogeneous nature of the ripple phase becomes apparent, with the spatial ordering, laterally within a leaflet and asymmetrically across the leaflets, being key to the ripple. The obvious question is: do these four distinct conformations exist and have finite lifetimes? The number of lipids in each of the clusters as a function of temperature is shown in Fig. 7 A, and the time dependence of the splay angle of each of the four species for one of the lipids at 315 K is shown in Fig. 7 B. As the figure shows, all of the components are present in the ripple phase and disappear in the disordered phase. Fig. 7 B further shows that the components are clearly distinct. The disordered lipid (orange) switches its angle as can be expected. The other three components are very clearly present for extended times.

Figure 7.

Number of lipids in each cluster at each simulation temperature for simulations of 512 lipids (A) and the splay angle of an example lipid from each of the clusters (B) taken from the 315 K simulation. The black dashed line shows the phase-transition temperature between 317 K and 318 K. The bulk lipid in each case is the linear lipid, ordered below the transition temperature and disordered above. Below $T_{\mathrm{m}}$ there exists disordered lipids and splayed lipids. By 320 K the only lipid component is the lipid disordered. The example splay plots show one of the key emergent differences between the clusters: the $L_{\mathrm{o}}$ and $L_{\mathrm{o},\mathrm{s}}$ lipids both have a low variance whereas the $L_{\mathrm{d}}$ and $L_{\mathrm{d},\mathrm{s}}$ lipids are highly mobile and show short time fluctuations. The $L_{\mathrm{d}}$ lipid can bee seen to transition to a splayed conformation briefly at 25 ns but returns to the more linear nature within 10 ns. Since $g_3$ is a time-averaged property the clustering is assigned on the basis of majority of time rather than instantaneous value. This transition behavior of a lipid was not a common occurrence. To see this figure in color, go online.

Discussion

In this study, we have applied a new radial-angular three-particle correlation function in combination with unsupervised ML to examine the phase transitions in DPPC lipid bilayers using data from atomistic MD simulations. The analysis revealed the presence of four distinct conformational populations of lipids in the ripple phase of DPPC lipid bilayers. The expected ordered and disordered lipids are found along with their splayed equivalents. The analysis using $g_3$ showed distinct differences in their gauche distribution and tail packing. PCA further confirmed the existence of these four lipid groups. Finite size effects influenced smaller (128 lipid) bilayers and only three clusters were identified, with no differentiation between the ordered-splayed and disordered-splayed lipids. The splayed lipids exist to stabilize the interface mismatch. To cover the interface region in smaller bilayer systems, a higher ratio of the lipids must be melted to splayed disordered. This was not the case in the small 128-lipid systems and thus those systems were influenced by finite size effects.

In a recent study, Walter et al. (5) also applied ML to study the main phase transition in DPPC bilayers. One fundamental difference between Walter et al. and our study is that they used supervised ML and trained their algorithm to distinguish between two predefined lipid conformations, fluid or gel. In our case we used unsupervised ML, and the number of lipid conformational categories was not fixed beforehand but emerged from data.

The structure of the ripple phase has remained an open question, and in their 2015 study Akabori and Nagle (4) state that the ripple structure that emerges from their scattering data does not agree with the ripple consisting of interdigitating ordered lipids as has been reported by several previous simulations (e.g., (10,11)). Akabori and Nagle dismissed the possibility of interdigitation of ordered lipids being the dominant behavior in the thinner minor arm, since the observed electron density is inconsistent with that scenario on a large enough scale. Instead, they proposed that the major arm consists of the usual ordered gel-like lipids and then hypothesized that the minor arm has five other lipid types of variable lengths and packing. Those lipids were classified as “more fluid than the gel phase” or intermediate, and suggested to exist on both sides of the minor arm. They did not elaborate these five additional lipid types further.

Our results contribute to the understanding of the nature of the ripple phase by providing atomistic insight into the different conformational structures of lipids in the ripple phase. First of all, as discussed above, conformational clustering using unsupervised ML (Fig. 2) revealed four distinct classes of lipids whose existence were subsequently verified by PCA. As Fig. 4, B and C show, disordered (orange) and disordered-splayed (red) lipids cluster in the groove region of the ripple only. This is unlike what has been suggested by Akabori and Nagle (4) based on x-ray scattering and by Khakbaz and Klauda (12), based on their MD simulations using 72 lipids, that the two sides of the ripple are symmetric in terms of lipid conformations (the two arms are asymmetric); specifically, that most fluid lipids are bounded on either side by fewer fluid lipids, forming an interface between the ordered lipids. Ordered lipids, as in the major arm, are not implicated to be a major component of the minor arm. In this work, the disordered lipids are bounded on one side by splayed lipids, but on the other side are the ordered lipids with no intermediate interface. Across the two leaflets this is a counter-parallel feature, combining to create a minor arm bounded on both sides by disordered lipids, in opposing leaflets but consisting of a mixture of ordered and more fluid lipids. As evident in Fig. 4, the convex part has the usual ordered (blue) and some ordered-splayed (green) lipids with some of them also distributed in the planar, gel-like regions. Furthermore, outside the disordered region, the minor arm consists of the usual ordered lipids (blue). Fig. 4, D–F also reveal that splayed lipids, both ordered and disordered splayed, tend to be present only on the minor arm side of ripple. The splayed lipids act as intermediates between the ordered and disordered lipids. The disordered-splayed lipids often adopt a conformation with one of the tails relatively ordered and the other much more fluid, seemingly half transitioned, forming an interfacial layer in the ripple. As Fig. 4 C also shows, there is some interdigitation but the presence of the fluid phase is the key here and clarifies the picture of Akabori and Nagle (4). In addition, Fig. 4, E and F show that the idea of dislocation lines consisting of lipids in the fluid phase put forward by Heimburg (44) over 20 years ago is indeed a very good description of the ripple phase. Although not addressed in the current article, we would also like to point out that the main phase transition has hysteresis, and the wavelength and symmetry of the ripples depends whether the transition is approached from below or above the main phase transition temperature (45).

The existence of the four distinct classes of lipids and their unique distribution in the convex and concave side of the ripple also show the shortcomings of current leading theories (42,43,46). While several of them do predict the ripple phase and the existence of the two arms of different lengths, none of them addresses the ripple structure or the asymmetry across the ripple. Coupling between the two leaflets and incorporation of the behavior of individual lipids appear to be the major issues that need to be addressed in future theories.

Author contributions

M.K. conceived the work; M.D., A.A.G., and A.D.R.-F. carried out the simulations and analyzed data; All authors wrote the manuscript; M.K. and D.F. supervised the project. All authors contributed to critical feedback on the manuscript and analysis.

Editor: Rumiana Dimova.

Data availability

Trajectory data are available from the authors upon request.