Significance
Economic experiments typically find that cooperation collapses. Yet paradoxically, if groups are asked to play again, cooperation resumes. This “restart effect” is puzzling because individuals are thought to be learning in games, either about their groupmembers, or about the payoffs in an unfamiliar setting, so why would anyone “restart”? We show that individuals only restart if they can either influence their groupmates' behavior or because they know that their groupmates will cooperate at high levels. Crucially however, we controlled for altruistic motivations by using computerized groupmates programmed to either increase or decrease their cooperation over time. Individuals tracked these changes, even though they knew they were playing with computers, suggesting that their cooperation levels reflect confusion, not altruism.
Keywords: Altruism, conditional cooperation, confusion, public goods game, social preferences
Abstract
Do economic games show evidence of altruistic or self-interested motivations in humans? A huge body of empirical work has found contrasting results. While many participants routinely make costly decisions that benefit strangers, consistent with the hypothesis that humans exhibit a biologically novel form of altruism (or “prosociality”), many participants also typically learn to pay fewer costs with experience, consistent with self-interested individuals adapting to an unfamiliar environment. Key to resolving this debate is explaining the famous “restart effect,” a puzzling enigma whereby failing cooperation in public goods games can be briefly rescued by a surprise restart. Here we replicate this canonical result, often taken as evidence of uniquely human altruism, and show that it 1) disappears when cooperation is invisible, meaning individuals can no longer affect the behavior of their groupmates, consistent with strategically motivated, self-interested, cooperation; and 2) still occurs even when individuals are knowingly grouped with computer players programmed to replicate human decisions, consistent with confusion. These results show that the restart effect can be explained by a mixture of self-interest and irrational beliefs about the game’s payoffs, and not altruism. Consequently, our results suggest that public goods games have often been measuring self-interested but confused behaviors and reject the idea that conventional theories of evolution cannot explain the results of economic games.
Economic games are often used to measure if individuals are willing to make sacrifices for the benefit of strangers (1–10). In the public goods game, individuals must decide how much to contribute to a group fund which is personally costly but benefits the group (11). Hundreds of experiments have found that average contributions begin at intermediate levels but then gradually decline if the game is repeated (12). Debate has continued for decades over whether these results, and thus human social behaviors more generally, are best explained by either altruistic (“prosocial”) or self-interested motivations (12–23).
The altruistic explanation often posits that contributions are motivated by a uniquely human desire to make sacrifices on behalf of the group and to conform with local levels of cooperation (1, 2, 4, 8, 21, 24, although see refs. 25–27). Initial contributions then unravel as disappointed cooperators learn that others are not as cooperative as they mistakenly thought (Conditional Cooperators hypothesis) (1, 4, 8, 12, 21). This altruistic interpretation assumes individuals fully understand the game and that the outcomes of their costly decisions can be used to infer their social motivations/preferences (28). For example, if individuals pay costs that benefit others in circumstances where they can never recoup those costs, as is common in economic experiments, then this approach assumes the behavior is evolutionarily altruistic (1, 2, 28–32)*. Consequently, the altruistic explanation often invokes new evolutionary theories to accommodate such altruistic behaviors via various forms of group selection (1, 2, 33, 34).
In contrast, the self-interested explanation posits that individuals initially contribute either to try to stimulate future reciprocal contributions in others (Strategic Cooperators hypothesis (35–38)), and/or out of a sense of confusion or uncertainty about the game’s payoffs (Confused Learners hypothesis, (12)). Contributions then decline as either the potential for future cooperation diminishes, or as confused individuals gradually learn about the game’s payoffs (12, 39). This approach assumes individuals are not well adapted to laboratory experiments, but that behavior will become more economically/evolutionarily rational with sufficient experience or in more realistic experiments (12, 17, 20, 23, 32, 40–43).
Although there is growing evidence that confusion and learning is important in public goods games (12–15, 19, 20, 22, 23, 26, 27, 39, 44–47), such conclusions are challenged by one intriguing phenomenon, the “Restart Effect” (21). When players in repeated public goods games are surprisingly told, after the final round, that they will play again, cooperation tends to immediately increase (36, 48–52). At first glance, this phenomenon seems to refute the idea that individuals are learning about the game’s payoffs and consequently favors the altruistic hypothesis by default (21). If individuals are learning about payoffs, then surely they would not increase their contributions after a restart, one could argue (21).
However, this argument is incomplete and unsatisfactory, for it does not explain why altruistic individuals, that like to cooperate with cooperators, would also increase their contributions after having just learned that people are not as cooperative as they thought. One hypothesis is that cooperators become more optimistic about their groupmates for the restart but this does not explain why they become more optimistic (52). In essence, both the Confused Learners and the Conditional Cooperators hypotheses posit that individuals are learning, either about the game’s payoffs in an unfamiliar environment, or about the cooperative nature of humans. It is therefore unclear why either hypothesis would predict a restart. In contrast, Strategic Cooperation could be favored at the start of a new game if there are repeated interactions and/or reputational benefits (35, 36). Resolving the restart-effect phenomenon is therefore crucial to solving the debate over whether humans are altruistic or self-interested in social dilemmas (8, 21, 53).
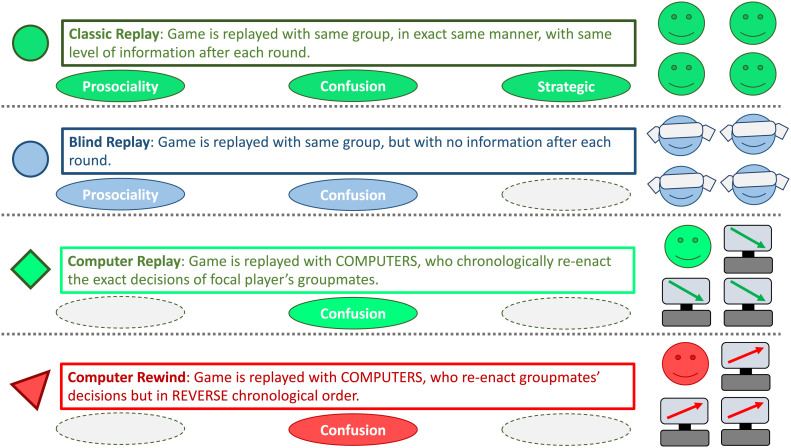
Here we test if the restart effect is driven by either altruistic or self-interested motivations, that may or may not be confused. We replicated the most common payoff parameters for linear public good games (12). Individuals could contribute up to 20 monetary units per round (20 MU = 0.5 Swiss Francs CHF). Individual contributions led to a group gain of 60% but also a personal loss of 60%. First, we made groups of four individuals play this public goods game together for nine rounds. We used constant groups (“partner” matching) rather than randomly shuffled groups each round (“stranger” matching) because prior research has shown that the restart effect only reliably occurs in constant groups (36, 48, 52). We then told each group that they would replay the nine-round game, and depending on randomly assigned session, this was either in the same manner as before (Classic Replay treatment), or according to one of three control conditions (Fig. 1). These control treatments allowed us to test if the size of the restart effect depended upon the possibility for social concerns and/or strategic cooperation (N = 80 individuals from 20 groups of four randomly assigned to each treatment).
Fig. 1.
Experimental design. We had four treatments, randomly assigned. In the Classic Replay, increased contributions can be explained by prosociality, confusion, and/or strategic investments. In Blind Replay, contributions are invisible, so participants cannot shape the behavior of their groupmates, eliminating strategic investments. In the Computer Replay and Computer Rewind treatments, individuals can neither affect the behavior or the welfare of their groupmates, who are computers, thereby eliminating both prosocial and strategic explanations. The relevant restart treatment was explained to participants before round one of the restart.
Results and Discussion
Our first control treatment allowed us to test the role of strategic cooperation. We compared a classical restart test, where the game is simply and surprisingly replayed in the same manner as before (Classic Replay), against a control treatment that removed all feedback on contributions and payoffs between each round of the second game (Blind Replay). If the restart effect is driven by optimistic beliefs among conditional cooperators trying to match their groupmates’ contributions, then they will increase their contributions in either treatment (52). However, by removing all feedback in the Blind Replay, we removed all possible reputational or signaling benefits and prevented participants from influencing the behavior of their groupmates. Therefore, if the restart is driven by strategic cooperation, or general reputation/audience effects (54, 55), then the Blind Replay treatment will not have a restart effect (35–38).
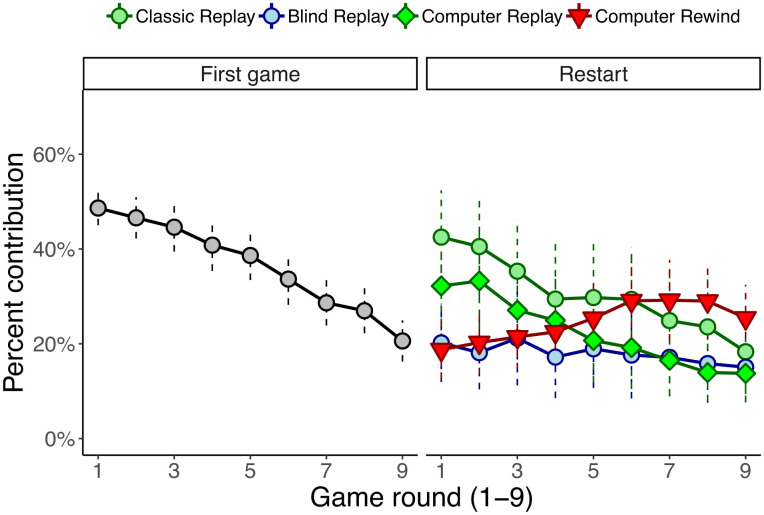
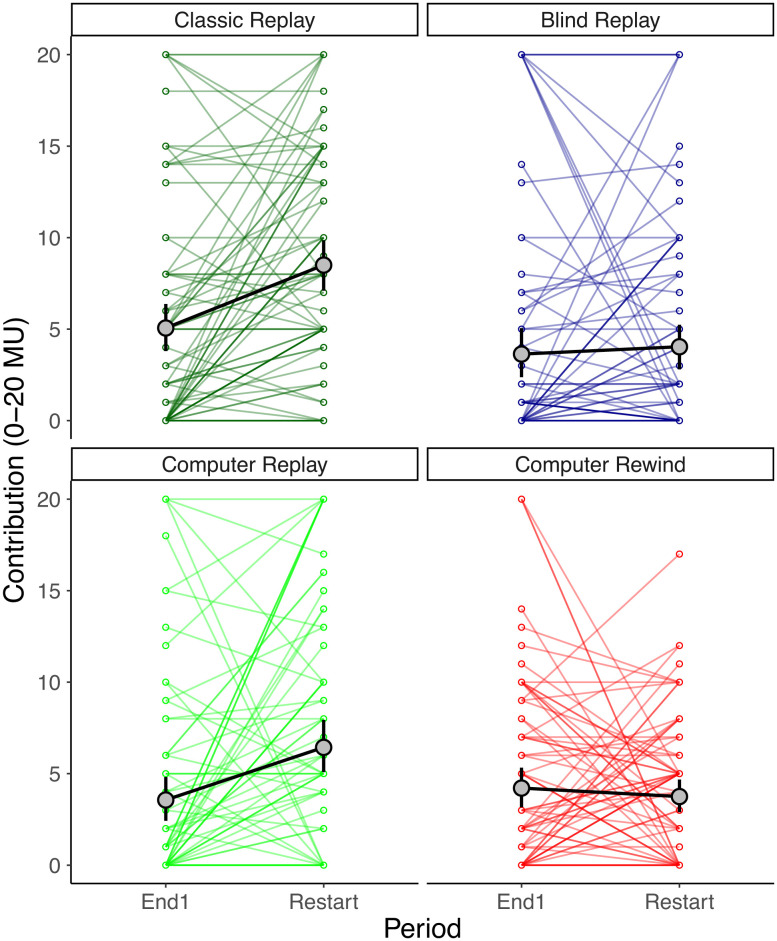
In support of the strategic cooperation hypothesis, we found that the restart effect was significantly larger in the Classic Replay treatment than in the Blind Replay treatment (LMM: t = 3.2, df = 80.0, P = 0.002, Table 1 and Figs. 2 and 3). In fact, a significant restart effect only occurred in the Classic Replay treatment and not in the Blind Replay treatment (Fig. 2 and SI Appendix, Fig. S1). Specifically, mean group contributions in the Classic Replay treatment significantly increased for the restart by 17 percentage points from 25 to 42% (Linear mixed model (LMM) on group means, LMM: Estimated increase ±SE = 17.2 ± 3.36%, t = 5.1, df = 80.0, P < 0.001, Table 1). By contrast, in the Blind Replay treatment, mean contributions only increased from 18 to 20% (4.0 MU), a non-significant increase of just 2 percentage points (LMM: Estimated increase ±SE = 2.0 ± 3.36%, t = 0.6, df = 80.0, P = 0.553]. Significantly more individuals increased their contribution for the restart in the Classic Replay treatment than in the Blind Replay treatment (57.5% versus 32.5%; 46/80 versus 26/80, Fisher’s Exact Test: P = 0.002, Fig. 3).
Table 1.
Restart effects
| Fixed effect | Estimate ± SE | Df | t-value | P-value |
|---|---|---|---|---|
| Intercept (Classic Replay) | 25.3 ± 4.07 | 111.6 | 6.2 | <0.001 |
| Blind Replay | -7.1 ± 5.75 | 111.6 | -1.2 | 0.218 |
| Computer Replay | -7.5 ± 5.75 | 111.6 | -1.3 | 0.195 |
| Computer Rewind | -4.3 ± 5.75 | 111.6 | -0.7 | 0.461 |
| Restart (Classic Replay) | 17.2 ± 3.36 | 80.0 | 5.1 | <0.001 |
| Restart*Blind Replay | -15.2 ± 4.75 | 80.0 | -3.2 | 0.002 |
| Restart*Computer Replay | -2.8 ± 4.75 | 80.0 | -0.6 | 0.556 |
| Restart*Computer Rewind | -19.5 ± 4.75 | 80.0 | -4.1 | <0.001 |
LMM on mean group contributions in the end of the first game and the start of the restarted game (reference treatment has been set to Classic Replay, values converted from MU to percentage contributions, N = 20 groups per treatment, model controls for group as a random effect).
Fig. 2.
Restart effects. Data show the mean contributions for the first game for all groups (N = 80 groups, grey circles); or for when individuals simply replayed the same game according to their randomly assigned restart treatment (Fig. 1). Dashed vertical lines show 95% confidence intervals based on group mean contributions. N = 20 groups for each restart treatment.
Fig. 3.
Individual restarts. Individual contributions in round 9 of the first game (“End1”) and the first round of the second game (“Restart”). Unique individuals are connected by straight colored lines. Overall means in grey circles with 95% confidence intervals are connected by thick black lines.
Further supporting the strategic cooperation hypothesis, we found that contributions gradually declined toward the end of the game in the Classic Replay treatment but not in the Blind Replay treatment (Fig. 2; LMM controlling for group: Classic Replay estimated decline ±SE = 2.8 ± 0.42 percentage points per round, df = 80.0, t = −6.6, P < 0.001; Blind Replay estimated decline ±SE = −0.6 ± 0.42, df = 80.0, t = −1.4, P = 0.170, Table 2). By the end of the experiment, when there was no longer the possibility of strategically investing in the future cooperation of groupmates, contributions had converged to approximately the same level of around 15–18% (Welch two sample t test on group mean contributions in final round: t = 0.6, df = 36.7, P = 0.561, estimated samples = 3.7 MU and 3.0 MU, 95% CI of difference = [−1.59, 2.89], Fig. 2).
Table 2.
Contributions over time
| Fixed effect | Estimate ± SE | Df | t-value | P-value |
|---|---|---|---|---|
| Intercept: Computer Replay | 35.6 ± 4.39 | 80.0 | 8.1 | <0.001 |
| Computer Rewind | -17.3 ± 6.21 | 80.0 | -2.8 | 0.007 |
| Classic Replay | 8.8 ± 6.21 | 80.0 | 1.4 | 0.159 |
| Blind Replay | -14.8 ± 6.21 | 80.0 | -2.4 | 0.020 |
| Game Round: Computer Replay | -2.6 ± 0.42 | 80.0 | -6.3 | <0.001 |
| Computer Rewind | 3.9 ± 0.60 | 80.0 | 6.5 | <0.001 |
| Classic Replay | -0.2 ± 0.60 | 80.0 | -0.3 | 0.782 |
| Blind Replay | 2.1 ± 0.60 | 80.0 | 3.4 | <0.001 |
LMM on mean group contributions during the nine rounds of the restarted game (reference treatment has been set to Computer Replay, values converted from MU to percentage contributions, N = 20 groups per treatment, model controls for group as a random effect).
In isolation, this result would suggest strategic cooperation (be it either consciously or subconsciously triggered) can explain the entirety of the restart effect (Fig. 2). While we consider this unlikely, the results do suggest that contributions in the early rounds of finitely repeated public goods games are inflated by the shadow of the future. Some individuals perhaps initially invest strategically but then taper their investments as the potential returns on strategic investments decrease. When the game is surprisingly restarted, they repeat their behavior (Fig. 1). When individuals know that their decisions can only affect the final earnings of their groupmates, but not their behavior, they contribute at significantly lower levels. This can also explain why studies where behavior is visible after each round have found that the restart effect is much more pronounced among constant groups compared to groups that are randomly shuffled each round (51, 52). In constant groups, there are repeated interactions (albeit anonymous) so it can appear financially worthwhile to try and shape the behavior of one’s groupmates. These results add to the hypothesis that the psychology of human cooperation has largely been shaped by repeated interactions with opportunities for signaling or reputational benefits (56–58). No altruistic nor prosocial concerns are required to explain this pattern of results.
The lack of a restart effect observed in the Blind Replay treatment above could also be due to conditional cooperators, for some unexplained reason, being more pessimistic about their groupmates in the Blind Replay treatment (4, 52, 59, 60). Although many studies on conditional cooperation elicit individual beliefs about their groupmates’ contributions (4), we did not because 1) doing so could shape the very behavior we are investigating, and 2) prior research has shown that soliciting beliefs tends to eliminate the restart effect, i.e., the phenomenon we are investigating (50, 52, 61). Instead, our next treatments, Computer Replay and Computer Rewind, controlled for the role of beliefs without affecting social preferences by fixing what the contributions of computerized groupmates would be.
In our Computer Replay treatment, we made participants play with computerized groupmates that would perfectly repeat the history of the focal player’s groupmates' decisions in the previous nine rounds, i.e., typically starting relatively high and then decreasing over time. Participants were told this and that there was nothing they could do to alter the behavior of the pre-programmed computers. Consequently, rational individuals who perfectly understand the game should contribute zero regardless of their social motivations. In other words, by replicating the decision environment but removing the social benefits of contributing (using an asocial control), we tested if those benefits were driving behavior. In contrast, if some individuals are confused conditional cooperators, who still mistakenly believe they can improve their own income by approximately matching (or undercutting) the contributions of their groupmates, they will replicate the classic restart effect (19, 22)†. To prevent further payoff-based learning, we did not show individuals their payoffs after each round in this second game, but they did see what the computers contributed after each round.
We found that we replicated the restart effect even when grouping individuals with computerized groupmates that could not possibly benefit nor be influenced, ruling out altruistic or strategic contributions (Computer Replay treatment, Figs. 2 and 3 and SI Appendix, Fig. S1). Specifically, in the Computer Replay treatment, mean contributions significantly increased from 18% in the final round with humans to 32% for the restart with computers (LMM: Estimated increase ±SE = 14.4 ± 3.36%, t = 4.3, df = 80.0, P < 0.001, Table 1). This increase of 14 percentage points was significantly larger than the increase of 2 percentage points in the Blind Replay treatment with humans (LMM: Estimated difference ±SE = 12.4 ± 4.75%, t = 2.6, df = 80.0, P = 0.011) and was comparably as large as the increase of 17 percentage points in the Classic Replay treatment (LMM: Estimated difference ±SE = 2.8 ± 4.75%, t = 0.6, df = 80.0, P = 0.556). Although if one ignores the first game end values, the restart for the Classic Replay could perhaps be argued to be greater, with contributions starting at 42% as opposed to 32% in the Computer Replay treatment, although this difference was not statistically significant (Linear model on group mean contributions in the first round of the restart, ignoring first game contributions: Estimated difference ±SE = 10.3 ± 5.56%, t = 1.86, df = 76, P = 0.067). Either way, approximately half of the individuals in the Computer Replay treatment increased their contributions for the restart (N = 38/80, 47.5%, 95% CI = [37%, 58%]), compared to 57.5% (N = 46/80) in the Classic Replay treatment (FET: P = 0.268) and 32.5% (N = 26/80) in the Blind Replay treatment (FET: P = 0.076) (Fig. 3).
Contributions in the Computer Replay treatment then significantly declined over time, just as they did in the Classic Replay treatment (LMM controlling for group: estimated decline ±SE = −2.6 ± 0.42 percentage points per round, df = 80.0, t = −6.3, P < 0.001, Table 2). This was because individuals were, on average, significantly tracking the contributions of their computerized groupmates (LMM regressing individual contributions on computerized groupmates’ contributions, controlling for individual: estimate ±SE = 0.28 ± 0.054, df = 649.1, t = 5.2, P < 0.001). The rate of decline was not significantly different from what was observed in the Classic Replay treatment (estimated difference in rate of decline between treatments ±SE = −0.2 ± 0.60 percentage points per round, df = 80.0, t = −0.3, P = 0.782, Table 2). These results, where participants “burn” money for no benefit to any participants, show that the costs of decisions in social experiments cannot be reliably used to infer social preferences (62). The patterns of behavior also suggest that confused conditional cooperation can account for a large part of the restart effect and the general pattern of contributions in public goods games, where behavior toward human and computerized groupmates is often strikingly similar, more so than in other simpler games (12, 15, 19, 20, 22, 45, 47, 63).
Finally, to really test if individuals were attempting to condition their contributions on those of their computerized groupmates, we used a third control treatment. Our Computer Rewind treatment was the same as the Computer Replay treatment, except that this time the computers replicated the previous human decisions in reverse chronological order. Participants were told that in round one the computers would replicate decisions from round nine of the previous game, and then in round two they would replicate round eight, and so on. This way individuals were grouped with computers that would, on average, gradually increase rather than decrease their contributions over time. An individual attempting to conditionally cooperate, but out of confusion and not a concern for fairness, would therefore increase rather than decrease their contributions over time in the second game.
We again found that we could replicate the restart effect with computers, but this time in reverse chronological order (Computer Rewind, Figs. 2 and 3 and SI Appendix, Fig. S1). As hypothesized, initial contributions showed no significant restart effect, resuming at just 19% after a previous finish of 21% (LMM: Estimated increase ±SE = −2.0 ± 3.36%, t = −0.7, df = 80.0, P = 0.493, Table 1). However, in contrast to all other treatments, contributions in the Computer Rewind treatment then significantly increased over the nine rounds to a peak of 29% (5.8 MU) and a finish of 25% in the final round (5.1 MU; Fig. 2, LMM, estimated increase ±SE = 1.3 ± 0.42 percentage points per round, df = 80.0, t = 3.0, P = 0.004, Table 2). Again, this was because individuals were on average, significantly tracking the contributions of their computerized groupmates (LMM: estimate ±SE = 0.20 ± 0.049, estimated df = 719.4, t = 4.2, P < 0.001). Fifty-one percent of individuals had a positive Pearson correlation between their contributions and game round (N = 41/80), significantly more than in any other treatment (N = 13, 14, or 17 out of 80 among the Computer Replay, Classic Replay, and Blind Replay treatments, respectively; respective Fisher’s Exact Tests: P < 0.001 in all cases).
Overall, only 22% of individuals played rationally with the computers and contributed 0 MU in every round (N = 35/160; 18/80 and 17/80 for Computer Replay and Computer Rewind respectively), compared to 29% in the Blind Replay treatment (N = 23/80; Fisher’s Exact Test on 35/160 versus 23/80, P = 0.265) and 4% in the Classic Replay treatment that allowed for strategic contributions (N = 3/80; Fisher’s Exact Test, P < 0.001). Therefore, no altruistic nor prosocial concerns are required to explain this pattern of results but a significant level of irrational decision making (“confusion”) among participants is.
Conclusion
The restart effect does not refute the confused learner’s hypothesis and does not show evidence of altruistic prosociality driven by fairness concerns. Instead, it can, in our data, be explained by confused conditional cooperation, as demonstrated with computers, and by strategic investments into the future cooperation of group partners when possible. These results add to the growing literature showing that human behavior in public goods games is not driven by altruistic motivations and does not require unique evolutionary explanations (12, 20, 22, 27, 39). In conclusion, evolutionary theory does not need expanding or reformulating to accommodate the results of public goods games.
Materials and Methods
We conducted 40 sessions in French language at the University of Lausanne (UNIL) Faculty of Business and Economics (HEC) Laboratory (HEC-LABEX facility). The laboratory staff recruited all participants using ORSEE (64), and the experiment was conducted entirely in z-Tree (65). We had 320 participants (159 female, 158 male, 1 other, and 2 declined to answer) who were mostly students at either UNIL or the Swiss Federal Institute of Technology (known as EPFL), aged under 25 (Under 20 = 134; 20–25 = 173; 26–30 = 11; 31–35 = 1; Over 35 = 1). Participants had to sign a consent form before starting and HEC-LABEX forbids all deception in experiments. Sessions were conducted either in the autumn semester of 2018 or 2019. Both times, we obtained ethical approval from the HEC-LABEX ethics committee.
A Note on Experimental Procedure.
The first game in this study, which set up groups for a test of the restart effect, formed a partial component of another, larger, study. In this other study, groups played for nine rounds and different groups received different levels of information after each round (N = 616 individuals in 154 groups). There were multiple treatments but here we just use the relevant treatments, which were those that both 1) experienced a first-game decline in contributions, and 2) then played one of our restart treatments (N = 320 individuals in 80 groups), otherwise no restart effect would be applicable.
Participants also played two special rounds for the purposes of the other study, either side of the first nine-round game, i.e., before and after, where they were knowingly grouped with computerized virtual players that contributed randomly. No feedback was provided in those two special rounds to prevent any forms of learning. After these 11 rounds, which form the entirety of the other study, participants then were told there would be a second game, for nine rounds (which forms the data for this study), and that the experiment would then be finished except for some brief questions.
The one extra round with the computers in-between the first game and the restart does not invalidate the results or value of the study, for the following reasons: 1) it was quick; 2) it contained no feedback on earnings so could not affect learning; 3) it was knowingly played with computers so could not have affected participants attitudes toward their human partners; and 4) players were then immediately and knowingly regrouped with the same original human partners (in the Classic and Silent Replay treatments). Finally, we replicated the standard restart effect in our Classic Replay treatment (Fig. 2), proving that our procedure did not invalidate the restart and is comparable to prior studies.
Public Good Game.
Participants first read on-screen instructions detailing the decision to contribute to the public good. The instructions were adapted from ref. 4 and involved standard control questions, and the correct answers were shown afterwards. Our game structure replicated the most common design for linear public good games, involving four group members and a return from contributing of 40%, necessitating an individual loss of 60% but a group gain of 60% (specifically, a multiplier of 1.6 for all contributions and a marginal per capita return of 0.4) (12). We endowed players with 20 monetary units (MU) per round (20 MU = 0.5 Swiss Francs CHF), and participants also earned a 10 CHF show-up fee. We informed them that they had been randomly grouped with three other participants and that the group would remain constant for 9 rounds of decision making.
In the first game preceding the restart treatments, all individuals saw, at the end of each round, their own payoff, and for half the groups, we also showed individuals social information on their groupmate’s contributions (N = 40 groups), either the group average, which is technically redundant information because it can in theory be calculated from one’s own payoff (N = 20 groups) or each individual decision, which can be used to calculate the group average (N = 20 groups; and the remaining 40 groups received just payoff information). Overall, mean contributions in the first game declined from 49%, 95% CI = [45.0%, 52.3%] in round one to 21%, 95% CI = [16.2%, 24.9%] in the final round (N = 320 individuals among 80 groups). Our analyses of the restarts control for each group’s history of contributions in the first game, except where stated otherwise.
The number of groups per restart treatment per first game treatment becomes quite small (N = 5 groups with each of the combined information treatments or 10 groups with just payoff information). Therefore, we decided to test if there were qualitative differences in restart effects depending on what level of information individuals received in the first game. We found no qualitative differences, so we combined all the data for analyses in the main text (three-way ANOVA comparing effect of restart treatment depending on information in the preceding first game, F6,80.0 = 1.8, P = 0.108; Table 3). A breakdown of the average restarts for each treatment conditioned on the level of information in the first game can be seen in the SI Appendix, Table S1.
Table 3.
LMMs using maximum likelihood on mean group contributions depending on the information shown in the first game (3 levels) and the restart treatment (4 levels) (N = 20 groups per restart treatment, 10 or 5 for the first game information level)
| Term \ Model | M1 P-value | M2*P-value | M3 P-value | M4 P-value |
|---|---|---|---|---|
| Stage† | <0.001 | <0.001 | <0.001 | <0.001 |
| Restart treatment‡ | 0.023 | 0.023 | 0.020 | 0.045 |
| First game info.§ | / | / | 0.217 | 0.210 |
| Stage*Restart treatment | / | <0.001 | <0.001 | <0.001 |
| Stage*First game info. | / | / | / | 0.094 |
| Restart treatment* First game info. | / | / | / | 0.952 |
| Stage*Restart treatment* First game info. | / | / | / | 0.108 |
| Number of observations¶ | 160 | 160 | 160 | 160 |
| Number of independent units# | 80 | 80 | 80 | 80 |
| Number of parameters | 7 | 10 | 12 | 26 |
| AIC | 1,372 | 1,357 | 1,358 | 1,370 |
| BIC | 1,393 | 1,388 | 1,395 | 1,450 |
| Significance of more complicated model|| | NA | <0.001 | 0.217 | 0.317 |
*This is the optimal model.
†Stage specifies the final round of the first game or the first round of the restarted game.
‡Specifies Classic Replay, Blind Replay, Computer Replay, or Computer Rewind
§Specifies Payoffs only, Payoffs plus group average contribution, or Payoffs plus individual contributions.
¶Each group contributed two data points, the end of the first game and the start of the restarted game.
#Models controls for group identity as a random effect.
||Model comparisons performed with a likelihood ratio test.
Restart Treatments.
We had four restart treatments, and individuals were always made aware of their treatment design before restarting the game. They also had to answer a series of true or false statement about the design, with the correct answers shown afterwards. In all four restart treatments, individuals either played with the same three individuals they had just played with, or with computerized virtual players.
Our Classic Replay treatment made individuals play again in the same group and with the same level of information (either combined social and payoff information or just payoff information). This treatment replicates the typical “partners” design documenting the restart effect (36, 48, 51).
Our Blind Replay treatment also made individuals play again in the same group, but this time, they knew that they and everyone else would receive no information on either decisions or payoffs in-between each round. This treatment controlled for strategic cooperation by preventing individuals from signaling their level of cooperation or influencing the behavior of their groupmates via their payoffs (39).
Our Computer Replay treatment made individuals replay the game but with computerized virtual groupmates. Participants knew that these virtual players would perfectly replicate the decisions of their groupmates from the first game, in chronological order for all nine rounds. This treatment is designed to detect the role that confused conditional cooperators play in the restart effect. Just because individuals can learn in the first game to contribute less does not mean they necessarily learn the dominant strategy (always contribute 0). Instead, they may still mistakenly believe they should anchor their contributions upon those of their groupmates, just to a lesser degree.
Our final treatment, Computer Rewind, also made individuals replay the game with computerized virtual groupmates. Again, participants knew that the computers would replicate the decisions of their groupmates from the first game, but this time in reverse chronological order. This treatment is designed to confirm the role of confused conditional cooperators by creating the circumstances for them to reverse the usual pattern of contributions and increase rather than decrease their contributions over time. In both the computer treatments, the instructions showed a table explaining how the round of the new game would correspond to the round of the previous game. Individuals also had to click a button to proceed saying “I understand that I am playing alone with simulated players.”
Analyses.
To examine the significance and relative size of the restart effects, we took the contributions data from the final round of the first game and the first round of the “restarted” game. We used the mean group contributions to be conservative as the behavior of participants from the same group for the first game is not fully independent. We then built a LMM, using the data from all the treatments, and controlled for group identity with random intercepts. We specified maximum likelihood rather than restricted maximum likelihood as this allowed us to compare nested models (Table 3). The model estimated the size of the restart effect for each of the four treatments, tested if the reference treatment’s restart was significantly different to zero, and significantly different from the other treatments. Degrees of freedom were estimated using Satterthwaite's method. Table 1 shows the estimates when the reference treatment is Classic Replay. To report the other comparisons in the text, we merely specified a different reference treatment.
To analyze the contribution dynamics over time in the second game, we built a similar model but only used the data from the restart games, using all nine rounds of data (Table 2). To analyze if individuals were conditioning their behavior on their computerized groupmates, we used a LMM on individual level data, with a random intercept for each individual. We controlled for game round by including each round as a separate fixed effect. We conducted analyses in RStudio (66), inputted the data with the zTree package (67), tested LMM significance with lmerTest (68), and made the data figures with ggplot2 (69).
Copy of key instructions translated into English.
For the restarts with humans. [Instant / Blind Replay treatment specifics]
You are now going to face the same decision again, as described in the instructions, with the same four people.
The situation is exactly the same [and you will receive the same types of information / except this time the participants will not receive any information.]
Again, you will take part in nine rounds of decision making.
You and the other members of your group will [receive the same type of information / will not receive any information after each round.
No-one will be able to know your investments.
Your earnings will not be shown after each round, but you will receive your money at the end of the experiment.]
After these nine rounds of decision making, the experiment will finish, except for some brief questions.
For the restarts with computers. [Computer Replay / Computer Rewind treatment specifics]
Again you will face the same decisions in a group of four.
However, this time, you find yourself in the special case with the computer.
Before you were in a group with people for nine rounds of decision making.
We will now call those rounds “Phase 1.”
Now you will take decisions for “Phase 2.”
During phase 2, you are going to take new decisions again for nine rounds.
But this time, there will only be you and the computer.
This time, the computer will not take decisions at random, but will reproduce the decisions of the other people in your group during Phase 1.
The computer will reproduce the decisions in [reverse] chronological order.
Therefore, in round 1 of this phase (Phase 2), the computer will reproduce the decisions of the three other people in your group in round [1 / 9] of Phase 1.
Then, in round 2, the computers will reproduce the decisions of the three other people in your group in round [2 /8] of phase 1.
Then in round 3, the computers will reproduce the decisions of round [3 / 7] and so on, until round 9, when it will reproduce the decisions of the [last / first] round of Phase 1.
The computer players will follow this plan, you cannot do anything to change their decisions.
You are the only person in your group and also the only person that will receive any money.
You are going to face nine rounds of decision making. For each round, you will be with the three simulated players.
These three simulated players will reproduce the decisions of the three other people in your group that you were grouped with before.
Your earnings will not be shown, but you will receive your money at the end of the experiment.
After these nine rounds of decision making, the experiment will finish, except for some brief questions.
The participants then saw the following table [Computer Replay / Computer Rewind ]
| Current round with computers | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Computer replicates decisions from human round | [1/9] | [2/8] | [3/7] | [4/6] | [5/5] | [6/4] | [7/3] | [8/2] | [9/1] |
After the instructions, individuals in all treatments had to answer the following true or false questions. They were then shown the correct answers.
Please confirm that you have understood the instructions. For each question, enter 1 if the statement is true, or 0 if it is false.
-
1)
You are in a group with computers
-
2)
You are in a group with humans
-
3)
People in your group will see your decision / the average group decision
-
4)
You will know the decisions of people in your group / the average group decision
-
5)
You will see your earnings after each round
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
General: Tiago Fernandes and Claire Guerin for practical assistance. Funding: Laurent Lehmann and the University of Lausanne Behaviour, Economics, and Evolution lecture series (BEE program).
Author contributions
M.N.B.-C. designed research; performed research; analyzed data; and wrote the paper.
Competing interests
The author declares no competing interest.
Footnotes
This article is a PNAS Direct Submission.
*Note that the altruistic/prosocial interpretation is not confined to altruistic motivations but is often defined in terms of the material consequences of decisions, regardless of motivations, for example see the hypothesis that “altruistic punishment” is motivated by “anger” (29). Of course, an important question is how the costs and benefits of laboratory behaviours correspond to the ancestral evolutionary costs and benefits (31).
†Although individuals can learn in the first game, learning is unlikely to be perfect or universal. For example, confused conditional cooperators may simply learn to deviate more from the group average, but not learn to ignore groupmates’ contributions.
Data, Materials, and Software Availability
All the data, analysis, and experiment files are freely available online at the Open Science Framework (https://osf.io/8nxbz/?view_only=7cfd4e1d26f14fa7ab07e96b2adccbb9) (70).
Supporting Information
References
- 1.Fehr E., Fischbacher U., The nature of human altruism. Nature 425, 785–791 (2003). [DOI] [PubMed] [Google Scholar]
- 2.Henrich J. et al. , "Economic man" in cross-cultural perspective: behavioral experiments in 15 small-scale societies. Behav. Brain Sci. 28, 795–815 (2005), discussion 815–55. [DOI] [PubMed] [Google Scholar]
- 3.Norenzayan A., Shariff A. F., The origin and evolution of religious prosociality. Science 322, 58–62 (2008). [DOI] [PubMed] [Google Scholar]
- 4.Fischbacher U., Gachter S., Social preferences, beliefs, and the dynamics of free riding in public goods experiments. Am. Econ. Rev. 100, 541–556 (2010). [Google Scholar]
- 5.Rustagi D., Engel S., Kosfeld M., Conditional cooperation and costly monitoring explain success in forest commons management. Science 330, 961–965 (2010). [DOI] [PubMed] [Google Scholar]
- 6.Gachter S., Schulz J. F., Intrinsic honesty and the prevalence of rule violations across societies. Nature 531, 496–499 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Purzycki B. G. et al. , Moralistic gods, supernatural punishment and the expansion of human sociality. Nature 530, 327–330 (2016). [DOI] [PubMed] [Google Scholar]
- 8.Fehr E., Schurtenberger I., Normative foundations of human cooperation. Nat. Human Behav. 2, 458–468 (2018). [DOI] [PubMed] [Google Scholar]
- 9.Thielmann I. et al. , Economic games: An introduction and guide for research. Collabra: Psychology. 7, 19004 (2021). [Google Scholar]
- 10.Sosis R. et al. , Introducing a special issue on phase two of the evolution of religion and morality project. Religion Brain Behav. 12, 1–3 (2022). [Google Scholar]
- 11.Chaudhuri A., Sustaining cooperation in laboratory public goods experiments: A selective survey of the literature. Experimental Economics 14, 47–83 (2011). [Google Scholar]
- 12.Burton-Chellew M. N., West S. A., Payoff-based learning best explains the rate of decline in cooperation across 237 public-goods games. Nat. Hum. Behav. 5, 1330–U77 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Andreoni J., Cooperation in public-goods experiments - kindness or confusion. Am. Econ. Rev. 85, 891–904 (1995). [Google Scholar]
- 14.Palfrey T. R., Prisbrey J. E., Altruism, reputation and noise in linear public goods experiments. J. Public Econ. 61, 409–427 (1996). [Google Scholar]
- 15.Houser D., Kurzban R., Revisiting kindness and confusion in public goods experiments. Am. Economic Rev. 92, 1062–1069 (2002). [Google Scholar]
- 16.Cooper D. J., Stockman C. K., Fairness and learning: An experimental examination. Games Economic Behav. 41, 26–45 (2002). [Google Scholar]
- 17.Hagen E. H., Hammerstein P., Game theory and human evolution: A critique of some recent interpretations of experimental games. Theor. Popul. Biol. 69, 339–348 (2006). [DOI] [PubMed] [Google Scholar]
- 18.Janssen M. A., Ahn T. K., Learning, signaling, and social preferences in public-good games. Ecol. Soc. 11, 21 (2006). [Google Scholar]
- 19.Ferraro P. J., Vossler C. A., The source and significance of confusion in public goods experiments. B E J. Economic Anal. Policy. 10 (2010). [Google Scholar]
- 20.Burton-Chellew M. N., West S. A., Prosocial preferences do not explain human cooperation in public-goods games. Proc. Natl. Acad. Sci. U.S.A. 110, 216–221 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Camerer C. F., Experimental, cultural, and neural evidence of deliberate prosociality. Trends Cogn. Sci. 17, 106–108 (2013). [DOI] [PubMed] [Google Scholar]
- 22.Burton-Chellew M. N., El Mouden C., West S. A., Conditional cooperation and confusion in public-goods experiments. Proc. Natl. Acad. Sci. U.S.A. 113, 1291–1296 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Andreozzi L., Ploner M., Saral A. S., The stability of conditional cooperation: Beliefs alone cannot explain the decline of cooperation in social dilemmas. Sci. Rep. 10, 13610 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Apicella C. L. et al. , Social networks and cooperation in hunter-gatherers. Nature. 481, 497–U109 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Burton-Chellew M. N., El Mouden C., West S. A., Social learning and the demise of costly cooperation in humans. Proc. Royal Soc. B-Biol. Sci. 284 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Burton-Chellew M. N., D’Amico V., A preference to learn from successful rather than common behaviours in human social dilemmas. Proc. Royal Soc. B-Biol. Sci. 288 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Burton-Chellew M. N., Guerin C., Decoupling cooperation and punishment in humans shows that punishment is not an altruistic trait. Proc. Royal Soc. B-Biol. Sci. 288 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Andreoni J., Miller J., Giving according to garp: An experimental test of the consistency of preferences for altruism. Econometrica 70, 737–753 (2002). [Google Scholar]
- 29.Fehr E., Gachter S., Altruistic punishment in humans. Nature 415, 137–140 (2002). [DOI] [PubMed] [Google Scholar]
- 30.Fehr E., Henrich J., "Is strong reciprocity a maladaptation? On the evolutionary foundations of human altruism" in Genetic and Cultural Evolution of Cooperation, Hammerstein P., Ed. (MIT Press, 2003), pp. 55–82. [Google Scholar]
- 31.West S. A., El Mouden C., Gardner A., Sixteen common misconceptions about the evolution of cooperation in humans. Evolution Hum Behav. 32, 231–296 (2011). [Google Scholar]
- 32.West S. A. et al. , Ten recent insights for our understanding of cooperation. Nat. Ecol. Evolution. 5, 419–430 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Richerson P. et al. , Cultural group selection plays an essential role in explaining human cooperation: A sketch of the evidence. Behav. Brain Sci. 39, e30 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Henrich J., Muthukrishna M., The origins and psychology of human cooperation. Ann. Rev. Psychol. 72, 207–240 (2021). [DOI] [PubMed] [Google Scholar]
- 35.Kreps D. M. et al. , Rational cooperation in the finitely repeated prisoners-dilemma. J. Econ. Theory 27, 245–252 (1982). [Google Scholar]
- 36.Andreoni J., Why free ride - Strategies and learning in public-goods experiments. J. Public Economics 37, 291–304 (1988). [Google Scholar]
- 37.Reuben E., Suetens S., Revisiting strategic versus non-strategic cooperation. Exp. Economics 15, 24–43 (2012). [Google Scholar]
- 38.Burton-Chellew M. N., El Mouden C., West S. A., Evidence for strategic cooperation in humans. Proc. Royal Soc. B: Biol. Sci. 284, 20170689 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Burton-Chellew M. N., Nax H. H., West S. A., Payoff-based learning explains the decline in cooperation in public goods games. Proc. Royal Soc. B-Biol. Sci. 282, 20142678 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Binmore K., Why experiment in economics? Economic J. 109, F16–F24 (1999). [Google Scholar]
- 41.Krupp D. B. et al. , Let’s add some psychology (and maybe even some evolution) to the mix. Behav. Brain Sci. 28, 828–829 (2005). [Google Scholar]
- 42.Smith V. L., Theory and experiment: What are the questions? J. Economic Behav. Organization. 73, 3–15 (2010). [Google Scholar]
- 43.Raihani N. J., Bshary R., Why humans might help strangers. Front. Behav. Neurosci. 9, 39 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Palfrey T. R., Prisbrey J. E., Anomalous behavior in public goods experiments: How much and why? Am Econ. Rev. 87, 829–846 (1997). [Google Scholar]
- 45.Shapiro D. A., The role of utility interdependence in public good experiments. Int. J. Game Theory. 38, 81–106 (2009). [Google Scholar]
- 46.Kummerli R. et al. , Resistance to extreme strategies, rather than prosocial preferences, can explain human cooperation in public goods games. Proc. Natl. Acad. Sci. U.S.A. 107, 10125–10130 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nielsen Y. A. et al. , Sharing money with humans versus computers: On the role of honesty-humility and (non-)social preferences. Social Psychol. Personality Sci. 13, 1058–1068 (2021), 10.1177/19485506211055622. [DOI] [Google Scholar]
- 48.Croson R. T. A., Partners and strangers revisited. Econ. Lett. 53, 25–32 (1996). [Google Scholar]
- 49.Cookson R., Framing effects in public goods experiments. Exp. Econ. 3, 55–79 (2000). [Google Scholar]
- 50.Croson R. T. A., Thinking like a game theorist: Factors affecting the frequency of equilibrium play. J. Econ. Behav. Organization 41, 299–314 (2000). [Google Scholar]
- 51.Andreoni J., Croson R., "Partners versus strangers: Random rematching in public goods experiments" in Handbook of Experimental Economics Results, Plott C. R., Smitt V. L., Eds. (North-Holland, Amsterdam., 2008), p. 776. [Google Scholar]
- 52.Chaudhuri A., Belief heterogeneity and the restart effect in a public goods game. Games 9, 96 (2018). [Google Scholar]
- 53.Arifovic J., Ledyard J., Individual evolutionary learning, other-regarding preferences, and the voluntary contributions mechanism. J. Public Econ. 96, 808–823 (2012). [Google Scholar]
- 54.Bateson M., Nettle D., Roberts G., Cues of being watched enhance cooperation in a real-world setting. Biol. Lett. 2, 412–414 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sparks A., Barclay P., Eye images increase generosity, but not for long: The limited effect of a false cue. Evolution Hum. Behav. 34, 317–322 (2013). [Google Scholar]
- 56.Trivers R. L., Evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–& (1971). [Google Scholar]
- 57.Kurzban R., Burton-Chellew M. N., West S. A., The evolution of altruism in humans. Annu. Rev. Psychol. 66, 575–599 (2015). [DOI] [PubMed] [Google Scholar]
- 58.Manrique H. M. et al. , The psychological foundations of reputation-based cooperation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 376, 20200287 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chaudhuri A., Paichayontvijit T., Smith A., Belief heterogeneity and contributions decay among conditional cooperators in public goods games. J. Econ. Psychol. 58, 15–30 (2017). [Google Scholar]
- 60.Columbus S., Böhm R., Norm shifts under the strategy method. Judgment Decis. Making 16, 1267–1289 (2021). [Google Scholar]
- 61.Gachter S., Renner E., The effects of (incentivized) belief elicitation in public goods experiments. Exp. Econ. 13, 364–377 (2010). [Google Scholar]
- 62.Wilson B. J., Social preferences aren’t preferences. J. Econ. Behav. Organization 73, 77–82 (2010). [Google Scholar]
- 63.Blount S., When social outcomes aren′t fair: The effect of causal attributions on preferences. Organizational Behav. Hum Decision Process. 63, 131–144 (1995). [Google Scholar]
- 64.Greiner B., Subject pool recruitment procedures: Organizing experiments with ORSEE. J. Econ. Sci. Association 1, 114–125 (2015). [Google Scholar]
- 65.Fischbacher U., z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 10, 171–178 (2007). [Google Scholar]
- 66.R. Team, RStudio: Integrated Development Environment for R (RStudio, PBC, Boston, MA, 2020). http://www.rstudio.com. [Google Scholar]
- 67.Kirchkamp O., Importing z-Tree data into R. J. Behav. Exp. Finance. 22, 1–2 (2019). [Google Scholar]
- 68.Kuznetsova A., Brockhoff P. B., Christensen R. H. B., lmerTest package: Tests in linear mixed effects models. J. Statis. Software 82, 1–26 (2017). [Google Scholar]
- 69.Wickham H., ggplot2: Elegant Graphics for Data Analysis (Springer-Verlag, New York, 2009). [Google Scholar]
- 70.Burton-Chellew M. N., The restart effect in social dilemmas shows humans are self-interested not altruistic. Open Science Framework. https://osf.io/8nxbz/. Deposited 6 May 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All the data, analysis, and experiment files are freely available online at the Open Science Framework (https://osf.io/8nxbz/?view_only=7cfd4e1d26f14fa7ab07e96b2adccbb9) (70).