Skip to main content
PMC home page
Journal of Structural Biology: X logoLink to Journal of Structural Biology: X
. 2023 Jan 24;7:100085. doi: 10.1016/j.yjsbx.2023.100085

Measuring the effects of ice thickness on resolution in single particle cryo-EM

Kasahun Neselu a, Bing Wang b, William J Rice b,c, Clinton S Potter a, Bridget Carragher a,⁎, Eugene YD Chua a,⁎
PMCID: PMC9894782  PMID: 36742017

Graphical abstract

graphic file with name ga1.jpg

Open in a new tab

Keywords: Cryo-EM, Ice thickness, Single particle analysis, Energy filter, High tension, Resolution

Highlights

  • •

    Resolution decreases with increasing ice thickness.

  • •

    20 eV energy filter slit has the greatest effect in thick ice > 200 nm.

  • •

    K3 super resolution mode provides greatest improvement compared to counting mode in 150–200 nm ice thickness.

  • •

    300 kV accelerating voltage provides greatest improvement compared to 200 kV for > 150 nm ice thickness.

  • •

    Integrating mode on a 200 kV microscope is most useful in < 50 nm ice.

Abstract

Ice thickness is a critical parameter in single particle cryo-EM – too thin ice can break during imaging or exclude the sample of interest, while ice that is too thick contributes to more inelastic scattering that precludes obtaining high resolution reconstructions. Here we present the practical effects of ice thickness on resolution, and the influence of energy filters, accelerating voltage, or detector mode. We collected apoferritin data with a wide range of ice thicknesses on three microscopes with different instrumentation and settings. We show that on a 300 kV microscope, using a 20 eV energy filter slit has a greater effect on improving resolution in thicker ice; that operating at 300 kV instead of 200 kV accelerating voltage provides significant resolution improvements at an ice thickness above 150 nm; and that on a 200 kV microscope using a detector operating in super resolution mode enables good reconstructions for up to 200 nm ice thickness, while collecting in counting instead of linear mode leads to improvements in resolution for ice of 50–150 nm thickness. Our findings can serve as a guide for users seeking to optimize data collection or sample preparation routines for both single particle and in situ cryo-EM. We note that most in situ data collection is done on samples in a range of ice thickness above 150 nm so these results may be especially relevant to that community.

Introduction

The goal of sample preparation for single particle cryo-electron microscopy (cryo-EM) is to capture the sample in optimal conditions on a cryo-EM grid. “Optimal conditions” means the biological sample is embedded in vitreous ice suspended over holes in the grid foil, has enough well-distributed particles in different orientations, and that the sample is found in ice that is as thin as possible, typically 10–100 nm (Noble et al., 2018). While the thinnest possible ice might be expected to yield the highest resolution reconstructions, there is usually a “Goldilocks” zone for ice thickness for each sample (Olek et al., 2022). If the ice is too thin, the sample can be excluded from the holes, adopt a preferred orientation, or break during imaging. On the other hand if the ice is too thick, increased inelastic scattering from the additional ice may negatively affect reconstruction resolutions (Wu et al., 2016). In most cases, the thinnest possible ice that yields good particles is desirable for data collection. This ideal ice thickness depends on the sample, and can range from 15 nm for apoferritin (12 nm in diameter) (Brown & Hanssen, 2022) to 750 nm for the Giant Mimivirus (500 nm in diameter) (Xiao et al., 2005). Quite often, however, ice much thicker than the diameter of the particle is required to avoid particles adopting a preferred orientation (e.g. Huntington et al., 2022).

Although ice thickness is an important parameter both for the sample integrity and optimal data collection, it is not currently possible to finely control ice thicknesses during cryo-EM sample preparation. With commonly-used plunge freezers, or even with modern automated sample preparation devices such as the chameleon (Darrow et al., 2019, Darrow et al., 2021), ice thicknesses often vary both within a grid square and across the grid. Some areas of a grid may have good particle distribution and ideal ice thickness while others may have too thin ice which excludes particles, or too thick ice that has reduced contrast.

Problems of variations in ice thickness on a grid can be solved in several ways. First, by setting automated data collection parameters to only collect on the desired ice thicknesses (Brown and Hanssen, 2022, Cheng et al., 2021, Rheinberger et al., 2021). Collecting good quality data by skipping over targets with too thin or too thick ice is important for optimizing data collection and storage efficiency, and for achieving highest resolution reconstructions. Second, post-specimen energy filters can be used (Schröder et al., 1990, Yonekura et al., 2006), which remove inelastically scattered electrons to reduce background noise, especially in regions with thicker ice. Using an energy filter should increase the upper range of ice thicknesses useful for achieving a desired resolution. Third, increasing the accelerating voltage of a microscope reduces the inelastic mean free path of scattering (Dickerson et al., 2022, Henderson, 1995, Martynowycz et al., 2021, Peet et al., 2019). This means that given the same sample thickness, electrons that have higher energy are less likely to undergo inelastic scattering than those with lower energy, and so will contribute less noise in those micrographs.

While the theoretical effects of ice thickness on single particle analysis and available strategies to optimize data collection are known, the practical effects of ice thickness on single particle analysis reconstruction resolutions have to our knowledge not been experimentally quantified. To this end we collected large apoferritin datasets over a wide range of ice thickness (15–500 nm) using a variety of instrumentation. This included both 200 kV and 300 kV microscopes (Glacios, Arctica, and Krios); direct electron detectors operating in integrating (Glacios with Falcon3), counting (Arctica with K3 and Krios with K3), and super resolution mode (Arctica with K3); and with a 20 eV energy filter slit inserted or retracted (Krios with K3). The data were sorted into groups based on ice thickness and each batch was independently processed to measure the impact of ice thickness and imaging technique on reconstruction resolution. We show that using a 20 eV energy filter slit has a greater effect in thicker ice; that operating at 300 kV instead of 200 kV accelerating voltage provides significant resolution improvements at an ice thickness above 150 nm; that collecting data in super resolution mode provides the most improvement in 150–200 nm thickness; and finally that using a detector operating in counting instead of linear mode has the greatest positive effect in < 150 nm ice thickness. Our findings can serve as a guide for users seeking to optimize data collection or sample preparation routines for both single particle and in situ cryo-EM. We also note that most in situ data collection is done on samples in a range of ice thickness above 150 nm so these results may be especially relevant to that community.

Methods

Sample preparation

Mouse apoferritin in a pET24a vector (Danev et al., 2019) was expressed in BL21(DE3) pLys cells. Cells were lysed, and apoferritin precipitated with 60% ammonium sulfate. After resuspension in 30 mM HEPES pH 7.5, 1 M NaCl, and 1 mM DTT, apoferritin was injected onto a HiTrap Q column and eluted with a 0–0.5 M NaCl gradient over 4 column volumes. The elution peak was pooled and concentrated for purification on a Superdex 200 16/60 column in 30 mM HEPES pH 7.5, 150 mM NaCl, and 1 mM DTT.

UltrAuFoil R1.2/1.3 300 mesh grids (Quantifoil) were plasma cleaned using a Solarus II (Gatan) with Ar:O₂ (26.3:8.7) at 15 W for 10 s. 3 μL mouse 8 mg/ml apoferritin was applied onto the plasma cleaned grids. After a 30 s incubation at 100% relative humidity and 22°C the grids were blotted for 4–5 s then plunge frozen into liquid ethane using a Vitrobot Mark IV (Thermo Fisher Scientific).

Data collection

Cryo-EM data was collected on three different microscopes. (1) A Titan Krios (Thermo Fisher Scientific) microscope operating at 300 kV and equipped with a BioQuantum energy filter (Gatan) and K3 camera (Gatan) in counting mode. Krios data was collected either with a 20 eV energy filter slit, or with the slit open, on the same grid during the same data collection session. (2) A Talos Arctica microscope operating at 200 kV and equipped with a K3 detector operating in counting or super resolution mode. Data was collected on a different apoferritin grid. (3) A Glacios microscope operating at 200 kV and equipped with a Falcon3 camera (ThermoFisher Scientific) operating in integrating mode. Data was collected on a third apoferritin grid. Data collection parameters are found in Table 1. Leginon (Cheng et al., 2021, Suloway et al., 2005) was used for automated data collection for all sessions. Ice thickness on the Arctica and Glacios was measured by using aperture limited scattering (ALS) method, and on the Krios by using the zero loss peak (ZLP) method (Rice et al., 2018). During data collection, the incoming images were motion corrected and dose weighted with motioncor2 (Zheng et al., 2017) in Appion (Lander et al., 2010).

Table 1.

Cryo-EM data collection parameters.

Dataset “Krios (Filtered and Unfiltered)” “Arctica (Counting and Super Resolution)” “Glacios”
Microscope Titan Krios Talos Arctica Glacios
Accelerating voltage (kV) 300 200 200
Energy filter slit width (eV) 20 N/A N/A
Pixel size (Å/pix) 1.083 1.096 1.204
Exposure time (ms) 2000 2400 2000
Frame time (ms) 40 50 40
Number of frames 50 48 50
Total dose (e/Å2) 51.22 50.34 50.53
Session name 22may20b 22sep21a, 22sep22a 22feb15b
Open in a new tab

Image processing

Frame-aligned and dose-weighted images were sorted into 5 different ice thickness groups (0–50 nm, 50–100 nm, 100–150 nm, 150–200 nm, and 200–500 nm) using a Python script. The micrographs were then imported into different workspaces and processed using cryoSPARC (Punjani et al., 2017). After importing the micrographs from each ice thickness group, the CTF was estimated. Next, the micrographs were manually curated to exclude bad micrographs, using the same exclusion criteria for all ice thickness groups. 200 micrographs were then randomly selected for further image processing. Particles were manually picked from some of these micrographs to generate good picking templates. Next, template picking was done on all 200 micrographs. The picks were then inspected, and obvious bad picks were excluded. The good picks were then extracted in a 256-pixel box and connected to a 2D class averaging job. The resulting 2D classifications were evaluated and only good class averages with good signal to noise ratio were kept. From the set of good particles, 2 to 4 mutually exclusive sets of 14,000 particles were created for further processing, depending on the number of particles available. Homogeneous refinement with defocus and CTF refinement was done on each set of particles, and the best and average reconstruction statistics are reported here. For the Glacios dataset, there was overfitting in the 3D reconstructions for ice thicknesses above 100 nm resulting in an overestimation of the resolution. To overcome this, the same soft mask around the apoferritin density was applied to all reconstructions from all Glacios ice thickness groups.

Analysis

Once a 3D reconstruction was obtained, the density was evaluated using UCSF Chimera (Pettersen et al., 2004). Reconstructions from the different microscopes and ice thickness groups were compared against one another to evaluate which ice thickness and microscope setup gave the best results. Linear regressions were done in Microsoft Excel using the midpoint of each ice thickness group as the value on the x-axis. Map-to-map Fourier shell correlations (FSCs) were calculated on the EMDB FSC server https://www.ebi.ac.uk/emdb/validation/fsc/.

Results

The thinner the ice, the better the resolution

To study the effects of ice thickness on resolution, we collected apoferritin data with a wide range of ice thicknesses (15–500 nm) on the Krios, Arctica, and Glacios microscopes. We observed the expected trend that as ice thickness increases, resolution decreases (Fig. 1 & Supplementary Fig. 1). With data collected on differently configured microscopes, we can quantify the contributions from the energy filter, accelerating voltage, and detector mode, to reconstruction resolutions at varying ice thicknesses. It is important to bear in mind that the numbers presented here are for a very specific data collection scenario, and do not represent the performance limit of these microscope setups. What a reconstruction can achieve practically will also depend on the number of particles, sample size, and homogeneity.

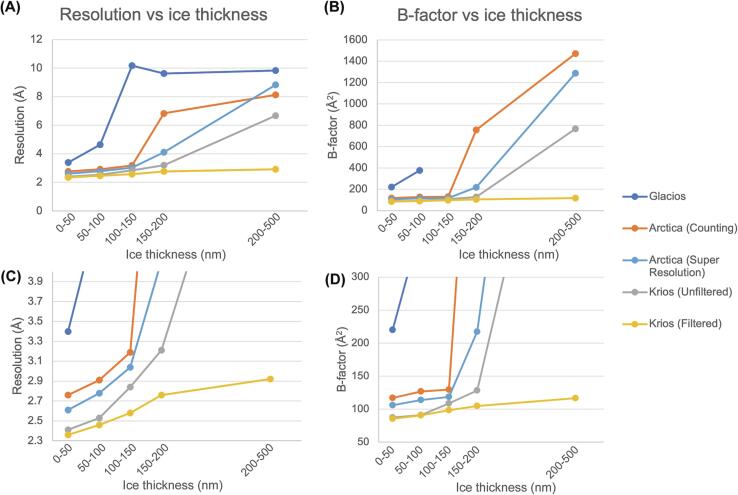
Fig. 1.

Fig. 1

Open in a new tab

(A) Plot of the best apoferritin resolutions obtained from micrographs of various ice thicknesses, and with microscopes of different configurations (see Table 1 for microscope configuration details). (B) Guinier plot B-factors from the best reconstructions versus ice thickness group. The data from each ice thickness group are plotted on the midpoint ice thickness value on the x-axis, i.e. 25, 75, 125, 175, and 350 nm. The numbers giving rise to these plots can be found in Table 2a, Table 2b. (C) Fig. 1(A) with a rescaled y-axis from 2.3 to 4 Å. (D) Fig. 1(B) with a rescaled y-axis from 50 to 300 Å2.

Here, we report both the best (Fig. 1 and Table 2a, Table 2b) and average (Supplementary Fig. 1 and Supplementary Table 1) reconstruction statistics from mutually exclusive sets of 14,000 particles processed with the same data processing parameters and settings, so as to have a holistic view on our processing, and to report on the variability we encountered in the process.

Table 2a.

Accompaniment table to Fig. 1A. Table of highest apoferritin reconstruction resolutions obtained from micrographs of various ice thicknesses, and with microscopes of different configurations (see Table 1 for microscope configuration details).

0–50 nm 50–100 nm 100–150 nm 150–200 nm 200–500 nm
Glacios 3.40 4.64 10.18 9.63 9.84
Arctica (Counting) 2.76 2.91 3.19 6.83 8.13
Arctica (Super Resolution) 2.61 2.78 3.04 4.11 8.82
Krios (Unfiltered) 2.41 2.53 2.84 3.21 6.67
Krios (Filtered) 2.36 2.46 2.58 2.76 2.92
Open in a new tab

Table 2b.

Accompaniment table to Fig. 1B. Table of Guinier plot B-factors from Table 1(A) for each ice thickness group. DNE = Did not estimate; that is, the 3D refinement job did not return a B-factor.

0–50 nm 50–100 nm 100–150 nm 150–200 nm 200–500 nm
Glacios 220.1 377.2 DNE DNE DNE
Arctica (Counting) 117 126.6 129.6 756.8 1470.7
Arctica (Super Resolution) 106 113.8 118.5 217.4 1287.1
Krios (Unfiltered) 87.5 91 108.5 128.4 766.4
Krios (Filtered) 85.5 90.7 98.3 104.8 116.7
Open in a new tab

The energy filter reduces the rate of resolution decay

Comparing the Krios datasets with and without the 20 eV energy filter slit shows that the main advantage of using the slit is to reduce the rate at which the resolution decays with increasing ice thickness. Fitting linear regressions into the 0–150 nm range of the resolution plot (Table 2a) reveals that both data have very similar intercepts (2.27 Å for unfiltered, and 2.30 Å for filtered), but the slope of the unfiltered data, at 0.0043 Å nm−1, is ∼ 2-fold higher than that of filtered data at 0.0022 Å nm−1 (Table 3a). This indicates that for apoferritin at the thinnest possible ice, the energy filter has minimal effect; however, with every nm of increasing ice thickness, the resolution of these reconstructions from data collected without an energy filter suffer 2-fold more than with an energy filter, up to 150 nm. Similarly, the rate of B-factor decay (Table 3b) on unfiltered data is 1.6-fold worse than that of filtered data, up to 150 nm ice thickness. Above 150 nm thickness, however, the resolution of unfiltered reconstructions starts to decay more rapidly, reaching a best of only 6.67 Å in 200–500 nm ice thickness, compared to 2.92 Å for energy filtered data. Practically speaking, most single particle data collected at the Simons Electron Microscopy Center is in ice thickness < 100 nm, for which the improvement in resolution by inserting the energy filter slit is small. This is expected since this ice thickness range is well below the inelastic mean free path of 350 ∼ 440 nm at 300 kV (Yonekura et al., 2006). Since the 20 eV slit provided the greatest resolution improvement in the thickest 200–500 nm ice thickness group (Fig. 1A and Table 1A), this may be of particular interest for in situ data collection from FIB-milled lamella where thickness is more likely to be in the range 150–250 nm.

Table 3a.

Linear regression fits into resolution vs ice thickness plots. Fits were done into the linear portions of the graph to allow for the best comparisons between plots. DNF = did not fit.

Dataset Fit range Linear regression R2
Glacios DNF DNF DNF
Arctica (Counting) 0–150 nm y = 0.0043x + 2.6308 0.9704
Arctica (Super Resolution) 0–150 nm y = 0.0043x + 2.4875 0.9856
Krios (Unfiltered) 0–150 nm y = 0.0043x + 2.2708 0.9389
Krios (Filtered) 0–150 nm y = 0.0022x + 2.3017 0.9973
Open in a new tab

Table 3b.

Linear regression fits into Guinier plot B-factor vs ice thickness plots.

Dataset Fit range Linear regression R2
Glacios DNF DNF DNF
Arctica (Counting) 0–150 nm y = 0.126x + 114.95 0.9162
Arctica (Super Resolution) 0–150 nm y = 0.125x + 103.39 0.9799
Krios (Unfiltered) 0–150 nm y = 0.21x + 79.917 0.871
Krios (Filtered) 0–150 nm y = 0.128x + 81.9 0.9884
Open in a new tab

Increasing high tension from 200 to 300 kV has the greatest effect in thicker ice

Next, we compared the Arctica counting data with the unfiltered Krios data. Since both microscopes were operated with a K3 detector in counting mode, we could concentrate on the effects of 200 vs 300 kV accelerating voltages. In ice of 0–150 nm, 200 kV data performed slightly worse than 300 kV data: linear regression fits reached intercepts of 2.63 Å (for 200 kV) vs 2.27 Å (for 300 kV), although the rates of resolution decay were the same, at 0.0043 Å nm−1 (Table 3a). The biggest differences were observed at > 150 nm ice thickness, where the 200 kV Arctica counting data achieved only 6.83–8.13 Å reconstructions, compared to 3.21–6.67 Å for 300 kV Krios counting data (Table 2a). The data shows that increasing the accelerating voltage from 200 to 300 kV provides the greatest improvement at the 150–200 nm thickness range. The corresponding ∼ 6-fold increase in B-factors (128.4 Å2 for 300 kV vs 756.8 Å2 for 200 kV) indicates that for this ice thickness, a much larger amount of 200 kV data would need to be collected to compensate for the loss of information due to inelastic scattering.

Super resolution > counting > integrating mode

In integrating mode, a direct electron detector integrates the total charge imparted by an electron, distributed by the microscope’s point spread function, across several pixels. Operating in counting mode allows for the localization of single electron events on the camera with pixel accuracy, reducing Landau and readout noise, and improving the DQE of a detector compared to integrating mode (Gatan., 2022, Li et al., 2013). A further improvement in DQE can be gained by collecting data in super resolution mode which makes use of high-speed detector electronics to determine the sub-pixel location of each electron event, digitally increasing the number of pixels by 4x (Booth, 2012, Li et al., 2013).

The poorer performance of 200 kV Arctica counting data compared to 300 kV Krios counting data in 150–200 nm ice can be somewhat rescued by collecting data in super resolution mode. This improved the reconstruction resolution from 6.83 to 4.11 Å, and the B-factors from 756.8 to 217.4 Å2 (Table 2a, Table 2b) which are more comparable to 300 kV Krios counting data.

By comparing Arctica data with Glacios data, we could compare the performance of a K3 detector operating in counting mode with a Falcon3 in integrating mode respectively. This is not an ideal comparison of counting vs integrating collection modes, since the Falcon3 and K3 have slightly different DQEs (Booth, 2019, Morado, 2020). Nevertheless, we include this data in the interest of completeness. We observed the most significant improvements from using counting mode below 150 nm ice thickness. Above 150 nm ice thickness, counting and integrating modes achieved similar resolutions and B-factors, suggesting that the noise from increased inelastic scattering and the subsequent reduction in image contrast dominates the gain in signal-to-noise from counting.

We observed that our Glacios data performs poorly at all ice thicknesses above 50 nm. While the data may appear to indicate that the resolution remains stable in 100–500 nm ice, in contrast to the other datasets where the resolutions and B-factors continued to worsen in the same ice thickness range (Fig. 1 and Supplementary Fig. 1), we believe this is just an artifact of generally poor reconstructions. Visual examination of the maps for reconstructions above 100 nm thickness revealed no real structural features that might be expected for a map 9 ∼ 10 Å in resolution, and instead showed that the ∼ 9.5 Å reported resolutions were due to misalignments to noise (Fig. 2). Map-to-map FSCs of the maps from thicker ice calculated against the map from 0 to 50 nm ice show that the Glacios maps from > 100 nm ice thickness have, at best, a 20 Å correlation to the map from 0 to 50 nm thickness (Supplementary Fig. 2). We conclude that Glacios data collected in integrating mode in ice thicker than 100 nm produces unreliable reconstructions that are, for apoferritin, significantly worse than 7 Å.

Fig. 2.

Fig. 2

Open in a new tab

Apoferritin reconstructions from Glacios data collected in integrating mode, by ice thickness group.

As ice thickness increases, we might expect a smooth decrease in reconstruction resolution. Instead, across all our datasets, we observed that resolution would decrease up to ∼ 4 Å, after which there is a “jump” to ∼ 7 Å without an intermediate 5–6 Å reconstruction (Fig. 1A and Table 1A). We hypothesize that this is because at better than ∼ 4 Å there are side chain densities that reconstruction programs can align to; however, for apoferritin, which contains only alpha helices and no beta sheets or any other significant structural features, the next feature that can be aligned are alpha helices at ∼ 7 Å, which results in the observed “jump” in resolution.

Discussion

Thicker ice produces more inelastic scattering events, which decreases single-to-noise ratios and worsens reconstruction alignment accuracy, resulting in poorer reconstruction resolutions. Here, we observe that using a 20 eV energy filter slit slows down the rate of resolution decay with increasing ice thickness by ∼ 2-fold on a 300 kV microscope. Using 300 kV accelerating voltage provides the greatest benefit over 200 kV at > 150 nm ice thickness, improving our apoferritin reconstruction from 6.83 to 3.21 Å in 150–200 nm ice. Using super resolution mode provides the most improvement in < 200 nm ice, and collecting data in counting instead of integrating mode improves reconstructions most noticeably in ice thinner than 150 nm. Combining these effects, we obtained the highest resolution reconstructions across all ice thickness groups from energy filtered 300 kV Krios data, followed by unfiltered Krios, 200 kV Arctica with a K3 in super resolution then counting mode, and lastly with a 200 kV Glacios with a Falcon3 in integrating mode. For 200 kV instruments, the best imaging setup of using a K3 in super resolution mode enabled high resolution reconstructions < 200 nm ice. In situations where thick (> 200 nm) ice cannot be avoided, for example with a large virus, large macromolecular complex, or in situ sample, it is most critical to use a microscope with high kV and an energy filter to obtain the highest resolution data.

In thin ice (0–50 nm), the best reconstructions from our comparable 200 and 300 kV data (Arctica with K3 in counting mode and Krios unfiltered) perform similarly, at 2.76 and 2.41 Å respectively. A visual examination of the maps showed little difference between the two (Supplementary Fig. 4). The advantages of using a lower accelerating voltage for single particle cryo-EM experiments have recently been more thoroughly described (Naydenova et al., 2019, Peet et al., 2019), and the data show that 200 keV electrons are better for single particle cryo-EM than 300 keV when specimen thickness is not considered (Peet et al., 2019). Specifically, the ratio of elastic scattering at 200 keV to 300 keV is 1.24, whereas the ratio of inelastic scattering at 200 keV to 300 keV is 1.14. For specimens thinner than ∼ 100 nm, electron energies lower than 300 keV were shown to contain more useful information for single particle cryo-EM (Peet et al., 2019). This improvement is likely somewhat offset by the detective quantum efficiency (DQE) of existing counting direct detectors being slightly worse at 200 keV than at 300 keV.

During processing, we observed that in thicker ice, reconstructions from mutually exclusive sets of 14,000 good particles randomly selected from each ice thickness group could achieve very different resolutions (Supplementary Fig. 1A). In the 200–500 nm ice thickness group, while the best reconstruction we obtained with filtered Krios data was 2.92 Å, across 4 independent reconstructions from mutually exclusive sets of 14,000 particles from the same dataset, we obtained reconstructions that ranged up to 10.74 Å, with an average of 7.39 Å (Supplementary Fig. 1A and Supplementary Table 1). This does not appear to be because some groups of 14,000 particles were from thinner ice than others. Analysis of the per-particle distribution of ice thicknesses for each of the four Krios filtered reconstructions from the 200–500 nm ice thickness group showed that particles that gave rise to the 2.92 Å reconstruction did not have significantly better ice thicknesses than the other 7–10 Å reconstructions (Supplementary Fig. 3). One hypothesis to explain this is that variability can arise during the random initialization process of 3D reconstruction: if a subset of higher quality particles happens to be selected to initialize the reconstruction, this could lead to better alignment and resolution for that reconstruction. However, since these high-quality particles are not ubiquitous in the thick ice data, obtaining these reconstructions can be hit-or-miss. Another interesting observation was that turning off both defocus and CTF optimization during 3D reconstruction in thick ice could sometimes give higher resolution reconstructions than if we turned on both options. For example, the best unfiltered Krios 200–500 nm reconstruction achieved 6.67 Å with defocus and CTF refinement, but 3.65 Å with both options deactivated. We think this could be because in thick ice the particles have very little high-resolution signal, so the defocus and CTF optimizing algorithms are fitting to noise, and turning them off can potentially yield a better reconstruction.

There are several additional considerations for improving on the existing imaging setups tested in this work. Firstly, considering that the inelastic mean free path is shorter for slower electrons, there will be more inelastic scattering in a 200 kV microscope, which means that installing a post-specimen energy filter will make a bigger impact on such a setup than on a 300 kV microscope. Secondly, on a microscope with a post-specimen energy filter, when collecting data in thick ice, it would also be beneficial to reduce the width of the energy filter slit to ∼ 10 eV to optimally eliminate inelastically scattered electrons and improve the reconstruction (Nakane et al., 2020, ThermoFisher Scientific, 2022). Thirdly, reducing inelastic scattering from ice by energy filtration will have the most benefit for small particles, since they have the lowest signal-to-noise ratios, and energy filtration also improves amplitude contrast allowing for better alignments during reconstruction (Danev et al., 2021). Since apoferritin has a molecular weight of ∼ 450 kDa, this same experiment should be done with a smaller protein of < 200 kDa to better evaluate the benefits for small macromolecules.

We observed that a Falcon3 detector in integrating mode (Glacios dataset) was only useful in the thinnest ice, < 50 nm. While using integrating mode on a Falcon3 reduces exposure times from 60 s to 1–2 s, making it much faster for a quick survey of the grid, the data from integrating mode is not likely to provide useful reconstructions except in very thin ice. For more challenging samples that prefer thicker ice or when working with suboptimal grids with thicker ice (as is commonly the case on a screening microscope), reconstructions obtained from the Glacios in integrating mode may not be an accurate reflection of what can be obtained from a better imaging setup. Here at the Simons Electron Microscopy Center, preliminary data are commonly collected on our Glacios in integrating mode before a full data collection on a Krios instrument. The data in this paper provide a useful benchmark for how reconstructions from a Glacios dataset can be extrapolated to reconstructions from a Krios dataset, given an ice thickness range. The case can be made here for either collecting data in counting mode on the Falcon3 on our Glacios microscope, or else for upgrading the camera, say to a K3, for faster speeds and better reconstructions.

Preparing samples in the thinnest ice possible remains the best global solution to obtaining high resolution. Where thick ice is necessary, for example with large macromolecules or in situ samples, using the best available imaging setup is essential for reaching high resolution with the greatest possible speed.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

Acknowledgements

We thank Dr. Masahide Kikkawa (University of Tokyo) for the apoferritin plasmid, and Dr. Brian Kloss (NYSBC) for expressing and purifying the apoferritin sample.

This work was supported by the Simons Electron Microscopy Center and National Resource for Automated Molecular Microscopy located at the New York Structural Biology Center, supported by grants from the Simons Foundation (SF349247) and the NIH National Institute of General Medical Sciences (GM103310). All Arctica data in this work was collected at the NYU Langone Health Cryo-EM core facility (RRID: SCR_019202).

Footnotes

Appendix A

Supplementary data to this article can be found online at https://doi.org/10.1016/j.yjsbx.2023.100085.

Contributor Information

Bridget Carragher, Email: bcarr@nysbc.org.

Eugene Y.D. Chua, Email: echua@nysbc.org.

Appendix A. Supplementary data

The following are the Supplementary data to this article:

Supplementary data 1
mmc1.docx (1.1MB, docx)

Data availability

Micrographs are available at EMPIAR-11397. Reconstructions are available on EMDB with the following accession codes: for Glacios 0-50 nm, EMD-29566; 50-100 nm, EMD-29567; 100-150 nm, EMD-29568; 150-200 nm, EMD-29569; 200-500 nm, EMD-29570. For Arctica in counting mode 0-50 nm, EMD-29573; 50-100 nm, EMD-29574; 100-150 nm, EMD-29575; 150-200 nm, EMD-29576; 200-500 nm, EMD-29577. For Arctica in super resolution mode 0-50 nm, EMD-29589; 50-100 nm, EMD-29591; 100-150 nm, EMD-29592; 150-200 nm, EMD-29593; 200-500 nm, EMD-29594. For Krios unfiltered 0-50 nm, EMD-29554; 50-100 nm EMD-29555; 100-150 nm, EMD-29556; 150-200 nm, EMD-29557; 200-500 nm, EMD-29558. For Krios filtered 0-50 nm, EMD-29536; 50-100 nm, EMD-29535; 100-150 nm, EMD-29559; 150-200 nm, EMD-29513; 200-500 nm, EMD-29393.

References

  1. Booth C. K2: a super-resolution electron counting direct detection camera for Cryo-EM. Microsc. Microanal. 2012;18(S2):78–79. doi: 10.1017/S1431927612002243. [DOI] [Google Scholar]
  2. Booth, C. (2019). Detection Technologies for Cryo-Electron Microscopy. https://cryoem.slac.stanford.edu/s2c2/sites/s2c2.cryoem.slac.stanford.edu/files/Cameras%20for%20Cryo-EM%20Stanford2019-Booth.pdf.
  3. Brown H.G., Hanssen E. MeasureIce: accessible on-the-fly measurement of ice thickness in cryo-electron microscopy. Commun. Biol. 2022;5(1):817. doi: 10.1038/s42003-022-03698-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cheng A., Negro C., Bruhn J.F., Rice W.J., Dallakyan S., Eng E.T., Waterman D.G., Potter C.S., Carragher B. Leginon: new features and applications. Protein Sci. 2021;30(1):136–150. doi: 10.1002/pro.3967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Danev R., Yanagisawa H., Kikkawa M. Cryo-electron microscopy methodology: current aspects and future directions. Trends Biochem. Sci. 2019;44(10):837–848. doi: 10.1016/j.tibs.2019.04.008. [DOI] [PubMed] [Google Scholar]
  6. Danev R., Belousoff M., Liang Y.-L., Zhang X., Eisenstein F., Wootten D., Sexton P.M. Routine sub-2.5 Å cryo-EM structure determination of GPCRs. Nat. Commun. 2021;12(1):4333. doi: 10.1038/s41467-021-24650-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Darrow M.C., Moore J.P., Walker R.J., Doering K., King R.S. Chameleon: next generation sample preparation for CryoEM based on Spotiton. Microsc. Microanal. 2019;25(S2):994–995. doi: 10.1017/S1431927619005701. [DOI] [Google Scholar]
  8. Darrow M.C., Booth T., Moore J.P., Doering K., Thaw P., King R.S. Enabling a Paradigm Shift in CryoEM Sample Preparation with chameleon. Microsc. Microanal. 2021;27(S1):524–525. doi: 10.1017/S1431927621002336. [DOI] [Google Scholar]
  9. Dickerson J.L., Lu P.-H., Hristov D., Dunin-Borkowski R.E., Russo C.J. Imaging biological macromolecules in thick specimens: The role of inelastic scattering in cryoEM. Ultramicroscopy. 2022;237 doi: 10.1016/j.ultramic.2022.113510. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gatan. (2022). Improving DQE with Counting and Super-Resolution. https://www.gatan.com/improving-dqe-counting-and-super-resolution.
  11. Henderson R. The potential and limitations of neutrons, electrons and X-rays for atomic resolution microscopy of unstained biological molecules. Q. Rev. Biophys. 1995;28(2):171–193. doi: 10.1017/S003358350000305X. [DOI] [PubMed] [Google Scholar]
  12. Huntington B., Zhao L., Bron P., Shahul Hameed U.F., Arold S.T., Qureshi B.M. Thicker Ice Improves the Integrity and Angular Distribution of CDC48A Hexamers on Cryo-EM Grids. Front. Mol. Biosci. 2022;9 doi: 10.3389/fmolb.2022.890390. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Lander, G. C., Stagg, S. M., Voss, N. R., Cheng, A., Fellmann, D., Yoshioka, C., Irving, C., Mulder, A., Lau, P.-W., Potter, C. S., & Carragher, B. (2010). Appion: An integrated, database-driven pipeline to facilitate EM image processing. 16. [DOI] [PMC free article] [PubMed]
  14. Li X., Mooney P., Zheng S., Booth C.R., Braunfeld M.B., Gubbens S., Agard D.A., Cheng Y. Electron counting and beam-induced motion correction enable near-atomic-resolution single-particle cryo-EM. Nat. Methods. 2013;10(6):584–590. doi: 10.1038/nmeth.2472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Martynowycz, M. W., Clabbers, M. T. B., Unge, J., Hattne, J., & Gonen, T. (2021). Benchmarking the ideal sample thickness in cryo-EM. Proceedings of the National Academy of Sciences, 118(49), e2108884118. https://doi.org/10.1073/pnas.2108884118. [DOI] [PMC free article] [PubMed]
  16. Morado, D. (2020). Some timing tests of the Gatan K3. https://forum.scilifelab.se/t/some-timing-tests-of-the-gatan-k3/139.
  17. Nakane T., Kotecha A., Sente A., McMullan G., Masiulis S., Brown P.M.G.E., Grigoras I.T., Malinauskaite L., Malinauskas T., Miehling J., Uchański T., Yu L., Karia D., Pechnikova E.V., de Jong E., Keizer J., Bischoff M., McCormack J., Tiemeijer P., Hardwick S.W., Chirgadze D.Y., Murshudov G., Aricescu A.R., Scheres S.H.W. Single-particle cryo-EM at atomic resolution. Nature. 2020;587(7832):152–156. doi: 10.1038/s41586-020-2829-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Naydenova K., McMullan G., Peet M.J., Lee Y., Edwards P.C., Chen S., Leahy E., Scotcher S., Henderson R., Russo C.J. CryoEM at 100 keV: A demonstration and prospects. IUCrJ. 2019;6(6):1086–1098. doi: 10.1107/S2052252519012612. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Noble A.J., Dandey V.P., Wei H., Brasch J., Chase J., Acharya P., Tan Y.Z., Zhang Z., Kim L.Y., Scapin G., Rapp M., Eng E.T., Rice W.J., Cheng A., Negro C.J., Shapiro L., Kwong P.D., Jeruzalmi D., des Georges, A., Carragher, B. Routine single particle CryoEM sample and grid characterization by tomography. Elife. 2018;7:e34257. doi: 10.7554/eLife.34257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Peet M.J., Henderson R., Russo C.J. The energy dependence of contrast and damage in electron cryomicroscopy of biological molecules. Ultramicroscopy. 2019;203:125–131. doi: 10.1016/j.ultramic.2019.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Pettersen E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., Ferrin T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
  22. Punjani A., Rubinstein J.L., Fleet D.J., Brubaker M.A. cryoSPARC: algorithms for rapid unsupervised cryo-EM structure determination. Nat. Methods. 2017;14(3):290–296. doi: 10.1038/nmeth.4169. [DOI] [PubMed] [Google Scholar]
  23. Rheinberger J., Oostergetel G., Resch G.P., Paulino C. Optimized cryo-EM data-acquisition workflow by sample-thickness determination. Acta Crystallogr. Sect. D Struct. Biol. 2021;77(5):565–571. doi: 10.1107/S205979832100334X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Rice W.J., Cheng A., Noble A.J., Eng E.T., Kim L.Y., Carragher B., Potter C.S. Routine determination of ice thickness for cryo-EM grids. J. Struct. Biol. 2018;204(1):38–44. doi: 10.1016/j.jsb.2018.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Schröder R.R., Hofmann W., Ménétret J.-F. Zero-loss energy filtering as improved imaging mode in cryoelectronmicroscopy of frozen-hydrated specimens. J. Struct. Biol. 1990;105(1–3):28–34. doi: 10.1016/1047-8477(90)90095-T. [DOI] [Google Scholar]
  26. Suloway C., Pulokas J., Fellmann D., Cheng A., Guerra F., Quispe J., Stagg S., Potter C.S., Carragher B. Automated molecular microscopy: The new Leginon system. J. Struct. Biol. 2005;151(1):41–60. doi: 10.1016/j.jsb.2005.03.010. [DOI] [PubMed] [Google Scholar]
  27. ThermoFisher Scientific. (2022). Selectris Applications Notes. https://cryoem.jhmi.edu/wp-content/uploads/2022/07/Selectris_apps_note_v2_1.pdf.
  28. Wu S., Armache J.-P., Cheng Y. Single-particle cryo-EM data acquisition by using direct electron detection camera. Microscopy. 2016;65(1):35–41. doi: 10.1093/jmicro/dfv355. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Xiao C., Chipman P.R., Battisti A.J., Bowman V.D., Renesto P., Raoult D., Rossmann M.G. Cryo-electron microscopy of the giant mimivirus. J. Mol. Biol. 2005;353(3):493–496. doi: 10.1016/j.jmb.2005.08.060. [DOI] [PubMed] [Google Scholar]
  30. Yonekura K., Braunfeld M.B., Maki-Yonekura S., Agard D.A. Electron energy filtering significantly improves amplitude contrast of frozen-hydrated protein at 300kV. J. Struct. Biol. 2006;156(3):524–536. doi: 10.1016/j.jsb.2006.07.016. [DOI] [PubMed] [Google Scholar]
  31. Zheng S.Q., Palovcak E., Armache J.-P., Verba K.A., Cheng Y., Agard D.A. MotionCor2: Anisotropic correction of beam-induced motion for improved cryo-electron microscopy. Nat. Methods. 2017;14(4):331–332. doi: 10.1038/nmeth.4193. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary data 1
mmc1.docx (1.1MB, docx)

Data Availability Statement

Micrographs are available at EMPIAR-11397. Reconstructions are available on EMDB with the following accession codes: for Glacios 0-50 nm, EMD-29566; 50-100 nm, EMD-29567; 100-150 nm, EMD-29568; 150-200 nm, EMD-29569; 200-500 nm, EMD-29570. For Arctica in counting mode 0-50 nm, EMD-29573; 50-100 nm, EMD-29574; 100-150 nm, EMD-29575; 150-200 nm, EMD-29576; 200-500 nm, EMD-29577. For Arctica in super resolution mode 0-50 nm, EMD-29589; 50-100 nm, EMD-29591; 100-150 nm, EMD-29592; 150-200 nm, EMD-29593; 200-500 nm, EMD-29594. For Krios unfiltered 0-50 nm, EMD-29554; 50-100 nm EMD-29555; 100-150 nm, EMD-29556; 150-200 nm, EMD-29557; 200-500 nm, EMD-29558. For Krios filtered 0-50 nm, EMD-29536; 50-100 nm, EMD-29535; 100-150 nm, EMD-29559; 150-200 nm, EMD-29513; 200-500 nm, EMD-29393.

Articles from Journal of Structural Biology: X are provided here courtesy of Elsevier

RESOURCES