Abstract
Electrolytes, consisting of salts, solvents, and additives, must form a stable solid electrolyte interphase (SEI) to ensure the performance and durability of lithium(Li)-ion batteries. However, the electric double layer (EDL) structure near charged surfaces is still unsolved, despite its importance in dictating the species being reduced for SEI formation near a negative electrode. In this work, a newly developed model was used to illustrate the effect of EDL on SEI formation in two essential electrolytes, the carbonate-based electrolyte for Li-ion batteries and the ether-based electrolyte for batteries with Li-metal anodes. Both electrolytes have fluoroethylene carbonate (FEC) as a common additive to form the beneficial F-containing SEI component (e.g., LiF). However, the role of FEC drastically differs in these electrolytes. FEC is an effective SEI modifier for the carbonate-based electrolyte by being the only F-containing species entering the EDL and being reduced, as the anion (PF6–) will not enter the EDL. For the ether-based electrolyte, both the anion (TFSI–) and FEC can enter the EDL and be reduced. The competition of the two species within the EDL due to the surface charge and temperature leads to a unique temperature effect observed in prior experiments: the FEC additive is more effective in modulating SEI components at a low temperature (−40 °C) than at room temperature (20 °C) in the ether-based electrolyte. These collective quantitative agreements with experiments emphasize the importance of incorporating the effect of the EDL in multicomponent electrolyte reduction reactions in simulations/experiments to predict/control the formation of the SEI layer.
1. Introduction
The increasing global energy demand1 and the pressing need to reduce fossil fuel consumption2 require further clean technology development including the improvement of energy density beyond that of lithium (Li)-ion batteries. The development of higher-energy-density electrode materials for Li-ion batteries is closely coupled with the design of electrolytes,3 as the design of electrolytes requires optimizing bulk transport properties as well as the interface/interphase with the electrodes. A typical liquid electrolyte is a liquid mixture of salts, solvents, and additives.4−6 These components jointly determine the electrolyte bulk properties and the electrode–electrolyte interface,7 where a solid electrolyte interphase (SEI) layer is formed by electrolyte reduction on the negative electrode (oxidation on the positive electrode). Constructing a robust and efficient SEI layer with electron resistance, fast ion transport, structural uniformity, and mechanical conformality on deforming electrodes is critical for avoiding dendrite growth and dead Li and for improving Coulombic efficiency.8−11 The SEI layer is a multifunctional nanocomposite—an inorganic inner layer (such as Li2CO3, LiF, and Li2O) near the electrode/SEI interface and an organic outer layer (such as lithium butylene dicarbonate and lithium ethylene dicarbonate) near the SEI/electrolyte interface.12,13 Despite tremendous experimental and modeling efforts, controlling the formation and growth of the nanometer-thick SEI films by electrolyte design remains critically challenging.14−19 It is even more challenging on Li-metal electrodes, where the electrolyte reduction reactions and Li deposition are intertwined.20 The reduction products of the electrolytes form the SEI layer, whose composition, heterogeneity, and thickness largely determine the Li-plating and stripping processes and thus the cycling performance.
Modeling of electrolyte reduction has provided tremendous atomistic insights into SEI formation processes, especially in light of the lack of direct experimental observations.14 Density functional theory (DFT) calculations of electrolyte species (salt, solvent, and additive) in the gas phase or with an implicit solvation model have revealed both the thermodynamics and kinetics of reduction processes,21−27 which have confirmed some of the reaction mechanisms deduced from experimental data.28,29Ab initio molecular dynamics (AIMD) simulations based on DFT became feasible for relatively large systems with the advancement of supercomputers.30 A series of reaction events were tracked within several picoseconds at the electrode/electrolyte interfaces using AIMD simulations.31−33 Nevertheless, the high costs of DFT-based calculations still limit the simulation size and time scale, so the electrolyte is often simplified to ion pairs in several solvent molecules and the long-range diffusion in the electrolyte is ignored. To address this issue, classical MD techniques with conventional or polarizable force fields have been developed to simulate the bulk electrolytes or the hybrid electrode/electrolyte systems, through which electrolyte structures and solvation environments have been extensively investigated.34−38 However, these MD simulations did not provide the details of electrolyte reduction reactions. Recently, two multiscale modeling methods were developed. Presampled reduction reaction pathways of solvent molecules coordinated with or without ions served as input for both the kinetic Monte Carlo (KMC) method and/or MD simulations to track chemical reactions and SEI formation in a longer time scale.39−41 In these simulations, the electric potential on the electrode was used to determine the reduction reactions, but their impact on the electrolyte structure was not included.
It is well known that ions in the electrolyte will redistribute near charged surfaces, forming the so-called electrical double layer (EDL) structure, which is different from the bulk electrolyte and varies as a function of the potential on the electrode. Furthermore, the electric potential on the electrode can reorient the polarizable solvent molecules, such as ethylene carbonate (EC).42 Since the SEI layer is mainly formed by electrolyte reduction reactions,43,44 they should be sensitive to the electrolyte structures within the EDL that are subject to an external electric field. However, the impact of the EDL on SEI formation has been rarely considered in the literature.45−48 As mentioned before, previous simulations mainly reported reduction reactions of simple solvent or Li+-coordinated solvent species without consideration of the EDL structures under the electric field for investigation of those reduction reactions.22,24−26,49−52 Therefore, it is critical to gain atomistic insights into the reduction reactions of the electrolyte species in the EDL to help predict and control the formation of the SEI layer as well as the Li-plating morphology.45
In this work, instead of taking DFT results as input to MD or KMC models, we feed MD-predicted EDL structures into DFT calculations. Specifically, MD simulations, which can deal with thousands to millions of atoms, are first used to capture the dynamics and statistics of the EDL structures of a realistic multicomponent electrolyte. Then, DFT calculations are used to compute the reduction potentials of the electrolyte species found in the EDL. Finally, the DFT-calculated reduction potentials of the Li+-coordinated clusters and free electrolyte species (without coordination to any Li+ ions) and their occurrence probabilities are ranked to show the sequence of reduction reactions while the potential on the electrode is lowered. The statistical representation of the reduced electrolyte species can be directly correlated with the SEI components observed in experiments.
We have applied this new interactive MD-DFT-data model to two types of essential multicomponent electrolytes, the carbonate-based electrolyte and the ether-based electrolyte, motivated by their applications for graphite and Li-metal electrodes, respectively. The carbonate-based electrolyte for typical Li-ion batteries consists of a 1 M concentration lithium hexafluorophosphate (LiPF6) salt dissolved in the mixed ethylene carbonate (EC) and ethyl methyl carbonate (EMC) solvent.5 However, it fails to be compatible with Li-metal anodes due to severe side reactions and the formation of a heterogeneous and unstable SEI layer, which results in whisker-shaped Li dendrite growth and short cycle life.53 Ether-based electrolytes, such as the mixed 1,3-dioxolane (DOL) and 1,2-dimethoxyethane (DME) solvent together with the lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) salt, show improved compatibility with the Li-metal anode54−57 owing to the better reductive stability of the ether solvent.58−60 In these electrolytes, fluoroethylene carbonate (FEC) is a common additive. The role of additives in SEI formation remains a mystery. However, the first question that needs to be addressed is whether the additive can enter the EDL and participate in the SEI formation process.
Recognizing the complexity of the SEI composition, structure, and properties, we will first focus on the F-containing component, as many recent studies have correlated LiF-rich SEI with improved cyclability for Li-metal electrodes.61−67 First, LiF is thermodynamically stable on a Li-metal surface, while Li2CO3 can be further reduced to Li2O.68 According to DFT calculations, LiF can block electron tunneling more effectively than Li2CO3.69 Crystalline LiF is not a good Li-ion conductor,70 but it can increase Li-ion conductivity when combined with Li2CO3 by forming a space charge layer.71 Experimentally, the ex situ-formed LiF SEI layer showed higher overpotential for Li-plating, but the regenerated LiF-containing SEI from the liquid electrolyte plays a more critical role in protecting the Li-surface.66 Therefore, it is reasonable to conclude that LiF-rich SEI formed from liquid electrolyte reduction reactions can be thermodynamically stable, mechanically repairing, electronically insulating, and ionically conductive. Compared to Li2O and Li2CO3, which are inevitable on the Li-metal surface when it is exposed to air, LiF can only form due to electrolyte decomposition. Therefore, we especially focus on the three components that can contribute to LiF formation, namely, PF6– and TFSI– anions as well as the FEC additive. Their involvement in the EDL and SEI formation will be compared in these two electrolyte systems. To focus on the role of EDL, we did not track the dynamics of SEI formation. The initial formation of SEI can gain many insights from modeling;47 however, the accumulation of the nanometer-thick SEI is beyond the current modeling capability.49 Since many intermediate species may eventually reduce to the thermodynamic stable phases on Li-metal, we consider that the species within the EDL that can be reduced above Li-metal reduction potential will be eventually converted to the stable SEI component, such as LiF.
The rest of the paper is organized as follows. First, we give a description of computational details of the interactive MD-DFT-data model, including MD simulations of bulk electrolytes, MD simulations of the EDL with interface models, DFT calculations of reduction potentials as well as data statistics for electrolyte reduction in the EDL. Then, we discuss the EDL structures and reduction reactions for the carbonate-based electrolyte, 1.0 M LiPF6@EC:EMC, as well as how FEC tunes the reduction of the EDL and SEI formation. After that, we discuss the EDL structures and reduction reactions for the ether-based electrolyte 0.9 M LiTFSI@DOL:DME. Finally, we discuss how FEC tunes the electrolyte reduction within the EDL and SEI formation for the ether-based electrolytes at both room and low temperatures and provide new insight into the temperature-dependent FEC additive effect.
2. Methodology
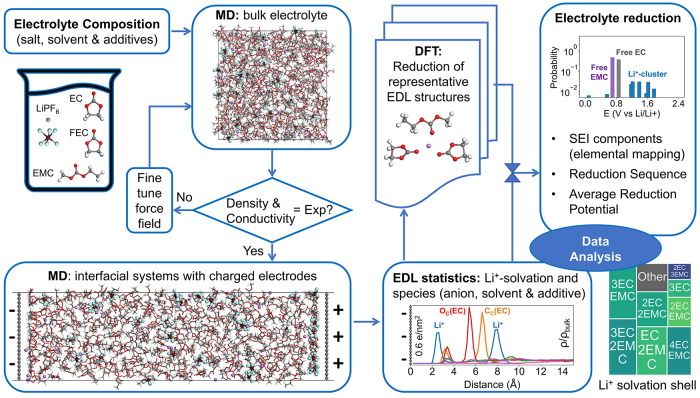
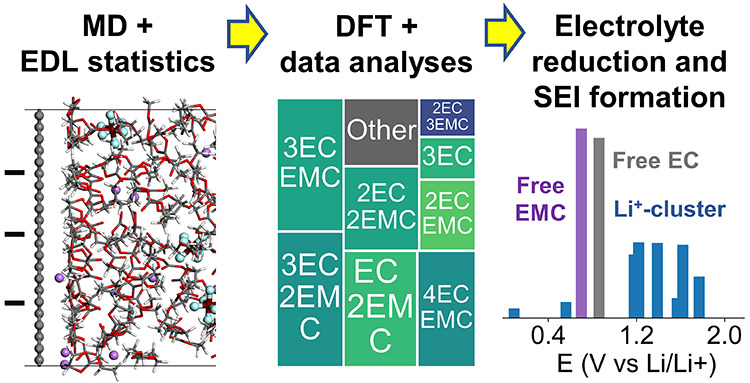
The scheme of our interactive MD-DFT-data model is shown in Figure 1. Five main steps of the modeling are: (1) MD simulations of bulk electrolytes to calibrate the force field setting; (2) MD simulations of the EDL structure with interface models; (3) statistical analysis of Li+-coordinated solvation clusters and free species in the EDL; (4) DFT-calculated reduction potentials and pathways for the representative structures in EDL; and (5) combining the EDL statistics and DFT results to obtain the statistics of the reduced species, average reduction voltage, SEI components, and SEI formation mechanism.
Figure 1.
Scheme of the MD-DFT-data interactive model proposed in this work to investigate the effect of the EDL on electrolyte reduction and SEI formation.
2.1. MD Simulations of Bulk Electrolytes
All MD simulations were carried out through the Forcite module as implemented in Materials Studio (MS) 2020.72 The COMPASS III force field73 was used along with optimized atom types and charges (see the Supporting Information (SI) and Figure S1 for details). A charging scaling of 0.7 is used for the cation (Li+) and anions since (1) it shows a good balance between cation–anion and cation–solvent interactions when compared to DFT-calculated binding energies (Figure S2) and (2) it gives accurate estimations of the electrolyte densities and Li+ ion conductivities (Figures S3–S6) when compared to previous theoretical and experimental values.34,56,61,74 The atomistic model for the carbonate-based electrolyte was constructed to be ∼1.0 M LiPF6 salt dissolved in the mixed solvent composed of 30 vol % EC and 70 vol % EMC. The atomistic model for the ether-based electrolyte was constructed to be ∼0.9 M LiTFSI salt dissolved in the mixed solvent composed of 80 vol % DOL and 20 vol % DME. Both electrolytes have FEC as an additive with a volume increase of less than 10% (see Li+ concentrations for different electrolytes in Figures S3–S6).
2.2. MD Simulations of the EDL Structure
An interface model, as shown in Figure 1 (as an inset), was used to obtain the EDL structures. The interface model consists of two graphene electrodes, an electrolyte that contains the same number of electrolyte species as those for bulk simulations, and a vacuum layer. The x- and y-dimensions of the periodic simulation cells are 25.6 Å × 27.1 Å. The electrolyte thickness between the two graphene electrodes thickness is ∼100.0 Å, obtained through equilibration simulations, which is large enough to ensure bulk electrolyte behavior in the middle region.75 The graphene electrodes were fixed for the subsequent simulations. They are negatively (left) and positively (right) charged and termed as anode and cathode, respectively. The vacuum layer is more than 3 times thicker than the electrolyte layer to eliminate the artificial image effects from the periodic cells. Both previous simulations76 and our tests showed that the vacuum space is large enough to produce the correct number and charge density profiles and thus to well describe the EDL structures. The SEI layer is not included in the interfacial model to simulate the initial steps of SEI formation,77 although its structure and chemistry will play a role in the growth of thicker SEI layers.37,78
We applied a surface charge density of σ = ±0.6 e/nm2, which is determined as the surface charge (0.5–0.7 e/nm2) at the electrochemical equilibrium condition for Li+/Li0 in EC based on DFT and density functional tight binding (DFTB) methods.42 Additional surface charge densities (0.0, ±0.4, ±0.8, and ±1.2 e/nm2) were also used to evaluate the effects of charge densities on the EDL to mimic the charging processes under different overpotentials. The surface charge is evenly distributed in all of the atoms of the graphene electrodes, which is a typical constant charge method, capturing a locally flat electrode surface in a one-dimensional EDL model.77,79−83
2.3. EDL Statistical Analysis
For each simulation (more details in the SI), the interfacial system was equilibrated for 2.0 ns under the NVT ensemble under uncharged conditions and then for 4.0 ns under each charge density condition followed by a production run for another 4.0 ns, whose trajectory was taken for statistical analyses. In this work, the EDL is defined as the region within 10.0 Å from the surface of the negatively charged graphene electrode.40 A species was considered to be located within the EDL if any of the atoms of the species was in the EDL (a distribution near the negatively charged surface is shown as an inset in Figure 1). Since the Li+ coordination can increase the reduction voltage of a solvent species dramatically,24 we analyzed the statistics of the electrolyte in the EDL in terms of (a) solvents/anions coordinated with Li+ in the first solvation shell and (b) free solvent/anions species (not coordinated to any Li+).
2.4. DFT Calculations of the Reduction Voltages
Each Li+-coordinated cluster (typically containing three to five solvent molecules and/or anions/additives) and free species (anion, solvent, or additive molecule) within the EDL was considered as an independent electron-capturing center that can be reduced. These local molecular structures are taken as input for DFT calculations to reoptimize the molecular geometry, followed by calculations of the reduction potential with an implicit solvation model. All DFT calculations were conducted using the Gaussian 09 code.84 The double hybrid functional M06-2X85 and the basis set 6-31+G(d,p) along with the D3 dispersion correction86 were used. The SMD87 solvation model was used to account for the solvation environment. The dielectric constants were set to ε = 20.5 for the carbonate-based electrolytes50,88 and ε = 7.2 for the ether-based electrolytes.89 The reduction potential with respect to (wrt) Li+/Li0 was calculated using the equation E(vs. Li/Li+) = −ΔG/F – 1.4, where ΔG is the Gibbs free energy change for the one-electron reduction reaction and F is the Faraday constant. The Gibbs free energy change was calculated as the difference between the Gibbs free energies of the reaction products and those of the reactants.
2.5. Statistical Representations of the SEI-Forming Species and Averaged Reduction Voltage
In the current model, the probability for reduction reactions due to electron tunneling as a function of the distance to the electrode surface90 was not yet considered for simplicity. We first consider which species in the EDL can be reduced. For the EDL structure, we have used molecule-based counting. For the onset of electrolyte reduction reactions, we used one-electron reduction-center-based counting. This means that each Li+-coordinated cluster was counted as one and the number of each Li+-coordinated cluster type, Ni, sums to the total number of Li+ ions, NLi = ∑iNi. A cutoff of 2.8 Å was used34 to determine whether a Li+ ion is coordinating with the O, F, and N atoms in the anion, solvent, or additive molecules. Each free species was counted as one, and the number of each species type, Nj, sums to the total number of free species, Nf = ∑jNj. Thus, the SEI formation probability for each Li+-coordinated cluster, i, is Pi = Ni/(NLi + Nf), while the SEI formation probability for each free species, j, is calculated as Pj = Nj/(NLi + Nf).
Furthermore, we can define an average reduction potential for the multicomponent electrolyte as Eave = ∑iPiEi + ∑jPjEj, where Ei and Ej are the corresponding reduction potentials of the Li+-coordinated cluster and free species, respectively. This simplification can serve as an input for continuum-level electrochemical simulations, such as the phase-field model, to quantitatively predict the SEI growth and Li-plating–stripping morphology.
Another statistical information we can obtain is the SEI components. We consider each reducible species (with a positive reduction potential with respect to Li+/Li0) will eventually be converted to SEI after a series of reduction reactions. Therefore, an atom-based counting of the F, C, and O species can be obtained to compare with atomic concentrations in the SEI layer reported in experiments.61
3. Results and Discussion
3.1. Statistics of the Solvent, FEC Additive, and Anion in the Solvation Shell of the Bulk Electrolytes
Before assessing the interfacial solvation structures in the EDL, the Li+ ion solvation behaviors were first analyzed in the bulk electrolytes. Four electrolyte systems were investigated in this study, namely, the carbonate-based electrolyte (i.e., ∼1.0 M LiPF6 salt in the mixed EC and EMC solvent) and ether-based electrolyte (i.e., ∼0.9 M LiTFSI salt in the mixed DOL and DME solvent) as well as the two electrolytes with FEC as an additive (see Figures S3–S6 for details).
Based on the average coordination numbers (CN) of each species in the Li+ ion solvation shell, it can be seen that EC molecules contribute the most to the first solvation shell of Li+ ions (average 2.26 out of 4.37 coordination number, CN), followed by EMC molecules (average 1.76 out of 4.37 CN) in the LiPF6@EC:EMC electrolyte (Figure S3). This reveals the coordination preference of cyclic over linear carbonate molecules to Li+ ions, which is consistent with previous experimental measurements91 and theoretical findings.92 In addition, the LiPF6 salt is found to be mostly dissolved in the mixed EC and EMC solvent considering the small contribution of the PF6– anions to the Li+ solvation shell (Figure S3).
In the LiTFSI@DOL:DME electrolyte (Figure S5), DME molecules (average 1.65 out of 3.37 CN) contribute the most to the first solvation shell of Li+ ions, followed by almost equal contributions by TFSI– and DOL, corroborating previous ab initio molecular dynamics study.91 The cation–anion coordination in the ether electrolyte becomes more significant than that in the carbonate-based electrolyte due to the smaller dielectric constant and less solvating ability of ether-based solvents, which is favorable for the appearance of contact ion pairs and thus the formation of anion-induced SEI components.6
Although FEC has been used as an additive to promote the LiF component in SEI,64,93 FEC participates in the Li+-ion solvation structure differently in the carbonate-based and ether-based electrolytes based on the solvation structure analyses. In the LiPF6@EC:EMC electrolyte, the solvation shells with the highest probabilities include Li+-2EC-2EMC, Li+-3EC-EMC, Li+-3EC-2EMC, and others (Figure S3e). After FEC is added to form the LiPF6@EC:EMC:FEC electrolyte, part of the solvation shell is replaced by FEC, but the top two solvation structures remain the same (Li+-2EC-2EMC and Li+-3EC-EMC) (Figure S4e). In contrast, the top two solvation shells (Li+-TFSI–-2DME and Li+-2DME-DOL) with the highest probabilities in LiTFSI@DOL:DME (Figure S5e) are replaced by Li+-2DME-FEC and Li+-TFSI–-DME-DOL-FEC after FEC is added (Figure S6e). The difference is caused by the relative binding energies to a Li+ ion, which ranks as Li+-TFSI– > Li+-PF6– > Li+-EC > Li+-FEC ∼ Li+-EMC > Li+-DME ∼ Li+-DOL (Figure S2). Therefore, FEC penetrates more into the DME-dominated solvation shells in the ether-based electrolytes than the EC-dominated solvation shells in the carbonate-based electrolytes.
3.2. EDL Structure and SEI Formation of the Carbonate-Based Electrolytes
3.2.1. Statistics of the EDL Structures in the LiPF6@EC:EMC Electrolyte with and without FEC
The characteristics of the EDL are clearly seen from the fluctuation of the electrolyte charge densities (Figure S7) for the carbonated-based electrolytes under different surface charge densities of the graphene electrode. The electrolyte charge densities start converging to zero as the distance gets beyond 10.0 Å, indicating the thickness of the EDL.
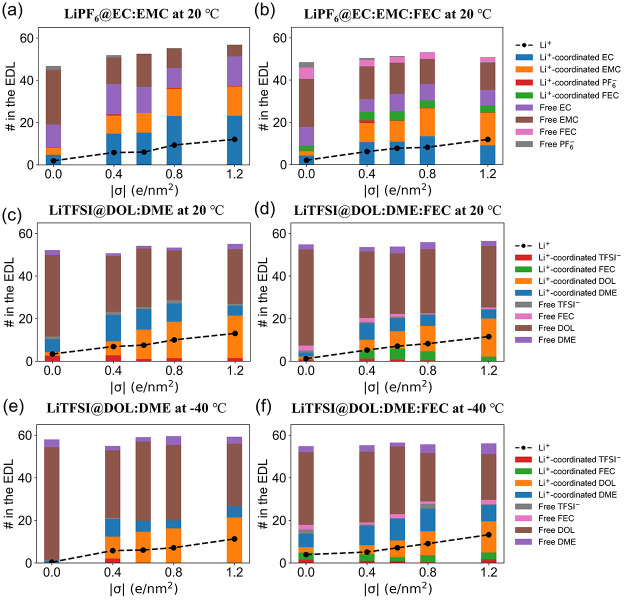
The numbers of the electrolyte species in the EDL for the carbonate-based electrolytes are summarized in Figure 2a,b (following molecule-based counting). Within the EDL near the negatively charged surfaces, not only do the number of Li+ ions increase with the charge density on the electrode, but also the numbers of solvent (EC and EMC), additive (FEC), and anion (PF6–) species vary with the surface charge, highlighting the importance of considering the reduction reactions of the electrolyte species within the EDL. In general, the number of free solvents decreases and that of Li+-coordinated solvents increases with more negative electron density on the electrode surface. The nonmonotonic change of EC in the EDL is mainly due to the first solvation shell change on charged surfaces.
Figure 2.
The number of species (Li+, EC, EMC, FEC, and PF6–) in the EDL for the carbonate-based electrolytes, (a) LiPF6@EC:EMC and (b) LiPF6@EC:EMC:FEC at 20 °C. The number of species (Li+, TFSI–, FEC, DOL, and DME) in the EDL for the ether-based electrolytes, (c) LiTFSI@DOL:DME and (d) LiTFSI@DOL:DME:FEC at 20 °C as well as (e) LiTFSI@DOL:DME and (f) LiTFSI@DOL:DME:FEC at −40 °C.
Figures S8 and S9 further showed the spatial distribution of each species within the EDL. The Li+ ion density peak becomes more prominent with more negative charges on the surface, and the peak position also gets closer to the surface. Two layers of Li+ ions are within the 10.0 Å thick EDL. The first-layer Li+ ions are at a distance of ∼2.0 Å and the second-layer Li+ ions are at ∼8.0 Å from the negatively charged surface (Figure S8). Figure S9 shows that the coordination numbers of different species around the first-layer Li+ ions vary with the surface charge density, while the coordination environments of the second-layer Li+ ions remain constant. It is important to notice that when the graphene electrode is not charged, the total Li+ coordination number to O/F is ∼4.4, with the largest contribution from EC, close to that obtained for the bulk electrolytes (Figures S3 and S4). When the graphene electrode is negatively charged, the total coordination number of the first-layer Li+ ions decreases as they lose part of the solvation shell when getting closer to the negatively charged surface. The loss mainly comes from the loss of EC in the first solvation shell and thus, EMC starts dominating the Li+ solvation shell. This is because EMC is less polar than EC, whose oxygen atoms are repelled away from the negatively charged surface.
3.2.2. Reduction of the LiPF6@EC:EMC Electrolyte in the EDL with and without FEC
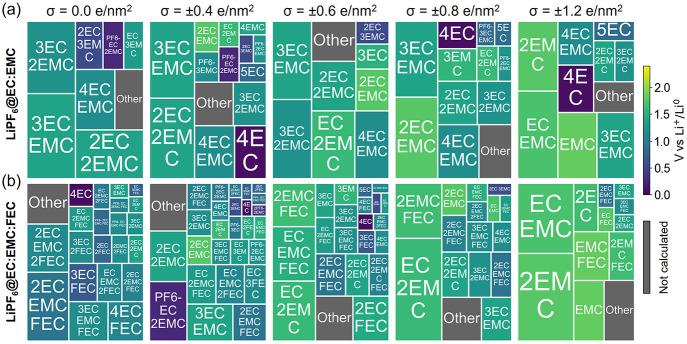
As we discussed above, the EDL presents complicated local structures that can dramatically change the reduction voltage and the composition and morphology of the SEI layer. With increasing surface electron densities on the electrode, more than half of the electrolytes in the EDL are coordinated with Li+-ions (e.g., Figure 2a). These Li+-coordinated species are represented as Li-ion solvation clusters (in Figure 3) for DFT reduction potential calculations. The percentage of each Li+-coordinated cluster within the EDL is represented as the area in Figure 3. All of the computed Li+-coordinated clusters accumulate to 90% of NLi. The reduction potential for each cluster is color-coded in Figure 3. With increasing negative charge density on the electrode, the Li+-coordinated clusters become smaller (also shown in Figure S9), and these smaller clusters tend to have higher reduction voltages. One would expect that at a lower voltage (corresponding to a more negatively charged surface), the EDL layer will favor more reduction reactions.
Figure 3.
Probability distributions of the solvation structures in the first solvation shell of Li+ ions within the EDL (10.0 Å from the negatively charged graphene electrode) under different graphene electrode charge densities: (σ = 0.0, ±0.4, ±0.6, ±0.8, and ±1.2 e/nm2) for the (a) LiPF6@EC:EMC and (b) LiPF6@EC:EMC:FEC electrolytes. Those solvation shell structures with the highest probabilities that accumulate up to 90% are shown with their reduction potentials (indicated by color coding), while the rest is labeled with “Other” (in gray).
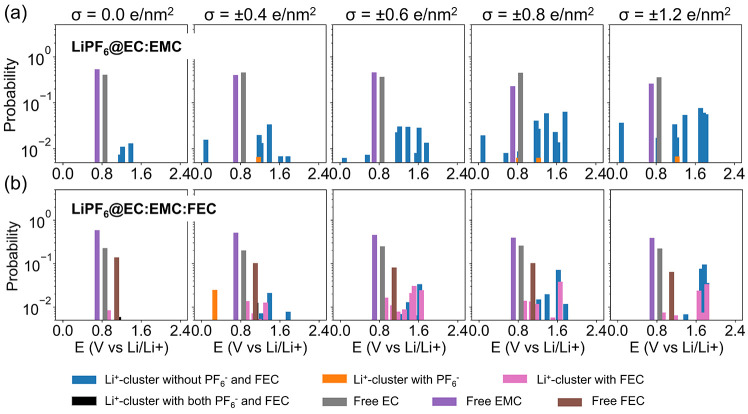
With increasing electron densities on the electrode, fewer free species appear in the EDL. The free species in the carbonate-based electrolyte, EC, EMC, and FEC, can be reduced above zero voltage, but free PF6– will not be reduced according to the computed reduction voltage (Figure S10). The well-studied EC has a cyclic shape and will be referred to as c-EC in the following discussions.26 It is energetically favorable for c-EC to open its ring upon reduction by breaking the bond that connects ethereal oxygen (OE) and ethereal carbon (CE),22 and to form the ring-opened EC anion (o-EC–).26 EMC has a reduction potential that is close to that of EC, as the DFT-calculated reduction potentials are 0.86 and 0.70 V vs. Li+/Li0 for c-EC and EMC, respectively (Figure S10), consistent with literature results.24,26 Free FEC has a slightly higher reduction potential (1.10 V vs. Li+/Li0) compared to c-EC and EMC.
As both Li+-coordinated clusters and free species can be reduced and contribute to SEI formation in LiPF6@EC:EMC, their probability (defined as Pi and Pj in the methods section) was plotted against their reduction potentials in Figure 4a. It is seen that free EC and EMC molecules make the most contributions to their abundance in the EDL. On the other hand, the Li+-coordinated clusters will be reduced prior to free EC and EMC molecules since they have generally higher reduction potentials.94 This means as the electric potential is lowered in SEI formation cycles (i.e., from higher to lower values),95 the Li+-coordinated clusters will be reduced first and form the initial SEI layer. The contribution of the reduction of Li+-coordinated clusters increases with a more negatively charged graphene electrode that attracts more Li+ ions.
Figure 4.
Probabilities in the logscale of DFT-calculated reduction potentials for (a) LiPF6@EC:EMC and (b) LiPF6@EC:EMC:FEC electrolytes under different surface charge densities of the graphene electrode. Contributions from different clusters and species are color-encoded, including free EC, free EMC, free FEC, and Li+-coordinated clusters with or without PF6– as well as Li+-coordinated clusters with or without FEC.
We have further calculated average reduction potentials based on the probabilities and the reduction voltage shown in Figure 4 for both the LiPF6@EC:EMC and LiPF6@EC:EMC:FEC electrolytes (Figure S11). The average reduction potentials increase as the graphene electrode charge density increases, being consistent with the general trend that more Li+-coordinated clusters appear in the EDL with a more negatively charged graphene electrode. The average reduction potentials can be used as inputs for phase-field simulations to quantitatively predict the SEI growth and Li-plating–stripping morphology,96−98 which is out of the scope of this work.
3.2.3. F-Containing SEI Species in LiPF6@EC:EMC with and without FEC
The two F-containing species are PF6– and FEC in the carbonate-based electrolytes. Free PF6– has a negative reduction potential (−0.65 V vs. Li+/Li0, Figure S10), which means it cannot be reduced, not to mention that it is mostly expelled from the negatively charged electrode (Figures 2 and S8). Although the reduction potential becomes positive by forming one LiF molecule when PF6– is coordinated with a Li+ ion (e.g., single LiPF6 has a reduction potential of 1.08 V vs. Li+/Li0, Figure S10), it barely contributes to reduction reactions considering its very small occurrence probability (orange bars in Figure 4a). Therefore, there will be no or little F-containing SEI component from reduction reactions of the LiPF6@EC:EMC electrolyte in the EDL. This also suggests that the experimentally identified F-containing SEI components can only come from the thermal decomposition of LiPF699 or chemical reactions triggered by the trace amount of water.100,101
When FEC molecules are added to form the LiPF6@EC:EMC:FEC electrolyte, they appear in the EDL (Figure 2b) as both free FEC and Li+-coordinated FEC by replacing EC. It is interesting to note that as the electrode surface becomes more negatively charged, the amount of Li+-coordinated FEC is less sensitive to the surface charge compared to EC and EMC. As a result, its contribution to the SEI layer formation becomes significant, as FEC shows up in many solvation shells of the Li+ ions in the EDL (Figures 3b and S9). FEC-containing Li+-coordinated clusters also start making significant contributions with a more negatively charged graphene electrode (Figure 4b). Li+-coordinated clusters that contain FEC have generally larger reduction potentials than their counterparts without FEC additive and free species (Figures 3 and S10), which means they will be reduced prior to other species.
Figure 5 shows the number of F atoms in the EDL that will be reduced (assuming its fate is LiF within the SEI upon reduction reactions) for both electrolytes with and without the FEC additive. The nonmonotonic increase of F is mainly due to the number of Li+ and PF6– ion pairs showing a nonmonotonic change with the surface charge, as more negative charges will attract Li+ but repel PF6– in the EDL. Overall, the LiPF6@EC:EMC:FEC electrolyte shows an increased number of F atoms in the EDL than LiPF6@EC:EMC without any additive. Therefore, FEC will greatly promote the LiF component in the SEI, which will then enhance the battery performance.64
Figure 5.
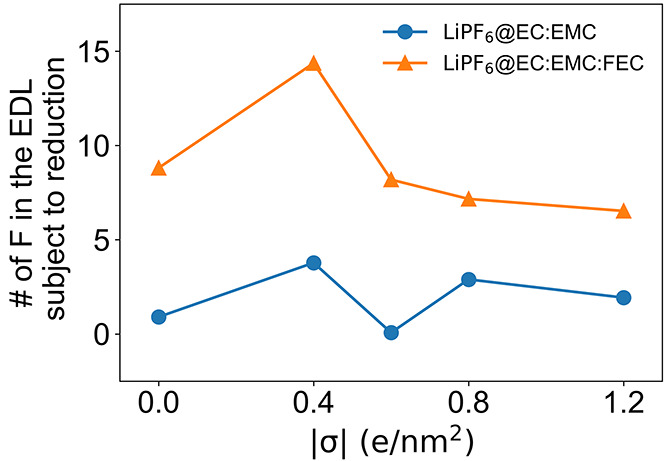
MD-calculated number of F atoms in the EDL in the LiPF6@EC:EMC (blue line and dots) and LiPF6@EC:EMC:FEC (orange line and dots) electrolytes as functions of the surface charge densities of the graphene electrode. Note that free PF6– has a negative reduction potential and thus its F atoms are not subject to the reduction reaction and are not counted here.
3.3. Ether-Based Electrolytes: Temperature Effects of the FEC Additive on Modifying the SEI Formation
3.3.1. EDL Structures of the Ether-Based Electrolyte (LiTFSI@DOL:DME) at Room Temperature
The electrolyte charge density and number density profiles for the ether-based electrolytes (LiTFSI@DOL:DME and LiTFSI@DOL:DME:FEC) also show clear EDL characteristics with two layers of Li+ ions within the EDL (Figures S12 and S13). Figure 2c–f shows the number of different species in the EDL as a function of the surface charge density of the graphene electrode at room temperature (20 °C) and a low temperature (−40 °C). Among the free species, DOL molecules dominate due to their abundance in the electrolyte (the volume ratio of DOL to DME is set to 8:2 for consistency with prior experiments,61 corresponding to a molar ratio of 6:1; see Figure S5). However, the Li+-ion-coordinated DME has a much higher percentage than the free DME in the EDL, as they are more preferred in the Li+-ion solvation shell, especially in the bulk electrolyte and when the surface charge is lower (σ = 0.0 or ±0.4 e/nm2). Figure S14 further calibrates that the Li+ ion solvation shell change with the surface charge density of the graphene electrode and the DME/DOL coordination number ratio decreases with more negative electron density on the graphene electrode as the negative charge on the surface repels DME more than DOL. Different from the PF6– anion, the TFSI– anion shows up in the EDL due to the strong ion pairing between Li+ and TFSI– and the less polar ether-based solvents. However, the number of TFSI– in the EDL will decrease with more negative charges on the electrode surface due to repulsion. These EDL structures are the results of balancing all of the interatomic interactions and electrostatic interactions with the charged electrode surface.
3.3.2. Reduction Reactions and the FEC Additive Effect for LiTFSI@DOL:DME at Room Temperature (20 °C)
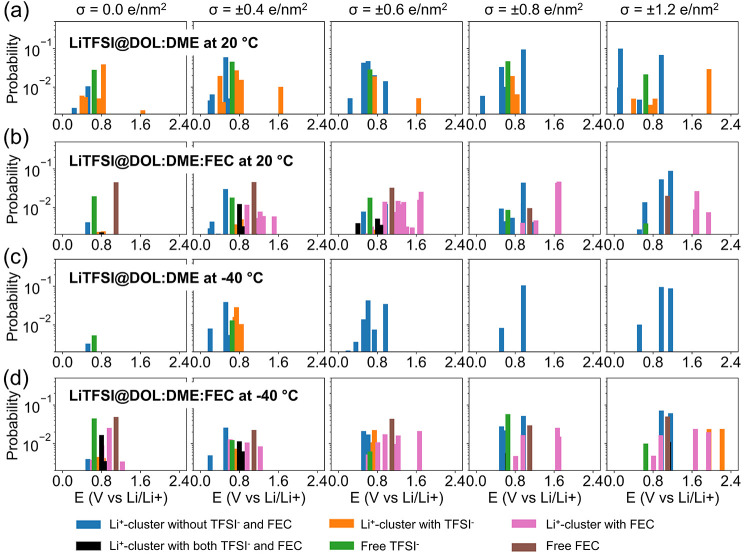
Following the same computational procedure of evaluating the reduction potentials of all of the species in the EDL in the ether-based electrolyte reveals several important differences from the carbonate-based electrolyte shown in Section 3.2. First, free DME and DOL molecules, which make the most contributions to the EDL structures, do not reduce on the Li-metal electrode (with a negative reduction potential, −1.01 V for DME and −0.43 V for DOL vs. Li+/Li0, see Figure S10). This means less SEI will be formed in the DME-DOL mixed electrolytes. Therefore, the Li+-coordinated clusters in the EDL of the LiTSI@DOL:DME electrolyte will dominate the SEI formation. Figure S15a,b shows the percentage of each dominating Li+-coordinated cluster and Figure 6a,b shows the probability (Pi) distributions of all of the reducible Li+-coordinated clusters against their reduction potentials for the ether electrolytes (with or without the FEC additive) at room temperature (20 °C). All F-containing free species (TFSI– and FEC) and almost all Li+-coordinated clusters (the exception is Li+-3DME) have positive reduction potentials, indicating they can be reduced once they show up in the EDL.
Figure 6.
Probabilities in the logscale of DFT-calculated reduction potentials for (a) LiTFSI@DOL:DME at 20 °C, (b) LiTFSI@DOL:DME:FEC at 20 °C, (c) LiTFSI@DOL:DME at −40 °C, and (d) LiTFSI@DOL:DME:FEC at −40 °C under different surface charge densities of the graphene electrode. Contributions from different clusters and species are color-encoded, including free TFSI–, free FEC, Li+-coordinated clusters with or without TFSI–, and Li+-coordinated clusters with or without FEC.
When FEC is added to form the LiTFSI@DOL:DME:FEC electrolyte, FEC replaces part of the solvation shell of Li+ ions (Figures 2 and S14). Both free FEC molecules and Li+-coordinated clusters that contain FEC molecules make significant contributions to reduction reactions in the EDL (Figure 6b). In the meantime, the contributions by TFSI– and Li+-coordinated clusters that contain TFSI– become much less compared to the base electrolyte without the FEC additive (LiTFSI@DOL:DME). As a result, there is no obvious gain in the number of F in the EDL (and thus LiF formed as an SEI component) by introducing the FEC additive at room temperature (20 °C) (Figure 7a).61 In the meantime, the number of C and O atoms in the EDL remains almost unchanged after adding FEC at 20 °C, indicating that inorganic Li2O and Li2CO3 and many other possible organic components in the SEI will vary little as well. As a result, the battery cycling performance is expected to change little, as has been observed in our previous experimental work.61
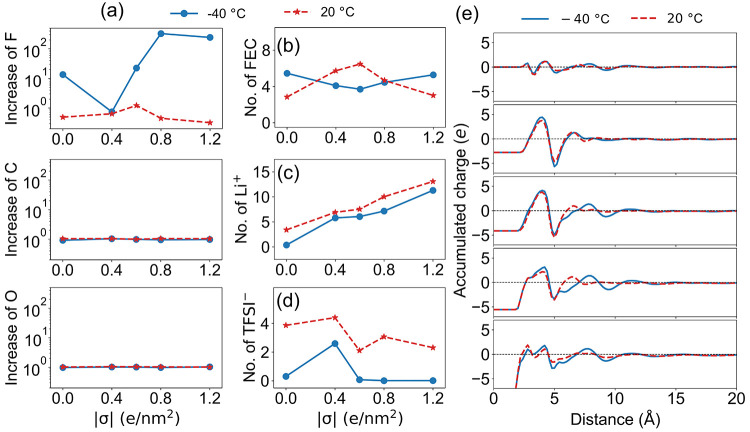
Figure 7.
(a) Increases in the number of F atoms (upper panels), C atoms (middle panels), and O atoms (lower panels) in the EDL after adding the FEC additive obtained from MD simulations conducted at a low temperature (−40 °C, blue solid lines) and room temperature (20 °C, red dashed lines). Note that each TFSI– has six F atoms, while each FEC has only one F atom. (b) Number of FEC molecules in the EDL for the LiTFSI@DOL:DME electrolyte with the FEC additive at a low temperature (−40 °C) and room temperature (20 °C). (c) Number of Li+ in the EDL for the LiTFSI@DOL:DME electrolyte at a low temperature (−40 °C) and room temperature (20 °C). (d) Number of TFSI– ions in the EDL for the LiTFSI@DOL:DME electrolyte at a low temperature (−40 °C) and room temperature (20 °C). It is seen that both the number of Li+ ions and TFSI– in the EDL at room temperature (20 °C) are larger than those at a low temperature (−40 °C). (e) Accumulated charges as functions of distance from the negatively charged graphene electrode at different surface charge densities of the graphene electrode. It is seen that the accumulated charge converges more quickly to zero at room temperature (20 °C), suggesting that the negative charge in the negatively charged graphene electrode is screened by the EDL more efficiently at room temperature (20 °C) than that at a low temperature (−40 °C).
3.3.3. FEC Becomes More Effective in Promoting LiF Formation at a Low Temperature (−40 °C) for LiTFSI@DOL:DME
Interestingly, the experimental study showed that (a) the LiTFSI@DOL:FECDME electrolyte showed worse cycling performance at low temperatures (≤−20 °C) compared to room temperature and (b) the FEC additive becomes more effective in generating inorganic SEI and improving performance at low temperatures (≤−20 °C).61 To understand this phenomenon, we have also conducted interfacial simulations at a low temperature of −40 °C to investigate the temperature effect on how the FEC additive tunes the formation of the SEI layer. Figure 6c,d shows the probability distribution of species against their reduction potentials for the LiTFSI@DOL:DME electrolyte with or without the FEC additive at −40 °C under different surface charge densities of graphene electrodes. In the base electrolyte, the number of TFSI– becomes much less near the negatively charged graphene electrode at −40 °C (Figure 6c) compared to that at 20 °C (Figure 6a), in agreement with the poorer SEI performance at −40°C. In the electrolyte with the FEC additive, FEC still appears in the EDL (Figure 7b) despite the lack of TFSI– in the EDL, leading to enhanced SEI performance. Therefore, the contribution of TFSI– in the EDL in the base electrolyte without the FEC additive determines how effectively FEC can tune the formation of LiF in the SEI layer.
Considering TFSI– is repulsive with the negatively charged graphene electrode, it can exist near the negatively charged graphene electrode only because the negative charge of the latter one is screened by the EDL. To be more specific, the negative charge of the electrode is mostly screened by the Li+ ions in the EDL, considering that both solvent and additive molecules are neutral. As shown in Figure 7c, the numbers of Li+ ions in the EDL at a low temperature (−40 °C) are constantly smaller than those in the EDL at room temperature (20 °C) at all surface charge densities of the graphene electrode due to less desolvation of Li+ ions from the bulk electrolyte that dictates the interfacial processes at low temperatures.102−106 With fewer Li+ ions in the EDL, less TFSI– comes to the EDL (Figure 7d) since the negative charge of the electrode is screened less efficiently (Figure 7e). As a result, there is only a smaller number of F in the EDL in the base electrolyte at a low temperature (−40 °C), and FEC becomes more effective in increasing the number of F in the EDL (Figure 7a). In this context, the FEC additive becomes more effective in promoting reduction reactions that can eventually lead to LiF formation and enhance the SEI quality at a low temperature (−40 °C). Note that the changes of C and O atoms in the EDL are both little at a low temperature (−40 °C) as well (Figure 7a), further suggesting the significant role of F in regulating the quality of the SEI layer and the underlying role of EDL in determining SEI components.62
4. Conclusions
In summary, we have developed an interactive MD-DFT-data model to investigate the reduction reactions of multicomponent electrolytes within the EDL. First, MD simulations based on a fine-tuned force field are conducted to capture the structures and statistics in the EDL. Then, DFT calculations are carried out to compute the reduction products and corresponding reduction potentials of the representative species in the EDL. We have applied this new model to both the carbonate-based electrolytes (LiPF6@EC:EMC) and the ether-based electrolytes (LiTFSI@DOL:DME), which are essential toward graphite and Li-metal electrodes, respectively. Our model demonstrates that the SEI formed in ether-based electrolytes is mainly from the Li-ion-coordinated solvents and anions, while the SEI formed in the carbonate-based electrolyte comes from both cation-coordinated and free solvents but not anions. FEC is considered an additive for both electrolyte systems. We found that FEC can enter the EDL region in the LiPF6@EC:EMC electrolyte. In addition, free FEC and FEC-containing Li+-coordinated clusters prefer to be reduced prior to EC and EMC, which thus benefits the formation of LiF and thus the SEI quality. For the ether-based electrolyte, LiTFSI@DOL:DME, at room temperature (20 °C), the FEC additive replaces the existing TFSI– in the EDL, and it does not lead to an obvious change of the F amount in the EDL. Thus, the LiF formation and SEI quality will be expected to change slightly. However, at a low temperature of −40 °C, only a very small amount of TFSI– can be found in the EDL in the pristine electrolyte without FEC due to fewer Li+ ions in the EDL that can screen the negative charge of the graphene electrode. Thus, when FEC is added, the amount of F in the EDL is significantly increased, which will possibly lead to more LiF formation in the SEI. This has clearly explained our previous experimental finding that FEC becomes more effective in promoting LiF formation at low temperatures. These collective agreements with experiments emphasized the importance of incorporating the EDL structure in SEI design, as just considering the bulk electrolyte compositions is insufficient.
The current model simplified the SEI formation process, which can be expanded within the simulation framework shown in Figure 1. For example, reorganization energies can also be computed in the DFT step and the data analysis will include reduction reaction kinetics to derive the SEI species. Furthermore, the DFT model can be replaced by AIMD simulations to determine the decomposition reaction intermediates. It is also possible to couple the AIMD simulations with the interface model to determine the distribution of the reaction intermediates in the EDL and the subsequent reduction reactions. Overall, this framework emphasizes that including the EDL on charged electrode surfaces is critically important in predicting the reduction reactions of the multicomponent electrolytes to accelerate the design of electrolytes with an optimized SEI layer.
Acknowledgments
Q.W. and Y.Q. thank NASA for financial support (grant no. 80NSSC21M0107) and insightful discussions with Drs. J.W. Lawson, M.R. Mehta, J.H. Stenlid, J.Z. Ji, and L.Q. Chen.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.2c11807.
MD simulation details; force field calibrations; bulk electrolyte simulations; EDL structures of carbonate-based electrolytes and their reduction potentials; and EDL structures of ether-based electrolytes and their reduction potentials (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Scheffran J.; Felkers M.; Froese R.. Economic Growth and the Global Energy Demand. In Green Energy to Sustainability; Wiley, 2020; pp 1–44. [Google Scholar]
- Stern P. C.; Janda K. B.; Brown M. A.; Steg L.; Vine E. L.; Lutzenhiser L. Opportunities and Insights for Reducing Fossil Fuel Consumption by Households and Organizations. Nat. Energy 2016, 1, 16043 10.1038/nenergy.2016.43. [DOI] [Google Scholar]
- Xu K. Li-Ion Battery Electrolytes. Nat. Energy 2021, 6, 763. 10.1038/s41560-021-00841-6. [DOI] [Google Scholar]
- Xu K. Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries. Chem. Rev. 2004, 104, 4303–4417. 10.1021/cr030203g. [DOI] [PubMed] [Google Scholar]
- Xu K. Electrolytes and Interphases in Li-Ion Batteries and Beyond. Chem. Rev. 2014, 114, 11503–11618. 10.1021/cr500003w. [DOI] [PubMed] [Google Scholar]
- Wang H.; Yu Z.; Kong X.; Kim S. C.; Boyle D. T.; Qin J.; Bao Z.; Cui Y. Liquid Electrolyte: The Nexus of Practical Lithium Metal Batteries. Joule 2022, 6, 588–616. 10.1016/j.joule.2021.12.018. [DOI] [Google Scholar]
- Wang Z.; Wang H.; Qi S.; Wu D.; Huang J.; Li X.; Wang C.; Ma J. Structural Regulation Chemistry of Lithium Ion Solvation for Lithium Batteries. EcoMat 2022, 4, e12200 10.1002/eom2.12200. [DOI] [Google Scholar]
- Winter M. The Solid Electrolyte Interphase - The Most Important and the Least Understood Solid Electrolyte in Rechargeable Li Batteries. Z. Phys. Chem. 2009, 223, 1395–1406. 10.1524/zpch.2009.6086. [DOI] [Google Scholar]
- Cheng X.-B.; Zhang R.; Zhao C.-Z.; Wei F.; Zhang J.-G.; Zhang Q. A Review of Solid Electrolyte Interphases on Lithium Metal Anode. Adv. Sci. 2016, 3, 1500213 10.1002/advs.201500213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X.; Zhang R.; Chen X.; Cheng X.; Li X.; Zhang Q. The Failure of Solid Electrolyte Interphase on Li Metal Anode: Structural Uniformity or Mechanical Strength?. Adv. Energy Mater. 2020, 10, 1903645 10.1002/aenm.201903645. [DOI] [Google Scholar]
- Wu H.; Jia H.; Wang C.; Zhang J.; Xu W. Recent Progress in Understanding Solid Electrolyte Interphase on Lithium Metal Anodes. Adv. Energy Mater. 2021, 11, 2003092 10.1002/aenm.202003092. [DOI] [Google Scholar]
- Peled E. The Electrochemical Behavior of Alkali and Alkaline Earth Metals in Nonaqueous Battery Systems—The Solid Electrolyte Interphase Model. J. Electrochem. Soc. 1979, 126, 2047–2051. 10.1149/1.2128859. [DOI] [Google Scholar]
- Peled E.; Golodnitsky D.; Ardel G. Advanced Model for Solid Electrolyte Interphase Electrodes in Liquid and Polymer Electrolytes. J. Electrochem. Soc. 1997, 144, L208–L210. 10.1149/1.1837858. [DOI] [Google Scholar]
- Cresce A. V.; Russell S. M.; Baker D. R.; Gaskell K. J.; Xu K. In Situ and Quantitative Characterization of Solid Electrolyte Interphases. Nano Lett. 2014, 14, 1405–1412. 10.1021/nl404471v. [DOI] [PubMed] [Google Scholar]
- Tripathi A. M.; Su W. N.; Hwang B. J. In Situ Analytical Techniques for Battery Interface Analysis. Chem. Soc. Rev. 2018, 47, 736–751. 10.1039/C7CS00180K. [DOI] [PubMed] [Google Scholar]
- Harks P. P. R. M. L.; Mulder F. M.; Notten P. H. L. In Situ Methods for Li-Ion Battery Research: A Review of Recent Developments. J. Power Sources 2015, 288, 92–105. 10.1016/j.jpowsour.2015.04.084. [DOI] [Google Scholar]
- Liu D.; Shadike Z.; Lin R.; Qian K.; Li H.; Li K.; Wang S.; Yu Q.; Liu M.; Ganapathy S.; et al. Review of Recent Development of In Situ/Operando Characterization Techniques for Lithium Battery Research. Adv. Mater. 2019, 31, 1806620 10.1002/adma.201806620. [DOI] [PubMed] [Google Scholar]
- Liu T.; Lin L.; Bi X.; Tian L.; Yang K.; Liu J.; Li M.; Chen Z.; Lu J.; Amine K.; et al. In Situ Quantification of Interphasial Chemistry in Li-Ion Battery. Nat. Nanotechnol. 2019, 14, 50–56. 10.1038/s41565-018-0284-y. [DOI] [PubMed] [Google Scholar]
- Zhou Y.; Su M.; Yu X.; Zhang Y.; Wang J. G.; Ren X.; Cao R.; Xu W.; Baer D. R.; Du Y.; et al. Real-Time Mass Spectrometric Characterization of the Solid–Electrolyte Interphase of a Lithium-Ion Battery. Nat. Nanotechnol. 2020, 15, 224–230. 10.1038/s41565-019-0618-4. [DOI] [PubMed] [Google Scholar]
- Xu R.; Yan C.; Huang J.-Q. Competitive Solid-Electrolyte Interphase Formation on Working Lithium Anodes. Trends Chem. 2021, 3, 5–14. 10.1016/j.trechm.2020.10.008. [DOI] [Google Scholar]
- Li T.; Balbuena P. B. Theoretical Studies of the Reduction of Ethylene Carbonate. Chem. Phys. Lett. 2000, 317, 421–429. 10.1016/S0009-2614(99)01374-3. [DOI] [Google Scholar]
- Wang Y.; Nakamura S.; Tasaki K.; Balbuena P. B. Theoretical Studies to Understand Surface Chemistry on Carbon Anodes for Lithium-Ion Batteries: How Does Vinylene Carbonate Play Its Role as an Electrolyte Additive?. J. Am. Chem. Soc. 2002, 124, 4408–4421. 10.1021/ja017073i. [DOI] [PubMed] [Google Scholar]
- Wang Y.; Nakamura S.; Ue M.; Balbuena P. B. Theoretical Studies to Understand Surface Chemistry on Carbon Anodes for Lithium-Ion Batteries: Reduction Mechanisms of Ethylene Carbonate. J. Am. Chem. Soc. 2001, 123, 11708–11718. 10.1021/ja0164529. [DOI] [PubMed] [Google Scholar]
- Borodin O.; Olguin M.; Spear C. E.; Leiter K. W.; Knap J. Towards High Throughput Screening of Electrochemical Stability of Battery Electrolytes. Nanotechnology 2015, 26, 354003 10.1088/0957-4484/26/35/354003. [DOI] [PubMed] [Google Scholar]
- Delp S. A.; Borodin O.; Olguin M.; Eisner C. G.; Allen J. L.; Jow T. R. Importance of Reduction and Oxidation Stability of High Voltage Electrolytes and Additives. Electrochim. Acta 2016, 209, 498–510. 10.1016/j.electacta.2016.05.100. [DOI] [Google Scholar]
- Leung K. Two-Electron Reduction of Ethylene Carbonate: A Quantum Chemistry Re-Examination of Mechanisms. Chem. Phys. Lett. 2013, 568–569, 1–8. 10.1016/j.cplett.2012.08.022. [DOI] [Google Scholar]
- Borodin O.; Olguin M.; Spear C. E.; Leiter K. W.; Knap J.; Yushin G.; Childs A. S.; Xu K. (Invited) Challenges with Quantum Chemistry-Based Screening of Electrochemical Stability of Lithium Battery Electrolytes. ECS Trans. 2015, 69, 113–123. 10.1149/06901.0113ecst. [DOI] [Google Scholar]
- Aurbach D.; Levi M. D.; Levi E.; Schechter A. Failure and Stabilization Mechanisms of Graphite Electrodes. J. Phys. Chem. B 1997, 101, 2195–2206. 10.1021/jp962815t. [DOI] [Google Scholar]
- Jin Y.; Kneusels N.-J. H.; Magusin P. C. M. M.; Kim G.; Castillo-Martínez E.; Marbella L. E.; Kerber R. N.; Howe D. J.; Paul S.; Liu T.; Grey C. P. Identifying the Structural Basis for the Increased Stability of the Solid Electrolyte Interphase Formed on Silicon with the Additive Fluoroethylene Carbonate. J. Am. Chem. Soc. 2017, 139, 14992–15004. 10.1021/jacs.7b06834. [DOI] [PubMed] [Google Scholar]
- Iftimie R.; Minary P.; Tuckerman M. E. Ab Initio Molecular Dynamics: Concepts, Recent Developments, and Future Trends. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6654–6659. 10.1073/pnas.0500193102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung K.; Budzien J. L. Ab Initio Molecular Dynamics Simulations of the Initial Stages of Solid-Electrolyte Interphase Formation on Lithium Ion Battery Graphitic Anodes. Phys. Chem. Chem. Phys. 2010, 12, 6583–6586. 10.1039/b925853a. [DOI] [PubMed] [Google Scholar]
- Camacho-Forero L. E.; Smith T. W.; Bertolini S.; Balbuena P. B. Reactivity at the Lithium–Metal Anode Surface of Lithium–Sulfur Batteries. J. Phys. Chem. C 2015, 119, 26828–26839. 10.1021/acs.jpcc.5b08254. [DOI] [Google Scholar]
- Leung K.; Qi Y.; Zavadil K. R.; Jung Y. S.; Dillon A. C.; Cavanagh A. S.; Lee S.-H. H.; George S. M. Using Atomic Layer Deposition to Hinder Solvent Decomposition in Lithium Ion Batteries: First-Principles Modeling and Experimental Studies. J. Am. Chem. Soc. 2011, 133, 14741–14754. 10.1021/ja205119g. [DOI] [PubMed] [Google Scholar]
- Borodin O.; Smith G. D. Quantum Chemistry and Molecular Dynamics Simulation Study of Dimethyl Carbonate: Ethylene Carbonate Electrolytes Doped with LiPF6. J. Phys. Chem. B 2009, 113, 1763–1776. 10.1021/jp809614h. [DOI] [PubMed] [Google Scholar]
- Borodin O. Polarizable Force Field Development and Molecular Dynamics Simulations of Ionic Liquids. J. Phys. Chem. B 2009, 113, 11463–11478. 10.1021/jp905220k. [DOI] [PubMed] [Google Scholar]
- Bedrov D.; Piquemal J. P.; Borodin O.; MacKerell A. D.; Roux B.; Schröder C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. 10.1021/acs.chemrev.8b00763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorn R.; Kumar R.; Abraham D. P.; Voth G. A. Atomistic Modeling of the Electrode-Electrolyte Interface in Li-Ion Energy Storage Systems: Electrolyte Structuring. J. Phys. Chem. C 2013, 117, 3747–3761. 10.1021/jp3102282. [DOI] [Google Scholar]
- Kim S.-P.; van Duin A. C. T.; Shenoy V. B. Effect of Electrolytes on the Structure and Evolution of the Solid Electrolyte Interphase (SEI) in Li-Ion Batteries: A Molecular Dynamics Study. J. Power Sources 2011, 196, 8590–8597. 10.1016/j.jpowsour.2011.05.061. [DOI] [Google Scholar]
- Takenaka N.; Suzuki Y.; Sakai H.; Nagaoka M. On Electrolyte-Dependent Formation of Solid Electrolyte Interphase Film in Lithium-Ion Batteries: Strong Sensitivity to Small Structural Difference of Electrolyte Molecules. J. Phys. Chem. C 2014, 118, 10874–10882. 10.1021/jp5018696. [DOI] [Google Scholar]
- Abbott J. W.; Hanke F. Kinetically Corrected Monte Carlo-Molecular Dynamics Simulations of Solid Electrolyte Interphase Growth. J. Chem. Theory Comput. 2022, 18, 925–934. 10.1021/acs.jctc.1c00921. [DOI] [PubMed] [Google Scholar]
- Spotte-Smith E. W. C.; Kam R. L.; Barter D.; Xie X.; Hou T.; Dwaraknath S.; Blau S. M.; Persson K. A. Toward a Mechanistic Model of Solid-Electrolyte Interphase Formation and Evolution in Lithium-Ion Batteries. ACS Energy Lett. 2022, 7, 1446–1453. 10.1021/acsenergylett.2c00517. [DOI] [Google Scholar]
- Li Y.; Qi Y. Energy Landscape of the Charge Transfer Reaction at the Complex Li/SEI/Electrolyte Interface. Energy Environ. Sci. 2019, 12, 1286–1295. 10.1039/C8EE03586E. [DOI] [Google Scholar]
- Attia P. M.; Das S.; Harris S. J.; Bazant M. Z.; Chueh W. C. Electrochemical Kinetics of SEI Growth on Carbon Black: Part I. Experiments. J. Electrochem. Soc. 2019, 166, E97–E106. 10.1149/2.0231904jes. [DOI] [Google Scholar]
- Das S.; Attia P. M.; Chueh W. C.; Bazant M. Z. Electrochemical Kinetics of SEI Growth on Carbon Black: Part II. Modeling. J. Electrochem. Soc. 2019, 166, E107–E118. 10.1149/2.0241904jes. [DOI] [Google Scholar]
- Chen F. Atomistic Modelling Approaches to Understanding the Interfaces of Ionic Liquid Electrolytes for Batteries and Electrochemical Devices. Curr. Opin. Electrochem. 2022, 35, 101086 10.1016/j.coelec.2022.101086. [DOI] [Google Scholar]
- Vatamanu J.; Borodin O. Ramifications of Water-in-Salt Interfacial Structure at Charged Electrodes for Electrolyte Electrochemical Stability. J. Phys. Chem. Lett. 2017, 8, 4362–4367. 10.1021/acs.jpclett.7b01879. [DOI] [PubMed] [Google Scholar]
- Borodin O.; Ren X.; Vatamanu J.; Von Wald Cresce A.; Knap J.; Xu K. Modeling Insight into Battery Electrolyte Electrochemical Stability and Interfacial Structure. Acc. Chem. Res. 2017, 50, 2886–2894. 10.1021/acs.accounts.7b00486. [DOI] [PubMed] [Google Scholar]
- Yao N.; Chen X.; Fu Z.; Zhang Q. Applying Classical, Ab Initio, and Machine-Learning Molecular Dynamics Simulations to the Liquid Electrolyte for Rechargeable Batteries. Chem. Rev. 2022, 122, 10970–11021. 10.1021/acs.chemrev.1c00904. [DOI] [PubMed] [Google Scholar]
- Wang A.; Kadam S.; Li H.; Shi S.; Qi Y. Review on Modeling of the Anode Solid Electrolyte Interphase (SEI) for Lithium-Ion Batteries. npj Comput. Mater. 2018, 4, 15 10.1038/s41524-018-0064-0. [DOI] [Google Scholar]
- Borodin O.; Behl W.; Jow T. R. Oxidative Stability and Initial Decomposition Reactions of Carbonate, Sulfone, and Alkyl Phosphate-Based Electrolytes. J. Phys. Chem. C 2013, 117, 8661–8682. 10.1021/jp400527c. [DOI] [Google Scholar]
- Halls M. D.; Tasaki K. High-Throughput Quantum Chemistry and Virtual Screening for Lithium Ion Battery Electrolyte Additives. J. Power Sources 2010, 195, 1472–1478. 10.1016/j.jpowsour.2009.09.024. [DOI] [Google Scholar]
- Han Y. K.; Jung J.; Yu S.; Lee H. Understanding the Characteristics of High-Voltage Additives in Li-Ion Batteries: Solvent Effects. J. Power Sources 2009, 187, 581–585. 10.1016/j.jpowsour.2008.10.137. [DOI] [Google Scholar]
- Fang C.; Wang X.; Meng Y. S. Key Issues Hindering a Practical Lithium-Metal Anode. Trends Chem. 2019, 1, 152–158. 10.1016/j.trechm.2019.02.015. [DOI] [Google Scholar]
- Li W.; Yao H.; Yan K.; Zheng G.; Liang Z.; Chiang Y.-M.; Cui Y. The Synergetic Effect of Lithium Polysulfide and Lithium Nitrate to Prevent Lithium Dendrite Growth. Nat. Commun. 2015, 6, 7436 10.1038/ncomms8436. [DOI] [PubMed] [Google Scholar]
- Peng H.-J.; Huang J.-Q.; Cheng X.-B.; Zhang Q. Review on High-Loading and High-Energy Lithium-Sulfur Batteries. Adv. Energy Mater. 2017, 7, 1700260 10.1002/aenm.201700260. [DOI] [Google Scholar]
- Thenuwara A. C.; Shetty P. P.; McDowell M. T. Distinct Nanoscale Interphases and Morphology of Lithium Metal Electrodes Operating at Low Temperatures. Nano Lett. 2019, 19, 8664–8672. 10.1021/acs.nanolett.9b03330. [DOI] [PubMed] [Google Scholar]
- Wang J.; Huang W.; Pei A.; Li Y.; Shi F.; Yu X.; Cui Y. Improving Cyclability of Li Metal Batteries at Elevated Temperatures and Its Origin Revealed by Cryo-Electron Microscopy. Nat. Energy 2019, 4, 664–670. 10.1038/s41560-019-0413-3. [DOI] [Google Scholar]
- Gofer Y.; Ben-Zion M.; Aurbach D. Solutions of LiAsF6 in 1,3-Dioxolane for Secondary Lithium Batteries. J. Power Sources 1992, 39, 163–178. 10.1016/0378-7753(92)80135-X. [DOI] [Google Scholar]
- Park M. S.; Ma S. B.; Lee D. J.; Im D.; Doo S.-G.; Yamamoto O. A Highly Reversible Lithium Metal Anode. Sci. Rep. 2014, 4, 3815 10.1038/srep03815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao R.; Yang J.; Xu Z.; Wang J.; Nuli Y.; Sun L. A New Ether-Based Electrolyte for Dendrite-Free Lithium-Metal Based Rechargeable Batteries. Sci. Rep. 2016, 6, 21771 10.1038/srep21771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thenuwara A. C.; Shetty P. P.; Kondekar N.; Sandoval S. E.; Cavallaro K.; May R.; Yang C. T.; Marbella L. E.; Qi Y.; McDowell M. T. Efficient Low-Temperature Cycling of Lithium Metal Anodes by Tailoring the Solid-Electrolyte Interphase. ACS Energy Lett. 2020, 5, 2411–2420. 10.1021/acsenergylett.0c01209. [DOI] [Google Scholar]
- Li T.; Zhang X. Q.; Shi P.; Zhang Q. Fluorinated Solid-Electrolyte Interphase in High-Voltage Lithium Metal Batteries. Joule 2019, 3, 2647–2661. 10.1016/j.joule.2019.09.022. [DOI] [Google Scholar]
- Tan J.; Matz J.; Dong P.; Shen J.; Ye M. A Growing Appreciation for the Role of LiF in the Solid Electrolyte Interphase. Adv. Energy Mater. 2021, 11, 2100046 10.1002/aenm.202100046. [DOI] [Google Scholar]
- Zhang X.-Q.; Cheng X.-B.; Chen X.; Yan C.; Zhang Q. Fluoroethylene Carbonate Additives to Render Uniform Li Deposits in Lithium Metal Batteries. Adv. Funct. Mater. 2017, 27, 1605989 10.1002/adfm.201605989. [DOI] [Google Scholar]
- Zhao J.; Liao L.; Shi F.; Lei T.; Chen G.; Pei A.; Sun J.; Yan K.; Zhou G.; Xie J.; et al. Surface Fluorination of Reactive Battery Anode Materials for Enhanced Stability. J. Am. Chem. Soc. 2017, 139, 11550–11558. 10.1021/jacs.7b05251. [DOI] [PubMed] [Google Scholar]
- He M.; Guo R.; Hobold G. M.; Gao H.; Gallant B. M. The Intrinsic Behavior of Lithium Fluoride in Solid Electrolyte Interphases on Lithium. Proc. Natl. Acad. Sci. U.S.A. 2020, 117, 73–79. 10.1073/pnas.1911017116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan X.; Ji X.; Han F.; Yue J.; Chen J.; Chen L.; Deng T.; Jiang J.; Wang C. Fluorinated Solid Electrolyte Interphase Enables Highly Reversible Solid-State Li Metal Battery. Sci. Adv. 2018, 4, eaau9245 10.1126/sciadv.aau9245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung K.; Soto F.; Hankins K.; Balbuena P. B.; Harrison K. L. Stability of Solid Electrolyte Interphase Components on Lithium Metal and Reactive Anode Material Surfaces. J. Phys. Chem. C 2016, 120, 6302–6313. 10.1021/acs.jpcc.5b11719. [DOI] [Google Scholar]
- Lin Y. X.; Liu Z.; Leung K.; Chen L. Q.; Lu P.; Qi Y. Connecting the Irreversible Capacity Loss in Li-Ion Batteries with the Electronic Insulating Properties of Solid Electrolyte Interphase (SEI) Components. J. Power Sources 2016, 309, 221–230. 10.1016/j.jpowsour.2016.01.078. [DOI] [Google Scholar]
- Pan J.; Cheng Y.-T.; Qi Y. General Method to Predict Voltage-Dependent Ionic Conduction in a Solid Electrolyte Coating on Electrodes. Phys. Rev. B 2015, 91, 134116 10.1103/PhysRevB.91.134116. [DOI] [Google Scholar]
- Zhang Q.; Pan J.; Lu P.; Liu Z.; Verbrugge M. W.; Sheldon B. W.; Cheng Y.-T.; Qi Y.; Xiao X. Synergetic Effects of Inorganic Components in Solid Electrolyte Interphase on High Cycle Efficiency of Lithium Ion Batteries. Nano Lett. 2016, 16, 2011–2016. 10.1021/acs.nanolett.5b05283. [DOI] [PubMed] [Google Scholar]
- Dassault Systèmes BIOVIA . Materials Studio; Dassault Systèmes: San Diego, 2020. [Google Scholar]
- Akkermans R. L. C.; Spenley N. A.; Robertson S. H. COMPASS III: Automated Fitting Workflows and Extension to Ionic Liquids. Mol. Simul. 2021, 47, 540–551. 10.1080/08927022.2020.1808215. [DOI] [Google Scholar]
- Saunier J.; Gorecki W.; Alloin F.; Sanchez J. Y. NMR Study of Cation, Anion, and Solvent Mobilities in Macroporous Poly(Vinylidene Fluoride). J. Phys. Chem. B 2005, 109, 2487–2492. 10.1021/jp048717m. [DOI] [PubMed] [Google Scholar]
- Rakov D.; Hasanpoor M.; Baskin A.; Lawson J. W.; Chen F.; Cherepanov P. V.; Simonov A. N.; Howlett P. C.; Forsyth M. Stable and Efficient Lithium Metal Anode Cycling through Understanding the Effects of Electrolyte Composition and Electrode Preconditioning. Chem. Mater. 2022, 34, 165–177. 10.1021/acs.chemmater.1c02981. [DOI] [Google Scholar]
- Yeh I. C.; Berkowitz M. L. Ewald Summation for Systems with Slab Geometry. J. Chem. Phys. 1999, 111, 3155–3162. 10.1063/1.479595. [DOI] [Google Scholar]
- Holoubek J.; Baskin A.; Lawson J. W.; Khemchandani H.; Pascal T. A.; Liu P.; Chen Z. Predicting the Ion Desolvation Pathway of Lithium Electrolytes and Their Dependence on Chemistry and Temperature. J. Phys. Chem. Lett. 2022, 13, 4426–4433. 10.1021/acs.jpclett.2c00770. [DOI] [PubMed] [Google Scholar]
- Jorn R.; Raguette L.; Peart S. Investigating the Mechanism of Lithium Transport at Solid Electrolyte Interphases. J. Phys. Chem. C 2020, 124, 16261–16270. 10.1021/acs.jpcc.0c03018. [DOI] [Google Scholar]
- Reed S. K.; Lanning O. J.; Madden P. A. Electrochemical Interface between an Ionic Liquid and a Model Metallic Electrode. J. Chem. Phys. 2007, 126, 084704 10.1063/1.2464084. [DOI] [PubMed] [Google Scholar]
- Vatamanu J.; Bedrov D.; Borodin O. On the Application of Constant Electrode Potential Simulation Techniques in Atomistic Modelling of Electric Double Layers. Mol. Simul. 2017, 43, 838–849. 10.1080/08927022.2017.1279287. [DOI] [Google Scholar]
- Vatamanu J.; Borodin O.; Smith G. D. Molecular Simulations of the Electric Double Layer Structure, Differential Capacitance, and Charging Kinetics for N-Methyl-N-Propylpyrrolidinium Bis(Fluorosulfonyl)Imide at Graphite Electrodes. J. Phys. Chem. B 2011, 115, 3073–3084. 10.1021/jp2001207. [DOI] [PubMed] [Google Scholar]
- Baskin A.; Lawson J. W.; Prendergast D. Anion-Assisted Delivery of Multivalent Cations to Inert Electrodes. J. Phys. Chem. Lett. 2021, 12, 4347–4356. 10.1021/acs.jpclett.1c00943. [DOI] [PubMed] [Google Scholar]
- Zeng L.; Wu T.; Ye T.; Mo T.; Qiao R.; Feng G. Modeling Galvanostatic Charge–Discharge of Nanoporous Supercapacitors. Nat. Comput. Sci. 2021, 1, 725–731. 10.1038/s43588-021-00153-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ort J. V.; Fox D. J.. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, 2016.
- Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- Hall D. S.; Self J.; Dahn J. R. Dielectric Constants for Quantum Chemistry and Li-Ion Batteries: Solvent Blends of Ethylene Carbonate and Ethyl Methyl Carbonate. J. Phys. Chem. C 2015, 119, 22322–22330. 10.1021/acs.jpcc.5b06022. [DOI] [Google Scholar]
- Oehme K.-L. Static Dielectric Constants of Pure Liquids and Binary Liquid Mixtures. Z. Phys. Chem. 1994, 185, 276–277. 10.1524/zpch.1994.185.Part_2.276a. [DOI] [Google Scholar]
- Takenaka N.; Fujie T.; Bouibes A.; Yamada Y.; Yamada A.; Nagaoka M. Microscopic Formation Mechanism of Solid Electrolyte Interphase Film in Lithium-Ion Batteries with Highly Concentrated Electrolyte. J. Phys. Chem. C 2018, 122, 2564–2571. 10.1021/acs.jpcc.7b11650. [DOI] [Google Scholar]
- von Cresce A.; Xu K. Preferential Solvation of Li+ Directs Formation of Interphase on Graphitic Anode. Electrochem. Solid-State Lett. 2011, 14, A154–A156. 10.1149/1.3615828. [DOI] [Google Scholar]
- Borodin O.; Olguin M.; Ganesh P.; Kent P. R. C.; Allen J. L.; Henderson W. A. Competitive Lithium Solvation of Linear and Cyclic Carbonates from Quantum Chemistry. Phys. Chem. Chem. Phys. 2016, 18, 164–175. 10.1039/C5CP05121E. [DOI] [PubMed] [Google Scholar]
- Markevich E.; Salitra G.; Aurbach D. Fluoroethylene Carbonate as an Important Component for the Formation of an Effective Solid Electrolyte Interphase on Anodes and Cathodes for Advanced Li-Ion Batteries. ACS Energy Lett. 2017, 2, 1337–1345. 10.1021/acsenergylett.7b00163. [DOI] [Google Scholar]
- Chen X.; Shen X.; Li B.; Peng H.; Cheng X.; Li B.; Zhang X.; Huang J.; Zhang Q. Ion–Solvent Complexes Promote Gas Evolution from Electrolytes on a Sodium Metal Anode. Angew. Chem., Int. Ed. 2018, 57, 734–737. 10.1002/anie.201711552. [DOI] [PubMed] [Google Scholar]
- Elgrishi N.; Rountree K. J.; McCarthy B. D.; Rountree E. S.; Eisenhart T. T.; Dempsey J. L. A Practical Beginner’s Guide to Cyclic Voltammetry. J. Chem. Educ. 2018, 95, 197–206. 10.1021/acs.jchemed.7b00361. [DOI] [Google Scholar]
- Chen L.; Zhang H. W.; Liang L. Y.; Liu Z.; Qi Y.; Lu P.; Chen J.; Chen L.-Q. Modulation of Dendritic Patterns during Electrodeposition: A Nonlinear Phase-Field Model. J. Power Sources 2015, 300, 376–385. 10.1016/j.jpowsour.2015.09.055. [DOI] [Google Scholar]
- Liang L.; Chen L.-Q. Nonlinear Phase Field Model for Electrodeposition in Electrochemical Systems. Appl. Phys. Lett. 2014, 105, 263903 10.1063/1.4905341. [DOI] [Google Scholar]
- Liu Z.; Li Y.; Ji Y.; Zhang Q.; Xiao X.; Yao Y.; Chen L.-Q.; Qi Y. Dendrite-Free Lithium Based on Lessons Learned from Lithium and Magnesium Electrodeposition Morphology Simulations. Cell Rep. Phys. Sci. 2021, 2, 100294 10.1016/j.xcrp.2020.100294. [DOI] [Google Scholar]
- Campion C. L.; Li W.; Lucht B. L. Thermal Decomposition of LiPF6-Based Electrolytes for Lithium-Ion Batteries. J. Electrochem. Soc. 2005, 152, A2327–A2334. 10.1149/1.2083267. [DOI] [Google Scholar]
- Ha Y.; Stetson C.; Harvey S. P.; Teeter G.; Tremolet de Villers B. J.; Jiang C.-S.; Schnabel M.; Stradins P.; Burrell A.; Han S.-D. Effect of Water Concentration in LiPF6-Based Electrolytes on the Formation, Evolution, and Properties of the Solid Electrolyte Interphase on Si Anodes. ACS Appl. Mater. Interfaces 2020, 12, 49563–49573. 10.1021/acsami.0c12884. [DOI] [PubMed] [Google Scholar]
- Cao C.; Pollard T. P.; Borodin O.; Mars J. E.; Tsao Y.; Lukatskaya M. R.; Kasse R. M.; Schroeder M. A.; Xu K.; Toney M. F.; Steinrück H. G. Toward Unraveling the Origin of Lithium Fluoride in the Solid Electrolyte Interphase. Chem. Mater. 2021, 33, 7315–7336. 10.1021/acs.chemmater.1c01744. [DOI] [Google Scholar]
- Li Q.; Lu D.; Zheng J.; Jiao S.; Luo L.; Wang C.-M.; Xu K.; Zhang J.-G.; Xu W. Li+-Desolvation Dictating Lithium-Ion Battery’s Low-Temperature Performances. ACS Appl. Mater. Interfaces 2017, 9, 42761–42768. 10.1021/acsami.7b13887. [DOI] [PubMed] [Google Scholar]
- Xu K.; Von Wald Cresce A. Li+-Solvation/Desolvation Dictates Interphasial Processes on Graphitic Anode in Li Ion Cells. J. Mater. Res. 2012, 27, 2327–2341. 10.1557/jmr.2012.104. [DOI] [Google Scholar]
- Xu K.; Von Cresce A.; Lee U. Differentiating Contributions to “Ion Transfer” Barrier from Interphasial Resistance and Li+ Desolvation at Electrolyte/Graphite Interface. Langmuir 2010, 26, 11538–11543. 10.1021/la1009994. [DOI] [PubMed] [Google Scholar]
- Abe T.; Fukuda H.; Iriyama Y.; Ogumi Z. Solvated Li-Ion Transfer at Interface Between Graphite and Electrolyte. J. Electrochem. Soc. 2004, 151, A1120–A1123. 10.1149/1.1763141. [DOI] [Google Scholar]
- Hubble D.; Brown D. E.; Zhao Y.; Fang C.; Lau J.; McCloskey B. D.; Liu G. Liquid Electrolyte Development for Low-Temperature Lithium-Ion Batteries. Energy Environ. Sci. 2022, 15, 550–578. 10.1039/D1EE01789F. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.