Statistical electromagnetics for industrial pharmaceutical lyophilization

Abstract

Lyophilization is a common unit operation in pharmaceutical manufacturing but is a prolonged vacuum drying process with poor energy utilization. Microwave-assisted vacuum drying has been investigated to accelerate the lyophilization process. However, the literature lacks methodical approaches that consider the lyophilizer, the lyophilizate, the microwave power uniformity, the resulting heat uniformity, and the scalability. We present a microwave–vacuum drying method based on the statistical electromagnetics theory. The method offers an optimum frequency selection procedure that accounts for the lyophilizer and the lyophilizate. The 2.45 GHz frequency conventionally utilized is proven to be far from optimum. The method is applied in a microwave-assisted heating configuration to pharmaceutical excipients (sucrose and mannitol) and different myoglobin formulations in a lab-scale lyophilizer. At 18 GHz frequency and 60 W microwave power, the method shows nearly three times speed-up in the primary drying stage of sucrose relative to the conventional lyophilization cycle for typical laboratory batches. The uniformity of the microwave power inside the chamber is controlled within ± 1 dB. The resulting heating uniformity measured through residual moisture analysis shows 12.7% of normalized SD of moisture level across the batch in a microwave-assisted cycle as opposed to 15.3% in the conventional cycle. Conventional and microwave lyophilized formulations are characterized using solid-state hydrogen-deuterium exchange-mass spectrometry (ssHDX-MS), solid-state Fourier transform infrared spectroscopy (ssFTIR), circular dichroism (CD), and accelerated stability testing (AST). Characterization shows comparable protein structure and stability. Heat and mass transfer simulations quantify further effects of optimal volumetric heating via the high-frequency statistical microwave heating.

Significance Statement.

Pharmaceutical lyophilization evolved through four historical milestones in over a century, the methodical publication of the process in 1880s by Richard Altmann, the independent rediscovery of the process by Shackell in 1909, the improvements in the freezing and condensing concepts through Tival’s and Elser’s patented lyophilization systems in 1927 and 1934, and the production of lyophilization at scale during and after WWII. This work presents a methodical approach for microwave-assisted lyophilization exploiting statistical electromagnetics that allows for large-area uniformity in electromagnetically complex enclosures with a frequency selection procedure that accounts for the lyophilizer and the lyophilizate. This method is scalable and directly applicable to production lyophilizers. It carries the potential to relieve bottlenecks in biopharmaceutical and vaccine manufacturing.

Introduction

Lyophilization, also referred to as freeze-drying, has been developed as an industrial process for preserving blood plasma around World War II and has since been applied to manufacturing thermally labile materials, including peptides, proteins, antibody–drug conjugates, and vaccines. Lyophilization is often the only method to produce room-temperature stable sterile powders suitable for long-term storage and shipping outside the cold chain. Lyophilized products urgently need increased production, including microbiologic standards for the SARS-CoV-2 virus, reagents for PCR diagnostic, monoclonal antibody (mAb), and other therapeutics. COVID-19 vaccines are already being developed in a lyophilized form to enable global distribution, as was the case for smallpox, the only human disease so far that has been globally eradicated by vaccination. While the COVID-19 pandemic put lyophilized products in daily news since 2020, the need for lyophilization capacity has constantly been increasing since the early 2000s with the growth in biopharmaceuticals. For example, from 1990 to 1998, the share of newly approved lyophilized injectable products was 11.9%. In 2011, it increased to 41%, and from 2013 to 2015, it grew to 50% (1, 2). Conventional lyophilizers used in production today follow a simple open-loop batch-based process that includes four main steps: pretreatment, freezing, primary drying, and secondary drying. Primary drying is the longest part of the freeze-drying cycle. It is a slow and expensive vacuum dehydration process, often taking several days or even a couple of weeks with high energy costs (3). Furthermore, it exhibits poor energy efficiency with a typical figure of about 5% (1). Accelerating the primary drying cycle would result in significantly higher throughput and, thereby lower manufacturing costs (4).

The current conventional freeze dryers use indirect heat transfer with a refrigerant fluid, typically a silicone oil, which significantly dampens the process response. This mechanism, in turn, inhibits the utilization of a high-refresh-rate dynamic freeze-drying process parameters. A closed-loop process would require rapid, nearly instantaneous control of the lyophilization parameters such as heat input. Consequently, the current primary drying method presents a severe limitation in moving from an open-loop to a closed-loop and, eventually, continuous lyophilization. To the best of our knowledge, closed-loop continuous lyophilization is unavailable. To perform a closed-loop control, one needs to know the endpoint of each stage of the lyophilization process, which is one of the most common lyophilization-related deficiencies (5). Even though the Pirani convergence to capacitance manometer (CM) (6) is considered to be the end of the primary drying cycle, the exact moment of the end of primary drying is not clear and the actual convergence may take several hours. The possible reasons for this phenomenon are the gas diffusion from the chamber to the condenser, batch heterogeneity, process conditions, and batch size (7). The real time measurement and control of product critical quality attributes (residual moisture and product temperature) through shelf temperature and chamber pressure along with the accurate criteria for the end of each stage of the freeze-drying cycle results in the closed-loop lyophilization process. Microwave heating is an attractive alternative heat transfer mechanism to address these challenges. The fundamental idea is to use high-frequency electromagnetic (EM) fields to energize the product on the molecular level. The frozen solvent, typically water, absorbs the induced heat that drives sublimation. This technology is widely used in the food industry (8–10). Copson (11) was one of the first who applied and described microwave-assisted freeze-drying (MAFD). While microwave heating is not new in general freeze-drying, practically all previous studies have not comprehensively covered the problem’s EM aspects. Very few studies addressed the topic of microwave freeze-drying (MWFD) in the pharmaceutical industry, such as (12–19). In (12) and (13), the main objective is to evaluate the stability of microwave freeze-dried products compared to conventionally freeze-dried ones. In (13), the authors pointed out that utilizing a different microwave setup increased the batch homogeneity. They attributed this to using solid-state semiconductor microwave generators with no EM study presented. The authors used a modified lab-scale Püschner WaveVac 0250FD vacuum drier. In (15) and (20), a mathematical model for heat and mass transfer and theoretical and experimental investigations of dielectric-assisted MWFD are introduced. Dielectric-assisted microwave heating uses an auxiliary dielectric material that is lossy at 2.45 GHz to avoid changing the frequency. The auxiliary material is volumetrically heated rapidly; however, lyophilizate heating happens through conduction. In (16), mechanistic models are derived for a MAFD process to predict the reduction in primary drying time. In (17), MWFD was applied to vaccines while using a first-principle model to identify mechanisms for faster drying. The authors utilized the REVTM drying technology. In (18), lattice acid bacteria’s survival rate and cell membrane integrity are evaluated under MWFD. The Püschner WaveVac 0150fd vacuum drier is used in this study. In (19), the MWFD process parameters are optimized for enzymes. To the best of our knowledge, none of the published studies on MWFD offered a methodical approach to design the underlying EM space utilized in MWFD such that it achieves uniformity, efficiency, and scalability. This highlights the gap that motivated the presented work. In his overview of MAFD for the food industry, Fan et al. (10) emphasize the need to further study the MWFD theory. Ambros et al. (21) highlighted the need for temperature control by variable microwave power input during the drying process. Moreover, in their study of the microwave–vacuum drying of lactic bacteria, they made a step toward the continuous process and, hence the closed-loop control of the freeze-drying process. Bosca et al. (22) used soft sensor for in-line monitoring of the primary drying step of a pharmaceutical freeze-drying process in vials. The list of related studies about microwave/microwave-assisted drying approach are summarized in Table S2 (Supplementary Material). The most critical EM aspects partially or fully overlooked in the previous studies are as follows:

1. EM wave propagation modeling inside the electromagnetically complex freeze dryer chamber. The chamber is geometrically irregular and has many cubic wavelengths in size, leading to complex propagation phenomena. Attempting to solve Maxwell’s equations analytically in such an environment is practically impossible and has to be conducted for each new chamber. On the other hand, EM full-wave numerical simulation is impractical as it comes at an enormous computational cost, even with modern supercomputers. Besides, it does not provide the necessary physical insight to predict and achieve uniformity of the EM power inside the lyophilization chamber. As a result, no straightforward modeling process has been devised for such an EM problem.

2. Frequency selection for the frozen state. Almost all previous attempts have used the conventional 2.45 GHz frequency (12,13, 15, 17, 19, 20, 23, 24–28), which is far from optimum for lyophilization as will be shown throughout the paper. While 2.45 GHz may be a convenient frequency to use due to widely available magnetron-based microwave power sources, the ice does not have a significant dielectric loss at this frequency and, as a result, the induced microwave heating at 2.45 GHz is low. In addition, the EM power uniformity may not exist at 2.45 GHz for most lyophilizer structures due to the limited intershelf spacing. Therefore, a frequency selection procedure that accounts for the lyophilizer and the lyophilizate is essential.

3. EM/Heating uniformity through large volumes to achieve a successful lyophilization process at scale. With numerous propagating EM modes being excited in the resonant cavity formed inside the freeze dryer, localized cold and hot spots evolve. This composition inhibits effective and predictable microwave-heating necessary for practical lyophilization for pharmaceutical manufacturing. Gitter et al. (12) outlined that microwave power used in their study was 2 kW, with only one-tenth of it going to the product chamber vs. 24.5 W in the present work (after excluding cable and antenna losses). In (17), a simulation-based comparison between a magnetron and a solid-state device (SSD) source is presented. The study revealed better uniformity of field distribution in the case of the SSD source. However, the study could not introduce a methodical approach capable of predicting/designing specific uniformity. Moreover, the power in the entire microwave cycle was 883 W on average, which is × 36 times more than the present study (24.5 W). Such a significant amount of power puts a severe limitation on scalability.

This work develops a new microwave-heating method based on statistical electromagnetics (SEM) theory to address these gaps. The idea is to create an SEM environment where the average-power distribution is uniform within a specified standard deviation. To that end, a frequency selection procedure is presented tailored to MWFD. This procedure accounts for both the lyophilizer and the lyophilizate. Even though the reported accelerations of the lyophilization cycles in the literature reach × 4.3 (12), × 3.6 (13) as opposed to × 2.9 reported in the presented work, the maximum reachable acceleration by this method is only bound by the power amplifier (PA) capability (100 W max), not by the method itself. The core contribution of the presented MWFD method is the underlying EM design approach. This method is scalable and efficient, introduces controlled uniformity of the heating energy, and is directly applicable to industrial lyophilizers. Model protein formulations with four typical lyoprotectant excipients are characterized by various methods to assess physical and chemical stability after conventional and microwave-assisted lyophilization. The work also presents a heat-and-mass-transfer-based simulation of the microwave-assisted primary drying process for a typical vial formulation to estimate primary drying process time. Hill and Jennings (29) modeled the heat source term responsible for microwave heating in the heat equation and showed the general derivation of the heat source term. Hossan et al. (30) performed the numerical modeling of microwave heating of cylindrical-shaped objects directly related to freeze-drying of vials. Nastaj and Witkiewicz (31) developed a detailed primary and secondary drying model for microwave heating. The microwave heating of magnetite at different frequencies was modeled by Peng et al. (32). This work uses LyoPRONTO lyophilization simulation and process optimization tool (33) modified to model volumetric microwave heating. The focus of the analysis is the comparison of the primary drying time during the microwave-assisted and conventional primary drying. The microwave modeling is calibrated with experimental data and applied for optimization in terms of variable power under the constraint on the maximum product temperature.

Results

SEM and microwave-heating in lyophilization

The SEM theory has been developed primarily to address electromagnetic interference (EMI) and electromagnetic compatibility (EMC) problems in electrically large cavities with complex EM fields. This class of problems has two main similarities with microwave-heating in lyophilization. First, they both involve electrically large, metallic, complex, and geometrically irregular cavities. These cavities are also not designed for a specific EM function, and their loadings (alien materials inside the cavity) are not known beforehand. Second, both classes of problems require a uniform average power distribution. This is particularly critical in microwave-heating since it directly translates to uniform heating necessary for uniform residual moisture and other product quality attributes. SEM is not focused on calculating the exact field strength at every point in the solution domain but rather on the measurable average quantities, such as average power and energy densities. Consequently, in SEM, we model the electric and magnetic field components in Maxwell’s equations as random variables and compute their distribution functions. All other parameters are derived from these random variables. In SEM, we model the electric field as (34)

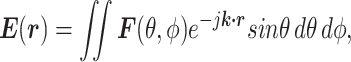where is the electric-field vector, is the position vector, 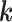is the propagation vector, and 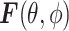is the angular spectrum vector of the electric field as a function of the angular spherical space coordinates, θ, and ϕ. This representation satisfies Maxwell’s equations, and 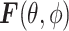carries all the statistical properties of an ideally random EM environment. In such an environment, the following assumptions hold. First, the means of the vector components of the angular spectrum, 〈F_θ〉 and 〈F_ϕ〉, are zero. Second, the angular spectrum orthogonal polarization components, 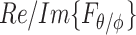and 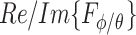, quadrature-phase components, 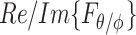and 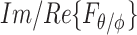, and components arriving from different angles, 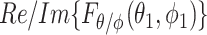and 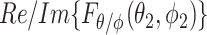, are uncorrelated (34). These assumptions have been experimentally validated in (35). As a result, two fundamental conclusions can be drawn. First, the expectation of the squared magnitude of the electric/magnetic-field vectors and the energy density are constants and independent of the position vector 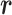, which translates to power distribution uniformity. Second, the real and imaginary parts of the measurable S-parameters follow a Gaussian distribution, and hence the received power at any position inside the chamber follows an exponential distribution. The significance of these results is demonstrated below.

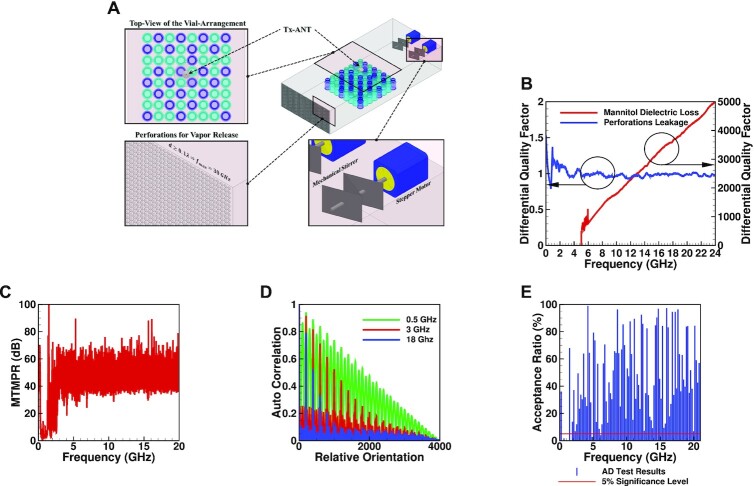
All microwave lyophilization runs are conducted in a lab-scale lyophilizer (LyoStar3 from SP Scientific) in the LyoHub facility at the Birck Nanotechnology Center, Purdue University. Lyophilizer chambers are commonly compartmentalized into multiple stainless-steel shelves. We constructed an auxiliary-chamber (AUXC) to enable dry-lab (outside the lyophilizer) design experiments. As shown in Figure 1A (top-right) and the closeup in the bottom-left, the front face of the AUXC has numerous 1-mm diameter perforations to allow for vapor release during primary and secondary drying. Since the diameter of each perforation is much smaller than the wavelength, λ, of the radiated waves (1 mm = 0.1 λ at 30 GHz), the AUXC can effectively trap the waves inside up to at least 30 GHz. To quantitatively evaluate any microwave leakage, we measured the differential quality factor. The differential quality factor is the difference between the AUXC’s composite quality factors before and after adding the perforations. The differential quality factor as measured using the method in (36) is plotted in Figure 1B vs. frequency (see the supplementary information for more details). Any microwave leakage due to the perforations will reduce the composite quality factor of the perforated chamber and, hence increase the differential quality factor. A differential quality factor of about 1 dB is maintained over frequency, indicating insignificant leakage due to the perforations.

Fig. 1.

The dry-lab experiments setup and results. (A) A 3D illustration of the designed auxiliary chamber (AUXC) with three closeups showing the mechanical stirrers (MS) for creating a statistical EM environment (bottom-right), the perforations for vapor flow (bottom-left), and a top view of a product batch with vials selected for moisture analysis in dark-blue (top-left). (B) The measured differential quality factors that evaluate the leakage due to perforations and the behavior of the dielectric loss factor of mannitol at −45°C vs. frequency. (C) The maximum-to-minimum power ratio (MTMPR) evaluated the field variations in the SEM environment. (D) The autocorrelation between the different EM field structures evaluates the independence between the different promoted field structures at 0.5, 3, and 18 GHz. (E) The Anderson Darling (AD) statistical test results are used to measure the lowest usable frequency (LUF) of the auxiliary chamber (AUXC).

To create the intended SEM environment inside the AUXC, the EM boundary conditions (BCs) must change continuously, and a sufficiently high number of EM modes must be excited. Continuously changing the BCs means that, at every moment, a new EM field structure emerges inside the chamber, and in general, a random behavior evolves. This can be realized by electronic-stirring (37) and/or mechanical-stirring (36, 38). Electronic stirring relies on continuously changing the source driving-frequency (frequency-stirring) or amplitude (noise-stirring). Mechanical stirring includes a continuously moving irregular metallic plate, which is the realization followed in the presented work. We designed two identical mechanical stirrers as depicted in the closeup in Figure 1A (bottom-right) and mounted them to the back wall of the AUXC. Each irregular metalic plate is driven by a stepper motor that is controlled by a customized computer code.

Dry-lab experiments

Dry-lab experiments aim to evaluate the created SEM environment in terms of the quality of stirring (QoS) and the number of modes excited inside the AUXC. A high QoS means that the emerging EM field structures are sufficiently different and independent. To evaluate the QoS, one MS is step-rotated by 20 steps and the other by 200 steps resulting in 4,000 variations (relative orientations of the MSs) representing 4,000 changes in the EM field structure. At each variation, we measure the voltage transfer function between a transmitting antenna (Tx-ANT) and a randomly positioned receiving antenna (Rx-ANT) at 33 different locations vs. frequency by a power-network-analyzer (PNA). With the knwoledge of the input power, the received power at all variations is then calculated and corrected for the Tx-ANT and Rx-ANT efficiencies. The maximum-to-minimum power ratio (MTMPR) indicates how different the EM field structures are. A 20 dB (or higher) MTMPR indicates sufficiently different field structures (39). From Figure 1C, we see that the measured MTMPR sustains a 45-dB level at frequencies higher than 3 GHz. Next, to evaluate the independence of these field structures, then at a single location of the Rx-ANT, we calculate the autocorrelation between the successive EM variations at selected frequencies spanning the entire producible frequency range in our lab, 0.5, 3, and 18 GHz. These are plotted in Figure 1D. At 18 GHz, the independence of the produced field structures is evident from the low (< 0.1) autocorrelation for almost all variations. At lower frequencies, these variations become more dependent, indicating lower QoS. In summary, based on these measurements, frequencies above 3 GHz are needed for high QoS. To ensure that a well randomized EM environment is created, a sufficiently large number of EM modes must be excited inside the chamber. To evaluate this, we measure the lowest usable frequency (LUF) of the AUXC. We can define the LUF as the lowest frequency below which an insufficient number of modes are excited such that the SEM assumptions no longer hold. Consequently, uniformity of power distribution is not guaranteed, and the probability distribution functions of the EM parameters are not established. Therefore, to measure the LUF, we run a goodness-of-fit (GoF) statistical test on samples of the received powers vs. frequency at 33 locations inside the AUXC. For each sample (frequency), the test outcome for a given sample decides, to a certain level of confidence, whether the sample is drawn from the exponential distribution (the null-hypothesis) with the alternative hypothesis being that the sample is drawn from other distribution. We used an Anderson Darling test with a 5% significance level (40). The test results (P-values) are plotted in Figure 1E. At frequencies with test outcome values higher than 5%, the test rejects the null hypothesis, and thereby we measured a LUF of 6.4 GHz, after which all the samples follow the null-hypothesis. Conclusively, to ensure exciting sufficiently numerous modes and a high QoS, the frequency selection should be higher than 6.4 GHz.

Dielectric heating of ice

The frequency selection procedure presented so far accounts for the chamber geometry. Accounting for the lyophilizate requires an understanding of the microwave dielectric heating. Upon exposure to EM waves, the power density dissipated as heat in the exposed dielectric material is (41)

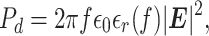where P_d is the power density dissipated as heat, f is the frequency of the incident EM wave, ϵ₀ is the absolute free-space permittivity, |E| is the magnitude of the incident EM wave, and ϵ_r(f) is the dielectric loss factor of the lyophilizate. Measurements in (42) provide the dielectric loss factor of ice at −15, −40, and −73^°C at four frequencies, 5, 10, 35, and 39 GHz. Results indicate a monotonic increase of the loss factor vs. frequency. To verify this behavior vs. frequency, we measure the differential quality factor, which is the difference between the composite quality factors of the empty and lyophilizate-loaded AUXC. The latter refers to the AUXC while placed on a lyophilizer’s shelves loaded with 100 vials filled with 3 ml of mannitol (5% v/v) each. Since the composite quality factor measures the loss in the EM energy in the cavity, the differential quality factor measures the loss in the EM energy dissipated as heat in the lyophilizate. The quality factor measurements were conducted while the shelf temperature is at −45^°C. The results, depicted in Figure 1B, validate the behavior in (42) for mannitol at −45^°C. It should be noted that the method in (36) for measuring the composite quality factor stipulates a well randomized SEM environment and, hence, all the measurements below the LUF should be discarded.

End of primary drying

It is essential to define the end of primary drying to enable a rigorous evaluation of the enhancement introduced by the microwave-heating. It is also critical to start the secondary drying after ensuring that all the ice has been sublimed. Otherwise, the product will collapse due to exceeding the critical temperature (4). Significant research has been conducted to define the end of primary drying. Here, we follow the approach outlined in (43). Specifically, we identify the end of primary drying when the Pirani and CM pressure readings converge within a specified tolerance. The CM pressure sensor reads the chamber’s absolute pressure while the Pirani gauge measures the pressure through the gas’s thermal conductivity in the chamber. In a lyophilizer chamber, two gases exist during primary drying, namely nitrogen and water vapor. The sterile nitrogen is used to control the pressure inside the chamber, while the water vapor is a direct result of sublimation from the frozen product. Since the thermal conductivity of water is ≈1.6 × the thermal conductivity of nitrogen, it is expected for the Pirani gauge readings to be about 60% higher than the CM as long as water vapor is the dominant gas inside the chamber due to sublimation. As the primary drying ends, the water vapor level decays, leading the Pirani and CM readings to converge. The end of primary drying is marked when the Pirani gauge and CM readings converge to a specified difference.

Microwave-assisted lyophilization experimental setup

The statistical microwave-setup integrated with the lab-scale lyophilizer is depicted in Figure 2. The AUXC is inserted in the LyoStar3 chamber. We use a PNA to generate the needed RF signal with a maximum output power of 19 dBmW. A PA with a maximum output power of 100 W is used to amplify the signal. Since the PA has a constant gain, we control the PA’s output power by changing the PNA signal power. Next, to relay the signal inside the AUXC and control the stepper motors, we use RF and DC bulkheads. These provide access to the RF and the motor power supply cables inside the lyophilizer without compromising the chamber sealing to maintain the desired vacuum level. A customized computer code controls the movement (relative-speed/speed and sense of rotation) of the MSs driven by the stepper-motors and automates the measurements of the composite quality factor, which requires 4,000 s-parameter measurements. The code also limits the current drawn by each stepper-motor to avoid heating the AUXC walls.

Fig. 2.

The statistical microwave system integrated with the LyoStar3 lyophilizer.

When a protein is dried, it is deprived of the hydrogen bonds provided by water molecules. This, in turn, tends to destabilize the protein. Excipients are used to replace these hydrogen bonds. Additionally, they provide a structure of the dried cake for fast reconstitution. It is essential for any lyophilization process that the dried cake keeps its elegance as a collapsed cake has a lower specific surface area and, thus slower secondary drying and longer reconstitution times (43). We examine the effectiveness of microwave-assisted lyophilization on both the bare excipients and the protein/excipient mixtures. We conducted microwave-assisted lyophilization runs with aqueous solutions of mannitol, sucrose, and four formulations of a model protein (myoglobin) with mannitol, sucrose, trehalose, and sodium chloride as excipients. The list of all the experiments as well as process recipes prescribing the duration of different process steps are summarized in Tables S1 and S3 (Supplementary Material).

In experiment#1, the AUXC is loaded with 114 vials filled with 3 ml of mannitol (5% v/w) each. A conventional cycle, whose primary drying lasts for 11.45 h, and four microwave-assisted cycles are conducted at 12, 14, 16, and 18 GHz with an output of 79 W out of the PA. The CM and PIRANI readings vs. drying time are plotted in Figure 3A. The primary drying durations for the microwave-assisted cycles are 6.7 h, 6.3 h, 6.2 h, and 5.6 h, respectively, indicating a primary drying speed-up of 1.43 ×, 1.52 ×, 1.55 ×, and 1.71 ×, respectively. The results confirm the behavior demonstrated by the differential quality factor in Figure 1B. Therefore, the microwave-assisted lyophilization runs, utilized to prepare the lyophilized model protein samples in experiment#4, are conducted at 18 GHz, which is the maximum producible frequency in the lab with the available equipment.

Fig. 3.

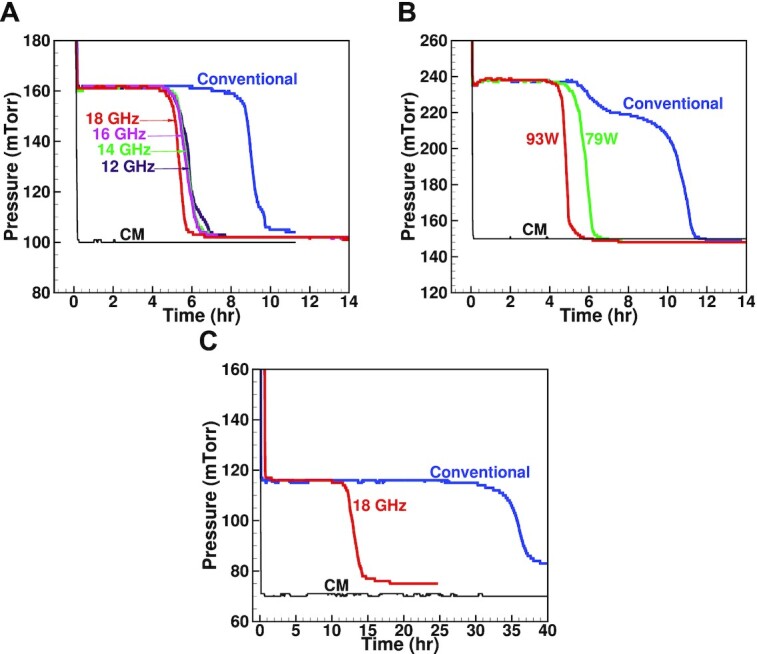
The CM and Pirani gauge pressure measurements vs. primary drying time for different lyophilization cycles. (A) A conventional cycle and four microwave-assisted cycles of mannitol (5% v/v, 6R-Vial, 3 ml fill volume, and 114 vials) at 12, 14, 16, and 18 GHz. (B) A conventional cycle and two microwave-assisted cycles of mannitol (5% v/v, 6R-Vial, 3 ml fill volume, and 100 vials) at different PA output powers, 79 and 93 W. (C) A conventional and microwave-assisted (71 W) lyophilization cycles of sucrose (5% v/v, 6R Vial, 3 ml fill volume, and 64 vials).

In experiment#2, the AUXC is loaded with 100 vials filled with 3 ml of mannitol (5% v/v) each. A total of three runs were conducted, a conventional cycle and two microwave-assisted cycles at 79 and 93 W of PA output power. The CM and PIRANI reading vs. drying time are plotted in Figure 3B. The primary drying durations are 11.5 h, 6.4 h, and 5.6 h, respectively, indicating a primary drying speed-up of 1.8 × and 2.1 ×, respectively. Recipe#1, tabulated in summarized in a Supplemental Material table, has been applied in experiment#1 and experiment#2.

In experiment#3, the AUXC is loaded with 64 vials filled with 3 ml of sucrose (5% v/v) each. A conventional cycle and an microwave-assisted cycle, at 18 GHz, are conducted. The CM and Pirani reading vs. drying time are plotted in Figure 3C. The primary drying durations are 38 h and 16 h, respectively, indicating a speed-up of 2.4 ×. The samples obtained from experiment#3 are utilized for the uniformity analysis.

In experiment#4, the AUXC is loaded with 144 vials filled with the four myoglobin formulations with 36 vials of each formulation. This experiment aims to compare the physical and chemical properties of the lyophilized model protein obtained from the conventional and the microwave-assisted lyophilization cycles. The primary drying duration in the conventional and microwave-assisted cycles are 16.3 h and 5.6 h, respectively, indicating a speed-up of 2.91 × in the primary drying duration. The samples obtained from experiment#4 are utilized for protein properties analysis.

Residual moisture testing

To assess the uniformity of the microwave-assisted lyophilization compared to the conventional process, we performed a moisture analysis for selected vials at different locations drawn from the samples obtained from experiment#3. The selected vials are highlighted in Figure 1A, and the top-left closeup indicates the locations of these vials. We used the Computrack VaporPro moisture-specific analyzer, which provides the moist percentatge detected upon excessive heating of the sealed vial under test. The results in Figure 5A show that the average moisture for the conventional cycle is 0.91%, while it is 0.38% in the microwave-assisted lyophilization. The conventional cycle shows a 15.3% normalized SD from the mean, while the microwave-assisted cycle shows a 12.7% normalized SD from the mean, indicating not only uncompromised, but also better uniformity in the case of microwave-assisted lyophilization. Visual inspection of vials in all the lyophilization cycles showed intact dry cakes without visible collapse and shrinkage (Fig. 4). The photographs of sucrose and formulation runs are provided in the supplementary information.

Fig. 5.

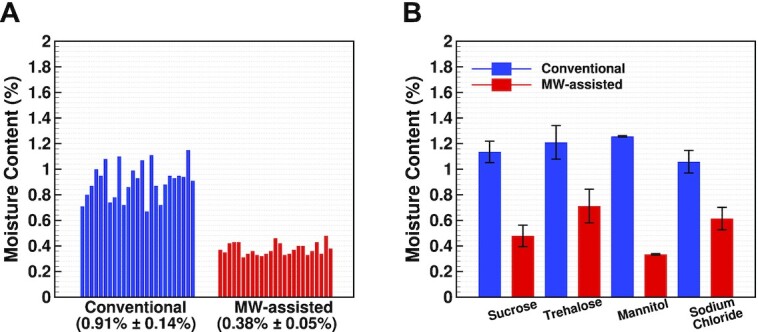
Residual moisture comparison between conventional and microwave-assisted lyophilization runs. (A) Residual moisture for sucrose samples prepared using conventional and microwave-assisted lyophilization. (B) Residual moisture after conventional (blue) or microwave-assisted (red) lyophilization for the four myoglobin with sucrose, trehalose, mannitol, or sodium chloride. N = 3 ± SD for each formulation.

Fig. 4.

Photograph of the batch with 3 ml mannitol 5% v/v filled in 6R Schott vials after the microwave-assisted lyophilization cycle (18 GHz, 79 W). There are no signs of product collapse.

The moisture results of the protein samples for all excipients in Figure 5B show that, overall, the microwave-assisted runs produced dryer samples than the conventional runs. In samples dried using conventional lyophilization, the residual moisture was the highest in mannitol (1.25%), whereas trehalose showed the highest residual moisture of all the formulations when dried using microwave heating (1.21%). The conventional samples showed residual moisture between 1% and 1.3% w/w, while the microwave samples showed residual moisture between 0.3% and 0.7% w/w.

Solid-state hydrogen-deuterium exchange-mass spectrometry

Solid-state hydrogen-deuterium exchange-mass spectrometry (ssHDX-MS) assesses the stability of lyophilized protein formulations by probing the backbone amide chains of a protein molecule. This method has been used successfully to correlate deuterium incorporation to long-term aggregation and protein-matrix interactions for a protein, mAb, and an antibody fragment (see the supplementary information for more details). The deuterium uptake in formulations dried using either of the two methods showed a dependence on the excipient (Figures 6A and 6C; Figures S1A and S1C, Supplementary Material). Sucrose and trehalose showed the slowest rate of deuterium uptake and the smallest value for total deuterium uptake over time. Mannitol and sodium chloride showed higher rates of deuterium uptake and total deuterium uptake throughout the experiment. This is potentially due to less or no hydrogen bonding occurring in crystalline formulations containing mannitol and sodium chloride as excipients and is consistent with previous results (44–46). Within mannitol and sodium chloride formulations, mannitol showed lower deuterium uptake than sodium chloride formulations irrespective of the drying method. Additionally, sucrose formulations dried using either conventional or microwave-assisted lyophilization showed a similar rate and extent of deuterium uptake over time (Fig. 6A). ANOVA analysis (Šídák’s multiple comparison test) on the two data sets showed no significant differences in deuterium uptake between sucrose formulations dried using conventional or microwave-assisted lyophilization (P < 0.1). Similarly, a 2-way ANOVA test was performed on trehalose, mannitol, and sodium chloride containing formulations to test if there was any difference in the rate and/or the extent of deuterium incorporation due to differences in the drying method employed. No significant differences were observed at any time point except at 48 h for trehalose formulations (Fig. S1A, Supplementary Material). In comparison, the mannitol (Fig. 6C) formulations showed differences at 3 h and 48 h and the sodium chloride (Fig. S1C, Supplementary Material) formulations showed no significant differences at any time point (all at P < 0.1). Individually, sucrose-containing formulations dried using conventional lyophilization showed deuterium uptake curves coinciding with microwave-assisted lyophilized formulations at almost all time points. In the case of trehalose, deuterium uptake curves obtained from microwave lyophilized samples showed consistently lower deuterium uptake starting at 24 h up until the end of the experiment (10 days). This trend was also true for mannitol, although differences in deuterium uptake were prominent starting at 48 h. Sodium chloride deuterium uptake curves showed some differences between drying methods but all time points were within experimental error.

Fig. 6.

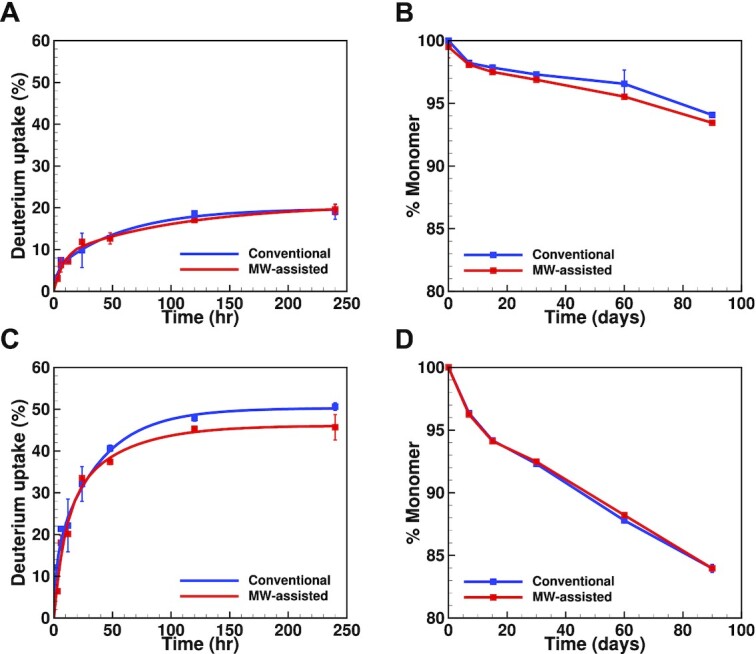
ssHDX-MS and 90 days accelerated stability testing (AST) results for myoglobin sucrose (A) and (B) and myoglobin mannitol (C) and (D) formulations, respectively. AST samples were analyzed using size exclusion chromatography (SEC). Conventional lyophilization data are shown in blue, while the microwave-assisted lyophilization results are shown in red. Samples were reconstituted with 300 μl of quench buffer (ssHDX-MS) or water (SEC) and diluted to appropriate concentrations before analysis. N = 3 ± SD for each time point for both ssHDX-MS and SEC analyses.

Solid-state Fourier transform infrared spectroscopy and circular dichroism

Solid-state Fourier transform infrared spectroscopy (ssFTIR) was performed to detect possible changes in the secondary structure of myoglobin on lyophilization. Sucrose and mannitol ssFTIR spectra are shown in Figures 7B and 7D, respectively. The ssFTIR spectra for trehalose and sodium chloride are shown in Figures S2B and S2D (Supplementary Material), respectively. Sucrose and sodium chloride spectra between microwave-assisted and conventional lyophilization showed little difference. The ssFTIR spectra of trehalose and mannitol samples dried using microwave-assisted lyophilization showed sharper and more intense peaks than the conventionally dried samples for the two formulations. All spectra, regardless of the drying method used, showed a peak around 1,650/cm indicating that the α-helical structure of myoglobin was preserved in the samples. Additionally, a peak around 1,670/cm was also present in all samples indicating that the random coil structure of myoglobin was preserved.

Fig. 7.

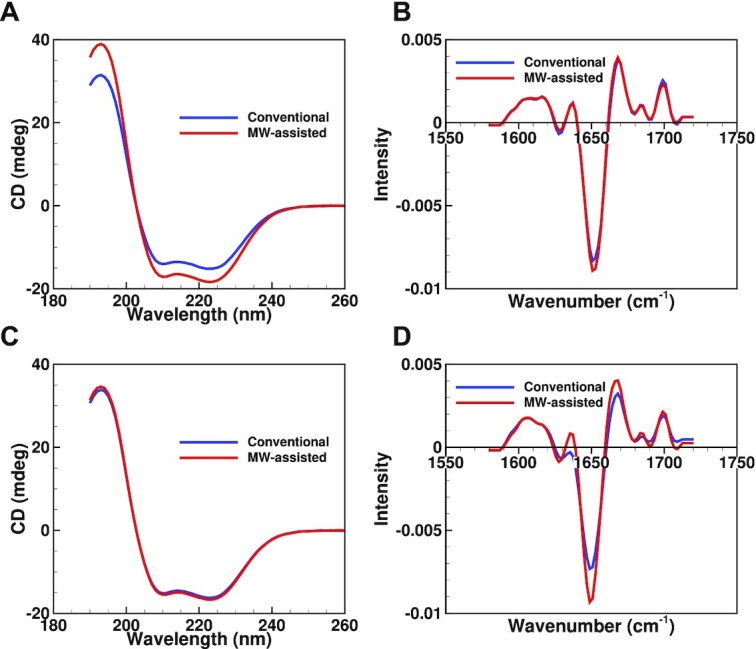
Circular dichroism (CD) and solid-state FTIR (ssFTIR) results for myoglobin sucrose (A) and (B) and myoglobin mannitol (C) and (D) formulations. CD samples were reconstituted with 300 μl of water and diluted to appropriate concentrations before analysis. Results for samples dried using a conventional lyophilization cycle are shown in blue, while the microwave-assisted lyophilization cycle results are shown in red.

Circular dichroism (CD) spectra were also obtained for samples dried using conventional and microwave-assisted lyophilization to detect conformational changes in the protein molecule on reconstitution. Figures 7A and 7C show representative CD spectra for myoglobin sucrose and myoglobin mannitol runs, respectively. CD spectra for myoglobin trehalose and myoglobin sodium chloride formulations are shown in Figures S2B and S2D (Supplementary Material), respectively. All samples showed two peaks between 210 and 230 nm consistent with the presence of α-helices in the protein molecule. CD spectra from both microwave-assisted and conventional runs were identical for all formulations except sucrose, where some intensity differences were observed.

Accelerated stability test

Accelerated stability testing (AST) was performed on all samples post drying to assess the stability differences due to the different drying methods. Results were plotted as a decrease in percent monomer (% monomer) over time. Figures 6B and 6D are representative SEC curves of decrease in monomer content vs. time for myoglobin sucrose and myoglobin mannitol formulations, respectively. All sample sets were tested right after lyophilization to detect initial aggregation if any, before stability testing was carried out ( t= 0). Sodium chloride showed the lowest t = 0 monomer content at 98% for both of the drying methods tested (Fig. S1D, Supplementary Material). Samples were also tested at the end of the 90 days incubation period at 40 ^°C and 6% relative humidity. Sucrose showed a gradual decrease in monomer content over the 90 days incubation period, with approximately 94% monomer remaining at the end of testing for samples dried using either conventional or microwave-assisted lyophilization (Fig. 6B). Trehalose (Fig. S1B, Supplementary Material) showed similar monomer content at 96% for both drying methods while mannitol had 84% monomer remaining. On the other hand, sodium chloride formulations showed differences in the final percent monomer remaining depending on the drying method employed with conventionally dried samples showing 91% monomer and microwave-assisted samples showing 89% monomer remaining.

Lyophilization modeling

Modeling of microwave-assisted vial heating is performed by a modified LyoPRONTO solver (33) for the 1D quasi-steady-state heat and mass transfer in the vial. The modeling process takes into account several heat transfer mechanisms. The conventional lyophilization process includes heat conduction due to the contact between vial bottom and shelf and through the gas between the vial a shelf, radiative heat transfer from the adjacent shelves, and lyophilizer walls. In addition to those, microwave volumetric heating term is present in the modeling process. The heat from the bottom of the vial is transferred to the sublimation front by the conduction and volumetric heating from the microwave source. The sublimation front propagates downward, increasing the porous “cake” length until it reaches the initial length of the frozen product. Equations are solved iteratively to obtain the product bottom temperature and sublimation flux as a function of time. The total energy (heat) balance is described as

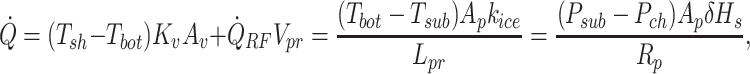where 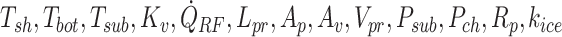, and δH_s are the shelf temperature, product bottom temperature, sublimation front temperature, vial heat transfer coefficient, microwave heat source, frozen product length, product area, vial area, product volume, sublimation front pressure, chamber pressure, product resistance, the thermal conductivity of ice, and heat of sublimation, respectively. The microwave-assisted heating is modeled by the volumetric microwave heat source 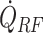, which can be tuned to supply varying heat.

Figure 8 shows the primary drying time of conventional and microwave-assisted runs. Figures 8A and 8B demonstrates the results based on the experimental data for 3 ml mannitol 5% and sucrose 5% filled in 6R Schott vials and recipes shown in Table S3 (Supplementary Material). Also, the strength of volumetric heat source was calibrated to match the overall drying time for mannitol 5% cycle with 79 W and 93 W: 150.6 mW/cm ³ and 205 mW/cm³ as well as 106.7 mW/cm³ for sucrose 5%, 79W case. The optimal (P(t)) microwave-assisted runs are modeled using the varying heat supply and the same process parameters as in recipes described in a Supplemental Material table. The optimal run or run with variable power (P(t)) corresponds to the process with variable 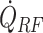. This process ensures the minimum drying time by keeping the product temperature at the highest value and accounting for the critical product temperature constraint. Figures 8C and 8D show the results of optimal microwave-assisted runs for mannitol 5% (Fig. 8C) and sucrose 5% (Fig. 8D) for 1 and 2 ml fill volumes and are obtained from the simulation.

Fig. 8.

Primary drying time for conventional drying (blue bars) and microwave-assisted drying (18 GHz) (red bars). (A) A volume of 3 ml mannitol 5% filled in Schott 6R vials and (B) 3 ml sucrose 5% filled in Schott 6R vials. Conventional and microwave-assisted results in (A) and (B) are based on experimental data. Conventional drying results in (C) and (D) are based on simulation and shown for 1 and 2 ml fill volumes with (C) mannitol 5% and (D) sucrose 5%. All the variable power (P(t)) drying results are obtained from the simulation where critical product temperatures were assumed to be −3^°C and −28^°C for mannitol and sucrose runs, correspondingly.

The modeling shows the possibility for further drying time reduction by increasing the power of the microwave heat source while avoiding the collapse of the product. In the microwave-assisted variable power (P(t)) runs, the results are compared to the conventional runs. In the P(t) case, the amount of heat supplied to the frozen product is found by solving the optimization problem, where the sublimation flux is maximized. Several equality and inequality constraints, such as critical product temperature, are taken into account during optimization. The primary drying cycle acceleration of 3.1 times can be reached for the 5% mannitol case, 3 ml fill volume. For 5% sucrose case, 3 ml fill-volume, the primary drying cycle is 2.5 times faster for optimized microwave-assisted heating. Based on the modeling results performed for 1 and 2 ml fill volumes of sucrose 5% and mannitol 5% cases, one can conclude that microwave-assisted cycle acceleration increases with reducing the fill volume. Indeed, for mannitol 5% case and 1 ml fill-volume, the modeled microwave-assisted cycle’s drying time was potentially 6.6 times shorter and 4 times shorter for 5% sucrose case.

Discussion

According to some estimates (47), sublimation and depressurization, collectively, consume more than 70% of the total energy cost of the lyophilization process. Thus, reducing the drying time reduces the energy cost significantly. This is best approached by converting the lyophilization process from the current open-loop form to a fully closed-loop form. In closed-loop lyophilization, the lyophilizer changes the recipe without interrupting the process to yield the maximum achievable drying rate and, thus, reduce the drying time. A dynamic recipe requires rigorous feedback and controllability over the running process. Feedback aims to provide a real-time sublimation rate through continuous monitoring of the pressure at the vicinity of the vial location (as opposed to the chamber absolute pressure) (48), and the product temperature (49). On the other hand, controllability aims to change the recipe—at the highest possible refresh rate—based on the feedback to result in the maximum real-time drying rate. The refresh rate essentially depends on the responsivity of the heating source to ON/OFF switching. Besides providing instantaneous ON/OFF switching of the heating source, the presented microwave-assisted lyophilization method provides uniform heating measured by 12.7% normalized SD of the moisture level across the vials compared to the 15.3% introduced by the conventional process. All the potential causes of nonuniformity in the conventional cycle, such as the edge effect (50), still applies to the presented microwave-assisted cycle. The reason is that, in the microwave-assisted cycle, microwave heating is utilized along with the conventional heating mechanism. Therefore, better uniformity can be justified by less exposure to conventional heating due to the reduced drying time. On the other hand, this predicts a significantly better uniformity when utilizing microwave-heating as the only heating mechanism. Additionally, the proposed method showed significant reductions in primary-drying times. Specifically, 42%, 65%, and 66% reductions in drying durations of mannitol, sucrose, and four myoglobin formulations, respectively, with microwave power as low as 79 W. Moreover, the proposed method accounts for the different geometrical shapes of the lyophilizer’s chamber and the lyophilizate and, therefore, is readily scalable and directly accessible to the lyophilization sector in the pharmaceutical and biotechnology industry.

Microwave-heating poses explicitly an additional challenge for product temperature monitoring. Traditionally, the temperature is monitored through Type T thermocouples, which display stability at extremely low-temperature applications with excellent repeatability in the −200 to 200^°C. They also demonstrate a good resolution of ± 1.0^°C accuracy. Nonetheless, inside an electromagnetically charged chamber, these characteristics could be compromised and strongly influenced by the high microwave power. The proposed microwave-assisted lyophilization method is directly applicable in the new and existing industrial lyophilizers. Since temperature monitoring is essential, even for the current open-loop batch-based lyophilization process, research effort needs to be directed toward investigating temperature-monitoring mechanisms compatible with the harsh EM environment imposed by the proposed method. Fiber-optical sensors, for instance, offer complete immunity to RF and microwave radiation while matching the high temperature operating capability of T-type probes. Even more, fiber optic temperature sensing is highly robust with resolutions of 0.01^°C and excellent accuracy of ± 0.15^°C. The ultrasmall diameter size of the probe and 10 ms response time makes them essential for MAFD application.

Conclusion

A new microwave-assisted lyophilization method based on the theory of statistical EMs is developed. It is a key to transforming the lyophilization process into a continuous closed-loop process with significantly higher efficiency. The method has been validated by applying to bare excipients and four formulations of a model protein—each with a different excipient. A speed-up of the primary drying of up to 2.4 × is measured through Pirani gauge and CM pressure measurement convergence. As a proof of concept, formulations were characterized using standard pharmaceutical techniques such as CD and ssFTIR to test the structural integrity of myoglobin post lyophilization and quantify the residual moisture content. Short-term AST and ssHDX-MS testing were also conducted on samples to analyze the long-term storage stability of the formulations. Results indicate that microwave-assisted lyophilization did not alter the protein structure despite producing drier samples. Additionally, long-term storage stability did not seem to differ significantly with the drying technique employed. Besides boosting the process efficiency via reducing the drying time and enhancing the heating uniformity, the proposed method is readily scalable and accounts for the lyophilizer and the lyophilizate, making it directly accessible to the lyophilization sector in the pharmaceutical and biological industries.

Notes

Competing Interest: Other than the patent US 11,289,946 B2 by (A.A., M.D.S., and D.P.), the authors declare no competing interests.

Funding

The development of computational modeling for RF/microwave-assisted lyophilization was supported by the NSF award 1827717.

Authors' Contributions

A.A. and D.P. conceived the application of high-frequency microwave-heating for lyophilization; A.A. developed the original statistical electromagnetics method, performed the EM computations/simulations, designed the dry-lab and microwave-assisted lyophilization experiments, and carried out the dry-lab experiments; M.D.S. designed, manufactured, and built the elements of the experimental setup; M.D.S. and A.A. carried out experiments #1, #2, and #3; R.T. and A.A. contributed to the sample preparation and carried out experiment #4; E.T. and R.T. designed the chemical and physical stability assays for the model protein formulations and R.T. performed the measurements by ssHDX-MS, ssFTIR, CD, and AST; and P.K. and A.A. designed the modeling of lyophilization with microwave heating effects and P.K. performed the simulations using a modified LyoPRONTO software to compare the microwave-assisted, microwave optimal, and conventional lyophilization processes. All authors wrote the manuscript, analyzed and discussed the results, and commented on the manuscript.

Previous Presentation

These results were not presented previously.

Preprints

A preprint of this article is published at (DOI).

Data Availability

The data underlying this article are available in the public repository Zenodo at https://zenodo.org/, and can be accessed with DOI: 10.5281/zenodo.6566581. Deposit number: 6566581