Mitigating long queues and waiting times with service resetting

Abstract

What determines the average length of a queue, which stretches in front of a service station? The answer to this question clearly depends on the average rate at which jobs arrive at the queue and on the average rate of service. Somewhat less obvious is the fact that stochastic fluctuations in service and arrival times are also important, and that these are a major source of backlogs and delays. Strategies that could mitigate fluctuations-induced delays are, thus in high demand as queue structures appear in various natural and man-made systems. Here, we demonstrate that a simple service resetting mechanism can reverse the deleterious effects of large fluctuations in service times, thus turning a marked drawback into a favorable advantage. This happens when stochastic fluctuations are intrinsic to the server, and we show that service resetting can then dramatically cut down average queue lengths and waiting times. Remarkably, this strategy is also useful in extreme situations where the variance, and possibly even mean, of the service time diverge—as resetting can then prevent queues from “blowing up.” We illustrate these results on the M/G/1 queue in which service times are general and arrivals are assumed to be Markovian. However, the main results and conclusions coming from our analysis are not specific to this particular model system. Thus, the results presented herein can be carried over to other queueing systems: in telecommunications, via computing, and all the way to molecular queues that emerge in enzymatic and metabolic cycles of living organisms.

Significance Statement.

Resetting can expedite the completion of random processes. From stochastic optimization, via first-passage and search, and onto chemical reactions: it has been repeatedly demonstrated that when stochastic fluctuations in the completion time of a random process are large—stopping the process and starting it anew will shorten its completion time. Here, we demonstrate how this general principle can be utilized to dramatically lower waiting times and improve overall performance of queueing systems (natural and man-made). Random service time fluctuations are notorious for causing major backlogs and delays in such systems. Yet, we show that when these fluctuations are intrinsic to the server—a remarkably simple service resetting protocol can reverse their deleterious effects and significantly cut down queues and waits.

Queueing theory is the mathematical study of waiting lines (1,2). Ranging from the all familiar supermarket and bank, to call centers (3, 4), airplane boarding (5,6), telecommunication and computer systems (7–9), production lines and manufacturing (10), enzymatic and metabolic pathways (11–14), gene expression (15–19), and transport phenomena (20–23), waiting lines and queues appear ubiquitously and play a central role in our lives. While the teller at the bank works at a (roughly) constant rate, other servers, e.g. computer systems (9), and molecular machines like enzymes (24–26), often display more pronounced fluctuations in service times. These fluctuations have a significant effect on queue performance (1,2): higher fluctuations in service times will result in longer queues as illustrated in Fig. 1(A). Service time variability is, thus a major source of backlogs and delays in queues (9), and this problem is particularly acute when encountering heavy tailed workloads (27).

Fig. 1.

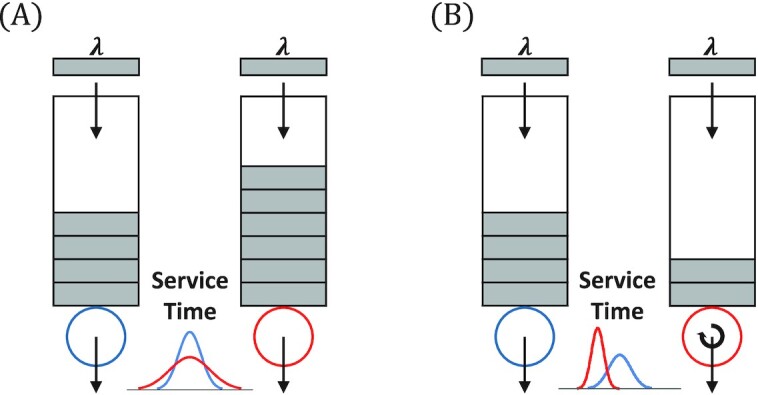
Backlogs and delays caused by service time fluctuations can be mitigated with service resetting. Panel (A): the mean number of agents—jobs, customers, molecules, and so on—in a queue is sensitive to stochastic fluctuations in the service time provided by the server (computer, cashier, enzyme, and so on). For a given arrival rate and mean service time, the queue stretching in front of a server whose service time distribution is more variable will be longer on average. This fact is schematically illustrated by the blue and red servers whose service time distributions have equal means. Yet, compared to the blue server, the larger variance of the red service time distribution leads to longer queues. Panel (B): in this paper, we show that when large service time fluctuations are intrinsic to the server, resetting service and starting it anew can dramatically improve performance. This is schematically illustrated by the red server whose service time distribution changed following the application of a service resetting policy (to be described in the main text). Comparing to panel (A), it can be seen that both the mean and variance of the red service time distribution have been reduced due to service resetting. The net outcome is a significant performance gain, which leads to shorter queues and waiting times.

Different strategies have been developed to mitigate the detrimental effect caused by stochastic service time fluctuations. In particular, when considering single server queues, various scheduling policies can be applied to reduce waiting times. For example, computer servers can be designed to serve smaller jobs first, rather than by order of arrival. While this policy can be criticized from the standpoint of fairness, it does reduce average waiting times by preventing situations where typically sized jobs (which are common) get stuck behind a single job that is very large (9). In situations where service can be stopped and continued from the same point at a later time, one can further improve performance by implementing a policy in which only the job with the shortest remaining service time is served (28). This policy can be proven optimal under certain conditions (29).

The problem with the above-mentioned scheduling policies is that they are ill-equipped to deal with situations where fluctuations in service times are intrinsic to the server itself. These are in fact prevalent. For example, stochastic optimization algorithms can take wildly different times to solve two instances of the exact same problem (30). Similarly, the time it takes an enzyme to catalyze a given chemical reaction varies considerably between turnover cycles — despite the fact that the incoming (substrate) and outgoing (product) molecules are chemically identical (24–26). Crucially, in these and similar cases the total service time of an incoming job is unknown a priori and the time remaining for a job in service cannot be determined by simple observation. Size-based scheduling policies are, thus impossible to implement, which calls for the development of new and novel approaches to the problem.

In this paper, we propose a complementary approach to solve the problems caused by service time fluctuations in queueing systems. Namely, we show that implementing a simple service resetting policy can reverse the deleterious effect of stochastic fluctuations when the latter are large and particularly harmful. The policy, which consists of random or deterministic resetting of the service process, may seem counterintuitive at first. After all, no benefit can possibly come from doing the exact same thing all over again. However, here we show that when service time fluctuations are intrinsic to the server itself, in the sense that jobs whose service has been reset are assigned fresh service times, service resetting can be used to drastically improve queue performance as illustrated in Fig. 1(B). Indeed, it has recently been shown that resetting has the ability to expedite the completion of random processes: from stochastic optimization (31–33), via first-passage and search (34–39), and onto chemical reactions (40, 41), and this general principle is, hereby, exploited in the context of queueing.

A different way in which resetting can be used to affect queue performance is by resetting of the jobs arrival process, which is interesting to consider e.g. in the context of intracellular transport (42). However, resetting the arrival process has no affect on service time fluctuations, which is further compounded by the fact that in most conventional queue structures the arrival process is extrinsic to the system and is, thus not subject to control or optimization. We, thus focus on queues with service resetting to which we devote this paper. Before moving forward to develop the theory and discuss examples, we mention in passing that the concept of resetting is also relevant in the context of reliability theory (43,44) and income dynamics (45). Resetting also appears when considering queues with catastrophic events (46–48). Note, however, that such catastrophic events lead to mass annihilation of jobs (agents) from the queue. On the contrary, service resetting conserves the number of jobs in the queue, as jobs whose service was reset would still require full service before they can leave the system. Thus, “resetting by catastrophe” should not be confused with the service resetting policy that is introduced and rigorously analyzed below.

The remainder of this paper is structured as follows. In the section “Queues: Models and Preliminaries,” we provide a brief review of the M/G/1 queuing model for which queue arrivals are Markovian and service is general. This queue will serve as the main modeling platform of this paper. We also review the Pollaczek–Khinchin formula, which provides the mean number of jobs in the M/G/1 queue at the steady-state, highlighting the sensitivity of the latter to service time fluctuations. Finally we provide a short overview of existing scheduling strategies aimed to mitigate service time fluctuations. In the section “Queues with Service Resetting,” we discuss service resetting and formulate a model for a single-server queue with service resetting. We show that the latter can be mapped onto a standard model of a single-server queue without service resetting, but with a modified service time distribution that depends on the underlying distributions of the service and resetting times. In particular, for the M/G/1 queue, this fact allows us to reapply the Pollaczek–Khinchin formula to study how the mean number of jobs in the queue depends on the resetting protocol. We focus on two prominent resetting protocols for which we provide detailed analysis: In the section “M/G/1 Queues with Poissonian Service Resetting,” we consider Poissonian resetting, i.e. resetting at a constant rate. We show that when the variability in the underlying service time distribution is high, the mean number of jobs in the system obtains a minimum as a function of the resetting rate. This means that resetting can drastically improve queue performance. Similarly, in the section “M/G/1 Queues with Sharp Service Resetting,” we study resetting at fixed time intervals (a.k.a. sharp resetting), and show that while this resetting protocol leads to similar qualitative results, the fixed inter-resetting time duration can be tuned to perform better than any other stochastic resetting protocol (Poissonian resetting included). In the section “Examples,” we illustrate the general results obtained for two well-established service time distributions, namely the log-normal and Pareto distribution, which are considered respectively in the subsections “Log-normal service times” and “Pareto service times.” Finally, in the section “Beyond the Mean Queue Length,” we go beyond the mean to explore how service resetting affects the distribution of customers in the system. In particular, we show that the z-transform of this fundamental distribution can be obtained analytically for the M/G/1 queue with service resetting. We end in the section “Conclusions and Outlook.”

In what follows we use f_Z(t), 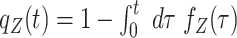, 〈Z〉, Var(Z), and 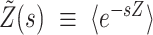to denote, respectively, the probability density function, the survival function, expectation, variance, and Laplace transform of a non-negative random variable Z.

Queues: Models and Preliminaries

Consider a queuing system that is composed of a queue in which jobs await to be served, and a server which serves one job at a time according to a First-Come, First-Served policy (FCFS). A queue can be identified as a stochastic process whose state space is denoted by the set N = {0, 1, 2, 3,...}, where the value corresponds to the number of jobs in the queue, including the one being served. In particular, an M/G/1 queue, written in Kendall’s notation (1,2,9), consists of a single server and queue to which jobs arrive according to a Poisson process with rate λ (1,2, 9). Thus, the M in Kendall’s notation stands for Markovian or memory-less arrival process. No assumptions are made on the service time of jobs, which comes from a general distribution, hence the G in Kendall’s notation. Denoting the service time by the random variable S (for service), whose density we denote by f_S(t), we define the service rate μ ≡ 1/〈S〉. It will prove convenient to introduce the utilization parameter ρ = λ/μ, which gives the fraction of time the server is working (not idle) in the steady state (1, 2, 9). The model attains a steady state as long as the arrival rate is smaller than the service rate, i.e, ρ < 1. For ρ > 1, the queue grows indefinitely long with time and the system does not attain a steady state. Thus, in what follows we will assume ρ < 1.

The number of jobs in an M/G/1 queue fluctuates with time. Thus, it is only natural to start the discussion with the average of this observable. The mean number of jobs 〈N〉 in the system (queue + server) is given by the famous Pollaczek–Khinchin formula (1, 2, 9)

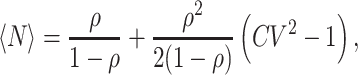(1)

where ρ is the utilization, and

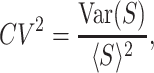(2)

is the squared coefficient of variation, or the variability in service time. As expected, the mean number of jobs is a monotonically increasing function of the utilization, with 〈N〉 tending to infinity as ρ → 1⁻. Thus, low service rates lead to long queues. Note, however, the appearance of CV² in the second term of Eq. (1). This indicates that the mean length of the queue is highly sensitive to stochastic fluctuations in the service time, which is a nontrivial effect that can be explained by the inspection paradox (9).

From the second term in Eq. (1), we see that the mean number of jobs is a monotonically increasing function of CV². Note, that when CV < 1, i.e. when service time fluctuations are relatively small, the contribution of the second term is negative, leading to shorter queues. On the other hand, when CV > 1, i.e. when service time fluctuations are relatively large, the contribution of the second term is positive, leading to longer queues. Importantly, there can be a “piling up” of jobs due to high service time variability. This can happen, for example, if short service times are occasionally followed by extremely long service times. In such situations CV² is large, thus resulting in long queues even in low utilization. It is, thus apparent that service time fluctuations are central to the behavior of the M/G/1 queue, and their effect in other queuing systems is similar.

Finally, we recall that the mean waiting time 〈T〉 of a job in the queue, i.e. the time elapsed from arrival to the end of service, follows from Eq. (1) by using Little’s law (1,2, 9), which states 〈T〉 = λ⁻¹ 〈N〉. Thus, we have

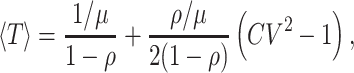(3)

and note that similar to the mean number of jobs, the mean waiting time crucially depends on fluctuations in service time.

To deal with the detrimental effect caused by service time fluctuations several different strategies have been developed. When considering single server queues, the main tools at our disposal are scheduling policies (a.k.a. service policies) (9). A scheduling policy is the rule according to which jobs are served in a queue. For example, servers can serve jobs according to the order of their arrival as e.g. happens in the supermarket. This simple FCFS policy seems fair when working with people as customers. However, when considering queues of inanimate objects, fairness is not necessarily the most important requirement and other service policies can also be considered.

The FCFS policy is an example of a nonsize-based policy—the server serves jobs based on their order of arrival rather than their size. However, in situations where jobs sizes are known, one can utilize this knowledge to devise size-based policies such as Shortest-Job-First (SJF). According to this policy, once free, the server chooses to work on the job with the smallest size, and hence also the shortest service time. In terms of the average waiting time of a job in the queue, the SJF policy performs better than the FCFS policy (9). This can be understood intuitively. In the FCFS policy, all jobs that arrive after a very large job will suffer from a long waiting time. This will not happen in the SJF policy, where extremely large jobs which are rare will not be selected for service before jobs of typical size. The latter are much more common and since they are served first they spend less time in the queue, resulting in smaller waiting times on average compared to Eq. (3).

In the SJF policy, the server chooses the smallest job waiting in the queue each time service is complete. This approach can be further developed allowing the server to inspect jobs’ sizes (including the one in service) continuously in time—constantly searching for the job with the shortest remaining service time. In such a queue, an arriving job can preempt the job in service if its own service time is lower. The service of the preempted job is resumed later, starting from the point where it was stopped. The above policy is called Shortest-Remaining-Processing-Time (SRPT) (28), and it was used e.g in web servers to reduce the waiting time of static HTTP requests whose sizes have been shown to follow a heavy-tailed distribution (9). It was proved in (29), that in single-server queues where the service time of jobs is known and preemption is possible, the SRPT policy is the optimal policy with respect to minimizing the mean waiting time.

Having readily available knowledge of job sizes and their remaining service times, as well as the ability to preempt jobs, is a luxury not shared by all queueing systems. For example, in nondeterministic algorithms, e.g. stochastic optimization methods, inputs of similar size can render significantly different run times (30), and the same can happen for consecutive runs of the algorithm using the same input. Size-based scheduling policies like the SJF and SRPT are then inapplicable. Instead, we will hereby show that in such cases the intrinsic randomness of the service process can be exploited via service resetting to achieve similar performance goals.

Queues with Service Resetting

In the section “Queues: Models and Preliminaries,” we reviewed the nontrivial dependence that the mean number of jobs in an M/G/1 queue has on service time fluctuations. Namely, large relative fluctuations lead to long queues. In this section, we analyze the effect of service resetting on the mean and variance of the service time. We emphasize that the analysis presented in this section is agnostic to the arrival process. Thus, the results obtained are not specific to the M/G/1 queue and apply broadly to queues with general arrivals.

To understand how restarting service affects the overall service time of a job, we consider two extreme scenarios. First, consider a situation where fluctuations in service times are extrinsic to the server. Thus, imagine a server that serves jobs of variable size at a constant rate. In this case, the service time is determined exclusively by the job size, i.e. the bigger the job the longer the service time, and vice versa. An example of such would be a supermarket cashier counter. The teller serves the customers at a (roughly) constant rate, and the service time is determined by the number of items each customer has. Thus, the fluctuations in service time originate solely from the variability in the number of items each customer brought. Imagine now that the teller decides to restart service from time to time. Since restart does not affect the number of items one has, this strategy is clearly detrimental. The time already spent in service is lost, while the customer’s required service time remains unaltered. Thus, in this case, restart results in wasted time and delays.

Now, consider a queue in which fluctuations in service times are intrinsic to the server, i.e. a queue in which all jobs are (roughly) identical but the time it takes to serve a job is nevertheless random. Example of such would be a computer server, which runs a stochastic algorithm. Such algorithms employ probabilistic approaches to the solution of mathematical problems, e.g. optimization. The run time of such an algorithm can vary considerably between runs. Importantly, stochastic fluctuations in run times come from the probabilistic solution method. This means that run times can be different even for two identical instances of the same problem. Thus, resetting such an algorithm in its course of action would result in a new and random run time, contrary to the case of a teller in a supermarket.

Another example of a queue in which fluctuations in service time are intrinsic to the server can be found in enzymatic reactions. In the context of enzymes, substrate molecules can be viewed as customers, forming a “waiting line” to the enzyme which acts as a server. Substrate molecules are identical, and require the same type of service: a catalytic process which converts a substrate molecule to a product molecule. Yet, at the single-molecule level, chemistry is stochastic as thermal fluctuations render the service (catalysis) time random. It is often the case that a substrate molecule unbinds the enzyme without completing service (40). In this case, service is reset, and a new and random service time is drawn upon rebinding.

Before going forward with the analysis, we once again point out that the two scenarios presented above are extremes in which the service time of a job is set by factors which are either completely extrinsic or completely intrinsic to the server. More generally, one can think of situations where a mix of extrinsic and intrinsic factors affect the service time. While such distinctions are rarely made or considered in traditional queueing theory, they have recently taken center stage in the analysis of queues with job redundancies (49). As explained above, understanding the source of service time variability is also important when considering queues with service resetting.

We proceed to consider queues in which service time fluctuations are completely intrinsic to the server. As explained above, in these queues resetting results in a newly drawn service time that is added to the time already spent in service. In what follows, we will quantify the effect of resetting on the mean and variance of the total service time. We will then go on to show that in certain situations resetting significantly expedites service, thus improving overall performance by shortening queues. This effect will be discussed in the next section.

Let us consider a server with service resetting. Assume that both the service and restart times are two independent and generally distributed random variables. The total service time under restart, S_R, is then described by the following renewal equation 

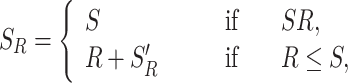(4)

where R is a random resetting time drawn from a distribution with density f_R(t), and 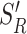is an independent and identically distributed copy of S_R. To understand this equation, observe that when service occurs before restart, S_R = S. However, if service is restarted at a time R ≤ S, then service starts over with newly drawn service and resetting times. In this case, .

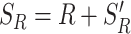Service can be seen as a first-passage process which ends when a job is served. A comprehensive framework for first-passage under restart was developed in (36,37). In the following, we show how the results obtained there can be used to gain insight on the general performance of queues with service resetting. We note that these results were obtained in continuous time, which will be considered henceforth. For an analogous set of results in discrete time, please see the recently developed framework for discrete time first-passage under restart (50).

Starting from Eq. (4), one can obtain the probability density of S_R in Laplace space (Methods). In what follows, we will first consider the first two moments of this distribution. These are given by (Methods)

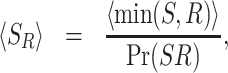(5)

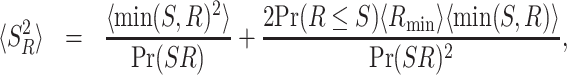(6)

where min(S, R) is the minimum between S and R, Pr(S < R) is the probability of service being completed prior to restart, and R_min = {R|R = min(R, S)} standing for the random restart time given that restart occurred prior to service. Finally, recall that the variance in the service time is given by 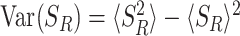, which will be useful in the next section. Equations (5) and (6) assert that the mean and variance of the service time under restart can be evaluated directly from the distribution of the resetting time and the distribution of the service time without resetting. Importantly, in cases where this cannot be done analytically, numerical methods can be used to obtain 〈S_R〉 and 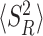and as long as the distributions of R and S are known or can be sampled from.

M/G/1 Queues with Poissonian Service Resetting

Poissonian resetting, i.e. resetting with a constant rate, has been extensively investigated (34–38) (see (39) for extensive review and (51) for discussion on the connection with the inspection paradox). As the name suggests, here resetting follows a Poisson process and the number of resetting events in a given time interval comes from the Poisson distribution. In this section, we quantify the effect of Poissonian resetting on the mean and variance of the service time in a general queueing system. With this result at hand, we specialize to determine the mean number of jobs in an M/G/1 queuing system with service resetting.

Consider service resetting with rate r. In other words, we take the restart time R in Eq. (4) to be an exponential random variable with mean 1/r, which renders service resetting a Poisson process with rate r. The mean and second moment of the service time can then be derived using Eqs. (5) and (6), giving (Methods)

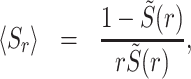(7)

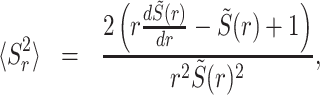(8)

where 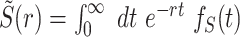is the Laplace transform of the service time, evaluated at the restart rate r.

The utilization of this queue is then given by ρ_r = λ〈S_r〉, and the squared coefficient of variation of the service time is 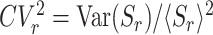. We can now write the mean queue length in an M/G/1 system with service resetting by replacing ρ by ρ_r, and CV² by 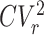, in Eq. (1). This yields

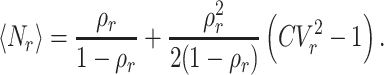(9)

Similarly, the mean waiting time 〈T_r〉 in the system can be derived from Little’s law (1, 2, 9), yielding an analogous result to Eq. (3).

To better understand the effect of resetting on the mean queue length, consider the introduction of an infinitesimal resetting rate δr. Utilizing Eq. (7), we then find

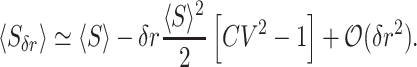(10)

As expected, the first term on the right hand side of Eq. (10) is the mean of the original service time, i.e. without resetting. The second term gives the first order correction, and note that its sign is governed by CV² of the original service time. Specifically, for CV² > 1, we have 〈S_δr〉 < 〈S〉 and vice versa. In other words, the introduction of Poissonian resetting to an M/G/1 queue will reduce the mean service time whenever the coefficient of variation of the original service time is greater than unity.

In Fig. 2, we consider a representative example for the effect of resetting on an M/G/1 queue with large fluctuations in service time. Starting from a service time distribution with CV > 1, we introduce resetting and plot the mean service time 〈S_r〉 vs. the resetting rate. As predicted by Eq. (10), we see that 〈S_r〉 initially decreases, obtaining a minimum at an optimal resetting rate r*. In addition, note that at this optimal resetting rate we have 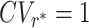. Remarkably, this observation is not specific to the service time distribution considered in Fig. 2, but is rather a universal property. Namely, it can be shown that (37)

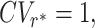(11)

for any resetting rate, 0 < r* < ∞, at which

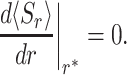(12)

Substituting Eq. (7) into Eq. (12) yields

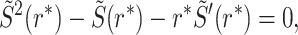(13)

which can be solved to obtain r*. Combining Eq. (11) with the Pollaczek–Khinchin formula given in Eq. (9), we have

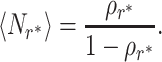(14)

Note that the mean number of jobs at optimality is equivalent to the mean number of jobs in an M/M/1 queue (9), for which the service time is exponentially distributed with mean 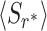. We return to this point in the section “Beyond the Mean Queue Length,” where we show that this result does not extend to the level of the distribution of number of jobs in the system.

Fig. 2.

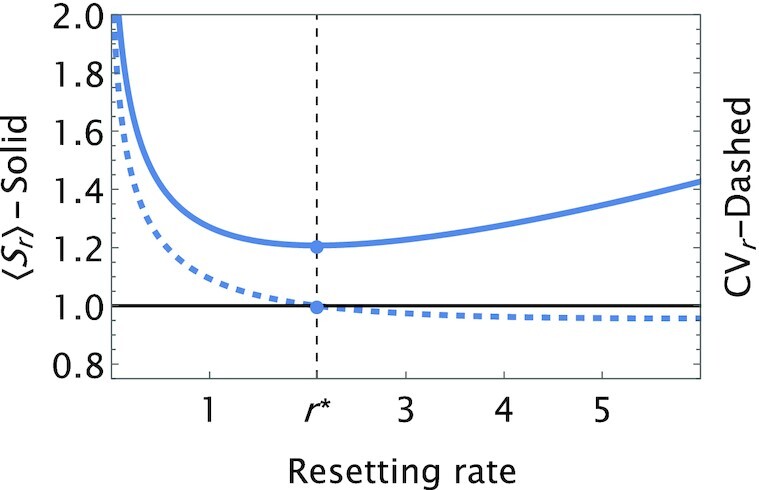
The mean (solid line) and CV (dashed line) of the service time with Poissonian resetting as a function of the resetting rate. Plots were made, using Eqs. (7) and (8), for an underlying service time taken from the inverse-Gaussian distribution whose density is given by 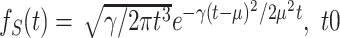. Here, μ = 2.5 and γ = 0.5. Observe that the mean service time with resetting, 〈S_r〉, is minimized at an optimal resetting rate r* ≃ 2.092, which was found using Eq. (13). At this optimal resetting rate we have .

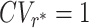Comparing Eqs. (1) and (14), we observe that 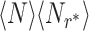. One can easily derive this inequality by substituting CV > 1 into Eq. (1). This yields

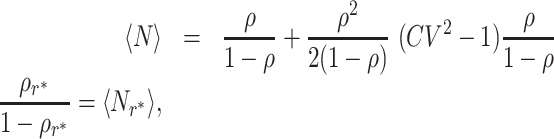(15)

where in the last inequality we used the monotonicity of the function 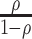on the interval [0,1), and the optimality of r*, which implies 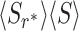resulting in .

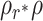We, thus see that whenever CV > 1 for the original service time, the mean number of jobs in the queue can be reduced by resetting service at an optimal rate. When doing so, one also sets the coefficient of variation of the optimally restarted service time to unity. Thus, resetting not only shortens the mean service time but also reduces the relative stochastic fluctuations around this mean, hence providing a double advantage.

M/G/1 Queues with Sharp Service Resetting

So far, we considered queues with resetting at a constant rate. In what follows, we consider a different extensively investigated resetting strategy, namely sharp (a.k.a deterministic or periodic) resetting (37,52–56). Strong motivation to study this strategy comes from the fact that, in terms of mean performance, sharp resetting either matches or outperforms any resetting strategy of the type considered above Eq. (4) (Poissonian resetting included) (37).

To see this, let us now consider service which is reset at fixed time intervals of length τ, i.e. when the received service time reaches a certain threshold. This simply means that the resetting time R in Eq. (4) is taken from the distribution f_R(t) = δ(t − τ), where δ(t) is the delta function. Equations (5) and (6), can then be simplified to give (Methods)

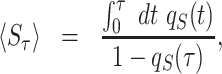(16)

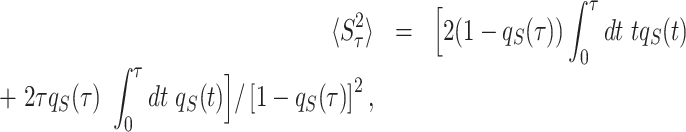(17)

where 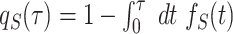is the survival function associated with the underlying service time.

The utilization of this queue is then given by ρ_τ = λ〈S_τ〉, and the squared coefficient of variation of the service time is 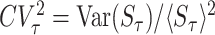. We can now obtain the mean queue length under service resetting by replacing ρ by ρ_τ, and CV² by 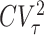, in Eq. (1). This yields

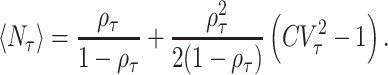(18)

In Fig. 3, we consider a representative example for the effect of sharp resetting on an M/G/1 queue with large fluctuations in service time. Starting from the same service time distribution used in Fig. 2 (CV > 1), we introduce resetting and plot the mean service time 〈S_τ〉 vs. the sharp resetting time τ. Once again, we observe that 〈S_τ〉 obtains a minimum at an optimal resetting time τ*. In addition, note that at this optimal resetting time we have 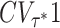. As for the case of Poissonian resetting, this observation is not specific to the service time distribution considered in Fig. 3, but is rather a universal property. Namely, it can be shown that (37)

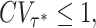(19)

for an optimal resetting time τ*, which brings 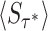to a global minimum. As before, τ* can be found by setting

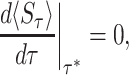(20)

which by substitution of Eq. (16) into Eq. (20), boils down to

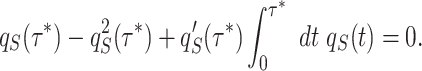(21)

Fig. 3.

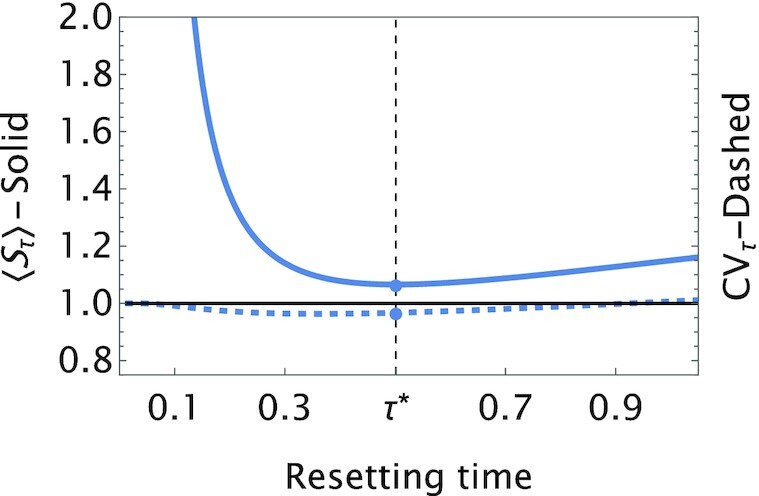
The mean (solid line) and CV (dashed line) of the service time with sharp resetting as a function of the resetting time. Plots were made, using Eqs. (16) and (17), for an underlying service time taken from the inverse-Gaussian distribution whose density is given by 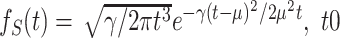. Here, μ = 2.5 and γ = 0.5. Observe that the mean service time with resetting, 〈S_τ〉, is minimized at an optimal resetting time τ* ≃ 0.501, which was found using Eq. (21). At this optimal resetting time we have .

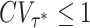Combining Eq. (19) with the Pollaczek–Khinchin formula given in Eq. (18), we have

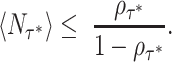(22)

It is interesting to compare Eqs. (22) and (14). To this end, we recall that the mean first passage time under optimal sharp resetting is always smaller or equal than that obtained under optimal Poissonian resetting (37). Translating this result to the language of queueing, we have 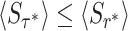, which implies  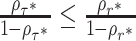, by monotonicity. We, thus have

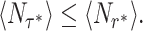(23)

Equation (23) is of great importance as it reveals that sharp resetting offers an additional improvement compared to the Poissonian resetting strategy. Once again, we see that whenever CV > 1 for the original service time, the mean number of jobs in the queue can be reduced by resetting service at an optimal time. When doing so, one also reduces the coefficient of variation of the optimally restarted service time below unity. Thus, sharp resetting further shortens the mean service time, while also reducing the relative stochastic fluctuations around this mean compared to Poissonian resetting. We now set out to illustrate the results obtained in the sections “M/G/1 Queues with Poissonian Service Resetting” and “M/G/1 Queues with Sharp Service Resetting” on two case studies of particular interest.

Examples

To demonstrate the power of our approach, we now consider two service time distributions, which are well-documented in the queuing literature: log-normal and Pareto (57–62). Note that we intentionally skip the exponential service time distribution as this distribution is memory-less, and therefore, unaffected by service resetting (51). In what follows, we first describe the effect of restart in the case of log-normal service times and discuss Pareto service times next.

Log-normal service times

Consider the case of an M/G/1 queue whose service time S is log-normally distributed

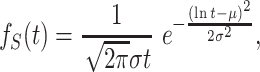(24)

for t > 0, where μ ∈ ( − ∞, ∞) and σ > 0. The survival function is then given by

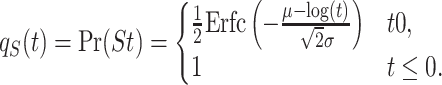(25)

The mean and variance of the service time in this case are given by

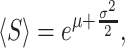(26)

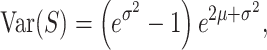(27)

such that

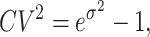(28)

which is independent of μ. In the discussion below, we set the mean service time 〈S〉 to be fixed, and vary σ, which controls the relative magnitude of fluctuations in service time via Eq. (28). Setting 〈S〉 and σ, μ is uniquely determined by Eq. (26).

For Poissonian resetting, the mean service time is given by Eq. (7), which requires the Laplace transform of the log-normal distribution. The latter, does not have an analytical closed-form, but it can be evaluated numerically for any choice of parameters. In the case of sharp resetting, the mean service time is given by Eq. (16), which requires the survival function q_S(t) given in Eq. (25). Here too, the mean service time under resetting can be computed by numerical evaluation of the required integrals. In Fig. 4, we set 〈S〉 = 1 and σ = 1.05, and plot the mean service time under Poissonian and sharp resetting. In both cases, a minimum is obtained at an optimal resetting rate or time, depending on the resetting scheme. Observe that the optimal mean service time under sharp resetting is indeed lower than that obtained for Poissonian resetting.

Fig. 4.

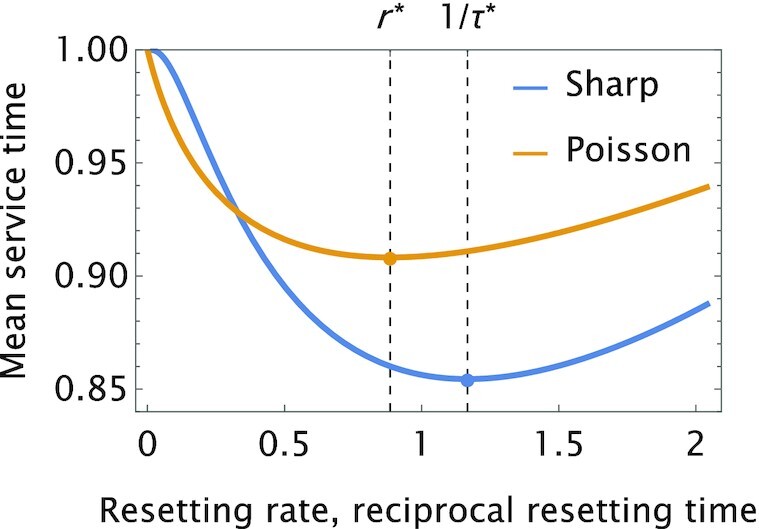
The mean service time with Poissonian (orange) and sharp (blue) resetting, as a function of the resetting rate and reciprocal resetting time. Plots were made, using Eqs. (7) and (16), for an underlying service time taken from the log-normal distribution whose density is given by Eq. (24). Here, 〈S〉 = 1 and σ = 1.05, yielding μ = −0.28125. The optimal resetting rate, r*, and resetting time, τ*, are indicated.

To find the optimal resetting rate in Fig. 4, we solve

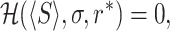(29)

where 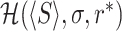denotes the left hand side of Eq. (13). This gives r* ≃ 0.885 for the given parameters. A similar minimization procedure can be carried out for sharp resetting. Substitution of the survival function for the log-normal distribution given in Eq. (25) into Eq. (21) yields the following equation for the optimal resetting time τ*

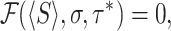(30)

where 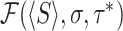denotes the left hand side of Eq. (21). This gives τ* ≃ 0.857.

Once in hand, the optimal resetting rate r* can be substituted into Eqs. (7) and (8), to obtain the mean and variance of the service time under optimal Poissonian resetting. Similarly, τ* can be substituted into Eqs. (16) and (17), for the mean and variance of the service time under optimal sharp resetting. Once these quantities are known, and given the arrival rate λ, the Pollaczek–Khinchin formula can be used directly to obtain the mean number of jobs in a queue with optimal service resetting.

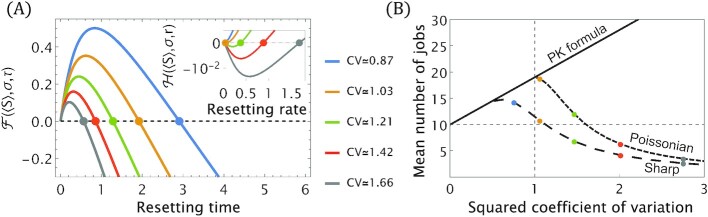
In Fig. 5, we extend the analysis presented in Fig. 4. Setting 〈S〉 = 1, we compute the optimal resetting rate and time for various values of the parameter σ (Fig. 5A), which controls the relative fluctuations in the log-normal service time via Eq. (28). We then compare between the mean number of jobs in a queue without service resetting and that obtained when optimal Poissonian and sharp resetting are applied (Fig. 5B). We observe that resetting can drastically shorten queues when stochastic fluctuations in the underlying service time are large (high CV). To this end, note that optimal sharp resetting outperforms optimal Poissonian resetting as predicted by Eq. (23). Also, note that for high CV values the mean queue lengths at optimal resetting drop below the mean queue length in the absence of service time fluctuations (CV = 0). This remarkable feature illustrates how resetting turns the problem of service time fluctuations into an advantageous benefit.

Fig. 5.

Panel (A): solutions of Eqs. (29) and (30) for the Log-normal service time distribution under Poissonian (inset) and sharp resetting (main). Here, we fix 〈S〉 = 1 for the mean service time without resetting and vary σ to control relative stochastic fluctuations, CV, via Eq. (28). The intersection points of the curves with the dashed horizontal line going through the origin give the optimal resetting times τ* (optimal resetting rates r* in the inset). Note that higher values of σ yield lower optimal resetting times (higher resetting rates). Panel (B): The mean number of jobs in a queue with arrival rate λ = 0.95, as a function of the underlying CV² of the service time distribution. The Pollaczek–Khinchin formula gives the familiar linear dependence of Eq. (1). Also plotted are the behaviors for the optimal Poissonian and sharp resetting protocols, with colored circles matching their counterparts in panel (A). Strong deviations from the Pollaczek–Khinchin behavior of the nonrestarted case are observed. While resetting provides no advantage for low CV values, it can drastically reduce queue lengths when CV is high.

Pareto service times

We now consider the case of an M/G/1 queue whose service time S is Pareto distributed

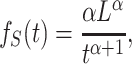(31)

for t ≥ L, where α, L > 0. The survival function is then given by

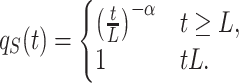(32)

The mean and variance of the service time in this case are given by

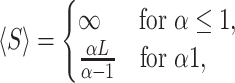(33)

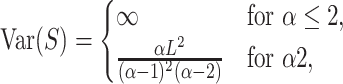(34)

such that

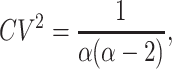(35)

for α > 2, and note that this coefficient of variation is independent of L. Next, we consider this queue with service resetting.

For Poissonian resetting, the mean service time is given by Eq. (7), which requires the Laplace transform of the Pareto distribution. This is given by

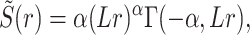(36)

where Γ(s, x) is the upper incomplete gamma function

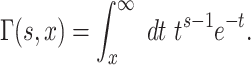(37)

By substituting the above into Eqs. (7) and (8), we get the following expressions for the mean

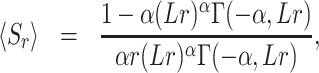(38)

and second moment

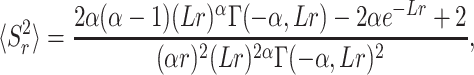(39)

of the service time under Poissonian resetting.

In the case of sharp resetting, the first two moments of the service time are given by Eqs. (16) and (17). Substituting the survival function (32) into Eqs. (16) and (17) yields

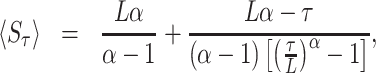(40)

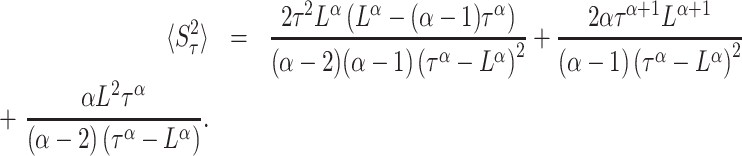(41)

Note that in the above we only considered resetting times τ > L as the support of the Pareto distribution is given by t ≥ L. Also, note that Eq. (40) is valid for α ≠ 1. Similarly, in Eq. (41) we require α ≠ 1, 2. These singular cases require separate treatment, following similar footsteps.

In Fig. 6, we set 〈S〉 = 1 and α = 2.1, and plot the mean service time under Poissonian and sharp resetting. In both cases, a minimum is obtained at an optimal resetting rate or time, depending on the resetting scheme. Once again, the optimal mean service time under sharp resetting is indeed lower than that obtained for Poissonian resetting.

Fig. 6.

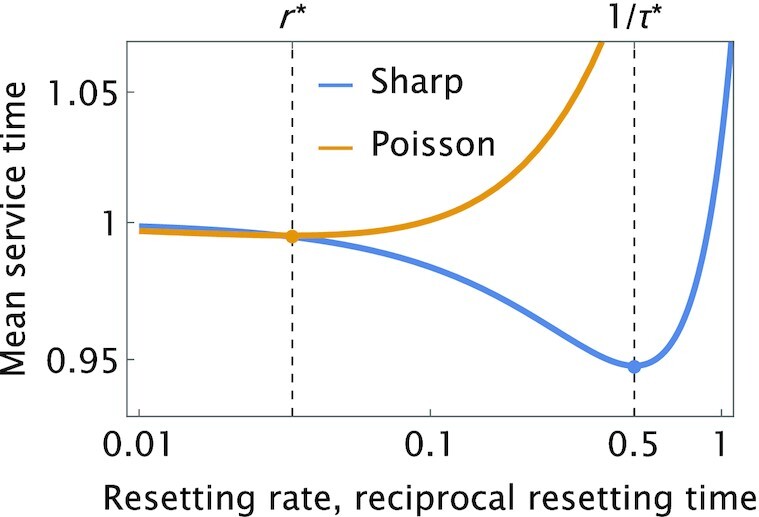
The mean service time with Poissonian (orange) and sharp (blue) resetting, as a function of the resetting rate and reciprocal resetting time (log-scaled). Plots were made, using Eqs. (38) and (40), for an underlying service time taken from the Pareto distribution whose density is given by Eq. (31). Here, 〈S〉 = 1 and α = 2.1, yielding L ≃ 0.524. The optimal resetting rate, r*, and resetting time, τ*, are indicated.

To find the optimal resetting rate in Fig. 6, we solve

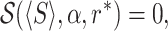(42)

where 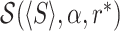denotes the left hand side of Eq. (13), after substituting the Laplace transform of Eq. (36). This gives r* ≃ 0.034. A similar minimization procedure can be carried out for sharp resetting. Substitution of the survival function for the Pareto distribution given in Eq. (32) into Eq. (21) yields the following equation for the optimal resetting time τ*

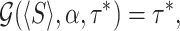(43)

where

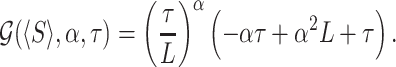(44)

Solving gives τ* ≃ 1.990.

The optimal resetting rate r* can be substituted into Eqs. (7) and (8), to obtain the mean and variance of the service time under optimal Poissonian resetting. Similarly, τ* can be substituted into Eqs. (16) and (17), for the mean and variance of the service time under optimal sharp resetting. Once these quantities are known along with the arrival rate λ, the Pollaczek–Khinchin formula can be used directly to obtain the mean number of jobs in a queue with optimal service resetting.

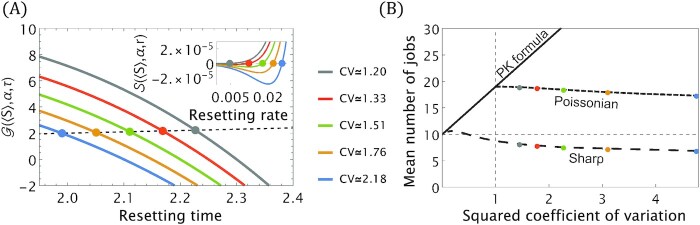
In Fig. 7, we extend the analysis presented in Fig. 6. Setting 〈S〉 = 1, we compute the optimal resetting rate and time for various values of the parameter α (Fig. 7A), which controls the relative fluctuations in the Pareto service time via Eq. (35). Here, we made sure that α > 2, so as to keep both the mean and variance of the service time without resetting finite. We then compare between the mean number of jobs in a queue without service resetting and that obtained when optimal Poissonian and sharp resetting are applied (Fig. 7B). Like in the previous example, here too, we observe that resetting can induce shorter queues when the underlying service time variability (CV) is large. Noteworthy in this case is the dominance of sharp resetting over Poissonian resetting as predicted by Eq. (23). Moreover, for high CV values the mean queue length at optimal sharp resetting drops below the mean queue length in the absence of service time fluctuations (CV = 0). This hallmark property demonstrates once again how resetting can take advantage of large stochastic fluctuations in the service time to drastically improve queue performance.

Fig. 7.

Panel (A): solutions of Eqs. (42) and (43) for the Pareto service time distribution under Poissonian (inset) and sharp resetting (main). The intersection points of the curves for different α (i.e. for different CV) with the dashed line give the optimal resetting times τ* (optimal resetting rates r* in the inset). Panel (B): the mean number of jobs in a queue with arrival rate λ = 0.95, as a function of the underlying CV² of the service time distribution. The Pollaczek–Khinchin formula gives the familiar linear dependence of Eq. (1). Also plotted are the behaviors for the optimal Poissonian and sharp resetting protocols, with colored circles matching their counterparts in panel (A). Strong deviations from the Pollaczek–Khinchin behavior of the nonrestarted case are observed. While resetting provides no advantage for low CV values, it can drastically reduce queue lengths when CV is high.

Finally, we utilize the Pareto case study to demonstrate that service resetting can also be useful in extreme situations where the variance, and possibly even mean, of the service time diverge. Indeed, while in such cases the mean number of jobs in the queue would normally diverge as well, service resetting can prevent the queue from “blowing up.” To see this, it is enough to observe that the first two moments of the service time under resetting, Eqs. (5) and  (6) correspondingly, are always finite—and as long as the mean resetting time is finite and the probability for service to complete before resetting is nonzero. Thus, service resetting acts to regularize moment divergence of the underlying service time distribution, which in turn allows queues with service resetting to operate under extreme heavy-load conditions that would not be accessible otherwise. This nontrivial conclusion is further illustrated in Fig. 8.

Fig. 8.

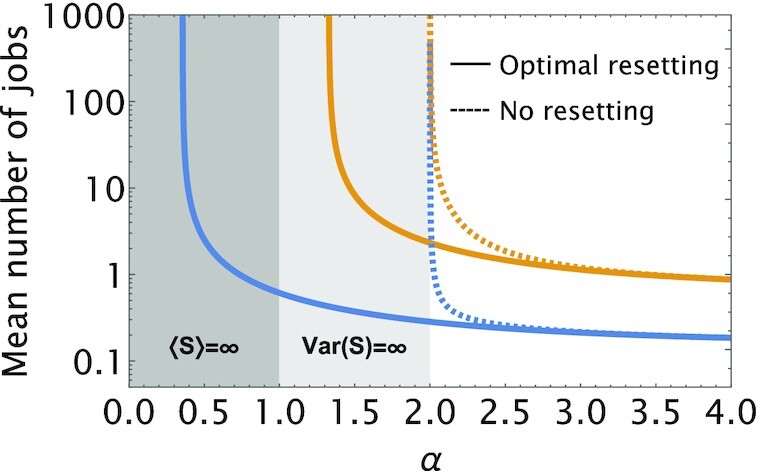
Queues with service resetting can operate under extreme heavy-load conditions that are not accessible to normal queues. To illustrate this, we plot in dashed lines the mean number of jobs for two queues with a Pareto service time distribution. Fixing L = 1 in Eq. (31), and setting the arrival rates to λ = 0.125 (blue) and λ = 0.4 (orange), we see that both queues “blow up” as α → 2. Indeed, recalling Eq. (34), we see that Var(S) = ∞ for α ≤ 2 and the divergence in the mean number of jobs follows from the Pollaczek–Khinchin formula. In contrast, we use solid lines to plot the mean number of jobs for the same queues, but with optimal sharp resetting. Observe that in both cases the mean number of jobs remains finite well below α = 2, and only diverges when the service rate (under optimal sharp resetting) drops below the corresponding arrival rate.

Beyond the Mean Queue Length

So far, we have only been concerned with the mean number of jobs in a queue with service resetting. We will now turn our attention to discuss the full distribution of the queue length. In an M/G/1 queue, the probability mass function of the number of jobs in the system, defined as P_N(n) = Pr(N = n), is not known explicitly. However, one can obtain an expression for the corresponding probability generating function

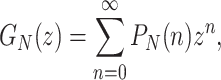(45)

using the Pollaczek–Khinchine transform equation (2)

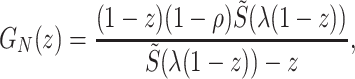(46)

where 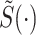is the Laplace transform of the service time, and ρ = λ〈S〉 is the utilization of the queue. Similarly, one can also compute the Laplace–Stieltjes transform, 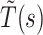, of the total time a job spends in the system. This is given by the corresponding Pollaczek–Khinchin transform equation which reads (9)

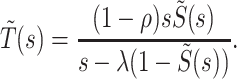(47)

Equations (46) and (47) apply to the standard M/G/1 queue. To obtain corresponding formulas with service resetting, we follow a similar procedure to that, which was applied for the mean number of jobs and mean waiting time in the queue. Namely, we replace ρ and 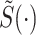in the above Pollaczek–Khinchin formulas by ρ_R and 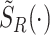, which are correspondingly the utilization of the queue and Laplace transform of the service time with service resetting. In general, the latter is given by Eq. (52) in the Methods section. In what follows, we will consider a specialized version of this general formula, which is of particular interest due to its analytical tractability and ubiquitous applicability. Namely, we consider the case of Poissonian resetting for which one can readily show that (36,37)

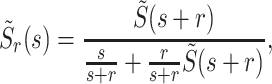(48)

with r standing for the resetting rate. For completeness, and to keep the presentation self-contained, this formula is also rederived in the Methods section.

In Fig. 9, we compare the distribution of the number of jobs in an M/G/1 queue, with and without optimal Poissonian service resetting. We assume the inverse-Gaussian service time distribution that was discussed in Fig. 2, and note that its Laplace transform is given by 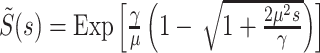, with γ, μ > 0. Substituting this result into Eq. (48), we obtain the Laplace transform of the service time with Poissonian resetting at a constant rate r:

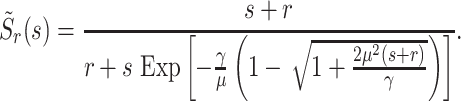(49)

We then substitute the Laplace transform of Eq. (49) into Eq. (46), and replace ρ by ρ_r in this equation, to obtain the probability generating function

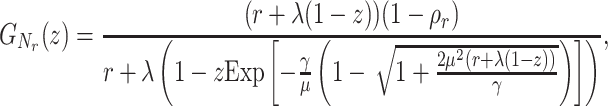(50)

Fig. 9.

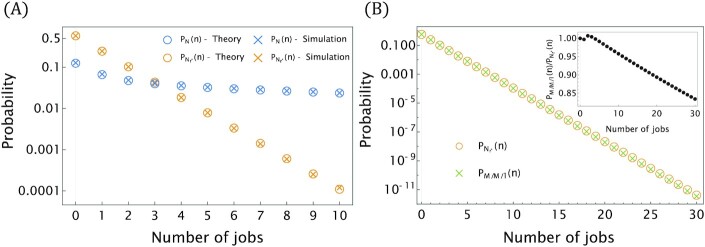
Panel (A): the probability mass function of the number of jobs in the system (queue + server) with (orange markers) and without (blue markers) optimal Poissonian service resetting. Here, the jobs arrival rate was set to λ = 0.35 and the service time was taken as in Fig. 2, i.e. from the inverse-Gaussian distribution 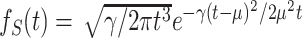, with parameters μ = 2.5 and γ = 0.5. The probability to find n jobs in the system with service resetting, 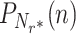, was computed via Eq. (51) for a resetting rate r* ≃ 2.092, which minimizes the mean service time for this choice of parameters (see Fig. 2). Similarly, the probability P_N(n) to find n jobs in the system without service resetting was computed by taking derivatives of Eq. (46). These analytical results (circles) were further corroborated with numerical simulations (X marks). Panel (B): the probability mass function 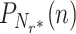from panel (A) is compared to the geometric probability distribution—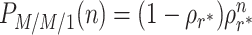—of an M/M/1 queue with the same mean service time, arrival rate, and utilization 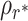(green). Equation (14) asserts that the mean number of jobs in these two queueing systems is identical, but note that this equivalence does not extend to their stationary probability distributions which are similar but not identical (inset).

of the number of jobs in the presence of service resetting. The probability to find n jobs in the system can then be computed from Eq. (50) via

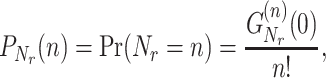(51)

where 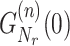stands for the nth derivative of 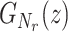evaluated at z = 0. The probability P_N(n) to find n jobs in the system without service resetting can be similarly computed by taking derivatives of Eq. (46).

The effect of service resetting can be seen in panel (A) of Fig. 9. It is evident that optimal service resetting with rate r* results in a stationary job distribution whose tail decays faster compared to the no resetting case. This, in turn, results in a lower mean queue length compared to that, which is obtained in the absence of resetting. In panel (B), we further compare the stationary queue length distribution to the geometric distribution of an M/M/1 queue that has the same mean service time, arrival rate, and utilization. Recall that Eq. (14) asserts that the mean number of jobs in an M/G/1 queue with optimal Poissonian service resetting is equal to the mean number of jobs in an M/M/1 queue that has the same utilization. This happens since the mean and standard deviation of the service time become equal under optimal Poissonian service resetting [see Eq. (11)], which is also a property of the exponential service time distribution of the standard M/M/1 queue (i.e. in the absence of resetting). As a result, the performance of the two queues is very similar, but not identical (inset). Indeed, while the mean and standard deviation of the service time identify under optimal Poissonian service resetting, the full service time distribution need not be exponential as in the M/M/1 queue. This, in turn, results in deviations from the geometric distribution for the number of jobs in the system.

Conclusions and Outlook

Regulating the number of jobs in a queue is an integral part of performance modeling and optimization of queuing systems. One problem that arises in this context is that large stochastic fluctuations in service times lead to significant backlogs and delays. In this paper, we showed how this problem can be mitigated by service resetting. Specifically, we have shown that when applied to servers with intrinsically high service time variability, resetting can dramatically reduce queue lengths and job waiting times.

To intuitively understand how this is possible, consider a scenario where service completes within τ₁ or τ₂ time units with equal probabilities; and further let τ₁ ≪ τ₂. It is then clear that if service did not complete after τ₁ time units, resetting service shortly after this time is beneficial. Indeed, as a new service time is drawn with each resetting, such resetting protocol would give a mean service time of ≈2τ₁, which is significantly shorter than the (τ₁ + τ₂)/2 that is obtained in the absence of resetting. More generally, it has been demonstrated repeatedly that when stochastic fluctuations in the completion time of a random process are large—stopping the process and starting it anew will shorten its mean completion time. This fact was proven rigorously for sharp resetting, which occurs periodically at fixed time intervals (52,53); and for Poissonian resetting where it was moreover shown to be a direct result of the inspection paradox (51).

In this paper, we further developed the theory of stochastic resetting and applied it to better the design and performance of queueing systems. The analysis presented was based on the canonical M/G/1 queuing model in which jobs arrive to the queue following a Poisson process and service times come from a general distribution. The renowned Pollaczek–Khinchin formula [Eq. (1)] asserts that the mean number of jobs in this queue grows linearly with the squared coefficient of variation, CV², of the service time. Employing the recently developed framework of first-passage under restart (36, 37) to the M/G/1 queue, we showed that Poissonian service resetting reduces both the mean and variance of the overall service time when CV > 1, i.e. exactly when service time fluctuations start to become a major source of concern. Sharp service resetting, performs even better and could in some cases lower the mean and variance of the service time even when CV < 1 (52). In both cases, this results in shorter queues and examples were given to show that mean queue lengths may even drop below those attained for servers with no service time fluctuations. Service resetting can thus turn a well-known drawback of queueing systems into a favorable advantage.

Our work is the first step toward the application of resetting as a fluctuations mitigation strategy in queueing systems. The analysis presented above yielded analytical formulas for the mean and distribution of the number of jobs in an M/G/1 queue under service resetting, thus generalizing the Pollaczek–Khinchin formula to this case. While obtaining similar analytical expressions in systems other than the M/G/1 queue requires additional work, it is important for us to emphasize that several results and conclusions coming from our analysis trivially carry over to other queueing systems. As realistic job arrival processes are often non-Poissonian, queues with non-Markovian arrivals are of prime importance in this regard. Crucially, such queues also suffer from service time fluctuations, which is most easily appreciated by examining Kingman’s approximation formula (63). The latter asserts that the mean number of jobs in a G/G/1 queuing system (general arrivals and service) grows linearly with the squared coefficient of variation of the service time, i.e. just like it does in the M/G/1 queue.

Interestingly, the application of service resetting in the G/G/1 queue will have the same effect on the service time distribution as in the simpler M/G/1 queue. To see this, one only needs to observe that in both queues the arrival process is completely decoupled from the service process, and moreover note that resetting only modifies the service time distribution. Thus, in all cases where service resetting is beneficial in the M/G/1 queue it would also be beneficial in the G/G/1 queue. Moreover, while an exact general expression for the mean number of jobs in the G/G/1 queue with service resetting is unknown, the results derived in the sections “Queues with Service Resetting,” “M/G/1 Queues with Poissonian Service Resetting,” “M/G/1 Queues with Sharp Service Resetting,” and in the Methods—regarding the service time distribution under resetting—can be applied directly to estimate this central quantity via Kingman’s approximation formula. Indeed, this can be done since no specialized properties of the M/G/1 queue were utilized in the derivation of these results, and since both Kingman’s approximation and the Pollaczek–Khinchin formula depend only on the first two moments of the service time distribution.

More generally, we observe that the results established in this paper utilize the independence of the arrival and service processes to map single-server queuing systems with service resetting onto single-server queuing systems without service resetting. Conclusions coming from this work, thus apply broadly to single-server queuing systems, and possible extensions to multiserver queues and queueing networks are left for future research. More sophisticated service resetting strategies, e.g. ones which can utilize full or partial information regarding the state of the queue or server, would also be interesting to consider as part of future research. Finally, note that we have assumed that resetting takes zero time, which is rarely the case in real world systems (40,41, 64). Accounting for this time, as well as other possible costs of service resetting in queuing systems, is crucial if we are to narrow the gap between theory and practice. This can be done by taking advantage of results established in (40,41, 51, 64–66).

Methods

In this section, we provide full derivation of central results that were announced in the main text. Some of these results were derived employing the framework of first passage under restart in (37).

We start by recalling that the Laplace transform of the distribution of the service time under resetting can be derived from Eq. (4) in the main text to give (37)

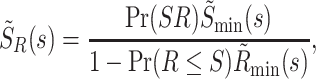(52)

where 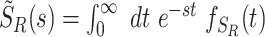. We also define two auxiliary random variables

(53)

In words, R_min is the restart time conditioned on the event that restart occurs before the service is over. Similarly, S_min is the service time conditioned on the event that service occurred prior to a restart. The probability density functions of R_min and S_min are given by (37)

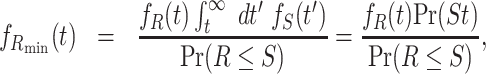(54)

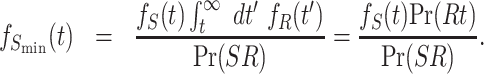(55)

Note, that the Laplace transforms of these distributions, 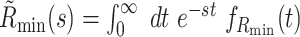and 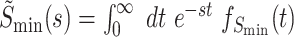, appear on the right hand side of Eq. (52).

The moments can now easily be computed from Eq. (52) by noting that

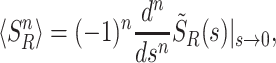(56)

which gives (37)

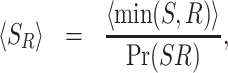(57)

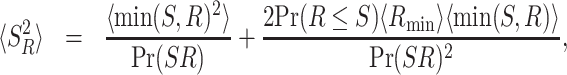(58)

where 〈R_min〉 can be computed directly from Eq. (54). The other components can also be systematically derived with the knowledge of individual time densities. For example, the numerator 〈min(S, R)〉 in Eq. (57) is given by

(59)

and the denominator in Eq. (57) is given by

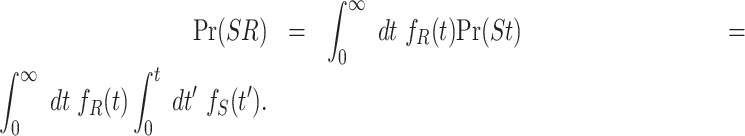(60)

Moments and Laplace transform of the service time under Poissonian resetting

Consider the case of Poissonian resetting. The restart time R is then exponential with probability density function

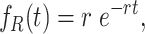(61)

and the cumulative distribution function is given by

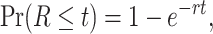(62)

where r is the resetting rate.

In the case of Poissonian resetting, the cumulative distribution function of min(S, R) can be written as

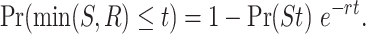(63)

Using the following formula for the expectation value of a non-negative random variable

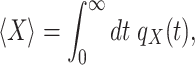(64)

where q_X(t) = Pr(X > t) is the survival function of X, one can easily show that

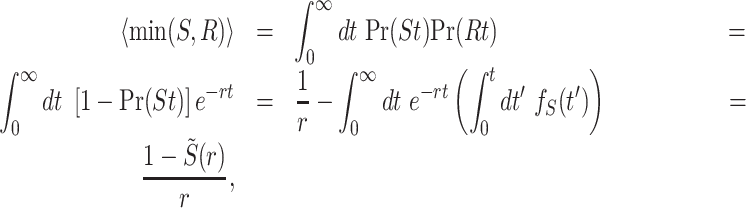(65)

where in the last step we used a known formula for the Laplace transform of a time-domain integration: 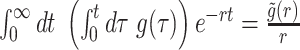, where 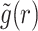is the Laplace transform of g(t). Similarly, we can use Eq. (60) to find

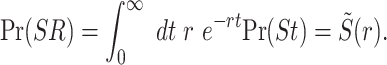(66)

Substituting Eqs. (65) and (66) into Eq. (57), we get the following formula for the mean service time under Poissonian resetting

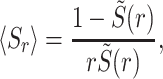(67)

which is Eq. (7) in the main text.

We now turn to derive a formula for 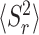, the second moment of the service time under Poissonian resetting. We start by deriving a formula for 〈min(S, R)²〉. By taking the derivative of Eq. (63), one can easily obtain the probability density function of min(S, R)

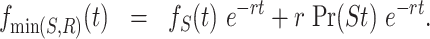(68)

Now, we can use the probability density function given in Eq. (68) to calculate 〈min(S, R)²〉

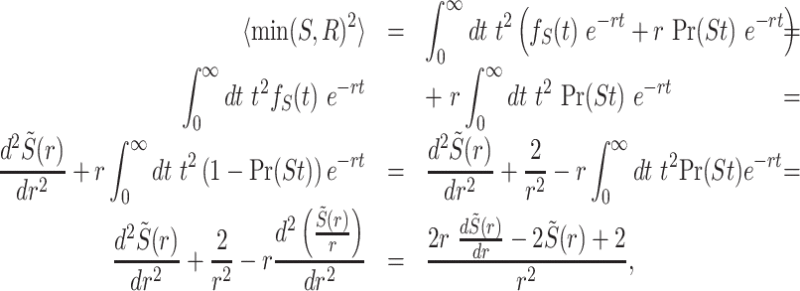(69)

where during the derivation we used a known property of Laplace transforms: 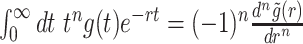, where n is a positive integer and 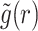standing for the Laplace transform of g(t).

We now turn to calculate 〈R_min〉. This can be explicitly done using Eq. (54)

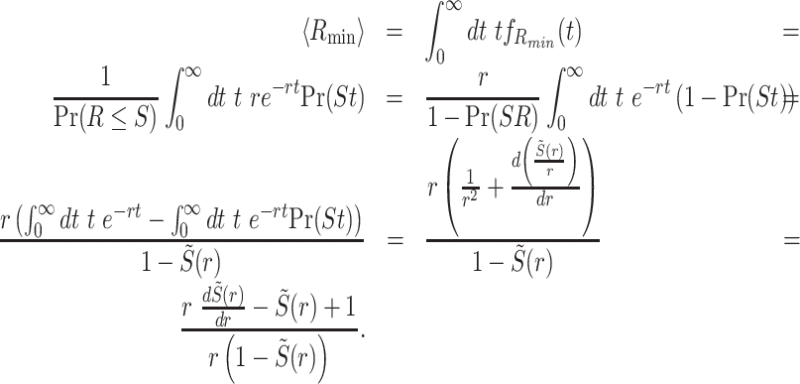(70)

Having all the terms on the right hand side of Eq. (58) in hand, we can now calculate

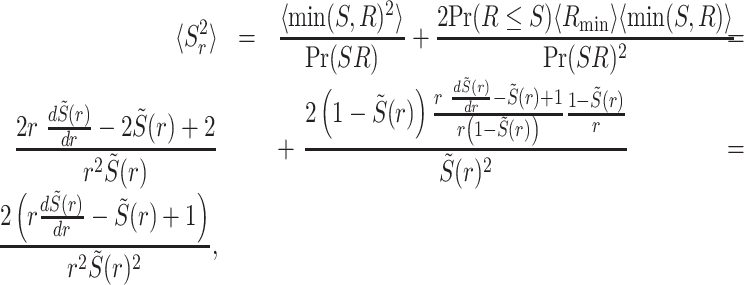(71)

which is Eq. (8) in the main text.

Finally, we turn to the derivation of the Laplace transform of the service time distribution under Poissonian resetting. The Laplace transform of the service time distribution under general resetting is given in Eq. (52), which is written in terms of the Laplace transforms of the auxiliary random variables R_min and S_min. Substituting Eqs. (61) and (66) into Eq. (54) we get

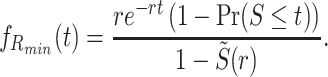(72)

Similarly, substituting Eqs. (62) and (66) into Eq. (55) yields the probability density function of the random variable S_min

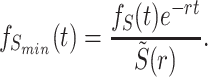(73)

Taking the Laplace transform of Eqs. (72) and (73) we get

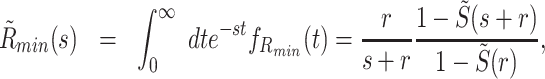(74)

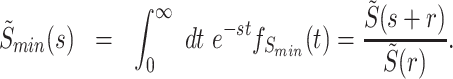(75)

Substituting Eqs. (66), (74), and (75) into Eq. (52) yields

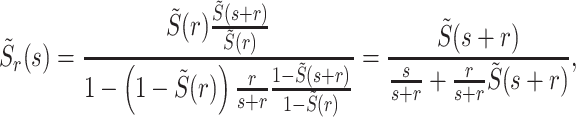(76)

which is Eq. (48) in the main text.

Moments of the service time under sharp resetting

Consider now the case of sharp, i.e. deterministic, resetting. When the restart time R is deterministic, its probability density function is given by

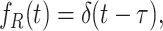(77)

where τ is the resetting time and δ( · ) is the delta function. In the case of sharp resetting, the cumulative distribution function of min(S, R) can be written as

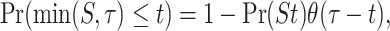(78)

where we have used 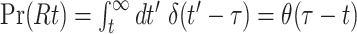, where θ is the Heaviside step function. Using Eq. (64) once again we have

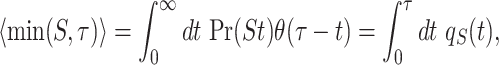(79)

where 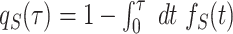is the survival function associated with the underlying service time. To derive Pr(S < R) we once again use Eq. (60) to find

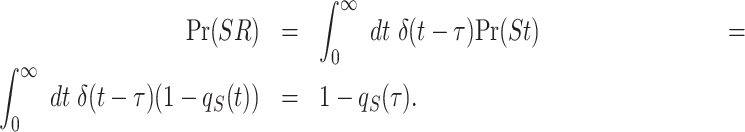(80)

Substituting Eqs. (79) and (80) into Eq. (57), we get the following formula for the mean service time under sharp restart

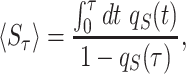(81)

which is Eq. (16) in the main text.

We now turn to derive a formula for 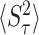, the second moment of the service time under sharp resetting. We start by deriving a formula for 〈min(S, τ)²〉. By taking the derivative of Eq. (78), one can easily obtain the probability density function of min(S, τ)

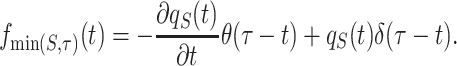(82)

Now, we can use Eq. (82) to compute 〈min(S, τ)²〉, which reads

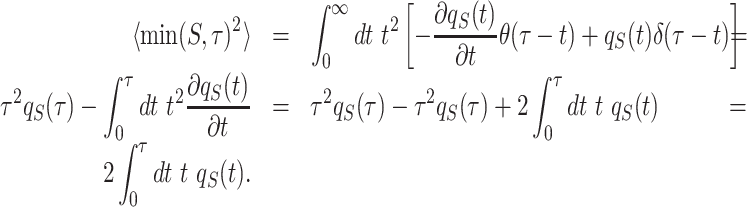(83)

We now turn to calculate 〈R_min〉. Since R is deterministic, 〈R_min〉 is simply τ. This can also be explicitly shown using Eq. (54)

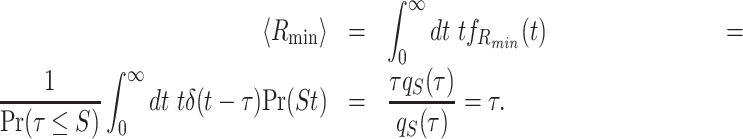(84)

Substituting Eqs. (79), (80), (83), and (84) into Eq. (58) we arrive at the following expression

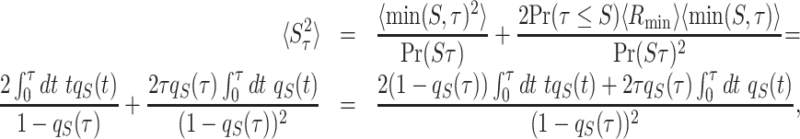(85)

which is Eq. (17) in the main text.

Notes

Competing Interest: The authors declare no competing interest.

Funding

S.R. acknowledges support from the Israel Science Foundation (grant no. 394/19). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 947731).

Authors’ contributions

All authors contributed to the design and undertaking of this research and to the writing of this paper.

Data Availability

All data are included in the article.