Abstract
In this paper we show that an autoregressive fractionally integrated moving average time-series model can identify two types of motion of membrane proteins on the surface of mammalian cells. Specifically we analyze the motion of the voltage-gated sodium channel Nav1.6 and beta-2 adrenergic receptors. We find that the autoregressive (AR) part models well the confined dynamics whereas the fractionally integrated moving average (FIMA) model describes the nonconfined periods of the trajectories. Since the Ornstein-Uhlenbeck process is a continuous counterpart of the AR model, we are also able to calculate its physical parameters and show their biological relevance. The fitted FIMA and AR parameters show marked differences in the dynamics of the two studied molecules.
I. INTRODUCTION
The advent of single-molecule techniques over the past two decades has revolutionized molecular biophysics. Amongst these techniques, single-particle tracking (SPT) has emerged as a powerful approach to study a variety of dynamic processes [1–4]. Individual trajectories have been obtained for diverse biological systems, including measurements in cell membranes [5–12], the cytoplasm [13–17], and the cell nucleus [18–22]. The dynamics of molecules in living cells typically exhibit complex behavior with a high degree of temporal and spatial heterogeneities, due to different factors such as spatial constraints and complex biomolecular interactions [23]. Each mechanism governing the diffusion process has different characteristics, which can give important information regarding the biological system [4,24–27].
A phenomenon often observed in single-molecule experiments is subdiffusion, with a characteristic sublinear meansquared displacement (MSD), which largely departs from the classical Brownian motion (BM). Determining the mechanisms underlying anomalous diffusion in complex fluids, e.g., in the cytoplasm of living cells or in controlled in vitro experiments [28–30], is a challenging problem. Subdiffusion can be rooted in different physical origins including immobile obstacles, binding, crowding, and heterogeneities [31]. Some of the theoretical models employed to describe subdiffusion are the continuous-time random walk [8], obstructed diffusion [32,33], fractional Brownian motion (FBM) [29,34], diffusion in a fractal environment [35,36], fractional Lévy stable motion (FLSM) [37], and fractional Langevin equation (FLE) [16,20,34].
A discrete-time model that generalizes the above fractional models is the autoregressive fractionally integrated moving average (ARFIMA) process [38,39]. From the physical point of view, it is a discrete-time analog of FLE that incorporates the memory parameter d [40]. Other popular models of subdiffusive dynamics like FBM and FLSM are the limiting cases of the ARFIMA with different noises [41]. ARFIMA exhibits power-law long-time dependencies, similar to FBM and FLSM. Long-time dependencies result in anomalous diffusion, evident in a nonlinear MSD [37]. In contrast to FBM and FLSM, ARFIMA can also describe various light- and heavy-tailed distributions and an arbitrary short-time dependence.
ARFIMA was previously suggested as an appropriate model for SPT dynamics for various biological experiments, namely the motion of individual fluorescently labeled mRNA molecules in bacteria [42,43] and transient anomalous diffusion of telomeres in the nucleus of eukaryotic cells [44]. A special case of the ARFIMA process, namely fractionally integrated moving average (FIMA), was proposed as a useful tool for estimating the anomalous diffusion exponent for particle tracking data with measurement errors [45]. FIMA was also useful in introducing so-called calibration surfaces, which are an effective tool for extracting both the magnitude of the measurement error and the anomalous exponent for autocorrelated processes of various origins [46]. Since ARFIMA models were successful in analyzing data in other fields (econometrics, see 2003 Nobel Prize in Economic Sciences for C. W. J. Granger and R. Engel; finance and engineering [47–49]), many statistical tools and computer packages are readily available, e.g., Interactive Time Series Modelling (ITSM) [50].
In this article, we focus on two types of motion in the plasma membrane, namely free and confined. Transient confinement within membrane domains is a very common feature in the plasma membrane [23]. Here, we focus on confinement within stable clusters. We propose the ARFIMA as a suitable model to characterize both types of dynamics. In Sec. II we discuss basic building blocks of the ARFIMA process: the autoregressive (AR), fractionally integrated (FI), and moving average (MA) parts. We show that the AR process is a discrete counterpart of the continuous-time Ornstein-Uhlenbeck (O-U) process. We also study the relationship between the ARFIMA and MSD. In Sec. III our fitting procedure (presented in detail in Appendix B) is applied to the motion of individual voltage-gated Na channels and beta-2 adrenergic receptors on the surface of live mammalian cells. In the described examples, we show that the increments of the nonconfined parts of the trajectories are well described by the FIMA process, whereas the confined parts can be modeled by the AR. The analysis also suggests that the beta-2 receptors appear to be more subdiffusive in the free state and have a lower autoregressive parameter in the confined state. Finally, the distribution of the estimated ARFIMA noise sequence appears to change from Gaussian in the free state to non-Gaussian in the confined state.
II. ARFIMA MODEL
The ARFIMA process is a generalization of the classical autoregressive moving average (ARMA) process that introduces the FI part with the long memory parameter d [38,39], see Appendix A for a presentation of general ARFIMA processes.
In this paper we concentrate on a special case of the ARFIMA proces, namely on the ARFIMA with AR and MA parts of order 1, which is denoted by ARFIMA(1, d, 1). The ARFIMA(1, d, 1) process X(t) for t = 0, ±1, … is defined as a stationary solution of the fractional difference equation [50]
| (1) |
where Z(t) is the noise (independent and identically distributed sequence usually Gaussian or in general belonging to the domain of attraction of Lévy stable law), |ϕ| < 1 and |ψ| < 1 are autoregressive and moving average parameters, respectively, and B is the backshift operator: BX(t) = X(t − 1). The fractional difference operator (1 − B)d is defined by means of the binomial expansion, namely , where and Γ is the Gamma function. In the finite variance case we assume that the memory parameter |d| < 1/2 and for the general Lévy α-stable case we assume that α > 1 and |d| < 1 − 1/α [51].
Let us emphasize here a very convenient “building block structure” of the ARFIMA (1, d, 1) model: ARFIMA(1, d, 1) = AR(1) + FI(d) + MA(1), where the AR(1), FI(d), and MA(1) are defined by the following equations:
| (2) |
| (3) |
| (4) |
respectively.
The FI(d) part, which is related to the fractional difference operator, leads to the regularly varying (power-law) correlations which are related to the classical definition of long-range dependence (long memory): lack of summability of correlations [52]. In this paper we will call all processes with power-law correlations long-range dependent even if the correlations are summable in contrast to the exponentially (so much faster) decaying correlations. Long-memory processes are often used to describe the dynamical behavior of complex systems. Consequently, ARFIMA models have already emerged in the physical literature, e.g., in the modeling of soft x-ray solar emissions [53,54], heartbeat interval changes, air temperature changes [55], and the motion of molecules in live cells [42–44,46].
The ARFIMA(1, d, 1) process offers a lot of flexibility in modeling long (power-law) and short (exponential or finite-time) dependencies by choosing the memory parameter d in the FI part, and appropriate AR(1) and MA(1) process parameters (ϕ and ψ). Hence, they can be tailored to different empirical data. To illustrate it, let us recall three standard models used in the biophysics literature: confinement by a potential well, FBM and Brownian motion. These models correspond to different components of the ARFIMA(1, d, 1) process, namely the AR(1) part, FI(d) part and partial sum process of MA(0) (which is MA(1) with ψ = 0, so a pure white sequence), respectively. Furthermore, the MA(1) which introduces a one-lag dependence can be associated with the measurement noise [45]. When added to the FI(d) process, we obtain the FIMA(d, 1) model: (1 − B)dX(t) = Z(t) − ψZ(t − 1), which corresponds to FBM with noise [45]. This leads to an efficient algorithm for extracting the magnitude of the measurement error for fractional dynamics based on the FIMA processes [46]. The relations between the different models are summarized in Table I.
TABLE I.
Physical (with and without measurement noise) and corresponding ARFIMA(1, d, 1) models.
| Physical model | ARFIMA(1, d, 1) |
|---|---|
| Confinement by a potential well (O-U) | AR(1) |
| O-U + noise | ARMA(1,1) |
| BM | MA(0) |
| BM + noise | MA(1) |
| FBM | FI(d) |
| FBM + noise | FIMA(d, 1) |
If the sample comes from an ARFIMA(1, d, 1) process with noise belonging to the domain of attraction of Lévy α-stable law, then for large sample lengths the time-averaged MSD behaves like
| (5) |
where the bar stands for the time average, ~ denotes asymptotic behavior and a = 2d + 1 [37]. Therefore, the memory parameter d controls the extent of the diffusion anomaly regardless of the underlying distribution. If d < 0, the process is subdiffusive, and if d > 0, the character of the process changes to superdiffusive.
Single-particle tracking data are commonly analyzed by the MSD of the trajectories. However, past work has shown that MSDs can be susceptible to errors and biases. To improve accuracy in single particle studies guidelines with respect to measurement length and maximum time lags have been proposed [56].
In this article, for the purpose of identifying diffusive motions in single-particle trajectories we apply two special cases of the ARFIMA(1, d, 1) model, namely AR(1) and FIMA(d, 1). FIMA(d, 1) is characterized by three parameters: fractional d giving rise to the long memory, the parameter ψ of the MA(1) part corresponding to the one-lag dependence, and the distribution of the noise sequence, which in the case of the Gaussian white noise is fully characterized by its variance σ2. The second model is AR(1), which is characterized by the AR parameter ϕ and the distribution of the noise sequence. This model is a discrete analog of the continuous-time O-U process X(t) defined by the overdamped Langevin equation
| (6) |
where ξ(t) is white Gaussian noise with 〈ξ(t)ξ(t′)〉 = 2Dδ(t – t′). A discretization of equation (6) gives
| (7) |
which is the AR(1) model equation with ϕ = −(kΔt/γ − 1) and Gaussian white noise Z(t) = Δtξ(t) with variance σ 2 = 2DΔt.
III. ANALYSIS OF INDIVIDUAL MEMBRANE PROTEIN TRAJECTORIES
Single-particle tracking on the plasma membrane of mammalian cells indicates that often molecules are subjected to transient confinement. Here we employ ARFIMA models to characterize the motion of Nav1.6 channels in the soma of transfected cultured rat hippocampal neurons and beta-2 adrenergic receptors (B2AR) in transfected human embryonic kidney (HEK-293) cells. Nav1.6 channels were biotinylated at an extracellular site and labeled with streptavidin-conjugated CF640R. The B2AR were tagged with hemagglutinin (HA) and labeled with anti-HA antibody conjugated to CF640. Transfected cells were imaged by total internal reflection microscopy at 20 frames/s and individual fluorescent molecules were tracked with the u-track algorithm [57]. Experimental details about cell culture, transfection, and imaging were published previously [36,58].
Following Ref. [59], we employed an automated algorithm to detect changes in molecule dynamics. This algorithm was based on a sliding-window MSD. As a result, we obtained trajectories belonging to two states: free and confined. Figure 1 depicts two representative free and two representative confined trajectories. Trajectories from the free state resemble Brownian diffusion, whereas confined-state trajectories appear as realizations of a stationary process.
FIG. 1.
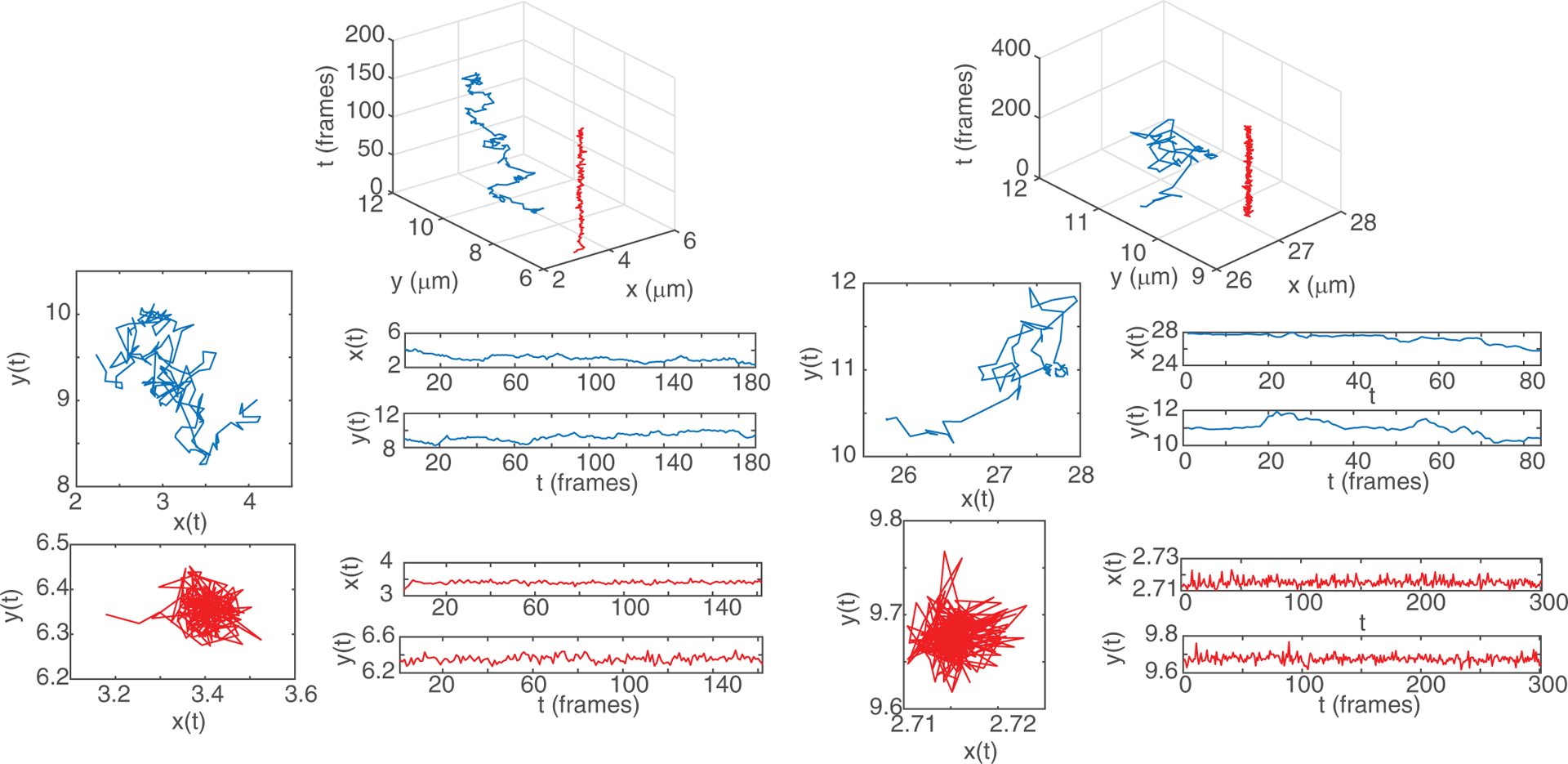
Representative Nav1.6 (left panel) and beta-2 receptor (right panel) trajectories. The top panel illustrates the receptor dynamics in three dimensions, where the z axis corresponds to time. The (upper) blue trajectories show molecules in the free state and the (lower) red trajectories show molecules in the confined state.
We selected five long representative trajectories corresponding to each motion (free and confined). The shortest were 174 (free state) and 153 (confined state) points for the the Nav1.6, and 84 (free state) and 300 (confined state) points for the beta-2 receptors. We focused on the x-coordinate of the motions. We first fitted the ARFIMA(d, 1) model to the increments of free-state trajectories. The simplest well-fitted model common to all trajectories is FIMA(d, 1). Figures 2 and 3 show a scatter plot of the estimated d and ψ parameters with the corresponding 95% confidence intervals obtained by Monte Carlo simulations. For the beta-2 receptor trajectories, the memory parameter d and the moving average parameter ψ are usually lower than for Nav1.6 trajectories. The MSD anomalous exponent a = 2d + 1 is also shown in the right axis of Fig. 2. The detailed results of the FIMA identification and validation procedure are presented in the Supplemental Material [60].
FIG. 2.
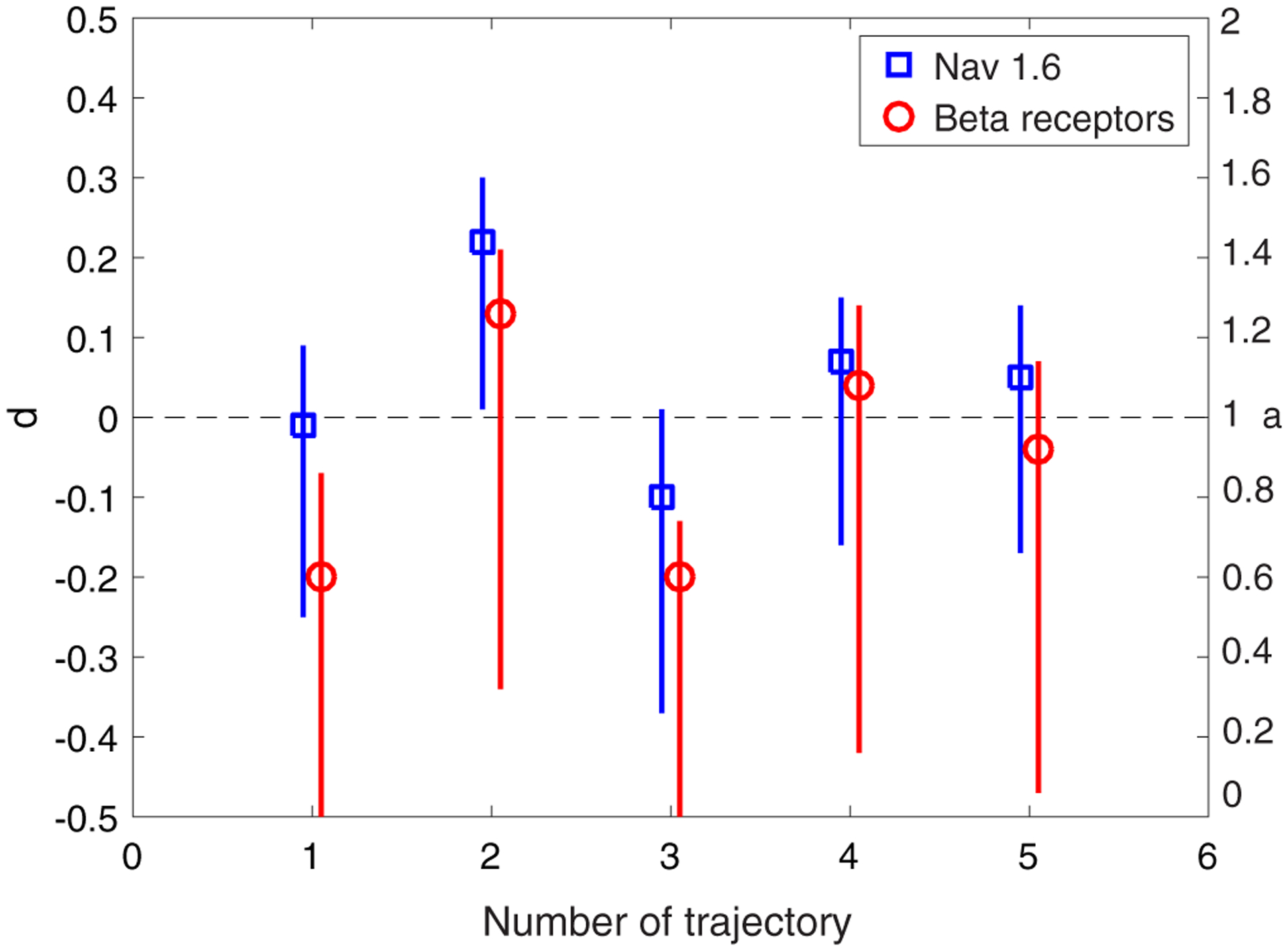
Fitted d parameter (with the 95% confidence interval) of the FIMA(d, 1) model to the increments of the free state Nav1.6 and beta-2 receptor five representative trajectories.
FIG. 3.
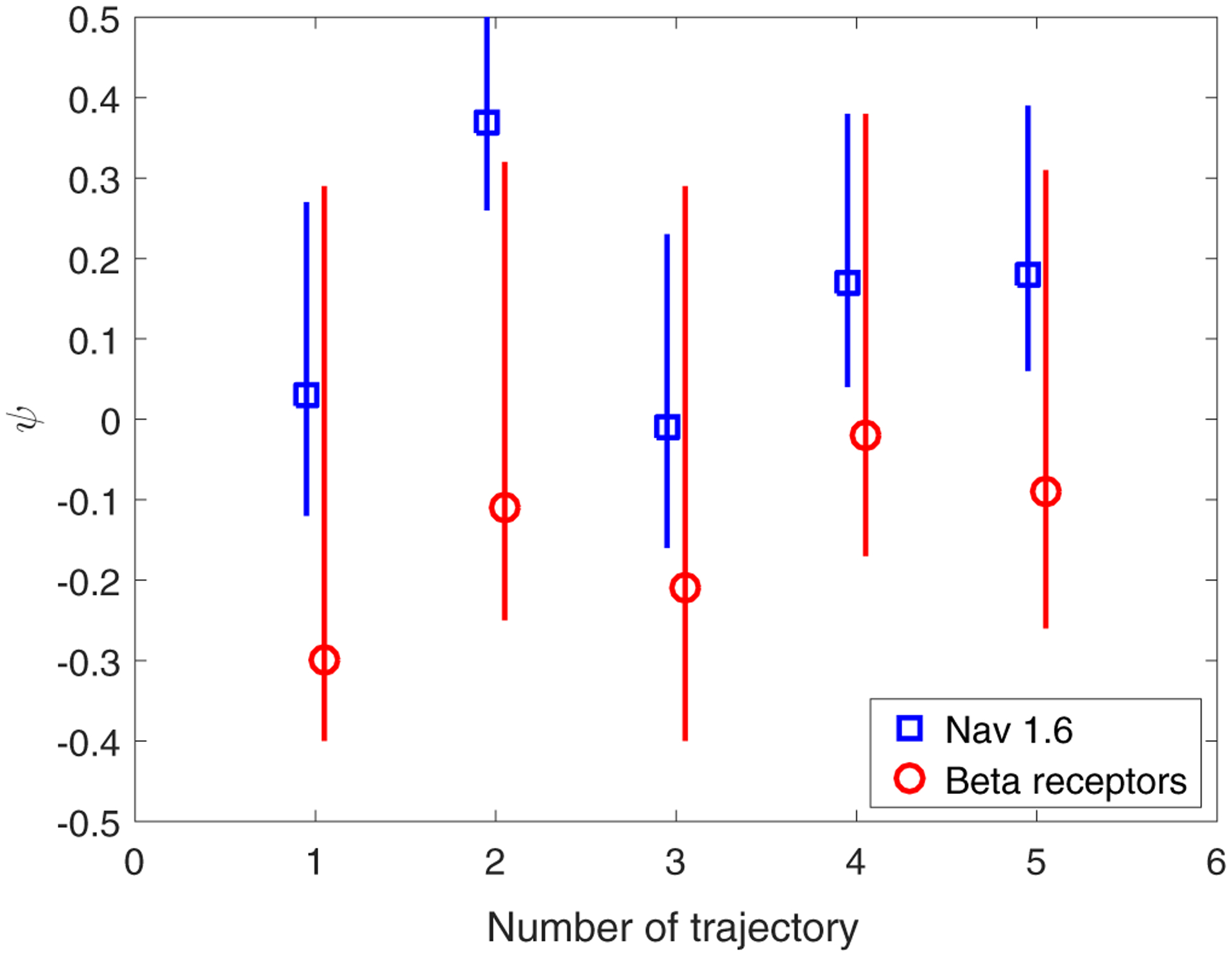
Fitted ψ parameter (with the 95% confidence interval) of the FIMA(d, 1) model to the increments of the free state Nav1.6 and beta-2 receptor five representative trajectories.
To check the goodness of fit of the FIMA model, we calculated the MSD for 1000 simulated trajectories of the model with parameters given in the Supplemental Material [60] and compared the results with the MSD values of the analyzed representative trajectories. We can see in Fig. 4 that the fitted FIMA processes reproduce the sample MSD well.
FIG. 4.
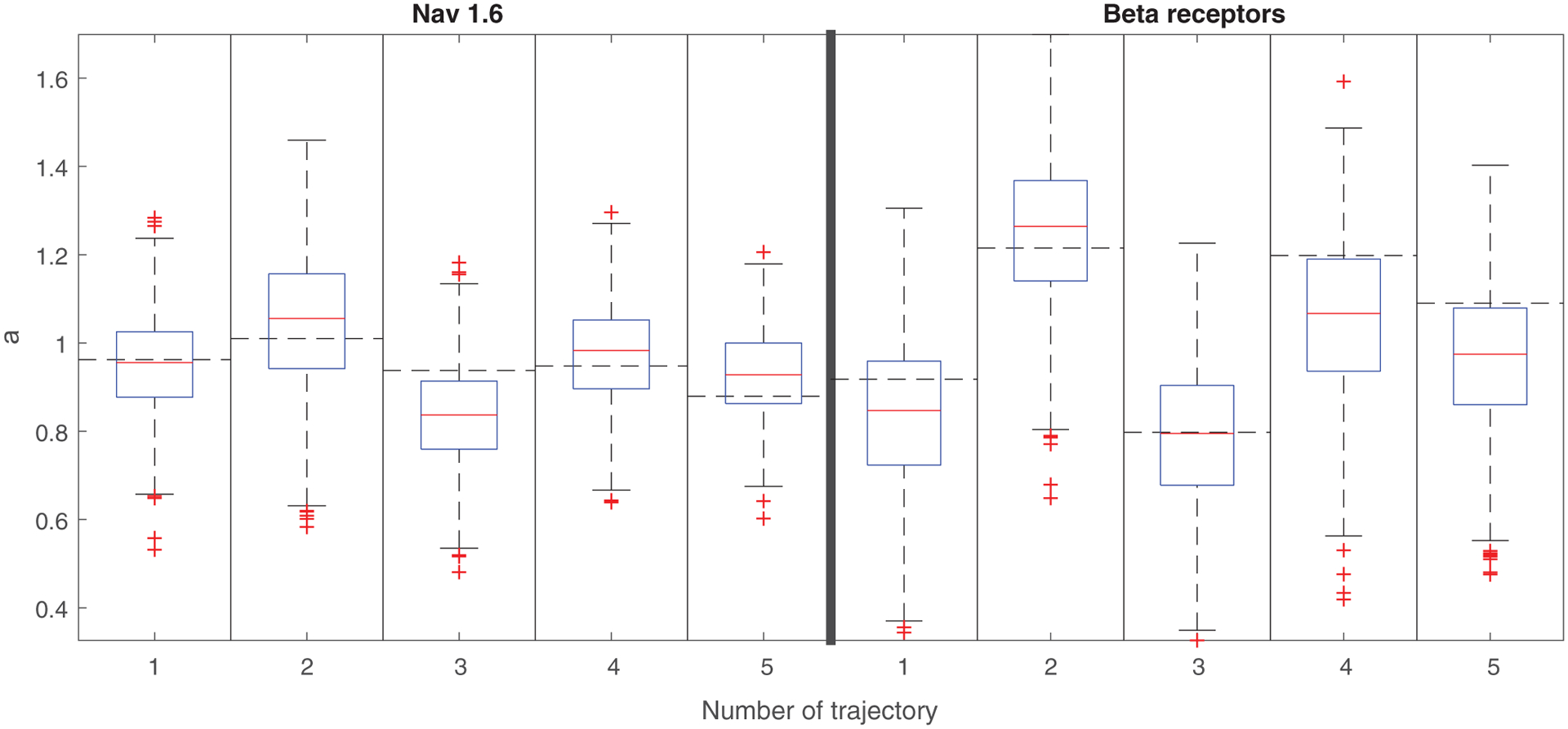
Boxplots of estimated MSD exponents for 1000 simulated trajectories of the fitted FIMA processes for free state Nav1.6 and beta-2 receptor five representative trajectories. The dashed horizontal line stands for the MSD exponent obtained for the analyzed empirical trajectory.
Some of the empirical MSD values fall outside the interquantile range but they are always contained in the 95% confidence interval [61], see Fig. S1 in the Supplemental Material [60]. By examining the width of the boxplots, we can also observe that the variability of the MSD exponent in the beta-2 receptor case seems bigger than in the Nav1.6 case, which suggests another difference between Nav 1.6 and beta-2 receptor dynamics.
We also checked the distribution of the model residuals. First, following the procedure in Appendix D we found that the residuals belong to the domain of attraction of the normal law. Next, it appeared that the residuals can be treated as Gaussian since the test was rejected only for one trajectory from the confined state. Hence we conclude that the increments of the trajectories in the free state can be modeled by the Gaussian FIMA(d, 1). Recall that this model represents a Gaussian fractional process with power-law memory, which corresponds to fractional Brownian motion with Hurst index H = d + 1/2 [41].
We performed the same analysis for the confined case and we found that a simpler ARFIMA model describes well the data, namely AR(1). Its estimated parameters are depicted in Fig. 5 with the corresponding 95% confidence intervals obtained by Monte Carlo simulations. Hence, with the use of the ARFIMA model we are able to distinguish between these two different states. Moreover, we can see that for beta-2 receptor trajectories the autoregressive parameter is usually lower than for the Nav1.6 trajectories. The detail results of the AR identification and validation procedure are presented in the Supplemental Material [60].
FIG. 5.
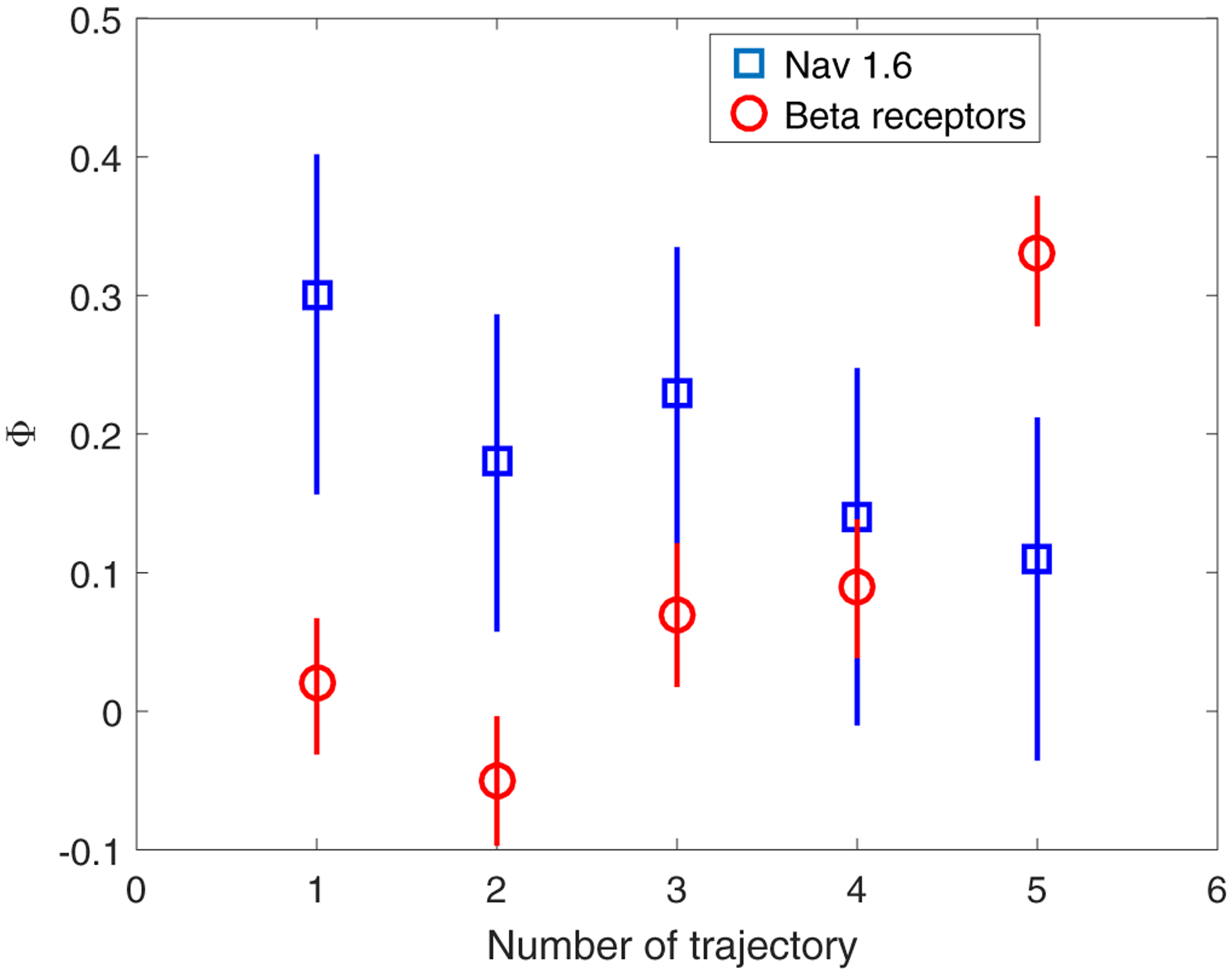
Fitted ϕ parameter (with the 95% confidence interval) of the AR(1) model to the confined state Nav1.6 and beta-2 receptor five representative trajectories.
As we showed in Sec. II, AR(1) corresponds to the O-U process. From a physical point of view, this model describes the motion of a Brownian particle in a harmonic potential with restoring force F = −kx and damping coefficient γ [Eq. (7)]. Therefore, we calculated the corresponding O-U parameters and, in turn, the corresponding physical parameters that characterize the protein motion (Tables II and III). Namely, the diffusion is D = σ2/(2Δt), where σ2 is the variance of the noise term Z(t) and, in our time series, Δt = 0.05 s. By considering the Einstein-Smoluchowski relation, γ = kBT/D with kBT being thermal energy at 37°C. Next the parameter ϕ yields the constant k = γ(1 – ϕ)/Δt. At last, by equipartition, the variance of the particle position, i.e., the square of the characteristic radius of the confining domain, is found, 〈X2〉 = kBT/k = σ2/[2(1 – ϕ)]. We note that in the analyzed trajectories, the confining radius of Nav1.6 channels is larger than the confining radius of B2AR, where the former yields a mean of 53 nm, while the latter has a mean of 23 nm.
TABLE II.
Ornstein-Uhlenbeck process parameters for the representative confined state Nav1.6 trajectories.
| Traj. | ϕ | σ2(nm2) | D(μm2/s) | γ(10−8kg/s) | k(pN/μm) | 〈X2〉(nm2) |
|---|---|---|---|---|---|---|
| 1 | 0.30 | 1948 | 0.019 | 22.0 | 3.08 | 1391 |
| 2 | 0.18 | 7966 | 0.080 | 5.4 | 0.88 | 4857 |
| 3 | 0.23 | 4319 | 0.043 | 9.9 | 1.53 | 2804 |
| 4 | 0.14 | 4053 | 0.041 | 10.6 | 1.82 | 2356 |
| 5 | 0.11 | 6105 | 0.061 | 7.0 | 1.24 | 3430 |
TABLE III.
Ornstein-Uhlenbeck process parameters for the representative confined state beta-2 receptor trajectories.
| Traj. | ϕ | σ2(nm2) | D(μm2/s) | γ(10−8kg/s) | k(pN/μm) | 〈X2〉(nm2) |
|---|---|---|---|---|---|---|
| 1 | 0.02 | 553 | 0.006 | 77.4 | 15.18 | 282 |
| 2 | −0.05 | 1327 | 0.0013 | 32.3 | 6.77 | 632 |
| 3 | 0.07 | 1485 | 0.015 | 28.8 | 5.36 | 799 |
| 4 | 0.09 | 1696 | 0.017 | 25.2 | 4.59 | 932 |
| 5 | 0.33 | 252 | 0.003 | 169.9 | 22.76 | 188 |
To check the goodness of fit of the AR model, we calculated the MSD for 1000 simulated trajectories of the model with parameters given in the Supplemental Material [60] and compared the results with the MSD values for the analyzed representative trajectories. We can see in Fig. 6 that the fitted AR processes reproduce the sample MSD well. Some of the empirical MSD values fall outside the interquantile range but they are always (even beta-2 receptor trajectory no. 3) contained in the 95% confidence interval [61], see Fig. S2 in the Supplemental Material [60]. By examining the width of the boxplots, we can also observe that the variability of the MSD exponent in the Nav 1.6 case seems bigger than in the beta-2 receptor case, which suggests another difference between Nav 1.6 and beta-2 receptor dynamics.
FIG. 6.
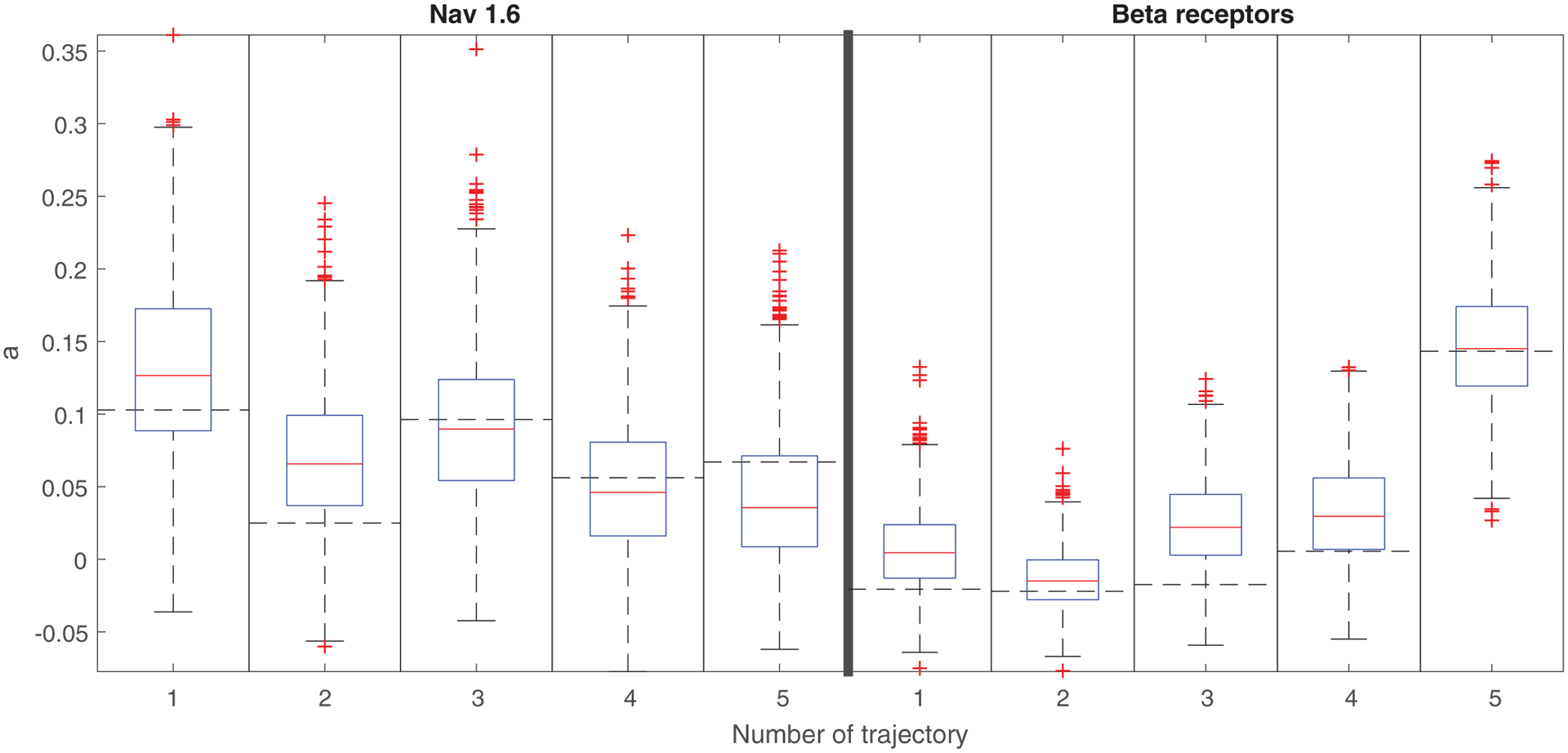
Boxplots of estimated MSD exponents for 1000 simulated trajectories of the fitted AR processes for the confined state Nav1.6 and beta-2 receptor five representative trajectories. The dashed horizontal line stands for the MSD exponent obtained for the analyzed empirical trajectory.
We also checked the distribution of the model residuals. Following the procedure in Appendix D, first we found that they belong to the domain of attraction of the normal law. However, in contrast to the free state, Gaussianity was rigorously rejected for almost all trajectories. Normal inverse Gaussian (NIG) and t location-scale distributions were not rejected for most of the trajectories. In order to make a rigorous conclusion about the model residuals one should analyze more trajectories. Hence we conclude that the confined state trajectories can be modeled by the non-Gaussian AR(1).
For the detailed goodness-of-fit analysis of identified AR(1) and FIMA (d, 1) models we refer the reader to the Supplemental Material [60].
IV. DISCUSSION AND CONCLUSIONS
In this paper we demonstrated that the ARFIMA(1, d, 1) model can identify two types of motions of membrane proteins. We analyzed five representative trajectories chosen from each of two categories: free and confined states of Nav1.6 and beta-2 adrenergic receptors. We found that the two special cases of the model, FIMA(d, 1) and AR(1), fully identify the free and confined state dynamics, respectively. These results allowed us to propose a new unified methodology to detect certain types of motion in complex systems.
In the free state, the beta-2 receptors appear to be more subdiffusive and, moreover, the moving average parameter is lower. In the confined state the autoregressive parameter for the beta-2 receptor trajectories seems to be lower than for Nav1.6 trajectories. Furthermore, the distribution changes from being Gaussian in the free to non-Gaussian in the confined state. Since the AR(1) is a discrete-time counterpart of the O-U process, we calculated the parameters of the corresponding O-U processes which, we found, are biologically meaningful. We note that the estimated FIMA memory parameters provide more accurate information on the subdiffusion type than the MSD exponents since they are more robust with respect to the measurement noise.
We would like to point out that a very popular model for subdiffusion continuous-time random walk (CTRW) [62] is not considered here, but it can be represented in the form of subordinated O-U process, i.e., AR with randomized time described by the inverse stable process [63,64].
Accurate motion analysis often requires a transient motion classification [65,66]. Many transient motion analysis algorithms employ either rolling windows analysis [67,68] or hidden Markov modeling [69,70]. Our studies show that one can also consider the ARFIMA model as a possible tool for such classification.
We believe that our methodology provides a simple unified way to gain deeper information into processes leading to anomalous diffusion in single-particle tracking experiments. Finally, we note that in order to model the whole trajectories (free and confined parts of the trajectories together) the ARFIMA process is not enough. One possible extension is ARFIMA with noise described by the generalized autoregressive conditional heteroskedasticity (GARCH) model [71,72]. Such models can be useful in description of changing diffusivity which results in so-called transient anomalous diffusion [73,74]. ARFIMA combined with GARCH can describe both power-law decay of the autocorrelation function with arbitrary finite-lag effects (ARFIMA part) and changing diffusion exponent (GARCH part). This is a subject of ongoing work.
Supplementary Material
ACKNOWLEDGMENTS
We thank Patrick Mannion, Sanaz Sadegh, and Laura Solé for useful discussions. K.B. and G.S. acknowledge the support by NCN Maestro Grant No. 2012/06/A/ST1/00258. Research of A.W. was supported by NCN-DFG Beethoven Grant No. 2016/23/G/ST1/04083. D.K. was supported by the National Science Foundation under Grant No. 1401432. M.M.T acknowledges the support of the National Institutes of Health under Grants No. R01GM109888 and No, RO1NS085142.
APPENDIX A: GENERAL ARFIMA MODEL
The ARFIMA(p, d, q) process X(t) for t = 0, ±1, … is defined as a solution of the equation
where Z(t) is the noise sequence (Gaussian or, in general, in the domain of attraction of Lévy stable law) and B is the backshift operator, i.e., BX(t) = X(t − 1) and BjX(t) = X(t − j) [39,50]. Moreover the Φp and Ψq are AR and MA polynomials, respectively, known in classical time-series theory:
The crucial part of the above definition of ARFIMA series is the fractional difference operator (1 − B)d defined as a power series
where with asymptotic behavior bj (d) ~ Γ(−d)−1j−d−1 and Γ is the Gamma function.
In the finite variance case we assume that |d| < 1/2 and for the general Lévy α-stable case we assume that α > 1 and |d| < 1 − 1/α [51]. The assumption about the exponent d ensures a proper definition of the operator for the Gaussian ARFIMA processes. The parameter d is called the memory parameter. From the physical point of view, it is known that ARFIMA is a discrete time analog of the fractional Langevin equation that takes into account the memory parameter [40,54].
In the Gaussian case, the autocovariance function r(k) of the ARFIMA process decays as k2d−1. Moreover, for d > 0 we have , which serves as a classical definition of long memory [52]. For the Lévy α-stable case with α < 2 the covariance does not exist and one has to replace it, e.g., with the codifference (see Ref. [75]). The codifference of the ARFIMA process was studied in Ref. [51], where it was proved that for d > 1 − 2/α the ARFIMA possesses long-term dependence in the classical sense.
A partial sum of the ARFIMA process is asymptotically self-similar with the Hurst index equal to d + 1/α, where α is the index of stability [76]. As a consequence Gaussian ARFIMA(0, 0, 0), which is just the pure white noise sequence, corresponds, in the limit sense, to BM. Similarly, ARFIMA(0, d, 0) corresponds to FBM with H = d + 1/2. For more information about the ARFIMA processes with their applications to biophysics see, e.g., Refs. [42,46].
The ARFIMA process (in the literature also called FARIMA) is a generalization of the classical stationary discrete-time ARMA process to account for the long-range dependence (powerlike decaying autcorrelation function) [50,52].
The ARMA models provide a general framework for studying stationary short memory phenomena, i.e., processes with exponentially decaying autocovariance. These models consist of two broad classes of time-series processes, namely the AR and the MA. The ARMA is usually referred to as the ARMA(p, q) model where p is the order of the autoregressive part and q the order of the moving average part.
Let us now concentrate on the ARMA(1, 1) case which is sufficient for many studies. The process X(t) is ARMA(1, 1) if it is stationary and satisfies (for every t) a linear difference equation with constant coefficients:
| (A1) |
where t = 0, ±1, …
The basic building blocks of the model are the AR(1): X(t) = ϕX(t − 1) + Z(t) and MA(1): X(t) = Z(t) − ψZ(t − 1) processes, where ϕ and ψ are real parameters and Z(t) is the noise term [50]. AR(1) stands for the autoregression and the explanatory variable is the observation immediately prior to our current observation. Its autocorrelation function r(k) decays as ϕk 〈X2(t)〉. The MA(1) part introduces one-lag dependence in the time series, namely X(t) is a stationary one-correlated time series: X(s) and X(t) are independent whenever |t − s| > 1. The dependence is fully controlled by the parameter ψ. A stationary solution of ARMA(1, 1) equation exists if and only if ϕ ≠ ±1. If |ϕ| < 1, then a unique stationary solution exists and is causal, since X(t) can be expressed in terms of the current and past values Z(s), s ⩽ t. Otherwise, if |ϕ| > 1, then the solution is not causal since X(t) is then a function of Z(s), s ⩾ t. Moreover, if |ψ| < 1 then X(t) is invertible, so the noise process Z(t) can be expressed in terms of past values X(s), s ⩽ t [50]. For the noise process Z(t) we only assume that it belongs to the domain of attraction of Lévy α-stable law for α ⩽ 2 [75,77]. It can be a finite variance white noise (uncorrelated random variables with mean zero and variance σ2, e.g., Gaussian or Student’s t) or infinite variance independent and identically distributed sequence (e.g., Lévy α-stable with α < 2 or Pareto).
The ARFIMA process is a d-differenced ARMA process, where d is a fractional memory parameter. As a consequence, ARFIMA(1, d, 1) process X(t) is defined as a stationary solution of the fractional difference equation [50]
| (A2) |
APPENDIX B: ARFIMA PARAMETER ESTIMATION
In order to estimate the ARFIMA parameters one can apply the maximum likelihood estimation method, which is implemented, e.g., in ITSM [50], or its approximation given by the Whittle estimator [78,79]. The Whittle estimator is particularly simple to implement in any computer software and it benefits from the elementary form of the ARFIMA spectral density. Briefly, let {x1, x2, …, xN} be a trajectory of length N. For the model FIMA(d, 1), we estimate the vector β = (ϕ, d). We denote the normalized periodogram by
| (B1) |
The Whittle estimator is defined as the vector argument (ϕ, d) for which the following function attains its minimum value:
| (B2) |
where
| (B3) |
For the AR(1) the estimator minimizes
| (B4) |
APPENDIX C: ARFIMA MODEL VALIDATION
Having fitted the ARFIMA process, the next step is to investigate the residuals obtained either by fractional differencing the data [80] or as prediction errors [50].
If there is no dependence among the residuals, we can regard them as observations of independent random variables and there is no further modeling to be done except to estimate their mean and variance [50].
If there is a significant dependence among the residuals, we need to evaluate a more complex stationary time-series model for the noise that accounts for the dependence, e.g. the GARCH process [71,72].
We now recall some simple tests for checking the hypothesis that the residuals are observed values of independent and identically distributed random variables. If they are, we conclude the model describes the data well.
First, we plot the sample autocorrelation function with its 95% confidence interval. In the Gaussian case about 95% of the sample autocorrelations should fall between the bounds . The same can be done for squares of the observations to check for a dependence in variance. Next, we apply the Ljung-Box, and McLeod-Li tests, which are portmanteau tests [50]. The Ljung-Box test relies on the sample autocorrelation function, which, at lag h, has a chi-squared distribution with h degrees of freedom. The McLeod-Li test is similar but on the squared data.
APPENDIX D: ARFIMA RESIDUAL DISTRIBUTION
Having found an appropriate ARFIMA model describing the data, we can identify the distribution underlying the noise sequence. Information about the distribution is helpful in determining confidence intervals for the estimated parameters and also in construction of prediction intervals. We now investigate the distribution of the residuals.
Following Ref. [81], we first check if the underlying distribution belongs to the domain of attraction of the Gaussian or non-Gaussian Lévy-stable distributions by examining its rate of convergence.
If the results suggest the Gaussian domain of attraction, we consider three typical light-tailed probability distributions for the residuals of the ARFIMA model, namely Gaussian, t location-scale and NIG.
If the non-Gaussian Lévy stable domain of attraction is suggested, we test for Lévy α-stable distributions.
The t location-scale distribution generalizes ordinary Student’s t distribution. The probability density function (PDF) of this distribution is given as
| (D1) |
where B is the beta function and n denotes the degrees of freedom parameter. This distribution is useful for modeling data with heavier tails than the normal. It approaches the Gaussian distribution as n approaches infinity and smaller values of n yield heavier tails.
A random variable X is said to have a NIG distribution if it has a PDF,
| (D2) |
The NIG distribution, introduced in Ref. [82], is described by four parameters (α, β, δ, μ), where α stands for tail heaviness, β for asymmetry, δ is the scale parameter, and μ is the location. The normalizing constant Kλ(t) in (D2) is the modified Bessel function of the third kind with index λ, also known as the MacDonald function. The NIG distribution is more flexible than the Gaussian distribution since it allows for fat-tails and skewness. The Gaussian distribution arises as a special case by setting β = 0, δ = σ2α, and letting α → ∞.
In order to check the goodness of fit of the distributions considered here, we apply the Anderson-Darling test [83], which is based on the A2 statistic:
| (D3) |
where FN (x) and F(x) denote the empirical and theoretical distribution functions, respectively. The test is one of the most powerful statistical tools for detecting most departures from normality [83].
References
- [1].Höfling F and Franosch T, Rep. Prog. Phys 76, 046602 (2013). [DOI] [PubMed] [Google Scholar]
- [2].Metzler R, Jeon J-H, Cherstvy AG, and Barkai E, Phys. Chem. Chem. Phys 16, 24128 (2014). [DOI] [PubMed] [Google Scholar]
- [3].Manzo C and Garcia-Parajo MF, Rep. Prog. Phys 78, 124601 (2015). [DOI] [PubMed] [Google Scholar]
- [4].Krapf D, Curr. Top. Membr 75, 167 (2015). [DOI] [PubMed] [Google Scholar]
- [5].Dahan M, Lévi S, Luccardini C, Rostaing P, Riveau B, and Triller A, Science 302, 442 (2003). [DOI] [PubMed] [Google Scholar]
- [6].Sergé A, Bertaux N, Rigneault H, and Marguet D, Nat. Methods 5, 687 (2008). [DOI] [PubMed] [Google Scholar]
- [7].Manley S, Gillette JM, Patterson GH, Shroff H, Hess HF, Betzig E, and Lippincott-Schwartz J, Nat. Methods 5, 155 (2008). [DOI] [PubMed] [Google Scholar]
- [8].Weigel AV, Simon B, Tamkun MM, and Krapf D, Proc. Natl. Acad. Sci. U.S.A 108, 6438 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Kusumi A, Suzuki KG, Kasai RS, Ritchie K, and Fujiwara TK, Trends Biochem. Sci 36, 604 (2011). [DOI] [PubMed] [Google Scholar]
- [10].Calebiro D, Rieken F, Wagner J, Sungkaworn T, Zabel U, Borzi A, Cocucci E, Zürn A, and Lohse MJ, Proc. Natl. Acad. Sci. U.S.A 110, 743 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Weigel AV, Tamkun MM, and Krapf D, Proc. Natl. Acad. Sci. U.S.A 110, E4591 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Masson JB, Dionne P, Salvatico C, Renner M, Specht CG, Triller A, and Dahan M, Biophys. J 106, 74 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Weiss M, Elsner M, Kartberg F, and Nilsson T, Biophys. J 87, 3518 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Tolić-Norrelykke IM, Munteanu E-L, Thon G, Oddershede L, and Berg-Sorensen K, Phys. Rev. Lett 93, 078102 (2004). [DOI] [PubMed] [Google Scholar]
- [15].Golding I and Cox EC, Phys. Rev. Lett 96, 098102 (2006). [DOI] [PubMed] [Google Scholar]
- [16].Jeon J-H, Tejedor V, Burov S, Barkai E, Selhuber-Unkel C, Berg-Sorensen K, Oddershede L, and Metzler R, Phys. Rev. Lett 106, 048103 (2011). [DOI] [PubMed] [Google Scholar]
- [17].Bálint Š, Vilanova IV, Sandoval Álvarez A, and Lakadamyali M, Proc. Natl. Acad. Sci. U.S.A 110, 3375 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Kues T, Peters R, and Kubitscheck U, Biophys. J 80, 2954 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Levi V, Ruan Q, Plutz M, Belmont AS, and Gratton E, Biophys. J 89, 4275 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Bronstein I, Israel Y, Kepten E, Mai S, Shav-Tal Y, Barkai E, and Garini Y, Phys. Rev. Lett 103, 018102 (2009). [DOI] [PubMed] [Google Scholar]
- [21].Gebhardt JCM, Suter DM, Roy R, Zhao ZW, Chapman AR, Basu S, Maniatis T and Xie XS, Nat. Methods 10, 421 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Izeddin I, Récamier V, Bosanac L, Cissé II, Boudarene L, Dugast-Darzacq C, Proux F, Bénichou O, Voituriez R, and Bensaude O, eLife 3, e02230 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Krapf D, Curr. Opin. Cell Biol 53, 15 (2018). [DOI] [PubMed] [Google Scholar]
- [24].Barkai E, Garini Y, and Metzler R, Phys. Today 65, 29 (2012). [Google Scholar]
- [25].Kepten E, Bronshtein I, and Garini Y, Phys. Rev. E 87, 052713 (2013). [DOI] [PubMed] [Google Scholar]
- [26].Bronshtein I, Kepten E, Kanter I, Berezin S, Lindner M, Abena B Redwood, Mai S, Gonzalo S, Foisner R, Shav-Tal Y, and Garini Y, Nat. Commun 6, 8044 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Zhang Y and Dudko OK, Annu. Rev. Biophys 45, 117 (2016). [DOI] [PubMed] [Google Scholar]
- [28].Pan W, Filobelo L, Pham NDQ, Galkin O, Uzunova VV, and Peter G Vekilov, Phys. Rev. Lett 102, 058101 (2009). [DOI] [PubMed] [Google Scholar]
- [29].Szymański J and Weiss M, Phys. Rev. Lett 103, 038102 (2009). [DOI] [PubMed] [Google Scholar]
- [30].Campagnola G, Nepal K, Schroder BW, Peersen OB, and Krapf D, Sci. Rep 5, 17721 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Jeon J-H and Metzler R, Phys. Rev. E 81, 021103 (2010). [DOI] [PubMed] [Google Scholar]
- [32].Weigel AV, Ragi S, Reid ML, Chong EKP, Tamkun MM, and Krapf D, Phys. Rev. E 85, 041924 (2012). [DOI] [PubMed] [Google Scholar]
- [33].Hellmann M, Klafter J, Heermann DW, and Weiss M, J. Phys.: Condens. Matter 23, 234113 (2011). [DOI] [PubMed] [Google Scholar]
- [34].Kepten E, Bronshtein I, and Garini Y, Phys. Rev. E 83, 041919 (2011). [DOI] [PubMed] [Google Scholar]
- [35].ben-Avraham D and Havlin S, Diffusion and Reactions in Fractals and Disordered Systems (Cambridge University Press, Cambridge, 2000). [Google Scholar]
- [36].Sadegh S, Higgins JL, Mannion PC, Tamkun MM, and Krapf D, Phys. Rev. X 7, 011031 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Burnecki K and Weron A, Phys. Rev. E 82, 021130 (2010). [DOI] [PubMed] [Google Scholar]
- [38].Hosking JRM, Biometrika 68, 165 (1981). [Google Scholar]
- [39].Granger CWJ and Joyeux R, J. Time Ser. Anal 1, 15 (1980). [Google Scholar]
- [40].Magdziarz M and Weron A, Studia Math. 181, 47 (2007). [Google Scholar]
- [41].Burnecki K and Weron A, J. Stat. Mech (2014) P10036.
- [42].Burnecki K, Muszkieta M, Sikora G, and Weron A, Europhys. Lett 98, 10004 (2012). [Google Scholar]
- [43].Burnecki K, J. Stat. Mech (2012) P05015.
- [44].Burnecki K, Sikora G, and Weron A, Phys. Rev. E 86, 041912 (2012). [DOI] [PubMed] [Google Scholar]
- [45].Burnecki K, Kepten E, Garini Y, Sikora G, and Weron A, Sci. Rep 5, 11306 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Sikora G, Kepten E, Weron A, Balcerek M, and Burnecki K, Phys. Chem. Chem. Phys 19, 26566 (2017). [DOI] [PubMed] [Google Scholar]
- [47].Crato N and Rothman P, Econom. Lett 45, 287 (1994). [Google Scholar]
- [48].Fouskitakis G and Fassois S, IEEE Trans. Signal Process 47, 3365 (1999). [Google Scholar]
- [49].Gill-Alana L, Econ. Bull 3, 1 (2004). [Google Scholar]
- [50].Brockwell PJ and Davis RA, Introduction to Time Series and Forecasting (Springer-Verlag, New York, 2002); ITSM for Windows: A User’s Guide to Time Series Modelling and Forecasting (Springer-Verlag, New York, 1994). [Google Scholar]
- [51].Kokoszka P and Taqqu MS, Stoch. Proc. Appl 60, 19 (1995). [Google Scholar]
- [52].Beran J, Statistics for Long-Memory Processes (Chapman & Hall, New York, 1994). [Google Scholar]
- [53].Stanislavsky A, Burnecki K, Magdziarz M, Weron A, and Weron K, Astrophys. J 693, 1877 (2009). [Google Scholar]
- [54].Burnecki K, Klafter J, Magdziarz M, and Weron A, Phys. A 387, 1077 (2008). [Google Scholar]
- [55].Podobnik B, Ivanov P. Ch., Biljakovic K, Horvatic D, Stanley HE, and Grosse I, Phys. Rev. E 72, 026121 (2005). [DOI] [PubMed] [Google Scholar]
- [56].Kepten E, Weron A, Sikora G, Burnecki K, and Garini Y, PLoS One 10, e0117722 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Jaqaman K, Loerke D, Mettlen M, Kuwata H, Grinstein S, Schmid SL, and Danuser G, Nat. Methods 5, 695 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Akin EJ, Solé L, Johnson B, Beheiry ME, Masson JB, Krapf D, and Tamkun MM, Biophys. J 111, 1235 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Weron A, Burnecki K, Akin EJ, Sole L, Balcerek M, Tamkun MM, and Krapf D, Sci. Rep 7, 5404 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].See Supplemental Material. at. http://link.aps.org/supplemental/10.1103/PhysRevE.99.012101 for detailed information about the fitted models.
- [61].Neyman J, Philos. Trans. A Math. Phys. Sci 236, 333 (1937). [Google Scholar]
- [62].Metzler R and Klafter J, Phys. Rep 339, 77 (2000). [Google Scholar]
- [63].Weron A and Magdziarz M, Phys. Rev. Lett 105, 260603 (2010). [DOI] [PubMed] [Google Scholar]
- [64].Magdziarz M and Weron A, Ann. Phys 326, 2431 (2011). [Google Scholar]
- [65].Vega AR, Freeman SA, Grinstein S, and Jaqaman K, Biophys. J 114, 1018 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Briane V, Kervrann Ch., and Vimond M, Phys. Rev. E 97, 062121 (2018). [DOI] [PubMed] [Google Scholar]
- [67].Liu Y-L et al. , Biophys. J 111, 2214 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Sikora G, Wyłomańska A, Gajda J, Solé L, Akin EJ, Tamkun MM, and Krapf D, Phys. Rev. E 96, 062404 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Monnier N et al. , Nat. Methods 12, 838 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Sungkaworn T, Jobin M-L, Burnecki K, Weron A, Lohse MJ, and Calebiro D, Nature 550, 543 (2017). [DOI] [PubMed] [Google Scholar]
- [71].Baillie R, Chung C-F, and Tieslau MA, J. Appl. Econ 11, 23 (1996). [Google Scholar]
- [72].Ling S and Li WK, J. Amer. Statist. Assoc 92, 1184 (1997). [Google Scholar]
- [73].Manzo C, Torreno-Pina JA, Massignan P, Lapeyre GJ Jr., Lewenstein M, and Garcia Parajo MF, Phys. Rev. X 5, 011021 (2015). [DOI] [PubMed] [Google Scholar]
- [74].Chechkin AV, Seno F, Metzler R, and Sokolov IM, Phys. Rev. X 7, 021002 (2017). [Google Scholar]
- [75].Samorodnitsky G and Taqqu MS, Stable Non-Gaussian Random Processes (Chapman & Hall, New York, 1994). [Google Scholar]
- [76].Stoev S and Taqqu MS, Fractals 12, 95 (2004). [Google Scholar]
- [77].Janicki A and Weron A, A Simulation and Chaotic Behaviour of α–Stable Stochastic Processes (Marcel Dekker Inc., New York, 1994). [Google Scholar]
- [78].Pipiras V and Taqqu MS, Long-Range Dependence and Self-Similarity (Cambridge University Press, Cambridge, 2017). [Google Scholar]
- [79].Burnecki K and Sikora G, IEEE Trans. Signal Process 61, 2825 (2013). [Google Scholar]
- [80].Burnecki K and Sikora G, Chaos Solitons Fractals 102, 456 (2017). [Google Scholar]
- [81].Burnecki K, Wyłomańska A, and Chechkin A, PLoS One 10, e0145604 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Barndorff-Nielsen OE, Normal Inverse Gaussian Processes and the Modelling of Stock Returns (Research Report 300. Department of Theoretical Statistics, University of Aarhus, 1995). [Google Scholar]
- [83].D’Agostino RB and Stephens MA, Goodness-of-Fit Techniques (Marcel Dekker, New York, 1986). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


