Abstract
Closed-loop neural interfaces with on-chip machine learning can detect and suppress disease symptoms in neurological disorders or restore lost functions in paralyzed patients. While high-density neural recording can provide rich neural activity information for accurate disease-state detection, existing systems have low channel counts and poor scalability, which could limit their therapeutic efficacy. This work presents a highly scalable and versatile closed-loop neural interface SoC that can overcome these limitations. A 256-channel time-division multiplexed (TDM) front-end with a two-step fast-settling mixed-signal DC servo loop (DSL) is proposed to record high-spatial-resolution neural activity and perform channel-selective brain-state inference. A tree-structured neural network (NeuralTree) classification processor extracts a rich set of neural biomarkers in a patient- and disease-specific manner. Trained with an energy-aware learning algorithm, the NeuralTree classifier detects the symptoms of underlying disorders (e.g., epilepsy and movement disorders) at an optimal energy-accuracy trade-off. A 16-channel high-voltage (HV) compliant neurostimulator closes the therapeutic loop by delivering charge-balanced biphasic current pulses to the brain. The proposed SoC was fabricated in 65nm CMOS and achieved a 0.227μJ/class energy efficiency in a compact area of 0.014mm2/channel. The SoC was extensively verified on human electroencephalography (EEG) and intracranial EEG (iEEG) epilepsy datasets, obtaining 95.6%/94% sensitivity and 96.8%/96.9% specificity, respectively. In-vivo neural recordings using soft μECoG arrays and multi-domain biomarker extraction were further performed on a rat model of epilepsy. In addition, for the first time in literature, on-chip classification of rest-state tremor in Parkinson’s disease (PD) from human local field potentials (LFPs) was demonstrated.
Keywords: Machine learning, neural network, decision tree, closed-loop neuromodulation, epilepsy, Parkinson’s disease, energy-efficient classification, seizure, tremor
I. Introduction
NEUROLOGICAL disorders are the second leading cause of global deaths and the leading cause of disability worldwide [1]. Epilepsy (>60M) and Parkinson’s disease (>10M) are among common examples, and many patients are living with medication-refractory symptoms of these disorders. Closed-loop brain stimulation has emerged as a promising therapeutic solution to treating such disorders [2]–[6], and a number of FDA-approved and research-based devices are currently available, including NeuroPace’s responsive neurostimulation and Medtronic’s Percept deep-brain stimulation (DBS) systems. However, these devices have a low channel count (4–6) and rely on simplistic symptom detection algorithms (e.g., feature thresholding), which could result in suboptimal detection accuracy and limited therapeutic efficacy.
Over the past decade, we have witnessed a growing adoption of machine learning (ML) for symptom prediction in a variety of neurological conditions such as epilepsy [7], Parkinson’s disease (PD) [8], depression [9], migraine [10], [11], and memory disorders [12]. Through neural signal acquisition, biomarker extraction, and ML-based classification, pathological disease states can be detected more accurately and suppressed more effectively than conventional methods. Moreover, ML intelligence can improve the accuracy of motor intention decoding in brain-machine interfaces (BMIs) for rehabilitation of motor impairments [13], [14]. Despite recent innovations, existing ML-embedded SoCs [5], [15]–[22] are limited in the following aspects:
1). Low channel count:
As the analog front-end (AFE) often dominates the overall area of a neural interface system, the channel count of existing ML-SoCs is limited to 8–32, which may not be sufficient to collect clinically meaningful information for accurate disease state prediction.
2). Low hardware efficiency:
Despite the low channel count, the area and energy consumption of the existing SoCs are prohibitive, making it difficult to scale up the number of channels. This is mainly due to their hardware complexity that grows proportional to the number of channels and biomarkers.
3). Limited application:
With limited sets of biomarkers and conventional classifiers, most neural interface SoCs reported so far have targeted a single task, epileptic seizure detection, while there exist many other conditions that could benefit from the closed-loop neural interface technology.
Closed-loop SoCs would advance further with a higher number of channels and greater adaptability to various neural classification tasks. In epileptic seizure detection, for instance, covering a larger brain area with a high-spatial-resolution electrocorticography (ECoG) array will enable more precise localization of epileptic foci and better mapping of seizure onset [23], thus enhancing the seizure detection accuracy of the trained classifier. In treating movement disorders such as PD and essential tremor, high-density DBS can engage target brain regions more effectively while reducing stimulation-induced side effects [24]. Furthermore, high-density sensing can enhance the accuracy of motor intention decoding in prosthetic BMIs by collecting higher-resolution motor and sensory information [25]. Fig. 1 presents the envisioned versatile neural interface platform that integrates a large number of channels. A patient- and disease-specific classifier detects the pathological symptoms of brain disorders and activates a neurostimulator to provide cortical or deep-brain stimulation for symptom suppression. In BMIs, motor intention can be decoded to control prosthetic devices and provide sensory feedback to the brain via electrical stimulation. This high-channel-count, versatile neural interface device could advance our understanding of complex brain dynamics and provide new therapeutic opportunities for people suffering from various neurological/psychiatric disorders and motor conditions. A miniaturized, energy-efficient implementation of such devices is a key to enabling next-generation closed-loop neural SoCs.
Fig. 1.
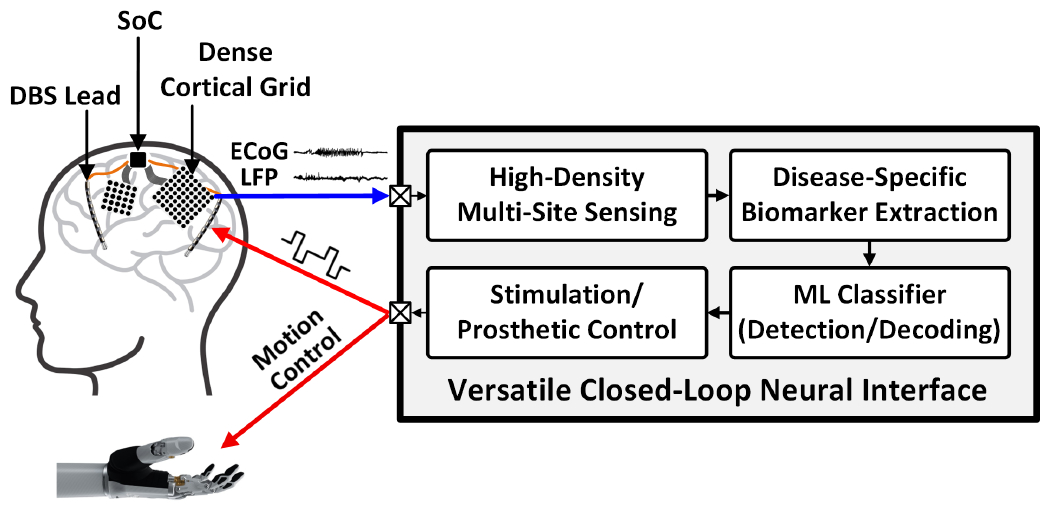
Versatile closed-loop neural interface platform with high-density sensing and stimulation capabilities.
To overcome the aforementioned limitations of existing systems and transition towards the next-generation closed-loop neural interface, this paper presents a 256-channel highly scalable, energy-efficient neural activity classification and closed-loop neuromodulation SoC. A 256-channel area-efficient AFE collects high-resolution neural activity for classifier training, and selectively processes informative channels via energy-efficient inference. Enhanced by multi-symptom biomarker extraction and a multi-class tree-structured neural network (NeuralTree) classifier, the SoC provides greater flexibility for a broader range of applications beyond seizure detection. Through efficient circuit implementation and circuit-algorithm co-design, this high-channel-count neural interface achieves a new class of energy-area efficiency.
This paper extends upon our prior work in [26] and presents a review of the state-of-the-art, detailed description of the proposed circuits/algorithms, and more extensive benchtop and in-vivo validation of the SoC. The paper is organized as follows. Section II provides a high-level description of the 256-channel SoC. Section III describes the system-level optimization of the AFE and introduces a 256-channel time-division multiplexed (TDM) architecture with a two-step fast-settling mixed-signal DC servo loop (DSL). Sections IV and V detail the NeuralTree classification processor and the 16-channel high-voltage (HV) compliant neurostimulator, respectively. Benchtop and in-vivo measurement results are demonstrated in Section VI. Finally, Section VII concludes the paper.
II. SoC Architecture
Fig. 2 presents the architecture of the proposed 256-channel neural activity classification and closed-loop neuromodulation SoC. Four 64-channel chopper-stabilized time-division multiplexed (CS-TDM) AFE modules perform high-density multi-site neural recording to train the classifier. A 16×16 switch matrix and row-multiplexing chopper (MUX-CHOP) connect the 256-channel neural inputs to the AFE modules for signal conditioning. In inference mode, the MUX-CHOP is configured such that any subset of 64 input channels can be selected and processed by the main AFE module (#1). The input selection can change dynamically on a window-by-window basis according to the trained input sequence, to perform channel-selective inference. Following signal conditioning by the main AFE module, a finite impulse response (FIR) filter and feature extraction engine (FEE) compute neural biomarkers in temporal, spectral, and phase domains. Up to 64 multi-symptom biomarkers are extracted on demand in a patient- and disease-specific manner. The extracted biomarkers are passed to the NeuralTree classifier for neural activity classification. The flexible NeuralTree model supports both binary and multi-class classification. Upon detection of pathological brain states, a 16-channel HV compliant neurostimulator delivers charge-balanced biphasic current pulses to the brain to close the therapeutic loop.
Fig. 2.
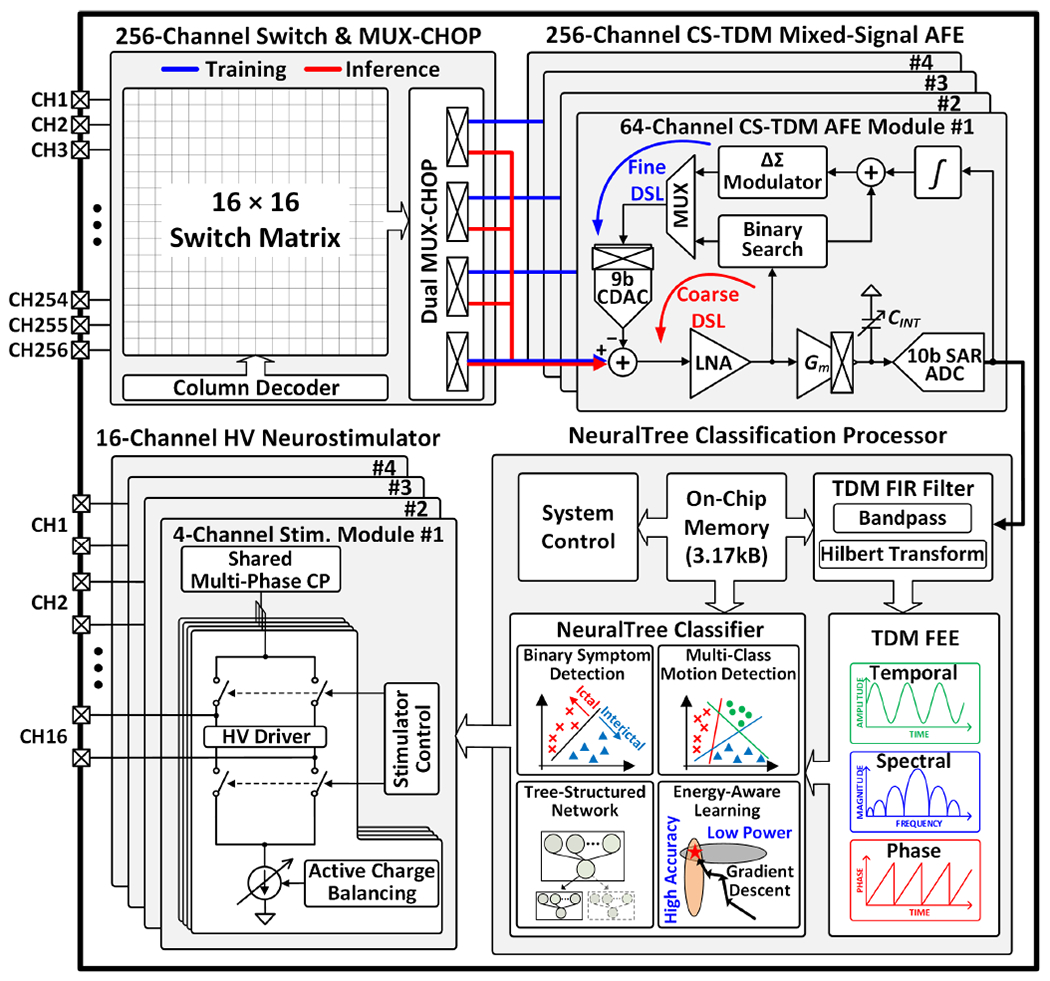
Proposed 256-channel scalable, versatile closed-loop SoC architecture.
The all-in-one integration of high-density recording and stimulation channels, multi-symptom neural biomarkers, and ML intelligence can easily grow the hardware complexity of the system. To overcome this challenge, the proposed SoC employs various circuit-algorithm innovations and system-level hardware optimization techniques, which will be discussed in the remainder of this paper.
III. 256-Channel Analog Front-End
As the sensor count increases, the area constraint on the AFE becomes more stringent and the complexity of the backend signal processing also grows significantly. We tackle these challenges with an area-efficient TDM AFE with a channel-selective inference scheme. Noting that only subsets of input electrodes capture disease-relevant neural activity, the channel-selective approach can greatly reduce the hardware overhead during inference. To validate this concept, we trained a classifier on 128-channel intracranial electroencephalography (iEEG) recorded from an epileptic patient [27] to assess the discriminative power of each channel. The NeuralTree classifier (detailed in Section IV-C) was trained using two common types of seizure biomarkers (line-length and multiband spectral energy) extracted from the 128 channels. The importance of each channel was then assessed based on the number of features extracted during inference using 5-fold cross-validation. The non-uniform channel importance in Fig. 3 implies that high-density training followed by channel-selective inference can save the inference cost significantly while maintaining the classification accuracy.
Fig. 3.
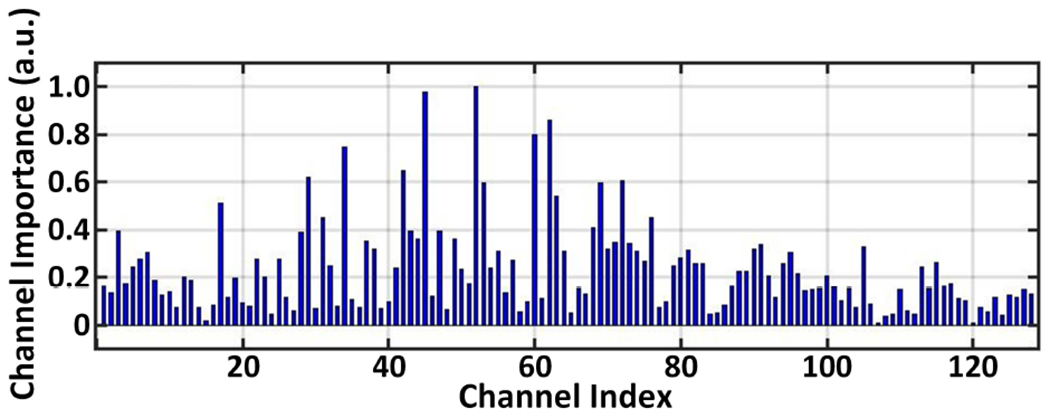
The relative importance of 128 iEEG channels recorded from an epileptic patient and evaluated with 5-fold cross-validation.
Fig. 4 depicts the AFE configurations during classifier training and inference. In training mode, the four 64-channel CS-TDM AFE modules acquire 256-channel neural signals to exploit high-resolution brain activity information. The digitized 256-channel neural data are then used for offline classifier training, during which informative channel indices and feature types are identified. After loading the trained parameters to an on-chip memory, the MUX-CHOP is configured to select any subset of up to 64 informative channels and connect them to the main AFE module via a shared input path. Here, the three auxiliary AFE modules are disabled to save system power. In the proposed NeuralTree model, the selected channels can change dynamically in each feature computation window to perform on-demand biomarker extraction, thus reducing the number of extracted features and enabling energy-efficient classification. However, the dynamic channel selection approach raises new concerns on electrode DC offset (EDO) cancellation that must be addressed.
Fig. 4.
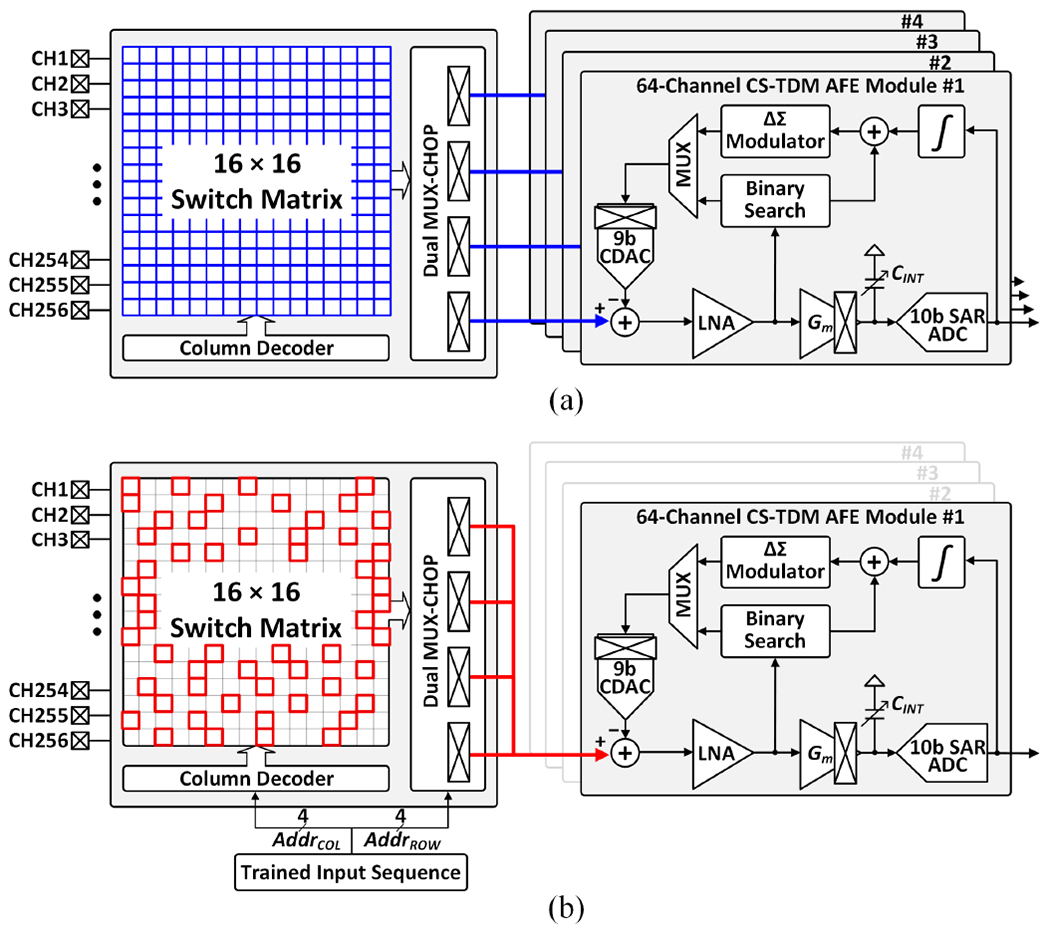
The AFE configurations for (a) classifier training with high-density sensing, and (b) channel-selective inference, where any subset of 64 input channels can be selectively processed on a window-by-window basis.
A. Challenges of Electrode DC Offset Cancellation
Electrochemical polarization at the electrode-tissue interface develops DC offsets between electrodes [28], the magnitude of which can be as large as ±50mV [29]. Each recording electrode in an array can develop a unique EDO with respect to a common reference electrode. When many electrodes with different EDOs are multiplexed to a single amplifier, these EDOs appear as a large signal that fluctuates at the multiplexing frequency, as shown in Fig. 5. Digitizing small neural signals (~1μ–1mV) and significantly larger EDOs simultaneously would require a high-resolution (~16 bits) analog-to-digital converter (ADC), which is nontrivial to design in a compact and power-efficient way. A high-resolution ADC would also increase the hardware complexity of the subsequent filtering and signal processing in the digital back-end (DBE). Another challenge imposed by the channel-selective inference scheme is that the EDO pattern at the amplifier input changes between successive feature extraction windows (Fig. 5). With a conventional large-time-constant DSL, the amplifier would saturate predominantly in each window (~1s), resulting in a significant loss of neural activity information.
Fig. 5.
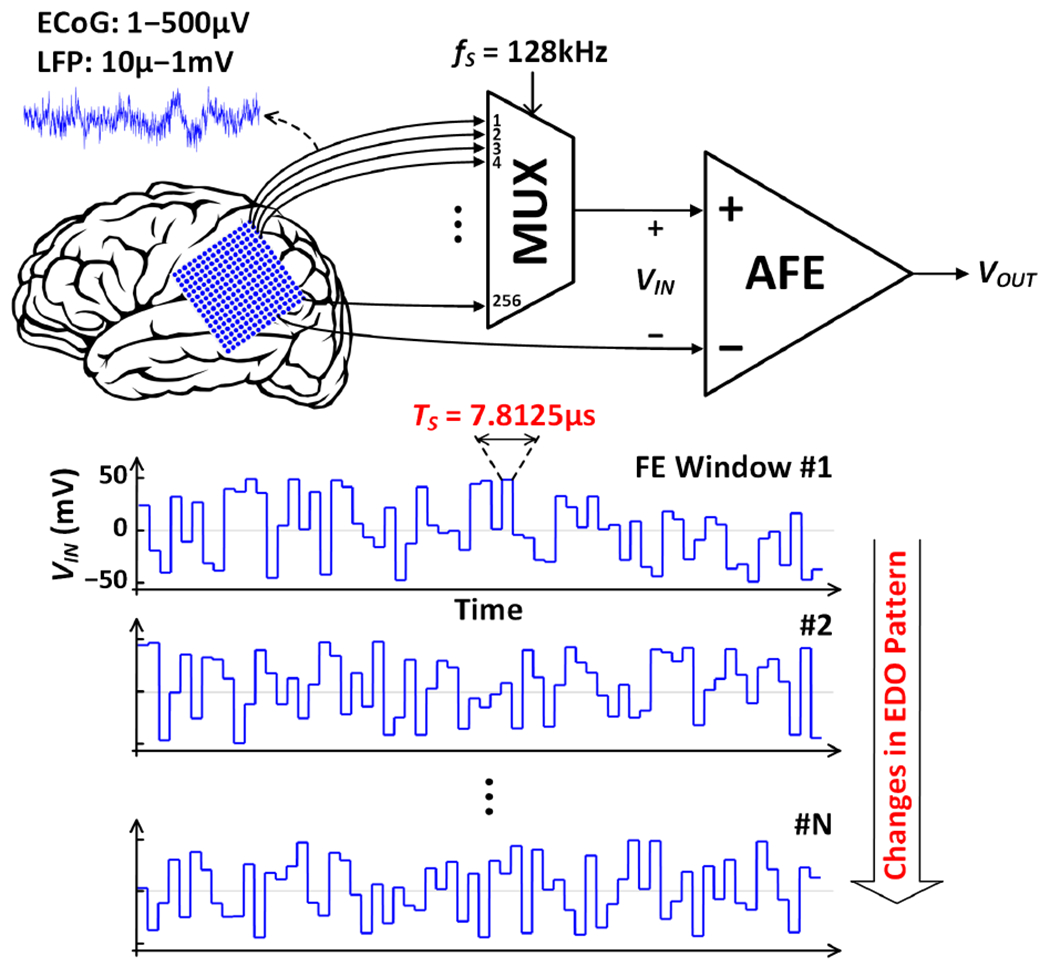
Illustration of EDO fluctuations at the input of the proposed TDM AFE in channel-selective inference mode. Among 256 input channels, up to 64 channels with unique EDOs are multiplexed to the AFE in each feature extraction window. Therefore, the AFE must cancel the EDOs that change abruptly between successive channels and feature extraction windows.
The 16-channel SoC in [5] multiplexed a low-noise amplifier (LNA) for every two channels to save chip area. Intermediate node voltages were stored on 1.5pF sampling capacitors for fast switching between channels with different EDOs. However, this analog S/H-based approach is area inefficient (~0.49mm2/channel) and thus, it is not a viable option for a high-channel-count system. A mixed-signal coarse-fine DSL was reported in [29]. The coarse loop canceled large EDOs using binary search, while the fine loop suppressed residual offsets. Despite achieving a small area of 0.013mm2/channel, the ADC-assisted binary search loop requires many samples to converge, making it inadequate for fast settling in the presence of abrupt EDO changes. Recently, hardware sharing via time-division multiplexing has been increasingly adopted to improve the area efficiency of high-channel-count AFEs. Specifically, to cancel EDOs between successive channels, several DSL designs were reported, including binary search [30], delta encoding [31], and least-mean-square filtering [32]. While these AFEs can ultimately settle for a fixed input EDO pattern, none are compatible with the channel-selective feature extraction scheme as the offset cancellation loops must resettle in each window when a new set of inputs (with unknown EDO patterns) is fed to the AFE.
B. Two-Step Fast-Settling Mixed-Signal DC Servo Loop
To enable an area-efficient AFE implementation and address the EDO cancellation challenge, a 256-channel CS-TDM AFE with a two-step fast-settling mixed-signal DSL is proposed, as shown in Fig. 6. The timing diagram of the two-step EDO cancellation process during inference is illustrated in Fig. 7. At the beginning of each feature extraction window, coarse offset cancellation using binary search is performed for 64 selected channels. A dynamic comparator detects the polarity of the LNA output, and a successive approximation register (SAR) logic subsequently updates the input code for a 9-bit capacitive digital-to-analog converter (CDAC). This process is repeated 9 times until the LNA output converges, and the EDO (≤±50mV) is digitized at 9-bit resolution. The 9-bit EDO code is then stored into a register. This 64-channel coarse EDO cancellation is performed only during the first sampling period (7.8μs/channel) of each window to enable fast settling and minimize neural data loss. Next, a fine loop is enabled to record neural signals and cancel any residual EDOs following the coarse offset cancellation (<±0.2mV). A low-pass filtering digital integrator extracts undesired low-frequency signal components including residual EDOs from the ADC output. The pre-stored 9-bit EDO is added to the 9 most significant bits of the 19-bit integrator output. This newly formed 19-bit code is then ΔΣ-modulated and fed back to the amplifier input via the 9-bit segmented (6-bit unary+3-bit binary) CDAC. Here, an oversampling ratio (OSR) of 50 increases the effective number of bits of the 9-bit CDAC to ~17 bits to suppress the DAC quantization noise to <1μV [33]. The output of the digital integrator can be bit-shifted to control the feedback gain for loop stability and adjust the highpass pole location in the closed-loop frequency response.
Fig. 6.
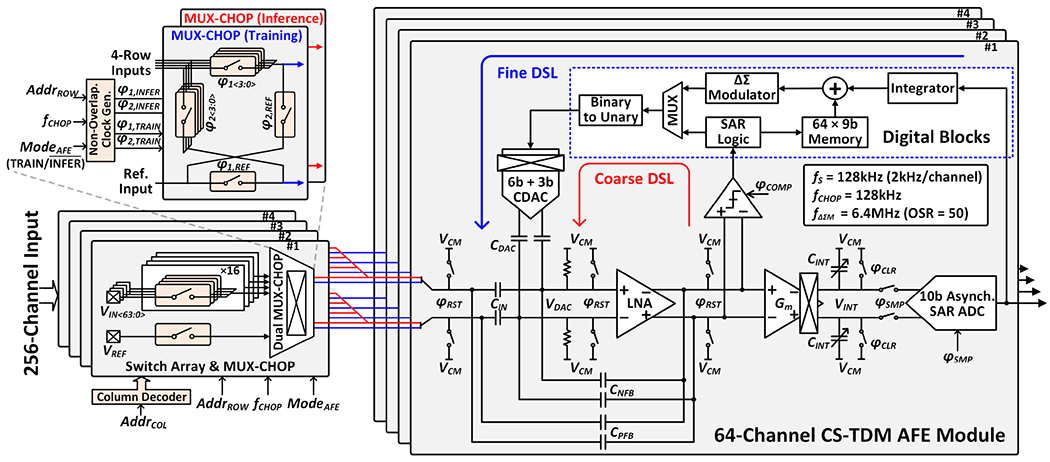
Modular architecture of the proposed 256-channel CS-TDM AFE with a two-step fast-settling mixed-signal DSL. In training mode, the 4×16 switch matrix in each AFE module sequentially selects 64 input channels (row-major order) for signal conditioning. In each feature extraction window during inference, the four MUX-CHOPs select up to 64 channels out of 256 and route them to the main AFE module via the shared input path drawn in red.
Fig. 7.
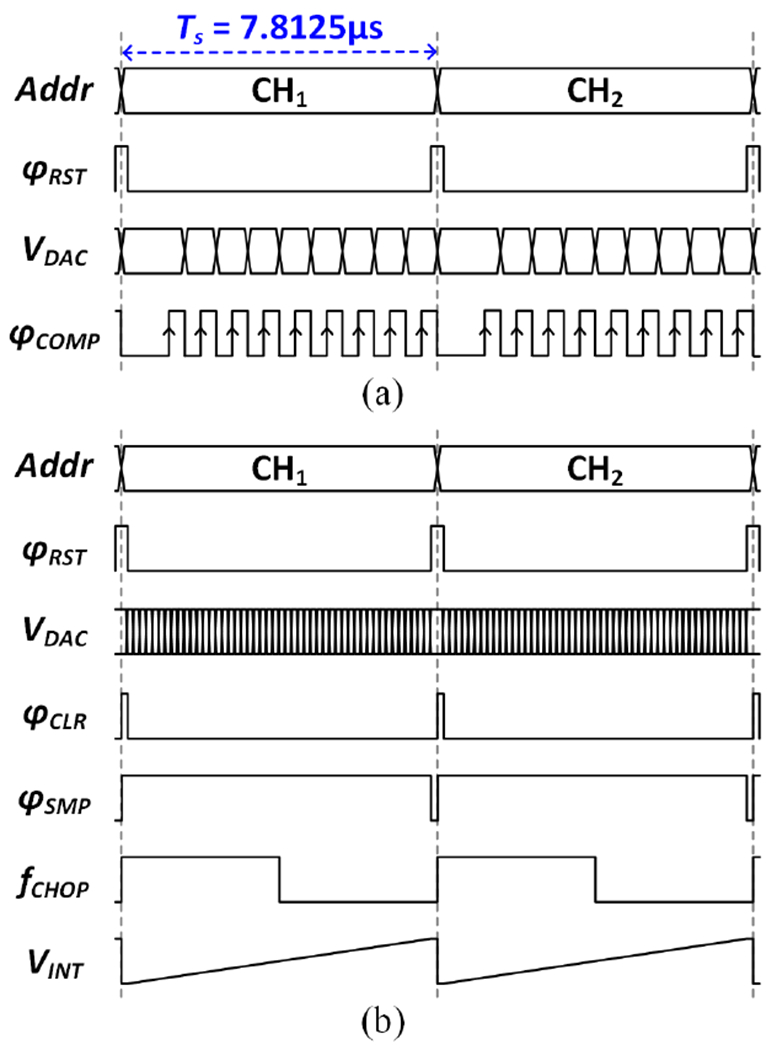
Timing diagram of the two-step (coarse/fine) DSL operation in channel-selective inference mode. (a) The coarse EDO cancellation using 9-bit binary search is performed in the first sampling period in each feature extraction window. (b) The ΔΣ fine loop for residual EDO cancellation operates for the rest of the feature extraction window.
C. Low-Noise Amplifier and Anti-Aliasing Integrator
The AFE forward path consists of a chopper-stabilized LNA and Gm-C integrator. The LNA is capacitively coupled to provide a precise, moderate closed-loop gain of 26dB (CIN/CNFB = 24pF/1.2pF). The positive feedback loop (CPFB) partially compensates for input impedance degradation due to chopping. Here, the value of CPFB is chosen equal to CNFB to avoid the instability condition (i.e., the total effective input capacitance being negative), and its noise contribution is negligible when referred to the electrode-tissue interface, given much higher electrode coupling capacitance (~1nF). The core amplifier in the LNA stage adopts an inverter-based current-reuse topology for improved noise efficiency [34] as shown in Fig. 8(a). The complementary input pairs are biased in weak inversion (gm/ID ≈ 25) and constructed using thick-oxide transistors to prevent gate leakage. The cascode transistors boost the open-loop gain to enable a precise closed-loop gain, while isolating the input devices from the amplifier output not to exacerbate the Miller effect on their Cgd.
Fig. 8.
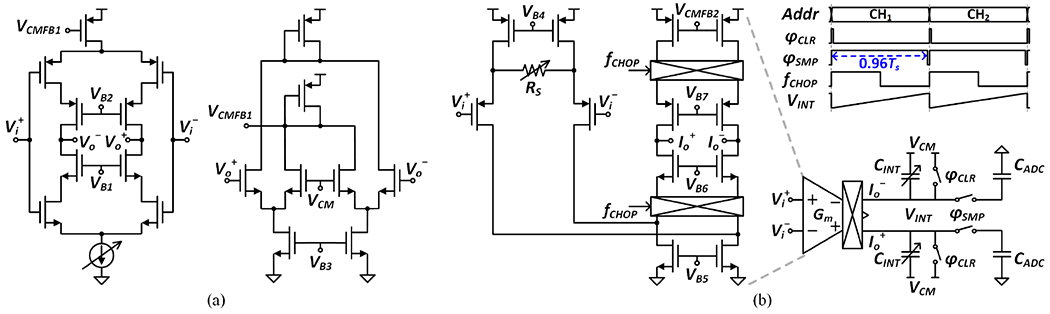
Circuit implementations of the forward-path amplifiers: (a) core amplifier in the LNA stage and its common-mode feedback (CMFB) circuit, and (b) Gm-C integrator and the timing diagram of operation.
With a ΔΣ frequency of 6.4MHz, the LNA bandwidth is set to 7MHz, which is much higher than the ADC sampling rate of 128kS/s. This high LNA bandwidth necessitates an anti-aliasing filter prior to digitization to avoid noise folding. Filtering is achieved by a charge sampling Gm-C integrator, which provides a sinc-shaped frequency response with notches at integer multiples of the sampling frequency [35], [36]. Fig. 8(b) presents the circuit implementation of the Gm-C integrator and the timing diagram of charge sampling operation. A folded-cascode amplifier with source degeneration is implemented for improved linearity. The integration time extends to the 96% of the sampling period, during which high-frequency ΔΣ noise and chopper ripples are attenuated. The charge sampling approach relaxes the settling requirement of the amplifier [35], obviating the need for a power-consuming ADC buffer. The 3-bit resistor (RS) and 5-bit capacitor (CINT) banks provide an additional programmable gain (14–34dB) in the forward path.
In a TDM front-end, samples of the current channel can be corrupted by previous channel residues, which manifests as inter-channel crosstalk. To prevent this, our CS-TDM AFE periodically resets the intermediate nodes along the forward path between successive channels. During this reset operation, the kT/C noise is sampled by the input capacitors at 2kHz per channel. With chopper stabilization, however, this kT/C noise is up-modulated to integer multiples of the chopping frequency (128kHz) and subsequently attenuated by the notches of the Gm-C integrator.
When the neurostimulator is triggered in closed-loop mode, the recording electrodes experience large differential- and common-mode stimulation artifacts, the amplitude of which can be a few 10s and 100s of mVpp, respectively, depending on the stimulation current amplitude [37]. To prevent amplifier saturation by these artifacts, the AFE inputs are disconnected from pads via multiplexing switches in the matrix (i.e., sensing is disabled during stimulation). A synchronous control of recording and stimulation allows the AFE operation to resume immediately after the last stimulation pulse. Therefore, only residual artifacts and stimulation-induced DC offsets that remain at the time of AFE reconnection corrupt recorded neural signals. The amplitude and duration of residual artifacts are minimized by the charge balancing capabilities of the biphasic stimulators (detailed in Section V). When the AFE inputs are reconnected, the brief reset operation at every sample aids in fast recovery (<5ms [38]) while the two-step DSL quickly cancels newly developed DC offsets (Fig. 7).
D. Asynchronous Analog-to-Digital Converter
A 10-bit SAR ADC digitizes the Gm-C integrator output at 128kS/s (2kS/s per channel). Following charge sampling in the Gm-C integrator, only a short time (312.5ns) is allocated to digitization. To avoid the use of an excessively high clock frequency, we adopt an asynchronous SAR control with a single sampling clock [39]. A 9-bit binary-weighted charge-redistribution DAC with top-plate sampling and monotonic switching is implemented, using 2.3fF metal-oxide-metal unit capacitors and bootstrapped switches [39]. An attenuation capacitor equal to the total 9-bit DAC capacitance is added to halve the effective input range of the ADC without an additional reference voltage generator [40]. This approach relaxes the linearity and gain requirements of the preceding amplifiers with only a marginal area overhead, which is amortized across 64 channels in the proposed TDM AFE.
IV. NeuralTree Classification Processor
The high-level architecture of the proposed NeuralTree classification processor is presented in Fig. 2. The configurable TDM FIR filter performs selective bandpass filtering (BPF) and Hilbert transformation (HT) depending on the type of feature being extracted. Following signal filtering, the multi-symptom TDM FEE extracts up to 64 patient- and disease-specific neural biomarkers in temporal, spectral, and/or phase domains. The NeuralTree classifier uses the extracted feature vectors to perform top-down brain-state inference along the most probable path of the tree. The end-to-end TDM implementation enables a seamless integration of key building blocks without the need for demultiplexing, thus achieving a new class of scalability and energy efficiency. Hardware-friendly feature approximations and energy-aware training algorithm further improve the NeuralTree’s hardware efficiency, as detailed in this section.
A. Bandpass Filtering and Hilbert Transform
Fig. 9 depicts the block diagram of the TDM FIR filter that processes digitized neural signals. To save silicon area, a single set of arithmetic units is shared between 64 channels for 32-tap bandpass filtering [5]. Band-specific FIR coefficients are retrieved from the on-chip memory and multiplexed into the multiplier array. The FIR filter can be reconfigured as a 31-tap Hilbert transformer to obtain analytic signals for instantaneous phase and amplitude extraction. The 64-channel BPF and HT register banks are clocked at 128kHz and selectively clock gated depending on the feature type. For temporal feature extraction, the ADC output is directly fed to the FEE and the FIR is bypassed.
Fig. 9.
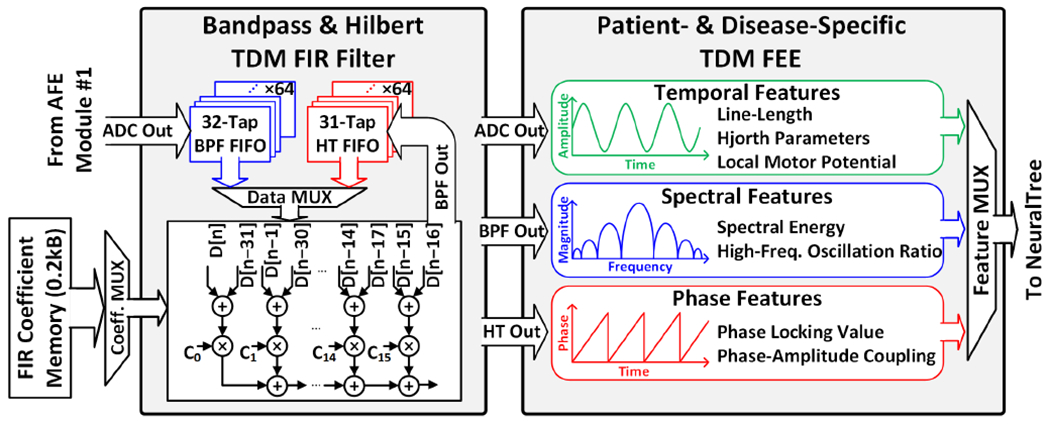
Configurable TDM FIR filter and multi-symptom TDM FEE.
B. Multi-Symptom Feature Extraction
To enhance the versatility of the SoC for a broad range of neural classification tasks, the FEE integrates multi-symptom neural biomarkers, as summarized in Table I. Without careful design considerations, integrating such a broad range of biomarkers can be hardware intensive. The following subsections describe hardware-friendly feature approximation algorithms and circuit techniques that enable low-complexity, yet accurate feature extraction in the proposed SoC.
TABLE I.
Task-Specific Neural Biomarkers Integrated on the SoC
| Epileptic Seizure | Description |
|---|---|
| Line-Length | Average of absolute temporal derivative |
| Hjorth Activity | Variance of signal |
| Delta Energy | Spectral energy in 1–4 Hz |
| Theta Energy | Spectral energy in 4–8 Hz |
| Alpha Energy | Spectral energy in 8–13 Hz |
| Beta Energy | Spectral energy in 13–30 Hz |
| Low-Gamma Energy | Spectral energy in 30–50 Hz |
| Gamma Energy | Spectral energy in 50–80 Hz |
| High-Gamma Energy | Spectral energy in 80–150 Hz |
| Ripple Energy | Spectral energy in 150–250 Hz |
| Phase-Amplitude Coupling | Coupling of the phase in 4–8 Hz to the amplitude envelope in 80–150 Hz |
| Phase Locking Value | Synchronization between two-channel phases in 13–30 Hz |
| Parkinsonian Tremor | Description |
|
| |
| Hjorth Activity | Variance of signal |
| Hjorth Mobility | Mean frequency of signal |
| Hjorth Complexity | Change in signal frequency |
| Tremor Energy | Spectral energy in 1–4 Hz |
| Beta Energy | Spectral energy in 13–30 Hz |
| Low-Gamma Energy | Spectral energy in 30–45 Hz |
| Gamma Energy | Spectral energy in 60–90 Hz |
| High-Gamma Energy | Spectral energy in 100–200 Hz |
| Slow High-Frequency Oscillation | Spectral energy in 200–300 Hz |
| Fast High-Frequency Oscillation | Spectral energy in 300–400 Hz |
| High-Frequency Oscillation Ratio | Ratio of the energy in 200–300 Hz to the energy in 300–400 Hz |
| Phase-Amplitude Coupling | Coupling of the phase in 13–30 Hz to the amplitude envelope in 150–400 Hz |
| Finger Movement | Description |
|
| |
| Local Motor Potential | Mean value of signal |
| Hjorth Activity | Variance of signal |
| Hjorth Mobility | Mean frequency of signal |
| Hjorth Complexity | Change in signal frequency |
| Alpha Energy | Spectral energy in 8–13 Hz |
| Beta Energy | Spectral energy in 13–30 Hz |
| Low-Gamma Energy | Spectral energy in 30–60 Hz |
| Gamma Energy | Spectral energy in 60–100 Hz |
| High-Gamma Energy | Spectral energy in 100–200 Hz |
1). Temporal features:
Line-length (LL) increases in the presence of high-amplitude or high-frequency neural oscillations and has been among powerful biomarkers of epileptic seizures [41]. LL is defined as in (1):
| (1) |
where N is the number of samples in a feature extraction window. Fig. 10(a) presents the hardware implementation of the proposed TDM temporal feature extractor. For LL extraction, the absolute differences between successive samples are accumulated with two adders and one absolute value calculator.
Fig. 10.
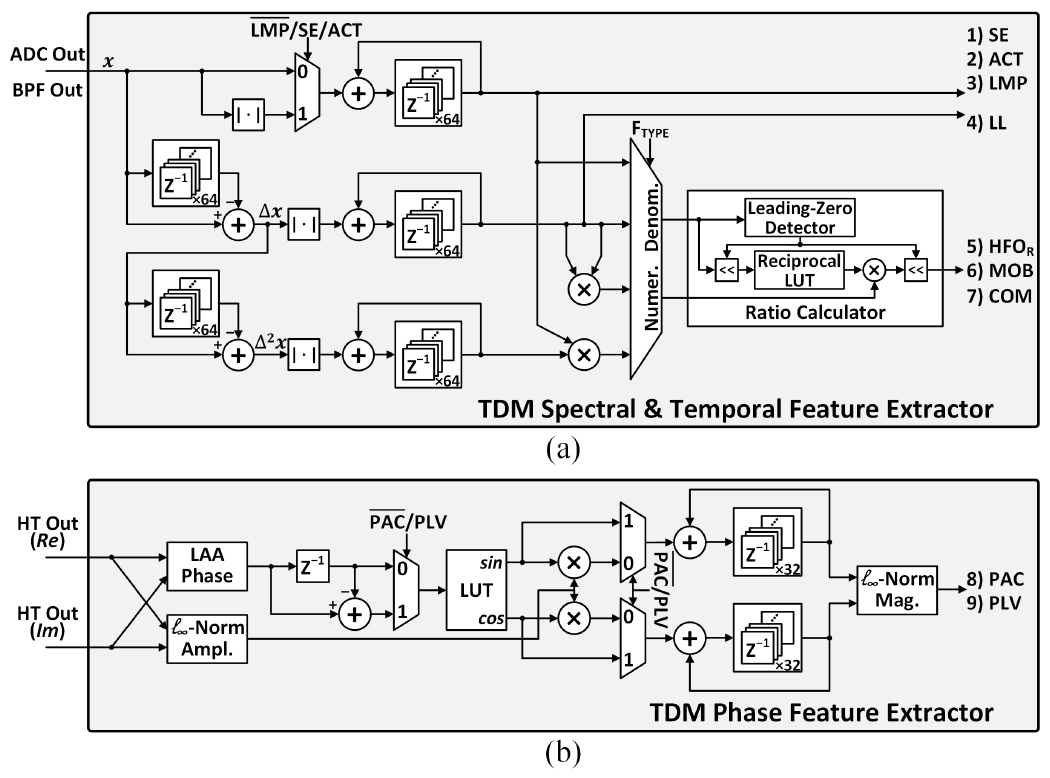
Hardware implementations of the TDM FEE: (a) temporal and spectral feature extractor, and (b) phase feature extractor.
The Hjorth statistical parameters are highly correlated with tremor in PD [8] and used in BMIs for finger movement [42] and gait [43] decoding. The Hjorth activity (ACT), mobility (MOB), and complexity (COM) measure the variance, mean frequency, and frequency change of a signal, respectively, as defined below [44]:
| (2) |
| (3) |
| (4) |
where μ, Δx, and Δ2x are the mean, first, and second derivatives of the signal x, respectively.
The three Hjorth parameters are difficult to efficiently compute in their original form, due to the intensive multiplication and square-root operations. Ref. [45] introduced a similar set of parameters, namely mean amplitude, mean frequency, and spectral purity index (SPI), in which the square and square-root operators are replaced by simple absolute value approximations. These new parameters are less intensive to compute while preserving a close relation to the measures of EEG amplitude and frequency. We adopt this approach to approximate the Hjorth features as in (5–(7), with a modification to the SPI parameter by taking its reciprocal, since it is better correlated with the original Hjorth complexity parameter:
| (5) |
| (6) |
| (7) |
To calculate the approximated Hjorth features, the absolute values of the input and its first and second derivatives are accumulated selectively, as shown in Fig. 10(a). For MOB and COM extraction, the subsequent multipliers and ratio calculator further process the accumulated derivatives to compute features in fractional form. The ratio calculator employs a reciprocal-multiply approach with bit shifting instead of a complex divider, as depicted in Fig. 10(a).
Local motor potential (LMP) has been used as a low-complexity yet effective marker for motor intention decoding in BMIs [46]. The LMP feature quantifies the mean value of a signal as defined in (8):
| (8) |
The accumulation function can be performed by reusing the ACT extractor and bypassing the absolute value calculator, as shown in Fig. 10(a).
2). Spectral features:
Spectral energy (SE) in multiple frequency bands of neural oscillations has been a commonly used biomarker in epilepsy [5], [16], [17], [19], [21], [22], [42], PD [8], [47], and BMIs [14], [48]. As a measure of signal power integrated over time, the SE can be defined in the discrete-time domain as follows:
| (9) |
where xBAND,t indicates the bandpass-filtered neural signal.
A common approximation method to avoid the square operation is to take the absolute output of the bandpass filter. The 16-channel EEG processor in [5] demultiplexed the output of the TDM FIR filter to 112 signal paths (16 channels×7 bands) to calculate 112 SE features in parallel. This approach requires an equal number of multi-bit adders and absolute value calculators with significant area overhead. To save chip area, the TDM spectral feature extractor in Fig. 10(a) directly receives the BPF output as the input without demultiplexing, and extracts up to 64 SE features using a single adder. The area efficiency is further improved by reusing the hardware already implemented for ACT and LMP extraction.
High-frequency (>200Hz) oscillations (HFOs) are prominent features in PD [49] and epilepsy (>80Hz) [50]. For instance, Ref. [51] reported the energy ratio between the slow (HFO1, 200–300Hz) and fast HFO (HFO2, 300–400Hz) as an indicator of rest tremor in PD:
| (10) |
The SE extractor is reused to calculate the slow and fast HFOs, while the ratio between the two is computed using the ratio calculator shared with the Hjorth feature extractor.
3). Phase features:
Different brain regions communicate with each other through neuronal oscillations. Abnormal cross-regional synchronization of neural oscillations can indicate disease-related pathological states in neurological and psychiatric disorders. In epilepsy, spatial and temporal changes in cross-channel phase synchronization, quantified by phase locking value (PLV), play as a key indicator of seizure state [52]. Phase-amplitude coupling (PAC) is another mechanism for within- and cross-regional brain communication. PAC quantifies the degree to which the low-frequency neural oscillatory phase modulates the amplitude of high-frequency oscillations [53]. Excessive PAC has been observed in disorders such as epilepsy [54], PD [55], and depression [56].
Measuring PLV and PAC requires Hilbert transformation to obtain analytic signals followed by several complex computations such as extraction of instantaneous phase and amplitude, trigonometric functions, and magnitude computation, as shown in (11) and (12):
| (11) |
| (12) |
where Δθt in (11) is the cross-channel phase difference, and θt and At in (12) are the modulating phase and modulated amplitude envelope, respectively.
The SoCs in [17], [57] employed multiple COordinate Rotation DIgital Computer (CORDIC) processors to compute these non-linear functions, consuming an excessive amount of power (>200μW). Alternatively, Fig. 10(b) depicts the proposed TDM phase feature extractor [26]. With band-specific analytic signals (Re and Im) as inputs, the instantaneous phase is approximated using a linear arctangent approximation (LAA) algorithm [58] followed by look-up table (LUT)-based error correction [59]. The l∞-norm is used to approximate the amplitude envelope of high-frequency oscillations in PAC, as well as the magnitude computations in (11) and (12). The TDM phase feature extractor can compute up to 32 PLV/PAC features on demand in a compact area of 0.033mm2, performing a higher degree of multiplexing compared to the architecture in [59].
To evaluate the accuracy of the proposed feature approximation algorithms, we analyzed the Pearson correlation coefficient between the ideal and approximated features in MATLAB. The phase and 8-band SE features were extracted from an epilepsy iEEG dataset [27], while a PD local field potential (LFP) dataset [8] was used to compute the HFO ratio and Hjorth features. The boxplot of correlation coefficients in Fig. 11 shows that the approximated features are highly correlated with their ideal counterparts, exhibiting median correlations above 0.9.
Fig. 11.
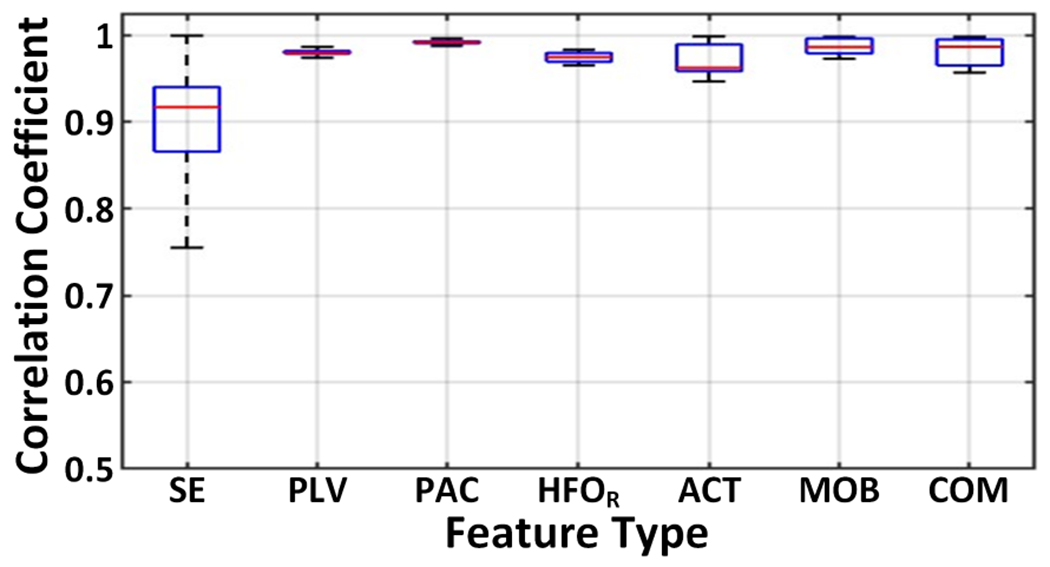
Boxplot of the Pearson correlation coefficients between the ideal and approximated features.
Thanks to feature approximations and hardware sharing, the proposed multi-symptom FEE occupies a small silicon area of 0.12mm2, even with the complex features integrated. Aggressive hardware sharing among different feature calculators is possible thanks to the on-demand TDM scheme, where only selected features are consecutively extracted. With a 128kHz clock, the FEE can generate any combination of up to 64 neural biomarkers in each programmable feature extraction window (0.25–2s). Any unused hardware units are selectively clock- and data-gated to reduce dynamic power dissipation.
C. Energy-Aware, Low-Complexity NeuralTree Model
Deployment of ML algorithms in closed-loop neural interfaces can provide a more accurate and personalized treatment option than conventional methods with feature thresholding [60]. Compared to approaches that utilize an external device (e.g., FPGA) for classification, ML-embedded closed-loop devices offer several advantages including more rapid closed-loop intervention, higher energy efficiency, and enhanced privacy/security, all thanks to relaxed data telemetry requirements [60]. These, however, come at the cost of lower flexibility of the on-chip algorithms, as well as their limited area and power budget. Such constraints become more restrictive as the demand for higher channel counts continues to grow.
Decision tree (DT)-based ML models are becoming popular for their lightweight inference and low memory utilization. The 32-channel seizure detection classifier in [16] employed an ensemble of 8 eXtreme Gradient-Boosted (XGB) DTs. A 41.2nJ/class DBE energy efficiency in 1mm2 area was achieved, thanks to the on-demand feature extraction and sequential node processing. The 8-channel seizure detection SoC with 1024 AdaBoosted trees in [18] reported low-complexity spectral feature extraction with bit-serial processing, and achieved a 36nJ/class DBE energy efficiency. However, a drawback of conventional DT-based classifiers is that the number of trees and signal processing units can significantly increase as the classification task becomes more complex.
To enhance the hardware efficiency of the on-chip classifier, we propose a hierarchical NeuralTree model. Fig. 12(a) illustrates a graphical representation of the NeuralTree classifier trained with a probabilistic routing scheme [42]. Unlike conventional axis-aligned binary DTs, the NeuralTree is a single oblique tree with probabilistic splits. With internal nodes represented by two-layer neural networks, the probability of splits in each internal node is computed using the sigmoid function. The feature vector xi is routed to each leaf node l with a probability p(l|xi; θ), where θ indicates the internal node parameters. The leaf nodes are parameterized by the class probability ϕ. The probability of xi belonging to class yi can be expressed as:
| (13) |
Fig. 12.
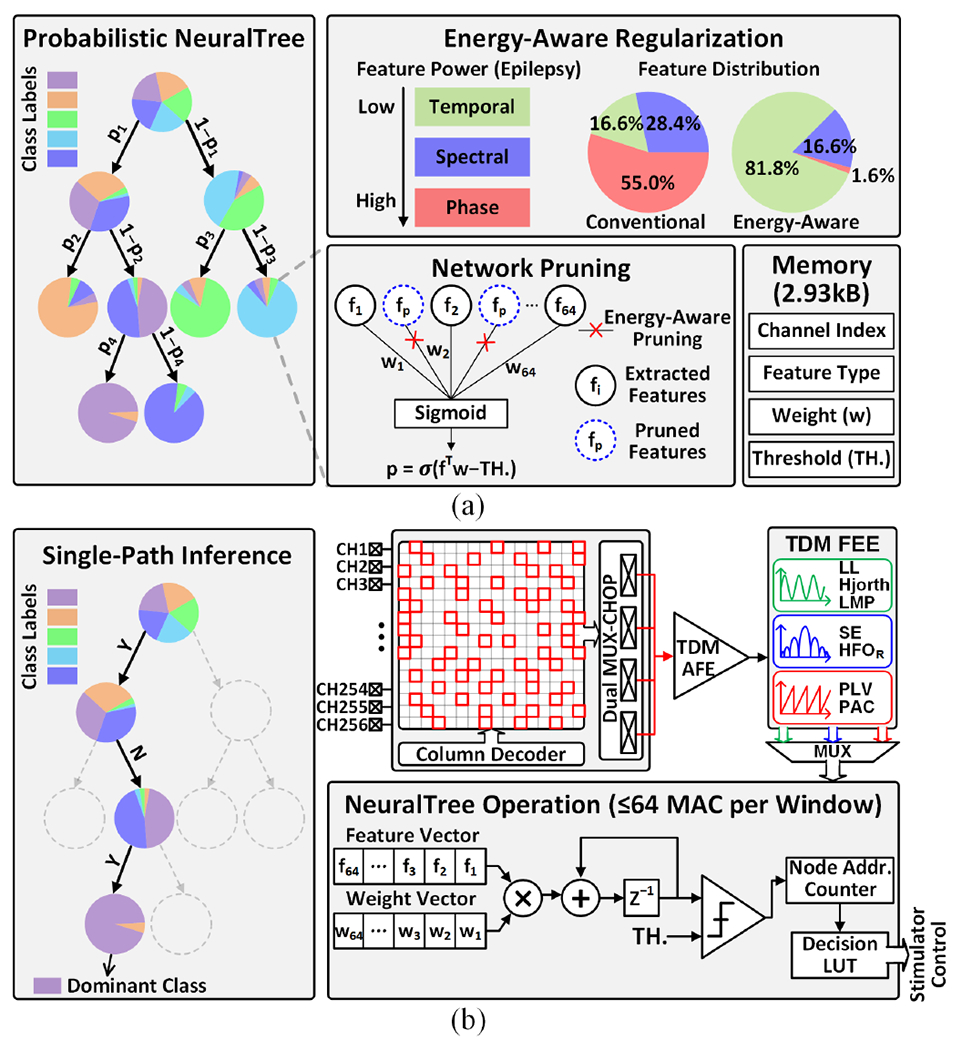
NeuralTree classifier: (a) probabilistic NeuralTree trained with energy-aware regularization and network pruning, and (b) the NeuralTree hardware implementation and system operation under the proposed singlepath channel-selective inference scheme. The NeuralTree is trained on neural activity from all 256 channels. Following the regularization and network pruning, each internal node contains an optimal set of up to 64 features, which can be associated with any input channels.
where ω = θ ∪ ϕ indicates the trainable weights in the NeuralTree, and L is the number of leaf nodes. In the training process, we simply minimize the cross-entropy loss on the training data:
| (14) |
The probabilistic NeuralTree is compatible with gradient-based optimization, which allows the use of hardware-efficient model compression techniques such as weight pruning and fixed-point quantization. To enable neural activity inference at an optimal energy-accuracy trade-off, the NeuralTree employs energy-aware regularization [61]. Here, the power consumed for feature computation is added to the objective function as a regularization term in the training objective. Specifically, we define the energy-aware regularization term as:
| (15) |
where I and D represent the number of internal nodes and feature types, respectively, and β is the normalized power cost for each feature type estimated using Synopsys PrimeTime. We use pi to represent the probability of visiting the internal node i and θi,j for the weight associated with feature j at node i. Combining (14) and (15), we derive an energy-aware objective function, which seeks to minimize the classification error as well as the energy consumption during inference:
| (16) |
Here, we introduce a hyperparameter C to control the energy-accuracy trade-off and penalize power-demanding features. The proposed NeuralTree is trained using TensorFlow [62] with Adam optimizer (learning rate: 0.001) [63]. Validated on the iEEG epilepsy dataset [27], the energy-aware regularization saves 64% power in filtering and feature extraction during inference, with only a marginal accuracy loss (<2%).
The regularization is applied on all types of features (Table I) extracted from 256 channels. Following this, network pruning is performed to compress the tree structure by reducing the number of extracted features (i.e., maximum 64 per node). The NeuralTree with a depth of 4 contains up to 15 internal nodes, each assigned a unique set of up to 64 features. Once an optimal feature set is determined for each node via regularization and pruning, the feature types and associated channel indices are stored in the on-chip memory for inference. Thanks to network pruning and fixed-point weight quantization (12 bits), the trained parameters of the compressed NeuralTree require only 2.93kB of memory. Through energy-aware regularization and network pruning, features with an optimal energy-accuracy trade-off are extracted in a patient- and disease-specific way.
Considering that most samples are routed with high certainty during training, the inference can be performed through top-down conditional computations, as depicted in Fig. 12(b). By reusing a single multiply-and-accumulate (MAC) unit and a comparator, the standalone NeuralTree occupies a significantly smaller area compared to large tree ensembles. In addition to conventional binary classification tasks (e.g., seizure or tremor detection), the NeuralTree further supports multi-class classification tasks such as finger movement detection. This additional functionality is achieved with only a marginal memory overhead to store multi-bit class labels in the decision LUT. As a proof of concept, a 6-class finger movement classification task was simulated using a human ECoG dataset [64], where the NeuralTree decoded finger movements with 73.3% accuracy.
During inference, the NeuralTree performs sequential node processing along the most probable path, thus reducing the number of computed features and weighted summations. Only one node is visited in each feature computation window, during which a maximum of 64 features are extracted from any subset of channels, as shown in Fig. 12(b). The NeuralTree is clocked at 128kHz but only activated during the last 64 clock cycles in each feature extraction window to perform 64 feature-weight MAC operations. The lightweight channel-selective inference coupled with energy-aware learning considerably enhances the model’s energy efficiency and scalability.
V. High-Voltage Compliant Neurostimulator
A single-chip integration of neurostimulator with other building blocks is desired to reduce the size of the implantable device and interconnection complexity. However, depending on the electrode impedance and stimulation amplitude, the voltage compliance required at the electrode-tissue interface can exceed the gate-oxide breakdown limits in standard CMoS processes [65]. To facilitate a seamless integration of the closed-loop neuromodulation system in a standard low-power CMoS process, a 16-channel neurostimulator is implemented with a stacked HV compliant architecture.
Fig. 13(a) presents the 12-stage 4-phase charge pump (CP) that generates an 8V supply for the current drivers. Each stage in the 4-phase CP consists of four elements in parallel, thus reducing output ripples by a factor of four without the need for large output capacitors [66]. To minimize the reversion loss in the CP, flying capacitors (CP) are controlled by a non-overlapping clock generator. The ring VCO generates a high-frequency clock at 1GHz, which allows the use of small flying capacitors (0.8pF) for improved area efficiency [65]. To further save chip area, a single CP is shared among four individually addressable stimulation channels with constraints on the maximum current when more than one channel is active.
Fig. 13.
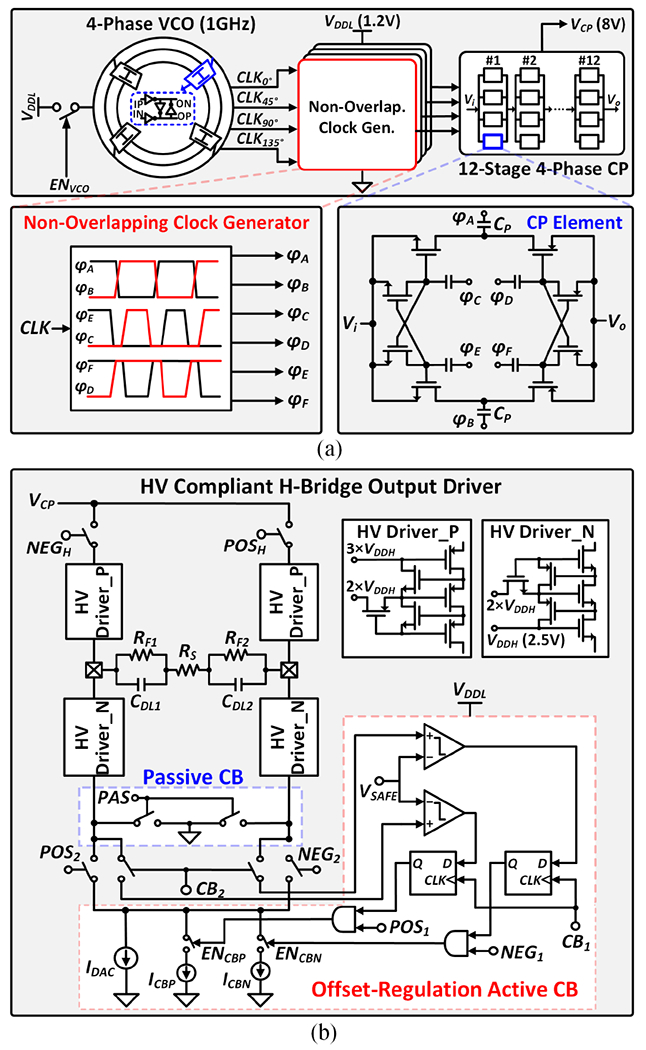
Architecture of the HV compliant neurostimulator: (a) 12-stage 4-phase charge pump with high-frequency clocking, and (b) HV compliant H-bridge output driver with charge balancing.
Fig. 13(b) shows the architecture of the stacked H-bridge output driver. A single current sink (IDAC) is used in both anodic and cathodic phases to reduce charge mismatch. To ensure precise charge balancing (CB), an offset-regulation active CB technique combined with passive discharging is employed [67]. The residual voltage at the electrode is monitored following biphasic stimulation. If the residual voltage exceeds the safety level (±VSAFE = ±50mV), the active CB is enabled to provide an additional current such that the two stimulation phases are balanced. Following active CB, any residual charges on the two electrodes are discharged to the ground. To provide sufficient flexibility for various applications, the stimulation parameters such as current amplitude, pulse width, and frequency are programmable.
VI. Measurement Results
The SoC was fabricated in a TSMC 65nm 1P9M low-power CMOS process with a chip dimension of 4mm×2mm. The chip micrograph and SoC power breakdown are presented in Figs. 14(a) and (b), respectively. The 256-channel SoC only occupies an active area of 3.48mm2 (0.014mm2/channel) and consumes 453μW at 1.2V supply voltage in inference mode.
Fig. 14.
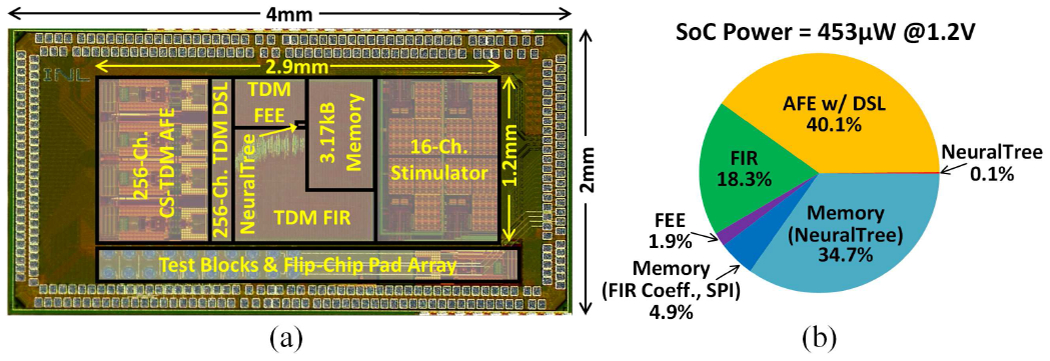
(a) Chip micrograph, and (b) SoC power breakdown.
A. AFE Characterization
The 256-channel TDM AFE including the digital DSL occupies an area of 1.1mm2 (0.004mm2/channel) and consumes 387μW (1.51μW/channel) in training mode. During channel-selective inference, the LNAs and DSLs in the three auxiliary AFE modules are disabled, reducing the AFE power to 182μW. Fig. 15(a) shows the measured AFE gain that is programmable between 40.7 and 57.9dB. The location of the high-pass pole can be adjusted by bit-shifting the output of the digital integrator, as demonstrated in Fig. 15(b). With a 2.5mVpp, 40.039Hz sine input, the entire AFE including the ADC achieved a signal-to-noise and distortion ratio (SNDR) of 49dB and a spurious-free dynamic range (SFDR) of 61.6dB, measured with 2048-point FFT. Fig. 15(d) presents the input-referred noise (IRN) performance measured with the high-pass corner set to 1Hz. The noise was measured at the ADC output and thus factored in noise folding incurred by the broadband Gm-C integrator as well as ADC noise. Without chopping, the measured IRN was 60.4μVrms in the 1–500Hz band. It is dominated by the kT/C noise resulting from the reset operation for crosstalk reduction. When chopping was enabled, the IRN reduced to 3.2μVrms with the kT/C and 1/f noise up-modulated by the chopper and filtered out by the Gm-C integrator, as discussed in Section III–C. With the fine DSL disabled, the IRN was measured at 1.5μVrms. This indicates that when the fine DSL is active, ~2× noise folding occurs due to the insufficient LNA bandwidth with respect to the Δω frequency [33]. The noise performance could be improved by increasing the LNA bandwidth and lowering the OSR with a higher-order ΔΩ modulator. Fig. 15(e) demonstrates the fast-settling behavior of the proposed coarse-fine DSL in the presence of abrupt EDO changes over 1s windows, which enables channel-selective inference. With the DSL disabled, the AFE was completely saturated by the offsets. When only the fine DSL was activated, the AFE failed to capture a significant portion of signals during its settling, as other existing DSLs would behave. With a 128kHz chopping frequency, the input impedance was measured to be 24.5MΩ at 100Hz (10.8MΩ without positive feedback in simulations). The limited impedance boosting (~2.3×) is due to process variations and parasitic effects [68]. A tunable capacitor bank could be incorporated to account for such non-idealities and further boost the input impedance, with a negligible impact on the per-channel area of our TDM AFE. The common-mode rejection ratio (CMRR) and power-supply rejection ratio (PSRR) at 50Hz were 70dB and 71dB, respectively. Crosstalk between channels was less than −79.8dB inter-module and −72.8dB intra-module.
Fig. 15.
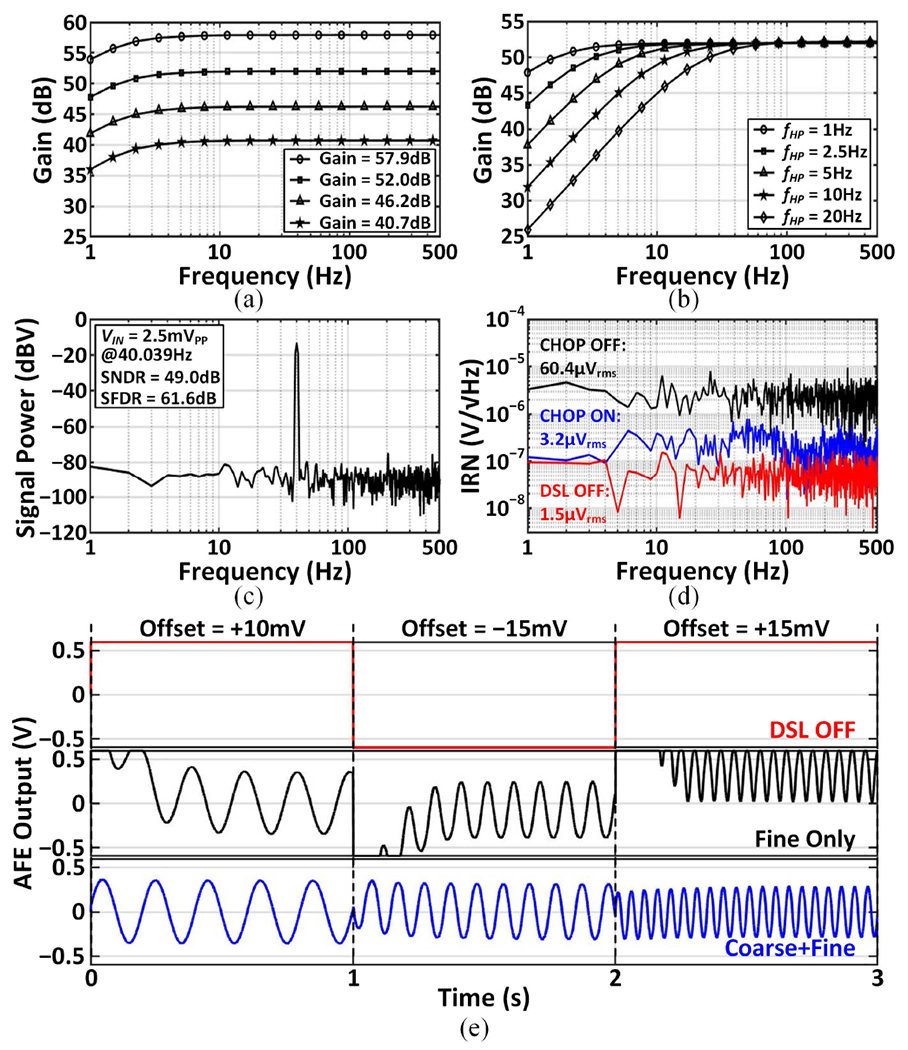
Measured AFE performance: (a) programmable gain, (b) programmable high-pass pole, (c) output power spectral density with a single-tone input, (d) input-referred noise spectral density, and (e) two-step fast-settling DSL operation in the presence of abrupt offset changes over three successive 1s windows.
B. Stimulator Characterization
The stimulator occupies a small area of 0.05mm2/channel, which is 4× and 7× more compact than the stacked architectures in [15] and [65], respectively. Figs. 16(a)–(c) present biphasic stimulation current outputs with different parameters, measured using a 6kΩ+330nF load. Each channel can generate moderate currents ranging from 65μA to 600μA. With a 640kHz input clock, the pulse width and frequency are programmable within 9.375μs–203.125μs and 9.6Hz–53.3kHz, respectively. The range of these parameters can be adjusted with a variable input clock depending on stimulation needs. The stimulator output measured in vitro using custom electrodes is presented in Fig. 16(d). Under the maximum load current condition, the charge mismatch between the anodic and cathodic phases was measured to be <0.1%.
Fig. 16.
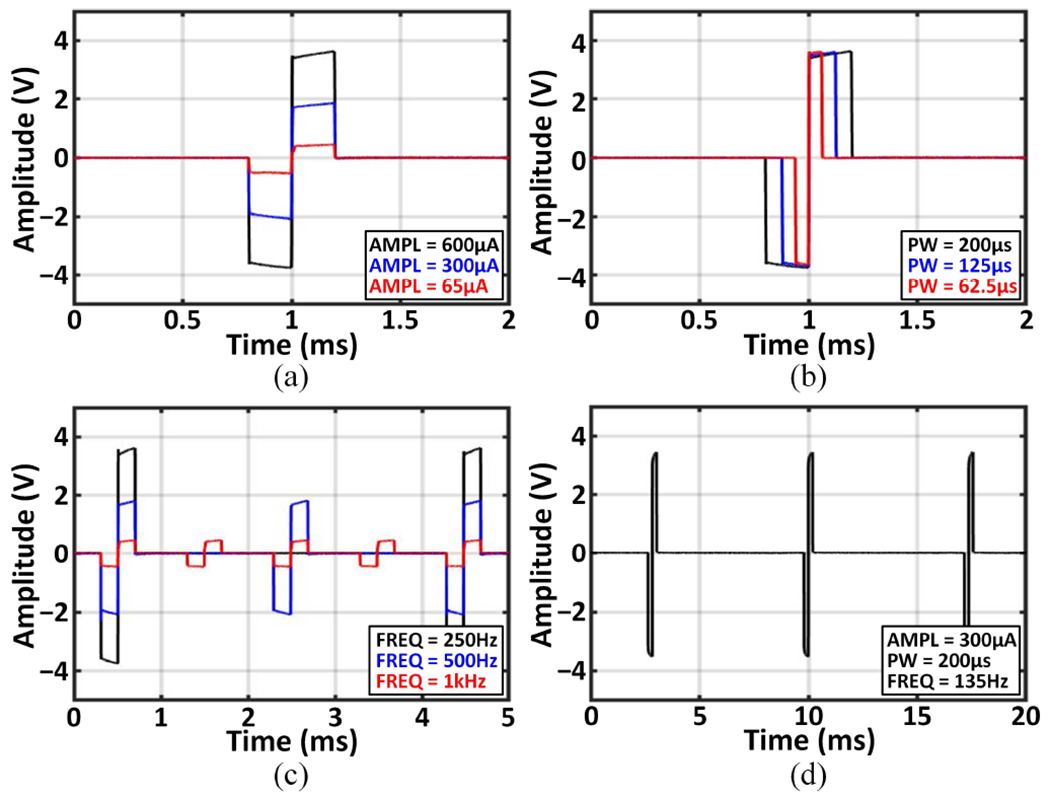
Biphasic outputs of the neurostimulator: (a) programmable current amplitude, (b) pulse width, (c) frequency, and (d) in-vitro measured output.
C. In-vivo Measurements
The neural recording and biomarker extraction capabilities of the SoC were validated in vivo in the experimental setup shown in Fig. 17(a). The animal experiments were performed with the approval of all experimental and ethical protocols and regulations granted by the Veterinary Office of the Canton of Geneva, Switzerland, under License No. GE/33A (33223). All procedures were in accordance with the Regulations of the Animal Welfare Act (SR 455) and Animal Welfare Ordinance (SR 455.1). We implanted two 15-channel 200μm-diameter soft μECoG arrays, shown in Fig. 17(b), into the somatosensory cortex of a Lewis rat. The μECoG arrays were fabricated using an e-dura technology with gold thin films [69]. Pentylenetetrazol (20mg) was injected intraperitoneally to the anesthetized rat to induce seizures [70]. Figs. 17(c) and (d) present ECoG recordings and neural biomarkers in a normal and seizure state, respectively. Prominent increases in temporal and spectral biomarkers at the seizure onset and strong cross-channel phase synchronization were observed during a seizure event in a short acute recording session. In future work, the real-time seizure detection capability of the SoC will be further validated in vivo with a collection of sufficient seizure activity and objective seizure annotation.
Fig. 17.
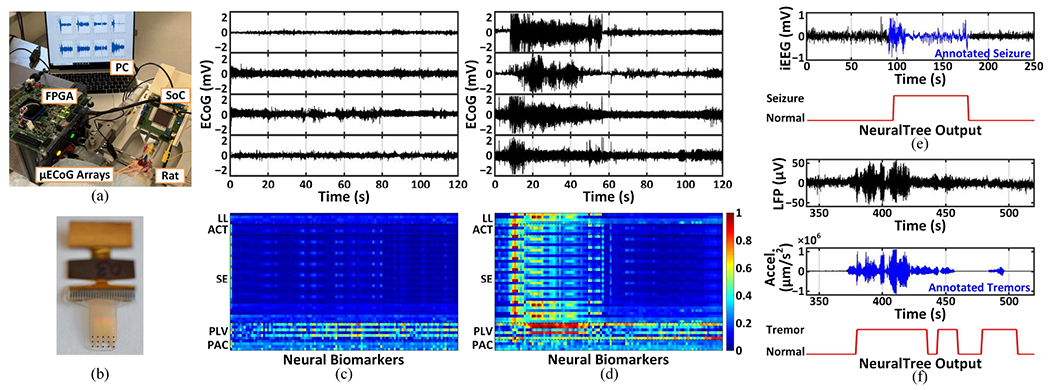
The SoC validation on a rat model of epilepsy and human datasets: (a) the experimental setup for in-vivo testing, (b) a 15-channel soft μECoG array with a flexible cable, (c) ECoG recordings and neural biomarker extraction in a normal state, (d) ECoG recordings and neural biomarker extraction in a seizure state, (e) epileptic seizure detection from iEEG, and (f) Parkinsonian tremor detection from LFPs.
D. Epileptic Seizure Detection
The classification performance of the SoC was validated on the CHB-MIT EEG [71] and iEEG.org [27] datasets of epileptic patients. We analyzed 983-hour EEG recordings of 24 patients and 596-hour iEEG recordings of 6 patients, which contain 176 and 49 annotated seizures, respectively. Blockwise data partitioning was used to avoid data leakage from training to inference [16]. We performed 5-fold cross-validation for most patients and adopted a leave-one-out approach for patients with fewer than 5 seizures. The number of correctly detected seizures was counted to assess the sensitivity, while the specificity was calculated based on the window-based true negative rate averaged over multiple runs.
In training mode, each patient’s multi-channel neural data (18–28 EEG and 47–108 iEEG channels) were fed to the AFE. The digitized AFE outputs were processed offline to extract features using a bit-accurate FEE model in MATLAB for training the classifier. The trained NeuralTree parameters were then stored in the on-chip memory for inference, and the NeuralTree performance on the test data was evaluated. The SoC achieved 95.6%/94% sensitivity and 96.8%/96.9% specificity on the EEG and iEEG datasets, respectively. The SoC’s seizure detection performance on an epileptic patient is demonstrated in Fig. 17(e).
E. Parkinsonian Tremor Detection
The SoC’s performance was further validated on a PD patient with rest-state tremor recruited by the University of Oxford [8]. A 4-channel DBS lead was implanted into the subthalamic nucleus to collect LFps, while the acceleration of the contralateral limb was used to label the tremor. Window-based true positive and negative rates were used to assess the sensitivity and specificity, respectively, using 5-fold cross-validation. The SoC achieved 82.6% sensitivity and 78.4% specificity. Fig. 17(f) presents an example of the SoC’s tremor detection performance, where tremor states with inconspicuous neural activity were successfully detected by the NeuralTree. To the best of our knowledge, this is the first demonstration of PD tremor detection with an on-chip classifier.
F. Comparison with the State-of-the-Art
Table II compares the proposed SoC with the state-of-the-art seizure detection SoCs with on-chip ML. The 256-channel SoC achieves an 8× improvement in channel count, 9.3× in per-channel area, and 4.3× in system energy efficiency over the state-of-the-art. The compressed NeuralTree takes up 2.93kB out of the 3.17kB on-chip memory, enabling more efficient memory utilization than SVM classifiers [5], [17], [19], [20], [22]. For instance, the recent SVM classifier in [22] utilized 70kB of memory to store 256 support vectors for 16 channels. The proposed SoC achieves better multi-channel scalability than previous DT-based SoCs [16], [18] thanks to the end-to-end TDM implementation. Moreover, the SoC integrates the broadest range of neural biomarkers reported so far to provide greater flexibility for multiple neural classification tasks. In this work, the classification performance on human datasets was validated using the entire system including the AFE. Furthermore, the NeuralTree was trained on all neural channels without any pre-selection. Such aspects should be considered when comparing the classification performance of different SoCs.
TABLE II.
Comparison with the State-of-the-Art Neural Interface SoCs with On-Chip ML
| Parameter | JSSC’15 [5] | JSSC’18 [15] | JETCAS’18 [16] | ISSCC’18 [17] | ISSCC’20 [18] | JSSC’20 [19] | TBioCAS’21 [20] | VLSI’21 [21] | JSSC’22 [22] | This Work | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Process (nm) | 180 | 180 | 65 | 130 | 65 | 40 | 180 | 28 | 40 | 65 | ||
| Supply Voltage (V) | 1.8/1 | 1.8 | 0.8 | 1.2 | 1.2 | 0.58 | 1.5 | 0.5 | 1.1/0.7 | 1.2 | ||
| # Recording Ch. | 16 | 16 | 32^ | 32 | 8 | 14^ | 8 | 8^ | 16 | 256 | ||
| # Stimulation Ch. | 1 | 16 | - | 32 | 1 | - | 2 | - | 1 | 16 | ||
| Area/ch.* (mm2) | 1.563 | 0.95 | 0.031^ | 0.237 | 0.244 | 0.182^ | 0.729 | 0.013^ | 0.13 | 0.014 | ||
| Energy Efficiency (μJ/class) | 2.73 | 64§ | 0.0412^ | 178.7§ | 0.036^ | 170.9^ | 174.4§ | 0.0015^ | 0.97 | 0.227 | ||
| Memory (kB) | 64† | - | 1 | 96† | - | 35.8† | 64 | 0.2 | 134† | 3.17‡ | ||
| Classifier | D2A-LSVM | Ridge Regression | XGB-DT | EDM-SVM | BrainForest | NL-SVM | Coarse (Th.) Fine (LS-SVM) | LR + SGD | GTCA-SVM | NeuralTree | ||
| Feature Set | SE | FFT, ApEn | LL, POW, VAR, SE | PLV, CFC, SE | RAF Neurons | SE | MODWT-KDE | SE, LL | SE | PLV, PAC, SE, HFOR, LL, LMP, Hjorth | ||
| Dataset (# Patients) | MIT (14) | Local (5) | iEEG (20) | EU-iEEG (-) | EU-iEEG (-) | MIT (24) | MIT (23) | UoM (3) | MIT (24) | MIT (24) | MIT (24) | iEEG(6) |
| Sensitivity (%) | 95.7 | 96 | 83.7 | 100 | 96.7 | 96.6 | 97.8 | 97.9 | 97.5 | 100 | 95.6 | 94 |
| Specificity (%) | 98 | 100 | 88.1 | 0.81FP/hr | 0.8FP/hr | 0.28FP/hr | 99.7 | 98.2 | 98.2 | 99.5 | 96.8 | 96.9 |
| Latency (s) | 1 | 0.76 | 1.1 | <0.1 | - | 0.71 | <0.3 | 2.6 | 1.6 | 0.74 | <1 | |
Estimated based on SoC area and # of recording channels
Including data storage
Digital back-end only
NeuralTree (2.93kB), FIR (0.2kB), and SPI (0.04kB)
Estimated based on AFE and DBE power consumption
VII. Conclusion
To pave the way towards next-generation closed-loop neural interfaces, this article presented a highly scalable, versatile neural activity classification and closed-loop neuromodulation SoC integrating an area-efficient dynamically addressable 256-channel mixed-signal front-end, multi-symptom biomarker extraction, an energy-aware NeuralTree classifier, and a 16-channel HV compliant neurostimulator. A channel-selective inference scheme was introduced to overcome the limited scalability and low hardware efficiency of existing SoCs. Through aggressive system-level time-division multiplexing and energy-efficient circuit-algorithm co-design, the proposed 256-channel SoC achieved the highest level of integration reported so far, as well as the highest energy and area efficiency. The versatility of the SoC was demonstrated using human epilepsy and Parkinson’s datasets with multiple signal modalities (EEG, iEEG, and LFP). This high-channel-count SoC with the multi-class NeuralTree model can be further used for motor intention decoding in prosthetic BMIs.
Acknowledgment
The authors acknowledge Ivan Furfaro for his contribution to the in-vivo experimental setup. This work was partially supported by the National Institute of Mental Health Grant R01-MH-123634, Swiss State Secretariat for Education, Research and Innovation (SERI) contract SCR0548363, and fundings from EPFL and Cornell University.
Biographies

Uisub Shin (Student Member, IEEE) received the B.E. degree in Electronics Engineering from Chungnam National University, Daejeon, South Korea, and the M.S. degree in Electrical Engineering from Korea Advanced Institute of Science and Technology (KAIST), Daejeon, South Korea, both with the highest honors in 2015 and 2017, respectively. Since 2018, he has been pursuing the Ph.D. degree in Electrical and Computer Engineering at Cornell University, Ithaca, NY, USA. He is currently at Swiss Federal Institute of Technology Lausanne (EPFL), Geneva, Switzerland, as a visiting Ph.D. student.
Uisub is a recipient of the 5-year Kwanjeong Educational Foundation Scholarship. His research interests lie in the design of low-power analog/mixed-signal and digital ICs, machine learning SoCs, and signal processing for biomedical applications.

Cong Ding (Student Member, IEEE) received the B.E. and M.S. degrees in Microelectronics from the University of Electronic Science and Technology of China, Sichuan, China, and Tsinghua University, Beijing, China, in 2017 and 2020, respectively. Since 2021, she has been working toward the Ph.D. degree in Electrical Engineering with Swiss Federal Institute of Technology, Lausanne, Switzerland.
Her research interests include low-power analog and RF circuit design for biomedical applications.

Bingzhao Zhu (Student Member, IEEE) received the B.Sc. degree in Opto-Electronics Science and Engineering from Zhejiang University, Hangzhou, China, in 2017. He is currently pursuing the Ph.D. degree in Applied and Engineering Physics and a minor in Computer Science, at Cornell University, Ithaca, New York, USA. Since 2020, he is a visiting PhD student at Swiss Federal Institute of Technology (EPFL), Geneva, Switzerland. His research interests include brain-computer interfaces (BCI), low-power machine learning, neural signal processing, and computational imaging.

Yashwanth Vyza received the B.Tech degree in electronics and instrumentation engineering from the National Institute of Technology (NIT), Rourkela, India, in 2017, and the M.Sc. degree in electrical engineering with a specialization in microelectronics from Technische Universiteit Delft (TU Delft), The Netherlands, in 2019. He is currently pursuing the Ph.D. degree with the Laboratory for Soft Bioelectronic Interfaces, Neuro-X Institute at the Ecole Polytechnique Fdrale de Lausanne (EPFL), Lausanne, Switzerland.
His research interests are toward hybrid integration and packaging of active electronics such as CMOS-based ASICs and wireless systems into soft, flexible, and stretchable implantable bioelectronics for translational applications.

Alix Trouillet received the B.S. degree in biochemistry from the University of Cergy-Pontoise, Cergy, France, in 2006, the M.S. degree in pathophysiology from Pierre et Marie Curie University (UPMC), Paris 6, Paris, France, in 2008, and the Ph.D. degree in neuroscience from University of Paris 6, Paris, working on retinal degenerative diseases with the Vision Institute, Paris, in 2014.
From 2015 to 2018, she was a Post-Doctoral Fellow with the Department of Otolaryngology, Stanford University, Stanford, CA, USA, working on the pathophysiology of mechanotransduction in models of deafness. In 2019, she joined the Laboratory of Soft Bioelectronic Interfaces, EPFL, Geneva, Switzerland, where she is currently a Research Scientist. Her work includes translational study toward the development of a new auditory brainstem implant to restore hearing and fundamental research in sensory restoration in rodents using cortical stimulation.

Emilie C. M. Revol (Student Member, IEEE) received the B.Sc. degree in life sciences and the M.S. degree in bioengineering with a minor in neuroprosthetics from the Ecole Polytechnique Federale de Lausanne (EPFL), Lausanne, Switzerland in 2016 and 2019, respectively. She is currently pursuing a Ph.D. degree within the Laboratory for Soft Bioelectronic Interfaces at the Neuro-X Institute of EPFL, Geneva, Switzerland. Her main research interests lie at the interface between engineering and neurosciences: implant design for cortical recording and modulation in various physiological phenomena, including auditory activity and spreading depolarizations in various animal models.

Stéphanie P. Lacour (Member, IEEE) received the Ph.D. degree in electrical engineering from the INSA de Lyon, Villeurbanne, France, in 2001. She completed Post-Doctoral Research at Princeton University, Princeton, NJ, USA, and the University of Cambridge, Cambridge, U.K. She joined the Ecole Polytechnique Fdrale de Lausanne (EPFL), Lausanne, Switzerland, in 2011. She holds the Bertarelli Foundation Chair in neuroprosthetic technology with the School of Engineering, EPFL. She is the director of EPFL interdisciplinary Neuro-X institute.
Dr. Lacour was a recipient of the 2006 MIT TR35, the ERC StG in 2011, and the SNSF ERC CG in 2016, and was nominated as a 2015 Young Global Leader by the World Economic Forum.

Mahsa Shoaran (Member, IEEE) received the B.Sc. and M.Sc. degrees from Sharif University of Technology in 2008 and 2010, respectively, and the Ph.D. degree in Electrical Engineering from Swiss Federal Institute of Technology (EPFL) in 2015. She was a Postdoctoral Fellow at the California Institute of Technology from 2015 to 2017. She is currently an Assistant Professor in the Institute of Electrical and Micro Engineering and Center for Neuroprosthetics of EPFL and director of the Integrated Neurotechnologies Laboratory. From 2017 to 2019, she was an Assistant Professor at the School of Electrical and Computer Engineering at Cornell University, Ithaca, NY. Mahsa is a recipient of the 2021 ERC Starting Grant, 2018 Google AI Faculty Research Award, and two Swiss NSF Postdoctoral Fellowships. She was named a Rising Star in EECS by MIT in 2015. Her research interests include low-power mixed-signal IC design for neural interfaces, machine learning SoCs, and neuromodulation therapies for neurological disorders. Dr. Shoaran serves on the Technical Program Committee of the IEEE ISSCC and CICC, the ISSCC SRP committee, and as chair in BioMedical Electronics for the IEEE International Conference on Electronics Circuits and Systems (ICECS).
Contributor Information
Uisub Shin, Institute of Electrical and Micro Engineering, EPFL, 1202 Geneva, Switzerland, and the School of Electrical and Computer Engineering, Cornell University, Ithaca, NY 14853, USA.
Cong Ding, Institute of Electrical and Micro Engineering and Center for Neuroprosthetics, EPFL, 1202 Geneva, Switzerland.
Bingzhao Zhu, Institute of Electrical and Micro Engineering, EPFL, 1202 Geneva, Switzerland, and the School of Applied and Engineering Physics, Cornell University, Ithaca, NY 14853, USA.
Yashwanth Vyza, Institute of Electrical and Micro Engineering and Center for Neuroprosthetics, EPFL, 1202 Geneva, Switzerland.
Alix Trouillet, Institute of Electrical and Micro Engineering and Center for Neuroprosthetics, EPFL, 1202 Geneva, Switzerland.
Emilie C. M. Revol, Institute of Electrical and Micro Engineering and Center for Neuroprosthetics, EPFL, 1202 Geneva, Switzerland.
Stéphanie P. Lacour, Institute of Electrical and Micro Engineering and Center for Neuroprosthetics, EPFL, 1202 Geneva, Switzerland.
Mahsa Shoaran, Institute of Electrical and Micro Engineering and Center for Neuroprosthetics, EPFL, 1202 Geneva, Switzerland.
References
- [1].Feigin VL et al. “Global, regional, and national burden of neurological disorders during 1990–2015: A systematic analysis for the global burden of disease study 2015,” The Lancet Neurology, vol. 16, no. 11, pp. 877–897, Nov. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Skarpaas TL and Morrell MJ, “Intracranial stimulation therapy for epilepsy,” Neurotherapeutics, vol. 6, no. 2, pp. 238–243, Apr. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Meidahl AC, Tinkhauser G, Herz DM, Cagnan H, Debarros J, and Brown P, “Adaptive deep brain stimulation for movement disorders: The long road to clinical therapy,” Movement disorders, vol. 32, no. 6, pp. 810–819, Jun. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zhu B, Shin U, and Shoaran M, “Closed-loop neural prostheses with on-chip intelligence: A review and a low-latency machine learning model for brain state detection,” IEEE Transactions on Biomedical Circuits and Systems, vol. 15, no. 5, pp. 877–897, Oct. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Altaf MAB, Zhang C, and Yoo J, “A 16-channel patient-specific seizure onset and termination detection SoC with impedance-adaptive transcranial electrical stimulator,” IEEE Journal of Solid-State Circuits, vol. 50, no. 11, pp. 2728–2740, Oct. 2015. [Google Scholar]
- [6].Shoaran M et al. “A 16-channel 1.1mm2 implantable seizure control SoC with sub-μW/channel consumption and closed-loop stimulation in 0.18μm CMOS,” in 2016 IEEE Symposium on VLSI Circuits (VLSI-Circuits). IEEE, Jun. 2016, pp. 1–2. [Google Scholar]
- [7].Shoeb AH, “Application of machine learning to epileptic seizure onset detection and treatment,” Ph.D. dissertation, Massachusetts Institute of Technology, 2009. [Google Scholar]
- [8].Yao L, Brown P, and Shoaran M, “Improved detection of Parkinsonian resting tremor with feature engineering and Kalman filtering,” Clinical Neurophysiology, vol. 131, no. 1, pp. 274–284, Jan. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Sani OG, Yang Y, Lee MB, Dawes HE, Chang EF, and Shanechi MM, “Mood variations decoded from multi-site intracranial human brain activity,” Nature biotechnology, vol. 36, no. 10, pp. 954–961, Nov. 2018. [DOI] [PubMed] [Google Scholar]
- [10].Zhu B, Coppola G, and Shoaran M, “Migraine classification using somatosensory evoked potentials,” Cephalalgia, vol. 39, no. 9, pp. 1143–1155, Aug. 2019. [DOI] [PubMed] [Google Scholar]
- [11].Taufique Z, Zhu B, Coppola G, Shoaran M, and Altaf MAB, “A low power multi-class migraine detection processor based on somatosensory evoked potentials,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 68, no. 5, pp. 1720–1724, Mar. 2021. [Google Scholar]
- [12].Ezzyat Y et al. “Closed-loop stimulation of temporal cortex rescues functional networks and improves memory,” Nature communications, vol. 9, no. 1, pp. 1–8, Feb. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Xie Z, Schwartz O, and Prasad A, “Decoding of finger trajectory from ECoG using deep learning,” Journal of neural engineering, vol. 15, no. 3, p. 036009, Feb. 2018. [DOI] [PubMed] [Google Scholar]
- [14].Yao L, Zhu B, and Shoaran M, “Fast and accurate decoding of finger movements from ECoG through Riemannian features and modern machine learning techniques,” Journal of Neural Engineering, vol. 19, no. 1, p. 016037, Feb. 2022. [DOI] [PubMed] [Google Scholar]
- [15].Cheng C-H et al. “A fully integrated 16-channel closed-loop neural-prosthetic CMOS SoC with wireless power and bidirectional data telemetry for real-time efficient human epileptic seizure control,” IEEE Journal of Solid-State Circuits, vol. 53, no. 11, pp. 3314–3326, Sep. 2018. [Google Scholar]
- [16].Shoaran M, Haghi BA, Taghavi M, Farivar M, and Emami-Neyestanak A, “Energy-efficient classification for resource-constrained biomedical applications,” IEEE Journal on Emerging and Selected Topics in Circuits and Systems, vol. 8, no. 4, pp. 693–707, Jun. 2018. [Google Scholar]
- [17].O’Leary G et al. “A recursive-memory brain-state classifier with 32-channel track-and-zoom Δ2Σ ADCs and charge-balanced programmable waveform neurostimulators,” in 2018 IEEE International Solid-State Circuits Conference-(ISSCC). IEEE, Feb. 2018, pp. 296–298. [Google Scholar]
- [18].O’Leary G et al. “A neuromorphic multiplier-less bit-serial weight-memory-optimized 1024-tree brain-state classifier and neuromodulation SoC with an 8-channel noise-shaping SAR ADC array,” in 2020 IEEE International Solid-State Circuits Conference-(ISSCC). IEEE, Feb. 2020, pp. 402–404. [Google Scholar]
- [19].Huang S-A, Chang K-C, Liou H-H, and Yang C-H, “A 1.9mW SVM processor with on-chip active learning for epileptic seizure control,” IEEE Journal of Solid-State Circuits, vol. 55, no. 2, pp. 452–464, Dec. 2019. [Google Scholar]
- [20].Wang Y et al. “A closed-loop neuromodulation chipset with 2-level classification achieving 1.5-Vpp CM interference tolerance, 35-dB stimulation artifact rejection in 0.5 ms and 97.8%-sensitivity seizure detection,” IEEE Transactions on Biomedical Circuits and Systems, vol. 15, no. 4, pp. 802–819, Aug. 2021. [DOI] [PubMed] [Google Scholar]
- [21].Chua A, Jordan MI, and Muller R, “A 1.5 nJ/cls unsupervised online learning classifier for seizure detection,” in 2021 Symposium on VLSI Circuits. IEEE, Jun. 2021, pp. 1–2. [Google Scholar]
- [22].Zhang M, Zhang L, Tsai C-W, and Yoo J, “A patient-specific closed-loop epilepsy management SoC with one-shot learning and online tuning,” IEEE Journal of Solid-State Circuits, vol. 57, no. 4, pp. 1049–1060, Feb. 2022. [Google Scholar]
- [23].Chang EF, “Towards large-scale, human-based, mesoscopic neurotechnologies,” Neuron, vol. 86, no. 1, pp. 68–78, Apr. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Anderson DN, Osting B, Vorwerk J, Dorval AD, and Butson CR, “Optimized programming algorithm for cylindrical and directional deep brain stimulation electrodes,” Journal of neural engineering, vol. 15, no. 2, p. 026005, Jan. 2018. [DOI] [PubMed] [Google Scholar]
- [25].Kaiju T et al. “High spatiotemporal resolution ECoG recording of somatosensory evoked potentials with flexible micro-electrode arrays,” Frontiers in neural circuits, vol. 11, p. 20, Apr. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Shin U et al. “A 256-channel 0.227μJ/class versatile brain activity classification and closed-loop neuromodulation SoC with 0.004mm2-1.51μW/channel fast-settling highly multiplexed mixed-signal front-end,” in 2022 IEEE International Solid-State Circuits Conference (ISSCC), vol. 65. IEEE, Feb. 2022, pp. 338–340. [Google Scholar]
- [27].International Epilepsy Electrophysiology Portal. [Online]. Available: http://www.ieeg.org/ [Google Scholar]
- [28].Cogan SF, “Neural stimulation and recording electrodes,” Annu. Rev. Biomed. Eng, vol. 10, pp. 275–309, Aug. 2008. [DOI] [PubMed] [Google Scholar]
- [29].Muller R, Gambini S, and Rabaey JM, “A 0.013 mm2, 5 μW, DC-coupled neural signal acquisition IC with 0.5 V supply,” IEEE Journal of Solid-State Circuits, vol. 47, no. 1, pp. 232–243, Sep. 2011. [Google Scholar]
- [30].Sharma M, Strathman HJ, and Walker RM, “Verification of a rapidly multiplexed circuit for scalable action potential recording,” IEEE transactions on biomedical circuits and systems, vol. 13, no. 6, pp. 1655–1663, Dec. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Uehlin JP, Smith WA, Pamula VR, Perlmutter SI, Rudell JC, and Sathe VS, “A 0.0023 mm2/ch. delta-encoded, time-division multiplexed mixed-signal ECoG recording architecture with stimulus artifact suppression,” IEEE Transactions on Biomedical Circuits and Systems, vol. 14, no. 2, pp. 319–331, Dec. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Fathy NSK, Huang J, and Mercier PP, “A digitally assisted multiplexed neural recording system with dynamic electrode offset cancellation via an lms interference-canceling filter,” IEEE Journal of Solid-State Circuits, vol. 57, no. 3, pp. 953–964, Mar. 2022. [Google Scholar]
- [33].Muller R et al. “A minimally invasive 64-channel wireless μECoG implant,” IEEE Journal of Solid-State Circuits, vol. 50, no. 1, pp. 344–359, Nov. 2014. [Google Scholar]
- [34].Song S et al. “A 430nW 64nV/vHz current-reuse telescopic amplifier for neural recording applications,” in 2013 IEEE Biomedical Circuits and Systems Conference (BioCAS). IEEE, Oct. 2013, pp. 322–325. [Google Scholar]
- [35].Xu G and Yuan J, “Comparison of charge sampling and voltage sampling,” in Proceedings of the 43rd IEEE Midwest Symposium on Circuits and Systems (Cat. No. CH37144), vol. 1. IEEE, Aug. 2000, pp. 440–443. [Google Scholar]
- [36].Mirzaei A, Chehrazi S, Bagheri R, and Abidi AA, “Analysis of first-order anti-aliasing integration sampler,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 55, no. 10, pp. 2994–3005, Apr. 2008. [Google Scholar]
- [37].Chandrakumar H and Marković D, “An 80-mVpp linear-input range, 1.6-GΩ input impedance, low-power chopper amplifier for closed-loop neural recording that is tolerant to 650-mVpp common-mode interference,” IEEE Journal of Solid-State Circuits, vol. 52, no. 11, pp. 2811–2828, Oct. 2017. [Google Scholar]
- [38].Heer F et al. “Single-chip microelectronic system to interface with living cells,” Biosensors and Bioelectronics, vol. 22, no. 11, pp. 2546–2553, Oct. 2007. [DOI] [PubMed] [Google Scholar]
- [39].Liu C-C, Chang S-J, Huang G-Y, and Lin Y-Z, “A 10-bit 50-MS/s SAR ADC with a monotonic capacitor switching procedure,” IEEE Journal of Solid-State Circuits, vol. 45, no. 4, pp. 731–740, Mar. 2010. [Google Scholar]
- [40].Harpe PJ et al. “A 26 μW 8 bit 10 MS/s asynchronous SAR ADC for low energy radios,” IEEE Journal of Solid-State Circuits, vol. 46, no. 7, pp. 1585–1595, May 2011. [Google Scholar]
- [41].Esteller R, Echauz J, Tcheng T, Litt B, and Pless B, “Line length: An efficient feature for seizure onset detection,” in 2001 Conference Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, vol. 2. IEEE, Oct. 2001, pp. 1707–1710. [Google Scholar]
- [42].Zhu B, Farivar M, and Shoaran M, “ResOT: Resource-efficient oblique trees for neural signal classification,” IEEE Transactions on Biomedical Circuits and Systems, vol. 14, no. 4, pp. 692–704, Jun. 2020. [DOI] [PubMed] [Google Scholar]
- [43].Shafiul Hasan S, Siddiquee MR, Atri R, Ramon R, Marquez JS, and Bai O, “Prediction of gait intention from pre-movement EEG signals: A feasibility study,” Journal of NeuroEngineering and Rehabilitation, vol. 17, no. 1, pp. 1–16, Dec. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Hjorth B, “EEG analysis based on time domain properties,” Electroencephalography and clinical neurophysiology, vol. 29, no. 3, pp. 306–310, Sep. 1970. [DOI] [PubMed] [Google Scholar]
- [45].Goncharova II and Barlow JS, “Changes in EEG mean frequency and spectral purity during spontaneous alpha blocking,” Electroencephalography and clinical neurophysiology, vol. 76, no. 3, pp. 197–204, Sep. 1990. [DOI] [PubMed] [Google Scholar]
- [46].Stavisky SD, Kao JC, Nuyujukian P, Ryu SI, and Shenoy KV, “A high performing brain–machine interface driven by low-frequency local field potentials alone and together with spikes,” Journal of neural engineering, vol. 12, no. 3, p. 036009, May 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Yao L, Brown P, and Shoaran M, “Resting tremor detection in Parkinson’s disease with machine learning and Kalman filtering,” in 2018 IEEE Biomedical Circuits and Systems Conference (BioCAS). IEEE, Oct. 2018, pp. 1–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].So K, Dangi S, Orsborn AL, Gastpar MC, and Carmena JM, “Subject-specific modulation of local field potential spectral power during brain–machine interface control in primates,” Journal of neural engineering, vol. 11, no. 2, p. 026002, Feb. 2014. [DOI] [PubMed] [Google Scholar]
- [49].Özkurt TE et al. “High frequency oscillations in the subthalamic nucleus: A neurophysiological marker of the motor state in Parkinson’s disease,” Experimental neurology, vol. 229, no. 2, pp. 324–331, Jun. 2011. [DOI] [PubMed] [Google Scholar]
- [50].Jacobs J et al. “High-frequency oscillations (HFOs) in clinical epilepsy,” Progress in neurobiology, vol. 98, no. 3, pp. 302–315, Sep. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Hirschmann J et al. “Parkinsonian rest tremor is associated with modulations of subthalamic high-frequency oscillations,” Movement Disorders, vol. 31, no. 10, pp. 1551–1559, Oct. 2016. [DOI] [PubMed] [Google Scholar]
- [52].Mormann F, Lehnertz K, David P, and Elger CE, “Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients,” Physica D: Nonlinear Phenomena, vol. 144, no. 3-4, pp. 358–369, Oct. 2000. [Google Scholar]
- [53].Canolty RT and Knight RT, “The functional role of cross-frequency coupling,” Trends in cognitive sciences, vol. 14, no. 11, pp. 506–515, Nov. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Guirgis M, Chinvarun Y, Carlen PL, and Bardakjian BL, “The role of delta-modulated high frequency oscillations in seizure state classification,” in 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE, Jul. 2013, pp. 6595–6598. [DOI] [PubMed] [Google Scholar]
- [55].De Hemptinne C et al. “Exaggerated phase–amplitude coupling in the primary motor cortex in Parkinson disease,” Proceedings of the National Academy of Sciences, vol. 110, no. 12, pp. 4780–4785, Mar. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Olbrich S, Tränkner A, Chittka T, Hegerl U, and Schönknecht P, “Functional connectivity in major depression: Increased phase synchronization between frontal cortical EEG-source estimates,” Psychiatry Research: Neuroimaging, vol. 222, no. 1-2, pp. 91–99, Apr. 2014. [DOI] [PubMed] [Google Scholar]
- [57].Abdelhalim K, Jafari HM, Kokarovtseva L, Velazquez JLP, and Genov R, “64-channel UWB wireless neural vector analyzer SoC with a closed-loop phase synchrony-triggered neurostimulator,” IEEE Journal of Solid-State Circuits, vol. 48, no. 10, pp. 2494–2510, Jul. 2013. [Google Scholar]
- [58].Rajan S, Wang S, Inkol R, and Joyal A, “Efficient approximations for the arctangent function,” IEEE Signal Processing Magazine, vol. 23, no. 3, pp. 108–111, May 2006. [Google Scholar]
- [59].Shin U, Ding C, Somappa L, Woods V, Widge AS, and Shoaran M, “A 16-channel 60μW neural synchrony processor for multi-mode phase-locked neurostimulation,” in 2022 IEEE Custom Integrated Circuits Conference (CICC). IEEE, Apr. 2022, pp. 1–2. [Google Scholar]
- [60].Yoo J and Shoaran M, “Neural interface systems with on-device computing: Machine learning and neuromorphic architectures,” Current opinion in biotechnology, vol. 72, pp. 95–101, Dec. 2021. [DOI] [PubMed] [Google Scholar]
- [61].Zhu B, Taghavi M, and Shoaran M, “Cost-efficient classification for neurological disease detection,” in 2019 IEEE Biomedical Circuits and Systems Conference (BioCAS). IEEE, Oct. 2019, pp. 1–4. [Google Scholar]
- [62].Abadi M et al. “TensorFlow: A system for large-scale machine learning,” in 12th USENIX symposium on operating systems design and implementation (OSDI 16), Nov. 2016, pp. 265–283. [Google Scholar]
- [63].Kingma DP and Ba J, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, Dec. 2014. [Google Scholar]
- [64].Miller KJ et al. “Human motor cortical activity is selectively phase-entrained on underlying rhythms,” PLOS Computational Biology, vol. 8, no. 9, p. e1002655, Sep. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Uehlin JP et al. “A single-chip bidirectional neural interface with high-voltage stimulation and adaptive artifact cancellation in standard CMOS,” IEEE Journal of Solid-State Circuits, vol. 55, no. 7, pp. 1749–1761, May 2020. [Google Scholar]
- [66].Van Breussegem T and Steyaert M, “A 82% efficiency 0.5% ripple 16-phase fully integrated capacitive voltage doubler,” in 2009 Symposium on VLSI Circuits. IEEE, Jun. 2009, pp. 198–199. [Google Scholar]
- [67].Noorsal E, Sooksood K, Xu H, Hornig R, Becker J, and Ortmanns M, “A neural stimulator frontend with high-voltage compliance and programmable pulse shape for epiretinal implants,” IEEE Journal of Solid-State Circuits, vol. 47, no. 1, pp. 244–256, Sep. 2011. [Google Scholar]
- [68].Fan Q, Sebastiano F, Huijsing JH, and Makinwa KA, “A 1.8 μW 60 nV/√Hz capacitively-coupled chopper instrumentation amplifier in 65 nm CMOS for wireless sensor nodes,” IEEE Journal of Solid-State Circuits, vol. 46, no. 7, pp. 1534–1543, May 2011. [Google Scholar]
- [69].Minev IR et al. “Electronic dura mater for long-term multimodal neural interfaces,” Science, vol. 347, no. 6218, pp. 159–163, Jan. 2015. [DOI] [PubMed] [Google Scholar]
- [70].Velisek L, Kubova H, Pohl M, Stankova L, Mareš P, and Schickerova R, “Pentylenetetrazol-induced seizures in rats: An ontogenetic study,” Naunyn-Schmiedeberg’s archives of pharmacology, vol. 346, no. 5, pp. 588–591, Nov. 1992. [DOI] [PubMed] [Google Scholar]
- [71].Goldberger AL et al. “PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals,” Circulation, vol. 101, no. 23, pp. e215–e220, Jun. 2000. [DOI] [PubMed] [Google Scholar]


