Uncovering Sociological Effect Heterogeneity Using Tree-Based Machine Learning

Abstract

Individuals do not respond uniformly to treatments, such as events or interventions. Sociologists routinely partition samples into subgroups to explore how the effects of treatments vary by selected covariates, such as race and gender, on the basis of theoretical priors. Data-driven discoveries are also routine, yet the analyses by which sociologists typically go about them are often problematic and seldom move us beyond our biases to explore new meaningful subgroups. Emerging machine learning methods based on decision trees allow researchers to explore sources of variation that they may not have previously considered or envisaged. In this article, the authors use tree-based machine learning, that is, causal trees, to recursively partition the sample to uncover sources of effect heterogeneity. Assessing a central topic in social inequality, college effects on wages, the authors compare what is learned from covariate and propensity score–based partitioning approaches with recursive partitioning based on causal trees. Decision trees, although superseded by forests for estimation, can be used to uncover subpopulations responsive to treatments. Using observational data, the authors expand on the existing causal tree literature by applying leaf-specific effect estimation strategies to adjust for observed confounding, including inverse propensity weighting, nearest neighbor matching, and doubly robust causal forests. We also assess localized balance metrics and sensitivity analyses to address the possibility of differential imbalance and unobserved confounding. The authors encourage researchers to follow similar data exploration practices in their work on variation in sociological effects and offer a straightforward framework by which to do so.

Heterogeneity in response to life events and circumstances is common. Individuals differ both in pretreatment characteristics (i.e., pretreatment heterogeneity) and in how they respond to a common treatment, event, or intervention (i.e., treatment effect heterogeneity). Treatment effect heterogeneity has important implications for social research and policy. The study of effect heterogeneity can yield valuable insights into how scarce social resources are distributed in an unequal society (e.g., Brand 2010; Brand and Xie 2010; Heckman, Humphries, and Veramendi 2018; Heckman, Urzua, and Vytlacil 2006), how events differentially affect populations with different expectations of their occurrence (e.g., Brand et al. 2019; Brand and Simon Thomas 2014; Clark, Knabe, and Rätzel 2010; Turner 1995), and what factors may explain response heterogeneity, including differential selection (e.g., Heckman and Vytlacil 2007; Zhou and Xie 2019, 2020). We may want to identify the most responsive subgroups to determine which individuals benefit most from, or are most harmed by, a treatment. In some cases, the same disruptive event could have significant consequences for some populations but less or even no effect among others (Brand et al. 2019). If policymakers understand patterns of treatment effect heterogeneity, they can more optimally assign different treatments to balance competing objectives, such as reducing costs and maximizing outcomes for targeted groups (Athey and Imbens 2019; Davis and Heller 2017).

Sociologists routinely partition their samples into subgroups by individual characteristics to explore how the effects of events or interventions vary across the population. Researchers often, for example, assume that effects vary by race and gender and indicators of socioeconomic status, like education or income. Despite their ubiquity, such interactions may not represent the most meaningful variation in effects or the partitions that are most consequential for a relationship of interest. Indeed, many researchers report stratified estimates by gender or race when the differences between groups are not statistically or substantively significant. Long-standing theoretical priors, strong convention, and biases that one should examine differences by particular characteristics often drive these decisions. The practices researchers use to examine heterogeneity via stratified groups or interaction effects also regularly fail to consider the causal assumptions and possible differential selection processes underlying subpopulation differences in estimated effects. That is, differences in effects across subgroups could be due to differential response to treatment or due to differential selection on unobserved variables (Carvalho et al. 2019; Kaufman 2019). Social scientists interested in causal inference also explore how effects vary by the likelihood of selection into treatment, including stratified analyses by propensity score strata, nonparametric methods of effect variation by propensity scores, or exploring variation across different parameters of interest that indicate selection into treatment (Brand and Simon Thomas 2013; Heckman et al. 2006; Morgan and Winship 2014; Xie, Brand, and Jann 2012). These latter approaches encourage researchers to interpret effects on the basis of both observed and unobserved selection into treatment (Brand et al. 2019; Brand and Xie 2010; Heckman and Vytlacil 2007; Zhou and Xie 2019, 2020). In both covariate- and propensity score–based partitioning methods, however, analysts determine the key subgroups.

Empirical papers are written largely to suggest that decisions about which subgroups to explore occur before any data analyses. Indeed, much social scientific inquiry labors under the delusion that methods of discovery reflect conjectural inspiration. In actuality, it is often difficult to know ex ante the subgroups most responsive to events or interventions. Social scientists routinely explore their data, running tens or hundreds of regressions to determine if subgroups of potential interest show meaningful differences in effect estimates, and then proceed to selectively report the effect estimates of those that do (known as p-hacking).¹ Conventional tests of statistical significance, however, are performed conditional on a null distribution derived from a hypothesis defined ex ante. When a large number of tests are performed without multiple testing correction, or when hypotheses are not prespecified, this type of statistical inference is invalid. Likewise, if researchers select which interactions to report as a result of exploratory analyses, and do not draw on cross-validation procedures or multiple-testing adjustments, they are subject to incorrectly rejecting a correct null hypothesis. Such ad hoc searches for responsive subgroups may reflect noise within the data rather than true response variation. Studies have shown that p-hacking, along with selective publication, is a substantial problem leading to misleading conclusions (Brodeur, Cook, and Heyes 2020). Additionally, undocumented serendipitous manual specification search procedures lack transparency and reproducibility (Freese and Peterson 2017). Finally, covariates may be most informative when considered jointly, in complex and nonlinear ways (e.g., upper income white individuals with strong religious beliefs, rather than white individuals). It is generally unclear which of the large number of possible covariate thresholds and interactions are best to consider.

We argue for an alternative data-driven approach based on machine learning that will help uncover essential sources of effect heterogeneity and more transparently depict the analyses that lead to a focus on particular subgroups. Machine learning methods, that is, computational and statistical approaches to extracting patterns and trends from data, are rapidly and dramatically affecting social science methodology (see recent reviews by Athey 2019; Brand, Koch, and Xu 2020; Molina and Garip 2019). Data-driven machine learning enables researchers to be systematic in the model selection procedure and fully describe the process by which the model was selected, which enables reproducibility. These advantages will likely make supervised machine learning procedures an integral part of empirical sociological practice going forward.

Statisticians and social and computer scientists have recently made progress in merging machine learning methods and causal inference. Because the goal of accurate prediction of response variables (typical of machine learning) differs from the goal of obtaining unbiased estimates of causal effects, machine learning methods must be tailored to causal objectives. Recent work has adapted tree-based methods to explore sources of treatment effect variation. Decision trees are a widely used machine learning approach that recursively split the data into increasingly smaller subsets where data-points bear greater similarity (Brand et al. 2020). The resulting hierarchical data structure can be represented with a tree. These models are attractive for social science applications because they are simple to understand and interpret. “Causal trees,” introduced in Athey and Imbens (2015, 2016), are decision trees adapted to uncover treatment effect heterogeneity. They allow researchers to identify subpopulations that respond differently to treatments by searching over high-dimensional functions of covariates and their interactions. Analysts use this approach to uncover key subpopulations that they had not prespecified and that may or may not accord with conventional sociodemographic partitions and theoretical priors. This method benefits from ease of use and interpretability and can be an effective tool for sociological inquiry and discovery.

In this article, we focus on the utility of causal trees for uncovering treatment effect heterogeneity in observational data. We apply causal trees to a key topic in the social inequality literature, the distributional effects of college on low-wage work over the life-course. Within the causal tree and forest literatures, there are limited examples of how to effectively apply these algorithms to observational data of sociological relevance. We use three different approaches for adjusting for confounding and estimating effects within leaves of the causal tree: inverse propensity weighting (IPW), nearest neighbor matching, and mapping estimates from a doubly robust causal forest. In addition, we consider localized (i.e., partition-specific) propensity score imbalance and apply localized sensitivity analyses to explore the effect of differential unobserved confounding. Next, we explore what we learn from causal trees relative to more conventional techniques for identifying treatment effect heterogeneity, namely covariate and propensity-score stratified effects. In our case study, we conclude that conventional stratified analyses (or interactions) do not identify some of the most responsive, and theoretically interesting, subgroups highlighted by the causal tree. We encourage researchers to follow similar practices in their work on exploring variation in sociological effects using observational data, and we provide straightforward guidelines and data visualization techniques by which to do so.

UNCOVERING HETEROGENEOUS TREATMENT EFFECTS

Let us consider a setup with units i = 1, . . . n, a pretreatment covariate vector X_i, a response Y_i, and a binary treatment indicator W_i ∈ {0, 1}. We assume potential outcomes for each unit $\left(Y_i^0,Y_i^1\right)$ and define the unit-level treatment effect as

$${\tau }_i=Y_i^1-Y_i^0,$$ (1)

where we never observe both outcomes: W_i = 1 indicates that the unit received the treatment, and W_i = 0 that the unit received the control. Observational data are used to identify causal associations of social processes that are not easily subject to experimental manipulation. Using observational data, we invoke an “unconfoundedness” or “selection on observables” assumption that once we condition on X, there are no additional confounders between the treatment and the outcomes of interest (Imbens and Rubin 2015):

$$W_i\coprod \left(Y_i^1,Y_i^0\right)\mid X_i\text{.}$$ (2)

As it is generally infeasible to condition on X in a fully nonparametric way, methods for estimating treatment effects under unconfoundedness often entail treating nearby units in the x-space as matches for the target treated unit. One approach to determine nearby cases is to use the propensity score to approximate the assignment mechanism (Imbens and Rubin 2015). A propensity score is the probability of treatment conditional on a set of observed covariates:

$$e(x)=pr\left(W_i=1\mid X_i=x\right).$$ (3)

The propensity score provides a summary measure of estimated selection into treatment. Machine learning methods, including classification and regression trees (CART), neural networks, and random forests, have increasingly been used to estimate propensity scores (Lee, Lessler, and Stuart 2009; McCaffrey, Ridgeway, and Morral 2004; Westreich, Lessler, and Funk 2010). If we know e(x), we can estimate average treatment effects using methods such as IPW or propensity score matching.

Covariate and Propensity Score–Based Partitioning

Our goal is to identify how treatment effects vary across a population. Sociologists routinely use regression interaction terms or stratified analyses to explore subgroup variation by selected theoretically motivated covariates. Let us refer to this practice as covariate partitioning. We define a conditional average treatment effect (CATE) using covariate partitioning by the average difference in potential outcomes within prespecified subgroups:

$$\tau (x)=E\left[Y_i^1-Y_i^0\mid X_i=x\right].$$ (4)

Such analyses generally amount to an ad hoc partitioning of the sample on the basis of factors presumed to account for variation (e.g., race, socioeconomic status), or by post hoc interpretations if variation across groups is serendipitously found. An alternative approach to assess effect heterogeneity is to partition the sample into strata of the estimated propensity score to determine whether subpopulations with lower or higher estimated probabilities of treatment differ in their treatment effects (Brand and Simon Thomas 2013; Xie et al. 2012). We define a CATE using propensity score–based partitions as

$$\tau (e(x))=E\left[Y_i^1-Y_i^0\mid e\left(X_i\right)=e(x)\right].$$ (5)

Tree-Based Machine Learning

Machine learning is a computational and statistical approach to extracting patterns and trends from data (Brand et al. 2020). Supervised learning algorithms learn to predict response variables from covariates.² A supervised learning model is first trained in one data set and then evaluated in another. Model selection is dictated by a model’s ability to generalize to unseen data in this evaluation set. An overfit model fits too closely to the training data, explaining idiosyncratic patterns (i.e., noise) in those data but generalizing poorly to new data. Thus, a learning algorithm must be flexible enough to fit the training data, yet not so complex that variance is high when fit to new data. Regularization approaches (e.g., shrinkage penalties) can reduce overfitting and model complexity to improve generalization. During training, supervised learning algorithms optimize in-sample performance for a loss function (also called objective or cost function), often the mean squared error (MSE) for regression tasks. After training, researchers use evaluation metrics to assess out-of-sample predictive performance of the model.

Decision trees are among the most widely used supervised machine learning algorithms. Decision trees recursively partition the data along covariate thresholds into increasingly smaller subsets where data bear greater similarity (i.e., have a smaller variance, entropy, or Gini coefficient) (Breiman et al. 1984). A tree represents the resulting hierarchical data structure. At each decision, splits are chosen by selecting a covariate and threshold that minimize the in-sample loss function (e.g., the MSE) within the remaining subsample of data. Cross-validation is used to select hyperparameters (e.g., for pruning the depth of a tree) that maximize predictive power without overfitting the data. Decision trees are easy to understand and interpret because they are “white box” algorithms, yielding a visually interpretable decision process.

As with all algorithms, however, decision trees have disadvantages. At each partition decision, the tree optimizes the loss function conditional only on the current subset of data, rather than on the heterogeneity of the complete data set. Although computationally inexpensive, this “greedy” design choice means that trees are not guaranteed to find a globally optimal solution. Random forests build on the decision tree algorithm by averaging over a large number of decision trees (Breiman 2001; Ho 1995). Each decision tree in the forest is constructed not on the original sample but by repeatedly resampling training data with replacement and generating a consensus prediction (i.e., bootstrap aggregating or “bagging”). Even with bagging, greedy trees tend to use the same features for similar decision sequences. Random forests thus combine bagging with a covariate resampling scheme that forces greedy trees to explore different decision sequences with other covariates. In other words, at each split, a given tree in the forest can only choose from a random subset of covariates. Random forests have gained popularity because of their predictive performance and ease of use.

Recursive Partitioning Using Causal Trees

Machine learning methods have been increasingly adapted to objectives for estimating causal effects in social science applications (for a review, see Athey 2019). This rise of machine learning to estimate causal effects has been closely trailed by interest in applying algorithms to estimate heterogeneous causal effects. Some scholars have proposed methods that formulate the search for effect heterogeneity as a variable selection problem using a least absolute shrinkage and selection operator (LASSO) (Imai and Ratkovic 2013; Tian et al. 2014). The treatment indicator is interacted with any number of covariates, and LASSO regularization is used to search for the most predictive interactions. Other algorithms for fitting heterogeneous response functions include approaches based on decision trees, such as Bayesian additive regression trees and Bayesian forests (Chipman, George, and McCulloch 2010; Hill 2011; Taddy et al. 2016) and CART and random forests (Foster, Taylor, and Ruberg 2011; Su et al. 2009; Zeileis, Hothorn, and Hornik 2008).

We focus here on the sociological utility of the causal tree algorithm developed by Athey and Imbens (2016) for identifying effect heterogeneity. Athey and Imbens extended decision trees to causal settings using a potential outcome approach and provided a framework for uncovering effect heterogeneity. A tree, or partitioning Π, corresponds to a partitioning of the covariate space $\mathbb{X}$. In standard decision trees, each leaf l represents the average value of Y for units in that leaf. If there are k covariates and N observations, we partition the covariate space $\mathbb{X}$ into M mutually exclusive leaves l₁, . . . l_M where we estimate the outcome for an individual in leaf l_M as the mean of the outcome for training observations in that leaf. This partitioning process is repeated until a regularization penalty selected through cross-validation limits the depth of the tree. The resulting leaves contain a group of units with similar values of Y.

Applying the potential outcome approach to decision trees to instead generate causal trees requires altering the objective function. In a causal tree, we want the best prediction of the treatment effect τ, not the outcome Y as in the standard regression tree algorithm. The causal tree algorithm is thus an adaptation of decision trees for causal inference that attempts to partition the data to minimize heterogeneity in within-leaf treatment effects (i.e., differences in potential outcomes), rather than minimizing heterogeneity within-leaf (observed) outcomes. The difficulty in predicting the leaf-specific treatment effect is that we have no “ground truth,” or no observed value of the true treatment effect, as we do when predicting the value of an observed outcome Y. This issue reflects the fundamental problem of causal inference: we do not observe the causal effect for any unit.

In addition to adapting the objective to maximize treatment effect heterogeneity across leaves, Athey and Imbens (2016) advanced “honest” estimation. In honest estimation, we split the sample and use different data for selecting the partitions of the covariate space $\mathbb{X}$ and for estimation of leaf-specific effects. That is, we construct a tree using a training sample S^tr, and we estimate leaf-specific treatment effects using an estimation sample S^es. Notably, the criteria for constructing the partitions and cross-validation change in anticipation of honest estimation.³ Athey and Imbens introduced a modified expected MSE for the tree construction loss function that accounts for both honest estimation and the move to minimizing the MSE of treatment effects rather than outcomes:

$$-\widehat{EMS}{E}_{\tau (x)}=\frac{1}{N^{tr}}\sum _{i\in S^{tr}}{\widehat{\tau }}^2\left(X_i;S^{tr},\Pi \right)-\left(\frac{1}{N^{tr}}+\frac{1}{N^{es}}\right)\sum _{l\in \Pi }\left(\frac{S_{S^{tr}(1)}^2(l)}{p(l)}+\frac{S_{S^{tr}(0)}^2(l)}{1-p(l)}\right),$$ (6)

where N^tr and N^es are the sample size of the training sample and estimation sample, respectively; Π is a potential partition of the covariate space; $S_{S^{tr}(1)}^2(l)$ and $S_{S^{tr}(0)}^2(l)$ are the sample variances for the treated and control units in leaf l, respectively; and p(l) is the proportion of treated units in leaf l. The first term is the variance of treatment effects across leaves; we prefer leaves with heterogeneous effects. The second term is the uncertainty about leaf treatment effects; we prefer leaves with good fit, or leaf-specific effects estimated precisely. Honest estimation accounts for the uncertainty associated with the yet to be estimated leaf-specific treatment effects by including a penalty term for leaf-specific variance. As indicated by the sign, there is a trade-off between these two terms: we prefer tree topologies where leaves capture distinct heterogeneous effects, but where the effect is estimated precisely within leaves. We prune the tree using cross-validation, just as in standard regression trees, but the performance of the tree is based on treatment effect heterogeneity rather than predictive outcome accuracy. Honest estimation enables standard asymptotic properties in leaf-specific treatment effects.⁴ We define a CATE in the causal tree as the average difference in treated and control potential outcomes within leaves:

$$\tau (x;\Pi )=E\left[Y_i^1-Y_i^0\mid X_i\in l(x;\Pi )\right].$$ (7)

Causal trees can find heterogeneous effects, but they cannot guarantee that confounding within leaves is addressed in observational studies. Athey and Imbens (2016) contended that causal trees can be adapted to observational studies under the assumption of unconfoundedness by adjusting for estimates within leaves. The functions defined above can be modified with adjustments such that the weighted function balances the units in the treated and control groups. We use inverse propensity weights in an effort to ensure that the tree structure represents differential response to treatment rather than differential confounding by observed covariates. Once constructed, the tree is a function of covariates. Using a distinct sample to conduct inference, the “problem reduces to that of estimating treatment effects in each member of a partition of the covariate space,” in which case we need to “modify the estimates within leaves to remove the bias from simple comparisons of treated and control units” (Athey and Imbens 2016:7358–59; see also Hirano, Imbens, and Ridder 2003). For demonstration, we use IPW, nearest neighbor matching, and a doubly robust causal forest (generalized random forest [grf]), where we estimate one causal forest and average the estimated treatment effects within partitions.⁵ We assess propensity score balance within each partition to determine whether we have differential imbalance and whether our adjustment strategy succeeds in balancing observed selection into treatment.

Our detection of treatment effect heterogeneity hinges on our input covariates. Input covariates should be pretreatment, that is, potential moderators and not post-treatment mediators. We include all covariates used in estimation of the propensity of treatment. Following VanderWeele (2019), we include covariates presumed to cause the treatment, the outcome, or both, and any proxy for an unmeasured variable that is a common cause of both the treatment and the outcome. We exclude known instrumental variables. And following Hahn, Murray, and Carvalho (2020), we include the propensity score as one of the input covariates. As Imbens and Rubin (2015) outlined in their iterative procedure, we also exclude variables that do not add to the estimation of the likelihood of treatment. Fewer input covariates will result in less precise detection of heterogeneity, but even a small set can yield informative patterns.⁶

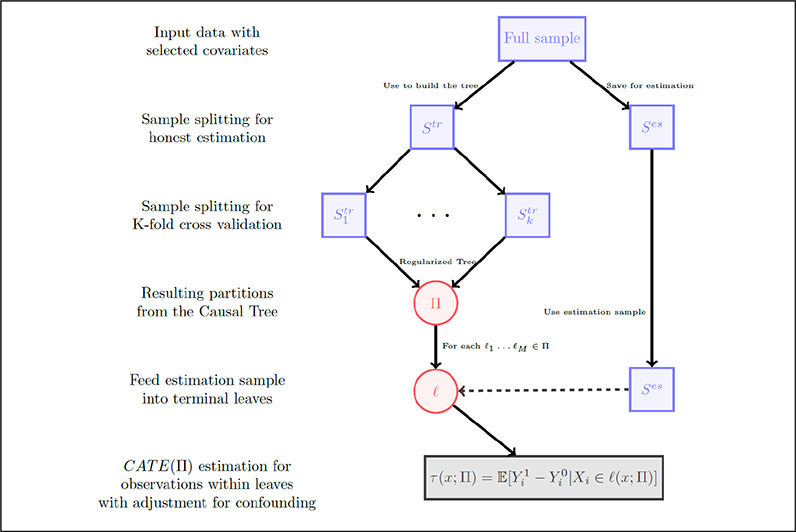
Our approach for using a causal tree to uncover treatment effect heterogeneity with observational data proceeds as follows: (1) input data with selected covariates; (2) draw a random subsample for training S^tr and retain a holdout sample for estimation S^es; (3) split the sample for k-fold cross-validation to regularize the tree in S^tr; (4) grow a tree via recursive partitioning in S^tr that maximizes heterogeneity across leaves and minimizes heterogeneity within leaves using adjustment (i.e., IPW); (5) feed the estimation sample into the leaves; and (6) estimate leaf-specific treatment effects in S^es using adjustment strategies, such as IPW, matching, and causal forests (grf). Figure 1 depicts this causal tree work flow.

Figure 1.

Causal tree work flow.

Note: We estimate leaf-specific treatment effects using inverse propensity weighting, nearest neighbor matching with four control units per treated unit on the linearized propensity score, and causal forests (grf). CATE = conditional average treatment effect.

Causal trees benefit from empirical discovery, important statistical properties, and interpretability. In contrast to methods that treat heterogeneity as a variable selection problem, trees search over possible combinations and thresholds of pretreatment covariates. In so doing, we uncover responsive subpopulations that we may not have considered prior to analysis. Moreover, in contrast to approaches that split the study population on the basis of outcome predictions, causal trees are optimized for treatment effect estimation within partitions of the covariate space and use sample splitting for “honest estimation” to provide leaf-specific, asymptotically unbiased estimates of average treatment effects with confidence intervals. In addition to these statistical guarantees, the causal tree is a particularly attractive tool for social science applications because the criteria used to make partitions are transparent to the end user. That is, the ability to plot the decision pathways of a causal tree renders it a powerful tool not just for uncovering treatment effect heterogeneity but also for interpreting and visualizing that heterogeneity.

As stated earlier, a disadvantage of single decision trees is that greedy optimization means the reported tree may not be the only valid tree or even the globally optimal tree. Different sample splits can result in different partitions and tree structures. To address these issues, Wager and Athey (2018) propose a causal forest for estimating treatment effects in the potential outcome framework assuming unconfoundedness with asymptotic guarantees. Several recent machine learning methods also flexibly combine supervised learning of the response variable with supervised learning of the propensity score to estimate average treatment effects. For example, Nie and Wager (2019) described a general class of two-step algorithms for heterogeneous treatment effects estimation in observational studies, and Athey, Tibshirani, and Wager (2019) proposed a grf that generates a doubly robust causal forest. This approach fits two separate regression forests to estimate $\widehat{e}(\cdot )$ and $\widehat{m}(\cdot )$ and then uses predictions from these two first-stage forests to grow a causal forest. We hereafter refer to this approach as a doubly robust causal forest or grf.

Causal forests (grf) have attractive properties for estimating heterogenous response functions yet lack the benefit of interpretability and identification of responsive subgroups. Although a causal forest (grf) does not give us a single, easily interpretable tree, we can generate useful metrics of heterogeneity, including an omnibus test of heterogeneity. We can also plot covariate importance by assessing the covariates chosen most often by the causal forest algorithm (i.e., a count of the proportion of splits on the variable of interest) and thus reveal the strongest determinants of the structure of the trees in the forest (O’Neill and Weeks 2018). Moreover, we can use the causal forest (grf) algorithm to estimate CATEs, including CATEs within partitions defined by covariates, propensity scores, or causal trees.

Overlap and Unconfoundedness

Estimating causal effects using observational data hinges on the overlap and unconfoundedness assumptions (D’Amour et al. 2020). Treatment effects are unidentified in regions that have no overlap. Matching methods restrict inference to the region of overlap, or common support; that is, we discard units that do not match, or the treated units with no comparable control units and the controls units with no comparable treated units, on the basis of observed covariates. Yet estimated treatment effects may be biased by unobserved covariates. Whether unconfoundedness is a reasonable assumption is a substantive issue, which depends on the quality of the covariates in capturing potential selection bias. Yet we recognize that even with a rich set of pretreatment covariates, potential confounders remain. Partitioning by propensity scores, selected covariates, or leaves within causal trees may involve differential selection bias. Because partitioning by propensity scores involves estimating subpopulation treatment effects by observed selection into treatment, the approach encourages attention to potential violations to the unconfoundedness assumption across partitions (see Zhou and Xie 2019, 2020). However, researchers evaluating covariate-stratified estimated treatment effects often fail to consider the possibility that unobserved confounding may differ across subgroups.

Here we relax the unconfoundedness assumption and conduct sensitivity analyses for differential hidden confounding within partitions defined by propensity scores, covariates, and leaves within the causal tree (Rosenbaum 2002). We subtract a bias factor from the point estimate and confidence interval of the treatment effects obtained under unconfoundedness (Arah 2017; Gangl 2013; VanderWeele and Arah 2011). The bias term is equal to the product of two parameters:

$$B=\gamma \lambda ,$$ (8)

where

$$\gamma =E(Y|U=1,W=w,X)-E(Y|U=0,W=w,X)$$ (9)

and

$$\lambda =P(U=1|W=1,X)-P(U=0|W=0,X).$$ (10)

That is, γ is the mean difference in the outcome associated with a unit change in an unobserved binary confounder, U, and λ is the mean difference in the unobserved confounder between treated and control units. Alternative approaches for sensitivity analyses are also possible (e.g., Cinelli and Hazlett 2020), but they follow the same general logic. Other strategies may more explicitly consider unobserved confounding that affects our conclusions as to treatment effect heterogeneity.

EMPIRICAL APPLICATION

To demonstrate the approach, we assess heterogeneity in the effect of college on reducing low-wage work over a career. The effects of college on wages is a key area of interest in social inequality research (Hout 2012). By focusing on low-wage work, we shift attention to how college may circumvent disadvantaged labor market outcomes for particular subpopulations. Some rhetoric suggests limiting college for segments of the population, particularly more disadvantaged students on the margin of school continuation (e.g., Caplan 2018). If we observe benefits for disadvantaged students that match, or even exceed, those of more traditional college students, we gain insight into whether college pays off for this subpopulation of potential college-goers. We draw on observational data and a highly selective treatment condition, completing college, to illustrate the use of causal trees and forests with observational data. We address four research questions: (1) Does college reduce the proportion of time in low-wage work over a career? (2) Does the effect of college on low-wage work vary by propensity score strata and by key covariates that influence the likelihood of completing college (i.e., parental income, mother’s education, measured ability, and race)? (3) Does the effect of college on low-wage work vary by subgroups we had not considered? and (4) How sensitive are the treatment effect estimates to unobserved confounding across partitions?

Our analysis proceeds as follows. First, we present descriptive statistics of the full sample. Second, we assess average effects of college on reducing low-wage work using three adjustment strategies: IPW, matching, and causal forest (grf). Third, we evaluate heterogeneous effects of college on reducing low-wage work for subgroups defined by the propensity of college, parental income, mother’s education, measured ability, and race, again using IPW, matching, and causal forest (grf). We estimate one causal forest for the full population, and then average those estimates within partitions. We compare balance metrics across partitions. Fourth, we evaluate heterogeneous effects for subgroups identified by the causal tree, using the same adjustment strategies and balance metrics. We offer descriptive statistics to help interpret the subgroups identified by the causal tree. We also discuss tree stability and offer a covariate importance plot from a causal forest. Fifth, we assess the sensitivity of partition-specific effect estimates to unobserved confounding.

Data and Descriptive Statistics

We use data from the Bureau of Labor Statistics 1979 to 2014 waves of the National Longitudinal Survey of Youth 1979 cohort. These nationally representative longitudinal data provide information on respondents’ sociodemographic background, achievement, skills, educational attainment, and long-term earnings trajectories from early to late career; the data have been widely used to assess the effects of college on wages. We restrict the sample to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582) and who had completed at least the 12th grade (n = 4,548). These sample restrictions ensure that all variables we use to predict college are measured precollege and that we compare college completers with those who completed at least a high school education. About one fifth of the sample completed college by age 25. We focus on the proportion of time spent in a low-wage job from 1990 to 2014, when respondents were roughly between the ages of 25 and 50. We measure low-wage work as less than two thirds of the median hourly wage for that year (Presser and Ward 2011). In Table 1, we report covariate means by college completion. We use covariates known to affect the likelihood of college completion, including measures of race, residence, parents’ income, parents’ education, father’s occupation, family structure, cognitive ability,⁷ college-preparatory program, psychosocial skills, juvenile delinquency, educational expectations and aspirations, school characteristics, and family formation. Descriptive statistics on our precollege covariates suggest well-documented socioeconomic differences in educational attainment.⁸

Table 1.

Descriptive Statistics of Precollege Characteristics and Wage Outcome

	Non–College Graduates		College Graduates
	Mean	S.D.	Mean	S.D.
Sociodemographic factors
Male (binary 0/1)	.497	—	.504	—
Black (binary 0/1)	.160	—	.069	—
Hispanic (binary 0/1)	.066	—	.026	—
Southern residence at age 14 (binary 0/1)	.325	—	.029	—
Rural residence at age 14 (binary 0/1)	.239	—	.186	—
Family background factors
Parents’ household income ($100s) (continuous 0 to 75)	190.959	110.173	286.006	150.934
Fathers’ highest education (0 to 20)	11.389	3.114	14.234	3.240
Mothers’ highest education (0 to 20)	11.345	2.412	13.317	2.437
Father upper-white-collar occupation (0/1)	.175	—	.507	—
Two-parent family at age 14 (binary 0/1)	.712	—	.847	—
Sibship size (continuous 0 to 19)	3.296	2.262	2.534	1.641
Cognitive and psychosocial factors
Cognitive ability ASVAB (continuous −3 to 3)	−.125	.673	.606	.553
High school college-preparatory program (0/1)	.236	—	.485	—
Rotter locus of control scale (continuous 4 to 16)	9.031	2.259	8.124	2.139
Juvenile delinquency activity scale (0 to 1)	.815	.389	.714	.452
Educational expectations (binary 0/1)	.309	—	.825	—
Educational aspirations (binary 0/1)	.434	—	.879	—
Friends’ educational aspirations (binary 0/1)	.358	—	.740	—
School factors
School disadvantage scale (0 to 99)	21.684	17.859	12.742	12.638
Family formation factors
Marital status at age 18 (binary 0/1)	.068	—	.003	—
Had a child by age 18 (binary 0/1)	.061	—	.002	—
Wage outcome
Proportion of time in low-wage work	.398	.363	.207	.246
Weighted sample proportion	.81		.19
n	3,531		851

Note: Data are from the National Longitudinal Survey of Youth (NLSY) 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. All descriptive statistics are weighted by the NLSY sample weight. ASVAB = Armed Services Vocational Aptitude Battery.

Average Effects of College on Low-Wage Work

In Table 2, we report estimates of the average effect of college completion on proportion of time in low-wage work over a career. We compare the unadjusted estimate to estimates adjusted by IPW, nearest neighbor matching on the basis of the linear propensity score (i.e., $logit(\widehat{e}(x))$)⁹ with four control units per treated unit, and causal forests (grf).¹⁰ To estimate the propensity of college, we use a random forest. We include the measures described in Table 1.¹¹ We find that college completion is associated with a significant 22 percentage point reduction in the proportion of time spent in a low-wage job across a career, an estimate that is reduced to about 19 percent using IPW and about 17.5 percent using matching and causal forest (grf). Appendix Figure A1 is an algorithm display detailing the steps of the causal forest estimation for the estimate reported in Table 2. More detailed code is available on Github. We perform an omnibus test for treatment effect heterogeneity, indicated by the line in Appendix Figure A1 for differential forest prediction, which suggests evidence at the p = .07 level for heterogeneity. Although this test does not indicate evidence for heterogeneity at the conventional .05 level, it remains plausible that the agnostic omnibus test is not capturing important heterogeneity along specific partitions of the covariate space (Athey and Wager 2019). We next assess possible sources of heterogeneity.

Table 2.

Effect of College Completion on Proportion of Time in Low-Wage Work

Wage Outcome	Unadjusted	IPW	NN Matching	Causal Forest (grf)
Proportion of time in low-wage work	−.223*** (.013)	−.189*** (.016)	−.174*** (.023)	−.176*** (.024)

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Estimates are based on IPW, NN matching with four control units per treated unit on the linearized propensity score, and on a causal forest (grf). grf = generalized random forest; IPW = inverse propensity weighting; NN = nearest neighbor.

^***p ≤ .001 (two-tailed tests).

Heterogeneous Effects of College on Low-Wage Work: Propensity Score and Covariate Partitioning

We examine stratified effects of college completion by propensity score strata and several a priori theoretically motivated covariates: parental income, mother’s education, ability, and race. We construct three propensity score strata to assess effects for low-, middle-, and high-propensity college-goers, where low ranges from 0 to less than .2, middle from .2 to less than .5, and high from .5 to 1. In addition, we partition by covariates that strongly influence selection into college and indicate levels of socioeconomic advantage: parental income, mother’s education, measured ability, and race. We divide parental income and ability into terciles of the distributions; divide mother’s education into categories of less than high school, high school degree, and some college or more; and divide respondents’ race into black, Hispanic, and white.

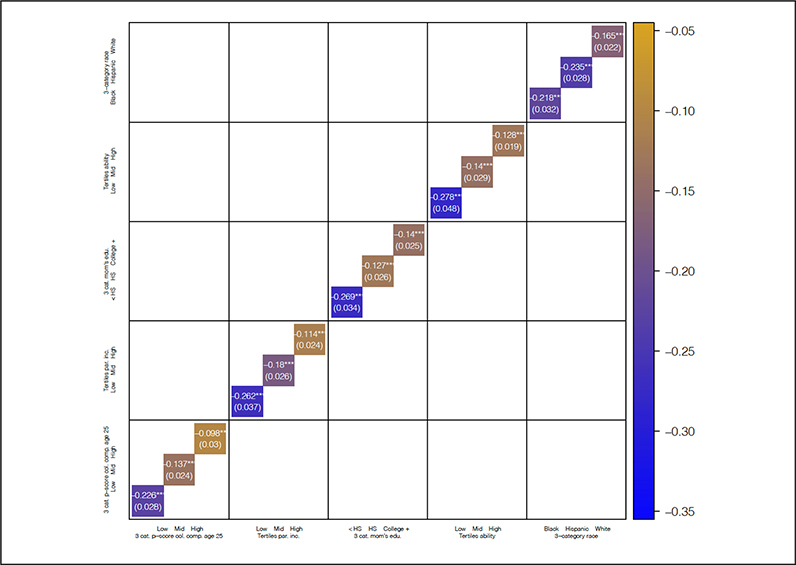
Figure 2 is a heatmap of estimated effects based on stratified models using IPW, where blue indicates larger treatment effects (i.e., larger negative effects indicating reductions in the proportion of time in low-wage work associated with a college degree) and yellow indicates smaller treatment effects (i.e., less negative effects, nearing zero). Table 3 reports estimated effects using IPW, matching, and a causal forest (grf); that is, we generate a causal forest (grf) and then average the estimated treatment effects within each partition. As shown in Figure 2 and Table 3, we find the largest effects of college on reducing low-wage work for respondents with a low propensity to complete college, low ability, low parental income, low mother’s education, and for black and Hispanic individuals. The effects of college on low-wage work for the most advantaged individuals are significant but smaller.¹² For example, we find a more than 20 percentage point lower proportion of time in low-wage work for college-educated workers with a low propensity of college versus a 10 percentage point lower proportion for those with a high propensity. The IPW estimates are somewhat larger than for matching and causal forest (grf), but the estimates are very similar for matching and causal forest (grf).¹³

Figure 2.

Covariate and propensity score–based partitioning: effect of college completion on the proportion of time in low-wage work.

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Estimated treatment effects are based on inverse propensity weighting. Standard errors are in parentheses. In the online version, blue indicates largest treatment effects, and yellow indicates smallest treatment effects. HS = high school.

Table 3.

Effects of College Completion on Proportion of Time in Low-Wage Work: Covariate and Propensity Score–Based Partitioning

	(a)			(b)			(c)
	IPW	NN Matching	Causal Forest (grf)	IPW	NN Matching	Causal Forest (grf)	IPW	NN Matching	Causal Forest (grf)
Propensity score strata: (a) = low, (b) = mid, (c) = high	−.226*** (.028)	−.205*** (.032)	−.208*** (.036)	−.137*** (.024)	−.132*** (.028)	−.134*** (.026)	−.098** (.030)	−.083** (.032)	−.101*** (.031)
Parental income terciles: (a) = low, (b) = mid, (c) = high	−.262*** (.037)	−.316*** (.034)	−.233*** (.046)	−.180*** (.026)	−.199*** (.033)	−.194*** (.043)	−.114*** (.024)	−.083 (.075)	−.091*** (.023)
Mothers’ education: (a) = less than HS, (b) = HS, (c) = college or higher	−.269*** (.034)	−.261*** (.034)	−.220*** (.042)	−.127*** (.026)	−.156*** (.030)	−.161*** (.038)	−.140*** (.025)	−.124*** (.031)	−.123*** (.025)
Ability terciles: (a) = low, (b) = mid, (c) = high	−.278*** (.048)	−.267*** (.040)	−.287*** (.063)	−.140*** (.029)	−.168*** (.030)	−.146** (.041)	−.128*** (.019)	−.118*** (.024)	−.120*** (.020)
Race: (a) = black, (b) = Hispanic, (c) = white	−.218*** (.032)	−.280*** (.053)	−.195*** (.048)	−.235*** (.028)	−.186*** (.046)	−.210** (.060)	−.165*** (.022)	−.189*** (.025)	−.157*** (.031)

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Propensity score strata and parental income and ability terciles are 1 for low, 2 for mid, and 3 for high. For mothers’ education, 1 indicates less than high school, 2 indicates a high school degree, and 3 indicates some college attendance or more. For race, 1 indicates black, 2 indicates Hispanic, and 3 indicates white (these categories were based on an ordering of the probability of college completion). Estimates are based on NN matching with four control units per treated unit on the linearized propensity score and on causal forest (grf) estimates applied to each partition. grf = generalized random forest; HS = high school; IPW = inverse propensity weighting; NN = nearest neighbor.

^**p ≤ .01 and

^***p ≤ .001 (two-tailed tests).

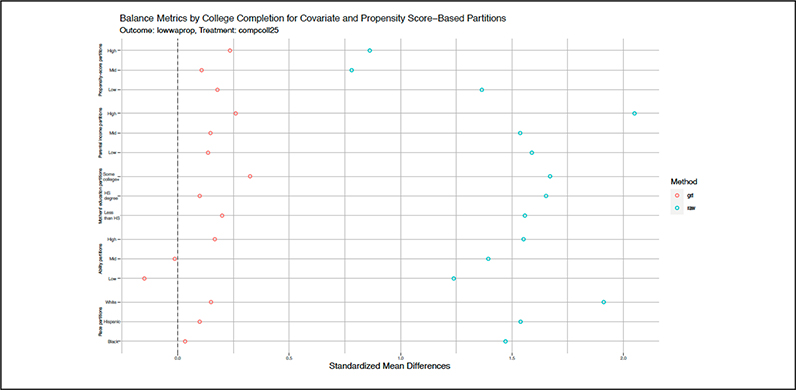
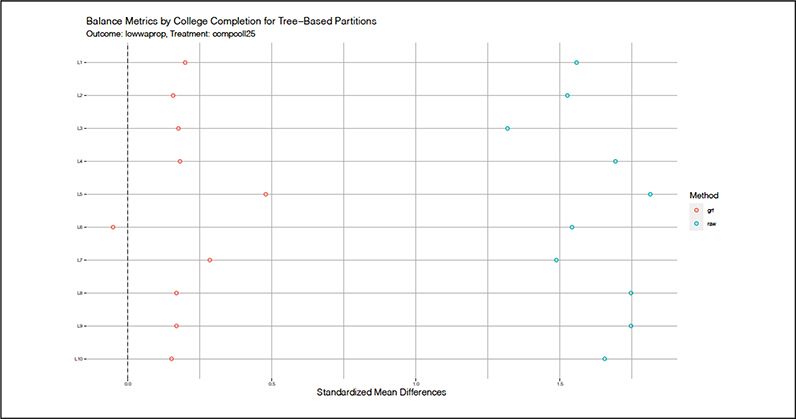
Next we attend to possible differential violations of covariate balance across subgroups. Figure 3 provides balance metrics defined by standardized mean propensity score differences across each of our partitions defined by propensity scores, parental income, mother’s education, ability, and race. If the numbers are close to zero, we achieve balance across covariates. We report raw differences and the balance achieved by causal forest (grf) estimation. In every case, we substantially reduce the raw imbalance by grf. The remaining imbalance is not zero, but it is generally no greater in the subgroups in which we observe large effects than in the subgroups in which we observe smaller effects. For example, the bias is close to zero for black respondents but relatively larger for Hispanic and white respondents. It is larger in the high propensity score and socioeconomic strata than in the low strata. Thus, although we are concerned about remaining imbalance, we are less concerned about differential imbalance that explains the patterns in heterogenous effects.

Figure 3.

Propensity score balance metrics by covariate and propensity score–based partitioning.

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548) and had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. The x-axis indicates standardized mean propensity score differences for raw and generalized random forest (grf) adjusted samples within each partition. The y-axis indicates the partition. HS = high school.

In the Appendix Figure A1 algorithm, we also report the best linear prediction of the CATE onto the propensity score from the causal forest. This suggests the effect of college on reducing low-wage work significantly decreases as the propensity of college increases, from a roughly 20 percentage point reduction for the lowest propensity of college to no effect for individuals with the highest propensity. R and Stata packages are available to generate these results. We also developed several possible causal tree visualizations that researchers can use, including an interactive tree (for our application, see https://htetree.shinyapps.io/hte_tree_ipw/, developed in collaboration with Stephanie Yee and Tony Chu of R2D3, http://www.r2d3.us).

Heterogeneous Effects of College on Low-Wage Work: Recursive Partitioning Using Causal Trees

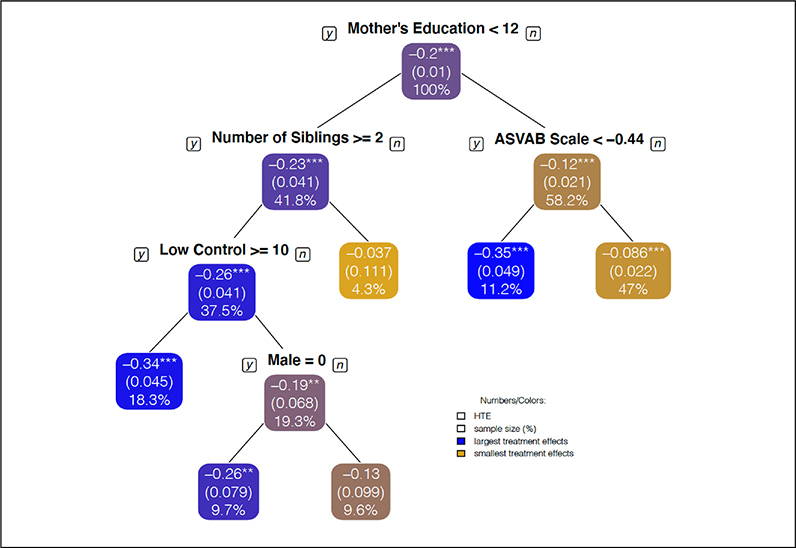
Figure 4 and Table 4 depict results of the causal tree for the effect of college completion on the proportion of time in low-wage work. The estimates displayed in the leaves of Figure 4 are based on IPW.¹⁴ Table 4 reports alternative estimates using nearest neighbor matching and a causal forest (grf). We include the 22 covariates described in Table 1 as well as the estimated propensity score as input splitting covariates, using the criteria to select covariates described earlier. We limit the depth of the tree by requiring at least 20 treated and 20 control units per leaf.¹⁵ Researchers may use a larger number of treated and control observations, such as 30 or 50, depending on sample size. Holding sample size constant, a larger minimum number of units will limit the depth of the tree and detection of heterogeneity. A larger sample size will enable more precise effect estimates within partitions and possible better adjustment of confounding. With more cases, researchers may use a larger number of control than treated observations to ensure better matches within partitions. We use 50 percent of the sample to train the data and grow the tree structure, and we reserve the remaining 50 percent of the sample as a holdout sample for estimation of leaf-specific treatment effects within that tree. The causal tree is color coded to indicate the size of the association, with blue indicating larger (negative) effects and yellow indicating smaller effects (nearing zero) (color coding in the online version). The color coding aligns with the results we report in Figure 2. As with the covariate and propensity partitioning, we estimate one causal forest for the full population and then average those estimates within the partitions. Appendix Figure A2 shows the baseline steps of the causal tree estimation, with more detailed code leading to the results in Table 4 (also available on Github).

Figure 4.

Recursive partitioning using a causal tree: effect of college completion on the proportion of time in low-wage work.

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Treatment effects are estimated by inverse propensity weighting. Standard errors are in parentheses. Blue indicates largest treatment effects, and yellow indicates smallest treatment effects. ASVAB = Armed Services Vocational Aptitude Battery; HTE = heterogeneous treatment effect.

Table 4.

Effects of College Completion on Proportion of Time in Low-Wage Work: Recursive Partitioning Causal Tree

	IPW	NN Matching	Causal Forest (grf)	n
L1: mothers’ education < 12	−.225*** (.041)	−.261*** (.034)	−.220*** (.042)	1,832
L2: L1 & number of siblings ≥ 2	−.264*** (.041)	−.291*** (.034)	−.251*** (.045)	1,645
L3: L2 & low control ≥ 10	−.343*** (.045)	−.372*** (.056)	−.318*** (.063)	800
L4: L2 & low control < 10	−.189** (.068)	−.099 (.150)	−.176*** (.064)	845
L5: L4 & female	−.255** (.079)	−.263** (.091)	−.179** (.065)	425
L6: L4 & male	−.133 (.099)	−.130 (.142)	−.170** (.098)	420
L7: L1 & number of siblings < 2	−.037 (.111)	−.110 (.070)	−.043 (.123)	187
L8: mother’s education ≥ 12	−.124*** (.021)	−.140*** (.023)	−.150** (.029)	2,550
L9: L8 & ASVAB scale < −.44	−.347*** (.049)	−.381*** (.050)	−.355* (.102)	490
L10: L8 & ASVAB scale ≥−.44	−.086*** (.022)	−.089*** (.018)	−.100* (.026)	2,060

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Estimates are based on IPW, NN matching with four control units per treated unit on the linearized propensity score, and causal forest (grf) estimates applied to each partition. ASVAB = Armed Services Vocational Aptitude Battery; grf = generalized random forest; IPW = inverse propensity weighting; L = leaf; NN = nearest neighbor. Shading indicates instability in the partitions.

^*p ≤ .05

^**p ≤ .01, and

^***p ≤ .001 (two-tailedtests).

The primary division depicted in Figure 4 occurs for mother’s education, with individuals whose mothers had less than a high school degree having larger negative effects of college on time spent in low-wage work. Individuals whose mothers have less than a high school degree have a 23 percentage point reduction in low-wage work, compared with a 12 percentage point reduction among those whose mothers have at least a high school degree. The largest effects accrue to respondents whose mothers did not complete high school, who grew up in large families, and who have low social control (i.e., in the top quartile of the low control distribution): a 34 percentage point reduction in low-wage work. For individuals with mothers with at least a high school degree and low ability (in the bottom quartile of the ability distribution), we see a similarly large effect (a 35 percentage point reduction). For respondents with less educated mothers who grew up in large families, yet had higher social control (below the top quartile of the low control distribution), we find larger effects for women than for men (26 percentage point lower proportion vs. a 13 percentage point lower proportion). We find substantially smaller effects for individuals whose mothers had less than a high school education but who came from smaller families. Respondents with mothers with at least a high school degree and relatively higher ability (above the bottom quartile of the ability distribution) have the smallest effect (a 9 percentage point reduction in low-wage work).¹⁶ Our substantive conclusions remain largely the same using alternative adjustment strategies (see Table 4).

Figure 5 provides balance metrics defined by standardized mean differences in propensity scores across each of our partitions defined by our causal tree. Again, we report the raw imbalance and the balance achieved by causal forest (grf) estimation. We substantially reduce the raw imbalance across leaves by our grf estimates. Leaves 3 and 9 are the most responsive partitions, yet the imbalance is no different here than in the less responsive partitions. Thus, again, although we are concerned about remaining imbalance, we are less concerned about differential imbalance that explains the patterns in heterogenous effects. Appendix Table A2 provides tests of significance across leaves, suggesting significant differences across most leaves.

Figure 5.

Propensity score balance metrics by recursive partitioning using a causal tree.

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. The x-axis indicates standardized mean propensity score differences for raw and generalized random forest (grf) adjusted samples within each partition. The y-axis indicates the partition.

As noted earlier, tree stability is a concern. That is, we may get different trees if we generate different random splits of the training and test data. To test tree structure stability, we generate 100 causal trees with different random splits of the training and test data. We find that 95 percent of the time we get the tree structure we present above with only one modification to the depth; that is, 36 percent of the time we do not see the split on gender. We thus shade the gender-partitioned estimates in Table 4. We get two additional trees accounting for the remaining 5 percent of trees. Thus, the tree we present in Figure 4 appears to be reasonably stable in our application.

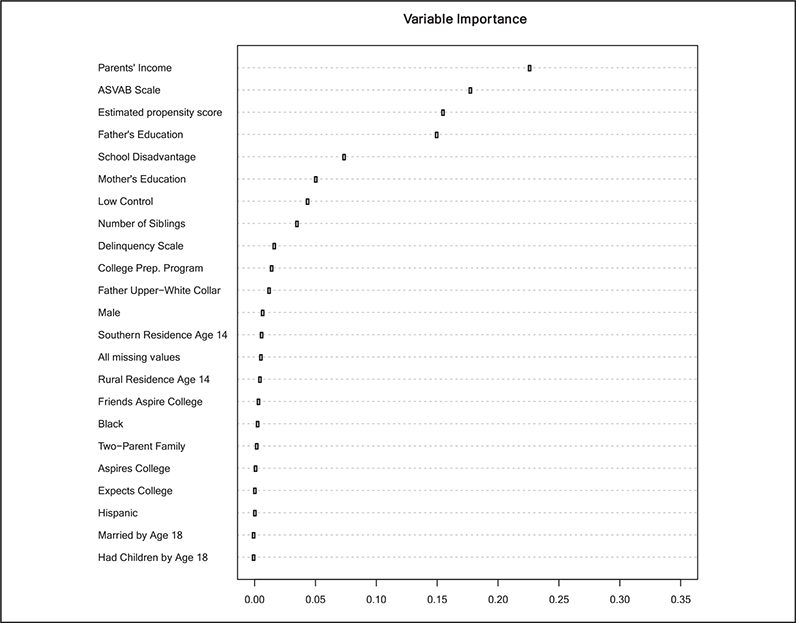
We also run causal forests (grf) with 4,000 trees. Figure 6 is a plot of covariate importance from a causal forest (grf), which can yield insight into how the ensemble of trees is making decisions. The x-axis indicates relative importance scores; we are concerned only with the relative strength across covariates. The covariates displayed at the top of the plot are the strongest determinants of generating the structure of the trees in the forest. The results suggest that parental income, ability, propensity of college, and father’s education are most important. School disadvantage, mother’s education, social control, and family size follow, with the remaining variables having minimal relative importance in terms of determining the structure of the trees. The covariates that generate the primary splits in the causal tree in Figure 6 are a subset of those identified here. This gives us confidence that the covariates selected by the tree are key axes of heterogeneity.

Figure 6.

Covariate importance plot based on a causal forest (generalized random forest) of the effect of college completion on the proportion of time in low-wage work.

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. The x-axis indicates relative importance scores; we are concerned only with the relative strength across covariates. The covariates displayed at the top of the plot are the strongest determinants of generating the structure of the trees in the forest. ASVAB = Armed Services Vocational Aptitude Battery.

In summary, more disadvantaged subpopulations, or those on the margin of school continuation, experience larger effects of college on reducing low-wage work. We identify this pattern across the various partitioning strategies. Yet the groups identified by the causal tree are not necessarily those we would identify by our theoretical priors. For example, although we consider strata on the basis of mother’s education in Table 3, we did not specifically consider individuals with mothers without a high school degree and who grew up in large families and had low social control, nor those with high school–educated mothers yet low ability.¹⁷ We should not go too far, however, in interpreting the selection of variables used for the splits (Athey and Imbens 2019). Instead, we should focus on the populations identified by the splits.

Table 5 provides leaf-specific selected covariate descriptive statistics. We report the most important covariates as defined by the covariate importance plot in Figure 6. Let us consider the subgroups in leaves 3 and 9 with the largest estimated treatment effects, that is, those whose mothers did not complete high school and who grew up in large families and had low social control (leaf 3), and those with more educated mothers who had low measured cognitive ability (leaf 9). In leaf 3, parental income is below average, school disadvantage is above average, and measured cognitive ability is below average. Fathers and mothers have below average levels of education. Three fourths of fathers have less than a high school degree, and all mothers have less than a high school degree (by definition of the leaf). About two thirds are black or Hispanic. In leaf 9, parental income is about average, school disadvantage is average, and measured ability is below average (more than a standard deviation below). Father’s education is about average, with three fourths having a high school degree or more, and mother’s education is above average, with all mothers (by definition of the leaf) holding a high school degree. About one fifth of mothers and fathers attended some college. More than two thirds are white. In both leaves 3 and 9, respondents report low social control, but particularly in leaf 3 (which is defined by low control). We thus have two distinct responsive subpopulations: individuals who are socioeconomically disadvantaged (i.e., leaf 3) and individuals with average socioeconomic status and below average measured cognitive ability (i.e., leaf 9). Almost 95 percent have a low propensity for college (in the bottom third of the propensity score distribution) in both leaves 3 and 9. Propensity of college is a key summary measure of responsiveness to college in reducing low-wage work.

Table 5.

Descriptive Statistics for Selected Covariates by Recursive Partitions

	Parental Income	Ability	Propensity Score	Fathers’ Education	School Disadvantage	Mothers’ Education	Low Control	Number of Siblings	Nonwhite
Ll: mothers’ education <12	121.669	−.239	.101	8.844	31.158	8.566	9.276	4.447	.611
L2: Ll & number of siblings ≥ 2	120.408	−.268	.095	8.754	31.635	8.512	9.338	4.855	.631
L3: L2 & low control ≥ 10	110.977	−.383	.078	8.554	32.464	8.382	11.222	5.008	.652
L4: L2 & low control <10	129.261	−.160	.112	8.941	30.857	8.646	7.570	4.711	.612
L5: L4 & female	129.287	−.124	.114	8.721	30.825	8.637	7.522	4.803	.621
L6: L4 & male	129.235	−.197	.109	9.161	30.889	8.655	7.618	4.618	.621
L7: Ll & number of siblings < 2	132.947	.020	.151	9.654	26.890	8.995	8.723	.796	.435
L8: mother’s education ≥ 12	215.123	.171	.256	12.827	19.314	12.894	8.717	2.922	.303
L9: L8 & ASVAB scale < −.44	170.699	−.875	.120	11.772	23.936	12.405	9.345	3.370	.304
L10: L8 & ASVAB scale ≥−.44	225.799	.422	.288	13.088	18.205	13.012	8.566	2.815	.302

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. ASVAB = Armed Services Vocational Aptitude Battery; L = leaf.

Leaves 7 and 10 are the least responsive subgroups. Individuals in leaf 10 have high levels of parental income, low levels of school disadvantage, high ability, and educated parents. More than 40 percent have college-educated fathers, and one third have college-educated mothers. Individuals in leaf 10 have the highest levels of advantage and the highest propensity of college among the partitioned subgroups. These individuals are most likely not at risk for working in low-wage jobs whether or not they attend and complete college. They can draw on their advantaged background to avoid such employment. Individuals in leaf 7 have average levels of parental income, school disadvantage, and ability, and below average levels of parent’s education, but they tend to be only children. These respondents may also be at a low risk for low-wage work if parents are more likely to assist an only child in securing employment.

Sensitivity Analyses

Tables 6 and 7 report sensitivity bounds on the estimated causal forest (grf) coefficients reported in Tables 3 and 4, respectively. The effect reaches nonsignificance when the unobserved confounder has a sizable difference between individuals who do and do not complete college (λ) or a strong effect on the proportion of time in low-wage work (γ). Suppose, for example, that idleness, unobserved in our data, increases the time in low-wage work over a career, and is lower among individuals who complete college than among those who do not. When λ equals −10 percent, we assume that the prevalence of idle individuals is 10 percent lower in the college-educated group than in the non-college-educated group. When γ equals 10 percent, we assume that idle individuals have a 10 percentage point higher level of low-wage work than those who are not idle (all else equal). We let the values of γ range from 10 to 40 percent and fix the value of λ at −10 percent.¹⁸

Table 6.

Sensitivity Parameters for Covariate and Propensity Score–Based Partitioning Results

		Treatment Effects
	Sensitivity Parameters		1		2		3
Partitions	γ	λ	CATE	CI	CATE	CI	CATE	CI
Propensity score	10%	−10%	−.198	(−.269 to −.127)	−.124	(−.175 to −.073)	−.091	(−.152 to −.030)
	20%	−10%	−.188	(−.259 to −.117)	−.114	(−.165 to −.063)	−.081	(−142 to −.020)
	40%	−10%	−.168	(−.239 to −.097)	−.094	(−.145 to −.043)	−.061	(−.122 to .000)
Parental income	10%	−10%	−.223	(−.313 to −.133)	−.184	(−.268 to −.100)	−.081	(−.126 to −.036)
	20%	−10%	−.213	(−.303 to −.123)	−.174	(−.258 to −.090)	−.071	(−.116 to −.026)
	40%	−10%	−.193	(−.283 to −.103)	−.154	(−.238 to −.070)	−.051	(−.096 to −.006)
Mothers’ education	10%	−10%	−.210	(−.292 to −.128)	−.151	(−.225 to −.077)	−.113	(−.162 to −.064)
	20%	−10%	−.200	(−.282 to −.118)	−.141	(−.215 to −.067)	−.103	(−.152 to −.054)
	40%	−10%	−.180	(−.262 to −.098)	−.121	(−.195 to −.047)	−.083	(−.132 to −.034)
Ability	10%	−10%	−.277	(−.400 to −.154)	−.136	(−.216 to −.056)	−.110	(−.149 to −.071)
	20%	−10%	−.267	(−.390 to −.144)	−.126	(−.206 to −.046)	−.100	(−.139 to −.061)
	40%	−10%	−.247	(−.370 to −.124)	−.106	(−.186 to −.026)	−.080	(−.119 to −.041)
Race	10%	−10%	−.185	(−.279 to −.091)	−.200	(−.318 to −.082)	−.147	(−.208 to −.086)
	20%	−10%	−.175	(−.269 to −.081)	−.190	(−.308 to −.072)	−.137	(−.198 to −.076)
	40%	−10%	−.155	(−.249 to −.061)	−.170	(−.288 to −.052)	−.117	(−.178 to −.056)

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Propensity score strata and parental income and ability terciles are 1 for low, 2 for mid, and 3 for high. For mothers’ education, 1 indicates less than high school, 2 indicates a high school degree, and 3 indicates some college attendance or more. For race, 1 indicates black, 2 indicates Hispanic, and 3 indicates white (these categories were based on an ordering of the probability of college completion). CATE = conditional average treatment effect; CI = confidence interval.

Table 7.

Sensitivity Parameters for Recursive Partitioning Results

Partitions	Sensitivity Parameters		Treatment Effects
	γ	λ	CATE	CI
L1: mothers’ education < 12	10%	−10%	−.210	(−.293 to −.127)
	20%	−10%	−.200	(−.283 to −.117)
	40%	−10%	−.180	(−.263 to −.097)
L2: L1 & number of siblings > 2	10%	−10%	−.241	(−.329 to −.153)
	20%	−10%	−.231	(−.319 to −.143)
	40%	−10%	−.211	(−.299 to −.123)
L3: L2 & low control ≥ 10	10%	−10%	−.308	(−.431 to −.185)
	20%	−10%	−.298	(−.421 to −.175)
	40%	−10%	−.278	(−.401 to −.155)
L4: L2 & low control < 10	10%	−10%	−.166	(−.291 to −.041)
	20%	−10%	−.156	(−.281 to −.031)
	40%	−10%	−.136	(−.261 to −.011)
L5: L4 & female	10%	−10%	−.160	(−.352 to .032)
	20%	−10%	−.150	(−.342 to .042)
	40%	−10%	−.130	(−.322 to .062)
L6: L4 & male	10%	−10%	.133	(.427 to −.162)
	20%	−10%	.143	(.437 to −.152)
	40%	−10%	.163	(.457 to −.132)
L7: L1 & number of siblings < 2	10%	−10%	−.033	(−.273 to .207)
	20%	−10%	−.023	(−.263 to .217)
	40%	−10%	−.003	(−.243 to .237)
L8: mother’s education ≥ 12	10%	−10%	−.140	(−.197 to −.083)
	20%	−10%	−.130	(−.187 to −.073)
	40%	−10%	−.110	(−.167 to −.053)
L9: L8 & ASVAB scale < −.44	10%	−10%	−.345	(−.546 to −.145)
	20%	−10%	−.335	(−.536 to −.135)
	40%	−10%	−.315	(−.516 to −.115)
L10: L8 & ASVAB scale ≥−.44	10%	−10%	−.090	(−.140 to −.039)
	20%	−10%	−.080	(−.130 to −.029)
	40%	−10%	−.060	(−.110 to −.009)

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. ASVAB = Armed Services Vocational Aptitude Battery; CATE = conditional average treatment effect; CI = confidence interval; L = leaf.

In Table 6, the effect of college on reducing low-wage work remains significant for the most disadvantaged college completers at each value we consider, even when unobserved differences have a substantial impact on low-wage work (γ = 40) and the prevalence of the unobserved factor differs between college graduates and non–college graduates by 10 percent (λ = −10). Estimates also remain significant for the middle propensity score, parental income, and middle and high mother’s education subpopulations, and for Hispanic and white respondents. Effects among individuals with a high propensity of college and high parental income are more sensitive to confounding when γ = 40. Table 7 provides sensitivity bounds on the estimated effects across leaves defined by the causal tree. The sizable leaf-specific estimates associated with the most responsive subpopulations are robust to unobserved confounding. For example, the largest estimate in leaf 3 remains significant even if the confounding variable reduced low-wage work by 40 percent (γ) and differed by 10 percent among college graduates and non–college graduates (λ).

DISCUSSION

Heterogeneity in response to an event or intervention is to be expected. We cannot reasonably presume that individuals respond identically to life events. We aim to understand heterogeneity, both in the characteristics that predispose some groups to experience particular events and how those characteristics govern differential response to events. One long-standing approach in sociology is to determine subgroups of interest who we theorize should respond differently and then test those possibilities in our data. There are many advantages to doing so, as we may have theoretical interest in whether black or white individuals, or men or women, or people who grew up in low-income versus high-income families are differentially affected by particular events. For example, we may want to know whether low-income students benefit more or less from college than high-income students, because our policies target recruitment of students by social class categories and we want to estimate the expected gain. We may likewise want to know whether students with a low estimated propensity of college benefit more or less, as such knowledge of the stratification process sheds light on the consequences of the unequal distribution of scarce resources. Such analyses also give us insight into how selection into treatments may confound the relationships we observe across subgroups.

Yet social scientists do not always know a priori which characteristics govern the distribution of responses. Often our data can tell us something we had not thought of before performing the analyses. Indeed, a great deal of the excitement of empirical social scientific work lies in unexpected discovery. Data-driven discoveries are common, but the analyses by which sociologists typically go about them are problematic. Indeed, researchers may estimate tens or hundreds of alternative specifications behind the scenes, without an established way to correct for the specification search process. It is difficult to be systematic or comprehensive in specifications when proceeding in an ad hoc way. Such procedures result in p-hacking and lack transparency and reproducibility. Most sociological analyses that explore covariate interactions also neglect how combinations of covariates and nonlinear interactions may best identify key subpopulations of interest. These analyses are thus limited in the subgroups considered, and they seldom move us beyond our expectations, and inherent biases, to consider new meaningful groups.

In this article, we used causal trees, a tree-based machine learning algorithm, to uncover sources of treatment effect heterogeneity. Uncovering heterogeneity using decision trees represents an especially promising use of machine learning methods for causal inference (Athey and Imbens 2017). Causal trees allow researchers to identify subpopulations that respond differently to treatments by searching over high-dimensional functions of covariates and their interactions. The algorithm partitions the data to minimize heterogeneity in within-leaf treatment effects. We used honest estimation, splitting the sample into subsamples to determine the model and estimating effects. Strategies such as these will increasingly be needed to justify analytic decisions in applied work (Athey 2019). Applying causal trees to observational data, we demonstrated how to use various adjustment strategies to address confounding within leaves, including IPW, nearest neighbor matching, and doubly robust causal forests. Other covariate adjustment strategies are possible to estimate leaf-specific effects. We compared results based on causal trees with traditional strategies based on conventional covariate and propensity score partitioning.

Our empirical application addresses a central question in research on social inequality, the effect of college on wages. We identified sources of heterogeneity in effects and unanticipated subgroups of notable interest. For example, instead of simply focusing on effect differences by mother’s education, as we did in our covariate partitioning, our recursive partitioning approach based on causal trees revealed a particularly responsive subgroup of individuals whose mothers had less than a high school degree, who grew up in large families, and who had low social control. Moreover, not all individuals whose mothers had more than a high school degree were equally less responsive. Those with low measured cognitive ability were particularly responsive. We thus identified responsive subgroups with different characteristics. The responsive subgroups identified by the causal tree, however, shared a low propensity of college. We also described distinct subgroups whose likelihood of low-wage work was less affected by college, that is, individuals with high levels of socioeconomic advantage and people with average background characteristics yet low levels of parental education.

The automation of some empirical tasks does not absolve our responsibility to carefully consider covariate imbalance, confounding, and the interpretation of estimated effects. In estimating heterogeneous treatment effects under unconfoundedness, we assume that the treatment effect varies by the subgroups identified and not by unobserved factors. We also face the possibility that the unconfoundedness assumption does not hold in our analyses, and that effects may be differentially biased across partitioned subgroups. In our application, for example, we know that continuing schooling is a highly selective process. Of the possible unobserved factors, some are systematic, reflecting individuals’ resistance to continuing their schooling. Expanding on the existing causal tree literature, we demonstrated several adjustment strategies at the estimation stage. We also assessed localized covariate balance, and we performed localized sensitivity analyses to assess the effect of differential unobserved confounding.

It is well known in the machine learning literature that predictions based on a single tree are sensitive to noise in the training set. The “greedy” optimization produces high-variance solutions. Minor modifications to the input data can produce large effects on the tree structure. Forests, or ensemble methods that average over many trees, tend to have lower variance than single decision trees. However, ensemble methods are black-box algorithms. The decrease in variance comes at the cost of interpretability. Causal trees are useful for uncovering interpretable responsive subpopulations. The tree-based machine learning literature, however, is rapidly evolving. New work in the literature on causal trees and forests continues to try and identify a “best” tree from the forest, to allow an interpretable tree similar to the causal tree we present here, while addressing the instability of single decision trees and retaining the advantages of the causal forest (e.g., see https://github.com/grf-labs/grf/issues/281). New approaches may ultimately result in a preferable tree structure. Still, the general principles we describe will continue to be applicable.

Our predetermined ideas as to which groups matter surely stifle social scientific progress. In this article, we adopted a machine learning approach based on decision trees to studying causal effects that allows us to uncover treatment effect heterogeneity and avoids common data-driven dangers. Machine learning algorithms are attractive for generating models where there may be numerous interaction effects a priori unknown to researchers. Causal trees offer a straightforward, intuitive analog to conventional covariate partitioning routinely used by sociologists, yet with more defensible statistical properties and reproducible search procedures, yielding the opportunity for meaningful data-driven discovery. These properties make causal trees a substantively powerful tool for sociological applications. Additional approaches will emerge that offer improvements to our understanding of treatment effect heterogeneity. We urge sociologists interested in variation in effects to apply these techniques to engage more explicitly with methods of discovery and improve research practices for exploring effect heterogeneity.

Biographies

Jennie E. Brand is a professor of sociology and of statistics at the University of California, Los Angeles (UCLA). She is director of the California Center for Population Research and codirector of the Center for Social Statistics at UCLA. She is chair of the Methodology Section of the American Sociological Association (ASA) and chair-elect of the Inequality, Poverty, and Mobility Section of the ASA. She is also a member of the board of the International Sociological Association Research Committee on Social Stratification and Mobility, a member of the Technical Review Committee for the National Longitudinal Surveys Program at the Bureau of Labor Statistics, and associate editor at Science Advances. Her research centers on social stratification and inequality and its implications for various outcomes that indicate life chances, with a methodological focus on causal inference and machine learning.

Jiahui Xu is a PhD student in sociology at Pennsylvania State University. She earned her master’s degree in applied economics at UCLA. Her research interests lie in causal inference and demography. She currently works on causal inference with machine learning and evaluation of sociological effect heterogeneity.

Bernard Koch is a PhD student in sociology at UCLA. He is interested in the science of science, cultural evolution, and computational methods. He is currently focused on the application of deep learning to network and causal inference problems to help identify how we can make science more equitable, efficient, and productive.

Pablo Geraldo is a PhD student in sociology at UCLA and student affiliate of the California Center for Population Research. His research examines inequality in education and the labor market, using a mixture of causal inference, network analysis, and machine learning approaches.

APPENDIX

Figure A1.

Causal forest (generalized random forest) algorithm.

Figure A2.

Causal tree algorithm.

Table A1.

t Tests for Propensity and Covariate Partitioning Results

		(a)	(b)
Propensity score	(a) Low
	(b) Mid	−2.41
	(c) High	−3.12	2.41
Parental income	(a) Low
	(b) Mid	−1.81
	(c) High	−3.36	−1.87
Mothers’ education	(a) Less than high school
	(b) High school	−3.32
	(c) College or higher	−3.06	.36
Ability	(a) Low
	(b) Mid	−2.46
	(c) High	−2.91	−.04
Race	(a) Black
	(b) Hispanic	.40
	(c) White	−1.36	−1.97

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Cells indicate unequal-variances t-test values for tests of difference between each of the pairs of subgroup effects.

Table A2.

t Tests for Recursive Partitioning Results

Leaf Legend	Leaf	1	2	3	4	5	6	7	8	9	10
L1: mothers’ education < 12	1
L2: L1 & number of siblings ≥ 2	2	−.67
L3: L2 & low control ≥ 10	3	−1.94	1.30
L4: L2 & low control < 10	4	−.45	−.94	−1.89
L5: L4 & female	5	.34	−.10	−.97	.63
L6: L4 & male	6	−.86	−1.22	−1.93	−.47	−.96
L7: L1 & number of siblings < 2	7	−1.59	−1.92	−2.55	−1.17	−1.60	−.65
L8: mother’s education ≥ 12	8	−2.19	−3.04	−4.41	−.91	−1.60	−.09	.77
L9: L8 & ASVAB scale < −.44	9	1.91	1.30	.06	1.89	.99	1.94	2.55	4.18
L10: L8 & ASVAB scale ≥ −.44	10	−2.99	−.94	−5.13	−1.44	−2.06	−.05	−.43	−1.25	4.86

Note: Data are from the National Longitudinal Survey of Youth 1979 cohort. The sample is restricted to individuals who were 14 to 17 years old at the baseline survey in 1979 (n = 5,582), who had completed at least the 12th grade (n = 4,548), and who had no missing data on the outcome (n = 4,382). College completion is measured as a 4-year degree completed by age 25. Cells indicate unequal-variances t-test values for tests of difference between each of the pairs of leaves represented by the leaf number. ASVAB = Armed Services Vocational Aptitude Battery; L = leaf.