Microtubule nucleation complex behavior is critical for cortical array homogeneity and xylem wall patterning

Significance

The plant cortical microtubule array is an established model system for self-organization, with a rich history of complementary experiments, computer simulations, and analytical theory. A hitherto unappreciated question is how array homogeneity is maintained given that new microtubules nucleate from existing microtubules. Based on detailed observations of the nucleation process, we derive a more realistic nucleation algorithm that promotes homogeneity. Our work highlights critical aspects of microtubule nucleation that warrant further experimental investigation and enables various lines of new quantitative, mechanistic research into how cells dynamically control their cell wall properties. At a mechanistic level, moreover, this work relates to the theory of cluster coexistence in Turing-like continuum models and demonstrates its relevance for discrete stochastic entities.

Abstract

Plant cell walls are versatile materials that can adopt a wide range of mechanical properties through controlled deposition of cellulose fibrils. Wall integrity requires a sufficiently homogeneous fibril distribution to cope effectively with wall stresses. Additionally, specific conditions, such as the negative pressure in water transporting xylem vessels, may require more complex wall patterns, e.g., bands in protoxylem. The orientation and patterning of cellulose fibrils are guided by dynamic cortical microtubules. New microtubules are predominantly nucleated from parent microtubules causing positive feedback on local microtubule density with the potential to yield highly inhomogeneous patterns. Inhomogeneity indeed appears in all current cortical array simulations that include microtubule-based nucleation, suggesting that plant cells must possess an as-yet unknown balancing mechanism to prevent it. Here, in a combined simulation and experimental approach, we show that a limited local recruitment of nucleation complexes to microtubules can counter the positive feedback, whereas local tubulin depletion cannot. We observe that nucleation complexes preferentially appear at the plasma membrane near microtubules. By incorporating our experimental findings in stochastic simulations, we find that the spatial behavior of nucleation complexes delicately balances the positive feedback, such that differences in local microtubule dynamics—as in developing protoxylem—can quickly turn a homogeneous array into a banded one. Our results provide insight into how the plant cytoskeleton has evolved to meet diverse mechanical requirements and greatly increase the predictive power of computational cell biology studies.

The plant cell wall is a highly versatile structure that has to adapt to diverse mechanical requirements (1–3). Wall mechanical properties are tuned through chemical composition and, critically, through anisotropic deposition of wall material (4–6). A key structure in this process is the cortical microtubule array, which determines where cell wall materials are inserted (7–10) and guides the deposition and, hence, orientation of cellulose microfibrils, the main load-bearing component of cell walls and determinant of their anisotropic mechanical properties (7, 11–13). The cortical array responds to various mechanical (14, 15), geometrical (16–18), developmental (19–21), and environmental (19) cues, integrating this information for future plant growth and function. This ability to respond to local wall stresses and other cues introduces a morphomechanical feedback loop that is considered the central ingredient of current plant growth models (22).

To make cell walls meet diverse mechanical requirements, the dynamic cortical microtubules can self-organize into various ordered structures (23), as illustrated by our focal examples: The arrays can be fully homogeneous, like the highly aligned transverse arrays of elongating interphase cells (Fig. 1A) (24) or locally patterned like the bands observed in developing protoxylem elements (Fig. 1B) (25). Both cases require an even distribution of wall material and, therefore, of microtubules, either over the entire membrane or among the bands. It has surfaced from multiple modeling studies (20, 26–29); however, that achieving the required degree of homogeneity is far from trivial. It remains an open question how plants meet this recurring homogeneity requirement.

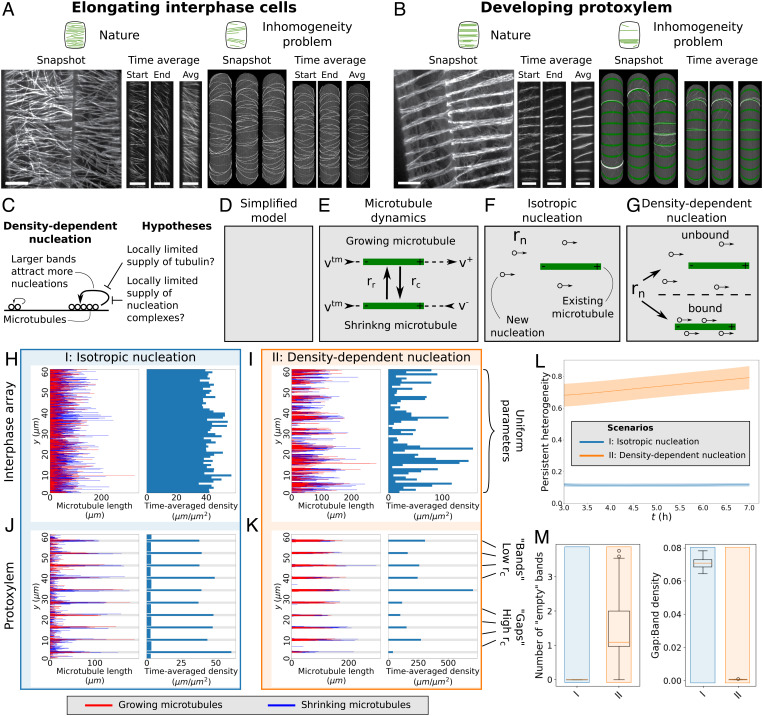
Fig. 1.

The inhomogeneity problem is reproduced by our simplified model. (A and B) Elongating interphase cells (A, Left) have homogeneous arrays of transversely oriented microtubules, while simulations with density-dependent nucleation (A, Right) yield highly inhomogeneous arrays. In developing protoxylem (B), microtubules are evenly distributed over a number of bands (B, Left), but in simulations with density-dependent nucleation, microtubules (white) accumulate in a small subset of the potential band positions, i.e., the green regions with favorable parameters for microtubule growth (B, Right). (Scale bars, 10 μm.) (C) Hypotheses for breaking the global competition caused by density-dependent nucleation. (D–G) Implementation of the simplified model with all microtubules perfectly transversely oriented (D). Under standard microtubule dynamics (E), microtubules grow or shrink at their plus ends with rates v⁺ and v⁻, respectively, retract at their minus ends with rate v^tm, and undergo spontaneous catastrophes and rescues at rates r_c and r_r, respectively. Under isotropic nucleation (F), microtubules nucleate at a fixed rate r_n at random (y-)positions. With density-dependent nucleation (G), nucleations still occur at a constant global rate r_n, but a portion of these nucleations is now distributed across existing microtubules proportional to their length. (H–K) Microtubule lengths and positions and time-averaged microtubule density of representative simulations using the simplified model for interphase arrays (H and I) and developing protoxylem (J and K). Protoxylem simulations were run for 2 h without an increased catastrophe rate in gaps followed by 5 h with an increase of a factor three. Other simulations were run for 7 h. Time-averaging was done over the last 3 h. See SI Appendix, Movie S1–S4 for time-lapse videos of the corresponding simulations. (L) Measure of persistent heterogeneity over time for simulations of the interphase arrays of elongating cells. Lines and shaded areas indicate mean and standard deviation, respectively. (M) The number of empty bands (bands with less than 25% of average microtubule density in bands) and ratio of microtubule density between gaps and bands for the protoxylem simulations. Boxplots are based on quantities averaged over the last 2 h of the simulations. Quantities in (L) and (M) were calculated from 100 independent simulations per nucleation mode.

The cortical microtubule array is a model system for self-organization. A rich tradition of biophysical models (26–28, 30–34) heavily founded upon quantitative experiments (35–39) has resulted in the current consensus model for spontaneous alignment dubbed “survival-of-the-aligned” (40). Simulation models continue to play a crucial role in understanding array behavior, for example, in the ongoing effort of unraveling how cells weigh the various and possibly conflicting cues for array orientation (18, 19, 41–45).

Currently, however, there are critical limitations to the application of these models as realistic simulators of the microtubule cytoskeleton, thus hampering progress on the above and other questions. The most striking shortcoming of this model is that, whenever the important aspect of microtubule-bound nucleation of new microtubules is incorporated, which is experimentally observed (38), this results in highly inhomogeneous arrays (Fig. 1 A and B) (20, 26–29). Arrays with such unrealistically large areas without microtubules would likely cause weak spots in the cell wall as cellulose synthase complexes (CESAs) are preferentially inserted at/near microtubules in hypocotyls (7). During localized secondary cell wall deposition, with known large gaps in the microtubule array, indeed hardly any CESAs are found in these gaps (46). Even if CESAs somehow wander into large gaps, the gaps may still jeopardize control over the cell’s expansion axis and morphology, as microtubules are required for rapid reorientation of CESA tracks, and without them, CESAs simply propagate the existing orientation of cellulose microfibrils by following previous CESA tracks (12).

This, what we call, inhomogeneity problem of the microtubule array arises because microtubule-based nucleation introduces positive feedback that amplifies fluctuations in local microtubule density. The existence of this positive feedback is supported by multiple experimental observations: In an established array, almost all microtubules are nucleated by γ-tubulin ring complexes (29, 47). These nucleation complexes are enriched in microtubule-dense regions (39) and occur almost exclusively in the microtubule bands of developing protoxylem once these are established (20). Microtubule-bound nucleation complexes, moreover, nucleate at a higher rate than unbound complexes (39). Therefore, some mechanism must balance this positive feedback. Such a mechanism would have to limit the extent of further microtubule growth or nucleation at a local level, as concentrating nucleation locations increases the local microtubule density. Two theoretical scenarios are 1) a local limitation of microtubule growth through the depletion of available tubulin subunits and 2) a local saturation of the amount of nucleation complexes that a microtubule-dense region can attract.

Microtubules grow through the incorporation of GTP–tubulin, mostly at their plus end, and their growth speed depends almost linearly on the GTP–tubulin concentration (48, 49). During shrinkage, tubulin subunits are typically released as GDP–tubulin (35, 50). Consequently, a high local density of dynamic microtubules implies both a high consumption and release of tubulin. The two different tubulin states, however, make that tubulin is released in an inactive form. In the context of small GTPase patterning, such a distinction provides a mechanism for the stable coexistence of multiple clusters as it allows redistribution of the substrate before it can be incorporated again (51). This process would suppress the peaks in local microtubule density and, consequently, yield more evenly distributed microtubule-based nucleations. Therefore, our first hypothesis is that local tubulin depletion could serve only as a homogenizing factor if the GDP–tubulin state is sufficiently long lived. The question remains whether this effect would be strong enough as simulations on small numbers of microtubules suggest that tubulin diffusion is so fast that local depletion has a very limited effect on concentration (52).

The second option for balancing the positive feedback and thus limiting the local increase of microtubule density may come naturally with revisiting the nucleation process. From pioneering work (27, 28, 30, 31) to current studies (17, 18, 33, 45), great progress has been made using isotropic nucleation, i.e., with uniform random location and orientation of new microtubules. In reality, however, most nucleations occur from nucleation complexes bound to existing microtubules, with new microtubules either parallel to their parent microtubules or branching at angles around 35° (38, 39, 53). So far, this microtubule-bound nucleation has been modeled as density-dependent nucleation: distributing the relevant nucleations over the existing microtubules proportional to their lengths (26–29). Density-dependent nucleation has several effects in simulations: it expands the range of biological parameters for which microtubules will spontaneously align, accelerates the alignment process in interphase arrays (26, 34), and speeds up protoxylem patterning (20). However, this density-dependent nucleation also leads to a global competition for nucleations, in which the microtubule densest region attracts the most nucleations (Fig. 1C), resulting in a strong local clustering of microtubules in simulated interphase arrays (26–28) and many missing bands in simulated protoxylem (20) (Fig. 1B). All quoted simulation studies with microtubule-based nucleation include branched nucleation, and this helps increase array homogeneity by colonizing adjacent empty membrane space (26). Nonetheless, the inhomogeneity problem surfaces in all these studies.

The core of the inhomogeneity problem is that with density-dependent nucleation, nucleation sites are distributed as if the system is well-mixed, so doubling the local density somewhere will double the probability that it will attract a specific nucleation at the expense of the rest of the array. In reality, however, the docking of a nucleation complex is primarily a local process. Although increasing the local microtubule density may speed up this process, it will affect only nearby but not distant nucleation complexes, so the local increase of nucleation must saturate. By liberally extending the analogy with small GTPase patterning—where decreasing benefits of increased local density favor cluster coexistence (54)—we arrive at our second hypothesis that such locally saturating nucleation rates would suppress the global competition for nucleations and support array homogeneity.

Here, we explore the potential of our two hypotheses for solving the inhomogeneity problem using a simplified stochastic simulation model of transversely oriented dynamic microtubules. We release this model as a simulation platform called CorticalSimple (55). Because of their different homogeneity requirements, we use both the basic homogeneous interphase array and the banded transverse array from developing protoxylem as model systems. Both systems depend on the well-studied process of microtubule alignment into a transverse array, which we here take for granted. This simplification provides a computationally attractive environment for exploring diverse mechanisms. As nucleation complex dynamics is not sufficiently studied yet to model it properly, we perform detailed observations of nucleation complex behavior, both under normal conditions and in sparse oryzalin-treated arrays.

This way, we discover that nucleation complexes predominantly appear at the plasma membrane near microtubules. Although this finding, at first glance, appears to aggravate the inhomogeneity problem, it turns out that our more realistic nucleation algorithm that includes this feature allows for homogeneity, while at the same time improving the ability to form patterned arrays. Our findings pave the way for a new generation of microtubule simulation models with broad biological applications.

Results

A Simplified Model of Transversely Oriented Microtubules Reproduces the Inhomogeneity Problem.

For solving the inhomogeneity problem, we simplified existing “full array models” (example snapshots in Fig. 1A and B) (26, 32) by taking alignment and orientation for granted. This means that all microtubules in our simulations are transversely oriented, i.e., they grow in the x-direction, and their positions are defined along the y-axis (Fig. 1D). The microtubules stochastically switch between growth and shrinkage (usually referred to as “catastrophe” and “rescue”), with parameters introduced in Fig. 1E and following the existing full array models. Example snapshots of the simplified arrays are shown in Fig. 1 H–K. The interphase array has uniform parameters, whereas in protoxylem, the catastrophe rate r_c is increased in predefined gap regions after a 2-h uniform initiation period, resulting in local destabilization of microtubules in an existing transverse array as experimentally observed and modeled by Schneider et al. (20). To validate our model, we use two types of microtubule nucleation from the full array models as a reference: isotropic nucleation, with uniformly distributed y-positions (Fig. 1F), and density-dependent nucleation, in which a density-dependent fraction of nucleation is “microtubule-bound,” with positions evenly distributed over all existing microtubule lengths (26) (Fig. 1G and SI Appendix, Materials and Methods).

With isotropic nucleation, we obtained homogeneous arrays and bands of similar density, whereas with density-dependent nucleation, arrays became inhomogeneous and band density varied substantially, often leaving bands largely empty (Fig. 1H–M). We thus validate the use of our model for studying the inhomogeneity problem by reproducing the effects of the two major nucleation modes used in the field so far.

Similar to full array simulations (20), the positive feedback inherent in density-dependent nucleation greatly enhanced the clearance of the gap regions. In the process, average microtubule density in the bands increased up to sixfold relative to isotropic nucleation, reflecting the surface covered by band regions (Fig. 1 J and K and SI Appendix, Fig. S1).

We did observe two quantitative differences with full array protoxylem simulations. First, we observed fewer empty bands with density-dependent nucleation than in the full array simulations (Fig. 1 B and K). Second, for both nucleation modes, we observed much larger differences in band vs. gap density, so that the experimentally observed ∼10-fold difference between bands and gaps (20) was easily reproduced even with isotropic nucleation, matching theoretical predictions of steady-state densities for noninteracting microtubules (see SI Appendix, Supplementary Text 1). Two differences from the full array simulations could underlie these quantitative effects: first, microtubules cannot leave the band or gap region they were nucleated in, and second, microtubule bundles—which tend to live longer than individual microtubules, even if the stability of individual microtubules is the same inside and outside bundles (56)—do not occur in the simplified model.

Tubulin Diffusion is Too Fast for Sufficient Local Variation in Microtubule Growth Velocities.

To test whether local tubulin depletion could solve the inhomogeneity problem, we made the microtubule growth speed dependent on the local (GTP–)tubulin concentration. Growing microtubules consumed (GTP–)tubulin, while shrinking microtubules released (GDP–)tubulin (Fig. 2A and SI Appendix, Materials and Methods). GDP–tubulin was recharged into GTP–tubulin at a constant rate β. We estimated that, with our default parameters, β should be less than β^* = 0.0425 s⁻¹ (SI Appendix, Supplementary Text 3) to have a chance that this mechanism could work.

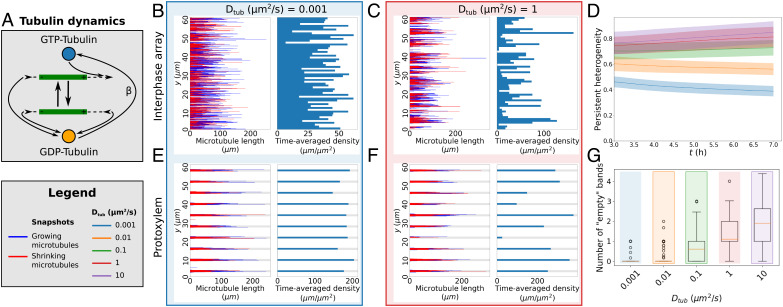
Fig. 2.

Local tubulin limitation requires unrealistically low tubulin diffusion to enhance homogeneity. (A) In our tubulin implementation, the v⁺ of the growing microtubules depends on the local GTP-tubulin pool, which is depleted as a result. Conversely, microtubule shrinkage increases the local GDP-tubulin concentration. GDP-tubulin is recharged at a constant rate β into the GTP-tubulin needed for growth. (B and C) Microtubule lengths and positions and time-averaged microtubule density of representative simulations using the simplified model with GTP- and GDP-tubulin with a tubulin recharge rate β = 0.01s⁻¹ (i.e., reactivations per particle per s) and two different tubulin diffusion coefficients (D_tub). Simulations were run for 7 h. Time-averaging was done over the last 3 h. See SI Appendix, Movie S5–S6 for time-lapse videos of the corresponding simulations. (E and F) Similar to (B and C), but for protoxylem. Simulations were run for two hours without increased catastrophe rate in gaps followed by 5 h with this increase. See SI Appendix, Movie S7–S8 for time-lapse videos of the corresponding simulations. (G) Number of empty bands (bands with less than 25% of average microtubule density in bands) for simulations with five different values of D_tub. Boxplots are based on quantities averaged over the last 2 h of the simulations. Quantities in (D) and (G) were calculated from 100 independent simulations using density-dependent nucleation.

With a plausible recharge rate of β = 0.01 s⁻¹ (i.e., reactivations per particle per s) (57), our simulations only produced nearly homogeneous arrays for tubulin diffusion coefficients of about 0.01 μm²/s and lower (Fig. 2 B and E). This apparent maximal diffusion coefficient for homogeneity increased with increasing β (SI Appendix, Fig. S2). However, no reasonable value of β could prevent inhomogeneity with diffusion coefficients of 1 to 10 μm²/s, similar to a measured cytoplasmic tubulin diffusion coefficient of 6 μm²/s in animal cells (58) (Fig. 2 C, D, F, and G and SI Appendix, Fig. S2).

As expected from theoretical considerations (51, 54), arrays were more homogeneous with the distinction between GTP– and GDP–tubulin than without (SI Appendix, Fig. S3). For the lowest diffusion coefficients, tubulin essentially was a local resource over the time of the simulation, and any observed array homogeneity simply reflected the homogeneous initial tubulin distribution (SI Appendix, Fig. S4).

These results suggest that, although the tubulin-depletion mechanism could improve homogeneity in principle, it does not ensure homogeneity in practice.

Nucleation Complexes Preferentially Appear at the Membrane Near Microtubules.

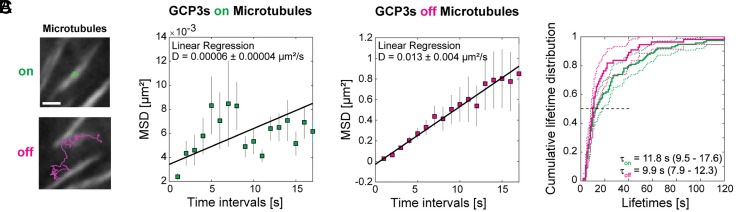
Since we found that local tubulin depletion does not solve the inhomogeneity problem, we next focused on nucleation. Little is known, however, about the mobility of nucleation complexes associated (directly or indirectly) with the membrane yet away from microtubules because normally most complexes are microtubule bound (38, 39). We, therefore, treated cells with the microtubule-depolymerizing drug oryzalin (59) to reduce the density of the cortical microtubules and observed GFP-labeled γ-tubulin complex protein (GCP)3, a component of the nucleation complex, using spinning disc confocal microscopy. We found that microtubule-bound complexes were indeed immobile, while complexes that appeared independent of microtubules at the plasma membrane showed diffusive behavior with a diffusion coefficient of approximately 0.013 μm²/s (Fig. 3 A and B and SI Appendix, Movie S9–S11). Lifetimes of bound and unbound nucleation complexes were similar to those found by others (39), validating the use of these cells.

Fig. 3.

Microtubule nucleation complexes are statically bound to microtubules and diffusively associated with plasma membranes. (A) Example trajectories of tracked GCP3 foci located on microtubules (green, Top) and off microtubules (magenta, Bottom). Scale bar, 1 μm. Time-lapse movies available as SI Appendix, Movie S9–S10. (B) Mean-squared displacement (MSD) calculated for 115 microtubule-bound and 55 diffusing GCP3 foci. Squares and line extensions represent means ± SDs for the given time intervals, and the solid line represents a weighted linear fit yielding the diffusion constant and fit error. The data were recorded from nine cells and five seedlings. (C) Cumulative lifetime distributions show that the median lifetime of the tracked GCP3 foci on microtubules (green) and off microtubules (magenta) are similar. Solid and dashed lines represent the empirical cumulative distribution function and the 95% lower and upper confidence bounds for the evaluated function values, respectively. The horizontal dashed line represents the median value.

By comparing new membrane associations in oryzalin-treated cells to those in mock-treated controls, we discovered that the appearance of nucleation complexes at the plasma membrane was preferentially near microtubules. For the control cells, we found that complexes appeared at an average rate of 0.0037 complexes μm⁻²s⁻¹ (SI Appendix, Table S1), which is similar to the 0.0045 complexes μm⁻²s⁻¹ we estimated to keep the overall nucleation rate consistent with previous simulations (SI Appendix, Supplementary Text 4). To maintain consistency, we used the latter number in our simulations. Even in the microtubule-sparse oryzalin-treated cells, we found an overrepresentation of nucleation complex appearances on the few remaining microtubules. Nucleation complexes appeared at an average rate of 0.00026 complexes μm⁻²s⁻¹, which could be separated in a rate of 0.013 complexes μm⁻²s⁻¹ for complexes appearing near/at microtubules and 0.000085 complexes μm⁻²s⁻¹ excluding these complexes (SI Appendix, Table S1). Because nucleation complexes colocalizing with microtubules may have appeared nearby and diffused toward them between frames, the first of these three values represents an upper bound and the last a lower bound. Still, as a conservative estimate, the rate at which new complexes appeared was at least an order of magnitude smaller in the absence of microtubules. Notably, the rate of 0.013 complexes μm⁻²s⁻¹ is only 3 to 3.5 times higher than in a normal density array, suggesting a strong local saturation of the nucleation complex appearance rate.

Local Limitation of Nucleation Complexes Can Solve the Inhomogeneity Problem.

Based on these experiments, we explicitly incorporated nucleation complexes into our simulations as particles that can associate with the membrane, here called “insertion” for simplicity of writing, move around diffusively in (effectively) two dimensions, attach to a microtubule upon encounter, and eventually either disassociate from the membrane or nucleate (Fig. 4A and SI Appendix, Materials and Methods). Note that the behavior of our model does not depend on the actual biochemical nature of this membrane association, only on observable parameters like typical duration. With this model, we investigated the impact of differential insertion rate (r_b within attraction radius R of any microtubule, r_{b, min} otherwise) and differential nucleation rates for complexes on (r_{n, bound}) or off (r_{n, unbound}) microtubules (39) on array homogeneity and patterning (Fig. 4).

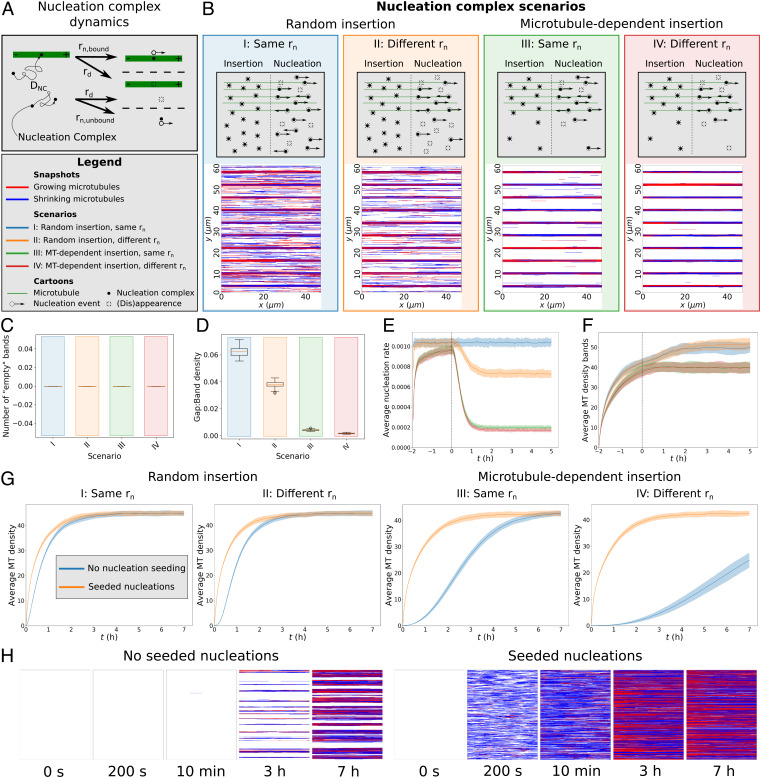
Fig. 4.

Local limitation of nucleation complex availability can ensure array homogeneity and enhance protoxylem band formation. (A) In our nucleation complex implementation, each complex moves within the two-dimensional plane of the membrane with diffusion coefficient D_NC and binds the first microtubule it encounters. A nucleation rate applies to each separate complex and, by default, this rate is higher for microtubule-bound complexes (r_{n, bound}) than for freely diffusing (r_{n, unbound}) ones. Complexes also disappear at rate r_d. Microtubule insertion into the membrane occurs at a constant rate r_b. For areas outside a distance R of a microtubule, this rate is reduced to r_{b, min} in case of microtubule-dependent nucleation complex insertion. (B) Final array snapshots of representative protoxylem simulations for four different nucleation complex scenarios: I, II: random insertion. III, IV: microtubule-dependent insertion. I, III: no difference between bound and unbound nucleation rates. II, IV: reduced nucleation rate for unbound complexes. See SI Appendix, Movie S12–S15 for time-lapse videos of the corresponding simulations. (C) Number of empty bands (bands with less than 25% of average microtubule density in bands) (D) Ratio of microtubule density between gaps and bands for the protoxylem simulations. (E) Average global nucleation rates. (F) Average microtubule density in band regions. (G) Average microtubule density for simulations without bands and gaps with and without seeded nucleations. (H) Snapshots at various time points of a simulated array with microtubule-dependent insertion and a reduced r_n for unbound complexes with and without seeding. See SI Appendix, Movie S16–S17 for time-lapse videos of the corresponding simulations. All summary statistics were calculated from 100 simulations. Lines and shaded areas indicate mean and SD, respectively. Boxplots are based on quantities averaged over the last 2 h of the simulations. Protoxylem simulations were run for two hours without an increased catastrophe rate in gaps followed by 5 h with this increase. Other simulations were run for 7 h.

We expected that our discovery of microtubule-dependent insertion, as yet another factor that favors microtubule-dense regions, would further aggravate the inhomogeneity problem. We found, however, that with a realistic attraction radius of R = 50 nm, twice the width of a microtubule, fully homogeneous arrays were formed over time (Fig. 4H). This was, however, a slow process, increasing the importance of a previously reported alternative source of nucleation early during de novo array establishment (29), here called “seeding” (Fig. 4 G and H). By halving R, small gaps started to appear in the array, in which nucleation complex insertion was not enhanced by microtubules, lowering the total microtubule density (SI Appendix, Fig. S5). The diffusion coefficient D_NC of unbound nucleation complexes would have had to be reduced by two orders of magnitude from our experimentally observed value to achieve a similar reduction of microtubule density. With further reductions, it would become impossible to sustain a normal density array (SI Appendix, Fig. S6).

For protoxylem patterning, we found that the differential insertion rate resulted in a more effective clearing of the gap regions than the differential nucleation rate, both for data-based rate differences (Fig. 4 B and D) as well as smaller r_b differences (SI Appendix, Fig. S7A) and artificially matched differences in r_b and r_n (SI Appendix, Fig. S8). Notably, the density in band regions increased only slightly during the separation process (Fig. 4F), in stark contrast to the large increase under density-dependent nucleation (SI Appendix, Fig. S1 B and D).

Homogeneity was robustly maintained, as bands were never lost (Fig. 4 B and C) except with very low diffusion coefficients ((SI Appendix, Fig. S7B). Increasing D_NC from low values reduced separation at most threefold. This observation strongly suggests that the measured value is roughly optimal for enhancing local array patterning and at the same time avoiding inhomogeneity and density loss problems ((SI Appendix, Fig. S7 C and D). A similar exploration with an equal insertion rate showed a window of optimal D_NC-values for separation with a reduced (but not equal) nucleation rate for unbound complexes (SI Appendix, Fig. S9). The default D_NC fell within this window for sufficiently large differences between bands and gaps only (starting from f_cat ≈ 3 to 4). This observation shows that, with sufficient (evolutionary) parameter tuning, reasonable degrees of separation could be obtained without preferential insertion at microtubules but only with large differences in microtubule dynamics. In conclusion, differential insertion increases the patterning potential of the array and makes this regime more accessible.

Discussion

We have developed a simplified model of transversely oriented microtubules and performed quantitative experimental observations of nucleation complex dynamics to investigate how plants ensure homogeneity of their cortical microtubule array and, consequently, cell wall. With our model and experiments, we identified the saturation of nucleation complex recruitment to microtubule-dense regions as a plausible mechanism for countering positive feedbacks inherent in microtubule-based nucleation that would otherwise cause severe array inhomogeneity. The key element of this mechanism is that the competition for nucleation complexes becomes local instead of global. This effect is achieved because the local probability of attracting specific nucleation now saturates with local microtubule density as opposed to the linear scaling under density-dependent nucleation. This mechanism is of a different nature than the contribution of branched nucleation to array homogeneity (26), as branched nucleation introduces only some local dispersal.

Besides the two factors already known, i.e., predominant nucleation from existing microtubules (38, 53) and reduced nucleation rate for unbound complexes (29, 39), we found that the appearance (or “insertion” for ease of writing) of nucleation complexes at the membrane is strongly biased toward microtubules. The molecular nature of this membrane association remains to be investigated, but our results clearly demonstrate the importance of the existence of this state. Together, these factors enable both completely homogeneous and complexly patterned arrays, as shown with our model systems of elongating interphase cells and developing protoxylem. Moreover, this “insertion” bias increases the importance of “seeding” the array with alternative (“GCP-independent”) nucleations as previously observed (29) to ensure its timely establishment.

We were unable to produce homogeneous arrays with realistic tubulin diffusion coefficients. The effect of the tubulin concentration on microtubule dynamics, however, is more complex than modeled here. Most importantly, the tubulin concentration also influences the nucleation rate (48, 49). However, GTP–tubulin profiles (52) are so flat for realistic tubulin diffusion coefficients that we do not expect a large impact from including such aspects. Furthermore, cytoplasmic streaming is likely to result in a greater effective diffusion coefficient for tubulin in plants compared to the available measurements from animal cells (58), making it even less likely that local tubulin depletion can effectively ensure homogeneity. So, while the existence of other mechanisms contributing to microtubule array homogeneity cannot be ruled out, the behavior of nucleation complexes in line with current experimental evidence likely plays a major role.

At the whole cell level, however, tubulin depletion can be an important factor in limiting microtubule density through changes in microtubule dynamics (32, 40). Markedly, using parameters measured in early interphase wild-type cells can result in unbound microtubule growth (40, 60), whereas with all parameter sets measured in established wild-type arrays, a finite steady-state microtubule density exists (20, 32, 37).

Our results demonstrate the value of our simplified model as a powerful tool for solving complex problems that can be interpreted as approximately one-dimensional. The simplification of abandoning microtubule-microtubule interactions, of course, introduces some quantitative differences with the full model, which can even increase our understanding of the real system. The largest difference is that, contrary to simulations with interacting microtubules (20), we observed strong band formation with isotropic nucleation while using the same parameters for microtubule dynamics. Two factors may underlie this difference: 1) Microtubule bundling, also without microtubule-based nucleation, increases the persistence of microtubule bundles, including those in the gap regions. Indeed, in Schneider et al. (20), it is shown that microtubule turnover is an important determinant of the band/gap-separation rate. 2) The effective nucleation rate in bands is higher in the simplified model because all nucleations inside a band give rise to microtubules that remain inside the band. In the full array model, a substantial part of these nucleations is “lost” because the microtubules quickly grow into the gap regions. Indeed, the authors also found a much stronger degree of separation with isotropic nucleation when the nucleation rate in bands was increased. Taken together, this suggests that the aspect of coalignment between parent and new microtubule (38) plays an important role in increasing the relevant nucleation rate inside bands and, hence, band stability. Band stability could additionally be enhanced by microtubule bundling itself.

Additional speedup of the separation process occurs if the band locations match well with density fluctuations in the (initial) microtubule array (20). This match is likely better in reality than in current models as gap regions are dynamically specified in the presence of the microtubule array. In metaxylem, gaps are specified by the small GTPase patterning protein Rho of plants 11 (AtROP11) and downstream effectors MIDD1 and kinesin-13A (61, 62). Various ROPs and the aforementioned effectors are also expressed during protoxylem formation (63, 64), and striated AtROP7 patterns are observed in protoxylem (65). The expected consequences, the regional differences in microtubule stability, are actually best quantified in protoxylem (20), which we also used as input for our simulations. Results so far, however, indicate that the corresponding microtubule patterns are not simply a readout of an ROP pattern, as changes in microtubule dynamics affect both the dynamics and outcome of the patterning process (20, 61, 66).

Notably, ROPs and other polarity factors are also indicated in the specification of the preprophase band (67), the single microtubule band that forms around the nucleus prior to cell division (68, 69), and altered microtubule dynamics are observed during its formation (37). Together, these phenomena suggest that integrating ROP patterning and microtubule dynamics into a single simulation environment will provide mechanistic insight into many processes.

How could ROPs and microtubules sometimes produce a homogeneous pattern, like in protoxylem and metaxylem, and sometimes a highly inhomogeneous one, like the preprophase band? Coincidentally, the literature on small GTPase patterning offers deeper insights. In the most common case, when GTPases are only interconverted between active and inactive states, the system can “phase separate” into a single cluster of active GTPases (54, 70–72). In contrast, multiple clusters can stably coexist by 1) the addition of GTPase turnover (i.e., production and degradation) (54, 73), 2) an inactive intermediate form that cannot be reincorporated into an (active) patch immediately (51)—much like the GDP–tubulin as intermediate modeled here—or 3) an additional factor that increasingly limits the growth of active patches as they get larger, like ROP GTPase activating proteins (GAPs) that increase ROP inactivation (54). All these options have in common that the growth of larger patches is specifically limited, and a baseline supply of raw material (inactive GTPases or nucleation of new microtubules) is guaranteed for smaller patches.

This comparison immediately stresses the significance of the uniform base insertion rate of nucleation complexes into the membrane of our model as a local supply. Our experiments on oryzalin-treated cells show that nucleation complexes are indeed inserted into empty regions in the plasma membrane. We expect that rapid diffusion of cytosolic nucleation complexes, likely enhanced by cytoplasmic streaming, can ensure a relatively uniform base insertion rate. Additionally, our data suggest that nucleation complexes are actively released from the membrane, because despite very different insertion rates, residence times near/at and away from microtubules are very similar (Fig. 3C), particularly for nonnucleating complexes (39). If, however, release were governed by thermodynamic equilibrium, complexes would have remained much longer when on microtubules. Active release would contribute to the sustenance of the cytosolic pool of nucleation complexes and, hence, the base insertion rate. As multiple nucleation complex subunits contain regulatory phosphorylation sites (74), the release could be in an inactive state, which would further support homogeneity (51). One form of density-dependent growth limitation the conceptual equivalent of GAP proteins (54) that is present in our model is the fact that a set of n isolated microtubules are more effective in capturing diffusing nucleation complexes from the membrane than a single bundle of n microtubules of the same length^*. Additionally, a similar but potentially stronger effect would occur if bundling of microtubules leads to shielding of part of the binding sites for nucleation complexes, thereby specifically reducing the per-length insertion rate of bundled microtubules.

The above mechanisms are not mutually exclusive and can enhance each other. Moreover, plant cells may operate close to the inhomogeneous regime of global competition as occurs with density-dependent nucleation, given the existence of inhomogeneous structures like the preprophase band. If cells are indeed close to this alternative regime, a substantial local increase in the factors that recruit nucleation complexes could over time trap a large fraction of these complexes to a specific region. The “group A” TPX2/TPXL proteins are ideal, though currently speculative, candidates for supporting preprophase band formation this way, as they are indicated in the recruitment of nucleation complexes to microtubules (75) and contain a nuclear importin domain (76), which could provide the correct perinuclear positioning of a high nucleation zone upon release. Simulations show that concentrating microtubule nucleation to the future band region can indeed reproduce a preprophase band-like structure (77).

Our observations of nucleation complex behavior and the solution they provide to the inhomogeneity problem pave the way for the next generation of microtubule simulation models. Some pressing biological questions that require detailed simulations including realistic nucleation are the following: 1) How do cells integrate all the different cues affecting array orientation (14–21) and resolve conflicts between them? 2) How can changes in the distribution of parent–offspring nucleation angles lead to substantial changes in cell morphology as, for example, in the tonneau2/fass (ton2) mutant (78)? 3) How can a continuous interaction between ROPs and their downstream effectors on the one hand (61, 62) and the microtubule array on the other hand lead to various complex wall patterns like in protoxylem and metaxylem? In summary, our work enables various lines of quantitative, mechanistic research that will improve our understanding of how cell wall properties are dynamically controlled.

Materials and Methods

Simulation Setup.

Cortical microtubules exist effectively on a two-dimensional surface on the inside of the membrane. Therefore, we chose our simulation domain to represent the cortex of a cylindrical cell, with a height of 60 μm and a radius of 7.5 μm as in Schneider et al. (20). This domain was represented by a rectangle with a horizontal periodic x-axis and a vertical y-axis representing the circumference and length of the cylinder, respectively. Except for the variant with nucleation complexes, horizontal positions were irrelevant and not tracked in the simulations. CorticalSimple (55) is written in Python and can be downloaded from git.wur.nl/Biometris/articles/corticalsimple.

Core Microtubule Dynamics.

Microtubule growth, shrinkage, and minus-end retraction (treadmilling) occur at speeds v⁺, v⁻, and v^tm, respectively, with catastrophes and rescues occurring at rates r_c and r_r, respectively (Fig. 1E). These are the same dynamics as described by Tindemans et al. (32), and parameters were based on (20) (see SI Appendix, Table S2 for parameter values).

Protoxylem Band and Gap Regions.

Protoxylem simulations used ten band regions of 1 μm separated by gap regions of 5 μm (with 2.5 μm gap regions on either end of the domain). Following (20), microtubule stability was reduced in the gap regions by increasing the catastrophe rate by a factor f_cat (default: f_cat  =  3) compared to the band regions. Before this increase in the gap catastrophe rate, simulations were run for two hours with homogeneous parameters (f_cat = 1), allowing a microtubule array to form.

Basic Nucleation Modes.

Isotropic nucleations were drawn at a constant global rate of r_n ⋅ A, where r_n is the nucleation rate in nucleations μm⁻²s⁻¹, and A is the domain area in μm² and given uniformly distributed y-positions (Fig. 1F).

Density-dependent nucleation was implemented as in Deinum et al. (26). Nucleation events were scheduled with a total rate r_n, of which a density-dependent fraction was assigned to microtubules, resulting in a bound rate r_{n, bound} following:

$$\begin{array}{c}\hfill r_{n,bound}=r_n\frac{\rho }{\rho +{\rho }_{\frac{1}{2}}},\end{array}$$ [1]

where ρ is the global microtubule density in μm microtubule per μm², and ${\rho }_{\frac{1}{2}}$ is the microtubule density at which half of all nucleations are bound. We then assigned y-positions to the unbound nucleations, as described for isotropic nucleation. The bound nucleations were distributed randomly across the total microtubule length and then got the y-position of their parent microtubule with a small normally distributed displacement (σ = 0.1 μm), which was redrawn for positions falling outside the simulation domain (Fig. 1G).

Tubulin Dynamics.

In one dimension, tubulin dynamics for a single tubulin follows the diffusion equation:

$$\begin{array}{c}\hfill \frac{\partial c_T}{\partial t}=D_{\mathit{tub}}\frac{{\partial }^2{c}_T}{\partial y^2}+f(MT),\end{array}$$ [2]

where c_T is the tubulin concentration, t is the time, y is the position along the longitudinal axis, D_tub is the tubulin diffusion coefficient, and f(MT) the function of microtubule dynamics that specifies the net release of tubulin from microtubules. This last term can be calculated directly from local changes in microtubule lengths at each integration time step. Similarly, when distinguishing GTP– and GDP–tubulin, we have:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\partial c_{T_1}}{\partial t}& =D_{\mathit{tub}}\frac{{\partial }^2{c}_{T_1}}{\partial y^2}+\beta c_{T_2}-f(M{T}_{\mathit{Growing}}),\hfill \\ \hfill \frac{\partial c_{T_2}}{\partial t}& =D_{\mathit{tub}}\frac{{\partial }^2{c}_{T_2}}{\partial y^2}-\beta c_{T_2}+g(M{T}_{\mathit{Shrinking}}),\hfill \end{array}\end{array}$$ [3]

where c_T1 and c_T2 are the concentrations of GTP– and GDP–tubulin, respectively, β is the recharge rate at which GDP–tubulin is converted back into GTP–tubulin, and f(MT_Growing) and g(MT_Shrinking) are the functions of microtubule dynamics that determine the tubulin consumption by growing microtubules and the tubulin release by shrinking microtubules, respectively. For convenience, we express tubulin concentrations in μm of microtubule length equivalent per μm².

Arrays were initiated without microtubules and with a uniform (GTP–)tubulin concentration of L_max/A, where A is the domain area and L_max is the maximum total microtubule length when all tubulin is in the microtubule form. Growth speed v⁺ was made linearly dependent on the local (GTP–)tubulin concentration (32), according to:

$$\begin{array}{c}\hfill v^{+}(y)=v_0^{+}\frac{c_T(y)}{c_{T,0}}=v_0^{+}\frac{A}{L_{\mathit{max}}}{c}_T(y),\end{array}$$ [4]

where v₀⁺ is the initial growth speed, and parameter c_{T, 0} is the initial homogeneous (GTP–)tubulin concentration.

The diffusion equations were integrated using a Crank–Nicolson algorithm (79) with integration steps of 0.01 s in time and 0.2 μm in space. Microtubule growth speeds were adjusted to the new tubulin concentration every time step and kept constant in between.

Nucleation Complexes.

In our nucleation complex implementation, membrane-associated complexes diffuse with diffusion coefficient D_NC. If a complex runs into a microtubule, it binds the microtubule and remains stationary. Therefore, to allow complexes to pass around the ends of microtubules, the x-positions and microtubule directions are tracked for this model variant.

Nucleation complexes are inserted at a constant rate r_b, which can be reduced to r_{b, min} for regions without a microtubule within a distance R in case of microtubule-dependent nucleation complex insertion.

Each individual complex can disassociate from the membrane at a rate r_d and nucleate at a rate r_n (Fig. 4A). Based on experimental data from Nakamura et al. (39), this nucleation rate is set a factor fifteen larger for microtubule-bound complexes than for unbound complexes (SI Appendix, Supplementary Text 4). Upon nucleation, the complex involved is removed from the simulation since experimental observations indicate that complexes that nucleated hardly ever nucleate a second time before disappearing (39). Positions of new microtubules are adopted from the parent nucleation complex, with the same small vertical displacement that is also used for density-dependent nucleation. The growing plus-end of each new microtubule is oriented either to the left or to the right with an equal probability.

Seeded nucleations are implemented by starting simulations with nucleation complexes with uniformly distributed complex-independent nucleations at a density of 1 nucleation per μm². This value has been chosen to be close to the steady-state microtubule density.

Nucleation complex diffusion has been implemented using two-dimensional Brownian motion simulations. Complexes move independently in both horizontal and vertical directions every time step by a distance of $\sqrt{2dt{D}_{\mathit{NC}}}N(0,1)$, where dt is the time step (0.01 s in our simulations), and N(0, 1) is a standard normally distributed random number.

Model Parameters.

All simulation parameters are given in SI Appendix, Table S2. Basic model parameters were chosen to be consistent with previous simulations of microtubule dynamics in protoxylem development (20). In the tubulin simulations, D_tub and β were varied to study their effect. L_max and v₀⁺ were tuned such that the average microtubule growth speed at steady state would be approximately equal to that used in simulations without tubulin (SI Appendix, Supplementary Text 2). Parameters r_b, r_d, r_{n, bound}, and r_{n, unbound} were estimated from data by Nakamura et al. (39) (SI Appendix, Supplementary Text 4). For simulations with microtubule-dependent nucleation complex insertion, we tried several values of r_{b, min} based on our experimental measurements and chose a distance R of 0.05 μm, which is about twice the width of a microtubule.

Measures of Heterogeneity.

For protoxylem simulations, we counted the number of largely empty bands, defined as bands with less than 25% of the average microtubule density in bands. The persistent heterogeneity measure for transverse interphase arrays was calculated as the SD of the values from a time-averaged microtubule density histogram divided by the average density. We used a histogram bin size of 1 μm and a time average over the last 3 h, with one measurement every 200 s.

Experimental Measurements.

Plant Material and Growth Conditions.

Arabidopsis (Arabidopsis thaliana, Columbia Col-0 ecotype) expressing the 35S promoter-driven VND7-VP16-GR (VND7) construct, the 35S promoter-driven mCherry-TUA5 microtubule marker, and the GCP3-GFP microtubule nucleation marker were used (20). Seeds were surface-sterilized and grown similar to ref. (20). To depolymerize MTs in epidermal cells, we applied 40 μM oryzalin for 4 h and subsequently focused on cells that showed remaining MT polymers in their cortex.

Induction of Protoxylem Formation.

Three-day-old dark-grown seedlings were transferred to half-strength MS, 1% sucrose plates supplemented with 10 μM dexamethasone (DEX). The unwrapped plates were then kept in the same phytotron for 24 h. Subsequently, seedlings were transferred to a microscope slide for imaging.

Spinning Disk Microscopy.

Imaging was performed similar to (20). Briefly, we used a spinning disc microscope consisting of a CSU-X1 spinning disk head (Yokogawa), an Eclipse TI (Nikon) inverted microscope body equipped with a perfect focus system, an Evolve CCD camera (Photometrics), and a CFI Apo TIRF 100x oil-immersion objective.

Image Analysis.

Confocal z-stack recordings of microtubules in noninduced and VND7-induced conditions were acquired (0.3 μm z-steps, 6 μm z-depth, and 300 ms integration time) and surface-projected using a custom-made MATLAB code used previously (80). Confocal single-plane time-lapse recordings of microtubules and GCP3 foci were acquired (1-s intervals, 2-min duration, 300-ms and 500-ms integration for microtubules, and GCP3, respectively) and analyzed using the open-source tracking software FIESTA (81). The in-built mean-squared displacement function was used to measure the diffusion constant of GCP3 foci. Cumulative lifetime distributions were made using the in-built MATLAB function ecdf.m.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Timelapse movie corresponding to Fig. 1H of a microtubule array simulation for an an elongating interphase cell with isotropic nucleation.

Movie S2.

Timelapse movie corresponding to Fig. 1I of a microtubule array simulation for an an elongating interphase cell with density-dependent nucleation.

Movie S3.

Timelapse movie corresponding to Fig. 1J of a microtubule array simulation for an a developing protoxylem cell with isotropic nucleation.

Movie S4.

Timelapse movie corresponding to Fig. 1K of a microtubule array simulation for an a developing protoxylem cell with density-dependent nucleation.

Movie S5.

Timelapse movie corresponding to Fig. 2B of a microtubule array simulation for an elongating interphase cell with isotropic nucleation and local tubulin limitation with a tubulin diffusion coefficient of 0.001 μm²/s.

Movie S6.

Timelapse movie corresponding to Fig. 2C of a microtubule array simulation for an elongating interphase cell with density-dependent nucleation and local tubulin limitation with a tubulin diffusion coefficient of 1 μm²/s.

Movie S7.

Timelapse movie corresponding to Fig. 2E of a microtubule array simulation for a developing protoxylem cell with isotropic nucleation and local tubulin limitation with a tubulin diffusion coefficient of 0.001 μm²/s.

Movie S8.

Timelapse movie corresponding to Fig. 2F of a microtubule array simulation for a developing protoxylem cell with density-dependent nucleation and local tubulin limitation with a tubulin diffusion coefficient of 1 μm²/s.

Movie S9.

Example of a GCP3-GFP focus stably bound to a cortical MT (ON). A single GCP3 focus stably bound to a remaining cortical MT polymer after four hours of 40 μM Oryzalin treatment. Single frames (left) of MTs (gray) and GCP3-GFP (green) and evolving maximum (MAX) projection (right). Temporal resolution is 2.6 seconds. Scale bar = 2 μm.

Movie S10.

Example of a diffusing GCP3-GFP molecule encountering cortical MTs without binding (OFF). A single GCP3 focus first diffusing in the vicinity of a cortical MT without binding to it then undergoes free diffusion in a MT-free manner (OFF) after four hours of 40 μM Oryzalin treatment. Single frames (left) of MTs (gray) and GCP3-GFP (magenta) and evolving maximum (MAX) projection (right). Temporal resolution is 2.6 seconds. Scale bar = 2 μm.

Movie S11.

Example of a freely diffusing GCP3-GFP molecule associated with the plasma membrane. A single GCP3 focus associates diffusively for about 30 seconds with the plasma membrane in complete absence of MTs (OFF) after four hours of 40 μM Oryzalin treatment. Single frames (left) of MTs (gray) and GCP3-GFP (magenta) and evolving maximum (MAX) projection (right). Temporal resolution is 1.3 seconds. Scale bar = 2 μm.

Movie S12.

Timelapse movie corresponding to Fig. 4B-I showing an overview of the simulated array of a microtubule array simulation for a developing protoxylem cell with explicit nucleation complexes using random complex insertion and the same nucleation rate on microtubules.

Movie S13.

Timelapse movie corresponding to Fig. 4B-II showing an overview of the simulated array of a microtubule array simulation for a developing protoxylem cell with explicit nucleation complexes using random complex insertion and a higher nucleation rate on microtubules.

Movie S14.

Timelapse movie corresponding to Fig. 4B-III showing an overview of the simulated array of a microtubule array simulation for a developing protoxylem cell with explicit nucleation complexes using microtubule-dependent complex insertion and the same nucleation rate on microtubules.

Movie S15.

Timelapse movie corresponding to Fig. 4B-IV showing an overview of the simulated array of a microtubule array simulation for a developing protoxylem cell with explicit nucleation complexes using microtubule-dependent complex insertion and a higher nucleation rate on microtubules.

Movie S16.

Timelapse movie corresponding to Fig. 4H showing an overview of the simulated array of a microtubule array simulation for an elongating interphase cell with explicit nucleation complexes using microtubuledependent complex insertion and a higher nucleation rate on microtubules. No seeded nucleations were used.

Movie S17.

Timelapse movie corresponding to Fig. 4H showing an overview of the simulated array of a microtubule array simulation for an elongating interphase cell with explicit nucleation complexes using microtubuledependent complex insertion and a higher nucleation rate on microtubules. Seeded nucleations were used.

Data, Materials, and Software Availability

Source code data have been deposited in Zenodo (https://www.doi.org/10.5281/zenodo.6401900).