Fast Bound and Pore Water Mapping of Cortical Bone with Arbitrary Slice Oriented 2D UTE

Abstract

Purpose:

Extend fast, 2D methods of bound and pore water mapping in bone to arbitrary slice orientation.

Methods:

To correct for slice profile artifacts caused by gradient errors of half pulse 2D UTE, we developed a library of predistorted gradient waveforms that can be used to interpolate optimized gradient waveforms for 2D UTE slice selection. We also developed a method to estimate and correct for a bulk phase difference between the two half pulse excitations used for 2D UTE signal excitation. Bound water images were acquired in three healthy subjects with adiabatic inversion recovery prepared 2D UTE, while pore water images were acquired after short-T2 signals were suppressed with double adiabatic inversion recovery preparation. The repeatability of bound and pore water imaging with 2D UTE was tested by repeating acquisitions after repositioning.

Results:

The library-based interpolation of optimized slice select gradient waveforms combined with the method to estimate bulk phase between two excitations provided compact slice profiles for half pulse excited 2D UTE. Quantitative bound and pore water values were highly repeatable — the pooled standard deviation of bound water across all three subjects was 0.38 mol ¹H/L, while pooled standard deviation of pore water was 0.30 mol ¹H/L.

Conclusion:

Fast, quantitative, 2D UTE-based bound and pore water images can be acquired at arbitrary oblique orientations after correcting for errors in the slice select gradient waveform and bulk phase shift between the two half acquisitions.

1. Introduction

In cortical bone, the water in pore spaces (pore water) and water bound the collagen matrix (bound water) have been shown to report on bone mechanical properties [1-8], and can be measured with MRI using various ultra-short echo time (UTE) methods [9-16]. Commonly, in order to minimize the delay between excitation and signal acquisition (i.e., echo time), UTE MRI uses a non-selective RF excitation pulse followed by a 3D center-out sampling of k-space. This approach provides good sensitivity to short-T₂ signals, but the necessary 3D encoding puts a lower limit on the scan time. For example, using adiabatic pulses to distinguish bound and pore water signals [9,12] and 3D radial sampling of k-space, ≈15 min scan times were needed to map bound or pore water concentrations in vivo in the tibia [15]. Alternative k-space sampling along with a bi-component strategy to fit the ratio of bound and pore signal amplitudes has shown potential for faster imaging [17, 18], but scan times remain limited by the necessity for 3D spatial encoding.

Spatial encoding requirements for UTE-MRI can be reduced to 2D by using slice-selective half-pulse (HP) RF excitation, which does not require a delay between excitation and acquisition for a gradient refocusing of transverse magnetization [19]. With these pulses, slice selection is achieved by summing signals from two HP acquisitions made with opposite slice-select gradient polarity. In summing these signals, the in-slice signals add constructively while the out-of-slice signals cancel. However, even small gradient waveform errors result in imperfect signal cancellation, which can substantially alter the result of a quantitative MRI method.

We have previously used an iterative pre-distortion method [20] to reduce gradient errors, and then applied this method to make rapid, accurate maps of bound and pore water concentrations in cortical bone with HP-2D-UTE [21]. This approach reduced total scan time from ≈30 min to as little as ≈30 sec, at the cost of a few minutes to pre-distort the slice select gradient waveform. However, these scans were limited to a slice located at the gradient isocenter and aligned to use only one physical gradient channel (X, Y, or Z). An off-center slice prescription introduces bulk signal phase shifts between excitations, which prevents effective out-of-slice signal cancellation, and an oblique slice orientation requires independent pre-distortion of each gradient channel, which mitigates the scan time benefit. This paper presents solutions to these technical challenges and demonstrates reliable and fast HP-2D-UTE mapping of bound and pore water concentrations with arbitrary slice prescription.

2. Methods

Two technical developments were needed for robust HP-2D-UTE with arbitrary slice prescription: 1) a library of pre-distorted gradient waveforms was generated for each physical gradient channel, enabling on-the-fly interpolation of an optimized gradient waveform for an arbitrary slice orientation, and 2) a slice-profile measurement was integrated into the scan protocol, which enabled a zeroth-order phase shift measurement and correction during image reconstruction.

Gradient Waveform Library

Gradient predistortion is an iterative procedure to update an applied waveform (G_app) based upon the error (Δ) between measured (G_obs) and ideal waveform (G_ideal). Briefly, for the i^th iteration,

$$G_{\text{app}}^i=G_{\text{app}}^{i-1}+\kappa {\left({\tilde{\mathbf{A}}}^{\mathrm{T}}\tilde{\mathbf{A}}+\lambda \mathbf{I}\right)}^{-1}\tilde{\mathbf{A}}{\Delta }^{i-1}.$$ (1)

Here, Ã is a Topelitz matrix representation of an estimate of the gradient impulse response function, while κ and λ are regularization parameters. Even though a linear approximation is taken at each iteration, the iterative process converges for nonlinear gradient systems.

Similar to previous studies [20, 21], the ideal gradient waveform (G_ideal) was designed as a minimum duration waveform, and calculated with a maximum gradient strength of 27 mT/m, maximum slew rate of 125 mT/m/ms, and maximum acceleration rate of 1000 mT/m/ms², providing sufficient gradient area to encode a slice thickness down to 5 mm. The library of gradient waveforms was developed using a uniform nickel-chloride phantom and an offset-slice gradient waveform measurement method [22-24]. The body coil was used for excitation, and 2 medium-sized flexible coils were used for signal reception. Regularization parameters were κ = 1 and λ = 0.2. The procedure was iterated three times on each gradient channel at 6 linearly-spaced amplitudes of the designed waveform per channel. Previous work demonstrated that three iterations were sufficient [20]. The total acquisition time to generate the gradient library was ≈45 min.

Phase Correction

In order to measure the bulk phase shift between the two HP acquisitions, slice profile measurements were incorporated into the 2D UTE imaging sequence by aligning the readout gradient with the slice-select direction. For each image acquisition, two profiles were acquired, S_p+(k) and S_p− (k), corresponding to the two HP gradient polarities. Both S_p+ (k) and S_p− (k) were measured from half-k-space acquisitions using the same center-out readout gradient used for UTE imaging. Spatial domain slice profiles were reconstructed from these k-space domain signals—acquired signals were density compensated [25-27], interpolated to a uniform 1D grid, and then inverse Fourier transformed [28] to generate a complex half-profiles, S_p+(z) and S_p−(z), where z is the slice profile direction. The full slice profile was then defined as the sum of these signals with the addition of a bulk phase term, ϕ, S_p(z) = S_p+(z) + S_p−(z)exp(iϕ). Ametric, m(ϕ), was defined to reflect the fraction of the signal coming from within the prescribed slice,

$$m(\varphi )=\mid \underset{z\in \text{slice}}{\int }dz{S}_{\mathrm{p}}(z)\mid /\underset{-\infty }{\overset{\infty }{\int }}dz\mid S_{\mathrm{p}}(z)\mid .$$ (2)

Then, the value of ϕ that maximized m was used to correct for the bulk phase difference between the two HP image acquisitions.

UTE MRI

Three healthy human volunteers (female/23, female/23 and female/21) were imaged with a 3T Philips Integra scanner after written, informed consent and IRB approval. After scout scans were acquired, a slice orientation was selected orthogonal to the long axis of the tibia, and slice selective gradient waveforms were linearly interpolated from the predistorted gradient waveform library. All UTE images were acquired with 200 mm × 200 mm FOV, 1.5 mm in plane resolution, and 5 mm slice thickness. A Gauss shaped half pulse was used for excitation[19], and variable rate selective excitataion (VERSE) was used to generate amplitude and frequency modulated waveforms on the time varying slice select gradient waveform [29]. The HP RF waveforms were calculated from the ideal gradient waveform.

Bound water images were acquired with an adiabatic inversion recovery-prepared (AIR) 2D UTE turbo field echo (TFE) sequence. Adiabatic inversion was achieved with a 6.2 ms HS8 pulse [30] with a maximum amplitude of 14 μT and bandwidth of 3600 Hz [9]. Other imaging parameters included: T_R = 400 ms, inversion delay = 84 ms, inter-excitation delay time of 3.28 ms, TFE factor of 16, and a schedule of flip angles with an effective 12.5° excitation and 60° effective saturation. Pore water images were acquired with a double adiabatic full passage (DAFP) prepared 2D UTE TFE imaging sequence. This sequence used a pair of the same HS8 inversion pulses used in the AIR sequence, T_R = 1 s, followed by a TFE readout train. For this sequence, the TFE factor was reduced to 4 to limit recovery of bound water signal. The excitation flip angle down the echo train used a schedule of flip angles with an effective 23° excitation and 60° effective saturation. The echo time was 0.1 ms. One set of AIR and DAFP image were acquired in approximately 6 minutes.

The full imaging protocol was repeated three times for each study subject, with the subject being repositioned each time. A fiducial marker placed on the leg was used to localize the same region of the tibia after respositioning. Repositioning was performed specifically to orient the tibia at different angles relative to the long axis of the magnet bore between ≈0° and 20°.

2D UTE images were reconstructed by gridding density compensated signals [25-27, 31] using measured radial center-out k-space trajectories. All UTE images were corrected for B₁ receive nonuniformity—$B_1^{-}$ receive maps were estimated from the ratio of signal intensity in T₁-weighted gradient echo images acquired with the medium sized flexible coil vs the body coil. A reference marker (H₂O + D₂O + 80 mM CuSO₄) with known T₁(= 17 ms), T₂(= 13 ms), and ¹H concentration (= 11.11 mol ¹H/L) in the FOV was used to convert AIR and DAFP signal intensities to quantitative concentration of bound water (C_bw) and pore water (C_pw), respectively. (note that the T₁ and T₂ relaxivities are similar for CuSO₄, [32]). Additional adjacent markers (with longer T₂) were used to extend the spatial coverage of the $B_1^{-}$ map, as described previously [12]. Using fixed relaxation rates (T₁ = 290 ms and T₂ = 0.35 ms, for bound water, and T₁ = 450 ms and T₂ = 100 ms for pore water [9], Bloch simulations of the pulse sequence were used to correct for relaxation differences between bone water and the reference marker. To minimize the impact of motion between scans, whole bone regions of interest (ROIs) were drawn on each image individually.

3. Results

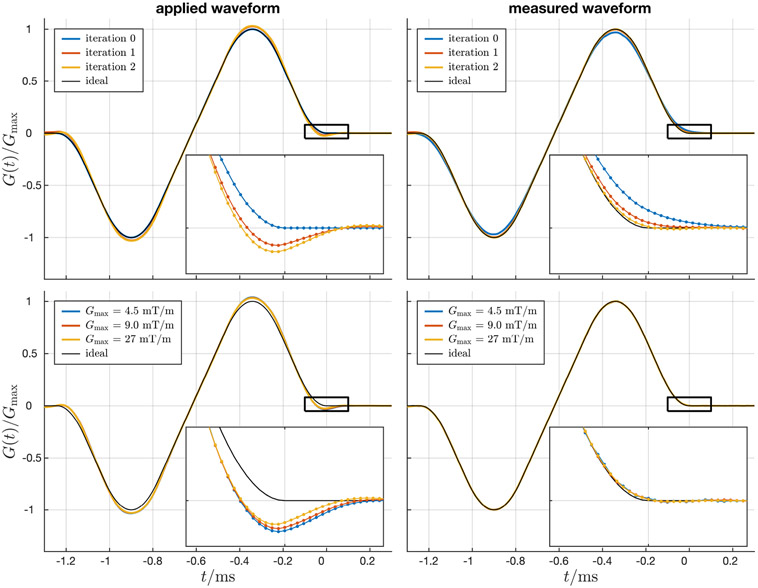
Example applied and measured slice select gradient waveforms are shown in Figure 1, with inset plots that highlight the errors. The top row shows the initial prescribed (blue) and desired (black) waveforms, as well as waveforms after one and two iterations of predistortion. The bottom row shows applied and measured waveforms at three different gradient amplitudes, G_max = 4.5, 9.0 and 27 mT/m. Note that some nonlinear effects of the gradient system are apparent: to produce a similar normalized gradient waveform (lower right panel), the overshoot on the applied waveform varies with gradient amplitude (lower left panel).

Figure 1:

Example slice selective gradient waveforms calculated using iterative predistortion applied to (left column) and measured on (right column) the gradient system. Inset plots highlight gradient errors at the end of the bipolar pulse. Top row: multiple iterations of predistortion are used to optimize the applied gradient waveform such that the observed waveform matches the ideal waveform. Bottom row: gradient amplitude dependent changes in the overshoot of the applied gradient waveform indicate nonlinear effects of the gradient system.

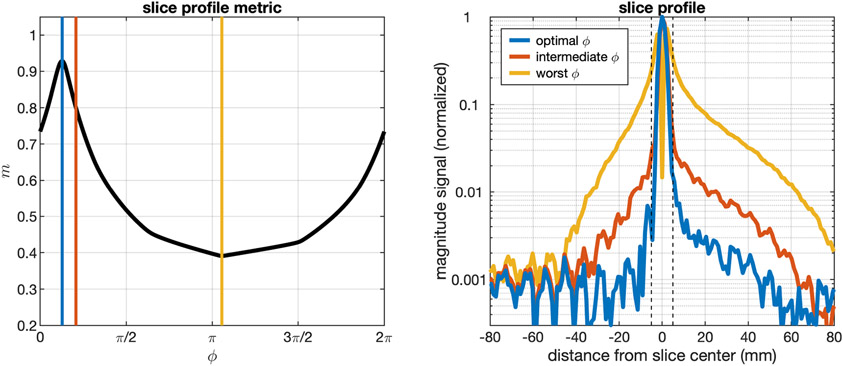
Figure 2 outlines an example result from the bulk phase correction algorithm used to estimate the 0-th order phase difference between the two HP excitations. The left panel shows the bulk phase correction metric, m(ϕ), from Equation 2, which reaches a value of 1 when all the excited comes from within the prescribed slice. Note that due to background noise in the magnitude slice projection the value of m(ϕ) will never reach 1. A blue line through the left panel indicates the optimal phase to combine the two excitations, the yellow line shows the least optimal phase, and the red line is an intermediate phase. The slice profiles estimated from this set of phases is shown in the right panel. The slice profile in blue is combined using the optimal phase and shows robust out-of-signal suppression, while the yellow and red lines have significant slice profile distortions and large out-of-slice signal contributions. The dashed vertical black lines define the prescribed slice used in the calculation of m(ϕ).

Figure 2:

Example result from the bulk phase correction algorithm. The left panel plots the metric m from Equation 2 from a representative slice profile calculation over a range of ϕ from 0 to 2π. Due to background noise in the magnitude slice projection, m(ϕ) will never reach 1. Reconstruction of the slice profile at the optimal m provides better out-of-slice signal suppression than other example values of ϕ.

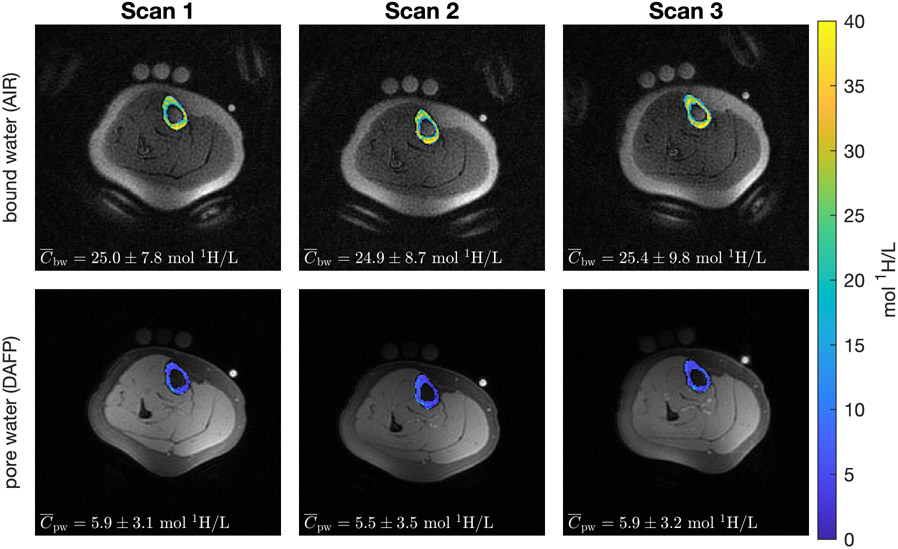
In Figure 3, AIR images overlaid with C_bw and DAFP images overlaid with C_pw illustrate the repeatability of quantitative bound water and pore water with 2D UTE. The three columns represent image acquisitions after repositioning the subject within the scanner. Average (across the ROI) C_bw and C_pw values from repeated scans and subjects are shown in Table 1. The pooled standard deviations (SD) of C_bw and C_pw were 0.38 mol ¹H/L and 0.30 mol ¹H/L, respectively.

Figure 3:

Example C_bw overlaid on AIR images and C_pw overlaid on DAFP images with a 2D-UTE acquisition. The patient was repositioned between each scan such that the angle between the tibia and the physical Z-axis varied between ≈ 0° and 20° across scans.

Table 1:

Mean (SD) of C_bw and C_pw computed over a cortical ROI in the tibia of three subjects and after repositioning three times. For each scan, each patient was repositioned such that the angle between the tibia and the Z-axis varied between ≈ 0° and 20°. The pooled SD values for each measure provides overall estimates of precision.

mol 1H/L	subject	scan number			SD of mean
		1	2	3
bound water	1	25.02 (7.84)	24.92 (8.71)	25.41 (9.82)	0.26
	2	22.50 (8.77)	22.45 (8.43)	22.91 (8.79)	0.25
	3	22.70 (8.75)	21.77 (7.88)	22.77 (9.19)	0.56
		–––– pooled SD ––––			0.38
pore water	1	5.87 (3.08)	5.54 (3.48)	5.86 (3.15)	0.19
	2	4.75 (2.08)	4.54 (2.17)	4.68 (2.21)	0.10
	3	5.24 (3.55)	5.66 (3.52)	6.18 (3.92)	0.47
		–––– pooled SD ––––			0.30

4. Discussion

This work presents technical developments that allow obliquely oriented, quantitative 2D UTE imaging of bound and pore water signals in the bone. This method was applied for imaging cortical bone in the tibia, and the repeatability of quantitative bound and pore water images in the tibia was evaluated after patient repositioning. Imaging at oblique orientations is important for patient comfort, as many imaging applications do not naturally align with a physical gradient axis. A previously published method for 2D BW and PW measurements used predistortion to achieve high quality slice profiles on the Z-axis [21]. To apply this method to oblique slice orientations, iterative predistortion would have to be applied on each gradient channel on a per-patient basis, as the ideal slice select gradient waveform will depend on the magnitude of the slice waveform projected onto each of the three physical gradient axes, requiring extra scan time and patient time in the scanner. This problem can be solved with a library of optimized gradient waveforms from which the desired waveform for any slice orientation can be interpolated.

To our knowledge, this is the first study to report on the repeatability of quantitative 2D UTE metrics after repositioning. Prior studies have used simpler methods to achieve visually high quality 2D UTE images. For instance, several of these studies had used linear systems theory to calibrate slice profiles for half pulse UTE [33, 34]. However, iterative predistortion will provide quality slice selection waveforms even in limits when the gradient system cannot be treated as a linear system. Nonlinear behavior of the gradient system is visible in Figure 1, where the relative magnitude of the overshoot on at the end of the slice select gradient depended on the magnitude of the waveform. Still other studies have suppressed out-of-slice signal using outer volume suppression techniques [35, 36]. However, these previously published methods have not been applied to quantitative imaging, and the repeatability of these methods have not been demonstrated. One previous study reported reproducibility in 3D UTE based bound and pore water measurements [15], reporting pooled standard deviations of the mean 3-5x worse than those reported here in Table 1. However, that study reported reproducibility over multiple scan sessions and locally defined ROIs within the bone. In contrast, this study was designed to only report on the repeatability at multiple orientations within the MRI system—scans were performed in same imaging session using a fiducial marker to ensure the same slice placement and an ROI that covered the whole bone.

There are several limitations to the proposed methods. Primarily, the method requires the collection of a library of predistored gradient waveforms. However, this library can be developed independently using phantoms rather than study subjects, and the library acquisition protocol can likely be optimized to require less than the ≈45 min used here. We used six linear spaced gradient amplitudes; however, it is possible that a smaller library, perhaps with non-linearly spaced waveform amplitudes, would be sufficient to produce reliable bound and pore water measurements from oblique slice orientations. Also, the method as proposed does not account for cross-terms between gradient channels and is prone to errors due to changes in gradient performance during a scanning session. In our experience, neither of these problems have been observed, but they could pose a limitation on other systems. In theory, the library can be extended to include the effect of cross-terms. Lastly, we have only tested this method on one system. Future studies should be aimed at comparing the reproducibility of 2D-UTE based bound and pore water measurements at multiple scanners or sites.

5. Conclusion

Using a library of predistorted slice select gradient waveforms and a novel method to correct for bulk phase differences between half pulse excitations, 2D UTE has been demonstrated effective for mapping bound and pore water concentrations in cortical bone with arbitrary slice orientation.