The Influence of Autoregressive Relation Strength and Search Strategy on Directionality Recovery in GIMME

Abstract

Unified structural equation modeling (uSEM) implemented in the Group Iterative Multiple Model Estimation (GIMME) framework has recently been widely used for characterizing within-person network dynamics of behavioral and functional neuroimaging variables. Previous studies have established that GIMME accurately recovers the presence of relations between variables. However, recovery of relation directionality is less consistent, which is concerning given the importance of directionality estimates for many research questions. There is evidence that strong autoregressive relations may aid directionality recovery and indirect evidence that a novel version of GIMME allowing for multiple solutions could improve recovery when such relations are weak, but it remains unclear how these strategies perform under a range of study conditions. Using comprehensive simulations that varied the strength of autoregressive relations among other factors, this study evaluated the directionality recovery of two GIMME search strategies: 1) estimating autoregressive relations by default in the null model (GIMME-AR), and 2) generating multiple solution paths (GIMME-MS). Both strategies recovered directionality best – and were roughly equivalent in performance – when autoregressive relations were strong (e.g., β = .60). When they were weak (β <= .10), GIMME-MS displayed an advantage, although overall directionality recovery was modest. Analyses of empirical data in which autoregressive relations were characteristically strong (resting state fMRI) versus weak (daily diary) mirrored simulation results and confirmed that these strategies can disagree on directionality when autoregressive relations are weak. Findings have important implications for psychological and neuroimaging applications of uSEM/GIMME and suggest specific scenarios when researchers might or might not be confident in directionality results.

Applied Abstract

Network modeling methods such as Group Iterative Multiple Model Estimation (GIMME) can provide valuable insights into person-specific processes present in time series data from multiple domains, including functional neuroimaging and intensive longitudinal studies of psychological variables. In these applications, the directionality of contemporaneous relations (those in which one variable predicts another at the same time point) is often of interest. However, the directionality of these relations is difficult to estimate in practice, and it is unclear what methods or features of data may facilitate accurate estimates. In this study, we assess the ability of two GIMME variants to estimate directionality in data sets in which autoregressive relations (those in which variables predict themselves at the next time point) are strong versus weak. The first variant (GIMME-AR) relies on strong autoregressive relations to inform directionality during model estimation, while the second variant (GIMME-MS) estimates multiple models with relations in opposite directions and allows these models to be compared after estimation with standard fit indices. We found that both methods performed best, and often provided similar directionality estimates, when autoregressive relations in data are strong (e.g., β = .60). When autoregressive relations were weak (β <= .10), GIMME-MS displayed a slight advantage over GIMME-AR, but overall performance was modest. These results indicate that GIMME-AR is likely preferable to GIMME-MS for analyzing data sets with strong autoregressive relations, such as functional neuroimaging data, while GIMME-MS may be preferable for analyzing data sets with weak autoregressive relations, such as daily diary or ambulatory assessment data.

Introduction

The promise of network models for characterizing individual-level processes in intensive longitudinal and functional neuroimaging time series data has precipitated a surge of interest across the behavioral and neural sciences. Many of these models were initially developed to characterize temporal and network dynamics of interactions between brain regions in functional magnetic resonance imaging (fMRI) data, leading to recent advances in the field’s understanding of the neural correlates of cognition and psychiatric syndromes (Beltz et al., 2018; Elbich et al., 2019; Gates et al., 2014; Litvina et al., 2019; Mumford & Ramsey, 2014; Nichols et al., 2014; Price, Lane, et al., 2017; Weigard et al., 2019; Wu et al., 2019). Applications of similar network models to data from daily diary and ambulatory assessment studies have also begun to provide key insights into the within-person dynamics of basic psychological phenomena (Bar-Kalifa & Sened, 2019; Hofmans et al., 2019; Lydon-Staley & Bassett, 2018; Yang et al., 2019) and to elucidate person-specific structures, and determinants, of psychopathology (Beltz et al., 2016; Dotterer et al., 2019; Ellison et al., 2019; Jongeneel et al., 2019; Stroe-Kunold et al., 2016; Wright et al., 2015; Yang et al., 2018). A unique strength of these approaches is their ability to account for heterogeneity in neural and psychological processes by characterizing person-specific relations between variables (Beltz et al., 2016). Indeed, several recent commentaries have posited that integration of person-specific network models with clinical care may improve patient outcomes by allowing clinicians to tailor personalized interventions (Epskamp, van Borkulo, et al., 2018; van der Krieke et al., 2015; Wright & Zimmermann, 2019).

The utility of these methods for advancing diverse research fields hinges on their ability to successfully characterize relations in time series data. However, ongoing questions remain about how, or even whether, such models should provide estimates of the directionality of relations between variables (Beltz & Molenaar, 2016; Epskamp, Waldorp, et al., 2018; Mumford & Ramsey, 2014). This question is especially relevant given that relations of interest in time series data can be both lagged (e.g., the relation between variable A at time t-1 and variable B at t) and contemporaneous (e.g., between variables A and B at t). Although the temporal ordering of lagged relations allows for inferences about directionality (e.g., A at t-1 influences B at t), such inferences are not straightforward for contemporaneous relations. In the absence of other information, a model coefficient that represents a directional relation from A to B at t (β_BA) will provide a description of the data that is statistically identical to one that represents the opposite relation from B to A (β_AB), leading to equivalent model solutions that prevent strong inferences about directionality (Beltz & Molenaar, 2016; Epskamp, van Borkulo, et al., 2018). Despite this challenge, questions about the directionality of contemporaneous relations are crucial to answer in many substantive applications. In the neuroimaging field, there has been a long history of interest in, and considerable controversy over, the development of methods that determine which brain regions directionally influence others (Friston, 2011; Friston et al., 2013; Liao et al., 2010; Mumford & Ramsey, 2014; Smith et al., 2011). In clinical contexts, researchers and providers could more effectively target person-specific psychopathology processes in patient populations if they were able to determine which variables have a directional influence on symptoms (Dotterer et al., 2019; Epskamp, van Borkulo, et al., 2018; van der Krieke et al., 2015). Hence, uncertainty about directionality is a limiting factor for many individual-level applications of these models.

Researchers have approached the challenges of estimating directionality in time series data in a variety of ways. One strategy is to exclusively focus on estimating the directionality of lagged relations between variables, for which inferences are inherently less problematic. This strategy is commonly implemented in dynamic structural equation modeling (DSEM) approaches (Hamaker et al., 2018; McNeish & Hamaker, 2020) and graphical vector autoregression (graphical VAR) approaches (Epskamp, Waldorp, et al., 2018; Wild et al., 2010). For example, in graphical VAR, an initial model that estimates autoregressive relations (e.g., variable A at t-1 with itself at t) and directional lagged relations is fit to the data, and residuals are subsequently used to estimate undirected contemporaneous relations. Proponents of this method argue that avoiding estimation of contemporaneous relations’ directionality, despite the associated limitations for inference, offers several key advantages, For instance, it reduces the presence of equivalent models and speeds up parameter estimation (Epskamp, Waldorp, et al., 2018).

Another strategy is to use algorithms that are explicitly designed to infer the directionality of contemporaneous relations by exploiting heuristics about directed acyclic graphs (DAGs), which are networks assumed to have directional relations but no feedback loops (e.g., in which both A influences B and B influences A) (Mumford & Ramsey, 2014). For example, the Greedy Equivalence Search (GES) approach (Chickering, 2002; Meek, 1997, 1995; Ramsey et al., 2010) conducts a two-stage (forward/backward) data-driven search in which DAGs with many possible combinations of directed edges are explored, and then a scoring algorithm that penalizes for model complexity (often the Bayesian Information Criterion or BIC) is used for DAG selection. Extensions of GES that leverage multi-subject data (Ramsey et al., 2010, 2011) and facilitate its use in high-dimensional (e.g., neuroimaging) data (Ramsey et al., 2017) have also been proposed. Finally, the Linear Non-Gaussian Acyclic Model (LiNGAM) approach (Shimizu et al., 2006) provides directionality inferences by assuming non-Gaussianity of errors, which yields additional information about directional relations in DAGs and allows for the use of either independent components analysis (ICA) or likelihood ratios (Hyvärinen & Smith, 2013) to infer the character of relations in the network. In general, GES, LiNGAM and similar algorithmic methods are designed to infer the directionality of contemporaneous relations without the use of information about autoregressive and lagged relations in the time series data.

Although the approaches outlined above have distinct merits, the VAR-based models have key limitations in research contexts in which contemporaneous relations are of interest (e.g., neuroimaging, daily diary), and the algorithmic/DAG methods may miss important features of network relations by not accounting the impact of temporal trends in the data. In contrast, approaches based on structural VAR models, such as unified structural equation modeling (uSEM), combine VAR and traditional SEM to permit simultaneous estimation of autoregressive relations, directed lagged relations, and directed contemporaneous relations (Gates et al., 2010; Kim et al., 2007). Although estimation of directed contemporaneous relations in this framework can lead to statistically and inferentially equivalent model solutions (Beltz & Molenaar, 2016), the combination of uSEM with the Group Iterative Multiple Model Estimation (GIMME) data-driven search strategy has nonetheless shown promise for producing accurate estimates of relation directionality (Gates & Molenaar, 2012).

Originally developed for use with neuroimaging data, GIMME leverages the fact that individuals in a group typically display some degree of commonality in their network features, as well as unique, individual-level features. GIMME begins by using Lagrange multiplier tests (Sörbom, 1989), which sequentially estimate relations that best improve fit of a null model, to determine which relations significantly improve fit for a majority (typically 75%) of individuals in a group. After group-level relations are established, GIMME then uses the group-level structure as the null model for individual-level searches, in which Lagrange multiplier tests are again used to sequentially estimate relations that best-improve fit to the individual-level data until the model achieves suitable fit according to traditional fit indices. Initial applications of uSEM and GIMME to simulated neuroimaging data (Smith et al., 2011) revealed that this approach outperformed contemporary network modeling methods, including, notably, the LiNGAM, GES¹, and VAR-based approaches (i.e., Granger causality), for estimating the directionality of relations between brain regions. GIMME successfully identified both the presence and directionality of approximately 90% of relations (collapsing across contemporaneous and lagged relations) in the simulated data (Gates & Molenaar, 2012). These simulated neuroimaging data, however, had strong autoregressive relations and a large proportion of lagged, relative to contemporaneous, relations. These features are not always present in neuroimaging data, especially for task-based designs, nor for behavioral time series data, especially when measurement intervals are large (e.g., 24 hours; Beltz & Molenaar, 2015).

Given the benefits of accurately estimating the directionality of contemporaneous relations in many research contexts, the work presented here seeks to elucidate best practices for doing so within the GIMME framework. Specifically, we evaluate the efficacy of two different GIMME-based search approaches for recovering directionality – the strengths and weaknesses of which have never been systematically evaluated in a side-by-side comparison – under a variety of conditions that are likely to be encountered when analyzing empirical data from behavioral and neuroimaging domains. To begin, we provide a conceptual introduction to both approaches, focusing on their estimation of contemporaneous relation directionality.

GIMME-AR

The standard search approach within GIMME (Gates & Molenaar, 2012), which we hereafter refer to as GIMME-AR (short for “GIMME with Default Autoregressive Relations”), uses lagged and autoregressive relations to inform the estimation of contemporaneous relations during data-driven model fitting from a Granger causality perspective. Granger causality evaluates whether, after controlling for two variables’ autoregressive relations, variable A better predicts variability in variable B, or vice versa. For example, without the inclusion of autoregressive relations, the estimation of a directional contemporaneous relation from variable A to variable B (β_BA) will provide an improvement in model fit that is identical to that provided by estimation of a relation in the opposite direction (β_AB). However, estimating autoregressive or lagged relations alters this dynamic through the inclusion of covariates. If variable A has a strong autoregressive relation that explains a large portion of its variance that would otherwise be explained by variable B, estimation of β_BA may yield a more substantial improvement in model fit than estimation of β_AB. Similarly, if there is a strong lagged relation from B to A, then estimating a contemporaneous relation from A to B may provide greater improvement in fit relative to a contemporaneous relation from B to A. Both scenarios would cause the contemporaneous relation from A to B (β_BA) to be selected during GIMME’s data-driven search, and this relation would therefore be assumed to best-reflect the directionality of the underlying process. Thus, covariates in the model influence detection of the directionality of the contemporaneous relation between two given variables. In this way, the final uSEM models obtained are strongly influenced by relations estimated early in the model search procedure. The GIMME-AR search strategy relies specifically on the use of autoregressive effects as covariates; in this approach, all individuals have all autoregressive relations estimated by default in the null model before the search commences to allow these relations to inform estimates of directionality.

Consistent with this approach, a recent simulation study focusing on the utility of GIMME-AR for analysis of ambulatory assessment data (Lane et al., 2019) highlighted the importance of autoregressive relations for recovering directionality. This study assessed how effectively a recently-developed variant of GIMME that allows for the creation of homogenous subgroups (S-GIMME) (Gates et al., 2017) recovered the presence and directionality of relations while varying the number of time points, participant sample size, and number of variables. Autoregressive relations were not varied systematically in these simulations and were, on average, roughly half the strength of between-variable lagged and contemporaneous relations. Recovery of both the presence and directionality of between-variable relations was quantified with two statistics: 1) “recall”, or the proportion of all simulated relations/directions that were recovered by the model, and 2) “precision”, or the proportion of relations/directions estimated by the model that were truly present in the simulated data.

Crucially, results indicated that both direction recall and direction precision were dramatically improved when all autoregressive relations were estimated by default in the null model, providing the first empirical demonstration that autoregressive relations play a key role in informing directionality estimates in GIMME (Lane et al., 2019). However, it is notable that even when autoregressive relations were estimated in the null model to inform the search process, recovery of directionality was far from perfect; average direction recall ranged from .43 to .72 under optimal conditions, while direction precision ranged from .57 to .79 (Lane et al., 2019).

GIMME-MS

An alternative approach to addressing directionality estimation in GIMME was introduced within a study on the presence of multiple solutions in data driven uSEM analyses (Beltz & Molenaar, 2016). Using both simulated and empirical data, the work demonstrated that – when autoregressive relations are not estimated in the null model – equivalent solutions in which contemporaneous relations of opposite directionality provide identical model fit are encountered throughout the data driven search process. Equivalent solutions were more common in data with relatively stronger contemporaneous relations than in data with relatively stronger lagged relations, because these strong contemporaneous relations are opened earlier in the search process, and lagged relations (i.e., covariates) are therefore unable to contribute information about their directionality (Beltz & Molenaar, 2016). The authors proposed that, rather than relying on lagged or autoregressive relations opening early in the search to inform estimation of contemporaneous relation directionality, it would be valuable to consider all possible solutions, with varying accounts of directionality, that result from the search process and subsequently use other objective or subjective criteria to select an optimal model.

The resulting GIMME for Multiple Solutions (GIMME-MS) uses the same search strategy implemented in standard GIMME, but with one critical change in search procedures (Beltz & Molenaar, 2016). Whenever, in the course of either the group- or individual-level search processes, estimation of two or more relations with the highest modification indices would provide an equivalent improvement in fit - a situation which almost always results from contemporaneous relations of opposing directionality - the algorithm estimates a separate model for each of these relations and continues the search procedure for all models in parallel. This strategy produces “trees” of parallel group- and individual-level searches that can result in multiple solutions at each level. After the GIMME-MS search process terminates, the researcher can then use several strategies to select an optimal model from these solutions, including cross-validating models in unseen data, eliminating solutions that are theoretically implausible, or using information from standard indices of absolute or relative model fit. Given that cross-validation and theoretical guidance are not always available and that absolute fit indices are inappropriate for model comparison, procedures that use relative fit indices for model selection may be most widely applicable.

One such principled solution reduction procedure proposed by Beltz and Molenaar (2016) that has been successfully adopted in subsequent work (Beltz et al., 2016; Dotterer et al., 2019; Kelly et al., 2020; Weigard et al., 2019) utilizes the AIC (Akaike, 1973), a log-likelihood-based index of relative model fit. Although the use of AIC can vary based on the research question, extant applications have taken an approach in which individual-level models are selected first and then used to determine the best group-level solution (e.g., Beltz et al., 2016; Dotterer et al., 2019; Kelly, Weigard, & Beltz, 2020; Weigard et al., 2019). Within each group-level solution, the AIC is first used to select a best-fitting model for each individual out of all of their possible individual-level solutions. Next, the AIC for these selected models is averaged across individuals within each group-level solution and the group-level solution with the lowest average AIC is then selected as the optimal model. In a small set of simulation studies aimed at validating these methods, GIMME-MS and AIC were found to recover all relations from the “true” model used to simulate several data sets that varied in their sample size, time series length, and relative strengths of contemporaneous and lagged relations (Beltz & Molenaar, 2016). Hence, the combination of GIMME-MS with an AIC-based solution reduction strategy offers an attractive option for researchers wishing to obtain valid directionality estimates in uSEMs, especially in situations in which autoregressive and lagged relations may be too weak to precisely inform estimates of directionality early in standard GIMME searches.

Current Study

Despite the clear value of the uSEM network modeling approach for characterizing person-specific processes in neuroimaging and intensive longitudinal behavioral data, the importance of obtaining directionality estimates in many applications warrants further examination of when directionality can be accurately recovered. The work reviewed above suggests that two search strategies within the GIMME framework may be effective for providing accurate directionality estimates: 1) autoregressive relations estimated by default in the null model (GIMME-AR), and 2) generation of multiple uSEM solutions during the search process that can later be compared using the AIC (GIMME-MS). Due to the wide breadth of application that uSEM and related methods have seen, features of lagged and autoregressive relations may differ considerably across empirical data sets analyzed with these approaches, which may in turn have implications for model fitting and directional relation recovery. For example, fMRI data are known to have a high degree of temporal autocorrelation, especially when collected during “resting state” scans (Arbabshirani et al., 2014; Beltz & Molenaar, 2015; Christova et al., 2011). In contrast, autoregressive relations in daily diary and ambulatory assessment data are often significantly weaker (Beltz et al., 2016; Beltz & Molenaar, 2016; Lane et al., 2019). The relative efficacy of GIMME-AR and GIMME-MS has not been evaluated under variable conditions of autoregressive and lagged relation strength (these factors were not varied by Lane et al., 2019), and GIMME-MS has yet to be tested in a large-scale, comprehensive simulation. Therefore, researchers currently have little guidance regarding how their choice of search strategy affects the integrity of directionality findings drawn from substantive applications of GIMME.

Our broad goal was to assess the absolute and relative efficacy of the GIMME-AR and GIMME-MS search strategies for recovering the directionality of contemporaneous relations in time series data under different realistic conditions that were expected to either facilitate or hinder recovery². Specifically, we aimed to gauge both strategies’ recall and precision (the same criteria used by Lane et al., 2019) in recovering the direction of contemporaneous relations from simulated data while varying: 1) the strength of autoregressive relations, 2) the relative strength of contemporaneous and lagged relations, and 3) time series length. Autoregressive relations were varied along a range that spanned from effectively null (average standardized β = .00, SD = .10) to strong (β = .60, SD = .10), which allowed us to evaluate recovery in data with autoregressive effects of the size commonly found across daily diary, ambulatory assessment, and fMRI data sets typically analyzed with GIMME (Beltz et al., 2016; Beltz & Molenaar, 2015, 2016; Lane et al., 2019). Contemporaneous relations were, in three different conditions: 1) roughly equivalent to lagged relations in strength, 2) systematically stronger than lagged relations, and 3) systematically weaker than lagged relations.

We hypothesized that GIMME-AR would display the highest rates of direction recall and direction precision when autoregressive relations in the simulated data were strong and when lagged relations were relatively stronger than contemporaneous relations. As GIMME-MS allows all possible outcomes of the data driven search process to be compared, rather than relying on strong autoregressive and lagged relations to guide the search toward a single solution, we hypothesized that the directionality recovery of GIMME-MS would be less influenced by the strength of autoregressive and lagged relationships, and that GIMME-MS would display relative advantages to GIMME-AR when autoregressive and lagged relations were weak. When autoregressive and lagged relationships were relatively strong, we hypothesized that the performance of the two search strategies would be similar, as previous work suggests that GIMME-MS may output fewer possible solutions, or only a single solution, when strong autoregressive and lagged relations are estimated early in the search (Beltz & Molenaar, 2016).

We then leveraged two empirical data sets to illustrate how the strength of naturally-occurring autoregressive relations influences results from GIMME-AR and GIMME-MS, and to guide recommendations for the application of GIMME in neuroimaging and behavioral data, including consideration of model assumptions. We applied both GIMME-AR and GIMME-MS to: 1) an archival resting state fMRI data set (Beltz & Molenaar, 2015), and 2) self-ratings of mood and psychopathology symptoms from a novel 100-day intensive longitudinal study. Given that autoregressive relations are typically substantially stronger in resting state fMRI data than in daily diary data, we hypothesized that GIMME-MS would identify a greater number of possible solutions for the daily diary data set. We also hypothesized that results obtained from GIMME-AR and GIMME-MS would be relatively similar for the resting state fMRI data, as the opening of strong autoregressive relations early in the GIMME-MS search process would be expected to lead the two search strategies to converge on similar models.

In the following sections, we first provide a detailed technical description of uSEM, GIMME, and the two different search strategies we assessed in this framework (GIMME-AR and GIMME-MS). Next, we describe the methods and results of the simulation study and include a discussion of the key substantive implications of these results. We then provide a description of the methods, results, and implications of our analyses of empirical resting state fMRI and daily diary data. Finally, we provide a general discussion of the broad implications of our findings for typical applications of GIMME and related network modeling methods.

Technical Description of GIMME and Search Strategies

Formal Definition of uSEM and GIMME

Unified structural equation modeling (uSEM), as first proposed by Kim et al. (2007), is a variant of structural vector autoregressive modeling, a framework that was developed for the analysis of time series data in econometrics (Lütkepohl, 2005). uSEM is formally defined as follows (assuming mean-centered data):

$${\eta }_t=A{\eta }_t+\varphi {\eta }_{t-1}+{\zeta }_t$$

where η_t is the current state of a multivariate time series with p variables at time t, A is a p × p matrix of coefficients for contemporaneous linear relations between variables (with a diagonal of 0), ϕ is a p × p matrix of coefficients for linear relations between variables at a lag of 1 (including autoregressive relations in the diagonal), and ζ contains Gaussian residuals which have a mean of 0 and are assumed to reflect white noise.

Within the GIMME framework (Gates & Molenaar, 2012), uSEM can be extended in the following way (assuming mean-centered data):

$${\eta }_{i,t}=\left(A_i+A_i^g\right){\eta }_{i,t}+\left({\varphi }_i+{\varphi }_i^g\right){\eta }_{i,t-1}+{\zeta }_{i,t}$$

where i represents each individual and g represents the group (i.e., full sample), A_i and $A_i^g$ contain coefficients estimated at the individual-level for relations present for a given individual and the whole sample, respectively, and ϕ_i and ${\varphi }_i^g$ contain the individual’s coefficients for lagged relations estimated individually and for the group, respectively. Hence, although GIMME leverages relations that are present for the majority of the sample to inform the estimation of individual-level models, all parameters, including those for relations that are common to the larger group, are estimated at the individual level.

GIMME-AR Search Strategy

The GIMME-AR search strategy is a straightforward implementation of the standard GIMME method (Gates & Molenaar, 2012), with the stipulation that all autoregressive relations are estimated in the null model (before the group-level search). First, null models are estimated for all individuals from the 2p × 2p block Toeplitz covariance matrices generated from the empirical time series (Box et al., 2015; Molenaar, 1985), with only specific parameters from the variance-covariance matrix of the process innovation being freely estimated in standard GIMME. In the GIMME-AR search strategy, specifically, autoregressive relationships in the diagonal of the ϕ matrix are also freely estimated in these null models. Second, the search process begins with Lagrange multiplier tests (modification indices) at the group level (Sörbom, 1989), which sequentially estimate relations that provide the best improvement of model fit across individuals. This process continues until no remaining relations significantly improve fit (defined as a Bonferroni-corrected p<.05) for a predetermined percentage of the group (typically 75%, as validated in early simulations; Gates & Molenaar, 2012). Third, following the group-level search, a “pruning” procedure is enacted to sequentially remove relations that are no longer significant for the same predetermined proportion of individuals. Fourth, individual-level solutions are generated by using the final group-level model structure as a starting point for Lagrange multiplier tests that sequentially estimate significant relations (defined as p<.01) for each individual. These individual-level searches continue until two of four common model fit indices suggest “excellent” (Brown, 2006) fit (RMSEA ≤ .05, SRMR ≤ .05, CFI ≥ .95, NNFI ≥ .95), and are followed by an individual-level pruning procedure that again removes relations that are no longer significant.

GIMME-MS Search Strategy

The GIMME-MS approach (Beltz & Molenaar, 2016) is similar to the GIMME-AR approach, with several critical exceptions. The search process similarly begins with the estimation of a null model, which is defined here as having no relations in the ϕ or A matrices estimated. Thus, unlike GIMME-AR, the autoregressive relations in the diagonal of ϕ are not freely estimated in GIMME-MS and are instead subject to the same criteria for estimation during the search process as other relations. After estimation of the null model, the group-level search process proceeds with Lagrange multiplier tests. However, at steps in the search in which the maximum modification index is not singular (i.e., when two or more parameters with identical modification indices display the maximal values), separate “solution paths” are created in which each relation with a maximal modification index value is estimated. The search process continues for these solution paths in parallel, with the possibility of additional paths being added in subsequent iterations. For each solution path, the search stops when no remaining relations significantly improve fit for a predetermined percentage of the group (again, typically 75%), and the standard GIMME pruning process is implemented. Next, within the group-level solutions that result from each solution path, individual-level search and pruning processes are conducted using the standard GIMME stopping criteria based on model fit. As in the group-level search, GIMME-MS generates multiple solution paths for a given individual-level model when maximum modification indices are not singular. Hence, the GIMME-MS procedure can result in multiple solutions for each individual that are nested within multiple group-level solutions.

Once all possible group- and individual-level solutions are obtained, researchers can use several strategies to select optimal solutions. The widely applicable AIC-based solution reduction procedures implemented in the current study to select final models for GIMME-MS fits to simulated and empirical data are described in detail below.

Simulation Study Methods

Simulation Design and Data Generation

We used Monte Carlo simulation procedures implemented in R (R Core Team, 2019), following Lane et al. (2019), to generate 8-variable time series data sets for simulated individuals. Data sets varied along several key factors: 1) number of time points (T = 50, 100, or 300), 2) autoregressive relation strength (β = .00, .10, .30, .50, or .60 all with SD = .10), and 3) relative strength of contemporaneous and cross-lagged (i.e., non-autoregressive lagged) relations (balanced, lagged-greater, or contemporaneous-greater). In the balanced (BA) condition, all contemporaneous relations in A were β = .30 (SD = .10) while cross-lagged relations in ϕ were β = −.30 (SD = .10)³. In the lagged-greater (LG) condition, contemporaneous relations in A were β = .30 (SD = .10) while cross-lagged relations in ϕ were β = −.60 (SD = .10). In the contemporaneous-greater (CG) condition, contemporaneous relations in A were β = .60 (SD = .10) while cross-lagged relations in ϕ were β = −.30 (SD=.10). The average absolute βs across these conditions allow evaluation of directionality recovery when contemporaneous and cross-lagged relations were either roughly as strong as the middle autoregressive strength condition (|β| = .30) versus when they were substantially stronger (|β| = .60). The range of βs for autoregressive relations was selected based on prior applications of GIMME to daily diary data, which typically display autoregressive effects at the lower end of this range, and based on applications from resting state fMRI data (including the specific data set used in the empirical example below; Beltz & Molenaar, 2015), which typically display autoregressive effects at the higher end. The final factorial design included 3 × 5 × 3 = 45 conditions, which were evaluated using 100 group-level replications each, leading to the generation of 5,000 individual-level data sets within each condition (100 replications × 50 subjects) and 225,000 individual-level data sets in total.

Following Lane et al. (2019), we generated data using an algebraic manipulation of the standard uSEM equation:

$${\eta }_{i,t}={\left(I_p-\left(A_i+A_i^g\right)\right)}^{-1}\left({\varphi }_i+{\varphi }_i^g\right){\eta }_{i,t-1}+{\left(I_p-\left(A_i+A_i^g\right)\right)}^{-1}{\zeta }_{i,t}$$

where I_p represents the identity matrix, and errors are generated to be Gaussian white noise for all variables and individual subjects. The first 50 observations of each simulated time series were discarded prior to generating the number of observations for each condition (T = 50, 100, or 300) in order to allow the time series to stabilize after initialization.

Individuals were nested within groups of 50 subjects each and shared 50% of their relations with other subjects in their group. The structure of A and ϕ was generated randomly for each replication and individual while holding overall network density to roughly 20% (not including autoregressive relations). Relations were roughly evenly distributed between A and ϕ and were evenly distributed between the group and individual level (i.e., for every subject, 50% of relations were unique to that individual rather than common to the group). In order to prevent unstable data generation, A matrices with maximum absolute eigenvalues greater than 1 were rejected, as they indicate that the density of positive input to given variable, or variables, would likely lead to uncontrolled growth.

All R scripts used to simulate the data, fit GIMME models to the simulated data, and evaluate directionality recovery, as well as all simulated data reported in the current study, are publicly available on the Open Science Framework (https://osf.io/zvfuh/).

Evaluation of Directionality Recovery

The GIMME-AR and GIMME-MS search strategies were applied separately to data from all simulation replications using the gimme (version 0.6–1) R package (Lane et al., 2019b). To select final models from the GIMME-MS fits, we used the AIC (Akaike, 1973), as the use of standard fit indices is likely to be the most widely applicable method, and as AIC has been previously applied for solution reduction in empirical studies using GIMME-MS (Beltz et al., 2016; Dotterer et al., 2019; Kelly et al., 2020; Weigard et al., 2019). First, the solution for each individual that displays the lowest AIC within each group-level solution was selected as the optimal individual-level solution for that group-level solution. Next, AIC was averaged across all selected individual-level solutions within each group-level solution, and the group-level solution with the lowest average AIC was selected.

Following the estimation and selection of final uSEMs in both frameworks, we used two indices to evaluate the efficacy of directionality recovery for contemporaneous relations (recovery for cross-lagged relations, although not to focus of this study, is also reported separately in Supplemental Materials): direction recall and direction precision (Lane et al., 2019). Direction recall is calculated as the proportion of directional contemporaneous relations present in the individual data-generating model that are successfully recovered in the uSEM (i.e., what fraction of the true relations did the model search recover?). Direction precision is calculated as the proportion of directional contemporaneous relations present in the individual uSEM that were also present in the data-generating model (i.e., what fraction of the relations recovered were in the data generating model?). In both cases, contemporaneous relations are considered to be correctly recovered if they are between the same variables and in the same direction as the data generating model. These indices each provide distinct, important information about recovery; recall evaluates how accurately the recovered model represents relations from the data-generating model by accounting for false negatives, while precision evaluates how likely recovered relations are to be true relations by accounting for false positives.

When considering the absolute values of recall and precision, it is important to note that GIMME is a sparse network mapping approach that prioritizes the inclusion of strong relations and does not typically estimate weaker relations. Additionally, we are simultaneously assessing both: 1) the recovery of a relation, and 2) the correct directionality. Other work (e.g., Gates & Molenaar, 2012; Lane et al., 2018; Smith et al., 2011) assesses the ability to recover a relation separately from the ability to detect the direction of the relation. The measure we use is more strict. Therefore, recall values considerably lower than 1 are expected, and precision values are expected to be higher than recall values. In substantive applications of GIMME, precision is also a central practical consideration because it is directly linked to questions about how confident a researcher should be in a given result (i.e., how likely is it that this directional relation is truly present in the data?). Precision statistics close to 1 are therefore optimal.

Simulation Study Results and Discussion

Convergence and Model Checking

Across the GIMME-AR and GIMME-MS search strategies, over 99.5% of models converged normally⁴. Model plausibility was also evaluated via the standardized error covariance matrix for assumption-violating values below 0 or above 1. Recovery analyses were conducted both including and excluding implausible models to ensure that inferences about directionality were robust. As these sensitivity analyses produced the same general patterns and inferences, results from the larger data set are reported below, and results with implausible models excluded are reported in Supplemental Materials.

Multiple Solutions by Simulation Condition

We first evaluated our prediction that data sets with weaker autoregressive/lagged than contemporaneous relations would produce more solutions in GIMME-MS. Figure 1 displays, for each condition, the average number of individual-level solutions (across all group-level solutions) in each replication (μIsol/rep). More detail on the levels of multiple solutions in each condition is available in Supplemental Materials. As expected, the relative strength of contemporaneous and lagged relations had a substantial influence on the number of solutions. Multiple solutions were rare in the lagged-greater (LG) condition (blue in Figure 1), with solution counts staying at, or a slight fraction above, 1 regardless of autoregressive relation strength or the number of time points. Furthermore, even in conditions in which multiple solutions were relatively common – contemporaneous-greater (CG) and balanced (BA) – they were infrequent when strong autoregressive relations were present. Notably, multiple solutions were extremely rare in the BA condition when autoregressive relations were systematically stronger than the off-diagonal contemporaneous and lagged relations (β = .50-.60 vs. β = |.30| for off-diagonal relations).

Figure 1.

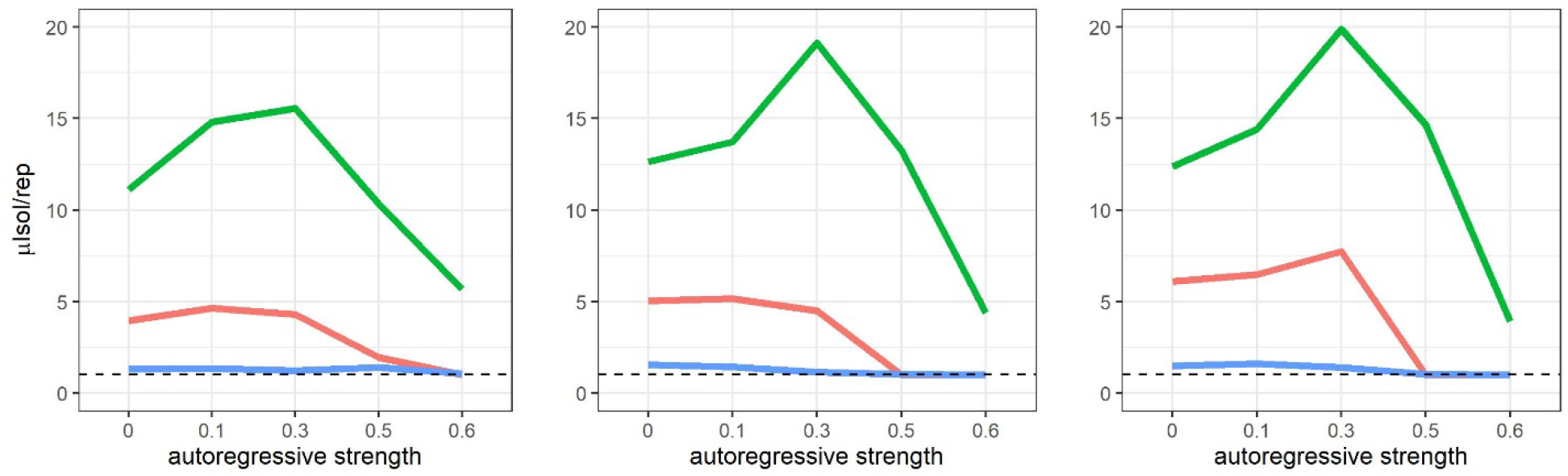
Average number of individual-level solutions per subject across all group-level solutions in each replication (μIsol/rep) for the balanced (red), lagged-greater (blue) and contemporaneous-greater (green) conditions. The black dashed line in each plot highlights the value of 1, where each statistic would fall if multiple solutions were not found. Plots that break down the solution counts by level (group/individual) are available in Supplemental Figure 1.

These results supported our prediction that GIMME-MS would generate fewer multiple solutions for data sets with relatively strong autoregressive or lagged relations than for those in which such relations are relatively weak. In fact, multiple solutions were exceedingly rare in conditions in which contemporaneous relations were either systematically weaker than lagged relations or systematically weaker than autoregressive relations. Under these conditions, the strong autoregressive or lagged relations are estimated early in the search process, preventing cases in which opening contemporaneous relations would lead to equivalent improvements in model fit. Therefore, when cross-lagged and/or autoregressive relations are strong, the GIMME-MS search process may closely resemble that of GIMME-AR and, in turn, may generate highly similar models.

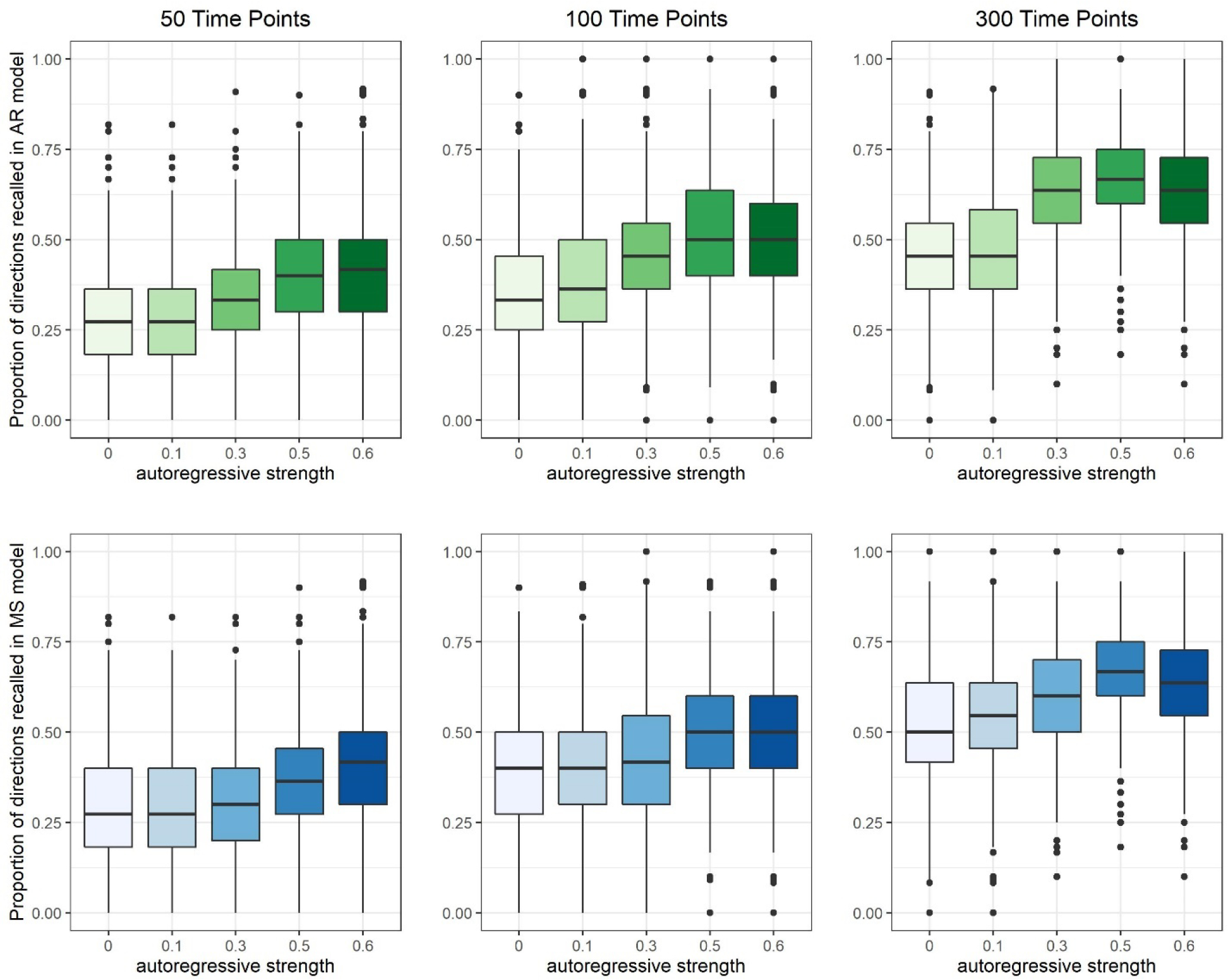
Directionality Recovery of Contemporaneous Relations

We next evaluated, and contrasted, the efficacy of GIMME-AR and GIMME-MS for recovering contemporaneous relation directionality. Table 1 provides a comprehensive summary of both search strategies’ direction recall and precision for contemporaneous relations, as well as the difference in recall and precision between the strategies. As discussed below, box plots of recall and precision values for individual-level models (Figures 2–5) show the effects of number of time points and autoregressive relation strength on contemporaneous direction recovery for the BA condition, as well as differences between search strategies in all conditions. Additional box plots of contemporaneous direction recovery in the LG and CG conditions and recovery statistics for cross-lagged relations are in Supplemental Materials.

Table 1.

Direction recall and direction precision for contemporaneous relations across all simulation conditions and the GIMME-AR and GIMME-MS search strategies, as well as the difference between strategies (GIMME-MS values minus GIMME-AR values). BA = balanced contemporaneous and lagged relations condition; LG = lagged-greater condition; CG = contemporaneous-greater condition; Auto. = autoregressive

			GIMME-AR			GIMME-MS			MS - AR Difference
Recovery Statistic	Time Points	Auto. Strength	BA	LG	CG	BA	LG	CG	BA	LG	CG
Direction Recall	50	0.00	0.27	0.29	0.31	0.30	0.36	0.37	0.03	0.07	0.06
		0.10	0.28	0.31	0.29	0.30	0.37	0.40	0.02	0.06	0.11
		0.30	0.33	0.37	0.36	0.31	0.36	0.46	−0.02	0.00	0.10
		0.50	0.40	0.41	0.65	0.35	0.37	0.49	−0.05	−0.04	−0.17
		0.60	0.42	0.43	0.70	0.42	0.42	0.54	0.00	−0.02	−0.16
	100	0.00	0.34	0.37	0.37	0.40	0.41	0.40	0.06	0.05	0.03
		0.10	0.38	0.38	0.33	0.41	0.46	0.46	0.04	0.08	0.13
		0.30	0.45	0.45	0.40	0.43	0.47	0.52	−0.03	0.02	0.12
		0.50	0.51	0.47	0.75	0.51	0.46	0.58	0.00	−0.01	−0.16
		0.60	0.51	0.48	0.81	0.51	0.48	0.69	0.00	0.00	−0.12
	300	0.00	0.45	0.43	0.38	0.51	0.47	0.47	0.06	0.04	0.10
		0.10	0.47	0.41	0.35	0.55	0.51	0.49	0.08	0.10	0.13
		0.30	0.63	0.51	0.47	0.60	0.55	0.57	−0.03	0.04	0.10
		0.50	0.67	0.56	0.76	0.67	0.55	0.63	0.00	−0.01	−0.14
		0.60	0.64	0.56	0.82	0.64	0.56	0.77	0.00	0.00	−0.05
Direction Precision	50	0.00	0.42	0.58	0.34	0.44	0.58	0.39	0.02	0.00	0.05
		0.10	0.42	0.58	0.32	0.44	0.60	0.41	0.02	0.02	0.10
		0.30	0.49	0.62	0.37	0.43	0.53	0.43	−0.06	−0.08	0.06
		0.50	0.56	0.64	0.66	0.46	0.50	0.42	−0.10	−0.14	−0.24
		0.60	0.60	0.66	0.70	0.58	0.60	0.47	−0.02	−0.07	−0.23
	100	0.00	0.47	0.72	0.37	0.51	0.67	0.41	0.05	−0.05	0.04
		0.10	0.51	0.71	0.32	0.53	0.72	0.46	0.02	0.01	0.13
		0.30	0.61	0.78	0.38	0.53	0.69	0.46	−0.08	−0.09	0.08
		0.50	0.71	0.83	0.75	0.70	0.77	0.50	−0.01	−0.06	−0.25
		0.60	0.76	0.83	0.83	0.75	0.81	0.64	−0.01	−0.02	−0.19
	300	0.00	0.55	0.68	0.35	0.61	0.65	0.46	0.05	−0.04	0.11
		0.10	0.55	0.60	0.32	0.63	0.69	0.47	0.07	0.09	0.15
		0.30	0.75	0.76	0.42	0.68	0.77	0.51	−0.07	0.01	0.09
		0.50	0.89	0.88	0.72	0.89	0.87	0.54	0.00	−0.02	−0.18
		0.60	0.91	0.90	0.80	0.91	0.90	0.72	0.00	0.00	−0.09

Figure 2.

Box plots of contemporaneous relation direction recall for individual-level models in the balanced (BA) simulation condition for GIMME-AR (top/green) and GIMME-MS (bottom/blue) search strategies.

Figure 5.

Box plots of contemporaneous relation direction precision differences between the two search strategies (GIMME-MS minus GIMME-AR) for individual-level models in all simulation conditions.

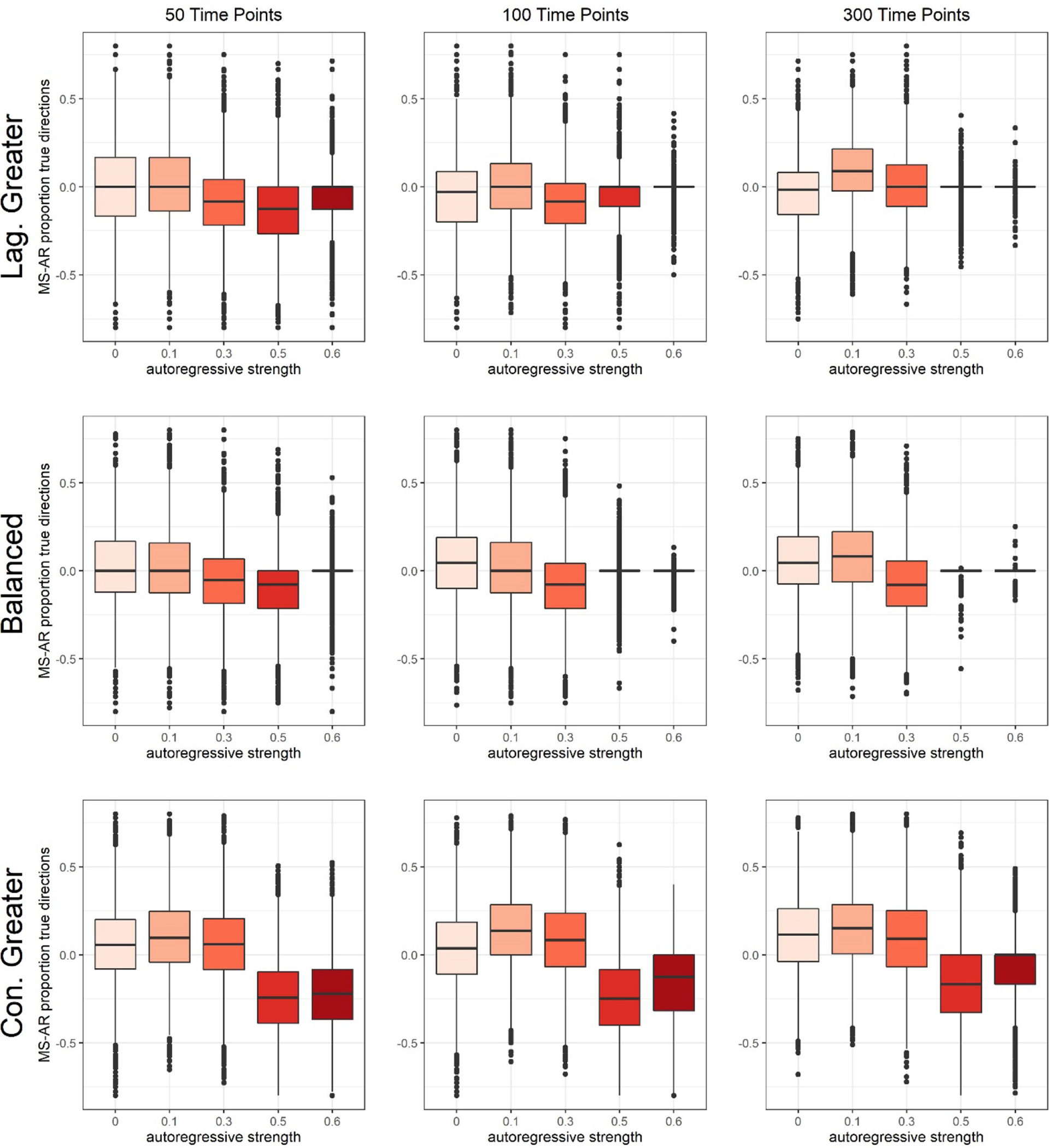
Contemporaneous direction recall for both strategies increased with the number of time points, consistent with previous work (Lane et al., 2019; Nestler & Humberg, 2021), and also increased dramatically at higher autoregressive relation strengths. Figure 2 illustrates both effects: Data sets with stronger autoregressive relations displayed better recall than those with weaker autoregressive relations across all time point conditions and, notably, across both GIMME-AR and GIMME-MS. Recall was typically below .50 for data sets with weak autoregressive relations, even with many time points, but data sets with autoregressive relations greater than or equal to the strength of off-diagonal relations in the BA condition (β = .30) displayed greater recall, especially at 300 time points. Differences between recall in the LG and CG conditions (Table 2) illustrate effects of the relative strength of lagged and contemporaneous relations: Across search strategies, recall was better for the CG than LG condition when autoregressive relations were strong (β =.50-.60), but was similar between the conditions when autoregressive relations were weak. Hence, contrary to our expectations, stronger contemporaneous relations did not substantially degrade direction recall; indeed, it improved it in some conditions. As the contemporaneous relations in CG may have been easier to detect because they were estimated early in the search process, this may have combined with conditions that are more favorable for discerning directionality (i.e., strong autoregressive relations) to improve recall overall.

Table 2.

Effects of the relative strength of contemporaneous and lagged relations on direction recall and direction precision for GIMME-AR (AR) and GIMME-MS (MS) search strategies. Values in the table represent difference scores obtained by subtracting recovery statistics in the contemporaneous greater (CG) condition from those in the lagged greater (LG) condition. Therefore, positive values indicate better recall or precision in the LG condition, whereas negative values indicate better recall or precision in the CG condition.

		Recall		Precision
Time Points	Auto. Strength	AR	MS	AR	MS
50	0.00	−0.02	−0.01	0.24	0.19
	0.10	0.01	−0.03	0.27	0.19
	0.30	0.00	−0.10	0.24	0.10
	0.50	−0.25	−0.11	−0.02	0.08
	0.60	−0.27	−0.12	−0.03	0.13
100	0.00	0.00	0.01	0.34	0.26
	0.10	0.05	0.00	0.39	0.26
	0.30	0.05	−0.05	0.39	0.23
	0.50	−0.27	−0.12	0.08	0.27
	0.60	−0.33	−0.21	0.00	0.17
300	0.00	0.05	−0.01	0.33	0.19
	0.10	0.05	0.02	0.27	0.22
	0.30	0.03	−0.02	0.34	0.26
	0.50	−0.21	−0.07	0.17	0.33
	0.60	−0.26	−0.21	0.10	0.18

Differences in contemporaneous relation direction recall between GIMME-AR and GIMME-MS across all simulation conditions are illustrated in Figure 3. At low to moderate autoregressive strengths (β = .00-.30), GIMME-MS showed improved direction recall relative to GIMME-AR. These improvements were marginal in the BA and LG conditions (.04 on average), but more substantial in the CG condition (.10 on average). However, at high autoregressive strengths, recall was typically identical between the two search strategies in the BA and LG conditions (as illustrated by the box plots in which most recall difference scores were 0), likely because the search strategies converged on identical models, and recall was substantially worse for GIMME-MS in the CG condition (by .13 on average). The advantage of GIMME-AR relative to GIMME-MS when both contemporaneous and autoregressive relations were relatively strong likely reflects the fact that strong autoregressive relations estimated in the null model in GIMME-AR provide guidance for the search, while strong contemporaneous relations may instead be estimated before them in GIMME-MS.

Figure 3.

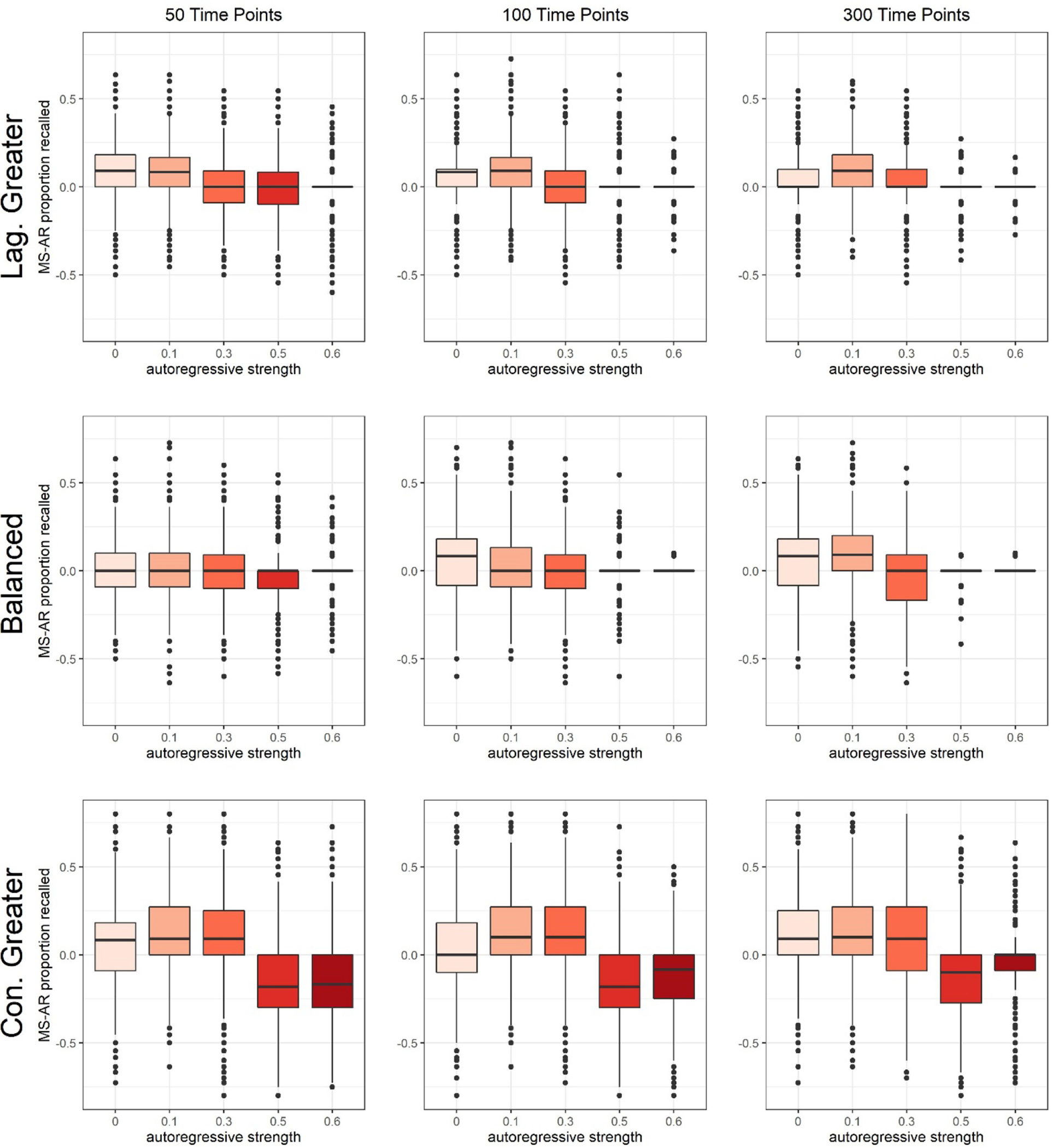
Box plots of contemporaneous relation direction recall differences between the two search strategies (GIMME-MS minus GIMME-AR) for individual-level models in all simulation conditions.

For contemporaneous direction precision, effects of the number of time points and the strength of autoregressive relations (Figure 4, Table 1) mirrored effects of direction recall, although precision statistics had higher absolute values because GIMME produces sparse and parsimonious networks by avoiding the estimation of weak (and potentially spurious) relations. Precision was consistently poor when autoregressive relations were weak (β = .00-.10) and gradually improved as the strength of these relations increased. Overall, optimal precision values were seen when autoregressive relations were strongest (β = .50-.60) and when 100 time points (average precision = .74) or 300 time points (average precision = .83) were available. In contrast to direction recall, however, direction precision was unambiguously better in the LG condition than in the CG condition (Table 2), with the only exceptions being for GIMME-AR at high autoregressive strengths. GIMME-AR obtained high precision with at least 100 time points in both conditions. Therefore, patterns in contemporaneous direction precision, but not contemporaneous direction recall, were consistent with our expectation that relatively stronger lagged relations would improve recovery.

Figure 4.

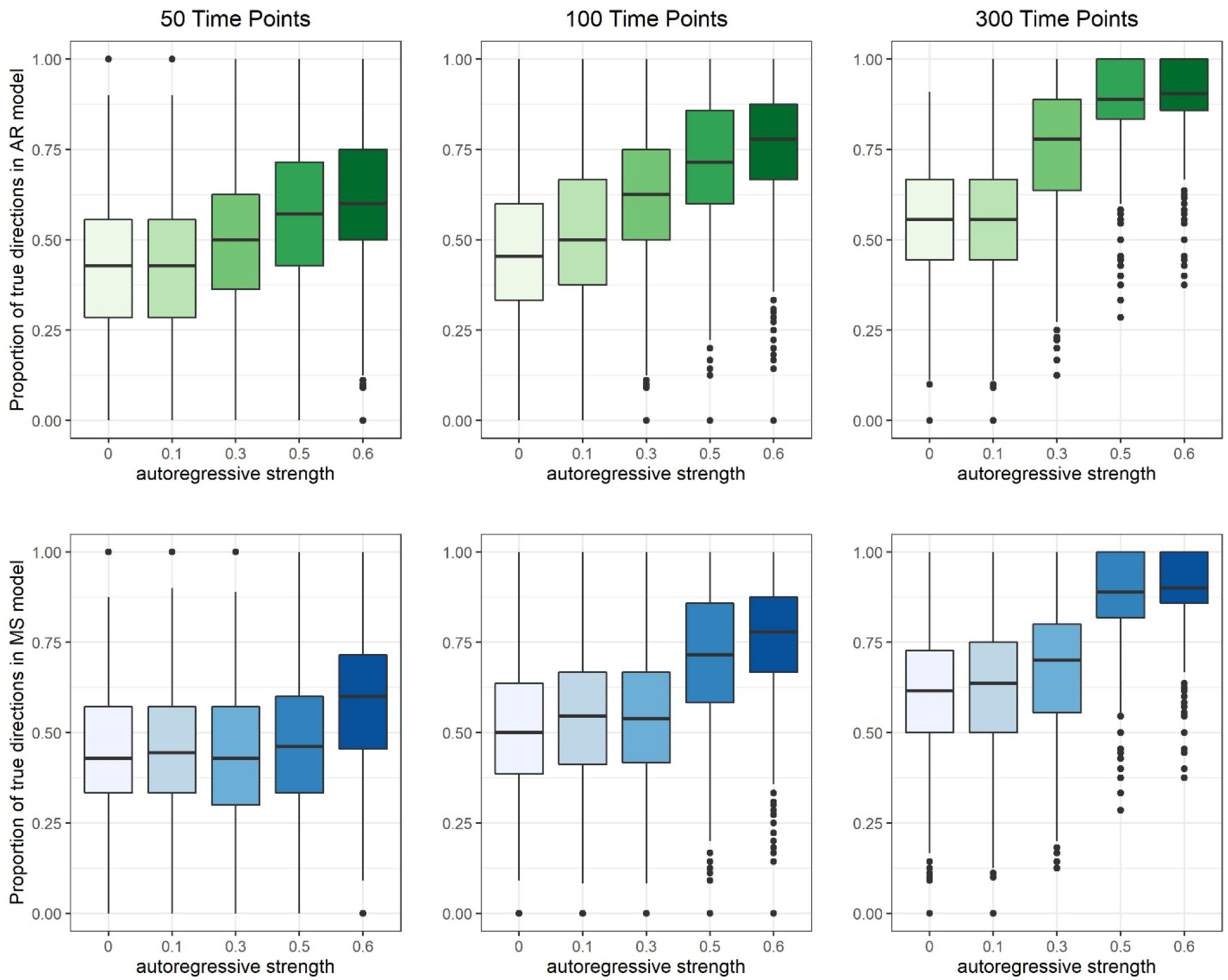
Box plots of contemporaneous relation direction precision for individual-level models in the balanced (BA) simulation condition for GIMME-AR (top/green) and GIMME-MS (bottom/blue) search strategies.

Differences in contemporaneous direction precision between GIMME-AR and GIMME-MS (Figure 5) were similar to those for contemporaneous direction recall. At low to moderate autoregressive strengths (β =.00-.30), GIMME-MS provided improved precision in the CG condition (by .09 on average), but no clear pattern emerged in the BA or LG conditions. At high autoregressive strengths, the search strategies had nearly identical precision in the BA and LG conditions, and GIMME-MS displayed markedly worse performance in the CG condition (by .20 on average), similar to the effects in recall.

In summary, contemporaneous direction recall and precision were both found to be substantially improved when autoregressive relations were stronger, consistent with our expectations. Effects of the relative strength of contemporaneous and lagged relations were more nuanced; precision was degraded, but recall was generally improved, when contemporaneous relations were stronger than lagged relations. Although effects of autoregressive and lagged relation strengths were generally consistent between GIMME-AR and GIMME-MS, GIMME-MS displayed incrementally better recall and precision than GIMME-AR when autoregressive relations were weak. When autoregressive relations were strong, performance of the methods was either equivocal, or, in situations in which contemporaneous relations were also strong, substantially worse for GIMME-MS. Hence, these findings present clear implications for whether GIMME-AR or GIMME-MS may be preferable in specific network modeling applications: GIMME-MS may be helpful for improving contemporaneous directionality recovery when autoregressive relations in empirical data are weak (e.g., intensive longitudinal or daily diary studies), whereas GIMME-AR appears preferable for data sets in which autoregressive relations are known to be strong (e.g., resting state fMRI).

Empirical Data Analysis Methods

We applied GIMME-AR and GIMME-MS (with AIC solution reduction) to two empirical data sets illustrating typical situations in which autoregressive relations are strong versus weak: resting state fMRI and daily diary data, respectively. In doing so, we: 1) evaluate whether effects of autoregressive relation strength on model features (e.g., number of solutions in GIMME-MS) identified in the simulation study are matched in empirical data, 2) assess similarities and differences between models estimated by GIMME-AR and GIMME-MS, and 3) provide practical insights to users planning to implement GIMME in similar empirical data, including important considerations about how features of these data sets may or may not align with assumptions of directionality modeling approaches, including GIMME.

Resting State fMRI

The first data set was previously analyzed in a study outlining a posteriori model validation procedures for standard GIMME models (Beltz & Molenaar, 2015), which includes a detailed description of the participants, procedures and pre-processing steps. Briefly, resting state fMRI data were collected from 32 young adult participants (all aged 20–21 years; 18 females) as part of a larger neuroimaging study on the neural reward and inhibitory processing of alcohol cues in university students. During a 2-hour neuroimaging and behavioral data collection session, participants were scanned using a 3-Tesla Siemens Trio scanner. MRI data included a high-resolution structural image as well as functional images collected in an EPI sequence (TR = 2000ms, TE = 25ms, FOV = 240mm, flip angle = 80°). During a resting state scan of 164 volumes (i.e., 164 separate measurement time points), participants were instructed to close their eyes and relax without falling asleep. Standard pre-processing steps included removal of the first 4 volumes, motion correction, non-brain removal, spatial smoothing with a 6mm Gaussian kernel, grand-mean signal intensity normalization, highpass filtering, removal of physiological noise via white matter and cerebrospinal fluid signal regression, and normalization to MNI space. Four regions of interest (ROIs), which are all central to the default mode network (DMN), were identified: posterior cingulate cortex (PCC; x = −5, y = −49, z = 40), 2), medial prefrontal cortex (MPFC; x = −1, y = 47, z = −4), right lateral parietal lobule (R LP; x = 46, y = −62, z = 32), and left lateral parietal lobule (L LP; x = −45, y = −67, z = 36). Mean BOLD signal from each region was then extracted for the remaining 160 volumes in the time series.

Daily Diary of Emotion Ratings

The second data set was drawn from a larger 100-day diary study of daily emotion in university community participants. Questionnaires administered daily included the widely-used Positive and Negative Affect Schedule (PANAS), in which participants rate their levels of 10 Positive emotions (e.g., “Enthusiastic”) and 10 Negative emotions (e.g., “Irritable”) on a 1–5 scale (Watson et al., 1988), and the 7 Up 7 Down inventory (Youngstrom et al., 2013), in which participants rate their levels of 7 Mania symptoms (e.g., “periods of extreme happiness and intense energy”) and 7 Depression symptoms (e.g., feeling “so down in the dumps you thought you might never come out of it”) on a 0–3 scale. We included data from 32 participants who were matched on gender (18 females) and who were in roughly the same age range (18–23 years old) as participants in the fMRI data set to ensure samples were structurally and demographically similar. As the fMRI data included 4 ROIs, we likewise selected 4 variables from the daily diary study which were likely to show relations with one another: Positive affect (daily composite from the PANAS), Negative affect (daily composite from the PANAS), Mania symptoms (daily composite from the 7 Up 7 Down inventory), and Depression symptoms (daily composite from the 7 Up 7 Down inventory).

Analyses

Prior to model fitting, we considered several features of each empirical data set to determine the extent to which basic assumptions of GIMME were met, including the assumptions of equal measurement intervals, weak stationarity, and Gaussian white noise errors that apply to GIMME and most other directionality modeling approaches. We then analyzed both data sets with GIMME-AR and GIMME-MS (with identical procedures to those used in the simulation study) and assessed several features of the results. First, we examined autoregressive relation strength in the two data sets by assessing the proportion of autoregressive relations estimated in GIMME-MS and the β weights of autoregressive relations estimated in GIMME-AR. We expected that the resting state fMRI data set would display both a greater proportion of autoregressive relations estimated in GIMME-MS and higher β weights of autoregressive relations estimated in GIMME-AR. Next, we examined the number of solutions generated by GIMME-MS in the two data sets. As the daily diary data were expected to have weaker autoregressive relations, we expected this data set to produce more solutions in GIMME-MS than the fMRI data set. Last, we examined the presence and directionality of relations in the final models obtained from each search strategy. We expected that GIMME-AR and GIMME-MS would display similar patterns of directionality when applied to the fMRI data set, but that their patterns of directionality for the daily diary data set would be discrepant (as the search strategies would differ in early-estimated relations).

Empirical Data Analysis Results and Discussion

Assumptions and Empirical Data Features

Simulation study data were explicitly derived from a data-generating process that met the assumptions of GIMME. However, it is possible (and perhaps likely) that empirical data sets violate these assumptions to some extent. Therefore, we begin by assessing several key assumptions in the empirical fMRI and daily diary data sets. These assumptions and other important considerations are reviewed in greater detail in prior GIMME tutorials (Beltz & Gates, 2017).

The assumption of equal measurement intervals is met in both empirical data sets. The fMRI data were collected at a precise interval (2000ms TR) and, in the daily diary study, participants were asked to respond to the mood measures between 8PM and bedtime each day and to reflect on how they generally felt throughout the past 24 hours.

The current implementation of uSEM within GIMME also assumes “weak stationarity”, or that data means, variances and covariances are stable across time. Preprocessing steps typically used to prepare resting state fMRI data for analysis help to maintain stationarity, and many of those steps were applied to these empirical fMRI data. They include high pass filtering, which removes low-frequency temporal trends from the data, and the covariation of nuisance signals (e.g., from white matter and cerebrospinal fluid), which removes variance associated with nonstationary contaminant processes like participant motion. Therefore, we expect that the stationarity assumption is met in the empirical fMRI data, although this assumption is naturally dependent on the success of preprocessing strategies for removing impactful non-stationary trends.

Stationarity considerations particularly relevant to intensive longitudinal behavioral data, such as the daily diary data analyzed here, include whether extreme values disproportionately influence model estimates. For example, a person experiencing a profoundly negative life event (e.g., loss of employment or the death of a loved one) may report extreme levels of negative affect on a small set of days. These outliers may not reflect the otherwise-stationary processes that govern the rest of the time series. To examine outliers in the empirical data, we standardized observations of each variable for each individual to Z-scores and plotted histograms of individuals’ most extreme Z-score absolute value for each variable (Supplemental Figure 14). Notable outliers were relatively uncommon in the resting state fMRI data. For each variable, fewer than half of individuals displayed a value >3SD from the mean, and there were only two instances (for two separate variables) in which a single individual displayed an outlier >6SD from the mean. In the daily diary data, however, the majority of individuals displayed values >3SD from the mean, and it was also common for individuals to display outliers >6SD, especially for Manic Symptoms (41% of the sample) and Depression Symptoms (34%). It is possible these two variables were more likely to display extreme values because they represent items that are infrequently endorsed by most individuals in non-clinical samples, and therefore, only display high levels on a subset of days during which individuals potentially experienced life events that had a substantial impact on their mood. Overall, the presence of more extreme values in the daily dairy data supports the notion that these data are more likely to contain influential cases than neuroimaging data and suggests that users of these data should consider sensitivity analyses to gauge the impact of outliers on inferences. Possible sensitivity analyses may include re-running GIMME while excluding these extreme values or including the severity of an individuals’ outliers as a covariate in follow-up tests.

A third basic assumption of uSEM within GIMME is that errors will reflect Gaussian “white noise”, or noise without any remaining temporal dependencies; although autoregressive effects of the first order, or even higher orders, may be present in empirical data, the first-order autoregressive terms in GIMME are assumed to be able to effectively model temporal dependencies, leaving only “white noise” in the residual time series. Figure 6 displays, for all variables and individuals in both data sets, the observed temporal autocorrelation coefficients at the first order (i.e., lag of 1, which GIMME estimates) through the seventh order. Note that this is the empirical data rather than the noise, so white noise is not expected. These coefficients indicate that the observed resting state fMRI data exhibited strong temporal dependencies. Autocorrelation was most pronounced at the first order, but also appears, on average, to be substantial (e.g., ≥0.20) at the second order, and many individuals displayed statistically significant autocorrelation effects at higher orders. In contrast, the daily diary data showed much weaker temporal dependencies; autocorrelation was only substantial for the first order, although these first-order effects were much smaller than those in the fMRI data, and few individuals displayed statistically significant autocorrelation effects at higher orders. This contrast suggests that the resting state fMRI data may require models with higher order autoregressive effects to fully account for all temporal dependencies. In fact, Beltz and Molenaar (2015) used this specific fMRI data set to explore, in depth, the validity of the assumption that the first-order effects modeled by default GIMME can adequately account for temporal dependencies in neuroimaging data. The authors found that 14 participants (44% of the sample) required the addition of a second order autoregressive term to produce white noise residuals. However, relevant to our focus in the current paper, this term only appeared to alter the estimation of contemporaneous relations for a minority of individuals.

Figure 6.

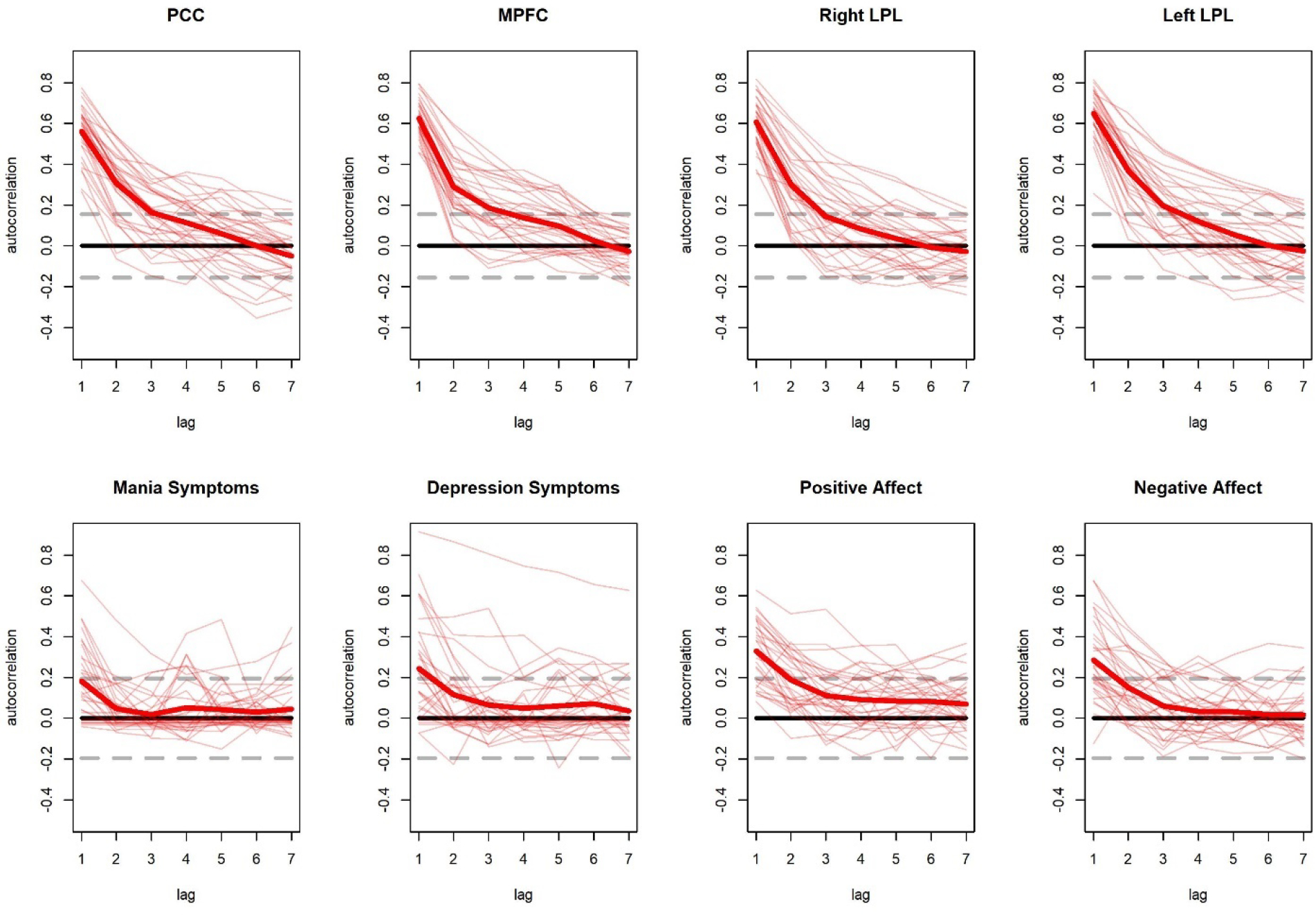
Observed temporal autocorrelation coefficients at lags of the first order (correlation between time t and time t-1) through the seventh order (correlation between time t and time t-7) for all variables in the resting state fMRI (top row) and daily diary (bottom row) data sets. The thick red line represents the sample average while the thinner and fainter lines represent the autocorrelation coefficients of each individual in the sample. Grey dashed lines represent the values that the autocorrelation coefficient would have to surpass to be considered significantly (p<.05) different from 0 given the time series length in each data set.

Although these daily diary data appear to exhibit relatively weak autocorrelation coefficients, a key consideration for intensive longitudinal behavioral data is whether mood or behavior follows cyclical trends, for instance across days of the week (e.g., feeling positive on Saturdays). If such trends exert a predominant effect on variation in the time series, or if they are of specific interest for a given research question, the current implementation of GIMME is not an ideal analysis option because it does not explicitly model such features. Figure 6 indicates that the daily diary data exhibited a generally monotonic decreasing pattern as orders increase and, importantly, that there was no uptick in autocorrelation at the seventh order, suggesting a lack of weekly trends. A handful of individuals (13–16%, depending on the variable) displayed small, statistically significant autocorrelation coefficients at the seventh order. However, this was also true at most other orders and even true for the seventh order of one of the fMRI variables (which is not on a weekly cycle). Hence, there is little evidence that systematic cyclical trends have a significant impact on these daily diary data.

Finally, prior to conducting any directionality modeling analysis, users should consider whether the method’s general assumptions about the functional form of relations between time series variables (in this case, linear) and the shape of the error distribution (e.g., Gaussian) are appropriate. It is possible that some neuroimaging or intensive longitudinal behavioral data sets may contain nonlinear relations or atypical error distributions, and methods for analyzing these data sometimes eschew these assumptions (e.g., the non-Gaussian errors assumed by the LiNGAM method; non-linear basis vectors in GIMME: (Duffy et al., 2021)). Therefore, researchers should carefully consider the possible limitations that these general assumptions entail for interpreting specific effects. In the current analysis, linearity and Gaussian errors were assumed, which follows most other network approaches.

GIMME Results

We next turn to summarizing the empirical results. Models from both search strategies successfully converged for all participants in the two empirical data sets. Final models for the fMRI data from GIMME-AR and GIMME-MS displayed identical average fit indices, which generally indicated good fit (RMSEA = .09, SRMR = .04, NNFI = .94, CFI = .97). Group-level autoregressive relations were present for all brain regions, along with group-level relations from the right lateral parietal lobe (R LP) to the left lateral parietal lobe (L LP) and from the L LP to posterior cingulate cortex (PCC). The presence of these group-level relations is consistent with their well-established role as “hubs” of the DMN (Buckner et al., 2008). For the daily diary data set, average fit indices for final models from both GIMME-AR (RMSEA = .04, SRMR = .06, NNFI = .99, CFI = .99) and GIMME-MS (RMSEA = .03, SRMR = .06, NNFI = .99, CFI = .98) also indicated good fit. No off-diagonal group-level relations were identified by either search strategy, though, possibly indicating a high degree of heterogeneity in the sample. However, as illustrated by models for three example participants displayed in Figure 7, individual-level relations were abundant and were generally consistent with conventional assumptions about the emotion variables in the data set. For example, participants tended to display a negative relation between Positive Affect and Negative Affect, positive relations between Negative Affect and Depression Symptoms, and positive relations between Positive Affect and Mania Symptoms. However, as discussed in detail below, GIMME-AR and GIMME-MS often provided differing estimates of the direction of these relations.

Figure 7.

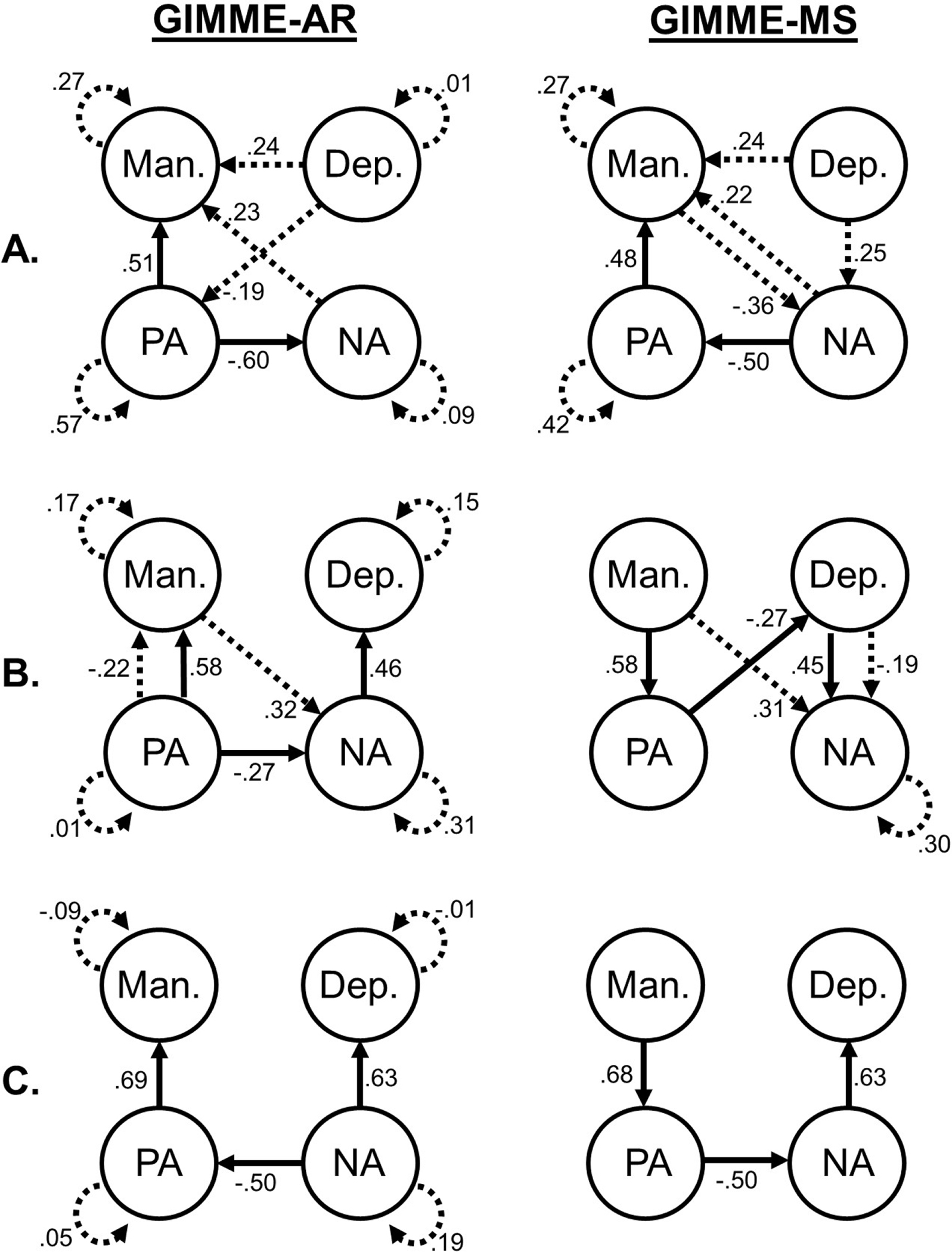
Schematics of networks generated by GIMME-AR and GIMME-MS for three example participants (A-C) from the daily diary data set. Circular arrows indicate autoregressive relations, straight dotted-lined arrows indicate lagged relations, and straight solid-lined arrows indicate contemporaneous relations. Numbers indicate β weights for recovered relations. Man. = Mania Symptoms; Dep. = Depression Symptoms; PA = Positive Affect; NA = Negative Affect

The fMRI data displayed substantially stronger autoregressive relations than the daily diary data, as illustrated by differences between the data sets in both the proportion of autoregressive relations opened in GIMME-MS and the average β weights of autoregressive relations estimated within GIMME-AR (Table 3). Moreover, β weights were all within the range of those used in the simulations; autoregressive relations in the daily diary data were of low to moderate strength (β =.11-.28) whereas those in the resting state fMRI data were comparable to the strongest simulated autoregressive relations (β =.43-.56). This correspondence was expected given that the simulation was informed by previous empirical applications of GIMME.

Table 3.

Proportion of individuals in the sample for which autoregressive relations were opened for each variable in GIMME-MS and the average β weights estimated for each variable’s autoregressive relation in GIMME-AR. Auto. = autoregressive; PCC = posterior cingulate cortex; MPFC = medial prefrontal cortex; LPL = lateral parietal lobule.

Data Set	Variable	GIMME-MS Auto. Proportion Opened	GIMME-AR Average Auto. β Weights
Resting State fMRI	PCC	1.00	0.43
	MPFC	1.00	0.56
	Right LPL	1.00	0.54
	Left LPL	1.00	0.48
Daily Diary	Mania Symptoms	0.16	0.11
	Depression Symptoms	0.34	0.20
	Positive Affect	0.44	0.28
	Negative Affect	0.34	0.18

There were also striking differences between the data sets in the number of solutions identified by GIMME-MS. There were no multiple solutions identified at either the group or individual levels for the fMRI data. In contrast, there was only one group-level solution identified for the daily diary data set (and this solution contained no group-level relations, as noted above), but GIMME-MS returned an average of 2.91 individual-level solutions per person (ranging from 1 to 6 across participants). Therefore, consistent with the simulation study findings, empirical data sets with weak autoregressive relations are the most likely to generate multiple solutions.

Inspection of the contemporaneous and lagged (excluding autoregressive) relations identified by GIMME-AR and GIMME-MS indicated that the two search strategies resulted in identical models for every single subject in the fMRI data set. Therefore, consistent with findings from the simulation study, GIMME-MS and GIMME-AR converge when applied to empirical data sets with strong autoregressive relations because GIMME-MS only detects multiple solutions if they are likely (due to identical modification indices). In contrast, recovered models for the daily diary data set were discrepant between search strategies. Only 59% and 53% of the lagged and contemporaneous relations, respectively, that were recovered by GIMME-AR were also recovered by GIMME-MS, and only 42% and 53% of the lagged and contemporaneous relations recovered by GIMME-MS were also recovered by GIMME-AR.

The discrepancies in recovered lagged relations, and the fact that far fewer of the lagged relations recovered by GIMME-MS were recovered by GIMME-AR than vice versa, can be explained in part by the fact that GIMME-MS identified more off-diagonal lagged relations (24 total) than GIMME-AR (17 total). This pattern may indicate that opening the autoregressive terms at the beginning of the search process in GIMME-AR causes signal from off-diagonal lagged relations to be incorrectly attributed to autoregressive relations.

Interestingly, out of the 70 total cases in which contemporaneous relations were discrepant between the GIMME-AR and GIMME-MS models, 50 (71%) were cases in which relations between the same two variables were identified, but the relation was modeled in the opposite direction in the two search strategies. Figure 7 illustrates this phenomenon in the three example participants; participants A and C display reversals in the directionality of relations between Positive Affect and Negative Affect, participants B and C display reversals in the directionality of relations between Positive Affect and Mania Symptoms, and B displays a reversal in the directionality of Depression Symptoms’ relation with Negative Affect. These results are generally consistent with previous work (Lane et al., 2019) showing that GIMME-AR is often able to effectively identify the presence of important relations in the network model, even in situations in which recovery of the directionality of these relations is poor or variable (as in the case with low autoregressive effects).

In summary, results from analyses of the empirical data sets were highly consistent with several aspects of the simulation study results. Notably, this consistency was apparent despite possible violations of GIMME’s assumptions, including higher-order temporal dependencies in a portion of the fMRI data and the presence of some extreme values in the daily diary data, and suggests that conclusions from the simulations are robust to minor violations. Therefore, guidelines derived from the simulations should be broadly applicable in real-world research projects involving data with relatively weak (daily diary) and relatively strong (fMRI) autoregressive relations.

General Discussion

The current study assessed the efficacy of two data-driven search strategies within the GIMME framework for correctly identifying the directionality of contemporaneous relations in person-specific network models. One strategy relies on the default estimation of autoregressive relations in the null model to inform estimation of directional relations during the search (GIMME-AR), whereas the second strategy estimates multiple solutions when relations of opposing directionality may lead to equivalent improvements in model fit that can be compared following the search (GIMME-MS). We assessed directionality recovery under conditions in which autoregressive and lagged relations were relatively strong versus relatively weak because we predicted that each search strategy would have unique strengths and weaknesses in these situations, which may in turn have important consequences for empirical applications. Through a principled simulation-recovery analysis paired with empirical examples, this study provides the first one-to-one comparison of GIMME-AR and GIMME-MS for directionality recovery under a variety of relevant conditions that may be encountered across different substantive applications. Notably, this also represents the first large-scale and comprehensive (i.e., involving many conditions and random replications) evaluation of the directionality recovery of GIMME-MS.

The overall pattern of findings suggests several important recommendations about which situations are most appropriate for the use of each strategy, and which features of empirical data allow researchers to place greater, or lesser, confidence in the resulting directionality estimates. As hypothesized, we found that direction recall (the proportion of relations in the “true” model that are recovered) and direction precision (the proportion of relations present in the estimated model that are also in the “true” model) were both dramatically improved when autoregressive relations in time series data were strong. Although we had initially expected this pattern to be more apparent for GIMME-AR, due to its reliance on strong autoregressive relations to guide the search, we found that the pattern was pronounced for both search strategies. However, each search strategy displayed relative advantages under certain conditions.

GIMME-MS displayed a clear advantage when autoregressive relations were very weak (β <= .10), likely because subjecting these relations to the same data-driven criteria for estimation as other relations may have prevented small or spurious autoregressive relation estimates from influencing the search process. In contrast, GIMME-AR and GIMME-MS often displayed highly similar direction recall and precision when autoregressive relations were strong (β > .30, or systematically stronger than contemporaneous relations). Both the simulation and empirical analyses suggested that this similarity resulted from the fact that GIMME-MS typically does not identify multiple solutions when autoregressive relations are strong, likely because these autoregressive relations are estimated early in the search. This causes GIMME-AR and GIMME-MS to converge on similar, or even identical, models for individuals. Notably, the latter occurred for all individuals in our analysis of empirical fMRI data with strong autoregressive relations.

GIMME-AR displayed markedly better direction recall and precision then GIMME-MS when autoregressive relations and contemporaneous relations were comparably strong (the contemporaneous greater, CG, condition in our simulations with autoregressive β >= .50). One possible reason for this is that GIMME-MS often estimates strong contemporaneous relations prior to estimating the strong autoregressive relations in these data sets, which prevents the latter from effectively guiding selection of the true direction of the contemporaneous relations. As these strong autoregressive relations are automatically estimated in the null model in GIMME-AR, this may explain GIMME-AR’s relative advantage in these situations. Correspondingly, the advantage of GIMME-MS for data sets with weak autoregressive relations (β <= .10) was also enhanced in the CG condition, which suggests that the relative strengths and weaknesses of each search strategy for contemporaneous relation direction recovery become more apparent when contemporaneous relations are stronger overall.

These patterns of results raise important implications for person-specific network modeling of time series data. The first major implication is that, if estimating contemporaneous relation directionality is important for a given research question, researchers should consider whether features of their empirical data set may be better suited for the application of GIMME-AR or GIMME-MS. Specifically, the application of GIMME-MS to daily diary, ambulatory assessment, and other intensive longitudinal behavioral data sets, which typically have weak autoregressive processes (Beltz et al., 2016; Beltz & Molenaar, 2016; Lane et al., 2019), should allow for improved contemporaneous directionality estimates. In contrast, GIMME-AR is likely to provide estimates of contemporaneous relation directionality that are comparable to, or even better than, those from GIMME-MS for empirical data sets with strong autoregressive processes, such as those drawn from fMRI (Arbabshirani et al., 2014; Beltz & Molenaar, 2015; Christova et al., 2011; Lund et al., 2006) and other neuroimaging methods such as functional near-infrared spectroscopy (Barker et al., 2016).

It should be noted that GIMME-MS often requires significantly more computing time than GIMME-AR due to the repetition of the search process for multiple solutions at the group and individual levels. GIMME-MS may also require more time and effort on the part of researchers to select optimal solutions after the search process ends. Therefore, despite the advantages of GIMME-MS in certain contexts, researchers may consider whether these trade-offs in human and computational resources are worth the improvements in directionality recovery that GIMME-MS allows. As the increases in direction recall and precision that GIMME-MS provides are often modest (typically in the .04 to .10 range depending on the index), GIMME-AR may still be preferable for addressing certain research questions that involve data with relatively weak autoregressive processes (e.g., applications in which contemporaneous relation directionality is not of great concern).

A second major implication follows from our finding that high direction precision for contemporaneous relations (e.g., .70-.90) was achieved in situations with strong autoregressive and/or cross-lagged relations (β >= .50) and a substantial number of observations (>=100), but that direction precision was often significantly lower without these features. Therefore, researchers should place greatest confidence in GIMME’s estimates of contemporaneous relation directionality for data sets that meet these specific criteria (e.g., fMRI data with hundreds of observations). Although these findings indicate limitations of directionality inferences for data sets with weak autoregressive and lagged relations or with limited time points, previous work demonstrates that, even in situations in which the directionality of relations is not recovered correctly, GIMME’s estimates of the presence versus absence of relations are often highly accurate (Lane et al., 2019). Hence, these limitations pose less of a problem for GIMME applications in which contemporaneous relation directionality is not central to the research question, or in which some amount of error in directionality estimates is deemed to be acceptable (e.g., when researchers focus on identifying general patterns across individuals or on using GIMME output for data driven prediction analyses).

This study also has several limitations that should be acknowledged. First, although we assessed the extent to which the example empirical data sets met GIMME’s assumptions and determined that the conclusions from the simulation study were mirrored in the empirical examples despite minor assumption violations in these data, GIMME’s assumptions may be violated to different degrees in different data sets. If major assumption violations are present, then the simulations results may not generalize to a given data set. Therefore, it is imperative that GIMME users take steps, such as those outlined in this study and in other GIMME tutorial papers (e.g., Beltz & Gates, 2017), to assess the degree to which assumptions are met and the ways in which violations may impact their conclusions; this is also true for other directionality modeling approaches.

Second, this study did not include the possibility of undirected contemporaneous relations between variables. Although such relations are assumed by alternate modeling methods (Epskamp, van Borkulo, et al., 2018; Epskamp, Waldorp, et al., 2018; Wild et al., 2010), they have only recently been considered within the GIMME framework (Luo et al., Submitted; Molenaar & Lo, 2016). Future extensions of the current study are needed to assess how the presence of undirected contemporaneous relations impacts the performance of the GIMME-AR and GIMME-MS search strategies under varying conditions of autoregressive relation strength.

Third, this study did not explore how GIMME’s subgrouping algorithm (Gates et al., 2017; Lane et al., 2019; Price, Gates, et al., 2017) impacts directionality recovery of the two search strategies. Significant theoretical work is required in order to fully integrate GIMME-MS with the subgrouping algorithm in the gimme R package.

Fourth, this study provides limited guidance about the use of approaches outside of the uSEM/GIMME frameworks for estimating directionality in time series data. Most of these approaches focus on inferring directionality from lagged relations (e.g., DSEM, graphical VAR) or, conversely, attempt to estimate contemporaneous relation directionality without considering relations of other temporal orders (e.g., GES, LiNGAM). Hence, the primary focus of our study – the influence of autoregressive and lagged relation strength on the recovery of contemporaneous relation directionality – has less or at least a substantially different meaning in these approaches, and future work is necessary to assess the possible impact of autoregressive relations on inferences from them.

In conclusion, we combined large-scale simulation studies that varied the strength of autoregressive relations with analyses of empirical data sets that shared the same autoregressive features to evaluate the efficacy of the GIMME-AR and GIMME-MS search strategies for recovering the directionality of contemporaneous relations in person-specific temporal network models. We found that both strategies performed best, and that their performance was often highly similar, when autoregressive relations were strong. GIMME-MS displayed specific advantages when autoregressive relations were weak, although overall directionality recovery under these conditions was still modest. Taken together, these findings have clear implications for methodological choices researchers encounter in common applications of GIMME and other person-specific network modeling methods to functional neuroimaging and behavioral data sets that naturally differ in the strength of autoregressive processes.