Dissecting the domains of PD: insights from longitudinal Item Response Theory modeling

Abstract

Background:

Longitudinal item response theory (IRT) models previously suggested that the MDS-UPDRS Motor Examination has two salient domains, tremor and non-tremor, that progress in time and in response to treatment differently.

Objectives:

Apply longitudinal IRT modeling, separating tremor and non-tremor domains, to reanalyze outcomes in the previously published clinical trial (SURE-PD3) that showed no overall treatment effects.

Methods:

We applied uni- and multidimensional longitudinal IRT models, to MDS-UPDRS Motor Examination items in 298 PD participants from the SURE-PD3 (placebo vs. inosine) study. We separated 10 tremor items from 23 non-tremor items and used Bayesian inference to estimate progression rates and sensitivity to treatment in overall motor severity and tremor and non-tremor domains.

Results:

The progression rate was faster in the tremor domain than the non-tremor domain before levodopa treatment. Inosine treatment had no effect on either domain relative to placebo. Levodopa treatment was associated with greater slowing of progression in the tremor domain than the non-tremor domain regardless of inosine exposure. Linear patterns of progression were observed. Despite different domain-specific progression patterns, tremor and non-tremor severities at baseline and over time were significantly correlated.

Conclusions:

Longitudinal IRT analysis is a novel statistical method addressing limitations of traditional linear regression approaches. It is particularly useful because it can simultaneously monitor changes in different, but related, domains over time and in response to treatment interventions. We suggest that in neurological diseases with distinct impairment domains, clinical or anatomical, this application may identify patterns of change unappreciated by standard statistical methods.

Introduction

Complex diseases have multiple dimensions of disability and impairment. Clinical monitoring of patient function and assessment of response to therapy in a clinical trial are often conducted using rating scale scores composed of multiple items, some clustered to cover distinct clinical domains. As one example, in Alzheimer’s disease, the Clinical Dementia Rating – Sum of Boxes (CDR-SB) Scale is composed of multiple items but measures two clinical domains of cognitive and functional performance.^{1, 2} Likewise, the Unified Huntington’s Disease Rating Scale³ has 74 items but is divided into four parts to cover different domains of disability and impairment. To analyze longitudinal data from a rating scale, the item scores are typically summed to obtain a total score, which is modeled as a continuous variable using either mixed models or generalized estimating equations (GEE). Reliance on the total score assumes a unidimensional underpinning to the disease being measured, equal importance of each item and any sub-scores relative to the total score, equal sensitivity to change at the item level, and equal discrimination of each item. However, such assumptions may not be valid,⁴ particularly when disease progression patterns or treatment effects apply to one domain of impairment differently from another.

Item Response Theory (IRT) modeling is a statistical framework that relates an individual’s response to rating scale items to the underlying disease severity, considered as the latent variable, termed theta. For example, Ueckert et al⁵ used a combined framework of IRT and pharmacometrics modeling to analyze item level baseline and longitudinal ADAS-cog data and demonstrated its capability of more effective and precise analysis than total score based methods. Ueckert ⁶ provides an excellent tutorial of modeling composite assessment data using IRT modeling. Typical IRT analyses usually operate under the assumption of unidimensionality, i.e., all items measure a single core attribute of the underlying disease. However, using the example of Parkinson’s disease (PD), there are two classic presentations of PD, termed tremor-dominant and akinetic-rigid (non-tremor dominant). In the contemporary era, these designations were formulated by Jankovic et al ⁷ with calculations provided for the applications of such archetypes with the MDS-UPDRS.⁸ Although there have not been extensive pharmacological studies of tremor-responsivity in comparison to the other features of parkinsonism, there is a well-established preferential improvement of tremor with deep brain stimulation, both at thalamic and subthalamic targets.⁹ Therefore, the separation of two domains or thetas is justified clinically. In our prior analysis of a cross-sectional database of over 6,000 MDS-UPDRS scores, we confirmed statistically with IRT that MDS-UPDRS Part 3 tremor and non-tremor items have very different relations to the construct of PD severity.¹⁰ To complement traditional clinical trial analyses that rely primarily on mixed models or GEE, multidimensional longitudinal item response theory (IRT) models with multiple latent variables offer the unique opportunity to investigate different progression patterns and treatment responses in more than one related, but nevertheless distinct, domains of diseases.^{11, 12} In this report, we demonstrate the added insights provided by IRT modeling when MDS-UPDRS Part 3 Motor Examination scores are reanalyzed from a recently published clinical trial (SURE-PD3) where traditional mixed modelling analyses failed to show any treatment effect.¹³

Methods

Overview

The SURE-PD3 study (ClinicalTrials.gov: NCT02642393) recorded MDS-UPDRS scores at all salient visits and prospectively followed subjects over a period of up to 24 months.¹³ We applied longitudinal IRT models to investigate Motor Examination (Part 3) score changes over time and in response to treatment for overall motor severity (unidimensional models) and for tremor and non-tremor domains (multidimensional models). Additionally, this approach allows use of longitudinal IRT to assess the strength of association between tremor and non-tremor domains. Because the MDS-UPDRS measurements in SURE-PD3 were numerous, we could thoroughly investigate linearity assumptions and models with random slopes, approaches not feasible in a prior IRT analysis that we conducted (STEADY-PD III study).¹²

Population

SURE-PD3 was a randomized, double-blind, placebo-controlled, phase 3 trial of oral inosine treatment of up to two years in early PD.¹³ 298 PD patients not yet requiring levodopa medication were randomized to either inosine (n=149) or placebo (n=149). The primary outcome was the rate of change in the MDS-UPDRS Parts 1 to 3 total score. The MDS-UPDRS was measured at baseline, weeks 3, 6, 12, and months 6, 9, 12, 15, 18, 21, 24. We excluded data from the following visits: the second screening visit, (298 visits) because it was very close to baseline visit (with 11 days to 58 days), washout visit (month 27, 247 visits) because it occurred after discontinuation of study drug, unscheduled visits (16 visits) because they could occur at any time during the study, and visits with missing MDS-UPDRS Part 3 scores (10 visits) due to the small amount of missing data. Because of the importance of an accurate baseline score, we excluded two subjects with missing values in their baseline MDS-UPDRS Part 3. Given that initiation of levodopa therapy greatly changes the MDS-UPDRS Part 3 scores, we created a “pre-levodopa therapy” dataset by removing all visits after levodopa therapy initiation and eight visits with missing data. The pre-levodopa therapy dataset consisted of 296 subjects and 2,313 visits. Our “levodopa therapy” dataset consisted of visits occurring after start of levodopa treatment with each subject’s the first visit on therapy used as their baseline. After deleting 3 visits with missing scores, the levodopa therapy dataset consisted of 151 subjects and 557 visits.

Statistical Analysis

Unidimensional longitudinal item response theory (IRT) model

The unidimensional longitudinal IRT model assumes a single latent variable, or theta, representing the underlying overall parkinsonian motor severity (higher value for more severe status) manifested by all 33 MDS-UPDRS Part 3 items. It consists of two levels (see Supplementary Section 1.1 and Figure S1). We applied the unidimensional longitudinal IRT model on the pre- and levodopa therapy datasets to investigate the progression in overall motor severity and the effects of inosine in comparison to placebo using 95% credible intervals (95% CI), the Bayesian equivalence of 95% confidence intervals, to determine significant effects. Only observed scores were modeled, omitting scores of any item (scores 3 or 4) that did not occur in the data.

Multidimensional longitudinal item response theory (IRT) model

Multidimensional longitudinal IRT approaches allow for multiple correlated latent variables. Based on our previous findings,¹⁰ we considered the latent variable of motor severity, termed theta, as multivariate with tremor and non-tremor function as separate, but correlated, theta components, the former captured by 10 tremor items (items 3.15a – 3.18 measuring tremor, with a total score range of 0 to 40) and the latter covering 23 non-tremor items (items 3.1 – 3.14 measuring bradykinesia, rigidity, gait, and posture, with a total score range of 0 to 92) (see Supplementary Section 1.2). The first level graded-response measurement models (Models (3) and (4) in the Supplemental Materials) are similar to the unidimensional longitudinal IRT model but account for the two domains. In the second level structural models (Models (5) and (6) in the Supplemental Materials), both the tremor theta component and the non-tremor theta component were regressed on time in years and the time by treatment interaction. We also included in the structural models subject-specific random intercepts and random slopes of time to allow each patient to have his/her own baseline severities and rates of progression in both tremor and non-tremor domains. To account for the relationship between the two theta components, the correlation among the random intercepts and random slopes in both domains was represented in a correlation matrix. To make the model estimable, the random intercepts were assumed to follow a standard normal distribution.

We adopted the multidimensional longitudinal IRT model on the pre- and levodopa therapy datasets to investigate the progression in tremor and non-tremor motor severities and the effects of inosine in comparison to placebo. Figure S2 (Supplemental material) displays an illustrative path diagram of the multidimensional longitudinal IRT model applying to the 10 tremor items and 23 non-tremor items. Because the latent variables, or theta components, are unitless, the rates of progression and drug responsivity in tremor and non-tremor domains can be directly compared and tested, thereby providing additional clinically relevant information not available in the unidimensional longitudinal IRT model.

To model the potential non-linear progression rates in both the unidimensional and multidimensional models, we have fit models with spline terms at year 1 and models with high-order terms for time (quadratic and cubic terms). For model comparison and selection, we used the Deviance Information Criterion (DIC), where lower values indicate better fit to the model.

Model fitting using Bayesian inference

The analyses were conducted using Bayesian inference based on Markov Chain Monte Carlo (MCMC) posterior simulations, implemented in Stan (version 2.28)¹⁴ via interface in R statistical program (version 4.1.2).¹⁵ We used vague (non-informative) prior information on all parameters in the models. The selection of prior distributions and parameters, initial values, and convergence assessment are detailed in our prior work.¹⁶

To facilitate clinical interpretation of the regression coefficients, typically expressed in unitless theta values of overall motor severity or the components of non-tremor and tremor domains, we can also apply simulation techniques to express them in terms of MDS-UPDRS point scores. These simulation strategies use posterior samples from Bayesian inference and necessarily are associated with increased variance. Therefore, we have analyzed and expressed the primary statistical results in unitless theta values, but provided the simulation MDS-UPDRS point-based results in the Supplemental Materials.

Diagnostics of model performance

The longitudinal IRT model performance was assessed comprehensively using diagnostics based on simulation and residual assessments. Specifically, based on the estimated parameters and the models, we simulated response of each category of all MDS-UPDRS Part 3 items across all visits. We compared the observed and simulated proportions via mirror plots and scatter plots. We computed the residual of each item (defined as the difference between the observed item value and this item’s respective weighted prediction score, which is the sum of each category score, i.e., 0–4, multiplied by this category’s simulated probability) and investigated the correlation between residuals. Lastly, we generated sum scores of all 33 Part 3 items, 10 tremor items, and 23 non-tremor items and compared with the observed data.

Results

Demographics and summary of IRT analyses.

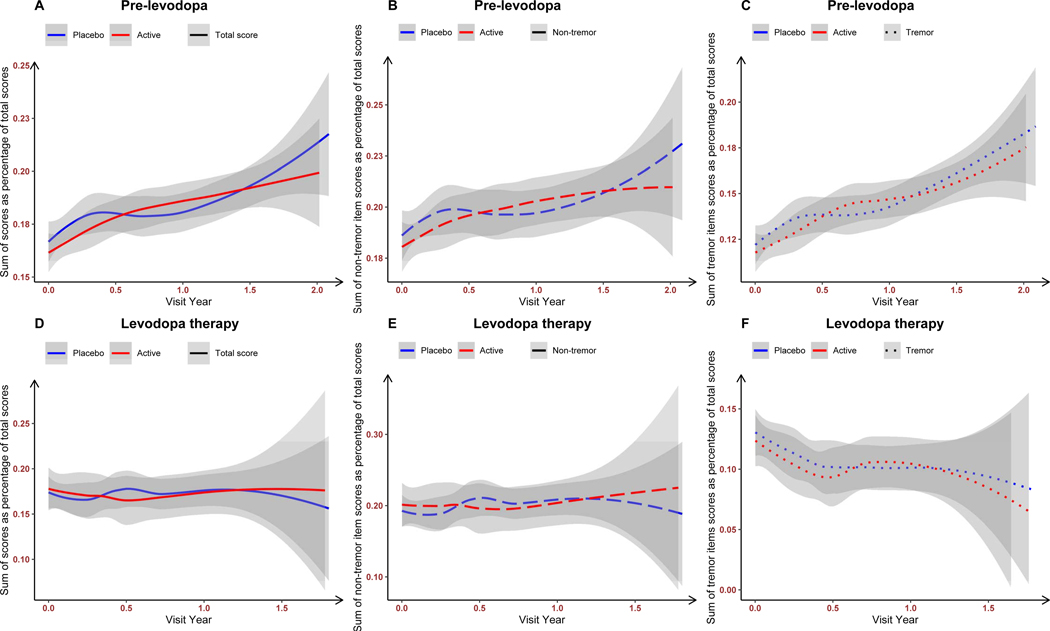
Table 1 displays the baseline characteristics of the original SURE-PD study (149 on inosine and 149 on placebo, Table 1A), of the pre-levodopa therapy dataset (Table 1B), and of the levodopa therapy dataset (Table 1C). The published SURE-PD3 analysis involved a mixed-effects model with random intercepts and slopes, examining the impact of inosine on parkinsonism manifested by the MDS-UPDRS parts I-III total score prior to initiation of levodopa medication and finding no beneficial treatment outcome.¹³ Our analysis examining total MDS-UPDRS Part 3 scores as well as tremor and non-tremor domains followed over the pre-levodopa therapy (Figure 1A–C) and levodopa therapy (Figure 1D–E) periods shows that before levodopa therapy, there is a significant motor severity deterioration in both tremor and non-tremor items in both placebo and inosine groups. However, in the presence of the levodopa therapy, there is stabilization of total motor severity and stable non-tremor motor severity in both placebo and inosine groups but declining (clinically improving) tremor motor severity regardless of placebo or inosine exposure.

Table 1.

Baseline characteristics of SURE-PD3 study participants (mean ± SD, or N (%)). In the levodopa therapy dataset, baseline is the first visit when patients started levodopa medication.

A. All SURE-PD3 study participants
	Inosine (n=149, 50%)	Placebo (n=149, 50%)
Age (years)	63±9.7	63.6±9.4
Sex (Male)	69 (46.3%)	82 (55%)
Education (years)	17.1±3.0	16±2.4
MAO-B Inhibitor	50 (33.6%)	62 (41.6%)
Modified H&Y Scale	1.7±0.5	1.8±0.4
Urate Level (mg/dl)	4.6±1.0	4.7±0.9
MDS-UPDRS-II Sum Score	21.5±8.6	22.5±9.2
MDS-UPDRS-III Sum Score	21.5±8.6	22.4±9.2
Resting Tremor	118 (79.2%)	122 (81.9%)
B. Pre- levodopa therapy dataset
	Inosine (n=147, 49.7%)	Placebo (n=149, 50.3%)
Age (years)	62.9±9.8	63.6±9.4
Sex (Male)	67 (45.6%)	82 (55.0%)
Education (years)	17.1±3.0	16±2.4
MAO-B Inhibitor	50 (34%)	62 (41.6%)
Modified H&Y Scale	1.7±0.5	1.8±0.4
Urate Level (mg/dl)	4.6±1.0	4.7±0.9
MDS-UPDRS-III Sum Score	21.5±8.6	22.5±9.2
Resting Tremor	118 (80.3%)	122 (81.9%)
C. Levodopa therapy dataset
	Inosine (n=63, 41.7%)	Placebo (n=88, 58.3%)
Age (years)	63.9±8.6	64.9±9.1
Sex (Male)	30 (47.6%)	47 (53.4%)
Education (years)	17.3±3.3	16.1±2.6
MAO-B Inhibitor	23 (36.5%)	33 (37.5%)
Modified H&Y Scale	1.8±0.5	1.8±0.5
Urate Level (mg/dl)	6.7±1.5	4.6±0.8
MDS-UPDRS-III Sum Score	23.5±10.2	23.1±11.2
Resting Tremor	46 (73.0%)	67 (76.1%)

Abbreviations: MAO-B, monoamine oxidase-B; H&Y, Hoehn and Yahr; MDS-UPDRS, Movement Disorder Society Unified Parkinson’s Disease Rating Scale

Figure 1:

LOWESS curves of MDS-UPDRS Part 3 total score (A and D), sum scores of non-tremor items (B and E), and tremor items (C and F) in the pre-levodopa therapy dataset (A-C, time zero is the baseline visit) and the levodopa therapy dataset (D-E, time zero is the visit when patients required levodopa medication) as percentages of the possible total scores. Abbreviations: LOWESS, locally weighted scatterplot smoothing.

Focused Analysis of the pre-levodopa therapy dataset

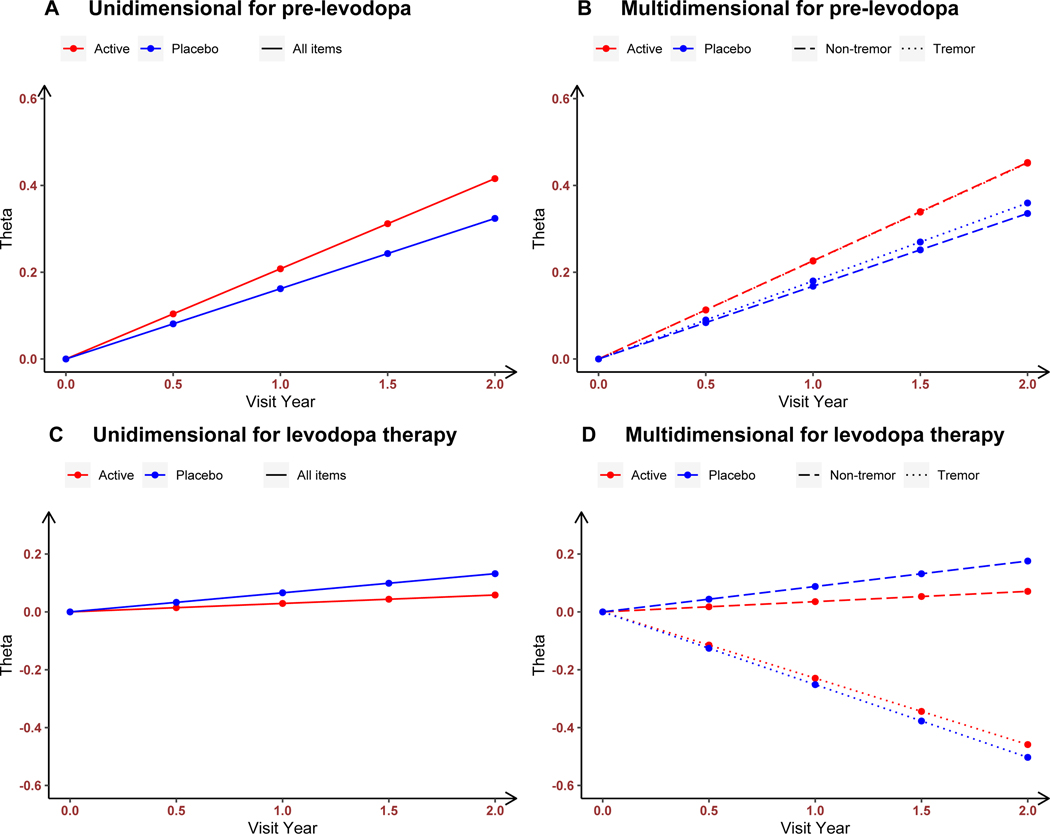
The unidimensional longitudinal IRT model used all 33 Part 3 items (Figure 2A). There was a significant time effect with deterioration in motor severity at the rate of 0.162 theta values per year (95% CI: [0.089, 0.230], Table 2A). Inosine was not associated with differential effects over the placebo group (0.046 theta values per year, 95% CI: [−0.046, 0.137]). Motor severity at baseline and its rate of progression were negatively but weakly correlated (correlation coefficient −0.168, 95% CI: [−0.340, 0.008]). Supplementary Section 2 presents the interpretation in terms of MDS-UPDRS point scores, and the location and discrimination parameters (Table S1).

Figure 2.

The estimated rates of progression among subjects in inosine and placebo groups in overall parkinsonian motor severity (from unidimensional longitudinal IRT models, A and C) and in tremor and non-tremor motor severities (from multidimensional longitudinal IRT model, B and D) in the pre-levodopa therapy dataset (A and B, time zero is the baseline visit) and in the levodopa therapy dataset (C and D, time zero is the visit when patients required levodopa medication).

Table 2.

Parameter estimates and 95% Credible Intervals (CI) for pre-levodopa dataset using the unidimensional and multidimensional longitudinal IRT models with random slopes. Statistically significant parameters are boldfaced.

A. Unidimensional longitudinal IRT model
Parameters	Mean	SD	95% CI
Time (in years)	0.162	0.036	0.089, 0.230
Time*Inosine	0.046	0.046	−0.046, 0.137
${\sigma }_{u1}$	0.303	0.026	0.254, 0.356
${\rho }_{01}$	−0.168	0.087	−0.340, 0.008
B. Multidimensional longitudinal IRT model
Tremor Domain
Time (in years)	0.180	0.042	0.094, 0.260
Time*Inosine	0.046	0.056	−0.062, 0.156
Non-tremor Domain
Time (in years)	0.168	0.037	0.096, 0.242
Time*Inosine	0.059	0.052	−0.045, 0.161

Note: 95% CI, 95% Credible Intervals; SD, standard deviation.

With the multidimensional longitudinal IRT model fitted to assess separately the 10 tremor and 23 non-tremor items, significant time effects for both placebo and inosine groups occurred with deterioration in both domains. For tremor severity, the rate of clinical decline was 0.180 theta component values per year (95% CI: [0.094, 0.260], Table 2B) whereas for non-tremor severity, the decline rate was 0.168 (95% CI: [0.096, 0.242]). Inosine was not associated with additional effects over placebo in either domain (tremor: 0.046 theta component values per year, 95% CI: [−0.062, 0.156]; non-tremor: 0.059, 95% CI: [−0.045, 0.161]). Tremor and non-tremor severities at baseline were negatively correlated (with significant correlation coefficient −0.262, 95% CI: [−0.377, −0.135]), suggesting that subjects with more pronounced tremor severity scores tend to have milder non-tremor severity ratings, and vice versa. However, the progression rates in both tremor and non-tremor domains were positively correlated (with significant correlation coefficient 0.396, 95% CI: [0.133, 0.615]), suggesting that subjects who progressed faster in tremor domain tend to also progress faster in non-tremor severity. Supplementary Section 2 presents the interpretation in terms of MDS-UPDRS point scores, the estimated correlation matrix of random effects (Table S2), and the location and discrimination parameters (Table S3).

Figure 2B displays in theta component values the different rates of progression of two treatment groups in the multidimensional model with both tremor and non-tremor domains. The multidimensional IRT model with random intercepts and random slopes (with DIC=127,262) had a superior fit than the unidimensional IRT model (DIC=131,034), the multidimensional IRT model with only random intercepts (DIC=127,734), and other multidimensional IRT model with nonlinear terms (e.g., models with spline terms at 1 year or models with quadratic and cubic terms of time).

In sum, the multidimensional longitudinal IRT model provides excellent goodness of fit and model performance in the analysis of the pre-levodopa therapy dataset. (Also see Supplementary Section 2.1).

Focused Analysis of the levodopa therapy dataset

For the unidimensional IRT model, (Figure 2C) there was a nonsignificant time effect for both placebo and inosine groups, with a slight clinical deterioration in motor severity at the rate of 0.066 theta values per year (95% CI: [−0.095, 0.222], Table 3A). Inosine was not associated with additional effects over the placebo group (−0.037 theta values per year, 95% CI: [−0.298, 0.204]). Motor severity at baseline and its rate of progression were negatively but weakly correlated (correlation coefficient −0.127, 95% CI: [−0.393, 0.158]). Supplementary Section 3 presents the interpretation in terms of MDS-UPDRS point scores, and the location and discrimination parameters (Table S4).

Table 3.

Parameter estimates and 95% Credible Intervals (CI) for levodopa dataset using the unidimensional and multidimensional longitudinal IRT models with random slopes. In the levodopa therapy dataset, baseline is the visit when patients started levodopa medication. Statistically significant parameters are boldfaced.

A. Unidimensional longitudinal IRT model
Parameters	Mean	SE	95% CI
Time (in years)	0.066	0.080	−0.095, 0.222
Time*Inosine	−0.037	0.125	−0.298, 0.204
${\sigma }_{u1}$	0.464	0.070	0.336, 0.612
${\rho }_{01}$	−0.127	0.145	−0.393, 0.158
B. Multidimensional longitudinal IRT model
Tremor Domain
Time (in years)	−0.251	0.105	−0.471, −0.051
Time*Inosine	0.022	0.139	−0.257, 0.292
Non-tremor Domain
Time (in years)	0.088	0.082	−0.077, 0.247
Time*Inosine	−0.052	0.129	−0.308, 0.204

Note: 95% CI, 95% Credible Intervals; SD, standard deviation.

For the multidimensional IRT model, with levodopa treatment, (Figure 2D) there was a significant negative (clinically improvement) time effect in tremor motor severity at the rate of −0.251 theta component values per year (95% CI: [−0.471, −0.051]). In contrast, there was nonsignificant time effect in non-tremor motor severity, with the rate of clinical decline being 0.088, (95% CI: [−0.077, 0.247]). Further, inosine was neither associated with additional effects over the placebo group in the tremor domain (0.022 theta component values per year, 95% CI: [−0.257, 0.292]), nor in the non-tremor domain (−0.052, 95% CI: [−0.308, 0.204]). Supplementary Section 3 presents the interpretation in terms of MDS-UPDRS point scores, and the location and discrimination parameters (Table S5). Tremor and non-tremor severities were positively correlated (with significant correlation coefficient 0.232, 95% CI: [0.034, 0.419]), suggesting that subjects with more pronounced tremor severity tend also to have worse non-tremor severity at the initiation of levodopa therapy. The progression rates in both tremor and non-tremor domains were positively correlated (correlation coefficient 0.530, 95% CI: [0.073, 0.866]), suggesting that subjects who progressed faster in tremor domain tend to also progress faster in non-tremor severity, after the initiation of levodopa therapy. See Table S6 (Supplemental material) for the estimated correlation matrix of random effects.

The multidimensional IRT model with random intercepts and random slopes (DIC= 29,985) had a superior fit than the unidimensional IRT model (DIC= 31,057), the multidimensional IRT model with only random intercepts (DIC=30,073), and other multidimensional IRT model with nonlinear terms (e.g., models with spline terms at 1 year or models with quadratic and cubic terms of time).

Similar to the results in the pre-levodopa therapy dataset, the multidimensional longitudinal IRT model had excellent goodness of fit and model performance in the levodopa therapy dataset. (See Supplementary Section 2.2)

Discussion

The novelty of new IRT applications

Applying longitudinal IRT models to the study of neurological diseases has increased recently. For example, to our knowledge, thirteen prior papers of relevance to our work, eight dealing with Parkinson’s disease and the others dealing with other neurological or psychiatric conditions^{5, 17–20} have been published on longitudinal IRT. All of them have made significant contribution to the field. Among the PD studies, using cross-sectional IRT modeling, Regnault et al ²¹ analyzed the pooled data of MDS-UPDRS Parts 2 and 3 from baseline, year 1, and year 2. Via longitudinal IRT models, Buatois et al ²² and Chen et al ²³ analyzed data of MDS-UPDRS and UPDRS, respectively, and concluded that IRT is a powerful tool to capture the heterogeneous nature of the rating scales and it markedly reduces sample size. Sheng et al ²⁴ and Chael et al ²⁵ analyzed the data of Part 3 of MDS-UPDRS and UPDRS, respectively, using two separate IRT models with the latent variable representing tremor and non-tremor symptoms, respectively. Similarly, Gottipati et al ²⁶ analyzed all three Parts of MDS-UPDRS using separate IRT models with the latent variable representing patient-reported responses, sided responses, and non-sided responses. Later, Gottipati et al ⁴ applied the models developed earlier²⁶ to the baseline UPDRS data from two clinical trials. Lastly, Arrington et al ²⁷ applied a unidimensional longitudinal IRT model to motor-related items in MDS-UPDRS Parts 2 and 3 and assessed the impact of reducing the number of items. Outside of PD, Ueckert et al ⁵ used IRT to study Alzheimer’s Disease, and Novakovic et al ¹⁸ used the technique in multiple sclerosis and concluded that IRT modeling is an effective tool to study disease progression with item-level data. In schizophrenia research, Krekels et al ¹⁷ fit separate longitudinal IRT models for three subscales of the Positive and Negative Symptom Scale as different domains. Finally, in dementia research, Vandemeulebroecke et al ¹⁹ and Bascoul-Mollevi et al²⁰ applied a unidimensional longitudinal IRT model to 14 items of two neuropsychological test batteries and 30 items of Quality of Life Questionnaire (QLQ-C30) and demonstrated its values as a powerful approach for progressive diseases.

In comparison, we consider our approach both novel and innovative, because our strategy has integrated three simultaneous analyses not conducted before in unison. Specifically, our longitudinal IRT modeling simultaneously estimated item-specific discrimination and location parameters in the measurement model and regression parameters in the structural models. As pointed out in Gottipati et al,²⁶ the sequential parameter estimation process had a worse fit to the data, as compared to the simultaneous counterpart. Next, our longitudinal IRT model fully accounts for the correlation among visits from the same subject exists in the longitudinal study as SURE-PD3. Lastly, our multivariate longitudinal IRT model can compare rates of progression in tremor and non-tremor domains and model their correlation. This ability to examine domain-specific changes and concurrent correlation between or among changing domains has not been previously possible.

Our longitudinal IRT approach offers a new alternative to the traditional analytic approaches (e.g., mixed model or GEE) which are based on sum scores. It directly addresses their limitations such as ignoring varying item sensitivities to change and the loss of information because the sum score ignores the differences between response patterns leading to the same sum score.^{11, 28} The Bayesian modeling we adopted is flexible and straightforward in fitting complex models such as multidimensional longitudinal IRT models. In contrast, with frequentist procedures it is much more difficult to develop and justify the theoretical properties for fitting such models.²⁹ Because of the high dimensional integration involved in fitting our models, maximum likelihood approaches are difficult to implement while Bayesian inference has computational advantages because it bases on Markov Chain Monte Carlo (MCMC) posterior simulations. Moreover, Bayesian analysis can easily incorporate information from relevant previous studies through an informative prior distribution, if needed. Lastly, the model fitting using Bayesian inference readily accounts for missing data as they can be sampled from their posterior distributions.

Direct application to PD

In spite of the negative findings reported in the original, more standard, trial analysis, our multidimensional longitudinal IRT model detected differential changes over time and in response to treatment in both tremor and non-tremor domains of the MDS-UPDRS. Our results are presented in unitless theta component values, and each contribution can be directly compared and tested, providing clinically important insights unavailable in the original trial analysis. In a longitudinal PD study, this strategy allows comparison of differential tremor and non-tremor progression rates under different treatment conditions. Given that safety rules and futility plans are usually incorporated into large clinical trials, even if global scores are not significantly changing, a more rapid treatment-associated decline in one pertinent severity domain could be identified with our methodology and serve as a valuable protective measure for patient safety and study integrity. Likewise, a selective improvement in one domain could potentially allow a study to continue even in the context of an overall futility assessment in the middle of a trial.

Our longitudinal IRT models account for PD patient heterogeneity by including both random intercepts and random slopes, allowing each patient to have his/her baseline motor severity incorporated into the subject-specific rate of progression. These models provide unique insight into the complex and informative correlation between tremor and non-tremor motor severities and their progression rates. In this study, those progression rates were positively correlated both before and after the initiation of levodopa therapy but in the event that a treatment improved one domain at the expense of exacerbating the other, this positive correlation would not hold. In the traditional mixed models or GEE analysis, these two effects would cancel one another in terms of a final score, but importantly, with our method, we can detect specific relationships that could guide treatment development and precision therapy.

Our analysis of tremor vs non-tremor change shows that in this single analysis, the modeling results support linear progression in total motor, tremor, and non-tremor scores both before and after the initiation of levodopa therapy. We emphasize that this finding is a study outcome and not a statistical assumption. The longitudinal IRT models can readily account for the non-linear progression and covariate effects if they exist. We plan to investigate possible non-linear progression patterns in other clinical trials and observation studies.

In an era of personalized medicine and precision therapy targets, defining specific treatment effects on tremor and non-tremor domains in PD has direct application. As shown in this analysis, tremor and non-tremor MDS-UPDRS Part III domains behave differently from one another, i.e., in one case tremor improving preferentially with levodopa therapy, and, in another case, inosine preferentially aggravating non-tremor function. Whereas clinical trials can focus on a primary outcome of changes in overall Part III MDS-UPDRS severity as a single concept or theta, sub-analyses may reveal selective treatment effects on one domain (tremor or non-tremor) and thereby offer clinicians the opportunity to tailor treatment recommendations according to the phenotypic domain of greater importance or impairment for the individual patient. Attributing the level of absolute domain-specific change that constitutes patient-pertinent improvement or decline [domain-based Minimal Clinically Important Difference] is a goal of future population research.

We continued throughout the analysis to monitor inosine treatment status, but because levodopa is considered a pivotal and highly pertinent clinical intervention, we focused on the pre and post events relative to this treatment. In this light, we were attentive to include all visits before levodopa was actually administered in the pre-levodopa analysis, and only visits that rated the patient on levodopa in the post-levodopa analysis. In this way, all visits in the studied are included without duplication and the two divisions could be re-fused without further manipulation if needed.

Applications beyond Parkinson’s disease

Wider IRT applications may be applicable to other neurological diseases within movement disorders with well-defined domains of impairment potentially progressing at different natural rates or responding differentially to treatment. One prototypic example is Huntington’s disease where motor, cognitive and behavioral deficits combine in a wide variety of phenotypes both for onset and disease progression. Outside of movement disorders, in Alzheimer’s disease, regulatory guidelines encourage that clinical trials demonstrate efficacy on both cognitive and functional measures.^{23, 24} To this end, the Clinical Dementia Rating – Sum of Boxes (CDR-SB) is intended to measure the influence of cognitive loss on the ability to conduct everyday activities and its six items may be broken down into cognitive and functional items.^{1, 2} Although not applied in published analyses, the multidimensional IRT modeling that we describe for PD is, in our view, ideally suited for a scale of this type and may provide novel insight and useful information to facilitate the development of AD treatments.

Limitations

Our study is a post-hoc analysis of a PD clinical trial with limited sample of de-novo patients and relatively short follow-up time which may not represent the whole PD severity continuum. Hence, the observed linear decline (clinically improvement) in tremor motor severity in response to the levodopa therapy should not be extrapolated to a longer observation period because of the levodopa-induced motor complications. To mitigate the influence of the initiation of the levodopa therapy on the MDS-UPDRS Part 3 scores, we have created the pre- and levodopa therapy datasets, which are not in the original design. Doing so, we created an artificial separation between the pre-dopa and post-dopa epochs and did not allow the testing for potential interactions between levodopa and inosine treatment in a continuous setting. In our study, tremor and non-tremor domains were modelled based on a data-driven dissociation of MDS-UPDRS Part 3 to analyze their progression in time and in response to treatment. Since the division of these two domains was driven by the data, its clinical implications are not clearly defined. Further work is needed to confirm the clinical usefulness of the tremor/non-tremor dichotomy in investigating treatment responsiveness. Moreover, we only investigated the motor severity manifested by Part 3, but not Parts 1 and 2. Lastly, the results rely on some statistical assumptions, e.g., independent censoring, and proportional odds assumption in modeling the ordinal item scores. In this analysis, we excluded data from the second screening visit, washout visit, unscheduled visits, and visits with missing data. Our longitudinal IRT models generally achieve better performance with larger amount of data being modeled.

Future Directions

Longitudinal IRT analysis of multidimensional neurological diseases is a novel statistical method addressing limitations of traditional linear regression approaches. It is particularly useful because it can simultaneously monitor changes in different, but related, domains over time and in response to treatment interventions. As molecular and pharmacologic targets are more refined, clinical trial outcomes may need to be monitored not only as a global rating scale measure, but also at the level of domain-specific changes where a change could impact patient autonomy even when the global rating does not reveal significant change.