A state of art review on estimation of solar radiation with various models

Abstract

Solar radiation is free, and very useful input for most sectors such as heat, health, tourism, agriculture, and energy production, and it plays a critical role in the sustainability of biological, and chemical processes in nature. In this framework, the knowledge of solar radiation data or estimating it as accurately as possible is vital to get the maximum benefit from the sun. From this point of view, many sectors have revised their future investments/plans to enhance their profit margins for sustainable development according to the knowledge/estimation of solar radiation. This case has noteworthy attracted the attention of researchers for the estimation of solar radiation with low errors. Accordingly, it is noticed that various types of models have been continuously developed in the literature. The present review paper has mainly centered on the solar radiation works estimated by the empirical models, time series, artificial intelligence algorithms, and hybrid models. In general, these models have needed the atmospheric, geographic, climatic, and historical solar radiation data of a given region for the estimation of solar radiation. It is seen from the literature review that each model has its advantages and disadvantages in the estimation of solar radiation, and a model that gives the best results for one region may give the worst results for the other region. Furthermore, it is noticed that an input parameter that strongly improves the performance success of the models for a region may worsen the performance success of another region. In this direction, the estimation of solar radiation has been separately detailed in terms of empirical models, time series, artificial intelligence algorithms, and hybrid algorithms. Accordingly, the research gaps, challenges, and future directions for the estimation of solar radiation have been drawn in the present study. In the results, it is well-observed that the hybrid models have exhibited more accurate and reliable results in most studies due to their ability to merge between different models for the benefit of the advantages of each model, but the empirical models have come to the fore in terms of ease of use, and low computational costs.

Nomenclature

AI

Artificial intelligence

AAPRE

Average absolute percent relative error

ANN

Artificial neural network

ANFIS

Adaptive network-based fuzzy inference system

BA_K

Boruta-based feature selection algorithm

BPNN

Back propagation neural network

C-SVM

Corrected support vector machine

CRO

Coral reefs optimization

CART

Classification and regression tree

CNN

Convolutional neural network

CS-OP-ELM

Cuckoo search based optimally pruned extreme learning machine

CSAWNN

Wavelet neural network based on cuckoo search algorithm

DA

Dragonfly algorithm

DE

Differential evolution

DL

Deep learning

DT

Decision tree

E

Relative percentage error

ELM

Extreme learning machine

erMAX

Maximum absolute relative error

FIS

Fuzzy inference systems

FFA

Firefly algorithm

FRF

Fuzzy regression function

GAMMF

Genetic approach combing multi-model framework

GFM

Generalized fuzzy model

GOA

Grasshopper optimization algorithm

GPI

Global performance index

GANN

Genetic algorithm neural network

GA

Genetic algorithm

GPR

Gaussian process regression

GRNN

Generalized regression neural network

GSO

Glowworm swarm optimization

GP

Genetic programming

GRU

Gated recurrent unit

GABPNN

Genetic algorithm based back propagation neural network

GWO

Grey wolf optimization

HMM

Hidden Markov model

KHA

Krill-herd algorithm

k-NN

K-nearest-neighbors

LSTM

Long short-term memory network

LES

Linear exponential smoothing model

LASSO

Least absolute shrinkage and selection operator

LM

Levenberg marquardt back propagation

LR

Linear regression

MARS

Multivariate adaptive regression spline

MAE

Mean absolute error

MLP

Multilayer perception

MPE

Mean percentage error

MARE

Mean absolute relative error

MLSR

Multivariable least squares regression

MABE

Mean absolute bias error

MRE

Mean relative error

M5

Model five

MLFFNN

Multilayer feedforward neural network

MBE

Mean biais error

M5Tree

Model five tree

MAPE

Mean absolute percentage error

MA

Moving average

NARX

Nonlinear autoregressive recurrent exogenous neural network

nRMSE

Normalized RMSE

NB

Naive bayes

NS

Nash-Sutcliffe model efficiency coefficient

nMBE

Normalized MBE

NSMOBA

Nondominated sorting-based multi-objective bat algorithm

nMAE

Normalized MAE

PSO

Particle swarm optimization

PV

Photovoltaic

R²

Coefficient of determination

RF

Random Forest

r

Correlation coefficient

RMSE

Root mean square error

RP

Resilient back propagation

RNN

Recurrent neural network

RSE

Relative standard error

RBFNN

Radial basis function neural network

RW

Random walk

RMSRE

Root mean squared relative error

RBF

Radial basis function

RRMSE

Relative root mean square error

SCG

Scaled conjugate gradient

SOM

Self-organizing map

SES

Simple exponential smoothing

SMAPE

Symmetric mean absolute percentage error

SARIMA

Seasonal autoregressive integrated moving average

SSRE

The sum of squares of relative errors

SSA

Salp swarm algorithm

SVM

Support vector machine

SVR

Support vector regression

SMGRT

Simple membership function and fuzzy rule generating technique

TDNN

Time delay neural network

U95

Uncertainty 95%

VAR

Vector autoregressive

WT

Wavelet transform

XGBoost

Extreme gradient boosting

1. Introduction

1.1. Research background

Solar radiation that crosses the atmosphere and reaches the Earth’s surface plays a critical role in the chemical, physical, and biological processes necessary for the survival of life [1,2,3]. Changes in solar radiation directly affect climate data, hydrologic cycle, sensible heat, latent heat, evaporation, ecological life, migration, and other many important parameters [1,4]. In addition to all these critical points, solar energy has a much lower environmental footprint compared to traditional energy sources such as fossil fuels. Because of all these characteristics, solar energy systems are look forwarded to play a key role in the mitigation of carbon emissions and new employment opportunities in the near future, exclusively in developing countries [5]. In brief, solar energy is seen as one of the most important renewable and sustainable energy sources that can suspend the global-scale energy crisis [6].

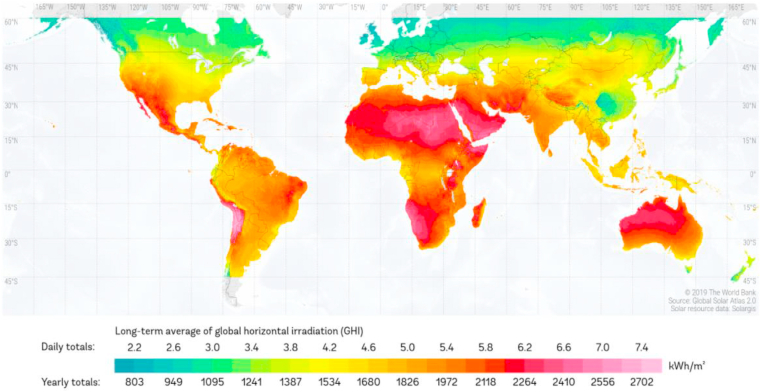
With the growing concerns on environmental issues, solar energy systems have begun to be widely used on a large scale in many countries in the world, exclusively in those with more solar energy potential. That is because the countries that relied on solar systems have witnessed their advantages such as economic, and environmental aspects in the short run and they started to enhance the share of solar systems in their electricity production methods. Many countries noticed these positive results in the short run and increased their solar power plant investment by revising their energy investments considering their solar energy potentials. The electrical energy potential that a country can obtain from the sun can be easily understood by the solar radiation of that country. In this framework, Fig. 1 shows the horizontal global solar radiation potential for all countries. As can be seen from the figure, especially Africa, Australia, South America, Southern Europe, and Asia (especially India) have a high solar energy potential. In these regions, solar energy has been often used in electricity and heat generation. In regions with low solar energy potential, concentrating the radiation (concentrated solar systems) is accepted as a simple solution method to enhance the solar radiation potential of the relevant regions.

Fig. 1.

The horizontal global solar radiation potential for all countries [7].

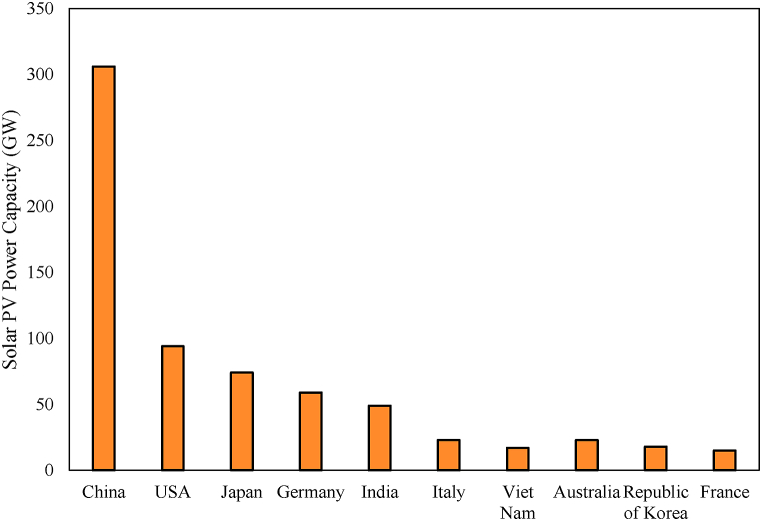
In today’s technology, it is possible to benefit from solar energy in different methods. These main methods can be listed as follows: Solar thermal electricity generation, solar heating systems, and photovoltaic cells (PV systems) [8–10]. Among all these methods, PV solar systems have a wide usage area all over the world, and it is easy to generate electricity from PV solar systems. Fig. 2 shows the top 10 countries with the highest solar PV power capacity for 2021 [11].

Fig. 2.

Solar PV power capacity for 2021 [11].

As can be seen in Fig. 2, China is the leading country with a new PV capacity of nearly 50 GW in the year 2021. China has about 300 GW of solar PV power, according to 2021 data. Considering the rest of the world, a significant increment transiting to solar energy has been well-noticed. The reason why the countries have considerable growth in their interest in solar energy is to ensure economic sustainability by reducing dependence on fossil fuels year by year and some agreements such as the Paris agreement and Kyoto protocol, etc in which countries are involved. Other important points regarding the growing capacities in solar PV capacities are counted as the energy security issues and the volatility of fossil-fuel prices. This growth is expected to continue in the upcoming years. For example, according to the International Energy Agency (IEA), Renewables 2021 report, it is foreseen that PV systems broke a new record in the capacity additions of renewable energy sources in the year 2021. According to the report, almost 290 gigawatts (GWs) of new renewable power was commissioned in 2021, which is 3% higher than 2020’s growth. PV systems alone account for more than half of all renewable power expansion in 2021, followed by wind energy and hydropower, respectively.

Although solar energy is a very useful source of renewable energy, the electricity generation capacity of PV modules largely depends on solar radiation, the climate of the location of the solar farm, and weather conditions [12]. Solar radiation reaching the PV cells significantly affects the power output of the cells. With the increase of solar radiation reaching the PV cell or module, the short-circuit current also increases [13,14,15,16]. This effect also increases the power output. With the increase in the installation of PV systems all around the world, it becomes important to estimate the solar radiation reaching the earth and the power obtained from these systems. In this way, both investment costs can be determined and electricity grid integration can be achieved.

1.2. Research significance

It is necessary to measure the solar radiation values in that region to determine the solar energy potential in a given geographical region. In this way, a future perspective for a solar energy system to be established in this region can be created. Solar radiation reaching a certain point on the earth is called direct and diffuse radiation. The sum of these two radiations is also called global solar radiation. Solar radiation is measured using devices such as a pyranometer, pyrheliometer, and solarmeter [17]. However, it is not practically possible to place these measurement devices in all regions due to their huge cost, measurement difficulties, and calibration problems. For example, Türkiye has 1798 meteorological measurement stations in 2020, but only 129 of these stations can measure solar radiation data. An important example of this case is from China. There are 756 meteorological measurement stations in China in 2012. Only 122 of these stations can measure the solar radiation data [9]. As can be clearly understood from these significant examples, access to solar radiation data for the installation of solar energy systems may be limited.

Estimation of solar radiation not only provides information for the installation of solar energy systems. The stochastic structure of solar radiation is mainly caused by the motion of cloud shadows between the sun and the PV array that usually causes a ramp event to consist over the solar modules. This event causes major, sudden, and unexpected floatings in the output power of PV modules [18]. The variability of energy from PV solar systems poses a serious challenge for energy companies and operators of the transmission system. The operator of the power grid needs production estimates for a safe and efficient supply [5,19]. Although production amounts can be estimated in conventional power plants, it is not easy to make this estimation in renewable power plants. Reliable, and robust estimates are significantly essential for efficient usage of the floating output of energy produced in PV systems.

Grid load estimated for the next two days provides the basis for scheduling of power plants and planning processings in the electricity market to balance the supply and demand of energy and to ensure reliable grid operation [20]. These load estimations are of great importance as they are used by utility companies, energy service providers, transmission system operators, and independent power producers in their scheduling, dispatching, and regulation of power [19].

To sum up, the estimation of solar radiation for solar energy systems (especially PV solar systems) is critical for several reasons. First and foremost, parameters such as system investment costs and operating costs can be determined with solar radiation data. In this way, the most optimum installation region for the investment can be determined. Second, estimates can be made for the fluctuating power output of solar PV systems. In this way, better integration can be achieved for power grids. Third, the knowledge of solar radiation can be a useful and very critical input to enhance the yield of crop growth in the agriculture sector. Furthermore, this estimation is of great importance to track and manage the possible future risk in the agriculture sector. Other important sectors using solar radiation data are tourism and health care. As it can be obviously understood, the accurate estimation of solar radiation is vital to very critical sectors. Accordingly, many researchers are dedicated to predicting solar radiation data with low errors and have improved many models for years. In this framework, there are quite different approaches in the literature for the estimation of solar radiation. While some of these approaches (empirical models, mathematical models, etc.) have been used for decades, some innovative approaches (machine learning approaches, hybrid models, etc.) are available in the literature in parallel to technological development in computer science. Empirical and mathematical methods are regarded as conventional, while others are artificial intelligence-based. Each used method has its characteristics, challenges, advantages, disadvantages, limitations, and accuracy. Among these models, artificial intelligence-based forecasting methods have superior advantages over traditional methods. Some of the superiorities of artificial intelligence-based methods include the capacity to work with incomplete inputs, reasoning capabilities, and ease of updates and maintenance [18,21]. The advantages of traditional methods can be listed as not requiring software knowledge, being easily applicable, and yielding results with less input. In addition to these, the estimation scale is also important. For example, traditional models give very satisfactory results in monthly estimations of solar radiation. However, in estimating daily or hourly solar radiation, the success of these models is highly worsening. The main reason for this case is that traditional methods do not have learning capabilities, unlike artificial intelligence (AI) based methods. However, the limited input data in traditional methods is one of the important factors affecting short-term estimation achievement.

Different parameters (measured solar radiation, wind speed, temperature, day length, sunshine duration, pressure, humidity, etc.) were used as inputs to predict solar radiation. Although the main aim of all these methods is considered to be higher accuracy estimation of solar radiation, this is not exactly true. High-performing estimations using fewer and more accessible inputs are far more important.

For these reasons, it is of major significance to reveal the estimation models performance of solar radiation under different conditions. The choice between models can be quite decisive for investors, companies, and decision makers. This study focused on an in-depth comparison of traditional and innovative solar radiation estimation methods. Accordingly, the rest of the paper is organized as follows: Section 2 gives a comprehensive literature review. This section is divided into five subsections. In the first four subsections, empirical models, time series methods, artificial intelligence methods, and hybrid methods are handled, respectively. In these subsections, after briefly explaining the models, which are frequently used in the estimation of solar radiation, information about the studies in the literature is given and the highlights of each work are detailed with the key findings. In the fifth subsection, studies based on different solar radiation estimation models using the same dataset are compared with each other. In this way, it has been aimed to make a more detailed comparison of the prominent models in the studies. In Section 3, the results obtained from the literature review are discussed in depth. An overall assessment of the key findings, such as the selection and importance of the inputs and the need for optimization in hybrid models, is presented thereof. One of the critical parts of the study is the research gaps, challenges, and future directions section. In Section 4, the general advantages, disadvantages, comparisons, challenges, and future directions of the models for the estimation of solar radiation are discussed. Finally, conclusions are drawn in Section 5.

2. Literature review

This section presents a literature review of the methods used to estimate solar radiation data. In this framework, the studies in the literature are divided into four subsections and discussed. These subsections provide a summary of studies in the literature using empirical models, time-series models, artificial intelligence models, and hybrid models, respectively. After briefly introducing the relevant estimation models in each subsection, prominent aspects of the literature studies are highlighted. The present section ends with an examination of studies that analyzed the performance of forecasting methods in different categories using the same dataset.

2.1. Empirical models

The importance of estimation and modeling solar radiation is known to everyone. Empirical models are used for years to predict solar radiation. The most widely used and oldest model is the Angstrom model [22]. Different models based on this model have been improved by many researchers. Models estimating solar radiation generally use sunshine duration, temperature, other meteorological parameters, and cloudiness index [23]. However, using all of these parameters at the same time complicates the empirical correlation, and generally, only a few parameters are used together in the developed models. In this case, the most preferred variables are sunshine duration and temperature parameters. Models developed according to these variables can only be used locally, even if they have a high accuracy rate.

Many parameters that affect solar radiation, and when these are entered as variables in an equation, it becomes very difficult to calculate. In the detailed literature study, it is seen that models using only a few variables generally make regional estimations. A summary of the study performed using empirical models for the estimation of solar radiation data is given in Table 1.

Table 1.

A summary of the studies regarding the prediction of solar radiation data using empirical models.

Location	Model	Input Parameters	Output Parameter	Data scale	Statistical Benchmarks	Key Findings	References
Ashanti, Owabide (Ghana)	Angstrom-Prescott and Hargreaves and Samani	Sunshine hours and air temperature	Global solar radiation	Five months from 2011: April, May, June, October, November	MBE, MPE, and RMSE	Proposed models using sunshine hours and air temperature compatible with measured solar radiation value.	[26]
Ghardaïa, Algeria	6 combined new models	Minimum and maximum temperature	Global solar radiation	365 days of 2006	RMSE, MBE, MAE, and MPE	GSR predicted well in all models, and MPE values found ±10%.	[27]
Yucatán Peninsula, Mexico	A novel empirical model (M5)	Average relative humidity, minimum temperature, maximum temperature, and transformed rainfall	Daily horizontal global solar radiation	From 6 different stations on different dates between 2000 and 2014.	MPE, MAPE, RMSE, MBE, MABE, and R2	The proposed model (M5) was calibrated using 12 existing models. If rainfall and relative humidity data are available, this model can be used.	[28]
India	32 empirical models in 4 different categories	Relative sunshine period, and clearness index	Global solar energy	1986–2000	MARE, MAE, RRMSE, RMSE, U95, t-stats, MPE, MBE, erMAX, r, and GPI	The power model with a clearness index shows great performance.	[29]
Tropical regions of China	6 temperature-based models (P1–P6)	Temperature, relative air humidity, vapor pressure deficit, transformed precipitation, and precipitation	Daily horizontal global solar radiation	1966–2015	R2, RMSE, NRMSE, and MBE	The second model (P2) has high accuracy when only air temperature is considered, but models 3 and 5 (P3 and P5) have higher accuracy when other variables (eg. precipitation and relative humidity) are considered for tropical regions of China.	[30]
Muğla, Türkiye	105 different regression models and set of new regression models	Sunshine duration, cloudless, and average sunshine duration	Global horizontal solar radiation	January 2007 to August 2015	MPE, MBE, MAPE, MABE, RMSE, and R2	7 new calibrated models were tested and found low error rates.	[31]
China	72 existing and developed empirical models	Meteorological and solar radiation data	Diffuse horizontal solar radiation	1966–2015	R2, RMSE, RRMSE, MAB, NRMSE, t-stat, U95, and GPI	In different categories, models were tested and developed.	[32]
India	Three Global Solar Radiation models (M-01, M-02, M-03)	Relative humidity, latitude, altitude, and sunshine duration	Global solar radiation	1986–2000	RMSE, MAE, R2, MPE, RMSRE MARE, MBE, t-stat, GPI, RRMSE, and U95	M-03 model contains 4 variables and can be applied with maximum 11.8935% MPE.	[33]
Morocco	Hybrid temperature-based models	Temperature	Daily global solar radiation	1996–2010	MBE, MSE, RMSE, R2, standard deviation, and performance score	4 ML models were used to optimize 42 temperature-based models and correlations (R2) increase.	[34]
China	Zone model	Surface meteorological measurements.	Daily global solar radiation	1970–2017	MABE, RMSE, and NSEC	With the zone method NSEC values greater than 0.8 and RMSE% less than 20% obtained.	[35]
Iran	Twenty-one sunshine-based empirical models	Number of days and sunshine	Daily solar radiation	2007–2017	R2, MAE, MBE, RRMSE, MAPE, RMSE, and MBE	21 different sunshine-based empirical models were compared and calibrated.	[36]
Adrar, Algeria	Proposed 6 temperature-based models	Daily air temperature	Daily average horizontal global solar radiation	4 years period	MBE, RMSE, and R2	Proposed M4 model shows best performance (R2 = 0.87).	[37]
Industrial City, the Kingdom of Saudi Arabia	Linear, Quadratic and Logarithmic	Relative humidity, ambient temperature, and sunshine duration	Global horizontal radiation	January–December 2016	r, R2, RMSE, MBE, MABE, and MAPE	3 different models were examined and compared, the quadratic model has the highest r and R2.	[38]
Eskişehir, Türkiye	Angström-Prescott model and improved versions of this model, also several typical models based on ambient temperature	Sun radiation, sunshine period, temperature, air pressure, wind speed, and relative humidity	Worldwide sun radiation	January 2011–December 2014	E, MPE, MAPE, SSRE, RSE, MBE, RMSE, t-sat, and R2	The author tested new model usage with 9 statistical techniques.	[39]
Peru	Multiple linear regression analysis	Temperature, precipitation, and relative humidity	Daily solar radiation	1990–2004 (calibration) and 2004–2010 (validation)	RMSE	Seven empirical models were employed for the prediction of daily solar radiation data.	[40]
Morroco	Temperature -Geographic factors model	Temperature- Geographic factors	Global solar radiation	August 2011–September 2015	r, nMAE, and nRMSE	22 empirical models and other machine learning methods were applied. Temperature-Geographic factors models recommend in all empirical models.	[41]
Iran	11 Newly Developed Empirical Models (NDEM)	Month number, solar declination, sunshine duration, RH, and cloud cover rank	Monthly, daily, and hourly diffuse solar radiation	January 2008 to December 2017	RMSE, NRMSE, and R2	11 newly developed models were tested. Errors do not exceed 10% for these models.	[42]
Ghana	Modified Angström-Prescot, modified Steyn-method, Ordinary kriging method	Sunshine duration	Global solar radiation, sky view factor, cloudiness index	2015–2018	r	Sky conditions were calculated by different methods for the 4 climate regions of Ghana.	[43]
China	Empirical PV power model, combined a sunshine-based model, and inverse distance weighting model	Minimum and maximum temperature, sunshine duration, relative humidity, and precipitation	Global solar radiation	1961 to 2018	RMSE, MAE, RRMSE, R2, and NS	New developed global solar radiation model can predict correctly.	[44]
Fiji island	20 empirical models	Sunshine duration, minimum, mean, and maximum temperatures, cloud cover, and relative humidity	Global solar radiation	1984 to 2018	ME, NSE, PME, RMSE, and r-value	20 models were analyzed by dividing into 3 different groups. Models with relative humidity in group 3 performed very well.	[45]
Irani (Ahvaz, BandarAbbas, and Kermanshah)	Eight Rs empirical models, (AP, GG, HS, S, An, Ch, Ba, Ab)	Extraterrestrial solar radiation, sunshine hours, air temperature, relative humidity, maximum possible sunshine hours, the function of daily range of air temperature, and station altitude	Solar radiation	2007 to 2017	RMSE, NMRSE, and R2	They compared 8 empirical models and SVM models. They do not recommend the use of empirical models instead of the SVM model, despite their high accuracy.	[46]

It is possible to examine the models used for the estimation of solar radiation in 2 groups. The first group model predicts global horizontal estimation of solar radiation (H-based), and the other is models based on different weather variables (non-H-based models) [24]. As seen in Table 1 many researchers create different models regionally. It is seen that most of the prediction models are H-Based. Due to their simplicity and high accuracy, H-based models are used in many applications. It has been stated in many studies that the dataset and the number of variables are important while developing the empirical model. The larger the dataset, the higher the accuracy of the empirical model. In addition, the increase of variables in the empirical models increases the accuracy parallel. However, in this case, the model can become complex. In empirical models, the simplicity of the model is as important as its accuracy. In addition, it is very critical to determine the key factor in a model for the simple and accurate, as in the study by Jamil and Bellos, 2018 (clearness index).

In recent studies, although the empirical models work with high accuracy in the region where they are tested, it has been observed that the opposite is the case in different climatic conditions and different regions. For this reason, some researchers have tried other predictive AI-based models combined with empirical models and developed hybrid models [25]. These models have been calibrated with other models, and their application areas and accuracy have also increased.

2.2. Time series methods

Time series methods are one of the most common statistical techniques used for the estimation of solar radiation. Time series can be described as the evolution of a series of observations that are sampled at regular intervals over time. The originality of time series models compared to other statistical methods is that they introduce time as one of their explanatory variables. Time series improve mathematical models that can predict future observations based on present data [47]. Time series models such as autoregressive integrated moving average (ARIMA), autoregressive (AR), autoregressive moving average (ARMA), an autoregressive moving average model with exogenous variables (ARMAX), autoregressive integrated moving average with exogenous variables (ARIMAX), autoregressive fractionally integrated moving average (ARFIMA), moving average (MA), and vector autoregressive (VAR) are used to estimate solar radiation.

The AR model shows a process where present values can correspond to a linear combination of past values. In contrast to the AR model, which uses the weighted total of the past values to ensure a time series representation, the MA model consolidates n number of past values to develop a time series. The ARMA model was improved by consolidating AR and MA models to ensure a stingy parameterization for a process. The ARMAX model ensures a multivariate time series representation to increase the accuracy of the univariate ARMA model by including suitable information in addition to subjected time series. For example, cloud cover, humidity, wind speed, and direction can be included as exogenic variables in an ARMA model to improve an ARMAX model for more accurate forecasting of solar radiation time series [48]. The ARIMA model is preferred for non-stationary time series. Distinct sections of nonstationary processes show some level of similarities, although they represent differences in local trend or level. A stable ARMA process with the n-th difference in the time series improves an ARIMA model [49]. The ARFIMA model is preferred for long memory prediction. ARFIMA generalizes ARIMA by authorizing the difference to get fractional values [50]. The ARIMAX model includes past values of the time series in ARIMA to improve its performance and accuracy. It is a more suitable model for time series with abrupt variations in trends. An ARIMA process containing the past values of an exogenic variable improves an ARIMA process [48]. The VAR model qualifies linear dependencies among two or more time series. The VAR model utilizations multiple variables to generalize the univariate AR model [51]. Summary of studies using time series models for the estimation of solar radiation is given in Table 2.

Table 2.

A summary of the studies regarding the prediction of solar radiation data using time series methods.

Location	Model	Input Parameters	Output Parameter	Data Scale	Statistical Benchmarks	Key Findings	References
Kansas, Denver, and Arizona, United States	ARIMA	Historical solar radiation	Daily average global horizontal solar radiation	January 01, 1987, to December 31, 1990	MAPE	ARIMA has better results when applied to the time-varying daily solar radiation prediction.	[52]
Many countries in Europe and Asia	ARIMA	Historical solar radiation	Daily solar radiation	9436 days from November 16, 1978	N/A	The time series in different climatic conditions depend on the long-range variability of solar radiation.	[53]
Jeddah, Saudi Arabia	AR	Historical solar radiation	Diffuse horizontal radiation, hourly global solar radiation, and direct normal radiation	1998–2002	RMSE and MBE	The applicable model developed with the entered parameters resulted in an accurate prediction.	[54]
Miami and Orlando, United States	ARIMA	Historical solar radiation	Hourly global solar radiation	January 1995 to December 2005	MBE and RMSE	It was observed that cloud cover information gives more accurate results in terms of prediction.	[55]
Awali, Bahrain	ARIMA	Historical solar radiation	Daily average solar radiation	May 2010 to April 2011	MAPE	It was observed that the different ARIMA models used effectively predict solar radiation.	[56]
Five cities in France	ARMA	Meteorological parameters	Hourly global solar radiation	October 2002 to December 2008	nRMSE	The nRMSE ranges from 18.9 to 21.1% in five different cities.	[57]
Ajaccio, France	ARMA	Meteorological parameters	Hourly solar radiation	2007–2008	nRMSE	ANN has better results than the ARMA model with a decrease of 1.3 points while performing error prediction.	[58]
Corsica Island, France	AR and ARIMA	Historical global solar radiation	Daily global solar radiation	January 1998 to December 2007	RMSE, nRMSE, MAE and MBE	An ANN with extrinsic and intrinsic data has better performance in univariate ARMA models.	[59]
Seoul, South Korea	ARIMA and SARIMA	Historical solar radiation data	Daily and monthly solar radiation	1981–2017	R2 and RMSE	While the ARIMA model has good results for daily solar radiation, SARIMA has more accurate results for monthly solar radiation estimation.	[60]
Oran, Algeria	ARMANAR	Meteorological parameters	Hourly global horizontal solar radiation	2010–2012	RMSE and nRMSE	nRMSE is 0.2634 and 0.3241, respectively for NAR and ARMA.	[61]
Seoul, South Korea	SARIMA NARX	Historical global solar radiation	Global solar radiation	1981–2015	RMSE and R2	R2 and RMSE are 0.95 and 0.23 MJ/m2, respectively for NARX.	[62]
New Delhi, India	ARIMA	Meteorological parameters	Monthly solar radiation	July 01, 1983, to December 31, 2007	RMSE, MAPE, MAE, and R2	MAPE, R2, RMSE, and MAE results are 6.556, 0.9293, 0.3529, and 0.2659, respectively.	[63]
Las Vegas, United States	ARMA	Historical solar radiation	Hourly solar radiation	1995–2004	MBE and nRMSE	MBE and nRMSE are 0.133% and 11.76%, respectively.	[64]
Morocco	ARMA and ARIMA	Historical solar radiation	Daily global solar radiation	2018 (November to December) and 2019 (January to March)	MBE RMSE, and MAPE	ARIMA has a better performance compared to the ARMA model.	[65]
Two cities (Algiers and Ghardaia) in Algeria	AR and NAR	Historical solar radiation	Daily global solar radiation	1 January 2005 to 31 December 2006	NRMSE, S, R2, RMSE, MAE and MBE	NAR has a better performance compared to the AR model.	[66]
Ghardaia, Algeria	ARMA, NARX, and AR	Historical solar radiation	Hourly global solar radiation	May 2013 to October 2013	RMSE, NRMSE, MAPE, NMBE and R	NARX estimated the solar radiation data more accurately than other models.	[67]

As seen in Table 2, time series models have generally yielded successful results in the estimation of solar radiation. Time series models make predictions using historical solar radiation data. In this framework, it makes predictions by ignoring other important climatic, environmental, and geographical changes. With the advancement of computer science, the use of AI algorithms has become widespread. AI algorithms applied to many engineering problems have provided very successful results. For example, [68], in their study, estimated solar radiation data for two different regions with a time series model, AI algorithm, and hybridization of these two models. The results were discussed with regards to RMSE, nRMSE, MBE, nMBE, MPE, and R² statistical metrics to determine the best method for these two regions as seen in Table 3.

Table 3.

Statistical comparison of time series, AI models, and their hybrid models on the same dataset [68].

Location	Model	R2	MBE (Wh/m2)	RMSE (Wh/m2)	MPE (%)	nMBE	nRMSE
Bouzaréah	ANN	0.802	−82.459	1334	24.062	−0.0192	0.31
	ARMA	0.716	−60.514	1553	28.611	−0.0141	0.361
	Hybrid	0.820	−48.591	1286	23.408	−0.0113	0.298
Ghardaia	ANN	0.907	−29.364	726.65	4.150	−0.0051	0.126
	ARMA	0.882	−7.493	813.32	5.626	−0.0013	0.141
	Hybrid	0.914	−31.458	701.18	4.092	−0.0054	0.119

Accordingly, the hybrid model gave the best result in all statistical metrics for the Bouzaréah region, while the AI-based algorithm gave the second-best result in 4 out of 6 statistical metrics. In the Ghardaia region, the hybrid algorithm had the best results in 5 of 6 statistical measures, while the AI-based algorithm showed the second-best performance in 4 of 6 statistical measures [68]. Accordingly, the higher performance success of prediction algorithms consisting of hybrids of AI and AI-time series has pushed researchers to use more AI or hybrid algorithms in recent years. In this framework, the effects of AI-based algorithms on the estimation of solar radiation are covered extensively in the following subsection.

2.3. Artificial intelligence methods

In recent years, it has been viewed that great, effective, and successful steps have been taken with the enormous technological development, particularly in computer science. These steps make human life easier in many stages of daily life. One of the significant steps is undoubtedly artificial intelligence (AI). AI is a relatively new application that is growing in both its popularity and the variety of its usage area. AI is a technology that is frequently applied today in medicine, textiles, energy, machinery, economy, and other many important fields, and its success is now proven and accepted by human beings. Although it emerged at first as an effective alternative approach to traditional methods, its performance success has surpassed traditional methods in almost every field where it is applied today. AI represents machines with human-like intelligence, and it has a very high learning ability with the mechanism it runs in the background. Compared to traditional methods, artificial intelligence is a very successful tool for dealing with uncertainties and especially sudden changes and making quick decisions/responses.

In particular, with its application to engineering problems, many time-consuming and costly problems are now solved in the computer environment. It is indispensable software for many sectors such as the economy, energy production, supply chains, logistics, crop yield in agriculture, etc. It also offers user optimization opportunities or investment advice by observing the minimum errors and results in advance. One of its wide usage areas is the energy sector. For this sector, it has been proven to offer very successful results about the energy potential at a given location, particularly with regards to solar and wind energy. Even decision-makers, as well as policymakers, have revised their future energy investment scenarios according to AI results and achieved maximum efficiency.

The fact that the estimation of solar radiation data is of major importance for many critical sectors and the devices’ high costs that measure this data has led to the derivation of empirical models in this field. Although accurate and satisfactory results could be achieved to a certain extent with these empirical models in the literature, errors have been minimized with the introduction of AI technology into this field. Many researchers have proven in their studies that AI methods give more accurate results than empirical models. In this section, it is aimed to give an extensive literature review on the estimation of solar radiation data with AI algorithms and to discuss the results of the relevant studies. Considering the literature studies, it has been observed that generally ANN, SVM, DL, k-NN, RNN, SP, RF, SMGRT, FIS, ANFIS, LSTM, ConvLSTM, CNN, XGBoost, NB, DT, ELM, GPR, and MLP have been dominantly used in the estimation of solar radiation data. A summary of the studies performed using AI algorithms for the estimation of solar radiation data is given in Table 4.

Table 4.

A summary of the studies regarding the prediction of solar radiation data using artificial intelligence algorithms.

Location	Model	Input Parameters	Output Parameter	Data Scale	Statistical Benchmarks	Key Findings	References
Cairo in Egypt	MLP, ANFIS, and SVM	Sunshine, temperature, meteorological parameters, and day number	Daily global solar radiation	2012–2015	R2, MBE, RRMSE, MPE, and RMSE	ANFIS and MLP models gave similar results, but SVM comes to the fore according to these two models.	[69]
Zonguldak in Türkiye	LR and GR	Humidity, wind speed, temperature, and pressure	Daily global solar radiation	One year period	MAE, MSE, and RMSE	GR exhibited more successful performance in estimating the solar radiation data than the LR model.	[70]
North China Plain in China	RF, GANN, ELM, and GRNN	Diffuse solar radiation	Daily diffuse solar radiation	2000–2014	RRMSE, MAE, NS, and RE	All models predicted diffuse solar radiation with a mean relative error between −5.8% to −5.4%. In general, the GANN model exhibited the best prediction performance, followed by ELM, RF, and GRNN methods, respectively.	[71]
Wuhan, Kunming, and Guangzhou in China	SVM and XGBoost	Minimum and maximum temperature, altitude, longitude, and latitude	Daily global solar radiation	1966–2015	MAE, RMSE, R2, and MBE	Statistical metric results demonstrate that the XGBoost model is better at estimating the daily global solar radiation than the SVM algorithm.	[72]
National laboratory in the USA	FoBa, leapForward, spikeslab, Cubist and bagEarthGCV	Historical solar intensity observations	Daily global solar irradiance	January 1, 2010, to December 31, 2015	r, R2, RMSE, and accuracy value	Experimental results demonstrate that for solar radiation forecasts from a few hours to two days, the algorithms predicted quite satisfactory results without the seasons being much affected by changes in weather conditions.	[73]
34 stations in Türkiye	DL	Minimum and maximum temperatures, cloud cover astronomical factor, sunshine duration, extraterrestrial radiation, and climatic variables,	Daily global solar radiation	2001–2007	R2, MAE, and RMSE	A total of 16 combinations of input parameters were tested, and it is reported that the sunshine duration is the most affecting parameter for GSR.	[74]
Abu Musa Island	ANFIS, RBFNN, SVR, MLFFNN, and FIS	Wind speed, local time, relative humidity, pressure, and temperature	Hourly solar radiation	N/F	r and RMSE	The correlation coefficient is bigger than 95% for most models in the prediction of hourly solar radiation.	[75]
Ghardaia in Algeria	SVM-R	Sunshine ratio	Daily global solar radiation	2005–2007	RMSE, rRMSE, and R2	The results showed that global solar radiation data is accurately predicted with very satisfied statistical R2, RRMSE, and RMSE of 97.4%, 8.46, and 1.59 (MJ/m2), respectively. Accordingly, the authors stated that only sunshine ratio data may be sufficient to predict the solar radiation data.	[76]
Gurugram in India	SVR	Pressure, relative humidity, day, temperature, and wind speed	Global solar radiation	2009–2011	RMSE	It has been shown that the most important parameter affecting the prediction performance of the SVR is the air temperature. The RMSE value in this model is found to be 14.3 MJ/m2.	[77]
Austin, TX in the USA	Naive Bayes	Dew point, temperature, sky coverage, and relative humidity	Two-day-ahead global horizontal irradiance	August 2013 to March 2014	E, MAE, RMSE, RMBE, MAPE, and MBE	The proposed NB is a significantly easy and rapid algorithm. This model requires small training data (less than two months) and utilizes publicly available input data. The results were very satisfying in terms of the six statistical metrics.	[78]
Odeillo in France	SP, ANN, and RF	Historical dataset	Solar radiation (diffuse horizontal, beam normal, and global horizontal)	3 years of hourly data	RMSE, MAE, nRMSE, and nMAE	RF had better forecasting results of solar irradiation as compared to SP, and ANN. Additionally, all models presented worse results in spring and autumn owing to the less reliable of data and high meteorological variability in these seasons.	[79]
India (Gorakhpur side)	RF, M5, MARS, and CART	Solar azimuth, dew point, pressure, rainfall, wind speed, global solar radiation, and minimum-maximum- average temperatures	One-day-ahead to six-day-ahead hourly solar radiation	January 1, 2017, to December 31, 2017	MAE, MBE, and RMSE	Among the prediction methods trained with the same dataset, the best prediction accuracy is obtained with RF, whereas the CART method is the worst.	[80]
Four provinces (Tekirdağ, Afyon, Ağrı, Sinop, and Hakkâri) in Türkiye	SVR, ANN, and DT	Hourly solar radiation	Hourly solar radiation	2012 to 2016	R2 and RMSE	It is observed that boosting the ensemble improves the prediction performance of the algorithms.	[81]
Toledo in Spain	SVR, GPR, MLP, and ELM	A clear-sky solar radiation model, a cloud index, and several reflectivity values	Hourly global solar radiation	May 2013 to April 2014	MBE, MAE, RMSE, and R2	The results demonstrated that the satellite measurements increased the input parameters and improved the predictability of global solar radiation of the machine-learning algorithm.	[82]
Isparta, Türkiye	DL, SMGRT, and ANFIS	Soil, and air temperature sunshine duration, relative humidity, cloudiness, and extraterrestrial solar radiation	Monthly global solar radiation	2007 to 2016	MBE, MSE, RMSE, and R2	Each model presented very satisfied results in predicting the GSR, but SMGRT comes to the fore according to the statistical metrics.	[83]
Tuscaloosa, Alabama in the USA	ANN, and RNN	Wind speed, dew-point temperature, outdoor air-dry bulb temperature, relative humidity, and wind direction	Daily global solar radiation	January 14, 2019, to January 21, 2019	RMSE, NMBE CV(RMSE), and R2	Cloud cover was a vital effect on the prediction of GSR. RNN had better prediction results, but it had 800 times higher computational costs than ANN.	[84]
Sapporo, Tateno, Fukuoka, Ishigakijima, and Minamitorishima in Japan	ANN	Relative humidity, precipitation, minimum and maximum temperature, altitude, longitude, months, latitude, sunshine duration, and wind speed	Global, direct, and diffuse solar radiation	2011–2016	R2, MAPE, and RMSE	Monthly diffuse, direct, and global solar radiation data could be predicted with very high accuracy via the developed models.	[85]
15 weather stations in China	SVM, RF, M5Tree, CatBoost and XGBoost	Relative humidity, maximum and minimum temperatures, and sunshine hour	Daily diffuse horizontal solar radiation	1996–2015	RMSE, MAE NRMSE, and R2	The same dataset of 15 different stations with different climate conditions predicted different algorithms, and the results showed that CatBoost gave lower error magnitudes against the varying climate conditions in comparison to other algorithms.	[86]
Ghardaia in India	MLP and RBF	Day, day duration, declination angle, air temperature (min, mean, and max), sunshine duration, atmospheric pressure, maximum elevation, and sunshine ratio	Global solar radiation	2014–2016	RMSE, rRMSE, and R2	Both algorithms gave a very low prediction error, but the MLP algorithm slightly comes to the fore as compared to the RBF algorithm.	[87]
Four different locations (Borno, Kano, Yobe, and Zamfara) in Nigeria	ANN, CNN, RNN, SVR, PR RF	Wind speed, sun height, and ambient temperature	Global and diffuse solar radiation	2005–2016	r, MAE, RMSE, and NMBE	It has been observed that deep learning methods achieve better prediction accuracy compared to machine learning methods. Overall, the application of RNN for the global solar radiation forecast in Yobe had the best performance with a 0.9546 r-value, 82.22 W/m2 of RMSE, and 36.52 W/m2 of MAE.	[88]
Johannesburg in South Africa	LSTM, ConvLSTM, CNN, RF, XGBoost, and SVM	Historical meteorological data	Hourly solar radiation	2009–2018	nRMSE	FR and CNN models gave the worst nRMSE values of 19.8%, and 12.61%, respectively. The best nRMSE result was obtained to be 1.51% for the ConvLSTM algorithm.	[18]
Four provinces (Karaman, Tokat, Nevşehir and Kırklareli) in Türkiye	ANN, DL, SVM, and k-NN	Extraterrestrial solar radiation, day length, minimum and maximum temperature, cloud cover, and solar radiation	Daily global solar radiation	January 1, 2018, to December 31, 2019	rRMSE, MAPE, RMSE, MBE, MABE, R2, and t-stat	ANN generally has lower error results than the other three ML algorithms.	[9]
Five cities (Dhaka, Bogura, Dinajpur, Chuadanga, and Satkhira) in Bangladesh	RNN, LSTM, and GRU	Minimum and maximum values of both temperature and humidity, wind speed, and solar radiation	Daily global solar radiation	2014–2019	MSE, MAE, RMSE, and MAPE	Among the three models, the GRU model gave the best result with a MAPE score of 19.28%.	[89]
Ghardaia, Algeria	SVM and C-SVM	Minimum, maximum, and mean temperatures	Daily global solar radiation	1 May 2013 to 31 December 2015	RMSE, rRMSE, MABE, and r	C-SVM gave the best performance, based on RMSE and r analysis.	[90]
Tamil Nadu, India	LM, SCG, and RP	Global and direct solar radiation, average ambient temperature, average wind speed, latitude, and longitude	Hourly solar radiation	N/F	MAD, MSE, RMSE, MAPE, and R	The LM algorithm has the advantage of converging in a shorter time and has reached the result with minimum error (R = 0.9376).	[91]

As seen in Table 4, most researchers trained AI algorithms using a large variety of input parameters and generally reported satisfactory results for each AI algorithm. On the other hand, considering the works where the same dataset is applied to different solo-AI algorithms, the number of studies emphasizing that there is a big difference between the algorithm successes in estimating the solar radiation data is very limited. Generally, AI algorithms give close estimation results to each other. Based on the literature review presented in Table 4, it is possible to conclude that it would not be correct to say that any AI algorithm gives the best results for all regions. In other words, it was well observed that while ANN gave the best estimation of solar radiation results for one region, it gave the worst result for another region. Furthermore, while the most significant parameter affecting the AI prediction results in a given region is the sunshine ratio, it may be temperature data for another region.

2.4. Hybrid methods

The continuous expansion of solar energy has made the subject of highly precise estimation of solar radiation important. Because of the atmospheric conditions variety and the non-steady action of solar radiation parameters, single prediction models such as empirical, artificial intelligence, and time series, may be insufficient to provide high forecasting performance [5]. From this point of view, researchers have focused on developing new models in which these methods are hybridized to eliminate the disadvantages of single estimation models and enhancement the estimation accuracy. A comprehensive literature review of recent trends in hybrid methods for the estimation of solar radiation data is presented in Table 5.

Table 5.

A summary of the studies regarding the prediction of solar radiation data using hybrid methods.

Location	Model	Input parameters	Output parameter	Data scale	Statistical benchmarks	Key findings	References
Gurgaon, India	ANN, ANFIS, and HMM-GFM	15 different combinations of inputs	Global solar radiation	2009 to 2011	r-value, RMSE, and MAPE	For the best prediction accuracy, the combination of input parameters is as follows: relative humidity, atmospheric pressure, sunshine, day number, and temperature. The proposed HMM-GFM method achieved the best estimation accuracy with 7.9124 MJ/m2 of RMSE, 3.0083% of MAPE, and 0.9921 of r-value.	[92]
Murcia, Spain	CRO–ELM, ELM, and SVR	Meteorological variables	Global solar radiation	January 1, 2010, to December 31, 2011	RMSE and MAE	The prediction accuracy of the CRO-ELM is higher than the conventional SVR and ELM algorithms.	[93]
Singapore	GAMMF, TDNN, ARMA (1,1), and ARMA-TDNN	Historical global solar radiation	5 min ahead solar radiation	2009 to 2010	SMAPE and RMSE	GAMMF achieved higher predictive accuracy compared to other methods.	[94]
Six locations in the USA	CS-OP-ELM, OP-ELM, ARMA, and BPNN	Eight input variables	Hourly clear and real sky global horizontal radiation	Hourly data from 2008 to 2010	MRE and RMSE	CS-OP-ELM had better prediction results of solar irradiation as compared to conventional OP-ELM, ARMA, and BPNN.	[95]
Four sites in the USA	RBF, Hard-ridge-RBF, DE-hard-ridge-RBF, and CS-hard-ridge-RBF	12 meteorological parameters	Monthly average global solar radiation	1998 to 2010	RMSE and MAPE	The RMSE and MAPE metric results showed that the hybrid methods (DE-hard-ridge-RBF and CS-hard-ridge-RBF) predict solar radiation with higher accuracy than conventional RBF and hard-ridge-RBF models.	[96]
USA (Colorado) and Singapore	SOM- SVR-PSO, ARIMA, SES, LES, and RW	Past 8-hour data	Hourly global solar radiation	USA (1997–2013) Singapore (2010–2013)	nRMSE and nMBE	The mean nRMSE value of the proposed hybrid model for USA data is on average 4% better than the ARIMA, LES, SES, and RW methods. For the Singapore data, the nMBE value of all models is usually less than 3%.	[97]
Three provinces (Maiduguri, Jos, and Iseyin) in Nigeria	GP, ANN, and SVM–FFA	Sunshine duration, min and max temperatures	Monthly mean horizontal global solar radiation	1987 to 2007	r, R2, RMSE, and MAPE	The proposed SVM-FFA gave the best prediction results with r, R2, RMSE, and MAPE of 0.8532, 0.7280, 1.8661 MJ/m2, and 11.5192%, respectively.	[98]
Four sites in the USA	SVM, SVM-HARD, GSO-SVM-HARD, and HARD-RIDGE-SVM	Meteorological variables	30 daily global solar radiations	One year	MSE, MAPE, and RMSE	It was observed that the hybrid GSO-SVM-HARD method achieved the best estimation accuracy in all regions. Also, the MAPE values of the hybrid method were between 5% and 15%.	[99]
Klang Valley, Malaysia	RFs–FFA, ANN-FFA, ANN, and RFs	Number of hours per day, humidity, day and month number ambient temperature, and sunshine ratio	Hourly global solar radiation	Hourly meteorological data for one year	MBE, MAPE, and RMSE	The proposed RFs-FA method is more successful in terms of prediction accuracy with 2.86% MBE, 6.38% MAPE, and 18.98% RMSE compared to hybrid ANN-FFA, ANN, and RFs models.	[100]
Four locations in India	DCGSO-LASSO, LASSO, SVM, and GRESH	Relative humidity, wind direction, wind speed, pressure, solar zenith angle, temperature, and precipitation	5 days global horizontal radiation	January 1, 2014 to December 31, 2014	RMSE, MAPE, and RMSE/Avg	The proposed DCGSO-LASSO achieved the best prediction accuracy for the four locations respectively with 16.815/23.02/22.354/11.437 of RMSE, 7.148%/13.101%/7.756%/1.782% of MAPE, and 2.991%/4.939%/4.423%/2.302% of RMSE/Avg.	[101]
Türkiye (65 locations)	FRF-SVM, ANFIS, and GenProg	Relative humidity, mean air temperature, altitude, latitude, and longitude	Horizontal global solar radiation	2000 to 2013	MAE, RMSE, IQR-AE, and MaxAE	In the training set, it was determined that the most suitable model was Gaussian kernel-based FRF-SVM with 0.531 of MAE and 1.571 of RMSE. In the testing, the error value of FRF-SVM-Gauss is slightly higher compared to the GenProg approach.	[102]
USA	NSMOBA, BPNN, GABPNN, GRNN, and CSAWNN	12 meteorological variables	Global solar radiation	1991 to 2010	MAE, MSE, and MAPE	The developed NSMOBA algorithm gave lower error values compared to other individual and hybrid prediction algorithms.	[103]
The Mashhad province of Iran	ANN-SA, ANN, SVM, MLSR, and GP	Relative humidity, atmospheric pressure, earth skin temperature, wind speed, minimum, average, and maximum air temperatures	Daily solar radiation	1995 to 2014	R2, MAE, and RMSE	The prediction results demonstrated that integrating the SA algorithm into the ANN modeling process increased prediction accuracy.	[104]
Malaysia (Kuala Terengganu)	ANFIS, ANFIS-DE, ANFIS-GA, and ANFIS-PSO	Clearness index, minimum and maximum temperature, monthly rainfall, and sunshine duration	Monthly global solar radiation	January 2006 to December 2014	r, R2, MABE, MAPE, RMSE, and RRMSE	ANFIS-PSO gave the best prediction results with 0.9963 of r, 0.9921 of R2, 0.2482 MJ/m2 of MABE, 1.4097% of MAPE, 0.3065 MJ/m2 of RMSE, and 1.7933% of RRMSE.	[105]
Eight provinces (Isfahan, Tabriz, Tehran, Zabol, Kermanshah, Bandar Abbas, Ahvaz, and Mashhad) of Iran	SVR-KHA and SVR	Historical global solar radiation data	Global solar radiation	1979 to 2014	MAE, MAPE, RMSE, R2 and RRMSE	SVR-KHA model gave low error compared to classical SVR with 0.93 of R2, 7.4% of MAPE, and 1.98 MJ/m2 of RMSE.	[106]
North Dakota, USA	ANFIS-muSG, ANFIS-GA ANFIS-GWO ANFIS-GOA, ANFIS-DA, ANFIS-SSA, ANFIS-PSO, and ANFIS	Minimum, mean, and maximum air temperatures	Global solar radiation	2010 to 2018	R2, MAE, RMSE, MARE, MRE, AAPRE, and RMSRE	Hybrid ANFIS-muSG performed 25.7%–54.8% better than its competitors in terms of RMSE metric for different locations of the studied region.	[107]
Three provinces (Dhahran, Riyadh, and Jeddah) in Saudi Arabia	SVR-GOA-BAK, ANN, DT, KNN, and RF	14 input variables	Global horizontal irradiance (at the 1-h ahead time horizon)	June 1, 2013, to May 31, 2017	R2, MAE, nMAE, MAPE, RMSE, and nRMSE	The hybrid SVR-GOA-BAK, achieved 32.15–39.69% better prediction accuracy in terms of MAPE performance criterion compared to the individual SVR methods.	[108]
China (Station of longitude 124.181 W and latitude 44.382 N)	Hybrid WT-CEEMDAN-IASO-ORELM, and nine competitive models	Historical solar radiation data	Short-term (10 min ahead) solar radiation	Different months of 2020 year: March, June, September, and December	MAPE, MAE, RMSE, and r-value	It has been observed that the proposed hybrid WT-CEEMDAN-IASO-ORELM model gives excellent results for short-term solar radiation prediction and is a prospective technology.	[109]
Queensland, Australia (Six solar farms)	CNN-REGST, CNN, LSTM, DNN, ELM, REGST, RFR, GBM, and MARS	Meteorological parameters	Daily global solar radiation	54 years of data	r-value, RMSE, MAE, RMSEr, RRMSE, RMAE, WI, NSE, LM, KGE, DS, APB, EVar	Given all metric results, it has been seen that the proposed hybrid CNN-REGST model exhibits a successful forecasting performance in daily GSR forecasting compared to deep learning and ML methods.	[110]
Four stations (Dori, Po, Gaoua and Boromo) in Burkina Faso	XGB-CMAES, adn MARS-CMAES	Minimum and maximum values of both weather temperature and humidity, wind velocity, evaporation, and vapor pressure deficit	Daily global solar radiation	January 1, 1998, to December 31, 2012	NSE, RMSE, MAE, R, and VAF	MARS-CMAES method gave better prediction performance compared to XGB-CMAES.	[111]

As can be seen in Table 5, researchers have successfully applied hybrid methods that combine the superior features of at the least two methods to solar radiation data estimation at different time horizons. For example, Ibrahim and Khatib [100] estimated the hourly global solar radiation of King Valley, Malaysia using a method called the random forests-firefly algorithm (RFs-FFA), which was developed by hybridizing the random forest technique and the firefly algorithm. The underlying reason for hybridizing these two methods is to develop the estimation accuracy of the traditional RFs method by finding the best number of trees and leaves per tree in the forest using the firefly algorithm. The authors evaluated the performance of the algorithms with regards to MAPE, RMSE, and MBE metrics. The hybrid RFs-FFA method achieved better prediction results with 6.38% of MAPE, 18.98% of RMSE, and 2.86% of MBE compared to single RFs. In another study, Mousavi et al. [104] estimated the daily solar radiation of the Mashhad province of Iran with an artificial intelligence-based hybrid algorithm. The authors hybridized the single ANN with the simulated annealing (SA) optimization algorithm to develop the calibration performance of the ANN method, which is frequently used in solar radiation prediction studies. The reason why the SA method was preferred in hybridization is that the algorithm is a non-greedy optimization approach and thus avoids local solution traps. The dataset used in the relevant study flaps the years 1995 and 2014 and it is separated into two stages: training and testing. The dataset between 1995 and 2009 was used to train the algorithms, while the remaining dataset (between 2010 and 2014) was used to confirm the fitting model. The authors reported that the predictive acuity of the hybrid ANN/SA method is superior to that of the single ANN as well as SVM and machine learning methods. Similarly, in numerous scientific papers, it has been observed that the researcher utilizes nature-inspired meta-heuristic optimizations in hybridization to improve the performance of single prediction methods. Table 5 details some existing literature studies focusing on hybridization with meta-heuristic algorithms. Accordingly, researchers used various meta-heuristic algorithms such as coral reefs optimization [93], cuckoo search algorithm [95], firefly algorithm [98], glowworm swarm optimization [99,101], nondominated sorting-based multiobjective bat algorithm [103], particle swarm optimization [105], genetic algorithm [105], differential evolution [105], grasshopper optimization algorithm [107], salp swarm algorithm [107], grey wolf optimizer [107], and dragonfly algorithm [107]. In the reference studies, metaheuristics were used to optimize the prediction structure and network parameters. In addition, new hybrid models have been proposed using different data pre-processing techniques or third methods to produce high-quality solutions to the estimation problems of solar radiation, which has a complex structure due to the distinct climatic conditions and estimation horizons of the studied regions. The HMM-GFM [92], GAMMF [94], FRF-SVM [102], SOM-SVR-PSO [97], and ANFIS-muSG [107] prediction algorithms can be given as examples of this type of hybridization. For example, Dong [97] applied the novel hybrid model based on self-organizing maps-support vector regression and particle swarm optimization (SOM-SVR-PSO) for the estimation of hourly solar radiation in the USA and Singapore. In the proposed hybrid method, the self-organization map, which is an example of the cluster-based ensemble learning approach, is used to separate the raw data into clusters with similar characteristics. While SVR is used to generate forecast data for each region, PSO is applied in the parameter selection of the SVR model.

As a result, many studies have declared that hybrid algorithms achieve higher prediction accuracy compared to single empirical, artificial intelligence, and time series prediction methods for the estimation of solar radiation. However, hybrid models have higher computational complexity in comparison to that of single methods.

2.5. Performance comparison of different-based models on the same dataset

This subsection evaluates literature studies involving performance comparison of the methods defined in the previous four subsections on the same dataset. Current studies comparing different models using the same dataset are given in Table 6. Let's examine some of these studies in detail. Bounoua et al. [41] applied 22 different empirical models, RF, MLP, Boost, and Bag models for different cities in Morocco to estimate solar radiation. Daily global estimation of solar radiation was made by using ambient temperature, relative humidity, wind speed, and solar radiation as input parameters. The dataset between 2011 and 2015 was used. Among the models, the RF model gave the best estimate. Performance parameters for the RF model were obtained as 87.753–96.22%, 5.84%–11.81%, and 7.85–15.33% for r, nMAE, and nRMSE, respectively. Among the machine learning models, the best performance was determined as 81.73%–95.14%, 5.88%–13.86%, and 8.22%–18% for R, nMAE, and nRMSE, respectively. Among the 22 empirical models, the model that gave the best performance was the TG1 model. For the TG1 empirical model was determined as 72.38%–93.46%, 6.96%–17.94%, and 9.89%–22.39% for R, nMAE, and nRMSE, respectively. Gürel et al. [112] ANN, Holt-Winters, RSM, and Angstrom type empirical models were used to estimate solar radiation for four different cities in Türkiye. Monthly and daily global estimation of solar radiation was made using ambient temperature, pressure, wind speed, sunshine duration, and relative humidity as input parameters. Meteorological data between 2008 and 2018 were used. ANN model gave the best performance among all models. MAPE, R², t-stat, RMSE, and MBE values were determined as 4.9263%, 0.9911, 0.582, 0.78 MJ/m²-day, and 0.1323 MJ/m²-day.

Table 6.

A summary of the studies comparing different models using the same dataset.

Location	Model	Input Parameters	Output Parameter	Data Scale	Statistical Benchmarks	Key Findings	References
China	ANN, and Empirical regression models (Model 1, Model 2)	Sunshine percentage, and clearness index	Monthly mean daily diffuse solar radiation	1995 to 2004	RMSE, MPE, and MBE	ANN is superior to empirical models. ANN estimated the actual values of Zhengzhou with 94.81% accuracy.	[113]
Türkiye (73 different locations)	ANN and MLR	Months of the year, latitude satellite-estimated LST, longitude, and altitude	Solar radiation forecasting	2000 to 2002	R2, RMSE, and MBE	ANN achieved high accuracy compared to MLR.	[114]
Iran	Five empirical models, WR, GEP, and ANN	Daylight hours, extraterrestrial global solar radiation, daily mean clearness index, and daily temperature	Daily global solar radiation	1982 to 2016	GPI, MAE, RMSRE, MBE, RMSE, RRMSE, U95, MARE, R2, erMAX, and t-stat,	The statistical metric results gave that the best prediction performance was exhibited by the ANN method.	[115]
Paris, France	ARMA, SIM, SVM, and NN	Global solar radiation	Hourly solar radiation	January 1, 2004, to December 31, 2015	nRMSE	NN model gave better performance than other models.	[116]
Kerman, Iran	3rd degree empirical model, ANN, SVM–RBF, SVM–WT	Daily clearness index	Diffuse solar radiation	2006 to 2012	r, RMSE, and MABE	The SVM–WT method has better estimation accuracy than its competitors with 0.9631 of r, 0.6940 MJ/m2 of RMSE, and 0.5757 MJ/m2 of MABE.	[117]
Tamil Nadu (India)	SVM, ANN, and empirical models	Relative humidity, longitude, day length, month, latitude, maximum and minimum temperature, and bright sunshine hours	Monthly mean daily global solar radiation	2003 to 2012	MBE, MAPE, RMSE, t-stat, and r-value	SVM algorithms gave better results than both those of ANN and empirical models.	[118]
Iran	Empirical models, ordinary and coupled ANN models	Sunshine duration, minimum and maximum air temperatures, and daily global solar radiation	Daily global solar radiation	1992 to 2015	R2, RMSE, and MBE	The prediction performance of the ordinary ANN models was enhanced considerably after being coupled with a genetic algorithm.	[119]
Abu Musa Island, Iran	SVR, MLFFNN, FIS RBFNN, and ANFIS	Inputs (N1): Wind speed, temperature, relative humidity, pressure, and local time Input (N2): Solar radiation	Hourly solar radiation	2010 to 2016	r, RMSE, and MSE	The results of N1 give that, MLFFNN and SVR methods exhibited the best prediction performance with r = 0.9999 and 0.9795, respectively. Furthermore, ANFIS, MLFFNN, and SVR methods obtained a correlation coefficient of over 0.95 in the test data for N2.	[75]
Four climatic zones of China	12 ML models, and 12 versions of the Ångström–Prescott model	Daily historical data	Daily global solar radiation	1966 to 2015	R2, RMSE, U95 MBE, t-stat, and NRMSE	Each prediction method used the same dataset and ML methods gave lower error values than empirical models. Among the ML methods, four models come to the fore: ANFIS, ELM, LSSVM, and MARS.	[120]
Four provinces (Şırnak, Kilis Ankara, and Karaman) in Türkiye	Angstrom type-empirical models, RSM, Holt-Winters, and ANN	Wind speed, pressure, relative humidity, ambient temperature, and sunshine duration	Monthly average daily global solar radiation	2008 to 2018	MAPE, RMSE, MBE, t-stat, and R2	Each model used the same dataset, and ANN exhibited the best results for global solar radiation data with R2, MAPE, RMSE, MBE, and t-stat of 0.9911, 4.93%, 0.78 MJ/m2, 0.1323 MJ/m2, and 0.58, respectively.	[112]
Five locations, Morocco	22 empirical models, RF, MLP, Boost, and Bag	Relative humidity, ambient temperature, wind speed, and solar radiation	Daily global solar radiation	2011 to 2015	r, nMAE, and nRMSE	RF method gave the best performance. r, nMAE and nRMSE are 81.73–95.14%, 5.88–13.86%, and 8.22–18%, respectively. Among the empirical models, the TG1 model was recommended. r, nMAE and nRMSE are 72.38–93.46%, 6.96–17.94%, and 9.89–22.39%, respectively.	[41]
Alabama, United States	KNNR, ANN, SVM, and BILSTM	Global solar radiation	Hourly solar radiation	May 1, 2011, to February 18, 2013	RMSE, MAE, and R2	The BILSTM model outperformed KNNR, ANN, and SVR methods in terms of RMSE, MAE, and R2 evaluation benchmarks.	[121]
North Carolina, and Southern Spain	MLP, ELM, GRNN, SVM, RF, and XGBoost	Temperature-based variables	Daily extraterrestrial solar radiation	2000 to 2018	MBE, RMSE, RRMSE, NSE, R2, and GPI	MLP and SVM are recommended for arid and semi-arid areas, while RF and XGBOOST are recommended for semi-humid and humid areas.	[122]
Tetouan in Morocco	ARIMA, FFNN, and k-NN	Top of atmosphere radiation, clearness index, maximum, average, delta, and ratio temperature	Daily global solar radiation	January 1, 2013, to December 31, 2015	MAPE, RMSE, MBE, NRMSE, Ts and σ	FFNN (6 × 10 × 1) gave better results than those of time series, and k-NN model with very low error magnitudes.	[123]

As seen in Table 6, time series models give better results than empirical models. AI models perform better when compared to time series models. Hybrid models, which are formed by combining single estimation models with each other, make a better estimation of solar radiation than all models.

3. Survey assessment

Nowadays, air pollution is becoming more visible, and rapidly growing public awareness has accelerated the transition to other clean, renewable, and sustainable energy sources, particularly solar energy. In addition to all these, the damage of non-renewable energy sources to the sustainable economic development of the government has made renewable energy sources very attractive in the short, medium, and long term. Even today, the energy production policy of governments is considered an indicator of the development level of that country. Until now, the demand for renewable resources, which was approached with prejudice, had slowed the transition of countries to these power systems. However, it has now been seen that renewable energy systems have offered very attractive results in high-level issues such as environmental pollution, economy, and energy security. Therefore, countries have revised their future energy investments and increased the level of renewable energy sources in total energy production as much as they can. In fact, many countries have made efforts to produce the main components that they can use for these power systems with their own technologies.

Solar radiation is a piece of very strategic information for a given region where the investment will be made before designing for solar energy systems. In order to provide this information, knowing the solar radiation value for a particular region in advance is of vital importance in the feasibility studies for that region. All these have been the subjects that have attracted researchers for the estimation of these data. In this regard, many models/methods have been developed and focused on estimating solar radiation data with the smallest possible error. Based on the comprehensive literature review, it is well-noticed that the solar radiation data have been estimated using different methods so far. As observed in the literature, solar radiation data was initially achieved by empirical mathematical models. Once the importance of solar radiation data was recognized and now widely used in many important sectors such as agriculture, energy production, tourism, etc. All these have led to ongoing attempts to estimate solar radiation more accurately in the upcoming years. One of the most considerable factors affecting the success of the estimation of solar radiation is undoubtedly the creation of the correct dataset for the relevant region. In this framework, many researchers have tried to estimate solar radiation data using distinct input parameters (see Fig. 3). A majority of the input parameters generally consist of the environmental and ecological input parameters such as sunshine duration, relative humidity, ambient temperature, sunshine ratio, minimum, maximum and mean air temperature, earth skin temperature, wind speed, wind direction, clear-sky estimates, satellite images, rainfall, and atmospheric pressure, etc. However, considering that solar radiation is a time-dependent variable, it has been observed that some of the researchers include data such as hours, days, months, and years in their algorithm for the training stages in addition to environmental and ecological input parameters. Furthermore, in addition to all these input parameters, a noteworthy number of researchers also considers that the solar radiation value is a location-dependent variable, they included some significantly important geographical data such as latitude, longitude, altitude, and elevation for the region to be studied. Consequently, it was viewed that while estimating solar radiation data for any region, it was possible to include the parameters directly related to solar radiation in that region. In other words, it was noticed from the published works that during the training of an algorithm, researchers did not face a problem due to insufficient/missing data to train their algorithms. In fact, they can create very big datasets, since much data about solar radiation is easily measurable and easily accessible. However, too many datasets may complicate the solution, control, and parameter optimization of algorithms. In this framework, it is reasonable that the researchers can use the most easily accessible data for the regions to be studied. Before starting the estimation, they can detect the correlation between each input parameter and solar radiation and perform feature extraction to enhance the performance achievement of the algorithms. Accordingly, researchers are dedicated to estimate the solar radiation data using various methods with the mentioned dataset. Based on the literature review, it is noticed that the number of studies that implemented the times series, and artificial intelligence methods have been exponentially increased. The previous papers have proved that solar radiation data can be estimated at a satisfactory rate with these methods. However, with advancing computer science, researchers focused on estimating these data with low errors. In this framework, the researchers deeply understood that each method has its own advantages and disadvantages in the estimation of solar radiation. All of this has resulted in the development of new hybrid models in which at least two methods are combined and which will generally reduce the disadvantages of single-model use. In the results, a large number of statistical error metrics are handled to discuss the performance success of the models in estimating the solar radiation data. Considering the results of the previous studies, it is obvious that there is no one model that is best for each region. That is, one model may estimate the solar radiation data with the lowest error at a given region, while the same model may do the worst solar radiation forecast at another region. This case may be attributable to the learning authority, size of the dataset, correlation of the dataset, and proper optimization of the model parameters. In this regard, the researchers tried to determine the usage dataset for the region where they focused on. As an overhead assessment, it is feasible to say that the hybrid models offer better results in estimating solar radiation data with lower errors than mono and empirical mathematical models. However, many researchers reported that empirical mathematical models have a considerable advantage with regards to facilitate of application and their estimation of solar radiation success is generally at a very satisfactory level for most regions.

Fig. 3.

Various inputs used in solar radiation data estimation.

In line with the major findings obtained from this review, it is possible to reach the following conclusions.

• ●It is very important that the dataset contains easily measurable data as well as its robust correlation with solar radiation. Furthermore, the availability of sufficient data for any region is among the issues of great importance for a more accurate estimation of solar radiation.
• ●The climatic characteristics of the studied region are of critical importance in the selection of the inputs. Therefore, appropriate inputs (temperature, humidity, pressure, etc.) should be selected according to the climatic characteristics of the region.
• ●Empirical models can be preferred in many studies in terms of easy application. However, the accuracy rates remain low compared to other machine learning-based estimation methods.
• ●In addition, it is very difficult to work with different variables in empirical models and to determine how much effect these variables have. For this reason, the results obtained are generally evaluated regionally.
• ●Time series models were improved based on statistical correlation. They generally have higher accuracy than empirical models, but do not describe well the nonlinear correlation between historical and other parameters.
• ●It can be said that time series models and ANN are equivalent in the quality of prediction under definite variability conditions, but the flexibility of ANN as a universal nonlinear approach is more preferred than time series models. In general, the accuracy of these methods relies on the quality of the training data.
• ●As a general conclusion, AI-based methods give very satisfactory results. However, the easy application of empirical models highlights the use of these models, especially in insignificant estimation differences.
• ●In general, ANN is seen as a “black box” in terms of engineering problems. In other words, ANN receives information from the outside and gives the outputs it produces to the outside. This problem may shake the trust in ANN. In contrast, time series and empirical models can be easily replicated by other researchers.
• ●Overall, it is possible to say that hybrid prediction methods created by combining two or more individual models produce better quality solutions to solar radiation problems at different time horizons compared to empirical, artificial intelligence, and time series models. The main goal of hybridization is to increase the final prediction accuracy by overcoming the various limitations of individual prediction methods.
• ●One of the components in double or triple hybridization is mostly meta-heuristic search algorithms. Because finding the most suitable parameters for the model is very important with regards to increasing the estimation accuracy. Recently, it is seen that researchers tend to use hybrid methods intensively in solar radiation prediction solutions.

4. Research gaps, challenges, and future directions

Solar radiation data is of immense importance in solar energy research. Where these data are not measured and meteorological data are not obtained, the estimation of solar radiation plays an important role. These estimation methods consist of empirical models, time series models, ANN (including machine learning algorithms), and hybrid methods. In the literature, these estimation methods are used to make the most precise estimation of solar radiation. However, these methods still require improvement. The research gaps, challenges, and future directions of estimation methods are outlined below.

• ●There is no model that works best for every region, an algorithm that works best for one region may give the worst result for another region. In this case, the estimation of solar radiation is dependent on the learning capabilities of the algorithms, as well as on the atmospheric, geographic, and climatic conditions of the given region, the size of the correlation value of the dataset with solar radiation, and the presence of sufficient data. Therefore, researchers should test multiple models for the given regions, and then they can only decide which model is better for the studied region.
• ●Based on the literature review, it is feasible to remark that the best results for the estimation of solar radiation are generally achieved with hybrid algorithms. However, advanced programming knowledge is required for that, and the establishment of the hybrid algorithm structure is a more time-consuming process than other methods. Considering the results obtained from the solo models and AI-based hybrid models, the differences are generally within very small limits.
• ●Researchers generally do not share their datasets, which means that another researcher does not have the opportunity to validate and develop the method for the relevant dataset. The fact that the data is generally handled on a large scale makes it difficult to share the dataset. Many algorithms that can probably achieve better results than the algorithm that many researchers find best, but these cannot be determined by future works.
• ●Particularly in artificial intelligence-based solar radiation predictions, the inability of researchers to derive a mathematical model limits their applicability by other researchers, although the results obtained from these studies are quite satisfactory.
• ●Although it seems like an advantage for time series models, only the long-term solar radiation data from the previous years are required. However, the lack of solar radiation data for the regions to be estimated or not recorded over long periods prevents time series from becoming widespread in estimating solar radiation. Furthermore, since time series models ignore many important environmental, geographic, and climatic parameters that directly affect solar radiation trends, it has a high potential to fail both in capturing sudden changes in solar radiation data and the case of a different trend from previous periods.
• ●Many researchers discuss the estimation of solar radiation of models using various types of statistical metrics in their studies. For example, the MSE metric, which is one of the most discussed statistical metrics in the discussions, is not suitable for discussing the prediction success models. By making predictions above and below the actual data, a model turns out to be quite small for the MSE and misleads the researcher. In this framework, it is more reasonable to use statistical metrics that take into account the absolute expressions of the errors or to use metrics that give the errors as a percentage. In addition, it will be also fairer to discuss all statistical metrics as normalized.
• ●In many studies, the same data types are commonly used as input parameters. Different ANN models should be developed and their accuracy checked by using different longitude, latitude, altitude, and extraterrestrial radiation for input parameters. This will be helpful for places where meteorological stations are not installed.
• ●Developing new models considering global warming and climate changes is a critical issue for future studies.
• ●The researchers have generally focused on the easy-to-measure meteorological station, satellite, and numerical weather parameters for the input data to reach the solar radiation of the relevant region. However, the performance of the models can be improved by using the feature selection methods (filter, wrapped, and embedded) in estimating the solar radiation data for a given region. The feature selection integrated solar radiation models have higher accuracy for global solar radiation, but their computational costs have been higher than that of the conventional/empirical solar radiation models.
• ●Owing to the fluctuations of solar radiation, error magnitudes in the estimation of solar radiation occur. Furthermore, researchers often suffer from the presence and lack of data required for model training. This is usually due to the malfunction/maintenance/non-existence of data measuring devices used in datasets. Thus, researchers encounter a challenging task in data preparation, feature selection, and model development stages, and the magnitude of the error in estimating solar radiation may be bigger.

5. Conclusion

This study deals with a detailed comparison of different methods used for the estimation of solar radiation works available in the literature. It is well understood that the dynamic nature of solar radiation noteworthy influences the reliability of most sectors including energy production, agriculture, and tourism in direct and/or indirect ways. Therefore, estimating solar radiation data with as few errors as possible will contribute to the development of these sectors. Many governments, investors, and decision-makers aim to maximize their profit margin by revising the location and size of their investments in these sectors according to the amount of solar radiation. However, it is well understood that the dynamic nature of solar radiation noteworthy complicates the estimation results and influences the reliability of most sectors in direct and/or indirect ways. From this point of view, the present review mainly discussed the estimation of solar radiation data by using empirical models, time series, artificial intelligence algorithms, and hybrid models. In conclusion, the findings of the study showed that each model has its own advantages and disadvantages in solar radiation prediction. That is, no optimal model/algorithm, which always gives satisfied results for all regions, was found. As a general assessment of the literature studies, it is noticed that hybrid methods developed to benefit from the advantages of single estimation methods generally give more accurate and reliable estimation results. However, hybrid models have higher computational complexity in comparison to single methods. From this point of view, using a single machine learning algorithm (particularly ANN and SVM) stands out as a very reasonable choice both in terms of an operational perspective and the success of the prediction results. On the other hand, it is seen that empirical models stand out with their features such as low computational costs, and ease of use. Since only historical solar radiation data is used in time series models, it has been concluded that it is an advantage that the data set is easy to create and easy to viable. Futhermore, the time series model provided not only simplicity and operability but also satisfied accuracy in estimating the solar radiation. In addition to the models, another important conclusion of the study is the creation of the dataset in a logical framework. While an input parameter has a great correlation in solar radiation data in one study and makes a significant contribution to the enhancement of the prediction success, in another study, it was found that the same input parameter worsened the prediction results. Therefore, researchers should be very meticulous while creating their dataset and make sure that each input parameter they use is at a correlational reasonable level. With the inclusion of improper input parameters in the dataset, the success of solar radiation estimation is negatively affected, which causes time loss, cost overruns, and computational complexities to a great extent. Accordingly, in order to improve the prediction success, it is of great significance to carefully examine the data set and perform cleansing and restructuring of historical datasets, because sudden changes observed in any parameter in the dataset, illogical results that may be caused by the time of measurement and the sensor, rapid climatic fluctuations, and incomplete data need to be cleaned. Finally, in recent years, tremendous developments in computer science and the ease of accessibility and availability of input data highly correlated to solar radiation are great important milestones that improve the success of solar radiation estimations. Knowledge of the solar radiation data for a given region is a very critical parameter, particularly for the energy, heating, tourism, and agriculture sectors, and since the estimation results should be obtained with as low errors as possible, and more, and more improvements, therefore, need to be gained to these sectors.

Author contribution statement

All authors listed have significantly contributed to the development and the writing of this article.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

The data that has been used is confidential.

Declaration of interest’s statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.