Magnetized mixed convection hybrid nanofluid with effect of heat generation/absorption and velocity slip condition

Abstract

Through a vertically shrinking sheet, a two-dimensional magnetic nanofluid is numerically analyzed for convection, heat generation and absorption, and the slip velocity effect. In this research, Al₂O₃–Cu/water composite nanofluid is studied, where water is deemed the base liquid and copper (Cu) and alumina (Al₂O₃) are the solid nanoparticles. Modern composite nanofluids improve heat transfer efficiency. Using the Tiwari-Das model, the current study examines the effects of the solid volume fraction of copper, heat generation/absorption, MHD, mixed convection, and velocity slip parameters on velocity and temperature distributions. Introducing exponential similarity variables converts nonlinear partial differential equations (PDEs) to ordinary differential equations (ODEs). MATLAB bvp4c solver is used to solve ODEs. Results showed dual solutions for suction with 0%–10% copper nanoparticles and 1%–500% heat generation/absorption. As copper (Cu) solid volume percentage increases from 0% to 10%, reduced skin friction $f^{″}\left(0\right)$ boosts in the first solution but falls in the second. When Cu is added to both solutions, heat transport $-{\theta }^{\prime }\left(0\right)$ decreases. As heat generation/absorption increases 1%–500%, $-{\theta }^{\prime }\left(0\right)$ decreases in both solutions. In conclusion, solution dichotomy exists when suction parameter $S\ge S_{ci}$ in assisting flow case, while no fluid flow is possible when $S<S_{ci}$.

1. Introduction

In late decades, the study of fluid mechanics has pulled in significant concern among analysts, scientists, and intellectuals from several areas as of an assortment of uses in science, technology, development, engineering, and construction. The most often addressed subjects are those concerning boundary layer flow. The boundary layer flow conception on a stretched layer was initially put forth by Sakiadis [1]. Crane [2] then updated Sakiadis' theories and used them to understand steady flow linear stretching surfaces as well as exponentials. According to his theory, the speed at which a layer stretches from a split is associated to the space between them. Because of technological advancements and increased demand for power, the world attempts to find specialized apparatus and appliances that develop thermal performance. Additionally, a wide variety of industrial applications for heat transfer deal with both rising and declining temperatures. Regular liquids, as oil and water, have less heat conductivity, which is the primary cause why engineering devices are insufficient.

The term "nanofluid" was generated by Choi [3] to entitle a mixture produced through scattering nanoparticles in a base fluid. Nanotechnology, according to him, is a kind of heat transmission dispersion that has improved thermal properties than normal fluid or regular fluids. "Nanofluids" are made up of minor amounts of dense particles that are 100 nm or slighter in volume. Nanofluids can be established through equally diffused solid nanoparticles in a normal fluid. Water, synthetic polymer remedies, oil and lubricants, organic fluids, and other typical liquids are examples of base fluids according by Asghar et al. [4] Solid nanoparticles with distinctive physical and chemical characteristics, like carbon nanotubes, oxides, carbides, or metals, are typically found in nanofluids by Nada et al. [5] In particular, when it comes to boosting the thermal conductivity of the standard liquids, nanofluids have been found to have greater thermal efficiency than their common fluid counterparts. As a result, nanofluids are used in a variety of heat transfer-related real-world applications. Drug delivery, agriculture, aerospace, microchips, and vehicles are just several illustrations of different applications Lund et al. [6] Throughout the period of the past two decades, a number of researchers have investigated both numerically and experimentally the thermophysical characteristics of nanofluids. Several articles have explained that nanofluids have a complex ratio of heat transmission than standard base liquids. Another attractive part that should be stated at this time is whether that stretching/shrinking problems are being introduced in polymer mechanism, which interacts also through stretching of plastic sheets, in addition to metallurgy, which includes cooling continuous strips. Infrequently these strips are stretched throughout the procedure of diagram Fisher [7]. Furthermore, it is generally agreed that Miklavic and Wang [8] were the first people to explore the viscous flow of fluid over a diminishing sheet using suction. They explained that mass suction is required in order to maintain flow past a diminishing sheet in the process of sustaining flow. Moreover, Bachok et al. [9] observed the flow of over a shrinking/stretching film by stagnation point. They noticed that the shrinking layer contained solutions that were non unique. Theoretical research on a nanofluid with boundary layer flow produced by a stretching/shrinking layer was then conducted by Bachok et al. [10] They found that the problem of sheet stretching and shrinking has two solutions. Sulochana and Naramgari [11] explored the influence that chemical reactions and radiation have on the stretching and shrinking of the layer when it occurs due to suction or injection. They came to the conclusion that the dual solution is only present in suction and injection parameters for a limited range. In their study of the mixed convection flow over the nanofluid, Ahmad and Pop [12] initiate that non-uniqueness of outcomes happens in only a minor variety of parameter values. Two dimensional electrical MHD nanofluid Stagnation steady flow slip boundary on a stretching sheet by mixed convection was investigated by KL Hsiao [13]. In the appearance of radiation, heat sink, and suction, Jamaludin et al. [14] analysed the diversified convections nanofluid stagnation-point with two-dimensional flow above a vertical stretched/shrunked layer. Besides, Lund et al. [15] explored the influence of mixed convection on the nanofluid and noticed four solutions.

Over the past few years, researchers from various fields have been paying particular attention to the progress made in the creation of improved heat transfer fluids. The term "hybrid nanofluid" refers to a new sort of nanofluid that is employed to enhance thermal effectiveness. A typical nanofluid is considered to be a hybrid nanofluid if it comprises nanoparticles that have been mixed with other types of nanofluid particles. According to the findings of Devi and Devi [16], the computational model that they developed of the hybrid nanofluid is significantly realistic than the other models because they associated their conclusions to the investigational outcomes of Suresh et al. [17] and observed that they were outstanding settlement. According to Huminic and Huminic [18], some of the most important applications for hybrid nanofluids provide plate cooling towers, helical coil chillers, microchannels coolants, mini channels, warmness pipes, cylinder heat condenser, cooling systems, and other similar applications. Waini et al. [19] studied hybrid nanofluids with an unstable flow over a layer of stretched and shrunked. Furthermore, Waini et al. [20] considered the flow and heat transmission of two-dimensional composite nanofluids above a shrinking/stretching curved surface through mass suction. They discovered that twofold solutions occur for a particular number of curvature, suction, and stretching/shrinking limitations. Waini et al. [21] observed the impact of transpiration flow on a layer that was expanding and contracting. In the literature, there are more references of hybrid nanofluid in this direction of stretching/shrinking layer [22,23].

Convection is a kind of heat transmission in which the transfer of heat takes place through the mass movement of the molecules of the fluid (gases or liquid). Over the heated plate, it appears when liquid particles develop less intense as they transfer from one area to another, holding the heat inside them due to temperature variations. This process takes place when the fluid is being heated. It is a significant contributor to the process of heat transmission, which may take place via diffusing, convection, or even both by Lund et al. [24] The cooling of the electronic components in the computer is accomplished by the process of convection. It can be observed that, in order to cool the electrical components, a tiny fan is typically attached to the side or the back of the casing. The casing also typically features vents on the side surface to facilitate the free flow of air. The movement of heat exchange is caused by body forces that occur since of density variations that develop owing to the temperature difference in the flow field in free convection. It is the main way of heat transfer due to numerous engineering and industrial applications. The difference in temperature between the fluid and the solid surface is what causes forced convection to occur. In this scenario, heat is transferred from the warmer phase to the cooler one by means of a process known as forced convection. In the process of forced convection, the movement of the fluid is produced by an exterior motive element such as a fan or a pump. The happenings of forced convection are also highly important and have a variety of applications in industries. For instance, the condenser process in an automobile, warming, and circulating of blood cools different areas of the body are examples of some of the uses of forced convection Waini et al. [25] The term "mixed convection" refers to the combination of free convection and forced convection. It is a mechanism of incredibly efficient heat transmission that is prevalent in numerous different transportation processes, both in engineered appliances and in natural environments. According to Prasad et al. [26] forced and free convection both give to the heat transmission mechanism in mixed convection. More probably, Merkin [27] the pioneer in this field, was the first expert to take into account the mixed convection influence of two-dimensional flow for the case of numerous solutions. He expanded his study on porous media and discovered twofold solutions later in 1986, according to Merkin [28]. Ghalambaz et al. [29] investigated the ${Al}_2{O}_3-Cu$/water hybrid nanofluid's mixed convection and heat transmission through a vertical layer. Moreover, in a porous medium the flow of steady mixed convection two dimensional with hybrid nanoparticles along a vertical layer is studied by Waini et al. [30] They exposed that while in the situation of opposing flow, there are two solutions. In hybrid nanofluid two-dimensional mixed convection and heat transmission by an exponentially vertical stretched/shrunked layer, Waini et al. [25] took this into consideration. Additionally, Yashkun et al. [31] looked into the constant flow with exponentially stretching/shrinking sheet, by Joule heating and mixed convection effects for hybrid nanofluid. Numerous researchers have used a wide variety of models and parameters in their investigations of mixed convection flow in hybrid nanofluids [32,33].

The impact of slip limitations on the flow of nanofluids, particularly hybrid nanofluids, has not been given significant study, according to a review of the existing literature. Significant physical applications include the production of cardiovascular system and interior cavities, as well as the cleaning of prosthetic heart valves Jamil and Khan [34]. It is worth remembering that non-slip condition does not true in fact. It is probable that Andersson [35] was the earliest person to propose the concept of a slip influence on boundary flows. Hayat et al. [36] examined that the effects of partial slip boundary and radiation for Ag–CuO/H₂O hybrid nanofluid. Additionally, in a hybrid nanofluid including viscous dissipation and partial slip, Aly and Pop [37] considered stretching/shrinking layer by MHD stagnation point flow. They concluded that, in comparison to ${Al}_2{O}_3$/water (Cu/water), it performs better also as cooler (heater) on the slip and stretching parameters.

The terms magneto (magnetic), hydro (fluids), and dynamics (motion) are combined to form the phrase magneto hydrodynamics (MHD). Magneto hydrodynamics is the study of the flow of electric conductivity fluids when a field of magnetism is present. Engineers employ magnetohydrodynamics principles in the creation and construction of generators, MHD pumps, geothermal energy extractors, flow metres, nuclear waste disposal, nuclear reactor cooling, and other industrial applications [38]. Devi and Devi [39] revealed the magnetized steady flow across a stretched layer using analytical methods, including suction and Newtonian heating in a hybrid nanofluid. They noticed that heat moves faster in hybrid nanofluids than in conventional nanofluids. Devi and Devi [39] noticed the hybrid nanofluid through a stretching surface. Lund et al. [24] inspected the stretching and shrinking surface with the impact of MHD and thermal radiation. Twofold solutions were attained in definite regions of the magnetic limitation. Waini et al. [40] considered the outcomes of hybrid nanoparticle radiation on the exponentially shrinking layer of MHD. The research articles include further references for these MHD studies [41,42].

The heat generation/absorption also has a significant impact on thermal efficiency. Since it has extensive uses in industrial purposes, such as geothermic supplies, chilling of atomic reactors and thermal insulation, the appearance and significance of heat absorption/generation on the boundary layer studies remain extremely important. These need the analysis of a temperature-dependent generation/absorption, which may change the aspect of heat transport. Ag–CuO/water hybrid nanofluid flow was examined by Hayat and Nadeem [43] in the occurrence of chemical processes, heat generation/absorption, and radiation. The impacts of heat generation/absorption, MHD on the hybrid nanofluid across a bidirectional exponentially stretched/shrunk layer were investigated by Zainal et al. [44] Under heat generation and slip conditions, Wahid et al. [45] examined that an exponentially extending and contracting permeable sheet. Several experts have looked into heat generation and absorption, including [46,47].

Waini et al. [25] analyzed vertical exponentially stretching/shrinking layer employing mixed convection short of accounting for MHD, heat generation/absorption, and velocity condition impacts for two-dimensional hybrid nanofluid. In addition, Yashkun et al. [31] looked into the influence of joule heating and mixed convection, MHD in a hybrid nanofluid flow that contained an exponentially stretching/shrinking layer for two-dimensional. However, these impacts were not taken into consideration, nor were the impacts of heat generation/absorption or velocity condition. By examining the implications of mixed convection, MHD, heat generation/absorption, and velocity condition, the current work seeks to close the gaps indicated in Waini et al. [25] and Yashkun et al. [31] Besides, both Waini et al. [25] and Yashkun et al. [31] did work on stretching and shrinking surface. The current study aims to investigate the innovative two-dimensional physical framework MHD mixed convection $Cu-A{l}_2{O}_3/H_{2}O$ composite nanofluid above a vertical enormously shrinking surface with velocity skid condition and heat generation/absorption, as motivated by the previous study. Using Tiwari and Das model [48], we have proposed a model with attention to the magnetic field over the vertical surface through the mixed convection, velocity slip condition, and heat generation/absorption. Alumina ($A{l}_2{O}_3$) and copper ($Cu$) are used for hybrid nanoparticles in this research. The $Cu-A{l}_2{O}_3/H_{2}O$ hybrid nanofluid is then developed by suspending both nanoparticles in water. For the purposes of comparison, the existing numerical outcome are compared to the results of past studies. The present numerical outcomes are original and haven't been published anywhere, as far as we know.

2. Mathematical modelling

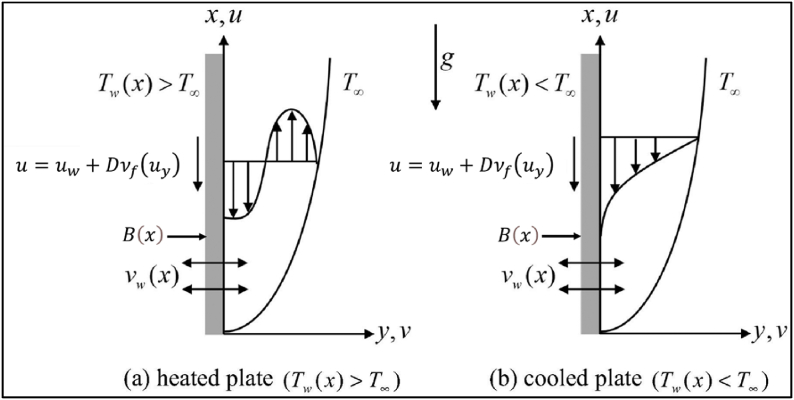
Fig. 1 depicts a vertical exponentially diminishing sheet with a Cartesian coordinate structure by MHD two-dimensional steady mixed convectional Al₂O₃–Cu/H₂O hybrid nanofluid. Where $T_w\left(x\right)=T_{\infty }+T_0{e}^{\raisebox{1ex}{$2x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}$, $T_{\infty }$ is free stream temperature, $T_0$ characteristic temperature. While temperature at the surface is $T_w\left(x\right)$. Furthermore, $l$ is the characteristic length. The velocity of the surface is $u=u_w=U_w{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}$ in the orientation of the $x$-axis. Where $U_w$ is a constant, and $u_w$ is the velocity of the surface. Both the cooled plate $\left(T_w\left(x\right)<T_{\infty }\right)$ and heated plate $\left(T_w\left(x\right)>T_{\infty }\right)$ are assumed. The acceleration related to gravity is specified by the symbol g. While in the direction of the $y-$ axis fluctuating magnetic field is $B\left(x\right)=B_0{e}^{x/2l}$ in which $B_0$ signifies the magnetic field's constant intensity.

Fig. 1.

The physical model for shrinking sheet.

The hybrid nanofluid model's (Yashkun et al. [31]; Yan et al. [49]) governing equations are listed below:

$$u_x+v_y=0$$ (1)

$$u{u}_x+v{u}_y=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}{u}_{yy}-\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}^{2}u+{\beta }_{hnf}\left(T-T_{\infty }\right)g$$ (2)

$$u{T}_x+v{T}_y=\frac{k_{hnf}}{{\left(\rho c_p\right)}_{hnf}}{T}_{yy}+\frac{q}{{\left(\rho c_p\right)}_{hnf}}\left(T-T_{\infty }\right)$$ (3)

The boundaries are as follows Yan et al. [49].

$$v=v_w\left(x\right),u=u_w+D{\nu }_f\left(u_y\right),T=T_w\left(x\right)=T_{\infty }+T_0{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}\mathrm{a}\mathrm{t}y=0$$ (4)

$$u\to 0,T\to T_{\infty },\mathrm{a}\mathrm{t}y\to \infty$$

In Equation (4), the letters $u$ and $v$ characterize the velocities across the $x-$ and $y$-axes, accordingly. The temperature of the fluid is denoted by $T$, while the kinematic viscosity is denoted by ${\nu }_f$. $D=D_1{e}^{-x/2l}$ is a component of velocity slip and $D_1$ denotes the first quantity of the velocity component. Furthermore, $v_w=-\sqrt{\frac{{\nu }_f{U}_w}{2l}}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}S$ as, the suction/injection parameter is denoted by $S$. where suction is correspond to by $S>0$, and injection is represented by $S<0$.

Moreover, ${\beta }_{hnf},{\left(\rho c_p\right)}_{hnf},k_{hnf},{\rho }_{hnf},{\mu }_{hnf}$ and ${\sigma }_{hnf}\text{,}$ are equivalent to a hybrid nanofluid's coefficient of thermal expansion, heat capacity, thermal conductivity, electrical conductivity, viscosity, and density. Additionally, $\mu ,c_p,\beta ,\rho ,k$ and σ which show the dynamic viscosity, specific heat capacity, thermal expansion coefficient, density, thermal conductivity and electrical conductivity, respectively. The hybrid nanofluid, nanofluid, fluid, "solid nano particles 1 ($\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$)" and "solid nano particles 2 ($\mathrm{C}\mathrm{u}$)" subscript specified by $hnf,nf,f,\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$ and $\mathrm{C}\mathrm{u}$ correspondingly. The thermophysical characteristics of the hybrid nanofluids utilized in Eqs. (2), (3) are provided after the definition of subscripts in Table 1. Besides, the thermophysical characteristics of the base fluid and solid nanoparticles for the hybrid are stated in Table 2. The solid volume fractions of $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$ and $\mathrm{C}\mathrm{u}$ are symbolized by ${\phi }_{A{l}_2{O}_3}$ and ${\phi }_{Cu}$ respectively, in Table 1.

Table 1.

A hybrid nanofluid's thermophysical characteristics Yashkun et al. [31].

Names	Properties
Dynamic Viscosity	${\mu }_{hnf}=\frac{{\mu }_f}{{\left(1-{\phi }_{Cu}\right)}^{2.5}{\left(1-{\phi }_{A{l}_2{O}_3}\right)}^{2.5}}$
Heat capacity	${\left(\rho c_p\right)}_{hnf}=\left(1-{\phi }_{Cu}\right)\left[\left(1-{\phi }_{A{l}_2{O}_3}\right){\left(\rho c_p\right)}_f+{\phi }_{A{l}_2{O}_3}{\left(\rho c_p\right)}_{A{l}_2{O}_3}\right]+{\phi }_{Cu}{\left(\rho c_p\right)}_{Cu}$
Thermal expansion coefficient	${\left(\beta \right)}_{hnf}=\left(1-{\phi }_{Cu}\right)\left[\left(1-{\phi }_{A{l}_2{O}_3}\right){\left(\beta \right)}_f+{\phi }_{A{l}_2{O}_3}{\left(\beta \right)}_{A{l}_2{O}_3}\right]+{\phi }_{Cu}{\left(\beta \right)}_{Cu}$
Density	${\rho }_{hnf}=\left(1-{\phi }_{Cu}\right)\left[\left(1-{\phi }_{A{l}_2{O}_3}\right){\rho }_f+{\phi }_{A{l}_2{O}_3}{\rho }_{A{l}_2{O}_3}\right]+{\phi }_{Cu}{\rho }_{Cu}$
Electrical conductivity	${\sigma }_{hnf}=\frac{{\sigma }_{Cu}+2{\sigma }_{nf}-2{\phi }_{Cu}\left({\sigma }_{nf}-{\sigma }_{Cu}\right)}{{\sigma }_{Cu}+2{\sigma }_{nf}+{\phi }_{Cu}\left({\sigma }_{nf}-{\sigma }_{Cu}\right)}\times \left({\sigma }_{nf}\right)$ where $\left({\sigma }_{nf}\right)=\frac{{\sigma }_{A{l}_2{O}_3}+2{\sigma }_f-2{\phi }_{A{l}_2{O}_3}\left({\sigma }_f-{\sigma }_{A{l}_2{O}_3}\right)}{{\sigma }_{A{l}_2{O}_3}+2{\sigma }_f+{\phi }_{A{l}_2{O}_3}\left({\sigma }_f-{\sigma }_{1A{l}_2{O}_3}\right)}\times \left({\sigma }_f\right)$
Thermal conductivity	$k_{hnf}=\frac{k_{Cu}+2k_{nf}-2{\phi }_{Cu}\left(k_{nf}-k_{Cu}\right)}{k_{Cu}+2k_{nf}+{\phi }_{Cu}\left(k_{nf}-k_{Cu}\right)}\times \left(k_{nf}\right)$ where $k_{nf}=\frac{k_{A{l}_2{O}_3}+2k_f-2{\phi }_{A{l}_2{O}_3}\left(k_f-k_{A{l}_2{O}_3}\right)}{k_{A{l}_2{O}_3}+2k_f+{\phi }_{A{l}_2{O}_3}\left(k_f-k_{A{l}_2{O}_3}\right)}\times \left(k_f\right)$

Table 2.

Water (base fluid) and solid nanoparticle thermophysical characteristics Waini et al. [25].

Fluids	Copper ($\mathrm{C}\mathrm{u}$)	Alumina ($\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$)	Water (${\mathrm{H}}_2\mathrm{O}$)
$c_p$(J/kg K)	385	765	4179
k (W/m K) $\beta \times {10}^{-5}\left(1/K\right)$	400 1.67	40 0.85	0.613 21
$\rho$(kg/m3)	8933	3970	997.1
$\sigma \left(\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$	5.96 × ${10}^7$	3.69 × ${10}^7$	0.05

The system is transformed into ordinary differential equations (ODEs) employing the corresponding similarity transformation variables [25,49].

$$\psi =\sqrt{2{\nu }_{f}l{U}_w}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}f\left(\eta \right);\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }};\eta =y\sqrt{\frac{U_w}{2{\nu }_{f}l}}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}$$ (5)

However, ${\nu }_f$ kinematic viscosity of fluid, the function of a stream is $\psi$ besides velocities are described such as

$u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x}$ and after it employs, we obtained Equation (6)

$$u=U_w{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}{f}^{\prime }\left(\eta \right);v=-\sqrt{\frac{U_w{\nu }_f}{2l}}{e}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2l$}\right.}\left(f\left(\eta \right)+\eta f^{\prime }\left(\eta \right)\right)$$ (6)

Equation (1) is completely satisfied, and after that by substituting Equation (6) in Equations (2), (3), we obtained that,

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{f}^{‴}+f^{″}f-2{\left(f^{\prime }\right)}^2-\frac{{\sigma }_{hnf}/{\sigma }_f}{{\rho }_{hnf}/{\rho }_f}M{f}^{\prime }+\left(\frac{{\beta }_{hnf}}{{\beta }_f}\right)2{\lambda }_1\theta =0$$ (7)

$$\frac{1}{\mathit{Pr}{\left(\rho c_p\right)}_{hnf}/{\left(\rho c_p\right)}_f}\left[\frac{k_{hnf}}{k_f}\right]{\theta }^{″}+{\theta }^{\prime }f-4\theta f^{\prime }+\frac{1}{{\left(\rho c_p\right)}_{hnf}/{\left(\rho c_p\right)}_f}Q\theta =0$$ (8)

Beside with boundary conditions.

$$f\left(0\right)=S,f^{\prime }\left(0\right)=-1+\delta f^{″}\left(0\right),\theta \left(0\right)=1$$ (9)

$$f^{\prime }\left(\eta \right)\to 0;\theta \left(\eta \right)\to 0\mathrm{a}\mathrm{s}\eta \to \infty$$

Where, prime shows the differentiation for $\eta$, the value of $M=\frac{{2l{B}_0}^2{\sigma }_f}{U_w{\rho }_f}$ refers to the magnetic parameter, ${\lambda }_1=\frac{{\beta }_f{T}_{0}l}{U_w^2}g$ shows the parameter of mixed convection, $\mathit{Pr}=\frac{{\left(\mu c_p\right)}_f}{k_f}$ is Prandtl number, Furthermore, $\delta =D_1\sqrt{\frac{{\nu }_f{U}_w}{2l}}$ is the velocity slip, and $Q=\frac{2q_L}{U_w{\left(\rho c_p\right)}_f}$ heat generation/absorption parameters.

The key physical factors are skin friction coefficient $C_f$ and local Nusselt number ${Nu}_x$ which are explained accordingly.

$$C_f=\frac{{\mu }_{hnf}}{{\rho }_f{u}_w^2}{\left(u_y\right)}_{y=0},{Nu}_x=\frac{2l}{k_f\left(T_w{-T}_{\infty }\right)}\left[-k_{hnf}{\left(T_y\right)}_{y=0}+{\left(q_r\right)}_{y=0}\right]$$ (10)

The following forms are formed, employing equations (5), (6), (10).

$${\left(Re\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right);{\left(Re\right)}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{Nu}_x=-\left[\frac{k_{hnf}}{k_f}+\frac{4Rd}{3}\right]{\theta }^{\prime }\left(0\right)$$ (11)

here, Equation (11) signified reduced skin friction and reduced Nusselt number.

where $Re=\frac{2u_{w}l}{{\nu }_f}$ is the local Reynolds number.

3. Results and discussion

The numerical solution to the system of higher order nonlinear ODEs expressed in Equation (7), (8), as well as the boundary conditions (9), is achieved by the implementation of the bvp4c solver, which is a component of the MATLAB computing software. Several professionals and scholars have widely employed this approach to resolve fluid flow problems. Jacek Kierzenka and Lawrence F. Shampine of Southern Methodist University in Texas developed the bvp4c solver by Hale [50]. The bvp4c solver is a finite modification algorithm that applies the three-stage Lobatto IIIA implicit Runge–Kutta method and yields numerical solutions of fourth order correctness. When an initial guess is given at the initial mesh points and step-size modifications, this approach delivers the desired accuracy. According to Waini et al. [25] the bvp4c solver gave adequate outcomes when compared to the shooting technique and Keller box.

The solution duality in the figures became achieved by utilizing various early estimates for $f^{″}\left(0\right)$ and $-{\theta }^{\prime }\left(0\right)$, with the result that both velocity profile and temperature profile fulfilled the boundary condition $\eta \to \infty$ asymptotically. In the existing study, hybrid nanofluid is analyzed by combining copper ($Cu$) nanoparticles with different volume fractions of ${Al}_2{O}_3$/water to generate the suitable hybrid nanofluid. The present results are verified using information from earlier studies to guarantee the algorithm's accuracy.

Additionally, In Table 3, we evaluate the values of $f^{″}\left(0\right)$ and $-{\theta }^{\prime }\left(0\right)$ from the Waini et al. [25] and Lund et al. [15] findings. As can be seen, the findings are consistent with the literature mentioned. However, Table 4 compares the values of $f^{″}\left(0\right)$ under the different findings of Ghosh and Mukhopadhyay [51], Hafidzuddin et al. [52], Yashkun et al. [31], and Waini et al. [40], the incredible congruence between those conclusions can be seen in Table 3, Table 4, respectively.

Table 3.

Values of $f^{″}\left(0\right)$ and $-{\theta }^{\prime }\left(0\right)$ for the numerous values of $\mathit{Pr}$ with ${\lambda }_1=-0.5,{\phi }_{A{l}_2{O}_3}={\phi }_{Cu}=\delta =Q=M=0$ and $S=5\text{.}$

	Lund et al. [15]	Lund et al. [15]	Waini et al. [25]	Waini et al. [25]	Present	study
$\mathit{Pr}$	$f^{″}\left(0\right)$	$-{\theta }^{\prime }\left(0\right)$	$f^{″}\left(0\right)$	$-{\theta }^{\prime }\left(0\right)$	$f^{″}\left(0\right)$	$-{\theta }^{\prime }\left(0\right)$
$1.0$	$4.449203$	$4.447507$	$4.449204$	$4.447507$	$4.4492038$	$4.4475074$
$1.6$	$4.540536$	$7.334577$	$4.540536$	$7.334578$	$4.5405362$	$7.3345777$
$1.8$					$4.5571615$	$8.3078434$
$2.0$	$4.570372$	$9.284828$	$4.570373$	$9.284829$	$4.5703728$	$9.2848287$
$2.2$					4.5811138	10.2648426
$2.4$	$4.590011$	$11.247347$	$4.590011$	$11.247348$	$4.5900111$	$11.2473478$
$2.8$					$4.6038793$	$13.2182324$
$3.0$					$4.6093825$	$14.2060090$
$4.5$					$4.6346512$	$21.6444129$
$6.2$			$4.648147$	$30.107416$	$4.6481472$	$30.1074164$
$6.5$					$4.6497747$	$31.6027444$
$7.0$					$4.6521678$	$34.0957891$
$7.5$					$4.6542325$	$36.5897057$
$8.0$					$4.6560319$	$39.0843414$
$9.0$					$4.6590152$	$44.0753173$
$10.0$					$4.6613871$	$49.0680252$

Table 4.

Values of $f^{″}\left(0\right)$ comprising various parameters ${\phi }_{A{l}_2{O}_3}={\phi }_{Cu}={\lambda }_1=\delta =Q=M=0$$\mathit{Pr}=0.7$, and $S=3\text{.}$

	First solution $f^{″}($ 0)	Second solution $f^{″}($ 0)
Ghosh and Mukhopadhyay [51]	$2.39082$	$-0.97223$
Hafidzuddin et al. [52]	$2.3908$	$-0.9722$
Yashkun et al. [31]	$2.390813$	$-0.972247$
Waini et al. [40]	$2.390814$	$-0.972247$
Present Study	$2.3908165$	$-0.9722473$

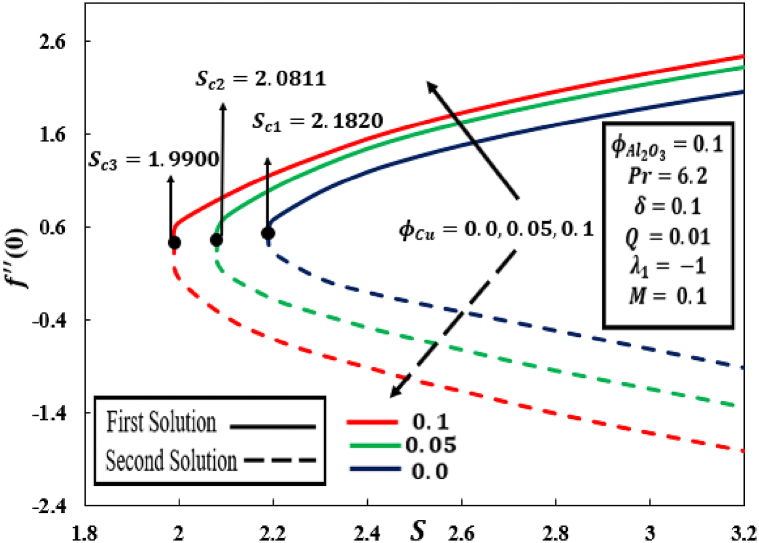
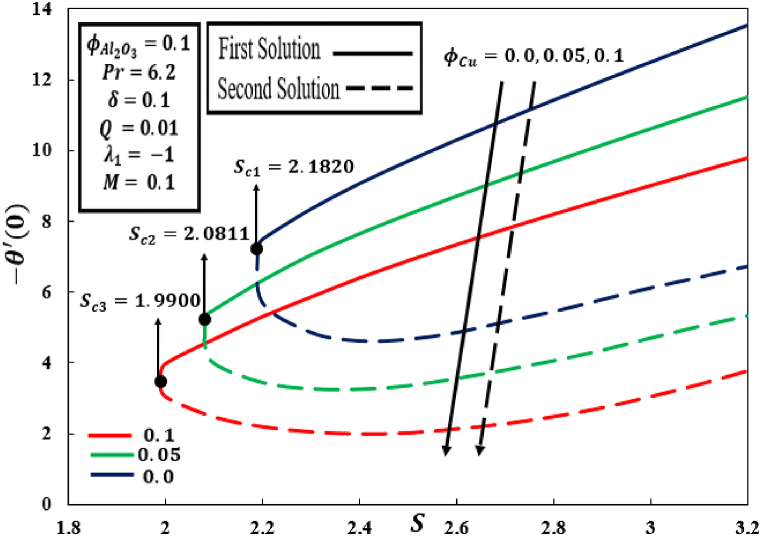
The effects of ${\phi }_{Cu}$ on the comportment of diminished skin friction $f^{″}\left(0\right)$ and rate of diminished heat transmission $-{\theta }^{\prime }\left(0\right)$, respectively displayed in Fig. 2, Fig. 3 d. In Fig. 2, Fig. 3, it can be seen that fluid flows towards $S$ until it reaches $S_{ci}$ where $i=1,2,3$, $S_{ci}$ is the precarious point in $S$ where the first and second solutions are connected. No solutions exist when $S<S_{ci}$. Here, it's important to state that while ${\phi }_{Cu}=0$, it is pure $\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3$ water-based nanofluid and $S_{c1}=2.1820$, subsequently 5% of ${\phi }_{Cu}$ is included and obtained $S_{c2}=2.0811$. As well, the value of $S_{c3}=1.9900$ appeared to enhance as 10% of the solid nano particles of ${\phi }_{Cu}$ is incorporated in the hybrid nanofluid. The falling action is depicted in both figures as ${\phi }_{Cu}$ grows $0\%\mathrm{t}\mathrm{o}10\%$ in the second solution. While, in the first solution, $f^{″}\left(0\right)$ increases with ${\phi }_{Cu}$. As opposed to that, $-{\theta }^{\prime }\left(0\right)$ decreases in both solutions when ${\phi }_{Cu}$ raises $0\%$ to 10%. Physically, the boundary layer separation was also expanded with the inclusion of ${\phi }_{Cu}$. Waini et al.²⁵ also came to similar conclusions.

Fig. 2.

Behaviour of $f^{″}\left(0\right)$ with the influence of ${\phi }_{Cu}$.

Fig. 3.

Behaviour of $-{\theta }^{\prime }\left(0\right)$ with the influence of ${\phi }_{Cu}$.

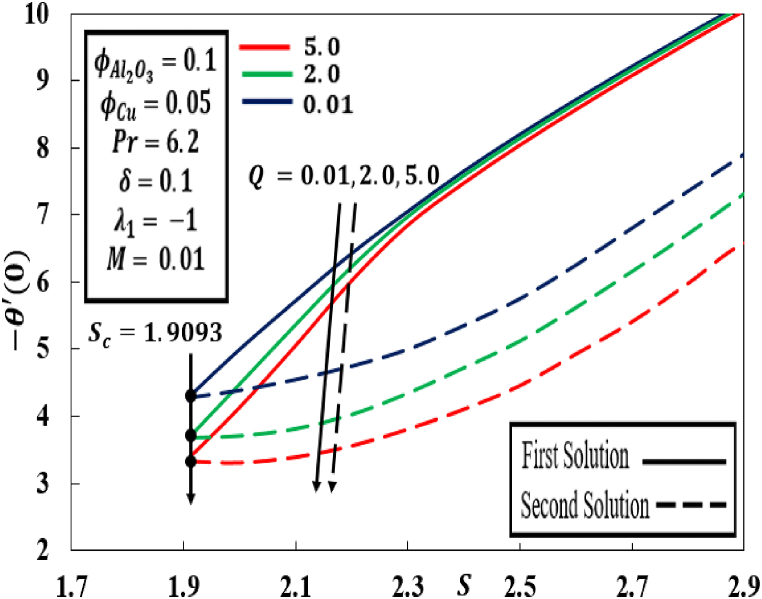
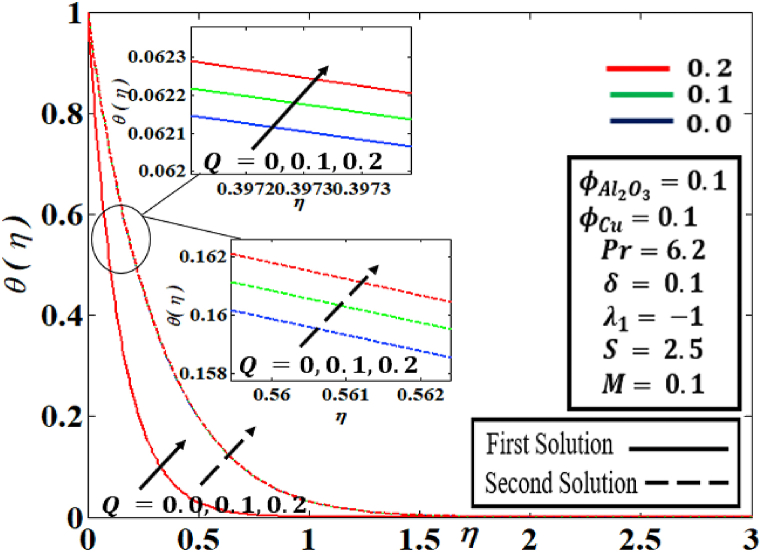
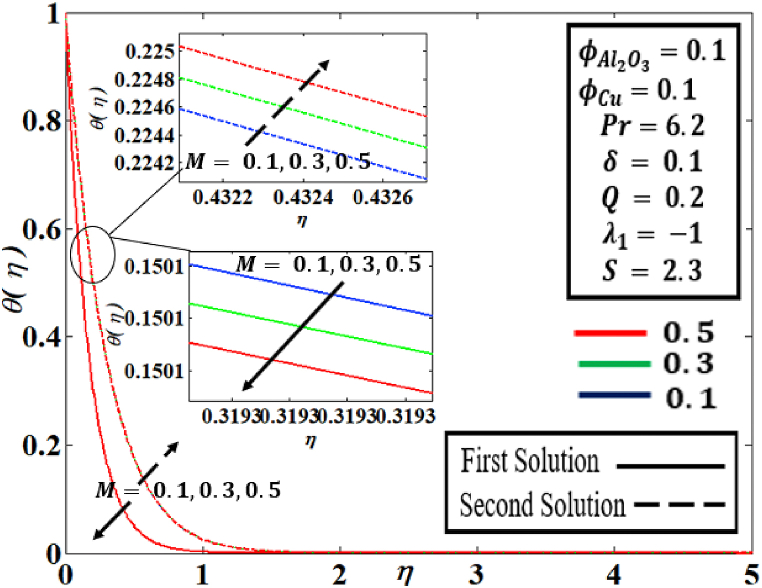
Fig. 4 shows the influence of heat generation/absorption $Q=0.01,2.0,5.0$ the rate of reduced heat transfer $-{\theta }^{\prime }\left(0\right)$ against suction $S$ under various parameters such as ${\phi }_{A{l}_2{O}_3}=0.1,{\phi }_{Cu}=0.05,\mathit{Pr}=6.2,\delta =0.1;{\lambda }_1=-1,\mathrm{a}\mathrm{n}\mathrm{d}M=0.01$. The unstable location in $S$ where the first and second solutions are combined is $S_c$. No solutions occur when $S<S_c$. For the various value of generation/absorption $Q$ parameter, dual solutions are seen, beginning at nearly the same critical levels which are $S_c=1.9093$. Furthermore, it can be seen when $Q$ is enhanced with large amount $1\%$ to 500%, $-{\theta }^{\prime }\left(0\right)$ declines in both solutions. Physically, this is because when the heat generation $Q>0$, the heat flux flow is reduced on the exponentially shrinking sheet, causing the heat exchange development to slow down. In addition, when heat absorption happens $Q<0$, the heat flux is larger, which speeds up the heat exchange progress.

Fig. 4.

Behaviour of $-{\theta }^{\prime }\left(0\right)$ with the influence of $Q$.

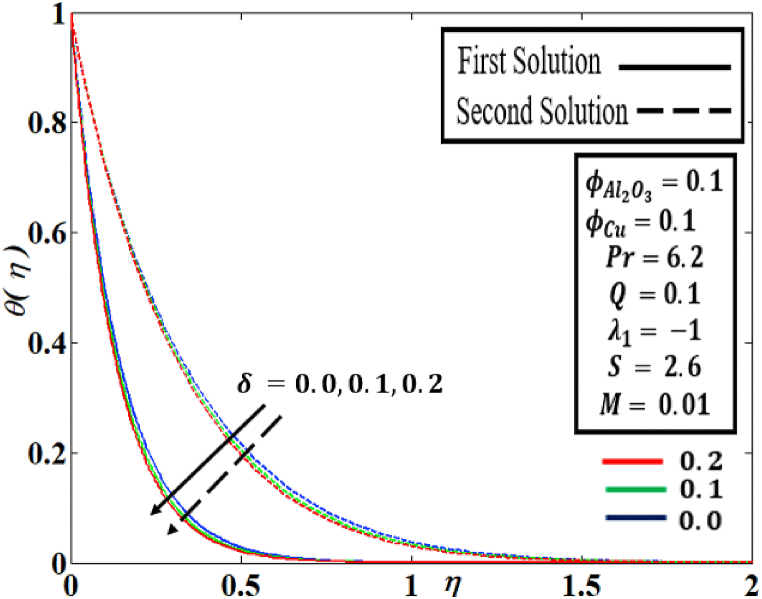
Fig. 5 demonstrates the temperature $\theta \left(\eta \right)$ profile of influence of heat generation/absorption $Q=0.0,0.1,0.2$ against $\eta$ under several parameters such as ${\phi }_{A{l}_2{O}_3}={\phi }_{Cu}=0.1,\mathit{Pr}=6.2,\delta =0.1,{\lambda }_1=-1,S=2.5\mathrm{a}\mathrm{n}\mathrm{d}M=0.1$. Because these factors have no effect on the velocity profile $f^{\prime }\left(\eta \right)$, in this investigation, just the temperature $\theta \left(\eta \right)$ profile is necessary. It is noted that when upsurges the percentage $0\%$ to $20\%$ value of $Q$, the temperature $\theta \left(\eta \right)$ profile of both solutions first and second are rising. Physically the thickness of the thermal boundary layer upsurges as the temperature gradient decreases when the heat generation effect $Q>0$. Besides, the thickness of the thermal boundary layer declines as the temperature gradient rises when the heat absorption effect $Q<0$. A solar collector is one illustration of an implementation. When the heat flux is larger, the heat exchange procedure from the solar board layer to the atmosphere is rapid, enhancing the performance of the solar panel process.

Fig. 5.

Behaviour of $\theta \left(\eta \right)$ with the influence of $Q$.

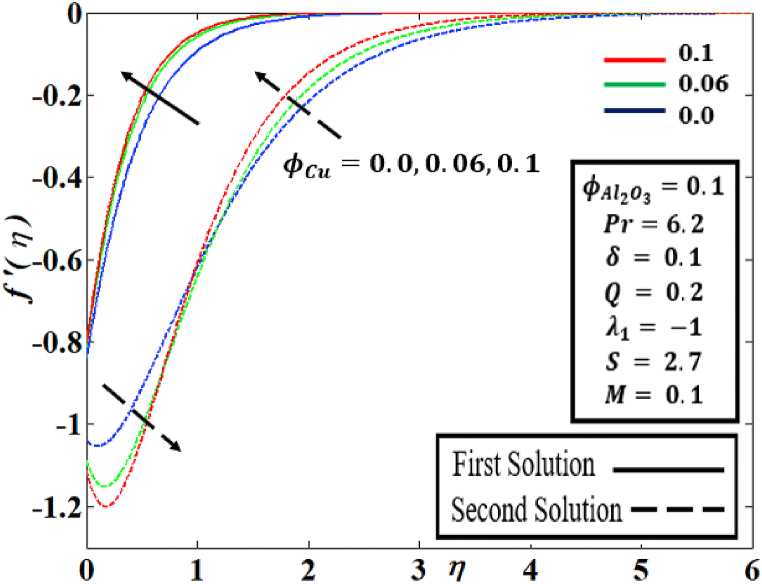
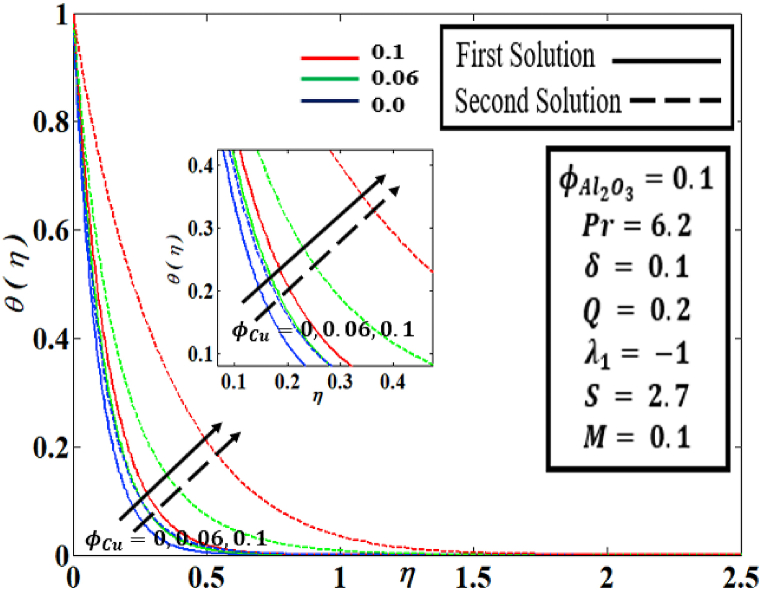
Fig. 6, Fig. 7 displays of velocity $f^{\prime }\left(\eta \right)$ profile and temperature $\theta \left(\eta \right)$ profile along solid volume fraction ${\phi }_{Cu}=0.0,0.06,0.1$ with different parameters ${\phi }_{A{l}_2{O}_3}=0.1,\mathit{Pr}=6.2,\delta =0.1;{Q=0.2,\lambda }_1=-1,S=2.7\mathrm{a}\mathrm{n}\mathrm{d}M=0.1$, respectively. As the value of ${\phi }_{Cu}\in [0\%,10\%$] grows, it can be noticed in Fig. 6 that the momentum boundary layer thickness in both solutions thickens. However, the opposite tendency can be seen subsequently $\eta <1$ in the second solution. This is due to collisions among dispersed nanoparticles. Besides, in Fig. 7, thermal boundary layer thickness upsurges for both solutions when ${\phi }_{Cu}\in [0\%,10\%$] increase. Physically, this tendency is in line with the premise that solid particles have a thermal conductivity that is larger than the base fluid's thermal conductivity. Wahid et al.⁴⁵ reported similar results in $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$.

Fig. 6.

Behaviour of $f^{\prime }\left(\eta \right)$ with the effect of ${\phi }_{Cu}$.

Fig. 7.

Behaviour of $\theta \left(\eta \right)$ with the influence of ${\phi }_{Cu}$.

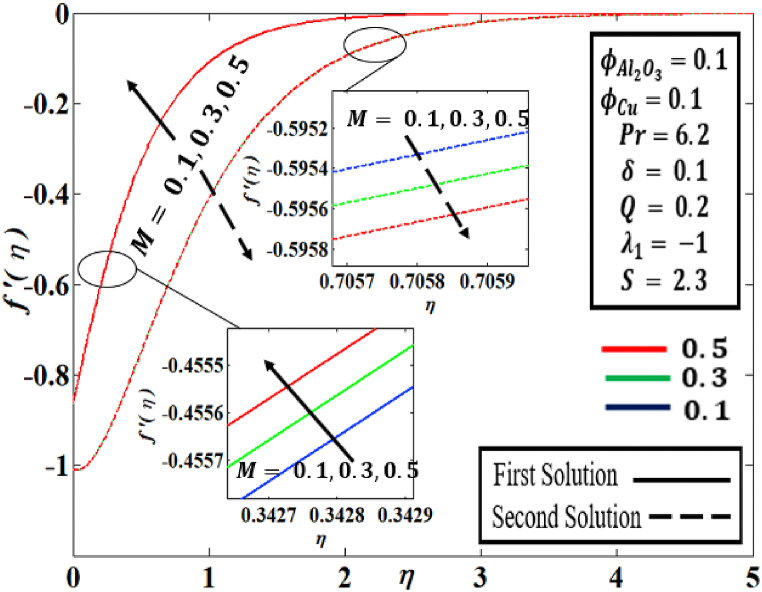
The graphs of the velocity $f^{\prime }\left(\eta \right)$ and temperature $\theta \left(\eta \right)$ profiles $M=0.1,0.3\text{,}$ and $0.5$ are described in Fig. 8, Fig. 9, respectively. While found in Fig. 8, the velocity $f^{\prime }\left(\eta \right)$ profile increases in the first solution but reduces in the second, showing that the rate of transmission substantially reduces as $M$ upsurges $10\%\mathrm{t}\mathrm{o}50\%$. Moreover, the first solution grows, and the second reduces solution, by an improving amount of, in the temperature $\theta \left(\eta \right)$ profile, as observed in Fig. 9. Physically, the movement mechanism became more resistive as a result of the Lorentz force generated by the magnetic field. $M$ therefore, lowers the surface's shear stress.

Fig. 8.

Behaviour of $f^{\prime }\left(\eta \right)$ with the influence of $M$

Fig. 9.

Behaviour of $\theta \left(\eta \right)$ with the influence of $M$

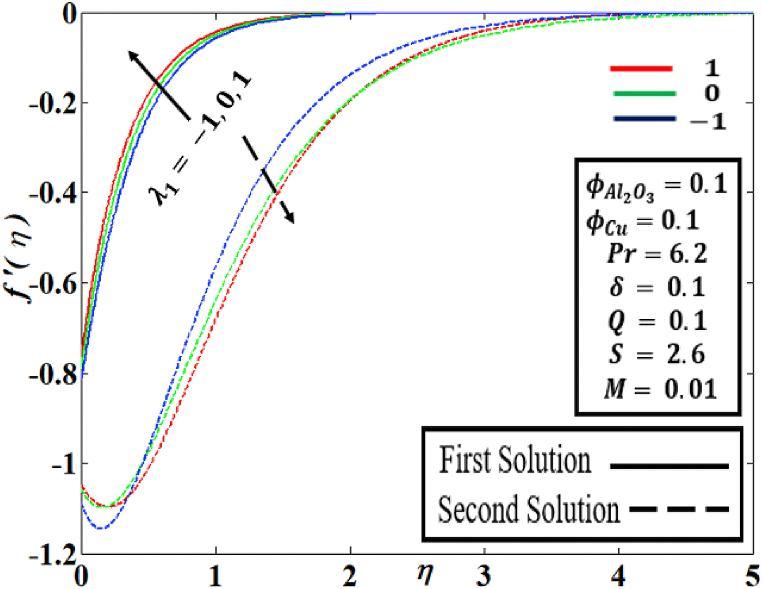
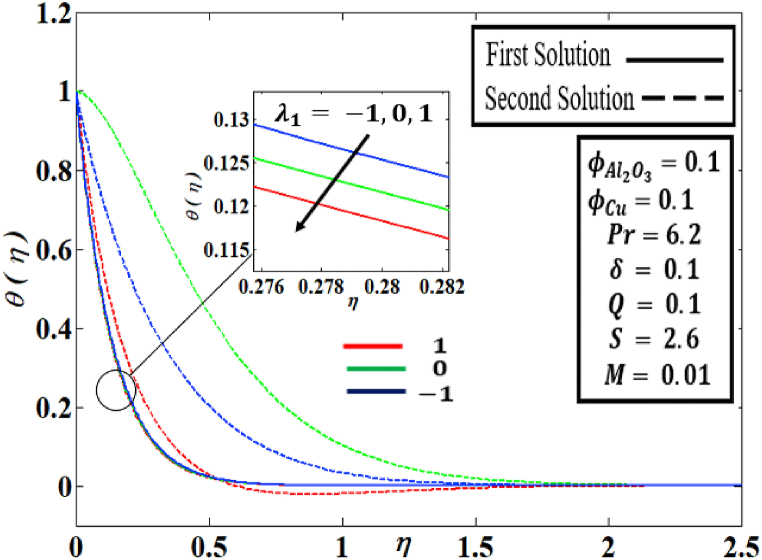
Fig. 10, Fig. 11 illustrate the graphs of the velocity $f^{\prime }\left(\eta \right)$ profile and the temperature $\theta \left(\eta \right)$ profile for the mixed convection parameter ${\lambda }_1=-1,0,1$ at several fixed parameters ${\phi }_{A{l}_2{O}_3}={\phi }_{Cu}=0.1,\mathit{Pr}=6.2,\delta =Q=0.1,S=2.6\mathrm{a}\mathrm{n}\mathrm{d}M=0.01$ respectively. It is examined that the first solution of $f^{\prime }\left(\eta \right)$ upsurge and drop in the second solution with the growing percentage values of ${\lambda }_1\in [-100\%-100\%$] in Fig. 10. Furthermore, in Fig. 11, the temperature $\theta \left(\eta \right)$ profile decrease in the first solution, but for the second solution, $\theta \left(\eta \right)$ rises in the range of $-1\le {\lambda }_1\le 0$ and reduces in the range of $0\le {\lambda }_1\le 1$ when the values of ${\lambda }_1$ is enhanced. Physically, it signifies that dual solutions for buoyancy-assisted flow are feasible.

Fig. 10.

Behaviour of $f^{\prime }\left(\eta \right)$ with the influence of ${\lambda }_1$.

Fig. 11.

Behaviour of $\theta \left(\eta \right)$ with the influence of ${\lambda }_1$.

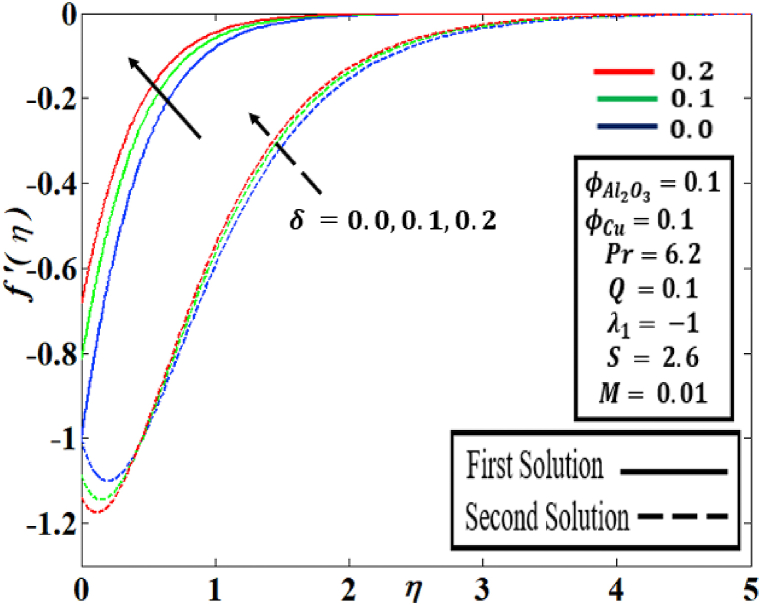
Fig. 12, Fig. 13 represent the following on distinct amounts of velocity slip parameter $\delta =0.0,0.1,\mathrm{a}\mathrm{n}\mathrm{d}0.2$ are the velocity $f^{\prime }\left(\eta \right)$ and temperature $\theta \left(\eta \right)$ profiles respectively in different parameters such as ${\phi }_{A{l}_2{O}_3}={\phi }_{Cu}=0.1,\mathit{Pr}=6.2,Q=0.1,{\lambda }_1=-1,S=2.6\mathrm{a}\mathrm{n}\mathrm{d}M=0.01$. From Fig. 12, the increasing behaviour for both solutions of velocity $f^{\prime }\left(\eta \right)$ profiles are observed when refining the percentage values of $\delta$ within range of $0\%\mathrm{t}\mathrm{o}20\%$. Additionally, From Fig. 13, the reducing performance of both solutions for temperature $\theta \left(\eta \right)$ profile is noticed when boosting the $\delta$ values. Significantly, it is clear that the absence of velocity skid has a greater impact on boundary layer separation in a hybrid nanofluid than the no-skid situation (for $\delta$ = 0).

Fig. 12.

Behaviour of $f^{\prime }\left(\eta \right)$ with the influence of $\delta$

Fig. 13.

Behaviour of $\theta \left(\eta \right)$ with the influence of $\delta$

4. Conclusion

The circumstance inspires this research that hybrid nanofluid has an extensive diversity of industrial uses. In this research, two-dimensional Al₂O₃–Cu/water hybrid nanofluid MHD mixed convection flow on an exponential vertical shrinking sheet by the influence of heat generation/absorption and velocity skid has been considered by bvp4c solver on the MATLAB program. Both the coding in the bvp4c solver and the physical model suggested in this study have been validated. To be more certain, all graphical and numerical results are achieved by solving a system of boundary-conditional higher-order ordinary differential equations (ODEs), which are similarly translated from the governing partial differential equations (PDEs). This study concentrations on the behaviour of the reduced skin friction $f^{″}\left(0\right)$ and heat transmission $-{\theta }^{\prime }\left(0\right)$ counter to suction limitation. The velocity and temperature profile under the effect of heat generation/absorption, solid volume fraction of copper, MHD, diversified convection, and velocity slip for the above-expressed hybrid nanofluid flow. The present research main conclusions are summarized:

• i.Given an appropriate set of characteristics, the viability of dual solutions has been established.
• ii.The motion of the hybrid fluid is flowed till an analytical point $S_{ci}$, although no flow of fluid is probable when $S<S_{ci}\text{.}$
• iii.Graphically and numerical findings have indicated that the accumulation of the hybrid solid volume fraction has led to an upsurge in the amount of heat transference and the addition of ${\phi }_{Cu}\in \left[0\%,10\%\right]$ extended the boundary layer separation.

Author contribution statement

Adnan Asghar, Zahir Shah, Narcisa Vrinceanu: Conceived and designed the analysis; Contributed analysis tools or data; Wrote the paper.

Abdul Fattah Chandio, Wejdan Deebani, Meshal Shutaywi, Liaquat Ali Lund: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data.

Funding statement

This work was supported by Lucian Blaga University of Sibiu (LBUS-IRG-2022-08).

Data availability statement

Data will be made available on request.

Declaration of interest’s statement

The authors declare no conflict of interest.